Расчет сопротивления параллельных резисторов онлайн. Расчет сопротивления параллельных резисторов: формулы, примеры и онлайн-калькулятор — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать общее сопротивление параллельно соединенных резисторов. Какие формулы использовать для двух и более резисторов. Примеры расчетов параллельных цепей. Где найти онлайн-калькулятор для быстрых вычислений.

Содержание

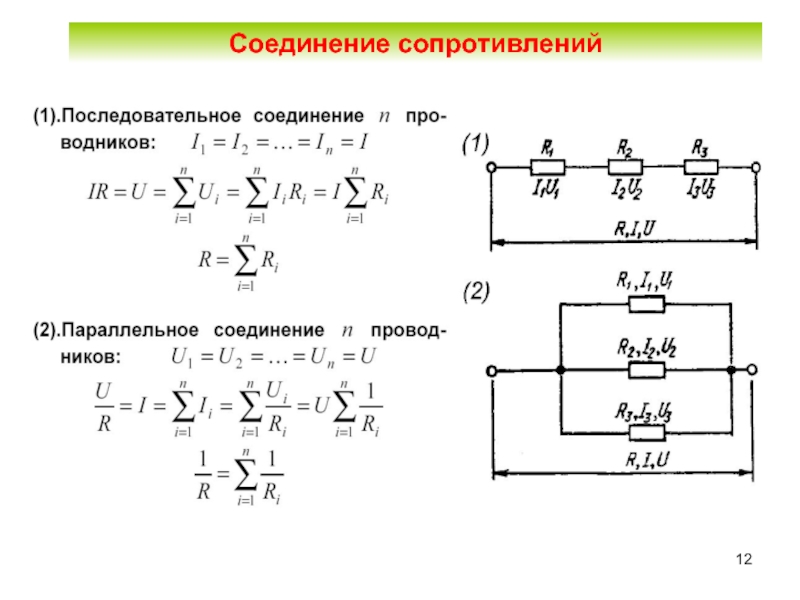
Что такое параллельное соединение резисторов

При параллельном соединении резисторов все их выводы соединяются в двух точках схемы. Такое соединение имеет ряд особенностей:

Напряжение на всех резисторах одинаковое
Общий ток равен сумме токов через каждый резистор
Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи

Параллельное соединение позволяет уменьшить общее сопротивление цепи по сравнению с отдельными резисторами. Это часто используется для получения нужного номинала, которого нет в наличии.

Формулы для расчета параллельного соединения резисторов

Для расчета общего сопротивления параллельно соединенных резисторов используются следующие формулы:

Формула для двух резисторов:

R = (R1 * R2) / (R1 + R2)

где R — общее сопротивление, R1 и R2 — сопротивления отдельных резисторов.

Формула для произвольного количества резисторов:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

Эту формулу можно преобразовать к виду:

R = 1 / (1/R1 + 1/R2 + 1/R3 + … + 1/Rn)

Примеры расчета параллельного соединения резисторов

Пример 1: Два резистора

Дано: R1 = 100 Ом, R2 = 200 Ом

Решение:

R = (100 * 200) / (100 + 200) = 20000 / 300 = 66.67 Ом

Пример 2: Три резистора

Дано: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом

Решение:

1/R = 1/10 + 1/20 + 1/30 = 0.1 + 0.05 + 0.033 = 0.183

R = 1 / 0.183 = 5.46 Ом

Онлайн-калькулятор параллельного соединения резисторов

Для быстрого расчета общего сопротивления параллельно соединенных резисторов можно воспользоваться онлайн-калькулятором. Вот несколько популярных вариантов:

Калькулятор на сайте RadioComponents.ru
Калькулятор на сайте Elektron.Start.Build
Калькулятор на сайте Qpick.ru

Такие калькуляторы позволяют быстро произвести расчеты для любого количества резисторов, просто введя их номиналы.

Когда применяется параллельное соединение резисторов

Параллельное соединение резисторов применяется в следующих случаях:

Для получения нужного номинала сопротивления, которого нет в наличии
Для уменьшения общего сопротивления цепи
Для увеличения мощности рассеивания
В делителях напряжения
В измерительных мостовых схемах

Понимание принципов параллельного соединения резисторов позволяет грамотно проектировать электрические цепи и подбирать нужные номиналы компонентов.

Особенности параллельного соединения резисторов

При использовании параллельного соединения резисторов важно учитывать следующие моменты:

Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи. Это позволяет уменьшать сопротивление участка цепи.

Ток в цепи распределяется обратно пропорционально сопротивлениям резисторов. Через резистор с меньшим сопротивлением течет больший ток.
Мощность, выделяемая на параллельно соединенных резисторах, суммируется. Это позволяет увеличить мощность рассеивания.
При выходе из строя одного резистора, остальные продолжают работать. Это повышает надежность схемы.
Параллельное соединение одинаковых резисторов позволяет уменьшить сопротивление в целое число раз (в 2, 3, 4 и т.д. раза).

Как правильно рассчитать параллельное соединение резисторов

Чтобы корректно рассчитать параллельное соединение резисторов, следуйте этим рекомендациям:

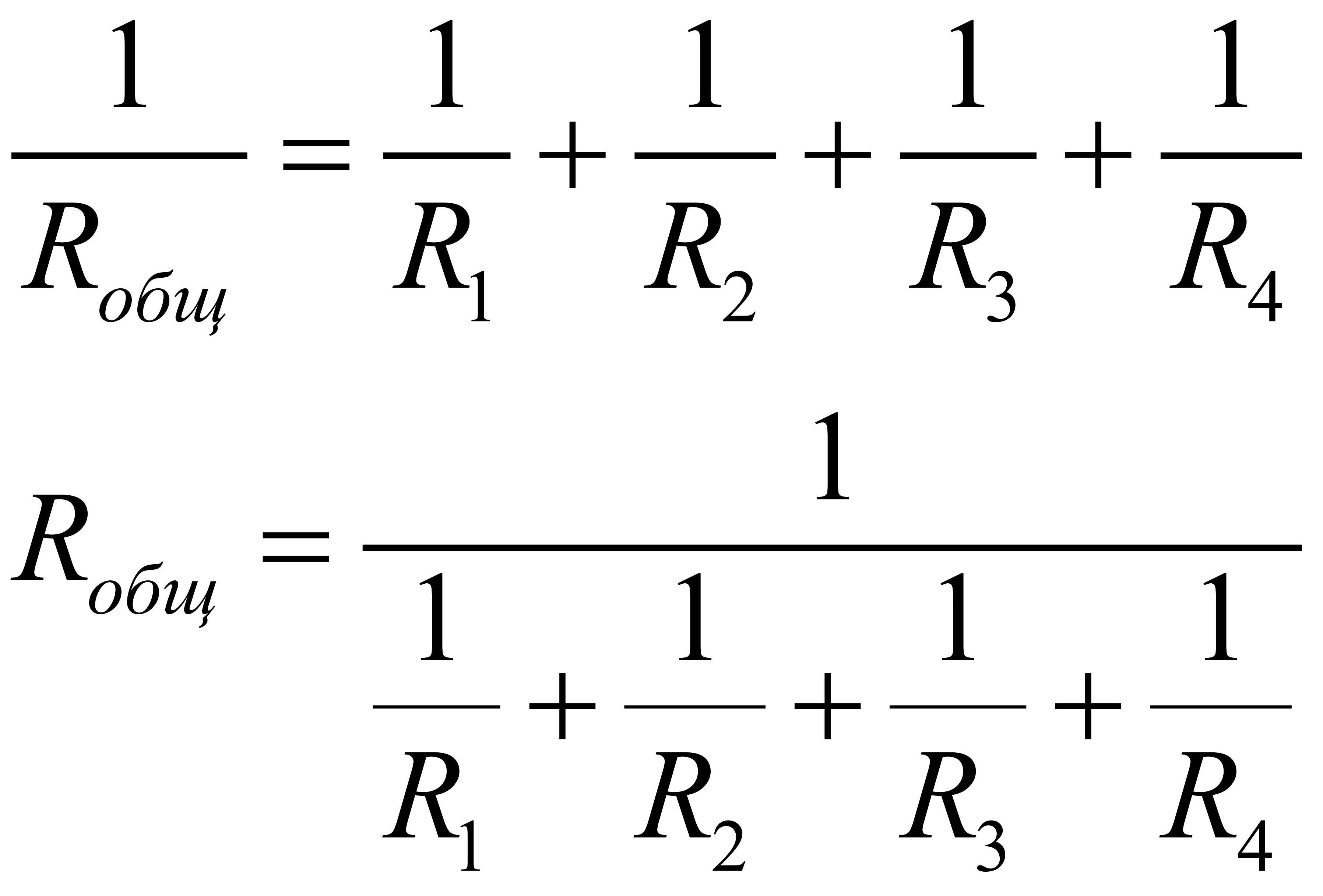
Определите количество параллельно соединенных резисторов
Запишите номиналы всех резисторов
Выберите подходящую формулу в зависимости от количества резисторов

Подставьте значения в формулу и произведите вычисления
Округлите результат до ближайшего стандартного номинала при необходимости
Проверьте результат, рассчитав общий ток через параллельную цепь

При сомнениях всегда лучше перепроверить расчеты или воспользоваться онлайн-калькулятором для подтверждения результата.

Сравнение параллельного и последовательного соединения резисторов

Параллельное и последовательное соединение резисторов имеют разные свойства:

Параметр	Параллельное соединение	Последовательное соединение
Общее сопротивление	Меньше наименьшего резистора	Сумма всех сопротивлений
Напряжение	Одинаковое на всех резисторах	Сумма напряжений равна общему
Ток	Общий ток равен сумме токов	Одинаковый через все резисторы
Мощность	Суммируется	Суммируется

Выбор типа соединения зависит от конкретной задачи и требуемых параметров цепи.

Расчет сопротивления цепи

Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью.

Пример 1

Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.

Допустим, что R₁=10 Ом R₂=20 Ом, тогда

Пример 2

Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R

1,R₂ такие же как и в примере 1)

Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз.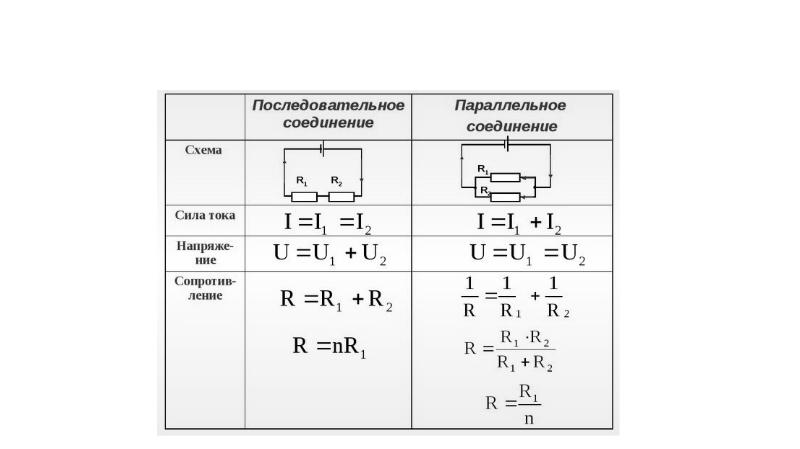

Пример 3

В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R₁,R₂ прежние, R₃=105 Ом)

Пример 4

Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R₁ и R₂ соединенных параллельно, а затем общее сопротивление, как сумму R₁₂ и R₃ соединенных последовательно.

Пример 5

Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.

R₄=20 Ом, R₅=40 Ом, R₆=15 Ом

Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.

Параллельное сопротивление — РадиоСхема

Калькулятор параллельных сопротивлений

Рассчитать общее сопротивление резисторов соединенных параллельно с легкостью!

Обзор

Расчет эквивалентного сопротивления (Rэкв) параллельных резисторов вручную может быть утомительным. Этот инструмент был разработан, чтобы помочь вам быстро рассчитать эквивалентное сопротивление, если у вас есть два или десять резисторов параллельно. Чтобы его использовать, просто указать, сколько параллельных резисторов имеется и значение сопротивления для каждого из них.

Уравнения

Когда у вас есть только два резистора в параллель:

Применение

Резисторы в серии эквивалентны одному резистору, сопротивление которого равно сумме каждого отдельного резистора. Результат эквивалентного сопротивления всегда меньше, чем каждый отдельный резистор.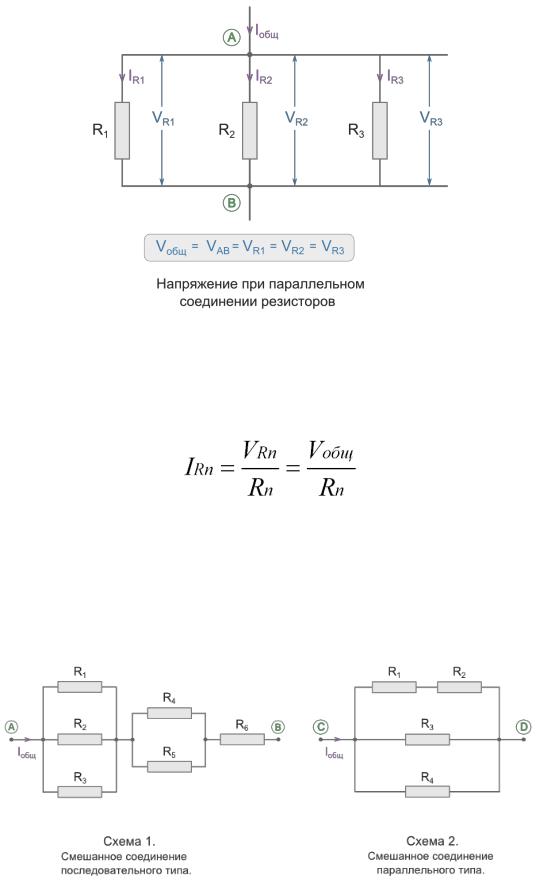 Если вдуматься, в этом есть смысл: если вы применяете напряжение через резистор, определенное количество тока. Если вы добавляете еще один резистор параллельно с первым, вы, по сути, открываете новый канал, через который может течь больший ток . Не важно, насколько большой второй резистор, общий ток, протекающий от источника питания будет немного выше, чем ток через один резистор. И если суммарный ток будет выше, то общее сопротивление должно быть ниже.

Вы можете легко вычислить эквивалентное сопротивление, когда у вас есть два одинаковых резистора параллельны: он наполовину состоит из отдельных сопротивления. Это удобно, когда вы нуждаетесь в определенном значении сопротивления и не имея соответствующего номинала в доступности. Например, если вы знаете, что нужно около 500 Ом, чтобы получить желаемую яркость из светодиодной цепи, вы можете использовать два по 1 кОм резистора параллельно.

Имейте в виду, что ток через индивидуальный резистор не меняется при добавлении резисторов в параллель, потому что добавление резистора параллельно влияет на напряжение на клеммах резисторов.

Программа для вычисления параллельной цепи резисторов

Предисловие.

Программа paralsop

Программа paresist
Онлайн расчёт цепи параллельных резисторов

Вначале было слово… И слово это было на бумаге. В общем, однажды меня достало расчитывать набор из параллельных сопротивлений, а потребность в этом периодически возникает, когда нет под рукой сопротивления нужного номинала. Процесс был стандартен: брался карандаш и листок бумаги, на котором составлялся путём гипотетического приспособления, интуиции и арифметических преобразований нужный номинал из кучки существующих в местной банке резисторов. Потому решил я избавиться от такой рутины и написал программку для оного действа. Первые варианты программы просто складывали сопротивления (конечно, не простым сложением, а правильным, по формуле 1/R=1/R1+1/R2+…..1/Rn ). Но это меня тоже неустраивало, поскольку часто приходится возвращаться к началу, ошибшись в выборе очередного резистора, включённого в цепь.

Потому, немного поразмыслив над кодом, доработал своё поделие и теперь программа не только прибавляет номиналы резисторов в параллельную цепь, но и исключает их оттуда. В общем Вот:

Описание.

Скачать программу paresist для расчёта сопротивления параллельной цепи (Linux)
Скачать программу paresist для расчёта сопротивления параллельной цепи (Win7-64)
Скачать программу paresist для расчёта сопротивления параллельной цепи (Win7-32)

Для начала работы с программой в Linux надо распаковать zip-архив, после чего копировать (или переместить) файл программы paralsop в каталог /bin или /usr/local/bin (естественно от имени root ), затем изменить права на файл
#chmod 777 /bin/paralsop
или если скопирован в каталог /usr/local/bin то:
#chmod 777 /usr/local/bin/paralsop
После этого Вы можете запустить программу от имени пользователя, набрав в терминале имя программы paralsop .

У меня эта программа — второй вариант, потому именуется paralsop2 — Вы можете тоже переименовать файл как угодно, например: parezist (параллельные резисторы 🙂 ) и тогда набирать в консоли придуманное имя вместо придуманного мной.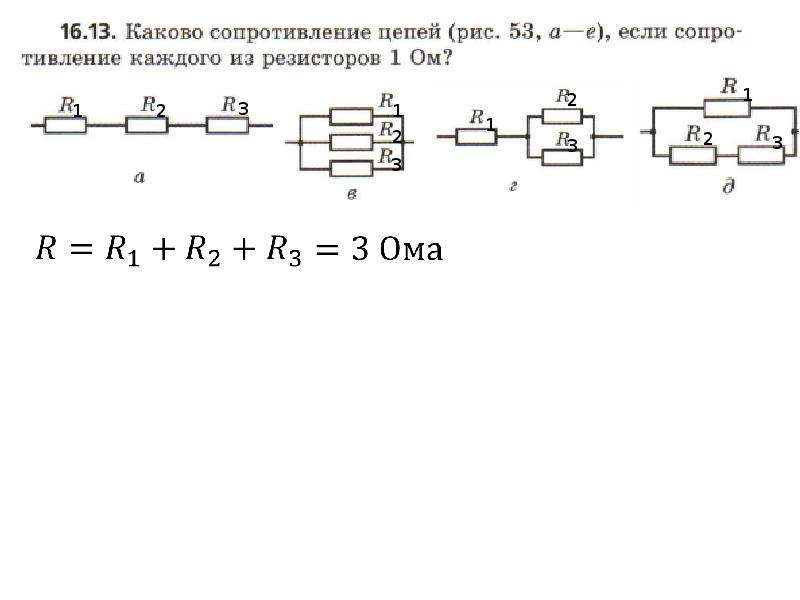 Нажимаем Enter

Интерфейс программы прост, как сковородка… Начинаем пользовать, и вводим номинал резистора, нажимаем Enter

Чуда не произошло, один резистор имеет своё собственное сопротивление, добавляем ещё, а потом отнимаем…

Естественно, отнимать можно только такие сопротивления, какие добавляли ( иначе в цепи спротивление будут создавать демоны 🙂 ) . Так до тех пор, пока не останется один единственный резистор. Если Вы и его решите изъять, то цепи как таковой небудет и требовать вычислений глупо ( но если хотите, то можно, только позвольте машине решать, как выйти из такой глупости 🙂 ). Чтобы завершить программу достаточно набрать 0 в качестве номинала и нажать Enter, поскольку нулём Вы замкнёте параллельную цепь накоротко, а в таком случае даже пробки вышибает 🙂

Для пользователей Windows 7 есть отличие в использовании программы. Её можно никуда не копировать и запускать с любого носителя, кликнув на распакованном файле программы мышкой.

Скачать программу можно отсюда, выбрав подходящий вариант для Вашей операционной системы.

Программа paresist предназначена для того-же самого, что и предыдущая, но применён немного другой подход к диалогу с пользователем. Её также следует распаковав из архива переместить в каталог /bin , сообщив файлу права на запуск, как программы. После этого запускаем её путём вызова командной строкой :
$paresist

Получаем приглашение программы:

Вводим предполагаемое количество резисторов для сборки цепи требуемого сопротивления, например — 4 шт. :

Затем нажимаем <Enter> и получаем приглашение к вводу номиналов резисторов в Омах.

Для выхода из программы в любой момент следует ввести значение 0 (ноль) и нажать <Enter> , поскольку при параллельном включении сопротивлений будет короткое замыкание 🙂 Потому вводятся значения отличные от нуля в положительную сторону.

После каждого номинала нажимаем <Enter>. По достижении заявленного количества резисторов в цепи программа автоматически подсчитывает их общее сопротивление и отображает все введённые номиналы в строке ( поскольку более 10 штук уже просматривать в терминале «столбиком» неудобно).

Если неустраивает результат, то можно пересчитать, введя 1 (единицу) и нажав <Enter>, тогда программа очистит экран и пригласит к новому расчёту. Если результат устраивает, то можно введя 0 (ноль) и нажав <Enter> выйти из программы, при этом весь расчёт останется на экране монитора. Программа собрана для отображения в локальной кодировке Utf8 под linux-i686-pae.

Скачать программу paresist для расчёта сопротивления параллельной цепи (для Linux i686)

Скачать для Windows-7/64 программу расчёта сопротивления параллельной цепи

Скачать для Windows-7/32 программу расчёта сопротивления параллельной цепи

Если у пользователей Windows 7 программа отображается «крякозябрами», то попытайтесь её запустить из командной строки путём ввода полного пути к файлу. Как правило в таком случае запускается cmd.exe с локалью UTF8 , тогда кодировки совпадают и программа нормально читается.
Онлайн расчёт цепи параллельных резисторов

Как рассчитать сопротивление параллельно соединенных резисторов

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.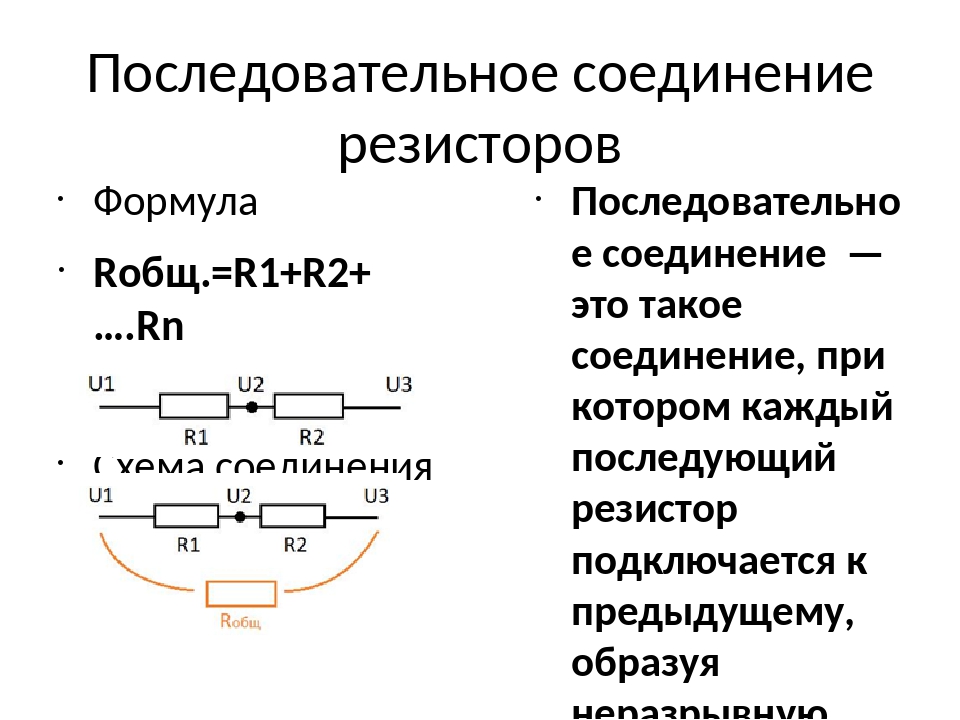

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт.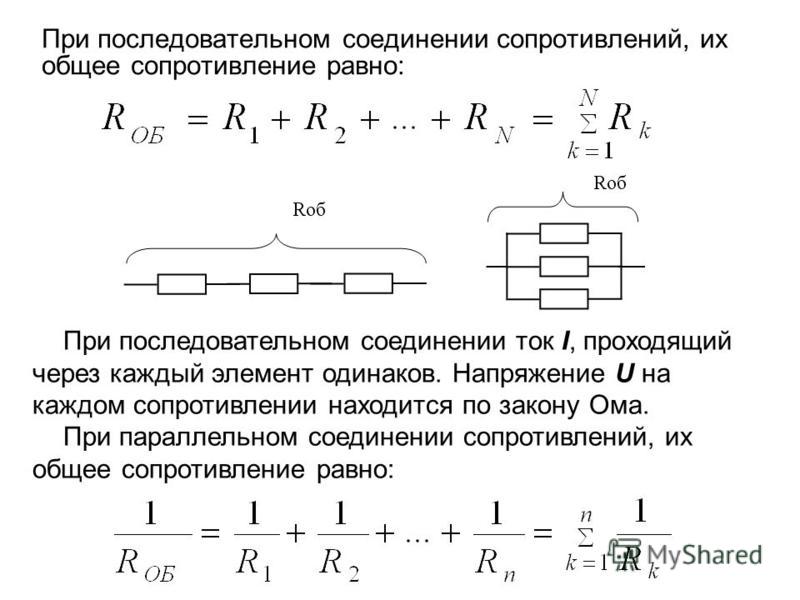 В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

Проводники (все металлы, ионизированный газ и электролитические растворы).
Полупроводники (Si, Ge, GaAs, InP и InSb).
Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

Температура окружающей среды и материала.
Электрические величины.
Геометрические свойства вещества.
Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
Визуально определить форму материала.
Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.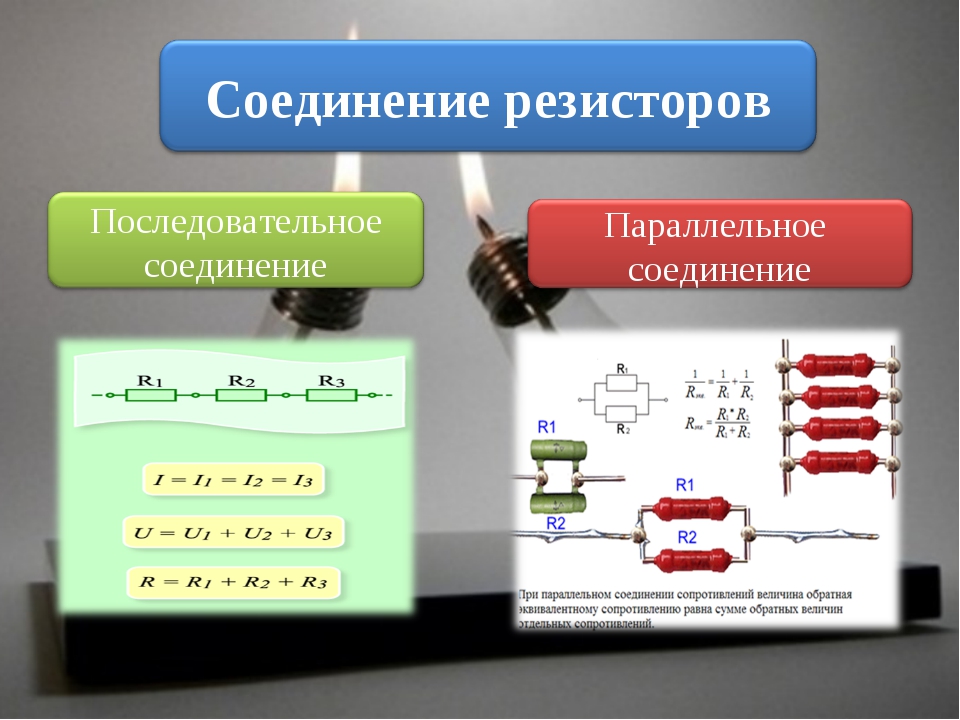

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

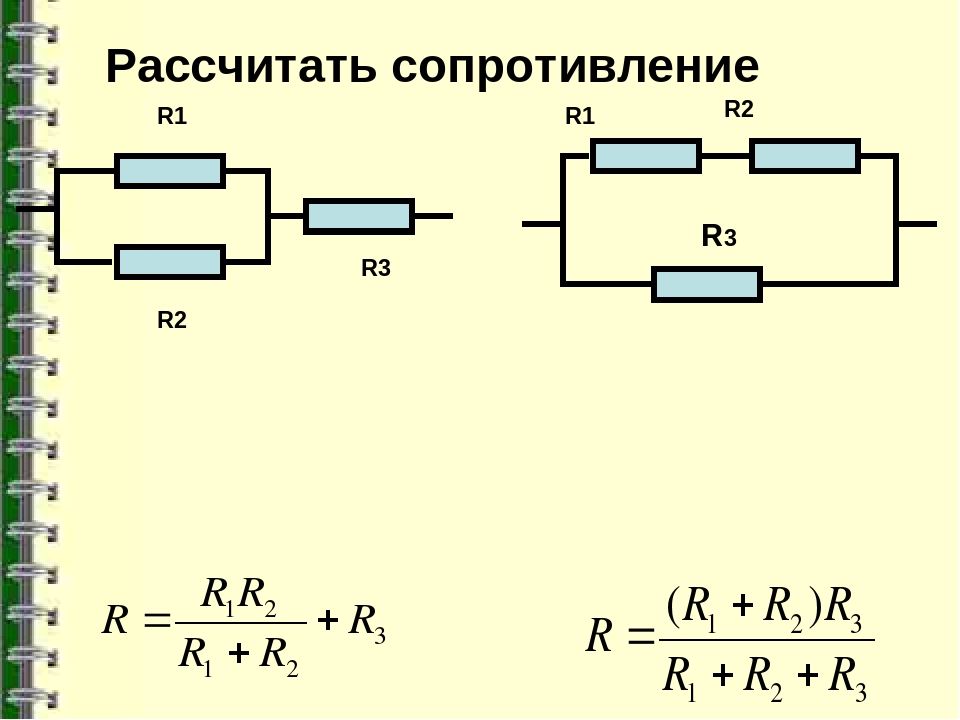
Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления.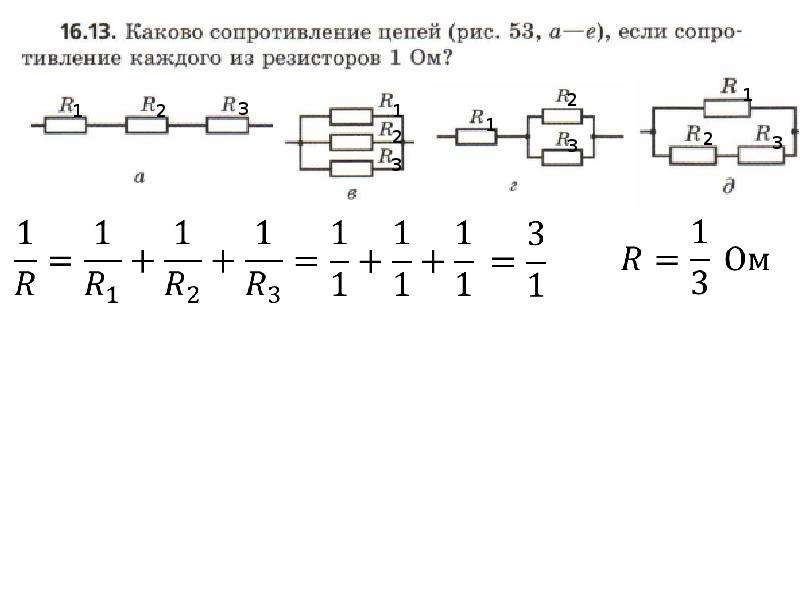 Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

Номинал резистора в 16 Ом подойдет.
Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
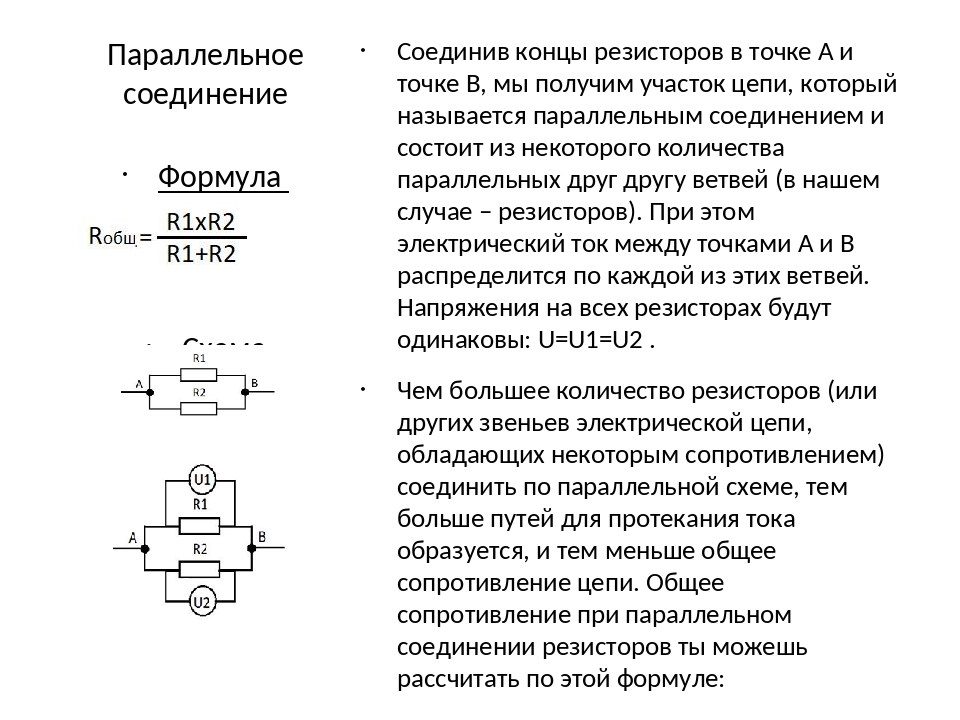
Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

Ток не изменяется на участке цепи.
Общее напряжение равно сумме падений напряжений на каждом резисторе.
Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

I = I1 = I2 = 0,5 (А).
Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

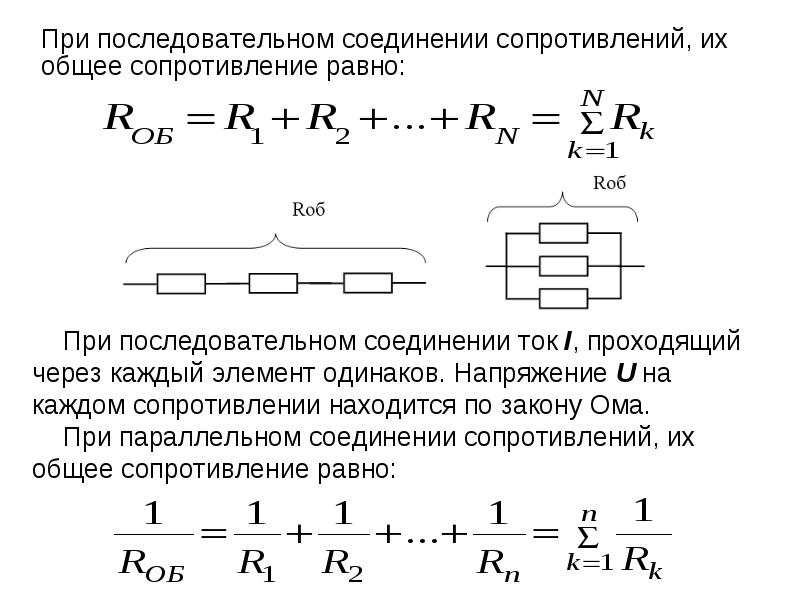
Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.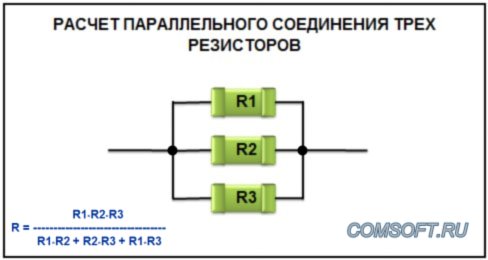

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.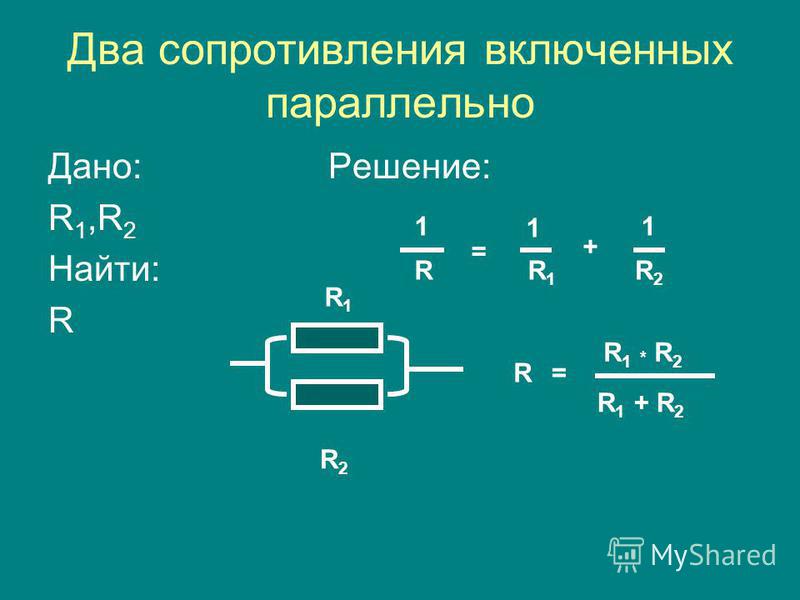

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Рассчитать сопротивление при параллельном соединении резисторов — онлайн калькуялтор

Онлайн калькулятор для расчета сопротивления в цепи при параллельном соединении резисторов.

Как пользоваться калькулятором

Введите заданное количество резисторов в цепи. Появятся поля с заданным количеством резисторов, укажите значение сопротивления каждого резистора в Ом. Нажмите на красную кнопку «Рассчитать». Результат появятся в поле снизу.

Примечание

Максимальное количество резисторов, которые можно ввести — 1000.
При параллельном соединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Теория

Резистор — пассивный элемент электроцепей, характеризуется сопротивлением электротоку.

Параллельное соединение — соединение, когда резисторы между собой соединены обоими контактами.

Ом — единица измерения сопротивления. Приставки увеличения: кило — килоом (тысяча Ом), мега — мегаом (миллион Ом).

Формула

Формула общего сопротивления при параллельном соединении нескольких резисторов:

Rобщ.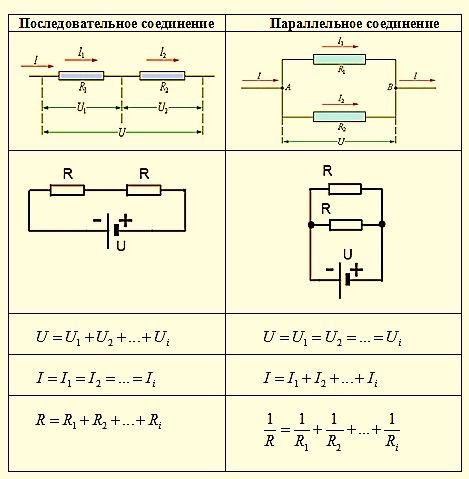 = 1 / Gобщ. = R1 * R2 * R2 / ((R1 * R2) + (R2 * R3) + (R1 * R3)).

где,

R1,R2,…Rn значение каждого отдельного резистора,
Rобщ. — общее сопротивление резисторов при параллельном соединении.

Пример

Известно сопротивление R1 = 2 Ом, R2 = 3 Ом, R3 = 4 Ом.

Требуется найти общее сопротивление в параллельной цепи резисторов.

Воспользуемся формулой:

Rобщ. = 1 / Gобщ. = R1 * R2 * R2 / ((R1 * R2) + (R2 * R3) + (R1 * R3)).

Rобщ. = 2 * 3 * 4 / ((2 * 3) + (3 * 4) + (2 * 4),

Rобщ. = 24 / 26 = 0,92.

Результат: Rобщ. = 0,92 Ом.

Задание

Рассчитайте с помощью онлайн программы правильно ли решен пример выше.

Онлайн определение эквивалентного сопротивления

Эквивалентное сопротивление при последовательном соединении

Альтернативное отображение

Эквивалентное сопротивление при паралельном соединении

Альтернативное отображение

Последовательное соединение

Что же такое эквивалентное сопротивление?

Все знаем что такое эквивалент.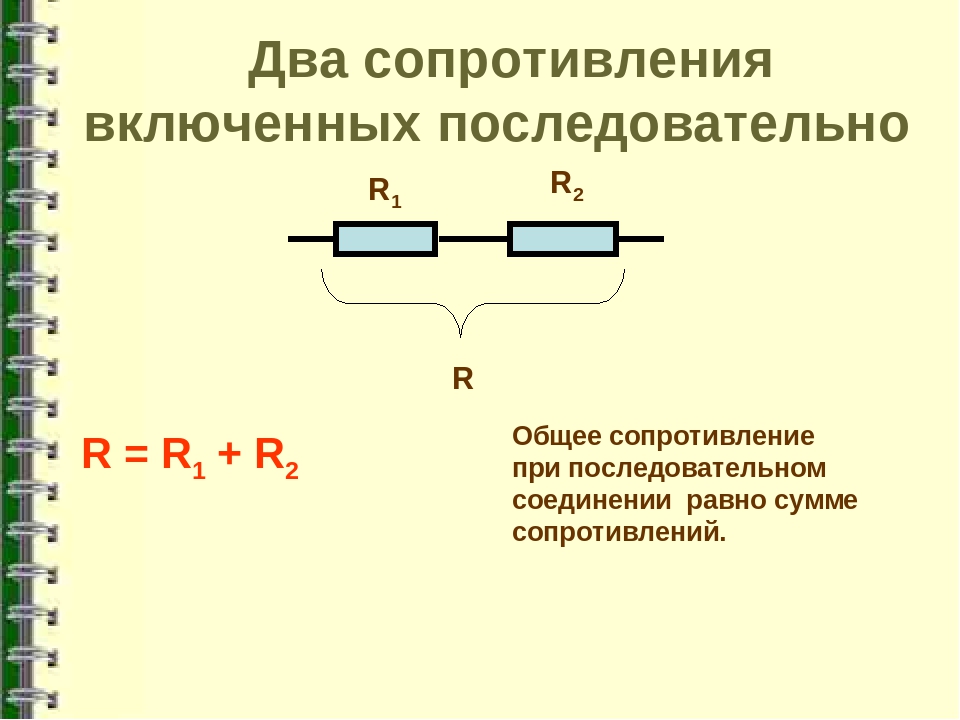 Это вещь или объект которое по своим характеристикам повторяет оригинал. В электротехнике эквивалент сопротивления это замена части схемы состоящей из нескольких резисторов — одним элементом(эквивалентом)

Сложные схемы соединений пока рассматривать не будем, а рассмотрим две самые простые схемы расчета эквивалентного сопротивления: последовательное и паралельное соединение

Вид последовательного соединения резисторов показан на рисунке ниже

И формула расчета эквивалентного сопротивления выглядит так

Параллельное СОЕДИНЕНИЕ

Паралельное соединение нескольних резисторов (сопротивлений) выглядит так, как показано на рисунке

А формула превращается в такую

Стоит обратить внимание, что по таким же формулам считается эквивалентное сопротивление индуктивностей, но совершенно другой прицип будет при расчете эквивалентной ёмкости конденсаторов

Синтаксис

Он очень прост

calc_e список сопротивлений с размерностями через запятую.

В ответе мы получим эквививалентное значение сопротивления при последовательном и паралельных соединениях.

Важное замечание: размерности нужно писать на русском языке. Для пользователей сайта, не знающих русский язык, можем по запросу добавить обработку англоязычных наименований приставок и размерностей. Это не сложно.

Примеры

Рассчитать эквивалентное сопротивление трех резисторов следующих номиналов: 10 Ом, 0.2кОм и 344кОм

В запросе так и пишем calc_e 10 Ом, 0.2кОм, 344кОм

Ответ не заставит себя долго ждать и выглядит вот так

Эквивалентное сопротивление при последовательном соединении

344.21килоОм

Альтернативное отображение

Эквивалентное сопротивление при паралельном соединении

9.5235458597492Ом

Альтернативное отображение

Удачи в расчетах!

Разложения в ряд Фурье периодических несинусоидальных функций. >>

Параллельные резисторы онлайн. Соединение резисторов

Определение параллельного соединения

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

Формулы для частного рассчета вытекают из основной формулы.

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:

Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

2. Делитель токов.

В этой теме можно привести множество примеров из нашей повседневной жизни, касающихся параллельного подключения сопротивлений. Параллельное соединение одинаковых сопротивлений — это наглядный пример подключения люстры с n-ым количеством ламп и с одинаковым сопротивлением для каждой лампы \рис.1\.

Если допустим в люстре состоящей из нескольких ламп \с одинаковым сопротивлением\ перегорела одна лампа и была произведена замена на лампочку другой мощности, — в этом случае, подключение люстры будет выглядеть как параллельное подключение с разным сопротивлением.

Какие еще можно привести примеры из практики — при параллельном подключении сопротивлений? Допустим, Вы подключили в своей квартире через удлинитель три бытовых электроприбора:

электроплиту;
стиральную машину;
телевизор.

Характер такого подключения примет значение как для параллельного подключения сопротивлений , разных по величине. То-есть, для каждого электроприбора, сопротивление имеет свое значение.

Расчет сопротивления при параллельном соединении

Как уже упоминалось, расчеты сопротивлений при параллельном соединении проводятся:

с одинаковым сопротивлением;
с разным сопротивлением,

а также, проводятся расчеты сопротивлений для смешанных соединений резисторов, при последовательном и параллельном соединениях \для одной цепи\. Расчет сопротивления для смешанных соединений резисторов, больше подходит к различным блок-схемам:

аудиотехники;
видеотехники.

К этой теме, расчеты для смешанных соединений, отношения не имеют.

Параллельное соединение одинаковых сопротивлений

Представим параллельное подключение, к примеру, трех сопротивлений \рис.2\ равных по величине, где R1=R2=R3=36 Ом \сопротивление лампы накаливания мощностью на 95 Вт\. К двум узловым точкам \А, В\ подключено напряжение 220 В. Нужно вычислить общее сопротивление всех трех ламп.

Для расчета общего сопротивления \Rобщ.\, нам необходимо 36 Ом разделить на количество сопротивлений. Решение простое, Rобщ.=12 Ом. То-есть, формула для расчета подобных вычислений выглядит как:

Rобщ. = R /n

Параллельное соединение разных сопротивлений

Допустим, возьмем выборочно три резистора, сопротивлением:

R1=20 Ом;
R2=40 Ом;
R3=10 Ом.

Нужно определить общее сопротивление резисторов при параллельном соединении. Для данного расчета воспользуемся формулой:

1/Rобщ.=1/R1+1/R2+1/R3.

Подставляем значения в формулу:

1/Rобщ. = 1/20+1/40+1/10=7/40=0,18

получаем: Rобщ.=1/0,18=5,5 Ом.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .

Параллельное соединение резисторов — онлайн калькулятор

Подведем итог

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.

Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление , используя нижеописанные формулы.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Расчет сопротивления

В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

R(общ)=R1*R2/R1+R2.

R(общ) – суммарное сопротивление;
R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Универсальная схема расчета

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

R(общ) – суммарное значение сопротивления;
R – номинал резистора, подсоединенного по параллельной схеме;
n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.

Пример расчета

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Заключение

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

Проверим справедливость показанных здесь формул на простом эксперименте.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Сопротивления

параллельно, онлайн калькулятор и формулы

Калькулятор и формулы для расчета резисторов параллельно

Рассчитать сопротивление параллельного включения

При параллельном подключении резисторов ток распределяется по отдельным резисторам.

Рассчитать общее сопротивление

Экспоненты не допускаются.Введите все значения в подходящих равных единицах измерения. Если вы введете все значения, например в кОм результат также отображается в кОм.

Для расчета введите значения отдельных резисторов, разделенных точкой с запятой.
Пример: 33; 12,1; 22

Вычислитель резисторов в параллель

Формулы резисторов, включенных параллельно

Чтобы рассчитать общее сопротивление нескольких резисторов, включенных параллельно, их значения проводимости складываются.Проводимость обратно пропорциональна сопротивлению. Формула для трех резисторов, соединенных параллельно:

\ (\ displaystyle \ frac {1} {R_ {ges}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \)

Если необходимо рассчитать общее сопротивление двух параллельных резисторов, можно использовать следующую формулу.

\ (\ Displaystyle R_ {ges} = \ гидроразрыва {R_1 · R_2} {R_1 + R_2} \)

Эта страница полезна? да Нет
Спасибо за ваш отзыв!
Прошу прощения за это
Как мы можем это улучшить?

послать

12.Параллельные цепи переменного тока

Вспомните закон Ома для чистых сопротивлений:

`V = IR`

В случае цепей переменного тока мы представляем сопротивление (эффективное сопротивление) в виде комплексного числа Z . Единицы равны Ом (Ом).

В этом случае закон Ома принимает вид:

В = ИЗ .

Напомним также, если у нас несколько резисторов ( R ₁, R ₂, R ₃, R ₄,…) подключено в параллели , тогда общее сопротивление R _T, выдается:

`1 / (R_T) = 1 / R_1 + 1 / R_2 + 1 / R_3 +…`

В случае цепей переменного тока это становится:

`1 / (Z_T) = 1 / Z_1 + 1 / Z_2 + 1 / Z_3 + …`

Простой кейс:

Если у нас есть 2 импеданса Z ₁ и Z ₂, соединены параллельно, затем общая сопротивление Z _T, равно

`1 / (Z_T) = 1 / Z_1 + 1 / Z_2`

Мы можем записать это как:

`1 / (Z_T) = (Z_2 + Z_1) / (Z_1Z_2)`

Находя взаимность обеих сторон, мы получаем:

`Z_T = (Z_1Z_2) / (Z_1 + Z_2)`

Пример 1

Найдите суммарный импеданс следующая цепь:

Ответ

Назовите импеданс, заданный верхней частью цепи Z ₁ и импеданс, определяемый нижняя часть Z ₂.

Мы видим, что Z ₁ = 70 + 60 j Ом и Z ₂ = 40-25 j Ом

Так

`Z_T = (Z_1Z_2) / (Z_1 + Z_2)`

`= ((70 + 60j) (40-25j)) / ((70 + 60j) + (40-25j))`

`= ((70 + 60j) (40-25j)) / (110 + 35j)`

(сложение комплексных чисел должно производиться в прямоугольной форме.

Теперь мы конвертируем все в полярную форму, а затем умножаем и делим как следует):

`= ((70 + 60j) (40-25j)) / (110 + 35j)`

`= ((92.текст (o) `

(Преобразуем обратно в прямоугольную форму.)

`= 37,22-5,93j`

(При умножении комплексных чисел в полярной форме мы умножаем r членов (числа на переднем плане) и складываем углы. При делении комплексных чисел в полярной форме мы делим члены r и вычитаем углы. См. раздел «Продукты и коэффициенты» для получения дополнительной информации.)

Таким образом, мы заключаем, что суммарный импеданс равен

`Z_T = 37-5.9j \ Omega`

Пример 2

Учитывая, что Z ₁ = 200-40 j Ом и Z ₂ = 60 + 130 Дж Ом,

найди

а) полное сопротивление

б) фазовый угол

в) общий ток строки

Ответ

a) `Z_T = frac {Z_1Z_2} {Z_1 + Z_2}`

`= frac {(200-40j) (60 + 130j)} {(200-40j) + (60 + 130j)}`

`= frac {(200-40j) (60 + 130j)} {260 + 90j}`

`= frac {(204.@ «A» `

Пример 3

Резистор 100 Ом, катушка индуктивности 0,0200 Н и Конденсатор 1,20 мкФ подключены параллельно с цепь, состоящая из резистора 110 Ом, включенного последовательно с `2.40 \ mu» F «` конденсатор. Питание `150 \» В «,` 60 \ «Гц» есть подключен к цепи.

Рассчитайте общий потребляемый ток от источника питания и его фазового угла.

Ответ

Для Z ₁ (верхняя часть цепь) имеем:

X _L = 2 π f L = 2 π (60) (0.@ `.

Резисторы и сопротивление

— MCAT Physical

Используйте следующую информацию, чтобы ответить на вопросы 1-6:

Кровеносная система человека — это замкнутая система, состоящая из насоса, который перемещает кровь по всему телу через артерии, капилляры и вены. Капилляры маленькие и тонкие, что позволяет крови легко перфузировать системы органов. Будучи замкнутой системой, мы можем моделировать систему кровообращения человека как электрическую цепь, делая модификации для использования жидкости, а не электронов.Сердце действует как основная сила для движения жидкости, жидкость движется по артериям и венам, и сопротивление кровотоку возникает в зависимости от скорости перфузии.

Чтобы смоделировать поведение жидкостей в системе кровообращения, мы можем изменить закон Ома V = IR на ∆P = FR, где ∆P — изменение давления (мм рт. Ст.), F — скорость потока (мл / мин), и R — сопротивление потоку (мм рт. ст. / мл / мин). Сопротивление потоку жидкости в трубке описывается законом Пуазейля: R = 8hl / πr ⁴, где l — длина трубки, h — вязкость жидкости, а r — радиус трубки.Вязкость крови выше, чем у воды из-за наличия клеток крови, таких как эритроциты, лейкоциты и тромбоциты.

Приведенные выше уравнения верны для гладкого ламинарного потока. Однако отклонения возникают при наличии турбулентного потока. Турбулентный поток можно охарактеризовать как нелинейный или бурный, с завихрением, слипанием или иным непредсказуемым расходом. Турбулентность может возникать при отклонении анатомического строения трубки, например, при резких изгибах или сжатиях. Мы также можем получить турбулентный поток, когда скорость превышает критическую скорость v _c, определенную ниже.

v _c = N _R h / ρD

N _R — постоянная Рейнольдса, h — вязкость жидкости, ρ — плотность жидкости, D — диаметр трубы. Плотность крови составляет 1060 кг / м 3 ³.

Другой ключевой особенностью системы кровообращения является то, что она устроена таким образом, что системы органов действуют параллельно, а не последовательно. Это позволяет телу изменять количество крови, поступающей к каждой системе органов, что было бы невозможно при последовательной конструкции.Эта установка представлена на Рисунке 1.

Предположим, что на рисунке 1 R1 = 1/2 мм рт. Ст. / Мл / мин, R2 = 2 мм рт. Ст. / Мл / мин, R3 = 4 мм рт. Ст. / Мл / мин и R4 = 4 мм рт. Ст. / Мл / мин.

Давление, создаваемое левым желудочком, составляет 100 мм рт. Ст., А давление, создаваемое правым желудочком, составляет 50 мм рт. Ст. Какая скорость потока через R3?

Пояснение:

В параллельной цепи напряжение остается постоянным. Аналогично, в этом сценарии давление остается постоянным.Если мы знаем давление и сопротивление, мы можем найти ток, протекающий через резистор, используя ∆P = FR.

В этом случае мы будем использовать только давление в левом желудочке, поскольку это давление, передаваемое остальной части тела, тогда как правый желудочек перекачивает только легкие. Используя ∆P = FR, мы можем изменить это так, чтобы получить F = ∆P / R. Подставляя числа, которые мы можем решить для F.

21.1 Последовательные и параллельные резисторы — College Physics

Сводка

Нарисуйте цепь с резисторами, включенными параллельно и последовательно.
Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
Контраст — способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
Рассчитайте общее сопротивление цепи, которая содержит смесь резисторов, включенных последовательно и параллельно.

Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи.Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.

Рис. 1. (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.

Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно.Например, если ток течет через человека, держащего отвертку, в землю, то на рисунке 1 (а) может быть сопротивление вала отвертки, сопротивление ее ручки, сопротивление тела человека и сопротивление его обуви. .

На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно.(Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. Это могло бы стать недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением. прибор, уменьшающий рабочий ток.)

Рисунок 2. Три резистора, подключенных последовательно к батарее (слева) и эквивалентному одиночному или последовательному сопротивлению (справа).

Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе на Рисунке 2.

Согласно закону Ома падение напряжения на резисторе при протекании через него тока рассчитывается по формуле, где равно току в амперах (A), а — сопротивление в омах. Другой способ думать об этом — это напряжение, необходимое для протекания тока через сопротивление.

Таким образом, падение напряжения равно, что есть, а что есть. Сумма этих напряжений равна выходному напряжению источника; то есть

Это уравнение основано на сохранении энергии и сохранении заряда.Электрическая потенциальная энергия может быть описана уравнением, где — электрический заряд, а — напряжение. Таким образом, энергия, подаваемая источником, равна, а энергия, рассеиваемая резисторами, равна

Связи: законы сохранения

Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.

Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, . Плата отменяется, уступая, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)

Теперь замена значений отдельных напряжений дает

Обратите внимание, что для эквивалентного сопротивления одиночной серии мы имеем

Это означает, что полное или эквивалентное последовательное сопротивление трех резисторов составляет

Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление последовательного соединения составляет

[/латекс]

, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.

Пример 1: Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи

Предположим, что выходное напряжение батареи на рисунке 2 равно, а сопротивления равны, и.а) Каково полное сопротивление? (б) Найдите ток. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)

Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:

Стратегия и решение для (b)

Ток определяется по закону Ома.Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:

Стратегия и решение для (c)

Напряжение — или падение — на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает

Аналогично

Обсуждение для (c)

Три капли добавляют к, как и прогнозировалось:

Стратегия и решение для (d)

Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля , где — электрическая мощность.В этом случае через каждый резистор протекает одинаковый полный ток. Подставляя закон Ома в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как

Аналогично

Обсуждение для (д)

Мощность также можно рассчитать с помощью либо, где — падение напряжения на резисторе (а не полное напряжение источника). Получатся те же значения.

Стратегия и решение для (e)

Самый простой способ рассчитать выходную мощность источника — использовать, где — напряжение источника.Это дает

Обсуждение для (e)

По совпадению обратите внимание, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, что соответствует мощности, выдаваемой источником. То есть

Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.

Основные характеристики резисторов серии

Сопротивления серии добавляют:.
Через каждый резистор последовательно проходит одинаковый ток.
Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.

На рисунке 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.

Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)

Рис. 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (предоставлено Дмитрием Г., Wikimedia Commons)

Чтобы найти выражение для эквивалентного параллельного сопротивления, давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны, и. Сохранение заряда подразумевает, что полный ток, производимый источником, является суммой этих токов:

Подстановка выражений для отдельных токов дает

Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает

Члены в круглых скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление параллельного соединения связано с отдельными сопротивлениями на

Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений.(Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.

Пример 2: Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи

Пусть выходное напряжение батареи и сопротивления при параллельном соединении на Рисунке 3 будут такими же, как в ранее рассмотренном последовательном соединении:,, и.а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)

Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения.Ввод известных значений дает

Таким образом,

(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)

Мы должны инвертировать это, чтобы найти полное сопротивление. Это дает

Суммарное сопротивление с правильным количеством значащих цифр —

Обсуждение для (а)

, как и предполагалось, меньше наименьшего индивидуального сопротивления.

Стратегия и решение для (b)

Полный ток можно найти из закона Ома, заменив полное сопротивление.Это дает

Обсуждение для (б)

Ток для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример). Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.

Стратегия и решение для (c)

Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,

Аналогично

Обсуждение для (c)

Общий ток складывается из отдельных токов:

Это соответствует сохранению заряда.

Стратегия и решение для (d)

Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. Давайте использовать, так как каждый резистор получает полное напряжение. Таким образом,

Аналогично

Обсуждение для (д)

Мощность, рассеиваемая каждым резистором параллельно, значительно выше, чем при последовательном подключении к тому же источнику напряжения.

Стратегия и решение для (e)

Общую мощность также можно рассчитать несколькими способами. Выбор и ввод полного тока дает

Обсуждение для (e)

Общая мощность, рассеиваемая резисторами, также составляет 179 Вт:

Это соответствует закону сохранения энергии.

Общее обсуждение

Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.

Основные характеристики параллельных резисторов

Параллельное сопротивление получается из, и оно меньше любого отдельного сопротивления в комбинации.
На каждый параллельно включенный резистор подается такое же полное напряжение источника. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
Параллельные резисторы не получают суммарный ток каждый; они делят это.

Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.

Комбинации последовательного и параллельного соединения можно свести к одному эквивалентному сопротивлению, используя метод, показанный на рисунке 4. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее уменьшаются, пока не останется единственное сопротивление.Процесс занимает больше времени, чем труден.

Рисунок 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто единичное эквивалентное сопротивление.

Самая простая комбинация последовательного и параллельного сопротивления, показанная на рисунке 5, также является наиболее поучительной, поскольку она используется во многих приложениях. Например, это может быть сопротивление проводов от автомобильного аккумулятора к его электрическим устройствам, которые включены параллельно.и мог быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.

Пример 3: Расчет сопротивления, падения, тока и рассеиваемой мощности: объединение последовательных и параллельных цепей

На рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного подключения. Мы можем считать сопротивление проводов, ведущих к и.(а) Найдите полное сопротивление. б) Что такое падение? (c) Найдите сквозной ток. (г) Какая мощность рассеивается?

Рисунок 5. Эти три резистора подключены к источнику напряжения, так что R ₂ и R ₃ параллельны друг другу, и эта комбинация идет последовательно с R ₁ .

Стратегия и решение для (а)

Чтобы найти полное сопротивление, отметим, что и находятся параллельно, а их комбинация — последовательно с.Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет

Сначала мы находим, используя уравнение для параллельных резисторов и вводя известные значения:

Инвертирование дает

Таким образом, общее сопротивление равно

Обсуждение для (а)

Общее сопротивление этой комбинации является промежуточным между значениями чисто последовательного и чистого параллельного (и, соответственно), найденными для тех же резисторов в двух предыдущих примерах.

Стратегия и решение для (b)

Чтобы найти падение, отметим, что через него протекает полный ток.Таким образом, его падение составляет

Мы должны найти, прежде чем сможем вычислить. Полный ток определяется по закону Ома для цепи. То есть

Вводя это в выражение выше, мы получаем

Обсуждение для (б)

Напряжение, приложенное к общему напряжению, и меньше его на величину. Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных и.

Стратегия и решение для (c)

Чтобы найти сквозной ток, мы должны сначала найти приложенное к нему напряжение.Мы называем это напряжением, потому что оно приложено к параллельной комбинации резисторов. Напряжение, приложенное к обоим и уменьшается на величину, так что оно составляет

Теперь ток через сопротивление находится по закону Ома:

Обсуждение для (c)

Ток меньше 2,00 А, которые протекали через R2R2 размером 12 {R rSub {размер 8 {2}}} {}, когда он был подключен параллельно к батарее в предыдущем примере параллельной цепи.

Стратегия и решение для (d)

Рассеиваемая мощность равна

Обсуждение для (д)

Мощность меньше 24.0 Вт этот резистор рассеивает при подключении параллельно источнику 12,0 В.

Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если протекает большой ток, провал в проводах также может быть значительным.

Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет.Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).

Что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, обозначенное значком, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение в проводах, представленных значком, уменьшая напряжение на лампочке (которая есть), которое затем заметно гаснет.

Рисунок 6. Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.

Проверьте свое понимание

1: Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную комбинации? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.

Стратегии решения проблем для последовательных и параллельных резисторов

Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
Точно определите, что необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, уменьшайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при нахождении [/ latex] латекса \ boldsymbol {R_p} [/ latex] необходимо с осторожностью относиться к обратному значению.
Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.

Концептуальные вопросы

1: Переключатель имеет переменное сопротивление, близкое к нулю в замкнутом состоянии и очень большое в разомкнутом, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рис. 7 на ток в разомкнутом и замкнутом состоянии.

Рис. 7. Переключатель обычно включен последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)

2: Какое напряжение на разомкнутом переключателе на рисунке 7?

3: На разомкнутом переключателе есть напряжение, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?

4: Почему мощность, рассеиваемая замкнутым переключателем, как на рисунке 7, мала?

5: Студент в физической лаборатории по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рис. 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и гаснет, когда он замкнут. (Не пытайтесь — батарея сильно разряжается!)

Рис. 8. Ошибка подключения: этот переключатель подключен параллельно устройству, представленному R .(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)

6: Зная, что сила удара зависит от величины тока, протекающего через ваше тело, вы бы предпочли быть последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он поражен током? Объяснять.

7: Были бы ваши фары тусклыми при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.

8: Некоторые гирлянды праздничных фонарей подключаются последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкаются накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?

9: Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.

10: Предположим, вы выполняете физическую лабораторию, которая просит вас вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?

11: Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление. Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор.Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.

12: У некоторых лампочек есть три уровня мощности (не включая ноль), полученные от нескольких нитей накала, которые индивидуально переключаются и подключаются параллельно. Какое минимальное количество нитей нити необходимо для трех режимов мощности?

Проблемные упражнения

Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.

1: (a) Какое сопротивление у десяти последовательно соединенных резисторов? (б) Параллельно?

2: (a) Какое сопротивление a и резистора, соединенных последовательно? (б) Параллельно?

3: Какие значения наибольшего и наименьшего сопротивления можно получить, соединив вместе резистор, резистор и резистор?

4: Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключаются к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?

5: Фара на 30,0 Вт и стартер на 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)

6: (a) Учитывая 48.Аккумулятор 0 В и резисторы, найдите ток и мощность для каждого из них при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.

7: Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, рассчитайте двумя следующими способами: (a) из известных значений и; (б) используя закон Ома для. В обеих частях явно показано, как вы выполняете шаги, указанные в Стратегиях решения проблем для последовательных и параллельных резисторов.

8: Ссылаясь на рисунок 5: (a) Рассчитайте и обратите внимание на то, как это соотносится с обнаруженными в первых двух примерах проблемами в этом модуле.(b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.

9: См. Рис. 6, где обсуждается затемнение света при включении тяжелого прибора. (a) Учитывая, что источник напряжения составляет 120 В, сопротивление провода равно, а номинальная мощность лампы составляет 75,0 Вт, какая мощность будет рассеиваться лампой, если при включении двигателя через провода пройдет в общей сложности 15,0 А? Предположите незначительное изменение сопротивления лампы. б) Какая мощность потребляет двигатель?

10: Линию электропередачи на 240 кВ подвешивают к заземленным металлическим опорам с помощью керамических изоляторов, каждый из которых имеет сопротивление.Рис. 9. (а) Какое сопротивление относительно земли 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Ясно покажите, как вы выполняете шаги, указанные в Стратегиях решения проблем для последовательных и параллельных резисторов.

Рис. 9. Линия электропередачи высокого напряжения (240 кВ), несущая 5,00 × 10 ² подвешен на заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает 1.00 × 10 ⁹ Ом по сопротивления каждый.

11: Покажите, что если два резистора и объединены, и один из них намного больше другого (): (a) Их последовательное сопротивление почти равно большему сопротивлению. (б) Их параллельное сопротивление почти равно меньшему сопротивлению.

12: Необоснованные результаты

Два резистора, один из которых имеет сопротивление, подключены параллельно, чтобы получить общее сопротивление. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

13: необоснованные результаты

Два резистора, один из которых имеет сопротивление, соединены последовательно, чтобы получить общее сопротивление.а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

Глоссарий

серии: последовательность резисторов или других компонентов, включенных в цепь один за другим

резистор: компонент, обеспечивающий сопротивление току, протекающему через электрическую цепь

сопротивление: вызывает потерю электроэнергии в цепи

Закон Ома: соотношение между током, напряжением и сопротивлением в электрической цепи:

напряжение: электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором

падение напряжения: потеря электроэнергии при прохождении тока через резистор, провод или другой компонент

текущий: поток заряда через электрическую цепь мимо заданной точки измерения

Закон Джоуля: взаимосвязь между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемая по формуле:

параллельно: разводку резисторов или других компонентов в электрической цепи, так что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы

Решения

Проверьте свое понимание

1: Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы.В таких случаях правила Кирхгофа, которые будут представлены в главе 21.3 «Правила Кирхгофа», позволят вам проанализировать схему.

Задачи Упражнения

1: (а)

(б)

3: (а)

(б)

5: 29,6 Вт

7: (а) 0,74 А

(б) 0,742 А

9: (а) 60,8 Вт

(б) 3,18 кВт

11: (а)

(б)

так что

13: (а)

(b) Сопротивление не может быть отрицательным.

(c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.

Оптимальные резисторы Найти инструменты

Эта страница представляет собой веб-приложение для разработки схем резисторов. Используйте эту утилиту, чтобы найти оптимальный набор резисторов для цепи резисторов из последовательности резисторов.

Пример расчета

Делитель напряжения

В1 (входное напряжение)	: В
В2 (желаемое выходное напряжение)	: В

Выберите последовательность резисторов: E6E12E24E48E96E192

Делитель напряжения2

В1 (входное напряжение)	: В
В2 (желаемое выходное напряжение)	: В
В3 (желаемое выходное напряжение)	: В

Выберите последовательность резисторов: E6E12E24E48E96E192

Параллельно и последовательно из двух резисторов

Эквивалентный резистор Ra		Параллельный	Ряд
	→

Выберите последовательность резисторов: E6E12E24E48E96E192
Ra (желаемое сопротивление):
Ом (10-1000 МОм)
Ra — это сопротивление для параллельного и последовательного размещения двух резисторов для создания нестандартного сопротивления.Этот инструмент найдет оптимальный набор резисторов R1, R2 и R3, R4 для желаемого значения Ra.

Расчет сопротивлений для деления напряжения (для разветвления тока)

Эквивалентный резистор Ra		Параллельный	Ряд
	→

Выберите последовательность резисторов: E6E12E24E48E96E192

N (общее количество резисторов)	: (2-99)
Ra (желаемое сопротивление)	: Ω (10-1000 МОм)

Схема «Еще три резистора» часто объединяется для деления напряжения (для разветвления тока).Этот инструмент находит оптимальный набор резисторов R1, R2… RN для желаемого значения Ra на основе близкого значения резистора, а также комбинирования сопротивлений.

19.3 Параллельные схемы | Texas Gateway

Robot

Роботы захватывают наше коллективное воображение уже более века. Теперь мечта о создании умных машин для выполнения нашей грязной работы, а иногда и просто для того, чтобы составить нам компанию, становится реальностью. Робототехника стала огромной областью исследований и разработок, некоторые технологии уже коммерциализированы.Подумайте, например, о небольших автономных пылесосах.

На рисунке 19.21 показаны лишь некоторые из множества различных форм, которые могут принимать роботы. Самые продвинутые роботы-гуманоиды могут ходить, наливать напитки и даже танцевать (хотя и не очень изящно). Другие роботы вдохновлены биологией, например, собачий робот , показанный на средней фотографии рис. 19.21. Этот робот может нести сотни фунтов груза по пересеченной местности. Фотография справа на рис. 19.21 показывает внутреннюю работу блока M, , разработанного Массачусетским технологическим институтом.Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться, переворачиваться в воздух и соединяться друг с другом в самых разных формах. Обмениваясь беспроводной связью между собой, они самостоятельно собираются в различные формы, такие как столы, стулья и, возможно, когда-нибудь даже здания.

Все роботы включают в себя огромное количество физики и инженерии. Простое наливание напитка было освоено роботами совсем недавно, после более 30 лет исследований и разработок! Баланс и выбор времени, которые мы, люди, считаем само собой разумеющимися, на самом деле являются очень сложной задачей, требующей отличного баланса, ловкости и обратной связи.Чтобы справиться с этим, требуются датчики для обнаружения баланса, вычислительная мощность для анализа данных и передачи соответствующих компенсирующих действий, а также соединения и приводы для выполнения требуемых действий.

Помимо определения силы тяжести или ускорения, роботы могут содержать несколько различных датчиков для обнаружения света, звука, температуры, запаха, вкуса и т. Д. Все эти устройства основаны на физических принципах, которые вы изучаете в этом тексте. Например, оптика, используемая для машинного зрения, аналогична оптике, используемой в ваших цифровых камерах: пиксельные полупроводниковые детекторы, в которых свет преобразуется в электрические сигналы.Для определения температуры можно использовать простые термисторы, которые представляют собой резисторы, сопротивление которых изменяется в зависимости от температуры.

Сегодня построить робота гораздо проще, чем несколько лет назад. Многие компании сейчас предлагают комплекты для сборки роботов. Они варьируются по сложности от чего-то подходящего для младших школьников до чего-то, что бросит вызов лучшим профессиональным инженерам. Если интересно, вы можете легко найти их в Интернете и начать создавать своего собственного робота уже сегодня.

Рис. 19.21 Роботы бывают разных форм и размеров, от классического гуманоида типа до собачьих роботов и небольших кубиков, которые самостоятельно собираются для выполнения различных задач.

ОПРЕДЕЛЕНИЕ ЭКВИВАЛЕНТНОГО СОПРОТИВЛЕНИЯ ЦЕПИ

Сопротивление было определено как отношение напряжения на компонент к току, протекающему через него. Итак, даже если компонент не называется «резистор», мы все еще можем найти цифру для его сопротивления.

Любая полезная схема обычно имеет несколько подключенных компонентов. вместе различными способами.

Теперь найдем выражение, позволяющее нам, чтобы рассчитать эквивалентное сопротивление компонентов, когда соединены последовательно друг с другом. С этого момента мы будем звонить резисторы, но имейте в виду, что они, в принципе, могут быть другими компонентами.

Эквивалентное сопротивление резисторов серии

Здесь мы видим три последовательно включенных резистора.
Так как они идут последовательно, одинаковые по току я протекает через все они.
Также, если напряжения на резисторах равны В ₁ В ₂ и V ₃, тогда, как показано здесь, мы можем написать

Следовательно, исходя из определения сопротивления, мы можем написать


Если этот единственный резистор R _E должен быть эквивалентом трех резисторы выше, мы имеем в виду, что он позволит протекать тому же току для такое же напряжение.Другими словами, он потреблял бы тот же ток от заданного аккумулятор как три резистора вместе.

Следовательно, ток I такой же, как в предыдущая схема, поэтому, снова используя определение сопротивления, мы имеем

Сложив их вместе и разделив на I, мы имеют (не совсем неожиданный) вывод

и, в более общем смысле, если есть N компонентов последовательно, результат может быть выражается как


Эквивалентное сопротивление параллельных резисторов
Здесь мы видим три резистора, включенных параллельно.

Поскольку они работают параллельно, мы знаем, что все они имеют одинаковые приложенное к ним напряжение.
Также мы знаем из действующего правила Кирхгофа

и из определения сопротивления


и, как и в случае серии, если R _E эквивалентен этим три резистора параллельно, тогда он должен потреблять тот же ток, что и все их от данной батареи.
Следовательно, имеем

Сложив эти два уравнения вместе и разделив на V, мы иметь

и, опять же, в более общем смысле, если в параллельно результат можно выразить как

Для упрощения расчетов стоит отметить, что если у нас N одинаковых резисторы, каждый из которых имеет сопротивление, R параллельно друг другу, затем их эквивалентное сопротивление дается