Расчет сопротивления резистора при параллельном соединении. Расчет сопротивления при параллельном и последовательном соединении резисторов: онлайн-калькулятор и формулы — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать общее сопротивление при параллельном и последовательном соединении резисторов. Какие формулы используются для расчета. Как работает онлайн-калькулятор для вычисления сопротивления резисторов. Какие преимущества и недостатки у параллельного и последовательного соединения.

Содержание

Основные принципы соединения резисторов

При создании электрических схем часто возникает необходимость соединять резисторы различными способами для получения нужного суммарного сопротивления. Существует два основных типа соединения резисторов:

Последовательное соединение
Параллельное соединение

Каждый из этих типов соединения имеет свои особенности и область применения. Рассмотрим их подробнее.

Последовательное соединение резисторов

При последовательном соединении резисторы подключаются друг за другом, образуя единую цепь. Основные свойства такого соединения:

Через все резисторы протекает одинаковый ток
Общее напряжение распределяется между резисторами
Общее сопротивление равно сумме сопротивлений всех резисторов

Формула для расчета общего сопротивления при последовательном соединении:

R = R1 + R2 + R3 + … + Rn

где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.

Параллельное соединение резисторов

При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи. Особенности такого соединения:

На всех резисторах одинаковое напряжение
Общий ток распределяется между резисторами
Общее сопротивление всегда меньше сопротивления наименьшего из резисторов

Формула для расчета общего сопротивления при параллельном соединении:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.

Онлайн-калькулятор для расчета сопротивления резисторов

Для удобства расчетов можно воспользоваться онлайн-калькулятором. Он позволяет быстро вычислить общее сопротивление при различных типах соединения резисторов.

Как пользоваться калькулятором:

Выберите тип соединения (последовательное или параллельное)
Введите значения сопротивлений отдельных резисторов
Нажмите кнопку «Рассчитать»
Получите результат расчета общего сопротивления

Калькулятор автоматически применяет нужную формулу в зависимости от выбранного типа соединения.

Преимущества и недостатки разных типов соединения

Каждый тип соединения имеет свои плюсы и минусы. Рассмотрим их:

Последовательное соединение:

Преимущества:

Позволяет получить большое общее сопротивление
Простота расчетов
Удобно для создания делителей напряжения

Недостатки:

При выходе из строя одного резистора размыкается вся цепь

Общий ток ограничен наименьшим сопротивлением

Параллельное соединение:

Преимущества:

Позволяет уменьшить общее сопротивление
Выход из строя одного резистора не нарушает работу остальных
Общий ток может быть больше, чем через каждый отдельный резистор

Недостатки:

Сложнее в расчетах
Требуется больше проводов для соединения

Практическое применение различных соединений резисторов

Знание особенностей соединения резисторов важно для практического применения в электронике. Рассмотрим несколько примеров использования:

Последовательное соединение:

Создание делителей напряжения
Ограничение тока в цепи
Получение нужного падения напряжения

Параллельное соединение:

Увеличение допустимой мощности рассеивания
Получение нестандартных номиналов сопротивлений
Создание токовых шунтов для измерительных приборов

Правильный выбор типа соединения резисторов позволяет оптимизировать работу электрической схемы и добиться нужных характеристик.

Расчет мощности при соединении резисторов

При соединении резисторов важно учитывать не только общее сопротивление, но и распределение мощности. Это позволяет избежать перегрева и выхода из строя компонентов.

Формулы для расчета мощности:

P = I^2 * R
P = U^2 / R

где P — мощность, I — ток, R — сопротивление, U — напряжение.

При последовательном соединении мощность распределяется пропорционально сопротивлению каждого резистора. При параллельном соединении мощность на каждом резисторе зависит от его сопротивления и общего напряжения.

Выбор номиналов резисторов для соединения

При проектировании электрических схем часто возникает необходимость получить определенное сопротивление, используя стандартные номиналы резисторов. Как правильно выбрать резисторы для соединения?

Определите требуемое общее сопротивление
Выберите тип соединения (последовательное или параллельное)
Подберите комбинацию стандартных номиналов, дающую нужное общее сопротивление
Проверьте расчеты с помощью онлайн-калькулятора
Учтите допуски и мощность выбранных резисторов

Правильный выбор номиналов и типа соединения позволяет оптимизировать схему и снизить стоимость компонентов.

Заключение

Понимание принципов соединения резисторов и умение правильно рассчитывать общее сопротивление — важные навыки для работы с электрическими схемами. Использование онлайн-калькуляторов значительно упрощает процесс расчетов и позволяет быстро подобрать нужную комбинацию резисторов.

Помните, что каждый тип соединения имеет свои особенности и область применения. Выбор оптимального варианта зависит от конкретной задачи и требований к схеме. Практика и опыт помогут вам эффективно использовать различные соединения резисторов в своих проектах.

О параллельном соединении резисторов: расчет подключения, определение мощности

Достаточно большое количество радиолюбителей занимается сборкой, модернизацией и ремонтом разнообразных схем; для кого-то это работа, а для кого-то просто увлечение или хобби. В любом случае необходимо иметь представление о процессах, происходящих в схеме, физических свойствах самих элементов цепи и особенностях взаимодействия элементов между собой.

Диагностика электронных схем

Компоненты электронных схем

Все множество компонентов и элементов делится на две основные группы:

Активные элементы, особенностью которых является возможность усиливать проходящий по ним сигнал. К такой группе, в первую очередь, относятся транзисторы и построенные на их основе схемы;
Пассивные элементы, которые не предназначены для усиления сигнала. Элементами, которые относятся к этой группе, являются резисторы, конденсаторы, катушки индуктивности, диоды и остальные аналоги данных компонентов.

Наиболее простым элементом по своим характеристикам и свойствам является резистор. Основное назначение резисторов заключается в ограничении величины тока, проходящего по нему. Все существующие резисторы подразделяются на два вида:

Постоянные – шунты, имеющие постоянное значение электрического сопротивления;
Переменные – шунты, сопротивление между контактами которого меняется механическим путем;

Центральными характеристиками резисторов являются:

Сила рассеивания, которая представляет собой максимальную мощность тока, выдерживаемую шунтом долгое время и рассеиваемую в виде тепла при постоянных характеристиках самого шунта;
Параметр точности представляет собой максимальное отступление от величины реального сопротивления в течение эксплуатации шунта;
Умение компонента противодействовать прохождению электротока в электрической цепи называется сопротивлением. Соответственно, с повышением сопротивления нарастает противостояние прохождению электротока.

Соединение резисторов

В радиотехнике встречается ряд конфигураций по состыковке компонентов в целом и шунтов в частности. Совмещение шунтов подразделяется на такие виды:

Набор параллельных резисторов;
Последовательное подключение шунтов;
Смешанное соединение резисторов.

Сопряжение резисторов

Последовательное соединение резисторов

Последовательным сопряжением компонентов называют такое сплочение нескольких шунтов, при котором каждый одиночный шунт подключается к следующему единичному шунту только в одной точке. Поскольку при последовательном включении по шунтам протекает одинаковый электрический ток, сталкивающийся постоянно с новой преградой в виде последующего сопротивления, то суммарное противодействие возрастает и равно сложению сопротивлений. Согласно картинке выше, при последовательном соединении суммарное последовательное сопротивление равно:

Rобщ=R1+R2, где:

Rобщ – суммарное противостояние цепи;
R1 – противодействие первого шунта;
R2 – противодействие второго шунта

Последовательное сопряжение шунтов

Напряжение при последовательном соединении компонентов понижается на любом отдельном элементе, опираясь на закон Ома, суммарное напряжение такого участка необходимо складывать. Соответственно, результирующий показатель напряжения возможно найти по выражению:

Uобщ=UR1+UR2, где:

Uобщ – суммарное напряжение участка;
UR1 – разность потенциалов на первом шунте;
UR2 – разность потенциалов на втором шунте.

Поскольку проходящий по компонентам электроток неизменный, то справедливо равенство:

Iобщ=IR1=IR2, где:

Iобщ – суммарная сила тока;
IR1 – электроток первого шунта;
IR2 – электроток второго шунта.

Дополнительная информация. При последовательной состыковке компонентов варьирование сопротивления любого элемента из этого участка влечет за собой как изменение сопротивления всего участка, так и изменение силы электротока этого участка.

Параллельное сопряжение резисторов

Параллельное соединение резисторов представляет собой такое соединение элементов, при котором резисторы подключаются друг к другу обоими выводами.

Дополнительная информация. В радиоэлектронике параллельные резисторы могут использоваться с целью снижения суммарного противодействия электротоку. Также мощность при параллельном стыковании компонентов возрастает сравнительно с каждым отдельным элементом.

При параллельном соединении шунтов через каждый единичный элемент потечет свой ток, и значение силы электротока будет обратно пропорционально сопротивлению компонента. Поскольку суммарная проводимость параллельного соединения возрастает, а общая сопротивляемость электротоку убывает, то, согласно закону Ома, общее сопротивление при параллельном соединении равняется:

Gобщ =1/Rобщ =1/R1+1/R2+1/R3;
Rобщ =1/Gобщ =R1R2R3/R1R2+R2R3+R1R3, где Gобщ – общая проводимость цепи.

Напряжение при параллельном соединении компонентов равняется разности потенциалов на каждом из компонентов:

Uобщ=UR1=UR2=UR3.

Направление токов в параллельной цепи

Калькулятор поможет определить суммарную силу тока цепи при параллельном совмещении, соответствующую сумме токов через каждый шунт:

Iобщ=IR1+IR2+IR3.

Смешанное соединение резисторов

Смешанное соединение резисторов представляет собой последовательное и параллельное соединение резисторов одновременно. Для определения суммарного противодействия цепи с разнотипной состыковкой шунтов требуется придерживаться последовательного алгоритма:

Схематически разделить цепь на отдельные участки, включающие в себя последовательное и параллельное соединение сопротивлений;
Рассчитать суммарный импеданс всех разделенных областей;
Представить первоначальную схему в виде сопротивлений, имеющих некоторую величину эквивалентного сопротивления;
Находите суммарное противодействие упрощенной схемы.

Понимание, что такое последовательное и параллельное соединение проводников, и поведения электрических характеристик при таком соединении позволит без особого труда проводить расчет, конструировать устройства различных конфигураций с требуемыми значениями параметров. Появится возможность упрощать и модернизировать схемы, вносить дополнительно какие-либо новшества в цепь.

Видео

Оцените статью:

Расчет параллельного соединения резисторов калькулятор онлайн

Параллельное соединение резисторов. Калькулятор для расчета

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

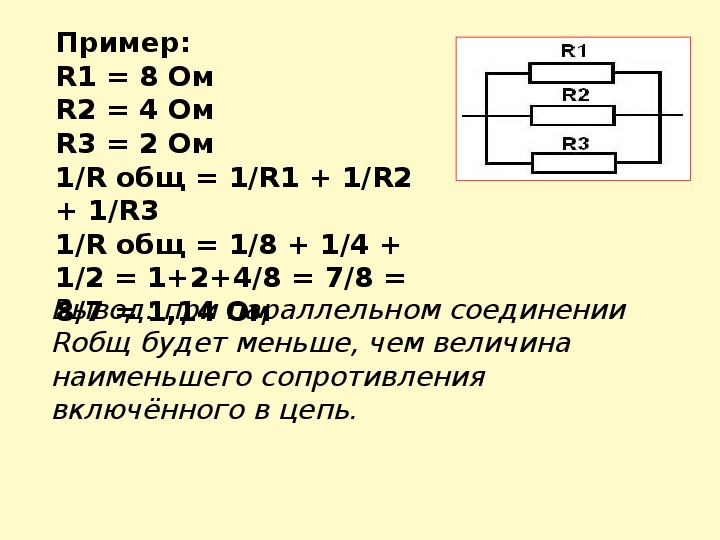
Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Калькулятор расчёта параллельного соединения резисторов

Вычислить сопротивление нескольких параллельно соединённых резисторов (до 10)

Впишите любое количество любых номиналов в омах и кликните мышкой в таблице.

Выбрать два имеющихся в наличии номинала E24 и получить результат их параллельного соединения

Если нужен номинал R и имеем резисторы стандарта E24 (+/-5%), тогда вписываем R и кликаем мышкой в таблице. Получим варианты параллельного соединения резисторов R₁ и R₂.

Ещё один калькулятор более точного подбора номинала из резисторов стандарта E48 (+/-2%).

Подбираем (меняем) нужный номинал из того что есть.

Калькуляторы могут быть полезны радиолюбителям-конструкторам, а так же ремонтникам РЭА при затруднении с выбором нужных номиналов резисторов для замены их в цепях электронных устройств.

Замечания и предложения принимаются и приветствуются!

Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:

Параллельное соединение резисторов

Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.

Для этого вам необходимо:

Указать в графе «количество резисторов» их число, в нашем примере их три;
После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
Далее нажмите кнопку «рассчитать» и в окошке «параллельное сопротивление в цепи» вы получите значение сопротивления в 10 Ом.

Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку «сбросить», чтобы обнулить значение параллельно включенных элементов калькулятора.

Для расчета суммарного сопротивления калькулятором используется такое соотношение:

R_сум — суммарное сопротивление параллельно соединенных элементов
R₁ — сопротивление первого резистора;
R₂ — сопротивление второго резистора;
R₃ — сопротивление третьего резистора;
R_n — сопротивление n-ого элемента.

Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:

Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:

Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.

Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах.

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

Параллельное соединение резисторов — онлайн калькулятор

Подведем итог

Конвертер величин

Калькулятор параллельных сопротивлений

Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов.

Пример. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно.

Введите величины сопротивлений в поля R₁, R₂ и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы сопротивления в миллиомах (мОм), омах (Ом), килоомах (кОм) или мегаомах (МОм) и нажмите кнопку Рассчитать.

1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.

Эквивалентное сопротивление R_eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.

Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:

Эта формула для R_eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:

Если параллельно соединены только два резистора, формула упрощается:

Если имеется n соединенных параллельно одинаковых резисторов R, то их эквивалентное сопротивление будет равно

Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.

Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.

При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Последовательное и параллельное соединение проводников, резисторов,

конденсаторов и катушек индуктивности. Онлайн расчёты.

«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »

«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью. »

Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо. », а заодно набросаю пару-тройку калькуляторов на заданную тему.

Итак.
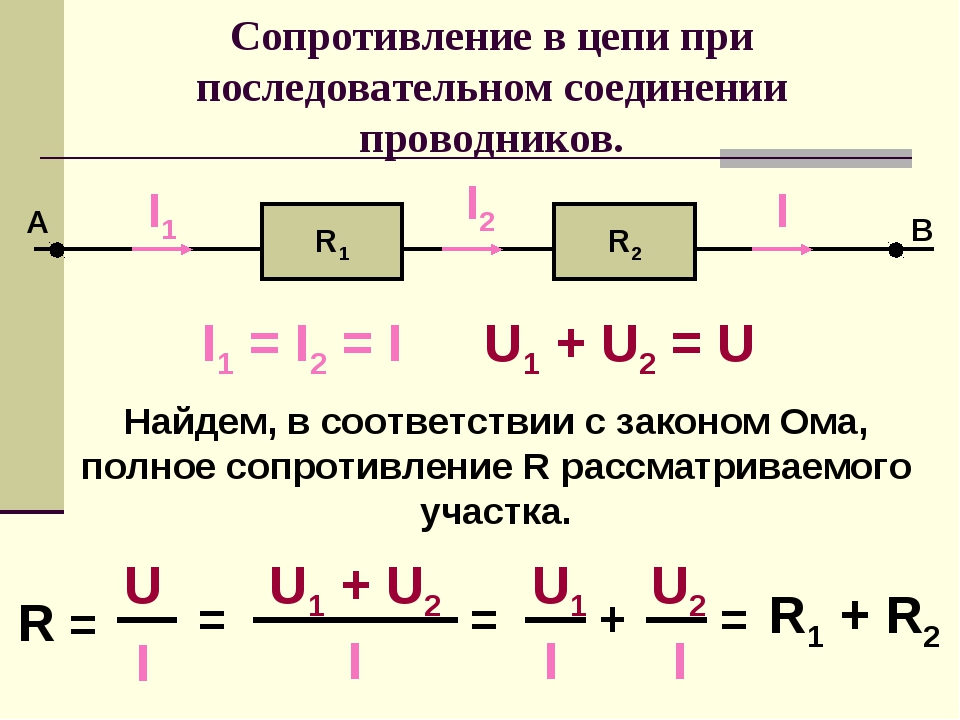
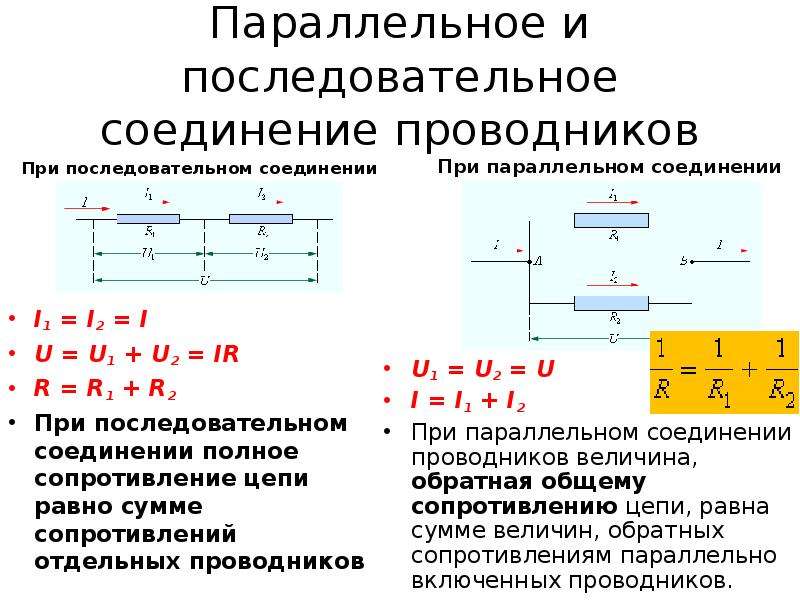
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.

Рис.1

Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить.
Короче, все вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников

Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.

Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.

Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:

С = С 1 + С 2 +. + С n и 1/L = 1/L 1 + 1/L 2 +. + 1/L n для параллельных цепей и
L = L 1 + L 2 +. + L n и 1/С = 1/С 1 + 1/С 2 +. + 1/С n для последовательных.

Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов

Ну и в завершении ещё одна таблица.

РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек

Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.

Расчет сопротивления параллельного соединения резисторов

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

Проводники (все металлы, ионизированный газ и электролитические растворы).
Полупроводники (Si, Ge, GaAs, InP и InSb).
Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

Температура окружающей среды и материала.
Электрические величины.
Геометрические свойства вещества.
Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
Визуально определить форму материала.
Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

Номинал резистора в 16 Ом подойдет.
Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

Ток не изменяется на участке цепи.
Общее напряжение равно сумме падений напряжений на каждом резисторе.
Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

I = I1 = I2 = 0,5 (А).
Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Расчет сопротивления резистора для светодиодов: онлайн-калькулятор

Светодиоды пришли на смену традиционным системам освещения – лампам накаливания и энергосберегающим лампам. Чтобы диод работал правильно и не перегорел, его нельзя подключать напрямую в питающую сеть. Дело в том, что он имеет низкое внутреннее сопротивление, потому если подключить его напрямую, то сила тока окажется высокой, и он перегорит. Ограничить силу тока можно резисторами. Но нужно подобрать правильный резистор для светодиода. Для этого проводятся специальные расчеты.

Расчет резистора для светодиода

Чтобы компенсировать сопротивление светодиода, нужно прежде всего подобрать резистор с более высоким сопротивлением. Такой расчет не составит труда для тех, кто знает, что такое закон Ома.

Математический расчет

Исходя из закона Ома, рассчитываем по такой формуле:

где Un – напряжение сети; Uvd – напряжение, на которое рассчитана работа светодиода; Ivd – ток.

Допустим, у нас светодиод с характеристиками:

2,1 -3, 4 вольт – рабочее напряжение (Uvd). Возьмем среднее значение 2, 8 вольт.

20 ампер – рабочий ток (Ivd)

220 вольт – напряжение сети (Un)

В таком случае мы получаем величину сопротивления R = 10, 86. Однако этих расчетов недостаточно. Резистор может перегреваться. Для предотвращения перегрева нужно учитывать при выборе его мощность, которая рассчитывается по следующей формуле:

Для наглядности рекомендуем посмотреть видео:

Графический расчет

Графический способ – менее популярный для расчета резистора на светодиод, но может быть даже более удобный. Зная напряжение и ток диода (их называют еще вольтамперными характеристиками – ВАХ), вы можете узнать сопротивление нужного резистора по графику, представленному ниже:

Тут изображен расчет для диода с номинальным током 20мА и напряжением источника питания 5 вольт. Проводя пунктирную линию от 20 мА до пересечения с «кривой led» (синий цвет), чертим пересекающую линию от прямой Uled до прямой и получаем максимальное значение тока около 50 мА. Далее рассчитываем сопротивление по формуле:

Получаем значение 100 Ом для резистора. Находим для него мощность рассеивания (Силу тока берем из Imax):

Онлайн-калькулятор расчета сопротивления

Задача усложняется, если вы хотите подключить не один, а несколько диодов.

Для облегчения самостоятельных расчетов мы подготовили онлайн-калькулятор расчета сопротивления резисторов. Если подключать несколько светодиодов, то нужно будет выбрать между параллельным и последовательным соединениями между ними. И для этих схем нужны дополнительные расчеты для источника питания. Можно их легко найти в интернете, но мы советуем воспользоваться нашим калькулятором.

Вам понадобится знать:

Напряжение источника питания.
Характеристику напряжения диода.
Характеристику тока диода.
Количество диодов.

А также нужно выбрать параллельную или последовательную схему подключения. Рекомендуем ознакомиться с разницей между соединениями в главах, которые мы подготовили ниже.

В каких случаях допускается подключение светодиода через резистор

Никакие диоды, в том числе светодиоды, нельзя включать без ограничения проходящего тока. Резисторы в таком случае просто необходимы. Даже небольшое изменения напряжения вызывают очень сильное изменение тока и, следовательно, перегрев диода.

Параллельное соединение

Для тех, кто уже сталкивался на практике со схемами подключения светодиодного освещения, вопрос о выборе между параллельным и последовательным соединением обычно не стоит. Чаще всего выбирают схему последовательного соединения. У параллельного соединения для светодиодов есть один важный недостаток – это удорожание и усложнение конструкции, потому что для каждого диода нужен отдельный резистор. Но такая схема имеет и большой плюс – если сгорела одна линия, то перестанет светить только один диод, остальные продолжат работу.

Почему нельзя использовать один резистор для нескольких параллельных диодов

Объясняется достаточно просто: если перегорит один светодиод, то на другой (-ие) может попасть больший ток и начнется перегрев. Потому при параллельной схеме подключения каждому диоду нужен отдельный резистор.

Последовательное соединение светодиодов

Именно такое соединение пользуется популярностью. Объясняется такой частый выбор простым примером. Представьте, что в елочной гирлянде для каждого светодиода подобран резистор. А в гирлянде этих лампочек бывает более сотни! Параллельное соединение в данном случае невыгодно и трудоемко.

Можно ли обойтись без резисторов

В бюджетных или просто старых приборах используются резисторы. Также они используются для подключения всего только нескольких светодиодов.

Но есть более современный способ – это понижение тока через светодиодный драйвер. Так, в светильниках в 90% встречаются именно драйверы. Это специальные блоки, которые через схему преобразуют характеристики тока и напряжения питающей сети. Главное их достоинство – они обеспечивают стабильную силу тока при изменении/колебании входного напряжения.

Сегодня можно подобрать драйвер под любое количество светодиодов. Но рекомендуем не брать китайские аналоги! Кроме того, что они быстрей изнашиваются, ещё могут выдавать не те характеристики в работе, которые заявлены на упаковке.

Если светодиодов не так много, подойдут и резисторы вместо достаточно высокого по цене драйвера.

Интересное видео по теме:

В заключение

Пишите комментарии и делитесь статьей в социальных сетях! Если возникли вопросы, можно найти в интернете дополнительные видео для расчета сопротивления резистора и на другие близкие темы.

Применение последовательного и параллельного соединения проводников. Сопротивление последовательное и параллельное соединение, соединения проводников

Содержание:

Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.

Напряжение при последовательном соединении

При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.

Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .

Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.

Напряжение при параллельном соединении

При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.

Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.

На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.

В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.

Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.

Gif?x15027″ alt=»Общий вид»>

Общий вид

Особенности включения

Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.

Для такого включения типичны следующие особенности:

Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.

В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.

Расчёт

Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).

Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:

I= U/R (одного из резисторов).

После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.

Типичные подключения

Пример №1

Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление. При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).

Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.

Из неё следует:

16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.

Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.

Пример №2

В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.

Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.

Gif?x15027″ alt=»Пример»>

В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:

1/R = 1/200+1/220+1/470 = 0,0117;

R=1/0,0117 = 85,67Ом.

В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.

Важно! Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.

Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.

Расчёт комбинированных схем

Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.

Gif?x15027″ alt=»Смешанная схема»>

Смешанная схема

Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.

Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.

В предыдущем конспекте был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R . Этот закон, установленный экспериментально, называется закон Ома (для участка цепи).

Закон Ома для участка цепи : сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника. Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).

Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи.

Д ва основных типа соединения проводников : последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.

Последовательное соединение проводников

При последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец — с началом третьего и т.д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.

Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: I 1 = I 2 = I .

Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений : R 1 + R 2 = R

. Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.

По закону Ома напряжение на каждом проводнике равно: U 1 = I* R 1 , U 2 = I*R 2 . В таком случае общее напряжение равно U = I ( R 1 + R 2) . Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике : U = U 1 + U 2 .

Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.

Для последовательного соединения проводников справедливы законы :

1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.

Параллельное соединение проводников

Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.

При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U .

При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I = I 1 + I 2 .

В соответствии с законом Ома I = U/R, I 1 = U 1 /R 1 , I 2 = U 2 /R 2 . Отсюда следует: U/R = U 1 /R 1 + U 2 /R 2 , U = U 1 = U 2 , 1/R = 1/R 1 + 1/R 2 Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.

При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г , то их общее сопротивление равно: R = г/2 . Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.

Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.

Для параллельного соединения проводников справедливы законы:

1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.

Сопротивление проводников. Параллельное и последовательное соединение проводников.

Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.

Сопротивление (часто обозначается буквой R или r ) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как

R — сопротивление;

U — разность электрических потенциалов (напряжение) на концах проводника;

I — сила тока, протекающего между концами проводника под действием разности потенциалов.

При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

По закону Ома, напряжения U 1 и U 2 на проводниках равны

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении (рис. 1.9.2) напряжения U 1 и U 2 на обоих проводниках одинаковы:

Этот результат следует из того, что в точках разветвления токов (узлы A и B ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд I Δt , а утекает от узла за то же время заряд I 1 Δt + I 2 Δt . Следовательно,I = I 1 + I 2 .

Записывая на основании закона Ома

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.

Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.

Последовательное соединение

Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.

При последовательном соединении сопротивления элементов суммируются.

Параллельное соединение

Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.

При параллельном соединении эквивалентное сопротивление находится как:

В случае двух параллельно соединенных резисторов

В случае трех параллельно подключенных резисторов:

Смешанное соединение

Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.

Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.

Итак, остается самое интересное и самое сложное соединение проводников.

Мостовая схема

Мостовая схема соединения представлена на рисунке ниже.

Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.

И находят сопротивления R 1 , R 2 и R 3 .

Мощность резисторов при последовательном и параллельном соединении

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Вычисление сопротивления и мощности при параллельном и последовательном соединении резисторов. (10+)

Расчет параллельно / последовательно соединенных резисторов, конденсаторов и дросселей

Параллельное или последовательное соединение (включение) применяется обычно в нескольких случаях. Во-первых, если нет резистора номинала. Во-вторых, если есть потребность получить резистор большей мощности. В-третьих, Если необходимо точно подобрать номинал детали, а устанавливать подстроечник нецелесообразно из соображений надежности. Большинство радиодеталей имеют допуски. Чтобы их компенсировать, например для резистора, последовательно с большим резистором устанавливают меньший в разы. Подбор этого меньшего резистора позволяет получить точно нужное значение сопротивления.

Вашему вниманию подборка материалов:

Практика проектирования электронных схем Искусство разработки устройств. Элементная база. Типовые схемы. Примеры готовых устройств. Подробные описания. Онлайн расчет. Возможность задать вопрос авторам

Ознакомьтесь также с:

Резисторы

Соединяем последовательно

[Сопротивление последовательно соединенных резисторов, кОм] = [Сопротивление первого резистора, кОм] + [Сопротивление второго резистора, кОм]

[Мощность, рассеиваемая первым резистором, Вт] = [Сопротивление первого резистора, кОм] * [Сила тока, мА] ^ 2 / 1000

[Мощность, рассеиваемая вторым резистором, Вт] = [Сопротивление второго резистора, кОм] * [Сила тока, мА] ^ 2 / 1000

Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 1 кОм, 4 Вт. 2 / [Сопротивление первого резистора, кОм] / 1000

Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 250 Ом, 4 Вт.

К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.

Практика проектирования электронных схем. Самоучитель электроники.
Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы.

Применение тиристоров (динисторов, тринисторов, симисторов). Схемы. Ис.
Тиристоры в электронных схемах. Тонкости и особенности использования. Виды тирис.

Биполярный транзистор. Принцип работы. Применение. Типы, виды, категор.
Все о биполярном транзисторе. Принцип работы. Применение в схемах. Свойства. Кла.

Плавная регулировка яркости свечения люминесцентных ламп дневного свет.
Схема драйвера для плавной регулировки яркости свечения ламп дневного света. Дра.

Проверка электронных элементов, радиодеталей. Проверить исправность, р.
Как проверить исправность детали. Методика испытаний. Какие детали можно использ.

RC — цепь. Резисторно — конденсаторная схема. Резистор, конденсатор. И.
Расчет RC — цепи, изменения напряжения на конденсаторе в зависимости от времени.

Силовой резонансный фильтр для получения синусоиды от инвертора.
Для получения синусоиды от инвертора нами был применен самодельный силовой резон.

Соединение резисторов разными способами позволяет получить необходимую величину сопротивления и мощности рассеивания одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное.

Последовательное соединение резисторов

Последовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются.
Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм и мощность рассеивания P = 0,25 Вт.

Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм.

Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт.

Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры:
Rобщ = 4 кОм; Pобщи = 1 Вт.

В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока.

Параллельное соединение резисторов

При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.

Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах [См] и обозначается большей латинской буквой G.

G = 1/R = 1/Ом = См

Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.

Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:

Если R1 = R2 = R3 = R4 = R , то

Rобщ = R/4.

Например, каждый из четырех резисторов имеет R = 10 кОм, тогда

Rобщ = 10 кОм/4 = 2,5 кОм.

Мощности рассеивания суммируются также, как и при последовательном соединении.

Смешанное соединение резисторов

Смешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, конденсаторов, диодов, транзисторов и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.

Общее (эквивалентное) сопротивление находится методом «сворачивания» схемы. Сначала определяется общее сопротивление одного отдельного соединения, затем последующего и так далее.

Теперь самостоятельно подсчитайте общее сопротивления схемы, приведенной ниже.

Параллельное соединение резисторов. Калькулятор для расчета

Что такое параллельное соединение резисторов, а также последовательное и смешанное. Что необходимо учитывать при подключении таких элементов. Формулы расчета мощности тока и сопротивления.

Свойства и технические характеристики резисторов

Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное.

На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.

Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.

Для соединения резисторов в схемах используются три разных способа подключения – параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Источник: http://electric-220.ru/news/moshhnost_pri_parallelnom_i_posledovatelnom_soedinenii_rezistorov/2016-10-31-1102

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

С правого края – правый.
С левого края – левый.

Источник: http://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html

Последовательное соединение[править | править код]

При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I = I 1 = I 2 = ⋯ = I n {displaystyle Imathrm {=} I_{1}=I_{2}=cdots =I_{n}} (так как сила тока определяется количеством электронов, проходящих через поперечное сечение проводника, и если в цепи нет узлов, то все электроны в ней будут течь по одному проводнику).

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника питания, равно сумме напряжений на отдельных участках цепи: U = U 1 + U 2 + ⋯ + U n {displaystyle Umathrm {=} U_{1}+U_{2}+cdots +U_{n}} .

Резисторы[править | править код]

Несколько резисторов, соединённых последовательно.

R = R 1 + R 2 + ⋯ + R n {displaystyle R=R_{1}+R_{2}+cdots +R_{n}}

Катушка индуктивности[править | править код]

L = L 1 + L 2 + ⋯ + L n {displaystyle L=L_{1}+L_{2}+cdots +L_{n}}

Электрический конденсатор[править | править код]

1 C = 1 C 1 + 1 C 2 + ⋯ + 1 C n {displaystyle {frac {1}{C}}={frac {1}{C_{1}}}+{frac {1}{C_{2}}}+cdots +{frac {1}{C_{n}}}} .

Мемристоры[править | править код]

M = M 1 + M 2 + ⋯ + M n {displaystyle M=M_{1}+M_{2}+cdots +M_{n}}

Выключатели[править | править код]

Цепь замкнута, когда замкнуты все выключатели. Цепь разомкнута, когда разомкнут хотя бы один выключатель. (См.также Логическая операция И).

Источник: http://ru.wikipedia.org/wiki/Последовательное_и_параллельное_соединение

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Источник: http://joyta.ru/7362-parallelnoe-soedinenie-rezistorov/

Понятие параллельного подключения резисторов

При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.

Источник: http://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html

Изображение резисторов на схемах

По стандарту резисторы изображаются прямоугольником с размерами 10 х 4 мм и обозначаются буквой R. Часто указывается мощность резисторов на схеме. Изображение этого показателя выполняется косыми или прямыми чёрточками. Если мощность более 2 Ватт, то обозначение производится римскими цифрами. Обычно это делается для проволочных резисторов. В некоторых государствах, например в США, применяются другие условные обозначения. Для облегчения ремонта и анализа схемы часто приводится мощность резисторов, обозначение которых выполняется по ГОСТ 2.728-74.

Источник: http://fb.ru/article/234301/kak-opredelit-moschnost-rezistorov-moschnost-rezistorov-pri-parallelnom-soedinenii

Параллельное соединение резисторов

> Теория > Параллельное соединение резисторов

Диагностика электронных схем

Компоненты электронных схем

Все множество компонентов и элементов делится на две основные группы:

Активные элементы, особенностью которых является возможность усиливать проходящий по ним сигнал. К такой группе, в первую очередь, относятся транзисторы и построенные на их основе схемы;
Пассивные элементы, которые не предназначены для усиления сигнала. Элементами, которые относятся к этой группе, являются резисторы, конденсаторы, катушки индуктивности, диоды и остальные аналоги данных компонентов.

Постоянные – шунты, имеющие постоянное значение электрического сопротивления;
Переменные – шунты, сопротивление между контактами которого меняется механическим путем;

Центральными характеристиками резисторов являются:

Сила рассеивания, которая представляет собой максимальную мощность тока, выдерживаемую шунтом долгое время и рассеиваемую в виде тепла при постоянных характеристиках самого шунта;
Параметр точности представляет собой максимальное отступление от величины реального сопротивления в течение эксплуатации шунта;
Умение компонента противодействовать прохождению электротока в электрической цепи называется сопротивлением. Соответственно, с повышением сопротивления нарастает противостояние прохождению электротока.

Соединение резисторов

Параллельное соединение резисторов

Набор параллельных резисторов;
Последовательное подключение шунтов;
Смешанное соединение резисторов.

Последовательное соединение резисторов

Rобщ=R1+R2, где:

Rобщ – суммарное противостояние цепи;
R1 – противодействие первого шунта;
R2 – противодействие второго шунта

Последовательное сопряжение шунтов

Uобщ=UR1+UR2, где:

Uобщ – суммарное напряжение участка;
UR1 – разность потенциалов на первом шунте;
UR2 – разность потенциалов на втором шунте.

Поскольку проходящий по компонентам электроток неизменный, то справедливо равенство:

Iобщ=IR1=IR2, где:

Iобщ – суммарная сила тока;
IR1 – электроток первого шунта;
IR2 – электроток второго шунта.

Параллельное сопряжение резисторов

Gобщ =1/Rобщ =1/R1+1/R2+1/R3;
Rобщ =1/Gобщ =R1R2R3/R1R2+R2R3+R1R3, где Gобщ – общая проводимость цепи.

Uобщ=UR1=UR2=UR3.

Направление токов в параллельной цепи

Iобщ=IR1+IR2+IR3.

Смешанное соединение резисторов

Схематически разделить цепь на отдельные участки, включающие в себя последовательное и параллельное соединение сопротивлений;
Рассчитать суммарный импеданс всех разделенных областей;
Представить первоначальную схему в виде сопротивлений, имеющих некоторую величину эквивалентного сопротивления;
Находите суммарное противодействие упрощенной схемы.

Источник: https://elquanta.ru/teoriya/parallelnoe-soedinenie-rezistorov-2.html

Источник: http://ugstroialyans.ru/summarnaya-moschnost-pri-parallelnom-soedinenii/

Мощность при последовательном соединение

При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I2 x R = 0,2562 x 390 = 25,55 Вт.

Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:

P1 = I2 x R1 = 0,2562 x 200 = 13,11 Вт;
P2 = I2 x R2 = 0,2562 x 100 = 6,55 Вт;
P3 = I2 x R3 = 0,2562 x 51 = 3,34 Вт;
P4 = I2 x R4 = 0,2562 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.

Источник: http://electric-220.ru/news/moshhnost_pri_parallelnom_i_posledovatelnom_soedinenii_rezistorov/2016-10-31-1102

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

Источник: http://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html

Что ещё нужно учитывать при подключении резисторов

Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.

При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.

Источник: http://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html

Типы проводников

Проводники (все металлы, ионизированный газ и электролитические растворы).
Полупроводники (Si, Ge, GaAs, InP и InSb).
Непроводники (диэлектрики или изоляторы).

Источник: http://morflot.su/raschet-moshhnosti-pri-parallelnom-soedinenii/

Чему равна сила тока в цепи при параллельном соединении резисторов

Согласно правилу Кирхгофа ток, поступающий в узел, равен току, выходящему из узла, – величина тока до группы параллельных резисторов и после нее должна быть неизменной.

Ток в группе параллельных резисторов распределяется по цепи в зависимости от их номинала, после прохождения через сопротивления суммируется в узле и выходит из него неизменным I = I1+I2+I3+…+In.

Источник: http://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html

Мощность при параллельном и последовательном соединении резисторов

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

Источник: http://usbravo.ru/kak-vychislit-moshchnost-pri-parallel-nom-soyedinenii/

Последовательное и параллельное соединение резисторов

Последовательное и параллельное соединение резисторов в схемах являются самыми распространенными, также – это база для расчета более сложных схем.

Последовательное подключение

Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше.

Рис. Последовательное подключение.

Обозначение:

Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим. Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях – складываем, в параллельных – это обратно пропорциональная величина.

Параллельное соединение

Рис. Параллельное подключение.

Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах – //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле.
Более наглядно это можно представить в виде формул:
1. Каждый вид соединения находится под одинаковым напряжением:
U = U1 = U2;
2. Суммарная сила тока равняется суммарному значению тока каждого участка
I = I1 + I2;
3. Сопротивление цепи равно сумме величина обратных сопротивлению участка:
1/R = 1/R1 + 17R2 + . . . + 1/Rn;
4. Сила тока пропорциональна сопротивлению каждого участка
I1/I2=R2/R1.
Далее рассмотрим схему как работает не только последовательное параллельное, но и смешанное соединение резисторов.

Смешанное подключение

Рис. Смешанное подключение резисторов

В электрических схемах используются не только типовые схемы, но и смешанное, созданное из критерий определенных требований. Чаще всего в схемах встречается третий вариант, представляющий набор из элементарных типов схем. В смешанных участках учитываются не только элементы, но и направления движения тока.
При вычислении мощности резисторов смешанного подключения используются формулы для параллельного и последовательного соединения резисторов, формула также является составной.

Основные законы электротехники, наиболее часто используемые для расчетов

Рассмотрим основные законы электротехники и свойства последовательного и параллельного соединения резисторов для участка цепи

Закон Ома

Напряжение находится по закону Ома по формуле I=U/R – чем больше сопротивление, тем меньше ток. Напряжение можно найти из этой же формулы. U=R*I, ток умножается на сопротивление. Запишем эту формулу для каждого участка U1=R1· I1, Un=Rn · In.

Законы Кирхгофа

Первый закон

Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два.

Рис. иллюстрация к пояснению действия первого закона Кирхгофа.

Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю.
Если посмотреть на схему, I1 – это ток, который заходит в узел, I2 и I3 – это электроны, которые вытекают из него.
Применяя формулировку первого закона можно записать формулу по-другому:
I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.

Второй закон Кирхгофа.

Рис. иллюстрация к пояснению действия второго закона Кирхгофа.

Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре.
E1- Е2 = – UR1 – UR2 или E1 = Е2 – UR1 – UR2.

Параллельное и последовательное соединение резисторов, решение задач

Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно.

Рис. Порядок замещения при расчете сложных позиций более простыми.

Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. Рассмотрим схему №1 на рис.
На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?

Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.

Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.
Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше (рис 3).

Теперь образовалась ситуация – включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех.

Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.
Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.

Схема с подключением сопротивлений «треугольником»

Рис. Расчетная схема соединения резисторов в треугольник.

Иногда некоторые затруднения возникают при разборе схемы соединения в треугольник.

Рассмотрим на примере рисунка расчет резисторов по этому подключению.
Из схемы видно, что R1 и R2 соединены последовательно Rэ12 будет соединяться R3 последовательно.

Затем Rэ123 соединяется с сопротивлением R4, R5 в последовательную цепь. Затем все это объединяется с Rэ в //.

Проведем несложные вычисления учитывая, что
R1, R2, R4, R5 равняется 1 Ом. R3, R7 – 2 Ом.
RЭ1,2 = R1+R2 = 1+1=2 Ом.

Вычисляем параллельное подключение: Rэ 12 с R3. Rэ1,3 = (Rэ12*R3) /(Rэ12+R3) = (2*2) /(2+2) = 1Ом.

Далее мы видим последовательное: RЭ123 + R4 + R5 = 1+1+1 = 3 Ом.
И последнее – Rэ123 4 5 с R6 – параллельное.

Общее сопротивление цепи Rц = Rоб = (RЭ1,2,3,4,5 *R6) /(RЭ1,2,3,4,5+R6) = (3 * 2) / (3+2) = 1,2 Ом. Как видно, что расчет подобного варианта также не сложный.

Расчет последовательного и параллельного подключения резисторов онлайн

Подсчитать значение мощность и сопротивлений подставляя их в формулы можно только в учебных целях, или, когда объемы не очень большие. Наиболее практичный вариант расчета является онлайн калькуляторы, которые расположены на многочисленных интернет ресурсах. Для расчёта любой сложности нужно правильно определить тип соединения резисторов последовательное или параллельное и внести данные для расчета в поля калькулятора.

Также такая форма расчета подойдет и для проверки результатов решения учебных задач.

Последовательное и параллельное соединение резисторов и конденсаторов

Электрические цепи состоят не только из резисторов, в них применяется большое количество различных деталей, например, конденсатор, которые подключаются в последовательное, // и смешанное соединение.

Рис. Замещения последовательно включенных элементов.

Определение этому элементу можно дать следующее: Конденсатор – это совокупность проводящих тел служащий для накопления электрического заряда.
Элементарный конденсатор имеет две пластины, форма этих пластин может быть различной: сферической, круглой, цилиндрической, прямоугольной – по форме пластин разделяется и тип конденсатора.

Важное свойство. Одно из важных свойств конденсатора: если заряжается одна пластина конденсатора, то благодаря явлению электростатической индукции заряжается и вторая половина, но с противоположным знаком.

Устройство конденсатора

Плоский конденсатор состоит из двух плоских пластин отстоящих друг от друга на маленькое расстояние. У конденсатора к двум пластинам припаивается вывод всего их получается два.

Типовые схемы подключения конденсаторов

Рассмотрим различные виды подключения конденсатора.

Последовательное

Первый вид — это последовательное соединение.
Предположим, что емкость этих конденсаторов будут равны. Тогда заряды также будут равны: q1=q2=q3, как и в примере с резисторами, сложный тип позиций с конденсатором можно упростить, заменив несколько элементов одним. У элементов соединенных друг за другом, общая емкость будет обратно пропорциональная всем имеющимся элементам. То есть: Rэк будет равняться 1/С1 + 1/С2 +…. 1/Сn/
Напряжение складывается, U эк = U1 + U2+ … Un.

Параллельное

Второй тип подключения конденсаторов – это соединение в паралель

Рис. Схема замещения элементов, включенных в параллель.

Соответственно эти конденсаторов обозначены C1, C2, … Cn заряды: Q1, Q2, … Qn и напряжение: U1, U2, … Un.

У элементов в // емкость складывается Сэ = C1 + C2 + … C n.
Напряжение Un на каждом конденсаторе будет равно напряжению на эквивалентном
Uэ = U1 = U2 =… = Un – это особенность параллельного подсоединения всех элементов цепи.

Емкость будет складываться из суммы отдельных элементов Сэ =С1 + С2 + … Сп.

Рис. Расчетные позиции элементов при различном включении.

Простая позиция, которая не требует преобразования №1 – последовательное подключение. По известной формуле для этих поз. запишем 1/Сэ = 1/С1 +1/С2 +1/С3, подставив формулу значения, которые даны в условии задачи, получим 1/Сэ = 1/С1 +1/С2 +1/С3 = 59 мФ.

Не требует преобразования и 2 схема: емкость общего конденсатора будет равняться сумме конденсаторов которые включены в параллельной цепи: Сэ =С1 +С2 +С3
Сэ = 100 + 200 + 500 = 800 мФ.

Рассмотрев рис. №3 видно, что пара конденсаторов включена параллельно и один последовательно. Алгоритм преобразования таких цепей мы уже рассматривали, поэтому: сразу же находим емкость конденсатора Сэ соединения: Сэ = С1+С2 = 200+500 = 700 мФ.

Теперь находим общие эквивалентную емкость элементов с последовательным подключением 1/Сэ = 1/С2,3 +1/ С1 = 89 мф.
Практическая задача решена.

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:

+7(499)403 39 91

Доставка подшипников по РФ и зарубежью.

Каталог подшипников на сайте themechanic.ru

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 128 22 34
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 646 00 12
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

Калькулятор онлайн для параллельного соединения резисторов: общие сведения, формулы расчета

Параллельное соединение резисторов. Калькулятор для расчета

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Как рассчитать сложные схемы соединения резисторов

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Таким образом, протекающий общий ток в цепи можно определить как:

I = I1 + I2

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

Параллельное соединение резисторов — онлайн калькулятор

Подведем итог

Источник: http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/

Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях — Help for engineer | Cхемы, принцип действия, формулы и расчет

Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений.

Состоит он из двух и более элементов (резисторов, реактивных сопротивлений). Элементарный делитель можно представить как два участка цепи, называемые плечами.

Участок между положительным напряжением и нулевой точкой – верхнее плечо, между нулевой и минусом – нижнее плечо.

Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений. Применяется для низкого напряжения и не предназначен для питания мощных машин. Простейший делитель состоит из двух последовательно соединенных резисторов:

На резистивный делитель напряжения подается напряжение питающей сети U, на каждом из сопротивлений R1 и R2 происходит падение напряжения. Сумма U1 и U2 и будет равна значению U.

В соответствии с законом Ома (1):

Падение напряжения будет прямо пропорционально значению сопротивления и величине тока. Согласно первому закону Кирхгофа, величина тока, протекающего через сопротивления одинакова. С чего следует, что падение напряжения на каждом резисторе (2,3):

Тогда напряжение на всем участке цепи (4):

Отсюда определим, чему равно значение тока без включения нагрузки (5):

Если подставить данное выражение в (2 и 3), то получим формулы расчета падения напряжения для делителя напряжения на резисторах (6, 7):

Необходимо упомянуть, что значения сопротивлений делителя должны быть на порядок или два (все зависит от требуемой точности питания) меньше, чем сопротивление нагрузки. Если же это условие не выполняется, то при приведенном расчете подаваемое напряжение будет посчитано очень грубо.

Для повышения точности необходимо сопротивление нагрузки принять как параллельно подсоединенный резистор к делителю. А также использовать прецизионные (высокоточные) сопротивления.

Пусть источник питания выдает 24 В постоянного напряжения, примем, что величина сопротивления нагрузки переменная, но минимальное значение равно 15 кОм. Необходимо рассчитать параметры резисторов для делителя, выходное напряжение которого равно 6 В.

Таким образом, напряжения: U=24 B, U2=6 В; сопротивление резисторов не должно превышать 1,5 кОм (в десять раз меньше значения нагрузки). Принимаем R1=1000 Ом, тогда используя формулу (7) получим:

выразим отсюда R2:

Зная величины сопротивления обоих резисторов, найдем падение напряжения на первом плече (6):

Ток, который протекает через делитель, находится по формуле (5):

Схема делителя напряжения на резисторах рассчитана выше и промоделирована:

Использование делителя напряжения очень неэкономичный, затратный способ понижения величины напряжения, так как неиспользуемая энергия рассеивается на сопротивлении (превращается в тепловую энергию). КПД очень низкий, а потери мощности на резисторах вычисляются формулами (8,9):

По заданным условиям, для реализации схемы делителя напряжения необходимы два резистора:

1. R1=1 кОм, P1=0,324 Вт.

2. R2=333,3 Ом, P2=0,108 Вт.

Полная мощность, которая потеряется:

Делитель напряжения на конденсаторах применяется в схемах высокого переменного напряжения, в данном случае имеет место реактивное сопротивление.

Сопротивление конденсатора рассчитывается по формуле (10):

где С – ёмкость конденсатора, Ф;

f – частота сети, Гц.

Исходя из формулы (10), видно, что сопротивление конденсатора зависит от двух параметров: С и f. Чем больше ёмкость конденсатора, тем сопротивление его ниже (обратная пропорциональность). Для ёмкостного делителя расчет имеет такой вид (11, 12):

Еще один делитель напряжения на реактивных элементах – индуктивный, который нашел применение в измерительной технике. Сопротивление индуктивного элемента при переменном напряжении прямо пропорционально величине индуктивности (13):

где L – индуктивность, Гн.

Падение напряжения на индуктивностях (14,15):

Источник: https://h5e.ru/komplektuyushchie/117

Расчет резистора для светодиода, калькулятор расчёта сопротивления

Светодиод имеет очень небольшое внутреннее сопротивление, если его подключить напрямую к блоку питания, то сила тока будет достаточной высокой, чтобы он сгорел.

Медные или золотые нити, которыми кристалл подключается к внешним выводам, могут выдерживать небольшие скачки, но при сильном превышении перегорают и питание прекращает поступать на кристалл.

Онлайн расчёт резистора для светодиода производится на основе его номинальной рабочей силы тока.

Онлайн калькулятор

Онлайн калькулятор покажет вам точное сопротивление в Омах. Как правило окажется, что резисторы с таким номиналом не выпускаются, и вам будет показан ближайший стандартный номинал. Если не удаётся сделать точный подбор сопротивления, то используйте больший номинал.

Подходящий номинал можно сделать подключая сопротивление параллельно или последовательно. Расчет сопротивления для светодиода можно не делать, если использовать мощный переменный или подстроечный резистор. Наиболее распространены типа 3296 на 0,5W.

При использовании питания на 12В, последовательно можно подключить до 3 LED.

Резисторы бывают разного класса точности, 10%, 5%, 1%. То есть их сопротивление может погрешность в этих пределах в положительную или отрицательную сторону.

Чтобы определить полярность можно подать небольшое напряжение или использовать функцию проверки диодов на мультиметре. Отличается от режима измерения сопротивления, обычно подаётся от 2В до 3В.

Основные параметры

Отличие характеристик кристаллов для дешевых ЛЕД

Так же при расчёте светодиодов следует учитывать разброс параметров, для дешевых они будут максимальны, для дорогих они будут более одинаковыми. Чтобы проверить этот параметр, необходимо включить их в равных условиях, то есть последовательно.

Уменьшая тока или напряжение снизить яркость до слегка светящихся точек. Визуально вы сможете оценить, некоторые будут светится ярче, другие тускло. Чем равномернее они горят, тем меньше разброс.

Калькулятор расчёта резистора для светодиода подразумевает, что характеристики светодиодных чипов идеальные, то есть отличие равно нулю.

Напряжение падения для распространенных моделей маломощных до 10W может быть от 2В до 12В. С ростом мощности увеличивается количество кристаллов в COB диоде, на каждом есть падение. Кристаллы включаются цепочками последовательно, затем они объединяются в параллельные цепи. На мощностях от 10W до 100W снижение растёт с 12В до 36В.

Этот параметр должен быть указан в технических характеристиках LED чипа и зависит от назначения:

цвета синий, красный, зелёный, желтый;
трёхцветный RGB;
четырёхцветный RGBW;
двухцветный, теплый и холодный белый.

Особенности дешёвых ЛЕД

Прежде чем подобрать резистор для светодиода на онлайн калькуляторе, следует убедится в параметрах диодов. Китайцы на Aliexpress продают множество led, выдавая их за фирменные. Наиболее популярны модели SMD3014, SMD 3528, SMD2835, SMD 5050, SMD5630, SMD5730. Всё самое плохое обычно делается под брендом Epistar.

Например, чаще всего китайцы обманывают на SMD5630 и SMD5730. Цифры в маркировке обозначают лишь размер корпуса 5,6мм на 3,0мм.

В фирменных такой большой корпус используется для установки мощных кристаллов на 0,5W , поэтому у покупателей диодов СМД5630 напрямую ассоциируется с мощностью 0,5W.

Хитрый китаец этим пользуется, и в корпус 5630 устанавливает дешевый и слабенький кристалл в среднем на 0,1W , при этом указывая потребление энергии 0,5W.

Китайские светодиодные лампы кукурузы

Наглядным примером будут автомобильные лампы и светодиодные кукурузы, в которых поставлено большое количество слабеньких и некачественных ЛЕД чипов. Обычный покупатель считает, чем больше светодиодов чем лучше светит и выше мощность.

Автомобильные лампы на самых слабых лед 0,1W

Чтобы сэкономить денежку, мои светодиодные коллеги ищут приличные ЛЕД на Aliexpress. Ищут хорошего продавца, который обещает определённые параметры, заказывают , ждут доставку месяц.

После тестов оказывается, что китайский продавец обманул, продал барахло. Повезёт, если на седьмой раз придут приличные диоды, а не барахло.

Обычно сделают 5 заказов, и не добившись результата и идут делать заказ в отечественный магазин, который может сделать обмен.

Источник: http://led-obzor.ru/raschet-rezistora-dlya-svetodioda-kalkulyator

Параллельное и последовательное соединение сопротивлений

Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил.

Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой.

Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение.

Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.

Способы подключения и их особенности

Внешний вид резисторов и обозначения в схемах

Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.

Последовательное соединение

Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего.

Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом.

Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений.

При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.

Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.

Схема последовательного соединения резисторов

Параллельное соединение

Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.

Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом.

В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления.

Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.

Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.

Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.

Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас.

При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе.

При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.

Параллельное соединение резисторов

Последовательно-параллельное соединение

Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.

Подведем итог

Подводя итог всему вышеизложенному можно сделать следующие выводы:

При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.

В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки.

По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники.

А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.

Источник: https://domelectrik.ru/baza/teoriya/rezistory-na-skheme

Последовательное и параллельное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление Rобщ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление Rобщ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление Rобщ

Для того чтобы посчитать общее сопротивление смешанного соединения:

Цепь разбивают на участки с только пареллельным или только последовательным соединением.
Вычисляют общее сопротивление для каждого отдельного участка.
Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

Если резисторы соединяются последоватеьно — складывать.
Если резисторы соединяются параллельно — использовать условное обозначение «||».
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

Ссылки по теме:

Источник: http://hightolow.ru/resistor3.php

Последовательное и параллельное соединение проводников, резисторов,конденсаторов и катушек индуктивности. Онлайн расчёт

«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская? — Ну, Света наверное.

— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! » «- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме? — С Божьей помощью, батюшка! С Божьей помощью…

» Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно набросаю пару-тройку калькуляторов на заданную тему. Итак.

При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках. Поясним рисунком с распределением напряжений, токов и формулами.Рис.1 Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными. Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить… Короче, все вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников

Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.

Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.

Почему переменными? А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.

Расчёт поведём на основании хрестоматийных формул:

и для параллельных цепей и

и для последовательных. Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов

Ну и в завершении ещё одна таблица.

РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек

Источник: http://vpayaem.ru/information12.html

Параллельное соединение резисторов. Расчеты общего сопротивления, общей мощности. :

Резистор – это элемент электрической схемы, который обладает сопротивлением электрическому току. Классифицируют два типа резисторов: постоянные и переменные (подстроечные). При моделировании той или иной электрической схемы, а также при ремонте электронных изделий, возникает необходимость использовать резистор определенного номинала.

Хотя и существует множество различных номиналов постоянных резисторов, в данный момент под рукой может не оказаться требуемого, либо резистора с таким номиналом не существует. Чтобы выйти из такой ситуации, можно использовать как последовательное так и параллельное соединение резисторов.

О том, как правильно произвести расчет и подбор различных номиналов сопротивлений, будет рассказано в этой статье.

Последовательное соединение резисторов – это самая элементарная схема сборки радиодеталей, оно применяется для увеличения общего сопротивления цепи.

При последовательном соединении, сопротивление используемых резисторов просто складывается, а вот при параллельном соединении необходимо производить расчет по нижеописанным формулам.

Параллельное соединение необходимо для снижения результирующего сопротивления, а также для увеличения мощности, несколько параллельно подключенных резисторов имеют большую мощность, чем у одного.

На фотографии можно увидеть параллельное подключение резисторов.

Ниже представлена принципиальная схема параллельного соединения резисторов.

Общее номинальное сопротивление необходимо рассчитывать по следующей схеме:

R(общ)=1/(1/R1+1/R2+1/R3+1/R n).

Где:

— R(общ) – общее сопротивление;

— R1, R2, R3 и Rn – параллельно подключенные резисторы.

Когда параллельное соединение резисторов состоит всего из двух элементов, в таком случае общее номинальное сопротивление можно высчитать по следующей формуле:

R(общ)=R1*R2/R1+R2.

Где:

— R(общ) – общее сопротивление;

— R1, R2 – параллельно подключенные резисторы.

В радиотехнике существует следующее правило: если параллельное подключение резисторов состоит из элементов одного номинала, то результирующее сопротивление можно высчитать, разделив номинал резистора на количество соединенных резисторов:

R(общ)=R1
.

Где:

— R(общ) – общее сопротивление;

— R – номинал параллельно подключенного резистора;

— n – количество соединенных элементов.

Важно учитывать, что при параллельном соединении результирующее сопротивление всегда будет ниже, чем сопротивление самого малого по номиналу резистора.

Приведем практический пример: возьмем три резистора, со следующими значениями номинального сопротивления: 100 Ом, 150 Ом и 30 Ом. Проведем расчет общего сопротивления, по первой формуле:

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

После расчета формулы мы видим, что параллельное соединение резисторов, состоящее из трех элементов, с наименьшим номиналом 30 Ом, в результате дает общее сопротивление в электрической цепи 21,28 Ом, что ниже наименьшего номинального сопротивления в цепи почти на 30 процентов.

Параллельное соединение резисторов чаще всего используют в тех случаях, когда необходимо получить сопротивление с большей мощностью.

В таком случае необходимо взять резисторы одинаковой мощности и с одинаковым сопротивлением.

Результирующая мощность в таком случае рассчитывается путем умножения мощности одного элемента сопротивления на общее количество параллельно подключенных резисторов в цепи.

Например: пять резисторов с номиналом в 100 Ом и с мощностью 1 Вт в каждом, подключенные параллельно, имеют общее сопротивление 20 Ом и мощность 5 Вт.

При последовательном подключении тех же резисторов (мощность так же складывается), получим результирующую мощность 5 Вт, общее сопротивление составит 500 Ом.

Источник: https://www.syl.ru/article/114725/undefined

Параллельное соединение резисторов

В случае последовательного соединения прохождение тока осуществляется только через один проводник. Параллельное соединение резисторов предполагает распределение электрического тока среди нескольких проводников. При добавлении еще одного резистора в электрическую цепь, ток будет частично проходить через разные резисторы.

Схемы последовательного и параллельного соединения

Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами.

При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений.

При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.

Если последовательное и параллельное соединение резисторов рассматривается с точки зрения радиоэлектроники, необходимо четко представлять себе, что представляет собой данный элемент и какова его роль в электронных схемах. Эта деталь является неотъемлемой частью многих устройств, благодаря такому свойству, как сопротивление электрическому току.

Резисторы могут быть двух типов – постоянными и переменными, то есть подстроечными. При создании тех или иных электрических схем требуется резистор установленного номинала, которого в данный момент может не оказаться в наличии.

Поэтому приходится использовать элементы с другими номинальными значениями, формула для каждого из которых подтверждает их физические свойства.

Последовательное соединение считается наиболее простым. Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.

Отличие параллельного и последовательного соединения

Последовательное и параллельное соединение резисторов отличаются между собой значениями напряжения. В каждой части параллельных контуров этот показатель будет одинаковым.

Однако, при одном и том же напряжении, сила тока в контурах будет разной.

Кроме того, сопротивление резисторов при параллельном соединении будет существенно отличаться от того же показателя при последовательном соединении.

В процессе использования последовательной схемы наблюдаются обратные явления. Сила тока в каждом сопротивлении будет одна и та же, а напряжение на каждом участке будет отличаться. Это связано с тем, что во время протекания тока, каждый резистор частично забирает приложенное напряжение.

Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено.

Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты.

Таким образом, параллельное соединение резисторов, находящихся под одинаковым напряжением, не влияет на режим работы каждого из них. То есть, они совершенно не зависят друг от друга, и ток, проходящий по одному приемнику, не может существенно влиять на другие приемники.

Формула расчета параллельного соединения резисторов

Свои особенности имеет и ток при параллельном соединении резисторов. Попадая в первый узел соединения, он разделяется на столько частей, сколько имеется резисторов, подключенных параллельно. То есть, через сопротивление R1 будет протекать ток I1, а через R2 – ток I2. При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2.

Если какой-либо резистор вышел из строя, то остальные будут нормально функционировать. В этом заключается основное преимущество параллельного соединения. Особенно, это касается двигателей и электрических ламп, работающих от определенного номинального напряжения.

Расчет общего номинального сопротивления осуществляется с помощью формулы: R(общ)=1/(1/R1+1/R2+1/R3+1/R n), где R(общ) – является общим сопротивлением, а R1, R2, R3 и Rn – параллельно подключенными резисторами. Если выполняется параллельное соединение двух резисторов, при котором используется всего лишь два элемента, то в этом случае для расчетов используется следующая схема: R(общ)=R1хR2/R1+R2.

Очень часто в радиоэлектронике приходится пользоваться следующим правилом: если резисторы, подключенные параллельно, имеют один и тот же номинал, то итоговое сопротивление высчитывается путем деления номинала на число подключенных элементов. Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1
, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов.

Для того чтобы рассчитать параллельное соединение резисторов, следует учитывать, что итоговое сопротивление всех подключенных элементов будет всегда ниже, чем сопротивление резистора с самым низким номиналом.

В качестве примера можно рассмотреть схему с тремя резисторами, сопротивления которых составляют 30, 100 и 150 Ом. При использовании основной формулы будет получен следующий результат: R(общ)=1/(1/30+1/100+1/150) =1/(0,03+0,01+0,007)=1/0,047=21,28Ом.

Таким образом, три резистора, соединенные параллельно, с минимальным номиналом 30 Ом, в итоге дадут общее сопротивление электрической цепи 21,28 Ом.

Онлайн калькулятор

В случае больших объемов вычислений, расчет параллельного соединения резисторов выполняется с помощью онлайн-калькулятора. Достаточно всего лишь ввести в нужные окна исходные данные, и после нажатия кнопки получить результат.

Источник: https://electric-220.ru/news/parallelnoe_soedinenie_rezistorov/2014-01-10-487

Онлайн-калькулятор параллельного соединения резисторов

instrument.guru > Электроника > Онлайн-калькулятор параллельного соединения резисторов

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент, присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет.

В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным.

Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:

Последовательное.
Параллельное.
Смешанное.

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно.

Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения.

После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно. То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

Освещение.
Розетки в квартире.
Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов.

Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно.

Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

Источник: https://instrument.guru/elektronika/onlajn-kalkulyator-parallelnogo-soedineniya-rezistorov.html

Параллельный резистор

— обзор

Используется метка задачи (3), закрепленная на днище металлического кузова автомобиля с помощью прокладки из пенопласта толщиной 5 мм. Рядом с металлической поверхностью серийная модель антенны становится 1,5 пФ и 10 нГн последовательно с 1 Ом. Напряжение холостого хода уменьшается от его значения в разомкнутом состоянии на 2 sin (2π (0,5 / 8,2)) = 0,19. Не обращайте внимания на любые изменения в соответствующих катушках индуктивности и рассчитайте значение напряжения, подаваемого на ИС, предполагая, что 1 В присутствует для того же освещения антенны с открытой меткой.

В (IC) = ______________ В

Что такое коэффициент передачи мощности?

τ = ______________

Если для включения тегу требуется 0,5 В, как это повлияет на диапазон чтения?

Получение последовательного параллельного преобразования: представьте, что у нас есть нагрузка (например, наша интегральная схема), подключенная через тройник, который мы моделируем как шунтирующий импеданс Z _sh, за которым следует последовательное сопротивление Z _ser.Можем ли мы найти значения Z _shtr и Z _sertr и, возможно, преобразованную нагрузку Z _ldtr, такие, что, если смотреть слева, серия — шунт и шунт –Серийные схемы имеют одинаковый импеданс, независимо от нагрузки?

Если это можно сделать, он должен работать для двух ограничивающих нагрузок: разомкнутой цепи и короткого замыкания ( Z _L = 0 и ∞).Используя формулы для последовательного и параллельного импедансов (Приложение 3), мы можем получить выражения для входного импеданса для нагрузок короткого замыкания и разомкнутой цепи, как показано на следующем рисунке

Теперь мы требуем, чтобы преобразованные версии были равны непреобразованные версии в обоих случаях:

Zsertr = ZserZshZser + Zsh; Zsh = Zsertr + Zshtr

Покажите, что преобразованный импеданс шунта равен:

Zshtr = (Zsh) 2Zser + Zsh

Обратите внимание, что оба они могут быть записаны аналогично:

Zshtr = βZsh; Zsertr = βZser; β≡ZshZser + Zsh

Используя этот факт, мы можем написать утверждение, что полное сопротивление одинаково для ЛЮБОЙ нагрузки, как:

Zsh (Zser + ZL ) Zsh (Zser + ZL) = Zsertr + ZshtrZLtrZshtrZLtrZsh (Zser + ZL) Zsh (Zser + ZL) = βZser + βZshZLtrβZshZLtr

Теперь самое сложное: ПОКАЗАТЬ, что это уравнение всегда верно, если: 9000Ltr

Может быть очень полезно отметить, что:

βZL + Zsh = β (ZL + Zser + Zsh)

9 0000 Калькулятор параллельных резисторов — [100% бесплатно]

Расчет эквивалентного сопротивления или REQ параллельных резисторов вручную может быть довольно утомительным.К счастью, этот калькулятор параллельных резисторов может помочь вам в расчетах независимо от того, сколько резисторов у вас параллельно. Вы также можете выполнить вычисления вручную, а затем использовать калькулятор параллельной схемы, чтобы проверить свой ответ.

Как использовать параллельный калькулятор резисторов?

Каким бы пугающим ни казался расчет параллельных резисторов, использование этого калькулятора параллельных резисторов является полной противоположностью. Этот онлайн-инструмент очень прост в использовании и понимании. Вот шаги, которые необходимо выполнить для использования этого калькулятора эквивалентного сопротивления или параллельного калькулятора сопротивления:

Сначала введите значение резистора 1.
Затем введите значения резистора 2, резистора 3, резистора 4 и резистора 5.
После ввода всех необходимых значений калькулятор параллельной цепи автоматически сгенерирует нужный вам результат. Поскольку единицей измерения для всех значений резистора является Ом, конечный результат также имеет ту же единицу измерения.

Что такое параллельный резистор?

Когда вы соединяете обе клеммы резисторов вместе параллельно, это означает, что вы соответственно подключили каждую из клемм к другому резистору или резисторам. В отличие от других схем, вы также можете классифицировать схему с параллельными резисторами как делитель тока.

Это связано с тем, что параллельные резистивные цепи могут проходить по нескольким путям, поскольку они имеют несколько путей, по которым может проходить ток.Поскольку этот тип схемы обеспечивает несколько путей для прохождения источника тока, сила тока может быть не одинаковой для всех ответвлений или путей.

Но падение напряжения, которое возникает на всех резисторах в параллельной цепи, остается неизменным. Это означает, что параллельные резисторы имеют общее напряжение, и этот факт применим ко всем элементам, соединенным параллельно.

По определению, параллельная резистивная цепь — это цепь, в которой резисторы имеют параллельные соединения или совместно используют одни и те же узлы или точки соединения.Кроме того, этот тип схемы имеет более чем один путь, подключенный к одному источнику напряжения.

Как рассчитать сопротивление в параллельной цепи?

Основной характеристикой параллельной цепи является общая разность напряжений или потенциалов на концах всех резисторов. Даже без использования калькулятора эквивалентного сопротивления, вы можете рассчитать эквивалентное сопротивление для этого типа цепи по следующей формуле:

1 / R = 1 / R1 + 1 / R2 +… + 1 / Rn

где:

R относится к эквивалентному параллельному сопротивлению
R1, R2,… Rn относится к сопротивлениям отдельных резисторов с номерами 1… n .2) в базовых единицах СИ

Вот несколько шагов, которые необходимо выполнить для расчета параллельного сопротивления без использования калькулятора параллельного сопротивления:

Сначала определите значения сопротивления всех резисторов, подключенных параллельно. Например, у нас есть три номинала резистора: 4 Ом , 3 Ом и 6 Ом .
Подставьте эти значения в приведенную выше формулу:

1 / R = 1/4 + 1/3 +1/6
, следовательно, , 1 / R = 0.75, а R = 1,33

Чтобы проверить точность ответа, введите значения в калькулятор параллельного резистора.

Как рассчитать сопротивление?

Прежде чем вы сможете выполнить расчет, вы должны сначала хорошо разбираться в параллельных цепях. Помните, что такая схема делится на несколько путей, а затем снова соединяется. Также имейте в виду, что ток течет по каждому из отдельных путей цепи.

Если в схеме есть резисторы на главном ответвлении или если в одном ответвлении имеется более одного резистора, следует выполнить другой расчет.Найдите общее сопротивление, используя значение сопротивления каждой из ветвей. Каждый из резисторов замедляет ток, проходящий через одну ветвь.

Но резисторы не так сильно влияют на общее сопротивление цепи. Следовательно, вы должны использовать формулу общего сопротивления:

1 / RT = 1 / R1 + 1 / R2 + 1 / R3 + 1 / R4… 1 / Rn

где:

R1 относится к сопротивлению 1-й ветви
R2 относится к сопротивлению 2-й ветви
R3 относится к сопротивлению 3-й ветви
R4 относится к сопротивлению 4-й ветви
и так далее, пока не дойдете до конечной ветки Rn .

Это самый простой способ рассчитать сопротивление. Но в некоторых случаях у вас может не быть значений отдельных сопротивлений. В таком случае вам нужно вместо этого использовать напряжение и ток. Вот шаги, которые необходимо выполнить:

В параллельных цепях напряжение в одной ветви имеет то же значение, что и общее напряжение, протекающее по всей цепи. Если вам известно значение напряжения одной из ветвей, вы можете выполнить расчет.
Вы также можете найти значение общего напряжения, равное источнику питания схемы, например, батарее. В параллельных цепях токи различаются от ветви к ветви. Вы должны знать значение общего тока. Без него вы не сможете рассчитать общее сопротивление.
Как только у вас есть общее напряжение и ток, вы можете вычислить общее сопротивление по закону Ома:

R = V / I.

Обратите внимание на любые ветви, у которых есть ноль. сопротивление.Если параллельная цепь имеет одну такую ветвь, весь ток течет через эту ветвь, и сопротивление становится равным нулю.

Почему при параллельном подключении эквивалентное сопротивление меньше?

По мере того, как вы продолжаете добавлять резисторы в параллельную цепь, это уменьшает эквивалентное сопротивление всей цепи. Однако это также увеличивает общий ток цепи. Это происходит потому, что добавление резисторов параллельно предоставляет схемам больше путей для прохождения тока.

11.2 закон Ома | Электрические цепи

Закон 11,2 Ома (ESBQ6)

temp text

Три основных параметра электрических цепей: ток, напряжение (потенциал разница) и сопротивление . Резюме:

Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
Разность потенциалов или напряжение \ (В \) — это количество энергии на единицу заряда, необходимое для перемещения этого заряд между двумя точками в цепи.
Сопротивление, \ (R \), является мерой того, насколько «трудно» протолкнуть ток через элемент схемы.

Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.

Георг обнаружил важную взаимосвязь между током, напряжением и сопротивлением в цепи. Симона Ома, и он называется Закон Ома .

Закон Ома

Величина электрического тока, протекающего через металлический проводник при постоянной температуре в цепи, равна пропорциональна напряжению на проводнике и может быть описана как

\ (I = \ frac {V} {R} \)

где \ (I \) — ток через проводник, \ (V \) — напряжение через проводник, а \ (R \) сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводник постоянен, независимо от приложенного к нему напряжения или проходящего через него тока.

Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводник прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на По оси X графика и тока по оси Y графика мы получим прямую.

Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R} \] Это можно изменить с точки зрения постоянного сопротивления как: \ [R = \ frac {V} {I} \]

временный текст

Закон Ома

Цель

Для определения взаимосвязи между током, протекающим через резистор, и потенциалом разность (напряжение) на одном и том же резисторе.

Аппарат

4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода

Метод

Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное напряжение на резисторе. и измерить результирующий ток в цепи. Во второй части мы будем варьировать ток в цепи и измерьте полученное напряжение на резисторе.После получения обоих наборов измерений, мы рассмотрим взаимосвязь между током и напряжением на резистор.

Изменение напряжения:
1. Установите схему в соответствии со схемой 1), начиная с одной ячейки.
2. Нарисуйте следующую таблицу в своем лабораторном журнале.
  Количество ячеек
  Напряжение, В (\ (\ text {V} \))
  Ток, I (\ (\ text {A} \))
  \ (\ text {1} \)
  \ (\ text {2} \)
  \ (\ text {3} \)
  \ (\ text {4} \)
3. Попросите учителя проверить электрическую цепь перед включением питания.
4. Измерьте напряжение на резисторе с помощью вольтметра, а ток в схему с помощью амперметра.
5. Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.
6. Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
Изменение тока:
1. Установите схему в соответствии со схемой 2), начиная только с 1 резистора в схема.
2. Нарисуйте следующую таблицу в своем лабораторном журнале.
  Напряжение, В (\ (\ text {V} \))
  Ток, I (\ (\ text {A} \))
3. Попросите учителя проверить вашу схему перед включением питания.
4. Измерьте ток и напряжение на единственном резисторе.
5. Теперь добавьте в цепь еще один резистор и измерьте ток и напряжение снова только на исходном резисторе. Продолжайте добавлять резисторы, пока не получите четыре последовательно, но не забывайте измерять напряжение только на исходном резистор каждый раз.Введите измеренные вами значения в таблицу.

Анализ и результаты

Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения. С напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная. и будет нанесен на ось \ (x \).Текущий является зависимой переменной и должен быть отложено по оси \ (y \).
Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом в случае, если независимая переменная — это ток, который должен быть нанесен на ось \ (x \), и напряжение является зависимой переменной и должно быть отложено по оси \ (y \).

Выводы

Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резистор при увеличении тока через резистор? я.е. Увеличивается или уменьшается?
Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.

Вопросы и обсуждение

Для каждого из ваших графиков вычислите градиент и по нему определите сопротивление оригинальный резистор. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?
Как бы вы смогли найти сопротивление неизвестного резистора, используя только мощность? питание, вольтметр и известный резистор \ (R_0 \)?

Закон Ома

Учебное упражнение 11.1

Постройте график напряжения (по оси X) и тока (по оси Y).

Какой тип графика вы получите (прямой, парабола, другая кривая)

прямая линия

Рассчитайте градиент графика.

Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжение:

\ begin {align *} m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\ & = \ текст {0,13} \ end {выровнять *}

Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.

Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.

Как бы вы смогли найти сопротивление неизвестного резистора, используя только мощность? питание, вольтметр и известный резистор \ (R_ {0} \)?

Вы начинаете с подключения известного резистора в цепь с источником питания.Теперь ваша очередь Считайте напряжение источника питания и запишите это.

Затем вы последовательно подключаете два резистора. Теперь вы можете проводить измерения напряжения. для каждого из резисторов.

Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:

\ [V = IR \]

Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток такой же везде в цепи мы можем найти неизвестное сопротивление.

\ begin {align *} V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ end {выровнять *}

Омические и неомические проводники (ESBQ7)

Проводники, подчиняющиеся закону Ома, имеют постоянное сопротивление при изменении напряжения на них или ток через них увеличивается.Эти проводники называются омическими проводниками . График ток в зависимости от напряжения на этих проводниках будет прямолинейным. Некоторые примеры омических жилы — резисторы цепи и нихромовая проволока.

Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Этот потому что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводники называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка распространенный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.

В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается из комнаты. температура до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, в результате увеличение тока вызывает повышение температуры нити, что увеличивает ее сопротивление.Это эффективно ограничивает увеличение тока. В этом случае напряжение и ток не изменяются. подчиняться закону Ома.

Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорируется. При применении металлических ламп накаливания, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \), и начиная с комнатной температуры) изменение довольно велико.

Как правило, для неомических проводов график зависимости напряжения от тока не будет прямолинейным, указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.

Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определяют, какой из них подчиняется закону Ома. Вы будете нужны лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр.Учащимся следует обнаружите, что резистор подчиняется закону Ома, а лампочка — нет.

Проводники омические и неомические

Цель

Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома

Аппарат

4 ячейки, резистор, лампочка, соединительные провода, вольтметр, амперметр

Метод

Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во втором — лампочка.Настройте обе схемы, указанные выше, начиная с 1 клетка. Для каждой цепи:

Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметр.
Измерить ток в цепи с помощью амперметра.
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.

Результаты

Нарисуйте в своей книге две таблицы, которые выглядят следующим образом. У вас должна быть одна таблица для измерения первой цепи с резистором и еще одна таблица для второй схемы измерения с помощью лампочки.

Количество ячеек	Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)

Анализ

Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs.\ (V \) (\ (x \) — ось), одна для резистора и один для лампочки.

Вопросы и обсуждение

Внимательно изучите свои графики и ответьте на следующие вопросы:

Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка резистору Ома? Закон?
Имеет ли лампочка омический или неомический провод?

Использование закона Ома (ESBQ8)

Теперь мы готовы увидеть, как закон Ома используется для анализа схем.

Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \) и напряжение на резисторе \ (\ text {5} \) \ (\ text {V} \), тогда мы можем использовать сопротивление Ома. Закон для расчета тока, протекающего через резистор. Наша первая задача — нарисовать схему диаграмма. При решении любой проблемы с электрическими цепями очень важно составить схему схему перед выполнением любых расчетов.Принципиальная схема этой проблемы выглядит следующим образом:

Уравнение закона Ома: \ [R = \ frac {V} {I} \]

, который можно изменить на: \ [I = \ frac {V} {R} \]

Ток, протекающий через резистор:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}

временный текст

Рабочий пример 1: Закон Ома

Изучите принципиальную схему ниже:

Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор — \ (\ text {4} \) \ (\ text {A} \).Какова разность потенциалов (напряжение) на резистор?

Определите, как подойти к проблеме

Нам задают сопротивление резистора и ток, проходящий через него, и просят рассчитать напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]

Решить проблему

Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \).\ begin {align *} R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}

Напишите окончательный ответ

Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).

Закон Ома

Учебное упражнение 11.2

Рассчитайте сопротивление резистора с разностью потенциалов \ (\ text {8} \) \ (\ text {V} \) через него, когда через него течет ток \ (\ text {2} \) \ (\ text {A} \). Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора равно:

\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}

Какой ток будет протекать через резистор \ (\ text {6} \) \ (\ text {Ω} \) при наличии разность потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Нарисуйте схему диаграмму перед расчетом.

Сопротивление неизвестного резистора равно:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ end {выровнять *}

Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \), когда ток \ (\ text {1,5} \) \ (\ text {A} \) течет через него? Нарисуйте принципиальную схему перед выполнением расчет.

Сопротивление неизвестного резистора равно:

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ end {выровнять *}

Переплет резисторов последовательно и параллельно (ESBQ9)

В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы подключены в последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. Параллельно В цепи есть несколько путей, по которым течет ток.

Когда в цепи более одного резистора, мы обычно можем рассчитать общую суммарную сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .

Эквивалентное последовательное сопротивление

В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление равно сумме сопротивлений всех резисторов.

Эквивалентное сопротивление в последовательной цепи,: Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]

Применим это к следующей схеме.

Резисторы включены последовательно, следовательно:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {выровнять *}

Эквивалентное параллельное сопротивление

В цепи, в которой резисторы включены параллельно, эквивалентное сопротивление определяется как следующее определение.

Эквивалентное сопротивление в параллельной цепи: Для резисторов \ (n \), включенных параллельно, эквивалентное сопротивление составляет:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]

Применим эту формулу к следующей схеме.

Какое полное (эквивалентное) сопротивление в цепи?

\ begin {align *} \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \Правильно) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text {1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text { Ω}} {\ text {10} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {выровнять *}

Последовательное и параллельное сопротивление

Учебное упражнение 11.3

Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) соединены последовательно. Рассчитать эквивалентное сопротивление.

Поскольку резисторы включены последовательно, мы можем использовать:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\ & = \ текст {20} \ текст {кОм} \ end {выровнять *}

Два резистора соединены последовательно.Эквивалентное сопротивление \ (\ text {100} \) \ (\ текст {Ω} \). Если один резистор \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.

Поскольку резисторы включены последовательно, мы можем использовать:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ R_ {2} & = R_ {s} — R_ {1} \\ & = \ text {100} \ text {Ω} — \ text {10} \ text {Ω} \\ & = \ текст {90} \ текст {Ω} \ end {выровнять *}

Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитать эквивалентное сопротивление.

Поскольку резисторы включены параллельно, можно использовать:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\ & = \ frac {1 + 10} {\ text {100}} \\ & = \ frac {11} {\ text {100}} \\ R_ {p} & = \ text {9,09} \ text {kΩ} \ end {выровнять *}

Два резистора подключены параллельно.Эквивалентное сопротивление \ (\ text {3,75} \) \ (\ текст {Ω} \). Если один резистор имеет сопротивление \ (\ text {10} \) \ (\ text {Ω} \), какое сопротивление у второго резистора?

Поскольку резисторы включены параллельно, можно использовать:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} \\ & = \ frac {1} {\ text {3,75}} — \ frac {1} {\ text {10}} \\ & = \ frac {\ text {10} — \ text {3,75}} {\ text {37,5}} \\ & = \ frac {\ text {6,25}} {\ text {37,5}} \\ R_ {2} & = \ текст {6} \ текст {Ω} \ end {выровнять *}

Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:

a) Резисторы включены параллельно, поэтому мы используем:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\ & = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\ & = \ frac {\ text {5}} {\ text {6}} \\ R & = \ текст {1,2} \ текст {Ω} \ end {выровнять *}

b) Резисторы включены параллельно, поэтому мы используем:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \\ & = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\ & = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\ & = \ frac {\ text {25}} {\ text {12}} \\ R & = \ text {0,48} \ text {Ω} \ end {выровнять *}

c) Резисторы включены последовательно, поэтому мы используем:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}

d) Резисторы включены последовательно, поэтому мы используем:

\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ текст {1} \ текст {Ω} \\ & = \ текст {10} \ текст {Ω} \ end {выровнять *}

Использование закона Ома в последовательных и параллельных цепях (ESBQB)

Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими настройками.

Последовательные цепи

Рассмотрим схему, состоящую из трех резисторов и одного одиночная ячейка соединена последовательно.

Первый принцип, который нужно понять в отношении последовательных цепей, заключается в том, что величина тока одинакова. через любой компонент в цепи. Это потому, что существует только один путь для движения электронов. в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении ток будет течь.Мы знаем, что ток по условию течет от положительного к отрицательному. Общепринятый ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к А.

Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:

\ [I = I_ {1} = I_ {2} = I_ {3}. \]

Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений по всем три резистора.Итак, мы можем написать:

\ [V = V_ {1} + V_ {2} + V_ {3} \]

Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления резисторов в серии, мы можем подойти к некоторым проблемам схемы.

Рабочий пример 2: Закон Ома, последовательная цепь

Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.

Определите, что требуется

Требуется рассчитать ток, протекающий в цепи.

Определите, как подойти к проблеме

Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако есть два резисторы в цепи и нам нужно найти общее сопротивление.

Найти полное сопротивление в цепи

Поскольку резисторы включены последовательно, общее (эквивалентное) сопротивление R составляет:

\ [R = R_ {1} + R_ {2} \]

Следовательно,

\ begin {align *} R & = \ текст {2} + \ текст {4} \\ & = \ текст {6} \ текст {Ω} \ end {выровнять *}

Применить закон Ома

\ begin {align *} R & = \ frac {V} {I} \\ R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\ I & = \ frac {V} {R} \\ & = \ frac {12} {6} \\ & = \ текст {2} \ текст {А} \ end {align *}

Напишите окончательный ответ

В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).

Рабочий пример 3: Закон Ома, последовательная цепь

Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найди сопротивление \ (R_ {2} \), учитывая, что ток, протекающий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ текст {V} \).\ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).

Нарисуйте схему и введите все известные значения.

Определите, как подойти к проблеме.

Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление с использованием:

\ [R = R_ {1} + R_ {2} \]

, потому что он находится в последовательной цепи.

Найдите общее сопротивление

\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {\ text {1,5}} {\ text {0,25}} \\ & = \ текст {6} \ текст {Ω} \ end {выровнять *}

Найдите неизвестное сопротивление

Мы знаем, что:

\ [R = \ text {6} \ text {Ω} \]

и что

\ [R_ {1} = \ text {1} \ text {Ω} \]

\ [R = R_ {1} + R_ {2} \] \ [R_ {2} = R — R_ {1} \]

Следовательно,

\ [R_ {1} = \ text {5} \ text {Ω} \]

Рабочий пример 4: Закон Ома, последовательная цепь

Для следующей схемы рассчитайте:

падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \), и \ (R_3 \)
сопротивление \ (R_3 \).

Определите, как подойти к проблеме

Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета напряжения падение через известные резисторы. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \).Теперь мы можем использовать эту информацию для найти напряжение на неизвестном резисторе \ (R_3 \).

Рассчитать падение напряжения на \ (R_1 \)

Используя закон Ома: \ begin {align *} R_1 & = \ frac {V_1} {I} \\ I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\ V_1 & = {I} \ cdot {R_1} \\ & = 2 \ cdot 1 \\ V_1 & = \ текст {2} \ текст {V} \ end {align *}

Рассчитать падение напряжения на \ (R_2 \)

Снова используя закон Ома: \ begin {align *} R_2 & = \ frac {V_2} {I} \\ I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\ V_2 & = {I} \ cdot {R_2} \\ & = 2 \ cdot 3 \\ V_2 & = \ текст {6} \ текст {V} \ end {align *}

Рассчитать падение напряжения на \ (R_3 \)

Так как падение напряжения на всех резисторах вместе должно быть таким же, как и падение напряжения через ячейку в последовательной цепи, мы можем найти \ (V_3 \), используя: \ begin {align *} V & = V_1 + V_2 + V_3 \\ V_3 & = V — V_1 — V_2 \\ & = 18-2-6 \\ V_3 & = \ текст {10} \ текст {V} \ end {align *}

Найдите сопротивление \ (R_3 \)

Нам известны напряжение на \ (R_3 \) и ток через него, поэтому мы можем использовать закон Ома, чтобы рассчитать значение сопротивления: \ begin {align *} R_3 & = \ frac {V_3} {I} \\ & = \ frac {10} {2} \\ R_3 & = \ text {5} \ Omega \ end {align *}

Напишите окончательный ответ

\ (V_1 = \ text {2} \ text {V} \)

\ (V_2 = \ text {6} \ text {V} \)

\ (V_3 = \ text {10} \ text {V} \)

\ (R_1 = \ text {5} \ Omega \)

временный текст

Параллельные цепи

Рассмотрим схему, состоящую из одной ячейки и трех резисторов, соединенных параллельно.

Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что напряжение одинаково на всех компонентах в цепи. Это потому, что есть только два набора электрически общие точки в параллельной цепи и напряжение, измеренное между наборами общих точек всегда должны быть одинаковыми в любой момент времени. Итак, для показанной схемы верно следующее:

\ [V = V_ {1} = V_ {2} = V_ {3}.\]

Второй принцип параллельной схемы состоит в том, что все токи, проходящие через каждый резистор, должны складываться. до полного тока в цепи:

\ [I = I_ {1} + I_ {2} + I_ {3}. \]

Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельной резисторов, теперь мы можем подойти к некоторым схемам, связанным с параллельными резисторами.

Рабочий пример 5: Закон Ома, параллельная схема

Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.

Определите, что требуется

Требуется рассчитать ток, протекающий в цепи.

Определите, как подойти к проблеме

Найдите эквивалентное сопротивление в цепи

Поскольку резисторы включены параллельно, общее (эквивалентное) сопротивление R составляет:

\ [\ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}}. \] \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {2 + 1} {4} \\ & = \ frac {3} {4} \\ \ text {Следовательно,} R & = \ text {1,33} \ Omega \ end {выровнять *}

Применить закон Ома

\ begin {align *} R & = \ frac {V} {I} \\ R \ cdot \ frac {I} {R} & = \ frac {V} {I} \ cdot \ frac {I} {R} \\ I & = \ frac {V} {R} \\ I & = V \ cdot \ frac {1} {R} \\ & = (12) \ left (\ frac {3} {4} \ right) \\ & = \ текст {9} \ текст {А} \ end {выровнять *}

Напишите окончательный ответ

В цепи протекает ток \ (\ text {9} \) \ (\ text {A} \).

Рабочий пример 6: Закон Ома, параллельная схема

Два омических резистора (\ (R_1 \) и \ (R_2 \)) подключены параллельно ячейке. Найди сопротивление \ (R_2 \), учитывая, что ток, протекающий через ячейку, равен \ (\ text {4,8} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ text {9} \) \ (\ text {V} \).

Определите, что требуется

Нам нужно рассчитать сопротивление \ (R_2 \).

Определите, как подойти к проблеме

Так как резисторы омические и нам даны напряжение на ячейке и ток через ячейку мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи. \ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {\ text {4,8}} \\ & = \ text {1,875} \ \ Omega \ end {align *}

Рассчитайте значение для \ (R_2 \)

Поскольку мы знаем эквивалентное сопротивление и сопротивление \ (R_1 \), мы можем использовать формулу для резисторов, включенных параллельно, найти сопротивление \ (R_2 \).\ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \ end {выровнять *} Переставляем решение для \ (R_2 \): \ begin {align *} \ frac {1} {R_2} & = \ frac {1} {R} — \ frac {1} {R_1} \\ & = \ frac {1} {\ text {1,875}} — \ frac {1} {3} \\ & = \ текст {0,2} \\ R_2 & = \ frac {1} {\ text {0,2}} \\ & = \ текст {5} \ \ Omega \ end {align *}

Напишите окончательный ответ

Сопротивление \ (R_2 \) равно \ (\ text {5} \) \ (\ Omega \)

temp text

Рабочий пример 7: Закон Ома, параллельная схема

Ячейка 18 В подключена к двум параллельным резисторам \ (\ text {4} \) \ (\ Omega \) и \ (\ text {12} \) \ (\ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов.

Сначала нарисуйте схему перед выполнением любых расчетов

Определите, как подойти к проблеме

Нам нужно определить ток через ячейку и каждый из параллельных резисторов. У нас есть была задана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для вычисления силы тока.

Рассчитать ток через ячейку

Чтобы рассчитать ток через ячейку, нам сначала нужно определить эквивалент сопротивление остальной части цепи. Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {4} + \ frac {1} {12} \\ & = \ frac {3 + 1} {12} \\ & = \ frac {4} {12} \\ R & = \ frac {12} {4} = \ text {3} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {18} {3} \\ I & = \ text {6} \ text {A} \ end {align *}

Теперь определите ток через один из параллельных резисторов

Мы знаем, что для чисто параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из параллельных резисторов.Для этой схемы: \ begin {align *} V & = V_1 = V_2 = \ text {18} \ text {V} \ end {выровнять *} Начнем с расчета тока через \ (R_1 \) по закону Ома: \ begin {align *} R_1 & = \ frac {V_1} {I_1} \\ I_1 & = \ frac {V_1} {R_1} \\ & = \ frac {18} {4} \\ I_1 & = \ text {4,5} \ text {A} \ end {align *}

Рассчитайте ток через другой параллельный резистор

Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_2 \): \ begin {align *} R_2 & = \ frac {V_2} {I_2} \\ I_2 & = \ frac {V_2} {R_2} \\ & = \ frac {18} {12} \\ I_2 & = \ text {1,5} \ text {A} \ end {выровнять *} Альтернативный метод вычисления \ (I_2 \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны составлять суммарный ток через клетка: \ begin {align *} I & = I_1 + I_2 \\ I_2 & = I — I_1 \\ & = 6 — 4.5 \\ I_2 & = \ text {1,5} \ text {A} \ end {align *}

Напишите окончательный ответ

Ток через ячейку равен \ (\ text {6} \) \ (\ text {A} \).

Ток через резистор \ (\ text {4} \) \ (\ Omega \) равен \ (\ text {4,5} \) \ (\ text {A} \).

Ток через резистор \ (\ text {12} \) \ (\ Omega \) равен \ (\ text {1,5} \) \ (\ text {A} \).

Закон Ома в последовательной и параллельной цепях

Учебное упражнение 11.4

Рассчитать номинал неизвестного резистора в цепи:

Сначала мы используем закон Ома для вычисления полного последовательного сопротивления:

\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {1} \\ & = \ текст {9} \ текст {Ω} \ end {выровнять *}

Теперь мы можем найти неизвестное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ R_ {4} & = R_ {s} — R_ {1} — R_ {2} — R_ {3} \\ & = 9 — 3 — 3 — 1 \\ & = \ текст {2} \ текст {Ω} \ end {выровнять *}

Рассчитайте значение тока в следующей цепи:

Сначала находим общее сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {1} + \ text {2,5} + \ text {1,5} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {5} \\ & = \ текст {1,8} \ текст {А} \ end {выровнять *}

Три резистора с сопротивлением \ (\ text {1} \) \ (\ text {Ω} \), \ (\ text {5} \) \ (\ text {Ω} \) и \ (\ text {10} \) \ (\ text {Ω} \) соответственно соединены в серия с \ (\ text {12} \) \ (\ text {V} \) батареей.Рассчитайте значение тока в схема.

Рисуем принципиальную схему:

Теперь мы находим общее сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ текст {1} + \ текст {5} + \ текст {10} \\ & = \ текст {16} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {12} {16} \\ & = \ текст {0,75} \ текст {A} \ end {выровнять *}

Рассчитайте ток через ячейку, если оба резистора омические по своей природе.

Сначала находим общее сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {3}} \\ & = \ frac {3 + 1} {\ text {3}} \\ & = \ frac {4} {\ text {3}} \\ & = \ текст {0,75} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {\ text {0,75}} \\ & = \ текст {12} \ текст {А} \ end {выровнять *}

Рассчитайте номинал неизвестного резистора \ (R_ {4} \) в цепи:

Сначала находим общее сопротивление:

\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {24} {\ text {2}} \\ & = \ текст {12} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать неизвестное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \\ \ frac {1} {R_ {4}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} — \ frac {1} {R_ {2}} — \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {12}} — \ frac {1} {\ text {120}} — \ frac {1} {\ text {40}} — \ frac {1} {\ text {60}} \\ & = \ frac {10 — 1 — 3 — 2} {\ text {120}} \\ & = \ frac {4} {\ text {120}} \\ & = \ текст {30} \ текст {Ω} \ end {выровнять *}

значение тока через аккумулятор

Рисуем принципиальную схему:

Чтобы вычислить значение тока через аккумулятор, нам сначала нужно вычислить эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {5}} + \ frac {1} {\ text {10}} \\ & = \ frac {10 + 2 + 1} {\ text {10}} \\ & = \ frac {13} {\ text {10}} \\ & = \ текст {0,77} \ текст {Ω} \ end {выровнять *}

Теперь можем посчитать ток через батарею:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {0,77}} \\ & = \ текст {26} \ текст {А} \ end {выровнять *}

значение тока в каждом из трех резисторов.

Для параллельной схемы напряжение на ячейке такое же, как и напряжение на каждой резисторов. Для этой схемы:

\ [V = V_ {1} = V_ {2} = V_ {3} = \ text {20} \ text {V} \]

Теперь мы можем рассчитать ток через каждый резистор. Начнем с \ (R_ {1} \):

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {1}} \\ & = \ текст {20} \ текст {А} \ end {выровнять *}

Затем мы вычисляем ток через \ (R_ {2} \):

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {5}} \\ & = \ текст {4} \ текст {А} \ end {выровнять *}

И наконец вычисляем ток через \ (R_ {3} \):

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {10}} \\ & = \ текст {2} \ текст {А} \ end {выровнять *}

Вы можете проверить, что они в сумме составляют общий ток.

Последовательные и параллельные сети резисторов (ESBQC)

Теперь, когда вы знаете, как работать с простыми последовательными и параллельными цепями, вы готовы к работе со схемами. которые объединяют эти две схемы, например, следующую схему:

Рисунок 11.1: Пример последовательно-параллельной сети. Пунктирными прямоугольниками обозначены параллельные участки цепи.

Проработать такие схемы относительно легко, потому что вы используете все, что у вас уже есть. узнал о последовательных и параллельных цепях. Единственная разница в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из двух параллельных частей. которые затем последовательно с ячейкой. Чтобы вычислить эквивалентное сопротивление для схемы, вы начнете с вычисление общего сопротивления каждой из параллельных частей, а затем сложение этих сопротивлений в серии. {- 1} \\ & = \ текст {5} \, \ Omega \ end {align *}

Теперь вы можете рассматривать схему как простую последовательную схему следующим образом:

Следовательно, эквивалентное сопротивление: \ begin {align *} R & = R_ {p1} + R_ {p2} \\ & = 5 + 5 \\ & = 10 \, \ Omega \ end {align *}

Эквивалентное сопротивление схемы на рисунке 11.1 — это \ (\ текст {10} \) \ (\ текст {Ω} \).

временный текст

Последовательные и параллельные сети

Учебное упражнение 11.5

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {4} + \ frac {1} {2} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:

\ begin {align *} R_ {s} & = R_ {3} + R_ {p} \\ & = \ текст {2} + \ текст {1,33} \\ & = \ текст {3,33} \ текст {Ω} \ end {выровнять *}

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {1} + \ frac {1} {2} \\ & = \ frac {3} {2} \\ R_ {p} & = \ text {0,67} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с тремя последовательно включенными резисторами, поэтому мы можем рассчитать эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {3} + R_ {4} + R_ {p} \\ & = \ текст {4} + \ текст {6} + \ текст {0,67} \\ & = \ текст {10,67} \ текст {Ω} \ end {выровнять *}

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}

\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}

ток \ (I \) через ячейку.

Чтобы найти ток \ (I \), нам сначала нужно найти эквивалентное сопротивление. Мы начинаем путем вычисления эквивалентного сопротивления параллельной комбинации:

\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}

Итак, ток через ячейку:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {12}} {\ text {2,652}} \\ & = \ текст {4,52} \ текст {А} \ end {выровнять *}

ток через резистор \ (\ text {5} \) \ (\ text {Ω} \).

Ток через параллельную комбинацию резисторов равен \ (\ text {4,52} \) \ (\ текст {A} \). (Сила тока одинакова при последовательной комбинации резисторов и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение через параллельную комбинацию резисторов (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалент сопротивление цепи):

\ begin {align *} V & = I \ cdot R \\ & = (\ text {4,52}) (\ text {0,652}) \\ & = \ текст {2,95} \ текст {V} \ end {выровнять *}

Поскольку напряжение на каждом резисторе в параллельной комбинации одинаковое, это также является напряжением на резисторе \ (\ text {5} \) \ (\ text {Ω} \).

Итак, теперь мы можем рассчитать ток через резистор:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {2,95}} {\ text {5}} \\ & = \ текст {0,59} \ текст {A} \ end {выровнять *}

Если ток, протекающий через ячейку, равен \ (\ text {2} \) \ (\ text {A} \), и все резисторы являются омическими, рассчитайте напряжение на ячейке и на каждом из резисторов \ (R_1 \), \ (R_2 \) и \ (R_3 \) соответственно.

Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление. Мы начинаем с расчет эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}

\ begin {align *} R_ {s} & = R_ {1} + R_ {p} \\ & = \ text {4,66} + \ text {1,33} \\ & = \ текст {5,99} \ текст {Ω} \ end {выровнять *}

Итак, напряжение на ячейке:

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {5,99}) \\ & = \ текст {12} \ текст {V} \ end {выровнять *}

Ток через параллельную комбинацию резисторов равен \ (\ text {2} \) \ (\ text {A} \).(Ток одинаков при последовательной комбинации резисторов, и мы можем рассмотреть весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с поиска напряжение на \ (R_ {1} \):

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {4,66}) \\ & = \ текст {9,32} \ текст {V} \ end {выровнять *}

Теперь находим напряжение на параллельной комбинации:

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {1,33}) \\ & = \ текст {2,66} \ текст {V} \ end {выровнять *}

Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторах \ (R_ {2} \) и \ (R_ {3} \).

ток через ячейку

Чтобы найти ток, нам сначала нужно найти эквивалентное сопротивление. Мы начинаем с расчет эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {1} + \ frac {1} {1} \\ & = 2 \\ R_ {p} & = \ text {0,5} \ text {Ω} \ end {выровнять *}

\ begin {align *} R_ {s} & = R_ {1} + R_ {4} + R_ {p} \\ & = \ text {2} + \ text {1,5} + \ text {0,5} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}

Итак, ток через ячейку:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {10}} {\ text {4}} \\ & = \ текст {2,5} \ текст {А} \ end {выровнять *}

падение напряжения на \ (R_4 \)

Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Текущий то же самое через последовательные комбинации резисторов, и мы можем рассмотреть все параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение через \ (R_ {4} \):

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2,5}) (\ текст {1,5}) \\ & = \ текст {3,75} \ текст {V} \ end {выровнять *}

ток через \ (R_2 \)

Используя это, мы можем найти ток через \ (R_ {2} \).

Сначала нам нужно найти напряжение на параллельной комбинации:

\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {0,5}) \\ & = \ текст {1,25} \ текст {V} \ end {выровнять *}

Теперь мы можем найти ток через \ (R_ {2} \), используя тот факт, что напряжение одинаково на каждом резисторе в параллельной комбинации:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {1,25}} {\ text {1}} \\ & = \ текст {1,25} \ текст {А} \ end {выровнять *}

Резисторы в последовательном и параллельном соединении

Последовательные и параллельные резисторы

В предыдущем посте о резисторах мы изучили различные типы резисторов.

В некоторых случаях, когда мы не получаем желаемых или конкретных значений резисторов, мы должны либо использовать переменные резисторы, такие как потенциометры или предварительные настройки, чтобы получить такие точные значения. Однако такие горшки слишком дороги, чтобы использовать их на все случаи жизни.

Другой способ сделать это — объединить два или более резистора для получения необходимых точных значений. Такие комбинации резисторов стоят очень меньше.

Теперь возникает вопрос, как комбинировать эти резисторы.

Резисторы можно комбинировать двумя способами, например:

Параллельные комбинации

Резисторы

серии

Считается, что резисторы

подключены в « Series », когда они соединены гирляндной цепочкой в одну линию.

Расчет значений для двух или более резисторов, соединенных последовательно, просто, просто сложите все значения.

Последовательное соединение гарантирует, что ОДИН ток течет через все резисторы.

В этом типе подключения R _Итого всегда будет БОЛЬШЕ, чем любой из включенных резисторов.

Общее сопротивление — это сумма всех резисторов, соединенных последовательно, и определяется выражением:

_{рандов Итого} = ₁ + ₂ + ₃ + …………

Пример:

Поскольку резисторы соединены последовательно, одинаковый ток проходит через каждый резистор в цепи, и общее сопротивление R _Всего цепи должно быть равно к сумме всех отдельных резисторов, сложенных вместе.Это

R _Итого = ₁ + ₂

Общее приложенное напряжение V делится на два резистора.
Ток в цепи определяется как:

Используя закон Ома, напряжения на R ₁ и R ₂ задаются как:

Следовательно, полное напряжение определяется как:

Например, если мы возьмем V = 6 В, R ₁ = 1 кОм и R ₂ = 2 кОм, тогда

R _Всего = 1 кОм + 2 кОм = 3 кОм

I = 6 В / 3 кОм = 2 мА

Напряжение на резисторе 1 кОм составляет В ₁ = 2 мА × 1 кОм = 2 В

Напряжение на резисторе 2 кОм составляет В ₂ = 2 мА × 2 кОм = 4 В

Итак, мы видим, что мы можем заменить два отдельных резистора, указанных выше, только одним единственным «эквивалентным» резистором, который будет иметь номинал 3 кОм.

Это общее сопротивление обычно известно как эквивалентное сопротивление и может быть определено как; « — единое значение сопротивления, которое может заменить любое количество последовательно подключенных резисторов без изменения значений тока или напряжения в цепи ».

Последовательное соединение можно охарактеризовать следующими пунктами:

Одинаковый ток протекает через все последовательно включенные резисторы.
Результирующий резистор представляет собой СУММУ всех последовательно включенных резисторов.
делят общее приложенное напряжение пропорционально их величине.

Схема делителя напряжения

Поскольку последовательные резисторы делят напряжение, эту идею можно использовать для получения меньшего напряжения на выходе источника питания.

Например, у нас есть блок питания с фиксированным выходом 10 В. Но мы хотим от него только 5В. Как получить его ?

Схема, показанная выше, состоит из двух резисторов, R ₁ и R ₂, соединенных последовательно через напряжение питания V _в.

Ток I определяется по формуле:

Поскольку ток I протекает через R ₁, а также через R ₂, следовательно, используя закон Ома, напряжение, развиваемое на R ₂, определяется как:

Если R ₁ = R ₂, то выход V = V _дюйм/2

Если к цепи последовательно подключено больше резисторов, то на каждом резисторе по очереди будут появляться разные напряжения в зависимости от их индивидуальных значений сопротивления, обеспечивая разные, но меньшие точки напряжения от одного источника.

Параллельные резисторы

Считается, что резисторы

соединены вместе в « параллельном », когда оба их вывода соответственно подключены к каждому выводу другого резистора или резисторов.

Параллельная комбинация

Рис. ниже показана схема параллельной комбинации резисторов, где два резистора R ₁ и R ₂ подключены параллельно через напряжение питания E.

Как видно из рис.выше:

Для Current доступны два пути. Следовательно, ток разделяется.
А вот напряжения на резисторах такие же.
Если два резистора равны, ток будет делиться поровну, и R _Total будет ровно половиной любого резистора или ровно одной третью, если есть три равных резистора.
В целом можно сказать:

Токи в параллельной цепи резистора

В цепи параллельных резисторов напряжение на каждом резисторе, подключенном параллельно, остается неизменным.Однако ток через каждый параллельный резистор не обязательно будет одинаковым, поскольку значение сопротивления в каждой ветви определяет ток в этой ветви.

Общий ток I _Total в параллельной цепи резистора — это сумма отдельных токов, протекающих во всех параллельных ветвях, которая может быть определена с помощью закона Ома.

Пример

Допустим, напряжение Е равно 6В.

Резисторы должны быть R ₁ = 1 кОм и R ₂ = 2 кОм.

Согласно закону Ома, ток через R ₁ = 6 В / 1 кОм = 6 мА и ток через R ₂ = 6 В / 2 кОм = 3 мА

Следовательно, общий ток составляет 6 мА + 3 мА = 9 мА

6 В будет генерировать 9 мА только тогда, когда полное сопротивление цепи равно:

6 В / 9 мА = 0,66 кОм

Следовательно, эффективное сопротивление параллельно соединенных R ₁ и R ₂ составляет 0,66 кОм.

Это эффективное сопротивление также можно рассчитать по следующей формуле:

Таким образом, параллельное соединение можно охарактеризовать:

На всех параллельно подключенных резисторах присутствует одинаковое напряжение.
Величина, обратная результирующему или общему сопротивлению, является суммой обратных величин всех резисторов, включенных параллельно.
Параллельные резисторы делят общий ток обратно пропорционально их величине.
Когда набор резисторов подключен параллельно, эффективное сопротивление всегда меньше самого маленького в наборе.

Например: пусть резисторы 1 кОм и 10 кОм включены параллельно.

Тогда результат будет (1 k × 10 k) / 11 k = 0.9 кОм, что меньше 1 кОм (наименьшее).

Последовательные и параллельные резисторы

В некоторых электрических и электронных схемах требуется соединять различные резисторы вместе в «ОБЕ» параллельном и последовательном соединении в одной и той же схеме и создавать более сложные резистивные цепи.

Теперь возникает вопрос, как рассчитать комбинированное или полное сопротивление цепи, токи и напряжения для этих резистивных комбинаций.

Цепи резисторов

, которые объединяют последовательно и параллельные цепи резисторов вместе, обычно известны как комбинация резисторов или схемы со смешанными резисторами.

Метод расчета эквивалентного сопротивления цепей такой же, как и для любой отдельной последовательной или параллельной цепи.

Самая важная вещь, которую следует иметь в виду при таких расчетах, — это то, что последовательно подключенные резисторы несут точно такой же ток и что резисторы, подключенные параллельно, имеют точно такое же напряжение на них.

Пример

Рассмотрим схему, изображенную на рис. ниже:

В приведенной выше схеме рассчитаем полный ток (I _T), снимаемый с источника питания 12 В.

Мы видим, что два резистора, R ₂ и R ₃ фактически соединены в комбинации «СЕРИЯ», поэтому мы можем сложить их вместе, чтобы получить эквивалентное сопротивление. Таким образом, результирующее сопротивление для этой комбинации будет:

R ₂ + R ₃ = 8 Ом +4 Ом = 12 Ом

Таким образом, мы можем заменить оба резистора R ₂ и R ₃, указанные выше, на один резистор с сопротивлением 12 Ом, как показано на рис. ниже:

Итак, наша схема теперь имеет единственный резистор R _A в «ПАРАЛЛЕЛЬНО» с резистором R ₄.Используя наши резисторы в параллельном уравнении, мы можем уменьшить эту параллельную комбинацию до одного эквивалентного резистора номиналом R _{(комбинация)}, используя следующую формулу для двух параллельно соединенных резисторов.

Резистивная цепь теперь выглядит примерно так:

Мы можем видеть, что два оставшихся сопротивления, R ₁ и R _{(комбинация)} соединены вместе в комбинации «ПОСЛЕДОВАТЕЛЬНОСТЬ», и снова их можно сложить (резисторы, включенные последовательно), так что общее сопротивление цепи дано как:

Одно сопротивление всего 12 Ом можно использовать для замены четырех исходных резисторов, соединенных вместе в исходной цепи.

Теперь, используя закон Ома, значение тока цепи (I) просто рассчитывается как:

Анализ последовательных и параллельных резисторов

Несколько резисторов подключаются одновременно, образуя цепь без ответвлений посередине, которая называется резистором в последовательной цепи. И цепь, которая соединяет два или более резистора между двумя точками в цепи с одинаковым напряжением на обоих концах резистора, называется резистором в параллельной цепи.Следующие разделы в основном посвящены схемам, методам расчета, характеристикам неисправностей и устранению неисправностей последовательно включенных и параллельных резисторов. И последняя часть вводит понятие — ESR, которое связано с последовательными резисторами и конденсаторами.

Каталог

I Резисторы в последовательной и параллельной цепях

1. Резисторы в последовательной цепи

Несколько резисторов подключаются одновременно, образуя цепь без ответвлений посередине, которая называется резистором в последовательной цепи.На рисунке ниже показан резистор в последовательной цепи, состоящей из двух резисторов.

Резисторы в последовательной цепи

Характеристики последовательной цепи:

(1) Ток в последовательной цепи везде одинаков.

Если n резисторов соединены последовательно, то

(2) Общее напряжение в цепи равно сумме разделенных напряжений на последовательных резисторах.

(3) Общее сопротивление цепи равно сумме последовательного сопротивления.

R называется эквивалентным сопротивлением последовательно соединенных R1 и R2. После замены R1 и R2 на R это не влияет на ток и напряжение в цепи.

На рисунке 1 (b) представляет собой эквивалентную схему (a).

Если n резисторов соединены последовательно, то

(4) Взаимосвязь между распределением напряжения и распределением мощности в последовательных цепях.

Поскольку ток в последовательной цепи везде одинаков, поэтому

Две приведенные выше формулы показывают, что напряжение на каждом резисторе в последовательной цепи пропорционально сопротивлению каждого резистора. Мощность, потребляемая каждым резистором, также пропорциональна сопротивлению каждого резистора. Следовательно, когда последовательная цепь состоит из n резисторов, может быть получена формула деления напряжения последовательной цепи.

Совет: на практике резисторы часто подключаются последовательно, чтобы расширить диапазон измерения вольтметра.

2. Резисторы в параллельных цепях

Цепь, которая соединяет два или более резистора между двумя точками в цепи с одинаковым напряжением на обоих концах резистора, называется резистором в параллельной цепи.

Резисторы в параллельных цепях

Характеристики параллельной цепи:

(1) Напряжение на каждом резисторе в цепи одинаковое.

(2) Суммарный ток резисторов в параллельной цепи равен сумме токов ветвей.

(3) Обратное полное сопротивление параллельной цепи равно сумме обратных сопротивлений каждого параллельного резистора.

(4) Взаимосвязь между распределением тока и распределением мощности резисторов в параллельных цепях.

В параллельной цепи напряжения на параллельных резисторах одинаковы, поэтому

Приведенная выше формула показывает, что ток каждой ветви в параллельной цепи обратно пропорционален сопротивлению.И мощность, потребляемая резисторами каждой ветви, обратно пропорциональна сопротивлению.

Когда два резистора соединены параллельно, ток через каждый резистор можно рассчитать с помощью уравнения шунта. Формула шунта:

Приведенная выше формула показывает, что в резисторе в параллельной цепи ток ветви с малым сопротивлением велик, а ток ветви с большим сопротивлением мал.

Примечание : Резисторы в параллельных цепях широко используются в повседневной жизни.Например, электрические приборы в цепях освещения обычно подключаются параллельно. Только при параллельном использовании электроприборов другие электроприборы могут нормально работать, когда одно из электроприборов отключено, замкнуто или неисправно.

II C расчет S и P параллельно R esistance

Один резистор может быть подключен вместе с множеством других резисторов последовательно и параллельно. образуют сложные резистивные цепи.

Если мы соединим различные резисторы параллельно и последовательно в одной цепи, как мы вычислим сумму сопротивления, тока и напряжения этих резисторов в цепи?

Резистивные цепи, в которых сочетаются последовательные и параллельные резисторы, обычно называются комбинациями резисторов или гибридными резисторными цепями. Метод расчета эквивалентного сопротивления цепи такой же, как и для любой одиночной последовательной или параллельной цепи. Теперь мы знаем, что последовательные резисторы имеют одинаковый ток, а параллельные резисторы имеют одинаковое напряжение.

1. Пример расчета 1

Рассчитайте полный ток (IT), потребляемый от источника питания 12 В в следующей схеме.

На первый взгляд это может показаться сложной задачей, но если мы внимательно рассмотрим ее, то увидим, что два резистора R 2 и R 3 фактически соединены вместе последовательно. Итак, мы можем сложить сопротивление. Следовательно, общее сопротивление этой комбинации составляет:

R2 + R3 = 8 Ом + 4 Ом = 12 Ом

Таким образом, мы можем заменить резисторы R2 и R3 на резистор 12 Ом

И теперь в схеме есть резистор RA и резистор. R4 включены параллельно.Затем мы можем уменьшить эту параллельную комбинацию до единственного эквивалентного значения сопротивления R (комбинации), используя следующую формулу сопротивления.

В результате резистивная цепь теперь выглядит так:

Мы видим, что два оставшихся сопротивления, R1 и R (гребенчатый), соединены последовательно, и их можно снова сложить между точками. A и B.

R = R comb + R1 = 6 Ом + 6 Ом = 12 Ом

Один резистор 12 Ом можно использовать для замены четырех исходных резисторов, подключенных в исходной цепи.

Теперь, используя закон Ома, текущее значение (I) схемы просто рассчитывается следующим образом:

Следовательно, используя вышеуказанные шаги для замены всех резисторов, соединенных последовательно или параллельно, мы можем уменьшить любой сложный Схема резистора, состоящая из нескольких резисторов в простую единую схему только с одним эквивалентным резистором.

Мы также можем получить два тока ответвления, I1 и I2, используя дополнительный метод Ом:

В (R1) = I * R1 = 1 * 6 = 6 В

В (RA) = VR4 = (12-VR1) = 6 В

, следовательно:

I1 = 6 В и деление; RA = 6 деление; 12 = 0.5 А или 500 мА

I2 = 6 В и деление R4 = 6 деление 12 = 0,5 А или 500 мА

Поскольку сопротивления обеих ветвей равны 12 Ом, I1 и I2 равны 0,5 А (или 500 мА). Следовательно, общий ток питания IT = 0,5 + 0,5 = 1,0А.

После этих изменений иногда легче рисовать или перерисовывать новые схемы со сложными комбинациями резисторов и цепями резисторов, что становится наглядным пособием по математике. Затем продолжайте заменять любую последовательную или параллельную комбинацию, пока не найдете эквивалентное сопротивление R _EQ.Давайте попробуем еще одну более сложную схему комбинации резисторов.

2. Пример расчета 2

Чтобы найти эквивалентное сопротивление REQ, используемое в следующей схеме комбинации резисторов.

Опять же, эта схема лестничных резисторов может показаться очень сложной на первый взгляд, но, как и прежде, это просто комбинация последовательно соединенных и параллельных резисторов. Начиная с правой стороны и используя упрощенную формулу двух параллельных резисторов, мы можем найти эквивалентное сопротивление / комбинацию R8 и R10 и назвать это RA.

(Формула 4-1)

Следовательно, RA + R7 = 4 + 8 = 12 Ом

Сопротивление 12 Ом теперь параллельно R6, и общее сопротивление можно рассчитать как RB.

(Формула 4-2)

RB + R5 = 4 + 4 = 8 Ом

Значение сопротивления 8 Ом теперь параллельно с R4 и может быть рассчитано как RC, как показано.

(Формула 4-3)

RC подключен последовательно с R3, поэтому общее сопротивление RC + R3 = 8 Ом, что показано на рисунке.

Сопротивление 8 Ом параллельно R2, и его можно рассчитать как RD:

RD подключен последовательно с R1, поэтому общее сопротивление составляет RD + R1 = 4 + 6 = 10 Ом, как показано на фигура.

В конечном итоге, исходная сеть комплексных резисторов, которая включает десять независимых резисторов, соединенных последовательно и параллельно, может быть заменена эквивалентным сопротивлением REQ 10 Ом.

Когда мы сталкиваемся с любыми цепями, состоящими из последовательно включенных и параллельных резисторов, сначала нам нужно определить простое последовательное и параллельное сопротивление каждой ветви, а затем заменить их эквивалентным сопротивлением.

Это позволит нам упростить схему и поможет преобразовать сложные комбинированные резистивные схемы в один эквивалентный резистор.

Однако расчет более сложных Т-образных аттенюаторов и цепей резистивных мостов нельзя упростить до простых параллельных или последовательных цепей с эквивалентным сопротивлением. Их необходимо решить, используя закон Кирхгофа и закон напряжения Кирхгофа.

III Fault C характеристики и T обработка R esistor s в S eries и параллельный

1.

Особенности короткого замыкания и обрыва в последовательной цепи

(1) Особенности короткого замыкания

На рисунке ниже показано короткое замыкание в последовательной цепи. В схеме резисторы R1 и R2 изначально были включены последовательно, но теперь резистор R2 закорочен. В это время в последовательной цепи произойдут следующие изменения.

Короткое замыкание в последовательной цепи

1) После короткого замыкания резистора R2 в последовательной цепи присутствует только резистор R1.В это время общее сопротивление цепи уменьшается, что равно сопротивлению резистора R1.

2) Поскольку рабочее напряжение постоянного тока + V в цепи не изменилось, а общее значение сопротивления последовательной цепи уменьшилось, ток последовательной цепи увеличится после короткого замыкания резистора R2.

Увеличение силы тока в цепи связано с сопротивлением сопротивления короткого замыкания R2. Если сопротивление R2 относительно велико, величина увеличения в последовательной цепи после короткого замыкания будет относительно большой, что вызовет перегрузку по току.Когда блок питания не выдерживает чрезмерного тока, он может сгореть. Так что короткие замыкания в последовательных цепях очень вредны.

3) В то же время, поскольку повышенный ток также течет через другие резисторы (например, R1) в последовательной цепи, он также вызовет перегрузку по току в других резисторах, что также приведет к их повреждению.

4) Если в последовательной цепи увеличивается ток, протекающий через определенный компонент, это указывает на короткое замыкание в цепи.Поскольку ток в последовательной цепи после короткого замыкания увеличится, ток, протекающий через другие резисторы, также увеличится, что также увеличит падение напряжения на других резисторах.

5) Короткое замыкание в последовательной цепи относится к серьезной неисправности. Это может вызвать повреждение всех компонентов в последовательной цепи, поскольку ток, протекающий в последовательной цепи, увеличивается.

(2) Характеристики Обрыв C цепи

Когда в резисторе в последовательной цепи происходит разрыв цепи, в цепи не будет протекать ток. какая часть последовательной цепи разомкнута.

Неисправность обрыва цепи обычно не вредит последовательным цепям. Однако иногда из-за разомкнутой цепи напряжение цепи возбуждения нагрузки повышается, что приводит к ее выходу из строя.

Обрыв в последовательной цепи

2 . F ault A анализ серии R esist ors

Следующая таблица представляет собой сводку анализа неисправностей последовательных цепей с резисторами R1 и R2.

9696000

000

9000 9000 9000

000

Название компонента	Тип неисправности	Анализ неисправности	Анализ мыслей	Обрыв цепи	Нет тока через R1 и R2, и невозможно измерить напряжение на R1 и R2	Нет тока через резистор, поэтому нет напряжения.
Короткое замыкание	Ток, протекающий через R2, увеличивается, что может привести к сгоранию R2	Общее сопротивление уменьшается, что увеличивает общий ток. Если ток, протекающий через R2, слишком велик, он сожжет R2.
Сопротивление увеличилось	Ток, протекающий через R1 и R2, уменьшается, напряжение R1 увеличивается, а напряжение R2 уменьшается.	После того, как сопротивление R1 увеличивается, общее сопротивление увеличивается, общий ток уменьшается, а падение напряжения R2 уменьшается, поэтому напряжение R1 увеличивается.
Сопротивление уменьшилось	Ток, протекающий через R1 и R2, увеличивается, напряжение R1 уменьшается, а напряжение R2 увеличивается	После увеличения сопротивления R1 общее сопротивление уменьшается, и общий ток увеличивается, так что напряжение на R1 уменьшается.
Плохой контакт	Схема будет работать нормально в одном случае и ненормально в другом.	Схема работает нормально, когда контакт нормальный, цепь работает ненормально, когда контакт ненормальный
R2	Вышеупомянутые пять неисправностей	Анализ отказов такой же, как и выше (замените R1 с R2)	Аналитическое мышление такое же, как указано выше (замените R1 на R2)

3. Ошибка D обнаружение R esist или S eries

Есть много способов проверить отказ резисторов в последовательной цепи.Например, значение сопротивления каждого резистора в цепи можно измерить с помощью диапазона Ом мультиметра. Однако при поиске и устранении неисправностей метод проверки часто выбирается гибко.

Структура мультиметра

(1) Метод обнаружения неисправности для Обрыв C схема

Если устройство работает в цепи постоянного тока, используйте диапазон напряжения постоянного тока мультиметра для измерения напряжения на R1 (два измерительных провода соответственно подключены к двум контактам R1), тогда вы можете определить, есть ли в цепи обрыв цепи или нет.

Если устройство работает в цепи переменного тока, переменное напряжение мультиметра и диапазон переменного напряжения цифрового измерителя можно использовать для измерения переменного напряжения на R1.

(2) F ault I nspection Средство для короткого замыкания C цепи

Теоретически вы также можете использовать описанный выше метод для измерения напряжения на R1 при проверке короткое замыкание резисторов в последовательной цепи.Если напряжение на R1 выше нормального значения, это можно объяснить коротким замыканием в цепи. Потому что только короткое замыкание в последовательной цепи увеличит ток и напряжение на R1.

Однако существует проблема с вышеупомянутым методом проверки короткого замыкания. Необходимо знать, каково нормальное напряжение на R1, иначе невозможно определить, увеличился ли ток в цепи.

4. F a ilure Testing параллельного R esist ors

( 1) F ault D etection M ethod для разомкнутой цепи

Когда цепь отключена, используйте резистивный редуктор мультиметра для измерения общего сопротивления параллельной цепи. В нормальных условиях измеренное значение общего сопротивления должно быть

Обнаружение обрыва в параллельных цепях

Если измеренное значение сопротивления больше, чем R1 и R2, это означает, что R1 или R2 в цепи разомкнут. В частности, чтобы определить, какая цепь разомкнута, мы можем измерить ток каждой ветви сопротивления.

( 2) S hort C ircuit F ault D etection M etho d

Если измеренное общее сопротивление ноль, это означает, что в параллельной цепи произошло короткое замыкание.Если вам нужно понять детальное положение и причину отказа, вам необходимо провести дальнейшие измерения. Это имеет большое значение для поиска и устранения неисправностей, которые определяют объем неисправной цепи и направление проверки.

IV E quivalent S eries R esistance

ESR — это сокращение от эквивалентного последовательного сопротивления. Это эквивалентное «последовательное» сопротивление, означающее, что при последовательном подключении двух резисторов это значение будет увеличиваться, а при параллельном подключении — уменьшиться.

Появление ESR привело к отклонению поведения конденсаторов от его первоначального определения. Теоретически идеальный конденсатор сам по себе не генерирует никаких потерь энергии, но, поскольку материал, из которого изготовлен конденсатор, имеет сопротивление, а изоляционная среда имеет потери энергии, конденсатор становится несовершенным. Эти потери выглядят внешне так, как если бы резистор был подключен последовательно с конденсатором, поэтому они называются «эквивалентным последовательным сопротивлением».

Считаем, что резкое изменение напряжения на конденсаторе невозможно.Когда к конденсатору внезапно подается ток, напряжение конденсатора возрастает с 0 из-за его собственной зарядки. Но с ESR сам резистор генерирует падение напряжения, которое вызывает внезапное изменение напряжения на конденсаторе. Несомненно, это снизит фильтрующий эффект конденсатора, поэтому во многих высококачественных источниках питания используются конденсаторы с низким ESR.

Аналогичным образом, в случае колебательных контуров, ESR изменяет функцию контура, вызывая серьезные последствия, такие как отказ контура или даже повреждение.

Таким образом, в большинстве случаев конденсаторы с низким ESR работают лучше, чем конденсаторы с высоким ESR. Но есть исключения, и иногда ESR используется для чего-то полезного.

Например, в цепи стабилизации напряжения при переходной нагрузке конденсатор с определенным ESR немедленно генерирует колебания и запускает цепь обратной связи. Такой быстрый отклик достигается за счет определенных переходных характеристик. особенно когда скорость отклика силовой лампы низкая, а объем или емкость конденсатора строго ограничены.Такая ситуация наблюдается в некоторых трехконтактных регуляторах напряжения с трубками mos в качестве регуляторов или аналогичными схемами. В это время низкое ESR снизит общую производительность.

На самом деле, существует больше случаев, когда требуется более низкое ESR, а конденсаторы большой емкости с низким ESR относительно дороги. Поэтому во многих импульсных источниках питания принято параллельное соединение. Люди подключают несколько алюминиевых электролитических конденсаторов с относительно высоким ESR параллельно, чтобы сформировать конденсатор с низким ESR. Часто оказывается выгодным пожертвовать определенным объемом места на печатной плате в обмен на снижение стоимости устройства.

Другой концепцией, аналогичной ESR, является ESL, что означает эквивалентную последовательную индуктивность. Ранние катаные конденсаторы часто имели очень высокий ESL, и чем больше емкость, тем больше ESL. ESL часто становится частью ESR, а также вызывает сбои некоторых цепей, например, последовательный резонанс. Однако с точки зрения емкости доля ESL слишком мала, и вероятность возникновения проблем очень мала. В дополнение к развитию процесса производства конденсаторов, ESL постепенно игнорируется, и ESR используется в качестве основного эталонного фактора помимо емкости.

Подавление ESL и ESR для конденсаторов

Кстати, емкость также имеет добротность Q, аналогичную индуктивности. Этот коэффициент обратно пропорционален ESR и связан с частотой. Также редко используется.

Отказы цепи, вызванные ESR, часто трудно обнаружить, а влияние ESR легко не заметить в процессе проектирования. Самый простой способ состоит в том, что во время моделирования, если вы не можете выбрать конкретные параметры конденсатора, вы можете попытаться искусственно подключить небольшой резистор последовательно с конденсатором, чтобы имитировать эффект ESR.Как правило, ESR танталовых конденсаторов обычно ниже 100 миллиом, а алюминиевые электролитические конденсаторы выше этого значения, а ESR некоторых типов конденсаторов может достигать даже нескольких Ом.

Типичное соотношение между ESR и частотой для танталовых конденсаторов

Связь между ESR и пульсационным напряжением можно выразить формулой:

V = R (ESR) × I

В этой формуле V равно пульсации напряжения, R — ESR конденсатора, I — ток.