Расчет сопротивления резисторов и калькулятор параллельных соединений: подробное руководство

Как правильно рассчитать сопротивление резисторов при последовательном и параллельном соединении. Какие формулы использовать для вычисления общего сопротивления цепи. Как подобрать номиналы резисторов с помощью калькулятора параллельных соединений.

Основные принципы расчета сопротивления резисторов

Резисторы — одни из самых распространенных компонентов в электронных схемах. Они используются для ограничения тока, снижения напряжения, создания делителей напряжения и во многих других целях. При проектировании схем часто возникает необходимость рассчитать общее сопротивление нескольких резисторов, соединенных последовательно или параллельно.

Для корректных расчетов важно помнить основные формулы:

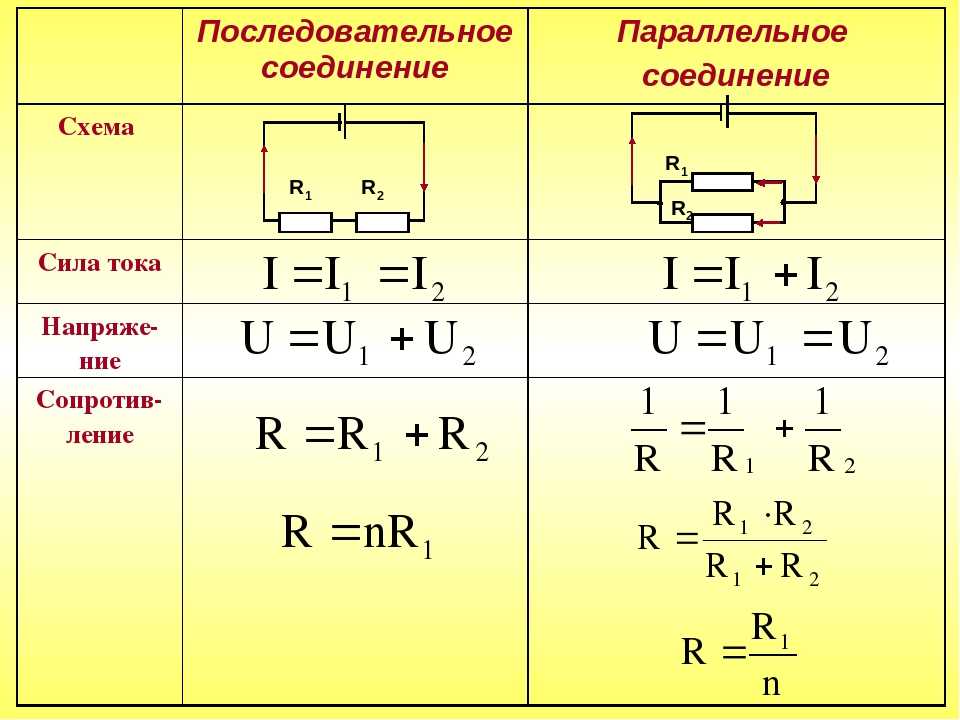
• При последовательном соединении: R общее = R1 + R2 + … + Rn
• При параллельном соединении: 1/R общее = 1/R1 + 1/R2 + … + 1/Rn

Эти базовые принципы позволяют вычислить суммарное сопротивление любой комбинации резисторов в схеме.

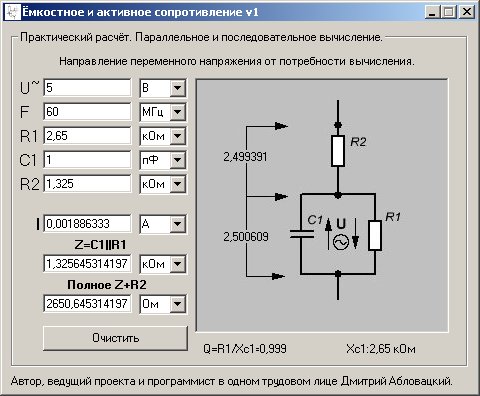
Последовательное соединение резисторов

При последовательном подключении резисторов их общее сопротивление равно сумме сопротивлений каждого из них. Это самый простой случай для расчетов.

Например, если необходимо получить сопротивление 100 кОм, а в наличии есть только резисторы на 47 кОм и 56 кОм, их можно соединить последовательно:

R общее = 47 кОм + 56 кОм = 103 кОм

Полученное значение очень близко к требуемому. В большинстве случаев такая точность является достаточной.

Параллельное соединение резисторов

Расчет параллельного соединения резисторов немного сложнее. Здесь используется обратная величина — проводимость. Общая проводимость равна сумме проводимостей отдельных резисторов.

Для двух резисторов формула упрощается:

R общее = (R1 * R2) / (R1 + R2)

Например, при параллельном соединении резисторов 1 кОм и 2 кОм получим:

R общее = (1000 * 2000) / (1000 + 2000) = 667 Ом

Важно помнить, что при параллельном подключении общее сопротивление всегда меньше сопротивления наименьшего из резисторов.

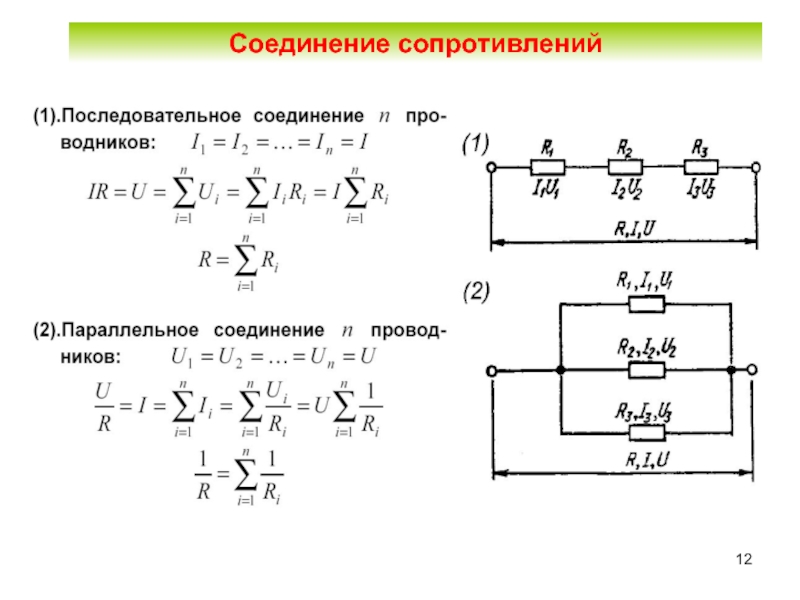
Применение калькулятора параллельных соединений

Для быстрого расчета сложных параллельных цепей удобно использовать специальные онлайн-калькуляторы. Они позволяют вводить номиналы нескольких резисторов и мгновенно получать результат.

Типичный калькулятор параллельных соединений имеет следующий функционал:

• Поля для ввода номиналов резисторов (обычно до 5-10 штук)
• Выбор единиц измерения (Ом, кОм, МОм)
• Кнопка расчета
• Поле с результатом

Использование таких инструментов значительно упрощает и ускоряет процесс подбора необходимых номиналов резисторов для схемы.

Подбор номиналов резисторов для получения нужного сопротивления

При проектировании схем часто возникает задача получить конкретное значение сопротивления, используя стандартные номиналы резисторов. Для этого применяются различные комбинации последовательного и параллельного соединения.

Например, требуется получить сопротивление 2,2 кОм. В наличии есть резисторы номиналом 1 кОм, 2 кОм и 4,7 кОм. Возможные варианты:

1. 1 кОм и 1,2 кОм последовательно
2. 4,7 кОм и 4,7 кОм параллельно
3. 2 кОм и 10 кОм параллельно

Выбор оптимального варианта зависит от конкретных требований схемы и доступных компонентов.

Особенности расчета мощности резисторов

При расчете сопротивлений важно учитывать и мощность резисторов. Мощность определяет способность резистора рассеивать тепло без повреждений.

Основные формулы для расчета мощности:

• P = U * I (мощность = напряжение * ток)
• P = U^2 / R (мощность = квадрат напряжения / сопротивление)
• P = I^2 * R (мощность = квадрат тока * сопротивление)

При последовательном соединении общая мощность равна сумме мощностей отдельных резисторов. При параллельном — сумме обратных величин мощностей.

Применение подтягивающих и стягивающих резисторов

Особую роль в электронных схемах играют подтягивающие (pull-up) и стягивающие (pull-down) резисторы. Они используются для задания определенного логического уровня на входах микросхем.

Подтягивающий резистор подключается между входом и напряжением питания. Он обеспечивает высокий логический уровень при отсутствии сигнала.

Стягивающий резистор соединяет вход с землей, задавая низкий уровень по умолчанию.

Типичные номиналы для таких резисторов — от 1 кОм до 100 кОм. Конкретное значение зависит от особенностей схемы и быстродействия сигналов.

Практические рекомендации по выбору резисторов

При проектировании электронных устройств важно учитывать не только расчетные значения сопротивлений, но и другие факторы:

• Допустимое отклонение (tolerance) — обычно от 1% до 20%
• Температурный коэффициент сопротивления
• Максимальное рабочее напряжение
• Уровень шумов
• Стоимость и доступность компонентов

Для ответственных узлов схемы рекомендуется использовать прецизионные резисторы с малым допуском и температурным коэффициентом.

Заключение

Правильный расчет и выбор резисторов — важный этап проектирования электронных устройств. Понимание основных принципов и формул, а также использование специализированных калькуляторов позволяет быстро подобрать оптимальные номиналы компонентов для любой схемы.

Регулярная практика в расчетах и эксперименты с реальными схемами помогут закрепить теоретические знания и развить интуитивное понимание работы резисторов в электронных цепях.

Расчет сопротивлений резисторов

Сопротивление резисторов R₁, R₂, R₄, R₅ в цепях делителей определяется по формулам:

,	(3.1)
,	(3.2)
,	(3.3)
,	(3.4)

где I_бэ= = 0,06 мА – постоянный ток базы,

I_кэ= = 1,6 мА – постоянный ток эмиттера,

U_кэ= = 5 В – постоянное напряжение коллектор-эмиттер,

U_бэ= = 0,276 В – постоянное напряжение база-эмиттер.

ΔU_э = 8 B

0,18 мА – ток делителя в цепях резисторов R₁, R₂, R₄, R₅.

Подставим числовые значений в формулы (3.1)–(3.4):

В соответствие с ГОСТ 28884-90 произведем подбор сопротивлений резисторов: R₁ = 16 кОм, R₂ =43 кОм, R₄ = 49 кОм, R₅ = 1,6 кОм.

Сопротивление нагрузки эмиттерного повторителя (резистор R₃ на принципиальной схеме) находится исходя из следующего условия:

.

(3.5)

Подстановкой значений в условие (3.5) получим

Ом

В соответствие с ГОСТ 28884-90 подберем сопротивления: R₆ =2,7 кОм, R₃ = 240 Ом.

Анализируя исходные данные курсовой работы, видим, что выходное напряжение генератора должно находиться в пределах U_вых=0÷5В. Исходя из произведенного графоаналитического расчета, определили, что U_КЭm = U_ВЫХmи равно 4 В. В связи с этим можно сделать вывод, что напряжения на выходе схемы должно сохраняться в пределах U_вых=0÷4В. Для этого следует использовать подстроечный резистор R₁₃. Определим параметры подстроечного резистора:

(3.6)

Подставляем числовые значения в формулу (3.6):

R₁₃=4/1,6∙10^-3=2,5 кОм

В соответствии с ГОСТ 28884-90 подберем ближайшее сопротивление по ряду Е24 (допуск 5%) значение R₁₃=2,7 кОм.

Теперь подберем конкретную модель подстроечного резистора по полученным данным:

R₁₃: СП5-16ВА-0,25 Вт

2. Расчет емкостей конденсаторов

На частоте генерации разделительные конденсаторы не должны вносить фазовых сдвигов. Величину их емкости находим из формулы:

(4.1)

где R_вху – входное сопротивление усилительного каскада, =105 Гц. Входное сопротивление усилительного каскада R_вху для усилительного каскада равно

R_вх2, для эмиттерного повторителя – R_вх1. На схеме C_р – это конденсаторы C₁ и C₂. Подстановкой значений в выражение (4.1), получим:

C₁=1/(6,28∙105∙0,1∙37500)=404 нФ,

C₂=1/(6,28∙105∙0,1∙750)=20,2 мкФ.

В соответствие с ГОСТ 28884-90 с допуском 5% выбираем C₁=470 нФ и C₂=22 мкФ.

Произведем подбор конденсаторов:

C₁: К10-17А-25В-Н50 — 0,47 мкФ — ±5% — ОЖ0. 460.174-М ТУ;

C₂: К50-35-16В – 22 мкФ — ±5% — ОЖ0.464.214 ТУ;

2. Расчет фазовращающей цепи

Найдем емкости конденсаторов (на принципиальной схеме С

3, С₄, С₅), фазовращающей цепочки, по формуле:

(5.1)

где =105 Гц, R — сопротивление фазовращающей цепи, вычисленное по формуле (1.7). Тогда

С= 1/(6,28∙105∙12500∙2,45)=49,5 нФ

В соответствие с ГОСТ 28884-90 с допуском 20% выбираем емкость С=68 нФ=0,068 мкФ.

Произведем подбор конденсаторов:

C_3, C_4, C₅:: К10-17А-Н50 — 0,068 мкФ — ±20% — ОЖ0. 460.174-М ТУ;

Анализируя задание курсовой работы, делаем вывод, что RC-генератор должен работать в двух диапазонах частот —

f₁=10÷50Гц, f₂=100÷200Гц. Поэтому нужно использовать тумблеры для выбора нужного диапазона частот, и от положения этих тумблеров будет зависеть, какие резисторы мы будем использовать для фазовращающей цепи. Также предусмотрим возможность точной настройки частоты f внутри каждого диапазона. Для этого будем использовать соединенные последовательно подстроечные резисторы (R₁₀, R_10’, R₁₁, R_11’, R₁₂, R_12’) и постоянные резисторы (R₇, R_7’, R₈, R_8’, R₉, R_9’). Схема генератора приведена в приложении. Проанализируем формулу для расчета сопротивлений резисторов фазовращающей цепи:

(5. 2)

Отмечаем, что при повышении частоты, уменьшается сопротивление R, и наоборот, при понижении частоты – сопротивление R увеличивается.

Поскольку подстроечный резистор соединен последовательно с постоянным резистором, то сумма их сопротивлений равна сопротивлению ветви.

Найдем сопротивления для граничных частот используемых диапазонов по формуле (5.2):

• для =10 Гц :

• для =50 Гц :

• для =100 Гц :

• для ₄=200 Гц :

Поскольку при точной настройке минимальное значение сопротивления ветви будет при максимальном значении частоты диапазона, то можно сделать вывод о том, что в этом случае сопротивление подстроечного резистора будет равно нулю, а сопротивление ветви будет определяться только сопротивлением постоянного резистора.

Следовательно, найдем значение постоянных регистров для обоих диапазонов частот:

R₇, R₈, R₉ = R _{f 4}=6,57 кОм;

R_7’, R_8’, R_9’ = R _{f 2}=26,3 кОм;

В соответствие с ГОСТ 28884-90 произведем подбор сопротивлений постоянных резисторов по ряду Е24 (допуск 5%):

R₇, R₈, R₉ = 6,8 кОм;

R_7’, R_8’, R_9’ = 27 кОм;

Тогда найдем максимальные значения сопротивлений для подстроечных резисторов R

10_m, R_10’m, R_11m, R_11’m, R_12m, R_12’m:

R_10m, R_11m, R_12m= 13,1 – 6,57 = 6,53 кОм;

R_10’m, R_11’m, R_12’m= 131 – 26,3 = 104,7 кОм;

В соответствие с ГОСТ 28884-90 произведем подбор сопротивлений постоянных резисторов по ряду Е24 (допуск 5%):

R_10m, R_11m, R_12m= 6,8 кОм;

R_10’m, R_11’m, R_12’m= 100 кОм;

Используя эти данные, подбираем конкретные модели подстроечных резисторов:

R₁₀, R₁₁, R₁₂ : СП5-16ВВ-0,125Вт — 6,8 кОм

R₁₀, R₁₁, R₁₂ : СП3-19А-0,5Вт – 100 кОм

Для переключения между резисторами, используемыми для диапазонов частот 10÷50 Гц и 100÷200 Гц, используем тумблеры типа ON-ON:

SA1, SA2, SA3: SMTS-102-A2 3 PIN (3A 125VAC) SPDT 3P

(Производитель: Jietong Switch)

Расчёт сопротивления резисторов и ёмкости конденсаторов

Автор: admin, 22 Мар 2013

Расчёт сопротивления резисторов и ёмкости конденсаторов

В этой статье рассмотрим как можно с помощью параллельного и последовательного включения резисторов и конденсаторов подобрать нужный номинал радиодетали, при отсутствии нужного.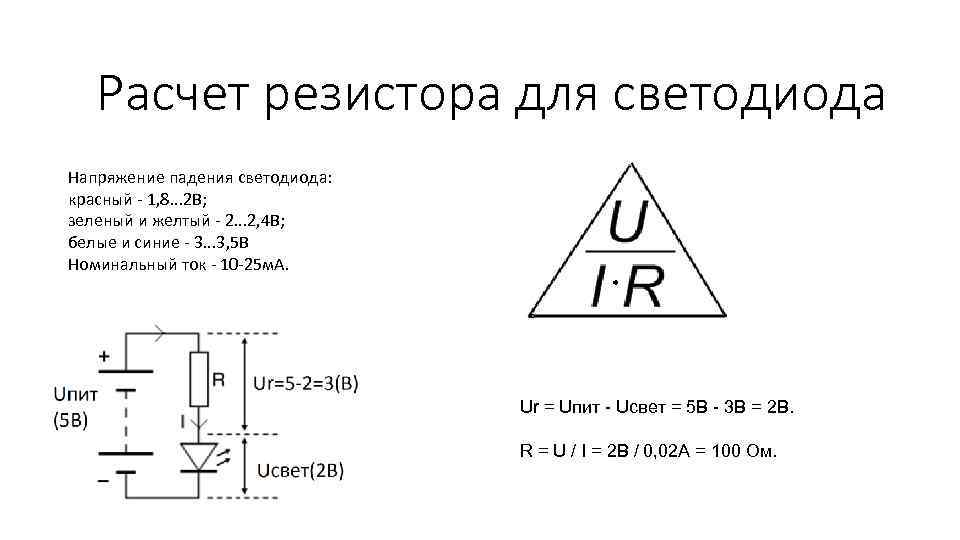 Расчёт производится по формулам расчёта сопротивления и ёмкости для параллельного и последовательного включения, а также с помощью удобной таблицы подбора ёмкости и сопротивления.

 

Резисторы

Широко применяются в радиоприёмниках, усилителях сигналов и во многих других схемах. Они служат для ограничения тока, создания падения напряжения, регулирования частоты, громкости и других сигналов. Обозначаются на схемах буквой R. Сопротивление резистора измеряется в Омах. Для больших сопротивлений используют единицы: килоомы (1кОм=1000Ом), мегаомы (1Мом=1000кОм). Кроме сопротивления резисторы характеризуются мощностью рассеяния, это такая наибольшая мощность, которую резистор может выдержать длительное время. Мощность рассеяния измеряется в ваттах (Вт). Ещё один показатель — это наибольшее возможное отклонение действительного сопротивления от  номинального, указанного на резисторе, выражается в %. Резисторы бывают постоянные (не изменяют своего сопротивления) и переменные(изменяют сопротивление в зависимости от положения движка резистора).

Иногда, при сборке схемы не оказывается под рукой резистора нужного номинала. В этом случае в большинстве случаев можно заменить резистор на ближайший по номиналу — например вместо 110 Ом можно использовать резистор номиналом 100 или 120 Ом. А если нет и ближайшего по номиналу или требуется точное значение сопротивления, то можно составить нужное сопротивление с помощью последовательного или параллельного соединения нескольких резисторов.

Последовательное соединение резисторов:

последовательное соединение резисторов

 

При последовательном соединении резисторов их общее сопротивление равно их сумме: Rобщ = R1+R2+…+Rn.

 

 

 

Параллельное соединение резисторов:

параллельное соединение резисторов

 

При параллельном соединении резисторов их общее сопротивление рассчитывается по формуле:

1/Rобщ = 1/R1 + 1/R2 +…+1/Rn или

Rобщ = 1/(1/R1 + 1/R2 +…+1/Rn).

На практике для подбора нужного сопротивления обычно включают параллельно два резистора, в этом случае формула примет вид:

Rобщ = R1*R2/(R1+R2).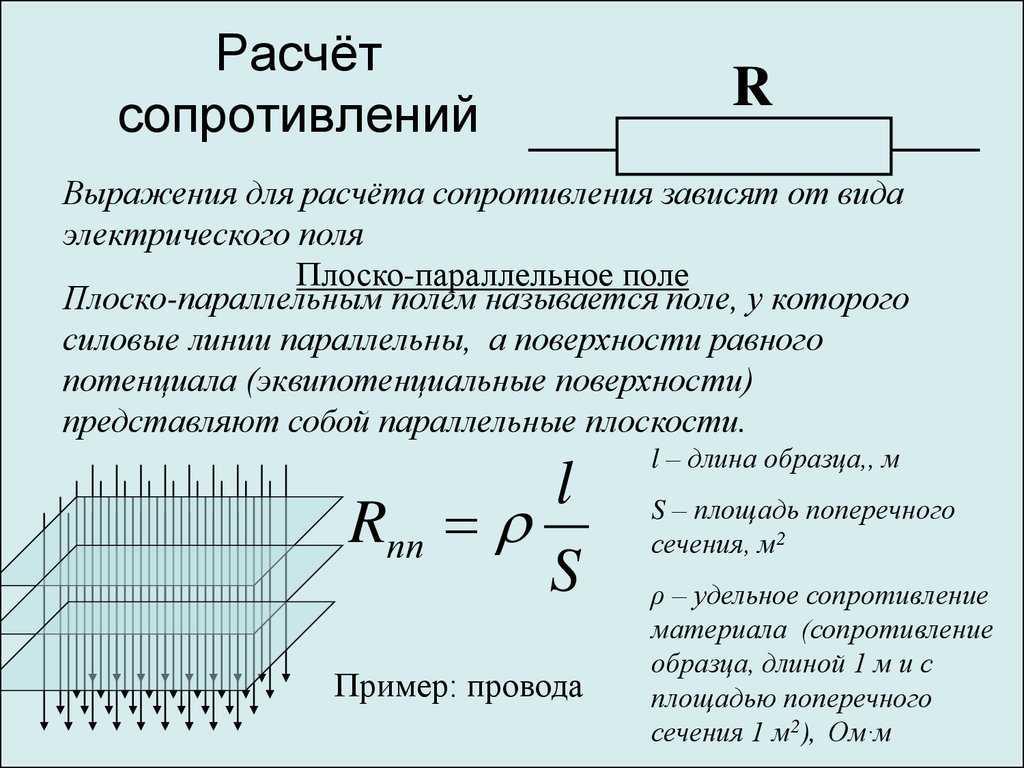

Ещё можно отметить, что при включении резисторов одинакового сопротивления, то их общее сопротивление будет равно половине сопротивления каждого их них. Мощность рассеяния, в этом случае, увеличится в 2 раза. Также при параллельном соединении общее сопротивление всегда меньше наименьшего из включенных в параллель резисторов.

Конденсаторы

Конденсаторы, как и резисторы, тоже очень широко применяются. Конденсатор это накопитель энергии, в простейшем виде это две пластины, между которыми находится диэлектрик, в качестве диэлектрика может быть просто воздух. Конденсаторы также бывают постоянной и переменной ёмкости. Единицей ёмкости является  фарада(Ф). На практике используют меньшие ёмкости, их выражают в микрофарадах(1Ф=1 000 000 мкФ), нанофарадах(1мкФ = 1 000 нФ), пикофарадах(1нФ=1 000 пФ). Также конденсаторы характеризуются рабочим напряжением, выражаемом в вольтах (В). Превышение на конденсаторе напряжения выше рабочего может привести к «пробою» диэлектрика конденсатора.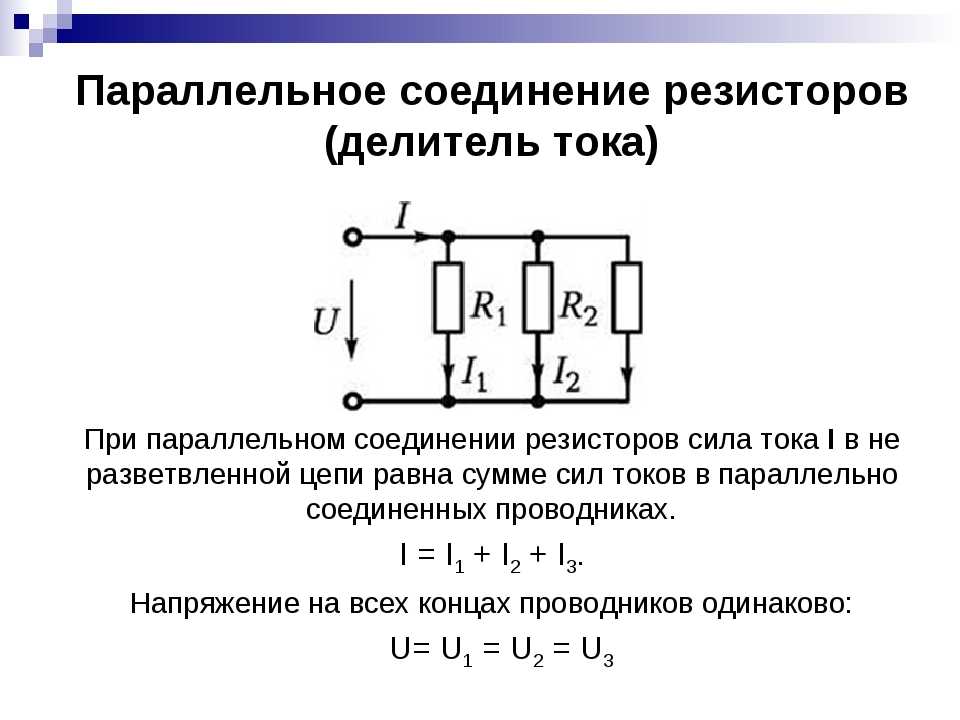

Конденсатор не проводит постоянный ток, а переменному току оказывает сопротивление, которое вычисляется по формуле:

Хс = 1/(2πfC), где

• Хс — емкостное сопротивление конденсатора, Ом;
• π — математическая константа, примерно равная 3,1416;
  
• f — частота переменного тока, Гц;
• С — ёмкость конденсатора, Ф.

Рассмотрим как можно собрать нужную ёмкость из имеющихся под рукой.

Последовательное включение конденсаторов:

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов их общая ёмкость рассчитывается по формуле, очень похожей на формулу для параллельного включения резисторов:

Собщ = 1/(1/С1+1/С2+…+1/Сn).

Но чаще тоже используют два конденсатора, тогда формула упрощается:

Собщ = С1*С2/(С1+С2).

Также, при включении конденсаторов с одинаковой ёмкостью их общая ёмкость будет в два раза меньше ёмкости каждого из них. Рабочее напряжение такого сборного конденсатора увеличится в 2 раза.

Параллельное включение конденсаторов:

Параллельное соединение конденсаторов

 

 

При параллельном соединении конденсаторов их общая ёмкость будет равна сумме всех емкостей.

Собщ = С1+С2+…+Сn.

При необходимости можно делать даже комбинированные соединения и параллельные и последовательные, в этом случае высчитывается ёмкость(или сопротивление) по одинаковым группам соединений, получают промежуточные значения, например Собщ1, Собщ2.., а потом уже из них высчитывают общее значение.

Но, как правило, более двух деталей для составления нужного номинала не используют, для параллельного соединения конденсаторов и последовательного резисторов всё просто — считаем сумму. А для последовательного соединения конденсаторов и параллельного соединения резисторов нужно считать, поэтому будет удобно пользоваться заранее составленной таблицей, которая подойдёт для обоих радиоэлементов.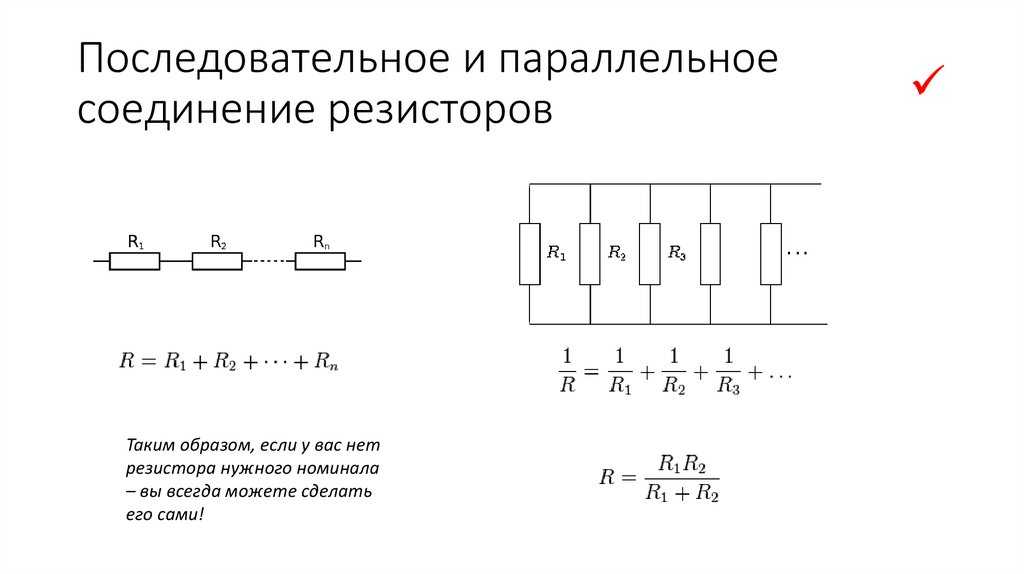

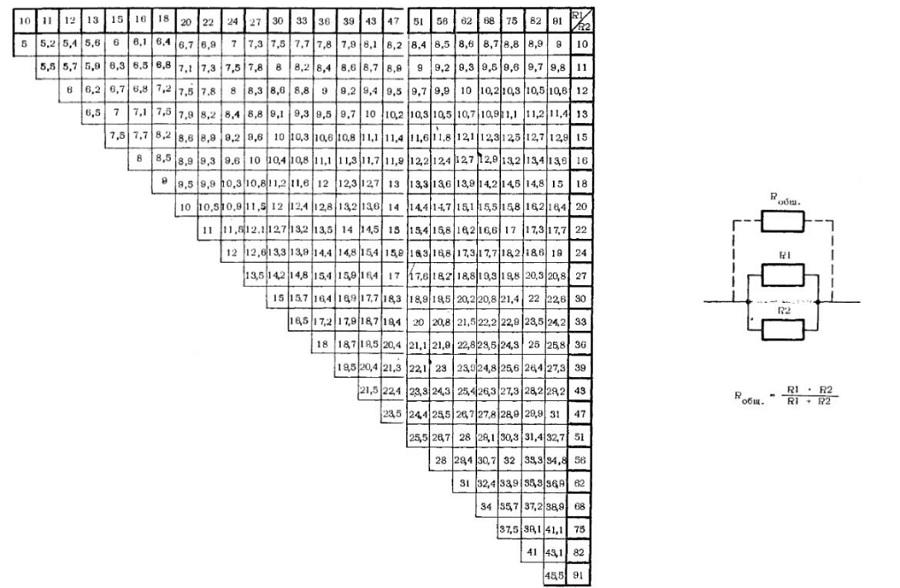
Таблица расчёта общего сопротивления (ёмкости) для двух параллельно соединённых резисторов (двух последовательно соединённых конденсаторов)

Таблица расчёта общего сопротивления(ёмкости)

По горизонтали смотрим значения, выделенные зелёным цветом, первого резистора(конденсатора) по вертикали второго. На перекрестии этих двух значений и будет общее сопротивление (ёмкость).

Будет интересно почитать:

Рубрики: Электронные устройства, Электросхемы
Метки: электроника, электросхема

ток — Расчет опорного резистора напряжения (шунт)

спросил 2 года 8 месяцев назад

Изменено 2 года, 8 месяцев назад

Просмотрено 888 раз

\$\начало группы\$

Я пытаюсь спроектировать схему, используя этот прецизионный эталон напряжения LM4040-5 для моего DAC8554, но я не могу понять, как правильно рассчитать номинал резистора, который нужно применить. Прямо сейчас LM4040-5V (референс 5 В) дает мне напряжения в диапазоне от 4,77 В до 5,11 В. Явно не очень точно!

Это базовая схема LM4040, приведенная в его техническом описании, а также формула, которую они предлагают для расчета номинала резистора:

---

---

Итак, для моего конкретного проекта В _S == +12 В , V _R == +5v , но где/как я могу получить значения для I _L (нагрузка) и I _Q (рабочий ток)?

• ток
• измерение тока
• ЦАП
• нагрузка
• опорное напряжение

\$\конечная группа\$

8

\$\начало группы\$

Это значения взяты из спецификаций соответствующих деталей. ЦАП показывает следующее:

Итак, вам нужно подать 250 мкА на ЦАП.

Тогда для правильной работы LM4040 требуется обратный ток:

Значит минимум 74мкА для версии -5.

Таким образом, минимальный ток через резистор должен быть 324 мкА. Если вы не считаете каждый мкА, я бы увеличил до 500 мкА, по крайней мере, чтобы убедиться, что у вас достаточно тока для допустимого отклонения входного питания и т. д.

С 12 В на одной стороне резистора и 5 В на другой, тогда максимальный резистор значение, которое вы можете иметь, составляет (12-5) В / 500 мкА или 14 кОм. Все, что выше, может не регулироваться должным образом.

Это, конечно, при условии, что к эталону не подключена никакая другая нагрузка.

\$\конечная группа\$

6

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Резисторы: Подтягивающие и подтягивающие резисторы

К Джиджи 2 года назад

Вы когда-нибудь задумывались над тем, почему резисторы так широко используются, но почти никто не отдает им должное за то, что они делают? Прежде чем мы углубимся в то, что именно представляют собой подтягивающие и подтягивающие резисторы, нам нужно сначала понять, что такое резисторы.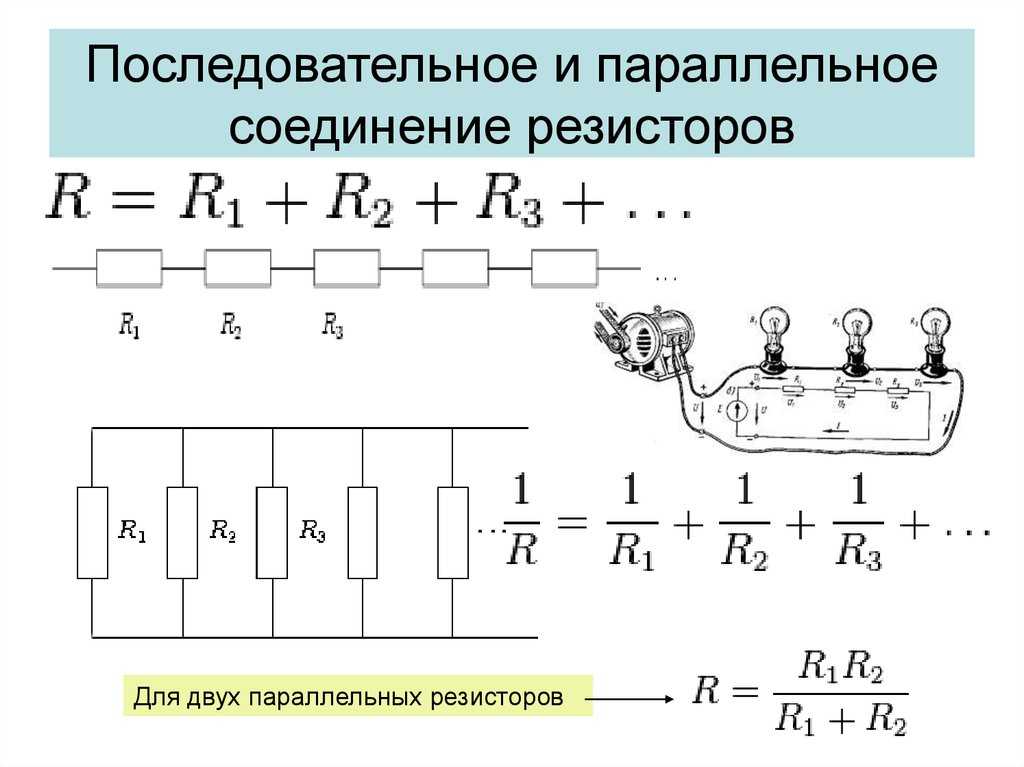

Итак, вот некоторые основы, которые вы должны понять о резисторах, прежде чем мы сможем приступить к нашей сегодняшней основной теме!

Резисторы

Резисторы определяются как пассивные электрические компоненты с двумя клеммами, которые реализуют электрическое сопротивление как элемент цепи.

Ссылка: Википедия

Таким образом, можно сказать, что основной задачей резисторов является регулирование или установка потока электронов (тока) через них с помощью типа проводящего материала, из которого они состоят.

Символ, обозначающий резисторы:

Существует много типов резисторов, но обычно их можно разделить на 4 группы :

• Углеродный резистор – Низкая мощность, изготовлен из угольной пыли или графитовой пасты.
• Полупроводниковый резистор – Высокочастотная/прецизионная тонкопленочная технология поверхностного монтажа.
• Резистор с проволочной обмоткой – Очень высокая номинальная мощность, металлический корпус для установки на радиатор.
• Пленочный или металлокерамический резистор – Очень низкая мощность, изготовлен из проводящей пасты на основе оксида металла.

Хотите узнать больше о резисторах? Кликните сюда!

---

Теперь, когда мы знаем больше о резисторах, мы можем перейти к тому, что будет освещено в этом блоге:

• Подтягивающий резистор
• Подтягивающий резистор
• Разница между подтягивающим и подтягивающим резистором
• Типичные области применения подтягивающего и подтягивающего резистора
• Расчет фактических значений подтягивающего и подтягивающего резистора
• Практический пример

---

Подтягивающие резисторы

Подтягивающие резисторы определяются как резисторы, которые используются для обеспечения натяжения провода до высокого логического уровня при отсутствии входного сигнала.

Это означает, что подтягивающие резисторы подключаются между источником напряжения и конкретным контактом, они также часто встречаются в цифровых логических схемах.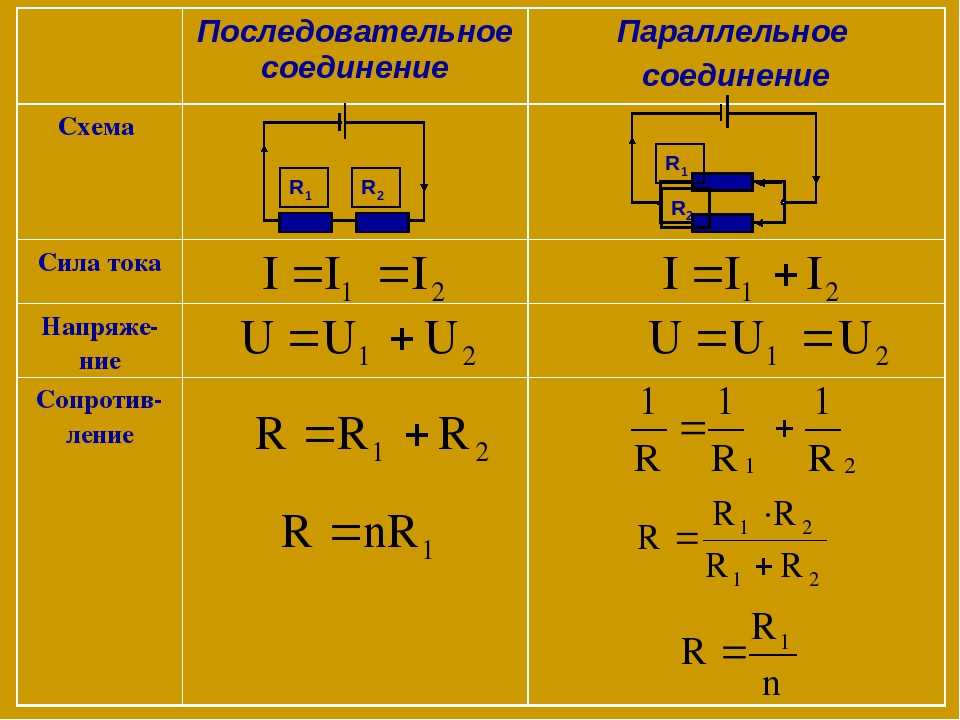

Ref: EEPower

Одна вещь, которую нужно знать перед использованием подтягивающего резистора, это логические состояния. Логические схемы имеют 3 логических состояния: высокий, низкий и плавающий (или высокий импеданс). Целью подтягивающего резистора является обеспечение того, чтобы входные контакты были эквивалентны напряжению земли или VCC (общий коллектор напряжения). Как правило, они также используются в сочетании с переключателями или транзисторами.

Подтягивающие резисторы

Подтягивающие резисторы определяются как резисторы, которые используются для обеспечения натяжения провода до высокого логического уровня при отсутствии входного сигнала.

Это означает, что подтягивающие резисторы подключаются между землей и соответствующим контактом на устройстве. Хотя они менее распространены, чем подтягивающие резисторы, они работают так же, как подтягивающие резисторы.

Ref: EEPower

Одно замечание по поводу подтягивающих резисторов: они должны иметь большее сопротивление, чем импеданс логической схемы, иначе они могут слишком сильно снизить общее напряжение. Это приведет к тому, что входное напряжение на выводе останется на постоянном низком логическом уровне.

---

Разница между подтягивающим и подтягивающим резисторами

Ref: Elprocus высокое состояние.

Подтягивающий резистор	Подтягивающий резистор
Подключение к нагрузке и заземление в низком состоянии

---

Типичные области применения подтягивающих и подтягивающих резисторов

Подтягивающие резисторы (чаще):

• Аналого-цифровые преобразователи для обеспечения управляемого потока тока в резистивный датчик.
• Шина протокола I2C
• Интерфейс коммутатора с микроконтроллером

Подтягивающие резисторы (реже):

• Выходы для обеспечения известного выходного импеданса.
• Шина протокола I2C

---

Расчет фактических значений подтягивающего и подтягивающего резисторов

Для расчета подтягивающего и подтягивающего сопротивления сначала необходимо применить формулу закона Ома: Сопротивление = напряжение/ Текущий или Р= В/И .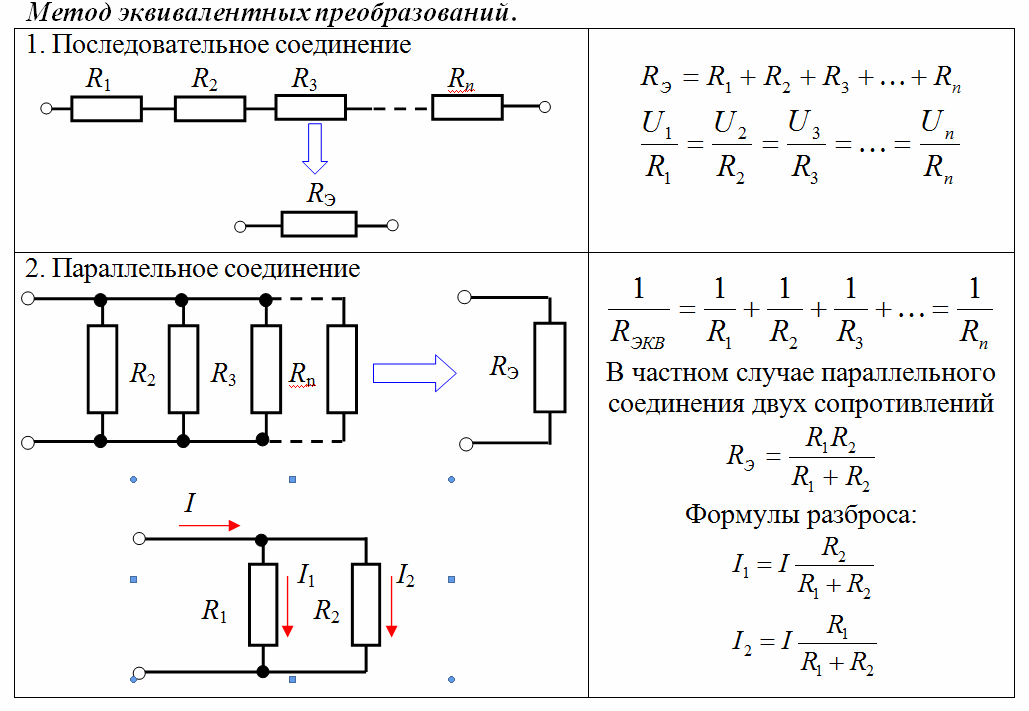

Однако, прежде чем мы сможем рассчитать фактические значения, вот несколько вещей, на которые следует обратить внимание при выборе номинала резистора:

• Значение резистора не должно быть слишком большим, поскольку оно влияет на протекание тока для функционирования входного контакта.
• Значение резистора не должно быть слишком низким, иначе через него может протекать избыточный ток, что может привести к короткому замыканию.

---

Практический пример

Чтобы лучше проиллюстрировать, как на самом деле рассчитать сопротивление натяжению вверх и вниз, вот пример того, как это сделать:

Подтягивающий резистор Пример:

Ссылка: gadgettronix

Предположим, что ток равен 100 мкА при +5 В постоянного тока (напряжение источника). Мы используем 4 В в качестве подтягивающего напряжения (минимальное напряжение), потому что наше напряжение Vcc равно 5, и наш подтягивающий резистор не должен ни превосходить Vcc, ни быть слишком низким.