Что такое размерность напряжения в сопротивлении материалов. Как определяется понятие напряжения. Какие бывают виды напряжений. Как рассчитывается размерность напряжения. Какова формула для расчета напряжения. Что такое деформация и как она связана с напряжением.
Что такое напряжение в сопротивлении материалов
Напряжение — это внутренняя сила, возникающая в материале при его деформации под действием внешних нагрузок. Напряжение характеризует интенсивность внутренних сил, действующих на единицу площади сечения тела.
Математически напряжение определяется как отношение силы, действующей на малый участок поверхности тела, к площади этого участка:
σ = F / A
где:
- σ — напряжение
- F — сила
- A — площадь
Единица измерения напряжения в СИ — паскаль (Па). 1 Па = 1 Н/м2.
Виды напряжений в сопротивлении материалов
В зависимости от характера действующих сил и вида деформации различают следующие основные виды напряжений:
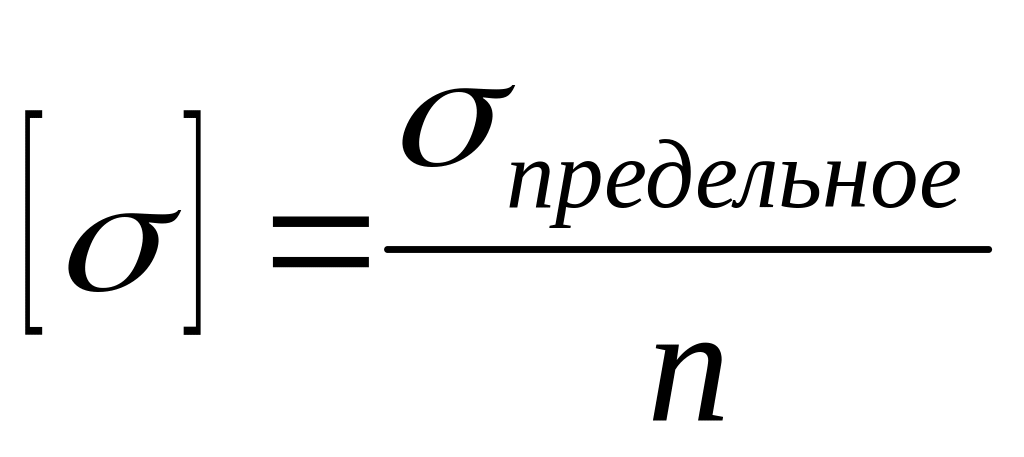
- Нормальные напряжения — возникают при растяжении-сжатии и изгибе
- Касательные напряжения — возникают при сдвиге и кручении
- Главные напряжения — максимальные и минимальные нормальные напряжения в данной точке тела
- Эквивалентные напряжения — используются для оценки сложного напряженного состояния
Размерность напряжения
Размерность напряжения можно определить из его физического смысла как отношения силы к площади:
[σ] = [F] / [A] = ML/T2 / L2 = M/(LT2)
Таким образом, размерность напряжения выражается формулой:
[σ] = M L-1 T-2
Где:
- M — размерность массы
- L — размерность длины
- T — размерность времени
Формула для расчета напряжения
Общая формула для расчета напряжения имеет вид:
σ = F / A
Для различных видов деформации используются свои формулы:
- При растяжении-сжатии: σ = N / A
- При изгибе: σ = M / W
- При кручении: τ = T / Wp
Где N — продольная сила, M — изгибающий момент, T — крутящий момент, W и Wp — моменты сопротивления сечения.
Связь напряжений и деформаций
Между напряжениями и деформациями существует прямая зависимость, которая в упругой области описывается законом Гука:
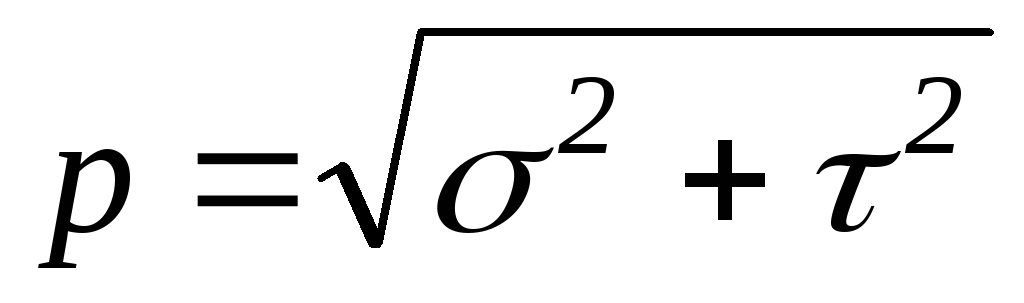
σ = E * ε
Где:
- σ — нормальное напряжение
- E — модуль упругости (модуль Юнга)
- ε — относительная деформация
Данная зависимость позволяет по известным напряжениям определять деформации и наоборот.
Допускаемые напряжения
При расчетах на прочность вводится понятие допускаемого напряжения [σ]. Оно определяется по формуле:
[σ] = σпред / n
Где:
- σпред — предельное напряжение для материала
- n — коэффициент запаса прочности
Условие прочности записывается в виде: σmax ≤ [σ]
Тензор напряжений
Напряженное состояние в точке тела полностью описывается тензором напряжений, который в общем случае имеет 9 компонент:
σx τxy τxz
τyx σy τyz
τzx τzy σz
Где σx, σy, σz — нормальные напряжения, τxy, τxz и т.д. — касательные напряжения.
Метод сечений для определения напряжений
Для определения внутренних усилий и напряжений в сечениях тела применяется метод сечений, который заключается в следующем:
- Мысленно рассекаем тело плоскостью
- Отбрасываем одну из частей
- Заменяем действие отброшенной части внутренними силовыми факторами
- Составляем уравнения равновесия
- Определяем внутренние усилия и напряжения в сечении
Этот метод позволяет определить распределение напряжений по сечению элемента конструкции.
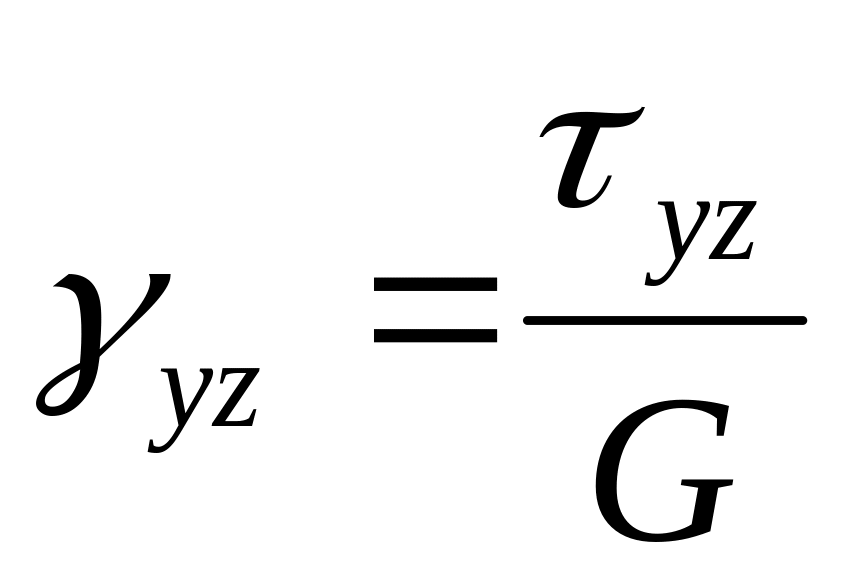
Концентрация напряжений
В местах резкого изменения формы или размеров детали (отверстия, выточки, галтели и т.п.) происходит концентрация напряжений — их значительное локальное увеличение. Это учитывается при расчетах на прочность с помощью коэффициента концентрации напряжений:
K = σmax / σnom
Где σmax — максимальное напряжение в зоне концентрации, σnom — номинальное напряжение в сечении.
Напряженно-деформированное состояние
Напряженно-деформированное состояние (НДС) конструкции характеризует распределение напряжений, деформаций и перемещений во всех точках рассматриваемого тела. Для определения НДС применяются аналитические и численные методы, в частности метод конечных элементов.
Знание НДС позволяет:
- Оценить прочность и жесткость конструкции
- Выявить опасные сечения и зоны концентрации напряжений
- Оптимизировать форму и размеры деталей
- Прогнозировать поведение конструкции под нагрузкой
Заключение
Понятие напряжения является ключевым в сопротивлении материалов и теории упругости. Знание размерности, формул и видов напряжений необходимо для выполнения прочностных расчетов и проектирования надежных конструкций. Связь напряжений и деформаций позволяет анализировать поведение материалов под нагрузкой и определять их механические характеристики.

Понятие о напряжениях и деформациях (Лекция №5)
Как отмечалось выше, внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Зафиксируем точку М в рассматриваемом сечении с единичным вектором нормали n. В окрестности этой точки выделим малую площадку F. Главный вектор внутренних сил, действующих на этой площадке, обозначим через P (рис. 1 а). При уменьшении размеров площадки соответственно
Рис.1. Композиция вектора напряжения.
уменьшаются главный вектор и главный момент внутренних сил, причем главный момент уменьшается в большей степени. В пределе при получим
Аналогичный предел для главного момента равен нулю. Введенный таким образом вектор рn называется вектором напряжений в точке. Этот вектор зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки F, характеризуемой вектором п. Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора п определяет напряженное состояние в этой точке.
Этот вектор зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки F, характеризуемой вектором п. Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора п определяет напряженное состояние в этой точке.
В общем случае направление вектора напряжений рn не совпадает с направлением вектора нормали п. Проекция вектора рnна направление вектора п называется нормальным напряжением , а проекция на плоскость, проходящую через точку М и ортогональную вектору
Размерность напряжений равна отношению размерности силы к размерности площади. В международной системе единиц СИ напряжения измеряются в паскалях: 1 Па=1 Н/м2.
При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.
е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.
Отнесем недеформированное тело к декартовой системекоординат Oxyz (рис. 2). Положение некоторой точки М в этой системе координат определяется радиус-вектором r(х, у, z). В деформированном состоянии точка М займет новое положение М/ , характеризуемое радиус-вектором r‘ (х, у, z). Вектор u=r’r называется вектором, перемещений точки М. Проекции вектора u на координатные оси определяют компоненты вектора перемещений и(х, у, z), v(х, у, z), w(х, у, z), равные разности декартовых координат точки тела после и до деформации.
Перемещение, при котором взаимное расположение точек тела не меняется, не сопровождается деформациями. В этом случае говорят, что тело перемещается как жесткоецелое (линейное перемещение в пространстве или поворот относительно некоторой точки). С другой стороны, деформация, связанная с изменением формы тела и его объема, невозможна без перемещения его точек.
С другой стороны, деформация, связанная с изменением формы тела и его объема, невозможна без перемещения его точек.
Рис.2. Композиция вектора перемещения
Деформации тела характеризуются изменением взаимного расположения точек тела до и после деформации. Рассмотрим, например, точку М и близкую к ней точку N, расстояние между которыми в недеформированном состоянии вдоль направления вектора s обозначим через (рис. 2). В деформированном состоянии точки М и N переместятся в новое положение (точки М’ и N), расстояние между которыми обозначим через s’. Предел отношения
называется относительной линейной деформацией в точке М в направлении вектора s, рис.3. Рассматривая три взаимно перпендикулярных направления, например, вдоль координатных осей Ох, Оу и Oz, получим три компоненты относительных линейных деформаций характеризующих изменение объема тела в процессе деформации.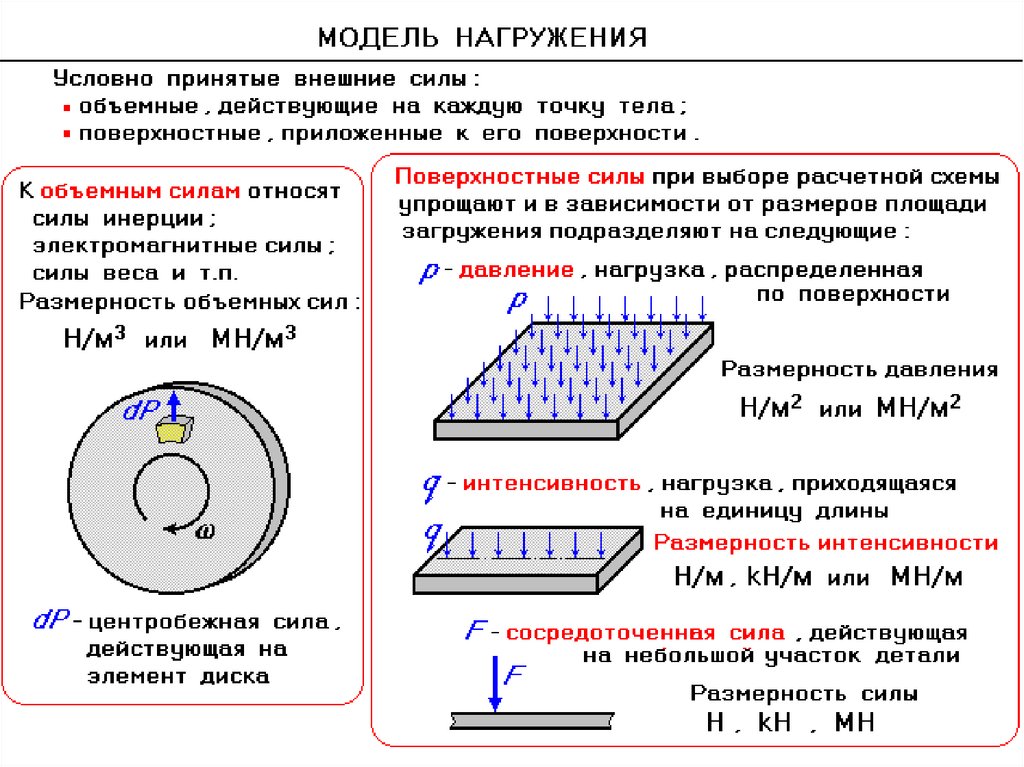
Для описания деформаций, связанных с изменением формы тела, рассмотрим точку М и две близкие к ней точки N и Р, расположенные в недеформированном состоянии в направлении двух взаимно ортогональных векторов s1 и s2. Расстояния между точками обозначим через и (рис. 4). В деформированном состоянии положение точек обозначим через М’, N’ и Р’. Угол между отрезками M’N’ и М’Р’ в общем случае будет отличным от прямого. При , изменение угла между двумя ортогональными до деформации направлениями называется угловой деформацией. Как видно из рис. 4, угловая деформация складывается из двух углов и , связанных с поворотами отрезков MN’ и М’Р’ ‘в.плоскости, образованной векторами s1 и s2, относительно этих векторов. Если заданы три взаимно ортогональных вектора, направленных вдоль координатных осей, то имеются три угловые деформации , и , которые вместе с тремя линейными деформациями , и

Рис.3. Композиция линейной деформации
Рис. 4. Композиция угловой деформации
НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ. ТЕНЗОР НАПРЯЖЕНИЙ
Вектор напряжений pn является физическим объектом, имеющим длину, направление и точку приложения. В этом смысле он обладает векторными свойствами. Однако этому объекту присущи некоторые свойства, не характерные для векторов. В частности, величина и направление вектора напряжений зависят от ориентации вектора n нормали бесконечно малого элемента поверхности dF. Совокупность всех возможных пар векторов п, рn в точке определяет напряженное состояние в данной точке. Однако для полного описания напряженного состояния в точке нет необходимости задавать бесконечное множество направлений вектора n, достаточно определить векторы напряжений на трех взаимно перпендикулярных элементарных площадках. Напряжения на произвольно ориентированных площадках могут быть выражены через эти три вектора напряжений. В дальнейшем лектор умышленно меняет ориентацию координат. Так, что ось Z продольная ось бруса, а X и Y координаты любой точки его поперечного сечения.
Напряжения на произвольно ориентированных площадках могут быть выражены через эти три вектора напряжений. В дальнейшем лектор умышленно меняет ориентацию координат. Так, что ось Z продольная ось бруса, а X и Y координаты любой точки его поперечного сечения.
Проведем через точку М три взаимно перпендикулярных плоскости с векторами нормалей, направления которых совпадают с направлениями координатных осей. Элементарные площадки образуем дополнительными сечениями, параллельными исходным плоскостям и отстоящими от них на бесконечно малые расстояния dx, dy, dz. В результате в окрестности точки М получим бесконечно малый параллелепипед, поверхность которого образована элементарными площадками dFх=dydz, dFн==dxdz, dFя=dxdy. Векторы напряжений px, py, pz, действующие на элементарных площадках, показаны на рис. 5.
Разложим каждый вектор напряжений на составляющие вдоль координатных осей (рис. 6). На каждой площадке действует одно нормальное напряжение , , , где индекс обозначает направление вектора нормали к площадке и два касательных напряжения с двумя индексами, из которых первый указывает направление действия компоненты напряжения, второйнаправление вектора нормали к площадке.
6). На каждой площадке действует одно нормальное напряжение , , , где индекс обозначает направление вектора нормали к площадке и два касательных напряжения с двумя индексами, из которых первый указывает направление действия компоненты напряжения, второйнаправление вектора нормали к площадке.
Рис. 5. Равновесное состояние бесконечно-малого параллелепипеда
Рис.6. Компоненты тензора напряженного состояния
Совокупность девяти компонент напряжений (по три на каждой из трех взаимно перпендикулярных площадок) представляет собой некоторый физический объект, называемый тензором напряжений в точке. Тензор можно представить в виде матрицы, соответствующим образом упорядочив девять компонент:
Для компонент тензора напряжений общепринятым является следующее правило знаков: компонента считается положительной, если на площадке с положительной внешней нормалью (т. е. направленной вдоль одной из координатных осей) эта компонента направлена в сторону положительного направления соответствующей оси. На рис. 6 все компоненты тензора напряжений изображены положительными. На площадках с отрицательной внешней нормалью (грани параллелепипеда, не видимые на рис. 5 и 6) положительная компонента направлена в противоположном направлении. Напряжения на трех взаимно ортогональных площадках с отрицательными направлениями нормалей также характеризуют напряженное состояние в точке. Эти напряжения, являющиеся компонентами тензора напряжений, определяются аналогично напряжениям на площадках с положительной нормалью. Они обозначаются теми же символами и имеют положительное направление, обратное изображенному на рис. 6.
е. направленной вдоль одной из координатных осей) эта компонента направлена в сторону положительного направления соответствующей оси. На рис. 6 все компоненты тензора напряжений изображены положительными. На площадках с отрицательной внешней нормалью (грани параллелепипеда, не видимые на рис. 5 и 6) положительная компонента направлена в противоположном направлении. Напряжения на трех взаимно ортогональных площадках с отрицательными направлениями нормалей также характеризуют напряженное состояние в точке. Эти напряжения, являющиеся компонентами тензора напряжений, определяются аналогично напряжениям на площадках с положительной нормалью. Они обозначаются теми же символами и имеют положительное направление, обратное изображенному на рис. 6.
общее понятие, виды, размерность. Допускаемые напряжения.
Предположим,
что внутренние силы в поперечном сечении
бруса непрерывно распределены по площади
сечения. Пусть на малую, но конечную
площадку ΔА действует внутренняя сила
ΔR
– равнодействующая внутренних сил,
действующих на этой площадке. Разложив
ΔR
на составляющие по осям z,
x,
y
получим ее компоненты ΔNz,
ΔQx,
ΔQy.
Разложив
ΔR
на составляющие по осям z,
x,
y
получим ее компоненты ΔNz,
ΔQx,
ΔQy.
Напряжение – интенсивность внутренних сил или внутреннее усилие, передаваемое через какое либо воображаемое плоское сечение, отнесенное к площади этого сечения.
Отношение вида Pср = ΔR/ ΔА определяет среднее напряжение на данной площадке.
Истинное (полное) напряжение в точке можно определить, уменьшая площадку: P = limΔA→0ΔR/ΔA = dR/dA. Размерность напряжения – Па (Паскаль) или МПа (Мегапаскаль).
Полное напряжение
обычно в расчетах не применяется, а
определяется его нормальная к сечению
составляющая σz
– нормальное напряжение, и касательные
τzx,
τzy– касательные
напряжения. Нормальное напряжение
считается положительным, если оно
направлено от сечения (растяжение), и
считается отрицательным, если оно
направлено к сечению (сжатие).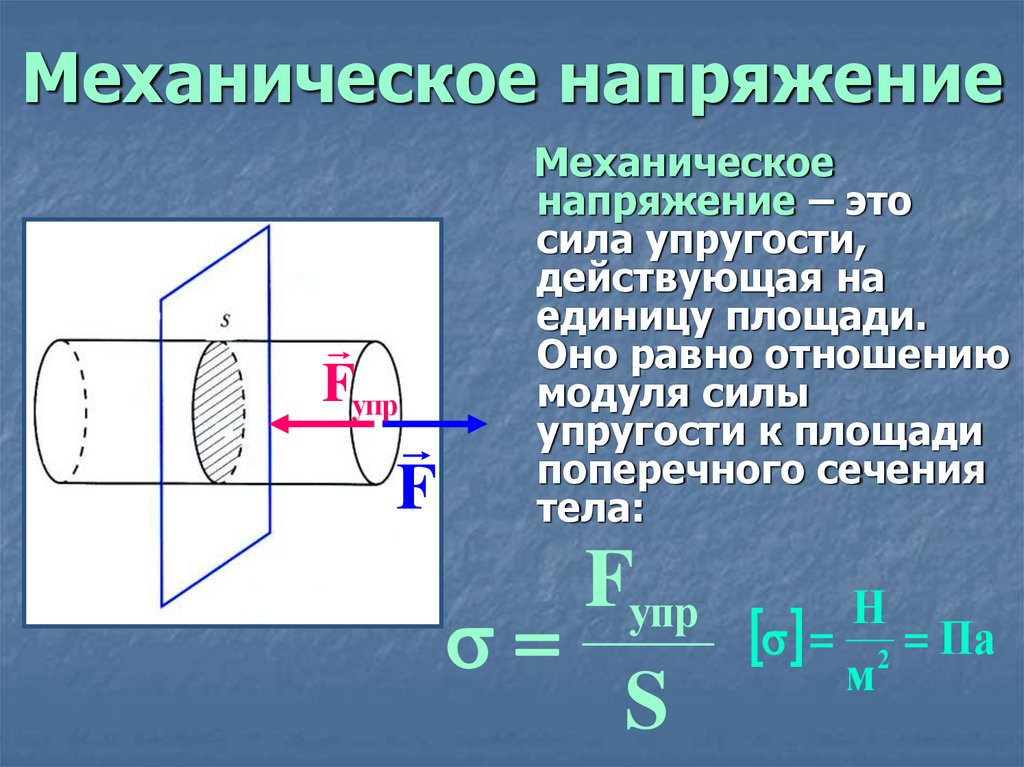 Полные
напряжения, приходящиеся на единицу
площади, можно выразить через нормальные
и касательные напряжения: P
= (σz+ τx
+ τy)1/2
Полные
напряжения, приходящиеся на единицу
площади, можно выразить через нормальные
и касательные напряжения: P
= (σz+ τx
+ τy)1/2
σz= limΔA→0 ΔNz/ΔA = dNz/dA
τzx= limΔA→0 ΔQx/ΔA = dQx/dA
τzy= limΔA→0 ΔQy/ΔA = dQy/dA
Первый индекс показывает, какой оси параллельна нормаль к площадке действия рассматриваемого напряжения, второй индекс показывает, какой оси параллельно данное напряжение.
Расчет на прочность и жесткость осуществляется двумя методами: методом допускаемых напряжений, деформаций и методом допускаемых нагрузок.
Предельное
напряжение
– напряжение, при котором образец из
данного материала разрушается или при
котором развиваются значительные
пластические деформации.
Допускаемое напряжение – напряжение, величина которого регламентируется техническими условиями
Допускаемое напряжение устанавливается с учетом материала конструкции и изменяемости его механических свойств в процессе эксплуатации, степени ответственности конструкции, точности задания нагрузок, срока службы конструкции, точности расчетов на статическую и динамическую прочность.
Определяется допускаемое напряжение по формуле: [σ] = σпр/[n]
σпр – предельное для данного материала напряжение
[n] – нормированный коэффициент запаса прочности
Между действующими напряжениями и внутренними силовыми факторами существует следующая связь:
Nz = ∫σzdA
Qy = ∫τzydA
Qx = ∫τzxdA
Mx = ∫yσdA
My = ∫xσdA
Mкр= ∫(τzyx – τzxy)dA
Нормальные и
касательные напряжения являются функцией
внутренних силовых факторов и
геометрических характеристик сечения. Эти напряжения, вычисленные по
соответствующим формулам, можно назвать
фактическими, или рабочими.
Эти напряжения, вычисленные по
соответствующим формулам, можно назвать
фактическими, или рабочими.
Наибольшее значение фактических напряжений ограничено предельным напряжением, при котором материал разрушается или появляются недопустимые пластические деформации.
Измерения напряжения – определение, вывод и пример
Формула измерения напряжения представлена в виде:
[M1 L-1 T-2]
Где,
Что такое напряжение?
Напряжение – это внешняя восстанавливающая сила, действующая на единицу площади, и обозначается σ. Обозначается как Н/м². Он используется для нахождения напряжения, приложенного к любому данному телу, когда сила и площадь, на которую оно действует, заданы в задаче.
Таким образом, \[σ = \frac{F}{A}\]
σ – это величина напряжения на объекте
F – сила, действующая на объект.
A – площадь поперечного сечения
, или можно также сказать, что напряжение – это сила, приложенная к объекту, заставляющая его полностью деформироваться. В терминологии физики мы нашли, как делается вывод формулы напряжения. Известно, что более крупные объекты могут противостоять большому количеству сил. Используя напряжение в качестве альтернативы силе, мы можем использовать один и тот же предел текучести для одного и того же материала, неважно, насколько велик объект.
Кроме того, стресс и деформация напрямую связаны друг с другом, и если увеличивается одно, автоматически увеличивается другое. Причем, чем больше напряжение объекта, тем большую деформацию он испытывает.
Получение величины напряжения
Напряжение = сила × площадь⁻¹ . . .. . (i)
Размерная формула площади = [M0 L² T0] . . .. (ii)
(ii)
Поскольку мы знаем,
Сила = M × a = MM × [M0 L¹ T⁻²]
Следовательно, размерная формула силы = M¹L¹T⁻²M¹L¹T⁻² . . . . (iii)
Подставив уравнения (ii) и (iii) в уравнение (i), мы получим:
Напряжение = Сила × Площадь⁻¹
Или Напряжение = M¹L¹T⁻²M¹L¹T⁻² × [M0 L ² T0]⁻¹ = M¹L⁻¹T⁻²M¹L⁻¹T⁻²
Таким образом, размерная формула напряжения представляется как M¹L⁻¹T⁻²M¹L⁻¹T⁻².
Пример решенной задачи
Вопрос: Если на упругую пружину действует сила 1000 Н на площади 0,2 м2. Рассчитать количество стресса?
Ответ: Как мы знаем из приведенной выше задачи,
F (сила) = 1000 Н,
A (площадь) = 0,2 м² {0.2}\]
σ = 5000 Н/м 2
Типы напряжения
1. Нормальное напряжение
Когда объект нагружен осевой силой. Нормальное напряжение представлено делением осевой силы на площадь поперечного сечения. Это произойдет, когда объект будет сжат.
Нормальное напряжение представлено делением осевой силы на площадь поперечного сечения. Это произойдет, когда объект будет сжат.
2. Продольное напряжение
Когда длина тела изменяется под действием приложенного нормального напряжения, это называется продольным напряжением.
Продольное напряжение представлено делением силы деформации на площадь поперечного сечения.
3. Объемное или объемное напряжение
Это стресс, при котором объем тела изменяется из-за нагрузки. Нормальное напряжение на объекте изменяет его длину или объем, а касательное напряжение приводит к изменению формы тела, которое называется объемным напряжением.
Напряжение сдвига — это сила, приложенная по касательной к площади поверхности плоскости. Когда силы, приложенные к поверхности, параллельны ей, а напряжение, действующее на поверхность, образует касательную, это называется напряжением сдвига.
4. Растягивающее напряжение
Это сила на единицу площади и напряжение, приложенное и увеличивающее длину тела из-за силы, называется растягивающим напряжением. Наблюдается при растяжении стержня по третьему закону движения. Типичным примером растягивающего напряжения является резина, а растяжение — это связанная с ним величина.
5. Напряжение сжатия
Это происходит, когда мы применяем тангенциальную силу к телу, и форма плюс объем объекта изменяются. Напряжение сжатия приводит к уменьшению длины объекта. Оно противоположно растягивающему напряжению.
Важность напряжения
Анализ напряжения является важной частью прикладной физики и помогает в классификации внутреннего распределения внутренних сил в твердых телах.
Являясь важной частью машиностроения, напряжения помогают в изучении и проектировании таких конструкций, как несущие конструкции, плотины, полозья и механические детали. Это также важно в других дисциплинах, например, в геологии, изучающей такие теории, как тектоника плит, вулканизм и лавины, а в биологии важно понимать анатомию живых существ.
Это также важно в других дисциплинах, например, в геологии, изучающей такие теории, как тектоника плит, вулканизм и лавины, а в биологии важно понимать анатомию живых существ.
Напряжение — это сила, которую мы прикладываем к объекту, чтобы он полностью деформировался. Кроме того, мы знаем о человеческом стрессе, но стресс в физике немного сложнее понять. Кроме того, в этой теме мы поговорим о напряжении, формуле напряжения, ее выводе и решенном примере.
Что происходит, когда объекты реагируют?
Чтобы сделать журавлика оригами, сложите лист бумаги. Кроме того, даже после того, как вы разгладите бумагу, оригами сохранит свою новую форму после завершения. Однако когда вы растягиваете резиновую ленту, она щелкает, когда вы отпускаете ее. Кроме того, некоторые объекты сохраняют некоторые из своих первоначальных форм при растяжении.
Кроме того, некоторые предметы меняют форму, когда к ним прикладывают силы, но не все предметы изменяются одинаково, даже если мы применяем одинаковое количество силы.
Стресс
Перед обсуждением стресса необходимо рассмотреть несколько понятий. Кроме того, напряжение определяется как количество силы (силы или энергии), которую мы прикладываем к объекту, деленное на площадь поперечного сечения, на которую действует сила.
Кроме того, более крупные объекты могут выдерживать большие нагрузки. Кроме того, используя напряжение вместо силы, мы можем использовать один и тот же предел текучести для одного и того же материала независимо от размера объекта.
Самое главное, стресс и напряжение неразрывно связаны, и по мере того, как увеличивается одно, другое следует за ним. Кроме того, чем большему напряжению подвергается объект, тем больше он деформируется, пока не выйдет из строя.
Кроме того, все объекты сначала испытывают упругую деформацию, но когда напряжение на объекте превышает определенный порог, он подвергается пластической деформации, и именно тогда происходит переключение и объект достигает предела текучести.
Кроме того, во всех материалах существует связь напряжений и деформаций, даже если размер каждой части варьируется. Кроме того, упругая деформация является линейной. Кроме того, на линию наклона влияют материалы, из которых построен объект. Кроме того, поскольку пластическая деформация не является линейной, ее сложнее моделировать.
Формула напряжения
Формула напряжения представляет собой силу, деленную на площадь поперечного сечения.
Сила/площадь = напряжение
\[σ = \frac{F} {A}\]
Вывод формулы напряжения
Величина напряжения на объекте обозначается =.σ
F = обозначает силу, действующую на объект .
А обозначает площадь поперечного сечения.
Пример формулы напряжения, которая была решена
Чтобы помочь вам лучше понять формулу, давайте рассмотрим несколько примеров.
Пример 1
Чему равно напряжение объекта с действующей силой 50 ньютонов (Н) и площадью поперечного сечения 5 мм 96\] Нм 2 .
Пример № 2
К упругой пружине приложили усилие 1000 Н на площади 0,2 м 2 . Итак, как рассчитать нагрузку на упругую пружину?
Решение:
Сначала запишите все, что мы узнали из формулы.
Сила (F) = 1000 Н
А равна 0,2 м 2 .
Теперь введите значения в формулу.
\[σ = \frac{F}{A}\]
\[σ = \frac{1000N}{0,2}\]
σ = 5000 Нм 2
В результате упругая пружина напрягается на величину 5000 Нм 2 .
Модуль упругости Юнга
Модуль Юнга — числовая константа, названная в честь английского врача и физика XVIII века Томаса Юнга, которая описывает упругие свойства твердого тела, подвергающегося растяжению или сжатию только в одном направлении, например металлического стержня. который возвращается к своей первоначальной длине после растяжения или сжатия по длине. Модуль Юнга — это мера способности материала противостоять изменениям длины при продольном растяжении или сжатии. Модуль Юнга, также известный как модуль упругости, равен продольному напряжению, деленному на деформацию. В случае металлического стержня, находящегося под напряжением, напряжение и деформация могут быть описаны следующим образом.
который возвращается к своей первоначальной длине после растяжения или сжатия по длине. Модуль Юнга — это мера способности материала противостоять изменениям длины при продольном растяжении или сжатии. Модуль Юнга, также известный как модуль упругости, равен продольному напряжению, деленному на деформацию. В случае металлического стержня, находящегося под напряжением, напряжение и деформация могут быть описаны следующим образом.
Когда металлический стержень с площадью поперечного сечения A тянут за оба конца с силой F, стержень растягивается от своей первоначальной длины L0 до новой длины L n . (В то же время поперечное сечение уменьшается.) Напряжение определяется как отношение растягивающей силы к площади поперечного сечения, или F/A. Деформация или относительная деформация определяется как разность длин L n L 0 , деленная на исходную длину, или (L n L 0 )/л 0 . (У прочности нет измерений. ) В результате модуль Юнга может быть выражен математически как
) В результате модуль Юнга может быть выражен математически как
Напряжение/деформация = (FL 0 )/A(L n L 0 ) = модуль Юнга
Это вариант закона упругости Гука. Модуль Юнга измеряется в фунтах на квадратный дюйм (psi) в английской системе и в ньютонах на квадратный метр (Н/м 2 ) в метрической системе. Алюминий имеет модуль Юнга около 1,0·107 фунтов на квадратный дюйм или 7,0·1010 Н/м 9 .0083 2 . Сталь имеет значение, которое примерно в три раза больше, а это означает, что для растяжения стального стержня требуется в три раза больше силы, чем для алюминиевого стержня аналогичной формы.
Модуль Юнга полезен только в том случае, когда напряжение пропорционально деформации и материал возвращается к своим первоначальным размерам после прекращения действия внешней силы. По мере увеличения напряжений материал может течь, постоянно деформироваться или, наконец, сломаться.
При удлинении натянутого металлического стержня его ширина немного уменьшается. Эта боковая усадка приводит к поперечной деформации, равной изменению ширины, деленному на первоначальную ширину. Коэффициент Пуассона – это отношение поперечной деформации к продольной деформации. Средний коэффициент Пуассона для стали равен 0,28, а для алюминиевых сплавов — 0,33. Материалы с коэффициентом Пуассона менее 0,50 расширяются при продольном растяжении и сжимаются при продольном сжатии.
Измерения напряжения — Infinity Learn
Напряжение, обозначаемое σ, представляет собой внешнюю восстанавливающую силу, действующую на единицу площади. Выражается в Н/м². . Он используется для расчета напряжения, приложенного к любому данному телу, когда сила и площадь, на которую оно действует, заданы в задаче. В результате σ = F/A
σ – это величина напряжения, приложенного к объекту
Зарегистрируйтесь, чтобы получить бесплатные пробные тестовые и учебные материалы
+91
Подтвердите код OTP (обязательно)
Я согласен с условиями и политикой конфиденциальности.
F обозначает силу, действующую на объект.
Площадь поперечного сечения обозначается буквой A.
Напряжение также можно определить как силу, приложенную к объекту, которая вызывает его полную деформацию. Мы обнаружили, как формула напряжения выводится в физической терминологии. Известно, что более крупные объекты более устойчивы к широкому диапазону сил. Мы можем использовать один и тот же предел текучести для одного и того же материала, независимо от того, насколько велик объект, используя напряжение вместо силы. Более того, стресс и напряжение неразрывно связаны, и по мере того, как увеличивается одно, вместе с ним растет и другое. И чем больше напряжение в объекте, тем большую деформацию он испытывает.
Типы напряжения
Нормальное напряжение
Нормальное напряжение возникает, когда объект нагружен осевой силой. Когда осевая сила делится на площадь поперечного сечения, представляется нормальное напряжение. Это произойдет, когда объект сжат.
Это произойдет, когда объект сжат.
Продольное растяжение
Продольное напряжение возникает, когда длина тела изменяется из-за приложения нормального напряжения. Продольное напряжение представлено делением деформирующей силы на площадь поперечного сечения.
Объемный и объемный стресс
Это тип стресса, при котором объем тела изменяется в результате стресса. Нормальное напряжение на объекте вызывает изменение его длины или объема, тогда как касательное напряжение вызывает изменение формы тела, известное как объем.
Деформация при растяжении
Напряжение при растяжении определяется как сила на единицу площади и напряжение, возникающее при приложении силы и увеличивающее длину тела в результате действия силы. Наблюдается при растяжении стержня в соответствии с третьим законом движения. Резина является распространенным примером растягивающего напряжения, и растяжение является величиной, связанной с ним.
Сжатие Напряжение
Когда мы прикладываем к телу касательную силу, форма и объем объекта изменяются. Длина объекта уменьшается в результате напряжения сжатия. Это обратное напряжение растяжения.
Прежде чем обсуждать стресс, необходимо рассмотреть несколько концепций. Кроме того, напряжение определяется как количество силы (силы или энергии), приложенной к объекту, деленное на площадь его поперечного сечения. Более крупные объекты также могут выдерживать большие силы. Кроме того, используя напряжение, а не силу, мы можем использовать один и тот же предел текучести для одного и того же материала независимо от размера объекта. Самое главное, стресс и напряжение неразрывно связаны, и по мере того, как растет одно, растет и другое. Кроме того, поскольку объект подвергается большему напряжению, он деформируется до тех пор, пока не выйдет из строя.
Dimensional Formula of Stress
The Stress dimensional formula is given by, [M 1 L -1 T -2 ]
Where,
- M = Mass
- L = Length
- T = Время
Напряжение = Сила [Площадь]-1. ., , (1)
., , (1)
Формула измерения площади = [M 0 L 2 T 0 ] . . . . (2)
Поскольку Сила = M × a = [M] × [M 0 L 1 T -2 ]
Формула измерения силы = [M 1 L 1 T -2 ] . . . . (3)
Когда мы подставляем уравнения (2) и (3) в уравнение (1), мы получаем
Напряжение = [Площадь]-1 Сила Альтернативно, Напряжение = [M 1 L 1 T — 2 ] × [M 0 L 2 T 0 ] -1 = [M 1 L -1 T -2 ]
[М 1 Л -1 Т -2 ].
Часто задаваемые вопросы
В. Что такое единица измерения и формула измерения напряжения?
Ответ: Сила, действующая на «маленькую» границу на единицу площади этой границы, определяется как напряжение.

