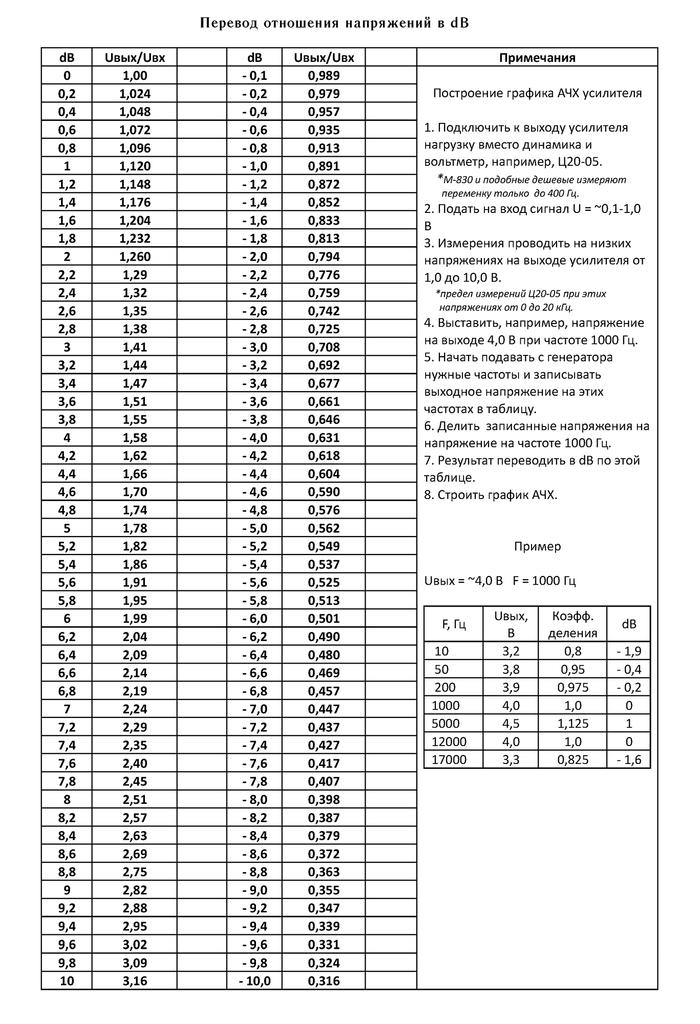
Что такое децибел и как он используется в радиотехнике. Как перевести децибелы в разы и наоборот. Почему логарифмическая шкала удобна для измерений в радиотехнике. Как связаны децибелы с оценкой силы сигнала по системе RST.
Что такое децибел и зачем он нужен
Децибел (дБ) — это логарифмическая единица измерения отношения двух величин. В радиотехнике децибелы широко используются для сравнения уровней мощности, напряжения и тока сигналов. Почему же децибелы так удобны?
- Децибелы позволяют заменить умножение и деление сложением и вычитанием
- Логарифмическая шкала удобна при работе с величинами, меняющимися в широком диапазоне
- Децибелы хорошо соответствуют восприятию звука человеческим ухом
- С помощью децибелов удобно оценивать усиление и ослабление сигналов
Основные формулы для работы с децибелами
Как же рассчитать значение в децибелах? Для этого используются следующие формулы:
- Для мощности: дБ = 10 * log(P1/P2)
- Для напряжения и тока: дБ = 20 * log(U1/U2) = 20 * log(I1/I2)
Здесь P1, U1, I1 — измеряемые величины, а P2, U2, I2 — опорные значения. Множитель 10 для мощности и 20 для напряжения/тока связаны с тем, что мощность пропорциональна квадрату напряжения или тока.

Перевод децибелов в разы и обратно
Как быстро перевести значение в децибелах в обычное отношение величин? Для этого полезно запомнить несколько ключевых соответствий:
- 3 дБ соответствует увеличению в 2 раза по мощности
- 6 дБ — увеличению в 4 раза по мощности или в 2 раза по напряжению/току
- 10 дБ — увеличению в 10 раз по мощности или в 3,16 раза по напряжению/току
- 20 дБ — увеличению в 100 раз по мощности или в 10 раз по напряжению/току
Зная эти соответствия, можно легко оценивать изменения сигналов, выраженные в децибелах.
Децибелы в оценке уровня сигнала
В радиолюбительской практике децибелы тесно связаны с системой оценки силы сигнала RST. Как они соотносятся?
- Каждый балл по шкале S соответствует изменению на 6 дБ
- S9 принято за 0 дБ (50 мкВ на входе приемника)
- Каждый балл ниже S9 означает уменьшение сигнала на 6 дБ
- Значения выше S9 указываются в децибелах (например, S9+20 дБ)
Таким образом, оценивая силу сигнала по шкале S, радиолюбители фактически оперируют логарифмической шкалой в децибелах.

Практическое применение децибелов в радиотехнике
Где же на практике используются децибелы в радиотехнике? Вот некоторые распространенные примеры:
- Оценка коэффициента усиления антенн и усилителей
- Измерение ослабления сигнала в фильтрах и аттенюаторах
- Расчет бюджета радиолинии
- Оценка чувствительности приемников
- Нормирование уровней побочных излучений передатчиков
Знание основ работы с децибелами позволяет быстро оценивать характеристики радиоаппаратуры и производить необходимые расчеты.
Особенности измерения уровней сигналов в децибелах
При измерении уровней сигналов в децибелах важно учитывать следующие моменты:
- Необходимо указывать опорный уровень (например, дБм — относительно 1 мВт)
- Для напряжения и тока нужно учитывать сопротивление цепи
- В нелинейных цепях соотношения для мощности, напряжения и тока могут нарушаться
- При каскадном соединении устройств их коэффициенты передачи в дБ складываются
Корректный учет этих особенностей позволяет избежать ошибок при работе с уровнями сигналов, выраженными в децибелах.
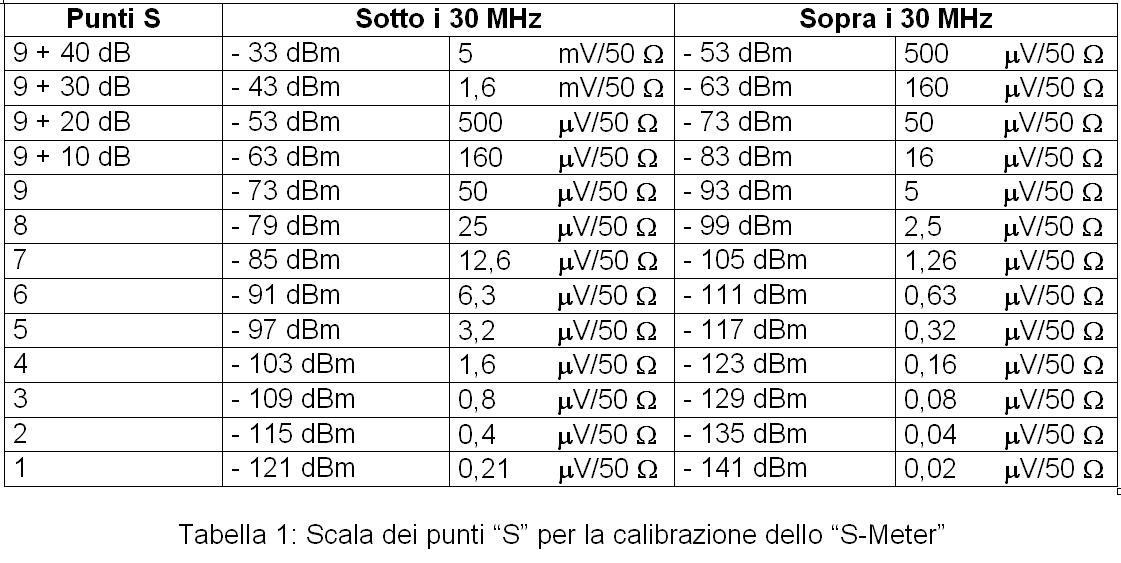
Децибелы и человеческое восприятие звука
Почему же децибелы так хорошо подходят для оценки громкости звука? Это связано с особенностями человеческого слуха:
- Ухо воспринимает относительные, а не абсолютные изменения громкости
- Закон Вебера-Фехнера говорит о логарифмической зависимости ощущений от силы раздражителя
- Изменение на 1 дБ — это минимально различимое на слух изменение громкости
- 6 дБ воспринимается как заметное изменение громкости
- 10 дБ примерно соответствует субъективному удвоению громкости
Таким образом, децибельная шкала очень удобна для оценки изменений громкости, воспринимаемых человеком.
Типичные ошибки при работе с децибелами
При использовании децибелов нужно быть внимательным, чтобы избежать распространенных ошибок:
- Путаница между децибелами для мощности и для напряжения/тока
- Сложение значений в децибелах и в разах
- Неправильный учет знака при ослаблении сигнала
- Забывание об опорном уровне при абсолютных измерениях
- Некорректное применение формул для нелинейных цепей
Понимание физического смысла децибелов и внимательность при расчетах помогут избежать подобных ошибок.

Децибелы ЭТО ОЧЕНЬ ПРОСТО!
Ю.БАЛТИН (YL2DX),
г.Рига.
Когда требуется сравнить какие-нибудь величины, это можно сделать по-разному. Можно, например, разделив эти величины одну на другую, сказать — Р1 больше чем Р2 в 3 раза, или Р1, меньше чем Р2 в 28 раз. Если нам понадобится далее вести какие-то расчеты, мы будем пользоваться отвлеченными числами 3, или 28, или 1/28 (иногда для уточнения добавляя слово «раз»).
В ряде случаев для расчетов или для большей наглядности сравнения оказывается удобнее логарифмировать отношение величин и оперировать далее с числом logа(Р1/Р2). Известно, что применение логарифмов упрощает математические расчеты, в частности, позволяет вместо умножения и деления пользоваться сложением и вычитанием. При большом диапазоне изменений какой-либо величины логарифмический масштаб позволяет лучше разглядеть на одном и том же графике и малые, и большие ее относительные изменения.
Чтобы различать, имеем ли мы дело с числом «раз» или с его логарифмом, а также чтобы зафиксировать, каким основанием мы пользуемся при логарифмировании (числом 10, числом e=2,71828 или иным), следует присвоить этому логарифму какое-нибудь название. В системе СИ в качестве относительной логарифмической единицы отношения мощностей Р1, и Р2 принят десятичный логарифм Ig(Р1/Р2). Эта единица называется бел (Б).
На практике этой довольно крупной единицей оказалось не очень удобно оперировать, поэтому ее «разменивают» на единицы, в десять раз меньшие — децибелы. Соотношение двух уровней мощности Р1 и Р2 в децибелах (дБ, или dB) выражают по следующей формуле:
Множитель 10 в формуле (1) появился потому, что десять децибел как раз и есть один бел. Таким образом, не повезло изобретателю телефона А.Г.Беллу — мало того, что единицу его имени укоротили на одну букву «л», так еще и пользуются лишь десятыми долями.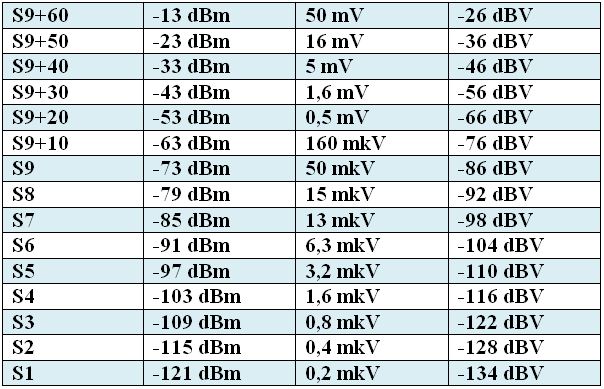
Теперь разберемся с отношениями напряжений или токов. Вспомним из школьного курса, что мощность в линейной цепи равна:
Отсюда легко видеть, что:
а значит:
Из школьного же курса вспомним:
Из равенств (2) и (3) вытекает следующее:
Это и есть формула взаимосвязи между «белами по мощности» и «белами по напряжению» в одной и той же цепи, если в ней выполняется закон Ома. Ну, а если мы намерены пользоваться десятыми долями бела, то обе половины этого уравнения необходимо умножить на 10. Отсюда следует, что при сравнении величин напряжений (U 1 и U2) или токов (I1 и l2), их соотношение в децибелах:
Полезно запомнить несколько характерных значений, приведенных в таблице.
Если напряжение на резисторе увеличить вдвое (на +6 дБ «по напряжению»), то и протекающий через него ток увеличится вдвое (на +6 дБ «по току»), а мощность, выделяемая этим резистором, станет вчетверо больше—опять-таки на +6 дБ («по мощности»). Чтобы уменьшить мощность в 10 раз (-10 дБ), нужно снизить приложенное к резистору напряжение в 3,162 раза (-10 дБ), отчего ток по закону Ома тоже уменьшится в 3,162 раза (-10 дБ).
Поскольку мощность в линейной цепи пропорциональна квадрату напряжения или тока, численные значения соотношений их величин, выраженные в децибелах, остаются одними и теми же как при сравнении мощностей, так и при сравнении напряжений или токов:
В случае ослабления сигнала (когда отношение Р1/Р2 меньше единицы), логарифм становится отрицательным, следовательно, отрицательным становится и коэффициент передачи данной цепи, выраженный в децибелах. Для вычисления общего коэффициента передачи нескольких последовательно соединенных цепей или устройств достаточно просуммировать значения в децибелах с учетом их знаков (+) или (-).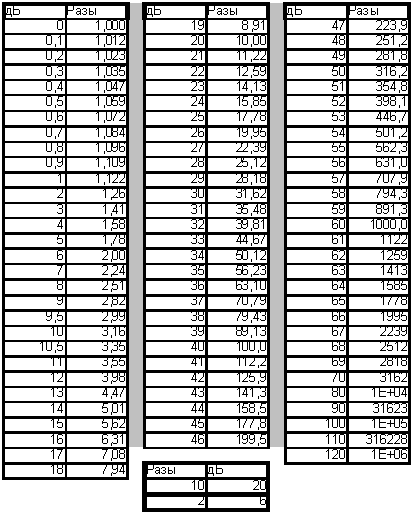 Это
Это
намного удобнее, чем перемножать исходные значения в разах.
При вычислении коэффициента передачи различных устройств (например, усилительного каскада) во многих случаях мы имеем дело с разными входным и выходным сопротивлениями; в нелинейных цепях напряжение и ток взаимно не пропорциональны, а мощность не связана с тем и другим квадратичной зависимостью. Коэффициенты передачи таких цепей по току:
и по напряжению:
различны и в разах, и в децибелах; коэффициент передачи по мощности:
а в децибелах:
поскольку
Равенство (6) к этим случаям не относится, но по отдельности изменения или соотношения величин тока или напряжения на одном и том же линейном сопротивлении (например, на сопротивлении нагрузки нелинейного усилителя) все равно выражаются в децибелах формулами (4) и (5), а изменения уровня мощности — формулой (1).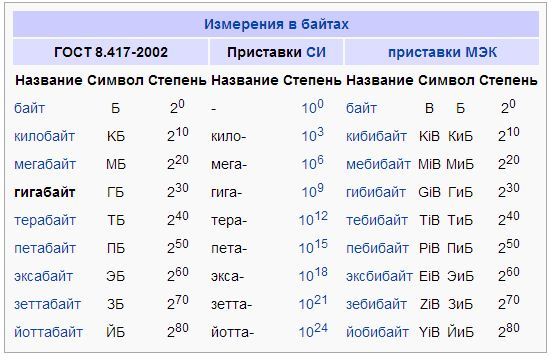
Зачем возиться с логарифмами? Во-первых, логарифмическая шкала наиболее естественна для наших органов чувств, в частности, для слуха. Закон логарифмической зависимости ощущений от силы воздействия сформулирован Вебером и Фехнером (обычно называется законом Вебера) — «одинаковые относительные изменения раздражающей силы вызывают одинаковые приращения слухового ощущения, т.е. слуховое ощущение пропорционально логарифму раздражающей силы».
Практически, 1 дБ — это наименьшая ступенька изменения интенсивности звука, едва обнаруживаемая на слух, изменение на 6 дБ воспринимается на слух как хорошо заметное (но небольшое — примерно вдвое громче), на 10 дБ — значительное, а на 20 дБ—как весьма большое. Каждый балл по шкале S системы RST — это 6 дБ (или 0,6 бела), так что мы, особо не задумываясь, занимаемся логарифмированием каждый раз, когда начинаем очередную связь в эфире, передавая рапорт корреспонденту.
Во-вторых, значения величин, с которыми нередко приходится сталкиваться, в обычном исчислении бывает трудно соразмерить—скажем, 1 микровольт отличается от 1 киловольта в 1 000 000 000 раз. А в децибелах разница выражается вполне удобной величиной 180 дБ. Мощности, которые выделятся на одном и том же сопротивлении при приложении к нему этих напряжений, будут отличаться астрономически — в 1 000 000 000 000 000 000 раз, а в децибелах — все на те же 180 дБ. С другой стороны, если, например, сравнивать 1,03 мА и 1,37 мА, то их отличие выразится вполне заметной величиной — 2,5 дБ.
А в децибелах разница выражается вполне удобной величиной 180 дБ. Мощности, которые выделятся на одном и том же сопротивлении при приложении к нему этих напряжений, будут отличаться астрономически — в 1 000 000 000 000 000 000 раз, а в децибелах — все на те же 180 дБ. С другой стороны, если, например, сравнивать 1,03 мА и 1,37 мА, то их отличие выразится вполне заметной величиной — 2,5 дБ.
|
Децибелы |
0 |
+1 (-1) |
+3 (-3) |
+6 (-6) |
+10 (-10) |
+20 (-20) |
+40 (-40) |
+60 (-60) |
|
Отношение мощностей P1/P2 |
1 |
1,26 (0,79) |
2 (0,5) |
4 (0,25) |
10 (0,1) |
100 (0,01) |
104 (10-4) |
106 (10-6) |
|
Отношение напряжений или токов U1/U2 или I1/I2 |
1 |
1,12 (0,89) |
1,41 (0,707) |
2 (0,5) |
3,16 (0,316) |
10 (0,1) |
100 (0,01) |
1000 (10-3) |
Если запомнить характерные значения из таблицы, то можно очень легко пересчитывать в уме и любые другие величины отношений в децибелы и обратно. Например, 4 дБ—это (3 дБ +1 дБ). Значит, отношение мощностей (2×1,26)= 2,52 раза или отношение напряжениий (1,41 х 1,12) =1,6 раза. Или, к примеру, отношение двух значений тока равно 17 раз, то есть (10×1,7). 10 раз по току — это 20 дБ, а 1,7 раза — между 1,41 и 2, значит, где-то около 4,5 дБ. В сумме (20 дБ + 4,5 дБ) = 24,5 дБ. Ну, а для чисел, кратных десяти, мнемоника очевидна.
Например, 4 дБ—это (3 дБ +1 дБ). Значит, отношение мощностей (2×1,26)= 2,52 раза или отношение напряжениий (1,41 х 1,12) =1,6 раза. Или, к примеру, отношение двух значений тока равно 17 раз, то есть (10×1,7). 10 раз по току — это 20 дБ, а 1,7 раза — между 1,41 и 2, значит, где-то около 4,5 дБ. В сумме (20 дБ + 4,5 дБ) = 24,5 дБ. Ну, а для чисел, кратных десяти, мнемоника очевидна.
Децибелы сами по себе — это величины не физические, а абстрактные, математические, такие же относительные, как и разы. Их нельзя пощупать руками как килограмм, метр или киловольт (нет… руками его, пожалуй, не стоит щупать… Hi). Их можно только вычислить, сравнивая реальные физические величины, и оперировать ими при расчетах. Но если мы устанавливаем в качестве эталона 0 дБ какое-то определенное значение физической величины, например, 1 Вт или 1 мкВ, то можем и прямо измерять в децибелах относительно него уровни мощности или, соответственно, напряжения. Обозначают такие единицы измерения теми же буквами «дБ», но с добавлением индекса: дБВт (децибел-ватт), дБмкВ (децибел-микровольт) и т. п. Например, мощность 27 дБВт—это то же самое, что 500 Вт, а -13 дБВт — 50 мВт. Напряжение -3 дБмкВ — 0,707 мкВ, а 23 дБмкВ — 14,14 мкВ.
п. Например, мощность 27 дБВт—это то же самое, что 500 Вт, а -13 дБВт — 50 мВт. Напряжение -3 дБмкВ — 0,707 мкВ, а 23 дБмкВ — 14,14 мкВ.
В акустике за 0 дБ однозначно принято пороговое звуковое давление 2-10 Па, и децибел без дополнительного индекса прямо используется в качестве единицы уровня звукового давления.
На коротких волнах, по системе оценки сигнала RST, напряжение, равное 50 мкВ, на 50-омном входе приемника (S=9), в сущности, принято за ноль децибел. Каждый балл ниже девяти — это -6 дБ (в 2 раза меньше) от этого напряжения, а если сигнал сильнее, то S-метр покажет, на сколько децибел. Чтобы напряжение на входе приемника изменилось на 1 балл, нужно на столько же изменить мощность передатчика — на 6 дБ, то есть в 4 раза. Если получен RS 59+20 dB, то можно (и нужно бы!) смело уменьшать мощность передатчика на 30 дБ (т.е. в 1000 раз!!!) — все равно будет слышно достаточно громко — больше чем на S=7 (с запасом +2 дБ) (конечно, если «+20» было сказано не ради красного словца. . .Hi).
. .Hi).
Надеюсь, что теперь понятно, почему «выжимать» 250 Вт из 200-ваттного передатчика просто глупо — увеличение силы сигнала менее чем на 1 дБ вообще никто не заметит, а вот сплэттер или щелчки по всему диапазону вполне реально могут испортить настроение многим.
О чувствительности приемника и S-метра
Чувствительность приемников часто измеряют в децибел-милливаттах (дБм) или дБмВт: 1 мВт = 0 дБм.
В сущности, измерять чувствительность в единицах мощности имеет больше смысла, чем в единицах напряжения, так так нам приходится иметь дело с сигналами разной формы — синусоидальными, шумовыми, шумоподобными и др. К тому же, мы избавляемся от необходимости уточнять, каково входное сопротивление приемника, и имеем возможность сравнивать чувствительность приемников с различными входными сопротивлениями. Эффективное напряжение 50 мкВ на 50-омном входе соответствует мощности -73 дБм. Этой же мощности соответствует напряжение 61,2 мкВ на 75-омном входе. Все это соответствует оценке S=9 сигнала по системе RST на частотах ниже 30 МГц. На УКВ за S=9 принята мощность -93 дБм (5 мкВ на 50-омном входе приемника).
Все это соответствует оценке S=9 сигнала по системе RST на частотах ниже 30 МГц. На УКВ за S=9 принята мощность -93 дБм (5 мкВ на 50-омном входе приемника).
Система оценки сигнала на слух по коду RST была предложена W2BSR в середине 30-х годов и с тех пор стала всемирно признанной. Стандарт градуировки S-метров был установлен IARU в 60-х годах, но когда его принимали, похоже, что ориентировались на не очень чувствительные приемники, а может быть, и на «тугоухих» операторов… (Hi). Впрочем, в те годы еще широко использовалась амплитудная модуляция (AM), в CW-приемниках сравнительно редко встречались хорошие узкополосные фильтры, а собственные шумы радиодеталей были побольше чем сейчас, так что чувствительность среднего любительского приемника была на порядок хуже, чем у современного.
Пороговая чувствительность порядка -130 дБм — очень высокая, но не редкая для современного КВ-приемника при узкой полосе в режиме CW (0,035 мкВ на 50-омном входе). Эта величина ниже, чем S=1 (-121 дБм) по S-метру. При таких уровнях имеется несоответствие слуховой (по таблице значений «S») и инструментальной (по S-метру) оценки силы сигнала — в чистом эфире, без помех, на хорошем приемнике сигнал с уровнем -125 или -130 дБм может вполне восприниматься на слух как хорошо читаемый «слабый», или «очень слабый» т.е. S=3 или S=2, a S-метр не будет показывать ничего. Но, по сути системы RST, если S=0, то сигнала просто не слышно совсем, a S=1 — это, по определению, «едва ощутимый сигнал». В тех же условиях сигнал мощностью -85 дБм может выглядеть как очень громкий (при достаточном коэффициенте усиления УНЧ приемника), но S-метр покажет не 9, а только 7 баллов — это типично, например, на 10-метровом диапазоне (впрочем, он как раз на границе KB и УКВ, где шкалы S-метров разные).
Эта величина ниже, чем S=1 (-121 дБм) по S-метру. При таких уровнях имеется несоответствие слуховой (по таблице значений «S») и инструментальной (по S-метру) оценки силы сигнала — в чистом эфире, без помех, на хорошем приемнике сигнал с уровнем -125 или -130 дБм может вполне восприниматься на слух как хорошо читаемый «слабый», или «очень слабый» т.е. S=3 или S=2, a S-метр не будет показывать ничего. Но, по сути системы RST, если S=0, то сигнала просто не слышно совсем, a S=1 — это, по определению, «едва ощутимый сигнал». В тех же условиях сигнал мощностью -85 дБм может выглядеть как очень громкий (при достаточном коэффициенте усиления УНЧ приемника), но S-метр покажет не 9, а только 7 баллов — это типично, например, на 10-метровом диапазоне (впрочем, он как раз на границе KB и УКВ, где шкалы S-метров разные).
В трансиверах разных фирм стандарт IARU не очень-то соблюдается. Кроме того, чувствительность одного и того же приемника на разных диапазонах различается и может ступенчато регулироваться оператором (включением или выключением преду-силителей ВЧ и аттенюаторов), а шкала S-метра остается одна на все случаи. Если включен аттенюатор, то следует величину его затухания прибавить к показаниям S-метра, а если включен дополнительный пре-дусилитель — то величину его усиления из показаний S-метра вычесть. Разумеется, это относится только к случаю использования для приема полноразмерных согласованных антенн. Когда действующая высота антенны мала, или антенна не согласована со входом приемника, показания S-метра сами по себе ничего не скажут о реальном уровне сигнала в эфире.
Если включен аттенюатор, то следует величину его затухания прибавить к показаниям S-метра, а если включен дополнительный пре-дусилитель — то величину его усиления из показаний S-метра вычесть. Разумеется, это относится только к случаю использования для приема полноразмерных согласованных антенн. Когда действующая высота антенны мала, или антенна не согласована со входом приемника, показания S-метра сами по себе ничего не скажут о реальном уровне сигнала в эфире.
В сущности, единственной полной и действительно объективной характеристикой уровня сигнала, создаваемого каким-либо передатчиком в точке приема, является напряженность поля, которую можно вычислить, разделив ЭДС на клеммах приемной антенны UA на ее действующую высоту hд:
Действующая высота (или действующая длина) антенны вычисляется по формуле:
т.е. зависит от длины волны l , коэффициента направленного действия D, КПД (?) антенны и ее входного сопротивления (идеальный полуволновой диполь в свободном пространстве имеет действующую длину l /?). Поэтому, если нужно более точно охарактеризовать силу сигнала от какой-либо станции, код RST надо дополнить сведениями об используемой приемной антенне и сообщить, показания ли это S-метра или оценка сделана на слух.
Поэтому, если нужно более точно охарактеризовать силу сигнала от какой-либо станции, код RST надо дополнить сведениями об используемой приемной антенне и сообщить, показания ли это S-метра или оценка сделана на слух.
КВ и УКВ №4, 2001 г.
Каталог радиолюбительских схем. Децибелы ЭТО ОЧЕНЬ ПРОСТО!
Каталог радиолюбительских схем. Децибелы ЭТО ОЧЕНЬ ПРОСТО!Децибелы ЭТО ОЧЕНЬ ПРОСТО!
Ю.БАЛТИН (YL2DX),
г.Рига.
Когда требуется сравнить какие-нибудь величины, это можно сделать по-разному. Можно, например, разделив эти величины одну на другую, сказать — Р1 больше чем Р2 в 3 раза, или Р1, меньше чем Р2 в 28 раз. Если нам понадобится далее вести какие-то расчеты, мы будем пользоваться отвлеченными числами 3, или 28, или 1/28 (иногда для уточнения добавляя слово «раз»).
В ряде случаев для расчетов или для большей наглядности сравнения оказывается удобнее логарифмировать отношение величин и оперировать далее с числом logа(Р1/Р2).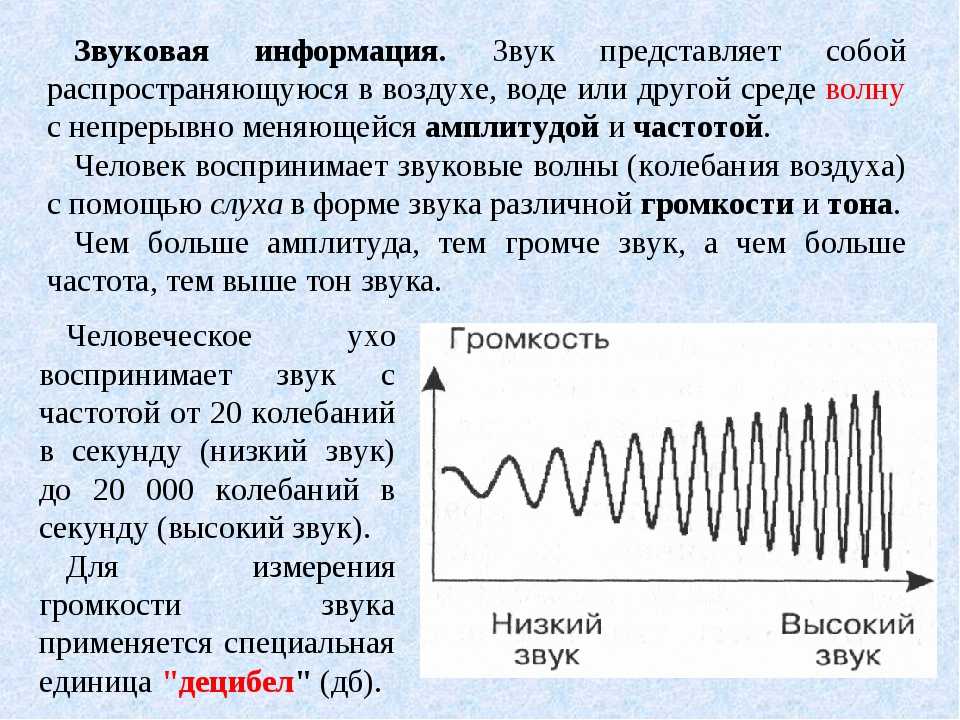 Известно, что применение логарифмов упрощает математические расчеты, в частности, позволяет вместо умножения и деления пользоваться сложением и вычитанием. При большом диапазоне изменений какой-либо величины логарифмический масштаб позволяет лучше разглядеть на одном и том же графике и малые, и большие ее относительные изменения.
Известно, что применение логарифмов упрощает математические расчеты, в частности, позволяет вместо умножения и деления пользоваться сложением и вычитанием. При большом диапазоне изменений какой-либо величины логарифмический масштаб позволяет лучше разглядеть на одном и том же графике и малые, и большие ее относительные изменения.
Чтобы различать, имеем ли мы дело с числом «раз» или с его логарифмом, а также чтобы зафиксировать, каким основанием мы пользуемся при логарифмировании (числом 10, числом e=2,71828 или иным), следует присвоить этому логарифму какое-нибудь название. В системе СИ в качестве относительной логарифмической единицы отношения мощностей Р1, и Р2 принят десятичный логарифм Ig(Р1/Р2). Эта единица называется бел (Б).
На практике этой довольно крупной единицей оказалось не очень удобно оперировать, поэтому ее «разменивают» на единицы, в десять раз меньшие — децибелы. Соотношение двух уровней мощности Р1 и Р2 в децибелах (дБ, или dB) выражают по следующей формуле:
Множитель 10 в формуле (1) появился потому, что десять децибел как раз и есть один бел. Таким образом, не повезло изобретателю телефона А.Г.Беллу — мало того, что единицу его имени укоротили на одну букву «л», так еще и пользуются лишь десятыми долями.
Таким образом, не повезло изобретателю телефона А.Г.Беллу — мало того, что единицу его имени укоротили на одну букву «л», так еще и пользуются лишь десятыми долями.
Теперь разберемся с отношениями напряжений или токов. Вспомним из школьного курса, что мощность в линейной цепи равна:
Отсюда легко видеть, что:
а значит:
Из школьного же курса вспомним:
Из равенств (2) и (3) вытекает следующее:
Это и есть формула взаимосвязи между «белами по мощности» и «белами по напряжению» в одной и той же цепи, если в ней выполняется закон Ома. Ну, а если мы намерены пользоваться десятыми долями бела, то обе половины этого уравнения необходимо умножить на 10. Отсюда следует, что при сравнении величин напряжений (U1 и U2) или токов (I1 и l2), их соотношение в децибелах:
Полезно запомнить несколько характерных значений, приведенных в таблице.
Если напряжение на резисторе увеличить вдвое (на +6 дБ «по напряжению»), то и протекающий через него ток увеличится вдвое (на +6 дБ «по току»), а мощность, выделяемая этим резистором, станет вчетверо больше—опять-таки на +6 дБ («по мощности»). Чтобы уменьшить мощность в 10 раз (-10 дБ), нужно снизить приложенное к резистору напряжение в 3,162 раза (-10 дБ), отчего ток по закону Ома тоже уменьшится в 3,162 раза (-10 дБ).
Чтобы уменьшить мощность в 10 раз (-10 дБ), нужно снизить приложенное к резистору напряжение в 3,162 раза (-10 дБ), отчего ток по закону Ома тоже уменьшится в 3,162 раза (-10 дБ).
Поскольку мощность в линейной цепи пропорциональна квадрату напряжения или тока, численные значения соотношений их величин, выраженные в децибелах, остаются одними и теми же как при сравнении мощностей, так и при сравнении напряжений или токов:
В случае ослабления сигнала (когда отношение Р1/Р2 меньше единицы), логарифм становится отрицательным, следовательно, отрицательным становится и коэффициент передачи данной цепи, выраженный в децибелах. Для вычисления общего коэффициента передачи нескольких последовательно соединенных цепей или устройств достаточно просуммировать значения в децибелах с учетом их знаков (+) или (-). Это
намного удобнее, чем перемножать исходные значения в разах.
При вычислении коэффициента передачи различных устройств (например, усилительного каскада) во многих случаях мы имеем дело с разными входным и выходным сопротивлениями; в нелинейных цепях напряжение и ток взаимно не пропорциональны, а мощность не связана с тем и другим квадратичной зависимостью.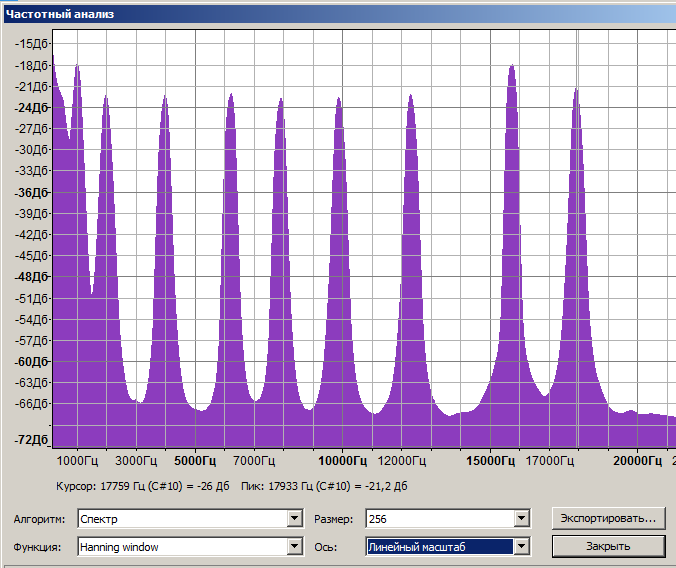 Коэффициенты передачи таких цепей по току:
Коэффициенты передачи таких цепей по току:
и по напряжению:
различны и в разах, и в децибелах; коэффициент передачи по мощности:
а в децибелах:
поскольку
Равенство (6) к этим случаям не относится, но по отдельности изменения или соотношения величин тока или напряжения на одном и том же линейном сопротивлении (например, на сопротивлении нагрузки нелинейного усилителя) все равно выражаются в децибелах формулами (4) и (5), а изменения уровня мощности — формулой (1).
Зачем возиться с логарифмами? Во-первых, логарифмическая шкала наиболее естественна для наших органов чувств, в частности, для слуха. Закон логарифмической зависимости ощущений от силы воздействия сформулирован Вебером и Фехнером (обычно называется законом Вебера) — «одинаковые относительные изменения раздражающей силы вызывают одинаковые приращения слухового ощущения, т.е. слуховое ощущение пропорционально логарифму раздражающей силы».
Практически, 1 дБ — это наименьшая ступенька изменения интенсивности звука, едва обнаруживаемая на слух, изменение на 6 дБ воспринимается на слух как хорошо заметное (но небольшое — примерно вдвое громче), на 10 дБ — значительное, а на 20 дБ—как весьма большое.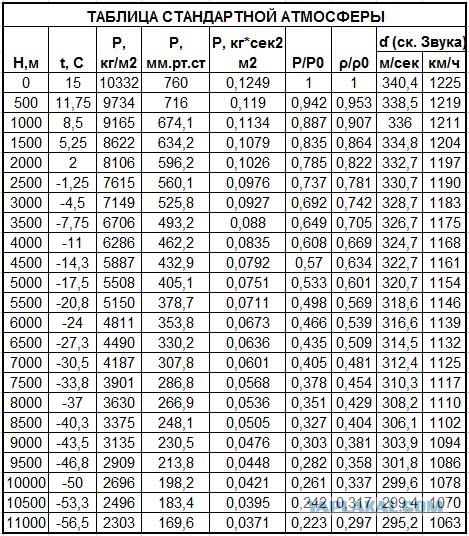 Каждый балл по шкале S системы RST — это 6 дБ (или 0,6 бела), так что мы, особо не задумываясь, занимаемся логарифмированием каждый раз, когда начинаем очередную связь в эфире, передавая рапорт корреспонденту.
Каждый балл по шкале S системы RST — это 6 дБ (или 0,6 бела), так что мы, особо не задумываясь, занимаемся логарифмированием каждый раз, когда начинаем очередную связь в эфире, передавая рапорт корреспонденту.
Во-вторых, значения величин, с которыми нередко приходится сталкиваться, в обычном исчислении бывает трудно соразмерить—скажем, 1 микровольт отличается от 1 киловольта в 1 000 000 000 раз. А в децибелах разница выражается вполне удобной величиной 180 дБ. Мощности, которые выделятся на одном и том же сопротивлении при приложении к нему этих напряжений, будут отличаться астрономически — в 1 000 000 000 000 000 000 раз, а в децибелах — все на те же 180 дБ. С другой стороны, если, например, сравнивать 1,03 мА и 1,37 мА, то их отличие выразится вполне заметной величиной — 2,5 дБ.
|
Децибелы |
0 |
+1 (-1) |
+3 (-3) |
+6 (-6) |
+10 (-10) |
+20 (-20) |
+40 (-40) |
+60 (-60) |
|
Отношение мощностей P1/P2 |
1 |
1,26 (0,79) |
2 (0,5) |
4 (0,25) |
10 (0,1) |
100 (0,01) |
104 (10-4) |
106 (10-6) |
|
Отношение напряжений или токов U1/U2 или I1/I2 |
1 |
1,12 (0,89) |
1,41 (0,707) |
2 (0,5) |
3,16 (0,316) |
10 (0,1) |
100 (0,01) |
1000 (10-3) |
Если запомнить характерные значения из таблицы, то можно очень легко пересчитывать в уме и любые другие величины отношений в децибелы и обратно. Например, 4 дБ—это (3 дБ +1 дБ). Значит, отношение мощностей (2×1,26)= 2,52 раза или отношение напряжениий (1,41 х 1,12) =1,6 раза. Или, к примеру, отношение двух значений тока равно 17 раз, то есть (10×1,7). 10 раз по току — это 20 дБ, а 1,7 раза — между 1,41 и 2, значит, где-то около 4,5 дБ. В сумме (20 дБ + 4,5 дБ) = 24,5 дБ. Ну, а для чисел, кратных десяти, мнемоника очевидна.
Например, 4 дБ—это (3 дБ +1 дБ). Значит, отношение мощностей (2×1,26)= 2,52 раза или отношение напряжениий (1,41 х 1,12) =1,6 раза. Или, к примеру, отношение двух значений тока равно 17 раз, то есть (10×1,7). 10 раз по току — это 20 дБ, а 1,7 раза — между 1,41 и 2, значит, где-то около 4,5 дБ. В сумме (20 дБ + 4,5 дБ) = 24,5 дБ. Ну, а для чисел, кратных десяти, мнемоника очевидна.
Децибелы сами по себе — это величины не физические, а абстрактные, математические, такие же относительные, как и разы. Их нельзя пощупать руками как килограмм, метр или киловольт (нет… руками его, пожалуй, не стоит щупать… Hi). Их можно только вычислить, сравнивая реальные физические величины, и оперировать ими при расчетах. Но если мы устанавливаем в качестве эталона 0 дБ какое-то определенное значение физической величины, например, 1 Вт или 1 мкВ, то можем и прямо измерять в децибелах относительно него уровни мощности или, соответственно, напряжения. Обозначают такие единицы измерения теми же буквами «дБ», но с добавлением индекса: дБВт (децибел-ватт), дБмкВ (децибел-микровольт) и т. п. Например, мощность 27 дБВт—это то же самое, что 500 Вт, а -13 дБВт — 50 мВт. Напряжение -3 дБмкВ — 0,707 мкВ, а 23 дБмкВ — 14,14 мкВ.
п. Например, мощность 27 дБВт—это то же самое, что 500 Вт, а -13 дБВт — 50 мВт. Напряжение -3 дБмкВ — 0,707 мкВ, а 23 дБмкВ — 14,14 мкВ.
В акустике за 0 дБ однозначно принято пороговое звуковое давление 2-10 Па, и децибел без дополнительного индекса прямо используется в качестве единицы уровня звукового давления.
На коротких волнах, по системе оценки сигнала RST, напряжение, равное 50 мкВ, на 50-омном входе приемника (S=9), в сущности, принято за ноль децибел. Каждый балл ниже девяти — это -6 дБ (в 2 раза меньше) от этого напряжения, а если сигнал сильнее, то S-метр покажет, на сколько децибел. Чтобы напряжение на входе приемника изменилось на 1 балл, нужно на столько же изменить мощность передатчика — на 6 дБ, то есть в 4 раза. Если получен RS 59+20 dB, то можно (и нужно бы!) смело уменьшать мощность передатчика на 30 дБ (т.е. в 1000 раз!!!) — все равно будет слышно достаточно громко — больше чем на S=7 (с запасом +2 дБ) (конечно, если «+20» было сказано не ради красного словца. . .Hi).
. .Hi).
Надеюсь, что теперь понятно, почему «выжимать» 250 Вт из 200-ваттного передатчика просто глупо — увеличение силы сигнала менее чем на 1 дБ вообще никто не заметит, а вот сплэттер или щелчки по всему диапазону вполне реально могут испортить настроение многим.
О чувствительности приемника и S-метра
Чувствительность приемников часто измеряют в децибел-милливаттах (дБм) или дБмВт: 1 мВт = 0 дБм.
В сущности, измерять чувствительность в единицах мощности имеет больше смысла, чем в единицах напряжения, так так нам приходится иметь дело с сигналами разной формы — синусоидальными, шумовыми, шумоподобными и др. К тому же, мы избавляемся от необходимости уточнять, каково входное сопротивление приемника, и имеем возможность сравнивать чувствительность приемников с различными входными сопротивлениями. Эффективное напряжение 50 мкВ на 50-омном входе соответствует мощности -73 дБм. Этой же мощности соответствует напряжение 61,2 мкВ на 75-омном входе. Все это соответствует оценке S=9 сигнала по системе RST на частотах ниже 30 МГц. На УКВ за S=9 принята мощность -93 дБм (5 мкВ на 50-омном входе приемника).
На УКВ за S=9 принята мощность -93 дБм (5 мкВ на 50-омном входе приемника).
Система оценки сигнала на слух по коду RST была предложена W2BSR в середине 30-х годов и с тех пор стала всемирно признанной. Стандарт градуировки S-метров был установлен IARU в 60-х годах, но когда его принимали, похоже, что ориентировались на не очень чувствительные приемники, а может быть, и на «тугоухих» операторов… (Hi). Впрочем, в те годы еще широко использовалась амплитудная модуляция (AM), в CW-приемниках сравнительно редко встречались хорошие узкополосные фильтры, а собственные шумы радиодеталей были побольше чем сейчас, так что чувствительность среднего любительского приемника была на порядок хуже, чем у современного.
Пороговая чувствительность порядка -130 дБм — очень высокая, но не редкая для современного КВ-приемника при узкой полосе в режиме CW (0,035 мкВ на 50-омном входе). Эта величина ниже, чем S=1 (-121 дБм) по S-метру. При таких уровнях имеется несоответствие слуховой (по таблице значений «S») и инструментальной (по S-метру) оценки силы сигнала — в чистом эфире, без помех, на хорошем приемнике сигнал с уровнем -125 или -130 дБм может вполне восприниматься на слух как хорошо читаемый «слабый», или «очень слабый» т. е. S=3 или S=2, a S-метр не будет показывать ничего. Но, по сути системы RST, если S=0, то сигнала просто не слышно совсем, a S=1 — это, по определению, «едва ощутимый сигнал». В тех же условиях сигнал мощностью -85 дБм может выглядеть как очень громкий (при достаточном коэффициенте усиления УНЧ приемника), но S-метр покажет не 9, а только 7 баллов — это типично, например, на 10-метровом диапазоне (впрочем, он как раз на границе KB и УКВ, где шкалы S-метров разные).
е. S=3 или S=2, a S-метр не будет показывать ничего. Но, по сути системы RST, если S=0, то сигнала просто не слышно совсем, a S=1 — это, по определению, «едва ощутимый сигнал». В тех же условиях сигнал мощностью -85 дБм может выглядеть как очень громкий (при достаточном коэффициенте усиления УНЧ приемника), но S-метр покажет не 9, а только 7 баллов — это типично, например, на 10-метровом диапазоне (впрочем, он как раз на границе KB и УКВ, где шкалы S-метров разные).
В трансиверах разных фирм стандарт IARU не очень-то соблюдается. Кроме того, чувствительность одного и того же приемника на разных диапазонах различается и может ступенчато регулироваться оператором (включением или выключением преду-силителей ВЧ и аттенюаторов), а шкала S-метра остается одна на все случаи. Если включен аттенюатор, то следует величину его затухания прибавить к показаниям S-метра, а если включен дополнительный пре-дусилитель — то величину его усиления из показаний S-метра вычесть. Разумеется, это относится только к случаю использования для приема полноразмерных согласованных антенн. Когда действующая высота антенны мала, или антенна не согласована со входом приемника, показания S-метра сами по себе ничего не скажут о реальном уровне сигнала в эфире.
Когда действующая высота антенны мала, или антенна не согласована со входом приемника, показания S-метра сами по себе ничего не скажут о реальном уровне сигнала в эфире.
В сущности, единственной полной и действительно объективной характеристикой уровня сигнала, создаваемого каким-либо передатчиком в точке приема, является напряженность поля, которую можно вычислить, разделив ЭДС на клеммах приемной антенны UA на ее действующую высоту hд:
Действующая высота (или действующая длина) антенны вычисляется по формуле:
т.е. зависит от длины волны l , коэффициента направленного действия D, КПД (η) антенны и ее входного сопротивления (идеальный полуволновой диполь в свободном пространстве имеет действующую длину l /
π). Поэтому, если нужно более точно охарактеризовать силу сигнала от какой-либо станции, код RST надо дополнить сведениями об используемой приемной антенне и сообщить, показания ли это S-метра или оценка сделана на слух.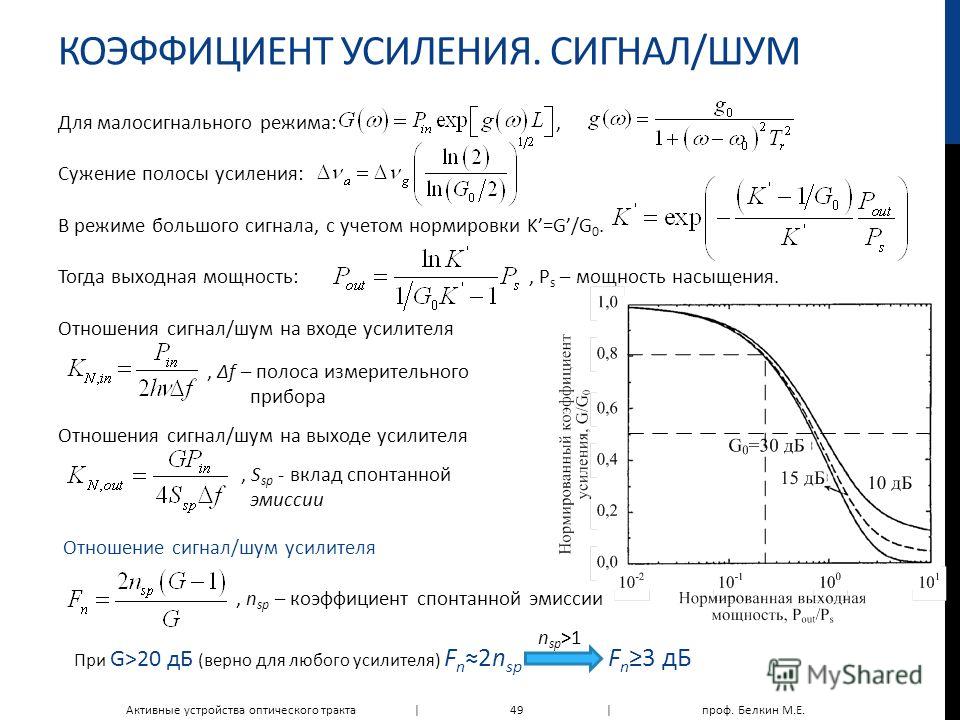
КВ и УКВ №4, 2001 г.
| Содержание | © Каталог радиолюбительских схемВсе права защищены. Радиолюбительская страница.Перепечатка разрешается только с указанием ссылки на данный сайт. Пишите нам. E-mail: [email protected] или [email protected]. |
Я радиолюбитель |
О децибелах (дБ) | GPII DeveloperSpace
О децибелах (дБ) | GPII DeveloperSpaceПерейти к основному содержанию
перевод
Введите ключевые слова
- Узнать
- Быстрые листы
- О децибелах (дБ)
Что такое децибел (дБ)?
дБ или децибел — это логарифмическая единица измерения соотношения между двумя числами.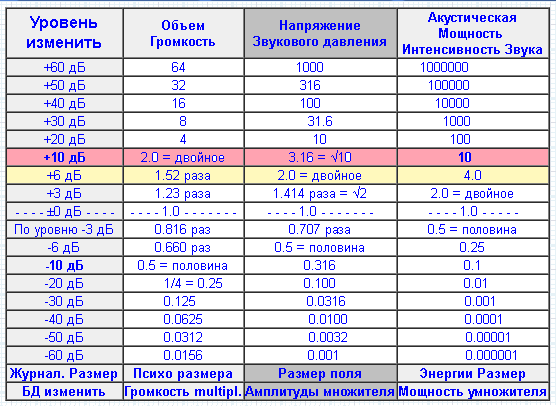
дБ и мощность (20 дБ = 100x)
Говоря о мощности, 3 дБ представляют отношение два к одному или удвоение мощности.
- Таким образом, усиление в 10 дБ соответствует отношению мощности десять к одному, поэтому 10 дБ в 10 раз больше мощности
- Прирост мощности в 40 дБ будет в 10 000 раз больше мощности.
дБ и усиление по напряжению (20 дБ = 10x)
Когда речь идет о напряжении, 6 дБ представляет собой соотношение два к одному или удвоение напряжения.
- 20 дБ будет представлять отношение напряжения десять к одному, поэтому 20 дБ будет в 10 раз больше напряжения.
- Прирост напряжения в 40 дБ будет в 100 раз больше напряжения.
дБ SPL (уровень звукового давления) (20 дБ = 10x)
Термин «SPL» означает уровень звукового давления. Меры SPL принимаются в отношении минимального порога человеческого слуха. Разница в 20 дБ в уровне звукового давления представляет собой отношение звукового давления десять к одному.
Разница в 20 дБ в уровне звукового давления представляет собой отношение звукового давления десять к одному.
- Таким образом, уровень звукового давления 40 дБ будет представлять собой уровень звукового давления, который в 100 раз превышает уровень звукового давления самого тихого звука, который может уловить нормальный человеческий слух.
Восприятие громкости (20 дБ = 4x)
Интересно, что наше восприятие громкости не совпадает с уровнем звукового давления. Хотя фактические формулы
несколько сложны, исходя из грубого эмпирического правила, увеличение уровня звукового давления на 10 дБ воспринимается примерно в два раза громче.
- Таким образом, усиление в 20 Дб кажется примерно в 4 раза громче.
- А усиление в 40 Дб кажется примерно в 16 раз громче.
дБ SPL в реальной жизни
Чтобы дать вам представление о том, как измерения дБ SPL соотносятся с повседневной жизнью, ниже приводится список приблизительных уровней звукового давления для различных звуков.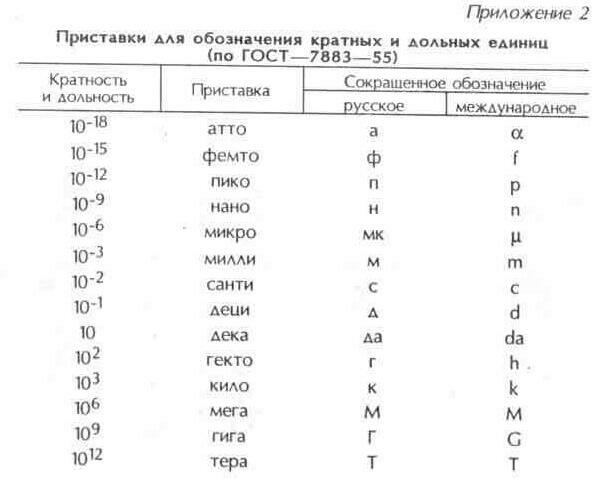 (Из http://www.state.me.us/spo/landuse/docs/NoiseTABulletin.pdf — с добавлением столбца «Приблизительная громкость») (см. также дБ SPL и дБ(A) SPL обсуждение на следующей странице)
(Из http://www.state.me.us/spo/landuse/docs/NoiseTABulletin.pdf — с добавлением столбца «Приблизительная громкость») (см. также дБ SPL и дБ(A) SPL обсуждение на следующей странице)
|
Звуковая среда |
Уровень звукового давления (дБА SPL) |
Приблизительная громкость обычного разговора |
|---|---|---|
|
Порог слышимости |
0 |
Ничего не слышу |
|
Интерьер студии вещания или шелест листьев |
10 |
1/32 громкость разговора |
|
Тихий интерьер дома или сельская ночь |
20 |
1/16 громкости |
|
Тихий интерьер офиса или тиканье часов |
30 |
1/8 громкости |
|
Тихая сельская местность или небольшой театр |
40 |
1/4 громкости |
|
Тихая пригородная зона или посудомоечная машина в соседней комнате |
50 |
1/2 громкости |
|
Интерьер офиса или обычный разговор |
60 |
Обычный разговор |
|
Пылесос на высоте 10 футов |
70 |
Вдвое громче |
|
Проезжающий автомобиль на расстоянии 10 футов или вывоз мусора на расстоянии 3 фута |
80 |
В 4 раза громче |
|
Проезжающий автобус или грузовик на расстоянии 10 футов или пищевой блендер на расстоянии 3 фута |
90 |
В 8 раз громче |
|
Проходящий поезд метро на расстоянии 10 футов или газовая газонокосилка на расстоянии 3 фута |
100 |
В 16 раз громче |
|
Ночной клуб с оркестром |
110 |
В 32 раза громче |
|
Порог боли |
120 |
В 64 раза громче разговора |
Хороший ресурс по этой теме (ссылка на сайт Американского акустического общества http://asa. aip.org/)
aip.org/)
- Campanella Acoustics — Часто задаваемые вопросы (FAQ)
В чем разница между dB SPL и dB(A) SPL?
Следующее взято из часто задаваемых вопросов Campanella Acoustics
Шумомер, который измеряет уровень звукового давления с «плоской» характеристикой, будет указывать силу низкочастотного звука с тем же акцентом, что и более высокочастотные звуки. Тем не менее, наше ухо воспринимает низкочастотный звук как менее громкий, чем более высокочастотный звук. Система барабанная перепонка-стремя-круглое окно ведет себя как механический преобразователь с конечной полосой пропускания. Говоря языком EE, частоты прокрутки «3 дБ» составляют примерно 500 Гц в нижней части и 8 кГц в верхней части. Используя электронный фильтр ослабления, равный тому, который, по-видимому, обеспечивает человеческое ухо для звука на каждой частоте (кривая отклика 40-фонов), измеритель уровня звука теперь будет сообщать числовое значение, пропорциональное человеческому восприятию силы этого звука. не зависит от частоты. Раздел 8.2 показывает таблицу этих весов.
не зависит от частоты. Раздел 8.2 показывает таблицу этих весов.
К сожалению, человеческое восприятие громкости по отношению к частоте меняется вместе с громкостью. Когда звук очень громкий — 100 дБ и более, восприятие громкости более стабильно во всем слышимом диапазоне частот. Веса «B» и «C» отражают эту тенденцию. Взвешивание «B» в настоящее время мало используется, но C-взвешивание добилось известности в оценке раздражающих общественных шумов, таких как низкочастотный звук, издаваемый артиллерийским огнем и рок-концертами под открытым небом. C-взвешивание также приведено в таблице в 8.2.
О первом электрическом шумомере сообщил Джордж У. Пирс в Proceedings of the American Academy of Arts and Sciences, v 43 (1907-8). Через пару десятилетий переход от конных повозок к автомобилям в городах привел к большим изменениям. в фоновом шумовом климате. Появление «звуковых радиостанций» — кинозвука — было большим стимулом для патентов на шумомеры того времени, но стандартного метода измерения звука все еще не было. «Шум» (нежелательный звук) стал достоянием общественности.
«Шум» (нежелательный звук) стал достоянием общественности.
Первый предварительный стандарт для шумомеров (Z24.3) был опубликован Американской ассоциацией стандартов в 1936, спонсируемый Американским акустическим обществом. Предварительный стандарт показывает две частотные взвешивающие кривые «А» и «В», которые были смоделированы на основе реакции человеческого уха на низкие и высокие уровни звука соответственно.
С появлением закона Уолша-Хили в 1969 году А-взвешивание звука де-факто считалось «подходящим» взвешиванием для представления уровня звука в виде одного числа (а не в виде спектра). С появлением интересов Федерального управления гражданской авиации США и Агентства по охране окружающей среды США в 70-х годах они также адаптировали показатель дБА. (Вместе с метрикой дБА возникла связанная с этим нехватка точности в точном представлении способности данного звука вызывать потерю слуха и способность создавать раздражение.)
[Примечание редактора: показатель с одним числом, такой как dBA, легче понять юридическим и административным должностным лицам, так что обнародование, обеспечение соблюдения и административные критерии и действия понятны большему количеству сторон, часто за счет более точного понимания и проектирования. способность к действию. Например, принудительное применение может быть основано на дБА, но схема контроля шума требует метрики спектральных данных октавной полосы или даже третьей октавы.]
способность к действию. Например, принудительное применение может быть основано на дБА, но схема контроля шума требует метрики спектральных данных октавной полосы или даже третьей октавы.]
аналогична той, что первоначально была определена как кривая «А» в 1936 стандарт. «С-взвешивание» дБ(С), которое используется иногда, имеет относительно плоскую характеристику. «U-взвешивание» — это недавнее взвешивание, которое используется для измерения слышимого звука в присутствии ультразвука и может быть объединено с A-взвешиванием для получения AU-взвешивания. Формула A-Weighting приведена в разделе 8 этого файла часто задаваемых вопросов.
В дополнение к частотной коррекции измерение уровня звукового давления может быть взвешено по времени в виде отклика «Быстрый», «Медленный» или «Импульсный». Измерения уровня звукового давления с A-взвешиванием и быстрым откликом также известны как «уровень звука».
Многие современные шумомеры могут измерять среднюю звуковую энергию за заданное время. этот показатель называется «эквивалентным непрерывным уровнем звука» (L sub eq). Совсем недавно в некоторых кругах стало принято предполагать, что это звуковое измерение было взвешено по шкале А, если не указан дескриптор взвешивания.
этот показатель называется «эквивалентным непрерывным уровнем звука» (L sub eq). Совсем недавно в некоторых кругах стало принято предполагать, что это звуковое измерение было взвешено по шкале А, если не указан дескриптор взвешивания.
Этот краткий обзор был подготовлен Греггом Вандерхейденом,
Trace R&D Center, University of Maryland, College Park.
dB Gain Calculator
Создано Joanna Śmietańska, кандидатом наук
Отредактировано Wojciech Sas, PhD и Adena Benn
Последнее обновление: 23 февраля 2023 г.
Содержание:- Что такое усиление?
- Формула для коэффициента усиления в дБ
- Коэффициент усиления по напряжению в дБ
- Как преобразовать коэффициент усиления в дБ? – example
- FAQ
Учитесь ли вы записывать музыку, быть инженером по микшированию или играть на своих первых гитарных педалях, ознакомьтесь с этим 9Калькулятор усиления 0030 дБ для регулировки громкости создаваемого вами звука. Думайте об усилении как о разнице в силе сигнала в вашей аудиосистеме или процессоре. Здесь вы можете указать усиление дБ как коэффициент изменения мощности или напряжения и рассчитать усиление по мощности или напряжению в дБ .
Думайте об усилении как о разнице в силе сигнала в вашей аудиосистеме или процессоре. Здесь вы можете указать усиление дБ как коэффициент изменения мощности или напряжения и рассчитать усиление по мощности или напряжению в дБ .
Понимание того, что такое усиление, может стать ключом к изменению звучания ваших миксов в лучшую сторону. Не беспокойтесь, если сейчас это звучит немного сложно! Читайте дальше, чтобы узнать, как можно создавать более качественные миксы, правильно используя усиление.
Что такое усиление?
Как правило, усиление звука описывает величину усиления, применяемого к сигналу, или просто громкость генерируемого звука . Если вы анализируете схемы в частотной области, будет удобнее сравнивать отношение выходных и входных значений в логарифмической шкале , чем в линейной шкале . Ознакомьтесь с нашим преобразователем мощности, чтобы узнать больше о единицах мощности.
Используя логарифмическое отношение двух величин, вы получите новую величину, которую можно представить числом 9.0030 децибел (или дБ для краткости). В названии децибел «деци» означает одну десятую ( 1/10 ) бел; следовательно, есть 10 децибел ( 10 дБ ) на бел или 1 бел = 10 децибел .
Чтобы понять , что означает дБ , помните , что это отношение используется для сравнения и расчета уровней изменения мощности . В отличие от напряжения или силы тока, которые измеряются соответственно в вольтах и амперах, децибел — это безразмерная величина . Если вам нужно найти уровни интенсивности звука в децибелах, посмотрите на наш калькулятор дБ.
💡 Термин «бел» в «децибелах» происходит от известного изобретателя телефона Александра Грэма Белла .
Формула для усиления в дБ
Мы можем использовать коэффициент усиления децибел для сравнения и расчета уровней изменения двух величин мощности.:no_upscale()/cdn.vox-cdn.com/uploads/chorus_asset/file/11469267/Screen_Shot_2018_06_03_at_11.25.38_AM.png) Этот калькулятор усиления дБ использует следующее уравнение для определения усиления мощности: (P2/P1)
Этот калькулятор усиления дБ использует следующее уравнение для определения усиления мощности: (P2/P1)
где:
- дБ\текст{дБ} дБ – усиление децибел в дБ ;
- P2P_2P2 – Конечный уровень мощности (выходной) в Вт ; и
- P1P_1P1 – Начальный уровень мощности (вход) в Вт .
Например, используйте входной сигнал 100 мВт для питания динамика и получите на выходе сигнал 100 Вт . Формула усиления в дБ будет следующей: дБ = 10log₁₀(100 Вт/0,1 Вт) = 10log₁₀(1000) = 30 дБ .
🙋 Вы ищете материал для приглушения громких звуков в вашем окружении? Тогда этот калькулятор коэффициента звукопоглощения будет полезен. Вы также можете проверить скорость звука в воздухе и других средах.
Коэффициент усиления по напряжению в дБ
При расчете коэффициента усиления по напряжению в дБ можно также использовать входное (V1V_1V1) и выходное (V2V_2V2) напряжения:
дБ=20log10(V2/V1)\small \text{dB} = 20 \log_{10} (V_2/V_1)dB=20log10(V2/V1)
Как видите, единственная разница между расчетами коэффициента усиления по мощности и напряжению в дБ касается констант 10 и 20 в уравнении. Также важно, чтобы отношение дБ было правильным во всех случаях, поэтому обе величины должны иметь одни и те же единицы , например ватт или вольт .
Также важно, чтобы отношение дБ было правильным во всех случаях, поэтому обе величины должны иметь одни и те же единицы , например ватт или вольт .
Как преобразовать усиление в дБ? – пример
Допустим, у нас есть усилитель, который выдает 2 Вт на входе и 400 Вт на выходе. Мы можем использовать этот калькулятор усиления дБ , чтобы легко найти усиление мощности в дБ :
- Введите значение
2 Втв поле «Начальная мощность». - Выберите значение
400 Вти укажите его в поле «Конечная мощность». - Считайте значение усиления мощности в дБ:
23,01.
В другом случае: входные и выходные значения совпадают, но уровень мощности выражен в вольт .
- Введите начальное напряжение
2 Ви конечное напряжение400 Вв соответствующие поля калькулятора усиления дБ.
- Проверить значение коэффициента усиления по напряжению в дБ:
46,02.
Обратите внимание, что в два раза больше усиления по мощности, чем , так как мы просто использовали коэффициент 20, а не 10 в уравнении.
Часто задаваемые вопросы
Что означает дБ?
дБ или децибел — это безразмерная единица , которая измеряет отношение между двумя числами . Мы используем децибелы, чтобы показать соотношение изменений мощности (увеличение или уменьшение). Он обычно определяется как , десятикратно превышающий логарифм по основанию 10 двух уровней мощности 9.0031 . Обратите внимание, что 1 ватт к 10 ваттам — это то же соотношение мощности, что и 9 ватт к 90 ваттам, или 1:10 , хотя существует большая разница в количестве ватт.
Может ли коэффициент усиления в дБ быть отрицательным?
Да . Такая ситуация возникает, если отношение мощностей P₂/P₁ или напряжений V₂/V₁ в формуле усиления в дБ на меньше 1 . Это означает, что в системе имеется вход , потеря мощности . Если отношение мощности или напряжения равно 1 , усиление равно 0 дБ , и поэтому схема не производит никакого усиления или проигрыша между сигналами.
Это означает, что в системе имеется вход , потеря мощности . Если отношение мощности или напряжения равно 1 , усиление равно 0 дБ , и поэтому схема не производит никакого усиления или проигрыша между сигналами.
Какой будет входная мощность, если усиление дБ равно 20, а выходная мощность 150 Вт?
1,5 Вт . Рассчитайте это легко следующим образом:
-
Поместите P₂ = 150 Вт и дБ = 20 в уравнение:
10log₁₀(150 Вт/P₁) = 20 .
-
Используйте антилог, чтобы найти P₂:
150 Вт/P₁ = 10 20/10 = 10 2 = 100 .
-
Найдите это:
150 Вт/P₁ = 100 и
P₁ = 150 Вт/100 = 1,5 Вт . -
Рассчитать максимальную начальную (входную) мощность как 1,5 Вт .