Реактивная сила определение. Реактивная сила в оборонной сфере: принципы, применение, перспективы

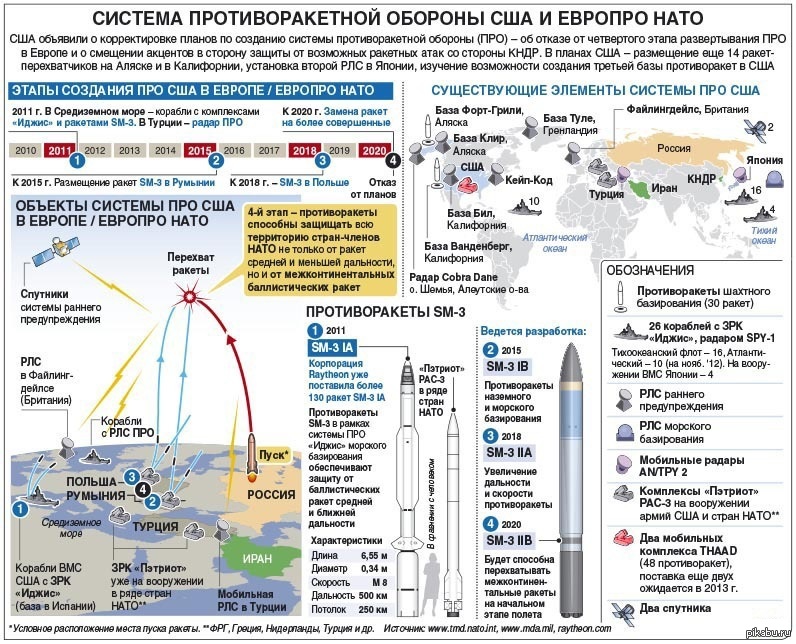
Что такое реактивная сила и как она используется в военной технике. Каковы основные принципы реактивного движения. Какие виды вооружений основаны на реактивной тяге. Каковы перспективы развития реактивных технологий в оборонной сфере.

Что такое реактивная сила и принцип ее действия

Реактивная сила — это сила, возникающая при истечении газа или жидкости из сопла. Она направлена в сторону, противоположную истечению рабочего тела, и является результатом действия третьего закона Ньютона.

Принцип действия реактивной силы основан на законе сохранения импульса. При выбросе массы рабочего тела в одном направлении возникает импульс силы в противоположном направлении. Это позволяет создавать тягу без опоры на внешнюю среду.

Основные характеристики реактивной силы:

• Не требует опоры на внешнюю среду
• Может создаваться в вакууме
• Величина силы зависит от скорости истечения и расхода рабочего тела
• Направлена противоположно истечению продуктов сгорания

Применение реактивной силы в оборонной сфере

Реактивный принцип широко используется в различных видах вооружений и военной техники. Основные области применения:

Ракетное вооружение

Ракеты различных классов и назначения являются самым распространенным применением реактивной тяги в военной сфере. К ним относятся:

• Баллистические ракеты
• Крылатые ракеты
• Зенитные ракеты
• Противотанковые ракетные комплексы
• Авиационные ракеты

Реактивный двигатель позволяет ракетам развивать высокую скорость и дальность полета.

Реактивная авиация

Реактивные двигатели широко применяются в военной авиации:

• Истребители
• Бомбардировщики
• Штурмовики
• Военно-транспортные самолеты

Реактивная тяга обеспечивает высокую скорость и маневренность боевых самолетов.

Виды реактивных двигателей в военной технике

В оборонной сфере применяются различные типы реактивных двигателей:

Жидкостные ракетные двигатели (ЖРД)

Используют жидкое топливо и окислитель. Обеспечивают высокий удельный импульс и возможность многократного включения. Применяются в баллистических ракетах, космических ракетах-носителях.

Твердотопливные ракетные двигатели (РДТТ)

Работают на твердом смесевом топливе. Более просты и надежны, но имеют меньший удельный импульс. Широко применяются в тактических ракетах, зенитных ракетных комплексах.

Воздушно-реактивные двигатели

Используют атмосферный воздух в качестве окислителя. Подразделяются на:

• Турбореактивные
• Турбовентиляторные
• Прямоточные

Применяются в авиации, крылатых ракетах.

Преимущества реактивного движения в военной технике

Использование реактивной тяги дает ряд важных преимуществ:

• Высокая скорость движения
• Большая дальность действия
• Возможность применения в любой среде, включая космос
• Высокая мощность и энерговооруженность
• Простота конструкции некоторых типов реактивных двигателей

Эти качества делают реактивное движение незаменимым для многих видов вооружений.

Развитие реактивных технологий в оборонной сфере

Основные направления совершенствования реактивных двигателей и вооружений:

Повышение удельного импульса

Позволяет увеличить дальность и скорость ракет. Достигается за счет новых видов топлива, совершенствования конструкции двигателей.

Улучшение массовых характеристик

Снижение массы конструкции при сохранении прочности позволяет увеличить полезную нагрузку ракет и летательных аппаратов.

Повышение надежности

Особенно важно для космических ракет и стратегических вооружений. Достигается за счет новых материалов и технологий производства.

Разработка гиперзвуковых технологий

Создание ракет и летательных аппаратов, способных развивать скорость более 5 Махов, является одним из приоритетных направлений.

Перспективные разработки реактивных вооружений

Ведущие страны мира активно работают над новыми видами реактивного оружия:

• Гиперзвуковые ракетные комплексы
• Беспилотные ударные летательные аппараты
• Космические системы вооружений
• Лазерное оружие с ядерной накачкой

Эти разработки могут значительно изменить расстановку сил в военной сфере в ближайшие десятилетия.

Проблемы и ограничения реактивных технологий

Несмотря на широкое применение, реактивное движение имеет ряд недостатков:

• Высокий расход топлива
• Сложность создания многоразовых систем
• Экологические проблемы при использовании некоторых видов топлива
• Высокая стоимость разработки и производства

Преодоление этих ограничений — важная задача для дальнейшего развития реактивных технологий.

Заключение

Реактивная сила играет ключевую роль в современных системах вооружений. Ракетная техника, реактивная авиация, космические системы во многом определяют военный потенциал ведущих держав. Несмотря на определенные недостатки, реактивные технологии продолжат активно развиваться и совершенствоваться в обозримом будущем.

Реактивные силы — определение термина

Термин и определение

силы, не создающие движения, но ограничивающие перемещения (препятствующие перемещениям) твёрдого тела (реакции связей).

Научные статьи на тему «Реактивные силы»

К указанным свойствам относят: сензитивность определяет силу воздействия внешних стимулов, вызывающих…
реакцию личности, скорость возникновения реакции; реактивность – степень непроизвольности реакции на…
внутренние или внешние воздействия одинаковой силы; активность – степень интенсивности воздействия личности…
на окружающую социально-природную среду; соотношение активности, реактивности определяет зависимость…

Данное свойство выступает обратным категории реактивности, повышение уровня сформированности которой

Статья от экспертов

Показан механизм возникновения реактивной силы, ускоряющей пылинку против ионного потока. Он основан на передаче импульса от потока дополнительно ускоренных в поле пылинки ионов атомам буферного газа (при перезарядке ионов на атомах буферного газа). В результате атомами (которые до перезарядки были ионами) из системы ’’ионы + пылинка” выносится больший импульс, чем вносился ими, что и создает реактивную силу, направленную против потока (отрицательная сила трения). Получена оценка ее величины.

Научный журнал

Creative Commons

Резонанс — это явление, при котором частота колебаний какой-либо системы увеличивается колебаниями внешней

силы…
Вынужденные колебания, источником которых является внешняя сила, увеличивают даже те колебания, амплитуда…
При условии неизменности в цепи и напряжения, и активного сопротивления $r$, сила тока при резонансе…
тока от реактивного сопротивления цепи.. ..
реактивной емкостной проводимости, т.е.

Статья от экспертов

В центре внимания статьи находится стратегия индийской «мягкой силы» в Южно-Азиатском субрегионе, как ключевой компонент современной политики Нью-Дели. Раскрыто понимание «мягкой силы» со стороны ведущих держав Азии. Индийско-китайские отношения в области «мягкой силы» рассмотрены через неологизм «Чиндия», который подразумевает не только конкуренцию двух держав, но и развитие смежных зон индийской и китайской цивилизаций, где в результате межкультурного диалога и обмена возникают своеобразные…

Научный журнал

Creative Commons

Повышай знания с онлайн-тренажером от Автор24!

• 📝 Напиши термин
• ✍️ Выбери определение из предложенных или загрузи свое
• 🤝 Тренажер от Автор24 поможет тебе выучить термины, с помощью удобных и приятных карточек

Закон сохранения импульса — опредление, формулы, формулировка

Импульс: что это такое

Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.

Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.

Импульс тела p — импульс тела [кг · м/с] m — масса тела [кг] v — скорость [м/с]

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Закон сохранения импульса

В физике и правда ничего не исчезает и не появляется из ниоткуда.

Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:

Закон сохранения импульса Векторная сумма импульсов тел в замкнутой системе постоянна

А выглядит — вот так:

Закон сохранения импульса pn — импульс тела [кг · м/с]

Простая задачка

Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?

Решение:

Запишем закон сохранения импульса для данного процесса.

— это импульс системы мальчик + лодка до того, как мальчик спрыгнул,

— это импульс мальчика после прыжка,

— это импульс лодки после прыжка.

Изобразим на рисунке, что происходило до и после прыжка.

Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид

Подставим формулу импульса.
, где:
— масса мальчика [кг]
— скорость мальчика после прыжка [м/с]
— масса лодки [кг]
— скорость лодки после прыжка [м/с]

Выразим скорость лодки :

Подставим значения:
м/с

Ответ: скорость лодки после прыжка равна 0,5 м/с

Задачка посложнее

Тело массы m₁ = 800 г движется со скоростью v₁ = 3 м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы m₂ = 200 г со скоростью v₂ = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.

Решение: Для данной системы выполняется закон сохранения импульса:

Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.

Спроецируем импульсы на ось х:

После неупругого удара получилось одно тело массы , которое движется с искомой скоростью:

Отсюда находим скорость тела, образовавшегося после удара:

Переводим массу в килограммы и подставляем значения:

м/с

В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.

Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на получившееся значение.

Ответ: скорость системы тел после соударения равна v = 0,2 м/с.

Второй закон Ньютона в импульсной форме

Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.

Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:

Применим выражение для ускорения

В этих уравнениях слева находится величина a. Так как левые части уравнений равны, можно приравнять правые их части

Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:

В правой части находится — это разница между конечной и начальной скоростью.

Преобразуем правую часть

Раскрыв скобки, получим

Заменим произведение массы и скорости на импульс:

Подставляем:

Или, сокращенно:

То есть, вектор – это вектор изменения импульса .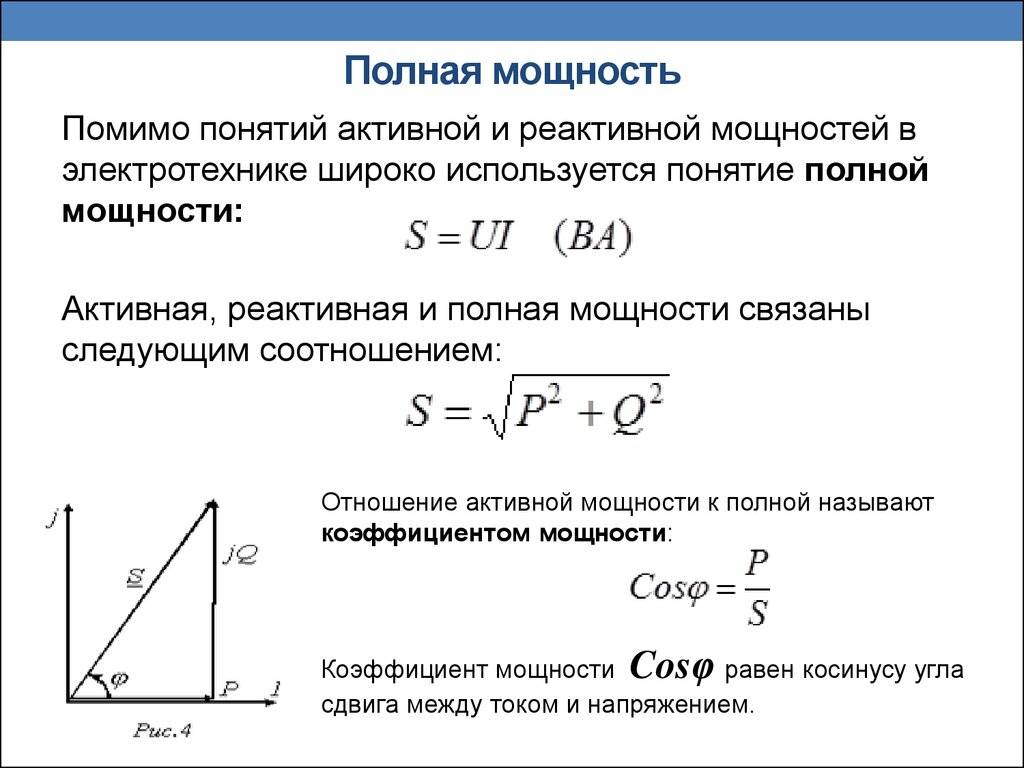

Тогда второй закон Ньютона в импульсной форме запишем так

Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.

Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?

Решение:

Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).

Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.

Реактивное движение

В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.

Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.

Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:

Сила называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.

Закон сохранения импульса позволяет оценить скорость ракеты.

m_г · v_г = m_р · v_р,
где m_г — это масса горючего,

v_г — скорость горючего,

m_р — масса ракеты,

v_р — скорость ракеты.

Отсюда можно выразить скорость ракеты:

v_р = m_г · v_г / m_р

Скорость ракеты при реактивном движении vр = mг · vг / mр mг — это масса горючего [кг] vг — скорость горючего [м/с] mр — масса ракеты [кг] vр — скорость ракеты [м/с]

Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

5.5 Третий закон Ньютона | University Physics Volume 1

Цели обучения

К концу раздела вы сможете:

• Сформулировать третий закон движения Ньютона
• Определить силы действия и реакции в различных ситуациях
• Применение третьего закона Ньютона для определения систем и решения задач движения

До сих пор мы рассматривали силу как толчок или притяжение; однако, если вы подумаете об этом, вы поймете, что ни толчок, ни притяжение никогда не возникают сами по себе. Когда вы толкаете стену, стена давит на вас. Это приводит нас к Третий закон Ньютона .

Третий закон движения Ньютона

Всякий раз, когда одно тело воздействует на другое тело, на первое тело действует сила, равная по величине и противоположная по направлению силе, которую оно оказывает.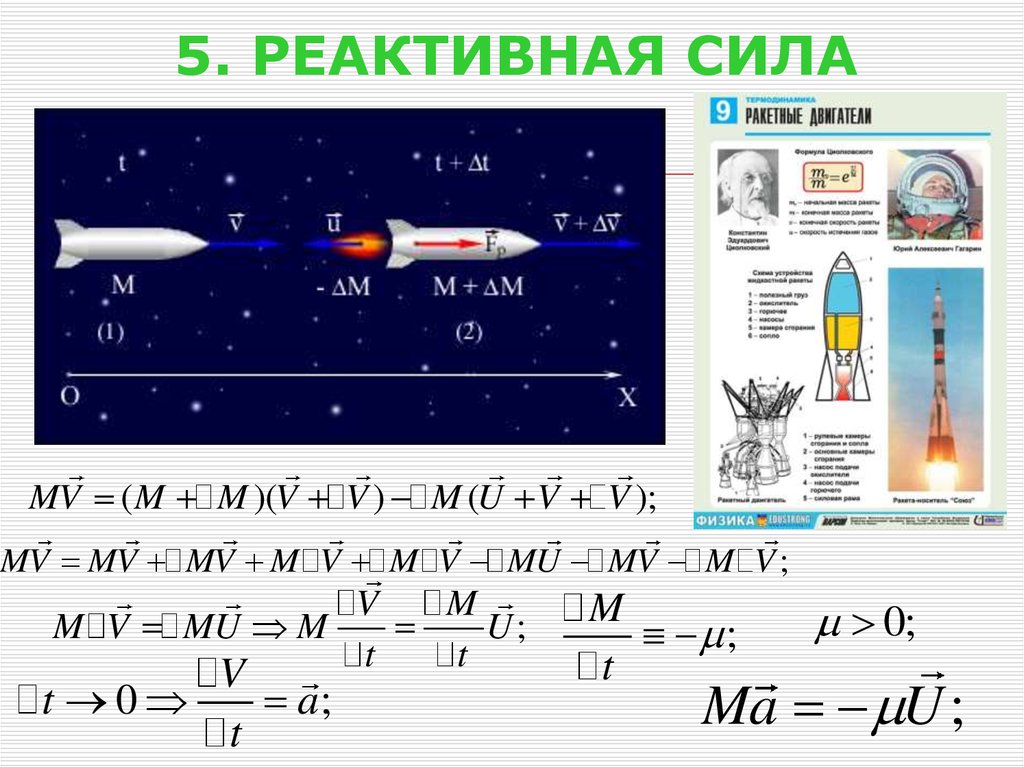 Математически, если тело A прикладывает силу [латекс] \overset{\to} {F} [/латекс] к телу B , тогда B одновременно оказывает силу [латекс] \text{−}\ overset{\to }{F} [/latex] на A , или в форме векторного уравнения,

[латекс] {\ overset {\ to {F}} _ {\ text {AB}} = \ text {−} {\ overset {\ to {F}} _ {\ text {BA}}. [/latex]

Третий закон Ньютона представляет собой определенную симметрию в природе: силы всегда возникают парами, и одно тело не может воздействовать силой на другое, не испытывая на себе силы. Иногда мы в общих чертах называем этот закон «действием-противодействием», где прилагаемая сила является действием, а сила, воспринимаемая как следствие, является противодействием. Третий закон Ньютона имеет практическое применение при анализе происхождения сил и понимании того, какие силы являются внешними по отношению к системе.

Мы легко можем увидеть третий закон Ньютона в действии, взглянув на то, как люди передвигаются. Рассмотрим пловца, отталкивающегося от края бассейна ((Рисунок)). Она упирается ногами в стенку бассейна и ускоряется в направлении, противоположном направлению ее толчка. Стена оказала на пловца равную и противоположную силу. Вы можете подумать, что две равные и противоположные силы нейтрализуют друг друга, но это не так , потому что они действуют на разные системы . В этом случае есть две системы, которые мы могли бы исследовать: пловец и стена. Если мы выберем пловца в качестве интересующей системы, как на рисунке, то [латекс] {F}_{\text{стена на ногах}} [/латекс] является внешней силой, действующей на эту систему и влияющей на ее движение. Пловец движется в направлении действия этой силы. Напротив, сила [латекс] {F}_{\text{футы на стене}} [/латекс] действует на стену, а не на нашу интересующую систему. Таким образом, [латекс] {F}_{\text{ноги на стене}} [/латекс] не влияет напрямую на движение системы и не отменяет [латекс] {F}_{\текст{стена на ногах} }. [/latex] Пловец отталкивается в направлении, противоположном тому, в котором он хочет двигаться. Таким образом, реакция на ее толчок идет в желаемом направлении. На диаграмме свободного тела, такой как показанная на (Рисунок), мы никогда не включаем обе силы пары действие-противодействие; в этом случае мы используем только [латекс] {F}_{\text{стена на ногах}} [/латекс], а не [латекс] {F}_{\текст{ноги на стене}} [/латекс].

Рисунок 5.16 Когда пловец прикладывает силу к стене, он ускоряется в противоположном направлении; другими словами, чистая внешняя сила, действующая на нее, действует в направлении, противоположном [латексу] {F} _ {\ text {ноги на стене}}. [/latex] Это противодействие возникает потому, что в соответствии с третьим законом Ньютона стена действует на пловца с силой [латекс] {F}_{\text{стена на ногах}} [/латекс] равной по величине, но в направлении, противоположном тому, которое она оказывает на него. Линия вокруг пловца указывает интересующую систему. Таким образом, диаграмма свободного тела показывает только [латекс] {F}_{\text{стена на ногах}}, [/латекс] w (сила гравитации) и BF, которая представляет собой выталкивающую силу воды, поддерживающую вес пловца. Вертикальные силы w и BF компенсируются, потому что нет вертикального ускорения.

Другие примеры третьего закона Ньютона найти несложно:

• Профессор шагает перед доской и прикладывает силу к полу. Пол оказывает на профессора силу реакции, которая заставляет его двигаться вперед с ускорением.
• Автомобиль ускоряется вперед, потому что земля давит на ведущие колеса вперед в ответ на то, что ведущие колеса толкают землю назад. Вы можете увидеть следы отталкивания колес назад, когда шины пробуксовывают на гравийной дороге и отбрасывают камни назад.
• Ракеты движутся вперед, выбрасывая газ назад с большой скоростью. Это означает, что ракета оказывает большую обратную силу на газ в камере сгорания ракеты; следовательно, газ оказывает большую реактивную силу на ракету вперед. Эта сила реакции, толкающая тело вперед в ответ на силу, направленную назад, называется тягой . Это распространенное заблуждение, что ракеты движутся сами по себе, отталкиваясь от земли или воздуха позади себя. На самом деле они лучше работают в вакууме, где они легче удаляют выхлопные газы.
• Вертолеты создают подъемную силу, толкая воздух вниз, тем самым испытывая направленную вверх силу реакции.
• Птицы и самолеты также летают, воздействуя на воздух в направлении, противоположном той силе, в которой они нуждаются. Например, крылья птицы толкают воздух вниз и назад, чтобы подняться и двигаться вперед.
• Осьминог передвигается в воде, выбрасывая воду через воронку из своего тела, подобно водному мотоциклу.
• Когда человек тянет вниз вертикальную веревку, веревка тянет человека вверх ((Рисунок)).

Рисунок 5.17 Когда альпинист тянет веревку вниз, веревка тянет альпиниста вверх.

Третий закон Ньютона имеет две важные особенности. Во-первых, прилагаемые силы (действие и противодействие) всегда равны по величине, но противоположны по направлению. Во-вторых, эти силы действуют на разные тела или системы: сила A действует на B и сила B действует на A . Другими словами, две силы являются различными силами, которые не действуют на одно и то же тело. Таким образом, они не отменяют друг друга.

Для ситуации, показанной на (Рисунок), третий закон указывает, что, поскольку стул давит на мальчика вверх с силой [латекс] \overset{\to }{C}, [/латекс] он давит на мальчика вниз стул с силой [латекс] \text{−}\overset{\to }{C}. [/latex] Точно так же он давит вниз с помощью сил [латекс] \text{−}\overset{\to }{F} [/latex] и [латекс] \text{−}\overset{\to }{T } [/latex] на полу и на столе соответственно. Наконец, поскольку Земля притягивает мальчика вниз с силой [латекс] \overset{\to }{w}, [/латекс] он притягивает Землю вверх с силой [латекс] \текст{−}\overset{\to }{ ш} [/латекс]. Если бы этот студент в отчаянии стучал кулаком по столу, он бы быстро усвоил болезненный урок (которого можно было бы избежать, изучая законы Ньютона), что стол наносит ответный удар так же сильно.

Человек, который идет или бежит, инстинктивно применяет третий закон Ньютона. Например, бегун на (рис.) толкает землю назад, так что она толкает его вперед.

Рисунок 5.18 Бегун сталкивается с третьим законом Ньютона. а) Бегун прикладывает силу к земле. (b) Сила реакции земли на бегущего толкает его вперед.

Пример

Силы, воздействующие на неподвижный объект

Пакет на (рис.) стоит на весах. На упаковку действуют следующие силы: [латекс] \overset{\to} {S}, [/latex], что связано с масштабом, и [латекс] \text{−}\overset{\to }{w}, [ /латекс], что связано с гравитационным полем Земли. Силы реакции, которые оказывает упаковка, равны [латекс] \текст{−}\overset{\to }{S} [/latex] на весах и [латекс] \overset{\to }{w} [/latex] на Земля. Поскольку пакет не ускоряется, применение второго закона дает

[латекс] \overset{\to }{S}-\overset{\to }{w}=m\overset{\to }{a}=\overset{\to }{0}, [/latex]

, так что

[латекс] \overset{\to {S}=\overset{\to }{w}. [/latex]

Таким образом, показания весов дают величину веса посылки. Однако весы не измеряют вес посылки; он измеряет силу [латекс] \text{−}\overset{\to }{S} [/latex] на его поверхности. Если система ускоряется, то [латекс] \overset{\to }{S} [/latex] и [латекс] \text{−}\overset{\to }{w} [/latex] не будут равны, так как объясняется в «Применениях законов Ньютона».

Рисунок 5.19 (a) Силы, действующие на упаковку, лежащую на весах, вместе с их силами реакции. Сила [латекс] \overset{\to }{w} [/латекс] – это вес упаковки (сила земного притяжения), а [латекс] \overset{\to }{S} [/латекс] – усилие весов на упаковке. (b) Изоляция системы пакет-масштаб и система пакет-Земля делает пары действия и противодействия ясными.

Пример

Подготовка к работе: выбор правильной системы

Профессор физики толкает тележку с демонстрационным оборудованием в лекционный зал ((Рисунок)). Ее масса 65,0 кг, масса тележки 12,0 кг, масса оборудования 7,0 кг. Вычислите ускорение, возникающее, когда профессор прикладывает к полу обратную силу 150 Н. Все силы, противодействующие движению, такие как трение о колеса тележки и сопротивление воздуха, составляют 24,0 Н.

Рис. Длины стрелок пропорциональны величине сил (за исключением [латекса] \overset{\to }{f}\text{,} [/латекса], потому что он слишком мал для масштабирования). Система 1 подходит для этого примера, потому что она запрашивает ускорение всей группы объектов. Только [latex] {\overset{\to }{F}}_{\text{floor}} [/latex] и [latex] \overset{\to }{f} [/latex] являются внешними силами, действующими на систему. 1 по линии движения. Все остальные силы либо отменяют, либо воздействуют на внешний мир. Система 2 выбрана для следующего примера таким образом, что [латекс] {\overset{\to }{F}}_{\text{проф}} [/латекс] является внешней силой и входит во второй закон Ньютона. Диаграммы свободного тела, которые служат основой для второго закона Ньютона, различаются в зависимости от выбранной системы.

Стратегия

Поскольку они ускоряются как единое целое, мы определяем систему как профессора, тележку и оборудование. Это Система 1 на (Рисунок). Профессор отталкивается назад с силой [латекс] {F}_{\text{фут}} [/латекс] в 150 Н. Согласно третьему закону Ньютона, на пол действует поступательная сила реакции [латекс] {F}_{ \text{floor}} [/latex] 150 Н в Системе 1. Поскольку все движения горизонтальны, мы можем предположить, что результирующая сила в вертикальном направлении отсутствует. Следовательно, задача является одномерной в горизонтальном направлении. Как уже отмечалось, трение f противостоит движению и, таким образом, находится в направлении, противоположном [латексу] {F} _ {\ text {пол}}. [/latex] Мы не включаем силы [latex] {F}_{\text{prof}} [/latex] или [latex] {F}_{\text{cart}} [/latex], потому что они внутренние силы, и мы не включаем [латекс] {F}_{\text{фут}} [/латекс], потому что он действует на пол, а не на систему. На Систему 1 не действуют никакие другие значительные силы. Если из всей этой информации можно найти чистую внешнюю силу, мы можем использовать второй закон Ньютона, чтобы найти требуемое ускорение. См. диаграмму свободного тела на рисунке.

Решение

Второй закон Ньютона равен

[латекс] a=\frac{{F}_{\text{net}}}{m}. [/latex]

Суммарная внешняя сила, действующая на Систему 1, выводится из (Рисунок) и предыдущего обсуждения как

[латекс] {F} _ {\ text {net}} = {F} _ {\ text { floor}}-f=150\,\text{N}-24.0\,\text{N}=126\,\text{N}\text{.} [/latex]

Масса Системы 1 равна

[латекс] m=(65.0+12.0+7.0)\,\текст{кг}=84\,\текст{кг}\текст{.} [/латекс]

Эти значения [латекс] {F}_ {\text{net}} [/латекс] и 9{2}. [/latex]

Значимость

Никакие силы между компонентами Системы 1, например, между руками профессора и тележкой, не вносят вклад в общую внешнюю силу, поскольку они являются внутренними по отношению к Системе 1. Другой способ взглянуть на это так: что силы между компонентами системы компенсируются, потому что они равны по величине и противоположны по направлению. Например, сила, приложенная профессором к тележке, приводит к равной и противоположной силе, действующей на профессора. В этом случае обе силы действуют на одну и ту же систему и поэтому сокращаются. Таким образом, внутренние силы (между компонентами системы) сокращаются. Выбор Системы 1 имел решающее значение для решения этой проблемы.

Пример

Сила, действующая на тележку: выбор новой системы

Рассчитайте силу, которую профессор оказывает на тележку (рисунок), при необходимости используя данные из предыдущего примера.

Стратегия

Если мы определим интересующую систему как тележку плюс оборудование (система 2 на (рис.)), то результирующая внешняя сила, действующая на систему 2, равна силе, которую профессор оказывает на тележку, за вычетом трения. Сила, которую она оказывает на тележку, [латекс] {F}_{\text{проф}} [/латекс], является внешней силой, действующей на Систему 2. [латекс] {F}_{\текст{проф}} [/latex] был внутренним по отношению к Системе 1, но он является внешним по отношению к Системе 2 и, таким образом, входит во второй закон Ньютона для этой системы.

Решение

Второй закон Ньютона можно использовать для нахождения [латекса] {F}_{\text{prof}}. [/latex] Начнем с

[латекс] a=\frac{{F}_{\text{net}}}{m}. [/latex]

Величина чистой внешней силы, действующей на Систему 2, равна

[latex] {F}_{\text{net}}={F}_{\text{prof}}-f. [/latex]

Решаем на [латекс] {F}_{\text{проф}} [/латекс], искомое количество:

[латекс] {F}_{\text{проф}}={ F} _ {\ text {net}} + f. [/latex]

Значение 9{2})=29\,\text{N}\text{.} [/latex]

Теперь мы можем найти искомую силу:

[латекс] {F}_{\text{prof}}={ F}_{\text{net}}+f=29\,\text{N}+24,0\,\text{N}=53\,\text{N}\text{.} [/latex]

Значение

Эта сила значительно меньше силы в 150 Н, которую профессор приложил назад к полу. Не вся эта сила в 150 Н передается на тележку; часть из них ускоряет профессора. Выбор системы — важный аналитический шаг как в решении задач, так и в глубоком понимании физики ситуации (что не обязательно одно и то же).

Проверьте свое понимание

Два блока покоятся и соприкасаются на поверхности без трения, как показано ниже, с [латекс] {м}_{1}=2,0\,\текст{кг}, [/латекс] [латекс ] {m}_{2}=6.0\,\text{kg}, [/latex] и приложенная сила 24 Н. (a) Найдите ускорение системы блоков. (b) Предположим, что блоки позже разделены. Какая сила будет придавать второму бруску массой 6,0 кг такое же ускорение, как и системе кубиков?

Показать решение

Посмотрите это видео, чтобы увидеть примеры действия и реакции.

Посмотрите это видео, чтобы посмотреть примеры законов Ньютона и внутренних и внешних сил.

Резюме

• Третий закон движения Ньютона представляет собой базовую симметрию в природе, с действующей силой, равной по величине и противоположной по направлению действующей силе.
• Две равные и противоположные силы не сокращаются, потому что они действуют на разные системы.
• Пары действие-противодействие включают пловца, отталкивающегося от стены, вертолеты, создающие подъемную силу, толкая воздух вниз, и осьминога, продвигающегося вперед, выбрасывая воду из своего тела. Ракеты, самолеты и автомобили толкаются вперед силой реактивной тяги.
• Выбор системы — важный аналитический шаг в понимании физики проблемы и ее решении.

Концептуальные вопросы

Определите силы действия и противодействия в следующих ситуациях: (а) Земля притягивает Луну, (б) мальчик пинает футбольный мяч, (в) ракета ускоряется вверх, (г) автомобиль ускоряется вперед, (e) прыгун в высоту прыгает, и (f) пуля стреляет из ружья.

Показать раствор

Предположим, вы держите в руке чашку кофе. Определите все силы, действующие на чашку, и реакцию на каждую силу. 9{2} [/латекс]. а) Какова сила трения между ногами проигравшего игрока и травой? (b) Какую силу прикладывает победивший игрок к земле, чтобы двигаться вперед, если его масса плюс снаряжение составляет 110,0 кг?

Книга по истории лежит поверх книги по физике на столе, как показано ниже; также показана диаграмма свободного тела. Учебники по истории и физике весят 14 Н и 18 Н соответственно. Определите каждую силу, действующую на каждую книгу, с помощью обозначения с двойным нижним индексом (например, контактная сила книги по истории, давящей на книгу по физике, может быть описана как [латекс] {\ overset {\ to } {F}} _ {\ text {HP }} [/latex]), и определить значение каждой из этих сил, объяснив используемый процесс. 9{2} [/латекс]. Найдите модуль ускорения автомобиля.

Глоссарий

Третий закон Ньютона

всякий раз, когда одно тело воздействует на другое тело, на первое тело действует сила, равная по величине и противоположная по направлению силе, которую оно оказывает

.

тяга

сила реакции, которая толкает тело вперед под действием обратной силы

ньютоновская механика — В чем разница между нормальной силой и силой реакции?

спросил 2 года, 4 месяца назад

Изменено 2 года, 3 месяца назад

Просмотрено 3к раз

$\begingroup$

Изучая силы и трения в данный момент, я не могу понять одну вещь: в чем разница между нормальной силой и силой реакции? Обе они действуют перпендикулярно поверхности и от нее, но в чем разница между обеими этими силами? Я пытался найти это в Интернете, к сожалению, безрезультатно.

• ньютоновская механика
• силы
• классическая механика
• терминология
• определение

$\endgroup$

$\begingroup$

Сила реакции относится к ее физическому содержанию — реакции на действие объекта. Нормальная сила относится к ее направлению — она ​​перпендикулярна поверхности. Многие силы могут быть нормальными силами и/или силами реакции, но не обязательно и теми, и другими. Элементарная физика, однако, часто использует термин нормальная сила в отношении силы, производимой опорой на объект. В данном случае это и нормальная (в описанном выше общем смысле), и реактивная сила.

$\endgroup$

$\begingroup$

В механике нормальная сила — это составляющая контактной силы, перпендикулярная поверхности, с которой контактирует объект.

Сила реакции является частью пары сил действия реакции согласно третьему закону Ньютона, snd может иметь компоненты как перпендикулярные, так и параллельные поверхности контакта.

Таким образом, нормальная сила может быть перпендикулярной составляющей реакции на силу, приложенную объектом к поверхности, но сила реакции не обязательно является нормальной силой.

Надеюсь, это поможет

$\endgroup$

$\begingroup$

Сила реакции действует в направлении, противоположном первоначальному действию, а не в перпендикулярном направлении. Если исходное действие направлено не в перпендикулярном направлении, то не будет и противодействующей силы (если только поверхность не лишена трения).

Это происходит, например, во время ходьбы. Нормальная сила по определению направлена ​​вверх, и она компенсирует направленную вниз гравитационную силу и направленный вниз толчок вашей ноги (чтобы не упасть под поверхность). Но вы также хотите двигаться вперед и, таким образом, отталкиваетесь ногой также и назад. Это компенсируется силой трения (чтобы вы не скользили). Сумма силы трения в параллельном направлении и нормальной силы в направлении вверх представляет собой силу диагональной реакции, которая является общей реакцией поверхности на вашу ногу.

$\endgroup$

$\begingroup$

В контексте, который вы описываете, они являются одной и той же силой и действительно действуют в одном направлении. То есть сила веса, действующая на объект, направлена ​​вниз, а сила «реакции» или «нормальная» сила действует в направлении вверх.

В этом контексте нет никакой разницы между ними (« реакция » и нормальный ). Оба термина используются для описания одного и того же. Но помните, что сила реакции — это сила, которая действует равно и противоположно другой силе и в общем случае не является перпендикулярной силой.