Реактивная составляющая сопротивления. Реактивное сопротивление в электрических цепях: виды, особенности и применение — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое реактивное сопротивление. Какие бывают виды реактивного сопротивления. Как рассчитывается реактивное сопротивление. Где применяется реактивное сопротивление в электротехнике. Как влияет реактивное сопротивление на работу электрических цепей.

Содержание

Что такое реактивное сопротивление и чем оно отличается от активного

Реактивное сопротивление — это сопротивление, которое оказывают переменному электрическому току в цепи индуктивные и емкостные элементы. В отличие от активного сопротивления, реактивное не приводит к необратимому преобразованию электрической энергии в тепловую.

Основные отличия реактивного сопротивления от активного:

Не приводит к рассеиванию энергии
Зависит от частоты переменного тока
Создает сдвиг фаз между током и напряжением
Может иметь как положительное, так и отрицательное значение

Реактивное сопротивление измеряется в омах, как и активное. Но оно не является постоянной величиной для элемента цепи, а зависит от частоты тока.

Виды реактивного сопротивления

Выделяют два основных вида реактивного сопротивления:

Индуктивное сопротивление

Индуктивное сопротивление создается катушками индуктивности. Оно пропорционально частоте переменного тока и индуктивности катушки:

X_L = ωL = 2πfL

где X_L — индуктивное сопротивление, Ом
ω — угловая частота, рад/с
f — частота, Гц
L — индуктивность, Гн

Емкостное сопротивление

Емкостное сопротивление создается конденсаторами. Оно обратно пропорционально частоте тока и емкости конденсатора:

X_C = 1 / (ωC) = 1 / (2πfC)

где X_C — емкостное сопротивление, Ом
C — емкость, Ф

Как рассчитать полное реактивное сопротивление цепи

Полное реактивное сопротивление цепи X рассчитывается как разность между индуктивным и емкостным сопротивлениями:

X = X_L — X_C

При последовательном соединении:

X = X_L1 + X_L2 + … — (X_C1 + X_C2 + …)

При параллельном соединении:

1/X = 1/X_L1 + 1/X_L2 + … — (1/X_C1 + 1/X_C2 + …)

Треугольник сопротивлений

Для наглядного представления соотношения между активным R, реактивным X и полным Z сопротивлениями цепи используется треугольник сопротивлений:

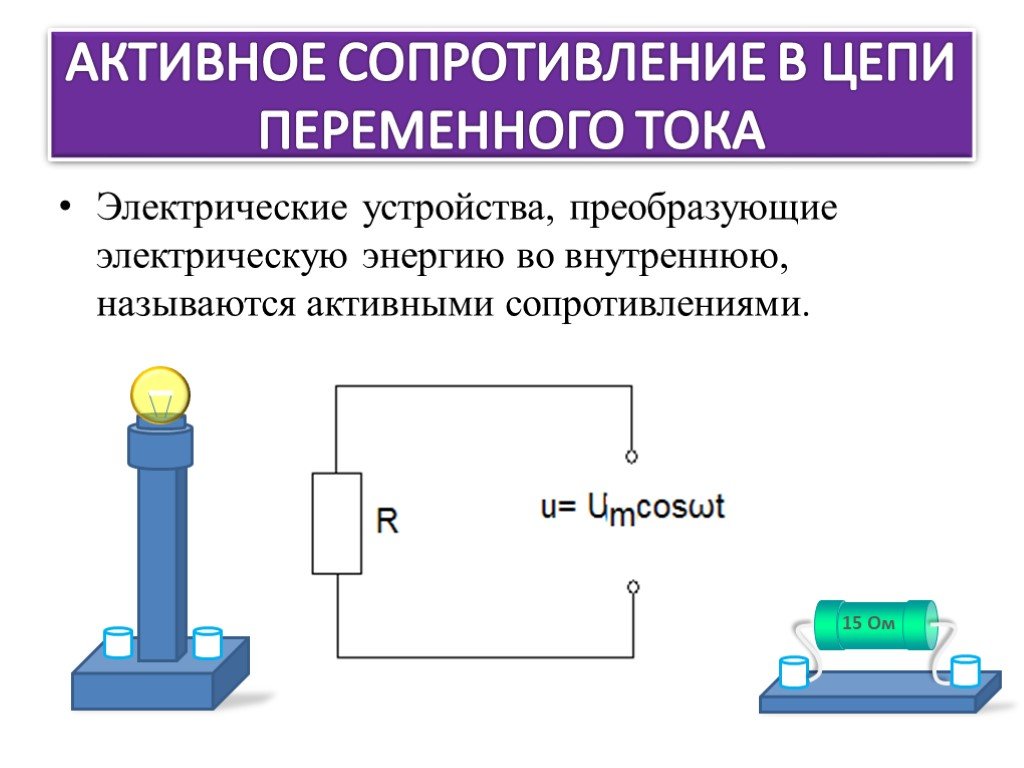
Z² = R² + X²

где Z — полное сопротивление цепи

Треугольник сопротивлений позволяет легко рассчитать любую из величин, зная две другие.

Влияние реактивного сопротивления на работу электрических цепей

Реактивное сопротивление оказывает существенное влияние на работу электрических цепей переменного тока:

Создает сдвиг фаз между током и напряжением
Ограничивает ток в цепи
Влияет на распределение напряжений на участках цепи
Приводит к возникновению реактивной мощности

Вызывает резонансные явления при определенных частотах

Поэтому при проектировании электрических устройств необходимо учитывать реактивные сопротивления элементов и принимать меры по компенсации их нежелательного влияния.

Применение реактивного сопротивления в электротехнике

Реактивное сопротивление широко используется в различных областях электротехники:

Фильтрация сигналов и помех
Создание резонансных контуров
Согласование импедансов
Компенсация реактивной мощности
Стабилизация напряжения
Ограничение токов короткого замыкания

Рассмотрим некоторые примеры применения более подробно.

Фильтрация сигналов

На основе реактивных элементов строятся различные фильтры для выделения или подавления определенных частот в сигнале:

Фильтры низких частот
Фильтры высоких частот

Полосовые фильтры
Заградительные фильтры

Такие фильтры широко применяются в радиотехнике, акустике, системах связи.

Компенсация реактивной мощности

В электроэнергетике для повышения коэффициента мощности и снижения потерь применяют компенсацию реактивной мощности. Для этого параллельно нагрузке подключают конденсаторные батареи, компенсирующие индуктивный характер нагрузки.

Измерение реактивного сопротивления

Для измерения реактивного сопротивления используются специальные приборы — измерители импеданса. Они позволяют определить как активную, так и реактивную составляющую полного сопротивления цепи.

Основные методы измерения реактивного сопротивления:

Мостовой метод
Резонансный метод
Векторный метод

При измерениях важно учитывать частоту тест-сигнала, так как реактивное сопротивление зависит от частоты.

Заключение

Реактивное сопротивление играет важную роль в работе цепей переменного тока. Понимание его природы и свойств необходимо для эффективного проектирования и эксплуатации электрических и электронных устройств. Грамотное использование реактивных элементов позволяет создавать различные полезные устройства — от простейших фильтров до сложных систем передачи энергии.

Активное и реактивное сопротивление. Треугольник сопротивлений

Активное и реактивное сопротивление — сопротивлением в электротехнике называется величина, которая характеризует противодействие части цепи электрическому току. Это сопротивление образовано путем изменения электрической энергии в другие типы энергии. В сетях переменного тока имеется необратимое изменение энергии и передача энергии между участниками электрической цепи.

Активное и реактивное сопротивление

При необратимом изменении электроэнергии компонента цепи в другие типы энергии, сопротивление элемента является активным. При осуществлении обменного процесса электроэнергией между компонентом цепи и источником, то сопротивление реактивное.

В электрической плите электроэнергия необратимо преобразуется в тепло, вследствие этого электроплита имеет активное сопротивление, так же как и элементы, преобразующие электричество в свет, механическое движение и т.д.

В индуктивной обмотке переменный ток образует магнитное поле. Под воздействием переменного тока в обмотке образуется ЭДС самоиндукции, которая направлена навстречу току при его увеличении, и по ходу тока при его уменьшении. Поэтому, ЭДС оказывает противоположное действие изменению тока, создавая индуктивное сопротивление катушки.

С помощью ЭДС самоиндукции осуществляется возвращение энергии магнитного поля обмотки в электрическую цепь. В итоге обмотка индуктивности и источник питания производят обмен энергией. Это можно сравнить с маятником, который при колебаниях преобразует потенциальную и кинетическую энергию. Отсюда следует, что сопротивление индуктивной катушки имеет реактивное сопротивление.

Самоиндукция не образуется в цепи постоянного тока, и индуктивное сопротивление отсутствует. В цепи емкости и источника переменного тока изменяется заряд, значит между емкостью и источником тока протекает переменный ток. При полном заряде конденсатора его энергия наибольшая.

В цепи напряжение емкости создает противодействие течению тока своим сопротивлением, и называется реактивным. Между конденсатором и источником происходит обмен энергией.

После полной зарядки емкости постоянным током напряжение его поля выравнивает напряжение источника, поэтому ток равен нулю.

Конденсатор и катушка в цепи переменного тока работают некоторое время в качестве потребителя энергии, когда накапливают заряд. И также работают в качестве генератора при возвращении энергии обратно в цепь.

Если сказать простыми словами, то активное и реактивное сопротивление – это противодействие току снижения напряжения на элементе схемы. Величина снижения напряжения на активном сопротивлении имеет всегда встречное направление, а на реактивной составляющей – попутно току или навстречу, создавая сопротивление изменению тока.

Настоящие элементы цепи на практике имеют все три вида сопротивления сразу. Но иногда можно пренебречь некоторыми из них ввиду незначительных величин. Например, емкость имеет только емкостное сопротивление (при пренебрежении потерь энергии), лампы освещения имеют только активное (омическое) сопротивление, а обмотки трансформатора и электромотора – индуктивное и активное.

Активное сопротивление

В цепи действия напряжения и тока, создает противодействие, снижения напряжения на активном сопротивлении. Падение напряжения, созданное током и оказывающее противодействие ему, пропорционально активному сопротивлению.

При протекании тока по компонентам с активным сопротивлением, снижение мощности становится необратимым. Можно рассмотреть резистор, на котором выделяется тепло. Выделенное тепло не превращается обратно в электроэнергию. Активное сопротивление, также может иметь линия передачи электроэнергии, соединительные кабели, проводники, катушки трансформаторов, обмотки электромотора и т.д.

Отличительным признаком элементов цепи, которые обладают только активной составляющей сопротивления, является совпадение напряжения и тока по фазе. Это сопротивление вычисляется по формуле:

R = U/I, где R – сопротивление элемента, U – напряжение на нем, I – сила тока, протекающего через элемент цепи.

На активное сопротивление влияют свойства и параметры проводника: температура, поперечное сечение, материал, длина.

Реактивное сопротивление

Тип сопротивления, определяющий соотношение напряжения и тока на емкостной и индуктивной нагрузке, не обусловленное количеством израсходованной электроэнергии, называется реактивным сопротивлением. Оно имеет место только при переменном токе, и может иметь отрицательное и положительное значение, в зависимости от направления сдвига фаз тока и напряжения. При отставании тока от напряжения величина реактивной составляющей сопротивления имеет положительное значение, а если отстает напряжение от тока, то реактивное сопротивление имеет знак минус.

Активное и реактивное сопротивление, свойства и разновидности

Рассмотрим два вида этого сопротивления: емкостное и индуктивное. Для трансформаторов, соленоидов, обмоток генераторов и моторов характерно индуктивное сопротивление. Емкостный вид сопротивления имеют конденсаторы. Чтобы определить соотношение напряжения и тока, нужно знать значение обоих видов сопротивления, которое оказывает проводник.

Реактивное сопротивление образуется при помощи снижения реактивной мощности, затраченной на образование магнитного поля в цепи. Снижение реактивной мощности создается путем подключения к трансформатору прибора с активным сопротивлением.

Конденсатор, подключенный в цепь, успевает накопить только ограниченную часть заряда перед изменением полярности напряжения на противоположный. Поэтому ток не снижается до нуля, так как при постоянном токе. Чем ниже частота тока, тем меньше заряда накопит конденсатор, и будет меньше создавать противодействие току, что образует реактивное сопротивление.

Иногда цепь имеет реактивные компоненты, но в результате реактивная составляющая равна нулю. Это подразумевает равенство фазного напряжения и тока. В случае отличия от нуля реактивного сопротивления, между током и напряжением образуется разность фаз.

Катушка имеет индуктивное сопротивлением в схеме цепи переменного тока. В идеальном виде ее активное сопротивление не учитывают. Индуктивное сопротивление образуется с помощью ЭДС самоиндукции. При повышении частоты тока возрастает и индуктивное сопротивление.

На индуктивное сопротивление катушки оказывает влияние индуктивность обмотки и частота в сети.

Конденсатор образует реактивное сопротивление из-за наличия емкости. При возрастании частоты в сети его емкостное противодействие (сопротивление) снижается. Это дает возможность активно его применять в электронной промышленности в виде шунта с изменяемой величиной.

Треугольник сопротивлений

Схема цепи, подключенной к переменному току, имеет полное сопротивление, которое можно определить в виде суммы квадратов реактивного и активного сопротивлений.

Если изобразить это выражение в виде графика, то получится треугольник сопротивлений. Он образуется, если рассчитать последовательную цепь всех трех видов сопротивлений.

По этому треугольному графику можно увидеть, что катеты представляют собой активное и реактивное сопротивление, а гипотенуза является полным сопротивлением.

Реактивное сопротивление

Реактивное сопротивление – это сопротивление прохождению переменного электрического тока в электрической цепи, обусловленное наличием в ней индуктивности или конденсатора.

Дело в том, что для постоянного тока индуктивность является обычным проводником и поэтому сопротивление его прохождению в цепи ничтожно мало. Конденсатор при тех же условиях для постоянного тока является диэлектриком – его электрическое сопротивление бесконечно велико.

Если же мы имеем дело с переменным током, то в этом случае сопротивление его прохождению по цепи индуктивности или конденсатора зависит от множества факторов: частоты самого тока, емкости конденсатора или индуктивности катушки.

Очень часто конденсатор и индуктивность из-за наличия в них реактивного сопротивления называют реактивными элементами или реактивными электронными компонентами.

Чем обусловлено реактивное сопротивление

В катушке

При протекании переменного электрического тока через катушку, он создает в ее витках магнитное поле, а оно в свою очередь обуславливает создание электродвижущей силы. Эта ЭДС направлена против внешнего тока, поэтому препятствует ему, то есть создает сопротивление. Как правило, реактивное сопротивление индуктивности называют еще индуктивным.

В конденсаторе

При протекании переменного тока через цепь конденсатора происходят процессы накопления и отдачи электрического заряда, связанные с действием в цепи электрического поля. Его действие также противоположно по направлению к внешнему току и поэтому создает для него сопротивление. Это сопротивление еще называют емкостным.

Интересно

Реактивное сопротивление катушки с увеличением ее индуктивности (количества витков) будет увеличиваться. В конденсаторе же рост емкости (увеличение площади электродов) приводит к прямо противоположному эффекту – уменьшению реактивного сопротивления.

< Предыдущая		Следующая >

Сопротивление реактивное — Справочник химика 21

Гаситель пульсации, как всякое неоднородное включение в трубопроводную систему, оказывает сопротивление движению потока. Полное сопротивление такого включения состоит из активной и реактивной составляющих, причем активная составляющая характеризует потери энергии потока на преодоление сил трения, а реактивная — перераспределение колебательной энергии гармоник в спектре колебаний давления.
[c.502]
Реактивные гасители основаны на принципе акустического фильтра, который не пропускает пульсаций на определенной частоте, зависящей от акустической массы и акустической емкости жидкости, заключенной в гасителе. Активное сопротивление реактивных гасителей невелико и не определяет их эффективности. Реактивные гасители имеют строго дискретный спектр гащения. [c.122]

Электрическое сопротивление нефтепродуктов своеобразно изменяется с температурой. На рис. 40 приведены кривые изменения электрического сопротивления реактивного топлива плотностью Р20 =0,789 и содержащего около 0,003% растворенной воды, в диапазоне температур от —25 до 200 °С [1в]. [c.152]

Кроме того, условием, необходимым для работы дуговой печи, через которую с огромной скоростью продувается струя воздуха, является, как уже сказано выше, стабилизация режима горения дуг. С этой целью в электрическую цепь печи вводят необходимые индуктивные сопротивления (реактивные или дроссельные катушки), обеспечивающие, во-первых, понижение напряжения на дуге в момент понижения ее сопротивления для ограничения силы проходящего через дугу тока и, во-вторых, подачу нужного высокого напряжения в момент зажигания дуги, когда сопротивление ее весьма велико.

[c.386]

Угол б называется углом диэлектрических потерь из (1.11) видно, что тангенс угла диэлектрических потерь реального конденсатора равен отношению его активного сопротивления в последовательной схеме замеш ения к сопротивлению реактивного участка этой цепи. [c.13]

Для реактивных четырехполюсников сопротивления холостого хода и короткого замыкания представляют собой сопротивления реактивных двухполюсников и, следовательно, можно записать [c.12]

Как видим, при весьма малых а практически можно считать все сопротивление реактивным (ввиду малости 7 по сравнению с У). Поэтому при малых а, принимая во внимание (64) и (70) и вспомнив прежние обозначения, можно полагать

[c.768]

Активные гасители (рис. 11.2) работают по принципу поглощения и рассеивания энергии пульсирующего потока в результате преодоления упругих сил вязкого или внутреннего трения. Их реактивное сопротивление незначительно активное сопротивление может быть включено последовательно (а, б) или параллельно (в). Активные гасители наиболее эффективно работают на высоких частотах, так как активное сопротивление пропорционально квадрату скорости, или в данном случае — частоты. [c.503]

Для исследования состояния поверхности металлических образцов и процессов адсорбции на ней, а также свойств окисных и защитных изоляционных пленок на поверхности металла применяют емкостно-омический метод (рис. 358). Емкость и сопротивление исследуемого электрода определяют компенсационным методом — подбором соответствующих величин емкости и сопротивления Из на мостике переменного тока с осциллографом в качестве нуль—инструмента. В электрохимических исследованиях этот метод сочетают с поляризационным методом, измеряя импеданс (полное активное и реактивное сопротивление цепи переменного тока) при различных значениях потенциала исследуемого электрода (см. 166). [c.465]

Реактивные и активные сопротивления короткой сети и печной установки. Расчет параметров х и г) произведен по методу, разработанному ЛенНИИГипрохимом, результаты расчета сведены в табл. 24. [c.141]

Значение реактивных и активных сопротивлений печной установки мощностью 60 МВА [c.141]

Участок Реактивные сопротивления Активные сопротивления [c.141]

Сопротивления повороту, оказываемое последними, вызывает на краях отверстий реактивные моменты, уменьшающие прогибы пластинки и которые можно рассматри,вать. как приложенные [c.452]

Пульсирующая сфера представляет собой поверхность, радиус которой tq колеблется с амплитудой А по гармоническому закону с круговой частотой (о. Полное комплексное сопротивление излучения пульсирующей сферы складывается из активной Rg и реактивной Xg частей [c.51]

Как упоминалось выше, для предотвращения перегрузки трансформаторов, возможной при увеличении проводимости электрического контура внутри электродегидратора, последовательно с первичной обмоткой трансформаторов включают реактивные катушки РОМ-13 6 мощностью 5 ква. При прохождении тока через катушку на ней возникает определенное падение напряжения в результате ее индуктивного сопротивления. Вследствие этого напряжение на первичной обмотке трансформатора снижается. Чем больше сила тока, том больше падает напряжение на реактивной катушке и тем меньше напряжение на трансформаторе. При коротком замыкании в трансформаторе почти все напряжение приходится на долю катушки, и сила тока в цепи ограничивается ее индуктивным сопротивлением. [c.60]

Индуктивность реактивной катушки РОМ-13/6 при включении всех витков составляет 0,1 гн, а ее индуктивное сопротивление при частоте тока 50 пер сек равно 31,4 ом. [c.60]

Для предотвращения аварийных ситуаций пр коротких замыканиях в высоковольтной цепи дегидратора повышающие трансформаторы включают последовательно с ограничителями тока, в качестве которых обычно употребляют катушки реактивной мощности, часто называемые просто реакторами (рис. 2.13). Увеличение силы тока в первичной цепи приводит к возрастанию сопротивления реактора и к увеличению на нем падения напряжения, что в свою очередь обусловливает уменьшение напряжения на первичной обмотке повышающего трансформатора и уменьшение силы тока в первичной цепи. [c.38]

Если Уно — максимальное значение реактивного (емкостного-сопротивления нагрузки, то минимально необходимое индуктивное сопротивление реактора будет определяться равенством [c.42]

Сварочные трансформаторы имеют падающую вольт-ампер-ную характеристику благодаря наличию реактивного индуктивного сопротивления во вторичной цепи, величину которого можно изменять, ограничивая тем самым максимальную величину сварочного тока. У трансформаторов типа СТЭ такое реактивное сопротивление (регулятор) оформлено в виде самостоятельного агрегата, который последовательно включен в цепь вторичной обмотки трансформатора. [c.94]

Под знаком суммы второго члена этого уравнения могут находиться такие внешние силы, как гравитационные, молекулярного притяжения, электростатические, а также силы, возникающие в результате воздействия на каплю несущего потока [13]. Последний член уравнения представляет собой реактивную силу, сообщаемую капле отходящими парами. Для расчетов тепло- и массообмена в вихревом газовом потоке преимущественное значение имеют центробежная сила (Рц) и сила вязкого сопротивления среды (F ), как наиболее важные по интенсивности действия и определяющие характер движения капли. Тогда суммарное воздействие сил, приложенных к капле, с учетом названных сил запишется следующим образом [c.176]

Однако, поскольку в схему моста входит источник переменного тока, балансировка моста осложнена влиянием индуктивностей и емкостей всей цепи. Емкость электролитической ячейки и цепи приводит к тому, что наряду с активной составляющей сопротивления измеряется реактивная составляющая. Выбирая оптимальные значения частоты и плотности тока, кон- [c.106]

Реактивные гасители (рис. 11.3) основаны на принципе акустического фильтра, препятствующего прохождению пульсации определенной частоты, которая зависит от массы и давления газа в ячейках гасителя. Активное сопротивление таких гасителей или гораздо меньше реактивного, или не определяет характера их работы. Реактивные гасители имеют сугубо дискретный спектр гашения. По виду амплитудно-частотной характеристики реактивные гасители можно разделить на широкополосные (а), резонансные (б) и смешанного типа (в). [c.503]

Хп — реактивное сопротивление. Ом/км (для проводов принимается равным 0,6) [c.53]

Применявшаяся нами электрическая измерительная схема неравновесного высокочастотного резонансного моста описана в [1, с. 254]. Эта схема позволяла регистрировать и записывать мгновенные значения изменений реактивного сопротивления датчика (йС, пропорциональные изменения локальной объемной концентрации бог или порозности бе = —бо. По-видимому, более однозначно связанной с объемной концентрацией твердой фазы а и менее зависящей от деталей структуры, является не реактивная составляющая сопротивления измерительного зонда, а тангенс угла диэлектрических потерь в материале зерен слоя [67, с. 291. [c.83]

Текучесть. Как и следовало предполагать, повышение температуры размягчения приводит к снижению текучести или тенденции к проседанию при температурах ниже температуры размягчения. Разработан метод, позволяющий измерять сопротивление текучести, которое сообщает каучук каменноугольным пекам, используемым в покрытиях, стойких к действию реактивного топлива. Этот же метод [c.219]

Простая установка с динамометром показана на рис. П-5. Весь узел привода смонтирован на упорном подшипнике и расположен выше сосуда с перемешиваемой жидкостью. При вращении мешалки создается механическое усилие, которому противодействует жидкость. Сопротивление жидкости передается от вала двигателя к мотору. Этот реактивный крутящий момент вызывает вращение привода на упорном подшипнике в направлении, [c.41]

При переменном токе полное сопротивление системы равно сумме активного и индуктивного (реактивного) сопротивлений [c.209]

Однако изменения сопротивления реактивной катушки можно добиться электрическим путем. С этой целью на сердечник (рис. 1-13,6) наматывается управляющая обмотка Шу, с помощью которой производится подмаг-ничивание сердечника постоянным током. От величины /у будет зависеть индуктивное сопротивление реактивной катушки переменному току. Зависимость такова с увеличением тока подмагничивания уменьшается индуктивное сопротивление и возрастает ток в нагрузочной цепи, и наоборот. Таким образом, магнитный усилитель позво-48 [c.48]

Использование электродных аналогов двойного электрического слоя электрода под током, простейшие из которых представлены на рис. 14.1, позволило разработать методы экспериментального разделения общей поляризационной емкости на ее слагаемые. Методы эти, однако, являются ирибллженными, так как двойнослойная и псевдоемкость взаимосвязаны и изменение одной приводит к изменению другой. Тем не менее они нашли широкое применение и дали возможность получить ценную информацию о поведении границы раздела электрод — электролит в условиях электродной йоляризации. Наиболее часто используются мостовые и другие схемы на переменном токг, которые позволяют находить величину, называемую импедансом 2 и характеризующую полное сопротивление (активное — R и реактивное — С) электрической цепи переменному току. Для цепи, моделирующей электрод, импеданс определяется уравнением [c.289]

Ороситель приводится в движение действием реактивного момента, возникающего при истечении пленочной струи, паправлениой в разные стороны относительгю оси вращения. Момент трения в подвеске оросителя и момент, обусловленный сопротивлением среды, а также гидравлическими потерями, компенсируется встроенной [c.170]

Допускаемые расхождения между параллельными определениями пределов прочности образцов резин после испытания в реактивных топливах не должны превышать 10% среднего арифметического значения. Считают, что топливо прошло испытание, если после контакта с ним образцы резины имеют сопротивление разрьту не менее 8,5 МПа, а относительное удлинение не менее 100%. [c.149]

В связи с зависимостью удельного сопротивления осадка от многих факторов и возникновением уравнения (111,39) сопоставлены величины удельного сопротивления с показателем степени в упомянутом уравнении, который назван кинетическим параметром [151]. Исследовано разделение 15 водных суспензий неорганических реактивных солей при плотности твердых частиц 2,1 — 7,0 г-см и среднем размере их в основном 5—30 мкм. Лабораторные опыты проведены на фильтре с перегородкой из фильтро-миткаля поверхностью 36 см при постоянной разности давлений З-Ю Па. Установлено, что удельное сопротивление осадка меньше для частиц с большей плотностью (хлорид талия), когда наблюдается быстрое оседание частиц и фильтрование происходит при скорости, приближающейся к постоянной это соответствует значениям т, близким к 1. Найдено, что удельное сопротивление осадка больше для тонкодисперсных частиц (сульфат бария), что соответствует значениям т, близким к 0,5. Отмечено, что соответствие между удельным сопротивлением осадка и кинетическим параметром лишь приближенное, причем в некоторых случаях расхождение существенное. Это объяснено влиянием искажающих микрЬ-факторов. [c.141]

Исследована зависимость удельного объемного сопротивления осадков ряда неорганических солей, образующихся при разделении их водных суспензий на фильтре, от концентрации твердых частиц в суспензии [206]. Использованы сульфаты кальция, бария и стронция, карбонат кальция, фторид лития и фосфат магния (МдНР04) реактивной степени чистоты, что сводит влияние примесей на удельное сопротивление осадка до минимума размер [c.188]

Виброгашение. Под виброгашением понимают умепь-ше 1ие уровня вибраций защищаемого объекта при введении в систему дополнительных реактивных сопротивлений. Чаще всего это достигается при установке агрегатов на виброгасящие основания (рис. 9.3). Массу фундамента подбирают таким образом, чтобы амплитуда колебаний подошвы фундамента [c.105]

При турбулентном характере потока образуются зоны вращательного движения газа, появляется дополнительное упругоинерционное воздействие на газовый поток, которое и характеризует реактивную часть полного сопротивления. Гасители, у которых реактивная часть сопротивления мала по сравнению с активной, можно считать чисто активными наоборот, гасители, активная часть сопротивления которых мала по сравнению с реактивной,—чисто реактивными. [c.503]

Вязкости от 0,5 до 3-10 сП могут быть измерены в реометре сопротивления. Этот аппарат в принципе аналогичен прибору Брукфильда. Он состоит из цилиндра (оканчивающегося с обеих сторон, конусами), вращающегося в сосуде с испытуемым материалом. Сопротивление испытуемого материала вращению шпинделя, передаваемое свободно подвешенному мотору, компенсируется градуированной пружиной. С корпусом мотора, испытывающим реактивный вращательный момент, связан указатель, который непр ывнр показывает вязкость на неподвижной шкале. [c.111]

Каменноугольный деготь в дорожных покрытиях. Смеси камен ноугольного дегтя с каучуком используют в дорожных покрытиях, стойких к действию реактивного топлива, и в смесях для герметизации стыков в цементобетоне. Благодаря введению эластомера повышается сопротивление изменению физических свойств от температуры. Деготь в большей степени, чем битум, хрупок при низкой температуре и излишне мягок при высокой температуре. Нит-рильные каучуки в виде крошки или гранул чаш,е всего используют во взлетно-посадочных полосах и площадках для стоянки самолетов, где происходит утечка авиационного топлива. [c.239]

Усилитель постоянного тока и линейные операционные блоки АВМ. Основным элементом большинсгва блоков электронных АВМ является операционный усилитель постоянного тока. Он состоит из трех элементов — собственно усилителя, цепи отрицательной обратной связи и входной цепи. Эти цепи могут содержать как активные, так и реактивные сопротивления. Усилители конструируют так, чтобы они имели очень большой (10″ —10 ) отрицательный коэффициент усиления по напряжению. Это означает, что напряжение, подаваемое с выхода усилителя через цепь обратной связи на ei o вход, уменьшает величину входного напряжения. При выполнении этого условия потенциал на входе усилителя относительно земли очень мал, а входной ток практически отсутствует. Усилитель обладает линейной характеристикой, если выходное напряжение не превышает допустимого значения. В ламповых усилителях это предельное значение составляет 100 В, в полупроводниковых— 10 или 30 В. Входное и выходное-напряжения усилителя имеют разные знаки. [c.327]

Теплогенерация за счет электрической энергии реализуется преодолением активного (омического) сопротивления, поэтому при использовании перемеиного тока нужно стремиться к уменьшению реактивного (индуктивного) сопротивления, являющегося следствием рассеяиия магнитной энергии. В отличие от постоянного тока при переменном токе эффект теплогенерации, кроме общего падения напряжения, зависит еще и от частоты тока. [c.239]

При разработке печей-теплогенератрров с электрическим режимом работы следует стремиться к соэдзегию такой конструкции, когда большая часть общего активного сопротивления сосредоточена в зоне технологического процесса. При этом увеличивается соотношение между активным и реактивным сопротивлениями, повышается os ф и наиболее эффективно используется электрическая энер- [c.241]

Входное и выходное сопротивления газопровода представляют собой эквивалентное сопротивление току, входящему в тело газопровода из земли и выходящему из тела газопровода (рис. 2), и содержат активную и реактивную составляющие. В общем случае не следует определять как входное сопротивление длинной линии с распределенными параметрами. На высоких частотах можно пренебречь активной составляющей входного и выходного сопротивлений и считать их чисто емкостными (Хв и Хвых), равными сопротивлению конденсаторов, образованных участками трубопровода длиной Lb x и землей. [c.105]

Что такое активное реактивное и полное сопротивление. Реактивное сопротивление XL и XC. Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления

Итак, катушки индуктивности и конденсаторы препятствуют протеканию переменного тока. Такое сопротивление по переменному току носит название реактивного сопротивления Х и измеряется в омах. Реактивное сопротивление зависит как от величины индуктивности и емкости, так и от частоты сигнала.

Катушка индуктивности имеет индуктивное реактивное сопротивление VL равное

где f — частота в герцах, a L — индуктивность в генри.
Так как ω = 2πf, то можно записать XL = ωL. Например, реактивное сопротивление катушки с индуктивностью 10 мГн, на которую подается сигнал частотой 1 кГц, равно

XL = 2π*1*103*10 *10-3 = 62,8 Ом.

Реактивное сопротивление катушки индуктивности возрастает с увеличением частоты сигнала (рис. 4.26).
Конденсатор имеет емкостное сопротивление XC равное

где С — емкость в фарадах. Например, реактивное сопротивление конденсатора емкостью 1 мкФ, на который подается сигнал частотой 10 кГц, равно

Рис. 4.26. Зависимость индуктивного Рис. 4.27.
сопротивления от частоты.

Рис. 4.28. Векторная сумма емкостного (XC)

и индуктивного (XL) сопротивлений.

Рис. 4.29.
(а) Катушка индуктивности, соединенная последовательно с резистором R.
(б) Векторное представление R, XL и их векторной суммы Z

Реактивное сопротивление конденсатора уменьшается с увеличением частоты сигнала (рис. 4.27).
Результирующее сопротивление цепи, включающей в себя емкостное сопротивление XC и индуктивное сопротивление XL, равно векторной сумме XC и XL. Векторы XC и XL, как видно из рис. 4.28(б), находятся в противофазе, т. е. разность фаз между ними равна 1800. Поэтому результирующее сопротивление просто равно разности между XC и XL. Например, пусть XL = 100 Ом, а XC = 70 Ом. Тогда результирующее реактивное сопротивление Х = 100 – 70 = 30 Ом и является индуктивным так как XL больше, чем XС.

Импеданс
Результирующее сопротивление цепи, содержащей как активное, так и реактивное (индуктивное либо емкостное) сопротивление, носит название импеданса или полного сопротивления цепи.
Импеданс Z является векторной суммой реактивного сопротивления Х и активного сопротивления R.
Рассмотрим, например, схему, изображенную на рис. 4.29. Она включает в себя индуктивное сопротивление XL соединенное последовательно с резистором R. Как видно из рис. 4.29(б), вектор XL опережает вектор R на 90°. Импеданс равен

Если XL = 400 Ом и R = 300 Ом, то Z = 500 Ом.

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности.

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U , подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение U , ток не может начаться мгновенно по причине противодействия ЭДС, равного -U , поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε ), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt) .
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t) , либо равная ей функция sin(t-π/2) .
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω .
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL , которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора.

Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

Если приложить к конденсатору напряжение U , мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt) .
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2) .
Тогда для синусоидального напряжения u = U amp sin(ωt) запишем выражение мгновенного значения тока следующим образом:

i = U amp ωCsin(ωt+π/2) .

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока.

Сопротивление, оказываемое проводником проходящему на нему переменному току, называется активным сопротивлением .

Если какой-либо потребитель не содержит в себе индуктивности и емкости (лампочка накаливания, нагревательный прибор), то он будет являться для переменного тока также активным сопротивлением.

Активное сопротивление зависит от частоты переменного тока, возрастая с ее увеличением.

Однако многие потребители обладают индуктивными и емкостными свойствами при прохождении через них переменного тока. К таким потребителям относятся трансформаторы, дроссели, электромагниты, конденсаторы, различного рода провода и многие другие.

При прохождении через них переменного тока необходимо учитывать не только активное, но и реактивное сопротивление , обусловленное наличием, в потребителе индуктивных и емкостных свойств его.

Активное сопротивление определяет действительную часть импеданса:

Где — импеданс, — величина активного сопротивления, — величина реактивного сопротивления, — мнимая единица.

Активное сопротивление — сопротивление электрической цепи или её участка, обусловленное необратимыми превращениями электрической энергии в другие виды энергии(в тепловую энергию)

Реакти́вное сопротивле́ние — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

Величина полного реактивного сопротивления

Индуктивное сопротивление () обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи.

Ёмкостное сопротивление ().

Здесь — циклическая частота

Полное сопротивление цепи при переменном токе:

z =

√

r 2 + x 2

√

r 2 +(x L −x C) 2

Билет №12.

1. 1) Согласование генератора с нагрузкой — обеспечение требуемой величины активного эквивалентного сопротивления нагрузки генераторной лампы, R э, при всех возможных значениях входного сопротивления антенного фидера, которое зависит от его волнового сопротивления и коэффициента бегущей волны (КБВ)

Согласование (в электронике) сводится к правильному выбору сопротивлений генератора (источника), линии передачи и приёмника (нагрузки). Идеального Согласование (в электронике) между линией и нагрузкой можно достичь при равенстве волнового сопротивления линии r полному сопротивлению нагрузки Zh = RH + j ХН, или при RH= r и XH= 0, где RH -активная часть полного сопротивления, XH — его реактивная часть. В этом случае в передающей линии устанавливается режим бегущих волн и характеризующий их коэффициент стоячей волны (КСВ) равен 1. Для линии с пренебрежимо малыми потерями электрической энергии Согласование и, благодаря ему, максимально эффективная передача энергии из генератора в нагрузку достигаются при условии, что полные сопротивления генератора Zr и нагрузки ZH являются комплексно-сопряжёнными, т. е. Zr = Z*H, или Rr = r = R Н =Xr- XH. В этом случае реактивное сопротивление цепи равно нулю, и соблюдаются условия резонанса, способствующие повышению эффективности работы радиотехнических систем (улучшается использование частотных диапазонов, повышается помехозащищенность, снижаются частотные искажения радиосигналов и т.п.). Оценку качества Согласование (в электронике) производят, измеряя коэффициент отражения и КСВ. Практически Согласование (в электронике) считают оптимальным, если в рабочей полосе частот КСВ не превышает 1,2-1,3 (в измерительных приборах 1,05). В отдельных случаях косвенными показателями Согласование (в электронике) могут служить реакции параметров генератора (частоты, мощности, уровня шумов) на изменение нагрузки, наличие электрических пробоев в линии, разогрев отдельных участков линии.

При таком режиме работы в приёмнике выделяется наибольшая мощность, равная половине мощности источника. В этом случае К.П.Д. =0,5. Такой режим используется в измерительных цепях, устройствах средств связи.

При передаче больших мощностей, например по высоковольтным линиям электропередач, работа в согласованном режиме, как правило, недопустима.

В цепь переменного электрического тока входят активные (содержащие внутренние источники энергии) и пассивные элементы (потребители энергии). К пассивным элементам относят резисторы и реактивные устройства.

Виды пассивных элементов

В электротехнике рассматривают два типа резисторов: активное и реактивное сопротивление. Активным – обладают приборы, в которых энергия электрического тока преобразуется в тепловую. В физике оно обозначается символом R. Единица измерения – Ом.

Этой формулой можно пользоваться для расчёта по мгновенным значениям тока и напряжения, максимальным или действующим.

Реактивные устройства энергию не рассеивают, а накапливают. К ним относятся:

катушка индуктивности;
конденсатор.

Реактивное сопротивление обозначается символом Х. Единица измерения – Ом.

Катушка индуктивности

Представляет собой проводник, выполненный в форме спирали, винта или винтоспирали. Благодаря высокой инерционности, прибор используют в схемах, которые применяются для уменьшения пульсаций в цепях переменного тока и колебательных контурах, для создания магнитного поля и т.д. Если она имеет большую длину при небольшом диаметре, то катушку называют соленоидом.

Для вычисления падения напряжения (U ) на концах катушки используют формулу:

U = –L·DI/Dt, где:

L – индуктивность прибора, измеряется в Гн (генри),
DI – изменение силы тока (измеряется в амперах) за промежуток времени Dt (измеряется в секундах).

Внимание! При любом изменении тока в проводнике возникает ЭДС самоиндукции, которая препятствует этому изменению.

Вследствие этого в катушке возникает сопротивление, которое называется индуктивным.

В электротехнике обозначается Х L и рассчитывается по формуле:

где w – угловая частота, измеряется в рад/с.

Угловая частота является характеристикой гармоничного колебания. Связана с частотой f (количество полных колебаний в секунду). Частота измеряется в колебаниях в секунду (1/с):

w = 2 · p · f.

Если в схеме используется несколько катушек, то при их последовательном соединении общее Х L для всей системы будет равно:

XL = XL1 + XL2 + …

В случае параллельного соединения:

1/XL = 1/XL1 + 1/XL2 + …

Закон Ома для такого соединения имеет вид:

где UL – падение напряжения.

Помимо индуктивного, устройство обладает и активным R.

Электрический импеданс в этом случае равен:

Емкостной элемент

В проводниках и обмотке катушки, кроме индуктивного и активного сопротивлений, присутствует и емкостное, которое обусловлено наличием ёмкости в этих приборах. Кроме резистора и катушки, в схему может быть включен конденсатор, который состоит из двух металлических пластин, между которыми размещён слой диэлектрика.

К сведению. Электрический ток протекает за счёт того, что в устройстве проходят процессы заряда и разряда пластин.

При максимальном заряде на пластинах прибора:

За счёт того, что резистивное устройство может накапливать энергию, его используют в приборах, которые стабилизируют напряжение в цепи.

Возможность накапливать заряд характеризуется ёмкостью.

Реактивное сопротивление конденсатора (ХС) можно рассчитать по формуле:

XC = 1/(w·C), где:

w – угловая частота,
С – ёмкость конденсатора.

Единица измерения ёмкости – Ф (фарада).

Учитывая, что угловая частота связана с циклической частотой, расчет значения реактивного сопротивления конденсатора можно выполнить по формуле:

XC=1/(2·p·f·C).

Если в цепи последовательно соединены несколько устройств, то общее X С системы будет равно:

XС = XС1 + XС2 + …

Если соединение объектов параллельное, то:

1/XC = 1/XC1 + 1/XC2+…

Закон Ома для этого случая записывается следующим образом:

где UС – падение напряжения на конденсаторе.

Расчёт цепи

При последовательном соединении I = const в любой точке и, согласно закону Ома, его можно рассчитать по формуле:

где Z – электрический импеданс.

Напряжение на устройствах рассчитывается следующим образом:

UR = I · R, UL = I · XL, UC = I · XC.

Вектор индуктивной составляющей напряжения направлен в противоположную сторону от вектора емкостной составляющей, поэтому:

следовательно, согласно расчётам:

Внимание! Для вычисления значения импеданса можно воспользоваться «треугольником сопротивлений», в котором гипотенузой является значение Z, а катетами – значения X и R.

Если в цепь подключены и конденсатор, и катушка индуктивности, то, согласно теореме Пифагора, гипотенуза (Z ) будет равна:

Так как X = XL – XC , то:

При решении электротехнических задач часто импеданс записывают в виде комплексного числа, в котором действительная часть соответствует значению активной составляющей, а мнимая – реактивной. Таким образом, выражение для импеданса в общем виде имеет вид:

где i – мнимая единица.

Для онлайн расчёта реактивного сопротивления можно использовать программу – калькулятор, которую можно найти в сети Интернет. Подобных сервисов достаточно много, поэтому вам не составит труда подобрать удобный для вас калькулятор.

Благодаря таким Интернет сервисам, можно быстро выполнить нужный расчёт.

Видео

Одной из основных проблем в сети переменного напряжения является наличие реактивной мощности. Она расходуется только на потери тепловые. Источником реактивной энергии есть накопители электрической энергии L и С. Я не буду очень глубоко рассматривать этот вопрос. Предлагаю рассмотреть этот вопрос на примере простых элементов цепи — индуктивности и емкости.

Индуктивный элемент L

Индуктивный элемент (рассмотрим на примере катушки индуктивности) представляют собой витки изолированного между собой провода. При протекании тока катушка намагничивается. Если изменить полярность источника, катушка начнет отдавать запасенную энергию обратно, стараясь поддержать величину тока в контуре. Поэтому при протекании через нее переменной составляющей, энергия запасенная при прохождении положительного полупериода, не успеет рассеяться и будет препятствовать прохождению отрицательного полупериода. В результате отрицательному полупериоду придется погасить энергию запасенную катушкой. В итоге напряжение(U), будет опережать ток (І) на какой-то угол φ. Ниже приведен результат моделирования работы на L-R нагрузку L=1*10 -3 Гн, R=0.5 Ом. U ист = 250 В, частота f=50 Гц.

φ – это разница фаз между U и I.

Реактивное сопротивление обозначается буквой X, полное Z, активное R.

Для индуктивности:

Где ω – циклическая частота

L – индуктивность катушки;

Вывод: чем выше индуктивность L или частота, тем больше будет сопротивление катушки переменному току.

Емкостной элемент

Емкостной элемент (рассмотрим на примере конденсатора) представляет собой двухполюсник с переменным или постоянным значением емкости. Конденсатор — накопитель электрических зарядов. Если подключить его к источнику питания, он зарядится. Если к нему приложить источник с переменной составляющей, он будет заряжаться при прохождении через него положительного полупериода. Когда направление полупериода изменится на отрицательное значение, конденсатор начнет перезаряжаться, то есть энергия, которая накопилась в нем, начнет противодействовать перезарядке. В итоге мы получим напряжение на конденсаторе противоположное источнику. В результате І, будет опережать U на какой- то угол φ. Ниже приведен результат моделирования работы на С-R нагрузку С=900*10 — 6 Фа, R=0.5 Ом, U ист = 250 В, частота f=50 Гц.

Рисунок 2. Работа источника на R-C нагрузку

Для емкости:

Где ω – циклическая частота

— частота питающего напряжения, Гц;

С — емкость конденсатора;

Вывод: чем выше емкость С или частота, тем меньше будет сопротивление переменному току.

Сравнение влияния реактивного сопротивления на активную мощность сети

Из рисунков 1 и 2 видно, что сдвиг фаз на рисунках не одинаков. Вывод — чем больше в полном сопротивлении Z будет влияние X L или X C тем больше будет разница фаз U и I.

Угол сдвига между током и напряжением называется φ .

Реактивная мощность однофазная:

Трехфазная:

U ф, I ф — фазные ток и напряжение

Вывод: реактивная мощность – не выполняет полезного действия.

Она «перегоняется» по сети нагревая кабели и увеличивая потери. На крупных промышленных предприятиях это особо ощутимо в силу наличия электроприводов и других крупных потребителей. Этот вопрос очень актуален для энергосбережения и модернизации производства. Поэтому на пром. предприятиях устанавливаются компенсаторы реактивной мощности. Они могут быть разного типа и кроме компенсации выполнять еще и роль фильтров. С помощью компенсаторов стараются сохранить баланс реактивной мощности для минимизации ее влияния на сеть и подогнать угол φ к нулю.

Для необходимо максимально сбалансировать в сети количество (L, C) элементов.

Расчёт реактивного сопротивления

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора.

Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = U_ampsin(ωt) запишем выражение мгновенного значения тока следующим образом:

i = U_ampωCsin(ωt+π/2).

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.

Калькулятор расчёта реактивного сопротивления

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Расчитать реактивное сопротивление ёмкости или индуктивности:

Реактивное сопротивление ёмкости
X_C = 1 /(2πƒC)

Реактивное сопротивление индуктивности
X_L = 2πƒL

Расчитать ёмкость и индуктивность от сопротивления:

Расчёт ёмкости: C = 1 /(2πƒX_C)

Расчёт индуктивности: L = X_L /(2πƒ)

Похожие страницы с расчётами:

Расcчитать импеданс.

Расcчитать частоту резонанса колебательного контура LC.

Расcчитать реактивную мощность и компенсацию.

Реактивная составляющая — входное сопротивление

Cтраница 2

При встречном включении ( рис. 7 — 7, б) следует изменить только знак перед М, в результате чего реактивная составляющая входного сопротивления уменьшается. [16]

Для этого расстояние х от максимума напряжения до точек подключения согласующего шунта должно быть выбрано так, чтобы активная составляющая входного сопротивления линии равнялась волновому сопротивлению фидера; реактивная составляющая входного сопротивления компенсируется равным по величине и противоположным по знаку реактивным сопротивлением шунта Хш. При этом выполняются условия согласования антенны с фидером. [18]

Расстройка любого из контуров делает входное сопротивление комплексным, но при частотах, меньших резонансной, реактивная составляющая входного сопротивления последовательного контура имеет емкостный характер, а параллельного — индуктивный; при частотах, больших резонансной, реактивная составляющая входного сопротивления последовательного контура имеет индуктивный характер, а параллельного — емкостный. [19]

Расстройка любого из этих контуров делает входное сопротивление комплексным, но при частотах, меньших резонансной, реактивная составляющая входного сопротивления последовательного контура имеет емкостный характер, а параллельного — индуктивный; при частотах, больших резонансной, реактивная составляющая входного сопротивления последовательного контура имеет индуктивный характер, а параллельного — емкостный. [20]

Характер входного сопротивления обычно определяется диапазоном усиливаемых частот. В области нижних частот реактивная составляющая входного сопротивления усилителя практически не учитывается. [22]

Хвх уменьшается по абсолютной величине. Знак минус в выражении ( 65) указывает на то, что реактивная составляющая входного сопротивления контура положительна при отрицательной расстройке и отрицательна при положительной расстройке. [24]

Входное сопротивление реальной линии имеет активную и реактивную составляющие. При этом, если она обладает длиной, кратной 0 25Х, то реактивная составляющая входного сопротивления равна нулю; ее входное сопротивление — активное. [25]

Параметр а, характеризующий расстройку, входит в числитель выражения ( 65) как множитель первой степени и в знаменатель как слагаемое во второй степени. Поэтому с изменением а от нуля до 1 числитель выражения изменяется в большей мере, чем знаменатель, и реактивная составляющая входного сопротивления контура Хвх возрастает по абсолютной величине. [26]

Величина а входит в числитель выражения ( 87) как множитель первой степени и в знаменатель как слагаемое во второй степени. Поэтому с изменением а от нуля до 1 числитель выражения изменяется в больней мере, чем знаменатель, и реактивная составляющая входного сопротивления контура Хвх возрастает по абсолютной величине. При дальнейшем увеличении расстройки влияние знаменателя сказывается в большей мере, чем числителя, и составляющая Хвх уменьшается по абсолютной величине. [27]

Входное сопротивление антенны состоит из активного сопротивления Ra, которое определяет подводимую к антенне мощность, и реактивного сопротивления Ха. Подобно колебательному контуру для эффективной работы антенны ее настраивают в резонанс. Реактивная составляющая входного сопротивления при этом становится равной нулю. [28]

Входное сопротивление антенны состоит из активного — сопротивления Rz, которое определяет подводимую к антенне мощность, и реактивного сопротивления Ха. Подобно колебательному контуру, для эффективной работы антенны ее настраивают в резонанс. Реактивная составляющая входного сопротивления при этом становится равной нулю. [29]

Измерение входных сопротивлений линий и определение момента резонанса производятся с помощью измерителя добротности. При резонансе напряжений, когда эквивалентное сопротивление отрезка линии мало, линия включается последовательно с образцовой катушкой куметра. В момент резонанса реактивная составляющая входного сопротивления кабеля равна нулю. Данное условие используется для определения момента резонанса подбором соответствующей частоты генератора. Ci-Сг / 2) и, изменяя ( увеличивая) частоту до / Р2, добиться резонанса. [30]

Страницы: 1 2 3

6.4. Сопротивление в цепи синусоидального тока

Если напряжение подключить к сопротивлению R, то через него протекает ток

(6.7)

Анализ выражения (6.7) показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе.
Формула (6.7) в комплексной форме записи имеет вид

(6.8)

где и — комплексные амплитуды тока и напряжения.
Комплексному уравнению (6.8) соответствует векторная диаграмма (рис. 6.4).

Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению.

Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току — активным сопротивлением.

Рис.6.4
Активное сопротивление больше омического из-за явления поверхностного эффекта. Поверхностный эффект заключается в том, что ток вытесняется из центральных частей к периферии сечения проводника.

6.5. Индуктивная катушка в цепи синусоидального тока

Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции

(6.9)

Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = e_L = 0.

(6.10)

Таким образом, ток в индуктивности отстает по фазе от напряжения на 90^o из-за явления самоиндукции.
Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:

(6.11)

Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0^oo), величина которого зависит от соотношения R и L. Выражение (6.11) в комплексной форме записи имеет вид:

(6.12)

где Z_L — полное комплексное сопротивление индуктивной катушки ;
Z_L — модуль комплексного сопротивления;
— начальная фаза комплексного сопротивления;
— индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).
Полное сопротивление индуктивной катушки или модуль комплексного сопротивления

Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).

Рис. 6.5

Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90^o.
В цепи переменного тока напряжения на участках цепи складываются не арифметически, а геометрически.
Если мы поделим стороны треугольника напряжений на величину тока I_m, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).

Из треугольника сопротивлений получим несколько формул:
; ;
Рис. 6.6

;

; .

6.6. Емкость в цепи синусоидального тока

Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

;

. (6.13)

Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90^o.

Выражение (6.13) в комплексной форме записи имеет вид:

, (6.14)

где — емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

Если комплексное сопротивление индуктивности положительно
, то комплексное сопротивление емкости отрицательно

На рис. 6.7 изображена векторная диаграмма цепи с емкостью.
Вектор тока опережает вектор напряжения на 90^o.

Рис. 6.7

6.7. Последовательно соединенные реальная индуктивная

катушка и конденсатор в цепи синусоидального тока

Катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно (рис.6.8). В схеме протекает синусоидальный ток

Определим напряжение на входе схемы.
В соответствии со вторым законом Кирхгофа,

(6.15)

Подставим эти формулы в уравнение (6.15). Получим:

(6.16)

Из выражения (6.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90^o, напряжение по емкости отстает по фазе от тока на 90^o.
Запишем уравнение (6.16) в комплексной форме:

(6.17)

Рис. 6.8

Поделим левую и правую части уравнения (6.17) на √2.
Получим уравнение для комплексов действующих значений токов и напряжений

, (6.18)

где — комплексное сопротивление цепи;
— модуль комплексного сопротивления, или полное сопротивление цепи;
— начальная фаза комплексного сопротивления.

При построении векторных диаграмм цепи рассмотрим три случая.

X_L > X_C, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис.6.9).
Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.6.10).
Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.6.11).

Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

Условие возникновения резонанса: , отсюда резонансная частота равна

Из формулы следует, что режима резонанса можно добиться следующими способами:

изменением частоты;
изменением индуктивности;
изменением емкости.

В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I₀ (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).

Рис. 6.9 Рис. 6.10 Рис. 6.11

6.8. Параллельно соединенные индуктивность, емкость

и активное сопротивление в цепи синусоидального тока

К схеме на рис. 6.12 подключено синусоидальное напряжение . Схема состоит из параллельно включенных индуктивности, емкости и активного сопротивления.
Определим ток на входе схемы.

В соответствии с первым законом Кирхгофа:
, (6.19)
где
— активная проводимость.

Рис. 6.12

Подставим эти формулы в уравнение (6.19). Получим:

, (6.20)

где — индуктивная проводимость;
— емкостная проводимость.

Из уравнения (6.20) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90^o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90^o.
Запишем уравнение (6.20) в комплексной форме.

, (6.21)

где — комплексная проводимость;
— полная проводимость;
— начальная фаза комплексной проводимости.

Построим векторные диаграммы, соответствующие комплексному уравнению (6.21).

Рис. 6.13 Рис. 6.14 Рис. 6.15

В схеме на рис. 6.12 может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением.
Из условия возникновения резонанса тока получим формулу для резонансной частоты тока

В режиме резонанса тока полная проводимость цепи — минимальна, а полное сопротивление — максимально. Ток в неразветвленной части схемы в резонансном режиме имеет минимальное значение. В идеализированном случае R = 0,

и .

Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр — пробкой.

6.9. Резонансный режим в цепи, состоящей

из параллельно включенных реальной индуктивной
катушки и конденсатора

Комплексная проводимость индуктивной ветви

где — активная проводимость индуктивной катушки;
   — полное сопротивление индуктивной катушки;
   — индуктивная проводимость катушки;
   — емкостная проводимость второй ветви.

В режиме резонансов токов справедливо уравнение:

или

Из этого уравнения получим формулу для резонанса частоты

(6.22)

На рисунке 6.16 изображена векторная диаграмма цепи в резонансном режиме.

Вектор тока I₂ опережает вектор напряжения на 90^o. Вектор тока I₁ отстает от вектора напряжения на угол φ,

где .

Разложим вектор тока I₁ на две взаимно перпендикулярные составляющих, одна из них, совпадающая с вектором напряжения, называется активной составляющей тока I_а1, другая — реактивной составляющей тока I_р1.

Рис. 6.16

В режиме резонанса тока реактивная составляющая тока I_р1 и емкостный ток I₂ , направленные в противоположные стороны, полностью компенсируют друг друга, активная составляющая тока I_а1 совпадает по фазе с напряжением (рис. 6.17). Ток I в неразветвленной части схемы совпадает по фазе с напряжением.

Рис. 6.17

Реактивные электронные компоненты и фазовый угол

Если вы брезгливо относитесь к электричеству или не заботитесь об электричестве, вы можете пропустить это. Но мы собираемся поговорить о некоторых вещах, которые являются довольно интересными, важными для мира электроники и совершенно классными, если вы хотите остаться.

В недавних блогах говорилось о резисторах, конденсаторах и индукторах, которые, наряду с диодами различного назначения, являются строительными блоками электронных схем. В этих блогах описывалось поведение устройств, когда они использовались вместе с источником постоянного напряжения.В этом блоге мы исследуем, что происходит, когда источником напряжения является переменный ток вместо постоянного.

Примечание. На рисунках ниже показаны примеры «устойчивого состояния». Уникальные условия, которые возникают при первом включении или отключении переменного тока или напряжения, не рассматриваются, поскольку они, хотя и интересны, в настоящее время не имеют отношения к теме.

Резистор —

Резисторы — это «пассивные» устройства.Это приятные и простые вещи — вы пропускаете через них ток, и возникает падение напряжения из-за их сопротивления потоку электричества. Они полностью соответствуют закону Ома: напряжение = сила тока, умноженная на сопротивление (E = IR). Ток в точности соответствует напряжению. Резисторы не накапливают энергию. Пока вы используете среднеквадратичные значения для измерений напряжения и силы тока, они работают точно так же с постоянным током, как и с переменным током. Энергия, которую они потребляют, рассеивается в виде тепла. Резисторы используются в основном как делители напряжения и ограничители тока в электронных схемах.Тостер — это просто большой резистор.

Реактивные компоненты —

Конденсаторы и катушки индуктивности — это «реактивные» компоненты, которые реагируют на изменения. В отличие от резисторов, конденсаторы и катушки индуктивности накапливают и выделяют энергию в зависимости от изменений приложенного напряжения или тока и не подчиняются закону Ома.

Конденсатор —

В случае конденсаторов электроны накапливаются на проводящих пластинах при увеличении напряжения. Они высвобождаются при уменьшении или снятии приложенного напряжения и приложении нагрузки («нагрузка» — это токопроводящий путь для электричества).Идеальный конденсатор с бесконечным внутренним сопротивлением, поскольку пластины изолированы друг от друга, поэтому в этом процессе не выделяется тепло. Фактически, конденсаторы имеют некоторое внутреннее сопротивление, поэтому неизбежно выделяется некоторое количество тепла, но, как правило, его очень мало.

Конденсаторы хранят электроны так же, как батарейки. В то время как батарея накапливает электроны, создавая химические изменения внутри батареи, конденсатор накапливает электроны непосредственно на проводящих пластинах и может делать это очень быстро по сравнению с батареей.Сохраненные электроны высвобождаются, когда приложенное напряжение уменьшается или снимается, а нагрузка подключается к заряженному конденсатору. Обратите внимание, что на приведенной выше иллюстрации с подключенным источником переменного напряжения, когда напряжение равно нулю, ток является самым высоким (или самым низким). Электрики сказали бы, что ток ведет к напряжению. Среднее общее потребление энергии равно нулю в течение цикла зарядки и разрядки. Конденсаторы в основном используются для поддержания постоянного напряжения в цепях, питаемых от переменного напряжения, как в случае переменного тока.Конденсаторы также могут использоваться для умножения напряжений, если они правильно настроены для хранения напряжения и последующего высвобождения его в последовательной конфигурации (например, несколько батарей, соединенных последовательно в фонарике, производят большее напряжение, чем одна батарея).

Индуктор —

В случае катушек индуктивности энергия накапливается в виде магнитного поля, создаваемого протеканием тока через катушку индуктивности. В отличие от идеального конденсатора с бесконечным сопротивлением, идеальный индуктор НЕ имеет внутреннего сопротивления, поэтому не выделяется тепло.На самом деле, у индукторов есть некоторое сопротивление, поэтому они рассеивают небольшое количество тепла.

Катушки индуктивности накапливают энергию в магнитном поле. Когда сохраненное магнитное поле схлопывается из-за изменения приложенного тока, энергия высвобождается в форме тока в попытке противостоять изменению. В этом случае ток отстает от напряжения. Катушка индуктивности фактически возвращает энергию источнику, чтобы обеспечить нулевое среднее потребление энергии (по крайней мере, в случае синусоидального возбуждения).Это немного сложно представить (по крайней мере, для меня), но если вы думаете о трансформаторе, на самом деле это индуктор со второй катушкой провода, отводящей магнитное поле, создаваемое первичной катушкой устройства. При отсутствии нагрузки на вторичную катушку трансформатор представляет собой просто индуктор и (теоретически) не потребляет энергию из линии электропередачи до тех пор, пока нагрузка не будет подключена ко второй катушке для отвода магнитного поля.

Значение вышесказанного заключается в том, что фазовый угол (выравнивание между напряжением и током во времени) электрического потока изменяется этими реактивными устройствами.Изменение фазового угла делает недействительным использование закона Ома в условиях переменного тока, переводя анализ цепей в совершенно новую область математики, включающую «мнимые числа», чтобы приспособиться к обратному потоку энергии к источнику. Некоторые из вас, возможно, слышали о терминах «прямая мощность» и «отраженная мощность». Здесь все начинается и может быть важным фактором при оценке производительности высокочастотного электронного оборудования, включая ультразвуковые устройства.

— JF —

Reactive Component — обзор

1.6.1 Значение

Потери энергии происходят во всех реальных пассивных компонентах, включая реактивные компоненты, такие как конденсаторы и катушки индуктивности. В разделе 1.3 мы показали, что все реальные пассивные компоненты должны быть представлены в виде резонансных цепей на микроволновых частотах, где энергия передается туда и обратно между индуктивными и емкостными элементами накопления энергии эквивалентной схемы, а некоторая часть энергии передается « проиграл »в паразитарных сопротивлениях. Учитывая наличие реальных потерь, мы можем определить меру Quality или « Q » для любой такой эквивалентной схемы следующим образом:

(1.6.1) Q = запасенная энергия Средняя рассеиваемая мощность

Более высокое значение Q указывает на более низкий уровень потерь мощности в цепи по сравнению с запасенной энергией.

Накопленная энергия — это сумма энергий, накопленных во всех реактивных элементах без потерь (катушки индуктивности и конденсаторы), тогда как рассеиваемая энергия — это сумма энергий, потерянных во всех резистивных элементах за цикл. Другими словами, схема, содержащая только идеальные реактивные элементы, будет иметь бесконечное число Q . Реальные компоненты и схемы демонстрируют некоторые электрические потери и, следовательно, имеют конечное значение Q .В случае отдельных реактивных компонентов, таких как конденсаторы и катушки индуктивности, чем выше Q , тем ближе компонент к идеалу.

На рисунках 1.16 и 1.17 показано, как Q рассчитывается для различных комбинаций реактивного компонента с последовательным и параллельным сопротивлениями, соответственно. Рассмотрим схему серии LR , показанную на рисунке 1.16 (b). Пиковая энергия, накопленная в катушке индуктивности, составляет ½ LI ², тогда как энергия, рассеиваемая в резисторе за один цикл, Тл , равна ½ I ² R _с T = ½ I ² R _s (1/ f ).Следовательно, для схемы рисунка 1.16 (б):

Рисунок 1.16. Q серийных комбинаций.

Рисунок 1.17. Q параллельных комбинаций.

(1.6.2) Qs = 2π12LImax212Imax2R1 / f = ωLR

, где ω — угловая частота ( ω = 2 πf ). Если мы теперь аналогичным образом рассмотрим энергию, запасенную в конденсаторе в последовательной RC-цепи на рисунке 1.16 (c), мы можем записать эквивалентное выражение для уравнения (1.6.2) как:

(1.6.3) Qs = 2π12Imax2 / ω2C12Imax2Rs1 / f = 1ωCRs

Это обобщено для произвольного реактивного сопротивления, X , на рисунке 1.16 (a). Читателю предоставляется в качестве упражнения вывести эквивалентные соотношения для Q параллельных цепей на рис. 1.17.

Теперь мы расширим приведенный выше анализ на схему серии RLC , показанную на рисунке 1.18 (a).

Рисунок 1.18. Цепи RLC. (a) Схема серии RLC . (b) Параллельная цепь RLC .

В резонансе накопленная электрическая энергия в цепи последовательного RLC передается взад и вперед между катушкой индуктивности и конденсатором один раз за каждый цикл. Когда энергия, запасенная в конденсаторе, максимальна, энергия, запасенная в катушке индуктивности, равна нулю, и наоборот. Таким образом, мы можем использовать уравнение (1.6.2) или (1.6.3) для вычисления Q в цепи RLC , так как оба этих выражения дадут одинаковый результат, как и для схемы на рисунке 1.18 (a) имеем

(1.6.4) Qs = ωoLR = 1ωoCR

На резонансной частоте ω ₀, чистое реактивное сопротивление цепи последовательного RLC равно нулю, поэтому полное сопротивление цепи Схема на Рисунке 1.18 (a) в резонансе — это просто R , что является наименьшим значением импеданса, достижимым для этой цепи на любой частоте.

Параллельная цепь RLC , показанная на Рисунке 1.18 (b), может рассматриваться как двойная, показанная на Рисунке 1.18 (a). Другими словами, чистая проводимость равна нулю в резонансе, поэтому полная проводимость равна 1/ R , что является наименьшим значением проводимости, достижимым для этой цепи на любой частоте.

В случае параллельной схемы RLC , показанной на Рисунке 1.18 (b), мы можем провести аналогичный анализ с точки зрения допусков. Следовательно, у нас есть следующие выражения для Q :

(1.6.5) Qp = RωoL = ωoCR

Все это имеет смысл, если учесть тот факт, что для бесконечного Q в случае рисунка 1.18 (a) требуется R = 0, тогда как бесконечное Q в случае рисунка 1.18 (b) требует R = ∞.

Теперь рассмотрим, например, импеданс последовательного резонансного контура, показанного на рисунке 1.18 (a), который можно записать следующим образом:

(1.6.6) Z = R + jωL + 1jωC

Мы можем исключить L или C из уравнения (1.6.6), отметив, что Резонансная частота, ω _o, связывает эти величины через ωo = 1 / LC. Таким образом, мы можем переписать уравнение (1.6.6) как:

(1.6.7) Z = R + jωωo2C + 1jωC = R + j1ωoCωωo − ωoω

Подставив выражение для Q последовательной цепи, как определено формулой уравнение (1.6.4) в уравнение (1.6.7) дает:

(1.6.8) Z = R1 + jQSωωo − ωoω

Большей ясности можно добиться, введя параметр дробной расстройки , « δ », который представляет собой отклонение на единицу от резонансного частота и определяется следующим образом:

(1.6.9) δ = ω − ωoωo

Используя это определение δ , мы можем переопределить величину внутри скобок уравнения (1.6.8) в терминах δ следующим образом [26]:

(1.6.10) ωωo − ωoω = 1 + δ − 11 + δ = δ2 + δ1 + δ

Уравнение (1.6.8) теперь принимает вид:

(1.6.11) Z = R1 + jδQS2 + δ1 + δ

Таким образом, проводимость на рисунке 1.18 (a) определяется как:

(1.6.12) Y = 1Z = 1R⋅11 + jδQS2 + δ1 + δ

Отметив, что проводимость на Рисунке 1.18 (a) в резонансе составляет Y _o = 1/ R , мы можем записать:

(1.6.13) YYo = 11 + j2δQS2 + δ1 + δ

Для очень малых отклонений частоты около резонансной частоты, то есть для δ ≪ 1, мы можем аппроксимировать уравнение (1.6.13) формулой [27]:

(1.6.14) YYo≈11 + j2δQS

График зависимости Y / Y _o от частоты показан на рисунке 1.19. точек половинной мощности показаны на рисунке 1.19, это частоты, обозначенные ω ₁ и ω ₂, по обе стороны от ω _o, где Y / Y _o падает до значения 0,707 от его значения при резонансе. Расстояние между ω ₁ и ω ₂ называется полосой пропускания половинной мощности , или Δ ω .Эти параметры связаны с Q следующим образом, который также служит другим рабочим определением Q для резонансного контура [25]:

Рисунок 1.19. Резонансная частота и Q .

(1.6.15) Q = ωoΔω = foΔf

Значение Q , вычисленное с использованием уравнения (1.6.15) для любой данной цепи, конечно, будет идентично вычисленному с использованием любого из других выражений для . Q , например уравнение (1.6.4) или (1.6.5).

Для каждой последовательной комбинации на рисунке 1.16 на заданной частоте существует эквивалентная параллельная комбинация, и наоборот. Возможность преобразования между последовательным и параллельным представлениями важна при проектировании сети. Это выполняется следующим образом:

Рассмотрим схему на Рисунке 1.16 (a). Мы можем записать проводимость как:

(1.6.16) Y = 1Rs + jX

(1.6.17) = Rs − jXRs2 + X2

(1.6.18) = RsRs2 + X2 − jXRs2 + X2

Что можно переписать как:

(1.6.19) Y = 1 / RsRs1 + XRs2 + 1 / XjRsX2 + 1

В терминах Q последовательной схемы рисунка 1.16 (a), Q _s, мы можем записать:

(1.6 .20) Y = 1Rs (1 + Qs2) + 1jX1Qs2 + 1

Итак, из уравнения (1.6.20) мы можем видеть, что последовательная комбинация на Рисунке 1.16 (a) эквивалентна параллельной комбинации на Рисунке 1.17 (a ), где параллельные элементы (проводимость и проводимость) равны:

(1.6.21) G = 1Rs (1 + Qs2)

(1.6.22) B = −QsX (1 + Qs2)

Поскольку проводимость, G , в уравнении (1.6.21) является обратной величиной эквивалентного параллельного сопротивления, R _p, мы можем установить следующую взаимосвязь между R _s и R _p:

(1.6.23) Rp = Rs ( 1 + Qs2)

Это означает, что R _p всегда будет больше R _s для любого Q _s> 0, как и следовало ожидать. Преобразуя уравнение (1.6.23), мы получаем следующую полезную формулу для Q резонансного контура с точки зрения последовательного и параллельного сопротивлений, которые будут неоднократно появляться в различных формах на протяжении всей этой книги и особенно в главе 9, где мы вводим соответствующий дизайн сети:

(1.6.24) Qs = RpRs − 1

Резистивный компонент — обзор

Пьезорезистор

Пьезорезистор — это устройство, которое демонстрирует изменение сопротивления при напряжении. В большинстве материалов пьезорезистивный эффект состоит из двух компонентов — геометрической и резистивной.

Геометрическая составляющая пьезорезистивности возникает из-за того, что напряженный элемент претерпевает изменение размеров. Эти изменения площади поперечного сечения и длины влияют на сопротивление устройства.

Хорошим примером геометрического эффекта пьезорезистивности является тензодатчик жидкости. Многие из этих устройств использовались много лет назад. Представьте себе эластичную трубку, наполненную проводящей жидкостью, например ртутью. Сопротивление ртути в трубке можно измерить с помощью пары металлических электродов, по одному на каждом конце, как показано на рисунке 19.1.1. Поскольку ртуть по существу несжимаема, силы, приложенные по длине трубки, растягивают ее, а также вызывают уменьшение диаметра трубки, в результате чего объем остается постоянным.Сопротивление тензодатчика равно

Рисунок 19.1.1. Жидкостный тензодатчик: ртутная трубка.

R = (сопротивление ртути) (длина трубки) / (площадь поперечного сечения трубки)

Так как

R = ρLA = ρL2V,

, то

dRdL = 2ρLV = 2RL

Мы определяем величина, называемая измерительным коэффициентом K , как:

K = dR / RdL / L

Поскольку

dRdr = 2RL,

мы имеем K = 2 для тензодатчика жидкости.

Это означает, что частичное изменение сопротивления в два раза превышает частичное изменение длины.Другими словами, при растяжении жидкостного тензодатчика на 1% его сопротивление увеличивается на 2%. Это верно для всех тензодатчиков жидкости, поскольку все, что нужно, — это чтобы среда была несжимаемой.

Жидкостные тензодатчики использовались в больницах для измерения колебаний артериального давления. Резиновый шланг, наполненный ртутью, натягивали вокруг конечности человека, колебания давления регистрировались на ленточном самописце, а форма импульсов давления использовалась для диагностики состояния артерий.Такие устройства были заменены твердотельными тензометрическими приборами в современных больницах, но этот пример все еще интересен с вводной точки зрения.

Металлическая проволока также может использоваться как тензодатчики. Как и в случае жидкостного тензодатчика, при растяжении провода его геометрия изменяется таким образом, что увеличивается сопротивление. Для металлической проволоки мы можем рассчитать коэффициент толщины, как мы это делали для жидкостного манометра, за исключением того, что мы не можем предполагать, что металл несжимаем, и мы не можем предполагать, что удельное сопротивление является постоянным:

R = ρLA = ρLπr2 = 4ρLπD2 dR = 4Lπd2dρ + ρπD2dL − 8ρLπD3dDdRR = dρρ + dLL − 2dDD

Тогда

K = dr / RdL / L = dρ / ρdL / L + 1−2dD / DdL / L −

/ DdL / L −
/ DdL / L −
/ L / L
определяется как коэффициент Пуассона, v, мы имеем
K = 1 + 2υ + dρ / ρdL / L
Для разных металлов эта величина зависит от свойств материала и деталей механизма проводимости.В общем, металлы имеют коэффициент измерения от 2 до 4.
Теперь, поскольку напряжение, умноженное на площадь, равно силе, а частичное изменение сопротивления равно коэффициенту измерения, умноженному на частичное изменение длины (деформации). , а напряжение — это модуль Юнга, умноженный на деформацию, имеем
F = σA = EAdLL = EAKdRR
или
dRR = FKEA
Таким образом, частичное изменение сопротивления тензодатчика пропорционально приложенной силе и пропорционально к коэффициенту толщины, деленному на модуль Юнга материала.Ясно, что мы предпочли бы иметь большое изменение сопротивления, чтобы упростить конструкцию остальной части измерительного прибора, поэтому мы обычно стараемся выбирать малые диаметры, малый модуль Юнга и большие измерительные коэффициенты, когда это возможно. Пределы упругости большинства материалов ниже 1%, поэтому мы обычно говорим об изменениях сопротивления в диапазоне от 1% до 0,001%. Ясно, что измерение таких сопротивлений нетривиально, и мы часто видим мосты сопротивления, предназначенные для создания напряжения, которое можно подавать в схемы усиления.
Обзор R, X и Z (сопротивление, реактивное сопротивление и импеданс) | Реактивное сопротивление и импеданс — R, L и C
Прежде чем мы начнем исследовать влияние резисторов, катушек индуктивности и конденсаторов, соединенных вместе в одних и тех же цепях переменного тока, давайте кратко рассмотрим некоторые основные термины и факты.
Сопротивление
Это по существу трение против потока тока. В той или иной степени он присутствует во всех проводниках (кроме проводов super !), Особенно в резисторах.Когда переменный ток проходит через сопротивление, возникает падение напряжения, синфазное с током. Сопротивление математически обозначается буквой «R» и измеряется в омах (Ом).
Реактивное сопротивление
По сути, это инерция против тока. Он присутствует везде, где электрические или магнитные поля развиваются пропорционально приложенному напряжению или току, соответственно; но особенно в конденсаторах и катушках индуктивности.
Когда переменный ток проходит через чистое реактивное сопротивление, возникает падение напряжения, которое на 90 ° не совпадает по фазе с током.Реактивное сопротивление математически обозначается буквой «X» и измеряется в омах (Ом).
Импеданс
Это исчерпывающее выражение любых форм противодействия протеканию тока, включая как сопротивление, так и реактивное сопротивление. Он присутствует во всех схемах и во всех компонентах.
Когда переменный ток проходит через полное сопротивление, возникает падение напряжения, которое не совпадает по фазе с током где-то между 0 ° и 90 °. Импеданс математически обозначается буквой «Z» и измеряется в единицах Ом (Ом) в сложной форме.
Идеальные резисторы обладают сопротивлением, но не реактивным сопротивлением. Идеальные катушки индуктивности и идеальные конденсаторы обладают реактивным сопротивлением, но не имеют сопротивления. Все компоненты обладают импедансом, и из-за этого универсального качества имеет смысл перевести все значения компонентов (сопротивление, индуктивность, емкость) в общие термины импеданса в качестве первого шага при анализе цепи переменного тока.
Идеальный резистор, катушка индуктивности и конденсатор.
Фазовый угол импеданса для любого компонента — это фазовый сдвиг между напряжением на этом компоненте и током через этот компонент.
Для идеального резистора падение напряжения и ток всегда в фазе друг с другом, поэтому угол импеданса резистора считается равным 0 °. Для идеального индуктора падение напряжения всегда опережает ток на 90 °, поэтому фазовый угол импеданса индуктора равен + 90 °.
Для идеального конденсатора падение напряжения всегда отстает от тока на 90 °, поэтому считается, что фазовый угол импеданса конденсатора составляет -90 °.
Полное сопротивление переменного тока ведет себя аналогично сопротивлению в цепях постоянного тока: они складываются последовательно и уменьшаются параллельно.Пересмотренная версия закона Ома, основанная на импедансе, а не на сопротивлении, выглядит так:
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Мощность в резистивных и реактивных цепях переменного тока | Коэффициент мощности
Рассмотрим схему для однофазной системы питания переменного тока, в которой источник переменного напряжения 120 В, 60 Гц подает питание на резистивную нагрузку: (рисунок ниже)
Источник переменного тока управляет чисто резистивной нагрузкой.
В этом примере ток нагрузки будет 2 ампера, среднеквадратичное значение. Мощность, рассеиваемая на нагрузке, составит 240 Вт.
Поскольку эта нагрузка является чисто резистивной (без реактивного сопротивления), ток находится в фазе с напряжением, и расчеты выглядят аналогично расчетам в эквивалентной цепи постоянного тока.
Если бы мы изобразили кривые напряжения, тока и мощности для этой схемы, это выглядело бы так, как показано на рисунке ниже.
Ток синфазен с напряжением в резистивной цепи.
Обратите внимание, что форма сигнала мощности всегда положительная, а не отрицательная для этой резистивной цепи.
Это означает, что мощность всегда рассеивается резистивной нагрузкой и никогда не возвращается к источнику, как это происходит с реактивной нагрузкой. Если бы источником был механический генератор, для поворота вала потребовалось бы 240 Вт механической энергии (около 1/3 лошадиных сил).
Также обратите внимание, что форма сигнала мощности не соответствует частоте напряжения или тока! Скорее, его частота составляет удвоить частоты сигнала напряжения или тока.
Эта другая частота запрещает наше выражение мощности в цепи переменного тока с использованием тех же сложных (прямоугольных или полярных) обозначений, которые используются для напряжения, тока и импеданса, потому что эта форма математического символизма подразумевает неизменные фазовые отношения.
Когда частоты не совпадают, фазовые соотношения постоянно меняются.
Как ни странно это может показаться, лучший способ продолжить вычисления мощности переменного тока — это использовать скалярную нотацию и обрабатывать любые соответствующие фазовые отношения с помощью тригонометрии.
Цепь переменного тока с чисто реактивной нагрузкой
Для сравнения рассмотрим простую цепь переменного тока с чисто реактивной нагрузкой на рисунке ниже.
Цепь переменного тока с чисто реактивной (индуктивной) нагрузкой.
Мощность не рассеивается в чисто реактивной нагрузке. Хотя он попеременно поглощается и возвращается к источнику.
Обратите внимание, что мощность одинаково чередуется между положительными и отрицательными циклами.(Рисунок выше) Это означает, что мощность поочередно поглощается и возвращается к источнику.
Если бы источником был механический генератор, для вращения вала не потребовалось бы (практически) никакой полезной механической энергии, потому что нагрузка не использовала бы никакой энергии.
Вал генератора легко вращается, а индуктор не нагревается, как резистор.
Цепь переменного тока с резистивной и чисто реактивной нагрузкой
Теперь давайте рассмотрим цепь переменного тока с нагрузкой, состоящей из индуктивности и сопротивления, как показано на рисунке ниже.
Цепь переменного тока с реактивным сопротивлением и сопротивлением.
При частоте 60 Гц индуктивность 160 миллигенри дает нам индуктивное реактивное сопротивление 60,319 Ом.
Это реактивное сопротивление в сочетании с сопротивлением 60 Ом образует полное сопротивление нагрузки 60 + j60,319 Ом, или 85,078 Ом 45,152 ^или. Если нас не интересуют фазовые углы (чего мы еще не достигли), мы можем рассчитать ток в цепи, взяв полярную величину источника напряжения (120 вольт) и разделив ее на полярную величину импеданса. (85.078 Ом).
При напряжении источника питания 120 вольт RMS ток нагрузки составляет 1,410 ампер. Это цифра, которую покажет амперметр RMS, если он подключен последовательно с резистором и катушкой индуктивности.
Мы уже знаем, что реактивные компоненты рассеивают нулевую мощность, поскольку они в равной степени поглощают мощность и возвращают мощность в остальную часть схемы.
Следовательно, любое индуктивное реактивное сопротивление в этой нагрузке также будет рассеивать нулевую мощность.
Единственное, что здесь осталось для рассеивания мощности, — это резистивная часть импеданса нагрузки.Если мы посмотрим на график формы волны напряжения, тока и полной мощности для этой схемы, мы увидим, как эта комбинация работает на рисунке ниже.
Комбинированная резистивно-реактивная цепь рассеивает больше мощности, чем возвращается к источнику. Реактивное сопротивление не рассеивает мощность; хотя резистор делает.
Как и в любой реактивной цепи, мощность с течением времени чередуется между положительными и отрицательными мгновенными значениями.
В чисто реактивной схеме чередование положительной и отрицательной мощности делится поровну, в результате чего рассеиваемая полезная мощность равна нулю.Однако в схемах со смешанным сопротивлением и реактивным сопротивлением, подобных этой, форма волны мощности по-прежнему будет чередоваться между положительной и отрицательной, но количество положительной мощности будет превышать количество отрицательной мощности.
Другими словами, комбинированная индуктивная / резистивная нагрузка потребляет больше энергии, чем возвращается к источнику.
Глядя на график формы волны для мощности, должно быть очевидно, что волна проводит больше времени на положительной стороне центральной линии, чем на отрицательной, что указывает на то, что нагрузка потребляет больше мощности, чем возвращается в цепь.
То небольшое возвращение мощности происходит из-за реактивного сопротивления; дисбаланс положительной и отрицательной мощности происходит из-за сопротивления, поскольку она рассеивает энергию за пределами цепи (обычно в виде тепла).
Если бы источником был механический генератор, количество механической энергии, необходимое для вращения вала, было бы суммой мощности, усредненной между положительным и отрицательным циклами мощности.
Математическое представление мощности в цепи переменного тока является сложной задачей, потому что волна мощности не имеет той же частоты, что и напряжение или ток.
Кроме того, фазовый угол для мощности означает нечто совершенно иное, чем фазовый угол для напряжения или тока. В то время как угол для напряжения или тока представляет собой относительный сдвиг по времени между двумя волнами, фазовый угол для мощности представляет собой отношение между рассеиваемой мощностью и возвращаемой мощностью.
Из-за того, что мощность переменного тока отличается от напряжения или тока переменного тока, на самом деле легче получить цифры для мощности, вычислив с помощью скаляра величин напряжения, тока, сопротивления и реактивного сопротивления, чем пытаться получить их. из вектор или комплексных величин напряжения, тока и импеданса, с которыми мы работали до сих пор.
ОБЗОР:
В чисто резистивной цепи вся мощность схемы рассеивается резисторами. Напряжение и ток синфазны.
В чисто реактивной цепи мощность цепи не рассеивается нагрузкой (ами). Напротив, мощность поочередно поглощается и возвращается к источнику переменного тока. Напряжение и ток сдвинуты по фазе на 90 °.
В цепи, состоящей из смешанного сопротивления и реактивного сопротивления, мощность, рассеиваемая нагрузкой (ями), будет больше, чем возвращаемая, но некоторая мощность определенно будет рассеиваться, а некоторая будет просто поглощаться и возвращаться.Напряжение и ток в такой цепи будут сдвинуты по фазе на величину где-то между 0 ° и 90 °.
СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:
В чем разница между сопротивлением, реактивным сопротивлением и импедансом?
Цепи постоянного тока относительно легко анализировать, поскольку ток течет в одном направлении, а сопротивление является основным элементом цепи. Цепи переменного тока, с другой стороны, более сложны, поскольку напряжение и ток меняют направление с заданной частотой.В то время как цепи постоянного тока имеют сопротивление, цепи переменного тока часто имеют сопротивление и другое свойство, известное как реактивное сопротивление. Импеданс — это комбинация сопротивления и реактивного сопротивления.
Компоненты, известные как резисторы, предотвращают протекание тока — другими словами, они обладают свойством сопротивления. Резисторы присутствуют как в цепях переменного, так и в постоянном токе, и энергия, которая не может течь, отводится в виде тепла. Математически сопротивление — это просто напряжение, разделенное на ток.
R = сопротивление (Ом)
В = напряжение (вольт)
I = ток (амперы)
Реактивное сопротивление — это свойство, которое противодействует изменению тока и присутствует как в катушках индуктивности, так и в конденсаторах. Поскольку оно влияет только на , изменяя ток , реактивное сопротивление зависит от мощности переменного тока и зависит от частоты тока. Когда присутствует реактивное сопротивление, оно создает фазовый сдвиг на 90 градусов между напряжением и током, причем направление сдвига зависит от того, является ли компонент катушкой индуктивности или конденсатором.
Реактивное сопротивление, возникающее в катушке индуктивности, известно как индуктивное реактивное сопротивление . Когда присутствует индуктивное реактивное сопротивление, энергия накапливается в виде изменяющегося магнитного поля, и форма сигнала тока отстает от формы сигнала напряжения на 90 градусов. Индуктивное реактивное сопротивление возникает из-за устройств, в которых провод намотан по кругу, таких как катушки (включая линейные реакторы), дроссели и трансформаторы.
X _L = индуктивное реактивное сопротивление (Ом)
f = частота (Гц)
L = индуктивность (Генри)
Реактивное сопротивление конденсатора известно как емкостное сопротивление .Емкостное реактивное сопротивление накапливает энергию в виде изменяющегося электрического поля и заставляет ток отводить от напряжение на 90 градусов. Емкость создается, когда две проводящие пластины размещаются параллельно друг другу с небольшим расстоянием между ними, заполненные диэлектрическим материалом (изолятором).
X _C = емкостное реактивное сопротивление (Ом)
C = емкость (фарады)
Импеданс — это комбинация сопротивления и реактивного сопротивления (как индуктивного, так и емкостного). и является комплексным числом, содержащим как действительную, так и мнимую части.(Реальная часть импеданса — это сопротивление, а мнимая часть — реактивное сопротивление.) Импеданс имеет как величину, так и фазу.
Z = величина импеданса (Ом) в последовательной цепи
X _T = полное реактивное сопротивление (Ом) = X _L — X _C
θ = фаза полного сопротивления (градусы)
Сопротивление, реактивное сопротивление и импеданс |
Х. Марк Бауэрс
Одним из моих рождественских подарков в декабре прошлого года была книга «Забытый гений Оливера Хевисайда — независимого представителя электротехники.Оливер Хевисайд был англичанином (1850–1925) и провел большую часть своей жизни, развивая свои теории в одиночку — настоящий гений-затворник. Я никогда не слышал о нем, но, похоже, он заслуживает гораздо большего признания, потому что он разработал многие теоретические концепции, которые мы сейчас принимаем как должное. В одной из своих ранее опубликованных работ Хевисайд переформулировал теорию электромагнетизма Максвелла (первоначально 12 уравнений, которые сбивали с толку большинство ученых его времени) в четыре уравнения Максвелла, теперь знакомые всем инженерам-электрикам.В той же статье, опубликованной в 1885 году, Хевисайд разработал формулу для потока энергии через электромагнитное поле, которая продемонстрировала, что электрическая энергия течет не по проводу, а скорее в пространстве рядом с ним. Большая часть работы Хевисайда собрана в пять томов, общий объем которых превышает 2500 страниц!
Цель этой и некоторых будущих статей — рассмотреть некоторые из этих основ, которым многих из нас учили на раннем этапе, но сейчас они используются редко. Здесь я начну с сопротивления, реактивного сопротивления и импеданса.Кроме того, позвольте мне заявить очевидное: этот столбец позволит только поверхностно изучить эти концепции, поскольку пространство не позволяет провести полный анализ.
Сопротивление
Сопротивление согласно определению закона Ома — это «характеристика цепи, ограничивающая ток». Сопротивление может возникать из-за дискретного компонента, такого как резистор, или может представлять совокупное сопротивление току провода (-ов), кабеля (-ов) или линии (-ов) передачи, включая коаксиальный кабель. Сопротивление, по определению, дает значение в омах при нулевой частоте (постоянный ток или постоянный ток).
На рис. 1 показаны соотношения по закону Ома между током, напряжением, сопротивлением и мощностью.
При работе с частотами больше нуля (переменный ток или переменный ток) мы обнаруживаем, что одного сопротивления недостаточно для правильной количественной оценки общего сопротивления току, протекающему в цепи. Это приводит нас к реактивному сопротивлению.
Реактивное сопротивление
Реактивное сопротивление (X) определяется как «часть общего сопротивления протеканию тока в цепи переменного тока из-за емкости, индуктивности или того и другого, и выражается в омах.«Реактивное сопротивление имеет как величину, так и фазу и далее разделяется на индуктивную и емкостную составляющие.
Индуктивное сопротивление
Индуктивное реактивное сопротивление (X _L) — это часть общего реактивного сопротивления цепи, вносимая катушками, дросселями и обмотками трансформатора. Любое устройство, в котором провод намотан по кругу, является индуктором. Катушки индуктивности имеют тенденцию противодействовать любому изменению тока с течением времени. Это связано с тем, что ток, протекающий через катушку индуктивности, создает магнитное поле.В цепи постоянного тока напряженность и направление магнитного поля остаются постоянными. В результате ток легко протекает через индуктор, поскольку он выглядит просто как кусок провода. Магнитные поля по своей природе сопротивляются изменениям и противодействуют любому изменению тока. В цепи переменного тока магнитное поле должно постоянно меняться при изменении величины и направления тока. Таким образом, катушка индуктивности легче пропускает низкие частоты, чем более высокие частоты. Это сопротивление изменению протекания тока является индуктивным реактивным сопротивлением и определяется формулой:
.
, где X _L — индуктивное реактивное сопротивление в Ом, π равно 3.14159 (…), F — частота в герцах, L — индуктивность в генри.
Емкостное реактивное сопротивление
Емкостное реактивное сопротивление (X _C) — это часть полного реактивного сопротивления цепи, обусловленная емкостью. Емкость возникает, когда две проводящие поверхности параллельны друг другу и разделены небольшим расстоянием с непроводящим веществом (диэлектриком). Примером может служить компонент дискретной схемы, называемый конденсатором. Конденсаторы являются устройствами ограничения напряжения, поскольку они имеют тенденцию противодействовать изменению напряжения с течением времени.
Когда на конденсатор подается постоянное напряжение, конденсатор потребляет ток и заряжается до значения приложенного напряжения. В цепи переменного тока, чем ниже частота приложенного напряжения, тем больше времени требуется конденсатору для зарядки, прежде чем напряжение изменит полярность и конденсатор начнет разряжаться. Следовательно, конденсатор тратит больше времени на полную зарядку и пропускает меньший ток, что приводит к меньшему протеканию тока (более высокому реактивному сопротивлению) на низких частотах. По мере увеличения частоты конденсатор переходит от зарядки к разрядке быстрее, позволяя протекать большему току (более низкое реактивное сопротивление).Поэтому емкостное реактивное сопротивление уменьшается с увеличением частоты. Фактическое значение X _C обратно пропорционально значению емкости и частоты, как показано в формуле:
, где X _C — емкостное сопротивление в омах, π — 3,14159 (…), F — частота в герцах, а C — емкость в фарадах.
Импеданс
Импеданс (Z) — это полное сопротивление току в цепи переменного тока, которая содержит сопротивление и реактивное сопротивление, и вот что интересно.Если бы цепь, например, была чисто индуктивной (без сопротивления), X _L представляла бы полное сопротивление протеканию тока. В этом примере Z и X _L идентичны и представлены значением некоторой величины с фазовым углом -90 ° (или тета). Если бы цепь была чисто емкостной, то было бы то же самое, за исключением того, что ɵ сдвигается на + 90 °. Фаза тока всегда указывается относительно напряжения (опережающая или запаздывающая). Сети переменного тока обычно содержат элементы сопротивления, индуктивности и емкости, и поэтому полное сопротивление должно быть комплексным значением с величиной и фазой (вектор).Величину Z в цепи можно вычислить, как показано в следующих формулах.
Импеданс последовательной цепи рассчитывается по
.
, где X _T = X _L — X _C (X _T — реактивное сопротивление комбинированной цепи).
Импеданс параллельной цепи рассчитывается по
.
где
Теперь рассмотрим схему на Рисунке 2, которая содержит комбинацию сопротивления и емкости (без индуктивности, чтобы не усложнять задачу).Обратите внимание, что резистивные и реактивные токи не суммируются численно, как можно было бы ожидать; 1,0 ампер резистивный ток плюс 1,0 ампер реактивный ток равны 1,414 ампера полного тока. Это сбивает с толку, пока мы не рассмотрим рисунок 3.
На рисунке 3 изображен текущий треугольник в качестве наглядного пособия для иллюстрации величины и фазы. Он показывает соотношение между резистивным, реактивным и полным токами, протекающими в нашей примерной схеме. Если мы построим резистивный ток в 1 ампер по оси x (0 ° тета) и реактивный ток в 1 ампер по оси y (+ 90 ° тета), общий ток будет представлен длиной гипотенузы в 1.414 ампер с опережающим фазовым углом 45 °.
Теперь очевидно, что импеданс и мощность в этой цепи также должны быть комплексными (векторами), и это действительно так. Использование формулы для Z (показанной ранее) для параллельной цепи дает 70,7 Ом для этой RC-цепи, но не обеспечивает фазовый угол. Треугольник импеданса может быть построен аналогично рисунку 3 (не показан). Однако для Z этот процесс непрост, так как сначала мы должны вычислить эквивалентную последовательную схему, а затем построить треугольник.Когда мы это делаем, результат дает комплексное Z 70,7 Ом с тета + 45 °.
В треугольнике мощности (также не показан) по горизонтальной оси отложена истинная мощность (резистивная, 100 Вт), реактивная мощность по вертикальной оси (100 ВА), а гипотенуза равна кажущейся мощности 141,4 вольт-ампера. Кроме того, косинус фазового угла 45 ° равен 0,707, что равно коэффициенту мощности (pf) в этой цепи. Коэффициент мощности — важное понятие в распределительных сетях электроэнергетики и, на мой взгляд, более простой способ концептуализации и расчета реактивных токов и мощности.
Подробную статью, включающую треугольники импеданса и мощности, см. На странице загрузок моего веб-сайта www.cablesoftengineering.com. Мы продолжим этот обзор в моей следующей колонке, когда перейдем к параметрам, относящимся к коаксиальному кабелю.
–
Рисунок 1. График закона Ома
Рисунок 2. Схема RC
Рисунок 3. Текущий треугольник
H.Марк Бауэрс,
Cablesoft Engineering, Inc.
[email protected]
Марк — вице-президент по инженерным вопросам в Cablesoft Engineering, Inc. Он занимается телефонией с 1968 года и кабельной промышленностью с 1973 года. Его последняя должность в отрасли была вице-президентом по корпоративному проектированию в Warner Cable Communications в Дублине, штат Огайо. Образование Марка включает в себя Школу ядерной инженерии ВМС США и степени бакалавра и магистра в области управления технологиями. Марк является членом SCTE • ISBE, IEEE, а также старшим членом и лицензированным главным инженером по телекоммуникациям в iNARTE.

Что такое реактивное сопротивление и чем оно отличается от активного

Виды реактивного сопротивления

Индуктивное сопротивление

Емкостное сопротивление

Как рассчитать полное реактивное сопротивление цепи

Треугольник сопротивлений

Влияние реактивного сопротивления на работу электрических цепей

Применение реактивного сопротивления в электротехнике

Фильтрация сигналов

Компенсация реактивной мощности

Измерение реактивного сопротивления

Заключение

Активное и реактивное сопротивление. Треугольник сопротивлений

Активное и реактивное сопротивление

Похожие темы:

Реактивное сопротивление

Чем обусловлено реактивное сопротивление

Интересно

Сопротивление реактивное — Справочник химика 21

Реактивное сопротивление катушки индуктивности.

Реактивное сопротивление конденсатора.

Индуктивный элемент L

Емкостной элемент

Сравнение влияния реактивного сопротивления на активную мощность сети

Расчёт реактивного сопротивления

Реактивное сопротивление катушки индуктивности.

Реактивное сопротивление конденсатора.

Калькулятор расчёта реактивного сопротивления

Расчитать реактивное сопротивление ёмкости или индуктивности:

Расчитать ёмкость и индуктивность от сопротивления:

Реактивная составляющая — входное сопротивление

Реактивная составляющая — входное сопротивление

6.4. Сопротивление в цепи синусоидального тока

6.5. Индуктивная катушка в цепи синусоидального тока

6.6. Емкость в цепи синусоидального тока

6.7. Последовательно соединенные реальная индуктивная

6.8. Параллельно соединенные индуктивность, емкость

6.9. Резонансный режим в цепи, состоящей

Реактивные электронные компоненты и фазовый угол

Reactive Component — обзор

1.6.1 Значение

Резистивный компонент — обзор

Пьезорезистор

Обзор R, X и Z (сопротивление, реактивное сопротивление и импеданс) | Реактивное сопротивление и импеданс — R, L и C

Сопротивление

Реактивное сопротивление

Импеданс

Мощность в резистивных и реактивных цепях переменного тока | Коэффициент мощности

Цепь переменного тока с чисто реактивной нагрузкой

Цепь переменного тока с резистивной и чисто реактивной нагрузкой

В чем разница между сопротивлением, реактивным сопротивлением и импедансом?

Сопротивление, реактивное сопротивление и импеданс |

Похожие записи

Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

Новорожденный какает слизью: причины появления слизи в кале грудничка

Гемангиома у новорожденных: причины, виды, лечение и профилактика

Добавить комментарий Отменить ответ