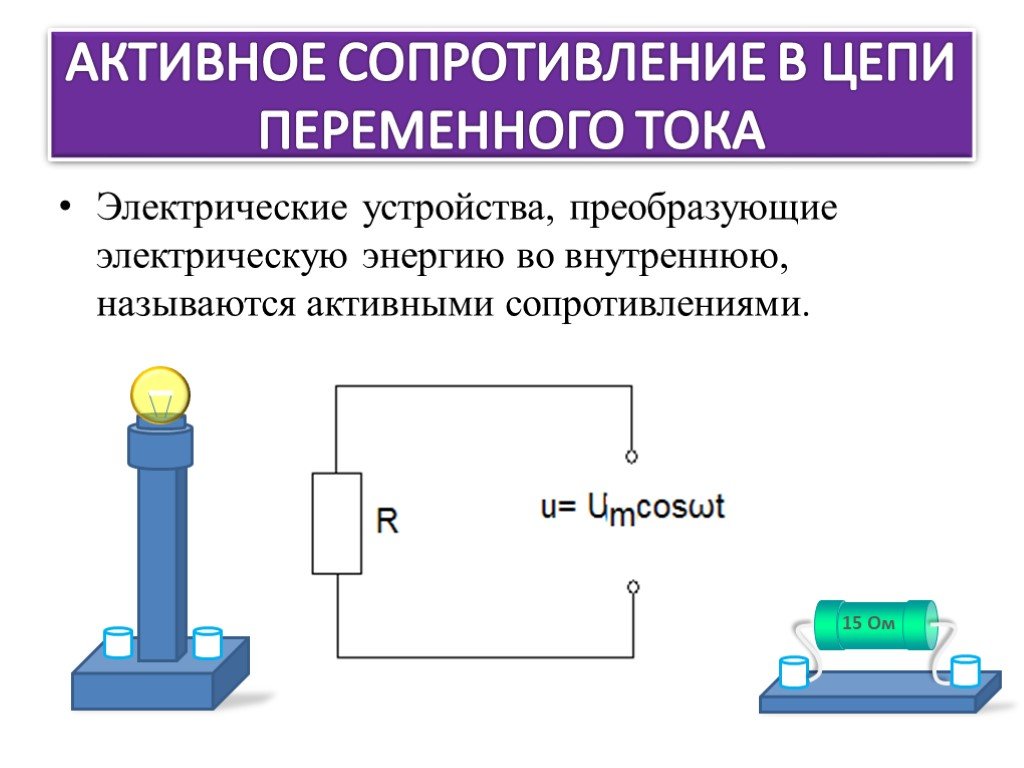
Что такое реактивное сопротивление. Как рассчитать емкостное и индуктивное сопротивление. Каковы особенности последовательных и параллельных RLC-цепей. Какое значение имеет реактивное сопротивление в электротехнике. Как влияет реактивное сопротивление на работу электрических цепей.
Что такое реактивное сопротивление и какие виды существуют
Реактивное сопротивление — это сопротивление, которое оказывают переменному току реактивные элементы электрической цепи — конденсаторы и катушки индуктивности. В отличие от активного сопротивления, реактивное сопротивление не приводит к необратимым потерям энергии.
Существует два основных вида реактивного сопротивления:
- Емкостное сопротивление (Xc) — создается конденсаторами
- Индуктивное сопротивление (XL) — создается катушками индуктивности
Емкостное и индуктивное сопротивления имеют противоположные свойства и в электрической цепи могут компенсировать друг друга.
Расчет емкостного и индуктивного сопротивления
Для расчета емкостного и индуктивного сопротивления используются следующие формулы:

Емкостное сопротивление:
Xc = 1 / (2πfC)
где:
- Xc — емкостное сопротивление (Ом)
- f — частота переменного тока (Гц)
- C — емкость конденсатора (Ф)
Индуктивное сопротивление:
XL = 2πfL
где:
- XL — индуктивное сопротивление (Ом)
- f — частота переменного тока (Гц)
- L — индуктивность катушки (Гн)
Особенности реактивного сопротивления в электрических цепях
Реактивное сопротивление обладает рядом важных особенностей:
- Зависит от частоты переменного тока
- Не вызывает потерь энергии
- Приводит к сдвигу фаз между током и напряжением
- Емкостное и индуктивное сопротивления компенсируют друг друга
- Измеряется в Омах, как и активное сопротивление
Эти свойства необходимо учитывать при анализе и расчете электрических цепей переменного тока.
Реактивное сопротивление в последовательных RLC-цепях
В последовательных RLC-цепях реактивное сопротивление определяется как разность между индуктивным и емкостным сопротивлениями:
X = XL — Xc
Если X > 0, цепь имеет индуктивный характер, если X < 0 - емкостный. При X = 0 возникает явление резонанса напряжений.
Полное сопротивление (импеданс) последовательной RLC-цепи рассчитывается по формуле:
Z = √(R^2 + X^2)
где R — активное сопротивление цепи.
Реактивное сопротивление в параллельных RLC-цепях
В параллельных RLC-цепях реактивная проводимость определяется как:
B = BC — BL
где BC — емкостная проводимость, BL — индуктивная проводимость.
Полная проводимость параллельной RLC-цепи:
Y = √(G^2 + B^2)
где G — активная проводимость.
Импеданс параллельной цепи равен обратной величине полной проводимости:
Z = 1 / Y
Значение реактивного сопротивления в электротехнике
Реактивное сопротивление играет важную роль во многих областях электротехники:
- Компенсация реактивной мощности в электрических сетях
- Создание резонансных контуров в радиотехнике
- Фильтрация сигналов разной частоты
- Согласование импедансов в линиях связи
- Накопление энергии в реактивных элементах
Понимание свойств реактивного сопротивления необходимо для эффективного проектирования и эксплуатации электрических и электронных устройств.

Влияние реактивного сопротивления на работу электрических цепей
Реактивное сопротивление оказывает существенное влияние на работу электрических цепей переменного тока:
- Изменяет амплитуду тока в цепи
- Вызывает сдвиг фаз между током и напряжением
- Влияет на резонансные явления
- Определяет реактивную мощность
- Воздействует на коэффициент мощности
Учет реактивного сопротивления позволяет корректно рассчитывать параметры цепей переменного тока и оптимизировать их работу.
Применение реактивного сопротивления на практике
На практике свойства реактивного сопротивления используются в различных устройствах и системах:
- Фильтры верхних и нижних частот
- Колебательные контуры радиоприемников
- Устройства компенсации реактивной мощности
- Импульсные источники питания
- Системы беспроводной передачи энергии
Понимание особенностей реактивного сопротивления позволяет создавать эффективные технические решения в различных областях электротехники и электроники.
Методы измерения реактивного сопротивления
Для измерения реактивного сопротивления применяются различные методы:
- Метод вольтметра-амперметра
- Мостовые методы
- Резонансный метод
- Метод векторных измерений
- Использование специализированных измерителей импеданса
Выбор метода измерения зависит от требуемой точности, диапазона частот и типа исследуемой цепи. Современные цифровые приборы позволяют проводить комплексный анализ импеданса в широком частотном диапазоне.
Заключение
Реактивное сопротивление является важной характеристикой электрических цепей переменного тока. Понимание его свойств и умение рассчитывать необходимо для анализа и проектирования различных электротехнических устройств. Учет реактивного сопротивления позволяет оптимизировать работу электрических систем и создавать эффективные технические решения.
Reactance
http://en.wikipedia.org Wikipedia, свободная энциклопедия
Реактивное сопротивление — это мнимая часть импеданса (импедансом называется полное (комплексное) сопротивление цепи переменного тока), которая показывает меру противодействия синусоидальному переменному току. Реактивное сопротивление возникает в присутствии индуктивности и ёмкости в цепи, и обозначается символом X; единица СИ — Ом.
(В этом разделе знак тильда (~) будет использован для обозначения векторов или комплексных величин, а буквы без дополнительных знаков обозначают модули векторов соответствующих величин, а также скалярные величины.)
Для определения импеданса требуется как реактивное сопротивление X, так и резистивное
(активное) сопротивление R.
Несмотря на то, что в некоторых обстоятельствах реактивное сопротивление может
доминировать, требуется хотя-бы приблизительное знание активного
сопротивления для определения импеданса.
Как модуль, так и фаза импеданса зависят от обоих сопротивлений – и от активного и от реактивного:
Модуль импеданса — это отношение амплитуд напряжения и тока, тогда как фаза - это разница между фазами напряжения и тока.
- Если X>0 говорят, что реактивное сопротивление является индуктивным
- Если X=0 говорят, что импеданс чисто резистивный (активный)
- Если X<0 говорят, что реактивное сопротивление является ёмкостным
Физическое значение
Определение соотношений между током и напряжением требует знания, как активного, так и реактивного сопротивлений. Реактивное сопротивление само по себе даёт только ограниченную физическую информацию об электрическом устройстве или электрической цепи:
- Величина реактивного сопротивления показывает меру
противодействия цепи только переменному току, и зависит от частоты
переменного тока.

- Положительное реактивное сопротивление подразумевает, что фаза напряжения опережает фазу тока, в то время как отрицательное реактивное сопротивление подразумевает, что фаза напряжения отстаёт от фазы тока.
- Нулевое реактивное сопротивление подразумевает, что ток и напряжение совпадают по фазе и наоборот, если реактивное сопротивление не равно нулю, тогда существует разность фаз между напряжением и током.
Есть случаи, когда в цепи есть реактивные элементы, но результируюшее реактивное сопротивление цепи равно нулю, для примера: резонанс в RLC-цепи случается, когда реактивные импедансы ZC и ZL взаимоуничтожаются. Это значит, что импеданс имеет фазу, равную нулю (специфический пример нулевого реактивного сопротивления для случая 3. выше).
Ёмкостное реактивное сопротивление
Ёмкостное реактивное сопротивление Xc обратнопропорционально частоте сигнала и ёмкости C.
Ёмкостной элемент называется конденсатором. Конденсатор состоит из двух проводников, отделённых друг от друга изолятором, тоесть диэлектриком.
При низких частотах или в цепи постоянного тока конденсатор разрывает (размыкает) цепь, так как ток не может течь через диэлектрик. Если к изначально разряженному конденсатору прикладывают постоянное напряжение – в начальный момент на обкладках конденсатора индуцируются заряды, электрическое поле котрых противоположно полю внешнего источника напряжения. Поэтому ток в этот начальный момент в цепи максимален. Затем потенциалы источника питания и конденсатора точно уравниваются, и ток в цепи прекращается.
Конденсатор, включённый в цепь переменного тока, будет успевать накапливать
только ограниченный заряд перед тем, как разность потенциалов изменит знак на
противоположный. Тоесть ток не будет успевать упасть до нуля, как в случае цепи
постоянного тока. Чем выше частота, тем меньший заряд будет аккумулироваться в
конденсаторе, и тем меньше конденсатор будет противодействовать внешнему току
(сопротивление уменьшается).
Индуктивное реактивное сопротивление
Индуктивное реактивное сопротивление XL прямопропорционально частоте сигнала и индуктивности L.
Индуктивный элемент представляет собой катушку индуктивности, тоесть длинный проводник, например проволока, намотанный в виде катушки. Изнутри катушка может быть пустая или содержать магнетик. Закон электромагнитной индукции Фарадея устанавливает, что ЭДС электромагнитной индукции в замкнутом контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Эта ЭДС часто называется противо-ЭДС.
Если индуктивность представляет собой катушку содержащую N витков.
В общем случае ЭДС является следствием изменения магнитного потока в
контуре. Но это изменение магнитного потока может иметь разные причины:
движение магнита, движение другой катушки с током, изменение собственного тока
контура. Последний случай носит название – явление самоиндукции, которое и
лежит в основе индуктивного реактивного сопротивления.
Последний случай носит название – явление самоиндукции, которое и
лежит в основе индуктивного реактивного сопротивления.
В свою очередь противо-ЭДС вызывает в контуре индукционный ток, который направлен противоположно току источника питания. Точная форма правила Ленца: индукционный ток в контуре имеет такое направление, что созданный им магнитный поток, через контур, препятствует изменению магнитного потока, вызвавшего этот ток.
Если к изначально неподключенной катушке индуктивности подключают источник постоянного тока – в начальный момент в катушке начинает течь ток от внешнего источника. Он вызывает изменение магнитного потока. Изменение магнитного потока порождает противо-ЭДС. Противо-ЭДС вызывает противоток. Этот противоток в начальный момент равен току источника.
При низких частотах или в цепи постоянного тока катушка индуктивности
проводит электрический ток беспрепятственно, и может рассматриваться как
короткозамкнутый участок цепи, тоесть проводник с низким сопротивлением. Если
к изначально неподключенной катушке индуктивности подключают источник
постоянного тока – в начальный момент в катушке возникает противоток, равный
току внешнего источника. Поэтому для идуктивного элемента в этот начальный
момент результирующий ток равен нулю, а напряжение максимально. Затем токи
источника и индуктивного элемента уравниваются и напряжение на индуктивном
элементе становится равным нулю.
Если
к изначально неподключенной катушке индуктивности подключают источник
постоянного тока – в начальный момент в катушке возникает противоток, равный
току внешнего источника. Поэтому для идуктивного элемента в этот начальный
момент результирующий ток равен нулю, а напряжение максимально. Затем токи
источника и индуктивного элемента уравниваются и напряжение на индуктивном
элементе становится равным нулю.
Ток в катушке индуктивности, включённой в цепь переменного тока, будет успевать возрасти только до определённого значения перед тем, как ток источника питания изменит знак на противоположный. Тоесть напряжение (на выводах катушки индуктивности) не будет успевать упасть до нуля, как в случае цепи постоянного тока. Чем выше частота, тем выше напряжение на выводах катушки индуктивности (сопротивление увеличивается).
Фазные соотношения
Фаза напряжения приложенного к чисто реактивному устройству (устройству с
нулевым активным сопротивлением) отстаёт от фазы тока на Pi/2 для ёмкости и опережает фазу тока на Pi/2 для индуктивности.
Причина различных знаков ёмкостного и индуктивного сопротивлений заключается в определении фазной переменной импеданса.
Для реактивного элемента цепи синусоидальное напряжение на элементе сдвинуто по фазе на 90 градусов (Pi/2 радиан) относительно тока. Элемент поочерёдно то поглащает энергию из сети, то затем возвращает энергию обратно в сеть, поэтому чисто реактивное сопротивление не поглащает энергию.
Реактивное емкостное сопротивление — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
| Характеристики крутизны для типовых пентагридных смесительных.| Компенсация связи через пространственный. [1] |
Реактивное емкостное сопротивление и положительное активное сопротивление элементов этой цепочки могут компенсировать связь через пространственный заряд в узком диапазоне частот. Для этого контур сигнальной сетки настраивают на частоту гетеродина и параметры компенсирующей цепи R и С подбирают так, чтобы на сигнальной сетке не появлялось заметное напряжение гетеродина.
[2]
Для этого контур сигнальной сетки настраивают на частоту гетеродина и параметры компенсирующей цепи R и С подбирают так, чтобы на сигнальной сетке не появлялось заметное напряжение гетеродина.
[2]
Как и активное, реактивное емкостное сопротивление оценивают в омах. Значение его зависит от емкости и частоты: чем больше емкость и частота, тем меньше сопротивление. Катушка индуктивности, включенная в цепь переменного тока, тоже обладает реактивным сопротивлением XL: ( uL2n L. Катушка с конденсатором образует колебательный контур. [3]
Сопротивление Хс называется реактивным емкостным сопротивлением. Оно отличается от активного сопротивления R, в котором вся мощность, отдаваемая источником тока, превращается в тепло и расходуется на нагревание сопротивления. В случае же емкостного реактивного сопротивления Хс вся работа, совершаемая источником тока при заряде конденсатора, преобразуется в энергию электрического поля, а при разряде вся энергия без остатка возвращается в источник. Потому сопротивление и называют реактивным.
[4]
Потому сопротивление и называют реактивным.
[4]
В диэлектрическом усилителе преобразование энергии источника питания в энергию усиливаемого сигнала производится нелинейным реактивным емкостным сопротивлением, роль которого играет конденсатор с сегнетодиэлектриком. [5]
При необходимости длину сварочной цепи можно нарастить, однако стабильность процесса в этом случае ухудшается ввиду увеличения активного, реактивного и емкостного сопротивления сварочной цепи и снижения возможностей источника питания по отработке возмущений, связанных с изменением вылета электрода и длины дуги. Сварочные кабели запрещено при работе укладывать в бухты или наматывать на вьюшки вследствие значительного увеличения индуктивного сопротивления сварочной цепи. [6]
Это происходит в том случае, когда в одних ветвях преобладает реактивное индуктивное сопротивление, а в других — реактивное емкостное сопротивление. [7]
Электрическая экни-валеитная схема РК. [8]
[8] |
При последовательной схеме замещения измеряемое сопротивление РК ( активная составляющая Ra) равно сумме первого и второго членов правой части выражения (3.24), третий член определяет реактивное емкостное сопротивление. [9]
В электрических цепях переменного тока при параллельном соединении реактивных сопротивлений может возникать резонанс токов. Это происходит в том случае, когда в одних ветвях преобладает реактивное индуктивное сопротивление, а в других — реактивное емкостное сопротивление. [10]
| Зависимость емкости бумажного ( а и слюдяного ( б конденсаторов от частоты ( между-слойная поляризавдя. [11] |
Практически о величине емкости конденсатора ( действующей емкости) мы судим по величине тока, потребляемого конденсатором. Наличие индуктивностиЬв конденсаторе дает увеличение его действующей емкости с ростом частоты ( рис. 30), так как ток будет возрастать за счет компенсации реактивного емкостного сопротивления индуктивным сопротивлением.
[12]
30), так как ток будет возрастать за счет компенсации реактивного емкостного сопротивления индуктивным сопротивлением.
[12]
В простейшем случае резонанс напряжений может быть получен в электрической цепи переменного тока при последовательном включении катушки индуктивности и конденсаторов. При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости С конденсаторов происходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах и активном сопротивлении катушки и активная, реактивная и полная мощности электрической цепи. [13]
В простейшем случае резонанс напряжений может быть получен в электрической цепи переменного тока при последовательном включении катушки индуктивности и конденсаторов. При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости С конденсаторов происходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах и активном сопротивлении катушки и активная, реактивная и полная мощности электрической цепи.
[14]
При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости С конденсаторов происходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах и активном сопротивлении катушки и активная, реактивная и полная мощности электрической цепи.
[14]
Страницы: 1
Глава 17. Резонансные цепи . Введение в электронику
ЦЕЛИ
После изучения этой главы студент должен быть в состоянии:
• Написать формулы для определения емкостного и индуктивного сопротивления.
• Описать, как реагируют на переменный ток и напряжение конденсаторы и катушки индуктивности.
• Дать определение реактивного сопротивления последовательной цепи и уметь определить характер цепи (индуктивный или емкостный).
• Дать определение термина импеданс.
• Уметь вычислять импеданс, который содержит как резистивную, так и емкостную или индуктивную составляющие.
• Объяснить, как должен быть модифицирован закон Ома перед использованием его для цепей переменного тока.
• Уметь вычислять Хс, XL, X, Z и Iт в последовательных RLC цепях.
• Уметь вычислять Ic, IL, Ix, IR и Iz в параллельных RLC цепях.
В предыдущих главах сопротивление, емкость и индуктивность в цепях переменного тока рассматривались по отдельности. В этой главе исследуется комбинация сопротивления, емкости и индуктивности в цепи переменного тока. Рассматриваемые вопросы не являются новым материалом, но применяют все изложенные ранее принципы.
Рассматриваемые вопросы не являются новым материалом, но применяют все изложенные ранее принципы.
Когда реактивное сопротивление катушки индуктивности равно реактивному сопротивлению конденсатора в цепи, возникает резонанс. Резонансные цепи широко используются в электронике.
17-1. РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ
Емкостное реактивное сопротивление — это противодействие, которое конденсатор оказывает переменному току. Оно измеряется в омах и обозначается символом Хс. Емкостное реактивное сопротивление вычисляется по формуле:
Хс = 1/2πfC
Заметим, что при использовании этой формулы емкость должна быть выражена в фарадах (а не в долях фарады).
Индуктивное реактивное сопротивление — это противодействие, которое катушка индуктивности оказывает переменному току. Оно измеряется в омах и обозначается символом XL.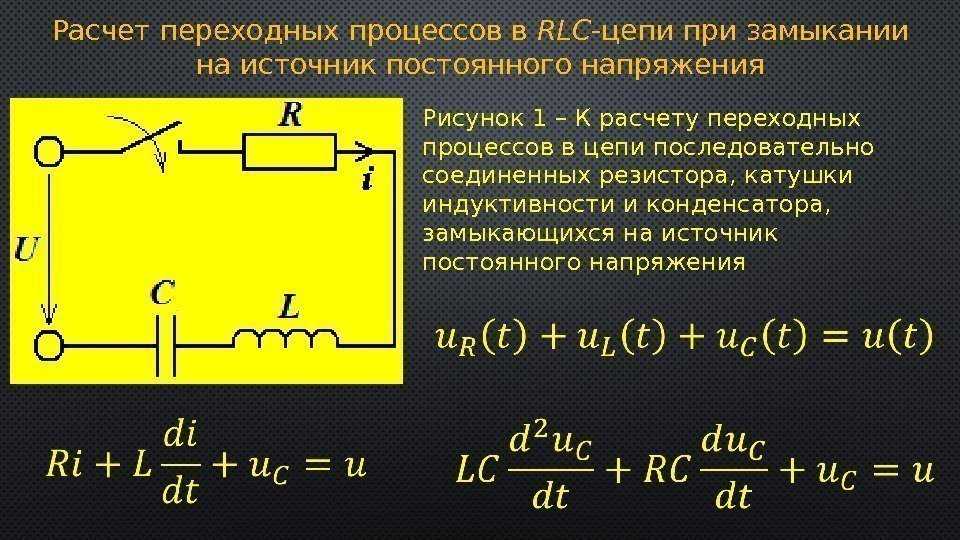 Индуктивное реактивное сопротивление вычисляется по формуле:
Индуктивное реактивное сопротивление вычисляется по формуле:
XL = 2πfL.
Заметим, что при использовании этой формулы индуктивность должна быть выражена в генри (а не в долях генри).
Емкостное реактивное сопротивление служит причиной того, что ток опережает по фазе напряжение. Индуктивное реактивное сопротивление служит причиной того, что ток отстает по фазе от напряжения. Емкостное и индуктивное реактивные сопротивления прямо противоположны по создаваемым эффектам и, следовательно, когда в цепи присутствуют и индуктивность и емкость, общий эффект определяется разностью их значений. Эта разность называется реактивным сопротивлением и обозначается символом X. Реактивное сопротивление может быть выражено следующими формулами:
X = Хс — XL или X = XL — Хс.
ПРИМЕР: Чему равно реактивное сопротивление цепи, содержащей конденсатор емкостью 1 мкФ, соединенный последовательно с индуктивностью 10 генри (рис. 17-1), работающей на частоте 60 герц?
Рис. 17-1
Дано:
f = 60 Гц; L = 10 Гн; С = 1 мкФ
Х =?
Решение:
Хс = 1/2πfC
Хс =1/(6,28)(60)(0,000001)
Хс =2654 Ом
XL = 2πfL
XL = (6,28)(60)(10)
XL = 3768 Ом
X = XL- XC = 3768–2654
X = 1114 Ом (индуктивное).
ПРИМЕР: Чему равно реактивное сопротивление цепи, содержащей конденсатор емкостью 1 мкФ, соединенный последовательно с индуктивностью 1 генри (рис. 17-2), работающей на частоте 60 герц?
Рис. 17-2
Дано:
f = 60 Гц; L = 1 Гн; С = 1 мкФ
Х =?
Решение:
Хс = 1/2πfC
Хс = 1/(6,28)(60)(0,000001)
Хс =2654 Ом
XL = 2πfL
XL = (6,28)(60)(1)
XL = 376,8 Ом
X = XC — XL = 2654 — 376,8
X = 2277,2 Ом (емкостное).
Эти примеры иллюстрируют важный момент. Когда емкостное и индуктивное реактивные сопротивления соединены последовательно, меньшее значение всегда вычитается из большего. Получающееся в результате реактивное сопротивление характеризуется большим значением.
17-1. Вопросы
1. Каково фазовое соотношение между током и напряжением на конденсаторе?
2. Каково фазовое соотношение между током и напряжением на катушке индуктивности?
3. По какой формуле определяется полное реактивное сопротивление последовательной цепи, когда известны значения Хс и XL?
4. Какова величина полного реактивного сопротивления (X) последовательной цепи, содержащей Хс = 50 ом и XL = 20 ом? Укажите, является X емкостным или индуктивным.
17-2. ИМПЕДАНС
Реактивное сопротивление, как емкостное, так и индуктивное, противодействует протеканию тока в цепях переменного тока. Активное сопротивление также препятствует протеканию тока в цепи. Комбинированное противодействие реактивного и активного сопротивлений называется импедансом и обозначается символом Z.
Активное сопротивление также препятствует протеканию тока в цепи. Комбинированное противодействие реактивного и активного сопротивлений называется импедансом и обозначается символом Z.
И активное, и реактивное сопротивления измеряются в омах. Следовательно, кажется логичным сложить эти сопротивления для того, чтобы получить импеданс. Однако этого делать нельзя, поскольку активное и реактивное сопротивления — величины векторные. В цепях переменного тока, содержащих только активное сопротивление, ток и напряжение находятся в фазе. И ток, и напряжение достигают своих максимальных значений одновременно.
Как упоминалось ранее, в цепях переменного тока, содержащих только реактивные сопротивления, ток будет либо опережать, либо отставать от напряжения на 90 градусов. Следовательно, напряжение в чисто реактивной цепи будет отличаться по фазе на 90 градусов от напряжения в чисто резистивной цепи.
Когда цепь содержит и активное, и реактивное сопротивление, импеданс будет больше любого их них. Кроме того, ток в такой цепи будет не в фазе с напряжением. Сдвиг по фазе будет в пределах от нуля до 90 градусов.
Кроме того, ток в такой цепи будет не в фазе с напряжением. Сдвиг по фазе будет в пределах от нуля до 90 градусов.
Для того чтобы найти импеданс, используется векторная диаграмма — прямоугольный треугольник сопротивлений. Это может быть сделано потому, что ток через резистор находится в фазе с напряжением на нем, а ток через реактивную нагрузку сдвинут по фазе на 90 градусов относительно напряжения на ней. Они находятся под прямым углом друг к другу.
ПРИМЕР: Чему равен импеданс последовательно соединенных резистора сопротивлением 150 ом и индуктивного реактивного сопротивления 100 ом?
В качестве первого шага нарисуем основание треугольника, представляющее резистор 150 ом. Далее нарисуем линию под углом 90 градусов к основанию, представляющую индуктивное сопротивление 100 ом. После этого соединим концы линий, образуя гипотенузу треугольника. Гипотенуза представляет импеданс цепи (рис. 17-3).
Рис.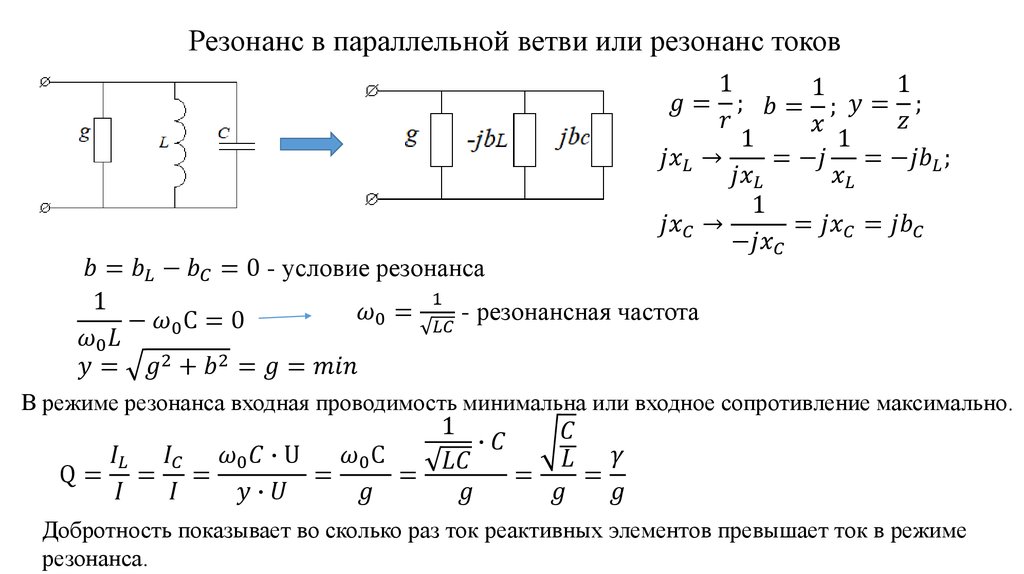 17-3. Векторная диаграмма.
17-3. Векторная диаграмма.
Теорема Пифагора утверждает:
с2 = а2 + Ь2,
где с — гипотенуза, а и b — катеты.
Графически это представлено на рис. 17-4.
Рис. 17-4. Векторная диаграмма, показывающая связь активного сопротивления, реактивного индуктивного сопротивления и импеданса в последовательной цепи.
Если импеданс, активное и реактивное сопротивления заменить соответствующими символами, то формула будет выглядеть следующим образом:
Z2 = R2 + X2.
Вернемся к определению импеданса последовательной комбинации резистора 150 ом и индуктивного сопротивления 100 ом.
Дано:
R = 150 Ом; XL = 100 Ом.
Решение:
Z2 = R2 + X2
Z2 =(150)2 + (100)2 = 32500
Z = √(32500) = 180,28 Ом.
Если вместо индуктивного в цепи находится емкостное сопротивление, то линию, представляющую емкостное сопротивление, обычно рисуют направленной вниз. Это показывает, что оно действует в направлении противоположном индуктивному сопротивлению, которое рисуют направленным вверх.
В последовательной цепи с емкостным реактивным сопротивлением формула для вычисления импеданса будет выглядеть следующим образом:
Z2 = R2 + Х2С.
ПРИМЕР: Чему равен импеданс цепи, содержащей резистор сопротивлением 220 ом, соединенный последовательно с конденсатором, имеющим емкостное реактивное сопротивление 270 ом?
Дано:
R = 220 Ом; Xc = 270 Ом.
Решение:
Z2 = R2 + X2c
Z2 = (220)2 + (270)2 = 121300
Z = √(121300) = 348,28 Oм.
Z = 348,28 Ом.
Если последовательная цепь содержит индуктивное и емкостное реактивные сопротивления, а также активное сопротивление, необходимо найти полное реактивное сопротивление (X). Реактивное сопротивление может быть либо индуктивным, либо емкостным. Следовательно, может быть использована одна из следующих формул:
Z2 = R2 + X2L;
Z2 = R2 + Х2с.
17-2. Вопросы
1. Как называется полное противодействие в цепи переменного тока?
2. Какая формула используется для вычисления величины полного противодействия в последовательной цепи?
3. Чему равно значение Z в последовательной цепи переменного тока, где Хс = 3 Ом, XL = 6 Ом, a R = 4 Ом?
17-3 ЗАКОН ОМА
Закон Ома не может быть применен в цепях переменного тока потому, что он не учитывает реактивное сопротивление. Модифицируя закон Ома путем учета импеданса, можно получить общий закон, который применим к цепям переменного тока.
I = E/R преобразуется в I = E/Z
Эта формула применима к переменному току, текущему в любой цепи.
ПРИМЕР: Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 250 ом и емкостное сопротивление 150 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?
Дано:
R = 510 Ом; XL = 250 Ом; Xc = 150 Ом; E = 120 В
Решение:
X = ХL + Хc = 250–150
X = 100 Ом (индуктивное)
Z2 = R2 + X2
Z2 =(510)2 +(100)2
Z = √(270100)
Z = 519,71 Ом
I = E/Z = 120/519,71
I = 0,23 А или 230 мА.
17-3. Вопросы
1. Каким образом модифицируется закон Ома, чтобы его можно было применить к цепям переменного тока для определения напряжения и тока?
2. Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 300 ом и емкостное сопротивление 375 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?
17-4. ЦЕПИ RLC
Материал, изложенный до сих пор, применим ко всем цепям переменного тока. В приведенных примерах рассматривались последовательные цепи. Понятия, рассмотренные в этом параграфе, не содержат нового материала, но используют все принципы, изложенные ранее.
ПРИМЕР: На рис. 17-5 показана последовательная RLC цепь. Необходимо вычислить Хс, XL, X, Z и IT.
Рис. 17-5. Последовательная цепь RLC.
Сначала вычислим Хс, XL и X.
Дано:
f = 60 Гц; С = 470 мкФ; L = 27 мГн.
Решение:
Xc = 1/2πfC
Xc = 1/(6,28)(60)(0,000470)
XC = 5,65 Ом
XL = 2πfL
XL = (6,28)(60)(0,027)
XL = 10,17 Ом
X = XL — Xc = 10,17 — 5,65
X = 4,52 Ом (индуктивное).
Используем значение X для вычисления Z.
Дано:
X = 4,52 Ом; R = 10 Ом.
Решение:
Z2 = R2 + X2
Z2 = (10)2 + (4,52)2 = 120,43
Z = √(120,43) = 10,97 Ом.
Это значение Z может быть использовано для вычисления полного тока (IT).
Дано:
Z = 10,97 Ом; E = 120 В.
Решение:
IT = E/Z = 120/10,97
IT = 10,94 A.
Помните, что во всех частях последовательной цепи течет один и тот же ток.
Если элементы в цепях соединены параллельно, то следует учесть одно главное различие между последовательными и параллельными цепями. При последовательном соединении по всей цепи течет один и тот же ток, а в параллельной цепи к каждой ветви приложено одинаковое напряжение. Вследствие этой разницы полный импеданс параллельной цепи должен вычисляться на основе тока в цепи.
При последовательном соединении по всей цепи течет один и тот же ток, а в параллельной цепи к каждой ветви приложено одинаковое напряжение. Вследствие этой разницы полный импеданс параллельной цепи должен вычисляться на основе тока в цепи.
В последовательной цепи RLC для вычисления реактивного сопротивления и импеданса используются следующие формулы:
X = Хс — XL или X = XL — Хс, Z2 = R2 + X2.
В случае параллельных цепей должны использоваться следующие формулы:
IX = Iс — IL или IX = IL — IX; I2Z = (IR)2 + (IX)2
Импеданс параллельной цепи находится с помощью формулы:
IZ = E/Z
Замечание: Если неизвестно напряжение (Е), приложенное к цепи, то для вычисления Ic, IL, Ix, IR и IZ можно использовать любое значение Е. То же значение напряжения должно использоваться для вычисления импеданса.
То же значение напряжения должно использоваться для вычисления импеданса.
ПРИМЕР: Найти значение Z для цепи, показанной на рис. 17-6.
Рис. 17-6. Параллельная цепь RLC.
Дано:
Е = 120 В; R = 60 Ом; Хс = 75 Ом; XL = 50 Ом.
Решение:
Первым шагом в вычислении Z является вычисление токов отдельных ветвей.
IR = E/R = 120/60 = 2 A
Ix = E/Xc = 120/75 = 1,6 A
IL = E/XL = 120/50 = 2,4 A
Используя значения IR, Ic, IL, вычислим Ix и Iz
IX = IL — Ic = 2,4 – 1,6
Ix = 0,8 А (индуктивный)
I2z = (IR)2 + (Ix)2
I2z = (2)2 + (0,8)2 = 4,64
Iz = √(4,64) = 2,15 A.
Используя значение Iz, вычислим Z.
Iz = E/Z
2,15 = 120/Z
Z = 120/2,15 = 55,8 Ом
В завершение этой главы отметим, что мы рассмотрели все блоки, из которых строятся электрические цепи. При изложении материала использовались ранее изученные понятия и соотношения.
17-4. Вопрос
1. Чем отличаются вычисления импеданса для последовательной цепи переменного тока и для параллельной цепи?
РЕЗЮМЕ
• Конденсатор в цепи переменного тока оказывает противодействие любому изменению напряжения, так же как он это делает в цепи постоянного тока.
• Ток опережает по фазе напряжение на конденсаторе на 90 градусов.
• Противодействие, оказываемое конденсатором переменному току, называется емкостным реактивным сопротивлением. Оно обозначается Хс и вычисляется по формуле:
XC = 1/2πfC
• Катушка индуктивности в цепи переменного тока противодействует любому изменению тока, так же как она это делает в цепи постоянного тока.
• На катушке индуктивности ток отстает по фазе от напряжения на 90 градусов.
• Противодействие, оказываемое катушкой индуктивности переменному току, называется индуктивным реактивным сопротивлением. Оно обозначается XL и вычисляется по формуле
XL = 2πfL.
• Полное реактивное сопротивление последовательной цепи переменного тока определяется формулами X = XC — XL или X = XL — XC.
• Полное реактивное сопротивление последовательной цепи переменного тока является либо емкостным, либо индуктивным, в зависимости от того, какая величина больше, ХC или XL.
• В параллельной цепи реактивное сопротивление определяется с помощью формул
IZ = E/Z
где Iz определяется формулой Iz2 = (IR)2 + (IX)2, а Iх вычисляется по формуле IX = IC — IL или IX = IL — IC.
• Реактивное сопротивление параллельной цепи также может быть емкостным или индуктивным, в зависимости то того, какая величина больше IC или IL.
• Полное сопротивление цепи переменного тока называется импедансом. Он обозначается символом Z. В последовательной цепи Z2 = R2 + X2. В параллельной цепи I2Z = (IR)2 + (IX)2 и
IZ = E/Z
• Получена формула для закона Ома, который можно применять для пеней переменного тока:
I = E/Z
Глава 17. САМОПРОВЕРКА
1. Чему равны значения ХС, XL, X, Z и IT для цепи, изображенной на рис. 17-7?
Рис. 17-7. Последовательная цепь RLC.
2. Чему равны значения IC, IL, IX, IR и IZ для цепи, изображенной на рис. 17-8?
Чему равны значения IC, IL, IX, IR и IZ для цепи, изображенной на рис. 17-8?
Рис. 17-8. Параллельная цепь RLC.
Активное сопротивление в цепи переменного тока: описание, формула
Метод векторных диаграмм
Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.
В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.
Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.
Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.
Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.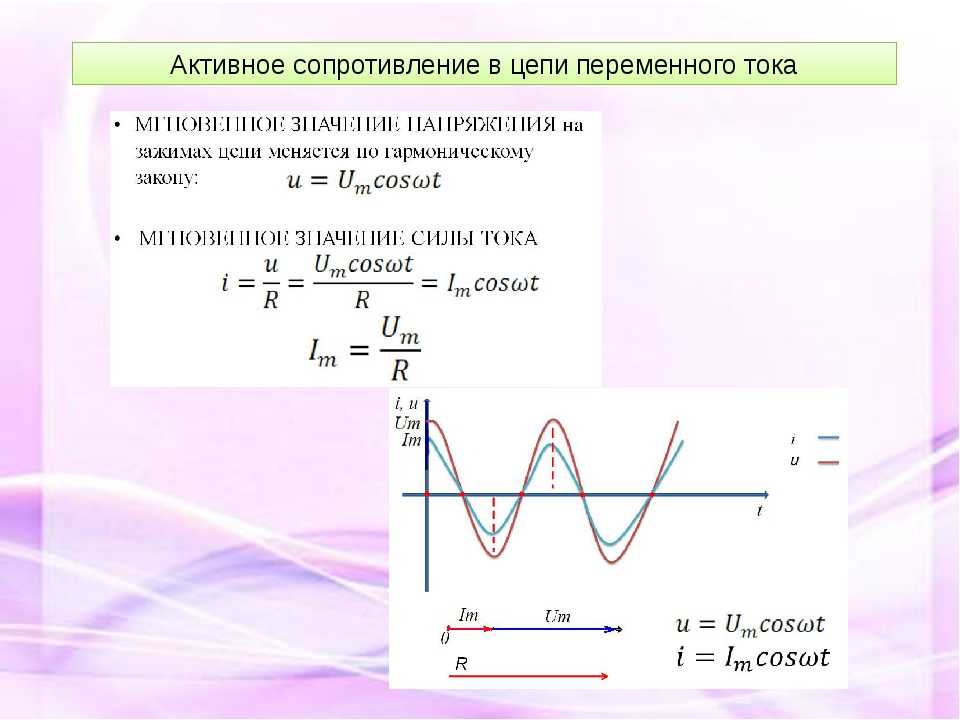
Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.
Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.
Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.
На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.
Векторная диаграмма напряжений представляет собой векторный треугольник напряжений
Последовательное соединение L R.
Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.
Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.
Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,
Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.
Векторная диаграмма строится так.
Треугольник сопротивлений
Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений
Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза. Величина и начальная фаза переменного тока, создаваемого переменным напряжением, зависят не только от величины сопротивлений, образующих электрическую цепь, но и от индуктивности и емкости этой цепи.Активное сопротивление в цепи переменного тока.Строго говоря, любая электрическая цепь обладает, кроме сопротивления, также индуктивностью и емкостью. Если по проводнику проходит ток, то вокруг него возбуждается магнитное поле, т.
Величина и начальная фаза переменного тока, создаваемого переменным напряжением, зависят не только от величины сопротивлений, образующих электрическую цепь, но и от индуктивности и емкости этой цепи.Активное сопротивление в цепи переменного тока.Строго говоря, любая электрическая цепь обладает, кроме сопротивления, также индуктивностью и емкостью. Если по проводнику проходит ток, то вокруг него возбуждается магнитное поле, т.
е. имеют место явления индуктивности. Ток возникает под действием электрического поля на заряды, следовательно, проводник должен обладать емкостью, так как в диэлектрической среде вокруг него возникает поток смещения.Однако в ряде случаев относительная роль двух из трех параметров R, L, С в электрической цепи практически незначительна.
Это позволяет рассматривать подобную цепь как обладающую только сопротивлением, или только индуктивностью, или только емкостью.Мы рассмотрим поочередно условия в трех таких простейших цепях переменного тока.В цепи, содержащей только сопротивление г, синусоидальное напряжени u = Um sin ?t источника электроэнергии создает ток:i = u : r = (Um: r ) sin ?tТак как сопротивление r от времени не зависит, то в этой цепи ток совпадает по фазе с напряжением (рис.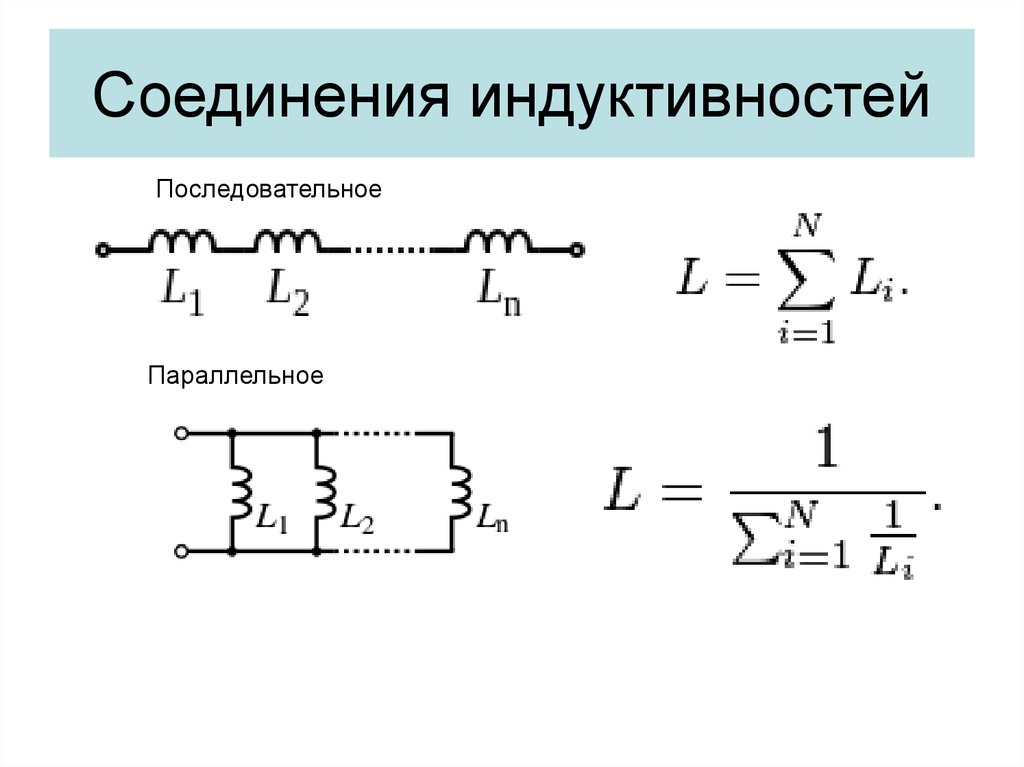 1) и изменяется также синусоидально:i = Imsin ?tздесь:Im= Um: rРисунок 1 Кривые мгновенных значений напряжения и тока в цепи,содержащей только сопротивление r.Разделив последнее выражение на , получим формулу закона Омадля действующих значений напряжения и тока:I = U : rКак видно из формулы, этот закон для цепей переменного тока, содержащих только сопротивление r, имеет такой же вид, как и закон Ома для цепи постоянного тока.В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.).Оно может существенно отличаться от сопротивления rпри постоянном токе.
1) и изменяется также синусоидально:i = Imsin ?tздесь:Im= Um: rРисунок 1 Кривые мгновенных значений напряжения и тока в цепи,содержащей только сопротивление r.Разделив последнее выражение на , получим формулу закона Омадля действующих значений напряжения и тока:I = U : rКак видно из формулы, этот закон для цепей переменного тока, содержащих только сопротивление r, имеет такой же вид, как и закон Ома для цепи постоянного тока.В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.).Оно может существенно отличаться от сопротивления rпри постоянном токе.
Сопротивление для постоянного тока называют омическим, чтобы отличить его от активного сопротивления для переменного тока.Различие между активным и омическим сопротивлениями обуславливается рядом причин. Одна из них – поверхностный эффект, частичное вытеснение переменного тока в поверхностные слои проводника.Чем больше частота переменного тока, тем это вытеснение значительнее.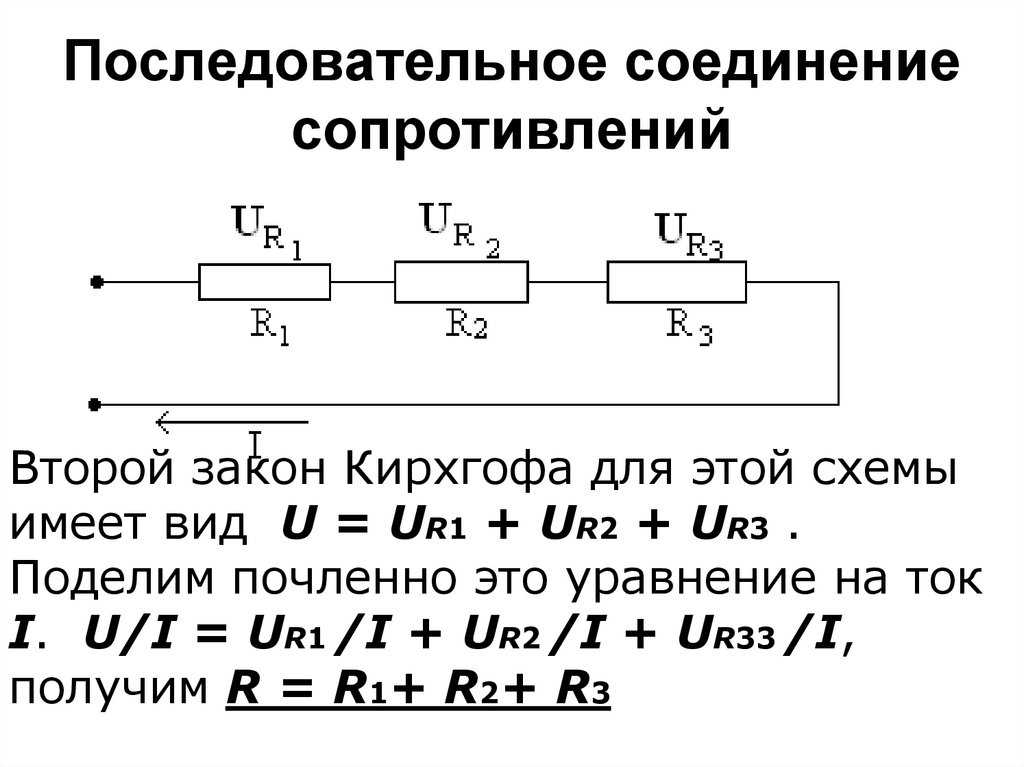 Из-за поверхностного эффекта сопротивлениеrоказывается уже существенно большим, чем вычисленное по формуле:r = ?
Из-за поверхностного эффекта сопротивлениеrоказывается уже существенно большим, чем вычисленное по формуле:r = ?
(l : S)Поверхностный эффект создается тем, что переменное магнитное поле индуктирует во внешних слоях проводника меньшую ЭДС самоиндукции, чем во внутренней его части.Особенно сильно поверхностный эффект увеличивает активное сопротивление стальных проводов. На активное сопротивление медных и алюминиевых проводов при промышленной частоте поверхностный эффект существенно влияет только при больших сечениях проводов (свыше 25 кв. мм).Кроме поверхностного эффекта, большое увеличение активного сопротивления электрической цепи могут вызывать потери энергии в переменном электромагнитном поле цепи от гистерезиса и вихревых токов.Поделитесь полезной статьей:
https://youtube.com/watch?v=NSxgxMNG2fwrel%3D0%26amp%3Bcontrols%3D0%26amp%3Bshowinfo%3D0
- electrosam.ru
- electrono.ru
- electroandi.ru
- fazaa.ru
Основные понятия
Ёмкостное сопротивление — это величина, которая создаётся конденсатором, включённым в цепь. Сопротивление подводящих проводов должно быть непренебрежимо большим. При подаче переменного тока возникают процессы, обусловленные периодическим зарядом и разрядом конденсатора.
Сопротивление подводящих проводов должно быть непренебрежимо большим. При подаче переменного тока возникают процессы, обусловленные периодическим зарядом и разрядом конденсатора.
Период разбивается на четыре четверти. В течение первой четверти напряжение растёт. В этот момент по цепи проходит зарядный ток, сила которого будет уменьшаться, достигнув нуля, когда электродвижущая сила достигнет положительного максимума. Конденсатор полностью заряжен. После этого начнётся спад напряжения. Конденсатор будет разряжаться через подключённую к нему нагрузку. По цепи потечёт ток.
К концу полупериода величина напряжения будет равна нулю, а сила тока будет наибольшей. Разрядка завершена. В начале третьей четверти электродвижущая сила будет возрастать, изменив своё направление. Вновь начнётся процесс заряда. Направление зарядного тока в третью четверть будет таким же, как и в предыдущую. По мере зарядки конденсатора эта величина будет убывать. К концу третьей четверти процесс зарядки будет завершён.
Вновь начнётся процесс заряда. Направление зарядного тока в третью четверть будет таким же, как и в предыдущую. По мере зарядки конденсатора эта величина будет убывать. К концу третьей четверти процесс зарядки будет завершён.
Электродвижущая сила достигнет своего наибольшего отрицательного значения. А на той обкладке, на которой в течение первого полупериода был положительный заряд, теперь будет отрицательный. Во время четвёртой четверти значение электродвижущей силы снова будет стремиться к нулю. Конденсатор будет разряжаться. Соответственно, в цепи появится постепенно нарастающий ток. Процесс повторяется. Таким образом, фаза переменного тока в конденсаторной цепи опережает фазу напряжения на 90 градусов.
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:
Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.
Почему на катушке ток отстает от напряжения?
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.
Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:
Все с точностью наоборот! Можно даже сказать, что катушка — это полная противоположность конденсатору 😉
Ну и напоследок давайте еще побалуемся частотой:
240 Килогерц
34 Килогерца
17 Килогерц
10 Килогерц
Вывод?
С уменьшением частоты сила тока через катушку увеличивается.
Емкостное сопротивление
В цепи, содержащей емкость и источник переменного тока происходят изменения заряда. Такой емкостью обладают конденсаторы, обладающие максимальной энергией при полном заряде. Напряжение емкости создает сопротивление, противодействующее течению переменного тока, которое считается реактивным. В результате взаимодействия, конденсатор и источник тока постоянно обмениваются энергией.
В конструкцию конденсатора входят токопроводящие пластины в количестве двух и более штук, разделенных слоями диэлектрика. Такое разделение не позволяет постоянному току проходить через конденсатор. Переменный ток может проходить через емкостное устройство, отклоняясь при этом от своей первоначальной величины.
Изменения переменного тока происходят под влиянием емкостного сопротивления. Чтобы лучше понять схему работы, найдем и рассмотрим принцип действия данного явления. Переменное напряжение, приложенное к конденсатору, изменяется в форме синусоиды. Под его воздействием на обкладках наблюдается всплеск, одновременно здесь накапливаются заряды электроэнергии с противоположными знаками. Их общее количество ограничено емкостью устройства и его габаритами. Чем выше емкость устройства, тем больше времени требуется на зарядку.
Их общее количество ограничено емкостью устройства и его габаритами. Чем выше емкость устройства, тем больше времени требуется на зарядку.
В момент изменения полупериода колебания, напряжение на обкладках конденсатора меняет свою полярность на противоположное значение, потенциалы также изменяются, а заряды пластин перезаряжаются. За счет этого удается создать течение первичного тока и находить способ противодействовать его прохождению, при уменьшении величины и сдвиге угла. Зарядка обкладок позволяет току, проходящему через конденсатор, опережать напряжение на 90.
Активное сопротивление
И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента – резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.
Индуктивное сопротивление катушки
Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением. Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.
Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.
При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).
Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).
Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.
Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.
Индуктивное сопротивление обозначается буквой XL и измеряется в омах.
Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле
XL=2π• f •L
где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн
Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:
Поэтому приведенная выше формула может быть представлена так:
Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.
Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.
Источник
Индуктивное сопротивление
Реактивное сопротивление подразделяется на два основных вида – индуктивное и емкостное.
При рассмотрении первого варианта следует отметить возникновение в индуктивной обмотке магнитного поля под действием переменного тока. В результате, в ней образуется ЭДС самоиндукции, направленной против движения тока при его росте, и по ходу движения при его уменьшении. Таким образом, при всех изменениях тока и наличии взаимосвязей, ЭДС оказывает на него противоположное действие и приводит к созданию индуктивного сопротивления катушки.
Под влиянием ЭДС самоиндукции энергия магнитного поля обмотки возвращается в электрическую цепь. То есть, между источником питания и обмоткой происходит своеобразный обмен энергией. Это дает основание полагать, что катушка индуктивности обладает реактивным сопротивлением.
В качестве типичного примера можно рассмотреть действие реактивного сопротивления в трансформаторе. Данное устройство имеет общий магнитопровод, с расположенными на нем двумя обмотками или более, имеющими общую зависимость. На одну из них поступает электроэнергия из внешнего источника, а из другой выходит уже трансформированный ток.
Под действием первичного тока, проходящего по катушке, в магнитопроводе и вокруг него происходит наведение магнитного потока. В результате пересечения витков вторичной обмотки, в ней формируется вторичный ток. При невозможности создания идеальной конструкции трансформатора, магнитный поток будет частично уходить в окружающую среду, что приведет к возникновению потерь.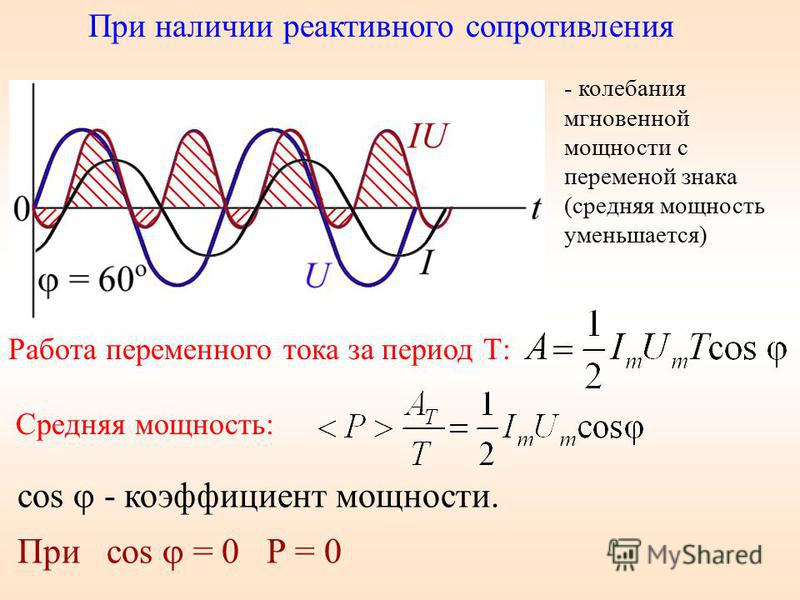 От них зависит величина реактивного сопротивления рассеяния, которая совместно с активной составляющей образуют комплексное сопротивление, называемое электрическим импедансом трансформатора.
От них зависит величина реактивного сопротивления рассеяния, которая совместно с активной составляющей образуют комплексное сопротивление, называемое электрическим импедансом трансформатора.
Применение на практике
Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:
- Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
- Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
- Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.

В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.
Измерение сопротивления конденсаторов.
Емкостное сопротивление
Оно имеет иную природу, чем индуктивное. Это понятие удобно проиллюстрировать на примере электрической цепи, состоящей из источника питания, клеммы которого соединены с обкладками конденсатора. Сразу после подключения на них будет постепенно накапливаться заряд, создавая ток в цепи.
После достижения предельной величины, которая определяется ёмкостью детали, ток не будет проходить по цепи. Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.
Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.
Если к конденсатору подключить источник переменного тока, то будет происходить следующее. С увеличением разности потенциалов заряд на обкладках конденсатора будет расти. Когда напряжение перейдёт в фазу уменьшения, накопленный заряд начнёт стекать с них, образуя ток противоположного направления. Затем разность потенциалов станет отрицательной, но по абсолютной величине будет расти до максимального значения. При этом конденсатор начнет вновь заряжаться, но при этом знак поступающих зарядов будет не такой, который был раньше.
Когда напряжение начнёт увеличиваться (уменьшаясь по абсолютной величине), заряд с обкладок конденсатора будет стекать. Когда разность потенциалов у источника достигнет нуля и продолжит увеличиваться, начнётся новый цикл изменений.
На каждом этапе описанной ситуации ток с обкладок конденсатора будет иметь направление противоположное тому, которое порождается переменной разностью потенциалов источника питания.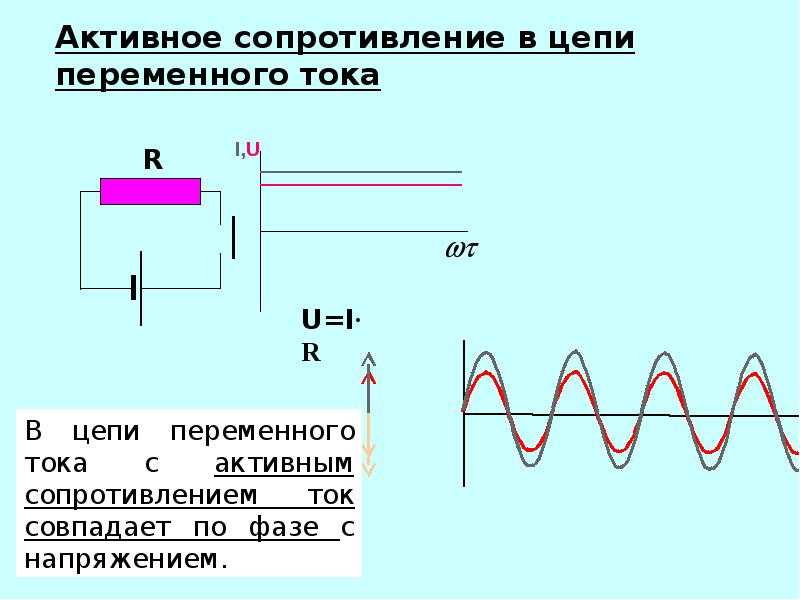
Происходящее таким образом уменьшение силы тока представляет собой физический смысл ёмкостного сопротивления. Оно обозначается буквами ХС и рассчитывается по формуле:
XС = 1/(w×C) = 1/(2π×f×C), где
- C — ёмкость используемого конденсатора;
- w — круговая частота переменного тока;
- π — число «пи»;
- f — частота переменного тока.
В рассматриваемом случае изменения тока отстают от напряжения.
Реактивное сопротивление
При прохождении переменного тока через реактивные элементы возникает реактивноесопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.
Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.
Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки
Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.
Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.
Сопротивление конденсатора можно рассчитать по формуле
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C.
RC цепь
Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU. Здесь U – напряжение источника питания.
Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.
Мощность в цепи с реактивными радиоэлементами
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:
Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π/2.
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность — это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком «плюс», а напряжение со знаком «минус». В итоге плюс на минус дает минус. Получается мощность со знаком «минус». А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:
Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?
С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем «плющить» пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно — это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо — это уже другая история.
В третий промежуток времени t3 и ток и напряжение у нас со знаком «минус». Минус на минус — это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
В результате за весь период у нас суммарное потребление энергии равно чему?
Правильно, нулю!
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
где
RL — это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L — собственно сама индуктивность катушки
С — межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
где
r — сопротивление диэлектрика и корпуса между обкладками
С — собственно сама емкость конденсатора
ESI (ESL) — эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Что надо знать про электрические процессы
Если говорить простым языком, то под сопротивлением принято понимать свойство среды, по которой протекает электрический ток, снижающее его величину.
Так работают провода и изоляторы высоковольтной линии электропередач, показанные на верхней картинке, да и любое вещество.
Изоляторы обладают очень высокими диэлектрическими свойствами, изолируют высоковольтное напряжение, присутствующее на токоведущих шинах от контура земли. Это их основное назначение.
Провода же должны максимально эффективно передавать транслируемые по ним мощности. Их создают так, чтобы они обладали минимальным электрическим сопротивлением, работали с наименьшими потерями энергии на нагрев.
В этом случае передача электричества от источника напряжения к потребителю на любое расстояние будет проходить эффективно.
Приведу для примера картинку из предыдущей моей статьи.
Ее, как и верхнюю, можно представить таким обобщенным видом.
На внешнем участке цепи токоведущие жилы отделены друг от друга воздушной средой и слоем изоляции с высокими диэлектрическими свойствами.
Хорошей проводимостью обладают токоведущие жилы. Подключенный к ним электрический прибор функционирует оптимально.
Как работает резистор
Ток в металлах проходит под действием приложенного напряжения за счет направленного движения электронов. При этом они соударяются, встречаются с положительно и отрицательно заряженными ионами.
Такие столкновения повышают температуру среды, уменьшают силу тока.
За направление электрического тока в электротехнике принято движение заряженных частиц от плюса к минусу. Электроны же движутся от катода к аноду.
Электрическое сопротивление металла зависит от его структуры и геометрических размеров.
Аналогичные процессы протекают в любой другой токопроводящей среде, включая газы или жидкости.
Какие существуют виды сопротивлений
В домашних электрических приборах используется большое разнообразие резисторов с постоянной или регулируемой величиной.
Они ограничивают величину тока всех бытовых устройств, а в наиболее сложных модулях их количество может достигать тысячи или более. Резисторы работают практически во всех схемах.
При использовании в цепях переменного тока они обладают активным сопротивлением, а конденсаторы и дроссели — реактивным.
Причем, на конденсаторах создается емкостное сопротивление, а у дросселей — индуктивное.
Реактивная составляющая на конденсаторах и дросселях сильно зависит от частоты электромагнитного колебания.
2 Шутки электриков о токах через конденсатор и дроссель
Их я привожу потому, что они позволяют запомнить характер прохождения тока через реактивные элементы.
Шутка №1 о емкости
В домашней сети и внутри многих приборов работают переменный и постоянный токи. Они по-разному ведут себя, если встречают на своем пути конденсатор.
Поскольку он состоит из двух токопроводящих пластин, разделенных слоем диэлектрика, то его обозначают на схемах двумя жирными черточками, расположенными параллельно. К их серединам подключены провода, нарисованные перпендикулярными линиями.
К их серединам подключены провода, нарисованные перпендикулярными линиями.
Переменный ток имеет форму гармоничной синусоиды, состоящей из двух симметричных половинок.
Такая гармоника движется от начала координат, встречает на своем пути обкладки, переваливается через них и, скатившись, начинает обгонять приложенное напряжение.
Постоянный ток таким свойством не обладает. Его тупой конец просто упирается в обкладку и останавливается. Пройти через конденсатор он не может. Это для него непреодолимое препятствие.
Шутка №2 о дросселе
Индуктивность выполнена витками изолированного провода. Любой ток проходит по нему. Но синусоида своими волнами путается в витках катушки, начинает отставать от напряжения.
Постоянка же спокойно перемещается внутри провода дросселя без ощущения какого-либо значительного противодействия. Поэтому постоянное напряжение может своим током спалить дроссель, созданный для работы на переменке.
Что же это за зверь: сверхпроводимость
Сто лет назад выявлена способность определенных металлов полностью терять свое сопротивление электрическому току при сверхнизких температурах. Выглядит этот процесс следующим образом.
Выглядит этот процесс следующим образом.
Со сверхпроводниками домашний мастер не работает
Но на верхнюю часть приведенного графика рекомендую обратить внимание: нагрев металла повышает его электрическое сопротивление
При электротехнических расчетах, требующих получения точного результата, необходимо учитывать температурный коэффициент, взятый из справочников.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Цепи RLC
Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.
В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.
Что мы узнали?
Сопротивление, на котором энергия электрического тока выделяется в виде тепла, называется активным. Оно не обладает инерционностью. Ток, протекающий через активное сопротивление, синфазен с напряжением на нем, и его можно найти по закону Ома для действующих значений. Мощность, выделяемая на активном сопротивлении, можно найти по закону Джоуля-Ленца для действующих значений.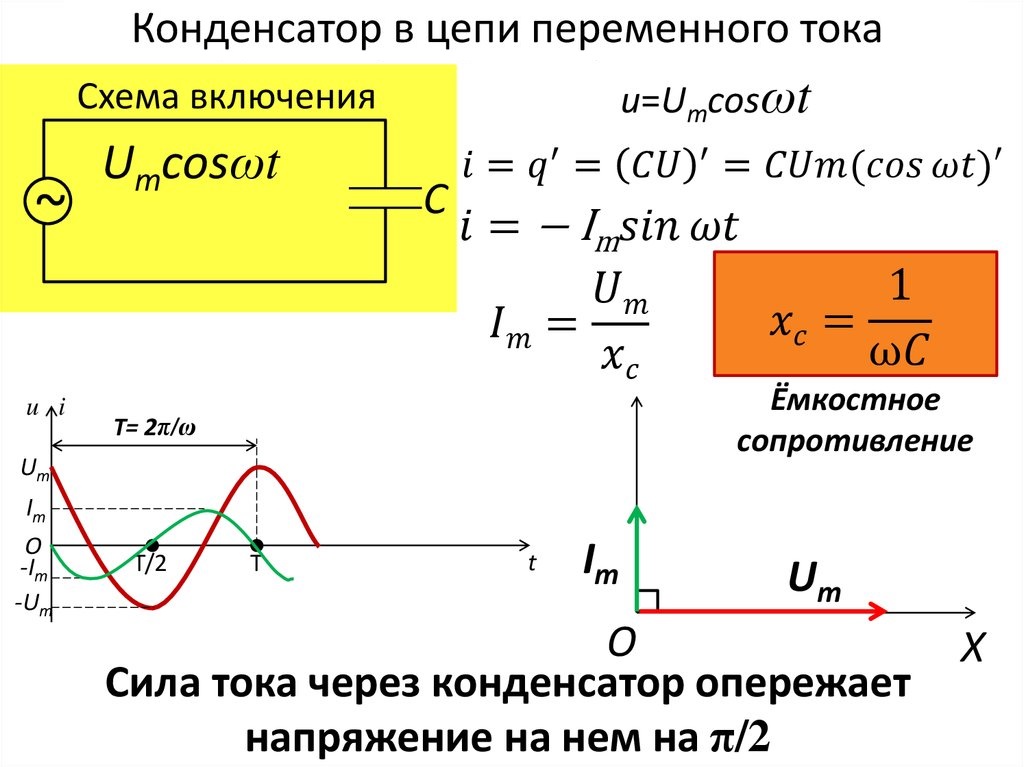
Предыдущая
ФизикаОткрытие электромагнитной индукции кратко и понятно о значении явления магнитного потока и что стало возможным появление (11 класс)
Следующая
ФизикаВиды излучений – кратко таблица характеристики и применения, диапазоны альфа, бета, гамма (11 класс)
|
Random converter |
Калькулятор импеданса катушки индуктивностиКалькулятор определяет импеданс катушки индуктивности для заданной частоты синусоидального сигнала. Определяется также угловая частота. Пример. Рассчитать импеданс катушки индуктивности 10 мкГн на частоте 25 МГц. Входные данные Индуктивность, L генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн) Частота, f герц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц) Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Угловая частота ω= рад/с Индуктивное реактивное сопротивление XL= Ом Введите значения индуктивности и частоты, выберите единицы измерения и нажмите кнопку Рассчитать. Для ввода значения бесконечность наберите inf. Отметим, что величина импеданса идеальной катушки индуктивности равна ее реактивному сопротивлению. Однако это не идентичные величины, так как между током и напряжением в индуктивной цепи существует фазовый сдвиг. Для расчетов используются указанная ниже формула: Здесь XL — реактивное сопротивление катушки в омах (Ом), ZL — импеданс катушки в омах (Ом), ω = 2πf — угловая частота в рад/с, f — частота в герцах (Гц), L — индуктивность в генри (Гн), j — мнимая единица. Для расчета выберите единицы измерения и введите индуктивность и частоту. Импеданс катушки индуктивности будет показан в омах. Катушка индуктивности представляет собой пассивный электрический элемент с двумя выводами, изготовленный, как правило, из изолированного провода в форме спирали, намотанного на магнитный сердечник или на оправку (без сердечника). Магнитный сердечник обычно изготовляется из ферромагнитного металла, например, железа или ферромагнитной керамики (феррита) и используется для усиления магнитного поля и, таким образом, для увеличения индуктивности катушки. Как и конденсаторы, катушки индуктивности используются для накопления и сохранения энергии. Однако, в отличие от конденсаторов, энергия в катушке хранится в форме окружающего ее магнитного поля. Катушки индуктивности применяются, в частности, в фильтрах для сглаживания постоянного тока или для предотвращения передачи высокочастотных помех по кабелям. Катушки индуктивности широко используются в колебательных контурах радиопередатчиков и радиоприемников, а также для изготовления трансформаторов. Высокодобротная катушка индуктивности без сердечника, установленная в радиопередатчике В отличие от конденсаторов, которые препятствуют изменению напряжения, приложенного к их обкладкам, катушки индуктивности препятствуют изменению текущего в них тока. В отличие от конденсаторов, которые не пропускают постоянный ток, катушки индуктивности пропускают его легко. Они препятствуют только прохождению переменного тока или иного изменяющегося тока и их способность препятствовать прохождению тока и называется индуктивностью. Индуктивность обозначается символом L в честь российского физика Эмиля Ленца и измеряется в генри — единицах, названных в честь американского ученого Джозефа Генри. В отличие от резисторов, которые препятствуют прохождению электрического тока вследствие падения напряжения на них, пропорционального протекающему току, катушки индуктивности препятствуют изменению протекающего через них тока. На них создается падение напряжения, прямо пропорциональное скорости изменения тока. График зависимости реактивного сопротивления катушки XL индуктивности и текущего через нее тока I от частоты f для нескольких величин индуктивности показывает прямую пропорциональную зависимость от частоты реактивного сопротивления и обратную зависимость от частоты протекающего через катушку тока Полное сопротивление Z, как и реактивное сопротивление, измеряется в омах (Ом) и состоит из двух частей — действительной и мнимой. Если реальная катушка индуктивности подключена к источнику постоянного напряжения, через нее протекает постоянный ток, ограниченный только сопротивлением провода, из которого намотана катушка. Когда катушка подключается к источнику постоянного напряжения, ток через нее медленно повышается от нуля до максимального значения, которое определяется внутренним сопротивлением источника и внутренним сопротивлением витков катушки. ЭДС самоиндукции, возникающая в катушке, препятствует резкому увеличению тока в ней. Эта ЭДС противодействует приложенному напряжению до тех пор, пока ток не достигнет максимального значения. Если источник постоянного напряжения отключить от катушки, протекающий через нее ток постепенно падает до нуля. В этом случае опять возникает ЭДС самоиндукции, которая снова препятствует, на этот раз, уменьшению тока и которая старается поддержать ток в неизменном состоянии. В конце концов, ток постепенно уменьшается до нуля. В чисто индуктивной цепи ток отстает от напряжения на π/2 радиан или 90°. 1 — в момент отрицательного максимума тока скорость его изменения нулевая и напряжение равно нулю; 2 — ток нулевой, скорость его изменения максимальная и напряжение равно положительному максимуму; 3 — ток положительный и максимальный, скорость его изменения нулевая и напряжение равно нулю; 4 — ток нулевой, скорость его изменения максимальная и напряжение равно отрицательному максимуму Если к катушке индуктивности приложено переменное синусоидальное напряжение, ток отстает от напряжения на некоторый фазовый угол, как показано на графике. В идеальной катушке индуктивности этот угол будет равен точно 90° или четверти цикла. Аналогичное явление можно наблюдать и в природе. Сравните: Солнце светит сильнее всего в астрономический полдень (солнечный свет — напряжение), однако самая жаркая часть дня обычно бывает через несколько часов после полудня (температура — ток). День зимнего солнцестояния в северном полушарии — в конце декабря, однако самые холодные месяцы еще впереди. Именно так ведет себя ток в катушке индуктивности Рассчитанный этим калькулятором импеданс представляет собой меру сопротивления катушки индуктивности протекающему через нее току на определенной частоте. Индуктивное реактивное сопротивление изменяется при изменении частоты приложенного переменного напряжения. Приведенные выше формула и график показывают, что реактивное сопротивление катушки индуктивности XL велико при высоких частотах и мало при низких частотах (конденсаторы ведут себя с точностью до наоборот). Импеданс измеряется в омах, так же, как и сопротивление. Импеданс мешает прохождению электрического тока так же, как и сопротивление, и показывает как сильно катушка противодействует прохождению тока через нее. Но тогда возникает вопрос: в чем же разница между импедансом и сопротивлением? А разница заключается в зависимости импеданса от частоты приложенного сигнала. Сопротивление от частоты не зависит, а импеданс катушек индуктивности от частоты зависит. Этот калькулятор предназначен для расчета импеданса идеальных катушек индуктивности. Реальные катушки всегда имеют сопротивление, которое на эквивалентной схеме изображают включенным последовательно с индуктивностью. Для расчета импеданса реальных катушек индуктивности пользуйтесь калькулятором импеданса RL-цепей. Катушки индуктивности в высокочастотном модуле телевизионного приемника Автор статьи: Анатолий Золотков Примеры расчетовРасчет реактивного сопротивления индуктивности 9,1мкГн на частоте 11 мегагерц Расчет реактивного сопротивления индуктивности 1,5миллигенри на частоте 1,8 килогерц Расчет реактивного сопротивления индуктивности 120миллигенри на частоте 150 килогерц Расчет реактивного сопротивления индуктивности 11мкГн на частоте 13 мегагерц Расчет реактивного сопротивления индуктивности 12миллигенри на частоте 15 килогерц Расчет реактивного сопротивления индуктивности 56миллигенри на частоте 68 килогерц Расчет реактивного сопротивления индуктивности 430микрогенри на частоте 510 мегагерц Расчет реактивного сопротивления индуктивности 33миллигенри на частоте 39 килогерц Расчет реактивного сопротивления индуктивности 160мкГн на частоте 200 мегагерц Расчет реактивного сопротивления индуктивности 51мкГн на частоте 62 мегагерц Вас могут заинтересовать и другие калькуляторы из группы «Электротехнические и радиотехнические калькуляторы»:Калькулятор резистивно-емкостной цепи Калькулятор параллельных сопротивлений Калькулятор параллельных индуктивностей Калькулятор емкости последовательного соединения конденсаторов Калькулятор импеданса конденсатора Калькулятор взаимной индукции Калькулятор взаимоиндукции параллельных индуктивностей Калькулятор взаимной индукции — последовательное соединение индуктивностей Калькулятор импеданса параллельной RC-цепи Калькулятор импеданса параллельной LC-цепи Калькулятор импеданса параллельной RL-цепи Калькулятор импеданса параллельной RLC-цепи Калькулятор импеданса последовательной RC-цепи Калькулятор импеданса последовательной LC-цепи Калькулятор импеданса последовательной RL-цепи Калькулятор импеданса последовательной RLC-цепи Калькулятор аккумуляторных батарей Калькулятор литий-полимерных аккумуляторов для дронов Калькулятор индуктивности однослойной катушки Калькулятор индуктивности плоской спиральной катушки для устройств радиочастотной идентификации (RFID) и ближней бесконтактной связи (NFC) Калькулятор расчета параметров коаксиальных кабелей Калькулятор светодиодов. Калькулятор цветовой маркировки резисторов Калькулятор максимальной дальности действия РЛС Калькулятор зависимости диапазона однозначного определения дальности РЛС от периода следования импульсов Калькулятор радиогоризонта и дальности прямой радиовидимости РЛС Калькулятор радиогоризонта Калькулятор эффективной площади антенны Симметричный вибратор Калькулятор частоты паразитных субгармоник (алиасинга) при дискретизации Калькулятор мощности постоянного тока Калькулятор мощности переменного тока Калькулятор пересчета ВА в ватты Калькулятор мощности трехфазного переменного тока Калькулятор преобразования алгебраической формы комплексного числа в тригонометрическую Калькулятор коэффициента гармонических искажений Калькулятор законов Ома и Джоуля — Ленца Калькулятор времени передачи данных Калькулятор внутреннего сопротивления элемента питания батареи или аккумулятора |
Реактивное сопротивление в электротехнике
Содержание
Реактивное сопротивление катушки индуктивности
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
Формула расчета реактивного сопротивления
В общем случае для деталей катушечного типа применяются выражения:
X = L*w = 2* π*f*L.
Для конденсаторов применяют формулы:
X = 1/(w*C)= 1/(2* π*f*C).
Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.
Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними. Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.
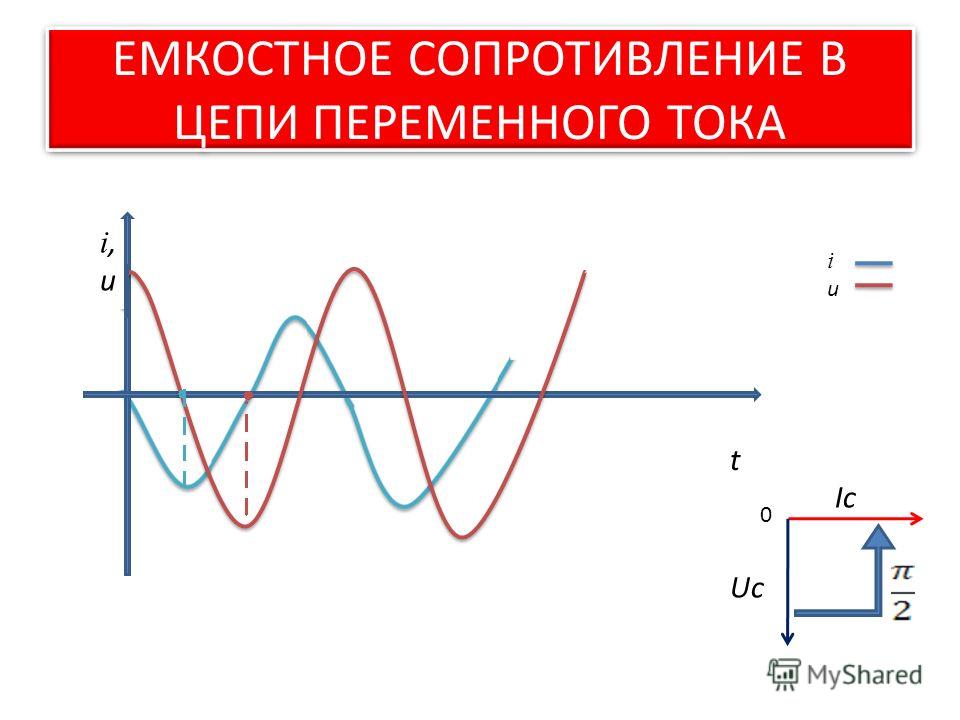
Таблицы максимальных значений емкости конденсаторов.
Действие индуктивного сопротивления кабельных линий
Полное сопротивление электрической цепи разделяется на активное и индуктивное сопротивление. Из них последнее является составной частью реактивного сопротивления, возникающего во время прохождения переменного тока через элементы, относящиеся к реактивным. Индуктивность считается основной характеристикой катушек, не учитывая активное сопротивление их обмоток. Как правило, реактивное сопротивление возникает под влиянием ЭДС самоиндукции. При ее росте, в зависимости от частоты тока, происходит одновременное увеличение сопротивления.
Таким образом, активное и реактивное сопротивление кабелей образуют полное сопротивление, которое есть ни что иное, как сумма квадратов каждой составляющей. Графически это отображается в виде прямоугольного треугольника, в котором гипотенуза является полным сопротивлением, а катеты – его составными элементами.
Очень быстро вычислить активное и индуктивное сопротивление кабелей помогает таблица, в которой отражаются основные характеристики наиболее распространенных проводников. Однако довольно часто требуется определить индуктивное сопротивление Х кабельной линии с определенной протяженностью. Для этого применяется простая первоначальная формула Х = Хl, где Х является индуктивным сопротивлением 1 км проводника, а l – длина этого проводника. Полученный результат измеряется в единицах Ом/км.
Однако довольно часто требуется определить индуктивное сопротивление Х кабельной линии с определенной протяженностью. Для этого применяется простая первоначальная формула Х = Хl, где Х является индуктивным сопротивлением 1 км проводника, а l – длина этого проводника. Полученный результат измеряется в единицах Ом/км.
В свою очередь Х определяется по другой формуле X = 0,145lg * (2Dср/d) + 0,0157 μт, в которой 2Dср является средним расстоянием между проводниками или центрами кабельных жил, d – диаметр этих проводников или жил, μт – отражает относительную магнитную проницаемость металла проводника. Таким образом, при увеличении сечения проводника реактивное сопротивление Х будет незначительно уменьшаться.
Формула индуктивного сопротивления
Активное и реактивное сопротивление
Сопротивление медного провода
Таблица перевода сечения кабеля AWG и GA в дюймы и миллиметры
Активная реактивная и полная мощность
Удельное сопротивление алюминия
Аналогия с электрическим сопротивлением проводника на примере резистора
Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.
Активное сопротивление
Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.
Резисторы – источники активного сопротивления
Реактивное сопротивление
К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.
Индуктивная нагрузка
Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:
R=U/I=0/I=0.
Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.
Катушка индуктивности
Емкостная нагрузка
При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.
Детали, обладающие емкостью
Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.
Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.
Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами
Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.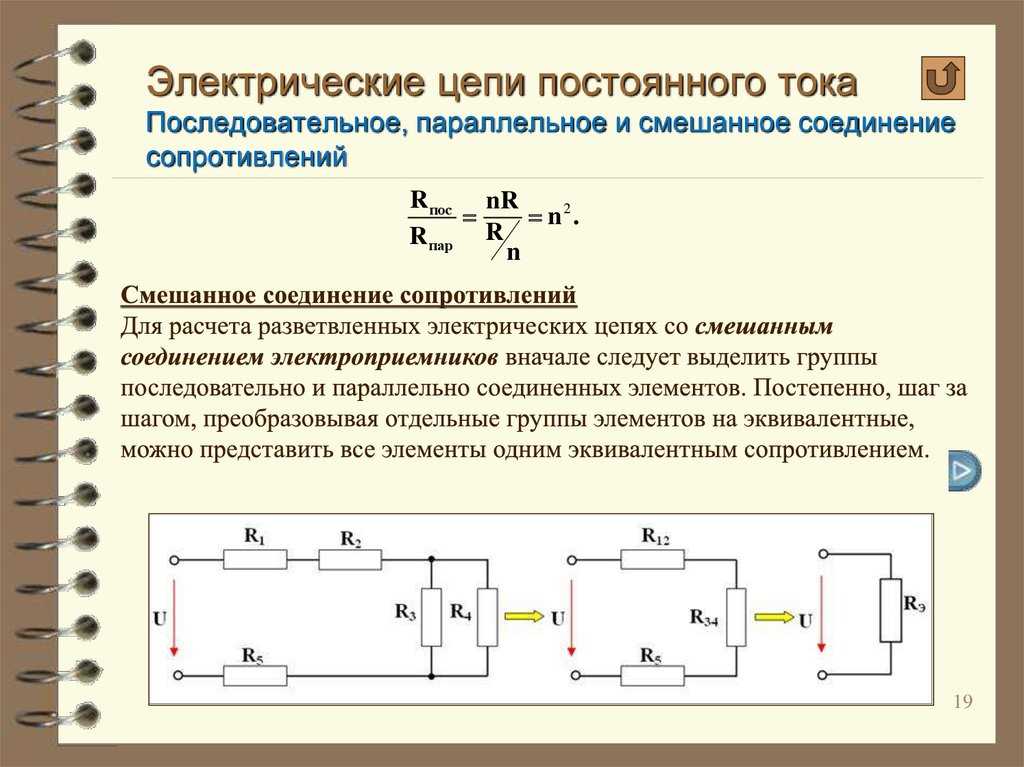
Принцип действия индуктивного сопротивления линий
Именно индуктивность признана главной характеристикой для катушек наряду с аналогичным показателем для их обмоток. R реактивного вида, проявляющееся под действием самоиндукционной ЭДС, растет в прямой пропорции с частотой тока.
Реактивная и активная составляющие обуславливают полное сопротивление, которое можно представить в виде суммы квадратов каждого показателя.
Оперативно справиться с поставленной задачей по расчету номинальных показателей помогут специальные таблицы. В них для самых распространенных проводников приведены все главные характеристики. Но на практике часто требуется узнать Х для участка с конкретной протяженностью. В этом случае главным инструментом является уже приводившееся выражение
Емкостная проводимость
Одним из эксплуатационных показателей остается данный параметр, обозначающий емкость между проводниками и землей, а также аналогичный показатель между самими токопроводниками.
Для его определения в трехфазной линии воздушных передач применяется выражение:
Можно увидеть прямую зависимость рабочей емкости от уменьшения расстояния между кабелями и их сечения. Следовательно, для линий низкого напряжения данная величина всегда будет больше, чем для высокого.
Проводимость подобного вида в воздушных линиях одноцепной конструкции рассчитывается так:Токи емкостного происхождения существенно влияют на работу линий с рабочими характеристиками напряжения лот 110 кВ и более, а также в магистралях уложенными кабелями с идентичными параметрами выше 10 кВ.
Попытка применить именно подобный способ для самостоятельного выполнения будет весьма непростой задачей, ведь в нем применяются и различные конструктивные нюансы типа геометрических характеристик, и диэлектрическая проницаемость изоляционного слоя, и многие другие вводные. Следовательно, оптимальным решением будет информация из таблиц, составленных производителями для конкретной марки кабеля. В каталогах все данные приведены с учетом номинального напряжения для каждой модификации.
Для начала линии, когда мы имеем дело с холостым ходом, емкостный ток определяется так:
Данный показатель будет объективным только при полностью обесточенных приемниках электричества.
Большое значение обозначенная емкость в любой рассматриваемой конструкции имеет для точного выполнения предварительных расчетов для устройств компонентов защиты и элементов заземления.
Для воздушной линии действительна такая формула:
Для кабельных магистралей:
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
Свойства ёмкостей.
Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:
Расчет сопротивления.
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Z = R + i X , где Z – импеданс, R – величина активного сопротивления , X – величина реактивного сопротивления, i – мнимая единица . В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:
- X > 0 – элемент проявляет свойства индуктивности .
- X = 0 – элемент имеет чисто активное сопротивление .
- X
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений.
Индуктивное сопротивление (X L ) обусловлено возникновением ЭДС самоиндукции . Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.
Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.
От чего зависит сопротивление конденсаторов цепей переменного тока
Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.
Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.
Вычисление Xc
Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.
При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.
График, отображающий эту величину конденсатора при непостоянном токе цепи, имеет форму гиперболы
Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.
Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.
При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.
Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку
Его электросопротивляемость является безваттной, реактивной.
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
Импеданс элемента.
Реактивное сопротивление конденсатора
Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.
В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = Uampsin(ωt) запишем выражение мгновенного значения тока следующим образом:
i = UampωCsin(ωt+π/2).
Отсюда выразим соотношение среднеквадратичных значений .
Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:
Реактивное сопротивление конденсатора называют ёмкостным.
Что такое реактивное сопротивление
Согласно известному закону Ома, достаточно приложить к концам электрической цепи различные напряжения, и под таким воздействием по проводникам будет протекать ток, сила которого будет зависеть от сопротивления сердечника.
Катушка
От источников напряжения переменный ток поступает к собранной схеме, повторяя очертания синусоиды. Когда цепь не работает на изменение направления потока электронов, и вектор, согласно фазе, соответствует приложенному напряжению, то на данном участке резистором создается активное чистое сопротивление. Если же отмечаются отличительные черты во вращении векторов, то такое сопротивление именуется реактивным.
Реактивное сопротивление у катушки индуктивности может возникнуть, если присоединить источник переменного напряжения и участок изолированной проволоки. Последняя подключается к генератору и на концы магнитопровода, используемого для улучшения поступления магнитных потоков. При замерах тока в обоих случаях отмечается, что его величина значительно снижена, а по фазе имеется отставание на заданный угол.
Генератор
Важно! Это явление отмечается при возникновении противодействующих индукционных сил, которые проявляются под воздействием закона Ленца
Электрический импеданс
Полное сопротивление цепи переменного тока или импеданс есть отражение трансформирующейся во времени величины тока. В электротехнической литературе обозначается латинской буквой Z. Импеданс является двумерной (векторной) величиной, включающей в себя две независимые скалярные одномерные характеристики: активное и реактивное противодействие переменному электротоку. Проще говоря, полное сопротивление — это активное и реактивное в сумме.
В электротехнической литературе обозначается латинской буквой Z. Импеданс является двумерной (векторной) величиной, включающей в себя две независимые скалярные одномерные характеристики: активное и реактивное противодействие переменному электротоку. Проще говоря, полное сопротивление — это активное и реактивное в сумме.
Активный компонент импеданса, обозначаемый буквой R, является критерием уровня, с которым материал противодействует потоку отрицательно заряженных частиц среди своих атомов. Низкоомными материалами принято считать:
- золото;
- серебро;
- медь.
Высокоомные материалы называют диэлектриками или изоляторами. К перечню таких материалов можно отнести:
- полиэтилен;
- слюду;
- оргстекло.
Вещества с промежуточной степенью противодействия относят к группе полупроводников. В эту группу входят:
- окисды металлов;
- сернистые соединения;
- соединения с селеном;
- химические элементы (мышьяк, германий, фосфор, кремний, сера, теллур, углерод, гален и др.
 ).
).
Полное сопротивление вычисляется по формуле: Z = √ R2 +(XL — XC)2, где: R — активное электросопротивление; XL — индуктивное сопротивление, единица измерения Ом; XC — емкостное противодействие, единица измерения Ом. Полное противодействие рассчитывается пошагово. Вначале рисуют схему, потом вычисляют равнозначные противодействия индивидуально для активного, индуктивного и емкостного компонентов нагрузки и вычисляется полное противодействие электрической цепи.
Характеристики потерь
При подсчете мощностного значения на компоненте цепи всегда принимаются во внимание потери, возникающие в сопротивлениях. Мощностные потери, характерные для активных сопротивлений, связаны с характеристиками проводниковых компонентов и качествами изоляционного покрытия
Реактивные потери в сети связаны с индуктивными противодействиями проводов, а также особенностями задействованных емкостных и катушечных элементов.
Чтобы суметь правильно рассчитать требуемые характеристики элементов сети, нужно знать, на какие составляющие делится сопротивление. Активная компонента связана с необратимым переходом энергии из одной формы в другую.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т
, равновеликого площади, ограниченной кривой р(t)
и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = S p
выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности P m.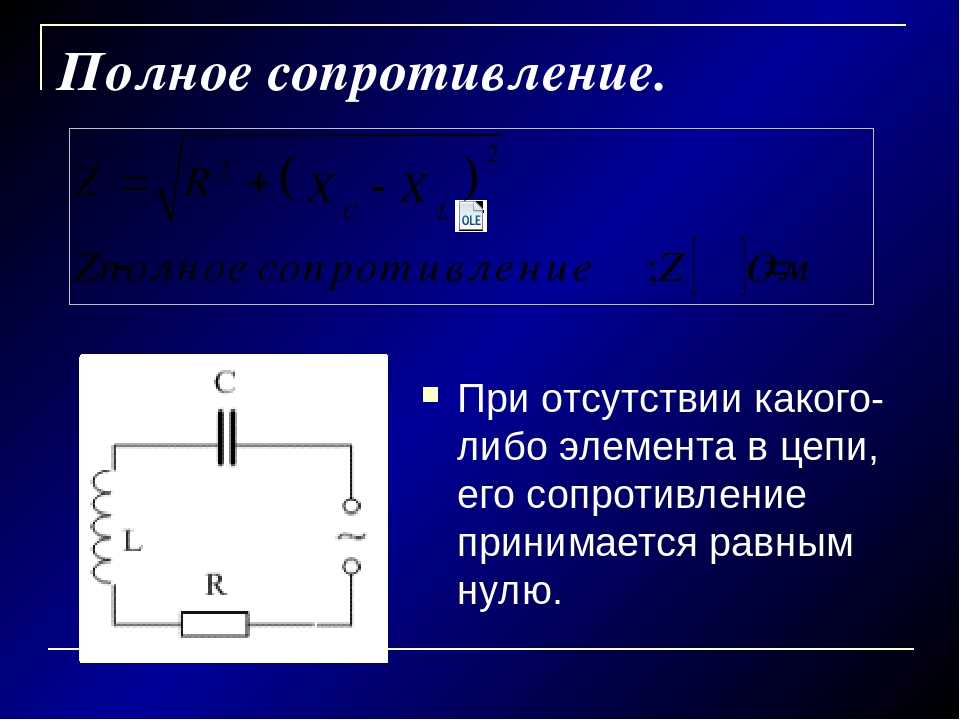
В этом случае часть площади Sp
, находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I 2 R = U 2 R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) .
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным , а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные .
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z
, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Индуктивное сопротивление в цепи переменного тока
Одной из основных характеристик электрических цепей является сопротивление, которое может быть активным и реактивным. Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу.
К реактивному относятся индуктивное и емкостное сопротивления, находящиеся в промежуточных преобразователях электроэнергии – индуктивных катушках и конденсаторах. Эти параметры в обязательном порядке учитываются при выполнении различных расчетов. Например, для определения общего сопротивления участка цепи, складываются активная и реактивная составляющие. Сложение осуществляется геометрическим, то есть, векторным способом, путем построения прямоугольного треугольника. В нем оба катета являются обоими сопротивлениями, а гипотенуза – полным. Длина каждого катета соответствует действующему значению того или иного сопротивления.
В качестве примера можно рассмотреть характер индуктивного сопротивления в простейшей цепи переменного тока. В нее входит источник питания, обладающий ЭДС (Е), резистор, как активная составляющая (R) и катушка, обладающая индуктивностью (L). Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру.
Таким образом, закон Ома для такой цепи переменного тока будет выглядеть в виде формулы: Е + Еси = I x R. Далее с помощью этой же формулы можно определить значение самоиндукции: Еси = -L x Iпр, где Iпр является производной тока от времени. Знак «минус» означает противоположное направление Еси по отношению к изменяющемуся значению тока. Поскольку в цепи переменного тока подобные изменения происходят постоянно, наблюдается существенное противодействие или сопротивление со стороны Еси. При постоянном токе данная зависимость отсутствует и все попытки подключения катушки в такую цепь привели бы к обычному короткому замыканию.
Для преодоления ЭДС самоиндукции, на выводах катушки источником питания должна создаваться такая разность потенциалов, чтобы она могла хотя-бы минимально компенсировать сопротивление Еси (Uкат = -Еси). Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности. В результате, между током и напряжением происходит смещение фаз.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.
а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
откуда:
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
Помогла ли вам статья?
Задать вопрос
Пишите ваши рекомендации и задавайте вопросы в комментариях
1.5: Реактивное сопротивление и импеданс — технические библиотеки LibreTexts
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 25164
- Джеймс М. Фиоре
- Муниципальный колледж Mohawk Valley
В отличие от резистора, у идеального конденсатора или идеальной катушки индуктивности напряжение и ток не совпадают по фазе. Для конденсатора ток опережает напряжение на конденсаторе на 90 градусов. Напомним, что напряжение на конденсаторе не может измениться мгновенно, \(i = C\, dv/dt\). Для катушки индуктивности напряжение опережает ток на 90 градусов. Точно так же ток через индуктор не может измениться мгновенно из-за \(v = L\, di/dt\). Хотя идеальные конденсаторы и катушки индуктивности не обладают сопротивлением, напряжение реагирует на ток. Неудивительно, что мы называем эту характеристику реактивным сопротивлением и обозначаем ее буквой \(X\). Реактивное сопротивление, как и сопротивление, представляет собой отношение напряжения к току. Мы определяем емкостное сопротивление как: 9{\circ}\), или, что более удобно, мы просто добавляем \(−j\), как в \(X_C = −j75 \Omega\).
Для катушки индуктивности напряжение опережает ток на 90 градусов. Точно так же ток через индуктор не может измениться мгновенно из-за \(v = L\, di/dt\). Хотя идеальные конденсаторы и катушки индуктивности не обладают сопротивлением, напряжение реагирует на ток. Неудивительно, что мы называем эту характеристику реактивным сопротивлением и обозначаем ее буквой \(X\). Реактивное сопротивление, как и сопротивление, представляет собой отношение напряжения к току. Мы определяем емкостное сопротивление как: 9{\circ}\), или, что более удобно, мы просто добавляем \(−j\), как в \(X_C = −j75 \Omega\).
Случай с индуктором аналогичен и оставлен в качестве упражнения. Индуктивное сопротивление \(X_L\) можно найти, используя:
\[X_L=+ j 2 \pi f L \label{1.9} \]
Примером может быть \(X_L = j68 \Omega\). Как уже говорилось, хотя сопротивление нельзя добавлять непосредственно к реактивному сопротивлению, реактивные сопротивления можно суммировать, если мы обращаем внимание на знаки. Например, если у нас есть последовательное емкостное сопротивление \(−j60 \Omega\) с индуктивным сопротивлением \(j100 \Omega\), результатом будет \(j40 \Omega\). Это связано с тем, что эти два элемента не совпадают по фазе на 180 градусов друг с другом, и поэтому они частично компенсируются. Помните, всегда добавляйте или вычитайте одинаковые элементы: реальный (сопротивление) к реальному и воображаемый (реактивный) к воображаемому.
Например, если у нас есть последовательное емкостное сопротивление \(−j60 \Omega\) с индуктивным сопротивлением \(j100 \Omega\), результатом будет \(j40 \Omega\). Это связано с тем, что эти два элемента не совпадают по фазе на 180 градусов друг с другом, и поэтому они частично компенсируются. Помните, всегда добавляйте или вычитайте одинаковые элементы: реальный (сопротивление) к реальному и воображаемый (реактивный) к воображаемому.
Уравнения \ref{1.8} и \ref{1.9} примечательны тем, что реактивное сопротивление является не только функцией емкости или индуктивности, но также функцией частоты. Реактивное сопротивление катушки индуктивности прямо пропорционально частоте, а реактивное сопротивление конденсатора обратно пропорционально частоте. На рисунке \(\PageIndex{1}\) показаны омические изменения резистора \(20 \Омега\), конденсатора 500 \(\мкФ\) и катушки индуктивности 500 \(\мкФ\)Гн. .
Мы видим, что значение сопротивления не меняется с частотой, в то время как индуктивное сопротивление увеличивается с частотой, а емкостное сопротивление уменьшается.
Из-за линейной шкалы частоты изменение конденсатора трудно увидеть. Если снова нанести это на график, но с использованием логарифмической шкалы частот, как показано на рисунке \(\PageIndex{2}\), симметрия станет очевидной.
Рисунок \(\PageIndex{2}\): Сопротивление и реактивное сопротивление в зависимости от частоты (логарифмическая ось).Влияние размера конденсатора и частоты показано на рисунке \(\PageIndex{3}\) с использованием логарифмической оси частоты: чем меньше конденсатор, тем больше емкостное сопротивление на любой конкретной частоте.
Рисунок \(\PageIndex{3}\): Изменение емкостного сопротивления в зависимости от емкости и частоты. Точно так же влияние размера катушки индуктивности и частоты показано на рисунке \(\PageIndex{4}\) с использованием линейной оси частот: чем больше катушка индуктивности, тем больше индуктивное сопротивление при любой заданной частоте.
Следует отметить, что графики на рисунках \(\PageIndex{3}\) и \(\PageIndex{4}\) относятся к идеальным компонентам. В действительности, все компоненты обладают некоторыми резистивными, емкостными и индуктивными эффектами из-за своей конструкции. Например, в конечном итоге индуктивные и резистивные эффекты приведут к тому, что кривые емкостного сопротивления на рисунке \(\PageIndex{3}\) начнут расти на высоких частотах. Точно так же резистивные и емкостные эффекты заставят кривые Рисунок \(\PageIndex{4}\) сгладиться на очень низких и очень высоких частотах.
Следует помнить интересное наблюдение: конденсаторы и катушки индуктивности немного похожи на химер. То есть они выглядят как разные вещи для разных источников, все смешанные вместе одновременно. Было бы неправильным думать, скажем, о конкретной катушке индуктивности как о «столько-то омах». Если исходный сигнал состоит из нескольких синусоидальных волн, таких как прямоугольная волна или музыкальная волна, катушка индуктивности «выглядит» как разное омическое значение для каждой из различных частотных составляющих одновременно.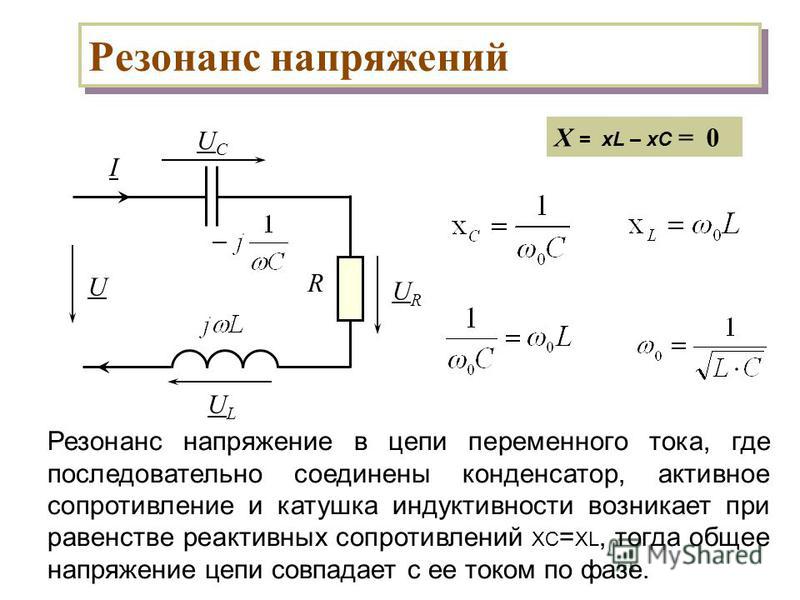 Это важная концепция, которую мы можем использовать, например, при разработке схем фильтров. 9{\circ} \Omega\), т. е. величина 600 Ом, которая включает сопротивление и индуктивное сопротивление (это должно быть индуктивное, а не емкостное сопротивление, поскольку знак угла положительный).
Это важная концепция, которую мы можем использовать, например, при разработке схем фильтров. 9{\circ} \Omega\), т. е. величина 600 Ом, которая включает сопротивление и индуктивное сопротивление (это должно быть индуктивное, а не емкостное сопротивление, поскольку знак угла положительный).
Чтобы завершить эту систему, у нас есть восприимчивость и проводимость. Восприимчивость, \(S\), является обратной величиной реактивного сопротивления. Адмиттанс \(Y\) является обратной величиной импеданса. Они аналогичны соотношению между проводимостью и сопротивлением и удобны для комбинаций параллельных цепей.
Пример \(\PageIndex{1}\)
Определите реактивные сопротивления катушки индуктивности 1 мГн и конденсатора 2 \(\мкФ) синусоидальной волне 2 кГц. Повторите для частоты 50 кГц.
Используйте уравнения \ref{1.8} и \ref{1.9}. Для конденсатора на 2 кГц имеем:
\[X_C =− j \frac{1}{2\pi f C} \nonumber \]
\[X_C = − j \frac{1}{2 \pi 1kHz 2 \mu F} \nonnumber \]
\[X_C =− j 79. 6\Omega \nonnumber \]
6\Omega \nonnumber \]
Для второго источника 50 кГц в 25 раз больше исходного, а емкостное сопротивление обратно пропорционально частоте. Следовательно, \(X_C\) в 25 раз меньше, или \(−j3,18 \Omega\).
Для катушки индуктивности на 2 кГц,
\[X_L = +j 2\pi f L \без номера \]
\[X_L = +j 2\pi 2 кГц 1 мГн \без номера \]
\[X L = +j 12.57\Omega \nonnumber \]
Индуктивное сопротивление прямо пропорционально частоте. Таким образом, увеличение f в 25 раз увеличивает \(X_L\) во столько же раз, что дает \(j314.2 \Omega\).
Пример \(\PageIndex{2}\)
Определите реактивную проводимость катушки индуктивности, реактивное сопротивление которой равно \(j400 \Омега\). Далее, если эту катушку индуктивности поставить последовательно с резистором \(1000 Ом\), определить результирующий импеданс в полярной форме, а также адмиттанс. 9{\circ} \mu S\).
Эта страница под названием 1.5: Reactance and Impedance распространяется в соответствии с лицензией CC BY-NC-SA 4. 0 и была создана, изменена и/или курирована Джеймсом М. Фиоре посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована Джеймсом М. Фиоре посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Автор
- Джеймс М. Фиоре
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
-
- Теги
-
- source@http://www.
 dissidents.com/resources/ACElectricalCircuitAnalysis.pdf
dissidents.com/resources/ACElectricalCircuitAnalysis.pdf
- source@http://www.
Электрическое реактивное сопротивление | Единицы измерения Wiki
в: Термины электроники, Физические величины, Измеряемые величины
| На этой странице используется контент из английской Википедии . Оригинальная статья была на Электрическом реактивном сопротивлении. Список авторов можно увидеть в история страниц . Как и в случае с Вики по единицам измерения, текст Википедии доступен по лицензии Creative Commons, см. Викия:Лицензирование. |
В электрических и электронных системах реактивное сопротивление — это сопротивление элемента цепи изменению электрического тока или напряжения из-за индуктивности или емкости этого элемента. Накопленное электрическое поле сопротивляется изменению напряжения на элементе, а магнитное поле сопротивляется изменению тока. Понятие реактивного сопротивления похоже на электрическое сопротивление, но они отличаются в нескольких отношениях.
Понятие реактивного сопротивления похоже на электрическое сопротивление, но они отличаются в нескольких отношениях.
Емкость и индуктивность являются неотъемлемыми свойствами элемента, как и сопротивление; их реактивное действие проявляется не при постоянном постоянном токе, а только при изменении условий в цепи. Таким образом, реактивное сопротивление зависит от скорости изменения и является постоянным только для цепей с переменным током постоянной частоты. При векторном анализе электрических цепей сопротивление представляет собой действительную часть комплексного импеданса, а реактивное сопротивление — мнимую часть. Оба используют одну и ту же единицу СИ, ом.
Идеальный резистор имеет нулевое реактивное сопротивление, тогда как идеальные катушки индуктивности и конденсаторы полностью состоят из реактивного сопротивления.
Содержимое
- 1 Анализ
- 2 Емкостное реактивное сопротивление
- 3 Индуктивное реактивное сопротивление
- 4-фазное соотношение
- 5 См.
 также
также - 6 Каталожные номера
- 7 Внешние ссылки
Analysis[]
В векторном анализе реактивное сопротивление используется для вычисления изменений амплитуды и фазы синусоидального переменного тока, проходящего через элемент цепи. Он обозначается символом .
Для расчета импеданса необходимы как реактивное сопротивление, так и сопротивление. В некоторых схемах один из них может доминировать, но приблизительное знание второстепенного компонента полезно, чтобы определить, можно ли им пренебречь.
- где
- — импеданс, измеренный в омах.
- — сопротивление, измеряемое в омах.
- — реактивное сопротивление , измеряемое в омах.
Как величина, так и фаза импеданса зависят как от сопротивления, так и от реактивного сопротивления.
- где комплексное сопряжение
Величина представляет собой отношение амплитуд напряжения и тока, а фаза представляет собой разность фаз напряжение-ток.
- Если , реактивное сопротивление называется индуктивным
- Если , то импеданс чисто резистивный
- Если , реактивное сопротивление называется емкостным
Емкостное реактивное сопротивление[]
- Основная статья: Емкость
Емкостное реактивное сопротивление является сопротивлением изменению напряжения на элементе. Емкостное реактивное сопротивление обратно пропорционально частоте сигнала (или угловой частоте ω) и емкости . [1]
Конденсатор состоит из двух проводников, разделенных изолятором, также известным как диэлектрик.
На низких частотах конденсатор имеет разомкнутую цепь, так как ток в диэлектрике отсутствует. Напряжение постоянного тока, приложенное к конденсатору, вызывает накопление положительного заряда на одной стороне и отрицательного заряда на другой стороне; электрическое поле из-за накопленного заряда является источником противодействия току. Когда потенциал, связанный с зарядом, точно уравновешивает приложенное напряжение, ток становится равным нулю.
Когда потенциал, связанный с зарядом, точно уравновешивает приложенное напряжение, ток становится равным нулю.
При питании от сети переменного тока конденсатор накапливает лишь ограниченное количество заряда, прежде чем разность потенциалов изменит полярность и заряд рассеется. Чем выше частота, тем меньше будет накапливаться заряд и тем меньше сопротивление току.
Индуктивное сопротивление[]
- Основная статья: Индуктивность
Индуктивное сопротивление — это сопротивление изменению тока на элементе. Индуктивное сопротивление пропорционально частоте сигнала и индуктивности.
Катушка индуктивности состоит из спирального проводника. Закон электромагнитной индукции Фарадея дает противоЭДС (напряжение, противодействующее току) из-за скорости изменения плотности магнитного потока через петлю с током.
Для индуктора, состоящего из катушки с петлями, это дает.
ПротивоЭДС является источником противодействия току. Постоянный постоянный ток имеет нулевую скорость изменения и рассматривает катушку индуктивности как короткое замыкание (обычно она изготавливается из материала с низким удельным сопротивлением). Переменный ток имеет усредненную по времени скорость изменения, пропорциональную частоте, что вызывает увеличение индуктивного сопротивления с частотой.
Постоянный постоянный ток имеет нулевую скорость изменения и рассматривает катушку индуктивности как короткое замыкание (обычно она изготавливается из материала с низким удельным сопротивлением). Переменный ток имеет усредненную по времени скорость изменения, пропорциональную частоте, что вызывает увеличение индуктивного сопротивления с частотой.
Соотношение фаз[]
Фаза напряжения на чисто реактивном устройстве (устройстве с нулевым сопротивлением) отстает от тока в радианах для емкостного реактивного сопротивления и опережает тока в радианах для индуктивного сопротивления . Обратите внимание, что без знания как сопротивления, так и реактивного сопротивления невозможно определить соотношение между напряжением и током.
Разные знаки емкостного и индуктивного сопротивления обусловлены фазовым коэффициентом импеданса.
Для реактивного компонента синусоидальное напряжение на компоненте находится в квадратуре (разность фаз) с синусоидальным током через компонент. Компонент попеременно поглощает энергию из цепи, а затем возвращает энергию в цепь, поэтому чистое реактивное сопротивление не рассеивает мощность.
Компонент попеременно поглощает энергию из цепи, а затем возвращает энергию в цепь, поэтому чистое реактивное сопротивление не рассеивает мощность.
См. также[]
- Электрические измерения
- Восприимчивость
- Магнитное реактивное сопротивление
Ссылки[]
- Pohl R. W. Elektrizitätslehre. — Берлин-Геттинген-Гейдельберг: Springer-Verlag, 1960.
- Попов В. П. Основы теории цепей. – М.: Высшая школа, 1985, 496 с. (На русском).
- Küpfmüller K. Einführung in die theoretische Elektrotechnik, Springer-Verlag, 1959.
- Янг, Хью Д.; Роджер А. Фридман и А. Льюис Форд (2004) [1949]. Sears and Zemansky’s University Physics (11-е изд.). Сан-Франциско: Аддисон Уэсли. ISBN 0-8053-9179-7.
- ↑ Ирвин, Д. (2002). Базовый анализ инженерных цепей , стр. 274. Нью-Йорк: John Wiley & Sons, Inc.
Внешние ссылки[]
- Интерактивное руководство по Java по индуктивному реактивному сопротивлению Национальная лаборатория сильного магнитного поля
- Индуктивное сопротивление: бесконечные примеры и упражнения
Контент сообщества доступен по лицензии CC-BY-SA, если не указано иное.
Емкостное реактивное сопротивление » Примечания по электронике
Емкостное реактивное сопротивление является мерой того, как конденсатор ограничивает протекание переменного тока, хотя и похоже на сопротивление, но не то же самое.
Емкость Учебное пособие Включает:
Емкость
Формулы конденсаторов
Емкостное реактивное сопротивление
Параллельные и последовательные конденсаторы
Диэлектрическая проницаемость и относительная диэлектрическая проницаемость
Коэффициент рассеяния, тангенс угла потерь, ESR
Таблица преобразования конденсаторов
Мы знакомы с тем, как резисторы ограничивают поток электрического заряда из-за своего сопротивления и закона Ома, но конденсаторы также могут препятствовать потоку электрического заряда с переменным током из-за своего реактивного сопротивления.
Важно знать, какое влияние окажет конденсатор на любую цепь, в которой он работает. Он не только предотвращает прохождение составляющей постоянного тока сигнала, но также влияет на любой переменный сигнал, который может появиться.
Возможность расчета уровня реактивного сопротивления важна, поскольку конденсаторы используются во многих электрических и электронных схемах. Также очень важно знать, как это реактивное сопротивление влияет на протекание тока с другими электронными компонентами.
Что такое емкостное сопротивление
В цепи постоянного тока, где могут быть батарея и резистор, именно резистор сопротивляется протеканию тока в цепи. Это основной закон Ома. То же самое справедливо и для цепи переменного тока с конденсатором.
Конденсатор с малой площадью пластины сможет хранить только небольшое количество заряда, и это будет препятствовать протеканию тока. Конденсатор большего размера позволит увеличить ток.
Принимая во внимание различные уровни накопления заряда, можно видеть, что если может быть сохранен только небольшой уровень заряда, это будет представлять более высокий уровень ограничения тока, который может проходить через конденсатор, чем тот, который может накапливать гораздо больше заряда.
«Ограничение» тока, который может проходить через конденсатор, называется реактивным сопротивлением конденсатора.
Реактивное сопротивление конденсатора отличается от сопротивления резистора, но тем не менее измеряется оно точно так же в Омах. Реактивное сопротивление конденсатора зависит от номинала конденсатора, а также от рабочей частоты. Чем выше частота, тем меньше реактивное сопротивление.
Установлено, что чем выше частота, тем ниже реактивное сопротивление, и для конденсатора заданного номинала видна кривая, подобная показанной ниже.
Емкостное сопротивление в зависимости от частотыРасчет реактивного сопротивления конденсатора
Можно представить, что чем больше конденсатор, тем больше заряда он может хранить и, следовательно, тем меньше он будет ограничивать протекание тока.
Большое влияние также оказывает частота изменения тока. Если частота выше, это означает большее изменение накопленного заряда и, следовательно, ограничение по току, т.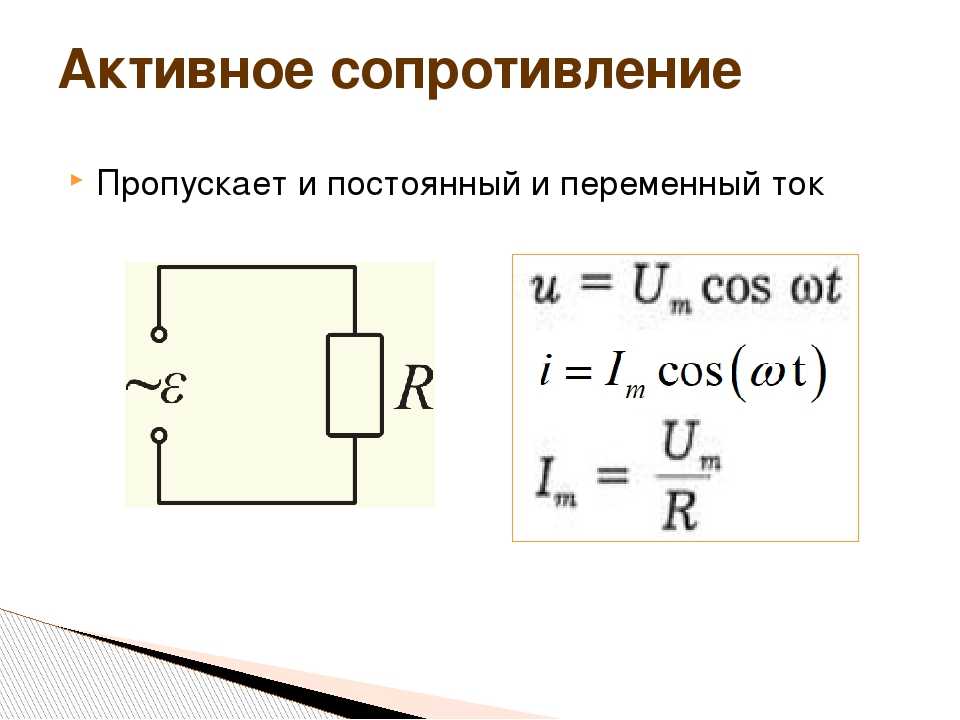 е. реактивное сопротивление меньше.
е. реактивное сопротивление меньше.
Основное уравнение реактивного сопротивления конденсатора:
Xc= 1ωC
Где
X c — емкостное реактивное сопротивление в Омах
ω — угловая скорость в радианах в секунду
C — емкостное сопротивление в фарадах
Однако обычно гораздо полезнее рассчитывать реактивное сопротивление, зная частоту. Частота в циклах в секунду или герцах используется как единица гораздо шире, чем угловая скорость.
Xc= 12πfC
Где
X c — емкостное сопротивление в омах
f — частота в герцах
C — емкостное сопротивление в фарадах
В качестве примера можно рассчитать реактивное сопротивление конденсатора емкостью 1 мкФ на частоте 1 кГц.
Непосредственная подстановка в уравнение и использование 2 π вместо 6, что является достаточно точным приближением для большинства расчетов.
Xc= 12π10310-6
Это упрощает, чтобы дать:
Xc= 166 Ом
Таким образом, можно увидеть, что очень легко вычислить реактивное сопротивление конденсатора. Главное, на что следует обратить внимание, это то, что все частоты и емкости измеряются в Гц и фарадах. Отслеживание нулей или степени десяти множителей на рисунках является ключом к получению правильного ответа.
Главное, на что следует обратить внимание, это то, что все частоты и емкости измеряются в Гц и фарадах. Отслеживание нулей или степени десяти множителей на рисунках является ключом к получению правильного ответа.
Текущие расчеты
На следующем этапе нужно посмотреть, как можно рассчитать ток, например, для конденсатора, подобного приведенному выше.
Если единственным присутствующим компонентом является конденсатор, то необходимо просто применить закон Ома и рассчитать напряжение или ток и т. д., зная две другие переменные. Также возможно рассчитать реактивное сопротивление, зная напряжение и ток.
В=I Xc
Это просто вопрос замены «R» в уравнении закона Ома на X c .
Можно также использовать треугольники закона Ома для вычисления значений неизвестной переменной.
Можно видеть, что сопротивление R, обычно наблюдаемое в уравнении закона Ома и треугольнике закона Ома, просто заменено емкостным сопротивлением X c .
Добавление сопротивления и реактивного сопротивления
Хотя сопротивление и реактивное сопротивление очень похожи, и их значения измеряются в Омах, они не совсем одинаковы. Ток и напряжение 90 ° не совпадают по фазе, а для резистора они совпадают по фазе.
В результате невозможно напрямую сложить сопротивление резистора и реактивное сопротивление конденсатора.
Вместо этого они должны суммироваться «векторно». Другими словами, необходимо возвести каждое значение в квадрат, а затем сложить их вместе и извлечь квадратный корень из этой цифры. Укажите в более математическом формате:
.Xtotal2 = Xc2+R2
Для удобства вычислений это можно выразить так:
Xtotal = Xc2+R2
Сложив таким образом две величины, можно рассчитать полное сопротивление комбинации резистора и конденсатора.
Также можно использовать закон Ома для расчета тока, напряжения и т. д. обычным способом.
Емкостное реактивное сопротивление является ключевой величиной во всех формах электрических электронных цепей. Поскольку конденсаторы используются практически во всех электронных устройствах, понимание того, как рассчитать реактивное сопротивление и как оно взаимодействует с резисторами и другими электронными компонентами, является ключевым элементом для многих электронных схем. Несмотря на то, что расчеты относительно просты, они очень важны во многих областях.
Другие основные понятия и руководства по электронике:
Напряжение
Текущий
Сила
Сопротивление
Емкость
Индуктивность
Трансформеры
Децибел, дБ
Законы Кирхгофа
Q, добротность
РЧ-шум
Сигналы
Вернуться в меню основных понятий электроники . . .
23.11 Реактивное, индуктивное и емкостное сопротивление – College Physics: OpenStax
Глава 23 Электромагнитная индукция, цепи переменного тока и электрические технологии
Резюме
- Зарисовка зависимости напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.

- Рассчитать индуктивное и емкостное сопротивление.
- Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.
Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.
Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис. 1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.
Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.
(б) График тока и напряжения на катушке индуктивности в зависимости от времени. График на рис. 2(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика 90 561 после 90 562 управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом: 9{\circ}}[/latex] фазовый угол.
Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует обратную ЭДС [латекс]\boldsymbol{V= -L(\Delta I/ \Delta t)}[/latex]. Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока [латекс]\boldsymbol{I}[/латекс] через катушку индуктивности [латекс]\жирный символ{L}[/латекс] определяется версией закона Ома:
Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока [латекс]\boldsymbol{I}[/латекс] через катушку индуктивности [латекс]\жирный символ{L}[/латекс] определяется версией закона Ома:
[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_L}},[/латекс]
, где [latex]\boldsymbol{V}[/latex] — среднеквадратичное напряжение на катушке индуктивности, а [latex]\boldsymbol{X_L}[/latex] определяется как
.[латекс]\boldsymbol{X_L = 2 \pi fL},[/латекс]
с [latex]\boldsymbol{f}[/latex] частотой источника переменного напряжения в герцах (анализ цепи с использованием правила цикла Кирхгофа и исчисления фактически дает это выражение). [latex]\boldsymbol{X_L}[/latex] называется индуктивным реактивным сопротивлением, потому что индуктор препятствует протеканию тока. [latex]\boldsymbol{X_L}[/latex] имеет единицы измерения в омах ([latex]\boldsymbol{1 \;\textbf{H}=1 \;\Omega \cdot \;\textbf{s}}[/latex ], так что частота, умноженная на индуктивность, имеет единицы измерения (циклы/с)([латекс]\boldsymbol{\Omega \cdot \;\textbf{s}}[/латекс])= [латекс]\boldsymbol{\Omega}[ /латекс]), в соответствии с его ролью эффективного сопротивления. Имеет смысл, что [латекс]\жирныйсимвол{X_L}[/латекс] пропорционален [латекс]\жирныйсимвол{L}[/латекс], поскольку чем больше индукция, тем больше его сопротивление изменению. Также разумно, что [латекс]\boldsymbol{X_L}[/латекс] пропорционален частоте [латекс]\жирныйсимвол{f}[/латекс], поскольку большая частота означает большее изменение тока. То есть [latex]\boldsymbol{\Delta I/ \Delta t}[/latex] велико для больших частот (большой [latex]\boldsymbol{f}[/latex] , маленький [латекс]\boldsymbol{\Delta t}[/латекс]). Чем больше изменение, тем больше сопротивление индуктора.
Имеет смысл, что [латекс]\жирныйсимвол{X_L}[/латекс] пропорционален [латекс]\жирныйсимвол{L}[/латекс], поскольку чем больше индукция, тем больше его сопротивление изменению. Также разумно, что [латекс]\boldsymbol{X_L}[/латекс] пропорционален частоте [латекс]\жирныйсимвол{f}[/латекс], поскольку большая частота означает большее изменение тока. То есть [latex]\boldsymbol{\Delta I/ \Delta t}[/latex] велико для больших частот (большой [latex]\boldsymbol{f}[/latex] , маленький [латекс]\boldsymbol{\Delta t}[/латекс]). Чем больше изменение, тем больше сопротивление индуктора.
Пример 1. Расчет индуктивного реактивного сопротивления, а затем тока
(a) Рассчитайте индуктивное реактивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Индуктивное сопротивление находится непосредственно из выражения [латекс]\boldsymbol{X_L = 2 \pi fL}[/латекс]. Как только [latex]\boldsymbol{X_L}[/latex] найден на каждой частоте, можно использовать закон Ома, указанный в уравнении [latex]\boldsymbol{I=V/X_L}[/latex], чтобы найти ток на каждой частоте. 94 \;\textbf{/s})(3,00 \;\textbf{мГн}) = 188 \;\Omega \;\textbf{at} 10 \;\textbf{кГц}}[/latex]
Как только [latex]\boldsymbol{X_L}[/latex] найден на каждой частоте, можно использовать закон Ома, указанный в уравнении [latex]\boldsymbol{I=V/X_L}[/latex], чтобы найти ток на каждой частоте. 94 \;\textbf{/s})(3,00 \;\textbf{мГн}) = 188 \;\Omega \;\textbf{at} 10 \;\textbf{кГц}}[/latex]
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении [латекс]\boldsymbol{I = V/X_L}[/латекс], при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первого частота, это дает
[латекс]\жирныйсимвол{I=}[/латекс][латекс]\жирныйсимвол{\гидроразрыва{V}{X_L}}[/латекс][латекс]\жирныйсимвол{=}[/латекс] [латекс]\boldsymbol{\frac{120 \;\textbf{V}}{1,13 \;\Omega}}[/latex][латекс]\boldsymbol{= 106 \;\textbf{A at} \; 60 \;\textbf{Гц}}.[/latex]
Аналогично, на частоте 10 кГц
[латекс]\boldsymbol{I=}[/латекс][латекс]\boldsymbol{\frac{V}{X_L}}[/латекс][латекс]\boldsymbol{=} [/латекс][латекс]\boldsymbol{\frac{120 \;\textbf{V}}{188 \;\Omega}}[/latex][латекс]\boldsymbol{= 0,637 \;\textbf{A at} \; 10 \;\textbf{кГц}}. [/latex]
[/latex]
Обсуждение
Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.
Обратите внимание, что, хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
График на рис. 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке a конденсатор полностью разряжен ([латекс]\boldsymbol{Q = 0}[/латекс] на нем), и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла: 9{\circ}}[/latex] фазовый угол.
Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла: 9{\circ}}[/latex] фазовый угол.
Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока [латекс]\boldsymbol{I}[/латекс] в цепи, содержащей только конденсатор [латекс]\boldsymbol{C}[/латекс] по другой версии закона Ома дается как
[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_C}},[/латекс]
, где [latex]\boldsymbol{V}[/latex] — среднеквадратичное значение напряжения, а [latex]\boldsymbol{X_C}[/latex] определяется (как и в случае [latex]\boldsymbol{X_L}[/latex], это выражение для [latex]\boldsymbol{X_C}[/latex] в результате анализа схемы с использованием правил Кирхгофа и исчисления) равно
[латекс]\boldsymbol{X_C =}[/латекс][латекс]\boldsymbol{\frac{1}{2 \pi fC}},[/латекс]
, где [latex]\boldsymbol{X_C}[/latex] называется емкостным реактивным сопротивлением, потому что конденсатор реагирует на сопротивление току. [latex]\boldsymbol{X_C}[/latex] измеряется в омах (проверка оставлена читателю в качестве упражнения). [латекс]\boldsymbol{X_C}[/латекс] обратно пропорциональна емкости [латекс]\жирныйсимвол{С}[/латекс]; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Это также обратно пропорционально частоте [латекс]\boldsymbol{f}[/латекс]; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
[latex]\boldsymbol{X_C}[/latex] измеряется в омах (проверка оставлена читателю в качестве упражнения). [латекс]\boldsymbol{X_C}[/латекс] обратно пропорциональна емкости [латекс]\жирныйсимвол{С}[/латекс]; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Это также обратно пропорционально частоте [латекс]\boldsymbol{f}[/латекс]; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
Пример 2. Расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Емкостное реактивное сопротивление находится непосредственно из выражения в [latex]\boldsymbol{X_C = \frac{1}{2 \pi fC}}[/latex]. 4 \;\textbf{/s})(5,00 \;\mu \ textbf{F})}} \\[1em] & \boldsymbol{3.18 \;\Omega \;\textbf{at} \; 10 \;\textbf{Гц}}. \end{массив}[/латекс]
4 \;\textbf{/s})(5,00 \;\mu \ textbf{F})}} \\[1em] & \boldsymbol{3.18 \;\Omega \;\textbf{at} \; 10 \;\textbf{Гц}}. \end{массив}[/латекс]
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в [latex]\boldsymbol{I = V/X_C}[/latex], при условии, что приложенное среднеквадратичное напряжение составляет 120 В. Для первой частоты это дает
[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_C}}[/латекс][латекс]\boldsymbol{=}[ /латекс][латекс]\boldsymbol{\frac{120 \;\textbf{V}}{531 \;\Omega}}[/latex][латекс]\boldsymbol{= 0,226 \;\textbf{A at} \ ; 60 \;\textbf{Гц}}.[/latex]
Аналогично, при 10 кГц,
[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_C}}[/латекс][латекс]\boldsymbol{=}[/латекс][латекс]\ boldsymbol{\frac{120 \;\textbf{V}}{3,18 \;\Omega}}[/latex][latex]\boldsymbol{= 37,7 \;\textbf{A at} \; 10 \;\textbf{кГц}}.[/latex]
Обсуждение
Конденсатор ведет себя совершенно по-разному на двух разных частотах, и совершенно противоположным образом реагирует катушка индуктивности. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), [latex]\boldsymbol{X_C}[/latex] стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .
Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .
Напомню, что на рис. 3 показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:
Рис. 3. (a) Источник переменного напряжения последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе. 9{\circ}}[/latex] фазовый угол.[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_L}},[/латекс]
, где [latex]\boldsymbol{V}[/latex] — среднеквадратичное напряжение на катушке индуктивности.
[латекс]\boldsymbol{X_L = 2 \pi fL},[/латекс] 9{\circ}}[/latex] фазовый угол.
[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_C}},[/латекс]
, где [latex]\boldsymbol{V}[/latex] — среднеквадратичное напряжение на конденсаторе.
[латекс]\boldsymbol{X_C =}[/latex][латекс]\boldsymbol{\frac{1}{2 \pi fC}}.[/latex]
Задачи и упражнения
1: При какой частоте дроссель 30,0 мГн будет иметь реактивное сопротивление [латекс]\boldsymbol{100 \;\Омега}[/латекс]
2: Какое значение индуктивности должно быть используется, если требуется [латекс]\boldsymbol{20,0 \;\textbf{k} \Omega}[/latex] реактивное сопротивление на частоте 500 Гц?
3: Какую емкость следует использовать для получения реактивного сопротивления [латекс]\boldsymbol{2,00 \;\textbf{M} \Omega}[/latex] на частоте 60,0 Гц?
4: При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление [латекс]\boldsymbol{0,250 \;\Омега}[/латекс]?
5: (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В. б) Какой будет сила тока на частоте 100 кГц?
б) Какой будет сила тока на частоте 100 кГц?
6: (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору [латекс]\boldsymbol{0,250 \;\мкФ}[/латекс]? б) Какой будет сила тока на частоте 25,0 кГц?
7: Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, создает ток силой 2,00 А. Индуктивность какая?
8: Источник 20,0 Гц, 16,0 В производит ток 2,00 мА при подключении к конденсатору. Какова емкость?
9: (a) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, устанавливается последовательно с компьютером. Какой минимальной индуктивностью он должен обладать, чтобы создавать реактивное сопротивление [латекс]\жирныйсимвол{2,00\;\текстбф{к}\Омега}[/латекс] для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?
10: Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. а) Какая емкость необходима для получения реактивного сопротивления [латекс]\жирныйсимвол{100\;\textbf{k}\Омега}[/латекс] на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. а) Какая емкость необходима для получения реактивного сопротивления [латекс]\жирныйсимвол{100\;\textbf{k}\Омега}[/латекс] на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
11: Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. (a) Какая емкость необходима для создания реактивного сопротивления [латекс]\boldsymbol{10,0 \;\textbf{м} \Омега}[/латекс] для сигнала 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
12: необоснованные результаты
При записи напряжений, вызванных активностью головного мозга (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
13: Создайте свою собственную задачу
Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.
Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.
- индуктивное сопротивление
- противодействие катушки индуктивности изменению тока; рассчитано по [латекс]\boldsymbol{X_L = 2 \pi fL}[/латекс]
- емкостное реактивное сопротивление
- сопротивление конденсатора изменению тока; рассчитано по формуле [латекс]\boldsymbol{X_C = \frac{1}{2 \pi fC}}[/latex]
23.11 Реактивное, индуктивное и емкостное сопротивление – College Physics
Глава 23 Электромагнитная индукция, цепи переменного тока и электрические технологии
Резюме
- Зарисовка зависимости напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.

- Рассчитать индуктивное и емкостное сопротивление.
- Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.
Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.
Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис. 1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.
Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.
(б) График тока и напряжения на катушке индуктивности в зависимости от времени. График на рис. 2(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика 90 561 после 90 562 управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом: 9{\circ}}[/latex] фазовый угол.
Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует обратную ЭДС [латекс]{V= -L(\Delta I/ \Delta t)}[/латекс]. Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока [латекс]{I}[/латекс] через катушку индуктивности [латекс]{L}[/латекс] определяется версией закона Ома:
Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока [латекс]{I}[/латекс] через катушку индуктивности [латекс]{L}[/латекс] определяется версией закона Ома:
[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {V} {X_L}}, [/ латекс]
, где [latex]{V}[/latex] — среднеквадратичное напряжение на катушке индуктивности, а [latex]{X_L}[/latex] определяется как 9.0032
[латекс] {X_L = 2 \pi fL},[/латекс]
с [latex]{f}[/latex] частотой источника переменного напряжения в герцах (анализ цепи с использованием правила цикла Кирхгофа и исчисления фактически дает это выражение). [латекс]{X_L}[/латекс] называется индуктивным реактивным сопротивлением, потому что индуктор препятствует протеканию тока. [latex]{X_L}[/latex] имеет единицы измерения омы ([latex]{1 \;\text{H}=1 \;\Omega \cdot \;\text{s}}[/latex], так что частота, умноженная на индуктивность, имеет единицы (циклы / с) ([латекс] {\ Omega \ cdot \; \ text {s}} [/ латекс]) = [латекс] {\ Omega} [/латекс]), что соответствует его роль эффективного сопротивления. Имеет смысл, что [латекс]{X_L}[/латекс] пропорционален [латексу]{L}[/латексу], поскольку чем больше индукция, тем больше его сопротивление изменению. Также разумно, что [латекс]{X_L}[/латекс] пропорционален частоте [латекс]{f}[/латекс], поскольку большая частота означает большее изменение тока. То есть [latex]{\Delta I/\Delta t}[/latex] велико для больших частот (большой [latex]{f}[/latex] , маленький [латекс] {\ Delta t} [/латекс]). Чем больше изменение, тем больше сопротивление индуктора.
Имеет смысл, что [латекс]{X_L}[/латекс] пропорционален [латексу]{L}[/латексу], поскольку чем больше индукция, тем больше его сопротивление изменению. Также разумно, что [латекс]{X_L}[/латекс] пропорционален частоте [латекс]{f}[/латекс], поскольку большая частота означает большее изменение тока. То есть [latex]{\Delta I/\Delta t}[/latex] велико для больших частот (большой [latex]{f}[/latex] , маленький [латекс] {\ Delta t} [/латекс]). Чем больше изменение, тем больше сопротивление индуктора.
Пример 1. Расчет индуктивного реактивного сопротивления, а затем тока
(a) Рассчитайте индуктивное реактивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Индуктивное сопротивление находится непосредственно из выражения [латекс]{X_L = 2 \pi fL}[/латекс]. Как только [латекс]{X_L}[/латекс] найден на каждой частоте, можно использовать закон Ома, указанный в уравнении [латекс]{I=V/X_L}[/латекс], чтобы найти ток на каждой частоте. 94 \;\text{/s})(3,00 \;\text{мГн}) = 188 \;\Omega \;\text{at} 10 \;\text{кГц}}[/latex]
Как только [латекс]{X_L}[/латекс] найден на каждой частоте, можно использовать закон Ома, указанный в уравнении [латекс]{I=V/X_L}[/латекс], чтобы найти ток на каждой частоте. 94 \;\text{/s})(3,00 \;\text{мГн}) = 188 \;\Omega \;\text{at} 10 \;\text{кГц}}[/latex]
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении [latex]{I = V/X_L}[/latex], при условии, что приложенное среднеквадратичное напряжение составляет 120 В. Для первой частоты это дает
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {X_L}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {120 \;\text{V}}{1.13 \;\Omega}}[/latex] [латекс]{= 106 \;\text{A at} \; 60 \;\text{Гц}}.[/latex]
Аналогично, на частоте 10 кГц
[латекс] {I=}[/латекс] [латекс]{\ гидроразрыва {V} {X_L}}[/латекс] [латекс] {=}[/латекс] [латекс ] {\ frac {120 \; \ text {V}} {188 \; \ Omega}} [/latex] [латекс] {= 0,637 \; \ text {A at} \; 10 \;\text{kHz}}. [/latex]
[/latex]
Обсуждение
Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.
Обратите внимание, что, хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
График на рис. 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке a конденсатор полностью разряжен ([латекс]{Q = 0}[/латекс] на нем), и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла: 9{\circ}}[/latex] фазовый угол.
Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла: 9{\circ}}[/latex] фазовый угол.
Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока [латекс]{I}[/латекс] в цепи, содержащей только конденсатор [латекс]{С}[/латекс], определяется другим выражением вариант закона Ома будет
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {X_C}}, [/латекс]
, где [латекс]{V}[/латекс] — среднеквадратичное значение напряжения, а [латекс]{X_C}[/латекс] определяется (как и в случае с [латекс]{X_L}[/латекс], это выражение для [латекс]{ X_C}[/latex] результат анализа схемы с использованием правил и исчисления Кирхгофа) равно
[латекс] {X_C =} [/латекс] [латекс] {\ гидроразрыва {1} {2 \ pi fC}}, [/латекс]
, где [латекс]{X_C}[/латекс] называется емкостным реактивным сопротивлением, потому что конденсатор препятствует протеканию тока. [latex]{X_C}[/latex] измеряется в омах (проверка оставлена читателю в качестве упражнения). [латекс]{X_C}[/латекс] обратно пропорциональна емкости [латекс]{С}[/латекс]; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Это также обратно пропорционально частоте [латекс]{ф}[/латекс]; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
[latex]{X_C}[/latex] измеряется в омах (проверка оставлена читателю в качестве упражнения). [латекс]{X_C}[/латекс] обратно пропорциональна емкости [латекс]{С}[/латекс]; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Это также обратно пропорционально частоте [латекс]{ф}[/латекс]; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
Пример 2. Расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Емкостное реактивное сопротивление находится непосредственно из выражения в [latex]{X_C = \frac{1}{2 \pi fC}}[/latex]. Как только [латекс]{X_C}[/латекс] найден на каждой частоте, можно использовать закон Ома, сформулированный как [латекс]{I = V/X_C}[/латекс], чтобы найти ток на каждой частоте. 4 \;\text{/s})(5,00 \;\mu \text{F})}} \\[1em]\;= & {3.18 \;\Omega \;\text{at} \; 10 \;\text{Гц}}. \end{массив}[/латекс]
4 \;\text{/s})(5,00 \;\mu \text{F})}} \\[1em]\;= & {3.18 \;\Omega \;\text{at} \; 10 \;\text{Гц}}. \end{массив}[/латекс]
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в [latex]{I = V/X_C}[/latex], при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первая частота, это дает
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {X_C}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ frac{120 \;\text{V}}{531 \;\Omega}}[/latex] [латекс]{= 0,226 \;\text{A at} \; 60 \;\text{Гц}}.[/latex]
Аналогично, при 10 кГц
[латекс]{I =}[/латекс] [латекс]{\ гидроразрыва {V} {X_C}}[/ латекс] [латекс] {=}[/ латекс] [латекс] {\ гидроразрыва {120 \; \ текст {V}} {3,18 \; \ Omega}} [/ латекс] [латекс] {= 37,7 \; \ текст {А в} \; 10 \;\text{кГц}}.[/latex]
Обсуждение
Конденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует индуктор. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), [латекс]{X_C}[/латекс] стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .
Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .
Напомню, что на рис. 3 показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:
Рис. 3. (a) Источник переменного напряжения последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе. 9{\circ}}[/latex] фазовый угол.[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {V} {X_L}}, [/ латекс]
, где [латекс]{В}[/латекс] — среднеквадратичное напряжение на катушке индуктивности.
[латекс] {X_L = 2 \pi fL},[/латекс]
с [latex]{f}[/latex] частотой источника переменного напряжения в герцах. 9{\circ}}[/latex] фазовый угол.
9{\circ}}[/latex] фазовый угол.
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {X_C}}, [/латекс]
, где [латекс]{В}[/латекс] — среднеквадратичное напряжение на конденсаторе.
[латекс] {X_C =} [/латекс] [латекс] {\ гидроразрыва {1} {2 \ pi fC}}. [/латекс]
Задачи и упражнения
1: При какой частоте индуктор на 30,0 мГн будет иметь реактивное сопротивление [латекс]{100 \;\Омега}[/латекс]
2: Какое значение индуктивности следует использовать, если [латекс]{20,0 \;\text{k} \Omega}[/latex] реактивное сопротивление необходимо при частоте 500 Гц?
3: Какую емкость следует использовать для получения реактивного сопротивления [латекс]{2,00 \;\text{M} \Omega}[/latex] на частоте 60,0 Гц?
4: При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление [латекс]{0,250 \;\Омега}[/латекс]?
5: (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В. б) Какой будет сила тока на частоте 100 кГц?
б) Какой будет сила тока на частоте 100 кГц?
6: (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору [латекс] {0,250 мкФ}[/латекс]? б) Какой будет сила тока на частоте 25,0 кГц?
7: Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, производит ток силой 2,00 А. Индуктивность какая?
8: Источник 20,0 Гц, 16,0 В производит ток 2,00 мА при подключении к конденсатору. Какова емкость?
9: (a) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, устанавливается последовательно с компьютером. Какой минимальной индуктивностью он должен обладать, чтобы создавать [латекс]{2,00 \;\текст{к} \Омега}[/латекс] реактивное сопротивление для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?
10: Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. а) Какая емкость необходима для получения реактивного сопротивления [латекс]{100 \;\text{k} \Омега}[/латекс] на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. а) Какая емкость необходима для получения реактивного сопротивления [латекс]{100 \;\text{k} \Омега}[/латекс] на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
11: Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекс]{10,0 \;\текст{м} \Омега}[/латекс] для сигнала 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
12: необоснованные результаты
При записи напряжений, вызванных активностью головного мозга (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
13: Создайте свою собственную задачу
Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.
Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.
- индуктивное сопротивление
- противодействие катушки индуктивности изменению тока; рассчитано по [латексу]{X_L = 2 \pi fL}[/латекс]
- емкостное реактивное сопротивление
- сопротивление конденсатора изменению тока; рассчитано по формуле [латекс]{X_C = \frac{1}{2 \pi fC}}[/latex]
Реактивное сопротивление и импеданс – формула
Значение импеданса – это мера общего сопротивления цепи переменного тока току, обозначаемому буквой Z. Проще говоря, это количество цепи, которая препятствует потоку изменений. Импеданс подобен сопротивлению, которое также учитывает влияние индуктивности и емкости. Единицей измерения импеданса является ом.
Единицей измерения импеданса является ом.
Поскольку импеданс учитывает влияние индуктивности и емкости и зависит от частоты тока, проходящего через цепь, он является более сложным, чем сопротивление. По сравнению с сопротивлением, которое постоянно независимо от частоты, импеданс зависит от частоты.
Когда дело доходит до определения реактивного сопротивления, это мера сопротивления индуктивности и емкости току. Давайте вкратце узнаем больше об этих двух терминах.
Формула импеданса
Математический символ импеданса — Z, а единица измерения — ом. Это надмножество сопротивления и реактивного сопротивления вместе взятых.
В терминах фазора импеданс Z характеризуется как сумма сопротивления R и реактивного сопротивления X следующим образом:
X = R + j X
емкостный X\[_{C}\].
X = X\[_{L}\] — X\[_{C}\]
Полное сопротивление, Z = \[\frac{V}{I}\]
В = напряжение в вольтах (В )
I = ток в амперах (А)
Z= полное сопротивление в омах (Ом)
R= сопротивление в омах (Ом)
Полное сопротивление можно разделить на две части:
Переменный ток опережает или отстает от напряжения в зависимости от характера реактивной составляющей импеданса (преимущественно индуктивной или емкостной).
Индуктивность и емкость вызывают фазовые сдвиги между током и напряжением, что означает, что сопротивление и реактивное сопротивление нельзя просто суммировать для получения импеданса. Вместо этого они должны быть суммированы как векторы с реактивным сопротивлением под прямым углом к сопротивлению, как показано на рисунке ниже. 9{2}}\]
Импеданс (Z) цепи определяют четыре электрические величины: сопротивление (R), емкость (C), индуктивность (L) и частота (f).
Что такое реактивное сопротивление?
Мера сопротивления индуктивности и емкости току в цепи переменного тока известна как реактивное сопротивление и обозначается буквой X. Оно зависит от частоты электрических сигналов и измеряется в омах.
Реактивное сопротивление бывает двух типов:
Формула реактивного сопротивления
Полное реактивное сопротивление (X) равно разности двух:
Полное реактивное сопротивление, X = X\[_{L}\]– X\[_{C}\]
a. Емкостное реактивное сопротивление X\[_{C}\]
Емкостное реактивное сопротивление X\[_{C}\]
Реактивное сопротивление, большое на низких частотах и малое на высоких частотах, известно как емкостное реактивное сопротивление ( X\[_{C}\] ). X\[_{C}\] бесконечно для устойчивого постоянного тока при нулевой частоте (f=0Hz). Это означает, что конденсатор пропускает переменный ток, но блокирует постоянный ток.
Емкостное реактивное сопротивление, X\[_{C}\] = 1/2fC
Где,
X\[_{C}\] = реактивное сопротивление в омах (Ом)
f = частота в герцах (Гц)
C = емкость в фарадах (Ф)
Например, конденсатор емкостью 1 мкФ имеет реактивное сопротивление 3,2. k для сигнала 50 Гц, но когда частота выше 10 кГц, реактивное сопротивление составляет всего 16.
b. Индуктивное реактивное сопротивление, X\[_{L}\]
Реактивное сопротивление, малое на низких частотах и большое на высоких частотах, называется индуктивным реактивным сопротивлением. X\[_{L}\] равно нулю для установившегося постоянного тока на нулевой частоте (f=0 Гц). Это означает, что катушка индуктивности пропускает постоянный ток, но блокирует переменный ток.
X\[_{L}\] равно нулю для установившегося постоянного тока на нулевой частоте (f=0 Гц). Это означает, что катушка индуктивности пропускает постоянный ток, но блокирует переменный ток.
Формула для расчета индуктивного сопротивления катушки:
Индуктивное сопротивление, или X\[_{L}\] является произведением удвоенной (pi), или 6,28, частоты переменного тока в герцах, индуктивность катушки в генри.
X\[_{L}\] = 2x f x L
L = значение индуктивности катушки в генри.
Индуктивное сопротивление, X\[_{L}\] = 2fL
Где,
X\[_{L}\] = реактивное сопротивление в омах (Ом)
f = частота в герцах (Гц)
L = индуктивность в генри (Гн)
Например, дроссель 1 мГн имеет реактивное сопротивление всего 0,3 для сигнала частотой 50 Гц, но когда частота выше 10 кГц, его реактивное сопротивление равно 63 Ом.
Формула реактивного сопротивления и импеданса
Элемент в цепи постоянного тока можно легко описать, используя только его сопротивление. Сопротивление конденсатора в цепях постоянного тока считается открытым соединением, тогда как сопротивление катушки индуктивности в цепи постоянного тока будет рассматриваться как короткое соединение или нулевое сопротивление. В отличие от цепей постоянного тока видно, что в цепях переменного тока импеданс элемента представляет собой значение того, насколько элемент имеет тенденцию противодействовать протеканию тока, когда на него подается переменное напряжение. Импеданс может быть представлен в виде комплексного числа, состоящего как из действительной, так и из мнимой частей, и может быть представлен следующим образом:
Сопротивление конденсатора в цепях постоянного тока считается открытым соединением, тогда как сопротивление катушки индуктивности в цепи постоянного тока будет рассматриваться как короткое соединение или нулевое сопротивление. В отличие от цепей постоянного тока видно, что в цепях переменного тока импеданс элемента представляет собой значение того, насколько элемент имеет тенденцию противодействовать протеканию тока, когда на него подается переменное напряжение. Импеданс может быть представлен в виде комплексного числа, состоящего как из действительной, так и из мнимой частей, и может быть представлен следующим образом:
Z = R + jX
Где Z представляет импеданс
R представляет значение сопротивления
X, мнимая часть, представляет реактивное сопротивление
Видно, что сопротивление в цепи всегда будет положительным, а наблюдаемое реактивное сопротивление будет либо положительным, либо отрицательным.
Знаете ли вы?
Когда ток и напряжение не соответствуют друг другу, это означает наличие фазового сдвига.




 Полярность индуцированного напряжения всегда такова, что это напряжение поддерживает изменяющийся ток в его текущем состоянии. Например, если ток растет, то напряжение препятствует этому росту и старается уменьшить ток. В то же время, если ток через катушку уменьшается, напряжение мешает этому уменьшению и поддерживает более высокий ток. Чем выше скорость изменения тока, тем больше амплитуда этого обратного напряжения. В связи с указанным свойством, это напряжение часто называют индуктивными выбросами или обратным током. Для того, чтобы как-то отличить это свойство от сопротивления, используют понятие реактивного сопротивления. Если к катушке индуктивности приложено синусоидальное напряжение, то при бóльших частотах катушка оказывает току большее сопротивление, следовательно, ее реактивное сопротивление также увеличивается, как показано на графике.
Полярность индуцированного напряжения всегда такова, что это напряжение поддерживает изменяющийся ток в его текущем состоянии. Например, если ток растет, то напряжение препятствует этому росту и старается уменьшить ток. В то же время, если ток через катушку уменьшается, напряжение мешает этому уменьшению и поддерживает более высокий ток. Чем выше скорость изменения тока, тем больше амплитуда этого обратного напряжения. В связи с указанным свойством, это напряжение часто называют индуктивными выбросами или обратным током. Для того, чтобы как-то отличить это свойство от сопротивления, используют понятие реактивного сопротивления. Если к катушке индуктивности приложено синусоидальное напряжение, то при бóльших частотах катушка оказывает току большее сопротивление, следовательно, ее реактивное сопротивление также увеличивается, как показано на графике.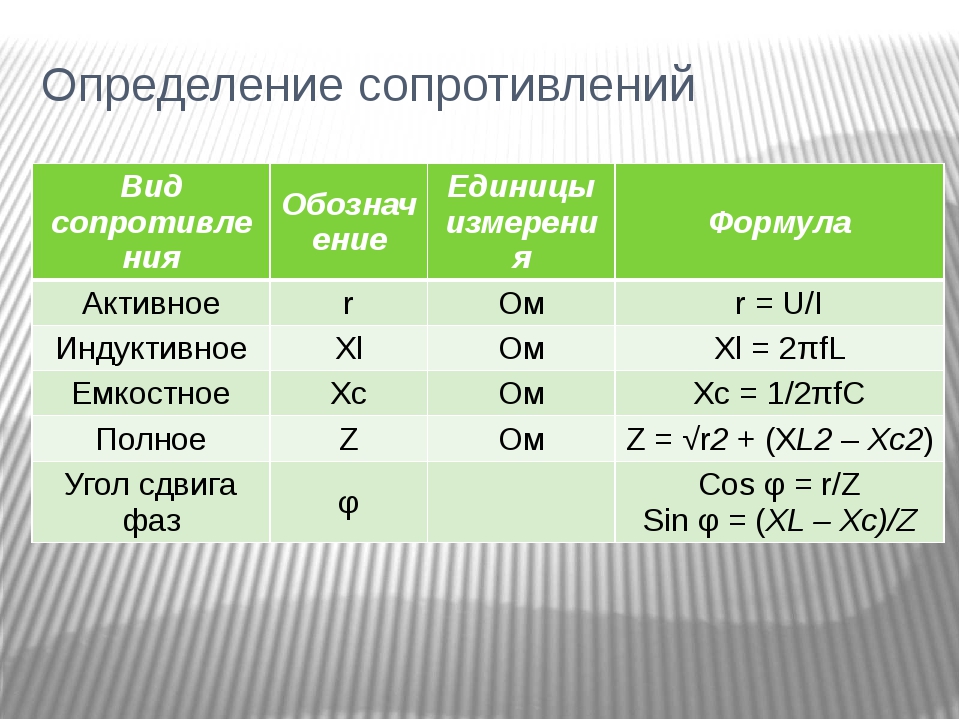 Первая из них представляет собой активное сопротивление R, которое затрудняет протекание тока в материале с плохой проводимостью и зависит от формы этого материала. Вторая часть — это рассмотренное выше реактивное сопротивление X. Оно также затрудняет протекание тока, но не вследствие свойств и формы проводящего материала, а из-за того, что протеканию тока мешает электрическое и магнитное поля.
Первая из них представляет собой активное сопротивление R, которое затрудняет протекание тока в материале с плохой проводимостью и зависит от формы этого материала. Вторая часть — это рассмотренное выше реактивное сопротивление X. Оно также затрудняет протекание тока, но не вследствие свойств и формы проводящего материала, а из-за того, что протеканию тока мешает электрическое и магнитное поля.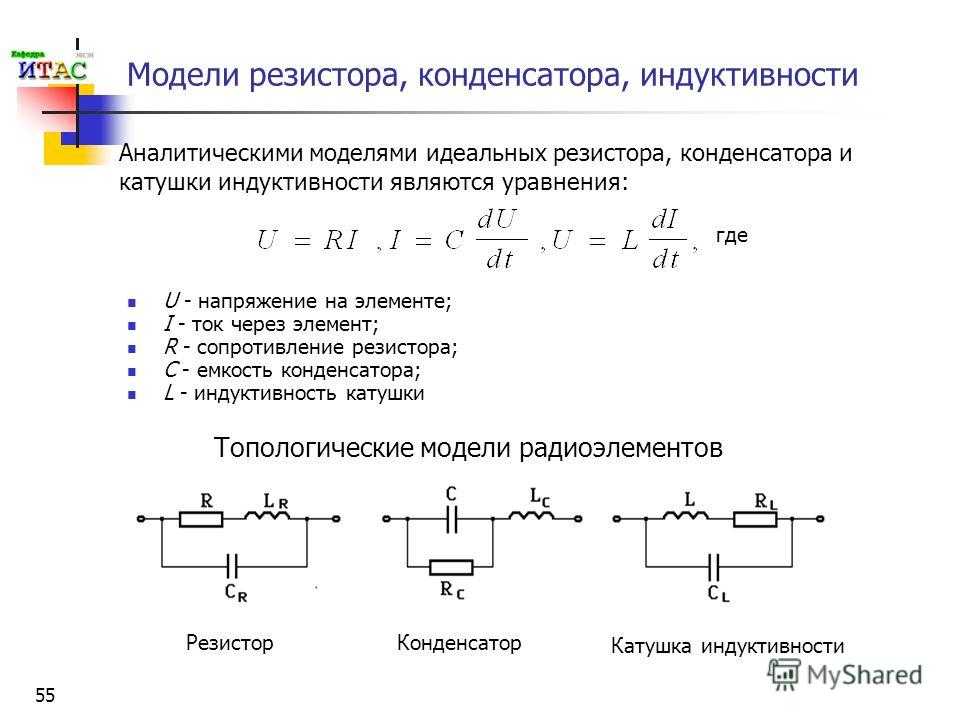
 В точке (ωt = π/2), временнóй оси, где ток нулевой, напряжение на катушке достигает своего положительного максимума. Затем ток постепенно увеличивается и вокруг катушки создается магнитное поле, которое, в свою очередь, создает ЭДС самоиндукции, направленную противоположно току. Эта ЭДС является реакцией катушки на изменение протекающего через нее тока, и она максимальна, когда ток нулевой, так как в этой точке скорость изменения тока максимальная. Когда же ток достигает своего максимального значения (положительного или отрицательного), скорость изменения синусоидального тока становится нулевой и в этих точках максимумов ток ЭДС самоиндукции (определяемая этой скоростью) также равна нулю. Это приводит к тому, что синусоида напряжения не совпадает по фазе с током на угол 90° или π/2 радиан. То есть, напряжение опережает ток или ток отстает от напряжения.
В точке (ωt = π/2), временнóй оси, где ток нулевой, напряжение на катушке достигает своего положительного максимума. Затем ток постепенно увеличивается и вокруг катушки создается магнитное поле, которое, в свою очередь, создает ЭДС самоиндукции, направленную противоположно току. Эта ЭДС является реакцией катушки на изменение протекающего через нее тока, и она максимальна, когда ток нулевой, так как в этой точке скорость изменения тока максимальная. Когда же ток достигает своего максимального значения (положительного или отрицательного), скорость изменения синусоидального тока становится нулевой и в этих точках максимумов ток ЭДС самоиндукции (определяемая этой скоростью) также равна нулю. Это приводит к тому, что синусоида напряжения не совпадает по фазе с током на угол 90° или π/2 радиан. То есть, напряжение опережает ток или ток отстает от напряжения. Или другой пример. День зимнего солнцестояния в северном полушарии (самый короткий день) — в конце декабря, однако самые холодные месяцы еще впереди. В зависимости от того, где вы живете, это будет январь или февраль. Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении индуктивности, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают катушки индуктивности.
Или другой пример. День зимнего солнцестояния в северном полушарии (самый короткий день) — в конце декабря, однако самые холодные месяцы еще впереди. В зависимости от того, где вы живете, это будет январь или февраль. Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении индуктивности, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают катушки индуктивности. При высоких частотах индуктивное реактивное сопротивление становится очень большим и очень сильно противодействует протекающему току. С другой стороны, при очень низких частотах или при постоянном напряжении катушка индуктивности проводит очень хорошо — отсюда правило, которое мы выучили в школе: катушки индуктивности не пропускают переменный ток и пропускают постоянный. Если частота очень низкая, катушки индуктивности пропускают сигнал очень хорошо. Именно поэтому их устанавливают в фильтрах громкоговорителей (кроссоверах), чтобы высокие частоты не попадали на низкочастотные динамические головки.
При высоких частотах индуктивное реактивное сопротивление становится очень большим и очень сильно противодействует протекающему току. С другой стороны, при очень низких частотах или при постоянном напряжении катушка индуктивности проводит очень хорошо — отсюда правило, которое мы выучили в школе: катушки индуктивности не пропускают переменный ток и пропускают постоянный. Если частота очень низкая, катушки индуктивности пропускают сигнал очень хорошо. Именно поэтому их устанавливают в фильтрах громкоговорителей (кроссоверах), чтобы высокие частоты не попадали на низкочастотные динамические головки. С увеличением частоты импеданс катушек уменьшается.
С увеличением частоты импеданс катушек уменьшается. Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов
Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов
 com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.