Резистивный делитель тока – » :

Делитель напряжения: теория и принцип действия

Делитель напряжения позволяет получить меньшее напряжение из большего, напряжение может быть как постоянным, так и переменным.

Рис. 1. Схема простейшего делителя напряжения

Простейшая схема делителя напряжения содержит минимум два сопротивления. Если величины сопротивлений одинаковы, то согласно закону Ома, на выходе делителя будет получено напряжение, в два раза меньшее, чем на входе, так как падение напряжений на резисторах будет одинаковым. Для других случаев величина падения напряжений на резисторах делителя определяется по формулам

U_R1 = I*R1; U_R2 = I*R2       (1)

где U_R1, U_R2 — падения напряжения на резисторах R1 и R2 соответственно, I — ток в цепи. В схемах делителей выходное напряжение обычно снимают с нижнего по схеме резистора.

Сумма падений напряжений U_R1, U_R2

на резисторах равна напряжению источника питания. Ток в цепи будет равен напряжению источника питания, делённому на сумму сопротивлений резисторов R1 и R2:

I = U_пит / (R1 + R2)       (2)

Рассмотрим практическую схему делителя постоянного напряжения (рис.2)

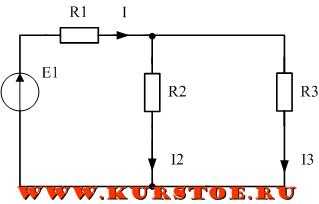
Рис. 2. Делитель постоянного напряжения.

Ток, протекающий в этой схеме, согласно формуле (2) будет равен

I = 10 / (10000+40000) = 0,0002 А = 0,2 мА.

Тогда согласно формуле (1) падение напряжения на резисторах делителя напряжения будет равно:

U_R1 = 0,0002*10000 = 2 В;
U_R2 = 0,0002*40000 = 8 В.

Если из формулы (1) вывести ток:

I = U_R1 / R1       (3)

И подставить его значение в формулу (2), то получится универсальная формула для расчёта делителя напряжения:

U_R1 / R1 = U_пит / (R1 + R2)

Откуда

U_R1 = U_пит * R1 / (R1 + R2)       (4)

Подставляя значения напряжения и сопротивлений в формулу (4), получим величину напряжения на резисторе R1:

U_R1 = 10 * 10000 / (10000+40000) = 2 В,

и на резисторе R2:

U_R2 = 10 * 40000 / (10000+40000) = 8 В.

Делитель напряжения с реактивными элементами в цепи переменного тока

В вышеприведённой схеме делителя напряжения (рис. 2) были использованы активные элементы — резисторы, и питание схемы осуществлялось постоянным напряжением (хотя схему можно питать и переменным током). Делитель напряжения может содержать так же и реактивные компоненты (конденсаторы, катушки индуктивности), но в этом случае для нормальной работы потребуется питание синусоидальным током (рис. 3).

Рис. 3. Ёмкостный делитель напряжения в цепи переменного тока.

Изображённый на рисунке 3 ёмкостный делитель напряжения работает аналогично резистивному делителю, но рассчитывается несколько иначе, поскольку реактивное сопротивление конденсаторов обратно пропорционально их ёмкости:

R_c = 1/(2 * π * f * C)

Здесь R_c — реактивное сопротивление конденсатора;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
C — ёмкость конденсатора, Фарад.

То есть чем больше ёмкость конденсатора, тем меньше его сопротивление, и следовательно в схеме делителя напряжения на конденсаторе с большей ёмкостью падение напряжения будет меньше, чем на конденсаторе с меньшей ёмкостью. Следовательно, формула (4) для ёмкостного делителя напряжения примет следующий вид:

U_С1 = U_пит * С2 / (С1 + С2)       (5)

U_С1 = 10 * 40*10^-9 / (10*10^-9+40*10^-9) = 8 В,
U_С2 = 10 * 10*10^-9 / (10*10^-9+40*10^-9) = 2 В.

Индуктивный делитель напряжения (рис. 4.) так же как и ёмкостный требует для своей работы синусоидальное питающее напряжение.

Рис. 4. Индуктивный делитель напряжения в цепи переменного тока.

Поскольку реактивное сопротивление катушки индуктивности в цепи переменного тока пропорционально номиналу катушки:

R_L = 2 * π * f * L

Здесь R_c — реактивное сопротивление катушки индуктивности;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
L — индуктивность катушки, Генри.

То следовательно и формула для расчёта индуктивного делителя напряжения будет точно такой же, как и формула для расчёта резистивного делителя напряжения (4), где вместо сопротивлений будут использоваться индуктивности:

U_L1 = U_пит * L1 / (L1 + L2)       (6)

Подставив в эту формулу параметры элементов из рисунка 4, получим:

U_L1 = 10 * 10*10^-6 / (10*10^-6+40*10^-6) = 2 В,
U_L2 = 10 * 40*10^-6 / (10*10

-6+40*10^-6) = 8 В.

В заключении следует отметить, что во всех расчётах величина нагрузки была принята равной бесконечности, поэтому полученные значения верны при работе рассмотренных делителей на сопротивление нагрузки, во много раз большее, чем величина собственных сопротивлений.

BACK

zpostbox.ru

Резистивные делители тока и напряжения

Резистивные делители широко применяются в электрических цепях приборов. Схемы простейших делителей тока и напряжения приве­дены на рис. 2-5, а, б. Коэффициенты передачи, или коэффициенты деления, делителей равны ; и определяются отношением сопротивлений входящих в них резисторов, поэтому точность коэффициента деления определя­ется не точностью самих сопротивлений резисторов, а лишь точностью поддержания их отношения. Приведенные выражения справедливы для случая, когда можно пренебречь внутренними сопротивлениями источников и нагрузок, полагая, что для делителя напряжения

R_H = ¥, а для делителя тока R_Н® 0.

 

 

 

 

 

 

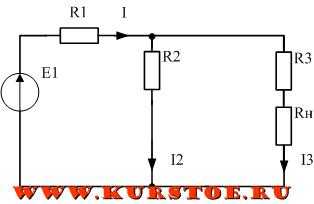
Рис. 2-5

 

 

С учетом сопротивлений источников и нагрузок выходной ток и выходное напряжение определяются формулами:

; .

Коэффициент деления тока не зависит от сопротивления цепи, вклю­ченной последовательно с делителем, т.е. от сопротивления источника. При постоянных сопротивлениях делителя и нагрузки изменение коэф­фициента деления учитывается формулами:

; .

Или, учитывая, что выходные сопротивления делителей составляют

, ,

коэффициенты деления можно представить в виде:

; .

Из приведенных формул легко определить погрешность делителей при изменении сопротивления нагрузки или выходных сопротивлений делителей. Однако, даже если нагрузки остаются неизменными, вклю­чение нагрузок, имеющих сопротивления, сравнимые с выходными сопротивлениями делителей, крайне нежелательно, так как это при­водит к существенному возрастанию погрешностей делителей под влиянием внешних факторов.

Для ненагруженных делителей погрешности от влияния внешних факторов пренебрежимо малы, так как используемые в них резисторы идентичны и отношение их сопротивлений является инвариантной величиной. По-разному влияют внешние воздействия на сопротивле­ния делителя и нагрузки, так как последние выполняются из различ­ных материалов, и поэтому возрастают соответствующие погрешности. Полагая, что под действием температуры относительная погрешность резисторов делителя составляет g_R, а относительная погрешность сопротивления нагрузки g_Rн можно написать следующие выражения для погрешностей коэффициентов деления:

; .

Если на вход резистивного делителя подается переменное напря­жение достаточно высокой частоты или напряжение, содержащее высо­кочастотные гармоники, то необходимо учитывать реактивные состав­ляющие сопротивлений, входящих в делитель резисторов.

Для того чтобы избежать частотной погрешности, должно выпол­няться следующее условие:

R₁/R₂ = L₁ /L₂ =C₂/C₁,

где L₁, L₂, C₁и C₂– параметры эквивалентной схемы резисторов.

Влияние индуктивной составляющей комплексного сопротивления обычно невелико, что объясняется соответствующей конструкцией не­проволочных резисторов и бифилярной намоткой высокочастотных проволочных резисторов. Емкостная же составляющая сопротивления может вносить заметную погрешность. Эту погрешность можно исключить, выравнивая постоянные времени резисторов делителя, для чего подбирают небольшие конденсаторы, включаемые параллельно ре­зисторам. Использование подобной емкостной коррекции позволяет снизить частотную погрешность делителей до десятых долей процента для частот звукового диапазона при применении микропроволочных резисторов типа МВСГ и для частот вплоть до нескольких десятков мегагерц при использовании непроволочных резисторов.

Дальнейшее снижение частотной погрешности возможно при при­менении более сложных схем частотной коррекции.

Существенно увеличиваются частотные погрешности делителей при включении сопротивления нагрузки. В рабочем диапазоне частот, где резисторы делителя имеют чисто активные сопротивления, частот­ные погрешности, вызванные реактивными составляющими сопротивле­ний нагрузок, определяются формулами:

; ,

если считать, как это и бывает в большинстве случаев, что нагрузка делителя тока имеет индуктивную составляющую, а нагрузка делителя напряжения – емкостную.

Многоступенчатые резистивные делители напряжения и тока приведены на рис. 2-5, г и д, где в качестве примеров указаны значения сопротивлений.

Подобные схемы используются для переключения пределов амперметров и аналоговых электронных вольтметров. Особую роль играют многоступенчатые делители с многозначными регу­лируемыми коэффициентами деления, используемые в современных цифровых приборах и компенсаторах ручного уравновешивания. В ка­честве примера на рис. 2-6 показан трехзначный делитель, который может выполняться как с ручным, так и с автоматическим изменением коэффициента деления. Принцип действия делителя поясняется рис. 2-6, а. Делитель состоит из идентичных резисторов, по которым перемещаются два механически соединенных, но электрически изоли­рованных движка. Часть резистора, к которой приложено напряже­ние, показана штриховкой; та часть резистора, с которой снимается напряжение, показана более густой штриховкой.На рис. 2-6,

б, в представлены построенные на этом принципе делитель с ручным управлением (при указанном положении движков U_ВЫХ = 0,120·U_ВХ) и с автоматическим управлением путем замыкания и размыкания соответствующих контактов реле (при указанном положе­нии контактов U_ВЫХ = 0,538 U_ВХ).

 

 

 

Рис. 2-6

 

Число знаков коэффициента деления определяется возможным диа­пазоном сопротивлений резисторов, поскольку, как видно из рис. 2-6, в,для того чтобы не сказывались остаточные параметры ключей, то сопротивление из них, которое меньше, должно быть на 1–2 порядка больше сопротивления r_к замкнутого ключа, а то, которое больше на 2–3 порядка меньше сопротивления R_к разомкнутого ключа.

Если предположить, что r_к = 0,01 Ом, а R_к = 10⁸ Ом, то можно реализовать пятизначный делитель, в котором коэффициент деления будет иметь погрешность, не превышающую последнего знака. Анали­зируя различные схемы делителей, нужно обратить внимание на следующие характеристики: постоянство входного сопротивления, постоянство выходного сопротивления, наличие общей шины между цепями входного и выходного напряжения, влияние остаточных пара­метров ключей, число используемых в делителе номиналов резисторов.

В современных цифровых приборах применяются лестничные делители тока и напряжения на выполненных по интегральной технологии мат­рицах резисторов, содержащих всего два номинала резисторов R и 2R. Схемы таких делителей показаны на рис. 2-7.

В делителе напряжения (рис. 2-7, a) используется один источник напряжения и усилитель с бесконечно большим входным сопротивле­нием, с выхода которого снимается нужная часть входного сигнала. В делителе тока (рис. 2-7, б) используется несколько идентичных источ­ников тока и суммирующий усилитель с бесконечно малым входным сопротивлением. На рис. 2-7, в и г показаны эквивалентные схемы того и другого делителя при замыкании (n–2)-го ключа в положе­ние 1.

а) б)

Рис. 2-7

 

Резистивная матрица имеет постоянное выходное сопротивление R_вых=R. Коэффициенты деления делителя тока и делителя напря­жения составляют:

,

где a_i принимают значения 0 и 1 в зависимости от положения ключей.

Лучшие делители имеют до 16 разрядов, погрешность линейности ±0,002%, температурную погрешность ±0,0007% на 1 К.

 



infopedia.su

Резистивные делители тока и напряжения

Резистивные делители широко применяются в электрических цепях приборов. Схемы простейших делителей тока и напряжения приве­дены на рис. 2-5, а, б. Коэффициенты передачи, или коэффициенты деления, делителей равны ; и определяются отношением сопротивлений входящих в них резисторов, поэтому точность коэффициента деления определя­ется не точностью самих сопротивлений резисторов, а лишь точностью поддержания их отношения. Приведенные выражения справедливы для случая, когда можно пренебречь внутренними сопротивлениями источников и нагрузок, полагая, что для делителя напряженияR_H = , а для делителя тока R_Н 0.

в)

Iвых 95R

Рис. 2-5

С учетом сопротивлений источников и нагрузок выходной ток и выходное напряжение определяются формулами:

; .

Коэффициент деления тока не зависит от сопротивления цепи, вклю­ченной последовательно с делителем, т.е. от сопротивления источника. При постоянных сопротивлениях делителя и нагрузки изменение коэф­фициента деления учитывается формулами:

; .

Или, учитывая, что выходные сопротивления делителей составляют

, ,

коэффициенты деления можно представить в виде:

; .

Из приведенных формул легко определить погрешность делителей при изменении сопротивления нагрузки или выходных сопротивлений делителей. Однако, даже если нагрузки остаются неизменными, вклю­чение нагрузок, имеющих сопротивления, сравнимые с выходными сопротивлениями делителей, крайне нежелательно, так как это при­водит к существенному возрастанию погрешностей делителей под влиянием внешних факторов.

Для ненагруженных делителей погрешности от влияния внешних факторов пренебрежимо малы, так как используемые в них резисторы идентичны и отношение их сопротивлений является инвариантной величиной. По-разному влияют внешние воздействия на сопротивле­ния делителя и нагрузки, так как последние выполняются из различ­ных материалов, и поэтому возрастают соответствующие погрешности. Полагая, что под действием температуры относительная погрешность резисторов делителя составляет _R, а относительная погрешность сопротивления нагрузки _Rн можно написать следующие выражения для погрешностей коэффициентов деления:

; .

Если на вход резистивного делителя подается переменное напря­жение достаточно высокой частоты или напряжение, содержащее высо­кочастотные гармоники, то необходимо учитывать реактивные состав­ляющие сопротивлений, входящих в делитель резисторов.

Для того чтобы избежать частотной погрешности, должно выпол­няться следующее условие:

R₁ /R₂ = L₁ /L₂ =C₂/C₁,

где L₁, L₂, C₁ и C₂ – параметры эквивалентной схемы резисторов.

Влияние индуктивной составляющей комплексного сопротивления обычно невелико, что объясняется соответствующей конструкцией не­проволочных резисторов и бифилярной намоткой высокочастотных проволочных резисторов. Емкостная же составляющая сопротивления может вносить заметную погрешность. Эту погрешность можно исключить, выравнивая постоянные времени резисторов делителя, для чего подбирают небольшие конденсаторы, включаемые параллельно ре­зисторам. Использование подобной емкостной коррекции позволяет снизить частотную погрешность делителей до десятых долей процента для частот звукового диапазона при применении микропроволочных резисторов типа МВСГ и для частот вплоть до нескольких десятков мегагерц при использовании непроволочных резисторов.

Дальнейшее снижение частотной погрешности возможно при при­менении более сложных схем частотной коррекции.

Существенно увеличиваются частотные погрешности делителей при включении сопротивления нагрузки. В рабочем диапазоне частот, где резисторы делителя имеют чисто активные сопротивления, частот­ные погрешности, вызванные реактивными составляющими сопротивле­ний нагрузок, определяются формулами:

; ,

если считать, как это и бывает в большинстве случаев, что нагрузка делителя тока имеет индуктивную составляющую, а нагрузка делителя напряжения – емкостную.

Многоступенчатые резистивные делители напряжения и тока приведены на рис. 2-5, г и д, где в качестве примеров указаны значения сопротивлений.

Подобные схемы используются для переключения пределов амперметров и аналоговых электронных вольтметров. Особую роль играют многоступенчатые делители с многозначными регу­лируемыми коэффициентами деления, используемые в современных цифровых приборах и компенсаторах ручного уравновешивания. В ка­честве примера на рис. 2-6 показан трехзначный делитель, который может выполняться как с ручным, так и с автоматическим изменением коэффициента деления. Принцип действия делителя поясняется рис. 2-6, а. Делитель состоит из идентичных резисторов, по которым перемещаются два механически соединенных, но электрически изоли­рованных движка. Часть резистора, к которой приложено напряже­ние, показана штриховкой; та часть резистора, с которой снимается напряжение, показана более густой штриховкой. На рис. 2-6, б, в представлены построенные на этом принципе делитель с ручным управлением (при указанном положении движков U_ВЫХ = 0,120·U_ВХ) и с автоматическим управлением путем замыкания и размыкания соответствующих контактов реле (при указанном положе­нии контактов U_ВЫХ = 0,538 U_ВХ).

Рис. 2-6

Число знаков коэффициента деления определяется возможным диа­пазоном сопротивлений резисторов, поскольку, как видно из рис. 2-6, в, для того чтобы не сказывались остаточные параметры ключей, то сопротивление из них, которое меньше, должно быть на 1–2 порядка больше сопротивления r_к замкнутого ключа, а то, которое больше на 2–3 порядка меньше сопротивления R_к разомкнутого ключа.

Если предположить, что r_к = 0,01 Ом, а R_к = 10⁸ Ом, то можно реализовать пятизначный делитель, в котором коэффициент деления будет иметь погрешность, не превышающую последнего знака. Анали­зируя различные схемы делителей, нужно обратить внимание на следующие характеристики: постоянство входного сопротивления, постоянство выходного сопротивления, наличие общей шины между цепями входного и выходного напряжения, влияние остаточных пара­метров ключей, число используемых в делителе номиналов резисторов.

В современных цифровых приборах применяются лестничные делители тока и напряжения на выполненных по интегральной технологии мат­рицах резисторов, содержащих всего два номинала резисторов R и 2R. Схемы таких делителей показаны на рис. 2-7.

В делителе напряжения (рис. 2-7, a) используется один источник напряжения и усилитель с бесконечно большим входным сопротивле­нием, с выхода которого снимается нужная часть входного сигнала. В делителе тока (рис. 2-7, б) используется несколько идентичных источ­ников тока и суммирующий усилитель с бесконечно малым входным сопротивлением. На рис. 2-7, в и г показаны эквивалентные схемы того и другого делителя при замыкании (n–2)-го ключа в положе­ние 1.

а) б)

Рис. 2-7

Резистивная матрица имеет постоянное выходное сопротивление R_вых=R. Коэффициенты деления делителя тока и делителя напря­жения составляют:

,

где _i принимают значения 0 и 1 в зависимости от положения ключей.

Лучшие делители имеют до 16 разрядов, погрешность линейности ±0,002%, температурную погрешность ±0,0007% на 1 К.

studfiles.net

3. Делители тока | 5. Схемы делителей и законы Кирхгофа | Часть1

3. Делители тока

Делители тока

Давайте проанализируем простую параллельную цепь и определим силу тока на каждом из ее резисторов:

 

 

Как вы уже знаете, напряжение на всех компонентах параллельной цепи одинаково. Исходя из этого можно заполнить верхнюю строчку рассмотренной ранее таблицы:

 

Теперь, используя закон Ома (I = U/R), мы можем рассчитать силу тока на каждом резисторе (в каждой ветви):

 

 

Один из принципов параллельных цепей гласит, что общая сила тока в таких цепях равна сумме отдельных токов. Поэтому, суммируя 6 мА, 2мА и 3мА, мы можем заполнить ячейку общей силы тока в нашей таблице:

 

 

И наконец, вычислим общее сопротивление нашей цепи. Сделать это можно при помощи закона Ома (R = U/I), или при помощи формулы параллельного соединения резисторов. В обоих случаях мы получим одинаковый ответ:

 

 

Из данной таблицы видно, что сила тока через каждый резистор связана с его сопротивлением (учитывая равенство напряжений на всех резисторах). Причем взаимосвязь эта обратнопропорциональна. К примеру, сила тока через резистор R₁ вдвое больше, чем через резистор R₃, хотя сопротивление последнего в два раза превышает сопротивление первого.

Если мы изменим напряжение питания этой схемы, то обнаружим, что пропорциональность соотношений не изменится:

 

 

Несмотря на то, что напряжение источника питания изменилось, ток через резистор R₁ по-прежнему в два раза превышает ток через резистор R₃. Таким образом, пропорциональность между токами различных ветвей цепи является исключительно функцией сопротивления.

Кроме того, токи отдельных ветвей цепи составляют фиксированные пропорции от ее общей силы тока. Несмотря на четырехкратное увеличение напряжения источника питания, соотношение между током любой ветви и общим током осталось неизменным:

 

 

Благодаря способности делить общий ток на пропорциональные части, параллельные цепи часто называют делителями тока. Поэкспериментировав немного с математикой, мы можем вывести формулу для расчета отдельных токов цепи, имея данные о сопротивлениях резисторов, общем сопротивлении цепи и общей силе тока:

 

 

Отношение общего сопротивления к отдельным сопротивлениям имеет ту же пропорцию, что и отношение отдельных токов к общей силе тока цепи. Полученная выше формула называется формулой делителя тока, с ее помощью легче определять токи отдельных ветвей параллельной цепи, если известна общая сила тока.

Давайте повторно рассчитаем токи каждой из ветвей нашей параллельной цепи, используя только что полученную формулу делителя тока (будем считать, что общая сила тока и общее сопротивление нам известны):

 

 

Если сравнить формулы делителя напряжения и делителя тока, то можно увидеть, что они удивительно похожи друг на друга. Однако, в формуле делителя напряжения R_n (отдельное сопротивление)  делится на  R_общ., а в формуле делителя тока — наоборот, R_общ. делится на R_n:

 

Именно из-за отношения сопротивлений очень легко перепутать эти формулы. В целях избежания путаницы вы должны знать, что отношение сопротивлений в обоих уравнениях должно быть меньше единицы (в конце концов это уравнения делителей, а не умножителей!). Если отношение будет больше единицы, значит вы перепутали уравнения. Зная, что общее сопротивление последовательной цепи (делитель напряжения) всегда больше любого из ее отдельных сопротивлений, R_общ. мы должны поставить в знаменатель отношения, а R_n — в числитель (только в этом случае отношение будет меньше единицы). И наоборот, зная что общее сопротивление параллельной цепи (делитель тока) всегда меньше любого из ее отдельных сопротивлений, R_общ. мы должны поставить в числитель отношения, а R_n — в знаменатель.

Схемы делителей токов, как и делителей напряжений,  нашли применение в электрических цепях измерительных приборов, где часть измеряемого тока необходимо пропустить через чувствительный прибор:

 

www.radiomexanik.spb.ru

Делитель тока — Википедия. Что такое Делитель тока

Материал из Википедии — свободной энциклопедии

Дели́тель то́ка — простейшая линейная электрическая цепь, выходной ток которой представляет собой часть входного тока. Это обеспечивается распределением тока между ветвями делителя.

В качестве делителя тока обычно применяют элементы с регулируемым сопротивлением (потенциометры), подключаемые параллельно.^{[источник не указан 775 дней]} Можно представить как русло реки, разделяющееся на несколько рек. Согласно первому закону Кирхгофа, сумма токов, входящих в узел и выходящих из узла, равна нулю. Применяемые сопротивления для деления токов могут быть как активными, так и реактивными. Реактивные сопротивления возможно использовать только на переменном токе.

Резистивный делитель тока

Простейший резистивный делитель тока — это два параллельно включённых резистора R1{\displaystyle R_{1}} и R2{\displaystyle R_{2}}, подключённых к источнику напряжения U{\displaystyle U}. Поскольку резисторы соединены параллельно, то к ним приложено одинаковое напряжение.

Ток через них можно определить согласно закону Ома:

 I1=U/R1{\displaystyle \ I_{1}=U/R_{1}}.

 I2=U/R2{\displaystyle \ I_{2}=U/R_{2}}.

Общий ток в цепи согласно первому закону Кирхгофа

 I=I1+I2{\displaystyle \ I=I_{1}+I_{2}}.

Применение

• Делитель тока имеет важное значение в схемотехнике в качестве элемента цепи для подключения устройства с номинальным током меньшим, чем протекающий в цепи.

• Датчик параметр-ток. На величину сопротивления влияют внешние факторы, например температура. Изменение температуры приводит к изменению сопротивления делителя тока. В результате изменяется ток через ветвь цепи.
• Измерение больших величин токов. Подключается два сопротивления. Через одно протекает малый ток (миллиамперы), через второе (называемое шунтом) — весь оставшийся ток. Измеряется ток через первое сопротивление. Далее выполняется расчет общего тока.

Ограничения в применении резистивных делителей тока

Для поддержания приемлемой точности работы делителя, необходимо, чтобы величина тока, протекающего через сопротивления делителя, была не менее чем в 10 раз больше, чем ток, протекающий в нагрузке (см. аналогичное требование у делителя напряжения). Увеличение этого показателя (до ×100,×1000 или больше) пропорционально увеличивает точность работы делителя, однако это также увеличивает поперечное сечение проводников, что увеличивает размеры, стоимость и снижает КПД схемы. Это одна из причин, по которой делители тока малопригодны в качестве источников постоянного тока для питания нагрузок. Для этой цели применяют иные схемотехнические решения, например стабилизаторы тока.

См. также

Ссылки

wiki.sc

Делитель тока — Википедия

Материал из Википедии — свободной энциклопедии

Дели́тель то́ка — простейшая линейная электрическая цепь, выходной ток которой представляет собой часть входного тока. Это обеспечивается распределением тока между ветвями делителя.

В качестве делителя тока обычно применяют элементы с регулируемым сопротивлением (потенциометры), подключаемые параллельно.^{[источник не указан 749 дней]} Можно представить как русло реки, разделяющееся на несколько рек. Согласно первому закону Кирхгофа, сумма токов, входящих в узел и выходящих из узла, равна нулю. Применяемые сопротивления для деления токов могут быть как активными, так и реактивными. Реактивные сопротивления возможно использовать только на переменном токе.

Резистивный делитель тока

Простейший резистивный делитель тока — это два параллельно включённых резистора R1{\displaystyle R_{1}} и R2{\displaystyle R_{2}}, подключённых к источнику напряжения U{\displaystyle U}. Поскольку резисторы соединены параллельно, то к ним приложено одинаковое напряжение.

Ток через них можно определить согласно закону Ома:

 I1=U/R1{\displaystyle \ I_{1}=U/R_{1}}.

 I2=U/R2{\displaystyle \ I_{2}=U/R_{2}}.

Общий ток в цепи согласно первому закону Кирхгофа

 I=I1+I2{\displaystyle \ I=I_{1}+I_{2}}.

Применение

• Делитель тока имеет важное значение в схемотехнике в качестве элемента цепи для подключения устройства с номинальным током меньшим, чем протекающий в цепи.

• Датчик параметр-ток. На величину сопротивления влияют внешние факторы, например температура. Изменение температуры приводит к изменению сопротивления делителя тока. В результате изменяется ток через ветвь цепи.
• Измерение больших величин токов. Подключается два сопротивления. Через одно протекает малый ток (миллиамперы), через второе (называемое шунтом) — весь оставшийся ток. Измеряется ток через первое сопротивление. Далее выполняется расчет общего тока.

Ограничения в применении резистивных делителей тока

Для поддержания приемлемой точности работы делителя, необходимо, чтобы величина тока, протекающего через сопротивления делителя, была не менее чем в 10 раз больше, чем ток, протекающий в нагрузке (см. аналогичное требование у делителя напряжения). Увеличение этого показателя (до ×100,×1000 или больше) пропорционально увеличивает точность работы делителя, однако это также увеличивает поперечное сечение проводников, что увеличивает размеры, стоимость и снижает КПД схемы. Это одна из причин, по которой делители тока малопригодны в качестве источников постоянного тока для питания нагрузок. Для этой цели применяют иные схемотехнические решения, например стабилизаторы тока.

См. также

Ссылки

wikipedia.green

Делитель тока — Википедия

Материал из Википедии — свободной энциклопедии

Дели́тель то́ка — простейшая линейная электрическая цепь, выходной ток которой представляет собой часть входного тока. Это обеспечивается распределением тока между ветвями делителя.

В качестве делителя тока обычно применяют элементы с регулируемым сопротивлением (потенциометры), подключаемые параллельно.^{[источник не указан 749 дней]} Можно представить как русло реки, разделяющееся на несколько рек. Согласно первому закону Кирхгофа, сумма токов, входящих в узел и выходящих из узла, равна нулю. Применяемые сопротивления для деления токов могут быть как активными, так и реактивными. Реактивные сопротивления возможно использовать только на переменном токе.

Резистивный делитель тока

Простейший резистивный делитель тока — это два параллельно включённых резистора R1{\displaystyle R_{1}} и R2{\displaystyle R_{2}}, подключённых к источнику напряжения U{\displaystyle U}. Поскольку резисторы соединены параллельно, то к ним приложено одинаковое напряжение.

Ток через них можно определить согласно закону Ома:

 I1=U/R1{\displaystyle \ I_{1}=U/R_{1}}.

 I2=U/R2{\displaystyle \ I_{2}=U/R_{2}}.

Общий ток в цепи согласно первому закону Кирхгофа

 I=I1+I2{\displaystyle \ I=I_{1}+I_{2}}.

Видео по теме

Применение

• Делитель тока имеет важное значение в схемотехнике в качестве элемента цепи для подключения устройства с номинальным током меньшим, чем протекающий в цепи.

• Датчик параметр-ток. На величину сопротивления влияют внешние факторы, например температура. Изменение температуры приводит к изменению сопротивления делителя тока. В результате изменяется ток через ветвь цепи.
• Измерение больших величин токов. Подключается два сопротивления. Через одно протекает малый ток (миллиамперы), через второе (называемое шунтом) — весь оставшийся ток. Измеряется ток через первое сопротивление. Далее выполняется расчет общего тока.

Ограничения в применении резистивных делителей тока

Для поддержания приемлемой точности работы делителя, необходимо, чтобы величина тока, протекающего через сопротивления делителя, была не менее чем в 10 раз больше, чем ток, протекающий в нагрузке (см. аналогичное требование у делителя напряжения). Увеличение этого показателя (до ×100,×1000 или больше) пропорционально увеличивает точность работы делителя, однако это также увеличивает поперечное сечение проводников, что увеличивает размеры, стоимость и снижает КПД схемы. Это одна из причин, по которой делители тока малопригодны в качестве источников постоянного тока для питания нагрузок. Для этой цели применяют иные схемотехнические решения, например стабилизаторы тока.

См. также

Ссылки

wiki2.red