Что такое параллельное соединение резисторов. Как рассчитать общее сопротивление при параллельном подключении. Какие преимущества дает использование параллельного соединения в электрических цепях. Где применяется параллельное соединение резисторов на практике.
Что такое параллельное соединение резисторов
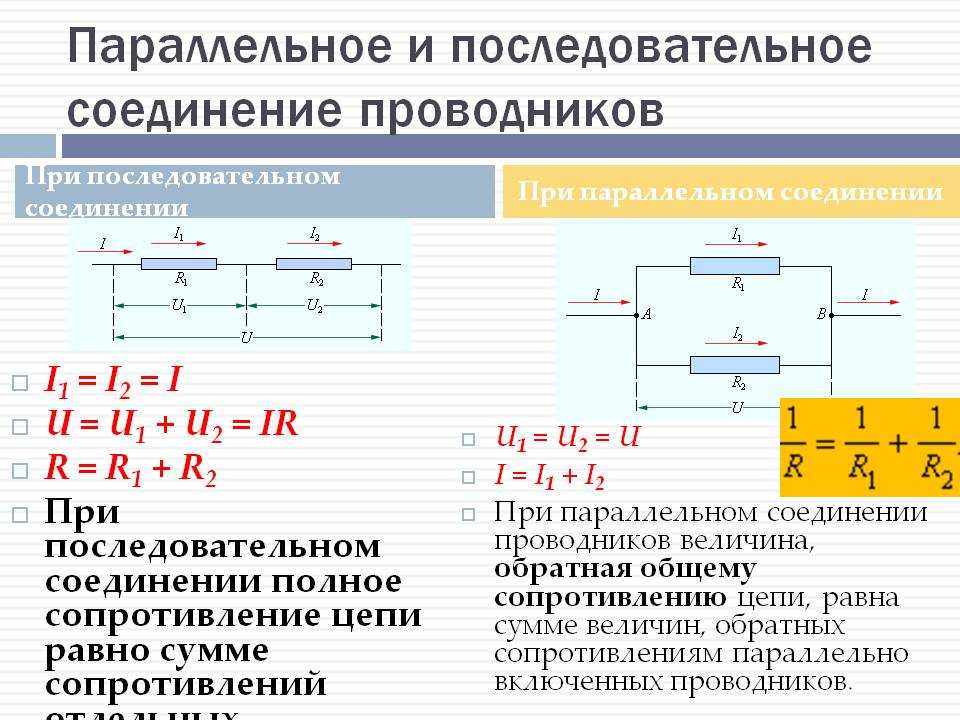
Параллельное соединение резисторов — это способ подключения двух или более резисторов, при котором начала всех резисторов соединены в одной точке, а концы — в другой. При таком соединении напряжение на всех резисторах одинаково и равно напряжению источника питания, а общий ток делится между резисторами.
Основные свойства параллельного соединения:
- Напряжение на всех резисторах одинаково
- Общий ток равен сумме токов через отдельные резисторы
- Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи
Параллельное соединение широко используется в электротехнике, так как позволяет разделить ток между несколькими потребителями и снизить общее сопротивление участка цепи.
Расчет общего сопротивления при параллельном соединении
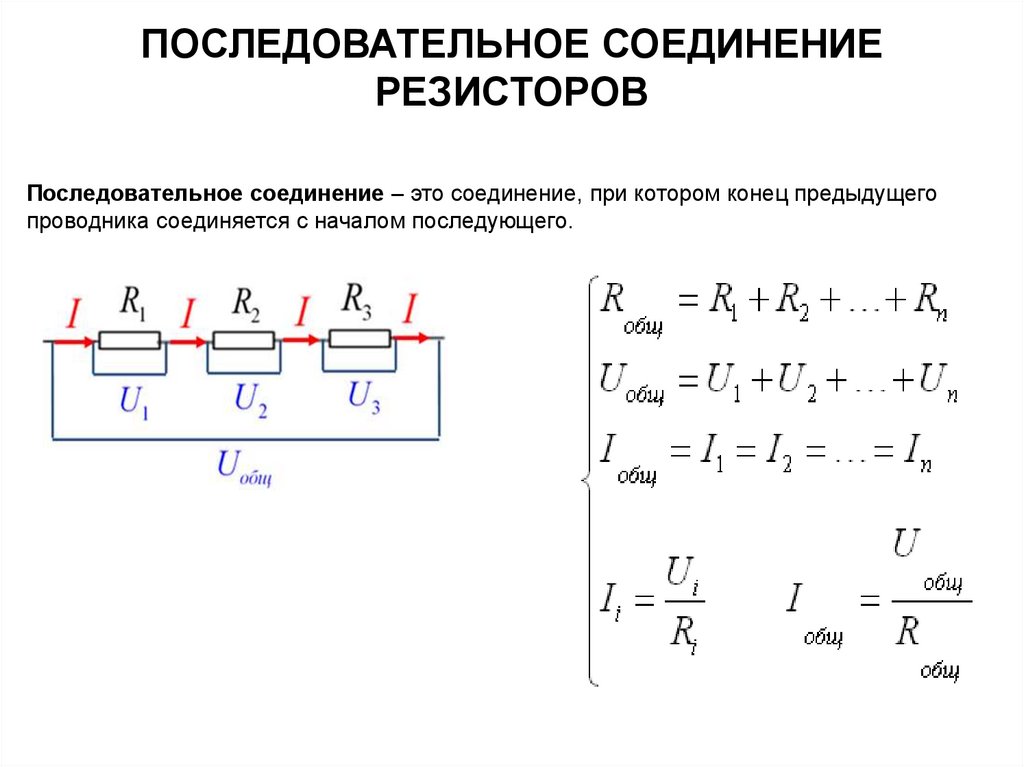
Для расчета общего сопротивления параллельно соединенных резисторов используется следующая формула:
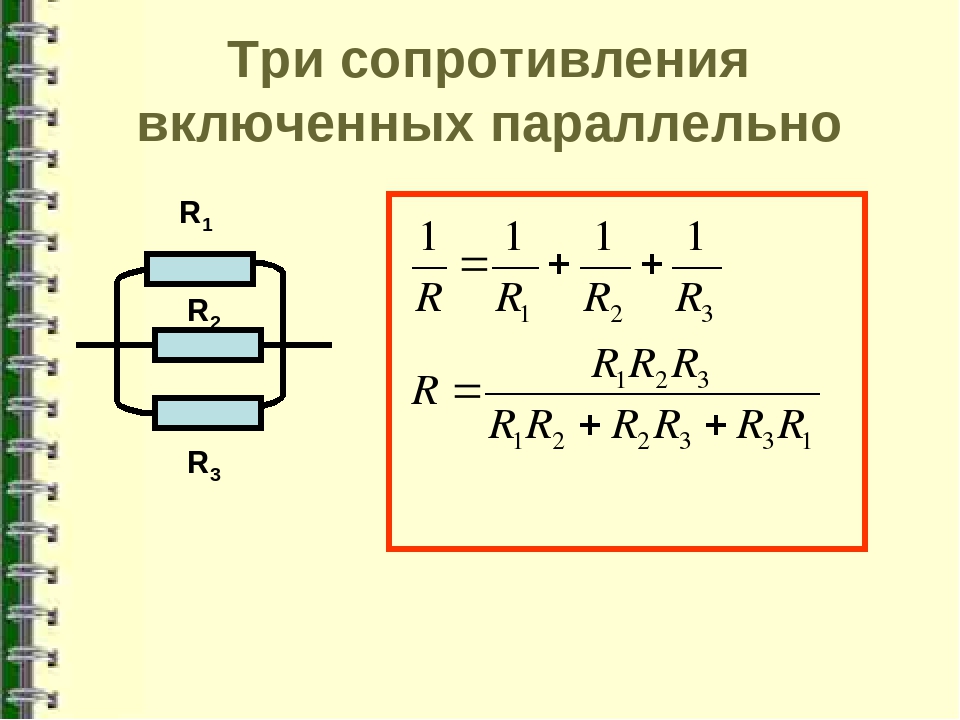
1/R = 1/R1 + 1/R2 + 1/R3 + …
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Для двух параллельно соединенных резисторов формула упрощается:
R = (R1 * R2) / (R1 + R2)
Как видно из формулы, общее сопротивление всегда меньше сопротивления наименьшего резистора в цепи. Это одно из ключевых свойств параллельного соединения.
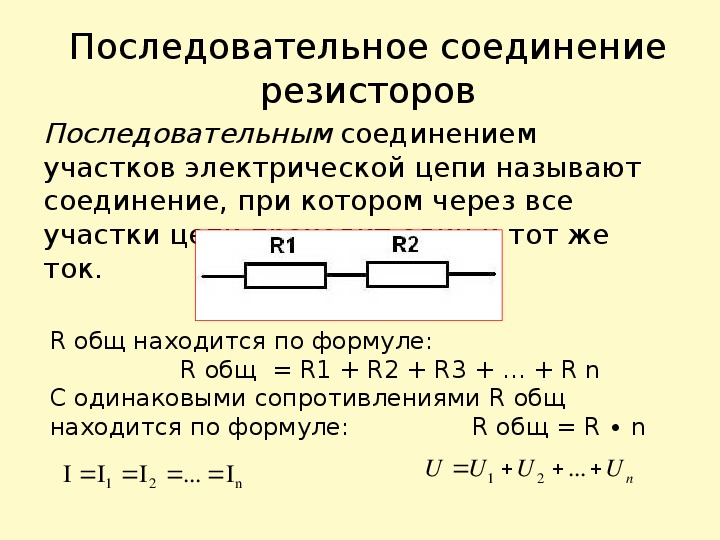
Распределение токов в параллельной цепи
При параллельном соединении общий ток делится между резисторами обратно пропорционально их сопротивлениям. То есть чем меньше сопротивление резистора, тем больший ток через него протекает.
Ток через отдельный резистор можно рассчитать по формуле:
I = U / R
где I — ток через резистор, U — напряжение (одинаковое для всех резисторов), R — сопротивление данного резистора.
Общий ток в цепи равен сумме токов через все резисторы:
I = I1 + I2 + I3 + …
Это позволяет разделить общий ток между несколькими потребителями, что часто используется на практике.
Преимущества параллельного соединения резисторов
Параллельное соединение резисторов имеет ряд важных преимуществ:
- Снижение общего сопротивления участка цепи
- Возможность разделения тока между несколькими потребителями
- Повышение надежности — при выходе из строя одного резистора цепь продолжает работать
- Возможность получения нестандартных номиналов сопротивлений
- Упрощение расчетов в сложных цепях
Благодаря этим преимуществам параллельное соединение широко применяется в различных электронных устройствах и электрических системах.
Практическое применение параллельного соединения резисторов
Параллельное соединение резисторов используется во многих областях электротехники и электроники:
- В системах электроснабжения — для распределения тока между потребителями
- В осветительных системах — для подключения нескольких лампочек
- В электронных схемах — для получения нужных номиналов сопротивлений
- В измерительных приборах — для расширения пределов измерения
- В системах защиты — для создания резервных цепей
Например, в бытовой электросети все розетки и электроприборы подключены параллельно. Это позволяет обеспечить одинаковое напряжение для всех устройств и разделить между ними общий ток.
Расчет параллельного соединения на практике
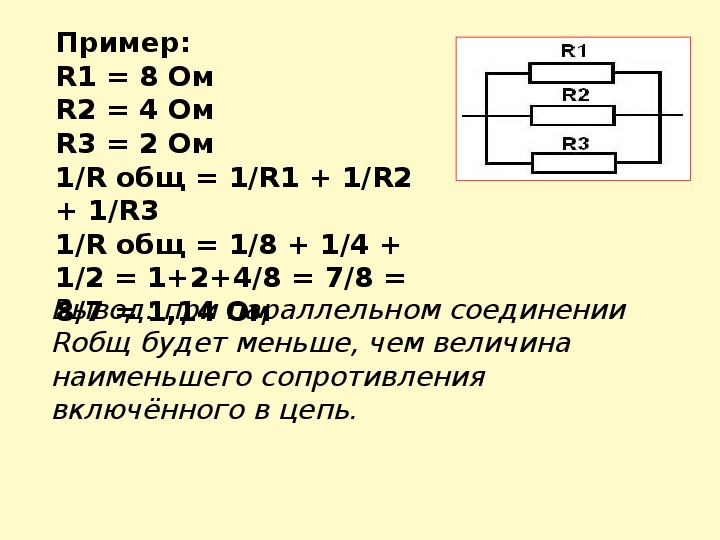
Рассмотрим пример расчета параллельного соединения трех резисторов:
Дано: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 12 В
1. Рассчитаем общее сопротивление:
1/R = 1/10 + 1/20 + 1/30 = 0.1 + 0.05 + 0.033 = 0.183
R = 1/0.183 = 5.46 Ом
2. Рассчитаем общий ток:
I = U/R = 12/5.46 = 2.2 А
3. Рассчитаем токи через каждый резистор:
I1 = U/R1 = 12/10 = 1.2 А
I2 = U/R2 = 12/20 = 0.6 А
I3 = U/R3 = 12/30 = 0.4 А
Как видим, общий ток 2.2 А разделился между резисторами обратно пропорционально их сопротивлениям.
Особенности параллельного соединения в цепях постоянного и переменного тока
Принципы параллельного соединения резисторов одинаковы для цепей постоянного и переменного тока. Однако в цепях переменного тока нужно учитывать ряд особенностей:
- Полное сопротивление (импеданс) зависит от частоты тока
- Необходимо учитывать реактивные составляющие — емкостное и индуктивное сопротивление
- Токи и напряжения могут быть сдвинуты по фазе
Поэтому расчеты для цепей переменного тока обычно более сложные и требуют использования комплексных чисел и векторных диаграмм.
Сравнение параллельного и последовательного соединения резисторов
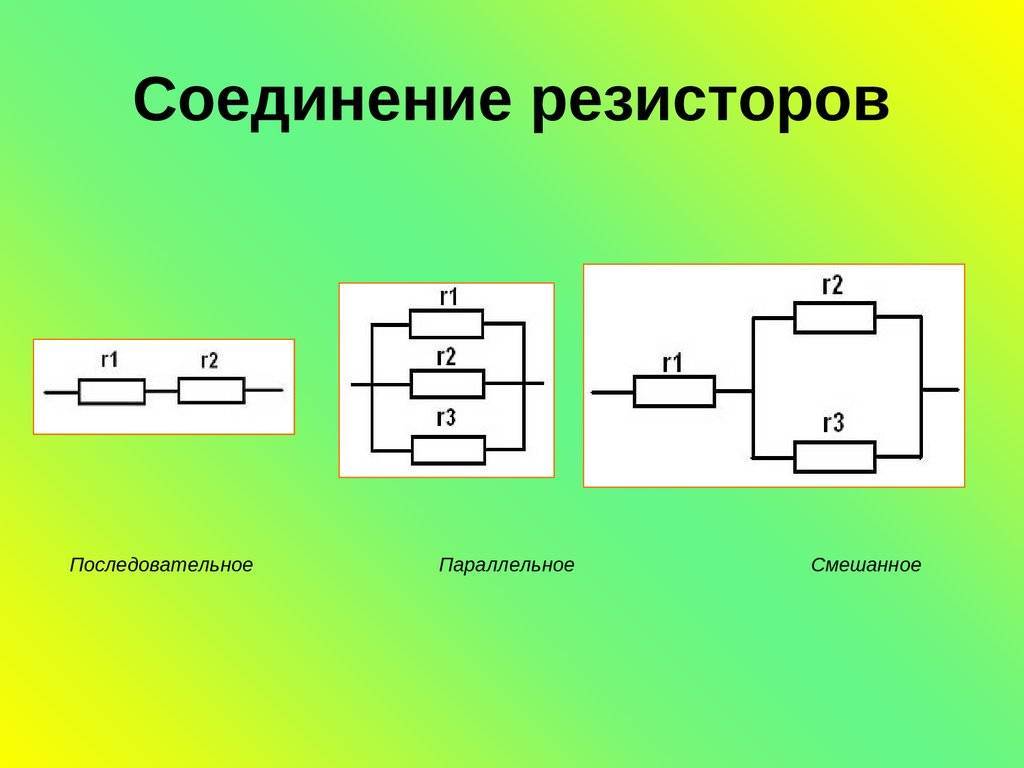
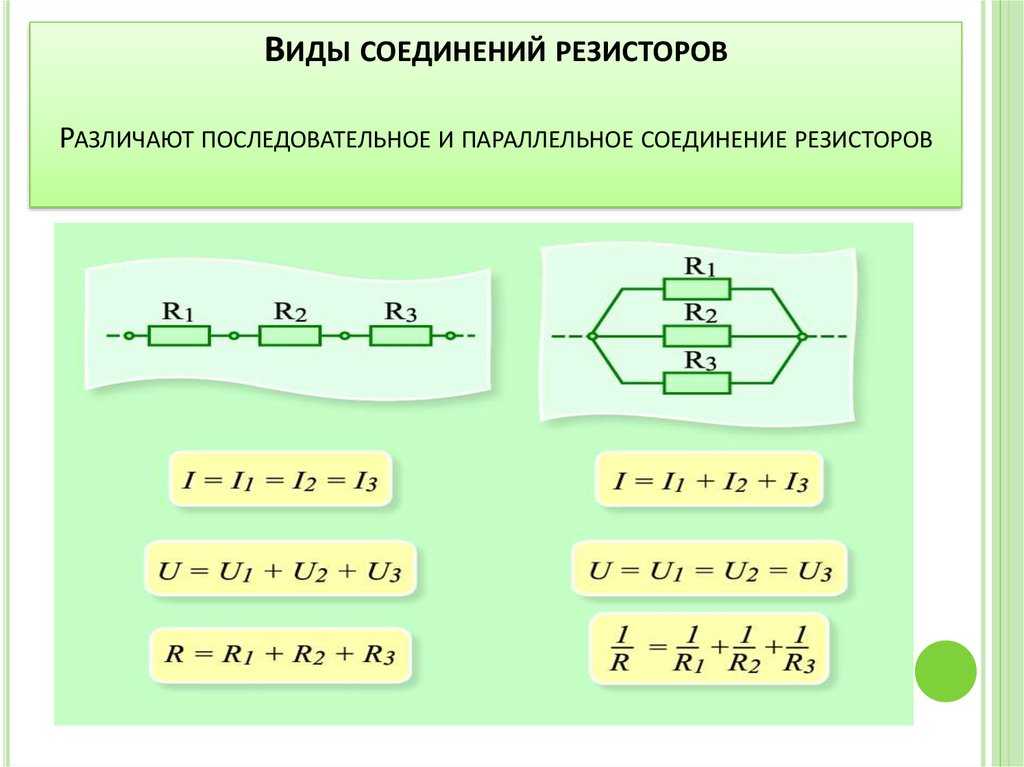
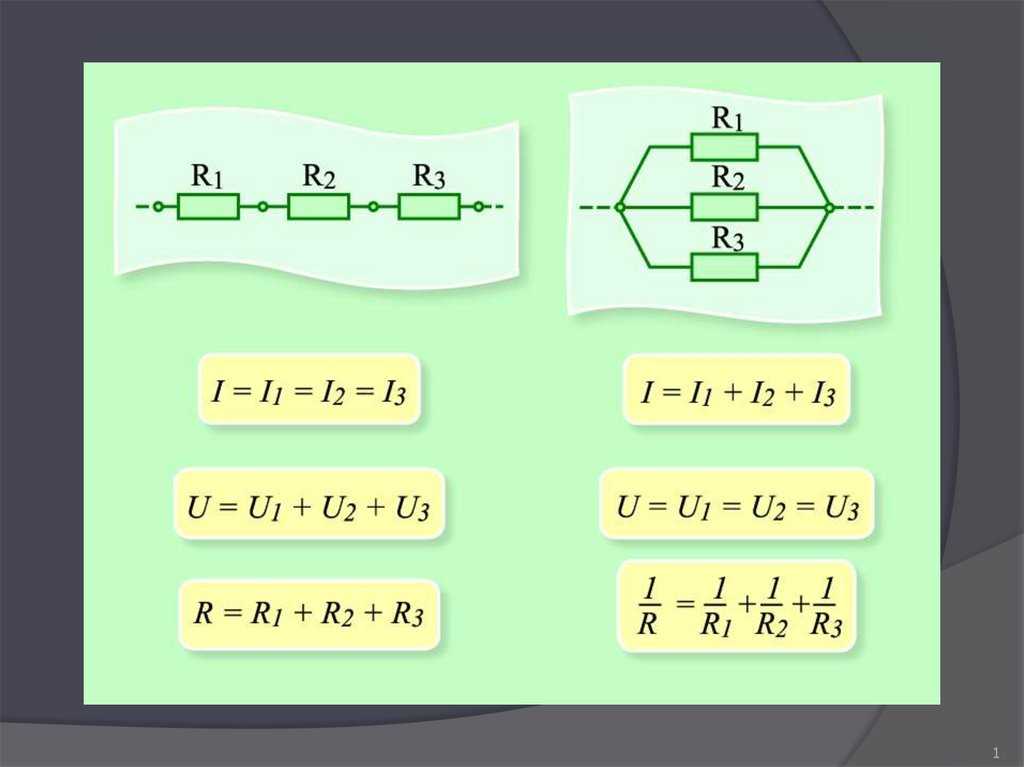
Параллельное и последовательное соединение резисторов имеют принципиальные различия:
| Параметр | Параллельное соединение | Последовательное соединение |
|---|---|---|
| Напряжение | Одинаково на всех резисторах | Сумма напряжений на резисторах |
| Ток | Сумма токов через резисторы | Одинаков во всей цепи |
| Общее сопротивление | Меньше наименьшего резистора | Сумма всех сопротивлений |
Выбор типа соединения зависит от конкретной задачи и требуемых параметров цепи.
Заключение
Параллельное соединение резисторов — важный принцип построения электрических цепей, позволяющий эффективно распределять ток и управлять сопротивлением участков цепи. Понимание особенностей параллельного соединения необходимо для проектирования и анализа различных электронных устройств и систем электроснабжения.
Основные преимущества параллельного соединения — снижение общего сопротивления, разделение тока между потребителями и повышение надежности — обеспечивают его широкое применение в современной электротехнике и электронике.

Решение задач по теме: «Смешанное соединение проводников» 8 класс онлайн-подготовка на Ростелеком Лицей
Необходимые для решения задач формулы и факты
Под соединением проводников подразумевается соединение резисторов – приборов, сделанных на основе сопротивления проводников. На предыдущих уроках были рассмотрены параллельное и последовательное соединения. На данном уроке будут рассмотрены задачи на смешанное соединение проводников, то есть когда в цепи присутствует и последовательное, и параллельное соединение.
Для решения задач сначала рассмотрим формулы для связи различных величин при параллельном и последовательном соединениях:
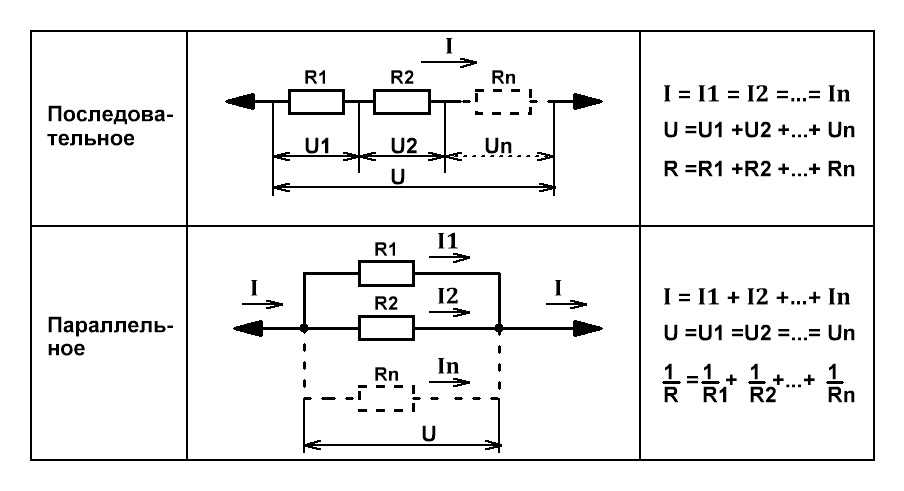
Если проводники соединены последовательно, то сила тока в них одинакова и равна силе тока в цепи. При этом общее напряжение в цепи будет состоять из суммы напряжений на каждом проводнике. А если говорить о сопротивлении этого участка цепи, в котором проводники соединены последовательно, то оно равно сумме сопротивлений проводников.
В параллельном соединении все по-другому. Сила тока в каждой ветке этой цепи будет различной, при этом общая сила тока в цепи будет вычисляться как сумма сил токов в проводниках. Напряжение на проводниках, соединенных последовательно, будет одинаковым. Общее сопротивление этого участка цепи, так называемое «эквивалентное сопротивление» R, будет вычисляться по следующей формуле: .
Также стоит отметить, что параллельное соединение обычно применяется при включении бытовых приборов, а последовательное – для того, чтобы создать длинную неразветвленную цепь.
Задача №1
Рассмотрим следующую задачу. Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом. Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В. Необходимо определить силу тока во всей электрической цепи (рис.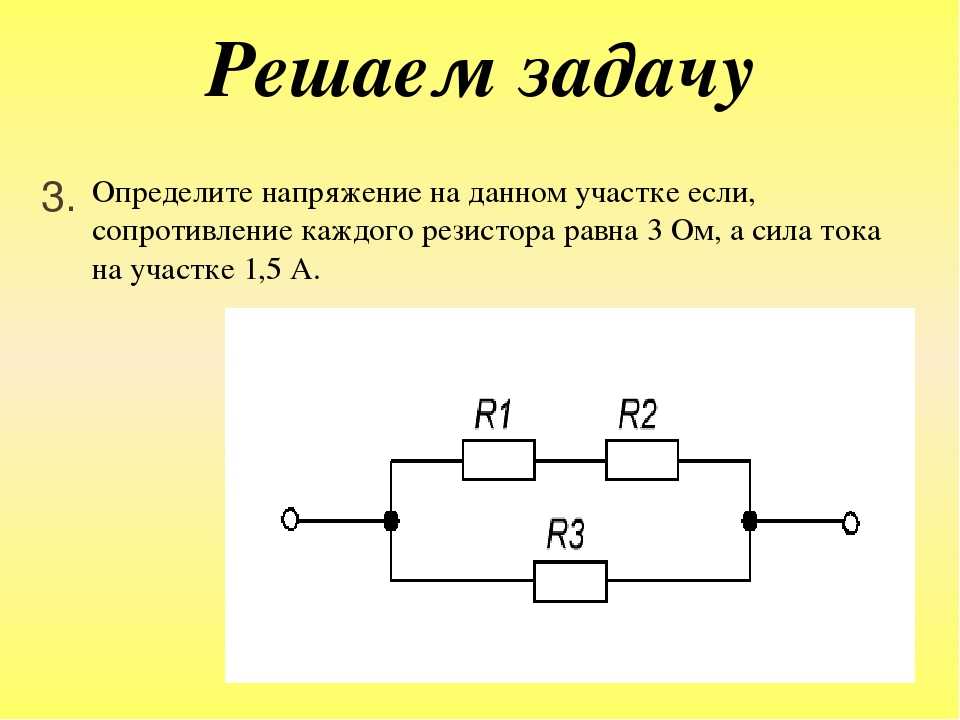 1).
1).
Рис. 1. Условия и рисунок задачи № 1
Как видим, резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним. Источник дает напряжение 2,4 В, соответственно, на участке АВ напряжение будет также 2,4 В. Сила тока, которую требуется найти, – это сила тока, протекающая через амперметр А.
Такое соединение проводников называется неразветвленным. В промышленности обычно изготавливается набор резисторов с четко определенными сопротивлениями, но для экспериментов могут понадобиться любые различные сопротивления. Тогда с помощью таких схем можно создавать нужное сопротивление для эксперимента или прибора.
Далее требуется определить эквивалентное сопротивление неразветвленной части. Сначала посмотрим, чему равно сопротивление R’ участка цепи АВ, который содержит только резисторы R1 и R2. Они соединены последовательно, тогда R′=R1+R2=2 [Ом]. Теперь можно перерисовать электрическую цепь, заменив сопротивления R1 и R2 эквивалентным им сопротивлением R’ (рис. 2).
2).
Рис. 2. Первая замена эквивалентным сопротивлением
Теперь можно сказать, что участок АВ включает в себя не три, а два сопротивления: R3 и R’. Эти два сопротивления соединены параллельно, соответственно, можно найти общее сопротивление электрической цепи по формуле . Выразив R и подставив значения , получаем:
Стоит отметить, что сопротивления были соединены, но общее сопротивление получилось все равно равным 1 Ом. Теперь электрическую цепь можно заменить следующей (рис. 3):
Рис. 3. Вторая замена эквивалентным сопротивлением
На рис. 3 сопротивление R=1 Ом называется эквивалентным сопротивлением, поскольку три сопротивления были заменены на одно. Чтобы рассчитать силу тока в цепи, надо использовать закон Ома для участка цепи: . Напряжение на сопротивлении R – это напряжение на участке АВ (Рис. 1), которое, в свою очередь, равно 2,4.Тогда . Это и будет значение силы тока в электрической цепи, которое покажет амперметр.
Задача №2
Теперь рассмотрим задачу, в которой также будет три сопротивления, но соединены они будут по-другому (рис. 4):
4):
Рис. 4. Условие задачи № 2
Два сопротивления R1 и R2 соединены параллельно (R1=R2=2 Ом), к ним еще последовательно присоединено сопротивление R3=1 Ом. Амперметр показывает силу тока в цепи, равную I=0,5 А. Требуется определить напряжение на концах участка этой цепи, то есть на участке АВ.
Для начала определим сопротивление участка цепи, содержащего сопротивления R1 и R2. Эти два сопротивления соединены параллельно, значит, их эквивалентное сопротивление R’ можно найти из формулы . Подставляя значения, получаем:
Теперь можно сказать, что цепь включает в себя только два сопротивления: R’и R3, которые соединены последовательно.
Рис. 5. Замена параллельного соединения эквивалентным сопротивлением
В задаче требуется определить напряжение. Для этого используется прибор, который называется вольтметр. В цепь он включается параллельно. И рассмотрим участок цепи, в котором все три сопротивления уже заменены эквивалентным.
Рис. 6. Включение вольтметра в цепь
6. Включение вольтметра в цепь
Вольтметр включен в месте, соответствующем участку АВ на рис. 4. Соответственно, он измеряет напряжение на это участке цепи. Чтобы найти значения этого напряжения, требуется сначала найти эквивалентное сопротивление. Сопротивления R’ и R3 соединены последовательно (рис. 5), значит, эквивалентное сопротивление определяется по формуле:
Теперь из закона Ома для участка цепи можно найти напряжение:
Значит, вольтметр должен будет показать значения напряжения в 1 В.
Расчет более сложных цепей
На уроке были рассмотрены соединения только трех сопротивлений, когда они были последовательные, к ним параллельно подключается третий, или когда два соединены параллельно, а к ним последовательно подключают третье сопротивление. Но реальные схемы значительно сложнее. Они содержат огромное количество различных элементов, сопротивлений, поэтому имеются достаточно сложные методы расчетов электрических цепей.
Впервые расчетами таких сложных электрических цепей озадачились ученые приблизительно в XIX веке, и появились новые правила, которые используются и по сей день. Немецкий ученый Кирхгоф разработал возможность расчета электрических сложных цепей, поэтому правила, которые используют для сложных цепей, называются «правилами Кирхгофа».
На следующих уроках будет рассмотрено понятие мощности и работы силы тока.
Список литературы
- Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
- Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Festival.1september.ru (Источник)
- Electroandi.ru (Источник)
- Bocharova.ucoz.ru (Источник)
Домашнее задание
- Стр.
 117: задачи № 4, 5. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
117: задачи № 4, 5. Перышкин А.В. Физика 8. – М.: Дрофа, 2010. - В каком случае эквивалентное сопротивление будет больше: если три проводника с сопротивлениями 1 Ом каждый соединить параллельно или последовательно?
- Два сопротивления R1=1 Ом и R2= 2 Ом соединены последовательно, к ним параллельно присоединено сопротивление 3 Ом. Чему равно эквивалентное сопротивление?
- Сколько различных цепей можно составить из трех резисторов с сопротивлениями 1 Ом каждый так, чтоб их эквивалентные сопротивления была различными?
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении. Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Интересное: Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является… Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 5 из 17Следующая ⇒ Понимание последствий параллельного или последовательного подключения резисторов очень важно и поможет вам понять и упростить схемы с помощью этих простых формул для последовательного и параллельного сопротивления: В этом примере схемы, R1 и R2 соединены параллельно, и могут быть заменены одним резистором R3 в соответствии с формулой: Кроме того, что эту формулу можно использовать для упрощения схем, она может быть использована для создания номиналов резисторов, которых у вас нет. Последовательно соединённые резисторы могут быть заменены одним резистором, значение которого будет равно сумме этих двух, в связи с тем, что это соединение обеспечивает дополнительное сопротивление тока. Таким образом, эквивалентное сопротивление R3 очень просто вычисляется: R3=R1+R2 В интернете есть удобные он-лайн калькуляторы для расчета последовательного и параллельного соединения резисторов. Токоограничивающий резистор Самая основная роль токоограничивающих резисторов — это контроль тока, который будет протекать через устройство или проводник. Для понимания их работы, давайте сначала разберём простую схему, где лампа непосредственно подключена к 9В батареи. Лампа, как и любое другое устройство, которое потребляет электроэнергию для выполнения определенной задачи (например, светоизлучение) имеет внутреннее сопротивление, которое определяет его текущее потребление. Теперь, когда лампа будет рассматриваться как резистор, мы можем использовать закон Ома для расчета тока, проходящего через него. Закон Ома гласит, что ток, проходящий через резистор равен разности напряжений на нем, поделенное на сопротивление резистора: I=V/R или точнее так: Теперь обратите внимание на рисунок выше, где добавлен токоограничительный резистор. Он будет ограничивать ток идущий к лампе, как это следует из названия. Вы можете контролировать, количество тока протекающего через лампу, просто выбрав правильное значение R1. Большой резистор будет сильно снижать ток, а небольшой резистор менее сильно (так же, как в нашей аналогии с водой). Математически это запишется так: Из формулы следует, что ток уменьшится, если значение R1 увеличится. Вы можете воспользоваться он-лайн калькулятором для расчета токоограничительного резистора светодиода. ⇐ Предыдущая12345678910Следующая ⇒ Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… |
резисторов параллельно
Мы говорим, что два резистора \(R_1\) и \(R_2\) соединены параллельно, если ток, поступающий в комбинацию, разделяется и рекомбинирует сразу после прохождения через каждый из резисторов, как показано на рисунке 36. 3.1. Два резистора в параллельной цепи также называются двумя ветвями схемы, а точки \(a\) и \(b\), где они разделяются или соединяются, называются соединениями или узлами .
3.1. Два резистора в параллельной цепи также называются двумя ветвями схемы, а точки \(a\) и \(b\), где они разделяются или соединяются, называются соединениями или узлами .
Еще одно свойство резисторов, включенных параллельно, заключается в том, что падение потенциала на каждом резисторе одинаково для всех резисторов, включенных параллельно, поскольку каждый резистор подключен к одним и тем же точкам соединения на двух концах.
Рисунок 36.3.1. Два резистора соединены параллельно. Ток \(I\), входящий в комбинацию на стыке \(a\) , разделяет с отдельными токами, входящими в два резистора, которые затем сразу же объединяются в стыке \(b\) после выхода из каждого резистора. Кроме того, падение потенциала каждого резистора одинаково, а именно, \(\Delta \phi_1 = \Delta\phi_2 = \phi_a — \phi_b\text{.}\)Подраздел 36.3.1 Падение потенциала на резисторах, включенных параллельно
На рисунке 36.3.1 резисторы параллельно подключены к источнику напряжения, так что мы устанавливаем одинаковую разность потенциалов на обоих резисторах.
\begin{уравнение} \Delta \phi_1 = \Delta \phi_2 = \phi_a — \phi_b = V.\label{eq-over-all-potential-drop-R-in-series}\tag{36.3.1} \end{уравнение}
Подраздел 36.3.2 Токи в резисторах, включенных параллельно
Применение закона Ома к двум резисторам по отдельности дает нам токи через отдельные резисторы сразу.
\начать{выравнивание} I_1 \amp = \dfrac{\Delta\phi_1}{R_1} = \dfrac{V}{R_1}\label{eq-resistors-in-parallel-current-I1}\tag{36.3.2}\\ I_2 \amp = \dfrac{\Delta\phi_2}{R_2} = \dfrac{V}{R_2} \label{eq-resistors-in-parallel-current-I2}\tag{36.3.3} \end{выравнивание}
Они показывают, что если \(R_1 \gt R_2\text{,}\), то \(I_1 \lt I_2\text{.}\) То есть больший ток будет течь по ветви с меньшим сопротивлением. Если ветвь не имеет сопротивления, то через любую другую ветвь не останется тока. Такие ответвления называются короткими в цепи.
Поскольку полный ток \(I\) входит в соединение \(a\), а токи \(I_1\) и \(I_2\) выходят и заряд не накапливается в \(a\text{,}\), мы можем применить сохранения заряда, чтобы заключить следующее сохранение тока в каждом переходе.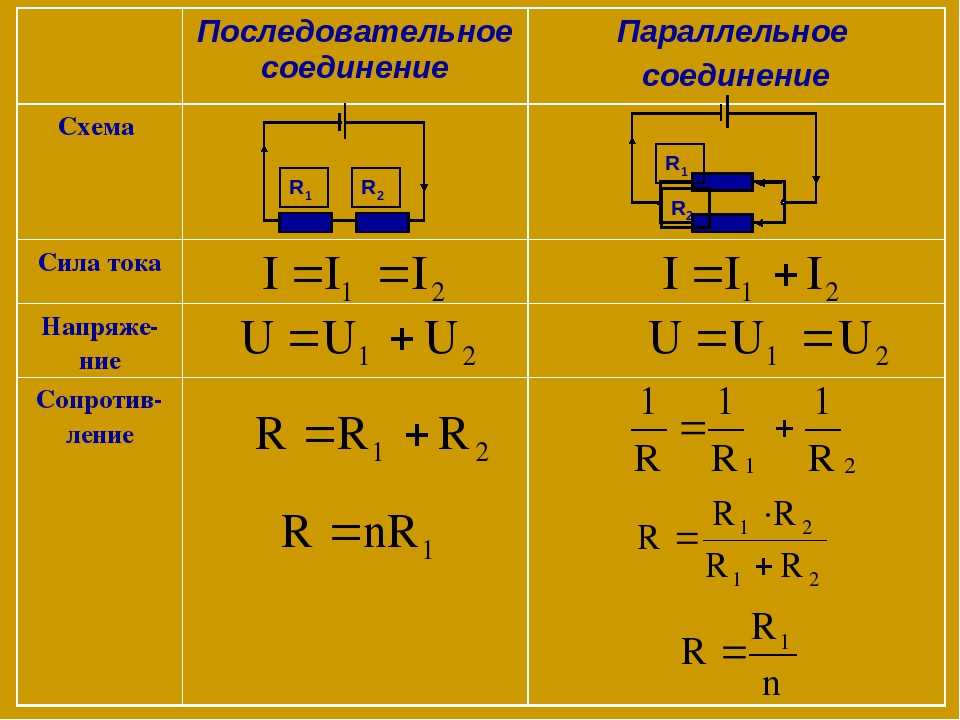
\begin{уравнение*} Я — И_1 — И_2 = 0, \end{уравнение*}
то есть общий ток в цепи
\begin{уравнение} I = I_1 + I_2 = \dfrac{V}{R_1} + \dfrac{V}{R_2} = V \left(\dfrac{1}{R_1} + \dfrac{1}{R_2} \right) .\ метка {экв-резисторы-в-параллельном-ток-сохранение}\тег{36.3.4} \end{уравнение}
Это показывает, что резисторы, включенные параллельно , делят между собой общий ток. Вот почему мы часто называем параллельные резисторы делителями тока . Решая это для \(V\) и используя его в уравнениях. (36.3.2) и (36.3.3), мы находим ток в каждой ветви через суммарный ток, входящий или выходящий из параллельных резисторов. После упрощения получаем следующие полезные формулы.
\начать{выравнивание} I_1 \amp = I\,\dfrac{R_2}{R_1+R_2},\label{eq-резисторы-параллельно-ток-I1-in-I}\tag{36.3.5}\\ I_2 \amp = I\,\dfrac{R_1}{R_1+R_2}. \label{eq-резисторы-параллельно-ток-I2-in-I}\tag{36.3.6} \end{выравнивание}
Обратите внимание, что резистор в числителе каждой формулы является резистором в другой ветви.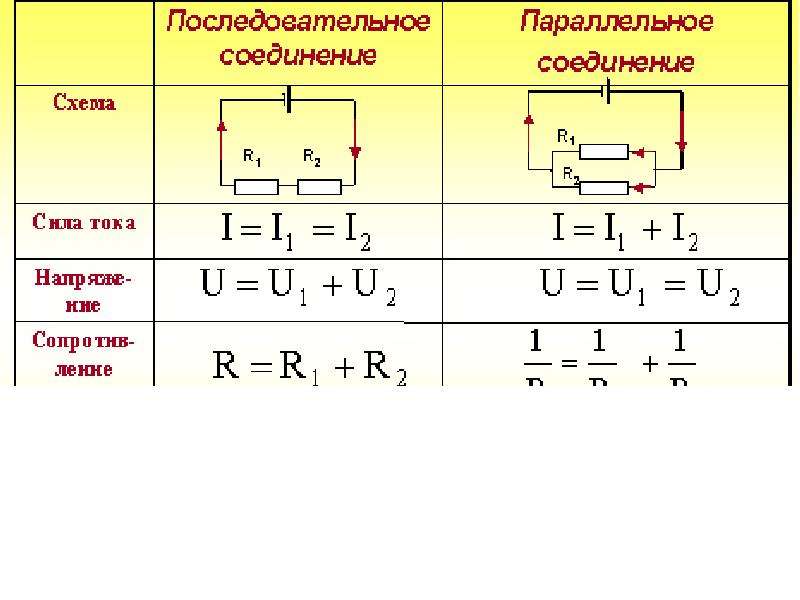 {-1} \text{.}\)
{-1} \text{.}\)
Мы будем часто писать уравнение. (36.3.7) как обратное сопротивление, т. е. соотношение проводимости.
\begin{уравнение} \dfrac{1}{R_\text{parallel}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} \Longleftrightarrow G_\text{parallel} = G_1 + G_2,\label{eq-equiv -res-parallel-resitors-inv-resistance}\tag{36.3.9} \end{уравнение}
, где я использовал обратную зависимость между проводимостью \(G\) и сопротивлением \(R\text{.}\)
\begin{уравнение*} G = \dfrac{1}{R}. \end{уравнение*}
Для \(N\) резисторов, включенных параллельно, вы можете показать, что
\begin{уравнение} \frac{1}{R_\text{parallel} } = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \cdots + \frac{1}{R_{N }},\тег{36.3.10} \end{уравнение}
и следующие для проводимости.
\begin{уравнение} G_\text{параллельно} = G_1 + G_2 + \cdots + G_N.\tag{36.3.11} \end{уравнение}
Следовательно, проводимости складываются в параллельной цепи. Ранее мы обнаружили, что сопротивления складываются последовательно.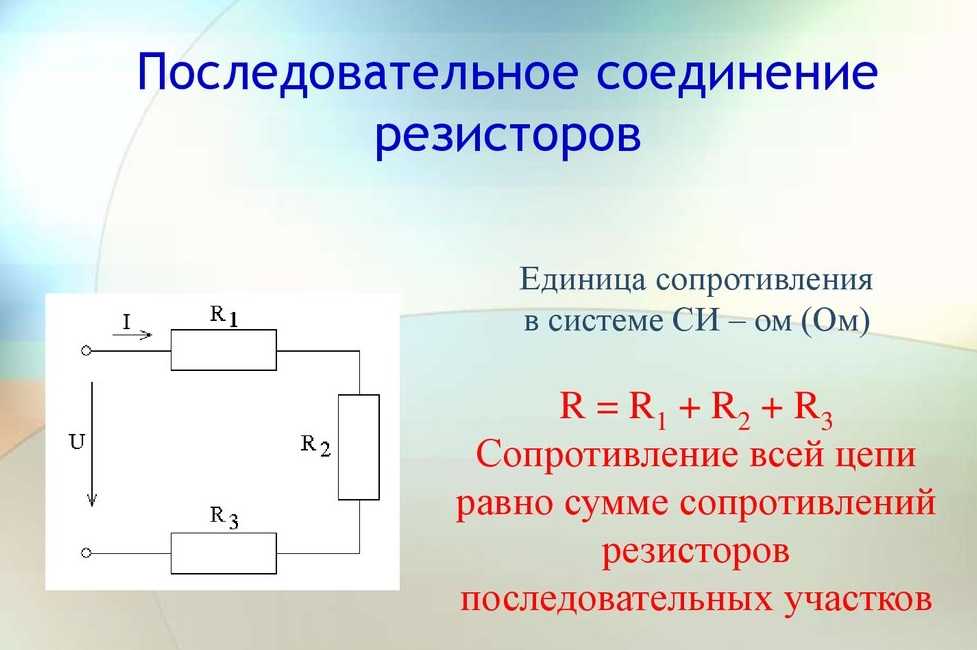
КПП 36.3.3. Делитель тока.
Рассмотрим схему, показанную на рисунке 36.3.4.
(а) Найдите процент тока, проходящего через каждый резистор.
(b) Найдите эквивалентное сопротивление источника напряжения.
(c) Найдите ток через источник напряжения.
(d) Найдите ток в каждом резисторе.
Рисунок 36.3.4.Подсказка
Используйте определения.
Ответ
(a) \(75\%,\ 25\%\text{,}\) (b) \(75\ \Omega \text{,}\) (c) \(267\text{ мА}\текст{,}\) (г) \(67\текст{ мА},\ 200\текст{ мА}\текст{.}\)
Решение 1 (a)
(a) В этом примере ток \(I_1\) будет больше тока \(I_2\), так как \(I_1\) проходит через меньшее сопротивление.
\begin{выравнивание*}
I_1 \amp = \left(\frac{300\Omega}{100\Omega + 300\Omega } \right) I = \frac{3}{4} I. \\
I_2 \amp = \left(\frac{100\Omega}{100\Omega + 300\Omega } \right) I = \frac{1}{4} I.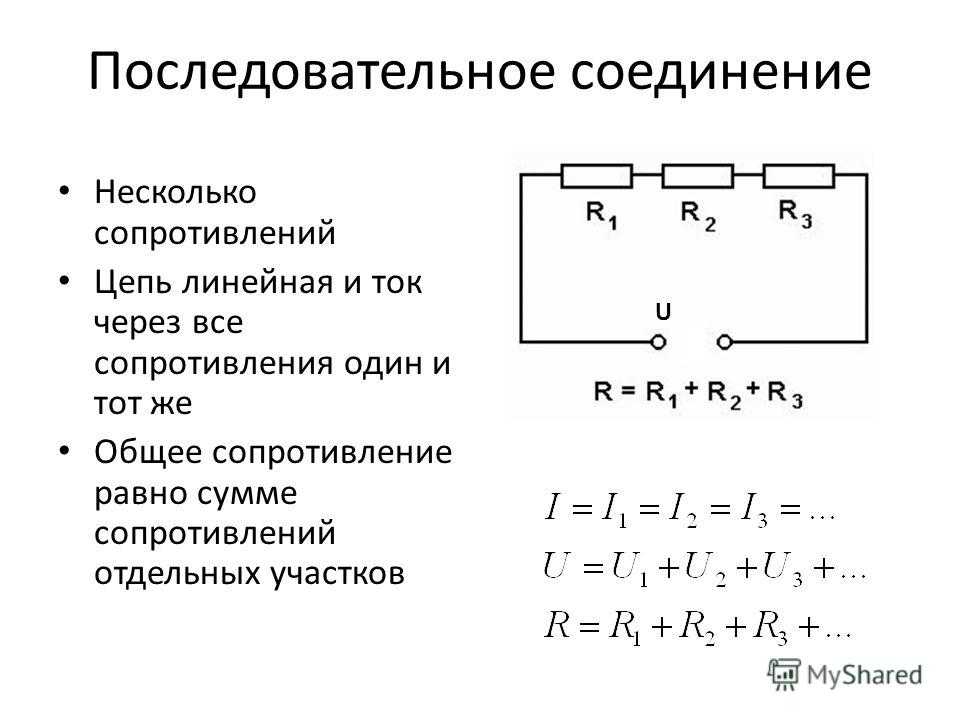 \end{align*}
\end{align*}
Следовательно, 75% всего тока проходит через резистор \(100\;\Omega\) и \(25\%\) через резистор \(300\; \Omega\). 9{-1} = \dfrac{R_1 R_2}{R_1 + R_2}\\ \amp = \dfrac{100\Omega \times 300\Omega }{100\Omega + 300\Omega } = 75\ \Omega. \end{align*}
Решение 3 (c)
(c) Эквивалентное сопротивление источника равно эквивалентному сопротивлению параллельных резисторов.
\begin{выравнивание*} I \amp = \dfrac{V}{R_\text{parallel}} = \dfrac{20\text{ V}}{75\ \Omega} = 267\text{ мА} \end{align*}
Решение 4 (d)
(d) Используя результаты (a) и (c), мы получаем
\begin{align*} I_1 \amp = \frac{3}{4} I = 67\text{ мА}.\\ I_2 \amp = \frac{1}{4} I = 200\text{ мА}. \end{выравнивание*}
КПП 36.3.5. Параллельная цепь из трех замаскированных резисторов.
Найдите ток через каждый резистор в цепи, показанной на рисунке 36.3.6.
Рисунок 36.3.6.Подсказка
Подумайте о разности потенциалов на каждом резисторе.
Ответ
\(\frac{1}{10}\text{ A},\ \frac{1}{20}\text{ A},\ \frac{1}{30}\text{ A} \)
Решение
Как и прежде, мы выберем отрицательную клемму батареи в качестве опорного нулевого потенциала. Затем положительная клемма аккумулятора находится на уровне 10 вольт. Из диаграммы на рисунке 36.3.7 видно, что ситуация с напряжением на каждом из резисторов одинакова: каждый резистор фактически подключен к двум клеммам батареи.
Рисунок 36.3.7. На этой диаграмме показано, что одна сторона каждого резистора подключена к минусу источника напряжения, а другая сторона подключена к плюсу. Это означает, что ток от источника напряжения разделится на три ветви, которые затем объединятся. Таким образом, три резистора на самом деле параллельны, хотя диаграмма не нарисована в традиционной параллельной диаграмме.Данная схема идентична трем резисторам, подключенным параллельно батарее. Следовательно, токи равны
\begin{выравнивание*}
I_1 \amp = \frac{10\text{ V}} {100\ \Omega} = \frac{1}{10}\text{ A}.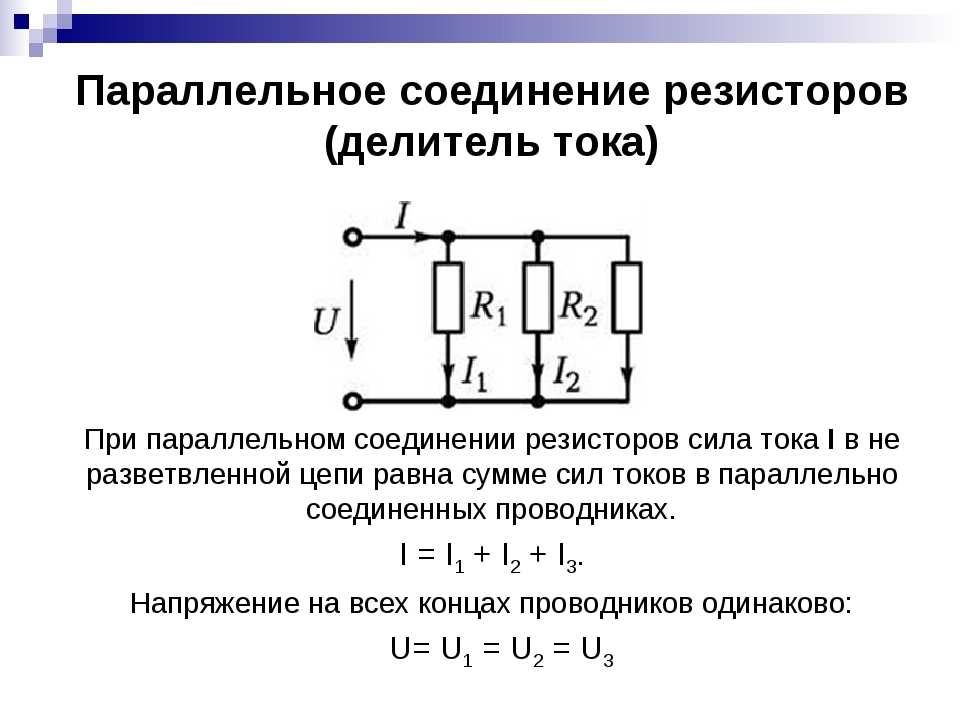 \\
I_2 \amp = \frac{10\text{ V}}{200\ \Omega} = \frac{1}{20}\text{ A}.\\
I_3 \amp = \frac{10\text{ V}}{300\ \Omega} = \frac{1}{30}\text{ A}.
\end{align*}
\\
I_2 \amp = \frac{10\text{ V}}{200\ \Omega} = \frac{1}{20}\text{ A}.\\
I_3 \amp = \frac{10\text{ V}}{300\ \Omega} = \frac{1}{30}\text{ A}.
\end{align*}
Определение эквивалентного сопротивления двух резисторов при параллельном соединении
Цель
Определить эквивалентное сопротивление двух резисторов при параллельном соединении.
Необходимые материалы
- Two resistors
- A battery eliminator
- Ammeter
- Plug key
- Connecting wires
- A piece of sandpaper
- Voltmeter
- Rheostat
Theory
When two or more resistors are connected together между двумя точками, то говорят, что они соединены параллельно.
Параллельное соединение,
- Разность потенциалов на каждом резисторе одинакова.
- Ток, протекающий через каждый резистор, разный.
The formula to calculate equivalent resistance in series is: 1/R p = 1/R 1 + 1/R 2 + 1/R 3
Circuit Diagram s Рис.
 (i) Рис. (ii) Рис. (iii)
(i) Рис. (ii) Рис. (iii) Процедура
- Настройте устройства, как показано на принципиальной схеме (i).
- Вставьте ключ и отрегулируйте реостат, перемещая его переменную клемму до тех пор, пока амперметр и вольтметр не покажут показания.
- Запишите показания вольтметра и амперметра. Выньте вилку из розетки или на мгновение выключите выпрямитель батареи.
- Повторите шаги 2 и 3 для других значений тока, изменяя скользящий контакт реостата.
- Рассчитайте сопротивление R 1 по формуле R = V/I.
- Аналогично вычислить R 2 и R p (параллельное эквивалентное сопротивление), выполнив описанные выше шаги.
Observation
For
R 1 :| S. No. | Voltmeter Reading (V) | Ammeter Reading (I) | Resistance ( R = V/I) |
1. | 0,02 В | 0,01 А | 2 Ом |
| 2. | 0.04 V | 0.02 A | 2 Ω |
| 3. | 0.08 V | 0.04 A | 2 Ω |
Mean value of R 1 = (2+2+2)/3 = 2 Ω
For
R 2| S. No. | Voltmeter Reading (V) | Ammeter Reading (I) | Сопротивление (R = V/I) |
| 1. | 0.01 V | 0.01 A | 1 Ω |
| 2. | 0.02 V | 0.02 A | 1 Ω |
| 3. | 0.04 V | 0.04 A | 1 Ω |
Mean value of R 2 = (1+1+1)/3 = 1 Ω
For
R p S. No No | Показания вольтметра (В) | Ammeter Reading (I) | Resistance (R = V/I) |
| 1. | 0.02 V | 0.03 A | ⅔ Ω |
| 2. | 0.04 V | 0.06 A | ⅔ Ω |
| 3. | 0.06 V | 0.09 A | ⅔ Ω |
Mean value of R p = (⅔+⅔+⅔)/3 = ⅔ Ом = 0,67 Ом
Расчет
= + = + =
или, R P = ω
Результат
- Расчетное значение эквивалентной сопротивления, R P
- . Расчетное значение эквивалентной сопротивления, R P
- . экспериментальное значение эквивалентного сопротивления, R p = ⅔ Ω = 0,67 Ω
- Эквивалентное сопротивление R p меньше отдельных сопротивлений.
- . Расчетное значение эквивалентной сопротивления, R P

 ..
..
 Таким образом, отныне, любое устройство может быть заменено на эквивалентное сопротивление.
Таким образом, отныне, любое устройство может быть заменено на эквивалентное сопротивление.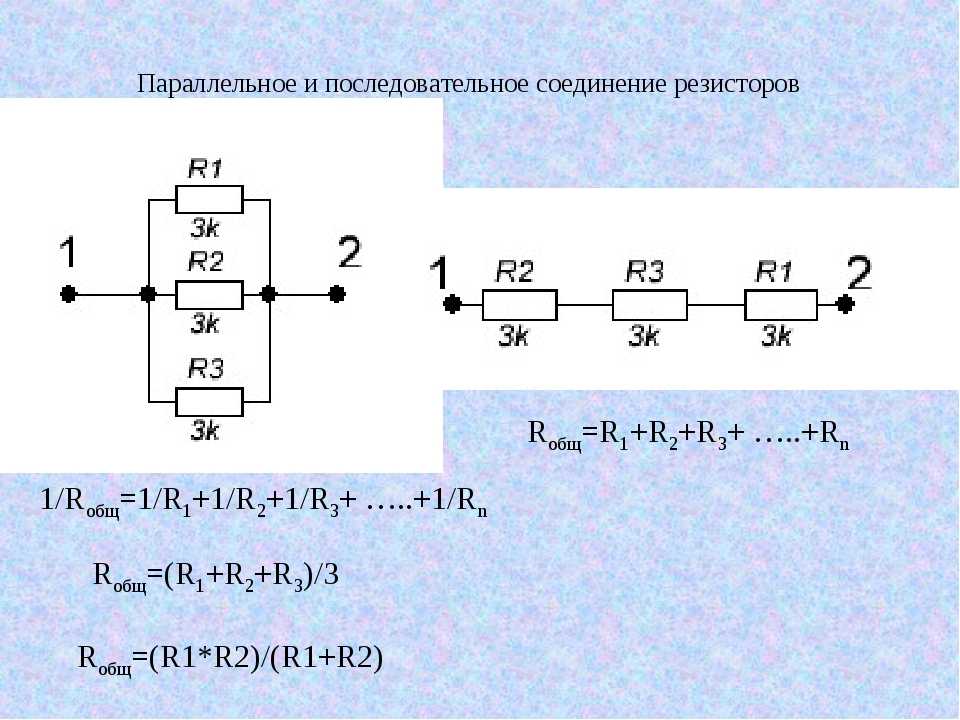 Таким образом, дополнительное сопротивление может быть использовано для ограничения тока. Однако важно отметить, что это приводит к нагреву резистора, и вы должны правильно рассчитать его мощность, о чем будет написано дальше.
Таким образом, дополнительное сопротивление может быть использовано для ограничения тока. Однако важно отметить, что это приводит к нагреву резистора, и вы должны правильно рассчитать его мощность, о чем будет написано дальше.