Что такое резонансная частота. Как она проявляется в природе и технике. Какое значение имеет в науке и технологиях. Каковы основные области применения резонанса.
Что такое резонансная частота и как она проявляется
Резонансная частота — это частота колебаний, при которой амплитуда вынужденных колебаний системы достигает максимального значения. Другими словами, это собственная частота колебаний системы, при которой даже небольшое внешнее воздействие вызывает резкое увеличение амплитуды колебаний.
Явление резонанса можно наблюдать во многих физических системах:
- Механические колебания (качели, мосты)
- Акустические системы (музыкальные инструменты)
- Электрические цепи (радиоприемники, генераторы)
- Оптические системы (лазеры)
- Квантовые системы (ядерный магнитный резонанс)
Физическая природа резонанса
Резонанс возникает, когда частота внешнего воздействия совпадает с собственной частотой колебаний системы. В этом случае энергия внешнего воздействия наиболее эффективно передается системе, вызывая увеличение амплитуды колебаний.
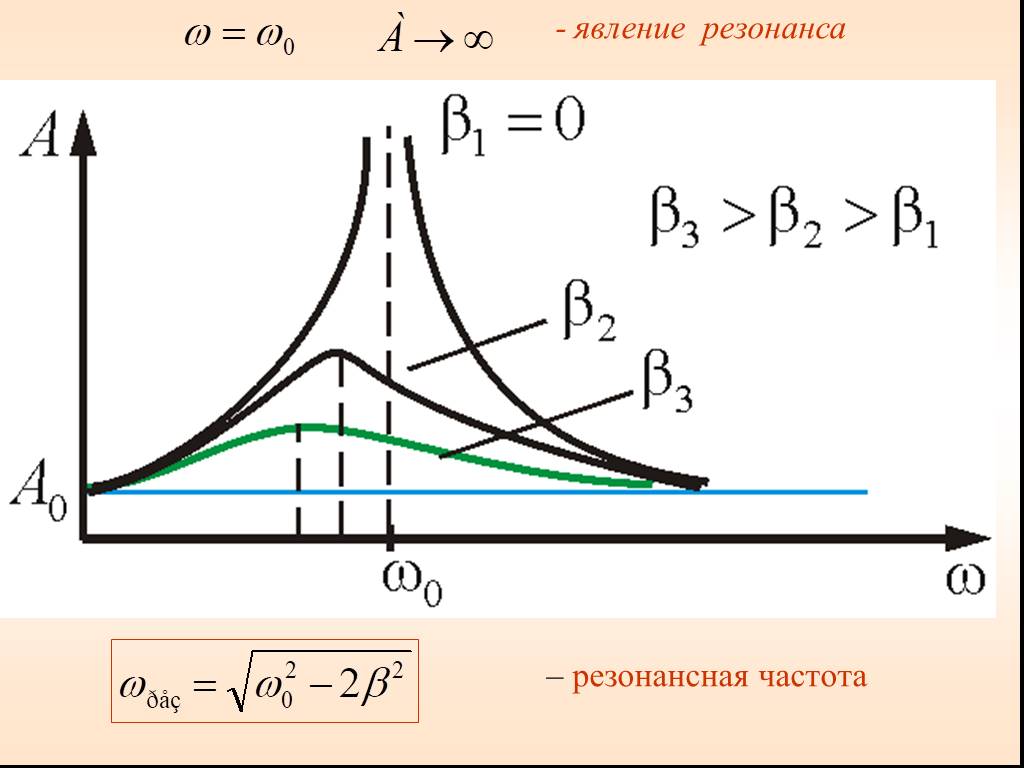
Какие физические процессы лежат в основе резонанса?
- Периодический обмен энергией между различными формами (кинетической и потенциальной)
- Синхронизация фаз внешнего воздействия и собственных колебаний
- Накопление энергии в системе при каждом периоде колебаний
Математическое описание резонанса
Резонансная частота ω0 для простых колебательных систем определяется формулой:
ω0 = √(k/m)
где k — коэффициент жесткости, m — масса.
Для электрического колебательного контура:
ω0 = 1/√(LC)
где L — индуктивность, C — емкость.
Примеры проявления резонанса в природе
Резонансные явления широко распространены в природе. Вот некоторые яркие примеры:
- Резонанс в акустических системах (эхо в пещерах, резонанс в музыкальных инструментах)
- Приливные резонансы в океанах и атмосфере
- Резонансы в орбитальном движении небесных тел
- Резонансное поглощение света атомами и молекулами
Применение резонанса в технике
Явление резонанса нашло широкое применение в различных областях техники:
- Радиотехника (настройка радиоприемников, фильтры)
- Акустика (музыкальные инструменты, акустические системы)
- Оптика (лазеры, оптические резонаторы)
- Механика (виброизоляция, демпфирование колебаний)
- Медицина (магнитно-резонансная томография)
Резонанс в электрических цепях
В электрических цепях резонанс возникает при определенном соотношении индуктивного и емкостного сопротивлений. Различают два основных вида резонанса:
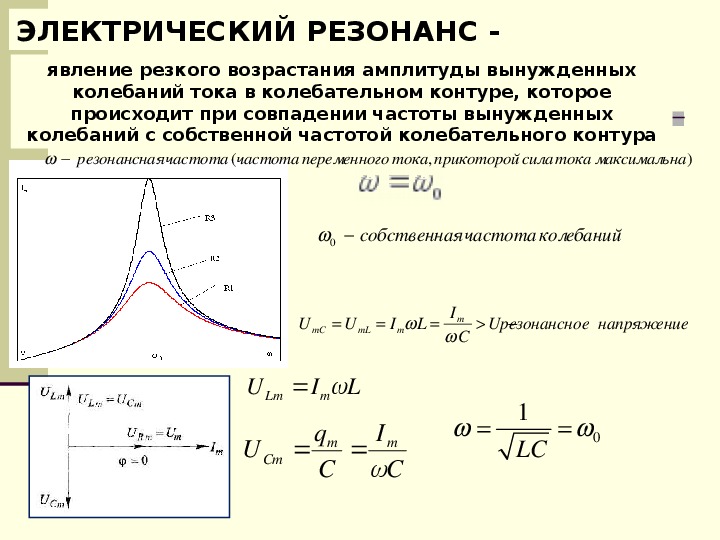
- Резонанс напряжений (в последовательном колебательном контуре)
- Резонанс токов (в параллельном колебательном контуре)
f = 1 / (2π√(LC))
где L — индуктивность, C — емкость.
Опасные проявления резонанса
Хотя резонанс широко используется в технике, в некоторых случаях он может представлять опасность. Известны случаи разрушения мостов и зданий из-за резонансных колебаний. Чтобы избежать этого, инженеры тщательно рассчитывают собственные частоты конструкций и принимают меры по демпфированию колебаний.
Какие меры применяются для предотвращения опасных резонансных явлений?
- Изменение собственной частоты конструкции
- Использование демпферов и амортизаторов
- Применение активных систем гашения колебаний
- Контроль внешних воздействий
Резонанс в квантовых системах
В квантовой механике резонанс проявляется в виде резкого увеличения вероятности взаимодействия частиц при определенных энергиях. Это явление лежит в основе многих важных физических эффектов:
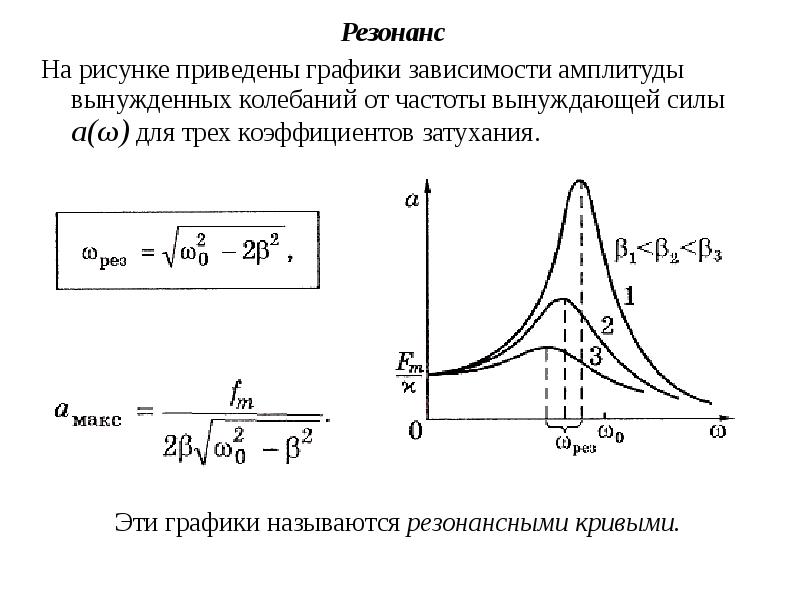
- Ядерный магнитный резонанс
- Электронный парамагнитный резонанс
- Резонансное туннелирование
- Фешбаховский резонанс
Методы исследования резонансных явлений
Для изучения резонансных явлений используются различные экспериментальные и теоретические методы:
- Анализ амплитудно-частотных характеристик
- Метод вынужденных колебаний
- Спектральный анализ
- Компьютерное моделирование
- Теория возмущений
Перспективы использования резонансных явлений
Исследование резонансных явлений продолжает открывать новые возможности для развития науки и техники. Вот некоторые перспективные направления:
- Беспроводная передача энергии на основе резонансной связи
- Разработка высокочувствительных сенсоров
- Создание новых типов квантовых вычислительных устройств
- Применение резонансных эффектов в нанотехнологиях
Таким образом, резонансные явления играют важную роль в современной науке и технике, открывая широкие возможности для создания новых технологий и устройств.
Резонансная частота | это… Что такое Резонансная частота?
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам.
Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы
Содержание
|
1 СтрунаМеханика
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
- ,
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).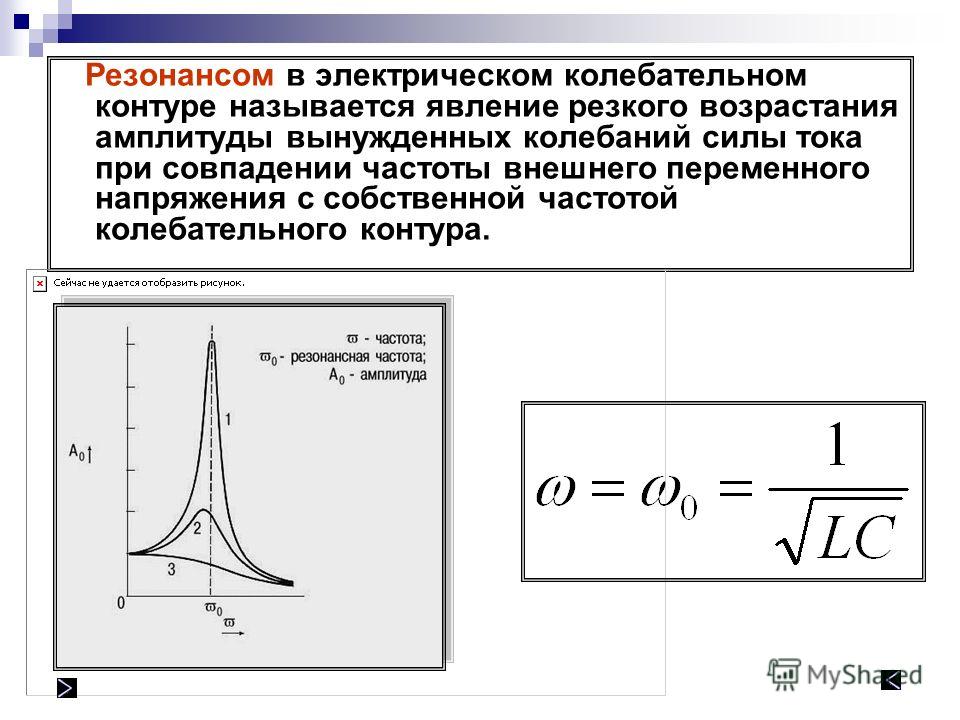
Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.
В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.
Другие механические системы могут использовать запас потенциальной энергии в различных формах.
Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.
Электроника
В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.
Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.
Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален.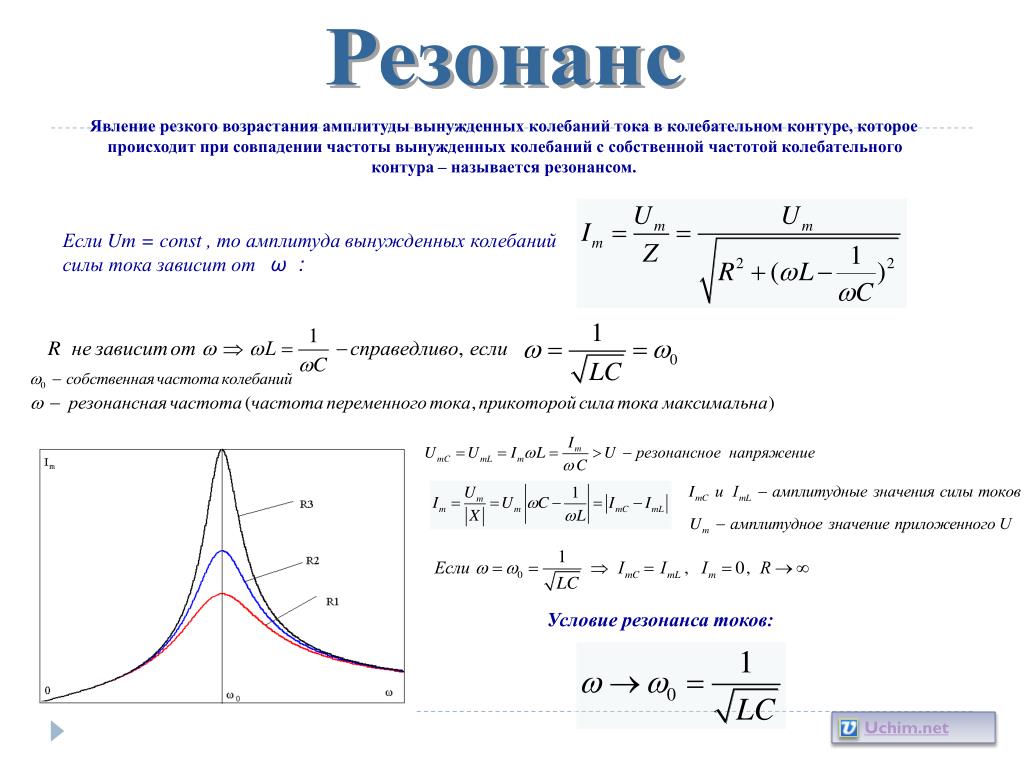
Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.
Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.
Акустика
Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.
Струна
Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:
где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:
Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:
- ,
где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.
Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.
Примечания
См. также
- Диссипативная структура
- Солитон
- Интерференция
- Журавлёв, Виктор Филиппович (см. в кн. «Прикладные методы в теории колебаний» (1988, совместно с Д. М. Климовым))
Ссылки
Richardson LF (1922), Weather prediction by numerical process, Cambridge.
Bretherton FP (1964), Resonant interactions between waves.
J. Fluid Mech., 20, 457-472.
Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.
Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.
Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.
Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.
Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.
Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука
Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М.
: Наука — 232 с.
Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука
Резонансная частота | это… Что такое Резонансная частота?
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений.
Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.
Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы
Содержание
|
Механика
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
- ,
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс.
(Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).
Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.
В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую.
Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.
Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.
Электроника
В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.
Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.
Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром.
Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.
Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте.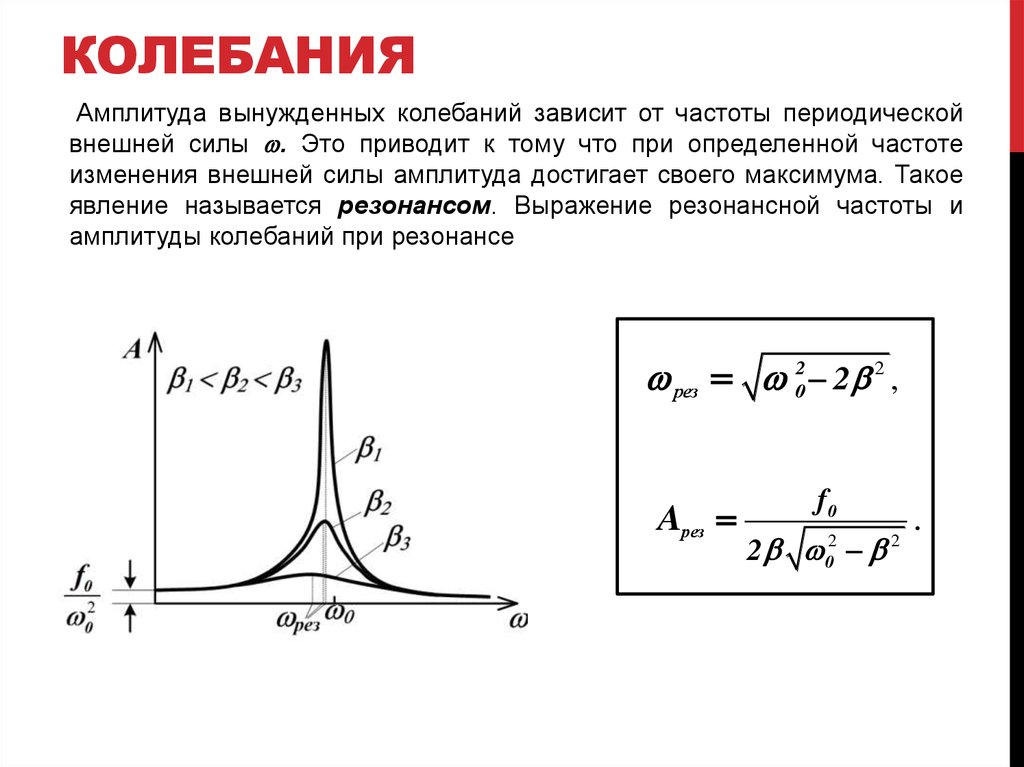
Ширина полосы пропускания определяется добротностью системы.
Акустика
Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.
Струна
Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:
где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:
Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:
- ,
где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.
Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.
Примечания
См. также
- Диссипативная структура
- Солитон
- Интерференция
- Журавлёв, Виктор Филиппович (см. в кн. «Прикладные методы в теории колебаний» (1988, совместно с Д. М. Климовым))
Ссылки
Richardson LF (1922), Weather prediction by numerical process, Cambridge.
Bretherton FP (1964), Resonant interactions between waves.
J. Fluid Mech., 20, 457-472.
Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.
Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.
Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.
Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.
Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.
Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука
Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М.
: Наука — 232 с.
Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука
Что такое резонансная частота?
То, что вы видели в мультфильмах, не обязательно является плодом буйного воображения писателей — некоторые сцены на самом деле уходят корнями в науку. В детстве я думал, что сцена ужасного певца, берущего высокую ноту и разбивающего осколок стекла, была забавной, только чтобы узнать, что это явление возможно в реальной жизни из-за того, что называется резонансной частотой.
Что такое резонансная частота и что она делает? В то время как паршивые навыки пения вряд ли разобьют стекло, воспроизведение звука, равного резонансной частоте стекла, будет. По крайней мере, это то, что я помню со школьного урока физики. Со временем я также обнаружил, что резонансная частота связана не только с разбиванием стекла, но и с важным принципом работы некоторых электронных устройств.
Что такое резонансная частота?
Резонансная частота — это собственная частота, при которой среда вибрирует с максимальной амплитудой
Почему стекло разбивается при воздействии звука? Звук – это акустическая волна, которая заставляет молекулы колебаться.
При проецировании от источника вибрация проходит через воздух на физическую структуру стекла. Если акустическая частота звука соответствует собственной частоте стекла, последнее начинает вибрировать с большей амплитудой, потенциально разрушая свою структуру.
Другими словами, стекло может разбиться, когда оно вибрирует на своей резонансной частоте. Резонансную частоту также можно определить как собственную частоту объекта, при котором он имеет тенденцию вибрировать с более высокой амплитудой. Например, вы могли бы почувствовать, как «трясется» мост, если бы общая сила колебаний от транспортных средств заставляла его вибрировать на своей частоте.
Термин «резонансная частота» также часто встречается в электронной технике, хотя он менее драматичен, чем осколки стекла или сильно трясущийся мост.
Резонансная частота в электронных схемах
Резонансная частота в электронных схемах выражается, когда схема демонстрирует максимальную колебательную характеристику на определенной частоте.
Это наблюдается для цепи, состоящей из катушки индуктивности и конденсатора.
Чтобы лучше понять, что такое резонансная частота и какую роль она играет в электронике, давайте рассмотрим последовательную RLC-цепь, которая питается от источника переменного тока. Известно, что величина емкостного и индуктивного сопротивления изменяется соответственно частоте. Емкостное реактивное сопротивление определяется уравнением X c = 1/(2ℼfC), а индуктивное сопротивление определяется уравнением X L = 2ℼfL.
Зависимость индуктивного и емкостного сопротивления от частот
На графике уменьшение емкостного сопротивления будет пересекаться с увеличением индуктивного сопротивления на определенной частоте. Частота, на которой оба параметра перекрываются, известна как резонансная частота цепи RLC. Следовательно, резонансную частоту можно получить, выразив равное значение как емкостного, так и индуктивного сопротивления следующим образом:
- Х Д = Х С
- 2ℼfL = 1/(2ℼfC)
- f r = 1/(2ℼ √LC)
В последовательной RLC-цепи импеданс минимален, когда он работает на резонансной частоте.
Полное сопротивление цепи выражается следующим уравнением:
Z = R + X L — X C
В резонансе X L равно X C , что означает, что они компенсируют друг друга. Это оставляет импеданс цепи чисто резистивным. В результате ток, протекающий через последовательную цепь RLC, достигает своего пика, когда он работает на своей резонансной частоте.
В параллельной RLC-цепи формула расчета резонансной частоты остается прежней. Однако вы обнаружите, что ток подавлен до минимума, так как полное сопротивление цепи максимально. Это происходит, когда LC цепи выглядит как разомкнутая цепь при параллельном соединении.
Применение резонансных цепей
Радиочастотные приемники пропускают сигналы, которые колеблются на резонансной частоте цепи
Концепция возбуждения цепи на ее резонансной частоте встречается в различных приложениях.
В генераторе в качестве колебательного контура используется параллельный LC, который приводится в движение на своей резонансной частоте. Результатом является непрерывная серия устойчивых, колеблющихся тактовых импульсов, которые управляют такими компонентами, как микроконтроллеры и коммуникационные ИС.
Резонансные контуры также используются в радиочастотных устройствах. Они становятся основой тюнера, усиливая сигналы, соответствующие его резонансной частоте, и подавляя те, которые выходят за пределы его полосы пропускания.
При проектировании резонансных цепей полезно работать с современным программным обеспечением для проектирования печатных плат. Allegro имеет все инструменты компоновки и моделирования, необходимые для обеспечения того, чтобы схема работала соответствующим образом на желаемой резонансной частоте. Вы также можете использовать InspectAR для точной оценки и улучшения печатных плат с помощью дополненной реальности и интуитивно понятного взаимодействия.
Проверка, отладка, доработка и сборка печатных плат никогда не были быстрее и проще.
Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов. Чтобы посмотреть видео по связанным темам или узнать, что нового в нашем наборе инструментов для проектирования и анализа, подпишитесь на наш канал YouTube.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетите вебсайт Больше контента от Cadence PCB Solutions
УЗНАТЬ БОЛЬШЕРезонанс
Резонанс В звуковых приложениях резонансная частота — это собственная частота вибрации, определяемая физическими параметрами вибрирующего объекта.
| Индекс Концепции резонанса | ||||||
| Назад |
Та же основная идея физически определенных собственных частот применяется во всей физике, в механике, электричестве и магнетизме, и даже во всей области современной физики. Вот некоторые из следствий резонансных частот: Легко заставить объект вибрировать на его резонансных частотах, трудно
на других частотах.
| Индекс Концепции резонанса | |||
| Назад |
Качели на детской площадке — пример маятника, резонансной системы только с одной резонансной частотой. Слегка толкая качели каждый раз, когда они возвращаются к вам, вы можете продолжать наращивать амплитуду качелей. Если вы попытаетесь заставить его качаться с удвоенной частотой, вам будет очень трудно, и вы можете даже потерять зубы в процессе!
