Сдвиг фаз в трехфазной сети: особенности, причины и влияние на работу электрооборудования

Что такое сдвиг фаз в трехфазной сети. Каковы причины возникновения сдвига фаз. Как сдвиг фаз влияет на работу электрооборудования. Какие существуют способы компенсации сдвига фаз в трехфазных сетях. Почему важно учитывать сдвиг фаз при проектировании и эксплуатации трехфазных систем.

Что такое сдвиг фаз в трехфазной сети

Сдвиг фаз в трехфазной сети — это угловое смещение синусоид напряжения или тока в разных фазах относительно друг друга. В идеальной трехфазной системе сдвиг фаз между соседними фазами составляет 120 градусов. Однако на практике из-за различных факторов может возникать дополнительный сдвиг, нарушающий симметрию системы.

Основные причины возникновения сдвига фаз

Существует несколько ключевых причин, приводящих к появлению сдвига фаз в трехфазных сетях:

• Несимметричная нагрузка по фазам
• Наличие реактивных элементов в цепи (индуктивностей и емкостей)
• Нелинейные нагрузки, генерирующие высшие гармоники
• Неравномерное распределение мощности по фазам
• Асимметрия параметров линий электропередачи

Влияние сдвига фаз на работу электрооборудования

Сдвиг фаз может оказывать существенное влияние на функционирование трехфазного электрооборудования:

Снижение коэффициента мощности

При наличии сдвига фаз между током и напряжением снижается коэффициент мощности, что приводит к увеличению потерь в сети и снижению эффективности передачи электроэнергии.

Дополнительный нагрев оборудования

Несимметричные токи, вызванные сдвигом фаз, приводят к дополнительному нагреву обмоток электродвигателей, трансформаторов и других устройств. Это ускоряет износ изоляции и сокращает срок службы оборудования.

Нарушение работы защитных устройств

Сдвиг фаз может вызывать ложные срабатывания или отказы в работе устройств релейной защиты и автоматики, что снижает надежность электроснабжения.

Способы компенсации сдвига фаз

Для уменьшения негативного влияния сдвига фаз применяются следующие методы:

• Симметрирование нагрузки по фазам
• Установка компенсирующих устройств (конденсаторных батарей, синхронных компенсаторов)
• Применение активных фильтров гармоник
• Использование специальных схем соединения обмоток трансформаторов
• Регулирование коэффициента мощности на подстанциях

Измерение и контроль сдвига фаз

Для определения величины сдвига фаз используются специальные приборы — фазометры. Они позволяют измерять угол сдвига между током и напряжением в каждой фазе. Современные цифровые анализаторы качества электроэнергии обеспечивают комплексный контроль параметров трехфазной сети, включая сдвиг фаз.

Какие параметры контролируются при измерении сдвига фаз?

При анализе сдвига фаз в трехфазных системах обычно контролируются следующие параметры:

• Углы сдвига между фазными напряжениями
• Углы сдвига между фазными токами
• Углы сдвига между током и напряжением в каждой фазе
• Коэффициенты несимметрии напряжений и токов
• Коэффициент мощности в каждой фазе и суммарный

Нормативные требования к сдвигу фаз

Согласно ГОСТ 32144-2013, в нормальных условиях эксплуатации электрических сетей должны соблюдаться следующие нормы по сдвигу фаз:

• Отклонение угла фазового сдвига между основными гармониками фазных напряжений от номинального значения 120° не должно превышать ±10°
• Коэффициент несимметрии напряжений по обратной последовательности не должен превышать 2% в течение 95% времени интервала в одну неделю

Влияние сдвига фаз на энергоэффективность

Сдвиг фаз оказывает существенное влияние на энергоэффективность трехфазных систем:

Как сдвиг фаз влияет на потери электроэнергии?

При наличии сдвига фаз между током и напряжением возникает реактивная составляющая мощности, которая не совершает полезной работы, но вызывает дополнительные потери в линиях электропередачи и трансформаторах. Это приводит к снижению коэффициента полезного действия системы электроснабжения.

Каково влияние на пропускную способность сетей?

Сдвиг фаз уменьшает активную составляющую полной мощности, что снижает пропускную способность линий электропередачи и трансформаторов. Это может потребовать увеличения сечения проводов или мощности трансформаторов для передачи той же полезной мощности.

Методы анализа сдвига фаз

Для исследования сдвига фаз в трехфазных системах применяются различные методы анализа:

Векторные диаграммы

Векторные диаграммы позволяют наглядно представить соотношения между токами и напряжениями в трехфазной системе. С их помощью можно определить углы сдвига фаз и оценить симметрию системы.

Анализ гармонического состава

Разложение кривых тока и напряжения на гармонические составляющие позволяет выявить причины возникновения сдвига фаз и оценить вклад высших гармоник.

Симметричные составляющие

Метод симметричных составляющих дает возможность представить несимметричную трехфазную систему в виде суммы трех симметричных систем, что упрощает анализ.

Заключение

Сдвиг фаз является важным параметром, характеризующим качество электроэнергии в трехфазных сетях. Его контроль и компенсация необходимы для обеспечения надежной и эффективной работы электрооборудования. Применение современных методов анализа и средств измерения позволяет своевременно выявлять и устранять проблемы, связанные со сдвигом фаз, повышая энергоэффективность и надежность электроснабжения.

Основы электропитания. Зачем нужен сдвиг фаз

Где R – сопротивление нагревательного элемента чайника.

Содержание

Основы электропитания. Зачем нам нужен сдвиг фаз?

В предыдущих частях этой серии мы обсудили общие аспекты производства и потребления электроэнергии, включая особенности ее передачи на большие расстояния. Теперь, когда вы знаете, что высоковольтные линии необходимы для передачи большой мощности, пришло время рассмотреть одну из самых важных частей энергосистемы, так называемую “последнюю милю”. – Кабели 230/400 В – поскольку именно к ним подключаются электрические розетки, как дома, так и на рабочем месте. Однако прежде чем анализировать характеристики пользовательского сегмента энергосистемы, необходимо сначала ответить на несколько теоретических вопросов, поскольку без этого будет непонятно, зачем это вообще было сделано.

Обратите внимание, что это эквивалентно ситуации, когда фаза изменилась бы от -180° до -270°. Теперь мы начинаем понимать, что питание емкостной нагрузки может вызвать неожиданные фазовые сдвиги, что может быть губительно для усилителя с неожиданной обратной связью.

Сдвиг фазы для реактивных нагрузок

Частотно-зависимый сдвиг фазы вызван влиянием реактивных компонентов, таких как конденсаторы и индукторы. Это относительная величина, поэтому она должна быть определена как разница разность фаз между двумя точками. В этой статье “сдвиг фаз” означает разность фаз между выходом и входом. Конденсатор заставляет напряжение отставать от тока на 90°, а индуктивность заставляет ток отставать от напряжения на 90°. В векторной форме это обозначается +j или -j для индуктивной и емкостной реактивности соответственно. Но емкость и индуктивность существуют в некоторой степени в все проводники. Почему же они не вызывают сдвиг фаз на 90°?

Все наши эффекты фазового сдвига будут моделироваться RC и RL цепями. Все цепи могут быть смоделированы как источник с некоторым внутренним сопротивлением, заданная цепь и нагрузка, следующая за цепью. Внутренний импеданс источника также называется его выходным импедансом. Мне проще всего говорить о входном сопротивлении, выходном сопротивлении и каскадах, поэтому я повторю: все цепи можно смоделировать как выход одного каскада с некоторым выходным сопротивлением, питающим следующий каскад, который нагружен входным сопротивлением следующего каскада. Это важно, поскольку позволяет снизить сложность схемы до гораздо более простых RLC-цепей, фильтров и делителей напряжения.

Посмотрите на приведенную ниже диаграмму.

Рисунок 1 – Шунтирующий конденсатор для предыдущего каскада и нагрузка 10kΩ

Это смоделирует некоторую схему источника (например, усилитель) с выходным сопротивлением 50 Ом, которая имеет нагрузку 10 кОм и шунтирована конденсатором 10 нФ. Должно быть понятно, что схема представляет собой RC-фильтр нижних частот, состоящий из R1 и C1. Из анализа основных схем мы знаем, что сдвиг фазы напряжения в RC-цепи будет изменяться от 0° до -90°, и моделирование подтверждает это.

Рисунок 2 – Логарифмическая амплитудно-частотная характеристика и частотная характеристика нашей схемы с шунтирующим конденсатором

На низких частотах выходная фаза не зависит от конденсатора. Когда мы достигаем частоты среза (f_ср.) RC-фильтра, фаза падает до -45°. Для частот выше частоты среза фаза приближается к асимптотическому значению -90°.

Эта фазочастотная характеристика моделирует сдвиг фаз, вызванный любым шунтирующим конденсатором. Шунтирующий конденсатор вызовет сдвиг фазы с резистивной нагрузкой в пределах от 0° до -90°. Конечно, необходимо также учитывать демпфирование.

Аналогичный взгляд на последовательный конденсатор (например, конденсатор емкостной связи переменного тока) показывает типичный эффект такой цепи.

Рисунок 3 – Цепь с последовательным конденсатором.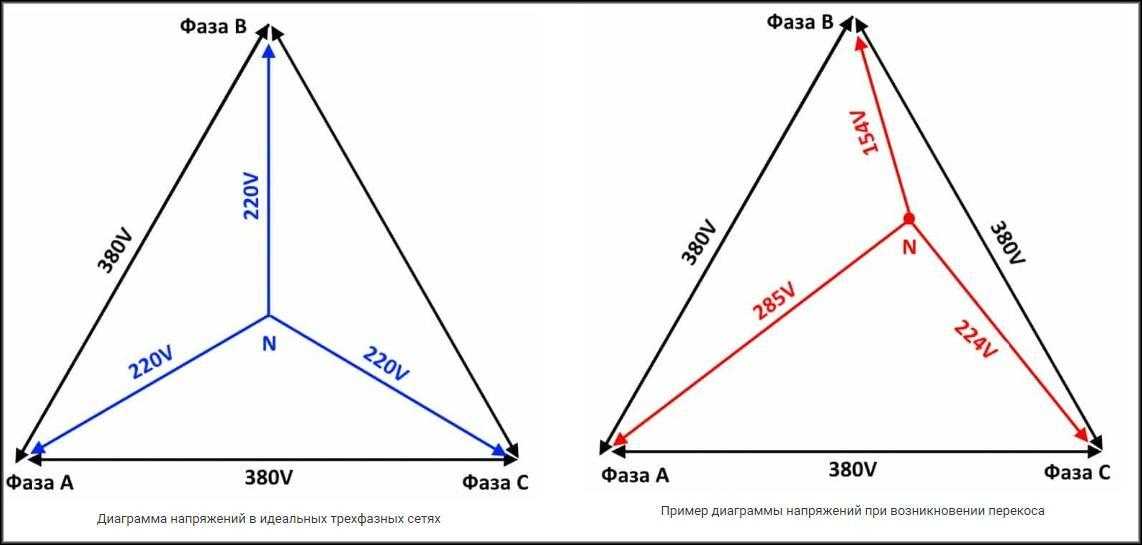 Рисунок 4 – . и графики его амплитудно-частотных и фазо-частотных характеристик

В этом случае сдвиг фазы начинается с +90°, а фильтр является фильтром высоких частот. Выше частоты среза он окончательно устанавливается на 0°. Таким образом, мы видим, что последовательный конденсатор всегда будет вносить сдвиг фазы между +90° и 0°.

Чем больше сдвиг фаз, тем длиннее те части периода, где мощность отрицательна, тем ниже будет средняя мощность тока.

Сдвиг фаз переменного тока и напряжения

Мощность постоянного тока, как мы уже знаем, равна произведению напряжения и тока. Однако в случае постоянного тока направления тока и напряжения всегда совпадают. В случае переменного тока направления тока и напряжения совпадают только в том случае, если в цепи тока нет конденсаторов или индукторов.

В этом случае формула для мощности

Кривая мгновенной мощности для этого случая (направления тока и напряжения совпадают) показана на рис. 1. Обратите внимание, что направления векторов напряжения и тока в этом случае совпадают, т.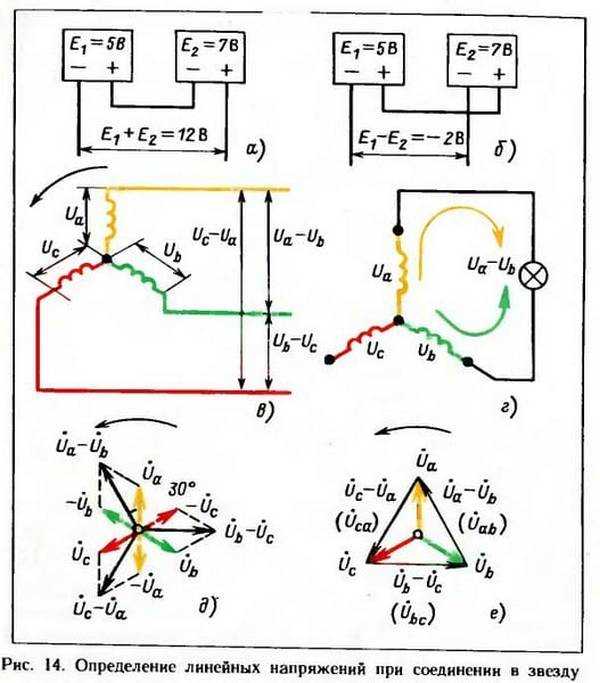 е. фазы тока и напряжения всегда одинаковы.

Рисунок 1. Фазовый сдвиг тока и напряжения. Сдвиг фаз отсутствует, и мощность всегда положительна.

Если в цепи переменного тока есть конденсатор или индуктор, фазы тока и напряжения не совпадают.

О причинах такого несоответствия читайте в моих учебниках по емкостным и индуктивным цепям, а сейчас давайте выясним, как это повлияет на величину переменного тока.

Представьте, что в начале вращения векторы тока и напряжения пучка имеют разные направления. Поскольку оба вектора вращаются с одинаковой скоростью, угол между ними будет оставаться неизменным во время их вращения. На рисунке 2 показан случай вектора тока с задержкой Im из вектора напряжения Um под углом 45°.

Рисунок 2. Фазовый сдвиг тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность становится отрицательной в определенные моменты времени.

Давайте посмотрим, как изменятся ток и напряжение в этом случае. Из синусоиды тока и напряжения видно, что когда напряжение проходит через ноль, ток отрицателен.

Затем напряжение достигает своего максимального значения и начинает уменьшаться, в то время как ток, хотя и положительный, еще не достиг своего максимального значения и продолжает увеличиваться. Напряжение изменило направление, но ток продолжает течь в том же направлении и т.д. Фаза тока всегда запаздывает по отношению к фазе напряжения. Существует постоянное смещение между фазами напряжения и тока Между фазами напряжения и тока существует постоянный сдвиг фазпод названием фазовый сдвиг.

Действительно, если мы посмотрим на рисунок 2, то увидим, что синусоида тока смещена вправо относительно синусоиды напряжения. Поскольку мы строим горизонтальную ось в градусах вращения, мы также можем измерить фазовый сдвиг в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между лучевыми векторами тока и напряжения.

Из-за задержки между фазой тока и фазой напряжения, в некоторые моменты времени его направление не совпадает с направлением напряжения. В эти моменты сила тока будет отрицательной, так как произведение положительной величины на отрицательную всегда будет отрицательным. Это означает, что внешняя цепь в эти моменты будет не потребителем электроэнергии, а ее источником. Часть энергии, которая вошла в цепь в течение той части периода, когда мощность была положительной, вернется к источнику энергии в течение той части периода, когда мощность отрицательна.

Чем больше сдвиг фаз, тем длиннее те части периода, где мощность отрицательна, тем ниже будет средняя мощность тока.

Если сдвиг фаз составляет 90°, то мощность будет положительной в течение одной четверти периода и отрицательной в течение другой четверти периода. Следовательно, средняя мощность тока составит нольи ток не будет производить никакой работы (рис. 3).

Рисунок 3. Фазовый сдвиг тока и напряжения. Фазы тока и напряжения смещены на 90. Мощность положительна в течение одной четверти периода и отрицательна в течение другой. Средняя мощность равна нулю.

Теперь понятно, что мощность переменного тока при наличии фазового сдвига будет меньше произведения среднеквадратичных значений тока и напряжения, т.е. формула

в этом случае не будет правильным.

ПОНРАВИЛАСЬ ЛИ ВАМ ЭТА СТАТЬЯ? ПОДЕЛИТЕСЬ ИМ СО СВОИМИ ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Фазовый сдвиг

Что такое фаза, фазовый угол и сдвиг фаз?

Говоря о переменном токе, часто используют такие термины, как “фаза”, “фазовый угол” и “сдвиг фаз”. Обычно под ним подразумевается синусоидально переменный ток или пульсирующий ток (получаемый путем выпрямления синусоидального тока).

Поскольку периодическое изменение электродвижущей силы сети или тока в цепи составляет является гармоническим колебательным процессоми функция, описывающая этот процесс, является гармонической, т. е. Эта функция является либо синусоидальной, либо косинусоидальной, в зависимости от начального состояния колебательной системы.

Аргументом функции в данном случае является фаза, т.е. положение колеблющейся величины (тока или напряжения) в данный момент времени относительно начала колебания. Сама функция принимает значение колеблющейся величины в один и тот же момент времени.

Чтобы лучше понять значение термина “фаза”, давайте рассмотрим график напряжения в однофазной сети переменного тока как функцию времени. Здесь мы видим, что напряжение изменяется от некоторого максимального значения Um до -Um, периодически проходя через ноль.

Изменяясь, напряжение в каждый момент времени принимает множество значений, периодически (через время T) возвращаясь к значению, при котором оно начало контролироваться.

Можно сказать, что в данный момент напряжение находится в определенной фазе, которая зависит от нескольких факторов: времени t, прошедшего с начала колебания, угловой частоты и начальной фазы. То, что указано в скобках, – это полная фаза колебания в текущий момент времени t. Psi – это начальная фаза.

Фазовый угол

Начальная фаза также называется в электротехнике начальный фазовый уголпотому что фаза измеряется в радианах или градусах, как и все обычные геометрические углы. Пределы изменения фазы лежат в диапазоне от 0 до 360 градусов или от 0 до 2*pi радиан.

На рисунке выше видно, что в момент начала наблюдения за переменным напряжением U его значение не было нулевым, т.е. фаза уже отклонилась от нуля на некоторый угол Psy, в данном примере равный примерно 30 градусам или пи/6 радианов – это начальный фазовый угол.

Как часть аргумента синусоидальной функции, Psi является константой, поскольку этот угол определяется в начале наблюдения переменного напряжения и в дальнейшем по существу неизменен. Однако его наличие определяет общий сдвиг синусоидальной кривой относительно начала.

При дальнейших колебаниях напряжения изменяется фазовый угол тока, а вместе с ним и напряжение.

Для синусоидальной функции, если общий фазовый угол (общая фаза, включая начальную фазу) равен нулю, 180 градусов (пи радиан) или 360 градусов (2*пи радиан), то напряжение равно нулю, а если фазовый угол равен 90 градусов (пи/2 радиан) или 270 градусов (3*пи/2 радиан), то напряжение максимально отклонено от нуля.

Фазовый сдвиг

Обычно при электрических измерениях в цепях с синусоидальным переменным током (напряжением) ток и напряжение в тестируемой цепи наблюдаются одновременно. Затем графики тока и напряжения строятся на общей координатной плоскости.

В этом случае частоты токов и напряжений одинаковы, но начальные фазы отличаются, если смотреть на графики. В этом случае мы говорим о сдвиг фаз между током и напряжением, т.е. разность их начальных фазовых углов.

Другими словами, сдвиг фазы определяет, насколько одна синусоида сдвинута во времени относительно другой. Фазовый сдвиг, как и фазовый угол, измеряется в градусах или радианах. Синусоида, период которой начинается раньше, находится в фазе до, а синусоида, период которой начинается позже, находится в фазе после. Фазовый сдвиг обычно обозначается буквой Phi.

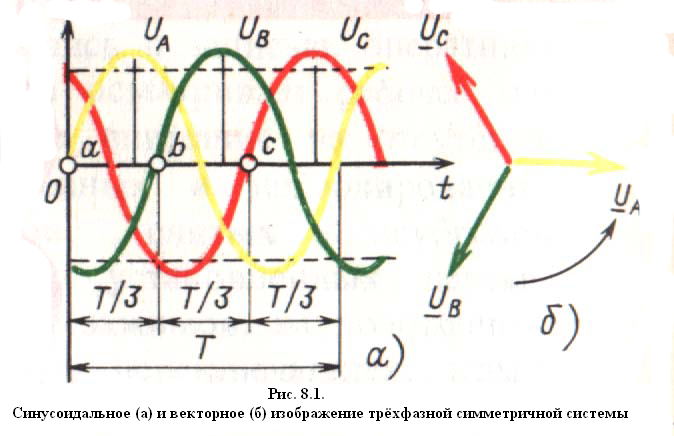
Например, сдвиг фаз между напряжениями на проводниках трехфазной сети переменного тока относительно друг друга постоянен и составляет 120 градусов или 2*pi/3 радиана.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет развитию нашего сайта!

– fázový posuv – fázový posuv (rozdíl) – fázový rozdíl

ФАЗОВАЯ СКОРОСТЬ

ФАЗОВОЕ ДВИЖЕНИЕ, начальная разность фаз фазы Начальная разность фаз между двумя переменными, которые изменяются по синусоиде с одинаковой частотой. Она измеряется в градусах, радианах или долях периода. В электротехнике S.f. между напряжением и током имеет большое практическое значение, определяя коэффициент мощности w Цепи переменного тока.

Смотреть что такое “PHASE RATE” в других словарях:

ДВИЖЕНИЕ ФАЗЫ

Разница в начальных фазах (см. Фаза) переменной, которая изменяется синусоидально с одинаковой частотой. Фаза измеряется в градусах.

PHASE MIG.

Величина, характеризующая временную задержку одного периодического (или квазипериодического) процесса относительно другого. Временная задержка одного периодического (или квазипериодического) процесса относительно другого. Для двух гармонических колебаний одинаковой частоты.

PHASE MIG.

Разница в начальных фазах физических величин, которые изменяются синусоидально с одинаковой частотой, например, напряжения в цепи синусоидального тока. Измеряется в градусах, радианах и долях периода.

. смотреть

ФАЗОВАЯ СКОРОСТЬ

ФАЗОВАЯ СКОРОСТЬ – это разность фаз исходных физических величин, которые изменяются синусоидально с одинаковой частотой (например, напряжение в цепи синусоидального тока). Она измеряется в градусах, радианах и долях периода.

ФАЗОВАЯ СКОРОСТЬ

PHASE SPLICE, начальная разность фаз физических величин, которые изменяются синусоидально с одинаковой частотой (например, напряжение в цепи синусоидального тока).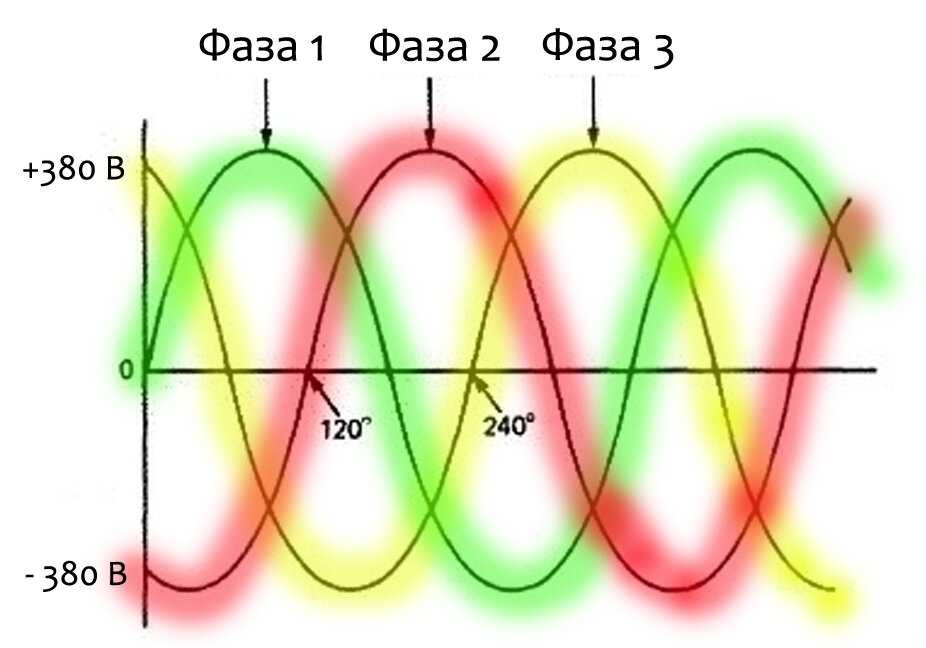 Измеряется в градусах, радианах и долях периода. см.

PHASE MIG.

РАЗНОСТЬ ФАЗ, начальная разность фаз физической величины, изменяющейся синусоидально на одной и той же частоте (например, напряжение в цепи синусоидального тока). Измеряется в градусах, радианах и долях периода. см.

РАЗНОСТЬ ФАЗ

– Разность фаз исходных физических величин, которые изменяются синусоидально с одинаковой частотой (например, напряжение в цепи синусоидального тока). Измеряется в градусах, радианах и долях периода. см.

РАЗНОСТЬ ФАЗ

Разность фаз исходных физических величин, которые изменяются синусоидально с одинаковой частотой. Измеряется в градусах, радианах и долях периода.

ДВИЖЕНИЕ ФАЗЫ

сдвиг фаз, сдвиг фаз времени, отставание, отставание

СДВИГ ФАЗЫ

– фазовый позув – фазовый роздыль

СДВИГ ФАЗЫ

Разность фаз между двумя периодическими переменными, не совпадающими по времени.

ДВИЖЕНИЕ ФАЗЫ

ДВИЖЕНИЕ ФАЗЫ

СДВИГ ФАЗЫ

сдвиг фаз, задержка

PHASE MIG.

СДВИГ ФАЗЫ

СДВИГ ФАЗЫ

СДВИГ ФАЗЫ

эл. фазовый сдвиг

СДВИГ ФАЗЫ

СДВИГ ФАЗЫ

ДВИЖЕНИЕ ФАЗЫ

СДВИГ ФАЗЫ

СДВИГ ФАЗЫ

СДВИГ ФАЗ МЕЖДУ НАПРЯЖЕНИЕМ И ТОКОМ

244 сдвиг фаз между напряжением и током Алгебраическая величина, определяемая вычитанием из начальной фазы синусоидального электрического тока.

СДВИГ ФАЗ МЕЖДУ НАПРЯЖЕНИЕМ И ТОКОМ

Это разность фаз между напряжением и током.

СДВИГ ФАЗ МЕЖДУ НАПРЯЖЕНИЕМ И ТОКОМ

Алгебраическая величина, определяемая путем вычитания начальной фазы синусоидального электрического тока из начальной фазы синусоидального электрического напряжения. Термины и определения основных понятий Телекоммуникационный словарь.2013.

СДВИГ ФАЗ СИНХРОННЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ (ВИБРАЦИЙ)

33. Сдвиг фаз синхронных гармонических колебаний (осцилляций) Сдвиг фаз Разность фаз между двумя синхронными гармоническими колебаниями (осцилляциями) в любой момент времени. смотреть

СДВИГ ФАЗ СИНХРОННЫХ КОЛЕБАНИЙ

21 Сдвиг фаз синхронных колебаний Разность фаз между двумя синхронными гармоническими колебаниями в любой момент времени Источник: РД 34.21.306-96: Метод. см. РД 34.21.306-96: Метод.

Фазовый сдвиг относится к временной задержке первого сигнала по отношению ко второму.

Заключение

Предположим, вы подключили две акустические системы (физически предполагается, что это ваши акустические системы) к выходу усилителя. Один динамик подключен как положено – плюс к плюсу, минус к минусу. А другой, смешанный, соединил плюс с минусом и минус с плюсом. Включите усилитель, что мы услышим? Скорее всего, жалкое подобие звука. Один динамик в какой-то мере ослабляет сигнал другого своими звуковыми волнами.

Следующие рисунки помогут объяснить это. Представьте, что вы видите это на экране осциллографа, который измеряет сигналы левого и правого каналов нашего усилителя.

На первом рисунке левый и правый каналы находятся в фазе. Сигнал одинаков в обоих каналах. Линии идеально следуют сигналу. Они имеют синхронизированную амплитуду по всему диапазону. Здесь мы можем сказать, что сигналы “в фазе“. Практически говоря, уровень суммирования сигнала будет усилен сигналами левого и правого каналов.

На втором рисунке показано полное несоответствие. “Горб” левого канала совпадает с “дном” правого канала. Чисто из школьной физики, результат добавления таких колебаний, в идеале, будет равен нулю. Сигналы будут отменять друг друга. Сигналы находятся вне фазы.

Фазовый сдвиг относится к временной задержке первого сигнала по отношению ко второму.

При двух гармонических колебаниях одинаковой частоты результатом сдвига фаз будет частичное затухание сигнала. Степень ослабления результирующего сигнала будет зависеть от этого фазового сдвига. В крайнем случае (в противофазе) выход будет равен абсолютному нулю.

Все эти образы и рассуждения о физических свойствах звуковых волн имеют мало отношения к практике, к реальности. Звук любого музыкального инструмента нельзя назвать “одночастотным сигналом”. (как осциллограмма на рисунках). Частичный сдвиг фазы может ослабить одни частоты по сравнению с другими. А иногда и усиливать некоторые из них.

Если вы обнаружили ошибку, выделите текст и нажмите кнопку Ctrl+Enter.

Читайте далее:

• Сколько электроэнергии потребляет трамвай?.
• Что такое сухие и мокрые нагревательные элементы в водонагревателе, бойлере, стиральной машине.
• Электрощиты на лестничных клетках: что должны делать сотрудники управляющих компаний – Рамблер/.
• Снижение потерь напряжения – Экономика энергетики.
• Трансконтинентальная суперсеть постоянного тока /.
• Электричество – это. Что такое производство электроэнергии?.
• Расчет потребления электроэнергии: онлайн-калькулятор.

Угол сдвига фаз между током и напряжением. Измерение и вычисление | ENARGYS.RU

Начальные фазы электромагнитных синусоидальных колебаний первичного и вторичного напряжения, с частотой одинаковой величины, могут существенно различаться на некоторый угол сдвига фаз (угол φ). Переменные величины могут неоднократно в течение определенного периода некоторого времени изменяются с определенной частотой. Если электрические процессы имеют неизменный характер, а сдвиг фаз равен нулю, это свидетельствует о синхронизме источников величин переменного напряжения, например, трансформаторов. Сдвиг фазы служит определяющим фактором коэффициента мощности в электрических сетях переменного тока.

Угол сдвига фаз находится при необходимости, тогда, если один из сигналов является опорным, а второй сигнал с фазой в самом начале совпадает с углом сдвига фаз.

Измерение угла сдвига фаз производится прибором, в котором присутствует нормированная погрешность.

Фазометр может производить измерение угла сдвига в границах от 0^о до 360^о в некоторых случаях от -180^оС до +180^оС, а диапазон измеряемых частот сигналов может колебаться от 20Гц до 20 ГГц. Измерение гарантируется в том случае если напряжение входного сигнала равно от 1 мВ до 100 В, если же напряжение входного сигнала превышает эти границы точность измерения не гарантируется.

Методы измерения угла сдвига фаз

Существует несколько способов измерения угла сдвига фаз, это:

1. Использование двухлучевого или двухканального осциллографа.
2. Компенсационный метод основан на сравнении измеряемого фазового сдвига, с фазовым сдвигом, который предоставляется образцовым фазовращателем.
3. Суммарно-разностный метод, он заключается в использовании гармонических или сформированных прямоугольных сигналов.
4. Преобразование сдвига фаз во временном интервале.

Как измеряется угол сдвига фаз осциллографом

Осциллографический способ можно отнести к самому простейшему с погрешностью в районе 5^о. Определение сдвига осуществляется при помощи осциллограмм. Существует четыре осциллографических метода:

1. Применение линейной развертки.
2. Метод эллипса.
3. Метод круговой развертки.
4. Использование яркостных меток.

Определение угла сдвига фаз зависит от характера нагрузки. При определении фазного сдвига в первичной и вторичной цепях трансформатора, углы могут считаться равными и практически не отличаются друг от друга.

Угол сдвига фаз напряжений, измеряемый по эталонному источнику частоты и при использовании измерительного органа лает возможность обеспечить точность всех последующих измерений. Фазные напряжения и угол сдвига фаз зависят от нагрузки, так симметричная нагрузка обуславливает равенство фазного напряжения , токов нагрузки и угол фазного сдвига, также будет равна нагрузка по потребляемой мощности на всех фазах электроустановки.

Угол сдвига фаз между током и напряжением в несимметричных трехфазных цепях не равны друг другу. Для того чтобы вычислить угол сдвига фаз (угол φ) в цепь включают последовательно присоединенные сопротивления (резисторы), индуктивности и конденсаторы (емкости).

Рис. №1. Последовательное соединение сопротивления, индуктивности и емкости для вычисления угла сдвига фаз. В этом контуре протекает переменный ток, который способствует возникновению ЭДС.

 

Рис. №2. Схема проведения опыта по определению сдвига фаз между током и напряжением. Слева показаны схемы подключения конденсаторов, катушек индуктивности и резисторов, справа показаны результаты опыта.

Из результатов опыта можно определить, что сдвиг фаз между напряжением и током служит при определении нагрузки и не может зависеть от переменных величины тока и напряжения в электрической сети.

Как вывод, можно сказать, что:

1. Составляющие элементы комплексного сопротивления, такие как резистор и емкость, а также проводимость не будут взаимообратными величинами.
2. Отсутствие одного из элементов делает резистивные и реактивные значения, которые входят в состав комплексного сопротивления и проводимости и делают их величинами взаимообратными.
3. Реактивные величины в комплексном сопротивлении и проводимости используются с противоположным знаком.

Угол сдвига фаз между напряжением и током всегда выражается, как главный аргументированный фактор комплексного сопротивления φ.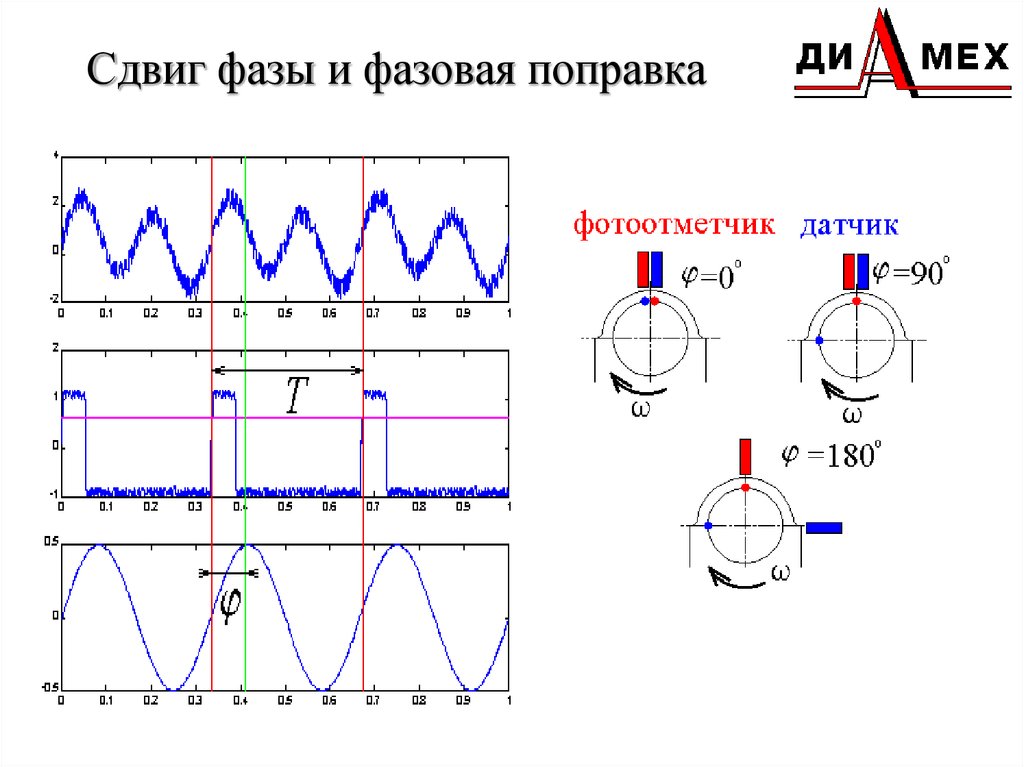

Использование формулы фазового сдвига в анализе цепи переменного тока

Ключевые выводы

●     Узнайте о формуле фазового сдвига.

●     Получите более полное представление о важности расчета фазового сдвига для анализа цепи переменного тока.

●     Узнайте, как рассчитать фазовый сдвиг.

 

Различные фазы синусоиды.

В любой отрасли, включая область электроники, смещение является синонимом той или иной формы изменения. В некоторых случаях этот сдвиг вызван внешними силами и может быть даже непреднамеренным. В других случаях сдвиг является внутренним и, возможно, преднамеренным, частично из-за функциональных требований.

Когда мы изучаем природу смещения в отношении частоты, эти изменения обычно могут отрицательно или положительно влиять на функциональность. Когда мы смотрим на понимание фазового сдвига в электронном дизайне, обнаруживаем, что различное фазное напряжение и амплитуда коррелируют с такими вещами, как периодическая функция, угловая частота, а затем соответствуют эффективности изменения фазы. Катушки индуктивности и низкочастотные устройства часто используют этот метод.

Что такое фаза и что такое фазовый сдвиг?

Мы определяем «фазу» как сигнал, имеющий ту же длину волны, тот же период и ту же частоту, что и другой сигнал, но при этом они представляют собой две (или более) формы волны, которые не точно выровнены. Фаза не является свойством отдельного радиочастотного сигнала; скорее, это касается отношения между этими двумя или более сигналами, которые также имеют одну и ту же частоту.

«Фазовый сдвиг» — это незначительное изменение между двумя формами сигнала. Как в электронике, так и в математике фазовый сдвиг — это задержка, присутствующая между этими двумя формами сигналов, имеющими одну и ту же частоту или период. Таким образом, мы выражаем фазовые сдвиги в терминах угла, который мы измеряем в радианах или градусах, которые могут быть положительными или отрицательными.

Например, положительный фазовый сдвиг на 90° составляет четверть полного цикла. В этом случае наша вторая волна опережает первую на 90°. Мы можем рассчитать фазовый сдвиг, используя временную задержку между ними и частоту сигналов.

Что такое формула фазового сдвига?

Во-первых, существует корреляция между синусоидальной волновой функцией и фазой. В области математики, а точнее, в тригонометрии, тригонометрическая синусоидальная функция генерирует гладкий волнообразный график. На этом графике чередуются минимальное и максимальное значения, и он повторяется каждые 360° (2 * пи радиан).

Note:

Pi radians = 180o

or

3.14159265359 * 57.295779513o = 180o

π rad = 180o

π = 3. 14159265359

A radian = 57.295779513o

1 рад = 180o/3,14159265359 = 57,295779513o

При 0o функция будет иметь нулевое значение, а при 90o она достигает максимального положительного значения. При 180° она стремится к нулю, а при 270° функция достигает максимального отрицательного значения. Однако на 360° он вернется к нулю, таким образом завершив полный цикл.

Любой угол больше 360° будет просто повторять предыдущий цикл. Кроме того, синусоида со сдвигом фазы будет начинаться и заканчиваться со значением, отличным от нуля, даже если во всех других аспектах она выглядит как стандартная синусоида. Это означает, что это s-образный сигнал, который является гладким и колеблется снизу, вверх или из стороны в сторону относительно нуля.

Вычисление фазового сдвига

Вычисление фазового сдвига включает сравнение двух сигналов, что также означает определение того, какая из этих двух волн является первой, а какая второй. В области электроники вторая волна обычно является выходом чего-то вроде усилителя, а вход мы обозначаем как первую волну.

В области математики первая волна может быть исходной функцией, а вторичная функция, конечно же, будет второй волной. Чтобы дополнительно проиллюстрировать это, мы можем использовать следующий пример: здесь ваша первая функция y = sin(x), а ваша вторая функция y = cos(x). Хотя порядок двух волн не влияет на абсолютное значение фазового сдвига, он определяет, является фазовый сдвиг отрицательным или положительным.

Когда мы сравниваем осциллограммы, мы организуем их так, чтобы они читались слева направо с использованием одних и тех же единиц времени или угла оси X. Например, график для обоих может начинаться с 0 секунд; здесь мы найдем пик на второй волне и найдем эквивалентный пик на первой. Всякий раз, когда мы ищем соответствующий пик, мы остаемся в пределах одного полного цикла, чтобы избежать неточностей разности фаз.

Примечание. Чтобы найти разницу, найдите значения по оси X для обоих пиков и вычтите их. Например, если пик первой волны приходится на 0,005 секунды, а пик второй волны приходится на 0,003 секунды, тогда разница составляет 0,005 — 0,003 = 0,002 секунды.

Вычисление фазового сдвига Продолжение

Таким образом, при вычислении фазового сдвига вам понадобятся период и частота волн. Например, осциллятор может генерировать синусоиду частотой 100 Гц. Мы определяем период или продолжительность цикла, разделив частоту на 1. Таким образом, в этом случае 1 ÷ 100 = 0,01 секунды для периода или продолжительности цикла.

Формула фазового сдвига выглядит следующим образом:

ps = 360 × (td ÷ p)

ps = фазовый сдвиг в градусах

td = разница во времени между сигналами 3 9 90 540 90 90 период

Используя вышеприведенные примеры, формула будет иметь следующий результат:

360 × (0,002 ÷ 0,01) = фазовый сдвиг (пс) в 72 градуса

Поскольку результатом является положительное число, фазовый сдвиг тоже положителен. С учетом этого вторая волна отстает от первой на 72 градуса. Чтобы вычислить разность фаз в радианах, мы используем следующее:

2 × pi × (td ÷ p)

Using the example results in the following solution:

2 × 3.14159265359 × (0.002 ÷ 0.01)

or

6.28 × 0.2 = 1.256 радианы

Мы используем формулу фазового сдвига, чтобы определить взаимосвязь между двумя сигналами и их результирующий фазовый угол. Это дает возможность проводить измерения в любом месте вдоль горизонтальной нулевой оси, в которой каждая волна проходит с одним и тем же направлением наклона, как отрицательным, так и положительным. Это важно, поскольку дает возможность описать взаимосвязь между напряжением и синусоидой тока в одной и той же цепи. Это жизненно важный инструмент в силовых цепях переменного тока, который служит основой для анализа цепей переменного тока.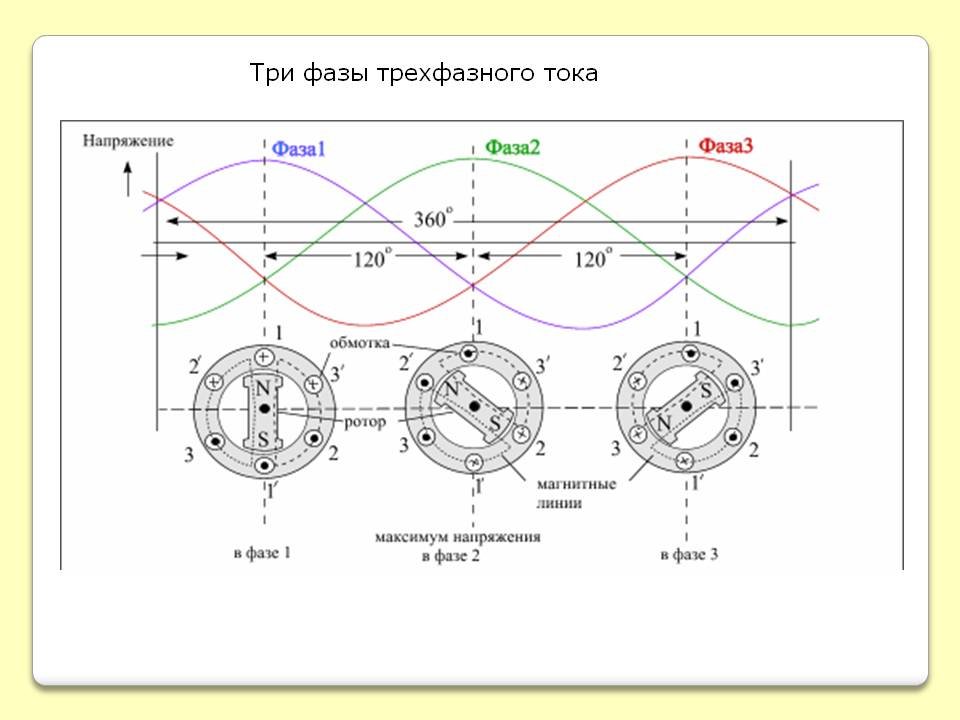

Части синусоиды.

Прежде чем беспокоиться об измерении фазового сдвига в цепях переменного тока, вы должны убедиться, что используете правильный набор программного обеспечения для проектирования, компоновки и анализа печатных плат. Allegro PCB Designer и полный набор инструментов проектирования Cadence помогут вам создавать проекты на основе проверенных моделей компонентов и анализировать все аспекты их функциональности. У вас также будет доступ к набору инструментов для проектирования MCAD и подготовки к производству. Наличие правильных инструментов может гарантировать, что ваш дизайн будет выполнен правильно с первого раза.

Если вы хотите узнать больше о том, какое решение может предложить Cadence, обратитесь к нам и нашей команде экспертов.

Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.

Подпишитесь на Linkedin Посетите вебсайт Больше контента от Cadence PCB Solutions

УЗНАТЬ БОЛЬШЕ

Как определить фазовый угол трехфазной цепи

спросил 7 лет, 11 месяцев назад

Изменено 1 год, 2 месяца назад

Просмотрено 9к раз

\$\начало группы\$

У меня возникли трудности с вопросом:

Сбалансированная трехфазная нагрузка, показанная на схеме, подключена к трехфазной сети 380 В, 50 Гц, последовательность фаз ABC. Напряжение В _АВ принято за эталонное.

Часть вопроса, на который я пытаюсь ответить, включает в себя преобразование схемы WYE в схему Delta, как я это сделал:

Теперь мой главный вопрос: как мне определить фазовый угол каждого компонента?
В моем учебнике нет примечаний о том, как определить фазовый угол. Все, что они говорят, это V _BC обычно используется в качестве эталонного вектора. Но в этом случае V _AB используется в качестве эталонного вектора, и я не знаю, как определить углы для векторной диаграммы. Я подумал о том, чтобы повернуть опорную диаграмму V _BC так, чтобы V _AB = 0, V _AC = 120 и V _BC = 240. Был бы я прав при таком подходе? Пожалуйста, сообщите

• трехфазный

\$\конечная группа\$

3

\$\начало группы\$

Теперь мой главный вопрос заключается в том, как определить фазовый угол каждого компонент?

Нарисуйте векторную диаграмму: —

В треугольнике нагрузки подключены к трем линейным напряжениям, а именно Vab, Vbc и Vca.