Что такое модуль Юнга. Как рассчитать модуль упругости материала. Почему модуль Юнга важен для инженеров и конструкторов. Где применяется модуль Юнга в повседневной жизни. Какие материалы имеют высокий и низкий модуль упругости.
Что такое модуль Юнга и как он определяется
Модуль Юнга — это фундаментальная характеристика материала, которая показывает его способность сопротивляться деформации при приложении нагрузки. Этот параметр определяется как отношение напряжения к относительному удлинению материала в области упругих деформаций.
Математически модуль Юнга (E) выражается формулой:
E = σ / ε
где σ — напряжение (сила на единицу площади), ε — относительная деформация (изменение длины, отнесенное к начальной длине образца).
Чем выше модуль Юнга, тем жестче материал и тем труднее его деформировать. Материалы с низким модулем Юнга, напротив, легко растягиваются или сжимаются под нагрузкой.
Как измеряется модуль упругости материалов
Измерение модуля Юнга обычно проводится в ходе испытаний на растяжение. Образец материала подвергается постепенно возрастающей нагрузке, при этом фиксируется зависимость между приложенным напряжением и возникающей деформацией.
Основные этапы определения модуля упругости:
- Подготовка стандартного образца материала
- Установка образца в испытательную машину
- Постепенное увеличение растягивающей нагрузки
- Измерение удлинения образца при разных значениях нагрузки
- Построение диаграммы «напряжение-деформация»
- Определение наклона линейного участка диаграммы, соответствующего модулю Юнга
Важно проводить измерения в области упругих деформаций, где сохраняется линейная зависимость между напряжением и деформацией. При превышении предела упругости материал начинает деформироваться необратимо.
Значение модуля Юнга для различных материалов
Модуль Юнга существенно различается для разных материалов. Вот некоторые характерные значения:
- Сталь: 200-210 ГПа
- Алюминий: 69-71 ГПа
- Медь: 110-120 ГПа
- Титан: 105-120 ГПа
- Бетон: 30-50 ГПа
- Дерево (вдоль волокон): 9-16 ГПа
- Полиэтилен: 0.2-1.4 ГПа
- Резина: 0.01-0.1 ГПа
Как видно, металлы обладают высоким модулем упругости, что делает их жесткими и прочными. Полимеры и эластомеры, напротив, имеют низкий модуль Юнга и легко деформируются.
Применение модуля Юнга в инженерных расчетах
Знание модуля упругости критически важно при проектировании различных конструкций и изделий. Рассмотрим основные области применения этого параметра:
Расчет деформаций
Модуль Юнга позволяет рассчитать, насколько деформируется деталь или конструкция под действием нагрузки. Это необходимо для обеспечения требуемой жесткости изделий.
Оценка прочности
Хотя модуль Юнга напрямую не определяет прочность, он помогает оценить напряженное состояние материала и спрогнозировать возможность разрушения.
Подбор материалов
Инженеры выбирают материалы с подходящим модулем упругости в зависимости от требований к жесткости конструкции.
Расчет собственных частот колебаний
Модуль Юнга входит в формулы для расчета частот собственных колебаний конструкций, что важно для предотвращения резонанса.
Влияние различных факторов на модуль Юнга
Модуль упругости материала может изменяться под влиянием различных факторов:
Температура
С повышением температуры модуль Юнга большинства материалов снижается. Это связано с увеличением подвижности атомов и молекул.
Влажность
Для некоторых материалов (например, древесины) повышение влажности приводит к снижению модуля упругости.
Структура материала
Наличие дефектов, пористость, размер зерна и другие структурные особенности влияют на модуль Юнга.
Направление нагрузки
Для анизотропных материалов (например, композитов) модуль упругости зависит от направления приложения нагрузки.
Взаимосвязь модуля Юнга с другими механическими свойствами
Модуль Юнга тесно связан с другими характеристиками материалов:
Коэффициент Пуассона
Этот параметр характеризует поперечную деформацию при растяжении. Вместе с модулем Юнга он полностью описывает упругие свойства изотропного материала.
Модуль сдвига
Для изотропных материалов модуль сдвига может быть рассчитан через модуль Юнга и коэффициент Пуассона.
Скорость звука
Скорость распространения звуковых волн в материале прямо пропорциональна квадратному корню из отношения модуля Юнга к плотности.
Особенности определения модуля Юнга для разных типов материалов
Методика измерения модуля упругости может различаться в зависимости от типа исследуемого материала:
Металлы
Полимеры
У полимеров модуль Юнга сильно зависит от скорости нагружения и температуры, что требует специальных методик испытаний.
Композиты
Для композиционных материалов важно учитывать анизотропию свойств и проводить испытания в различных направлениях.
Тонкие пленки
Определение модуля упругости тонких пленок требует специальных методов, например, наноиндентирования.
Точное определение модуля Юнга — важная задача материаловедения, требующая учета особенностей структуры и поведения каждого конкретного материала.
Физика — Модуль Юнга — Бирмингемский университет
Одним из самых важных тестов в технике является знание того, когда объект или материал будет изгибаться или ломаться, и свойство, которое говорит нам об этом, — модуль Юнга. Это мера того, насколько легко материал растягивается и деформируется.
Введение | Видео | В фокусе | Заключение | Следующие шаги |
Согнется или сломается?
Провода подчиняются закону Гука, как и пружины. Когда приложена сила F , она распространится на некоторое расстояние x , что можно просто описать уравнением F = kx
В то время как k для пружины — это жесткость пружины, степень растяжения проволоки зависит от ее площади поперечного сечения, длины и материала, из которого она изготовлена.
Модуль Юнга ( E ) — это свойство материала, которое говорит нам, насколько легко он может растягиваться и деформироваться, и определяется как отношение растягивающего напряжения ( σ ) к деформации растяжения ( ε ). Где напряжение представляет собой количество силы, приложенной к единице площади (
Поскольку сила F = мг , мы можем получить модуль Юнга проволоки, измерив изменение длины ( dl ), поскольку применяются гири массой м (при условии, что г = 9,81 метра в секунду в квадрате).
Относится ли модуль Юнга к исследованиям?
Имеет ли модуль Юнга отношение к исследованиям?
Что важно знать?
Для разных типов материалов графики напряжения-деформации могут выглядеть очень по-разному. Хрупкие материалы, как правило, очень прочные, потому что они могут выдерживать большие нагрузки, они не сильно растягиваются и могут внезапно сломаться.
Пластичные материалы имеют большую область упругости, где зависимость между напряжением и деформацией является линейной, но при первом обороте (предел упругости) линейность нарушается, и материал больше не может вернуться к своей первоначальной форме. Второй пик — это предел прочности при растяжении, и он говорит нам о максимальном напряжении, которое материал может выдержать до разрыва. Пластмассовые материалы не очень прочные, но выдерживают большую нагрузку. Модуль Юнга задается градиентом линии на графике напряжения-деформации.
В эксперименте, показанном на видео выше, мы измерили модуль Юнга медной проволоки, которая не сильно растягивается. Таким образом, можно использовать реперный маркер, например, ленту, чтобы определить исходную и увеличенную длину. Выполнение многократных измерений с различными массами увеличит количество точек на графике напряжения-деформации и сделает расчет модуля Юнга более надежным. Еще одна вещь, о которой нужно позаботиться, — это измерение площади поперечного сечения провода.
Как это применимо ко мне?
Изучение механических свойств материалов важно, потому что оно помогает нам понять, как ведут себя материалы, и позволяет нам разрабатывать новые продукты и улучшать существующие. В качестве примера темы исследования в Бирмингеме рассматривалась разработка шестов для прыжков, используемых спортсменами, занимающимися прыжками в высоту, для достижения максимальной производительности. Эти шесты должны быть легкими, чтобы обеспечить быстрый разбег, но также должны сохранять энергию упругой деформации при изгибе шеста. Шест должен преобразовывать энергию упругости в кинетическую энергию по мере того, как он выпрямляется, и быть в состоянии выдерживать нагрузки, вызванные весом прыгуна, а также выдерживать многократные использования спортсменом.
В небольших масштабах существует множество продуктов, содержащих биологические (например, фармацевтические препараты, препараты для лечения бесплодия, тканевая инженерия) и небиологические микрочастицы (например, химикаты, сельское хозяйство, товары для дома).
Благодаря пониманию их механических свойств мы можем прогнозировать их поведение при производстве и обработке, максимизировать их эксплуатационные возможности.
Модуль Юнга материала полезно знать, чтобы предсказать поведение материала под действием силы. Это важно практически для всего, что нас окружает, от зданий до мостов, транспортных средств и многого другого.
Следующие шаги
Эти ссылки предоставляются для удобства и только в информационных целях; они не являются подтверждением или одобрением Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте. Университет Бирмингема не несет ответственности за точность, законность или содержание внешнего сайта или последующих ссылок. Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы, касающиеся его содержания.
61
40
29
1
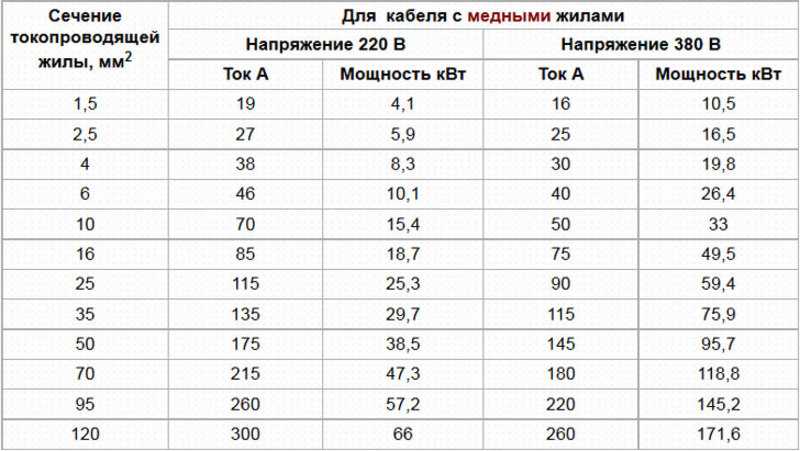14
