Что такое сортировка выбором. Как работает алгоритм сортировки выбором. Каковы преимущества и недостатки сортировки выбором. Как реализовать сортировку выбором на разных языках программирования. Какова сложность алгоритма сортировки выбором. Где применяется сортировка выбором на практике. Как оптимизировать алгоритм сортировки выбором.
Что такое сортировка выбором и как она работает
Сортировка выбором (Selection Sort) — это простой алгоритм сортировки, основанный на сравнении элементов. Его основная идея заключается в том, чтобы многократно находить минимальный элемент из несортированной части массива и помещать его в начало.
Принцип работы алгоритма:
- Находим минимальный элемент в несортированной части массива
- Меняем его местами с первым элементом несортированной части
- Сдвигаем границу отсортированной части на одну позицию вправо
- Повторяем шаги 1-3, пока весь массив не будет отсортирован
Рассмотрим пример работы алгоритма на массиве [64, 25, 12, 22, 11]:
- Шаг 1: [11, 25, 12, 22, 64] — 11 минимальный, меняем с первым элементом
- Шаг 2: [11, 12, 25, 22, 64] — 12 минимальный в оставшейся части
- Шаг 3: [11, 12, 22, 25, 64] — 22 минимальный в оставшейся части
- Шаг 4: [11, 12, 22, 25, 64] — 25 уже на своем месте
В результате получаем отсортированный по возрастанию массив.
Реализация алгоритма сортировки выбором на разных языках
Рассмотрим реализацию сортировки выбором на нескольких популярных языках программирования.
Python
Реализация на Python будет выглядеть следующим образом:
«`python def selection_sort(arr): n = len(arr) for i in range(n): min_idx = i for j in range(i+1, n): if arr[j] < arr[min_idx]: min_idx = j arr[i], arr[min_idx] = arr[min_idx], arr[i] return arr # Пример использования arr = [64, 25, 12, 22, 11] sorted_arr = selection_sort(arr) print("Отсортированный массив:", sorted_arr) ```Java
А вот как будет выглядеть реализация на Java: «`java public class SelectionSort { public static void selectionSort(int[] arr) { int n = arr.length; for (int i = 0; i < n-1; i++) { int minIdx = i; for (int j = i+1; j < n; j++) { if (arr[j] < arr[minIdx]) { minIdx = j; } } int temp = arr[minIdx]; arr[minIdx] = arr[i]; arr[i] = temp; } } public static void main(String[] args) { int[] arr = {64, 25, 12, 22, 11}; selectionSort(arr); System.out.println("Отсортированный массив:"); for (int i : arr) { System.out.print(i + " "); } } } ```Сложность алгоритма сортировки выбором
Важной характеристикой любого алгоритма является его сложность. Для сортировки выбором сложность можно оценить следующим образом:
- Временная сложность: O(n^2) во всех случаях (лучшем, среднем, худшем)
- Пространственная сложность: O(1), так как сортировка выполняется на месте
Почему временная сложность квадратичная. Алгоритм использует два вложенных цикла: внешний выполняется n-1 раз, а внутренний — от n-1 до 1 раза. Это дает нам формулу (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2, что в итоге дает квадратичную сложность O(n^2).
Преимущества и недостатки сортировки выбором
Как и любой алгоритм, сортировка выбором имеет свои сильные и слабые стороны. Рассмотрим основные преимущества:
- Простота реализации и понимания алгоритма
- Работает на месте, не требуя дополнительной памяти
- Минимальное количество обменов элементов (не более n-1)
Теперь обратимся к недостаткам:
- Квадратичная сложность делает алгоритм неэффективным на больших наборах данных
- Нестабильность — алгоритм может изменить порядок равных элементов
- Производительность не зависит от исходного порядка элементов
Применение сортировки выбором на практике
Несмотря на свою простоту, сортировка выбором находит применение в определенных сценариях:
- Сортировка небольших массивов (до 10-20 элементов)
- Обучение основам алгоритмов сортировки
- Ситуации, где важно минимизировать количество обменов элементов
- Как часть более сложных алгоритмов сортировки (например, Introsort)
Однако для больших объемов данных обычно используются более эффективные алгоритмы, такие как быстрая сортировка или сортировка слиянием.
Оптимизация алгоритма сортировки выбором
Хотя базовая версия сортировки выбором имеет квадратичную сложность, существуют способы её оптимизации:
- Двусторонняя сортировка выбором: поиск минимального и максимального элемента за один проход
- Использование бинарного поиска для нахождения позиции вставки
- Комбинирование с другими алгоритмами для улучшения производительности на определенных типах данных
Рассмотрим пример двусторонней сортировки выбором на Python:
«`python def bidirectional_selection_sort(arr): left = 0 right = len(arr) — 1 while left < right: min_idx = left max_idx = right for i in range(left, right + 1): if arr[i] < arr[min_idx]: min_idx = i if arr[i] > arr[max_idx]: max_idx = i if min_idx != left: arr[left], arr[min_idx] = arr[min_idx], arr[left] if max_idx == left: max_idx = min_idx if max_idx != right: arr[right], arr[max_idx] = arr[max_idx], arr[right] left += 1 right -= 1 return arr # Пример использования arr = [64, 25, 12, 22, 11, 61, 1, 100] sorted_arr = bidirectional_selection_sort(arr) print(«Отсортированный массив:», sorted_arr) «`Эта оптимизация позволяет уменьшить количество проходов по массиву почти вдвое, что может дать заметный прирост производительности на больших наборах данных.
Сравнение сортировки выбором с другими алгоритмами
Чтобы лучше понять место сортировки выбором среди других алгоритмов, сравним её с некоторыми популярными методами сортировки:
- Пузырьковая сортировка: оба алгоритма имеют сложность O(n^2), но сортировка выбором обычно выполняет меньше обменов
- Сортировка вставками: в среднем эффективнее сортировки выбором, особенно на почти отсортированных данных
- Быстрая сортировка: значительно эффективнее на больших наборах данных со средней сложностью O(n log n)
- Сортировка слиянием: стабильный алгоритм со сложностью O(n log n), но требует дополнительной памяти
Выбор алгоритма сортировки зависит от конкретной задачи, размера данных и требований к памяти и стабильности.
Визуализация работы алгоритма сортировки выбором
Для лучшего понимания работы алгоритма сортировки выбором, давайте создадим простую визуализацию с помощью React компонента:
«` import React, { useState, useEffect } from ‘react’; const SelectionSortVisualization = () => { const [array, setArray] = useState([]); const [currentIndex, setCurrentIndex] = useState(0); const [minIndex, setMinIndex] = useState(0); useEffect(() => { // Генерируем случайный массив const randomArray = Array.from({length: 10}, () => Math.floor(Math.random() * 100)); setArray(randomArray); }, []); useEffect(() => { if (currentIndex < array.length - 1) { const timer = setTimeout(() => { let minIdx = currentIndex; for (let j = currentIndex + 1; j < array.length; j++) { if (array[j] < array[minIdx]) { minIdx = j; } } setMinIndex(minIdx); const newArray = [...array]; [newArray[currentIndex], newArray[minIdx]] = [newArray[minIdx], newArray[currentIndex]]; setArray(newArray); setCurrentIndex(currentIndex + 1); }, 1000); return () => clearTimeout(timer); } }, [array, currentIndex]); return (Визуализация сортировки выбором
Текущий шаг: {currentIndex + 1}
Этот компонент создает визуальное представление работы алгоритма сортировки выбором. Каждый столбец представляет элемент массива, а его высота — значение элемента. Синий столбец показывает текущую позицию, красный — найденный минимальный элемент, а зеленые — уже отсортированную часть массива.
Оператор SQL ORDER BY: синтаксис, примеры
Оператор SQL ORDER BY выполняет сортировку выходных значений. Оператор SQL ORDER BY можно применять как к числовым столбцам, так и к строковым. В последнем случае, сортировка будет происходить по алфавиту.
Оператор SQL ORDER BY имеет следующий синтаксис:
ORDER BY column_name [ASC | DESC]
Сортировка может производиться как по возрастанию, так и по убыванию значений.
- Параметр ASC (по умолчанию) устанавливает порядок сортирования во возрастанию, от меньших значений к большим.
- Параметр DECS устанавливает порядок сортирования по убыванию, от больших значений к меньшим.
Примеры оператора SQL ORDER BY. Имеется следующая таблица Artists:
| Singer | Album | Year | Sale |
| The Prodigy | Invaders Must Die | 2008 | 1200000 |
| Drowning Pool | Sinner | 2001 | 400000 |
| Massive Attack | Mezzanine | 1998 | 2300000 |
| The Prodigy | Fat of the Land | 1997 | 600000 |
| The Prodigy | Music For The Jilted Generation | 1994 | 1500000 |
| Massive Attack | 100th Window | 2003 | 1200000 |
| Drowning Pool | Full Circle | 2007 | 800000 |
| Massive Attack | Danny The Dog | 2004 | 1900000 |
| Drowning Pool | Resilience | 2013 | 500000 |
Пример 1.
Вывести все записи таблицы, упорядоченные по названию исполнителя с помощью оператора SQL ORDER BY:
SELECT * FROM Artists ORDER BY Singer
| Singer | Album | Year | Sale |
| Drowning Pool | Sinner | 2001 | 400000 |
| Drowning Pool | Full Circle | 2007 | 800000 |
| Drowning Pool | Resilience | 2013 | 500000 |
| Massive Attack | Mezzanine | 1998 | 2300000 |
| Massive Attack | 100th Window | 2003 | 1200000 |
| Massive Attack | Danny The Dog | 2004 | 1900000 |
| The Prodigy | Invaders Must Die | 2008 | 1200000 |
| The Prodigy | Fat of the Land | 1997 | 600000 |
| The Prodigy | Music For The Jilted Generation | 1994 | 1500000 |
Пример 2.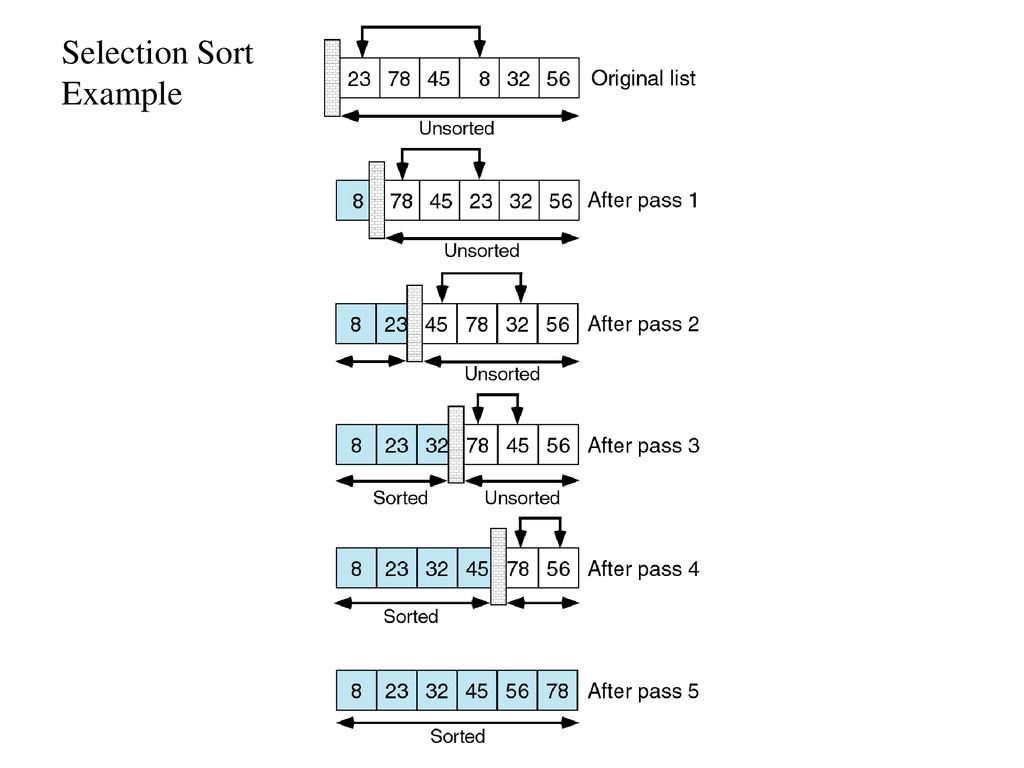
С помощью оператора SQL ORDER BY вывести названия исполнителя, альбома, год выпуска тех альбомов, которые выпущены после 2005 года, упорядоченные по убыванию года:
SELECT Singer, Album, Year FROM Artists WHERE Year > 2005 ORDER BY Year DESC
Результат:
| Singer | Album | Year |
| Drowning Pool | Resilience | 2013 |
| The Prodigy | Invaders Must Die | 2008 |
| Drowning Pool | Full Circle | 2007 |
Selection Sort — Interview Kickstart
Если вы разработчик программного обеспечения и готовитесь к техническому собеседованию, вы попали по адресу! Большинство технологических компаний используют проблемы со структурой данных для проверки мастерства разработчиков программного обеспечения. Вы должны хорошо разбираться не только во всех концепциях структуры данных, но и в различных методах сортировки данных.
Сортировка выбором — один из таких методов, который вы должны освежить в своем цикле кодирования. В этой статье мы рассмотрим:
- Что такое сортировка выбором?
- Как это работает — с примером
- Выбор алгоритма сортировки
- Выбор сортировки псевдокоды
- Код сортировки
- Сложность сортировки выбора
- Преимущества выбора сортировки
- Дисп. Сортировка выбором?
По определению, сортировка выбором — это алгоритм сортировки на основе сравнения на месте. Этот алгоритм сортировки известен своей простотой и эффективностью использования памяти — он не занимает лишнего места. Метод сортировки выбором многократно ищет «оставшиеся элементы», чтобы найти наименьший элемент, и перемещает его в конечное место.
Давайте углубимся в то, что это значит.
Принцип работы сортировки выбором
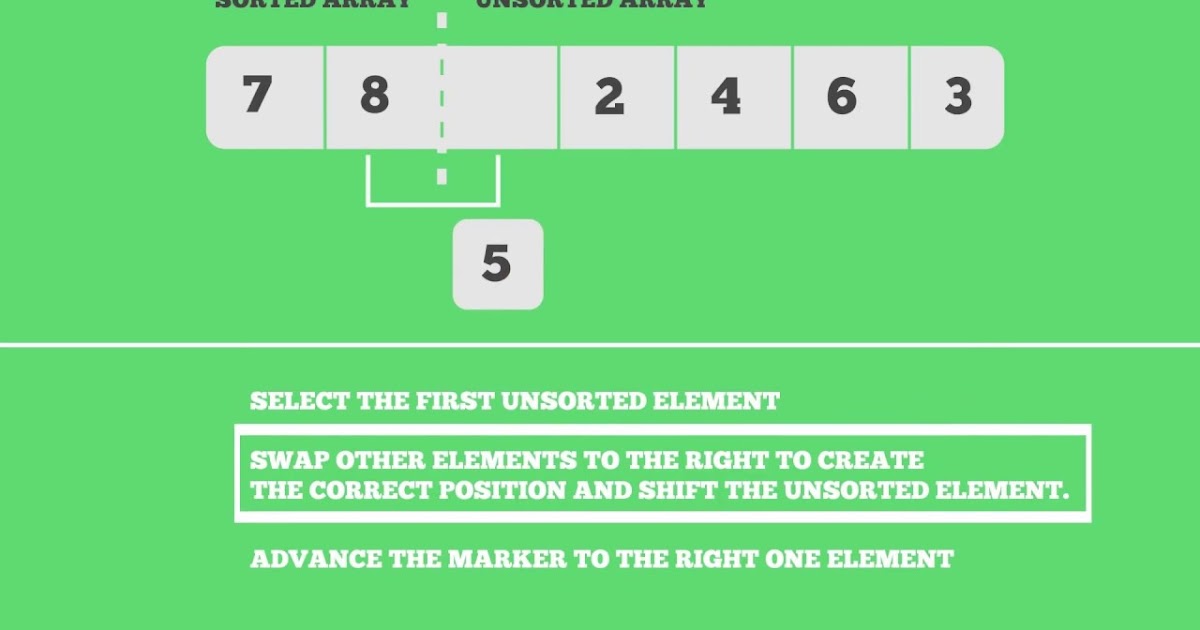
Этот алгоритм делит входной массив на две части — отсортированную часть и несортированную часть.
Изначально отсортированная часть массива пуста, а несортированная часть является входным массивом. Алгоритм работает по принципу нахождения наименьшего числа из несортированной части массива и последующей замены его первым элементом несортированной части. Это делается снова и снова, пока весь массив не будет отсортирован (в порядке возрастания).
Пример сортировки выбором
Рассмотрим следующий пример:
Входной массив:
arr [ ]= 19 10 4 8 3
Сначала мы ищем наименьшее число в arr[0-4] для замены это с первым элементом несортированной части. Итак, мы меняем местами 3 на 19, и массив изменяется следующим образом:
arr[ ]= 3 10 4 8 19
Далее нам нужно найти наименьшее число в arr[1-4] для обмена с первым элементом несортированного массива. Итак, меняем местами 4 на 10.
arr[ ]= 3 4 10 8 19
Теперь мы должны найти наименьшее число в arr[2-4] и поменять местами.
ARR [] = 3 4 8 10 19
сделайте то же самое для ARR [3-4]
ARR [] = 3 4 8 10 19
, и наш массив сортируется!
Алгоритм сортировки выбором
Теперь, когда вы знаете, как работает сортировка выбором, следовать шагам алгоритма будет довольно легко:
- Шаг 1: Установить minIndex в позицию 0
(minIndex будет содержать индекс наименьшего числа в несортированном подмассиве) - Шаг 2: Поиск наименьшего элемента в несортированном подмассиве и обновление minIndex
- Шаг 3: Поменять местами элемент в позиции minIndex с первым элементом несортированного подмассива.
- Шаг 4: Снова установите minIndex в первую позицию несортированного подмассива
- Шаг 5: Повторяйте шаги со 2 по 4, пока массив не будет отсортирован.
Псевдокод сортировки выбором
Как только вы поймете логику, написание кода для сортировки выбором станет довольно простым.
Вот псевдокод, который поможет вам написать код на любом языке по вашему выбору.
сортировка выбора процедуры arr : массив целых чисел n : размер массива для i = от 1 до n-1 // устанавливаем текущий элемент как minIndex мининдекс=я // проверить все остальные элементы (правая сторона текущего элемента) для j =i+1 до n если (обр [j]
Код сортировки выбором в C++
Мы выбрали C++ для демонстрации сортировки выбором. Вы можете использовать это как ссылку на код на C, Java, Python или любом другом языке программирования, который вы предпочитаете.
#включать использование пространства имен std; void selectionSort(int arr[], int n) { for (int i = 0; i Вывод:
Отсортированный массив:
3 4 8 10 19
Объяснение кода
Мы использовали те же входные данные, что и в примере выше. .
Первоначально текущий элемент был 19. Мы использовали цикл for, чтобы найти наименьшее число в массиве — 3.
2 для n элементов 92) в каждом случае - Шаг 1: Установить minIndex в позицию 0
Изначально отсортированная часть массива пуста, а несортированная часть является входным массивом. 
2 для n элементов 92) в каждом случаеЧасто задаваемые вопросы по сортировке выбором
Вопрос 1: Является ли алгоритм сортировки выбором встроенным алгоритмом сортировки на основе сравнения?
Ответ: Алгоритм сортировки выбором — это алгоритм сортировки на месте, основанный на сравнении. В основном это означает, что этот алгоритм преобразует заданный ввод (в данном случае массив) без использования какой-либо другой структуры данных. В таких случаях ввод обычно перезаписывается выводом.
Вопрос 2: Сколько перестановок делает алгоритм сортировки выбором?
Ответ: Алгоритм сортировки выбором делает n-1 свопов в худшем случае и ноль свопов в лучшем случае. Следовательно, он никогда не делает больше O(n) свопов. Таким образом, это удобно в ситуациях, когда «запись в память» является дорогостоящей операцией.
Вопрос 3. Является ли алгоритм сортировки выбором более быстрым, чем пузырьковая сортировка?
Ответ: Как сортировка выбором, так и пузырьковая сортировка имеют сложность в наихудшем случае O(n^2).
Однако алгоритм сортировки выбором по-прежнему быстрее пузырьковой сортировки в худшем случае, когда «запись в память» является дорогостоящей операцией. Это связано с тем, что сортировка выбором делает меньше свопов по сравнению с пузырьковой сортировкой.
Готовы ли вы пройти следующее собеседование по программированию?
Если вам нужны рекомендации и помощь в начале работы, зарегистрируйтесь на наш бесплатный вебинар. Являясь пионерами в области подготовки к техническим собеседованиям, мы обучили тысячи инженеров проходить самые сложные собеседования по программированию и получать работу в компаниях своей мечты, таких как Google, Facebook, Apple, Netflix, Amazon и других!
Зарегистрируйтесь прямо сейчас!
———-
Статья предоставлена Deepak Kumar
Алгоритмы сортировки: сортировка выбором | Мариам Джалуди | Стартап
Сортируем! В этой серии я расскажу об алгоритмах сортировки. Большинство языков программирования имеют встроенную функцию сортировки, но для того, чтобы писать более качественный код, вам нужно знать, что происходит в фоновом режиме.
- Bubble Sort
- Вставка Сорта
- Выбор сортировки
- Сорт сортировка
- Quick Sort
- Radix/Bucket Sort
- Heap Sort
Сорт является третьим в нашем списке Arasy-to-undlond Algorithms (Sorte Sorts-третий в нашем списке Easy-to-undlond (
. Пузырьковая сортировка и сортировка вставками — первые два). Подобно алгоритмам пузырьковой сортировки и сортировки вставками, сортировка выбором не является быстрым алгоритмом, но, тем не менее, его важно знать.
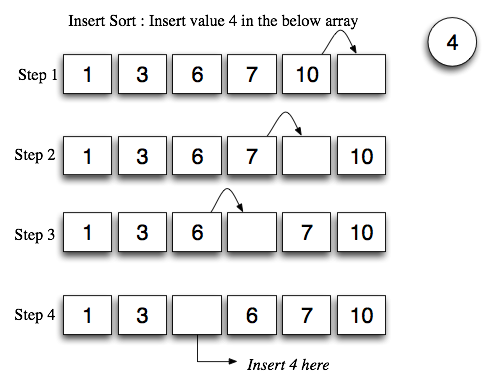
Вернемся к примеру с массивом, который мы использовали в предыдущих разделах:
Мы собираемся отсортировать этот список, разделив его на два отдельных списка внутри этого списка. Один подсписок будет представлять наши отсортированные числа, а другой будет представлять наши несортированные числа.
Изначально весь наш массив представляет собой несортированный список.
Мы будем искать в нашем массиве наименьшее число. Как только мы нашли наименьшее число, мы добавляем его в наш отсортированный список (то есть освобождаем место для него в начале массива). Это происходит на месте во входном массиве.
Если мы просматриваем наш массив, мы начинаем с индекса 0 и рассматриваем все, что там есть, как наше наименьшее значение.
Продолжайте просматривать массив, и если вы найдете какое-либо значение, которое меньше того, что было сохранено ранее, измените наименьшее значение на новое. Итак, если наименьший = 6, и мы переходим к следующему индексу, мы видим, что 3 меньше, чем 6, поэтому наименьший теперь равен 3. Продолжайте по всему массиву, пока не найдете наименьшее значение. В нашем случае мы находим, что 2 — это наименьшее значение.
Что теперь? Возьмите самое левое значение и замените его наименьшим значением. Теперь ваш массив разделен на две части: синяя часть — это отсортированный массив, а остальная часть — несортированный массив.
Давайте посмотрим на другую итерацию:
На этот раз наш несортированный массив начинается с индекса 1, потому что наш отсортированный массив имеет зарезервированный индекс 0. Мы устанавливаем наименьшее значение, которое находится в индексе 1 (наименьшее = 3). Мы будем сравнивать наименьшее значение со всеми остальными значениями в массиве, если есть какое-либо значение, которое меньше, мы устанавливаем наименьшее значение для этого значения. В данном случае мы видим, что 3 — это наименьшее значение. Нам не нужно менять местами 3 сам с собой, поэтому 3 теперь становится частью отсортированного массива.
Следующая итерация:
Начнем с индекса 2 с наименьшим значением = 9. Перебрав весь массив, мы находим, что 4 является наименьшим значением. 9 и 4 поменять местами.
Мы продолжаем увеличивать размер нашего отсортированного массива таким образом, пока не получим полностью отсортированный массив:
Чтобы отсортировать массив с помощью сортировки выбором, вы должны пройти по массиву один раз для каждого значения, которое у вас есть в массиве.
Если у нас есть n значений в нашем массиве, сортировка выбором имеет временную сложность O(n²) в худшем случае. В лучшем случае у нас уже есть отсортированный массив, но нам нужно пройти через массив O(n²) раз, чтобы быть уверенным! Следовательно, временная сложность сортировки выбором в лучшем и худшем случае одинакова.
Как насчет пространственной сложности? Сортировка выбором сортирует на месте , то есть нам не нужно выделять память для сортировки. Сложность пространства составляет O(1) .
Давайте посмотрим на сортировку выбором в Python:
Мы определяем наш selectionSort и принимает массив целых чисел. Теперь нам нужно начать итерацию по нашему массиву. Установите все, что находится в индексе 0, как наименьшее.
def selectionSort(array):
for i in range(len(array)):
наименьший = массив[i]
наименьшийIdx = i
Затем проверьте остальную часть массива на любое меньшее значение .
