Сила демпфирования в колебательных системах: виды, примеры и применение

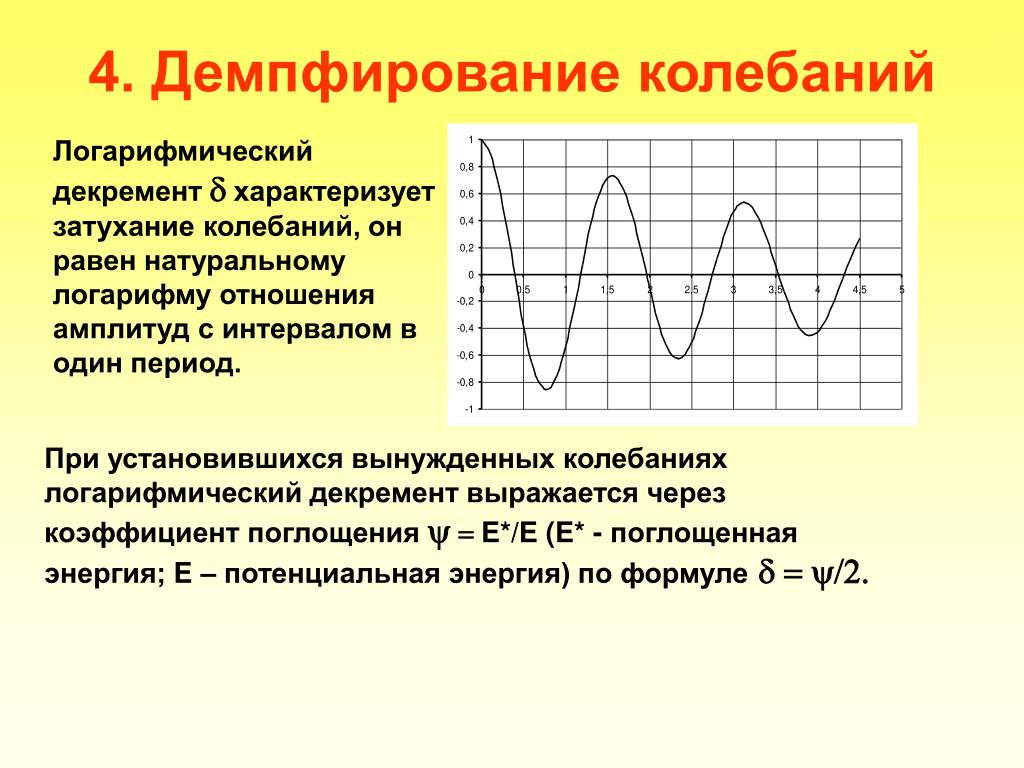
Что такое сила демпфирования. Какие существуют виды демпфирования в колебательных системах. Как демпфирование влияет на колебания. Где применяется демпфирование на практике.

Что такое сила демпфирования

Сила демпфирования — это сила, которая противодействует движению колеблющейся системы и приводит к уменьшению амплитуды колебаний с течением времени. Эта сила возникает из-за рассеяния энергии колебаний в окружающую среду.

Основные характеристики силы демпфирования:

• Направлена противоположно скорости движения
• Пропорциональна скорости движения
• Приводит к затуханию колебаний
• Преобразует механическую энергию колебаний в тепловую

Демпфирование играет важную роль во многих колебательных системах, ограничивая амплитуду колебаний и предотвращая резонанс.

Виды демпфирования в колебательных системах

Существует несколько основных видов демпфирования в колебательных системах:

1. Вязкое демпфирование

Вязкое демпфирование возникает при движении тела в вязкой среде, например, в жидкости или газе. Сила вязкого трения пропорциональна скорости движения:

F = -bv

где b — коэффициент вязкого трения, v — скорость.

2. Сухое трение

Сухое трение возникает между твердыми поверхностями при их относительном движении. Сила сухого трения постоянна по величине и не зависит от скорости:

F = -μN sign(v)

где μ — коэффициент трения, N — сила нормального давления.

3. Гистерезисное демпфирование

Гистерезисное демпфирование связано с внутренним трением в материале при циклических деформациях. Энергия рассеивается из-за необратимых процессов в структуре материала.

4. Демпфирование излучением

Демпфирование излучением происходит, когда энергия колебаний рассеивается в виде волн в окружающую среду, например, при излучении звука или электромагнитных волн.

Влияние демпфирования на колебания

Демпфирование оказывает существенное влияние на характер колебаний системы:

• Уменьшает амплитуду колебаний с течением времени
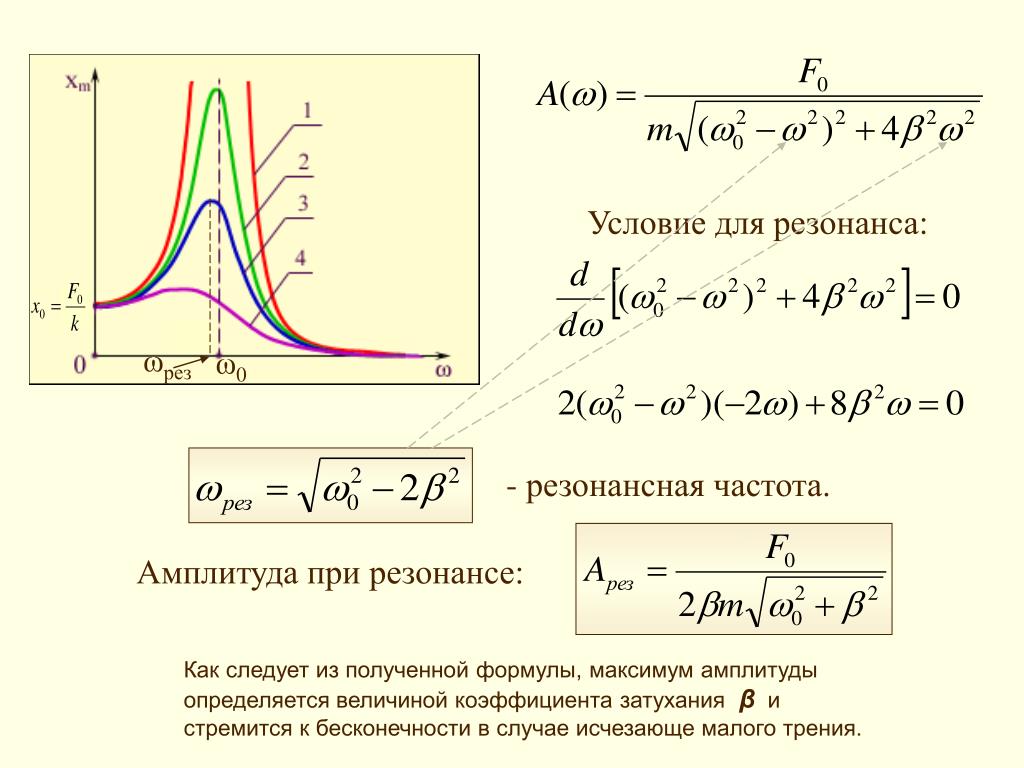
• Снижает резонансную частоту системы
• Ограничивает максимальную амплитуду при резонансе
• Увеличивает ширину резонансной кривой
• Приводит к отставанию по фазе вынужденных колебаний от вынуждающей силы

При слабом демпфировании колебания затухают медленно, при сильном — быстро. Критическое демпфирование обеспечивает наиболее быстрое затухание без перерегулирования.

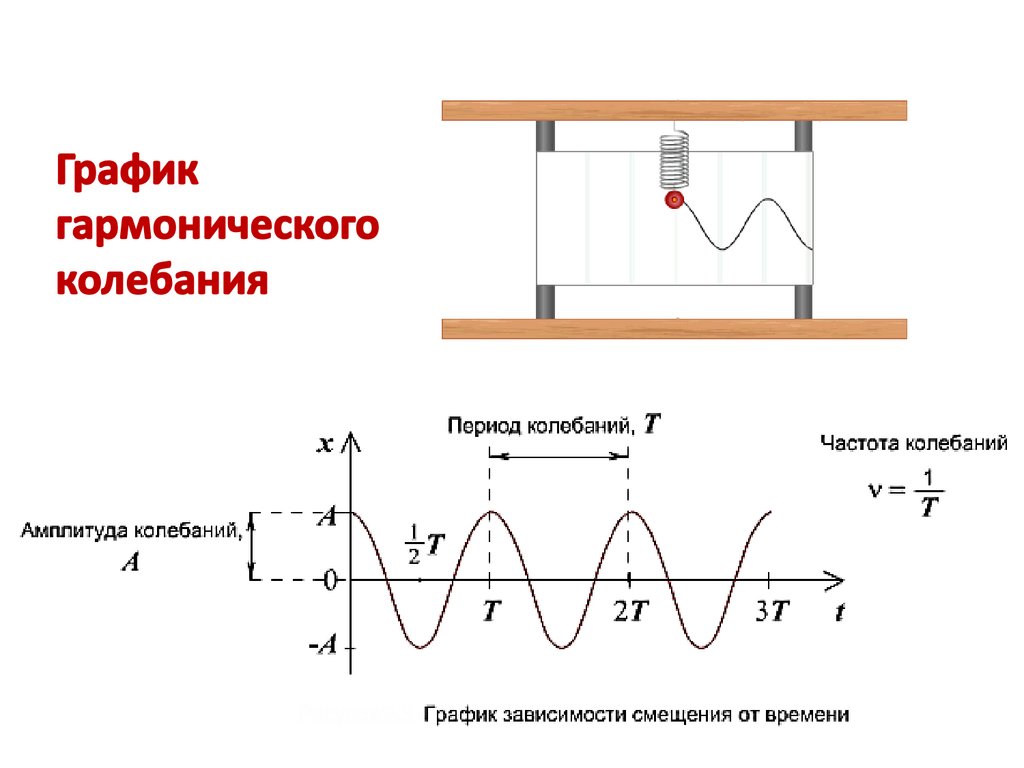
Примеры демпфирования в реальных системах

Демпфирование широко встречается в природе и технике. Некоторые примеры:

• Амортизаторы в автомобиле гасят колебания подвески
• Демпферы в музыкальных инструментах ограничивают время звучания
• Демпфирующие покрытия снижают вибрации конструкций
• Воздушное демпфирование ограничивает колебания маятника
• Электромагнитное демпфирование используется в измерительных приборах

В природных системах демпфирование обеспечивает затухание колебаний после воздействия внешних сил.

Применение демпфирования на практике

Демпфирование активно применяется в различных областях техники:

• Виброизоляция оборудования и конструкций
• Гашение колебаний в транспортных средствах
• Сейсмозащита зданий и сооружений
• Стабилизация прецизионных приборов
• Снижение шума механизмов
• Демпфирование колебаний в электрических цепях

Правильный выбор параметров демпфирования позволяет обеспечить требуемые динамические характеристики систем.

Расчет силы демпфирования

Для расчета силы демпфирования в колебательной системе используются различные модели:

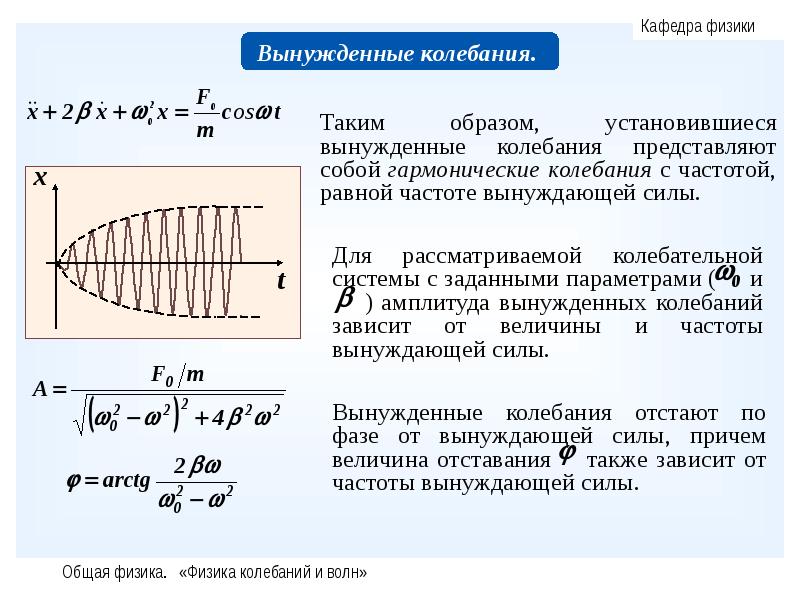
Линейное вязкое демпфирование

Сила пропорциональна скорости:

F = -bv

где b — коэффициент демпфирования, v — скорость.

Квадратичное демпфирование

Сила пропорциональна квадрату скорости:

F = -cv|v|

где c — коэффициент квадратичного демпфирования.

Гистерезисное демпфирование

Сила пропорциональна смещению и не зависит от частоты:

F = -hx

где h — коэффициент гистерезисного демпфирования, x — смещение.

Выбор модели демпфирования зависит от конкретной системы и требуемой точности расчетов.

Влияние демпфирования на собственные частоты системы

Демпфирование оказывает влияние на собственные частоты колебательной системы:

• Уменьшает собственные частоты по сравнению с недемпфированной системой
• Приводит к появлению мнимой части у собственных частот
• Вызывает расщепление кратных собственных частот
• Изменяет собственные формы колебаний

Учет демпфирования важен при анализе динамических характеристик реальных систем.

Проблемы, связанные с демпфированием

При использовании демпфирования могут возникать следующие проблемы:

• Нежелательное рассеяние энергии в некоторых системах
• Нелинейность демпфирующих сил
• Зависимость демпфирования от амплитуды и частоты колебаний
• Сложность точного измерения параметров демпфирования
• Температурная зависимость демпфирующих свойств материалов

Решение этих проблем требует тщательного анализа и подбора оптимальных параметров демпфирования.

Введение в исследование колебательных систем

Колебания: Введение в исследование колебательных систем

Магнус К. Колебания: Введение в исследование колебательных систем. Пер. с нем.— М.: Мир, 1982.— 304 с. В систематической и доступной форме описываются различные виды колебаний. Книга содержит много примеров и задач (в том числе нелинейных). Она может служить учебным пособием, методическим руководством и справочником. Автор, известный западногерманский ученый, знаком советским читателям по переводу его монографии «Гироскоп» (М.: Мир, 1974). Для математиков-прикладников, специалистов по теории колебаний, инженеров, преподавателей, аспирантов и студентов университетов и втузов. Оглавление Предисловие к переводу От автора 1. Основные понятия и определения. Графическое изображение колебательных процессов 1.2. Изображение колебаний в плоскости х, t 1.3. Векторное изображение колебаний и их представление в комплексной плоскости 1.4. Фазовые траектории и фазовый портрет 1.5. Переходная функция, частотные характеристики и годограф колебательной системы 1.6. Типы колебаний и их признаки 2. Собственные колебания 2.1. Недемпфированные собственные колебания 2.1.1.2. Электрический колебательный контур. 2.1.1.3. Жидкость в U-образной трубке и резонатор Гельмгольца. 2.1.1.5. Гравитационный маятник. 2.1.1.6. Осциллятор с непрерывно распределенными накопителями энергии. 2.1.2. Поведение линейных осцилляторов 2.1.2.2. Энергетические соотношения. 2.1.2.3. Влияние массы пружины. 2.1.2.4. Определение собственной частоты по величине стрелы прогиба. 2.1.3. Поведение нелинейных осцилляторов 2.1.3.2. Плоский гравитационный маятник. 2.1.3.3. Применения гравитационного маятника. 2.1.3.4. Циклоидальный маятник. 2.1.3.5. Осциллятор с кусочно линейной восстанавливающей силой. 2.1.3.6. Приближенные методы. 2.2. Демпфированные собственные колебания 2.2.2. Линейный осциллятор 2.2.2.2. Решение уравнений движения. 2.2.2.3. Поведение решений. 2.2.2.4. Фазовый портрет. 2.2.3. Нелинейный осциллятор 2.2.3.2. Осциллятор с сухим трением. 2.2.3.3. Сила демпфирования, пропорциональная квадрату скорости. 2.2.3.4. Энергетический метод решения уравнений колебаний. 2.3. Задачи 3. Автоколебания 3.1.2. Баланс энергии и фазовый портрет 3.2. Методы расчета 3.2.2. Линеаризация исходных уравнений 3.2.3. Метод Ритца — Галеркина 3.2.4. Метод медленно меняющихся амплитуд 3.3. Примеры автоколебательных систем 3.3.1.2. Движение маятника при импульсном периодическом возмущении и линейном демпфировании. 3.3.1.3. Движение маятника при импульсном возмущении и сухом трении. 3.3.2. Ламповый генератор 3. 3.3. Фрикционные колебания маятника Фроуда 3.4. Разрывные колебания 3.4.2. Колебания в релейном контуре регулирования (регулятор температуры) 3.4.2.1. Регулятор с гистерезисом. 3.4.2.2. Регулятор с временным запаздыванием. 3.4.3. RC-генератор 3.5. Задачи 4. Параметрические колебания 4.1. Примеры осцилляторов с параметрическим возбуждением 4.1.2. Колебания в спарнике электровоза 4.1.3. Электрический колебательный контур с периодическими параметрами 4.1.4. Колеблющаяся струна с переменным натяжением 4.1.5. Движение в окрестности стационарных колебаний 4.1.6. Математический маятник переменной длины 4.2. Колебания качелей 4.2.1. Нарастание амплитуды колебаний 4.2.2. Влияние демпфирования и сухого трения 4.3. Параметрические колебания линейных систем 4.3.2. Поведение осциллятора, описываемого уравнением Матье 4.3.3. Приближенные методы решений 4.4. Математический маятник с параметрическим возбуждением 4.4.2. Периодические решения 4. 4.3. Амплитудная частотная характеристика для периодических решений при … 4.4.4. Приближенные решения для случая … 4.5. Задачи 5. Вынужденные колебания 5.1. Реакция линейной системы на внешние непериодические возмущения 5.1.2. Переходные функции при импульсном возмущении 5.1.3. Выбор оптимальных параметров приборов 5.1.4. Возмущающие функции общего вида 5.2. Периодические возмущения в линейных системах 5.2.1.2. Амплитудные и фазовые характеристики. 5.2.1.3. Мощность и работа при вынужденных колебаниях. 5.2.1.4. Передаточная функция и частотные характеристики. 5.2.1.5. Переходные процессы при вынужденных колебаниях. 5.2.2. Периодическое возмущение общего вида; решение методом разложения в ряд Фурье 5.2.3. Статистически распределенные возмущения 5.2.4. Общее периодическое возмущение; решение методом припасовывания 5.3. Применение теории резонанса 5.3.2. Защита машин и приборов от воздействий колебаний 5.3.3. Настройка, избирательность и искажения в радиотехнике 5. 4. Вынужденные колебания нелинейных осцилляторов 5.4.2. Гармоническое возмущение недемпфированного осциллятора с разрывной восстанавливающей силой 5.4.2.2. Сравнение точного и приближенного решений. 5.4.2.3. Устойчивость периодических решений. 5.4.3. Гармоническое возмущение демпфированных нелинейных осцилляторов 5.4.3.2. Сухое трение и линейная восстанавливающая сила. 5.4.4. Верхние, нижние и комбинационные частоты при вынужденных колебаниях 5.4.5. Выпрямление вынужденных колебаний 5.4.6. Вынужденные колебания в автоколебательных системах 5.5. Задачи 6. Связанные колебания 6.1.1. Связанные колебания недемпфированного осциллятора 6.1.2. Главные колебания и главные координаты 6.1.3. Собственные частоты как экстремальные значения частного Релея 6.1.4. Гравитационный маятник на упругой нити 6.1.5. Вынужденные колебания связанных осцилляторов 6.1.6. Влияние демпфирования на связанные колебания 6.2. Колебательная система с произвольным числом степеней свободы 6. 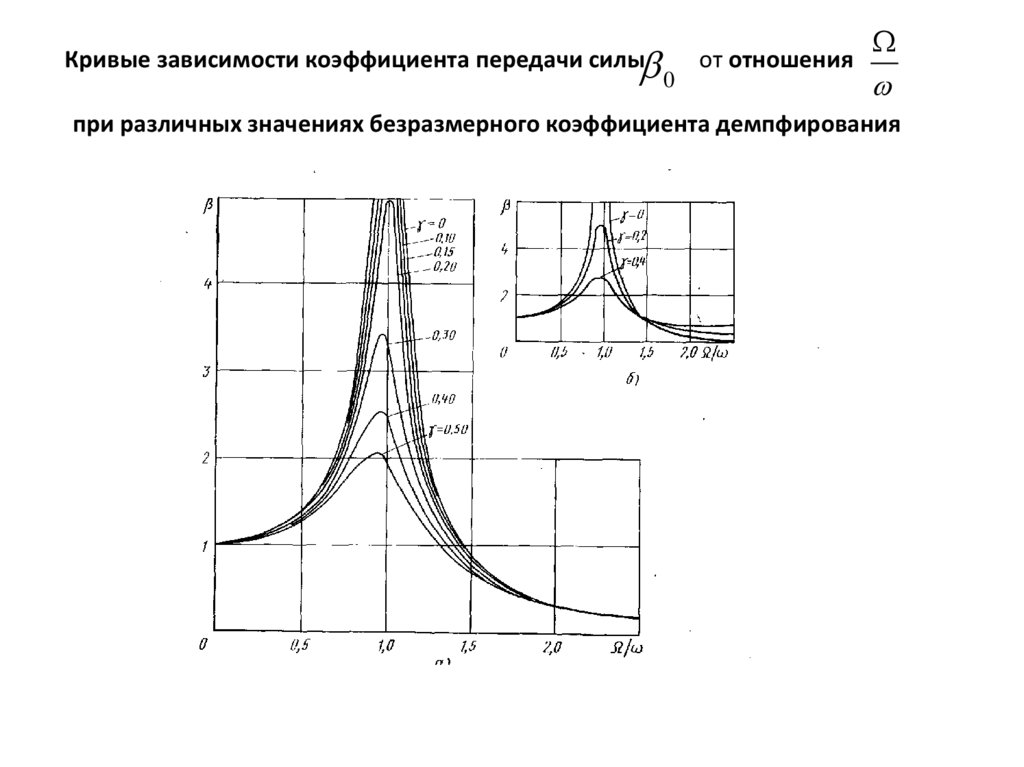2.2. Главные координаты и главные колебания 6.2.3. Колебательные цепи 6.2.4. Фильтры 6.2.5. Переход к колебаниям сплошной среды 6.3. Задачи Ответы к задачам Список литературы

Контактная стабилизация | Клуб пользователей ANSYS

Когда дело доходит до выполнения нелинейного анализа, сообщения об ошибках сходимости являются наиболее распространенным камнем преткновения. Нелинейность, или другими словами, изменение матрицы жесткости при выполнении расчета может быть связано с податливостью (пластичностью), деформацией конструкции (например, при деформации удочки) или изменением статуса контакта.

При использовании неявной схемы интегрирования, как правило, невозможно заранее предсказать, как изменится жёсткость конструкции, поэтому при настройке модели следует соблюдать особую осторожность.

Одна из основных трудностей, возникающих при выполнении нелинейного анализа, заключается в обнаружении изменения статуса контакта.

В конечно-элементном анализе, контакты обрабатываются как пружины, которые создаются между контактными поверхностями для достижения желаемого поведения контакта. Эти пружины включены в общую матрицу жесткости. Итак:

        F_c = K_c·X_p

        F_c: контактная сила
        K_c: контактная жесткость
        X_p: величина проникновения

В качестве примера рассмотрим случай, когда контакт не был установлен из-за начальных зазоров в файле CAD. Зазор означает, что X_p будет нулевым, а результирующие контактные силы (F_c) будут равны нулю. Это приводит к дисбалансу сил, и поскольку в статическом анализе не учитываются инерционные эффекты, узлы в теле будут иметь бесконечные скорости. Типичное сообщение об ошибке решателя приведено ниже:

 

В таблице «Initial Information» в «Contact Tool» будут выделены неправильно заданные контакты. Проверка этой информации перед решением модели является хорошей практикой и может сэкономить много времени на решение и отладку.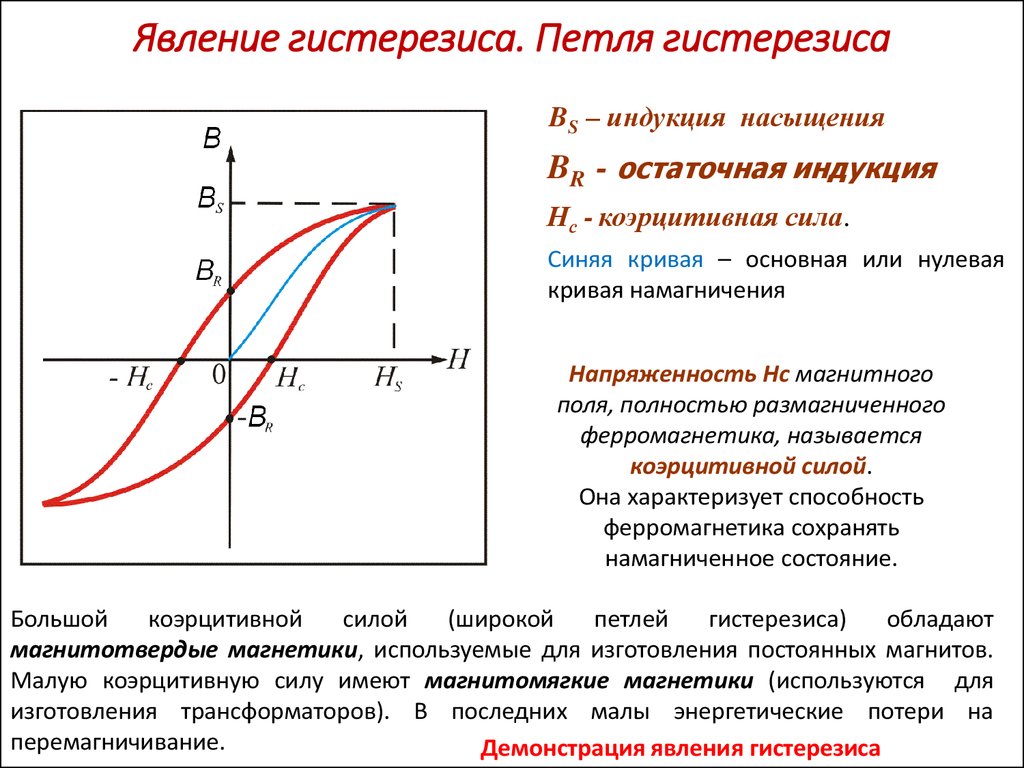 В этом примере проблема заключается в начальном зазоре 0,14204 мм, который привел к возникновению контактов в начале решения.

Одним из подходов к решению этой проблемы было бы задание начального шага нагрузки, на котором применяется перемещение к телу с недостающими ограничениями, для установления контакта на последующих шагах, на которых применяются рабочие нагрузки. Это перемещение затем может быть деактивировано, так как модель будет стабилизирована.

Хотя этот подход будет работать, он потребует дополнительных усилий пользователя для настройки и тестирования дополнительного шага нагрузки, который не является необходимой частью желаемых результатов анализа.

Чтобы решить эту проблему, в релизе 14 версии ANSYS, была добавлена функция, называемая демпфированием контакта.

Поскольку контакт не обнаружен, зазор приводит к возрастанию псевдоскорости между подшагами, и рассчитывается демпфирующая сила, чтобы предотвратить «улетание». Коэффициенты демпфирования рассчитываются как функция от зазора и радиуса срабатывания контакта «pinball radius».

Этот параметр находится в разделе «Advanced» в окне «Details» для интересующего контакта. Важным шагом сейчас является задание стабилизирующего коэффициента демпфирования.

Какое значение нужно использовать? Какая демпфирующая сила необходима? Как можно проверить результаты?

Это функция проиллюстрировано с помощью простого контактного анализа.

Контурный график величины зазора в «Contact Tool» показывает, что расстояние между контактными элементами достигает 1 мм.

На первом этапе (LS1 = 1 с) применяется простая нагрузка «Bearing load», и предполагается, что контакт будет инициирован, затем будет применено вращение на 45°, которое, как ожидается, приведет к перемещению из-за коэффициента трения 0,4 (LS2 = 2с).

Для получения результата энергии (/ POST26 ENERSOL в интерфейсе Mechanical APDL) использовался фрагмент вставки команд APDL для автоматической записи в текстовый файл в пользовательской папке проекта «user_file».

Чтобы определить влияние коэффициента демпфирования, были получены четыре решения с коэффициентом, варьирующимся от 1 до 0,001.

Искусственная энергия из-за стабилизации контакта

Этот график показывает искусственную энергию, созданную контактным демпфированием, чтобы облегчить процесс инициации контакта. Количество итераций, необходимых для решения модели, варьировалось от 189 до 211 от самого низкого до самого высокого коэффициента демпфирования.

Сила демпфирования прямо пропорциональна коэффициенту демпфирования, указанному пользователем (по умолчанию = 1). Это также зависит от перемещения во времени на текущем подшаге и радиуса действия контакта «pinball radius».

        

        d_n: коэффициент демпфирования в нормальном направлении
        FDMN: стабилизирующий коэффициент демпфирования в нормальном направлении (по умолчанию = 1.0)
        PINB, U_pinb: радиус действия контакта «pinball radius»
        U_n: контактный зазор в нормальном направлении

Если коэффициент демпфирования очень велик, прилагаемая сила может быть слишком высокой, следовательно, сходимость может стать более трудной.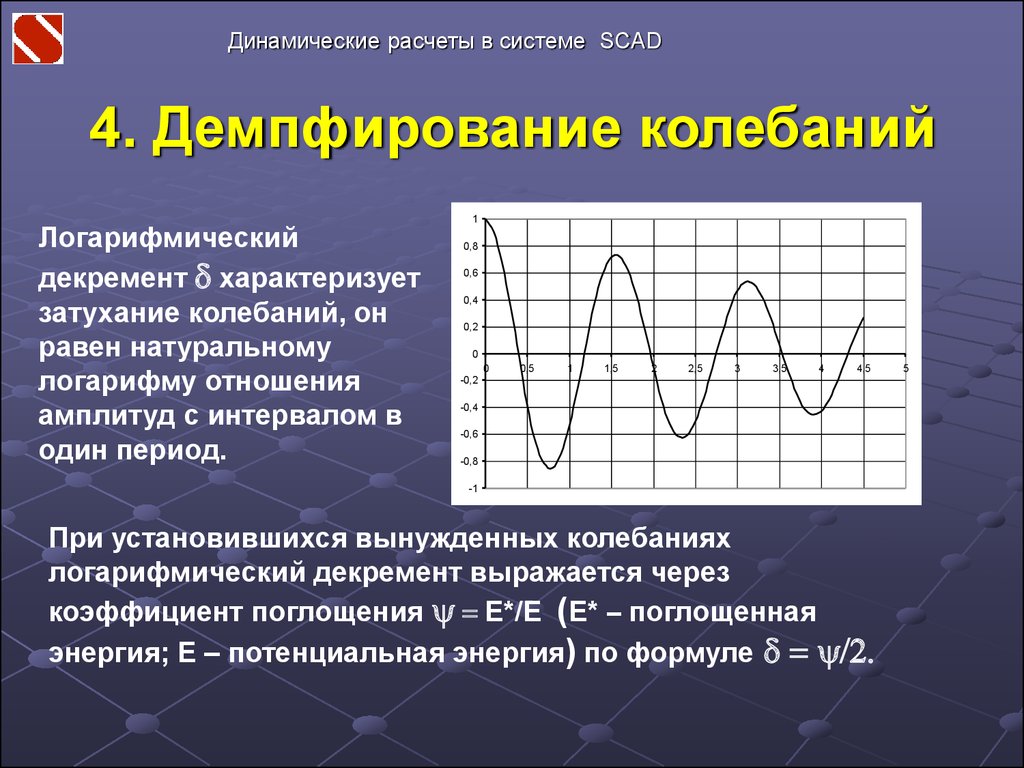 Это иллюстрируется количеством необходимых итераций.

В этом конкретном случае демпфирующая сила требуется только для стабилизации модели и предотвращения «улетания» колеса, поэтому меньший коэффициент демпфирования, например, 0,01, может быть достаточен.

Другое преимущество этого метода состоит в том, что эффект, подразумеваемый формулами, является временным. Когда контакт инициируется, конструкция стабилизируется, и демпфирующие силы постепенно исчезают.

Во время второго этапа нагружения возникает скачок демпфирующей силы, который усиливается вместе со значением FDMN. Причина в том, что демпфирование действует как для нормального, так и для касательного направления контакта.

        

        d_t: коэффициент демпфирования в касательном направлении
        FDMN: стабилизирующий коэффициент демпфирования в нормальном направлении (по умолчанию = 1.0)
        FDMT: стабилизирующий коэффициент демпфирования в касательном направлении (по умолчанию = 0. 001)
        PINB, U_pinb: радиус действия контакта «pinball radius»
        U_n: контактный зазор в нормальном направлении

Это касательное демпфирование использует ранее определенный коэффициент нормального демпфирования (FDMN), рассчитанное по коэффициенту демпфирования в касательном направлении (FDMT), обеспечивающее эффект стабилизации в этом направлении.

Это выглядит просто великолепно, теперь можно применять нагружение моментом без опасений, вместо использования вращения, описанного выше.

Искусственная энергия за счет стабилизации контакта/энергии жесткости

Этот график искусственной энергии стабилизации/энергии жесткости элемента показывает, что искусственная энергия доминирует в начале решения, но постепенно становится незначительной по мере стабилизации решения и получения реалистичного отклика.

Оба подхода, рассмотренные здесь, дают хорошее решение для этой конкретной задачи, однако возможны сценарии, в которых подход начального смещения не будет подходящим или будет неудобным из-за других особенностей модели. Стабилизация контакта обеспечивает упрощенный метод для достижения решения модели, содержащей контактные нелинейности. Настройка модели не должна быть искусством или чем-то вроде черной магии, и приятно видеть, что усовершенствования функционала в ANSYS признали необходимость упростить этот процесс.

Оригинал статьи: NON-LINEAR FEA: CONTACT STABILISATION

 

Демпфирование | Определение, типы и примеры

затухающие волны

Просмотреть все материалы

Похожие темы:

вязкое демпфирование демпфирование квадрата скорости радиационное затухание магнитное демпфирование Демпфирование Ландау

См. все связанное содержимое →

демпфирование , в физике сдерживание вибрационных движений, таких как механические колебания, шум и переменные электрические токи, путем рассеивания энергии. Если ребенок не будет продолжать качать качели, их движение затихнет из-за демпфирования.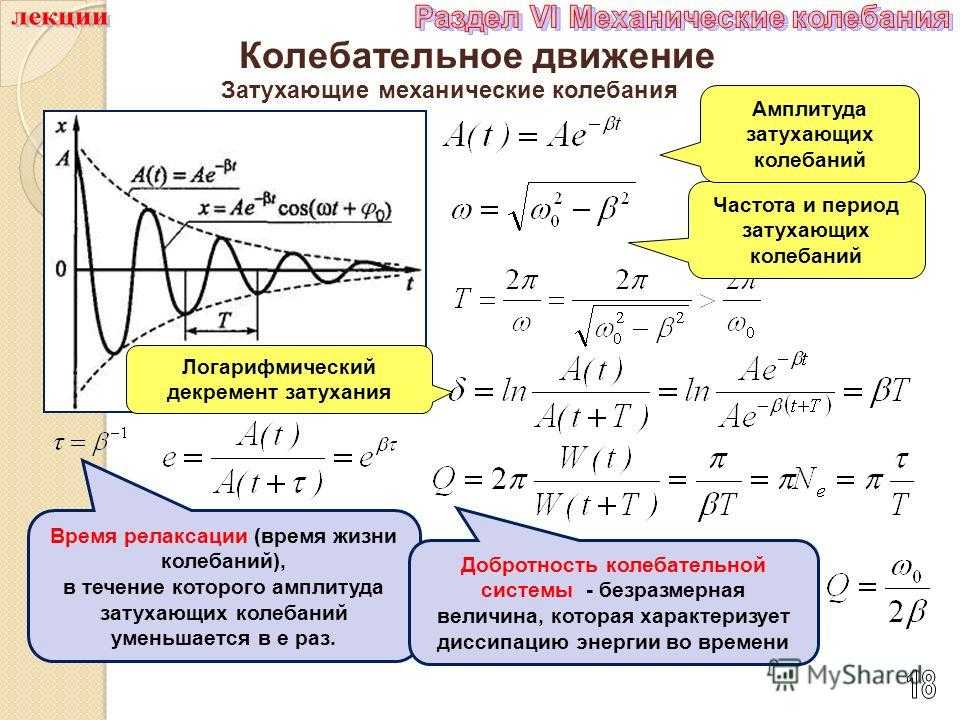 Амортизаторы в автомобилях и ковровые покрытия являются примерами демпфирующих устройств.

Система может быть настолько демпфирована, что не сможет вибрировать. Критическое демпфирование просто предотвращает вибрацию или достаточно для того, чтобы позволить объекту вернуться в исходное положение за кратчайший период времени. Автомобильный амортизатор является примером критически демпфирующего устройства. Дополнительное демпфирование вызывает чрезмерное демпфирование системы, что может быть желательно, как в некоторых дверных доводчиках. Вибрации системы с недостаточным демпфированием постепенно сужаются до нуля.

Британская викторина

Физика и естественное право

Существует множество типов механического демпфирования. Трение, также называемое в этом контексте сухим, или кулоновским, демпфированием, возникает главным образом из-за электростатических сил притяжения между скользящими поверхностями и превращает механическую энергию движения или кинетическую энергию в теплоту.

Вязкое демпфирование вызвано такими потерями энергии, которые происходят при жидкой смазке между движущимися частями или при проталкивании жидкости через небольшое отверстие поршнем, как в автомобильных амортизаторах. Сила вязкостного демпфирования прямо пропорциональна относительной скорости между двумя концами демпфирующего устройства.

Движение колеблющегося тела также проверяется его трением о газ или жидкость, через которые оно движется. Демпфирующая сила жидкости в этом случае прямо пропорциональна величине, несколько меньшей квадрата скорости тела, и поэтому называется демпфированием, квадратичным по скорости.

Помимо этих внешних видов демпфирования, существуют потери энергии внутри самой движущейся конструкции, которые называются гистерезисным демпфированием или, иногда, структурным демпфированием. При гистерезисном демпфировании часть энергии, связанной с повторяющейся внутренней деформацией и восстановлением исходной формы, рассеивается в виде случайных колебаний кристаллической решетки в твердых телах и случайной кинетической энергии молекул в жидкости.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас

Существуют и другие типы демпфирования. Резонансные электрические цепи, в которых переменный ток скачет туда-сюда, как в радио- или телеприемнике, гасятся электрическим сопротивлением. Сигнал, на который настроен приемник, синхронно подает энергию для поддержания резонанса.

При демпфировании излучения энергия колебаний движущихся зарядов, таких как электроны, преобразуется в электромагнитную энергию и излучается в виде радиоволн, инфракрасного или видимого света.

При магнитном демпфировании энергия движения преобразуется в тепло посредством электрических вихревых токов, индуцируемых либо в катушке, либо в алюминиевой пластине (прикрепленной к колеблющемуся объекту), которая проходит между полюсами магнита.

Редакторы Британской энциклопедии Эта статья была недавно отредактирована и дополнена Эриком Грегерсеном.

Сила демпфирования — значение, виды и примеры

Определение силы демпфирования в физике используется, когда вибрационное движение сдерживается, например, переменными электрическими токами, шумом, механическими колебаниями, рассеиваемой энергией.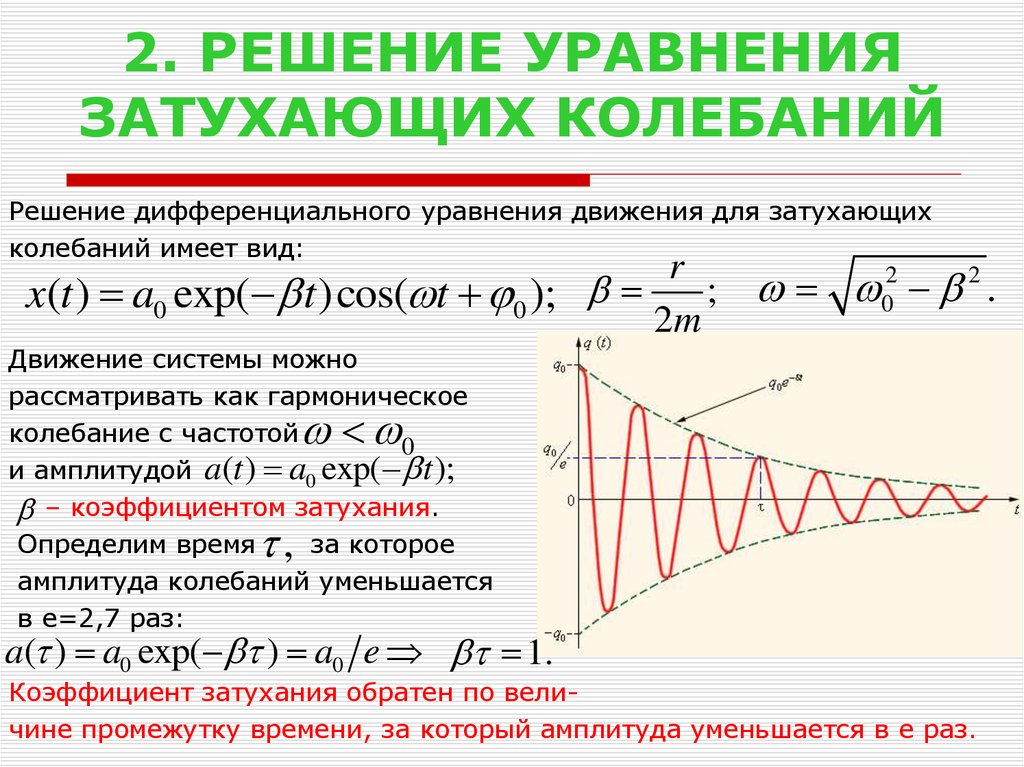 Это влияние на колеблющуюся систему или в ней, которое приводит к предотвращению или уменьшению колебательного движения. Когда мы говорим о физических системах, это явление является результатом процессов, которые в конечном итоге приводят к рассеянию энергии. Например, ребенок качается взад и вперед на качелях — движение стихнет из-за демпфирования, если ребенок перестанет толкать качели в любом направлении.

С другой стороны, могут быть системы настолько демпфированные, что вибрация вообще отсутствует. Критическое демпфирование — это то, что останавливает вибрацию или достаточно для того, чтобы объект мог как можно скорее вернуться в исходное положение. Одним из примеров этого является автомобильный амортизатор. Дополнительное демпфирование может привести к передемпфированию, и в некоторых случаях это необходимо, например, в дверных доводчиках. В недемпфированных системах вибрации со временем сходят на нет.

Некоторыми примерами демпфирования являются коврики, вибрирующие пружины, амортизаторы в автомобилях, звуки, издаваемые камертонами на больших расстояниях, часовой маятник, колебания ветки дерева, схемы RLC и т. д. Трение влияет на демпфирование как относительное движение между двумя поверхностями, толкающими друг друга, вызывающими диссипацию энергии. Кинетическая энергия при демпфировании преобразуется в тепло за счет трения.

(Изображение будет загружено в ближайшее время)

Электромагнитное демпфирование

Электромагнитное демпфирование является одним из интересных методов демпфирования, в котором используются токи, индуцируемые электромагнитным путем, чтобы иметь возможность замедлять движение движущегося объекта без физического воздействия. контакта с движущимся объектом.

Чтобы понять это конкретное явление, нам нужно понять вихревые токи и электромагнитную индукцию. Последнее представляет собой явление, при котором в проводнике индуцируется электродвижущая сила, и это происходит при изменении магнитного поля. Это индуцируется, когда проводник помещается в переменное магнитное поле или когда он движется поперек постоянного магнитного поля.

Затухание вибрации

Говорят, что вибрации затухают, когда трение и другие сопротивления приводят к рассеянию энергии вибрирующей системы. Вибрации уменьшаются или изменяются по интенсивности или частоте постепенно или даже прекращаются, и это приводит к тому, что система находится в равновесии.

При наличии возвращающей силы колебательное движение любой системы будет продолжаться бесконечно, если нет силы сопротивления. Трение уменьшит механическую энергию этой системы, и это называется затуханием вибрации. Затем демпфирование будет постепенно уменьшать амплитуду колебаний.

 

Одним из примеров такой вибрации является подвеска транспортных средств, которая демпфируется установленными на место амортизаторами.

Демпфирование также включает изучение собственной частоты затухающих и незатухающих колебаний.

Типы демпфирования

Даже при изучении демпфирования важно понимать, что существует несколько основных типов демпфирования и чем они отличаются друг от друга.

• Гашение света

Здесь наблюдаются определенные колебания, но их амплитуда медленно уменьшается со временем.

(Изображение будет загружено в ближайшее время)

• Критическое демпфирование

Здесь система вернется в положение равновесия как можно скорее без каких-либо колебаний.

(Изображение будет загружено в ближайшее время)

• Тяжелое демпфирование

Здесь также система возвращается в положение равновесия без колебаний, но это происходит очень медленно. Когда силы сопротивления превышают критическое демпфирование, происходит сильное демпфирование.

(Изображение будет загружено в ближайшее время)

Критическое демпфирование необходимо для того, чтобы можно было избежать значительного количества колебаний, а также слишком большого временного разрыва, когда система не может реагировать на возникающие возмущения. Электрические счетчики и весы — это инструменты, которые имеют критическое демпфирование, так что стрелка без колебаний перемещается в правильное положение, колеблясь.

Для критического демпфирования подвески автомобиля используются амортизаторы, чтобы предотвратить возникновение вибрации, поскольку это может привести к повреждению или затруднить управление.

Важность демпфирования

Демпфирование используется для ограничения вибраций, и это важно для защиты системы, в которой оно используется. Это то, что происходит с ящиками или дверными пружинами, поскольку демпфирование предотвращает удары, когда они открываются и закрываются. В гораздо большем масштабе той же цели служат системы демпфирования настила моста.

 

Если есть динамическая синусоидальная нагрузка, воздействующая на конструкцию здания, теоретически движения будут увеличиваться, и конструкция будет медленно падать. Вот почему демпфирование чрезвычайно важно для сохранения и предотвращения повреждений, независимо от того, используется ли оно для небольшого предмета домашнего обихода, такого как дверная пружина, или даже для чего-то гораздо большего, как уже упоминалось.