Смешанное соединение проводников формула. Смешанное соединение проводников: формулы, схемы и особенности расчета

alexxlabРазное
Что такое смешанное соединение проводников в электрической цепи. Как рассчитать общее сопротивление при смешанном соединении. Какие формулы применяются для расчета токов и напряжений в цепях со смешанным соединением. Какие особенности нужно учитывать при анализе смешанных цепей.

Содержание

Что такое смешанное соединение проводников

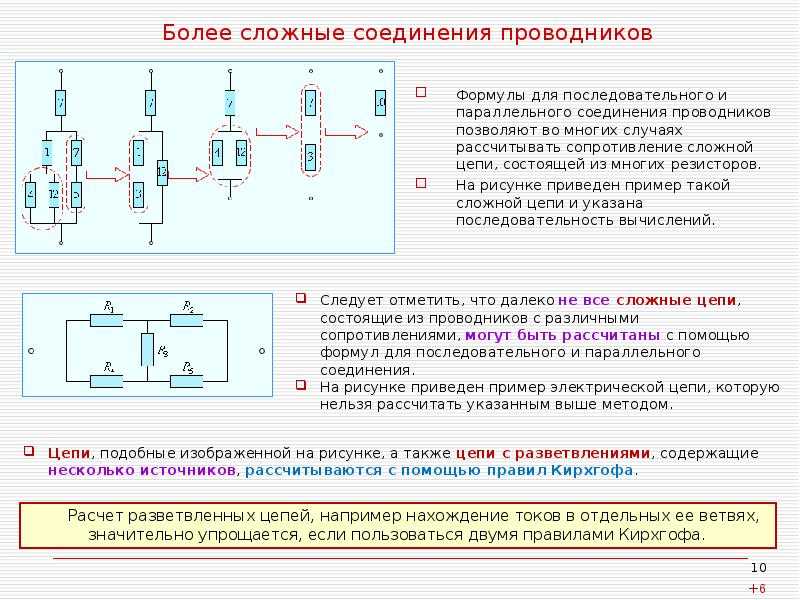
Смешанное соединение проводников представляет собой комбинацию последовательного и параллельного соединения в одной электрической цепи. Такой тип соединения часто встречается в реальных электрических схемах и устройствах.

Основные особенности смешанного соединения:

  • Содержит как последовательно, так и параллельно соединенные участки
  • Позволяет создавать сложные электрические цепи с нужными характеристиками
  • Требует поэтапного расчета отдельных участков для определения общих параметров
  • Дает возможность комбинировать преимущества обоих типов соединений

Формулы для расчета смешанного соединения

При анализе цепей со смешанным соединением используются следующие основные формулы:


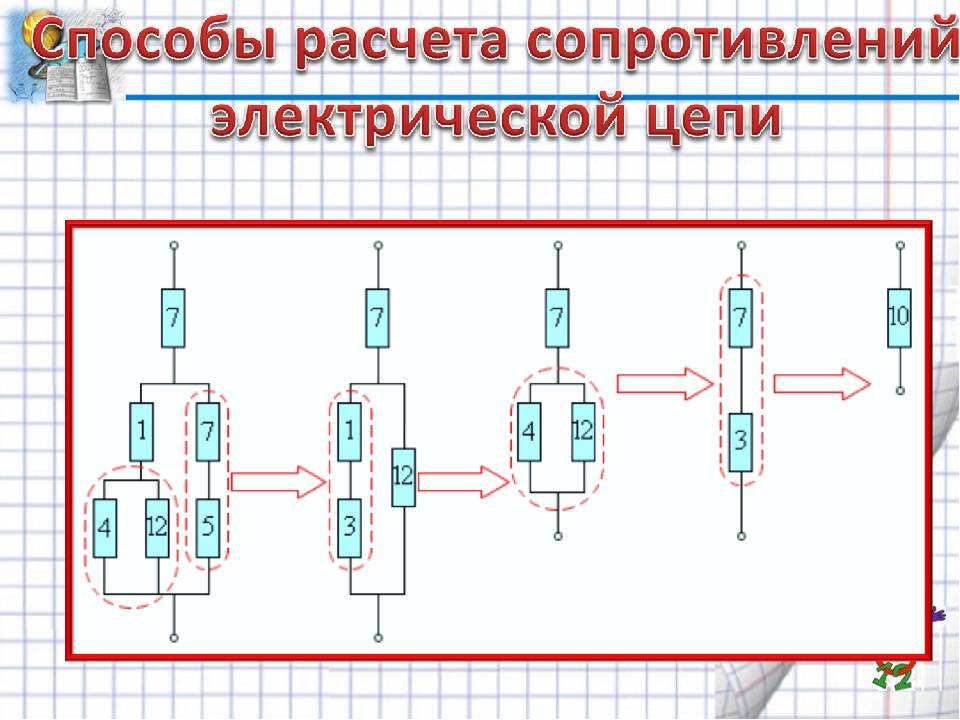
Общее сопротивление параллельного участка:

1/R = 1/R1 + 1/R2 + … + 1/Rn

Общее сопротивление последовательного участка:

R = R1 + R2 + … + Rn

Закон Ома для участка цепи:

I = U / R

Первое правило Кирхгофа:

I = I1 + I2 + … + In

Второе правило Кирхгофа:

U = U1 + U2 + … + Un

Эти формулы позволяют поэтапно рассчитать параметры сложной смешанной цепи.

Порядок расчета смешанного соединения

Чтобы правильно рассчитать цепь со смешанным соединением, необходимо придерживаться следующего алгоритма:

  1. Разбить схему на простые последовательные и параллельные участки
  2. Рассчитать сопротивление каждого простого участка
  3. Заменить простые участки их эквивалентными сопротивлениями
  4. Повторять шаги 1-3, пока не останется одно общее сопротивление
  5. Определить общий ток в неразветвленной части цепи
  6. Рассчитать напряжения и токи на всех участках в обратном порядке

Такой подход позволяет корректно проанализировать даже сложные смешанные схемы.

Пример расчета смешанного соединения

Рассмотрим пример расчета простой смешанной цепи:


  • Дано: R1 = 2 Ом, R2 = 3 Ом, R3 = 6 Ом
  • R2 и R3 соединены параллельно, их участок последовательно соединен с R1
  • Напряжение источника U = 12 В

Расчет:

  1. Находим сопротивление параллельного участка R23: 1/R23 = 1/R2 + 1/R3 = 1/3 + 1/6 = 1/2 R23 = 2 Ом
  2. Общее сопротивление цепи: R = R1 + R23 = 2 + 2 = 4 Ом
  3. Общий ток: I = U/R = 12/4 = 3 А
  4. Напряжение на R1: U1 = I * R1 = 3 * 2 = 6 В
  5. Напряжение на параллельном участке: U23 = I * R23 = 3 * 2 = 6 В
  6. Токи в параллельных ветвях: I2 = U23/R2 = 6/3 = 2 А I3 = U23/R3 = 6/6 = 1 А

Таким образом, мы полностью рассчитали параметры данной смешанной цепи.

Особенности анализа смешанных соединений

При работе со смешанными цепями важно учитывать следующие моменты:

  • Необходимо четко выделять последовательные и параллельные участки
  • Расчет ведется от общего к частному — сначала определяется общее сопротивление
  • Токи рассчитываются от общего к ветвям, напряжения — наоборот
  • Нужно проверять выполнение законов Кирхгофа для контроля
  • Сложные цепи удобно анализировать с помощью специальных программ

Понимание этих особенностей позволит корректно рассчитывать даже самые сложные смешанные соединения.


Применение смешанных соединений

Смешанные соединения проводников широко используются в различных областях электротехники и электроники:

  • В схемах электропитания для получения нужных напряжений
  • В фильтрах и частотных разделителях аудиотехники
  • В измерительных мостовых схемах
  • В цепях согласования импедансов в радиотехнике
  • В схемах защиты и коммутации электрооборудования

Понимание принципов работы смешанных цепей необходимо для грамотного проектирования и анализа электронных устройств.

Преимущества и недостатки смешанного соединения

Смешанное соединение проводников имеет свои плюсы и минусы:

Преимущества:

  • Позволяет создавать сложные цепи с нужными характеристиками
  • Дает возможность комбинировать достоинства разных типов соединений
  • Обеспечивает гибкость при проектировании электрических схем

Недостатки:

  • Усложняет расчет и анализ электрической цепи
  • Требует более тщательного контроля параметров
  • Может приводить к неочевидным эффектам при изменении режимов

Учет этих особенностей позволяет грамотно применять смешанные соединения в электротехнике.


Заключение

Смешанное соединение проводников — важный элемент современной электротехники, позволяющий создавать сложные и эффективные электрические цепи. Понимание принципов расчета и анализа таких соединений необходимо для проектирования надежных электронных устройств.

Ключевые моменты:

  • Смешанное соединение сочетает последовательные и параллельные участки
  • Расчет ведется поэтапно от общего к частному
  • Применяются законы Ома и Кирхгофа
  • Важно четко выделять характер соединения на разных участках
  • Такие цепи широко используются в различных областях электроники

Грамотное применение смешанных соединений открывает широкие возможности для создания эффективных электрических схем.


Решение задач по теме: «Смешанное соединение проводников» 8 класс онлайн-подготовка на Ростелеком Лицей

Необходимые для решения задач формулы и факты

 

Под соединением проводников подразумевается соединение резисторов – приборов, сделанных на основе сопротивления проводников. На предыдущих уроках были рассмотрены параллельное и последовательное соединения. На данном уроке будут рассмотрены задачи на смешанное соединение проводников, то есть когда в цепи присутствует и последовательное, и параллельное соединение.

 

Для решения задач сначала рассмотрим формулы для связи различных величин при параллельном и последовательном соединениях:

 

Если проводники соединены последовательно, то сила тока в них одинакова и равна силе тока в цепи. При этом общее напряжение в цепи будет состоять из суммы напряжений на каждом проводнике. А если говорить о сопротивлении этого участка цепи, в котором проводники соединены последовательно, то оно равно сумме сопротивлений проводников.

В параллельном соединении все по-другому. Сила тока в каждой ветке этой цепи будет различной, при этом общая сила тока в цепи будет вычисляться как сумма сил токов в проводниках. Напряжение на проводниках, соединенных последовательно, будет одинаковым. Общее сопротивление этого участка цепи, так называемое «эквивалентное сопротивление» R, будет вычисляться по следующей формуле: .

Также стоит отметить, что параллельное соединение обычно применяется при включении бытовых приборов, а последовательное – для того, чтобы создать длинную неразветвленную цепь.

 

Задача №1

 

 

Рассмотрим следующую задачу. Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом. Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В. Необходимо определить силу тока во всей электрической цепи (рис. 1).

 

Рис. 1. Условия и рисунок задачи № 1

Как видим, резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним. Источник дает напряжение 2,4 В, соответственно, на участке АВ напряжение будет также 2,4 В. Сила тока, которую требуется найти, – это сила тока, протекающая через амперметр А.

Такое соединение проводников называется неразветвленным. В промышленности обычно изготавливается набор резисторов с четко определенными сопротивлениями, но для экспериментов могут понадобиться любые различные сопротивления. Тогда с помощью таких схем можно создавать нужное сопротивление для эксперимента или прибора.

Далее требуется определить эквивалентное сопротивление неразветвленной части. Сначала посмотрим, чему равно сопротивление R’ участка цепи АВ, который содержит только резисторы R1 и R2. Они соединены последовательно, тогда R′=R1+R2=2 [Ом]. Теперь можно перерисовать электрическую цепь, заменив сопротивления R1 и R2 эквивалентным им сопротивлением R’ (рис. 2).

Рис. 2. Первая замена эквивалентным сопротивлением

Теперь можно сказать, что участок АВ включает в себя не три, а два сопротивления: R3 и R’. Эти два сопротивления соединены параллельно, соответственно, можно найти общее сопротивление электрической цепи по формуле . Выразив R и подставив значения , получаем:

Стоит отметить, что сопротивления были соединены, но общее сопротивление получилось все равно равным 1 Ом. Теперь электрическую цепь можно заменить следующей (рис. 3):

Рис. 3. Вторая замена эквивалентным сопротивлением

На рис. 3 сопротивление R=1 Ом называется эквивалентным сопротивлением, поскольку три сопротивления были заменены на одно. Чтобы рассчитать силу тока в цепи, надо использовать закон Ома для участка цепи: . Напряжение на сопротивлении R – это напряжение на участке АВ (Рис. 1), которое, в свою очередь, равно 2,4.Тогда . Это и будет значение силы тока в электрической цепи, которое покажет амперметр.

 

Задача №2

 

 

Теперь рассмотрим задачу, в которой также будет три сопротивления, но соединены они будут по-другому (рис.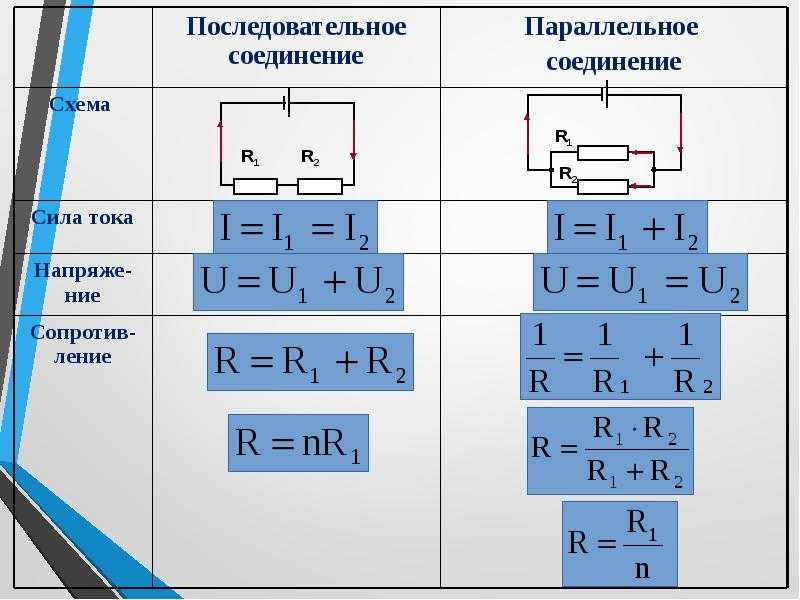 4):

 

Рис. 4. Условие задачи № 2

Два сопротивления R1 и R2 соединены параллельно (R1=R2=2 Ом), к ним еще последовательно присоединено сопротивление R3=1 Ом. Амперметр показывает силу тока в цепи, равную I=0,5 А. Требуется определить напряжение на концах участка этой цепи, то есть на участке АВ.

Для начала определим сопротивление участка цепи, содержащего сопротивления R1 и R2. Эти два сопротивления соединены параллельно, значит, их эквивалентное сопротивление R’ можно найти из формулы . Подставляя значения, получаем:

Теперь можно сказать, что цепь включает в себя только два сопротивления: R’и R3, которые соединены последовательно.

Рис. 5. Замена параллельного соединения эквивалентным сопротивлением

В задаче требуется определить напряжение. Для этого используется прибор, который называется вольтметр. В цепь он включается параллельно. И рассмотрим участок цепи, в котором все три сопротивления уже заменены эквивалентным.

Рис. 6. Включение вольтметра в цепь

Вольтметр включен в месте, соответствующем участку АВ на рис. 4. Соответственно, он измеряет напряжение на это участке цепи. Чтобы найти значения этого напряжения, требуется сначала найти эквивалентное сопротивление. Сопротивления R’ и R3 соединены последовательно (рис. 5), значит, эквивалентное сопротивление определяется по формуле:

Теперь из закона Ома для участка цепи можно найти напряжение:

Значит, вольтметр должен будет показать значения напряжения в 1 В.

 

Расчет более сложных цепей

 

 

На уроке были рассмотрены соединения только трех сопротивлений, когда они были последовательные, к ним параллельно подключается третий, или когда два соединены параллельно, а к ним последовательно подключают третье сопротивление. Но реальные схемы значительно сложнее. Они содержат огромное количество различных элементов, сопротивлений, поэтому имеются достаточно сложные методы расчетов электрических цепей.

 

Впервые расчетами таких сложных электрических цепей озадачились ученые приблизительно в XIX веке, и появились новые правила, которые используются и по сей день. Немецкий ученый Кирхгоф разработал возможность расчета электрических сложных цепей, поэтому правила, которые используют для сложных цепей, называются «правилами Кирхгофа».

На следующих уроках будет рассмотрено понятие мощности и работы силы тока.

 

Список литературы

  1. Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
  2. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
  3. Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

  1. Festival.1september.ru (Источник)
  2. Electroandi.ru (Источник)
  3. Bocharova.ucoz.ru (Источник)

 

Домашнее задание

  1. Стр. 117: задачи № 4, 5. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
  2. В каком случае эквивалентное сопротивление будет больше: если три проводника с сопротивлениями 1 Ом каждый соединить параллельно или последовательно?
  3. Два сопротивления R1=1 Ом и R2= 2 Ом соединены последовательно, к ним параллельно присоединено сопротивление 3 Ом. Чему равно эквивалентное сопротивление?
  4. Сколько различных цепей можно составить из трех резисторов с сопротивлениями 1 Ом каждый так, чтоб их эквивалентные сопротивления была различными?

 

 

Последовательное и смешанное соединение проводников в электрической цепи | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Загрузка…

Источники элект­рического тока (гальванические элементы, аккумуляторы, разнообразные генераторы и т.п.), потребители тока (электрические дви­гатели, нагреватели, осветительные лампы и т.п.), измерительные приборы (ампермет­ры, вольтметры, счетчики и т.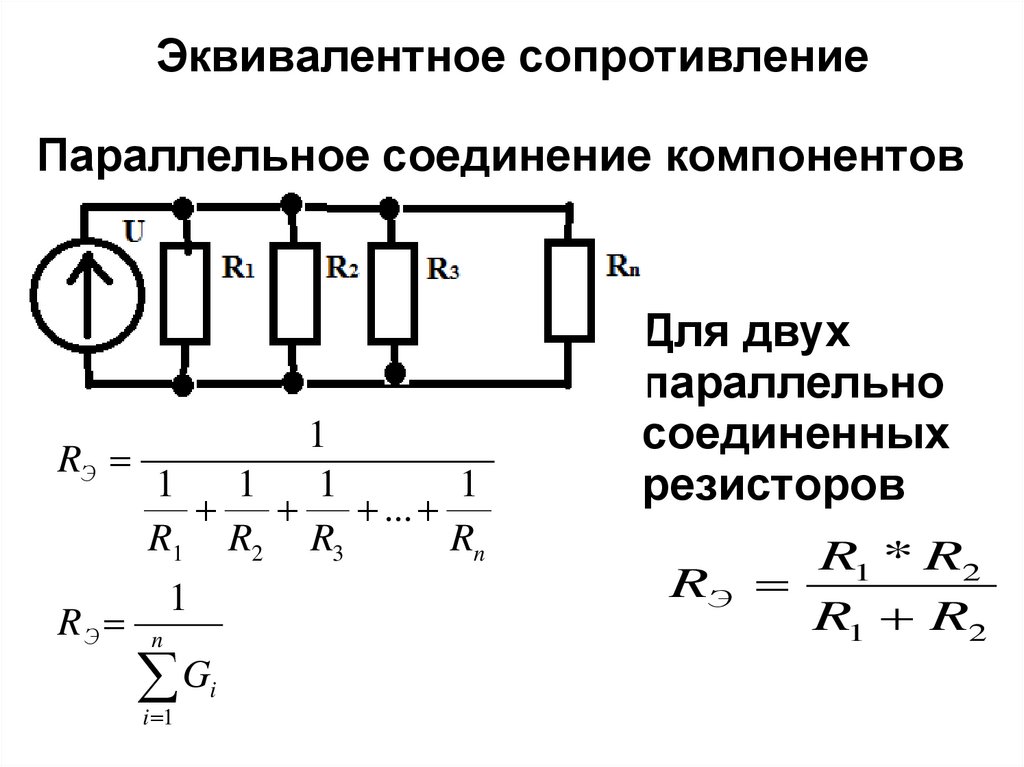 п.), регули­ровочные устройства (выключатели, пере­ключатели, реостаты и т.п.) соединяются с помощью проводников в электрические це­пи. Соединение элементов электрических це­пей может быть последовательным, парал­лельным или смешанным.

Последовательным считается такое со­единение, когда ток проходит сначала по проводнику 1, потом — по проводнику 2, по проводнику 3 и т. д. (рис. 5.7), сопро­тивления которых R1

, R2 и R3.

При установлении тока в таком соедине­нии сила тока I в каждой точке такого участка цепи одинакова.

Если потенциалы в точках соединения соответственно φ1, φ2, φ3, и φ4, то для каждого из проводников можно записать:

Рис. 5.7. Последовательное соединение проводников (резисторов)

φ1 — φ2 = IR1,

Загрузка. ..

φ2 — φ3 = IR2,

φ3 — φ4

= IR3,

I1 = I2 = I3 = const.

Сложив полученные уравнения и обо­значив общее сопротивление участка цепи R, получаем

φ1 — φ4 = I(R1 + R2 + R3) = IR.

Таким образом,

R = R1 + R2 + R3.

Этот вывод можно легко распространить на любое количество последовательно со­единенных проводников:

R = Σni=1 Ri. Материал с сайта http://worldofschool.ru

Если иметь в виду, что при прохождении тока в проводнике напряжение на нем рав­но разности потенциалов, то для последова­тельного соединения можно сделать вывод: U = U1 + U2 + U3, а для произвольного коли­чества проводников

U = Σni=1 Ui.

В электрических цепях практически не бывает только последовательных или только параллельных соединений элементов, они встречаются в определенных соединениях. Такие цепи называются смешанными. Так, например, выключатели или ампер­метры всегда включаются последовательно, а вольтметры — параллельно участку цепи, на котором измеряется напряжение.

На этой странице материал по темам:

  • Физика. электрическая цепь: последовательное соединение

  • Физика параллельное последовательное смешанное соединение

  • Физика смешанное соединение проводников с ключом

  • Лекция смешанное соединение проводников

  • Смешанное соединение проводников цепи

Вопросы по этому материалу:

  • Какие соединения проводников считаются последовательными? Приведите примеры.

  • Каким является общее сопротивление последовательно соединен­ных проводников?

  • Какой является сила тока в последовательно соединенных провод­никах?

  • Чему равно напряжение на всем участке последовательно соеди­ненных проводников?

Материал с сайта http://WorldOfSchool.ru

Органический смешанный ионно-электронный проводник для силовой электроники

1. Винтер-Дженсен Б., Винтер-Дженсен О., Форсайт М., Макфарлейн Д. Р., Наука 2008, 321, 671. [PubMed] [Google Scholar]

2. Мильчарек Г., Инганес О., наука 2012, 335, 1468. [PubMed] [Google Scholar]

3. Rivnay J., Leleux P., Hama A., Ramuz M., Huerta M., Malliaras G.G., Owens R.M., Sci. Респ. 2015, 5, 11613. [Бесплатная статья PMC] [PubMed] [Google Scholar]

4. Линь Ю., Фанг С., Су Д., Бринкман К.С., Чен Ф., Nat. коммун. 2015, 6, 6824. [Бесплатная статья PMC] [PubMed] [Google Scholar]

5. Посудиевский О.Ю., Козаренко О.А., Котенко И.Е., Бойко О.П., Шкавро А.Г., Кошечко В.Г., Походенко В.Д., Теор. Эксп. хим. 2014, 50, 197. [Google Scholar]

6. Кочергинский Н. М., Ван З., Synth. Встретил. 2006, 156, 1065. [Google Scholar]

7. Форрест С. Р., Природа 2004, 428, 911. [PubMed] [Google Scholar]

8. Heeger AJ, Angew. хим. Междунар. Эд. 2001, 40, 2591. [PubMed] [Google Scholar]

9. MacDiarmid A.G., Heeger A.J., Synth. Встретил. 1980, 1, 101. [Google Scholar]

10. Канадзава К.К., Диаз А.Ф., Гейсс Р.Х., Гилл В.Д., Квак Дж.Ф., Логан Дж.А., Раболт Дж.Ф., Стрит Г.Б., J. Chem. соц., хим. коммун. 1979, 854–855. [Google Scholar]

11. Ширакава Х., Икеда С., Synth. Встретил. 1980, 1, 175. [Google Scholar]

12. Бубнова О., Хан З. У., Ван Х., Браун С., Эванс Д. Р., Фабретто М., Ходжати-Талеми П., Дагнелунд Д., Арлин Дж.-Б., Гертс Ю. Х., Десбиф С., Брейби Д. В., Андреасен J.W., Lazzaroni R., Chen W.M., Zozoulenko I., Fahlman M., Murphy P. J., Berggren M., Crispin X., Nat. Матер. 2014, 13, 190. [PubMed] [Google Scholar]

13. Ким Н., Кан Х., Ли Дж.-Х., Ки С., Ли С. Х., Ли К., Adv. Матер. 2015, 27, 2317. [PubMed] [Google Scholar]

14. Ким Ф. С., Рен Г., Дженекхе С. А., Chem. Матер. 2010, 23, 682. [Google Scholar]

15. Лонг Ю.-З., Ли М.-М., Гу С., Ван М., Дювей Ж.-Л., Лю З., Фань З., Prog. Полим. науч. 2011, 36, 1415. [Google Scholar]

16. Персано Л., Кампосео А., Писиньяно Д., Prog. Полим. науч. 2015, 43, 48. [Google Scholar]

17. Groenendaal L., Jonas F., Freitag D., Pielartzik H., Reynolds J.R., Adv. Матер. 2000, 12, 481. [Google Scholar]

18. Wang H.D., Ail UD, Gabrielsson R.D., Berggren M.P., Crispin X., Adv. Энергия Матер. 2015, 5, 1500044. [Google Scholar]

19. Ви Г., Ларссон О., Сринивасан М., Берггрен М., Криспин Х., Мхайсалкар С., Adv. Функц. Матер. 2010, 20, 4344. [Google Scholar]

20. Аргун А.А., Эшкрафт Дж.Н., Хаммонд П.Т., Adv. Матер. 2008, 20, 1539. [Google Scholar]

21. Gu X., Knorr D.B. Jr., Wang G., Overney R.M., Thin Solid Films 2012, 520, 1872. [Google Scholar]

22. Nguyen C.A., Xiong S., Ma J., Lu X., Lee P.S., Phys. хим. хим. физ. 2011, 13, 13319. [PubMed] [Google Scholar]

23. Саруватари Х., Кубоки Т., Киши Т., Микошиба С., Таками Н., Дж. Источники энергии 2010, 195, 1495. [Google Scholar]

24. Сехон С. С., Бюлл. Матер. Наука 2003, 26, 321. [Google Scholar]

25. Камая Н., Хомма К., Ямакава Ю., Хираяма М., Канно Р., Ёнемура М., Камияма Т., Като Ю., Хама С., Кавамото К., Мицуи А., Нат. Матер. 2011, 10, 682. [PubMed] [Google Scholar]

26. Wada H., Amiel O., Sato A., J. Alloys Compd. 1995, 219, 55. [Google Scholar]

27. Янг В., Ионика твердого тела 1986, 20, 277. [Google Scholar]

28. Инагума Ю., Ликуан С., Ито М., Накамура Т., Учида Т., Икута Х., Вакихара М., Solid State Commun. 1993, 86, 689. [Google Scholar]

29. Ren X., Pickup P.G., J. Chem. Soc., Faraday Trans.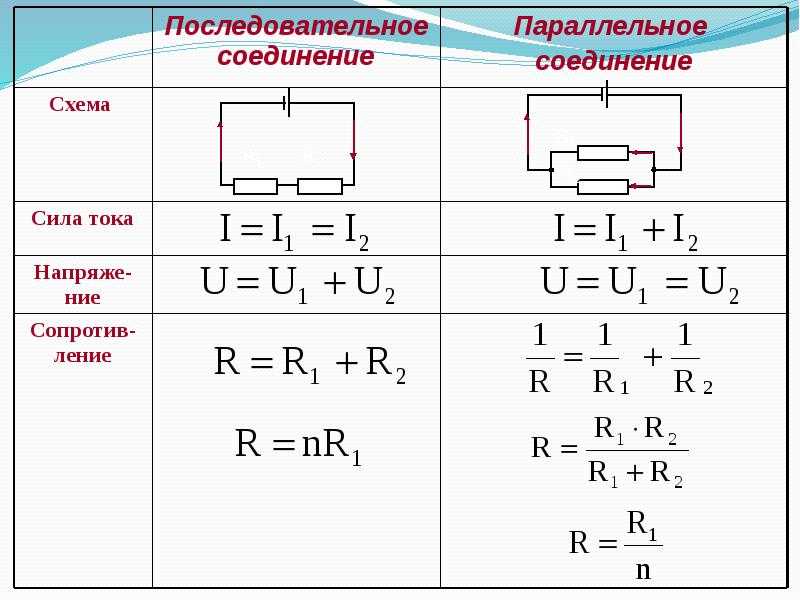 1993, 89, 321. [Google Scholar]

30. Duffitt G.L., Pickup P.G., J. Chem. Soc., Faraday Trans. 1992, 88, 1417. [Google Scholar]

31. Канг Х.К., Гекелер К.Э., Полимер 2000, 41, 6931. [Google Scholar]

32. статья о полупроводниковых устройствах, global.britannica.com/technology/semiconductor‐device, дата обращения: май 2015 г.

33. Serway R. A., Principles of Physics, Saunders College Publishing, Philadelphia, PA, USA, 1998. [Google Scholar]

34. Зотти Г., Зекчин С., Шиавон Г., Лувет Ф., Грюнендал Л., Криспин Х., Осикович В., Саланек В., Фалман М., Макромолекулы 2003, 36, 3337. [Google Scholar]

35. Hohnholz D., Okuzaki H., MacDiarmid AG, Adv. Функц. Матер. 2005, 15, 51. [Google Scholar]

36. Хенрикссон М., Берглунд Л. А., Исакссон П., Линдстрем Т., Нишино Т., Биомакромолекулы 2008, 9, 1579. [PubMed] [Google Scholar]

37. Гречински Г., Куглер Т., Саланек В. Р., Тонкие твердые пленки 1999, 354, 129. [Google Scholar]

38. Ланган П., Нишияма Ю., Чанзи Х., Биомакромолекулы 2001, 2, 410. [PubMed] [Google Scholar]

39. Винтер-Дженсен Б., Форсайт М., Уэст К., Андреасен Дж. В., Бэйли П., Пас С., МакФарлейн Д. Р., Полимер 2008, 49, 481. [Google Scholar]

40. Нардес А. М., Кемеринк М., Янссен Р. А. Дж., Phys. Преподобный Б 2007, 76, 085208. [Google Scholar]

41. Ван Т., Пирсон А., Данбар А. Ф., Станец П., Уоттерс Д., Коулз Д., Йи Х., Ираки А., Лидзи Д., Джонс Р. Л., Eur. физ. Дж. Э. 2012, 35, 1. [PubMed] [Google Scholar]

42. Оуян Дж., Сюй К.Ф., Чу К.В., Ян Ю., Ли Г., Шинар Дж., Полимер 2004, 45, 8443. [Google Scholar]

43. Ким Г. Х., Шао Л., Чжан К., Пайп К. П., Nat. Матер. 2013, 12, 719. [PubMed] [Google Scholar]

44. Huang J.-H., Chu C.-W., Electrochim. Акта 2011, 56, 7228. [Google Scholar]

45. Нюхольм Л., Нистрём Г., Мигранян А., Стрёмме М., Adv. Матер. 2011, 23, 3751. [PubMed] [Google Scholar]

46. Тараскон Дж. М., Арманд М., Природа 2001, 414, 359.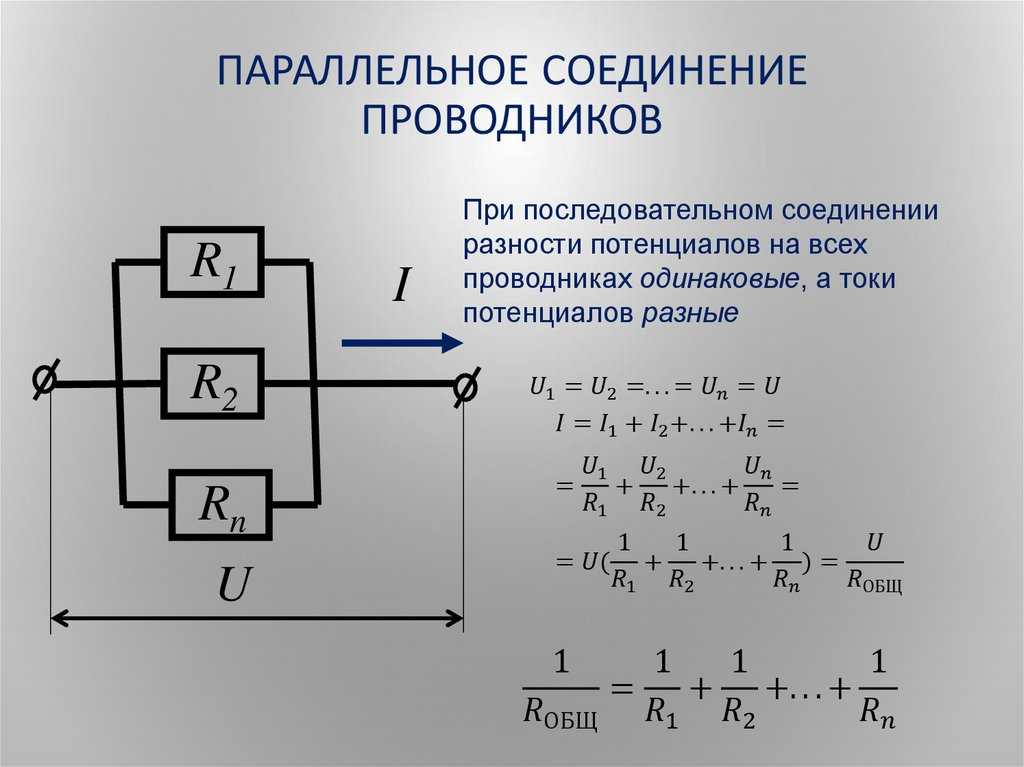 [PubMed] [Google Scholar]

47. Ходахоли Д., Ривнай Дж., Сессоло М., Гурфинкель М., Леле П., Джимисон Л.Х., Ставриниду Э., Эрве Т., Санаур С., Оуэнс Р. М., Маллиарас Г. Г., Нац. коммун. 2013, 4, 2133. [Бесплатная статья PMC] [PubMed] [Google Scholar]

48. Инал С., Ривнай Дж., Лелё П., Ферро М., Рамюз М., Брендель Дж. К., Шмидт М. М., Телаккат М., Маллиарас Г. Г., Adv. Матер. 2014, 26, 7450. [PubMed] [Google Scholar]

49. Hess L.H., Hauf M.V., Seifert M., Speck F., Seyller T., Stutzmann M., Sharp I.D., Garrido J.A., Appl. физ. лат. 2011, 99, 033503. [Google Scholar]

50. Сюй Х., Чжан З., Сюй Х., Ван З., Ван С., Пэн Л.-М., ACS Nano 2011, 5, 5031. [PubMed] [Google Scholar]

51. Sasa S., Ozaki M., Koike K., Yano M., Inoue M., Appl. физ. лат. 2006, 89, 053502. [Google Scholar]

52. Юань Х., Симотани Х., Цукадзаки А., Отомо А., Кавасаки М., Иваса Ю., Adv. Функц. Матер. 2009, 19, 1046. [Google Scholar]

53. Чо Дж. Х., Ли Дж., Ся Ю., Ким Б.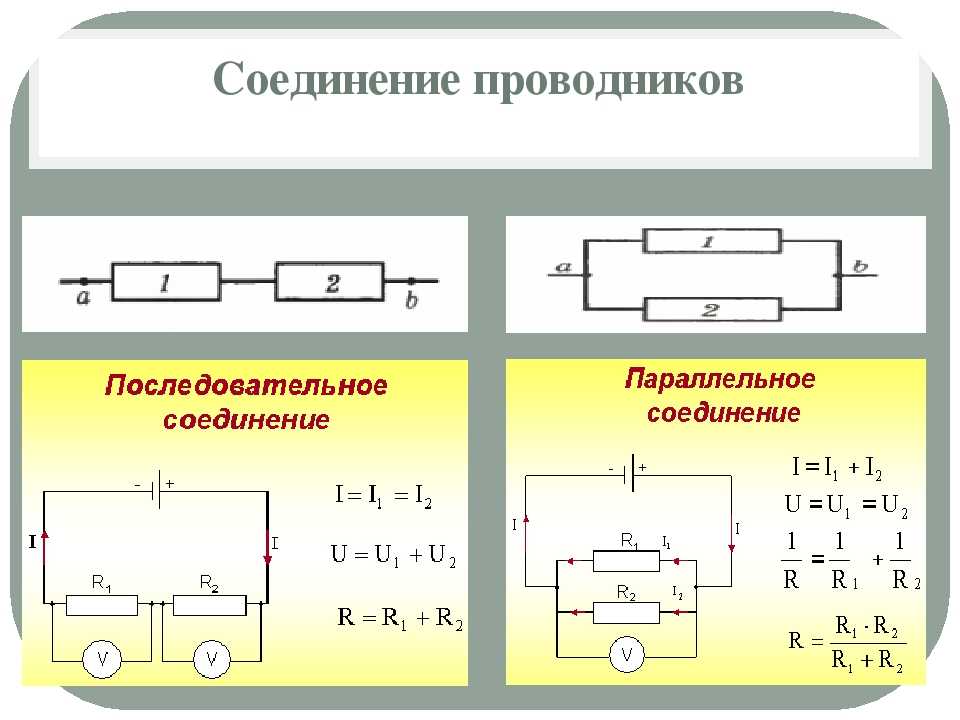 , Хе Ю., Ренн М. Дж., Лодж Т. П., Дэниел Фрисби С., Nat. Матер. 2008, 7, 900. [PubMed] [Google Scholar]

Обработка импеданса модели эквивалентной цепи со смешанными проводниками и явные приближенные решения

  • DOI:10.1149/1.1392611
  • ID корпуса: 94979608
 @article{Jamnik1999TreatmentOT,
  title={Обработка импеданса модели эквивалентной цепи со смешанными проводниками и явные приближенные решения},
  автор={Янко Ямник и Иоахим Майер},
  journal={Журнал Электрохимического общества},
  год = {1999},
  объем = {146},
  страницы={4183-4188}
}
  • J. Jamnik, J. Maier
  • Опубликовано 1 ноября 1999 г.
  • Материаловедение
  • Journal of The Electrochemical Society

Феноменологически смоделирован электрохимический импеданс смешанного проводника с двумя носителями заряда, зажатыми между двумя равными электродами.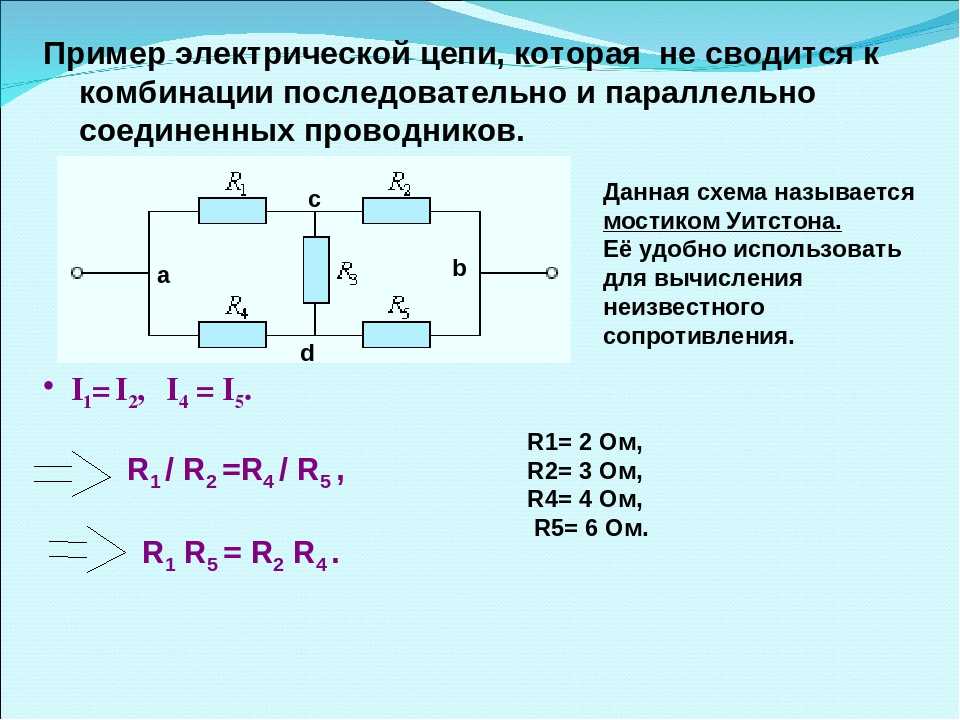 Найдена простая аналитическая аппроксимация, которая применима в очень широком окне параметров материалов (произвольные подвижности и концентрации носителей), если гарантируется линейный отклик и толщина образца велика по сравнению с длиной Дебая. Аппроксимация применима как к обратимым, избирательно блокирующим, так и к частично…

Просмотр через Publisher

Моделирование отклика импеданса тонкопленочных электродов со смешанной проводимостью.

Разработана новая численная модель импеданса для тонких пленок со смешанной проводимостью, работающих в качестве электродов для твердооксидных топливных элементов, и показано, что с помощью этой модели можно получить экспериментально согласованные объемные импедансы и поверхностные емкости.

Обобщенные эквивалентные схемы для смешанных проводников: сульфид серебра как модельная система самозакодированная программа на Фортране.

Обобщенные эквивалентные схемы для переноса массы и заряда: химическая емкость и ее значение Точная эквивалентная схема, включая концевые части, унифицированно учитывающая электрические и химические параметры контроля, получена для ячейки со смешанным проводником (или…

Спектроскопия импеданса как инструмент химического и электрохимического анализа смешанных проводников: A Пример использования Церии

  • Wei Lai, S. Haile

  • Материаловедение

  • 2005

Реакция полного сопротивления переменного тока смешанных ионных и электронных проводников (MIEC) получена из первых принципов и количественно сравнена с экспериментальными данными. Хотя подход не совсем новый,…

Электрический импеданс для электролизера.

  • Ф. Фрейре, Г. Барберо, М. Скалеранди

  • Физика

    Физический обзор. E, Статистическая, нелинейная физика и физика мягкого вещества

  • 2006

Показано, что объемное распределение ионов вблизи электродов отличается от полученного с помощью линейного анализа уже при малых амплитудах приложенного напряжения, и понятие электрического импеданса остается в силе.

Спектроскопия импеданса как инструмент химического и электрохимического анализа смешанных проводников: пример церия

  • Wei Lai

  • Материаловедение

  • 2005

Реакция импеданса переменного тока смешанных ионных и электронных проводников (MIEC) получена из первых принципов и количественно сравнена с экспериментальными данными. Хотя этот подход не совсем нов,…

Комплексное рассмотрение универсальных дисперсионных частотных характеристик в твердых электролитах с помощью спектроскопии иммитанса: низкотемпературный случай AgI поведение AgI. Ряды графиков Боде полной проводимости и емкости при разных температурах…

Новый вычислительный подход для импеданса SOFC из подробных электрохимических моделей реакции -диффузии

  • W. Bessler

  • Материалогические науки

  • 2005

на концепции электрического импульса для Электролитического Электрика

.

Похожие записи

21.11.2024 0

Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

19.11.2024 0

Новорожденный какает слизью: причины появления слизи в кале грудничка

19.11.2024 0

Гемангиома у новорожденных: причины, виды, лечение и профилактика

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *