Что такое идеальный источник ЭДС и идеальный источник тока. Каковы их основные характеристики и отличия. Как выглядят вольт-амперные характеристики реальных источников. Как преобразовать источник ЭДС в источник тока и наоборот.
Понятие идеальных источников электрической энергии
В теории электрических цепей используются понятия идеальных источников электрической энергии:
- Идеальный источник ЭДС (источник напряжения)
- Идеальный источник тока
Эти источники обладают следующими ключевыми свойствами:
Идеальный источник ЭДС
Идеальный источник ЭДС представляет собой активный элемент с двумя зажимами, напряжение на которых не зависит от протекающего через источник тока. Основные характеристики:
- Напряжение на зажимах всегда равно ЭДС источника
- Внутреннее сопротивление равно нулю
- Ток через источник может принимать любые значения
Идеальный источник тока
Идеальный источник тока — это активный элемент, ток которого не зависит от напряжения на его зажимах. Ключевые особенности:

- Ток источника постоянен при любом напряжении на зажимах
- Внутреннее сопротивление бесконечно велико
- Напряжение на зажимах может принимать любые значения
Вольт-амперные характеристики идеальных источников
Вольт-амперные характеристики (ВАХ) наглядно отражают свойства идеальных источников:
ВАХ идеального источника ЭДС
Представляет собой вертикальную прямую линию, параллельную оси токов. Это означает, что напряжение источника остается постоянным при любом токе нагрузки.
ВАХ идеального источника тока
Имеет вид горизонтальной прямой линии, параллельной оси напряжений. Это показывает, что ток источника не меняется при изменении напряжения на его зажимах.
Реальные источники электрической энергии
В действительности любой источник электрической энергии обладает конечным внутренним сопротивлением. Поэтому реальные источники описываются более сложными моделями:
Реальный источник ЭДС
Схема замещения реального источника ЭДС включает:- Идеальный источник ЭДС E
- Последовательно включенное внутреннее сопротивление r0
Напряжение на зажимах реального источника ЭДС определяется выражением:

U = E — I * r0
где I — ток нагрузки.
Реальный источник тока
Схема замещения реального источника тока содержит:
- Идеальный источник тока J
- Параллельно включенное внутреннее сопротивление r0
Ток реального источника тока описывается уравнением:
I = J — U / r0
где U — напряжение на зажимах источника.
Вольт-амперные характеристики реальных источников
ВАХ реальных источников электрической энергии отличаются от идеальных:
ВАХ реального источника ЭДС
Представляет собой наклонную прямую линию. При увеличении тока нагрузки напряжение на зажимах источника уменьшается из-за падения напряжения на внутреннем сопротивлении.
ВАХ реального источника тока
Также имеет вид наклонной прямой. При росте напряжения на зажимах ток источника несколько уменьшается из-за ответвления части тока через внутреннее сопротивление.
Преобразование источников электрической энергии
При анализе электрических цепей часто возникает необходимость преобразования источников ЭДС в источники тока и наоборот. Такое преобразование возможно для источников конечной мощности.

Преобразование источника ЭДС в источник тока
Источник ЭДС с последовательным внутренним сопротивлением может быть заменен эквивалентным источником тока:
- Ток источника: J = E / r0
- Внутреннее сопротивление: r0 (не изменяется)
Преобразование источника тока в источник ЭДС
Источник тока с параллельным внутренним сопротивлением может быть заменен эквивалентным источником ЭДС:
- ЭДС источника: E = J * r 0
- Внутреннее сопротивление: r0 (не изменяется)
Такие преобразования позволяют упростить расчет сложных электрических цепей, содержащих различные типы источников.
Режимы работы источников электрической энергии
Источники электрической энергии могут работать в различных режимах в зависимости от параметров нагрузки:
Режим холостого хода
Нагрузка отключена, ток равен нулю. Для источника ЭДС напряжение на зажимах равно ЭДС. Для источника тока напряжение стремится к бесконечности.
Режим короткого замыкания
Зажимы источника замкнуты накоротко. Для источника ЭДС ток максимален и ограничен только внутренним сопротивлением. Для источника тока напряжение равно нулю.

Номинальный режим
Режим, на который рассчитан источник. Обеспечивает оптимальные условия работы с высоким КПД.
Согласованный режим
Режим передачи максимальной мощности в нагрузку. Достигается при равенстве сопротивления нагрузки внутреннему сопротивлению источника.
Применение идеальных и реальных моделей источников
Выбор модели источника электрической энергии зависит от решаемой задачи:
- Идеальные источники применяются для упрощенного анализа цепей
- Реальные модели используются для более точных расчетов
- Преобразование источников позволяет оптимизировать методы расчета
Понимание свойств различных типов источников электрической энергии необходимо для эффективного анализа и проектирования электрических цепей.
Идеальный источник тока
Источники напряжения и тока, их свойства, характеристики и схемы замещения. Законы Ома и Кирхгофа.
Источник ЭДС (идеальный источник напряжения) — двухполюсник, напряжение на зажимах которого постоянно (не зависит от тока в цепи). Напряжение может быть задано как константа, как функция времени, либо как внешнее управляющее воздействие.
В простейшем случае напряжение определено как константа, то есть напряжение источника ЭДС постоянно.Реальные источники напряжения
Рисунок 2
Идеальный
источник напряжения (источник ЭДС)
является физической абстракцией, то
есть подобное устройство не может
существовать. Если допустить существование
такого устройства, то электрический
ток I,
протекающий через него, стремился бы к
бесконечности при подключении нагрузки,
сопротивление RH которой
стремится к нулю. Но при этом получается,
что мощность источника
ЭДС также стремится к бесконечности,
так как .
Но это невозможно, по той причине, что
мощность любого источника энергии
конечна.
Но при этом получается,
что мощность источника
ЭДС также стремится к бесконечности,
так как .
Но это невозможно, по той причине, что
мощность любого источника энергии
конечна.
В реальности, любой источник напряжения обладает внутренним сопротивлением r, которое имеет обратную зависимость от мощности источника. То есть, чем больше мощность, тем меньше сопротивление (при заданном неизменном напряжении источника) и наоборот. Наличие внутреннего сопротивления отличает реальный источник напряжения от идеального. Следует отметить, что внутреннее сопротивление — это исключительно конструктивное свойство источника энергии. Эквивалентная схема реального источника напряжения представляет собой последовательное включение источника ЭДС —
где
— падение напряжения на внутреннем сопротивлении;
—
падение напряжения
на нагрузке.
При коротком замыкании (), то есть вся мощность источника энергии рассеивается на его внутреннем сопротивлении. В этом случае токбудет максимальным для данного источника ЭДС. Зная напряжение холостого хода и ток короткого замыкания, можно вычислить внутреннее сопротивление источника напряжения:
Исто́чник то́ка (также генератор тока) — двухполюсник, который создаёт ток , не зависящий от сопротивления нагрузки, к которой он присоединён. В быту «источником тока» часто неточно называют любой источник электрического напряжения (батарею, генератор, розетку), но в строго физическом смысле это не так, более того, обычно используемые в быту источники напряжения по своим характеристикам гораздо ближе к источнику ЭДС, чем к источнику тока.
Свойства:
Напряжение на клеммах идеального источника тока зависит только от сопротивления внешней цепи:
Мощность, отдаваемая источником тока в сеть, равна:
Так
как для источника тока ,
напряжение и мощность, выделяемая им,
неограниченно растут при росте
сопротивления.
Реальный источник тока, так же как и источник ЭДС, в линейном приближении может быть описан таким параметром, как внутреннее сопротивление . Отличие состоит в том, что чем больше внутреннее сопротивление, тем ближе источник тока к идеальному (источник ЭДС, наоборот, чем ближе к идеальному, тем меньше его внутреннее сопротивление). Реальный источник тока с внутренним сопротивлением эквивалентен реальному источнику ЭДС, имеющему внутреннее сопротивление и ЭДС .
Напряжение на клеммах реального источника тока равно:
Сила тока в цепи равна:
Мощность, отдаваемая реальным источником тока в сеть, равна:
Схемы замещения источников энергии
Простейшая электрическая цепь и ее схема замещения, как указывалось, состоят из одного источника энергии с ЭДС Е и внутренним сопротивлением rвт и одного приемника с сопротивлением r. Ток
во внешней по отношению к источнику
энергии части цепи, т. е. в приемнике с
сопротивлением r,
принимается направленным от точки а с
большим потенциалом к
точке b с
меньшим потенциалом .
Направление
тока будем обозначать на схеме стрелкой
с просветом или указывать двумя индексами
у буквы I, такими
же, как и у соответствующих точек схемы.
Так, для схемы рис. 1.3 ток в приемнике I = Iаb,
где индексы а и b обозначают направление
тока от точки а к точке b.
Покажем,
что источник энергии с известными
ЭДС E и
внутренним сопротивлением rвт,
может быть представлен двумя
основными схемами замещения (эквивалентными
схемами).
Как
уже указывалось, с одной стороны,
напряжение на выводах источника энергии
меньше ЭДС на падение напряжения внутри
источника:
с
другой стороны, напряжение на
сопротивлении r
Ввиду
равенства из
(1.5а) и (1.56) получается или
В
частности, при холостом ходе (разомкнутых
выводах а и b)
получается E=Uх,
т. е. ЭДС равна напряжению холостого
хода.
Ток
во внешней по отношению к источнику
энергии части цепи, т. е. в приемнике с
сопротивлением r,
принимается направленным от точки а с
большим потенциалом к
точке b с
меньшим потенциалом .
Направление
тока будем обозначать на схеме стрелкой
с просветом или указывать двумя индексами
у буквы I, такими
же, как и у соответствующих точек схемы.
Так, для схемы рис. 1.3 ток в приемнике I = Iаb,
где индексы а и b обозначают направление
тока от точки а к точке b.
Покажем,
что источник энергии с известными
ЭДС E и
внутренним сопротивлением rвт,
может быть представлен двумя
основными схемами замещения (эквивалентными
схемами).
Как
уже указывалось, с одной стороны,
напряжение на выводах источника энергии
меньше ЭДС на падение напряжения внутри
источника:
с
другой стороны, напряжение на
сопротивлении r
Ввиду
равенства из
(1.5а) и (1.56) получается или
В
частности, при холостом ходе (разомкнутых
выводах а и b)
получается E=Uх,
т. е. ЭДС равна напряжению холостого
хода.
Из
(1.7 6)
следует, что rвт источника
энергии, так же как и сопротивление
приемника, ограничивает ток.
На
схеме замещения можно показать элемент
схемы с rвт,
соединенным последовательно с элементом,
обозначающим ЭДС E (рис.
1.7, а). Напряжение U зависит от тока
приемника и равно разности между
ЭДС E источника
энергии и падением напряжения rвтI (1.6а).
Схема источника энергии, показанная на
рис. 1.7, а, называется первой
схемой замещения или
схемой с источником ЭДС.
Если rвт<<r и
напряжение Uвт<<U,
т. е. источник электрической энергии
находится в режиме, близком к холостому
ходу, то можно практически пренебречь
внутренним падением напряжения и
принять Uвт = rвт =
0.
В этом случае для источника энергии
получается более простая эквивалентная
схема только с источником ЭДС, у которого
в отличие от реального источника
исключается режим короткого замыкания
(U =0). Такой источник энергии без внутреннего
сопротивления (rвт =
0),
обозначенный кружком со стрелкой внутри
и буквой E (рис.
1.7,6), называют идеальным
источником ЭДС или источником
напряжения (источником
с заданным напряжением). Напряжение на
выводах такого источника не зависит от
сопротивления приемника и всегда равно
ЭДС E.
Его внешняя характеристика — прямая,
параллельная оси абсцисс (штриховая
прямая ab на
рис. 1.4).
Такой источник энергии без внутреннего
сопротивления (rвт =
0),
обозначенный кружком со стрелкой внутри
и буквой E (рис.
1.7,6), называют идеальным
источником ЭДС или источником
напряжения (источником
с заданным напряжением). Напряжение на
выводах такого источника не зависит от
сопротивления приемника и всегда равно
ЭДС E.
Его внешняя характеристика — прямая,
параллельная оси абсцисс (штриховая
прямая ab на
рис. 1.4).
1.3. Источники ЭДС и тока
Теория / 1.3. Источники ЭДС и тока
К активным элементам электрических цепей относятся источники ЭДС и источники тока.
Источники ЭДС
Идеализированный источник ЭДС – это активный элемент с двумя зажимами, напряжение на которых не зависит от проходящего через источник тока. Перемещение зарядов в источнике от точки с меньшим потенциалом к точке с большим потенциалом осуществляется за счет сторонних сил, присущих источнику.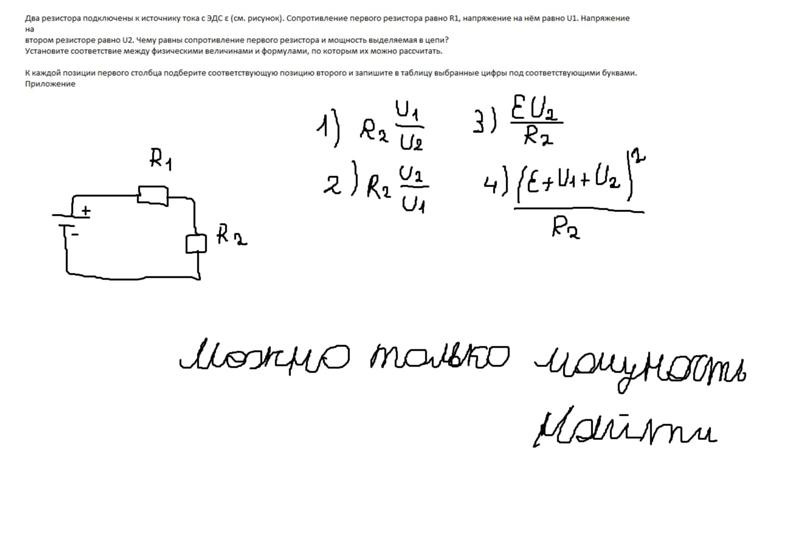 Обозначение идеализированных источников ЭДС на электрических схемах показано на рис. 1.5.
Обозначение идеализированных источников ЭДС на электрических схемах показано на рис. 1.5.
Электродвижущая сила (ЭДС) – это количество энергии, затраченное сторонними силами на перенос единичного положительного заряда от меньшего потенциала к большему
За положительное направление э.д.с. принимается направление возрастания потенциала (рис. 1.6).
Таким образом, положительные направления ЭДС и напряжения всегда противоположны.
Численно ЭДС равна разности потенциалов между выводами источника при разомкнутой цепи.
Если внутри источника ЭДС не содержится пассивных элементов, то его внутреннее сопротивление r0 равно нулю. Такой источник является идеальным.
На практике обычно приходится иметь дело с реальными источниками ЭДС, обладающими некоторым внутренним сопротивлением (рис. 1.7).
В таких источниках напряжение на зажимах зависит от тока в нагрузке.
Напряжение на зажимах реального источника в работающей цепи определяется соотношением
Это выражение называют внешней характеристикой источника ЭДС.
Анализируя внешнюю характеристику источника, можно сделать вывод, что напряжение на зажимах источника в режиме нагрузки всегда меньше ЭДС на величину падения напряжения на внутреннем сопротивлении источника. Зависимость напряжения от тока нагрузки показана на рис. 1.8 пунктирной линией. В свою очередь величина тока нагрузки зависит от сопротивления внешней цепи, поэтому можно считать, что напряжение на зажимах реального источника зависит от сопротивления внешней цепи.
В случае идеального источника внутренне сопротивление равно нулю. Напряжение на зажимах такого источника не зависит от тока нагрузки и равно ЭДС источника U = E. Зависимость напряжения от тока в идеальном источнике показана на рис. 1.8 сплошной линией.
Источники тока
Идеализированный источник тока – это активный элемент, ток которого не зависит от напряжения на его зажимах.
Считается, что внутреннее сопротивление идеального источника бесконечно велико, поэтому параметры внешней цепи не будут оказывать влияния на ток в источнике тока.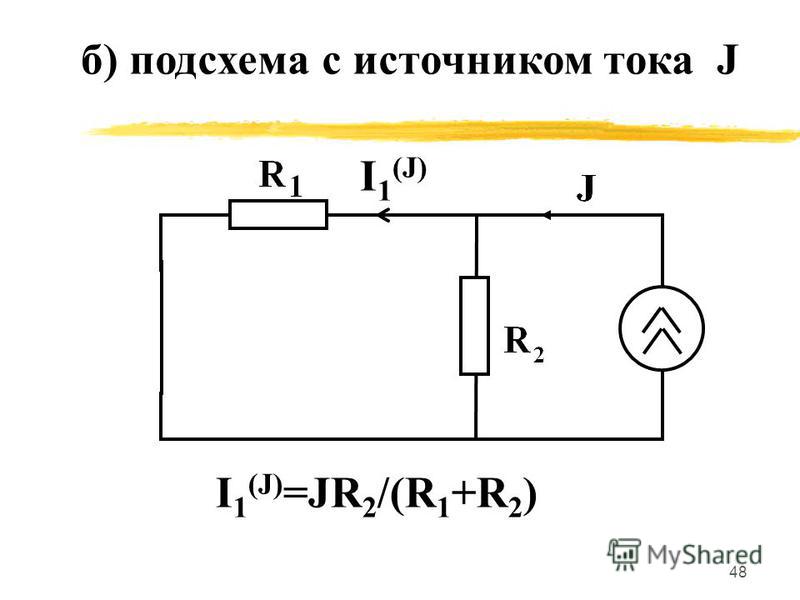 На электрических схемах источник тока обозначается так, как показано на рис. 1.9.
На электрических схемах источник тока обозначается так, как показано на рис. 1.9.
Реальный источник тока обладает конечным внутренним сопротивлением или отличной от нуля проводимостью. Схема реального источника представлена на рис. 1.10. Ток реального источника определяется разностью тока идеального источника J и внутреннего тока I0:
где U – напряжение, приложенное к зажимам источника. Полученное выражение называют внешней характеристикой источника тока.
Зависимость тока источника от напряжения на его зажимах показано на рис. 1.11. В случае идеального источника внутренняя проводимость равна нулю и, исходя из уравнения внешней характеристики, можно заключить, что ток, идущий от источника равен току короткого замыкания источника. Эта зависимость показана на рис. 1.11 сплошной линией.
В случае реального источника g0 ≠ 0 и часть тока будет ответвляться через внутреннюю проводимость. Чем больше напряжение, приложенное к источнику, тем больший ток ответвляется и тем меньший ток поступает в нагрузку.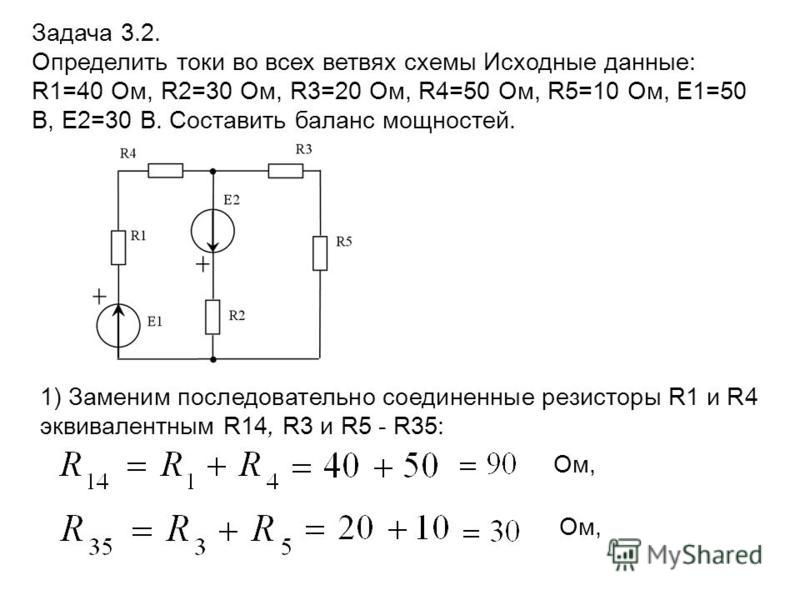 Вольт-амперная характеристика реального источника показана на рис. 1.11 пунктирной линией. Источник тока – это теоретическое понятие, но оно часто применяется для расчета электрических цепей. Примером источника тока может служить пентод.
Вольт-амперная характеристика реального источника показана на рис. 1.11 пунктирной линией. Источник тока – это теоретическое понятие, но оно часто применяется для расчета электрических цепей. Примером источника тока может служить пентод.
Эквивалентное преобразование источников конечной мощности
Преобразование какого-либо участка цепи по отношению к внешним зажимам называют эквивалентным, если напряжение u и ток i на внешних зажимах при этом не изменяются.
Рассмотрим условие эквивалентности реальных источников напряжения и тока, представленных на рис. 1.12, а,б. Воспользуемся уравнением внешней характеристики источника ЭДС
Поделим почленно это уравнение на r0
Здесь I – ток, протекающий через нагрузку;
Jкз = E/r0 – ток короткого замыкания источника ЭДС;
I0 = U/r0 – ток, протекающий через внутреннее сопротивление.
Отсюда можно заключить, что I0 = Jкз — I или I = Jкз — I0, то есть получили внешнюю характеристику источника тока.
Следовательно, схему источника ЭДС можно заменить схемой источника тока при условии, что ток короткого замыкания источника и внутренняя проводимость определятся выражениями:
В свою очередь, схему источника тока можно заменить схемой источника ЭДС при условии, что внутреннее сопротивление и э.д.с. источника определятся выражениями:
Мощность источника ЭДС определяется произведением электродвижущей силы источника и тока в нагрузке
Мощность источника тока определяется произведением тока короткого замыкания и напряжения на зажимах источника:
Основы электротехники и электроники: Курс лекций, страница 2
Величина, обратная сопротивлению, называется проводимостью (обозначается буквой g, имеет размерность Ом – 1 или См, Сименс).
В линейных
цепях сопротивление ветвей постоянно, определяется лишь физическими свойствами
материала проводников и не зависит от источников, токов и напряжений в ветвях.
Если источники в цепи создают на своих выводах напряжения и токи, которые не изменяются во времени, цепь называется электрической цепью постоянного тока. В цепи постоянного тока сопротивление индуктивностей равно нулю, сопротивление конденсаторов бесконечно велико.
Далее будут рассмотрены линейные цепи постоянного тока.
2. ИСТОЧНИКИ ЭДС И ИСТОЧНИКИ ТОКА
ЭДС – это максимальное напряжение, которое могут создать сторонние силы на выводах источника при отсутствии в цепи тока. В качестве сторонних сил могут выступать, например, химические реакции в гальванической батарее или момент на валу электрической машины, работающей в режиме генератора.
Для удобства анализа источники электрической энергии представляют либо с помощью идеального источника ЭДС, либо с помощью идеального источника тока. Идеальный источник ЭДС и идеальный источник тока называют также источниками бесконечно большой мощности.
На Рис. 2.1 а
показана вольт-амперная характеристика идеального источника ЭДС.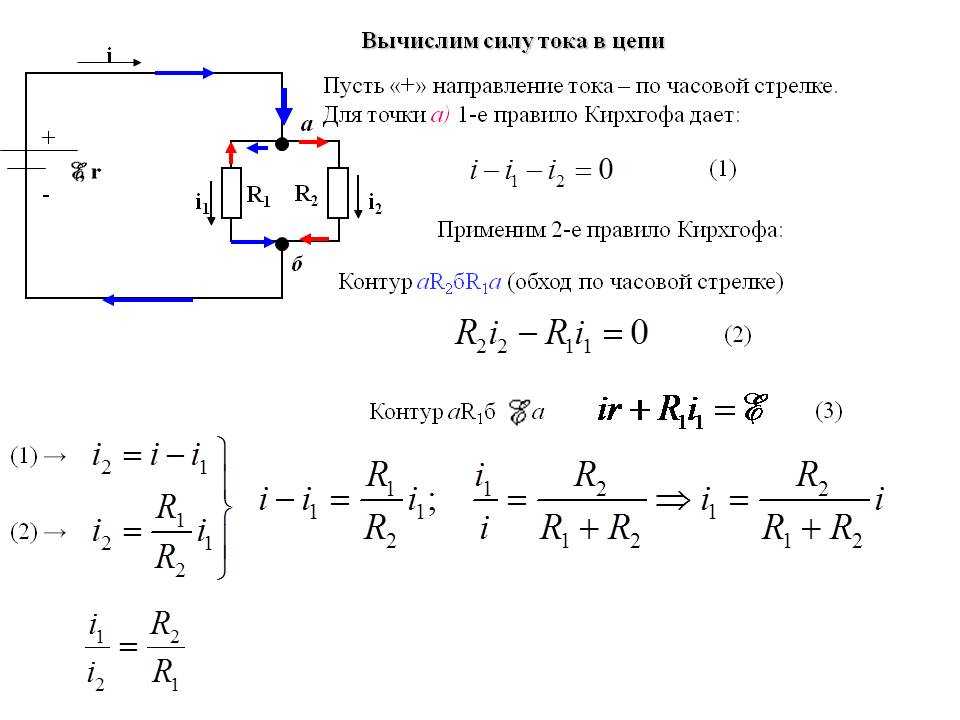 Этот источник
отличается тем, что напряжение на его выводах равно значению ЭДС независимо от
тока нагрузки. На Рис. 2.1 б показана вольт-амперная
характеристика идеального источника тока. Он сохраняет постоянство тока вне
зависимости от напряжения на своих выводах.
Этот источник
отличается тем, что напряжение на его выводах равно значению ЭДС независимо от
тока нагрузки. На Рис. 2.1 б показана вольт-амперная
характеристика идеального источника тока. Он сохраняет постоянство тока вне
зависимости от напряжения на своих выводах.
Рис. 2.1
Если к данным вольт-амперным характеристикам применить закон Ома (см. формулу (1.1))
,
можно сделать вывод, что сопротивление идеального источника ЭДС равно нулю, а сопротивление идеального источника тока равно бесконечности.
Реальный источник электрической энергии обладает конечным внутренним сопротивлением, его вольт-амперная характеристика показана на Рис. 2.2 и может быть описана выражением:
(2.1)
где – внутреннее сопротивление источника;
– напряжение холостого хода источника.
Рис. 2.2
2.2
Когда источник отключен от нагрузки, на его зажимах существует напряжение холостого хода , равное ЭДС источника. Если соединить накоротко зажимы источника, напряжение на зажимах будет равно нулю, а ток между зажимами будет равен току короткого замыкания .
Сравнивая вольт-амперные характеристики идеальных источников и реального источника, можно заключить, что реальный источник можно смоделировать либо с помощью эквивалентного идеального источника ЭДС и последовательно включенного внутреннего сопротивления, либо с помощью эквивалентного идеального источника тока и параллельно включенного внутреннего сопротивления (Рис. 2.3).
Рис. 2.3
Внутреннее сопротивление реального источника вычисляется как
.
ЭДС эквивалентного источника ЭДС равна напряжению холостого хода реального источника.
Ток эквивалентного источника тока равен току короткого замыкания реального источника.
ЭДС эквивалентного источника ЭДС и ток эквивалентного источника тока связаны соотношением:
(2. 2)
2)
Это соотношение говорит о том, что любой источник ЭДС с последовательно включенным сопротивлением может быть заменен источником тока с параллельно включенным таким же сопротивлением и наоборот.
Какой из двух эквивалентных замен воспользоваться, совершенно безразлично, и определяется лишь удобством расчета в каждом конкретном случае.
Заметим, что ЭДС идеального источника ЭДС всегда направлена от меньшего потенциала к большему, а ток идеального источника тока всегда направлен в ту же сторону, что и ток реального источника.
3. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ ЦЕПИ
Для упрощения расчетов электрическую цепь можно преобразовывать, уменьшая количество ветвей и узлов. При этом необходимо помнить, что после расчета преобразованной цепи следует выполнить обратное преобразование, чтобы вернуться к исходной цепи.
Любые
преобразования цепей должны быть эквивалентными, то есть преобразование какого-либо
участка цепи не должно изменять токораспределения в непреобразованной части
схемы. А это возможно лишь тогда, когда в процессе преобразования потенциалы
узлов в непреобразованной части схемы и токи, подтекающие извне к
преобразованному участку, сохраняются неизменными.
А это возможно лишь тогда, когда в процессе преобразования потенциалы
узлов в непреобразованной части схемы и токи, подтекающие извне к
преобразованному участку, сохраняются неизменными.
Простейшими преобразованиями электрической цепи являются свертки последовательно-параллельных соединений элементов цепи.
При последовательном соединении элементов конец предыдущего соединяется с началом последующего (Рис. 3.1). Главный признак последовательного соединения – один и тот же ток в каждом из элементов.
Рис. 3.1
Если к последовательному соединению элементов применить закон Ома (1.1), можно заключить, что напряжения на элементах распределяются прямо пропорционально сопротивлениям, а общее сопротивление последовательного соединения равно сумме сопротивлений элементов:
(3.1)
Итак, если на
участке цепи несколько элементов соединены последовательно, они могут быть
заменены одним эквивалентным элементом, сопротивление которого равно сумме
сопротивлений отдельных элементов. ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
СОПРОТИВЛЕНИЯ СКЛАДЫВАЮТСЯ!
ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
СОПРОТИВЛЕНИЯ СКЛАДЫВАЮТСЯ!
При параллельном соединении элементов начала всех элементов соединены в один узел, а концы всех элементов соединены в другой узел (Рис. 3.2).
Рис. 3.2
Главный признак параллельного соединения – одно и то же напряжение на каждом из элементов.
Если на участке цепи несколько элементов соединены параллельно, они могут быть заменены одним эквивалентным элементом, проводимость которого равна сумме проводимостей отдельных элементов. ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ СКЛАДЫВАЮТСЯ ПРОВОДИМОСТИ!
(3.2)
Источники электрической энергии в теоретических основах электротехники
Любой источник электрической энергии (источник питания) можно представить в виде источника напряжения или источника тока.
Идеальный источник напряжении (источник ЭДС) представляет собой идеализированный источник электрической энергии, напряжение на зажимах (выходное напряжение) которого равно ЭДС, и не зависит от протекающего через него тока.
Принято считать, что выходное сопротивление источника ЭДС равно нулю. Важнейшей характеристикой источника напряжения является внешняя характеристика , представляющая собой зависимость напряжения на зажимах нагруженного источника от тока в электрической цепи.
Условное графическое обозначение источника постоянной ЭДС приведено на рис. 1.6,а. Стрелка внутри кружка указывает положительное направление ЭДС, т. е. направление возрастания потенциала, а именно от вывода «-» к выводу «+».
Если к зажимам источника ЭДС подключить сопротивление нагрузки (рис 1.6,б), то ток . Уменьшение сопротивления вызывает неограниченное увеличение этого тока, но выходное напряжение источника ЭДС не изменится и останется равным ЭДС источника, т.е. . Мощность источника и равная ей мощность нагрузки стремятся к бесконечности.
Внешней характеристикой идеального источника постоянного напряжения является прямая линия, параллельная оси токов (рис. 1.7, а).
Реальный источник напряжения (источник напряжения).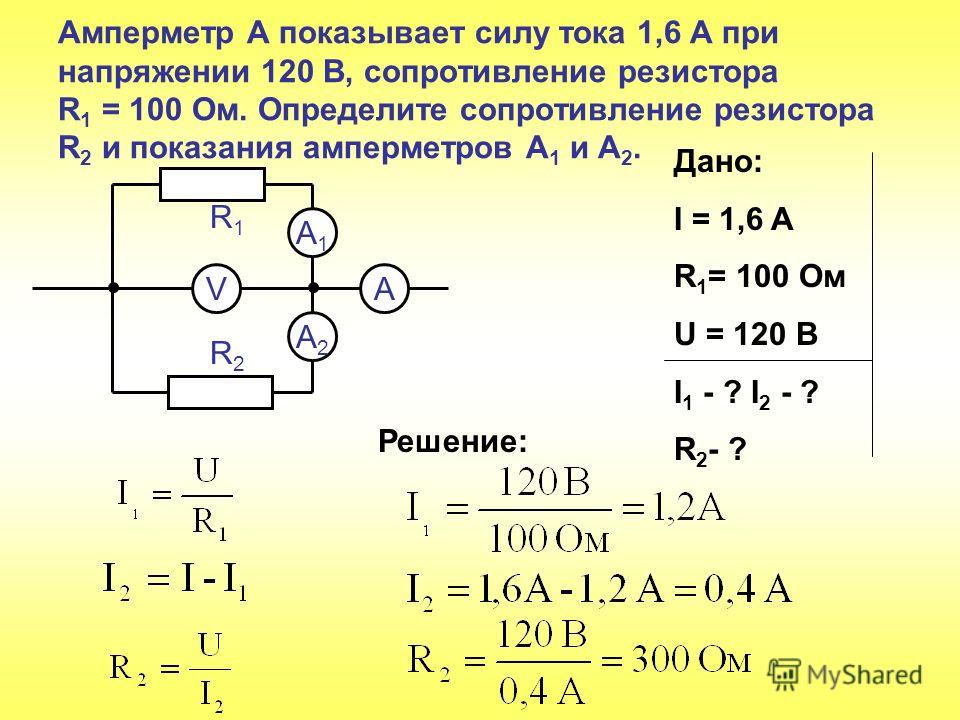 Схема замещения реального источника напряжения может быть представлена источником ЭДС и соединенным последовательно с ним внутренним сопротивлением источника (рис. 1.6,в). Значение невелико по сравнению с сопротивлением нагрузки .
Схема замещения реального источника напряжения может быть представлена источником ЭДС и соединенным последовательно с ним внутренним сопротивлением источника (рис. 1.6,в). Значение невелико по сравнению с сопротивлением нагрузки .
Зависимость напряжения на зажимах источника напряжения от тока, протекающего через внешние зажимы, определяется уравнением . Это уравнение и определяет внешнюю характеристику реального источника постоянного напряжения (рис. 1.7,6).
Она пересекает ось напряжения при работе источника в режиме холостого хода (точка 1 на рис. 1.7,б), когда и выходное напряжение источника (напряжение холостого хода) равно ЭДС, т.е. .
В режиме короткого замыкания (точка 4 на рис. 1.7,6) и ток источника (ток короткого замыкания) определяется его внутренним сопротивлением . Для большинства источников режим короткого замыкания является аварийным. Поэтому их защищают от короткого замыкания с помощью предохранителей, автоматических выключателей.
Кроме предельных режимов (холостой ход, короткое замыкание), источники могут работать в номинальном и согласованном режимах. Номинальным называют режим, па который рассчитан и изготовлен источник. В данном режиме источник работает долговременно с достаточно высоким коэффициентом полезного действия. Обычно . Поминальному режиму соответствует точка 2 на рис. 1.7, б.
Номинальным называют режим, па который рассчитан и изготовлен источник. В данном режиме источник работает долговременно с достаточно высоким коэффициентом полезного действия. Обычно . Поминальному режиму соответствует точка 2 на рис. 1.7, б.
Согласованным называют режим, при котором от источника в нагрузку передастся максимальная мощность . Этот режим выполняется, когда сопротивление нагрузки равно внутреннему сопротивлению источника, . При этом в источнике теряется 50% мощности.
Согласованный режим в основном применяется в маломощных цепях, когда определяющим условием является получение максимальной мощности в нагрузке, а не высокий КПД. Для силовых цепей характерен режим при обеспечивающий высокий КПД.
Идеальный источник тока (генератор тока) — это идеализированный источник электрической энергии, ток которого не зависит от напряжения на его зажимах (от сопротивления нагрузки). Принято считать, что выходное сопротивление идеального источника тока равно бесконечности.
Важнейшей характеристикой источника тока является внешняя характеристика , представляющая собой зависимость тока нагруженного источника от напряжения на его зажимах. Условное графическое обозначение генератора постоянного тока приведено на рис. 1.8,я. Двойная стрелка внутри кружка показывает положительное направление тока внутри источника.
Если к внешним выводам источника тока подключить сопротивление нагрузки , то напряжение на сопротивлении нагрузки . При увеличении напряжения на нем возрастает, а ток идеального источника тока не изменяется. Внешняя характеристикой генератора тока — прямая линия, параллельная оси напряжений (рис. 1.9,а).
Реальный источник тока. Схема замещения реального источника тока может быть представлена идеальным источником тока и соединенным параллельно с ним внутренним сопротивлением (рис. 1.8, в). Значение велико по сравнению с сопротивлением нагрузки .
Ток сопротивления нагрузки . Увеличение сопротивления вызывает уменьшение за счет увеличения тока .
Чем больше сопротивление нагрузки по сравнению с внутренним сопротивлением источника, тем больше ток нагрузки отличается от тока источника. Только в режиме короткого замыкания .
Внешняя характеристика реального источника тока приведена на рис. 1.9, б.
Эта теория взята со страницы помощи с заданиями по электротехнике:
Помощь по электротехнике
Возможно эти страницы вам будут полезны:
|
Стр 1 из 10Следующая ⇒ В теории электрических цепей используют понятия идеальные источники электрической энергии: источник напряжения и источник тока. Им приписывают следующие свойства: Источник напряжения представляет собой активный элемент с двумя зажимами, напряжение на котором не зависит от тока, проходящего через источник
Рис.2. Идеальный источник напряжения и его вольтамперная характеристика(BAX).
Предполагается, что внутри идеального источника напряжения пассивные сопротивление, индуктивность и емкость отсутствуют и, следовательно, прохождение тока не вызывает падения напряжения. Упорядоченное перемещение положительных зарядов в источнике напряжения от меньшего потенциала к большему возможно за счет работа сторонних сил, которые присущи источнику. Величина работы, производимой данными сторонними силами по перемещению единицы положительного заряда от отрицательного полюса источника напряжения к положительному по полюсу, называется электродвижущей силой (э.д.с.) источника и обозначается e(t). На рис.2(а) указано направление напряжения на зажимах идеального источника, которое всегда равно э.д.с. источника по величине и противоположно ей по направлению. Идеальный источник напряжения называют еще источником бесконечноймощности. Это — теоретическое понятие. Величина тока в пассивной цепи зависит от параметров этой цепи и e(t). Если зажимы идеального источника напряжения замкнуть накоротко, то ток цепи должен быть теоретически равен бесконечности. В действительности при замыкании зажимов источника ток имеет конечное значение, так как реальный источник обладает внутренним сопротивлением. Обычно внутренние параметры источника конечной мощности незначительны по сравнению с параметрами внешней цепи и в не которых случаях (по условию задачи) могут вообще не учитываться. Внутреннее сопротивление источника э.д.с.(r0) на схемах замещения изображается последовательно соединенным с самим источником.
Рис.3. Источник напряжения конечной мощности.
Источник тока представляет собой активный элемент, ток которого не зависит от напряжения на его зажимах.
Рис.4. Идеальный источник тока и его вольтамперная характеристика.
Предполагается, что внутренне сопротивление идеального источника тока равно бесконечности, и поэтому параметры внешней цепи, от которых зависит напряжение на зажимах источника тока, не влияют на ток источника. При увеличении напряжения внешней цепи, присоединенной к источнику тока, напряжение на его зажимах, и следовательно, мощность возрастают. Источник тока конечной мощности изображен на рис.5. g0 – внутренняя проводимость источника. Она характеризует внутренние параметры источника и ограничивает мощность, отдаваемую в цепь. Рис.5. Источник тока конечной мощности.
Часто при решении задач методом эквивалентных преобразований возникает необходимость заменить реальный источник напряжения эквивалентным источником тока или наоборот. Преобразование осуществляется по схеме и формулам рис.6.
(1)
Рис.6. Преобразования источников конечной мощности. Сопротивление. Сопротивлением называется идеализированный элемент цепи в котором происходит необратимый процесс преобразования электрической энергии в тепловую. Кроме того, данный термин применяется для количественной оценки величины, равной отношению напряжения на данном элементе к току, проходящему через него: [Ом] (2) Формула 2 выражает закон Ома. Сопротивление всегда положительно. Величина обратная сопротивлению носит название проводимости: [См] (3)
Рис.7. Графическое изображение сопротивления с выбранными положительными направлениями тока и напряжения.
Мгновенная мощность, поступающая в сопротивление равна: Pr = Ui = i2r = U2q (4) Параметр r в общем случае зависит от тока i (например, вследствие нагревания проводника током). Вольтамперная характеристика (зависимость напряжения на сопротивлении от тока) носит нелинейный характер.
Рис.8. BAX сопротивления: а – нелинейная; б – линейная.
Если сопротивление не зависит от тока, то имеет место прямая пропорциональность, выражающая закон Ома. В этом случае сопротивление называется линейным. Индуктивность. Индуктивностью называется идеализированный элемент электрической цепи, приближающейся по свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля. При этом термин «индуктивность» и его обозначение L применяется как для обозначения самого элемента цепи, так и для количественной оценки отношения потокосцепления самоиндукции к току в данном элементе: [Гн] (5) Индуктивность всегда положительна, так как потокосцепления и ток имеют одинаковые знаки. В общем случае индуктивность зависит от тока и является нелинейной. Если зависимостьy(i) линейная, то индуктивность – величина постоянная.
Рис.9. Зависимость потокосцепления от тока: а — нелинейная, б – линейная.
Рис.10. Графическое изображение индуктивности. (6) eL — электродвижущая сила самоиндукции, которая по закону Ленца противодействует изменению потокосцепления, что учитывается знаком « — ». Если индуктивность L величина постоянная (не зависит от тока), то = (7) Напряжение на индуктивности определяется: (8) Ток на индуктивности: (9) Формулы (8) и (9) выражают закон Ома дифференциальной и интегральной форме для индуктивности. Мгновенная мощность, поступающая в индуктивность равна: (10) Мощность индуктивности связана с процессом нарастания или убывания энергии магнитного поля. Емкость.
Емкостью называется идеализированный элемент электрической цепи приближенно заменяющий конденсатор, в котором накапливается энергия электрического поля. При этом данный термин применяется как для обозначения самого элемента, так и для количественной оценки отношения заряда к напряжению на этом элементе: [Ф] (11) Емкость всегда положительна, так как заряд и напряжение имеют одинаковый знак. В общем случае зависимость заряда от напряжения носит нелинейный характер и, следовательно, параметр С зависит от напряжения. Если зависимость заряда от напряжения линейная, емкость C – величина постоянная.
Рис.11. Зависимость электрического заряда от напряжения, а – нелинейная, б – линейная.
Ток емкости равен производной электрического заряда по времени: (12) Формула (12) выражает закон Ома для емкости. Напряжение на емкости: (13) Условное графическое изображение емкости указано на рис.11. Там же даны положительные направления тока и напряжения.
Рис.12. Условное обозначение емкости.
Мгновенная мощность, поступающая в емкость, равна: (14) Мощность емкости связана с процессом накопления или убыли электрического заряда в емкости. Когда заряд положительный и возрастает ток положительный и в емкость поступает электрическая энергия из внешней цепи. Когда заряд положителен, но убывает, т.е. ток отрицателен, энергия, ранее накопленная в электрическом поле емкости, возвращается во внешнюю цепь. Контрольные вопросы:
1. Изложите основные задачи электротехники. 2. Элементы электрической цепи, их классификация. 3. Определение электрического тока, падения напряжения. 4. Что понимают под положительными направлениями тока и напряжения. 5. Изложите основные сведения об источниках тока и источниках напряжения, их взаимном преобразовании. 6. Чем отличается идеальный источник энергии от источника энергии конечной мощности. 7. Дать краткую характеристику следующим элементам и терминам, их определяющим: сопротивление, емкость, индуктивность.
Законы электрических цепей Цель лекции № 2. Ознакомившись с лекцией № 2 по электротехнике студент должен уметь: 1. В смешанном соединении электрических элементов определять участки с последовательным и параллельным их соединением. 2. Определять потенциал любой точки электрической цепи относительно базиса. 3. 4. Определять необходимое количество узловых и контурных уравнений и составлять систему уравнений по законам Кирхгофа. 5. Записывать выражение баланса мощностей для сложной электрической цепи.
12345678910Следующая ⇒ Читайте также: |
Источник эдс. идеальный и реальный источники
Содержание
История
Электричество как источник энергии было известно ещё с древних времён, ведь сама природа генерирует его в огромных объёмах. Яркий пример — молния или электрический скат. Несмотря на такую близость к человеку, обуздать эту энергию удалось лишь в середине семнадцатого века: Отто фон Герике, бургомистр из Магдебурга, создал машину, позволяющую генерировать электростатический заряд. В середине восемнадцатого века Питер фон Мушенбрук — учёный из Голландии — создаёт первый в мире электрический конденсатор, названный Лейденской банкой в честь университета, где он работал.
Пожалуй, отсчёт эпохи настоящих открытий, посвящённых электричеству, принято начинать с работ Луиджи Гальвани и Алессандро Вольта, изучивших соответственно электрические токи в мышцах и возникновение тока в так называемых гальванических элементах. Дальнейшие исследования открыли нам глаза на связь электричества и магнетизма, а также на несколько очень полезных явлений (таких как электромагнитная индукция), без которых сегодня невозможно представить нашу жизнь.
Но мы не будем углубляться в магнитные явления и остановимся только на электрических. Итак, разберём, как же возникает электричество в гальванических элементах и что это вообще такое.
Идеальный источник тока (генератор)
Для начала рассмотрим абстрактный вариант: сила тока, созданная в этом устройстве, всегда одинаковая. Опираясь на закон Ома, можно легко сделать заключение, что напряжение находится в зависимости лишь от сопротивления подключенной нагрузки. Внутреннее сопротивление такого элемента питания имеет бесконечную величину, поэтому не воздействует на основной параметр.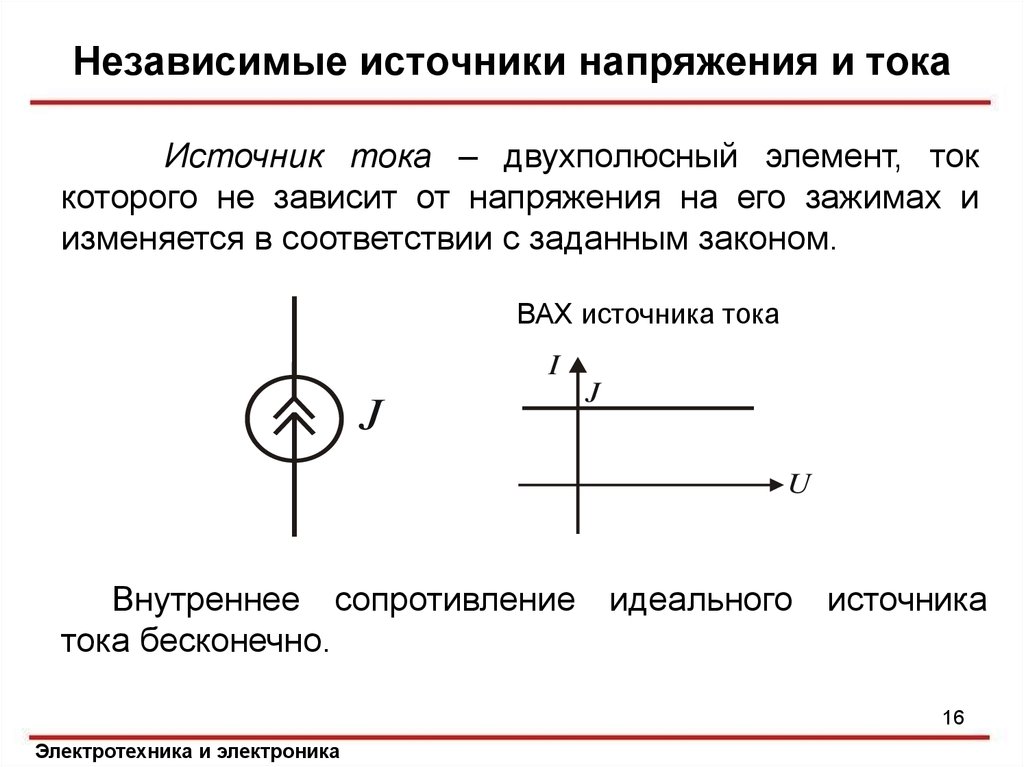 Вследствие того, что сила тока значение постоянное, то на значение мощности теоретического агрегата влияет только сопротивление подключенной нагрузки. В устройстве, при возникновении короткого замыкания, также сохраняется основное свойство источника.
Вследствие того, что сила тока значение постоянное, то на значение мощности теоретического агрегата влияет только сопротивление подключенной нагрузки. В устройстве, при возникновении короткого замыкания, также сохраняется основное свойство источника.
Такой идеальный элемент можно создать лишь в теории, его применяют при моделировании электромагнитных процессов. На практике такой системы достичь невозможно, поэтому рассмотрим материальную вариацию.
Принцип действия
Каждая маркировка источников тока определяет принцип его действия. В стандартной ситуации выработка энергии производится посредством взаимодействия составляющих частей, а именно:
- Механический тип. В результате взаимодействия деталей механизма, возникает трение. Благодаря такому явлению, возникает статическое электричество, преобразуемое в ток.
- Механические конструкции работают посредством образования последовательно движущихся заряженных частиц. Явление возникает благодаря взаимодействию химического элемента с электролитом.
 Заряженные частицы покидают структуру кристаллической решётки металла, входя в состав проводящей жидкости.
Заряженные частицы покидают структуру кристаллической решётки металла, входя в состав проводящей жидкости. - Солнечные батареи (световые источники) работают за счет выбивания заряженных частиц из диэлектрической (кремниевой) основы под воздействием светового потока. Благодаря этому возникает постоянное напряжение.
- Тепловые. Как правило, это 2 последовательно соединенных металлических основания. Одна часть нагревается, а вторая остается охлажденной. При изменении температурного режима возникает разница температур, в результате чего происходит движение заряженных частиц.
Важно! Любое изменение в строении вещества может привести к необратимым последствиям, которые проявятся при работе устройства
Конструкция
Конструкция элемента влияет на принцип его работы. Каждый источник, который выдает электрический ток, имеет определенную конструкцию:
Самый простой бытовой аккумулятор включает в себя металлический корпус, внутри которого используется щелочная среда. Дополнительными элементами являются свинцовые пластины, на которых накапливаются катоды и аноды.
Дополнительными элементами являются свинцовые пластины, на которых накапливаются катоды и аноды.
Аккумулятор
Обычная бытовая батарейка с входящим в её состав сухим элементом имеет металлический корпус, в который помещен стержень-накопитель катодов. Всё прочее пространство заполнено солевым электролитом.
Батарейка
Генератор переменного тока – это устройство, состоящее из трещоток или металлической рамки.
Механический принцип устройства
Тепловой источник тока, который уже включен в цепь. Это обычная рамка, установленная на подставке из диэлектрика. Обычно, конструкция подключена к измерительному прибору, типа амперметра. Источник тепла – это пламя или внешний электрический импульс.
Тепловое устройство
Важно! Подобная конструкция помогает точно понять, как образуется энергия, которая впоследствии преобразуется в ток. Каждый вариант строения обычно заключен в специальный корпус из диэлектрического материала
Так в чем же отличие
Для лучшего понимания, в чем состоит разница электродвижущей силы от напряжения, рассмотрим пример.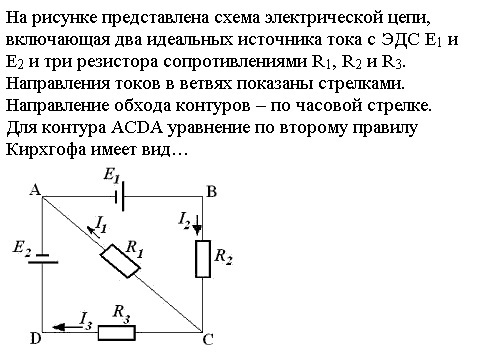 Имеется источник электрической энергии бесконечной мощности, в котором отсутствует внутреннее сопротивление. В электрической цепи смонтирована нагрузка. В этом случае будет справедливо утверждение, что ЭДС и напряжение тождественно равны, т.е между этими понятиями отсутствует разница.
Имеется источник электрической энергии бесконечной мощности, в котором отсутствует внутреннее сопротивление. В электрической цепи смонтирована нагрузка. В этом случае будет справедливо утверждение, что ЭДС и напряжение тождественно равны, т.е между этими понятиями отсутствует разница.
Однако, это идеальные условия, которые в реальной жизни не встречаются. Эти условия используют исключительно при расчетах. В реальной жизни учитывается внутреннее сопротивление источника питания. В этом случае ЭДС и напряжение имеют отличия.
На рисунке представлено, какая разница будет в значениях электродвижущей силы и напряжении в реальных условиях. Вышеприведенная формула закона Ома для полной цепи описывает все процессы. При разомкнутой цепи на клеммах батарейки будет значение 1,5 Вольта. Это значение ЭДС. Подключив нагрузку, в данном случае это лампочка, на ней будет напряжение 1 вольт.
Разница от идеального источника заключается в наличии внутреннего сопротивления источника питания. На этом сопротивлении и происходит падение напряжения. Эти процессы описывает закон Ома для полной цепи.
На этом сопротивлении и происходит падение напряжения. Эти процессы описывает закон Ома для полной цепи.
Если измерительный прибор на зажимах источника электроэнергии показывает значение 1,5 Вольта, это будет электродвижущая сила, но повторим, при условии отсутствия нагрузки.
При подключении нагрузки на клеммах будет заведомо меньшее значение. Это и есть напряжение.
Применение
Рисунок 2. Генератор тока типа «токовое зеркало», собранный на биполярных транзисторах
Источники тока широко используются в аналоговой схемотехнике, например, для питания измерительных мостов, для питания каскадов дифференциальных усилителей, в частности операционных усилителей.
Концепция генератора тока используется для представления реальных электронных компонентов в виде эквивалентных схем. Для описания активных элементов для них вводятся эквивалентные схемы, содержащие управляемые генераторы:
- Источник тока, управляемый напряжением (ИТУН). Применяется в основном для полевых транзисторов и электронных ламп.

- Источник тока, управляемый током (ИТУТ). Применяется, как правило, для биполярных транзисторов.
В схеме токового зеркала (рисунок 2) ток нагрузки в правой ветви задается равным эталонному току в левой ветви, так что по отношению к нагрузке R2 эта схема выступает как источник тока.
Реальный генератор
Главное различие между реальным и идеальным устройством — наличие внутреннего сопротивления. Чем выше данный параметр, тем ближе элемент к улучшенному варианту. Из этого следует, что напряжение и мощность значения конечные, т. е имеют определенный рабочий диапазон. При этом система также обладает ограничением по присоединяемой нагрузке. При решении задач, реальное устройство изображают в качестве идеального, с подключенным в параллель внутренним сопротивлением.
Эксплуатация данного агрегата возможна при холостом ходе (без внешней нагрузки) вследствие того, что имеем замкнутый контур за счет внутреннего сопротивления. Ток на выходе во время такого режима снижается до нулевого значения. При подключении накоротко (режим короткого замыкания) получим максимальную величину, а выходное напряжение опустится до 0.
При подключении накоротко (режим короткого замыкания) получим максимальную величину, а выходное напряжение опустится до 0.
В качестве примера такого устройства, обратимся к катушке индуктивности. Это положение справедливо в момент размыкания цепи. Так разность потенциалов в таком режиме резко увеличивается по сравнению с предыдущим состоянием. Все дело в ЭДС самоиндукции возникающей в этом элементе. При увеличении напряжения катушка накапливает энергию, при снижении отдает ее в сеть.
Еще одним примером является вторичная обмотка трансформатора тока, которая в нормальных условиях работы всегда должна быть закорочена. В противном случае, если в ней произойдет разрыв, то она станет генератором. Все дело в законе сохранения энергии, так мощность на первичной и вторичной обмотке должна быть одинаковой. Параметры первичной обмотки неизменны, вследствие конструктивных особенностей трансформатора (обмотка имеет один виток). При обрыве во вторичной обмотке, упорядоченного движения заряженных частиц не будет, соответственно напряжение резко возрастет.
Примеры
Источником тока является катушка индуктивности, по которой шёл ток от внешнего источника, в течение некоторого времени (t≪LR{\displaystyle t\ll L/R}) после отключения источника. Этим объясняется искрение контактов при быстром отключении индуктивной нагрузки: стремление к сохранению тока при резком возрастании сопротивления (появление воздушного зазора) приводит к резкому возрастанию напряжения между контактами и к пробою зазора.
Вторичная обмотка трансформатора тока, первичная обмотка которого последовательно включена в мощную линию переменного тока, может рассматриваться как почти идеальный источник переменного тока. Следовательно, размыкание вторичной цепи трансформатора тока недопустимо. Вместо этого при необходимости перекоммутации в цепи вторичной обмотки (без отключения линии) эту обмотку предварительно шунтируют.
Определение полюсов
Чтобы определить, который полюс источника постоянного напряжения является положительным, а какой — отрицательным, используются специальные «полюсоискатели», действие которых основано на явлении электролиза. Полюсоискатель представляет собой стеклянную ампулу, заполненную раствором поваренной соли с добавкой фенолфталеина. В ампулу снаружи введены электроды. При подключении к электродам источника напряжения начинается электролиз: на отрицательном полюсе идёт выделение водорода и образуется щелочная среда. Из-за наличия щёлочи фенолфталеин меняет свою окраску — краснеет, по красной окраске у электрода и судят о том, что он соединён с отрицательным полюсом источника напряжения.
Полюсоискатель представляет собой стеклянную ампулу, заполненную раствором поваренной соли с добавкой фенолфталеина. В ампулу снаружи введены электроды. При подключении к электродам источника напряжения начинается электролиз: на отрицательном полюсе идёт выделение водорода и образуется щелочная среда. Из-за наличия щёлочи фенолфталеин меняет свою окраску — краснеет, по красной окраске у электрода и судят о том, что он соединён с отрицательным полюсом источника напряжения.
Условия работы источников тока
Любой источник тока работает при определенных условиях. В отсутствие химической реакции внутри элементов не смогут образовываться заряженные частицы. Если будет отсутствовать анод и катод, то движения частиц не возникнет даже при наличии реакции.
В аккумуляторах происходит похожий процесс, но толчком для возникновения химической реакции является замыкание во внешней электрической цепи. Заряженные элементы начинают двигаться от анода к катоду и наоборот, создавая постоянный поток.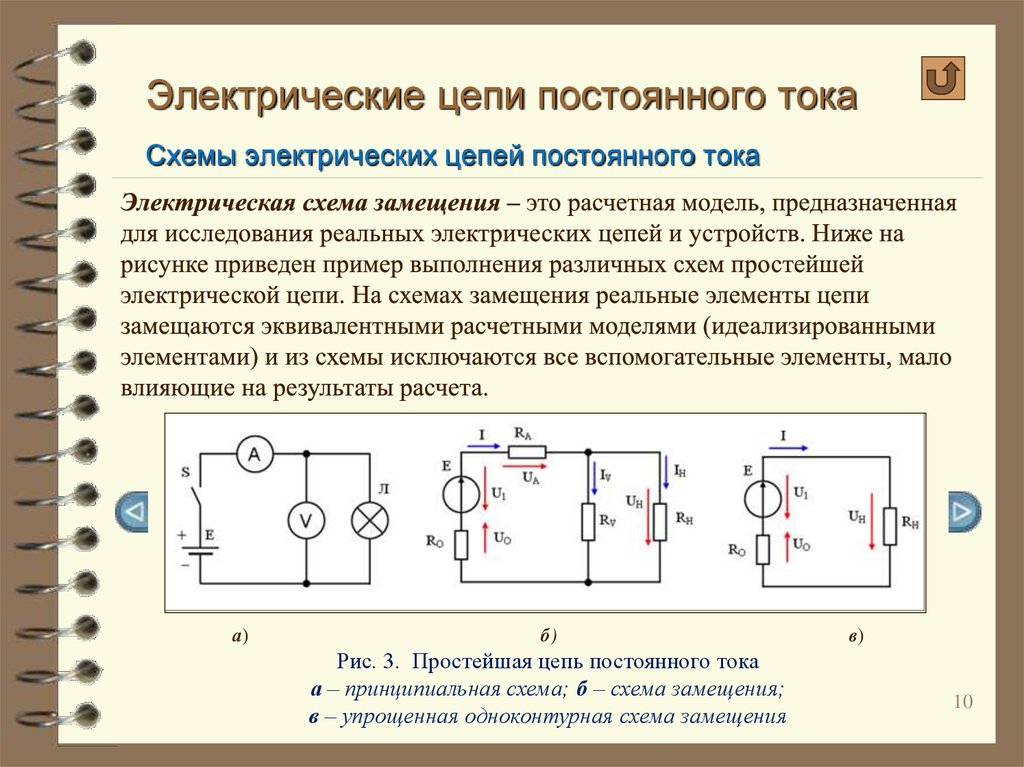
Идеальный и реальный
Световые типы не могут работать без наличия источника света. КПД зависит от типа используемого диэлектрического элемента. Дополнительно необходимо иметь в наличии приспособление ля преобразования полученной энергии.
Тепловой вариант не будет работать, если в его основу входит 1 тип металла. Если будет отсутствовать источник тепла, то ни о каком возникновение движущихся частиц не может быть и речи.
Источники
Для выработки электрической энергии требуется выбрать источник тока, соответствующий потребностям в конкретной сфере применения. Существует несколько вариантов таких приспособлений, каждый из которых имеет определенное строение, принцип работы и индивидуальные технические показатели.
Свойства
Идеальный источник тока
Сила тока, текущего через идеальный источник тока, всегда одинакова по определению:
- I=const{\displaystyle I={\text{const}}}
Напряжение на клеммах идеального источника тока (не путать с реальным источником!) зависит только от сопротивления R{\displaystyle R} подключенной к нему нагрузки:
- U=I⋅R{\displaystyle U=I\cdot R}
Мощность, отдаваемая источником тока в нагрузку:
- P=I2⋅R{\displaystyle P=I^{2}\cdot R}
Поскольку ток через идеальный источник тока всегда одинаков, то напряжение на его клеммах и мощность, передаваемая им в нагрузку, с ростом сопротивления нагрузки возрастают, достигая в пределе бесконечных значений.
Реальный источник
В линейном приближении любой реальный источник тока (не путать с описанным выше источником тока — моделью!) или иной двухполюсник может быть представлен в виде модели, содержащей, по меньшей мере, два элемента: идеальный источник и внутреннее сопротивление (проводимость). Одна из двух простейших моделей — модель Тевенина — содержит источник ЭДС, соединенный последовательно с сопротивлением, а другая, противоположная ей, модель Нортона — источник тока, соединенный параллельно с проводимостью (т. е. идеальным резистором, свойства которого принято характеризовать значением проводимости). Соответственно, реальный источник в линейном приближении может быть описан при помощи двух параметров: ЭДС E{\displaystyle {\mathcal {E}}} источника напряжения (или силы тока I{\displaystyle I} источника тока) и внутреннего сопротивления r{\displaystyle r} (или внутренней проводимости y=1r{\displaystyle y=1/r}).
Можно показать, что реальный источник тока с внутренним сопротивлением r{\displaystyle r} эквивалентен реальному источнику ЭДС, имеющему внутреннее сопротивление r{\displaystyle r} и ЭДС E=I⋅r{\displaystyle {\mathcal {E}}=I\cdot r}. {2}}}.}
{2}}}.}
Реальные генераторы тока имеют различные ограничения (например, по напряжению на его выходе), а также нелинейные зависимости от внешних условий. В частности, реальные генераторы тока создают электрический ток только в некотором диапазоне напряжений, верхний порог которого зависит от напряжения питания источника. Таким образом, реальные источники тока имеют ограничения по нагрузке.
Источник ЭДС и его характеристика.
Электродвижущей
силой источника (ЭДС) называется скалярная величина, численно равная
работе сторонних сил при перемещении единицы положительного заряда; ЭДС
источника числено равна разности потенциалов на концах разомкнутого элемента (без
нарузки). Электродвижущая сила измеряется в тех же единицах, что и
напряжение. = / = Дж/Кл = В×А×с/А×с
= В (вольт). Тогда разность потенциалов (напряжение)
1 вольта равна 1 джоулю энергии необходимому для перемещения заряда в 1 кулон
из одной точки проводника в другую.
ЭДС
возникает при диффузии ионов в электролитах, при электромагнитной индукции, при
электромагнитной индукции, при освещении светом полупроводниковых элементов и
т.д.
Источник
электродвижущей силы – это источники электромагнитной энергии,
характеризирующейся электродвижущей силой E и
внутренним электрическим сопротивлением Rвт.
Принципы
работы независимого источника ЭДС рассмотрим на примере простейшей цепи,
состоящей из этого источника ЭДС и резистивного элемента-приемника с переменным
сопротивлением R (сопротивлением проводов
пренебрегаем). На схеме замещения источник ЭДС представляют в виде двух
элементов: идеального источника ЭДС E,
внутреннее сопротивление которого равно нулю, и последовательного соединенного
с ним резистора, сопротивление которого Rвт.
Электродвижущая
сила E численно равна разности потенциалов или
напряжению U12X
между положительным 1 и отрицательным 2 зажимами источника энергии при
отсутствии в нем тока ( I=0 ), т. е. в режиме холостого
е. в режиме холостого
хода (ХХ),
и
действует в источнике от зажима с меньшим потенциалом ( 2 ) к зажиму с большим
потенциалом (1). Направление действия ЭДС указывается в кружочке стрелкой. При
подключении к выводам 1 и 2 нагрузки R в замкнутом контуре
цепи возникает ток I; при этом напряжение на зажимах 1
и 2 уже не будет равно ЭДС E вследствие падения
напряжения на внутреннем сопротивлении Rвт источника ЭДС:
Зависимость напряжения на зажимах источника ЭДС от
тока в нем носит название внешней характеристики источника, т.е. U12 = f (I).
При увеличении тока от нуля до номинального значения I = I1 напряжение на зажимах источника ЭДС убывает
практически по прямолинейному закону. При дальнейшем увеличении тока (при
уменьшении сопротивления R) эта пропорциональность нарушается (кривая 1) при
этом величена ЭДС E
у некоторых источников уменьшается и возрастает значение внутреннего
сопротивления Rвт.

Что такое источники тока
Источники тока – это элементы электрической цепи, который поддерживают энергию с заданными параметрами. При этом, энергоснабжение цепи не зависит от характеристик элементов, входящих в её состав, в частности, сопротивления.
Прибор для выработки тока
Различают идеальные и реальные устройства для выработки тока:
- Идеальные определяются только благодаря гипотезам и теоретическим выкладкам. Так, учёные нередко определяют ряд условий, при которых ток имеет максимальные значения, приближенные к идеалу. То есть, осуществляется имитация идеального источника.
- Реальные условия поддерживают заданные параметры выходного тока и напряжения. Любой прибор обеспечивает свою работу, при условии, что это позволяют сделать его технические характеристики.
Важно! Таким образом, максимальное значение тока и напряжения дают возможность определить, какой именно вариант источника будет использован в цепи – идеальный или реальный
Вывод
Из вышесказанного можно сделать вывод, что основная разница между ЭДС и напряжением состоит:
- Электродвижущая сила зависит от источника питания, а напряжение зависит от подключенной нагрузки и тока, протекающего по цепи.

- Электродвижущая сила это физическая величина, характеризующая работу сторонних сил неэлектрического происхождения, происходящих в цепях постоянного и переменного тока.
- Напряжение и ЭДС имеет единую единицу измерения – Вольт.
- U -величина физическая, равная работе эффективного электрического поля, производимой при переносе единичного пробного заряда из точки А в точку В.
Таким образом, кратко, если представить U в виде столба воды, то ЭДС можно представить что это насос, поддерживающий уровень воды на постоянном уровне. Надеемся, после прочтения статьи Вам стало понятно основное отличие!
Материалы по теме:
- Чем отличается трансформатор от автотрансформатора
- Разница между контактором и пускателем
- Как узнать, есть ли напряжение в розетке
Опубликовано:
15.08.2019
Обновлено: 15.08.2019
Помогла ли вам статья?
Задать вопрос
Пишите ваши рекомендации и задавайте вопросы в комментариях
Электромагнетизм.
 Если идеальный источник тока имеет бесконечное сопротивление, как возможен ток?
Если идеальный источник тока имеет бесконечное сопротивление, как возможен ток? Спросил
Изменено 5 лет, 11 месяцев назад
Просмотрено 4k раз
$\begingroup$
Откуда берется ток, если идеальный источник тока имеет бесконечное сопротивление? Ток не может проходить через источник тока из-за сопротивления, поэтому я не совсем понимаю, как и почему идеальный источник тока имеет бесконечное сопротивление.
- электромагнетизм
- электрические цепи
- электрическое сопротивление
$\endgroup$
$\begingroup$
Я думаю, вы можете ответить на свой вопрос, сопоставив простейшую возможную схему, просто подключив ваш источник к внешнему резистору R. Для идеального источника напряжения, которым по сути является батарея, вам нужно пренебрежимо малое сопротивление внутри источника, поэтому полное сопротивление очень близок к R, и тогда через него будет течь I=V/R, так что I буду зависеть от R, а V — нет (тогда как, если бы в источнике было сопротивление R’, вы бы получили снижение в эффективном V на IR’, так что это будет близко к VR’/R, и у вас будет только 1-R’/R желаемого V). Но обратите внимание на ключевой момент: если вы меняете R, постоянным остается V, а не I, поэтому у вас есть хороший источник V, но паршивый источник I.
Для идеального источника напряжения, которым по сути является батарея, вам нужно пренебрежимо малое сопротивление внутри источника, поэтому полное сопротивление очень близок к R, и тогда через него будет течь I=V/R, так что I буду зависеть от R, а V — нет (тогда как, если бы в источнике было сопротивление R’, вы бы получили снижение в эффективном V на IR’, так что это будет близко к VR’/R, и у вас будет только 1-R’/R желаемого V). Но обратите внимание на ключевой момент: если вы меняете R, постоянным остается V, а не I, поэтому у вас есть хороший источник V, но паршивый источник I.
Чтобы получить хороший источник I, перейдите к противоположному пределу огромного R’ в источнике. Тогда не будет иметь значения, какой R вы прикрепите к источнику, потому что R’ все равно будет доминировать. Вы всегда будете приближаться к I=V’/R’ для любого R, поэтому I остается близким к постоянному, так как V’. Однако V на резисторе R будет подчиняться V=IR=V’R/R’, поэтому оно вообще не будет постоянным, оно будет пропорционально R.
Ваш вопрос в пределе, как R’ уходит в бесконечность, разве это не убивает I, но ответ на этот вопрос таков: если вам нужен фиксированный источник I, вам нужно увеличивать V’ пропорционально R’. Ни R’, ни V’ не могут быть бесконечными, но хитрость в том, что вы должны сделать их обоих очень большими (и пропорционально этому), чтобы получить фиксированный источник I. Я полагаю, это дает ответ на ваш вопрос: «Вот почему невозможно иметь действительно идеальный источник тока».
$\endgroup$
$\begingroup$
Идеальный источник тока с бесконечным внутренним сопротивлением — это абстракция, используемая в теории цепей. Как следует из названия, это просто источник постоянного тока, который не реагирует на приложенное напряжение. Поэтому бесконечное сопротивление. Реальный источник тока моделируется идеальным источником тока, дающим постоянный ток параллельно с конечным внутренним сопротивлением.
$\endgroup$
4
$\begingroup$
Откуда берется ток, если идеальный источник тока имеет бесконечный сопротивление?
Наклон ВАХ для идеального источника тока равен нулю, как и в случае бесконечного сопротивления. Сказать, что идеальный источник тока имеет бесконечное внутреннее сопротивление Ом, значит сказать, что ток через него не зависит от напряжения на нем.
С другой точки зрения, для источника тока с конечное внутреннее сопротивление $r_s$, сопротивление нагрузки параллельно внутреннему сопротивлению, поэтому при делении тока ток нагрузки зависит от сопротивления нагрузки и определяется выражением
$$I_L = I_S \frac{r_s} {r_s + R_L}$$
Обратите внимание, что в пределе $r_s \rightarrow \infty$ ток нагрузки становится постоянным $I_L = I_S$. Таким образом, мы говорим, что у идеального источника тока, который производит ток нагрузки , независимый от $R_L$, внутреннее сопротивление бесконечно.
Таким образом, мы говорим, что у идеального источника тока, который производит ток нагрузки , независимый от $R_L$, внутреннее сопротивление бесконечно.
$\endgroup$
$\begingroup$
«Идеальный» в данном контексте означает, что не учитывается, как на практике могут быть достигнуты идеальные свойства (постоянный ток независимо от нагрузки, бесконечное сопротивление). Как говорит Фричарли, это абстрактное понятие.
Процесс анализа электрических цепей начинается с моделирования реальных электрических компонентов, которые обладают несколькими свойствами, как комбинации идеальных элементов (например, в химии), каждый из которых имеет одно свойство — чистый резистор/конденсатор/индуктор, чистый источник напряжения/тока и т. д.
Ни один реальный источник тока не обладает свойствами идеального источника тока, и спрашивать, как идеальный источник тока может иметь бесконечное сопротивление, но генерировать конечный ток, так же бессмысленно, как и спрашивать, как любая реальная струна может быть нерастяжимой. оказывать конечное натяжение, когда вы тянете за него. Однако для целей анализа электрических цепей большинство реальных источников тока можно с достаточной точностью смоделировать как идеальный источник тока с параллельным конечным внутренним сопротивлением. Реальный источник тока также будет иметь некоторую емкость и индуктивность, которые становятся значительными при высокой частоте.
оказывать конечное натяжение, когда вы тянете за него. Однако для целей анализа электрических цепей большинство реальных источников тока можно с достаточной точностью смоделировать как идеальный источник тока с параллельным конечным внутренним сопротивлением. Реальный источник тока также будет иметь некоторую емкость и индуктивность, которые становятся значительными при высокой частоте.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
идеальных источников | Абсолютная электроника, книга
Ultimate Electronics: практическое проектирование и анализ схем
≡ Оглавление
«
2.3
Напряжение и ток»
2,5
ЗемляИдеальные источники напряжения, идеальные источники тока и неидеальные источники с внутренним сопротивлением. 7 мин чтения
Идеальные источники напряжения и тока являются примитивными понятиями для моделирования цепей. Мы обсуждали напряжение и ток в предыдущем разделе.
Вот схематические символы для этих двух идеальных источников:
Символы идеального напряжения и источника тока
Circuitlab.com/cq8x2vnv3vhc5
Править — Моделирование
Символ идеального источника напряжения помечен положительными и отрицательными выводами, указывающими его направление. Он определяется всего одним параметром V : разностью напряжений на его клеммах.
Он определяется всего одним параметром V : разностью напряжений на его клеммах.
Идеальный источник напряжения поддерживает одинаковую разность напряжений на своих клеммах независимо от величины тока, направления тока или общего подаваемого заряда.
Идеальных источников напряжения в физической реальности не существует. Батарея (электрохимическая ячейка) ведет себя как идеальный источник напряжения, но это приближение не работает, когда токи велики и/или когда батарея разряжена. Мы обсудим батареи более подробно позже.
Когда какой-либо ток поступает в идеальный источник напряжения или выходит из него, напряжение на нем остается прежним. Вот простая симуляция, которая показывает этот эффект:
Развертка постоянного тока идеального источника напряжения
Circuitlab.com/cqvc3cr6qcn9k
Править — Имитация
Упражнение Щелкните цепь, затем нажмите «Симуляция» и «Запустить развертку постоянным током». Он настроен на регулировку тока, вводимого или выходящего из источника напряжения V1.
Он настроен на регулировку тока, вводимого или выходящего из источника напряжения V1.
График напряжения показывает, что напряжение остается постоянным (прямая линия на уровне 5 вольт) независимо от тока. Это скучная симуляция, но она показывает, что идеальный источник напряжения делает именно то, что должен!
Символ идеального источника тока имеет стрелку, указывающую направление тока – при заданном параметре тока I положительный.
Идеальный источник тока выдает определенное постоянное количество заряда за раз, независимо от напряжения, энергии или общего заряда.
Источник тока также иногда называют стоком тока , в зависимости от того, с какого направления мы на него смотрим. Термин источник тока может использоваться в любом направлении.
Не существует простого физического почти соответствующего компонента, подобного приведенному выше аккумулятору. Однако механические аналоги существуют. Водяной насос, который всегда выталкивает воду с заданной постоянной скоростью, независимо от того, насколько сильно он должен давить на какие-либо препятствия в трубе, является разумным гидравлическим приближением к источнику тока.
Эта аналогия намекает на проблемы, с которыми мы столкнемся в электронике: что произойдет, если мы соединим идеальный водяной насос с расходом 1 литр/час последовательно с идеальным водяным насосом с расходом 2 литра/час? Какой из них победит? Ответ заключается в том, что что-то должно дать. Два идеальных источника тока, соединенные последовательно, несовместимы.
Точно так же, что если мы возьмем наш идеальный водяной насос производительностью 1 литр/час и полностью перекроем его выходную трубу? Это похоже на то же самое, потому что заблокированный выход подобен источнику тока 0 литров в час. Так что, в конце концов, что-то должно дать сбой — либо помпа, либо препятствие, — но математически мы создали невозможную ситуацию.
Хотя они могут не встречаться в природе, источник тока является ценным методом моделирования, поскольку в довольно широком диапазоне некоторые вещи ведут себя как источники тока, и/или полезно строить источники тока как подкомпонент других систем или модели.
Вот простая симуляция, показывающая, что независимо от приложенного напряжения ток остается неизменным:
Развертка постоянного тока идеального источника тока
Circuitlab.com/cxwrktp8xekry
Править — Имитация
Упражнение Щелкните цепь, нажмите «Симуляция» и «Запустить развертку постоянным током».
Опять же, это скучная плоская симуляция, но источник тока поддерживает ток 10 А независимо от приложенного напряжения.
Моделирование неидеальных источников требует размышлений о сопротивлении и законе Ома, а также о том, как напряжения и токи ведут себя в сети в соответствии с законом Кирхгофа о напряжении и током Кирхгофа. Однако эти модели тесно связаны с идеальными источниками, поэтому мы кратко представим их здесь.
Практический источник напряжения моделируется в первом порядке с внутренним сопротивлением серии :
Неидеальный источник напряжения первого порядка
Circuitlab. com/c95f355g6h7m2
com/c95f355g6h7m2
Править — Имитация
Это означает, что фактическое внешнее напряжение падает по мере того, как от него отбирается ток. (В качестве альтернативы внешнее напряжение возрастает, если в него подается ток.)
Иногда этот эффект важен, а иногда нет: он зависит от величины падения напряжения и от того, рассчитана ли остальная часть вашей системы на то, чтобы выдерживать что.
На самом деле это не всегда линейно. Это даже не всегда монотонно: например, посмотрите защита от перегрузок , чтобы увидеть, как разработчики источников питания иногда намеренно хотят, чтобы нелинейное поведение сопротивления защищало цепь от перегрузки и перегрева.
Сравните эту симуляцию неидеального источника напряжения с симуляцией идеального источника напряжения выше:
Развертка постоянного тока неидеального источника напряжения первого порядка
Circuitlab. com/cnqwa9q3g92fe
com/cnqwa9q3g92fe
Править — Имитация
Упражнение Щелкните цепь, нажмите «Симуляция» и «Запустить развертку постоянным током». Теперь, когда внутреннее сопротивление не равно нулю, график напряжения больше не плоский. Наклон зависит от значения внутреннего сопротивления.
Поскольку батареи часто моделируются как источники напряжения, важно помнить, что настоящие гальванические элементы батареи также имеют внутреннее сопротивление. Это сопротивление зависит от химического состава батареи, конструкции и истории. Свежие, высококачественные батареи будут иметь более низкое внутреннее сопротивление, чем старые, бывшие в употреблении батареи. Когда люди, плохо знакомые с электроникой, рассматривают возможность питания большой нагрузки от батарей, они часто забывают учитывать падение напряжения из-за внутреннего сопротивления, которое может привести к тому, что система не сможет обеспечить ожидаемую мощность нагрузки. Кроме того, падение напряжения может привести к перезагрузке цифровых систем или вызвать колебания напряжения питания в прецизионных аналоговых системах. Подумайте, может ли внутреннее сопротивление батареи повлиять на остальную часть вашей системы.
Подумайте, может ли внутреннее сопротивление батареи повлиять на остальную часть вашей системы.
Практический источник тока моделируется в первом порядке с параллельным внутренним сопротивлением :
Неидеальный источник тока первого порядка
Circuitlab.com/c6m6cgvzv43vg
Править — Моделирование
Почему этот дополнительный резистор в параллелен здесь, а не в рядом с как для неидеального источника напряжения? Это потому, что последовательный резистор ничего не сделает с идеальным источником тока. (Источник тока не заботится о падении напряжения, поэтому любое дополнительное падение напряжения из-за последовательного резистора не повлияет на идеальный источник внутри.) Вместо этого параллельный резистор указывает, что потребляемый ток будет варьироваться в зависимости от приложенного напряжения: идеальный источник и резистор потребляют ток одновременно.
Сравните эту неидеальную симуляцию источника тока с симуляцией идеального источника тока выше:
Развертка постоянного тока неидеального источника тока первого порядка
Circuitlab.com/c3fv379ry9327
Править — Имитация
Упражнение Щелкните цепь, нажмите «Симуляция» и «Запустить развертку постоянным током». Теперь, когда имеется конечное (уже не бесконечное) внутреннее сопротивление, график тока больше не является плоским при внешнем приложенном напряжении.
Поскольку идеальных источников напряжения и тока не существует в природе, у проектировщика есть три варианта:
- Моделирование всего нелинейного поведения источника. Это часто очень сложно и трудно для понимания.
- Смоделируйте линеаризованное поведение источника вблизи его рабочей точки. Это намного проще и проще для понимания.
- Считать неидеальный источник «достаточно близким» к идеальному (нулевое или бесконечное внутреннее сопротивление).
 Это наименее сложно и легче всего понять.
Это наименее сложно и легче всего понять.
На практике это решение может и должно быть принято инженером. Обычно моделирование как № 2 или № 3 в некотором ограниченном диапазоне, где мы считаем, что эффект «достаточно плоский, чтобы линеаризовать» или «достаточно мал, чтобы его игнорировать», является хорошим решением, если только мы не проектируем намеренно нелинейный источник.
Неидеальные источники напряжения и тока, показанные на этой странице, также называются эквивалентными цепями Thevenin и Norton, которые мы изучим в следующем разделе.
В следующем разделе, «Земля», мы поговорим о концепции единой точки отсчета нулевого напряжения — концепции, которая невероятно широко используется и невероятно сбивает с толку многих новичков.
≡ Оглавление
«
2.3
Напряжение и ток»
2,5
Земля Роббинс, Майкл Ф. Абсолютная электроника: проектирование и анализ практических схем. CircuitLab, Inc., 2021, Ultimateelectronicsbook.com. Доступ . (Авторское право © 2021 CircuitLab, Inc.)
Абсолютная электроника: проектирование и анализ практических схем. CircuitLab, Inc., 2021, Ultimateelectronicsbook.com. Доступ . (Авторское право © 2021 CircuitLab, Inc.)
[РЕШЕНО] — вход/выход/внутреннее сопротивление идеального источника тока
Добро пожаловать на EDAboard.com
Добро пожаловать на наш сайт! EDAboard.com — это международный дискуссионный форум по электронике, посвященный программному обеспечению EDA, схемам, схемам, книгам, теории, документам, asic, pld, 8051, DSP, сети, радиочастотам, аналоговому дизайну, печатным платам, руководствам по обслуживанию… и многому другому. более! Для участия необходимо зарегистрироваться. Регистрация бесплатна. Нажмите здесь для регистрации.
Регистрация Авторизоваться
JavaScript отключен. Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.
- Автор темы судьба м
- Дата начала
- Статус
- Закрыто для дальнейших ответов.
судьба м
Младший член уровня 3
Это из моего учебника: «идеальный источник тока
будет иметь нулевое входное сопротивление. Идеальный источник тока имеет высокое выходное сопротивление
»
Я понимаю, что идеальный источник тока имеет бесконечное ВНУТРЕННЕЕ сопротивление, так что ток выходит из его и перейти к нагрузке, я просто не получаю входное и выходное сопротивление идеального амперметра … Почему входное сопротивление должно быть равно нулю, а выходное высокое? что означает внутреннее и выходное/входное сопротивление идеального амперметра?? Насколько они разные? Я смущен:-?:-?
KlausST
Супер модератор
Привет,
амперметр не является источником тока. Это совершенно разные вещи.
***
Идеальный источник тока имеет бесконечное выходное сопротивление. Но входное сопротивление не представляет интереса, но уж точно оно далеко от нуля.
(источник тока может иметь только два соединения = цепь постоянного тока с дистанционным питанием. Тогда вы не сможете различать входное и выходное сопротивление)
***
Амперметр имеет только два контакта. Поэтому только одно сопротивление. В идеале нулевое сопротивление.
Клаус
шризбф
Расширенный член уровня 5
[
Существует смесь ссылок на источник тока, а затем на амперметр.
Какой запрашивается?
судьба м
Младший член уровня 3
Вы правы, амперметр и источник тока совершенно разные :смеясь:
Почему у ИСТОЧНИКА ТОКА большое выходное сопротивление?
на самом деле это полная часть, которую я не понимаю в своей книге: «Поскольку измерение тока лучше всего делать
с низким сопротивлением, как, например, в амперметре, идеальный источник тока
будет иметь нулевое входное сопротивление. Идеальный источник тока имеет высокое выходное сопротивление
Идеальный источник тока имеет высокое выходное сопротивление
»
судьба м
Младший член уровня 3
источник тока, зря я сказал амперметр 😐 извините
KlausST
Супер модератор
Привет,
Источник тока:
Пример:
* Источник питания: 24 В
* Цепь постоянного тока: 20 мА (обе дают источник тока)
* один светодиод (A) в качестве нагрузки с V_f = 2 В при 20 мА
* другой светодиод (B) в качестве нагрузки с V_f = 10 В при 20 мА
Теперь мы различаем «R» и «r».
R — обычное сопротивление = V / I
r — дифференциальное сопротивление delta_V / delta_I
Со светодиодом (A):
Общее напряжение 24 В, общий ток 20 мА, поэтому общее сопротивление 24 В/20 мА = 1200 Ом
R светодиода: 2В/20мА = 100 Ом.
R цепи постоянного тока: (24В-2В)/20мА = 22В/20мА = 1100 Ом
(Проверка: 100 Ом + 1100 Ом = 1200 Ом. Верно)
Верно)
Со светодиодом (B):
Общее сопротивление 24 В/20 мА = 1200 Ом
R светодиода = 10 В/20 мА = 500 Ом
R цепи постоянного тока: (24 В -10 В) / 20 мА = 14 В/20 мА = 700 Ом Ом
(Проверка: 500 Ом + 700 Ом = 1200 Ом. Верно)
Теперь к дифференциальному сопротивлению «r».
объединяет оба случая «A» и «B»
В случае (A) источник постоянного тока 22 В и 20 мА
В случае (B) источник постоянного тока 14 В и 20 мА
r = (V1 -V2) / ( I1 — I2) = (22 В — 14 В) / ( 20 мА — 20 мА) = 8 В / 0 мА —> бесконечность
***
Истина такова: НЕ «R» источника тока бесконечно, НО «r».
Клаус
судьба м
Младший член уровня 3
Хорошо, спасибо за ответ, но извините, это был не мой вопрос… я думаю, что я расплывчата… например, представьте себе очень простое токовое зеркало КМОП, входное сопротивление которого составляет почти 1/гм, что мало, и выходное сопротивление высокое, я имею в виду перед тем, как нарисовать модель слабого сигнала и рассчитать Rin и Rout, для разработки такого зеркального источника тока, почему меньшее входное сопротивление и большее выходное сопротивление делают его лучшим источником тока? Надеюсь, я смог объяснить лучше. ..
..
д123
Расширенный член уровня 5
Привет,
Не уверен, возможно, не в этом: когда я делаю токовые зеркала из BJT, они не являются практичными источниками тока для моих намерений, в отличие от версии BJT/LED, которая стабильна при различных нагрузках, потому что они не могут хорошо справляться с изменениями нагрузки. . Это будет связано с моей любительской реализацией. Я предполагаю — и, без сомнения, любой, кто правильно понимает теорию, исправит это предположение — высокое выходное сопротивление может быть связано с тем, что ток постоянен на нагрузках? Входное сопротивление минимально, чтобы позволить току течь в источник по мере необходимости без сопротивления? Возможно нет.
KlausST
Супер модератор
Привет,
@OP: пожалуйста, предоставьте схему, чтобы мы могли ее обсудить.
Клаус
костыль
Расширенный член уровня 5
судьба м сказала:
Хорошо, спасибо за ответ, но извините, это был не мой вопрос… я думаю, что я расплывчата… например, представьте себе очень простое токовое зеркало КМОП, входное сопротивление которого составляет почти 1/гм, что мало, и выходное сопротивление высокое, я имею в виду перед тем, как нарисовать модель слабого сигнала и рассчитать Rin и Rout, для разработки такого зеркального источника тока, почему меньшее входное сопротивление и большее выходное сопротивление делают его лучшим источником тока? Надеюсь, я смог объяснить лучше…
Нажмите, чтобы развернуть…
В целях определения, управляемый током источник тока в идеале должен иметь нулевое входное сопротивление и бесконечное выходное сопротивление.
Источник тока, управляемый напряжением, будет иметь нулевое входное сопротивление и бесконечное выходное сопротивление.
Эти идеальные значения таковы, что на источник не будет влиять внешний импеданс того, что питает источник, а выходной ток не будет зависеть от любого импеданса нагрузки.
Единственным местом, где вы найдете такой идеальный источник, является симулятор, такой как Spice.
Практические источники стремятся к этим идеалам, но часто имеют импедансы, значительно отличающиеся от них.
Например, возьмем BJT (транзистор).
Он в основном действует как управляемый током источник тока с входным сопротивлением, возможно, в пару тысяч Ом, и выходным сопротивлением, возможно, в 50 кОм.
Казалось бы, не очень идеально, но достаточно близко для многих приложений.
судьба м
Младший член уровня 3
Почти получилось, всем спасибо!
asdf44
Расширенный член уровня 4
Лично я считаю, что термин импеданс слишком часто используется в сценариях, когда еще пара слов описывает конкретный сценарий или требование. Это особенно неинтуитивно, когда вы пытаетесь преподавать новый предмет, такой как текущий источник.
Это особенно неинтуитивно, когда вы пытаетесь преподавать новый предмет, такой как текущий источник.
Источники тока регулируют ток, а идеальные остаются постоянными независимо от напряжения. Если вы последуете приведенному выше примеру Клауса, это все захваты с «бесконечным импедансом». Бесконечный импеданс означает, что ток не сильно меняется в зависимости от напряжения, точно так же, как бесконечный резистор поддерживает один и тот же ток (почти нулевой) независимо от напряжения.
Что делает этот случай неинтуитивным, так это то, что источники тока имеют ненулевой ток, в то время как бесконечный импеданс (например, резисторы) должен, по-видимому, все время иметь почти нулевой ток (или потребуется бесконечное напряжение, чтобы иметь какой-либо ток). Однако следует уяснить, что импеданс в этом контексте фиксирует реакцию источника на изменить .
костыль
Расширенный член уровня 5
asdf44 сказал:
Лично я считаю, что термин импеданс слишком часто используется в сценариях, когда еще пара слов описывает конкретный сценарий или требование.
Это особенно неинтуитивно, когда вы пытаетесь преподавать новый предмет, такой как текущий источник.
……………….Нажмите, чтобы развернуть…
Вы правы. Простое объяснение может быть более интуитивно понятным для новичка.
Идеальный источник тока поддерживает постоянный выходной ток независимо от импеданса или напряжения выходной нагрузки.
Идеальный источник напряжения поддерживает постоянное выходное напряжение независимо от импеданса или тока выходной нагрузки.
Выходное сопротивление нужно делать для каждого из источников следует из описания.
- Статус
- Закрыто для дальнейших ответов.
-
А
Выходной каскад источника тока
- Автор: AlexandreRibas
- Ответов: 7
Разработка аналоговой схемы
-
п
сопротивление источника при приведенном к входу шуму тока
- Автор: patricku09
- Ответов: 1
Разработка аналоговой схемы
-
Вт
«Идеальный» дифференциальный усилитель в SPICE
- Автор: wes_s01
- Ответов: 1
Разработка аналоговой схемы
-
Е
идеальный входной/выходной импеданс балуна
- Начато опытным путем
- Ответов: 2
Разработка аналоговой схемы
-
С
Источник тока Howland
- Автор s.h.bagherzdeh
- Ответов: 3
Разработка аналоговой схемы
Делиться:
Фейсбук Твиттер Реддит Пинтерест Тамблер WhatsApp Эл. адрес Делиться Ссылка на сайт
Верх
3041 Примечания — C
3041 Примечания — C Эти заметки не могут распространяться или копироваться в любой форме, печатной или электронной, без разрешения. Разрешается устанавливать электронные гипертекстовые ссылки только на эти оригинальные документы.
Эти заметки не могут распространяться или копироваться в любой форме, печатной или электронной, без разрешения. Разрешается устанавливать электронные гипертекстовые ссылки только на эти оригинальные документы. Вернитесь к предыдущей теме, рассеиваемой мощности.
Анализ цепи постоянного тока
В большинстве случаев анализ цепей можно выполнить с помощью нескольких простых правил оценки напряжений и токов. Сначала мы рассмотрим цепи постоянного тока — те цепи, в которых протекают токи и присутствуют напряжения. являются независимыми от времени. Серияи параллельные сопротивления:
Резисторы или другие устройства с двумя выводами (имеющие только два соединения) называются последовательными, если через оба устройства должен протекать один и тот же ток. Сохранение электрического заряда требует, чтобы любой заряд, поступающий в устройство, либо выходил из устройства с той же скоростью, либо накапливался внутри устройства. Заряд не может просто исчезнуть или спонтанно появиться из ниоткуда в наших цепях. Поскольку наша модель резисторов не предусматривает накопление и сохранение заряда (это то, что конденсаторы будут делать для нас), ток, входящий в резистор, должен быть равен току, выходящему из него. Если два резистора соединить один за другим, то один и тот же ток, I , должен протекать через оба. Пример показан на рисунке ниже. В этой цепи появляется символ батареи, источника разности потенциалов или напряжения. Положительный (более высокий потенциал) вывод батареи связан с более длинной из пар чередующихся длинных и коротких линий.
Поскольку наша модель резисторов не предусматривает накопление и сохранение заряда (это то, что конденсаторы будут делать для нас), ток, входящий в резистор, должен быть равен току, выходящему из него. Если два резистора соединить один за другим, то один и тот же ток, I , должен протекать через оба. Пример показан на рисунке ниже. В этой цепи появляется символ батареи, источника разности потенциалов или напряжения. Положительный (более высокий потенциал) вывод батареи связан с более длинной из пар чередующихся длинных и коротких линий. В этом случае падение напряжения на R 1 должно быть
В 1 = IR 1
а падение напряжения на R 2 должен быть
В 2 = ИК 2 .
Сумма падений напряжения должна добавить к общему приложенному напряжению В от батареи:
В = В 1 + В 2 = IR 1 + IR 2 .

Затем ток определяется как I = V / (R 1 + R 2 ) ,
, что является тем же током, который протекал бы, если бы два резистора были заменены одним резистором,
R экв. =R 1 +R 2 .
Этот аргумент можно распространить на любое количество резисторов, соединенных последовательно. Эквивалентное сопротивление будет просто суммой отдельных сопротивлений:
R eq = R 1 + R 2 + R 3 + ….. .
Если два или более резистора (или других устройств) должны иметь одинаковое падение напряжения на них, они включены параллельно. В этом случае через каждый резистор протекает отдельный ток, но токи должны быть распределены так, чтобы
V = I 1 R 1 = I 2 R 2 .
Общий ток I , протекающий через такую конфигурацию, составляет всего
I = I 1 + I 2
I = В/Р 1 + В/Р 2
I = V(1/R 1 + 1/R 2 ).
Такой же общий ток будет течь, если два резистора заменить одним резистором
R eq = (1/R 1 + 1/R 2 ) -1 .
Это правило также легко обобщается на произвольное количество параллельно соединенных резисторов:
1 / R eq = 1/R 1 + 1/R 2 + 1/R 3 + ….
Для параллельных резисторов эквивалентное сопротивление всегда меньше, чем у любого из отдельных резисторов. Обратные сопротивления называются проводимостями, и при параллельном размещении сопротивлений становится доступным несколько путей для проводимости, увеличивая общую проводимость и уменьшая эффективное сопротивление. Меньшие резисторы в такой сети пропускают больший ток.
Последовательное применение правил последовательного и параллельного резисторов может упростить приведенную ниже схему, уменьшив ее до одного эквивалентного сопротивления, что позволит найти общий ток. Зная общий ток, можно рассчитать последовательные падения напряжения, а также токи через отдельные резисторы.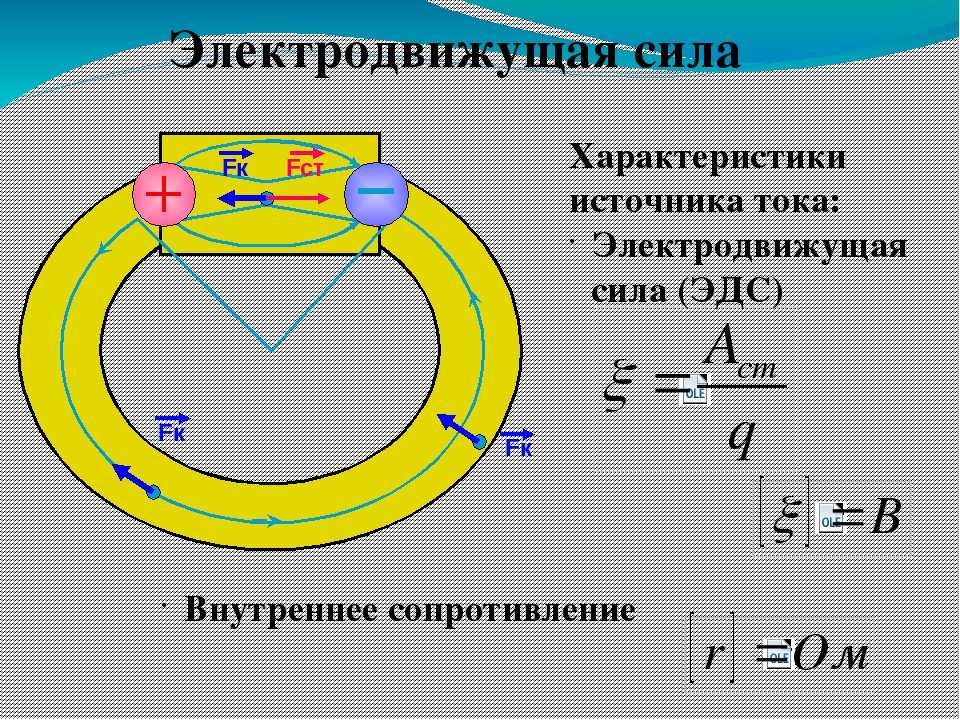
Упрощение здесь.
Правила Кирхгофа
Правила последовательного и параллельного сопротивления достаточны во многих ситуациях для анализа цепей. В некоторых случаях требуются более общие методы. Это могут быть ситуации с несколькими источниками напряжения или даже довольно простые схемы резисторов, которые не подходят для последовательной или параллельной конфигурации. Чтобы справиться с такими ситуациями, можно применить два правила.- Правило узла или соединения Кирхгофа требует, чтобы общий ток, входящий в соединение (место, где два разных провода соединены и заряды могут выбрать направление движения), должен равняться общему току, выходящему из соединения.
- Правило контура Кирхгофа гласит, что сумма падений напряжения на любом замкнутом пути в цепи постоянного тока должна быть равна нулю.
 Мы можем рассматривать правило петель как следствие сохранения энергии. Представьте, что вы следуете за зарядом в поездке по замкнутому пути в цепи. Заряд получает некоторую потенциальную энергию от батареи или другого источника напряжения в цепи. Проходя по цепи, заряд теряет эту энергию, превращая ее в тепловую энергию в резисторах. Когда заряд возвращается к батарее, она теряет именно то количество энергии, которое ей было дано, и ее энергия такая же, как и в начале. Изменения энергии заряда на каждом этапе определяются разностью напряжений на каждом резисторе или батарее, поэтому, если чистое изменение напряжения на пути равно нулю, то и чистое изменение энергии равно нулю.
Мы можем рассматривать правило петель как следствие сохранения энергии. Представьте, что вы следуете за зарядом в поездке по замкнутому пути в цепи. Заряд получает некоторую потенциальную энергию от батареи или другого источника напряжения в цепи. Проходя по цепи, заряд теряет эту энергию, превращая ее в тепловую энергию в резисторах. Когда заряд возвращается к батарее, она теряет именно то количество энергии, которое ей было дано, и ее энергия такая же, как и в начале. Изменения энергии заряда на каждом этапе определяются разностью напряжений на каждом резисторе или батарее, поэтому, если чистое изменение напряжения на пути равно нулю, то и чистое изменение энергии равно нулю.
Чтобы применить эти два правила, можно использовать следующую процедуру:
- Изучите схему, чтобы увидеть, можно ли применить правила последовательного или параллельного соединения для предварительного упрощения какой-либо части схемы. Если возможно, перерисуйте схему с эквивалентными сопротивлениями для этих частей.
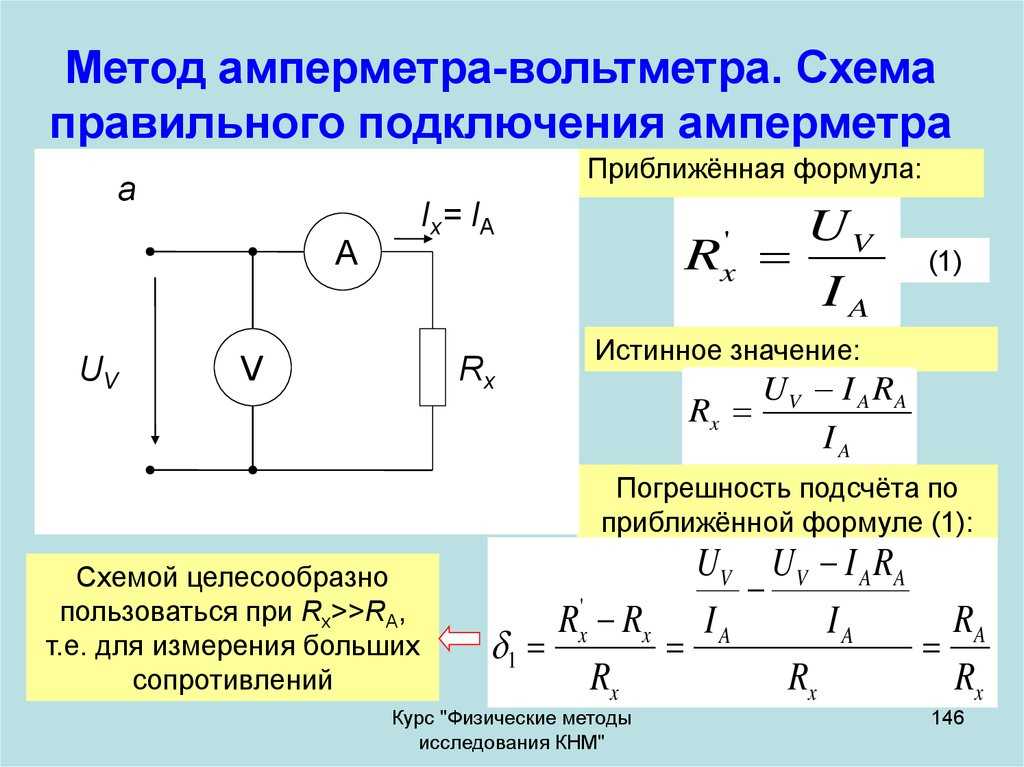
- Назначьте ток каждому резистору в цепи, например, обозначьте резисторы R 1 , R 2 , R 3 ,… и назначьте соответствующий ток I 1 , I 2 , I 3 ,… должны проходить через каждый резистор. Обязательно укажите предполагаемое направление течения тока. Обычно эти токи являются неизвестными величинами, которые вы будете решать.
- Определите узлы или соединения и запишите уравнение узла для каждого соединения.
- Определите замкнутые пути для использования в правиле цикла. Часто проще всего использовать самые маленькие замкнутые контуры в цепи. Запишите уравнения цикла для каждого из этих циклов.
- Определите, сколько у вас неизвестных токов. Затем найдите равное количество независимых уравнений, чтобы использовать их для решения неизвестных токов. Это часто бывает сложно, так как некоторые из уравнений, которые вы записываете, могут быть избыточными, т. е.
 они представляют одну и ту же математическую информацию и не являются независимыми.
они представляют одну и ту же математическую информацию и не являются независимыми.
- Решите уравнения методом грубой силы, матричными методами или с помощью программного обеспечения. Когда токи известны, можно также рассчитать любые падения напряжения. Если вы обнаружите, что получили отрицательный ток, это просто указывает на то, что ток течет в направлении, противоположном тому, которое предполагалось в начале процесса. Нет ничего плохого в том, чтобы с самого начала сделать неверное предположение о том, каким образом ток течет через резистор.
Токовые петли
Более прямой метод применения этих методов известен как метод Максвелла или метод сетки-петли. Это устраняет необходимость записи узловых уравнений (они выполняются автоматически) и систематически предоставляет нужное количество независимых уравнений.- Назначьте ток, I 1 , I 2 , I 3 ,… каждому из наименьших «подконтуров» в схеме.
 Представьте, что ток циркулирует по контуру, не зная об остальной части цепи.
Представьте, что ток циркулирует по контуру, не зная об остальной части цепи.
- Запишите уравнение цикла для каждого подконтура. Имейте в виду, что для некоторых резисторов вы должны учитывать два контурных тока, поскольку через один и тот же резистор будут протекать два разных контурных тока.
- Решите контурные токи, снова используя ваш любимый метод решения нескольких или многих одновременных уравнений. Уравнения, созданные этим методом, автоматически обеспечивают достаточное количество независимых уравнений.
- Используя контурные токи, найдите токи через каждый резистор и соответствующее напряжение падает по мере необходимости.
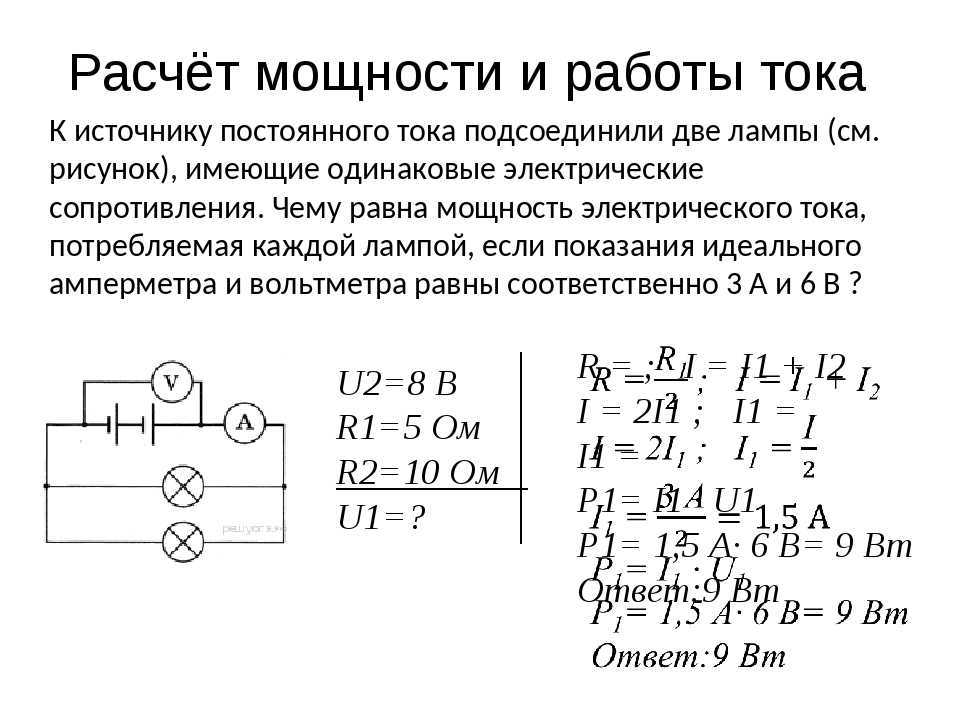 Если вы обнаружите, что трассируете путь, который проходит в направлении, противоположном предполагаемому направлению тока, падение напряжения будет отрицательным (- IR ), поскольку путь, по которому вы следуете, ведет от конца резистора с низким потенциалом (напряжением) к концу резистора с высоким потенциалом, и потенциал не падает, а увеличивается — отрицательное уменьшение ! Аналогичные правила применяются при столкновении с батареями или источниками напряжения на вашем пути. Если путь, по которому вы идете, ведет от клеммы + к клемме -, падение напряжения для контура равно + В , но если ваш путь проходит от клеммы — к +, то соответствующее падение напряжения составляет — В . Кроме того, при использовании метода токовой петли вы должны понимать, что некоторые резисторы будут включать в себя два контурных тока , и соответствующее падение напряжения будет зависеть либо от суммы (оба контурных тока протекают через резистор в одном направлении), либо от разности (контурный ток токи текут в противоположных направлениях) двух петлевых токов.
Если вы обнаружите, что трассируете путь, который проходит в направлении, противоположном предполагаемому направлению тока, падение напряжения будет отрицательным (- IR ), поскольку путь, по которому вы следуете, ведет от конца резистора с низким потенциалом (напряжением) к концу резистора с высоким потенциалом, и потенциал не падает, а увеличивается — отрицательное уменьшение ! Аналогичные правила применяются при столкновении с батареями или источниками напряжения на вашем пути. Если путь, по которому вы идете, ведет от клеммы + к клемме -, падение напряжения для контура равно + В , но если ваш путь проходит от клеммы — к +, то соответствующее падение напряжения составляет — В . Кроме того, при использовании метода токовой петли вы должны понимать, что некоторые резисторы будут включать в себя два контурных тока , и соответствующее падение напряжения будет зависеть либо от суммы (оба контурных тока протекают через резистор в одном направлении), либо от разности (контурный ток токи текут в противоположных направлениях) двух петлевых токов. Может быть полезно вспомнить гравитационный аналог потенциала. Каждый раз, когда ваши путешествия по пути ведут вас «под гору», падение напряжения положительное. Если ваш путь ведет вас в гору, падение напряжения отрицательное. Подъемник аналогичен аккумулятору: если вы поднимаетесь на нем вверх, ваша потенциальная энергия (и потенциал) увеличиваются — «отрицательное уменьшение».
Может быть полезно вспомнить гравитационный аналог потенциала. Каждый раз, когда ваши путешествия по пути ведут вас «под гору», падение напряжения положительное. Если ваш путь ведет вас в гору, падение напряжения отрицательное. Подъемник аналогичен аккумулятору: если вы поднимаетесь на нем вверх, ваша потенциальная энергия (и потенциал) увеличиваются — «отрицательное уменьшение».
Пример метода текущего цикла здесь.
Делитель напряжения
Простая, но очень важная схема — делитель напряжения. В некоторых ситуациях он обеспечивает способ получения небольших стабильных напряжений от источника фиксированного напряжения, который может быть полезен в других частях схемы. Это более важно, поскольку его поведение и анализ обеспечивают прототип для оценки многих других схем. Важно полностью понимать, как анализировать схему и уметь прогнозировать ее поведение в различных предельных случаях, не прибегая к подробным расчетам. Типичный делитель напряжения показан ниже.Выход делителя обычно принимают за падение напряжения на нижнем резисторе.
 (Мы указали, что V = 0 в нижней части схемы, включив символ заземления, общую точку отсчета, которой присвоен потенциал нулевого вольта. Тогда вы можете говорить о напряжении в любой точке цепи. Любой такой примечание. Например, «Напряжение в точке А составляет 5 вольт» на самом деле является утверждением о разности потенциалов между точкой А и точкой в цепи, выбранной в качестве земли. Использование точки заземления в цепи в качестве точки отсчета всегда подразумевается в любом утверждении о напряжениях «в точке» в цепи. Анализ прост. Выполните два простых шага: сначала оцените протекающий ток, а затем найдите падения напряжения, которые должны присутствовать на отдельных резисторах. Ток, который течет по цепи следует из последовательного включения резисторов:
(Мы указали, что V = 0 в нижней части схемы, включив символ заземления, общую точку отсчета, которой присвоен потенциал нулевого вольта. Тогда вы можете говорить о напряжении в любой точке цепи. Любой такой примечание. Например, «Напряжение в точке А составляет 5 вольт» на самом деле является утверждением о разности потенциалов между точкой А и точкой в цепи, выбранной в качестве земли. Использование точки заземления в цепи в качестве точки отсчета всегда подразумевается в любом утверждении о напряжениях «в точке» в цепи. Анализ прост. Выполните два простых шага: сначала оцените протекающий ток, а затем найдите падения напряжения, которые должны присутствовать на отдельных резисторах. Ток, который течет по цепи следует из последовательного включения резисторов: I = V в / ( R 1 + R 2 ).
The voltage drop across the lower resistor is just
V out = IR 2 = V in R 2 / ( R 1 + R 2 ) .
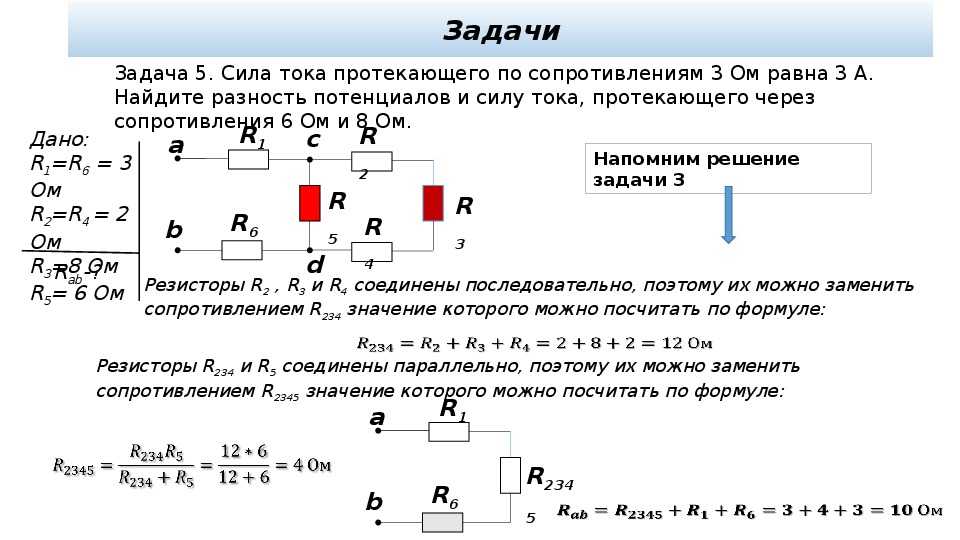 Выходное напряжение всегда меньше входного. По мере уменьшения второго резистора уменьшается и выходное напряжение. Если второй резистор намного больше первого, выходное и входное напряжения практически совпадают. Если резисторы равны, выход равен половине входа. Мы обнаружим, что анализ делителя напряжения неоднократно оказывается полезным при анализе цепей переменного тока и фильтров, смещении транзисторных схем и при настройке коэффициентов усиления в цепях с использованием операционных усилителей.
Выходное напряжение всегда меньше входного. По мере уменьшения второго резистора уменьшается и выходное напряжение. Если второй резистор намного больше первого, выходное и входное напряжения практически совпадают. Если резисторы равны, выход равен половине входа. Мы обнаружим, что анализ делителя напряжения неоднократно оказывается полезным при анализе цепей переменного тока и фильтров, смещении транзисторных схем и при настройке коэффициентов усиления в цепях с использованием операционных усилителей.
Источники напряжения и тока
Идеальный источник напряжения — это тот, который обеспечивает постоянное напряжение, независимое от требуемого от него тока. Такого устройства не существует. Каждый реальный источник напряжения ограничен максимальным током, который он может обеспечить. В простой цепи с переменным сопротивлением нагрузки требуемый ток увеличивается по мере уменьшения сопротивления нагрузки. Идеальный источник напряжения будет поддерживать постоянное напряжение на нагрузке при любых условиях. Подаваемый ток неограниченно возрастает по мере уменьшения сопротивления. Такой источник может подавать на резистор бесконечную мощность, подавая фиксированное напряжение и постоянно увеличивающийся ток по мере уменьшения сопротивления нагрузки, поскольку Р=IV .
Подаваемый ток неограниченно возрастает по мере уменьшения сопротивления. Такой источник может подавать на резистор бесконечную мощность, подавая фиксированное напряжение и постоянно увеличивающийся ток по мере уменьшения сопротивления нагрузки, поскольку Р=IV . На практике напряжение будет падать по мере увеличения тока, потребляемого от источника напряжения. Сначала уменьшение будет незначительным, но в какой-то момент напряжение на нагрузке станет значительно меньше номинального значения источника напряжения. Неидеальное поведение часто моделируют, предполагая наличие дополнительного сопротивления в самом источнике напряжения. Это сопротивление по-разному называют внутренним сопротивлением, сопротивлением источника или выходным сопротивлением. Тогда модель реального источника напряжения представляет собой просто идеальный источник напряжения, включенный последовательно с сопротивлением R из . (Эта величина часто обозначается как Z из .
 Z обычно используется для обозначения импеданса, обобщения идеи сопротивления, которое мы подробно рассмотрим при обсуждении цепей переменного тока.)
Z обычно используется для обозначения импеданса, обобщения идеи сопротивления, которое мы подробно рассмотрим при обсуждении цепей переменного тока.) В результате любой нагрузочный резистор, подключенный к источнику, фактически образует делитель напряжения. Ток, который будет протекать через нагрузку, равен
I = В / ( R out + R нагрузка ).
Это имеет максимальное значение V/R out , что происходит, когда выходные провода закорочены или «закорочены» вместе сопротивлением нагрузки, равным 0. Когда нагрузка представляет собой разомкнутую цепь (бесконечное сопротивление нагрузки), ток не течет, а выходное напряжение такое же, как идеальное напряжение источника. Всякий раз, когда нагрузка потребляет какой-либо ток, выходное напряжение должно быть ниже идеального значения, поскольку падение напряжения будет равно IR 9.0232 из на внутреннем последовательном сопротивлении, оставляя падение В — IR из на выходе.
 Чем меньше значение R из , тем более идеальным является источник напряжения. Если сопротивление нагрузки намного больше, чем внутреннее сопротивление источника, источник кажется почти идеальным. Однако если сопротивление нагрузки сравнимо с внутренним сопротивлением или меньше его, необходимо учитывать неидеальность источника.
Чем меньше значение R из , тем более идеальным является источник напряжения. Если сопротивление нагрузки намного больше, чем внутреннее сопротивление источника, источник кажется почти идеальным. Однако если сопротивление нагрузки сравнимо с внутренним сопротивлением или меньше его, необходимо учитывать неидеальность источника.
Источники тока обеспечивают постоянный ток через нагрузку, не зависящий от сопротивления нагрузки. Идеальный источник тока будет работать, даже если сопротивление нагрузки станет очень большим. Это потребует постоянно возрастающего напряжения, генерируемого источником тока. На практике это не так. Реальные источники тока ограничены по напряжению, которое они могут генерировать. Этот предел называется напряжением соответствия. Когда этот предел достигнут, источник тока действует как источник напряжения.
Неидеальное поведение источника тока можно смоделировать, подключив резистор параллельно идеальному источнику тока, как показано на рисунке. В качестве
R нагрузка увеличивается, больший ток будет протекать через внутренний резистор вместо нагрузки. Чтобы источник тока был полезным, внутреннее сопротивление должно быть большим по сравнению с сопротивлением нагрузки, которое будет встречаться при использовании.
В качестве
R нагрузка увеличивается, больший ток будет протекать через внутренний резистор вместо нагрузки. Чтобы источник тока был полезным, внутреннее сопротивление должно быть большим по сравнению с сопротивлением нагрузки, которое будет встречаться при использовании.
Эквивалентные схемы
Сложные двухполюсные (имеющие два провода для подключения нагрузки) сети, построенные из источников напряжения и резисторов, можно упростить до двух элементов эквивалентной схемы. Здесь следует упомянуть два типа эквивалентных схем: эквивалентные схемы Thevenin и Norton, в которых используются источники напряжения и тока соответственно.
Эквивалентная схема Thevenin состоит из одного идеального источника напряжения, последовательно соединенного с одним резистором. Эквивалентное напряжение Thevenin, В TH , находится путем расчета напряжения между двумя выходными соединениями, когда сопротивление нагрузки бесконечно, т. е. «напряжения холостого хода». Сопротивление Thevenin, R TH , находится из
Сопротивление Thevenin, R TH , находится из
R TH = V TH / I КОРОТКИЙ
где I КОРОТКОЕ — ток, протекающий через нагрузку, когда сопротивление нагрузки уменьшается до 0, т.е. выход закорочен.
Эквивалентная схема Нортона заменяет сеть одним идеальным источником тока, подключенным параллельно с одним резистором. Ток Нортона, I N , является выходным током короткого замыкания ( R нагрузка = 0). Сопротивление Нортона находится по напряжению холостого хода, V open (infinite R load ):
R N = V open / I N = V TH / I N = Р ТХ .
Обратите внимание, что эти эквивалентные схемы аналогичны нашим моделям для реальных источников напряжения и тока. Хотя нам не нужно часто оценивать эти эквивалентные схемы, стоит помнить, что они могут служить отправной точкой для моделирования еще более сложных схем, которые могут содержать более сложные компоненты, в том числе
транзисторы и операционные усилители, с которыми мы столкнемся позже.
Хотя нам не нужно часто оценивать эти эквивалентные схемы, стоит помнить, что они могут служить отправной точкой для моделирования еще более сложных схем, которые могут содержать более сложные компоненты, в том числе
транзисторы и операционные усилители, с которыми мы столкнемся позже.
Перейдите к следующей теме, Цепи переменного тока.
Источники напряжения и тока — вопросы и ответы по теории сетей
Этот набор вопросов и ответов с множественным выбором по теории сетей (MCQ) посвящен «Источникам напряжения и тока».
1. Выберите неверное утверждение из следующих.
а) Катушка индуктивности — пассивный элемент
б) Источник тока — активный элемент
в) Резистор — пассивный элемент
г) Источник напряжения — пассивный элемент
View Answer
Ответ: b
Объяснение: Источники энергии (источники напряжения или тока) — это активные элементы, способные подавать питание на какое-либо внешнее устройство.
2. Чтобы пренебречь источником напряжения, клеммы на источнике должны быть ___________
Чтобы пренебречь источником напряжения, клеммы на источнике должны быть ___________
a) заменены катушкой индуктивности
b) закорочены
c) заменены некоторым сопротивлением
d) разомкнуты
Просмотреть ответ
Ответ: b
Объяснение: Если источником напряжения пренебречь, его можно заменить просто с помощью провода, т. е. его следует замкнуть накоротко.
3. Источник напряжения и напряжение на клеммах могут быть связаны как ___________
а) напряжение на клеммах выше ЭДС источника
б) напряжение на клеммах равно ЭДС источника
в) напряжение на клеммах всегда ниже ЭДС источника
г) напряжение на клеммах не может превышать э.д.с. источника
View Answer
Ответ: c
Объяснение: Практический источник напряжения может быть представлен сопротивлением, включенным последовательно с источником. Следовательно, на резисторе будет некоторое падение напряжения, а напряжение на клеммах всегда ниже, чем ЭДС источника.
объявление
объявление
4. Идеальные источники тока имеют ___________
Идеальные источники тока имеют ___________
а) нулевое внутреннее сопротивление
б) малое значение напряжения
в) большое значение тока
г) бесконечное внутреннее сопротивление
Посмотреть ответ
Ответ: d
Объяснение: Для идеальных источников тока ток полностью не зависит от напряжения и имеет бесконечное внутреннее сопротивление.
5. В сети, состоящей из линейных резисторов и идеального источника напряжения, если номинал резисторов удвоить, то напряжение на каждом резисторе ___________
а) увеличится в четыре раза
б) останется неизменной
в) удвоится
г) уменьшится вдвое
Просмотреть ответ
Ответ: б
Пояснение: Даже при изменении номиналов линейных резисторов напряжение остается постоянным в случае идеального источника напряжения.
6. Практический источник тока также может быть представлен как ___________
а) сопротивление, параллельное идеальному источнику напряжения
б) сопротивление, параллельное идеальному источнику тока
в) сопротивление, включенное последовательно с идеальным источником тока
d) ни один из упомянутых
View Answer
Ответ: b
Объяснение: Фактический источник тока может быть представлен резистором, подключенным параллельно с идеальным источником тока.
7. Практический источник напряжения также может быть представлен как ___________
а) сопротивление, включенное последовательно с идеальным источником тока
б) сопротивление, включенное последовательно с идеальным источником напряжения
в) сопротивление, включенное параллельно идеальному источнику напряжения
г) ни один из упомянутых
Посмотреть ответ
Ответ: b
Объяснение: Практический источник напряжения может быть представлен резистором, включенным последовательно с идеальным источником напряжения.
объявление
8. Источник постоянного напряжения ___________
а) активный и двусторонний
б) пассивный и двусторонний
в) активный и односторонний
г) пассивный и односторонний
Просмотреть Ответ
Ответ: в
Пояснение: Источник напряжения активным элементом и является односторонним.
9. Что из следующего верно в отношении идеального источника напряжения?
а) нулевое сопротивление
б) малая ЭДС
в) большая ЭДС
г) бесконечное сопротивление
объявление
10.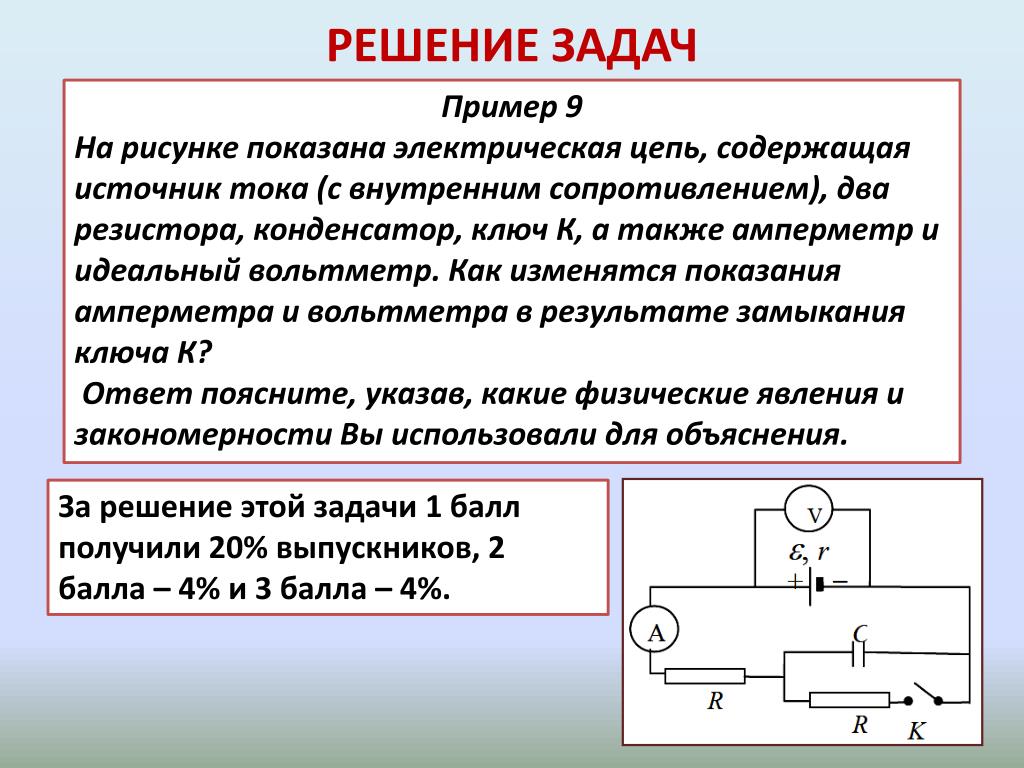 Зависимый источник ___________
Зависимый источник ___________
а) может быть источником тока или источником напряжения
б) всегда является источником напряжения
в) всегда является источником тока
г) ни один из упомянутых
Просмотреть ответ
Ответ: a
Объяснение: Зависимые источники могут быть либо источниками тока, либо источниками напряжения.
11. При некотором начальном изменении при t = 0+ конденсатор будет действовать как ___________
а) разомкнутая цепь
б) короткое замыкание
в) источник тока
г) источник напряжения
Посмотреть ответ
Ответ: г
Объяснение: При t=0+ конденсатор начинает заряжаться до определенного напряжения и действует как источник напряжения.
12. Если источником тока пренебречь, клеммы на источнике ___________
a) заменяются сопротивлением источника
b) разомкнутая цепь
c) заменен конденсатором
d) закорочен
View Answer
Ответ: b
Объяснение: Поскольку идеальный источник тока имеет бесконечное сопротивление, им можно пренебречь, разомкнув клеммы.
13. Источник постоянного тока подает электрический ток силой 200 мА на нагрузку 2 кОм. Когда нагрузка изменится на 100 Ом, ток нагрузки будет ___________
а) 9 мА
б) 4 А
в) 700 мА
г) 12 А
Посмотреть ответ
Ответ: б
Пояснение: По закону Ома сопротивление обратно пропорционально Текущий.
14. Источник напряжения с напряжением холостого хода 200 В и внутренним сопротивлением 50 Ом эквивалентен источнику тока ___________
а) 4 А при 50 Ом параллельно
б) 4 А при 50 Ом последовательно
в) 0,5 А при 50 Ом параллельно
d) ни один из упомянутых
Просмотреть ответ
Ответ: a
Пояснение: Источник напряжения с последовательным сопротивлением можно заменить источником тока с параллельным сопротивлением.
15. Источник напряжения 300 В имеет внутреннее сопротивление 4 Ом и питает нагрузку с таким же сопротивлением. Мощность, потребляемая нагрузкой, равна?
a) 1150 Вт
b) 1250 Вт
c) 5625 Вт
d) 5000 Вт
Посмотреть ответ
Ответ: c
Объяснение: Потребляемая мощность = I 2 R.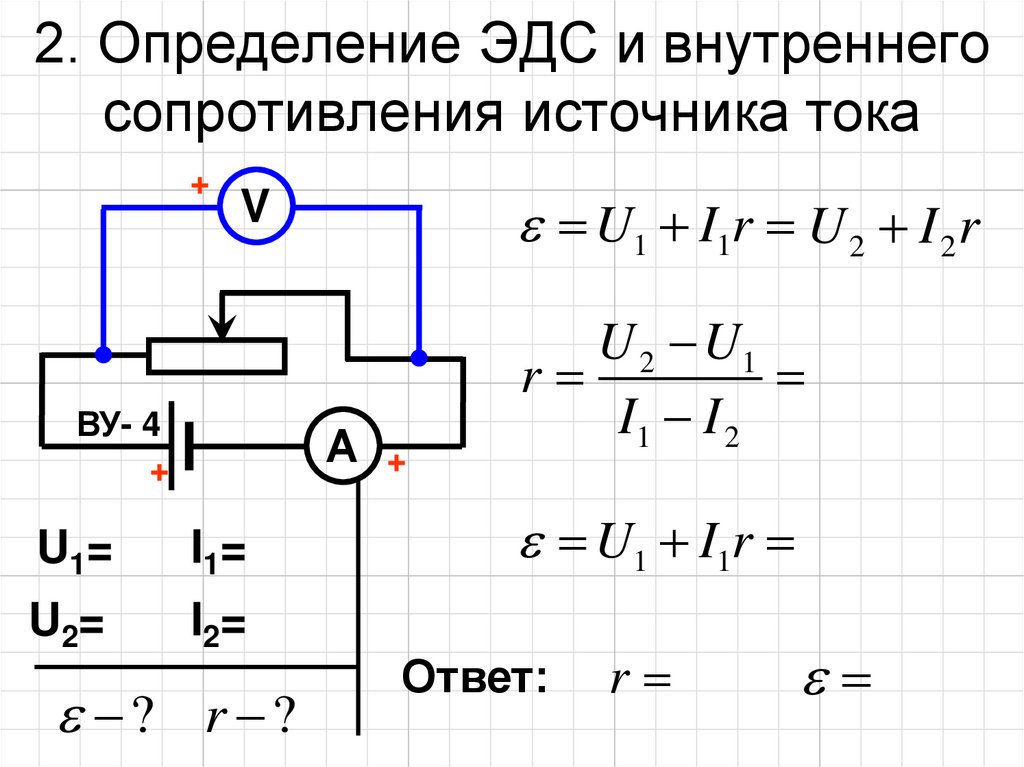
Sanry Education Series Сетевая теория.
Чтобы попрактиковаться во всех областях теории сетей, здесь есть полный набор из более чем 1000 вопросов и ответов с несколькими вариантами ответов .
Следующие шаги:
- Получите бесплатный сертификат о заслугах в области теории сетей
- Примите участие в конкурсе сертификации по теории сетей
- Стать лучшим игроком в теории сетей
- Сдайте тесты по теории сетей
- Практические тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
- Пробные тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
реклама
реклама
Подпишитесь на наши информационные бюллетени (тематические). Участвуйте в конкурсе сертификации Sanfoundry, чтобы получить бесплатный Сертификат отличия. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Ютуб | Телеграмма | Линкедин | Инстаграм | Фейсбук | Твиттер | Пинтерест
Маниш Бходжасиа, ветеран технологий с более чем 20-летним стажем работы в Cisco и Wipro, является основателем и техническим директором компании Sanfoundry . Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms.
Оставайтесь на связи с ним в LinkedIn.
Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms.
Оставайтесь на связи с ним в LinkedIn.
Подпишитесь на его бесплатные мастер-классы на Youtube и технические обсуждения в Telegram SanfoundryClasses.
Идеальные элементы и источники | Spinning Numbers
Цепь состоит из элементов . Обычно по крайней мере один элемент представляет собой источник , который обеспечивает энергию, чтобы заставить схему что-то делать. Источник соединяется с одним или несколькими компонентами , которые делают что-то полезное.
Мы определяем источники и компоненты как идеальные математические абстракции.
Следующая статья посвящена реальным элементам схемы, приближенным к идеальному варианту.
Автор Вилли Макаллистер.
Содержимое
- Идеальные источники
- Источник постоянного напряжения
- Источник переменного напряжения
- Источник постоянного тока
- Резистор
- Закон Ома
- Мощность резистора
- Конденсатор
- Мощность и энергия в конденсаторе
- Индуктор
- Мощность и энергия в индукторе
Начните с некоторых определений,
Элементы являются источниками или компонентами.
Источники обеспечивают питание цепи. Существует два основных типа:
- Источник напряжения
- Источник тока
Компоненты бывают трех основных типов, каждый из которых характеризуется различным соотношением тока и напряжения:
- Резистор
- Конденсатор
- Индуктор
Эти источники и компоненты имеют две клеммы или точки подключения. Неудивительно, что они называются $2$-терминальными элементами .
Позже мы узнаем о компонентах (транзисторах), которые имеют более двух выводов.
Идеальные источники
Источник постоянного напряжения
Два общих символа для источников постоянного напряжения выглядят следующим образом:
Символ слева — это батарея. Длинная горизонтальная линия представляет собой положительную клемму аккумулятора, а короткая горизонтальная линия — отрицательную клемму. Иногда батарея не помечена знаками $+$ и $-$, так что эту длинную и короткую линию нужно запомнить.
Символ батареи напоминает о самой первой батарее, изобретенной Вольтой. Стопка чередующихся разнородных металлических дисков,
Символ в виде круга обозначает какой-либо другой источник напряжения, блок питания или генератор. Лучше всего рисовать знаки $+$ и $-$ внутри круга, а не снаружи. Таким образом, они не будут перепутаны с другими метками напряжения, добавленными на схему позже.
Идеальный источник постоянного напряжения имеет фиксированное выходное напряжение, не зависящее от тока,
График зависимости тока от напряжения для источника постоянного напряжения. Ток определяется компонентами, подключенными к источнику напряжения.
Уравнение $i$-$v$ для источника постоянного напряжения: $v = \text V$, где $\text V$ — некоторое постоянное напряжение, например $v=3\,\text V$. Обратите внимание, что ток не упоминается в уравнении $i$-$v$.
Очевидным именем переменной для напряжения является $v$, но также часто используется переменная $e$, связанная с напряжением.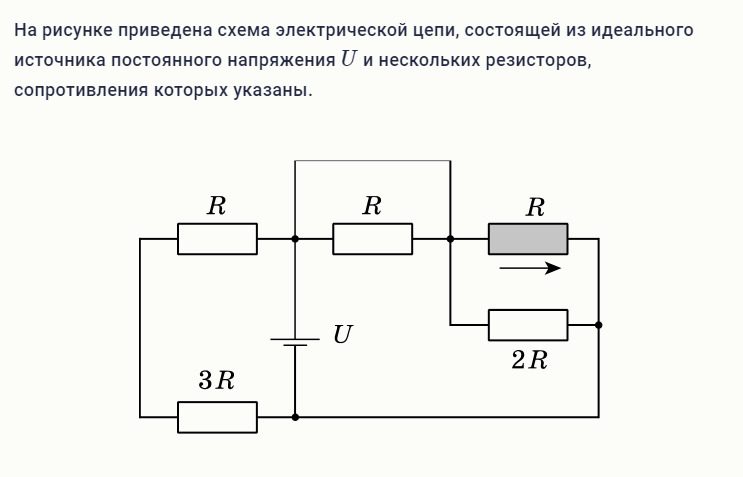 Это происходит от термина «электродвижущая сила» или ЭДС . Технически ЭДС относится к напряжению, создаваемому генератором, но $e$ используется как общий термин для обозначения напряжения. Вы можете использовать либо $v$, либо $e$, и все поймут, что вы имеете в виду.
Это происходит от термина «электродвижущая сила» или ЭДС . Технически ЭДС относится к напряжению, создаваемому генератором, но $e$ используется как общий термин для обозначения напряжения. Вы можете использовать либо $v$, либо $e$, и все поймут, что вы имеете в виду.
График выше является примером системы координат, которую мы часто используем. Независимой переменной по горизонтальной оси является напряжение, $v$. Зависимая переменная на вертикальной оси — текущая, $i$. Это называется графиком $i$-$v$.
Источник переменного напряжения
Источник переменного напряжения генерирует известное напряжение как функцию времени,
График зависимости напряжения от времени для источника переменного напряжения.
Определяющее уравнение для источника переменного напряжения: $v = v(t)$. Напряжение может быть любым изменяющимся во времени напряжением. Примеры: синусоидальная волна, одиночный импульс напряжения или повторяющаяся прямоугольная волна.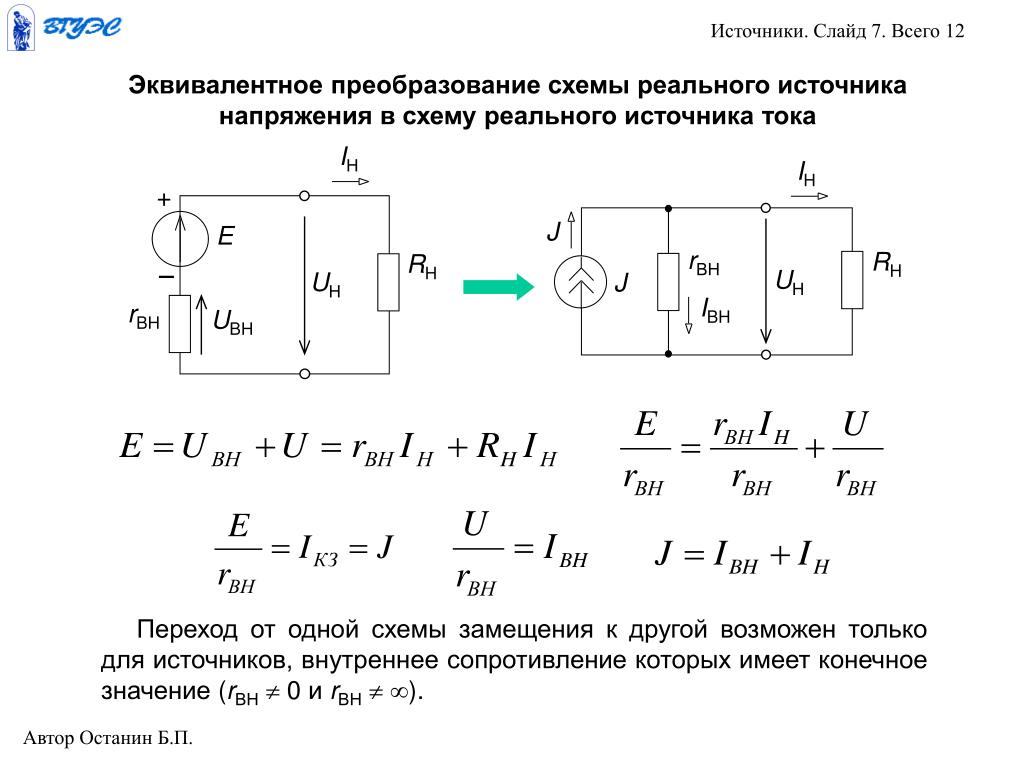 Еще
Еще
Ступенчатое напряжение
Прямоугольная волна
Треугольная волна
Пилообразная волна
Символ источника переменного напряжения выглядит так или в некоторых вариациях,
Загогулина внутри круга указывает на генератор синусоидальной волны. Вы столкнетесь с различными версиями этого символа для других форм сигналов.
Если в цепи требуется большой ток, идеальная математическая модель источника напряжения это обеспечивает. Конечно, в реальной жизни так не бывает. Когда вы моделируете цепь, вы можете случайно увидеть гигантские токи. Компьютер не возражает против тока в миллионы ампер, это просто число внутри компьютера, но, вероятно, это не то, что вы хотели.
Источник постоянного тока
Символ источника постоянного тока выглядит следующим образом:
Стрелка указывает направление протекания тока.
Идеальный источник постоянного тока имеет фиксированный выходной ток, не зависящий от напряжения, подаваемого на его клеммы.
График зависимости тока от напряжения для источника постоянного тока. Напряжение определяется компонентами, подключенными к источнику тока.
Уравнение для источника постоянного тока: $i = \text I$, где $\text I$ — постоянный выходной ток, например, $i=2\,\text{мА}$.
Обратите внимание, что в уравнении $i$-$v$ не упоминается напряжение. Ток один и тот же независимо от того, какое напряжение появляется на источнике. Для идеального источника тока напряжение на клеммах — это то, что требуется для выталкивания постоянного тока, даже если это напряжение гигантское.
Когда мы строим реальные источники тока, конечно, диапазон операций значительно ограничен по сравнению с абстракцией идеального источника тока.
Идея источника тока довольно странная, но важная.
реальные источники тока Аккумулятор имеет постоянное напряжение и переменный ток. Вот почему это хороший реальный пример идеального источника напряжения. Источник тока, наоборот, источник постоянного тока и переменного напряжения.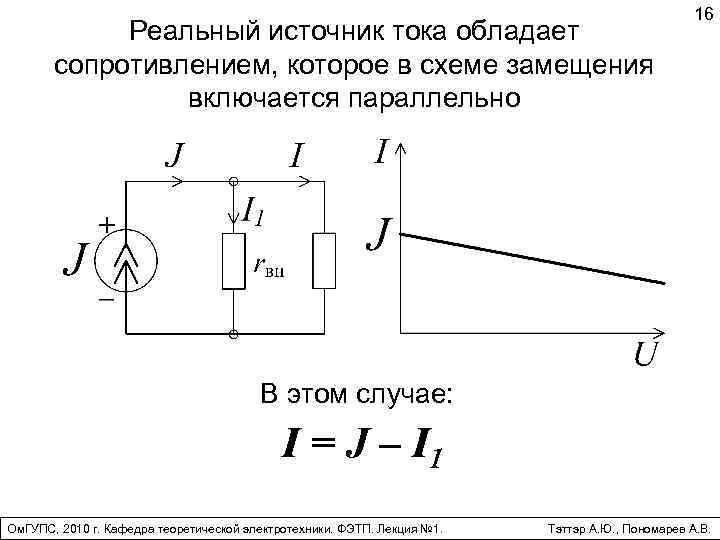 Они менее привычны, потому что вы не можете пойти в продуктовый магазин и купить источник тока.
Они менее привычны, потому что вы не можете пойти в продуктовый магазин и купить источник тока.
Можно построить источник тока как достаточно сложный прибор.
Источники тока часто используются при моделировании транзисторов в компьютерном моделировании. Область поведения транзистора очень похожа на источник тока.
Это обозначение транзистора MOSFET,
Это график $i$-$v$ МОП-транзистора. Горизонтальная ось представляет собой напряжение между клеммой стока и клеммой истока. Вертикальная ось — это ток, втекающий в Сток и выходящий из Истока. Каждая синяя линия представляет различное напряжение затвора, $\text V_{\text{GS}}$.
Статья в Википедии о МОП-транзисторах.
Обратите внимание, что синие линии справа от красной кривой горизонтальны — область, отмеченная цифрой 9.0049 область насыщения . В этом диапазоне напряжений стока ток постоянен при любом значении $\text V_{\text{DS}}$.
В области насыщения МОП-транзистор действует как источник тока. Мы используем идеальный источник тока в имитационной модели полевого МОП-транзистора, чтобы создать такое горизонтальное поведение.
Мы используем идеальный источник тока в имитационной модели полевого МОП-транзистора, чтобы создать такое горизонтальное поведение.
Имитационная модель полевого МОП-транзистора включает источник тока , управляемый напряжением (ромбовидная форма). Его ток определяется напряжением, найденным в другом месте модели.
Резистор
Два символа резистора выглядят следующим образом:
В США и Японии символом резистора является зигзаг. В Великобритании, Европе и других частях мира резистор нарисован в виде коробки.
Закон Ома
Напряжение на резисторе прямо пропорционально протекающему через него току.
$\large v = \text R \, i$
Это соотношение известно как закон Ома . Вы будете использовать это уравнение много в вашей работе со схемами. Это самое важное уравнение в электронике.
$\text R$ представляет сопротивление резистора. Мы измеряем сопротивление в единицах Ом , обозначаемых греческой заглавной буквой Омега, $\Omega$.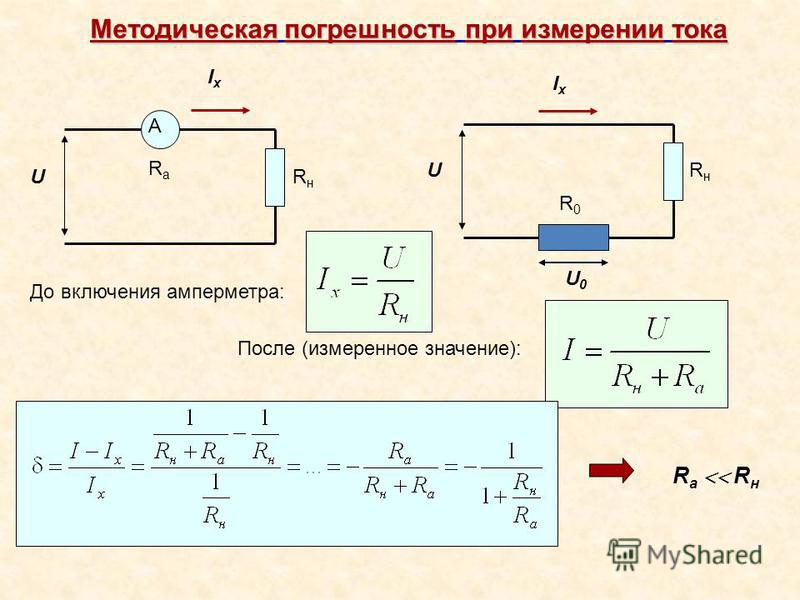 $\text R$ действует как константа пропорциональности в законе Ома.
$\text R$ действует как константа пропорциональности в законе Ома.
Вот график $i$-$v$ для резистора. Линия на графике представляет собой закон Ома, решенный для тока,
$i = \dfrac{1}{\text R}\,v\qquad$ Наклон линии равен $1/\text R$.
График зависимости тока от напряжения для резистора.
Каково сопротивление этого конкретного резистора?
показать ответНам нужно вычислить наклон линии. Один из способов определить линию — найти две точки. Давайте сделаем это.
Линия резистора всегда проходит через начало координат , что дает нам одну точку на линии, $(0, 0)$.
Вы можете выбрать любую другую точку на линии, чтобы найти наклон. Оглянитесь вокруг и выберите легкое. Выберем точку вверху справа, $(v = 3\,\text V, i = 4\,\text{mA})$.
Таким образом, наклон равен $\dfrac{4\,\text{мА} — 0}{3\,\text V -0}$.
Это означает, что $\text R$ равно 1/наклон или
$\text R = \dfrac{3\,\text V}{4\,\text{мА}} = 750 \,\Omega$
Закон Ома можно записать несколькими способами. Вы будете использовать все эти формы все время,
Вы будете использовать все эти формы все время,
$v = i\,\text R \qquad\qquad i = \dfrac{v}{\text R} \qquad\qquad \text R = \dfrac{v} {i}$
, помня закон ОмаВот два совета для запоминания закона Ома,
Способ, которым я запомнил закон Ома, состоял в том, чтобы запомнить одну форму. я повторил
$e = i\text R \qquad e \, i\,\text R \qquad e \, i\,\text R \qquad e\, i\,\text R \quad…$
, пока он не въелся в мой мозг, как мантра. (оба символа $e$ и $v$ используются для обозначения напряжения). Мне нравится звук $e$ в моей мантре.)
Произнеся мантру, я быстро вывел другие формы с помощью простой ментальной алгебры.
Этот рисунок — еще один способ запомнить закон Ома,
Наведите указательный или большой палец на нужную переменную $(v$, $i$ или $\text R)$ и прочитайте уравнение. Например, чтобы найти $\text R$, закройте $\text R$ и прочитайте $v/i$. Чтобы найти $v$, закройте $v$ и прочитайте $i\,\text R$.
Выберите метод, который поможет вам запомнить закон Ома.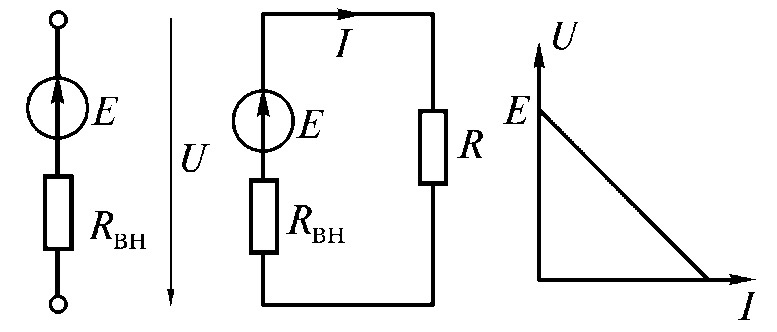 Это стоит усилий.
Это стоит усилий.
Закон Ома стоит запомнить.
Мощность резистора
Мощность рассеивается резистором, когда через него протекает ток.
что такое мощность?Мощность
Power — это скорость , энергия скорости $(U)$ преобразуется или передается.
Физик определяет мощность самым общим образом,
$p = \dfrac{dU}{dt}$
$U$ — энергия, измеряемая в джоулях. Джоуль — это количество энергии, затрачиваемое на перемещение тела с силой в один ньютон на расстояние в один метр.
Мощность — это скорость изменения энергии, измеряемая в джоулях в секунду.
$1$ джоуль также известен как $1$ ватт .
Электроэнергия
Электричество несет энергию. Как мы можем выразить $dU/dt$ в более привычных терминах?
Напряжение – это энергия, передаваемая на единицу заряда, $v = dU/dq$.
Ток – скорость потока заряда, $i = dq/dt$.
Разобьем $dU/dt$ и представим мощность как
$p = \dfrac{dU}{dt} = \left (\dfrac{dU}{dq}\right ) \cdot \left (\dfrac{dq}{dt}\right ) = \left (v \right ) \cdot \left (i \right )$
Таким образом, в электрических системах мощность является произведением напряжения и силы тока,
$p = v \,i $
Энергичные электроны, движущиеся через резистивный материал, сталкиваются с атомами материала.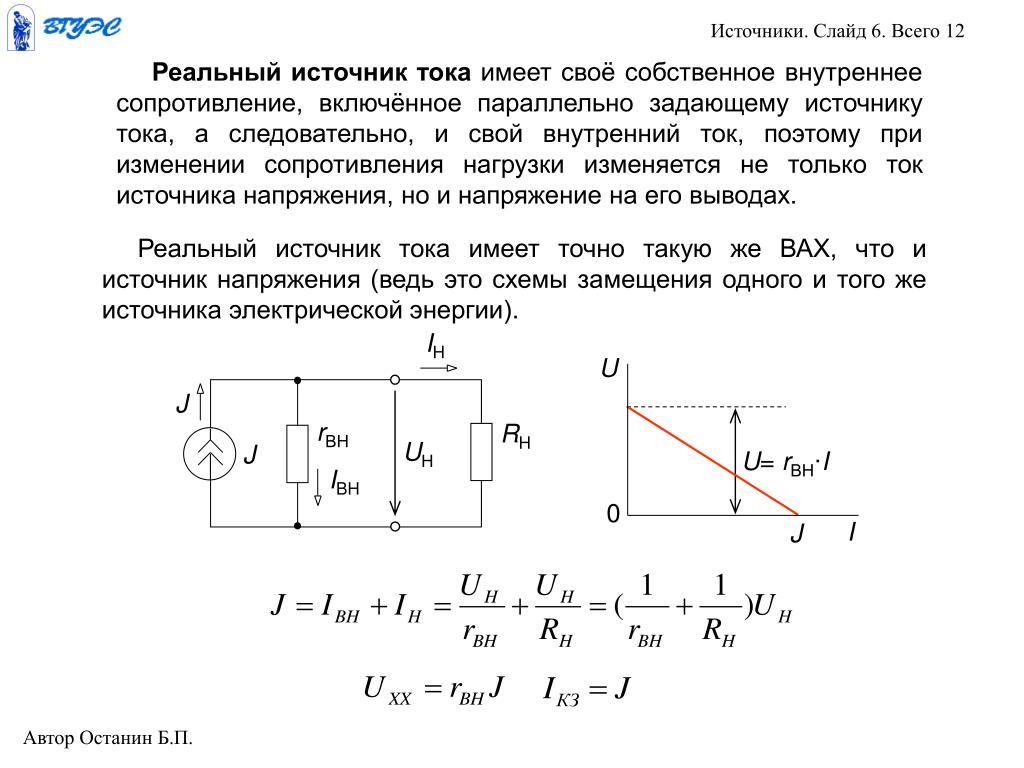 2$. Если вы уменьшите напряжение или ток в 2 раза, мощность снизится в 4 раза. 92$, поэтому снижение тока в два раза также снижает мощность в 4 раза.
2$. Если вы уменьшите напряжение или ток в 2 раза, мощность снизится в 4 раза. 92$, поэтому снижение тока в два раза также снижает мощность в 4 раза.
В целом Аарон и Бет уменьшили мощность в $4\times4 = 16$.
Конденсатор
Основное уравнение, описывающее конденсатор, связывает заряд $\text Q$ на конденсаторе с напряжением $\text V$ на конденсаторе.
$\text Q = \text C\,\text V$
Константа пропорциональности $\text C$ равна емкости . Единицей емкости является фарад $(\text F)$, и из приведенного выше уравнения видно, что $1 \,\text{фарад} = 1 \,\text{кулон}/\text{вольт}$
узнать больше о Q = CVВ этом видео вы узнаете, как устроен конденсатор, и посмотрите, как получается $\text Q = \text C\,\text V$.
Если заряд $\text Q$ может двигаться, у нас есть термин для этого: движущийся заряд называется текущий . Ток – это скорость изменения заряда во времени,
$i = \dfrac{dq}{dt}$
Используя идею о том, что движущийся заряд является током, вернемся к $\text Q = \text C\,\ текст V$ и возьмем производную от обеих сторон по времени и посмотрим, что мы получим. (Когда я начинаю говорить о том, что вещи меняются со временем, я переключаюсь с имен переменных в верхнем регистре на строчные: $q$, $i$ и $v$.)
(Когда я начинаю говорить о том, что вещи меняются со временем, я переключаюсь с имен переменных в верхнем регистре на строчные: $q$, $i$ и $v$.)
$\dfrac{dq}{dt} = \text C \, \dfrac{dv}{dt}$
и мы получаем уравнение, согласно которому ток в конденсаторе прямо пропорционален времени скорость изменения напряжения на конденсаторе,
$i = \text C \, \dfrac{dv}{dt}$
Это уравнение отражает зависимость $i$-$v$ для конденсаторов. Это также говорит нам о том, что электрические цепи могут меняться с течением времени.
что означает $d$?$d$ в $dq/dt$ — это запись из исчисления. $d$ означает дифференциал .
$d$ означает «небольшое изменение в …». Выражение $dt$ означает крошечное изменение во времени .
Когда вы видите $d$ в соотношении, таком как $dv/dt$, это означает «мизерное изменение $v$ (напряжения) на каждое крошечное изменение $t$ (времени)».
Выражение типа $dv/dt$ называется производным. Это то, что вы изучаете в дифференциальном исчислении.
Это то, что вы изучаете в дифференциальном исчислении.
Некоторые обозначения конденсатора выглядят следующим образом:
Версия с изогнутой линией используется для конденсаторов, у которых требуется, чтобы один вывод имел положительное напряжение по отношению к другому выводу («электролитические» конденсаторы). Изогнутая линия указывает на клемму, на которой должно быть более отрицательное напряжение. 9{\,T} i\,dt$
$-\infty$ нижний предел интеграла предполагает, что напряжение конденсатора в момент времени $T$ зависит не только от тока конденсатора в данный момент, но и от всей прошлой истории тока. Это было давно, поэтому мы часто пишем этот интеграл, начиная с некоторого известного напряжения $v_0$ в некоторое известное время, например $t=0$, а затем отслеживаем изменения оттуда.
$\int$ — это исчисление. Зацикленный символ $\int$ тоже из исчисления. Это интегральный признак. Принцип работы аналогичен символу суммирования $\Sigma$ (заглавная греческая буква сигма).
В приведенном выше уравнении знак интеграла говорит вам сложить произведение тока, $i$, на крошечный интервал времени, $dt$, для каждого $t$, начиная с момента времени $t=-\infty$, и остановка в момент времени $t=T$. Интегрирование противоположно взятию производной. Вы изучаете интегралы в интегральном исчислении.
Мощность и энергия в конденсаторе
Мгновенная мощность в ваттах, связанная с конденсатором, равна
$p = v\,i$
$p = v\,\text C \,\dfrac{dv}{dt } $ 92$
В отличие от резистора, в котором энергия уходит на тепло, в идеальном конденсаторе энергия не рассеивается. Вместо этого энергия в конденсаторе в виде накопленного заряда восстанавливается, когда заряд вытекает обратно из конденсатора.
Катушка индуктивности
Напряжение на катушке индуктивности прямо пропорционально скорости изменения во времени тока через катушку индуктивности. Мы можем выразить зависимость индуктора $i$-$v$ в математической записи как
$v = \text L \, \dfrac{di}{dt}$
Это свойство чувствительности к изменению тока обусловлено способностью индуктора накапливать энергию в окружающем магнитном поле. Энергия, запасенная в магнитном поле индуктора, может вернуться в цепь и генерировать электрический ток. Это довольно сложное электромагнитное явление, выходящее за рамки данной статьи. Так что сейчас я просто хочу, чтобы вы запомнили и приняли уравнение $i$-$v$ для катушки индуктивности.
Энергия, запасенная в магнитном поле индуктора, может вернуться в цепь и генерировать электрический ток. Это довольно сложное электромагнитное явление, выходящее за рамки данной статьи. Так что сейчас я просто хочу, чтобы вы запомнили и приняли уравнение $i$-$v$ для катушки индуктивности.
Чтобы узнать больше об индукторах и магнитных полях, см. раздел о магнитных полях в Khan Academy Physics.
Константа пропорциональности $\text L$ называется индуктивностью . Единицей индуктивности является генри, обозначаемый заглавной буквой H.
L и HСимвол для индуктивности $\text L$ чествует русского физика Генриха Ленца за его новаторскую работу в области электромагнетизма. (Символ $\text I$ уже был принят за ток, который нельзя было назвать $\text C$, потому что он уже был занят кулонов.)
единицей индуктивности является генри , $\text H$, названная в честь американского ученого Джозефа Генри, первого секретаря Смитсоновского института (и изобретателя дверного звонка).


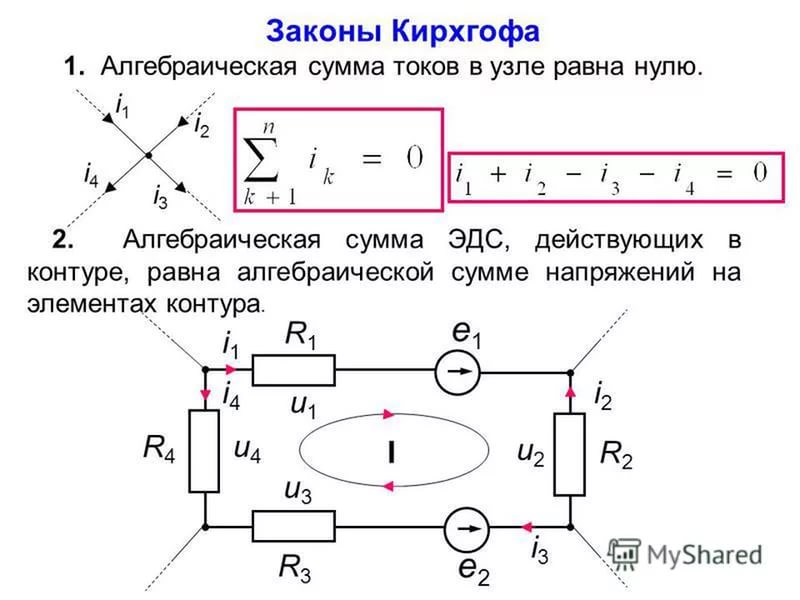
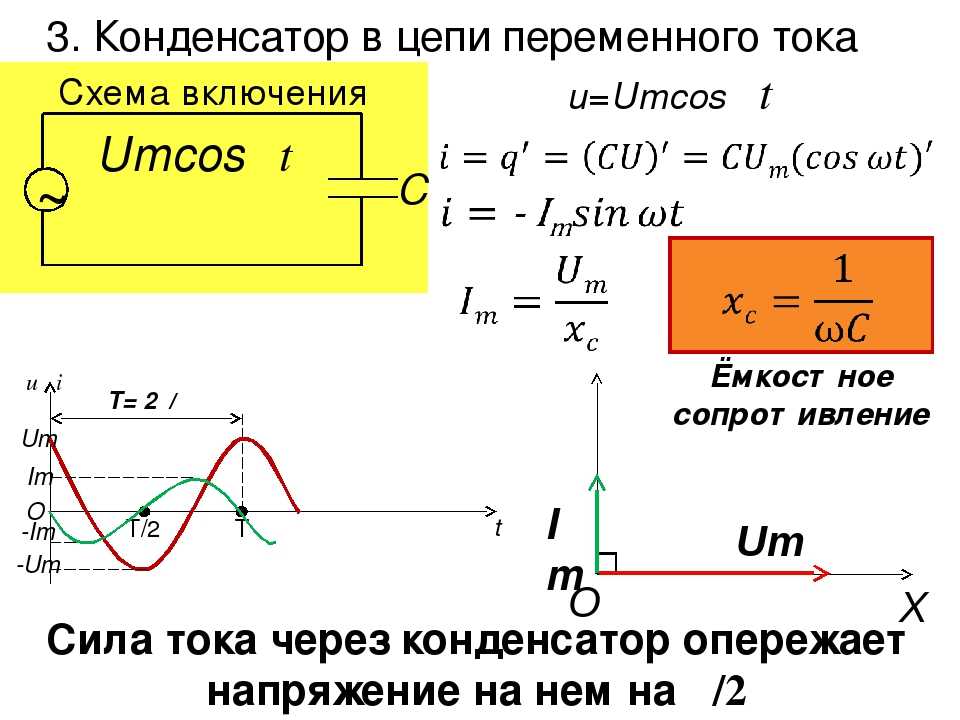 Поэтому идеальный источник тока теоретически так же рассматривается как источник бесконечной мощности.
Поэтому идеальный источник тока теоретически так же рассматривается как источник бесконечной мощности.




 Применять обобщенный закон Ома для активного участка ветви.
Применять обобщенный закон Ома для активного участка ветви.