Как рассчитать общее сопротивление при параллельном и последовательном соединении резисторов. Какие формулы использовать для вычислений. Примеры расчетов и онлайн-калькулятор для быстрого определения эквивалентного сопротивления.
Последовательное соединение резисторов
При последовательном соединении резисторов общее сопротивление цепи равно сумме сопротивлений всех резисторов:
R общ = R1 + R2 + R3 + … + Rn
Где:
- R общ — общее сопротивление цепи
- R1, R2, R3, …, Rn — сопротивления отдельных резисторов
Ключевые особенности последовательного соединения:
- Общее сопротивление всегда больше сопротивления любого отдельного резистора в цепи
- Ток через все резисторы одинаковый
- Напряжение на резисторах пропорционально их сопротивлению
Параллельное соединение резисторов
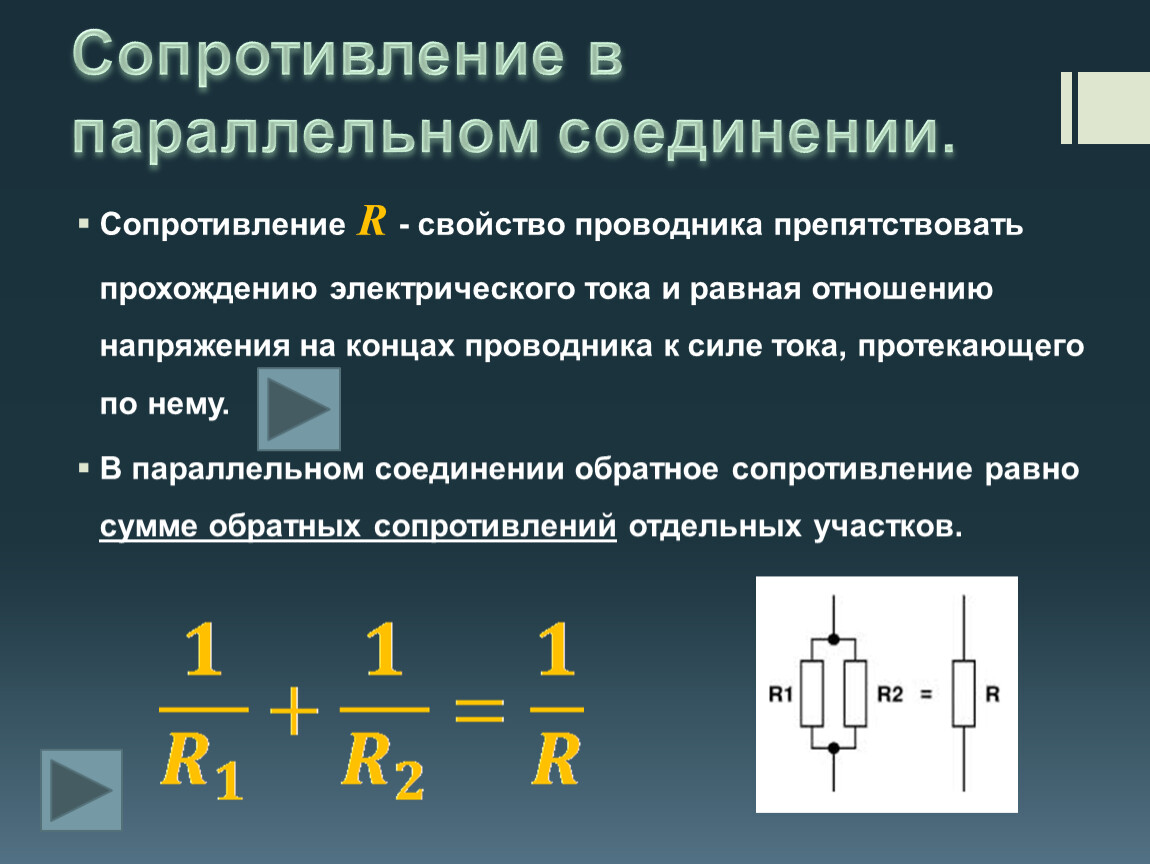
При параллельном соединении резисторов общее сопротивление цепи рассчитывается по формуле:
1/R общ = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
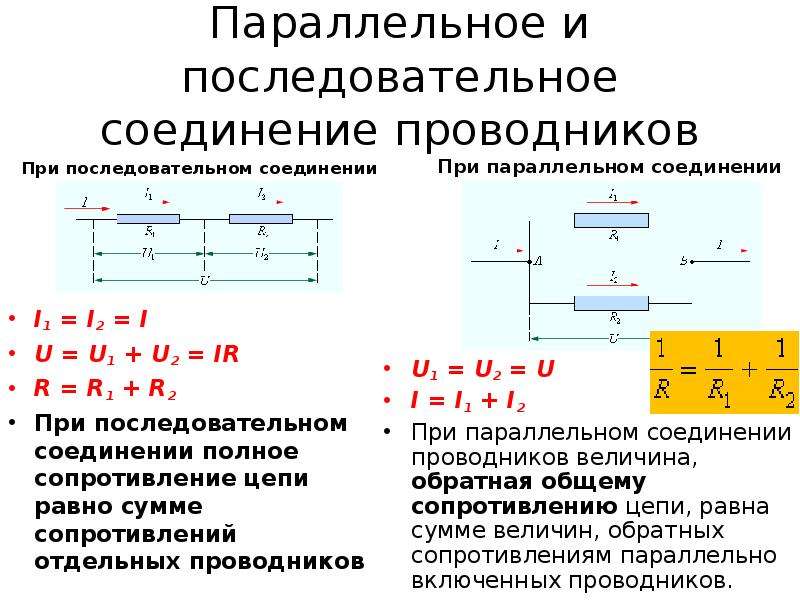
Для двух параллельно соединенных резисторов формула упрощается:
R общ = (R1 * R2) / (R1 + R2)
Особенности параллельного соединения:
- Общее сопротивление всегда меньше сопротивления любого отдельного резистора
- Напряжение на всех резисторах одинаковое
- Ток делится между резисторами обратно пропорционально их сопротивлению
Примеры расчетов
Последовательное соединение
Рассчитаем общее сопротивление трех последовательно соединенных резисторов: 100 Ом, 220 Ом и 470 Ом.
R общ = 100 Ом + 220 Ом + 470 Ом = 790 Ом
Параллельное соединение
Найдем эквивалентное сопротивление двух параллельно соединенных резисторов: 300 Ом и 600 Ом.
R общ = (300 Ом * 600 Ом) / (300 Ом + 600 Ом) = 200 Ом
Онлайн-калькулятор для расчета сопротивления
Для быстрого расчета эквивалентного сопротивления при параллельном и последовательном соединении резисторов вы можете воспользоваться онлайн-калькулятором:
«` import React, { useState } from ‘react’; import { Button, Input, Select } from ‘@/components/ui/input’; const ResistorCalculator = () => { const [resistors, setResistors] = useState([», »]); const [connectionType, setConnectionType] = useState(‘parallel’); const [result, setResult] = useState(null); const addResistor = () => { setResistors([…resistors, »]); }; const handleResistorChange = (index, value) => { const newResistors = […resistors]; newResistors[index] = value; setResistors(newResistors); }; const calculateResistance = () => { const values = resistors.map(r => parseFloat(r)).filter(r => !isNaN(r)); if (values.length === 0) return; let totalResistance; if (connectionType === ‘parallel’) { totalResistance = 1 / values.reduce((sum, r) => sum + 1/r, 0); } else { totalResistance = values.reduce((sum, r) => sum + r, 0); } setResult(totalResistance.toFixed(2)); }; return (Калькулятор сопротивления резисторов
Общее сопротивление: {result} Ом
 )}
)}
С помощью этого калькулятора вы можете быстро рассчитать эквивалентное сопротивление для параллельного и последовательного соединения резисторов.
Практическое применение расчетов сопротивления
Знание формул и умение рассчитывать общее сопротивление при различных соединениях резисторов очень важно в электронике и электротехнике. Вот несколько примеров, где это может пригодиться:
- Проектирование электронных схем — для подбора нужных номиналов резисторов
- Ремонт электроники — для замены вышедших из строя компонентов
- Создание делителей напряжения
- Расчет токоограничивающих резисторов для светодиодов
- Подбор шунтов для измерительных приборов
Ошибки при расчетах сопротивлений
При расчетах общего сопротивления цепи важно избегать следующих распространенных ошибок:
- Применение формулы для последовательного соединения к параллельному и наоборот
- Забывание о том, что при параллельном соединении общее сопротивление всегда меньше наименьшего из резисторов
- Неправильный перевод единиц измерения (например, путаница между Ом и кОм)
- Ошибки в расстановке скобок при расчетах для сложных цепей
Выбор типа соединения резисторов
Как выбрать, какой тип соединения использовать — последовательный или параллельный? Это зависит от конкретной задачи:
- Последовательное соединение используют, когда нужно увеличить общее сопротивление или разделить напряжение
- Параллельное соединение применяют для уменьшения общего сопротивления или разделения тока
- Иногда используют комбинацию обоих типов соединений для достижения нужных характеристик цепи
Влияние температуры на сопротивление
При точных расчетах важно учитывать, что сопротивление резисторов может меняться в зависимости от температуры:
- У большинства металлических проводников сопротивление растет с повышением температуры
- У полупроводников сопротивление обычно уменьшается при нагревании
- Существуют специальные резисторы с малым температурным коэффициентом сопротивления
Этот фактор особенно важен при проектировании устройств, работающих в широком диапазоне температур.
Заключение
Понимание принципов последовательного и параллельного соединения резисторов, а также умение рассчитывать общее сопротивление — важный навык для любого, кто работает с электроникой. Эти знания позволяют грамотно проектировать схемы, подбирать нужные компоненты и эффективно решать задачи в области электротехники.
Последовательное и параллельное соединения источников тока
Решение:
Внутреннее сопротивление элементов
Сопротивление параллельно включенных резисторов
Общая э. д. с. элементов e0=2e Согласно закону Ома для полной цепи
15 Сопротивления резисторов R1 и R2 и э. д. с. ε1 и ε2 источников тока в схеме, изображенной на рис. 127, известны. При какой э.д.с. ε3 третьего источника ток через резистор R3 не течет?
Решение:
Выберем направления токов I1, I2 и I3 через резисторы R1, R2 и R3, указанные на рис. 363. Тогда I3=I1+I2. Разность потенциалов между точками а и b будет равна
Если
Исключая I1 находим
16 Цепь из трех одинаковых последовательно соединенных элементов с э.д.с. ε и внутренним сопротивлением r замкнута накоротко (рис. 128). Какое напряжение покажет вольтметр, подключенный к зажимам одного из элементов?
Решение:
Рассмотрим ту же схему без вольтметра (рис. 364). Из закона Ома для полной цепи находим
Из закона Ома для участка цепи между точками а и b получим
Подключение вольтметра к точкам, разность потенциалов между которыми равна нулю, ничего не может изменить в цепи. Поэтому вольтметр будет показывать напряжение, равное нулю.
17 Источник тока с э.д.с. ε0 включен в схему, параметры которой даны на рис. 129. Найти э.д.с. ε источника тока и направление его подключения к выводам а и b, при которых ток через резистор с сопротивлением R2 не идет.
Решение:
Подключим источник тока к выводам а и b и выберем направления токов, указанные на рис. 365. Для узла е имеем I=I0+I2. При обходе контуров aefb и ecdf по часовой стрелке получим
Используя условие I2 = 0, находим
Знак минус показывает, что полюсы источника тока на рис. 365 нужно поменять местами.
18 Два элемента с одинаковыми э.д.с. ε включены в цепь последовательно. Внешнее сопротивление цепи R = 5 Ом. Отношение напряжения на зажимах первого элемента к напряжению на зажимах второго элемента равно 2/3. Найти внутренние сопротивления элементов r1 и r2, если r1=2r2.
Решение:
19 Два одинаковых элемента с э.д.с. ε=1,5 В и внутренним сопротивлением r = 0,2 Ом замкнуты на резистор, сопротивление которого составляет в одном случае R1=0,2 Oм, В другом — R2 = 20 Ом. Как нужно соединить элементы (последовательно или параллельно) в первом и во втором случаях, чтобы получить наибольший ток в цепи?
Решение:
При параллельном соединении двух элементов внутреннее сопротивление и э.д.с. равны r/2 и ε при последовательном соединении они равны 2r и 2ε. Через резистор R при этом текут токи
Отсюда видно, что I2>I1, если R/2+r<R+r/2, т. е. если r1=r; следовательно, токи при параллельном и последовательном соединениях одинаковы. Во втором случае R2>r.Поэтому ток больше при последовательном соединении.
20 Два элемента с э.д.с. ε1=4В и ε2 = 2В и внутренними сопротивлениями r1 = 0,25 Ом и r2 = 0,75 Ом включены в схему, изображенную на рис. 130. Сопротивления резисторов R1 = 1 Ом и R2 = 3 Ом, емкость конденсатора С=2 мкФ. Найти заряд на конденсаторе.
Решение:
21 К батарее из двух параллельно включенных элементов с э.д.с. ε1 и ε2 и внутренними сопротивлениями r1 и r2 подключен резистор с сопротивлением R. Найти ток I, текущий через резистор R, и токи I1 и I2 в первом и втором элементах. При каких условиях токи в отдельных цепях могут быть равными нулю или изменять свое направление на обратное?
Решение:
Выберем направления токов, указанные на рис. 366. Для узла b имеем I-I1-I2=0. При обходе контуров abef и bcde по часовой стрелке получим
Из этих уравнений находим
Ток I=0 тогда, когда изменена полярность включения одного из элементов и, кроме того, выполнено условие
Ток I1=0 при
а ток I2 = 0 при
Токи I1 и I2 имеют направления, указанные на рис.366, если
Они меняют свое направление при
22 Батарея из n одинаковых аккумуляторов, соединенных в одном случае последовательно, в другом— параллельно, замыкается на резистор с сопротивлением R. При каких условиях ток, текущий через резистор, в обоих случаях будет один и тот же?
Решение:
При n(R-r) = R-r. Если R=r, то число элементов произвольно; если R№r, задача не имеет решения (n=1).
23 Батарея из n = 4 одинаковых элементов с внутренним сопротивлением r=2 Ом, соединенных в одном случае последовательно, в другом — параллельно, замыкается на резистор с сопротивлением R=10Ом. Во сколько раз показание вольтметра н одном случае отличается от показания вольтметра в другом случае? Сопротивление вольтметра велико по сравнению с R и r.
Решение:
где V1 — показание вольтметра при последовательном соединении элементов, V2-при параллельном.
24 Как изменится ток, текущий через резистор с сопротивлением R = 2 Ом, если n =10 одинаковых элементов, соединенных последовательно с этим резистором, включить параллельно ему? Э.д.с. элемента ε = 2 В, его внутреннее сопротивление r = 0,2 Ом.
Решение:
25 Батарея составлена из N=600 одинаковых элементов так, что n групп соединены последовательно и в каждой из них содержится т элементов, соединенных параллельно. Э.д.с. каждого элемента ε = 2 В, его внутреннее сопротивление r = 0,4 Ом. При каких значениях n и m батарея, будучи замкнута на внешнее сопротивление R = 0,6 Ом, отдаст во внешнюю цепь максимальную мощность? Найти при этом ток, текущий через сопротивление R.
Решение:
Общее число элементов N=nm (рис. 367). Ток во внешней цепи
где r/m— внутреннее сопротивление группы из т параллельно соединенных элементов, а nr/m — внутреннее сопротивление n групп, соединенных последовательно. Максимальная мощность отдается во внешнюю цепь при равенстве сопротивления R внутреннему сопротивлению батареи элементов nr/m, т. е.
При этом через сопротивление R течет точек I=46 А.
26 Емкость аккумулятора Qo=80А⋅ч. Найти емкость батареи из n = 3 таких аккумуляторов, включенных последовательно и параллельно.
Решение:
При последовательном соединении через все аккумуляторы батареи течет один и тот же ток, поэтому все они разрядятся в течение одного и того же времени. Следовательно, емкость батареи будет равна емкости каждого аккумулятора:
При параллельном соединении n аккумуляторов через каждый из них течет 1/n часть общего тока; поэтому при том же разрядном токе в общей цепи батареи будет разряжаться в n раз дольше, чем один аккумулятор, т. е. емкость батареи в п раз больше емкости отдельного аккумулятора:
Заметим, однако, что энергия
отдаваемая батареей в цепь, и при последовательном и при параллельном соединении n аккумуляторов в n раз больше энергии, отдаваемой одним аккумулятором. Это происходит потому, что при последовательном соединении э. д. с. батареи в n раз больше э. д. с. одного аккумулятора, а при параллельном соединении э.д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в n раз.
27 Найти емкость батареи аккумуляторов, включенных по схеме, изображенной на рис.131. Емкость каждого аккумулятора Q0=64 А⋅ч.
Решение:
Каждая группа из пяти аккумуляторов, включенных последовательно, имеет емкость
Три параллельно включенные группы дают общую емкость батареи
28 Мост для измерения сопротивлений сбалансирован так, что ток через гальванометр не идет (рис. 132). Ток в правой ветви I=0,2 А. Найти напряжение V на зажимах источника тока. Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 1 Ом.
Решение:
29 Найти токи, протекающие в каждой ветви цепи, изображенной на рис. 133. Э.д.с. источников тока ε1 = 6,5 В и ε2 = 3,9 В. Сопротивления резисторов R1=R2=R3=R4=R5=R6=R=10 Ом.
Решение:
Составляем уравнения Кирхгофа в соответствии с направлениями токов, указанными на рис. 133: I1 + I2 — I3 = 0 для узла b;
I3 — I4 — I5 =0 для узла h; I5 — I1 — I6 = 0 для узла f: при этом
Для контура abfg (обход по часовой стрелке),
Для контура bcdh (обход против часовой стрелки) и
для контура hdef (обход по часовой стрелке). Решая эту систему уравнений с учетом, что все сопротивления одинаковы и равны R=10 Ом, получим
Отрицательные значения токов I2, I4 и I6 показывают, что при данных э.д.с. источников и сопротивлениях резисторов эти токи текут в стороны, противоположные указанным на рис. 133.
Параллельное соединение проводников
1103. Нарисуйте схему параллельного соединения проводников.
1104. В квартирах освещение и розетки для бытовой техники всегда соединяют параллельно. Почему?
Что бы при обрыве цепи, остальные потребители могли работать.
1105. На рисунке 114 изображены две параллельно соединенные проволоки одинаковой длины и одинакового сечения, но из разного материала: железная и медная. По какой из них пойдет ток большей силы? Почему?
Больший ток пойдет по той, у которой сопротивление меньше, т.е по медной.
1106. На рисунке 115 изображена схема параллельного соединения двух проводников сопротивлением 10 Ом каждый. Определите общее сопротивление цепи.
1107. Чему равно общее сопротивление цепи на рисунке 116, если сопротивление каждой электролампочки равно 200 Ом?
1108. На участке цепи параллельно соединены две лампы сопротивлением 20 Ом и 5 Ом. Каково общее сопротивление этого участка цепи?
1109. Кусок изолированного провода имеет сопротивление 1 Ом. Его разрезали посередине и получившиеся половинки скрутили вместе по всей длине. Чему будет равно сопротивление скрутки?
1110. Лампа 1 сопротивлением R1 = 6 Ом и лампа 2 сопротивлением R2 = 12 Ом соединены параллельно и подключены к напряжению 12 В. Какова сила тока:
а) в лампе 1;
б) в лампе 2;
в) во всей цепи?
1111. Сопротивления R1 = 24 Ом и R2 = 12 Ом соединены параллельно и подключены к напряжению 24 В. Определите силу тока:
а) в сопротивлении R1;
б) в сопротивлении R2;
в) во всей цепи.
1112. Три лампы сопротивлениями 10 Ом, 25 Ом и 50 Ом соединены параллельно и включены в сеть с напряжением 100 В. Каково общее сопротивление этого участка цепи? Какова сила тока в нем?
1113. Три лампочки сопротивлением R1 = 2 Ом, R2 = 4 Ом и R3 = 5 Ом соединены параллельно. В первой лампочке сила тока равна 2 А. Какова сила тока во второй и третьей лампочках?
1114. Проводник сопротивлением 200 Ом включен параллельно с неизвестным сопротивлением так, что общее сопротивление стало 40 Ом. Найдите неизвестное сопротивление.
1115. Начертите схему цепи, состоящую из источника, двух лампочек, соединенных параллельно, и амперметров, измеряющих силу тока в каждой лампочке и в проводе, подводящем ток к лампочкам. Допустим, что в цепи, составленной по вашей схеме, один из амперметров, измеряющий ток в лампочках, показал 0,1 А, а амперметр, измеряющий ток в подводящем проводе, — 0,15 А. Какой ток проходит через вторую лампочку?
1116. В комнатной электропроводке включено параллельно 4 лампы, каждая сопротивлением 330 Ом. Ток в каждой лампе 0,3 А. Определить ток, текущий по электропроводке, и сопротивление всей группы ламп.
1117. От группового распределительного щитка ток идет на две параллельные группы. В первой группе включено параллельно 10 ламп, каждая с сопротивлением 250 Ом, во второй группе 5 ламп, каждая с сопротивлением 300 Ом. Найдите ток в каждой группе, если ток, подводимый к щитку, равен 6,8 А.
1118. Между точками А и В включены три сопротивления (рис. 117). Определите общее сопротивление разветвленной части цепи, напряжение на концах разветвленной части цепи, ток в каждом из проводников, если ток в неразветвленной части цепи 5 А.
1119. Больше или меньше суммы сопротивлений общее сопротивление двух проводников, включенных последовательно?
1120. Больше или меньше суммы сопротивлений общее сопротивление двух проводников, включенных параллельно?
1121. Что больше: сопротивление одного проводника или общее сопротивление двух, включенных параллельно?
1122. Две проволоки — алюминиевая и никелевая — одинаковой длины и одинакового сечения включены в цепь параллельно. По какой из этих проволок пойдет ток большей силы? Почему?
1123. К каждой из двух лампочек накаливания подводится напряжение 120 В. Сопротивление первой лампочки 480 Ом, второй 120 Ом (рис. 118).
а) Чему равен ток в той и другой лампочке?
б) Какая будет гореть ярче?
1124. Те же две лампочки накаливания, что и в предыдущей задаче, включены в сеть с напряжением 120 В так, как показано на рисунке 119.
а) Сколько электрической энергии расходуется при прохождении одного кулона электричества от А до В (т.е. через обе лампочки)?
б) В какой из лампочек расходуется больше энергии?
в) Напряжение на какой из лампочек будет больше и во сколько раз?
г) Какая из лампочек будет гореть ярче?
д) Чему равно напряжение на каждой лампочке?
е) Чему равен ток через каждую лампочку?
ж) Чему равно сопротивление всего участка?
1125. Между двумя точками А и В (рис. 120) поддерживается напряжение 120 В.
а) Как между этими точками включить две лампочки, чтобы они горели так же ярко, как каждая в отдельности?
б) Какова будет сила тока в проводе, подводящем ток?
в) Чему равно сопротивление всего участка в этом случае?
1126. В сеть с напряжением 220 В включены параллельно 200 осветительных приборов, каждый сопротивлением 240 Ом. Каково сопротивление всего участка цепи? Какова сила тока, проходящего через каждый прибор? Какова сила тока во всей цепи?
1127. Провод сопротивлением 98 Ом разрезали на несколько одинаковых частей и получившиеся куски соединили параллельно. Измерили сопротивление этого участка — оно оказалось 2 Ом. На сколько частей разрезали провод?
1128. В сеть с напряжением 120 В включены пять одинаковых ламп (рис. 121), каждая сопротивлением 200 Ом. Какова сила тока в цепи?
1129. На рисунке 122 изображен участок цепи с двумя группами параллельно соединенных электроламп. В левой группе 8 лампочек сопротивлением по 400 Ом каждая, в правой группе 5 лампочек сопротивлением по 200 Ом каждая. Напряжение на каждой лампочке 120 В. Какова сила тока, проходящего через левую группу? через правую группу?
1130. На рисунке 123 приведена схема электрической цепи с тремя одинаковыми лампами. Изменится ли накал ламп 1 и 2 после замыкания ключа, если напряжение в обоих случаях одинаково? Если да, то как именно?
1131. Одинаковые сопротивления, каждое из которых равно 4 Ом, соединены параллельно (рис. 124). Определите общее сопротивление и силу тока, если напряжение на клеммах 12 В.
1132. На рисунке 125 изображено соединение четырех одинаковых сопротивлений, каждое из которых равно 4 Ом. Напряжение на клеммах равно 12 В. Определите общее сопротивление и силу тока.
1133. Четыре одинаковых сопротивления, каждое из которых равно 4 Ом, соединены как показано на рисунке 126. Каково общее сопротивление и сила тока, если напряжение на клеммах равно 12 В?
1134. Сопротивления по 4 Ом каждое включены в цепь по схеме на рисунке 127. Напряжение между клеммами равно 12 В. Каково общее сопротивление? Какова сила тока в цепи?
1135. На рисунке 128 приведено соединение четырех одинаковых сопротивлений, каждое из которых равно 4 Ом. Напряжение на клеммах 12 В. Определите общее сопротивление и силу тока в цепи.
1136. Для схемы соединения на рисунке 129 посчитайте общее сопротивление и силу тока в цепи, если сопротивления одинаковые — по 4 Ом каждое, а напряжение на клеммах равно 12 В.
1137. Одинаковые сопротивления, каждое из которых равно 4 Ом, соединены как показано на рисунке 130. Каково общее сопротивление и сила тока, если напряжение на клеммах равно 12 В?
1138. Сопротивления по 4 Ом каждое соединены как показано на рисунке 131. Напряжение между клеммами равно 12 В. Каково общее сопротивление? Какова сила тока в цепи?
Каково общее сопротивление трех параллельно соединенных резисторов — MOREREMONTA
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Как правильно соединять резисторы?
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов.
В жизни последовательное соединение резисторов имеет вид:
Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов.
Можно соединять резисторы и параллельно:
Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное и последовательное соединение проводников. — Объяснение нового материала.
Комментарии преподавателя Последовательное соединение проводниковЭлектрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.
На рисунке а изображена цепь последовательного соединения двух электрических ламп, а на рисунке б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.
Рис. Последовательное включение лампочек и источников питания
Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.
I = I1 = I2
А чему равно сопротивление последовательно соединённых проводников?
Соединяя проводники последовательно, мы как бы увеличиваем длину проводника. Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Последовательное соединение проводников
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
R = R1 + R2
Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:
U1 = IR1, U2 = IR2.
Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
U = U1 + U2.
Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.
Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.
Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Запишем условие задачи и решим её.
Расчет параметров электрической цепи
при параллельном соединении сопротивлений:
1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках
2. напряжение на всех параллельно соединенных участках цепи одинаково
3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :
( R — сопротивление проводника,
1/R — электрическая проводимость проводника)
Если в цепь включены параллельно только два сопротивления, то:
( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )
4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме работ на отдельных участках:
A=A1+A2
5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:
P=P1+P2
Для двух сопротивлений:
т.е. чем больше сопротивление, тем меньше в нём сила тока.
Использованные источники:
- http://www.tepka.ru/fizika_8, http://class-fizika.narod.ru
- https://www.youtube.com/watch?v=AW3n2XP4CQE
- https://www.youtube.com/watch?v=Bo1UwoBicew
Файлы
Нет дополнительных материалов для этого занятия.
Последовательное и параллельное соединение светодиодов
При конструировании различных электронных устройств часто возникает необходимость в последовательном, параллельном или комбинированном включении элементов. Не стали исключением и светодиоды. Учитывая их небольшие размеры, а также с целью повышения яркости, в одном корпусе осветительного прибора можно разместить несколько LED-чипов.
Как правильно собрать электрическую цепь, чтобы надёжность схемы была на высоком уровне? Что нужно знать о светодиодах, соединяя их параллельно или последовательно?
Параллельное соединение
Необходимость в параллельном включении возникает в случае, когда напряжения источника питания недостаточно для запитки нескольких последовательно соединённых светодиодов. Теоретически, в самом простом варианте можно было бы отдельно объединить все аноды и все катоды излучающих диодов. После чего подключить их к источнику напряжения с соблюдением полярности.
Но такая схема не работоспособна, так как дифференциальное сопротивление открытого светодиода чрезмерно мало, что провоцирует режим короткого замыкания. В результате все светодиоды в цепи единожды вспыхнут и навсегда погаснут.Но как говорят: «Правило без исключений не бывает». В китайских игрушках и зажигалках с подсветкой можно увидеть, что светодиоды запитаны прямо от батареек без каких-либо промежуточных элементов. Почему они не перегорают? Дело в том, что ток в цепи ограничен внутренним сопротивлением круглых батареек типа AG1. Их мощности недостаточно, чтобы нанести вред светодиоду.
Ограничить резкое нарастание тока в нагрузке можно с помощью резистора. О том, как это грамотно сделать с одним светодиодом, подробно написано в данной статье. Для цепи из нескольких параллельно подключенных LED с одним резистором схема примет следующий вид.
Но и этот вариант не пригоден для конструирования осветительных устройств с высокой надёжностью. Почему? Ответ на этот вопрос кроется в особенностях строения полупроводников. В процессе производства полупроводниковых элементов невозможно получить два абсолютно одинаковых прибора. Даже у светодиодов из одной партии будет разное дифференциальное (внутреннее) сопротивление, от которого зависит величина прямого напряжения. Это касается не только светодиодов, но и других полупроводников. Среди диодов, транзисторов и тиристоров тоже не найти двух приборов с равными электрическими параметрами.Из второй схемы видно, что резистор R1 ограничивает только суммарный ток цепи, который затем распределяется по ветвям со светодиодами в зависимости от их сопротивления. По закону Ома светодиод с наименьшим сопротивлением p-n-перехода получит наибольшую порцию тока. И скорее всего он будет больше номинального значения, что ускорит деградацию кристалла. Работа светодиода в режиме перегрузки по току рано или поздно приведёт к выходу из строя на обрыв. Оставшиеся в работе светодиоды распределят между собой ток сгоревшего элемента, что также приведёт к резкой потере яркости.
Как и в первом варианте, китайцы не стесняются конструировать светильники на базе «полурабочих» схем. Схему с одним резистором часто можно встретить в дешёвых фонариках и маломощных светильниках на пальчиковых батарейках. А чтобы светодиоды проработали хотя бы год, сопротивление резистора умышленно завышают, как бы, исключая возможные перегрузки.
Ниже приведен единственно верный вариант параллельного включения светодиодов.
Здесь последовательно с каждым светодиодом подключен ограничительный резистор. Такое схемотехническое решение позволяет выровнять токи в каждой отдельной ветви, не позволяя им превышать рабочее значение.Подключать светодиоды через резистор рекомендуется только от стабилизированного источника постоянного напряжения.
Пример расчета
Для закрепления теоретических знаний параллельное соединение светодиодов рассмотрим на конкретном примере.
В схеме включены два светодиода: слаботочный красный и мощный одноваттный белый, которые для удобства можно запитать от разных выключателей.Дано:
- источник напряжения U = +5 В;
- LED1 – красного свечения с ULED1 = 1,8 В и ILED1 = 0,02 А;
- LED2 – белого свечения с ULED2 = 3,2 В и ILED2 = 0,35 А.
Требуется рассчитать параметры и выбрать резисторы R1 и R2.
При параллельном включении к обеим ветвям (R1-LED1 и R2- LED2) прикладывается одинаковое напряжение, равное 5 В. Сопротивление каждого резистора определим по формуле:
Округляем полученное значение R2 до ближайшего большего значения из стандартного ряда E24 – 5,1 Ом. Подставив его обратно в формулу, находим реальный ток во второй ветви: С учетом возможного отклонения сопротивления выбранного резистора, которое для ряда Е24 может достигать 5%, ток 0,33 А является оптимальным. Снижение рабочего тока примерно на 4% сильно не повлияет на яркость, но позволит светодиоду работать без перегрузок.Мощность, которую должны рассеивать резисторы, определим с учетом пересчёта тока LED2 по формуле:
Резистор R1 подойдёт любой как планарный, так и с выводами сопротивлением 160 Ом и мощностью 0,125 Вт. Корпус резистора R2 должен эффективно отводить тепло в течение длительной работы светильника. Поэтому его выбираем с двойным запасом по мощности, а именно: 5,1 Ом – 1 Вт.Последовательное соединение
В последовательном включении светодиодов нужно соблюдать правило: «Напряжение источника питания должно быть больше суммы падений напряжений на светодиодах».
Остаток напряжения в неравенстве гасится одним единственным резистором R, правильное включение которого показано на схеме. Все светодиоды подключаются поочередно от анода к катоду. Сопротивление резистора задаёт ток цепи. Это значит, что соединять последовательно можно светодиоды только с одинаковым рабочим током.Пример расчета
Расчет сопротивления и мощности резистора проведём на примере включения трёх белых светодиодов из серии Cree XM-L, для которых характерным является ток ILED = 0,7 А и прямое напряжение ULED = 2,9 В. Взяв за основу цветовую температуру и требуемую яркость, можно последовательно подключать светодиоды из разных групп в пределах серии XM-L. Например, один Cree XM-L-T6 с ТС=5000°K и два Cree XM-L-T2 с ТС=2600°K, которые в итоге дадут мощный поток нейтрального света.
Питание на схему поступает от блока стабилизированного напряжения U = +12 В. Сопротивление резистора находим по закону Ома: Ближайший стандартный номинал – 4,7 Ом, при котором ток теоретически будет равен 0,702 А. Это не критично, но следует быть уверенным, что сопротивление резистора не изменится под влиянием температуры во время работы. Поэтому устанавливать нужно либо прецизионный резистор с допуском менее 1%, либо последовательно с R1 = 4,7 Ом запаять ещё одно сопротивление 0,1-0,2 Ом такой же мощности.Найдём мощность резистора:
По аналогии с расчётами для первой схемы устанавливать нужно резистор примерно с двойным запасом по мощности, то есть один на 5 Вт. Можно его заменить на два штуки по 2 Вт, но тогда придётся пересчитать сопротивление.Два важных момента
В момент первого включения желательно измерить мультиметром ток в цепи и падение напряжения на каждом светодиоде. Если полученные данные будут отличаться от расчётных, то нужно пересчитать сопротивление резистора. Иначе, ток в схеме может оказаться слишком заниженным (с потерей яркости) или завышенным (с перегревом чипа светодиода).
Как в последовательном, так и в параллельном включении светодиодов нельзя делать расчеты, ссылаясь исключительно на способность источника питания обеспечить нужный ток или напряжение. Важны оба этих параметра, произведение которых даёт мощность. Мощность блока питания всегда должна быть больше мощности потребления, чтобы гарантировать стабильную и продолжительную работу всего устройства.
|
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток: |
|
Последовательное соединение. 1. Сила тока во всех последовательно соединенных участках цепи одинакова: I1=I2=I3=…=In=… 2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке: U=U1+U2+…+Un+… 3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка: R=R1+R2+…+Rn+… Если все сопротивления в цепи одинаковы, то: R=R1. N При последовательном соединении общее сопротивление увеличивается (больше большего). |
Параллельное соединение. 1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках. I=I1+I2+…+In+… |
2. Напряжение на всех параллельно соединенных участках цепи одинаково: U1=U2=U3=…=Un=… 3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению):
Если все сопротивления в цепи одинаковы, то: При параллельном соединении общее сопротивление уменьшается (меньше меньшего). |
4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. A=I2Rt=I2(R1+R2+…+Rn+…)t. 5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. силы тока во всех участках одинаковы, то: U1:U2:…:Un:… = R1:R2:…:Rn:… Для двух резисторов: — чем больше сопротивление, тем больше напряжение. |
4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. .
5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. напряжения на всех участках одинаковы, то: I1R1= I2R2=…= I3R3=… Для двух резисторов: — чем больше сопротивление, тем меньше сила тока. |
Как рассчитать полное сопротивление параллельной цепи?
Как рассчитать полное сопротивление параллельной цепи?
Эффективное сопротивление резисторов, подключенных параллельно
- Есть три важных характеристики в параллельной цепи :
(a) Разность потенциалов одинакова на каждом резисторе.
(b) Ток, который проходит через каждый резистор, обратно пропорционален сопротивлению резистора.
(c) Полный ток в цепи равен сумме токов, проходящих через резисторы в ее параллельных ветвях.
- Когда два или более сопротивления подключены между двумя общими точками так, что к каждой из них приложена одинаковая разность потенциалов, они считаются подключенными параллельно.
Когда такая комбинация сопротивлений подключена к батарее, все сопротивления имеют одинаковую разность потенциалов на концах. - Вывод математического выражения параллельной комбинации:
Пусть, V будет разностью потенциалов между двумя общими точками A и B.Тогда из закона Ома
Ток, проходящий через R 1 , I 1 = V / R 1 … (i)
Ток, проходящий через R 2 , I 2 = V / R 2 … (ii)
Ток, проходящий через R 3 , I 3 = V / R 3 … (iii) - Если R — эквивалентное сопротивление, то по закону Ома полный ток, протекающий по цепи, определяется выражением
I = V / R… (iv)
и I = I 1 + I 2 + I 3 … (v) - Подставляя значения I, I 1 , I 2 и I 3 в уравнение.(v),
\ (\ frac {\ text {V}} {\ text {R}} = \ frac {\ text {V}} {{{\ text {R}} _ {\ text {1}} }} + \ frac {\ text {V}} {{{\ text {R}} _ {\ text {2}}}} + \ frac {\ text {V}} {{{\ text {R}} _ {\ text {3}}}} \ text {} …… .. \ text {(vi)} \) - Отменяя общий термин V, получаем
\ (\ frac {\ text {1}} {\ text {R}} = \ frac {\ text {1}} {{{\ text {R}} _ {\ текст {1}}}} + \ frac {\ text {1}} {{{\ text {R}} _ {2}}} + \ frac {\ text {1}} {{{\ text {R} } _ {3}}} \)
Эквивалентное сопротивление параллельной комбинации сопротивлений меньше, чем каждое из всех отдельных сопротивлений. - Эквивалентная схема показана на рисунке.
Важные результаты о параллельной комбинации:
- Полный ток в цепи равен сумме протекающих по ней токов.
- В параллельной комбинации резисторов напряжение (или разность потенциалов) на каждом резисторе одинаково и равно приложенному напряжению, то есть В 1 = В 2 = В 3 = В.
- Ток, протекающий через каждый резистор, обратно пропорционален его сопротивлению, поэтому чем выше сопротивление резистора, тем меньше ток, протекающий через него.
Люди также спрашивают
Проблемы параллельной цепи с решениями
- Три резистора, R 1 , R 2 и R 3 , подключены параллельно к батарее, как показано на рисунке.
Рассчитайте
(a) разность потенциалов на каждом резисторе,
(b) эффективное сопротивление R цепи,
(c) ток, I, в цепи,
(d) токи, I 1 , I 2 и I 3 , проходящие через каждый резистор.
Решение:
(a) Поскольку это параллельная схема, разность потенциалов на каждом резисторе составляет 6 В, то же самое, что и разность потенциалов на батарее, которая составляет 6 В.
Основное электрическое оборудование | Сопротивление параллельно
Параллельные схемы
Параллельная цепь определяется как цепь, в которой более одного пути тока подключены к общему источнику напряжения. Следовательно, параллельные цепи должны иметь два или более сопротивления нагрузки, которые не соединены последовательно.Каждый путь имеет отдельные резисторы (нагрузки) и может работать независимо от других путей. Различные пути прохождения тока обычно называют ветвью параллельной цепи.
Параллельное сочетание резистора
Два или более резистора считаются подключенными параллельно, если один конец резистора подключен к одному концу другого резистора, а второй конец первого резистора подключен ко второму концу другого резистора так, что разность потенциалов на каждом резисторе одинаковый.
Одним из преимуществ параллельной схемы является то, что в случае обрыва одной ветви это не повлияет на работу компонентов в других ветвях, поскольку они все еще подключены к источнику питания. В параллельной цепи напряжение одинаково на всех компонентах цепи.
- Устройства подключаются параллельно, когда они образуют петлю, не охватывающую другие элементы.
- Устройства подключаются параллельно, если у них есть два общих узла.
Эквивалентное сопротивление параллельной цепи
Суммарное сопротивление (или результирующее сопротивление) ряда сопротивлений или резисторов, соединенных параллельно, можно рассчитать с помощью закона комбинации сопротивлений, включенных параллельно. По закону сочетания сопротивлений параллельно. Сумма, обратная суммарному сопротивлению нескольких параллельно включенных сопротивлений, равна сумме обратных величин всех отдельных сопротивлений .Например, если несколько сопротивлений, R 1 , R 2 , R 3, и т. Д. Подключены параллельно, то их суммарное сопротивление R определяется по формуле:
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3
Предположим, что сопротивление R 1 на 4 Ом, R 2 на 6 Ом и третье сопротивление R 3 = 12 подключены параллельно, и мы хотим узнать их суммарное сопротивление R.
Мы знаем, что
1 / R экв = 1/4 + 1/6 + 1/12
1 / R экв. = 6/12
R экв. = 2 Ом
Это означает, что если мы соединим три сопротивления 4 Ом, 6 Ом и 12 Ом параллельно, то их общее сопротивление составит всего 2 Ом, что меньше, чем любое из трех отдельных сопротивлений (4 Ом, 6 Ом и 12 Ом). . Таким образом, когда несколько сопротивлений соединены параллельно, их суммарное сопротивление меньше наименьшего индивидуального сопротивления. Это связано с тем, что когда у нас есть два или более сопротивлений, соединенных параллельно друг другу, то один и тот же ток получает дополнительные пути для протекания, и общее сопротивление уменьшается.
Примечание: — Если в параллельной цепи только два пути, можно использовать следующую формулу:
R экв. = ( 1 R 2 ) ⁄ ( 1 + 2 )
Два сопротивления умножаются, а затем складываются.При использовании этой формулы нет необходимости находить значения, обратные значениям сопротивления. Эту формулу можно использовать только при наличии двух сопротивлений в параллельной цепи. Если имеется более двух сопротивлений, необходимо использовать формулу обратного сопротивления.
Другой простой метод определения общего сопротивления в параллельной цепи — это когда все значения сопротивления одинаковы. Примером параллельной цепи со всеми одинаковыми сопротивлениями является гирлянда, соединенная параллельно. Каждая лампа имеет одинаковое сопротивление.Когда все сопротивления равны, чтобы найти общее сопротивление, разделите значение сопротивления каждого резистора на количество путей, пять резисторов 10 Ом подключены параллельно, общее сопротивление равно 10, разделенному на 5, или 2 Ом.
Напряжение в параллельной цепи резистора
Любое количество резисторов (компонентов) может быть подключено параллельно. Рассмотрим параллельную схему с тремя резисторами, каждый из которых имеет обозначения сопротивления: R 1 , R 2, и R 3 .
Предположим, что разность потенциалов между точками A и B равна V. Разность потенциалов между любыми двумя точками не зависит от пути, пройденного между точками. Разность потенциалов между любыми двумя точками — это единственная фиксированная скалярная величина. Работа, выполняемая между этими двумя точками, не зависит от пути, пройденного испытательным зарядом. Технический способ сказать это — «электрическое поле консервативно», что также известно как закон напряжения Кирхгофа.
Поскольку каждое сопротивление подключено между одними и теми же двумя точками A и B, следовательно, разность потенциалов на каждом сопротивлении будет одинаковой и будет равна приложенной разности потенциалов V.Следовательно, напряжение на всех трех сопротивлениях, то есть R 1 , R 2 и R 3 , будет равно напряжению питания (В).
Это главное преимущество параллельной схемы и причина того, почему большинство повседневных цепей подключаются параллельно. Это гарантирует, что на все компоненты подается одинаковое напряжение. Например, каждая цепь в доме подключена параллельно, обеспечивая подачу 230 В (или 120 В в Северной Америке) на каждый компонент.Лампа на 230 В может быть подключена параллельно к пылесосу на 230 В и электрокамину на 230 В, все к источнику питания 230 В, и все они имеют одинаковое напряжение питания.
Ток в параллельной цепи резистора
Если мы поместим амперметры в параллельную цепь, как показано на рисунке, мы обнаружим, что сумма текущих показаний в каждой ветви будет равна току, потребляемому от источника питания.
Компоненты в параллельной цепи работают независимо друг от друга.Когда два или более блока соединены параллельно, каждый блок будет получать часть общего протекания тока в цепи. То есть полный ток схемы делится в одной или нескольких точках, и часть проходит через каждое сопротивление цепи. Обычно, когда мы анализируем схему этого типа, мы предполагаем, что сопротивление провода незначительно, а источник питания не имеет внутреннего сопротивления. Полный ток в параллельной цепи равен сумме токов в отдельных компонентах.Уравнение, выражающее это утверждение, следующее:
I T = I 1 + I 2 + I 3 + ——– I N
Обычно, когда мы анализируем параллельную цепь, мы предполагаем, что сопротивление провода незначительно и источник питания не имеет внутреннего сопротивления. Параллельная цепь всегда содержит более одного пути для прохождения тока; следовательно, ток может «выбирать», через какую единицу нагрузки проходить. Из-за природы физики (и закона Ома) больше электронов будет идти по пути более низкого сопротивления, а меньшее количество электронов будет идти по пути более высокого сопротивления.Таким образом, в параллельной цепи любой путь с более высоким сопротивлением, естественно, получает меньше тока, а цепи с низким сопротивлением будут получать больший ток.
Согласно закону Кирхгофа, сумма токов, приближающихся к любому соединению в цепи, равна сумме токов, выходящих из того же соединения, и может быть выражена следующим образом:
I = I 1 + I 2 + I 3
Из закона Ома
I = E / R
Подставляя значение I, получаем
E / R T = E / R 1 + E / R 2 + E / R 3
Поскольку напряжение питания E является общим для каждого сопротивления, мы можем разделить приведенное выше уравнение на E:
E / R T = E / E. 1 + E / E.R 2 + E / E.R 3
1 / R T = 1 / R 1 + 1 / R 2 + 1 / R 3
Где R T — полное сопротивление цепи
Обзор параллельных цепей
- При разделении цепи на ветви напряжение не падает; следовательно, на каждую ветвь цепи подается одинаковое напряжение.
- Полный ток в цепи равен сумме токов в ее параллельных ветвях.
- Обратное эквивалентное сопротивление равно сумме обратных величин отдельных сопротивлений.
- Общее сопротивление параллельной цепи всегда меньше, чем сопротивление ветви с наименьшим сопротивлением.
- Если один из параллельных путей разорван, ток будет продолжать течь по всем другим путям.
Преимущества параллельных цепей в домашней проводке
Расположение светильников и различных других электроприборов в параллельных цепях используется в бытовой электропроводке из-за следующих преимуществ:
- В параллельных цепях, если одно электрическое устройство перестает работать из-за какого-либо дефекта, все остальные устройства продолжают работать нормально. Например, если несколько лампочек подключены в параллельные цепи и одна лампочка перегорела (или перегорела), то все остальные лампочки будут продолжать светиться.
- В параллельных цепях каждый электроприбор имеет собственный выключатель, благодаря которому его можно включать и выключать независимо, не влияя на другие электроприборы. Например, все лампы, включенные в параллельную цепь в доме, имеют отдельные выключатели, благодаря которым мы можем включать или выключать любую лампочку по мере необходимости, не затрагивая другие лампы в доме.
- В параллельных цепях каждый электроприбор получает такое же напряжение (220 В), что и линия электропитания. Благодаря этому вся бытовая техника будет работать исправно. Например, все лампочки, включенные в параллельные цепи, получают одинаковое напряжение 220 вольт линии питания и поэтому светятся очень ярко.
- При параллельном подключении электроприборов общее сопротивление бытовой цепи снижается, из-за чего ток от источника питания велик. Таким образом, каждое устройство может потреблять необходимое количество тока. Например, в параллельных цепях даже приборы с высокой мощностью, такие как электрические утюги, водонагреватели, кондиционеры и т. Д., Могут потреблять большой ток, необходимый для их правильного функционирования.
Решенный пример параллельной цепи резистора
Вопрос.1. Схема состоит из трех параллельно соединенных резисторов, каждый из которых имеет сопротивление 2 Ом, 4 Ом, 16 Ом соответственно.Если цепь подключена к источнику питания 120 В, рассчитайте:
(1). Ток через каждую ветку
(2). Ток питания
(3). Полное сопротивление.
Sol: — Принципиальная схема вышеуказанного вопроса показана на рисунке
.
1). Ток через каждую ветку
⇒ I 1 = E / R 1 = 120/6
I 1 = 20 А
⇒ I 2 = E / R 2 = 120/12
I 2 = 10 А
⇒ I 3 = E / R 3 = 120/16
Я 2 = 7.5 А
2.) Ток питания
I T = I 1 + I 2 + I 3
Я Т = 20 + 10 + 7,5
I T = 37,5 A
(3) . Общее сопротивление
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3
1 / R экв. = 1/6 + 1/12 + 1/16
1 / R экв. = 15/48
R экв = 48/15 = 3.2 Ом
Для Последовательное сопротивление | Последовательная схема Нажмите здесь
Основы электротехники Щелкните здесь
Чтобы узнать о влиянии температуры на сопротивление, нажмите здесь
Для ознакомления с концепцией сопротивления и закона Ома нажмите здесь
Для основных величин и единиц нажмите здесь
резисторов в параллельной комбинации — инженерные проекты
Здравствуйте, ребята, надеюсь, у вас все отлично.В сегодняшнем руководстве мы обсудим параллельные резисторы . Существует 2 основных типа подключения, которые используются для создания схем. Один — последовательный контакт, второй — параллельный. Если компоненты в схемах параллельны друг другу, они имеют свою собственную ветвь. Эти ответвления обеспечивают разные пути прохождения тока. В параллельных схемах ток имеет разное значение в каждом сегменте схемы, а напряжение на каждой части равно входному напряжению.Чтобы решить вашу параллельную схему сопротивления, вы должны попробовать наш онлайн-калькулятор параллельного сопротивления
В сегодняшнем посте мы рассмотрим такие схемы, в которых есть параллельные сопротивления, и продемонстрируем, как мы можем найти эквивалентное сопротивление схемы, а также ток и напряжение на них. каждый компонент. Итак, давайте начнем с резисторов , подключенных параллельно.
Параллельная комбинация резисторов
- В электрических схемах сопротивления подключаются параллельно, если их обе конечные точки соединены с другими конечными точками сопротивления или сопротивлений.
- Как и в схеме последовательного сопротивления, ток может течь по одному пути, но в параллельной схеме есть много путей для тока. Благодаря этому параллельные схемы также считаются схемами делителя тока.
- Поскольку существует множество способов передачи тока в параллельных схемах, разные токи будут протекать через каждую часть схемы. Напряжение будет одинаковым для всех сопротивлений схемы.
- В приведенной ниже схеме есть 3 сопротивления Rx, Ry, Rz, напряжение на каждом из них будет одинаковым.
VRx = VRy = VRz = 12 В
- Чтобы найти эквивалентное сопротивление, нужно просто сложить все последовательные сопротивления в схеме, но при параллельном подключении сопротивлений мы добавляем обратную величину каждого сопротивления для эквивалентного сопротивления.
1 / Rt = 1 / Ra + 1 / Rb + 1 / Rc… ..1 / Rn
Токи в параллельной цепи резистора
- Чистый ток, проходящий через схему параллельных сопротивлений, эквивалентен суммированию токи, проходящие через каждое сопротивление схемы.
- Но ток через каждую ветвь схемы не будет одинаковым, в заключение, каждое сопротивление ветви схемы говорит о токе, протекающем через эту ветвь.
- Например, поскольку напряжение на каждом параллельном резисторе одинаково, и из-за различных значений сопротивления ток не будет одинаковым.
- Создадим схему с двумя параллельными сопротивлениями, как показано на рисунке.
- Ток, проходящий через каждое сопротивление, равен IRx и IRy, если мы применим закон Кирхгофа к этой схеме, чем мы.
It = IRx + IRy
- Если мы применим закон Ома к обоим сопротивлениям, мы сможем найти ток, проходящий через них.
IRx = V / Rx = 12/20 = 0,6 ампера
IRy = V / Ry = 12/47 = 0,255 ампера
- Таким образом, общий ток будет.
It = 0,6 + 0,255 = 0,855 ампер
Свойства параллельных резисторов
- На данной диаграмме показана параллельная резистивная схема, которая имеет 3 сопротивления Rx, Ry, Rz, включенных параллельно, и один источник тока.
- Ток Ix течет от источника к трем сопротивлениям схемы и делится на три разных пути.
- Если мы применим закон Ома к этой схеме, то получим это выражение.
Ix = IRx + IRy + IRz
- Напряжение на каждом сопротивлении будет.
VRx = (IRx). (Rx)
VRy = (IRy). (Ry)
VRz = (IRz). (Rz)
- Теперь используйте эти значения напряжения каждого сопротивления и найдите ток, протекающий по ним.
IRx = VRx / Rx
IRy = VRy / Ry
IRz = VRz / Rz
- Если мы сложим эти 3 тока, результирующее значение будет равно текущему источнику.
Закон Ома и параллельные резисторы
- Чтобы связать закон Ома и параллельную комбинацию резисторов, мы возьмем пример схемы, в которой 3 резистора, подключенных параллельно, и источник напряжения соединены с ними.
- Напряжение на каждом сопротивлении равно источнику напряжения.Если мы применим закон Ома, ток на каждом сопротивлении будет.
I1 = (V) / (Rx)
I2 = (V) / (Ry)
I3 = (V) / (Rz)
- Согласно принципу сохранения заряда, полный ток, протекающий в цепи будет равняться току, проходящему через эти три сопротивления.
It = (I1 + I2 + I3)
- Если мы поместим значения протекающих токов в 3 сопротивления, то получим.
I = (V) / (Rx) + (V) / (Ry) + (V) / (Rz)
I = V (1 / Rx + 1 / Ry + 1 / Rz)
- От Из этого соотношения можно сделать вывод, что полное сопротивление в параллельной схеме эквивалентно суммированию обратных сопротивлений каждого резистора.
- Итак, эквивалентное сопротивление в параллельной схеме составляет.
Rn = 1 / Rx + 1 / Ry + 1 / Rz + ……… + 1 / Rn
Применения параллельной цепи сопротивления
- Вот некоторые применения параллельных цепей сопротивления.
- Почти в каждом доме на Земле используется параллельная комбинация для электропроводки, поскольку мы можем включать и выключать бытовые приборы, не удаляя все устройства из схемы.
- В случае короткого замыкания на одном устройстве или его повреждения из-за некоторых электрических неисправностей, мы отключим цепь именно этого устройства, а не всю схему для устранения неисправности.
- Параллельные схемы используются не только в домашних условиях, но также используются для передачи и распределения электроэнергии в большие здания и различные районы.
- В настоящее время наши сетевые станции проектируются в соответствии с комбинациями параллельных цепей, когда цепь фидера отключена, другие фидеры в сети продолжают свою работу и подают мощность на нагрузку.
Калькулятор параллельного сопротивления
- Сейчас, когда мы обсуждали наш Калькулятор параллельного сопротивления, мы обсудим, как вы можете использовать его для решения ваших схем.
- Вы можете видеть на данном рисунке параллельный калькулятор сопротивления, это две части этого калькулятора, сначала слева, где вы можете сложить значения сопротивлений ваших цепей, а на правой стороне показано физическое представление схемы.
- Как вы можете видеть на данной диаграмме, я ввел пять различных значений в поле значений и получил эквивалентное сопротивление схемы. Если ваша схема не имеет большого сопротивления, вы можете добавить дополнительные значения сопротивления с помощью опции Добавить больше сопротивления .Вы также можете принимать значения в килоомах и мегаомах.
Это подробная статья о параллельных резисторах, если у вас есть какие-либо вопросы, задавайте их в комментариях. Спасибо за прочтение.
Автор: Захид Али
Я профессиональный писатель технического контента, мое хобби — узнавать новые вещи и делиться ими с новыми учениками. Также имею опыт работы в различных отраслях в качестве инженера. Теперь я делюсь своими техническими знаниями со студентами инженерных специальностей.
Пост-навигация
Сопротивление параллельно — диаграмма, формулы и числа
Последнее обновление: 28 апреля 2020 г., Teachoo
Здесь разные резисторы подключены между 2 точками, параллельными друг другу.
Пример
Это сделано для уменьшения чистого сопротивления цепи.
В этом случае полное сопротивление цепи равно сумме обратных величин индивидуального сопротивления резисторов.
1 / R = 1 / R 1 + 1 / R 2 + 1 / R 3
ВАЖНЫЕ МОМЕНТЫ
Когда 2 резистора подключены параллельно
-
Через каждый резистор протекает разный ток, но общий ток, протекающий по цепи, остается неизменным.
Следовательно, мы можем сказать, что
Суммарный ток = ток, протекающий через первый резистор + ток, протекающий через второй резистор + ток, протекающий через третий резистор
Я = Я 1 + Я 2 + Я 3
-
Потенциальная разница для всех обоих резисторов остается одинаковой (поскольку они оба находятся между одинаковыми точками)
Следовательно, мы можем сказать, что
Разница потенциалов = V
То же самое для резистора 1 и резистора 2.
Теперь мы знаем, что по закону Ома
Разница потенциалов = ток * сопротивление
Потенциальная разница / сопротивление = ток
Ток = потенциальный перепад / сопротивление
I = V / R
Как выводится формула сопротивления — для параллельных цепей?
Примечание — В случае параллельного подключения общее сопротивление всегда меньше, чем сопротивление индивидуальный резисторы.
При параллельном подключении резисторов полное сопротивление будет самым низким.
Вопросов
NCERT Вопрос 5 — Каким образом в цепь включается вольтметр для измерения разности потенциалов между двумя точками?
Посмотреть ответ
Q1, стр. 216 —
Оцените эквивалентное сопротивление при параллельном подключении следующих компонентов:
(а) 1 Ом и 10 6 Ом,
(b) 1 Ом, 10 3 Ом и 10 6 Ом.
Посмотреть ответ
Q2 Стр. 216 — К источнику 220 В. параллельно подключены электрическая лампа на 100 Ом, тостер сопротивлением 50 Ом и водяной фильтр сопротивлением 500 Ом. Какое сопротивление у электрического утюга, подключенного к тому же источнику, который потребляет такой же ток, как и все три прибора, и какой ток проходит через него?
Посмотреть ответ
Q4 Стр. 216 — Как можно соединить три резистора с сопротивлением 2 Ом, 3 Ом и 6 Ом, чтобы получить общее сопротивление (а) 4 Ом, (б) 1 Ом?
Посмотреть ответ
Q5 Стр. 216 — Какое (а) наибольшее, (б) наименьшее общее сопротивление, которое может быть обеспечено комбинацией четырех катушек с сопротивлением 4 Ом, 8 Ом, 12 Ом, 24 Ом?
Посмотреть ответ
Пример 12.8 —
На принципиальной схеме, приведенной на рис. 12.10, предположим, что резисторы R 1, R 2 и R 3 имеют значения 5 Ом, 10 Ом, 30 Ом соответственно, которые были подключены к батарее на 12 В. Рассчитайте
(а) ток через каждый резистор,
(б) полный ток в цепи, и
(в) полное сопротивление цепи.
Посмотреть ответ
Пример 12.9 —
Если на рис. 12.12 R 1 = 10 Ом, R 2 = 40 Ом, R 3 = 30 Ом, R 4 = 20 Ом, R 5 = 60 Ом, и к устройству подключена батарея на 12 В.Рассчитать
(а) полное сопротивление в цепи, и
(б) полный ток, протекающий в цепи.
Посмотреть ответ
Вопрос 5 — Какое минимальное сопротивление можно получить, используя пять резисторов по 1/5 Ом каждый?
(а) 1/5 Ом
(б) 1/25 Ом
(в) 1/10 Ом
(г) 25 Ом
Посмотреть ответ
Калькулятор параллельного и последовательного сопротивления
Параллельный и последовательный
Сопротивление
| Параллельное сопротивление | XXXX Ом |
| Сопротивление серии | XXXX Ом |
Рассчитать Прозрачный
⚠️ Сообщить о проблеме
Сопротивление — это электрический элемент, который не позволяет легко протекать через него току.В нашей повседневной жизни сопротивление используется во многих электрических цепях и устройствах. Внутри этих электрических устройств сопротивления расположены в различных конфигурациях.
Вы также, должно быть, наблюдали, выполняя соединения на макетной плате в своей лаборатории электроники, как резисторы подключаются по-разному. В зависимости от способа соединения их концов различают два основных типа цепей сопротивления:
- Цепи серии
- Параллельные схемы
По мере продвижения в этом посте мы поймем работу, сравнение, вычисления и различия между этими последовательными цепями и параллельными цепями.
Цепи серииДва или более резистора считаются подключенными последовательно, если ток, протекающий через них, одинаков. Другими словами, ток, исходящий от источника, или общий ток не будет разветвляться по какому-либо другому пути, а будет двигаться только по одному прямому пути.
При последовательном соединении сопротивлений чистое сопротивление цепи является суммой всех сопротивлений цепи.
На следующей принципиальной схеме показаны три последовательно соединенных сопротивления R 1 , R 2 и R 3 .Общее сопротивление этой последовательной цепи составляет R нетто = 1 R 2 + 3 R.
Обычно, если «n» сопротивлений соединены последовательно, общее сопротивление составляет R net = R 1 + R 2 +…. Р н .
Например, если в цепи есть три последовательно соединенных резистора по 10 Ом, и источник напряжения 30 В, то ток, протекающий в цепи и через каждый из них, определяется выражением I = V / R = 10/30 = 0. .33 А.
Параллельные цепи
Два или более резистора считаются подключенными параллельно, если они соединены головками на одной стороне и выводами на другой стороне цепи. В параллельной цепи ток, исходящий от источника, или полный ток будет ветвиться в месте соединения, где головки сопротивлений встречаются, а затем течет в разных количествах в каждом резисторе, а затем снова объединяется в точке встречи хвостов резисторы и течет в сторону начала координат.
При параллельном подключении сопротивлений сопротивление цепи, обратное сопротивлению цепи, является суммой значений, обратных сопротивлению всех сопротивлений цепи.
На следующей принципиальной схеме показаны три параллельно включенных сопротивления R 1 , R 2 и R 3 . Общее сопротивление этой параллельной цепи составляет 1 / R net = 1 / R = 1 / R 1 + 1 / R 2 + 1 / R 3 .
Как правило, если «n» сопротивлений подключены параллельно, общее сопротивление составляет:
1 / R net = 1 / R = 1 / R + 1 / R 2 + 1 / R 3 +….+ 1 / R n
Например, если три резистора 4 Ом, 8 Ом и 8 Ом подключены параллельно в цепи с питанием 10 В, то общее сопротивление цепи определяется как: 1 / Rnet = 1/4 + 1/8 + 1/8 = ½ или Rnet = 2 Ом
Тогда ток, протекающий по цепи, равен V / I = 10/2 = 5 ампер.
Если вы хотите рассчитать ток в каждом резисторе, вы можете использовать закон Ома:
Ток через резистор 4 Ом I 1 = 10/4 = 2.5 А
Ток через резистор 8 Ом I 1 = 10/8 = 1,25 A
Ток через резистор 4 Ом I 1 = 10/8 = 1,25 A
Обратите внимание: если вы сложите отдельные токи через каждый резистор, вы получите общий ток, протекающий в цепи.
Комбинация последовательных и параллельных резисторов
Если вы найдете схему, в которой резисторы включены последовательно и параллельно, то вам нужно решить комбинацию резисторов шаг за шагом, учитывая, находятся ли они последовательно или параллельно с соседними, и затем прийти к окончательному сопротивлению цепи.
Баллов о последовательном и параллельном соединении резисторов:
- Эффективное сопротивление последовательной цепи всегда больше, чем сопротивление каждого резистора в цепи.
- Эффективное сопротивление параллельной цепи всегда меньше, чем сопротивление каждого резистора в цепи.
- Ток в каждом из последовательно соединенных резисторов одинаков, а напряжение на каждом параллельном резисторе одинаково.
- В цепи последовательных резисторов, если одно сопротивление повреждается, вся цепь разрывается и ведет себя как разомкнутая цепь.
- В схеме параллельных резисторов, если один резистор поврежден, ток продолжает течь в других резисторах, и схема будет продолжать работать, но с другим значением сопротивления цепи.
Как вам помогает калькулятор последовательного и параллельного сопротивления CalculatorHut?
В нашей повседневной жизни мы сталкиваемся с последовательным и параллельным сочетанием резисторов во многих местах. Например, для цепей освещения мы используем параллельное соединение, а для приборов, которые работают непосредственно от сети, дается последовательное соединение.
CalculatorHut, универсальный центр научных и ненаучных онлайн-калькуляторов, предлагает бесплатный онлайн-калькулятор последовательного и параллельного сопротивления, который решит все ваши потребности в онлайн-калькуляторе бесплатно. Вы можете рассчитать до десяти резисторов, которые подключены последовательно или параллельно, с помощью этого удобного онлайн-калькулятора последовательного и параллельного сопротивления. Это очень удобный инструмент для студентов, который помогает им проверить правильность расчетов сопротивления.
CalculatorHut также предлагает широкий выбор более 100 калькуляторов по различным темам — калькуляторы здоровья, финансовые калькуляторы, калькуляторы транспортных средств, физические калькуляторы, химические калькуляторы, математические калькуляторы и многие другие бесплатные онлайн-калькуляторы для научных расчетов.
Наши читатели также могут получить бесплатный виджет любого калькулятора из нашего широкого спектра калькуляторов для встраивания в качестве виджетов на свои веб-сайты. Для этого они могут написать нам письмо по адресу [email protected].
Мы пропустили какой-нибудь бесплатный онлайн-калькулятор? Пожалуйста дай нам знать.Мы будем более чем счастливы удовлетворить ваши потребности в бесплатном онлайн-калькуляторе бесплатно и всегда!
Вот еще одна фантастическая новость! Вы можете бесплатно носить с собой в кармане наш широкий ассортимент онлайн-калькуляторов. Да! Бесплатное приложение CalculatorHut — ваш друг, который упрощает и упрощает любые вычисления! Удачных расчетов!
Сопротивление в последовательных, параллельных или последовательно-параллельных цепях
Сопротивление в последовательных, параллельных или последовательно-параллельных цепяхХотите сделать этот сайт своей домашней страницей? Это быстро и просто…
Да, сделайте эту страницу моей домашней!
|
|
A Passion Production opyright 2000
параллельных резисторов
Обзор
Резисторы в цепи могут быть подключены последовательно или параллельно.Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Параллельные резисторы
Параллельные резисторы, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Параллельные резисторы
Параллельное соединение резисторов.
Каждый резистор потребляет такой же ток, как если бы он был единственным резистором, подключенным к источнику напряжения.Это верно для схем в доме или квартире. Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.
Закон Ома и параллельные резисторы
Каждый резистор в цепи имеет полное напряжение. Согласно закону Ома токи, протекающие через отдельные резисторы, равны $ I_1 = \ frac {V} {R_1} $, $ I_2 = \ frac {V} {R_2} $ и $ I_3 = \ frac {V} {R_3 } $. Сохранение заряда подразумевает, что полный ток является суммой этих токов:
Параллельные резисторы
Три резистора, подключенных параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление.
$ I = I_1 + I_2 + I_3. $
Подстановка выражений для отдельных токов дает:
$ I = \ frac {V} {R_1} + \ frac {V} {R_2} + \ frac {V} {R_3} $
или
$ I = V (\ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3}) $
Это означает, что полное сопротивление в параллельной цепи равно сумме инверсии каждого отдельного сопротивления. Следовательно, для каждой цепи с числом $ n $ или параллельно подключенными резисторами
$ R_ {n \; (parallel)} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3}… + \ frac {1} {R_n}. $
Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений. Когда резисторы подключены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Каждый резистор, включенный параллельно, имеет одинаковое полное напряжение источника, приложенного к нему, но делит общий ток между ними. Примером может служить соединение двух лампочек в параллельную цепь с 1.Аккумулятор 5 В. В последовательной цепи две лампочки будут вдвое менее тусклыми при подключении к одному источнику батареи. Однако, если бы две лампочки были подключены параллельно, они были бы столь же яркими, как если бы они были подключены к батарее по отдельности. Поскольку к обеим лампочкам подается одинаковое полное напряжение, батарея также разряжается быстрее, поскольку она по существу обеспечивает полную энергию обеими лампочками.

