Сопротивление в параллельном соединении. Последовательное и параллельное соединение резисторов: особенности, расчеты и применение

Как рассчитать общее сопротивление при последовательном и параллельном соединении резисторов. Что такое делители напряжения и тока. Как решать задачи на комбинированные схемы с резисторами. Какие формулы применяются для расчета сопротивления в сложных цепях.

Особенности последовательного соединения резисторов

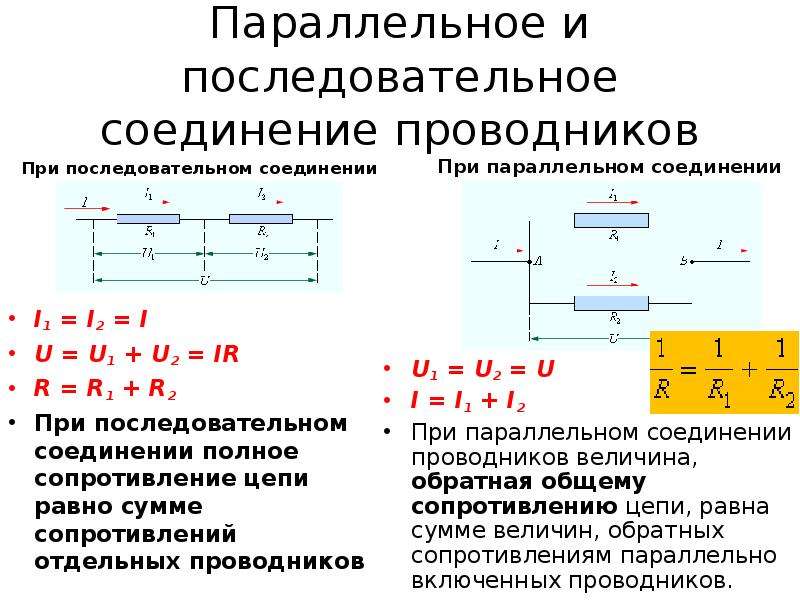
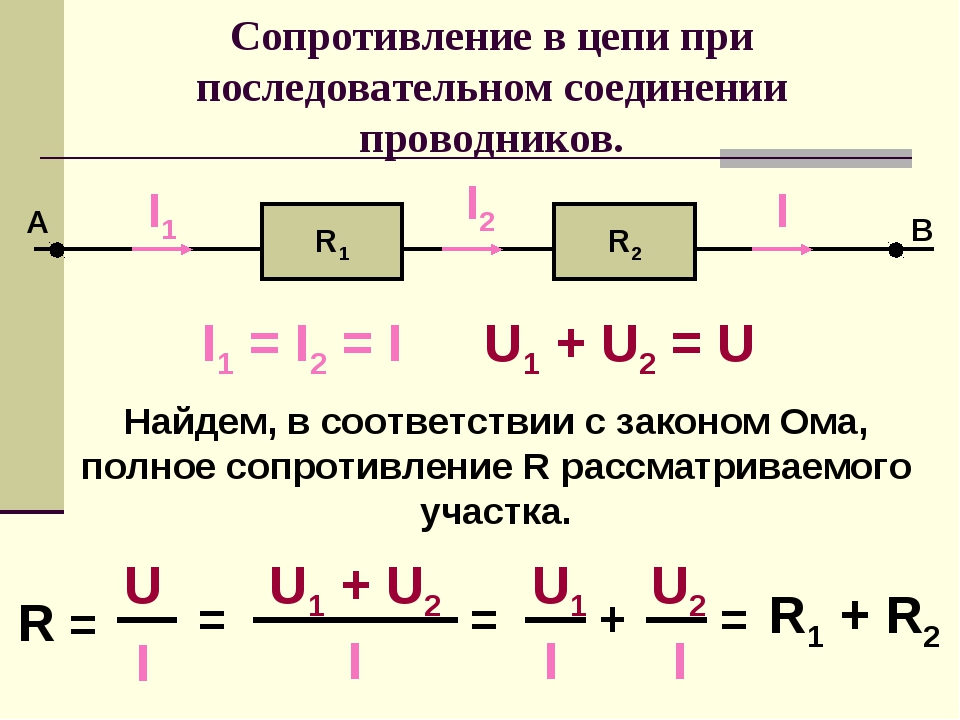
При последовательном соединении резисторы подключаются друг за другом в одну линию. Это приводит к ряду важных особенностей:

• Общее сопротивление цепи увеличивается при добавлении новых резисторов
• Через все резисторы протекает одинаковый ток
• Напряжение распределяется между резисторами пропорционально их сопротивлению

Для расчета общего сопротивления при последовательном соединении используется простая формула суммирования:

R_общ = R₁ + R₂ + R₃ + …

Где R_общ — общее сопротивление цепи, а R₁, R₂, R₃ — сопротивления отдельных резисторов.

Пример расчета последовательного соединения

Рассмотрим схему с тремя последовательно соединенными резисторами:

• R₁ = 100 Ом
• R₂ = 200 Ом
• R₃ = 300 Ом

Общее сопротивление составит:

R_общ = 100 Ом + 200 Ом + 300 Ом = 600 Ом

Как видим, расчет достаточно прост и не требует сложных вычислений.

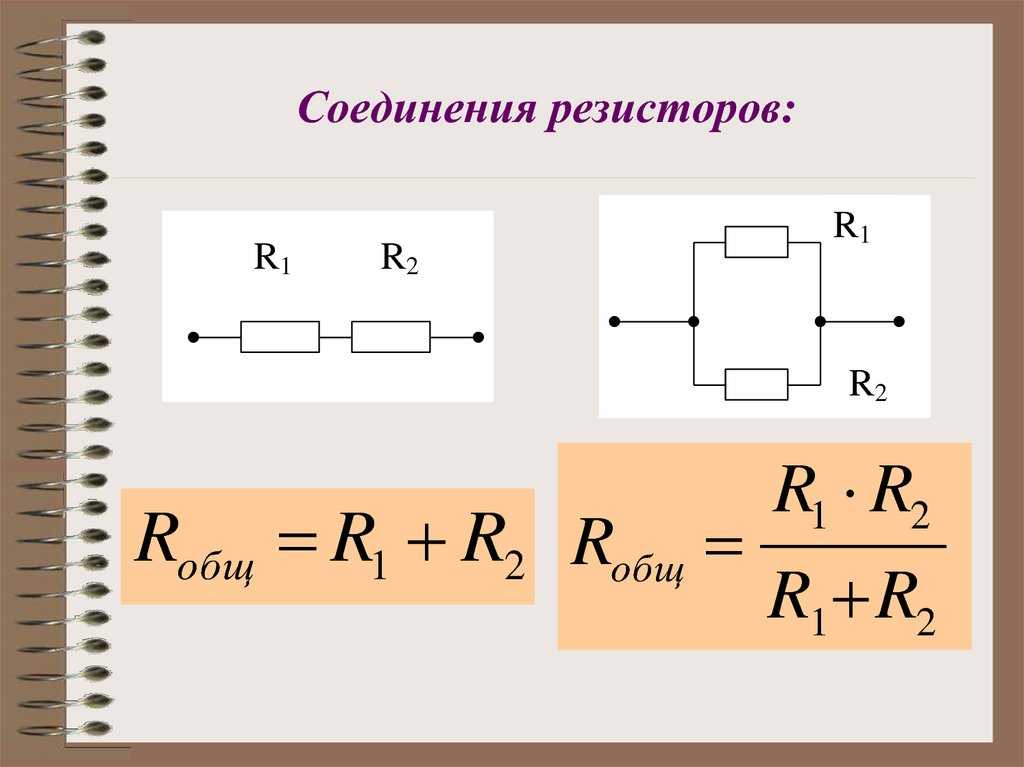
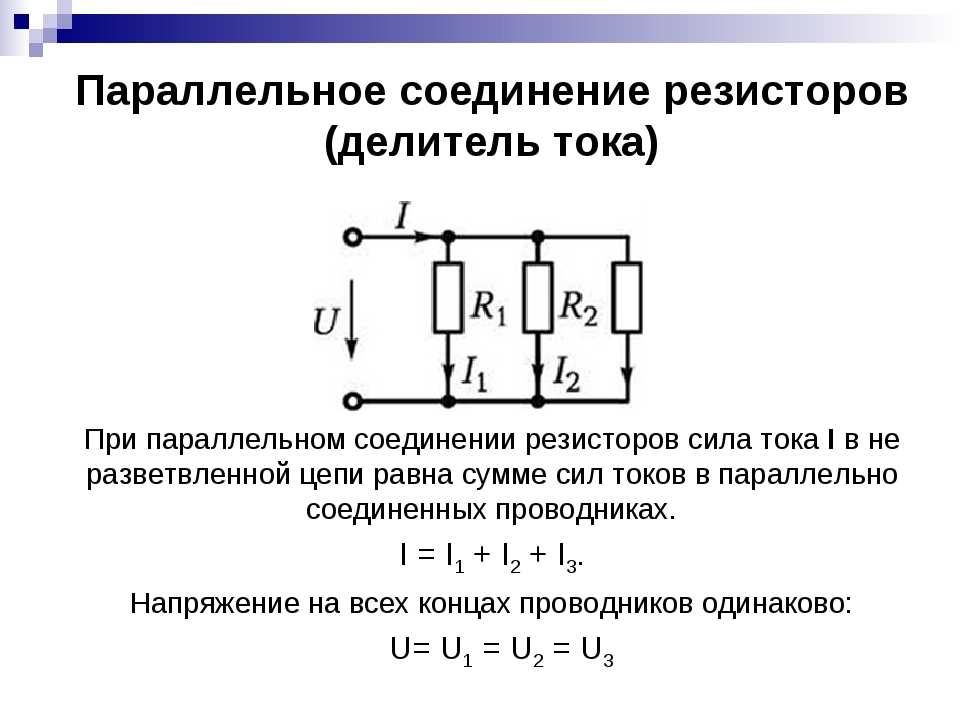
Параллельное соединение резисторов и его свойства

При параллельном соединении резисторы подключаются между одними и теми же двумя точками цепи. Это приводит к следующим особенностям:

• Общее сопротивление цепи уменьшается при добавлении новых параллельных ветвей
• Напряжение на всех резисторах одинаковое
• Ток делится между резисторами обратно пропорционально их сопротивлению

Для расчета общего сопротивления при параллельном соединении используется более сложная формула:

1/R_общ = 1/R₁ + 1/R₂ + 1/R₃ + …

Где R_общ — общее сопротивление, а R₁, R₂, R₃ — сопротивления отдельных параллельных ветвей.

Пример расчета параллельного соединения

Рассмотрим схему с тремя параллельно соединенными резисторами:

• R₁ = 100 Ом
• R₂ = 200 Ом
• R₃ = 300 Ом

Подставляем значения в формулу:

1/R_общ = 1/100 + 1/200 + 1/300 = 0.01 + 0.005 + 0.00333 = 0.01833

Отсюда находим общее сопротивление:

R_общ = 1 / 0.01833 ≈ 54.5 Ом

Как видим, общее сопротивление при параллельном соединении всегда меньше сопротивления любого из резисторов.

Делители напряжения и их применение

Делитель напряжения — это схема из последовательно соединенных резисторов, позволяющая получить на одном из них напряжение, меньшее входного. Такие схемы широко применяются в электронике для снижения напряжения.

Напряжение на любом резисторе делителя рассчитывается по формуле:

U_R = U_вх * R / R_общ

Где U_R — напряжение на резисторе, U_вх — входное напряжение, R — сопротивление резистора, R_общ — общее сопротивление делителя.

Пример расчета делителя напряжения

Рассмотрим делитель из двух резисторов:

• R₁ = 1 кОм
• R₂ = 3 кОм
• U_вх = 12 В

Общее сопротивление делителя:

R_общ = 1 кОм + 3 кОм = 4 кОм

Напряжение на R₁:

U_R1 = 12 В * 1 кОм / 4 кОм = 3 В

Напряжение на R₂:

U_R2 = 12 В * 3 кОм / 4 кОм = 9 В

Таким образом, входное напряжение 12 В разделилось на 3 В и 9 В.

Делители тока в параллельных цепях

Делитель тока — это параллельное соединение резисторов, в котором общий ток распределяется между ветвями обратно пропорционально их сопротивлению. Такие схемы применяются для измерения больших токов и защиты чувствительных приборов.

Ток в любой ветви делителя рассчитывается по формуле:

I_R = I_общ * R_общ / R

Где I_R — ток через резистор, I_общ — общий ток, R_общ — общее сопротивление параллельной цепи, R — сопротивление резистора.

Пример расчета делителя тока

Рассмотрим делитель из двух параллельных резисторов:

• R₁ = 100 Ом
• R₂ = 200 Ом
• I_общ = 300 мА

Общее сопротивление:

1/R_общ = 1/100 + 1/200 = 0.015

R_общ ≈ 66.7 Ом

Ток через R₁:

I_R1 = 300 мА * 66.7 Ом / 100 Ом = 200 мА

Ток через R₂:

I_R2 = 300 мА * 66.7 Ом / 200 Ом = 100 мА

Как видим, ток распределился обратно пропорционально сопротивлениям ветвей.

Комбинированные схемы с последовательно-параллельным соединением

В реальных электрических цепях часто встречаются комбинации последовательного и параллельного соединения резисторов. Расчет таких схем производится поэтапно:

1. Находим эквивалентное сопротивление параллельных участков
2. Заменяем параллельные участки их эквивалентными сопротивлениями
3. Рассчитываем общее сопротивление получившейся последовательной цепи

Пример расчета комбинированной схемы

Рассмотрим схему, где два параллельных резистора R₂ и R₃ соединены последовательно с R₁:

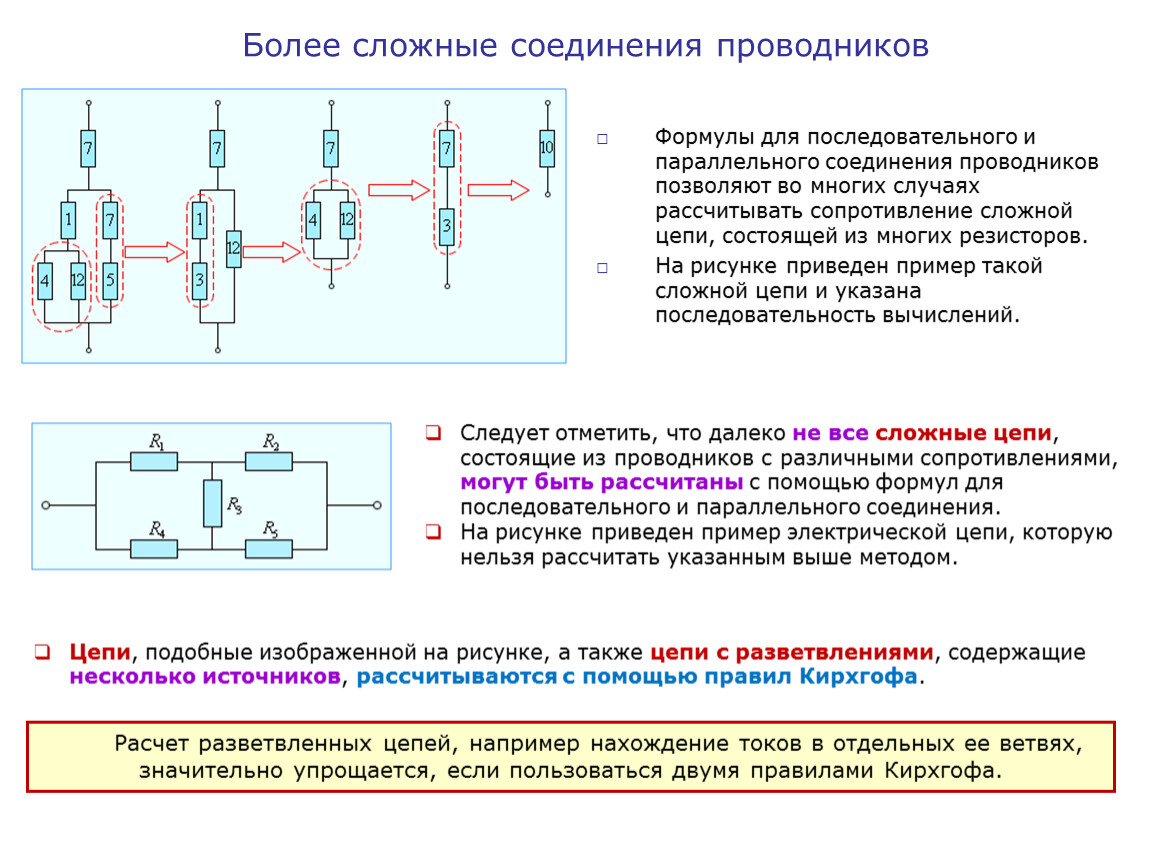
• R₁ = 100 Ом
• R₂ = 200 Ом
• R₃ = 300 Ом

Сначала найдем эквивалентное сопротивление R₂₃ параллельной части:

1/R₂₃ = 1/200 + 1/300 = 0.00833

R₂₃ = 120 Ом

Теперь рассчитаем общее сопротивление последовательной цепи:

R_общ = R₁ + R₂₃ = 100 Ом + 120 Ом = 220 Ом

Таким образом, общее сопротивление комбинированной схемы составляет 220 Ом.

Применение резисторов в электронных схемах

Резисторы широко используются в электронике для решения различных задач:

• Ограничение тока в цепи
• Создание падения напряжения
• Деление напряжения и тока
• Согласование импедансов
• Создание времязадающих цепей
• Линеаризация характеристик нелинейных элементов

Рассмотрим некоторые типичные применения резисторов:

Токоограничивающий резистор

Часто используется для защиты светодиодов. Если известны прямое напряжение светодиода U_LED и требуемый ток I, то сопротивление резистора рассчитывается как:

R = (U_пит — U_LED) / I

Подтягивающий резистор

Применяется для задания определенного логического уровня на входе микроконтроллера. Типичные значения — от 1 кОм до 100 кОм.

Резистор обратной связи

В схемах с операционными усилителями определяет коэффициент усиления. Для инвертирующего усилителя коэффициент усиления равен:

K = -R_ос / R_вх

Расчет мощности резисторов в электрических цепях

При проектировании схем важно правильно выбрать мощность резисторов. Мощность, рассеиваемая на резисторе, рассчитывается по одной из формул:

• P = I² * R
• P = U² / R
• P = U * I

Где P — мощность, I — ток через резистор, U — напряжение на резисторе, R — сопротивление.

Выбранная мощность резистора должна быть в 1.5-2 раза больше расчетной для обеспечения надежной работы.

Пример расчета мощности резистора

Рассмотрим резистор 100 Ом, через который протекает ток 100 мА. Рассеиваемая мощность составит:

P = (0.1 А)² * 100 Ом = 1 Вт

В этом случае следует выбрать резистор мощностью 2 Вт для надежной работы.

резисторов последовательно и параллельно | Комбинации резисторов

Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.

Результаты обучения

• Рассчитайте общее сопротивление различных комбинаций резисторов, т. е. последовательных, параллельных и последовательно-параллельных.
• Покажите, как резисторы используются в качестве делителей напряжения и тока.
• Рассчитайте сопротивление и мощность резистора последовательного падения напряжения.

Отдельные резисторы могут быть соединены последовательно, параллельно или последовательно и параллельно. Это приводит к более сложной схеме, общее сопротивление которой представляет собой комбинацию отдельных резисторов.

Серия

Комбинация резисторов

Чтобы соединить резисторы серии ,  они соединяются встык  в одну линию, как показано на рисунке . Характеристики последовательно соединенных резисторов можно резюмировать следующим образом:

• Общее сопротивление цепи ( R _T ) увеличивается, если дополнительные резисторы соединены последовательно, и уменьшается, если резисторы удалены.
• Чтобы определить общее сопротивление цепи, просто найдите сумму сопротивления отдельных нагрузок.
• В этом примере, если резисторы помечены R ₁ , R ₂ и R ₃ , затем общее сопротивление R _T — вычисленная с использованием Formula R _T — это Calmula R _T . Использование с использованием формы R _T — это Cormula R _T .

  Рис. 1 Резисторы соединены последовательно.

  ПРИМЕР 1

  Проблема: Три резистора, R ₁ (4 Ом), R ₂ (50 Ом) и R ₃ (75 Ом) подключены в серии. 2 . Определить значение общего сопротивления комбинированной цепи.

  Рисунок 20005 Рисунок 3 . Делители напряжения широко используются в цепях, где один источник напряжения должен обеспечивать несколько разных значений напряжения для разных частей цепи.

  Характеристики схемы последовательного делителя напряжения можно резюмировать следующим образом:

  • Одинаковая величина тока протекает через каждый резистор.
  • Входное напряжение распределяется пропорционально между последовательно соединенными резисторами.
  • Падение напряжения на резисторе в последовательной цепи прямо пропорционально омическому сопротивлению резистора.
  • Чем выше значение сопротивления, тем больше падение напряжения.

  Рисунок 3  Схема делителя напряжения.

  Для схемы делителя напряжения падение напряжения на каждом резисторе обычно является фактором, который необходимо определить. Падение напряжения на любом резисторе пропорционально отношению его сопротивления к общему сопротивлению цепи.

  Формула делителя напряжения позволяет рассчитать падение напряжения на любом из последовательно соединенных резисторов без предварительного расчета значения тока в цепи. Формула:

  Пример 2

  Резисторы R ₁ (5 кОм), R ₂ (3 Kω) и R ₃ (2 Kω подключены к сериям). для формирования делителя напряжения, как показано на рис. 4 . Если к цепи приложено входное напряжение 9 вольт, рассчитайте значение падения напряжения на каждом из резисторов, используя формулу делителя напряжения.

  Рисунок 4  Схема для примера 2. 9Пример 3 Рисунок 5 ). Определите значение последовательного сопротивления падению и требуемую мощность. Рисунок 5  Схема для примера 30006

  Резисторы соединяются параллельно , соединяя их бок о бок  поперек друг друга, как показано на Рис. 6 . Обратите внимание, что два конца резисторов подключены к одним и тем же двум точкам.

  Характеристики параллельно соединенных резисторов можно резюмировать следующим образом:

  • Общее сопротивление (R _T ) образованной цепи на меньше, чем на  наименьшее значение сопротивления, присутствующего в любой из ветвей.
  • Каждый резистор обеспечивает отдельный параллельный путь для протекания тока.
  • Если у вас параллельно подключено несколько резисторов одинакового номинала, то общее сопротивление проще всего найти, разделив общее значение сопротивления на количество подключенных резисторов. Для трех 150-омных резисторов, соединенных параллельно, общее сопротивление составляет

  . Рисунок 6. Резисторы, соединенные параллельно.

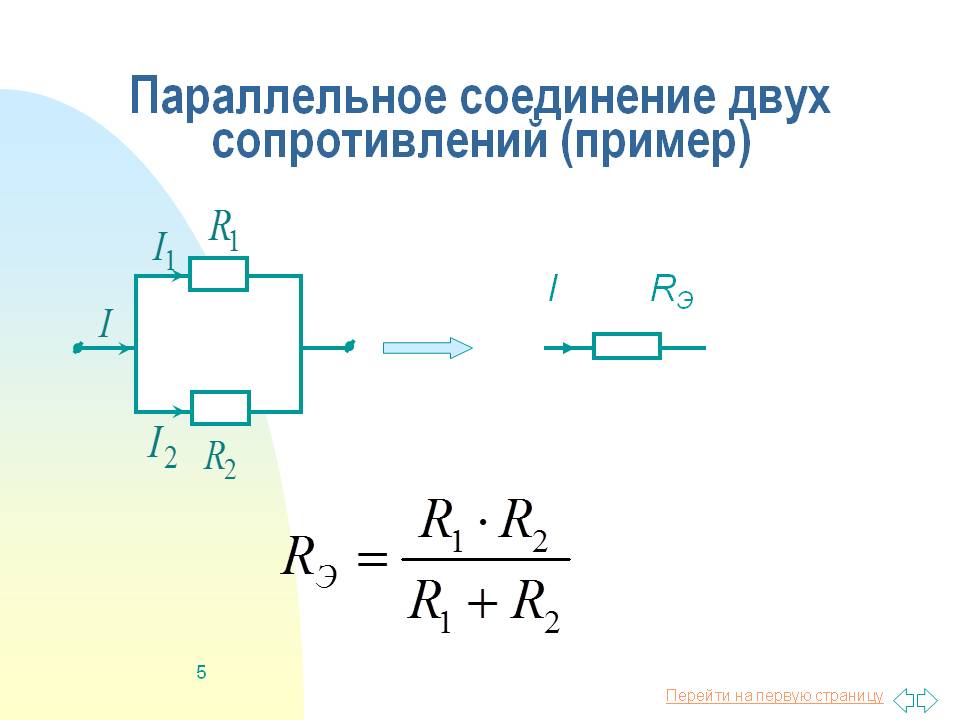
  Чтобы найти общее сопротивление двух параллельно соединенных резисторов разного номинала (очень распространенное применение), используется формула произведения на сумму. Эта формула 9Пример 4 Определите значение общего комбинированного сопротивления двух элементов, используя формулу произведения на сумму. Рис. 7 Там, где параллельно подключено более двух резисторов, их использование становится более сложным и менее практичным. Для более чем двух параллельно соединенных резисторов разного номинала используется общая формула для полного сопротивления параллельной цепи. Эта формула

  EXAMPLE 5

  Problem:  Three resistors,  R ₁  (120 Ω),  R ₂  (60 Ω), and  R ₃  (40 Ω) соединены параллельно, как показано на  Рисунок 8 . Определить значение общего сопротивления комбинированной цепи.

  Рис.80005 делители тока  потому что ток разделяется или делится между различными резисторами, как показано на  рис. 9 .

  Характеристики параллельной схемы делителя тока можно резюмировать следующим образом:

  • Ток, протекающий через каждый ответвленный резистор, обратно пропорционален значению его сопротивления.
  • Чем меньше значение сопротивления, тем больше ток, и наоборот.
  • Резисторы с одинаковым омическим сопротивлением будут иметь одинаковую величину тока через них.
  • Формула, описывающая делитель тока, аналогична формуле для делителя напряжения и может быть выражена следующим образом:

  Пример 6

  Проблема: Резисторы R ₁ R ₂ и R ₃ (2 ω, 3 ω и 6 ω, соответственно), подключены параллель), подключены к паралле. как показано на Рис. 10 . Используйте формулу делителя тока, чтобы вычислить значение тока, протекающего через каждый из нагрузочных резисторов, если общий ток, протекающий по цепи, составляет 10 ампер.

  Рисунок 10 Схема, например 6.

  Решение:

  Пример 7

  Задача: Поскольку дополнительные нагрузки подключены к параллелю Общее сопротивление цепи .  Для схемы, показанной на  Рисунок 11 , определите общее сопротивление цепи при каждом из следующих рабочих условий:

  1. Переключатели 1 и 2 замкнуты.
  2. Переключатели 1, 2 и 3 замкнуты.

  Рисунок 11 Схема, например, 7.

  Решение:

  СЕРИЯ ПАРЕЛЕЛЬНА СЕРИЯ КОМБОЛОВА резисторы последовательно с резисторами параллельно, как показано на Рисунок 12 .

  Правила, регулирующие эти цепи, такие же, как и правила, разработанные для последовательных и параллельных цепей. Сначала находится сопротивление объединенного полного сопротивления параллельного участка. Затем к любому последовательному сопротивлению прибавляется полное сопротивление параллельной части, чтобы найти общее сопротивление последовательно-параллельной комбинированной цепи.

  Рисунок 12  Последовательно-параллельное соединение резисторов.

  ПРИМЕР 8

  Задача: Резистор 9 Ом,

  R ₁ , и резистор 60 Ом, R ₂ , соединены последовательно друг с другом 40 Резистор Ом, R ₃ , как показано на Рисунок 13 . Определить общее сопротивление этой последовательно-параллельной комбинации резисторов.

  Рисунок 13  Схема для примера 8.

  Решение:

  ПРИМЕР 9

  Проблема:  Показания сопротивления можно использовать для проверки цепей на наличие неисправностей. Как определено в предыдущем примере, нормальное общее сопротивление этой последовательно-параллельной схемы Рисунок 14 составляет 60 Ом.

  1. Определите, какое новое значение R _T  было бы, если бы резистор R ₁  был поврежден
     размыкался  при значениях сопротивления R ₂ и R ₃ остаются прежними.
  2. Аналогично, найдите, каким будет новое значение R _T , должно быть резистор R ₃ Будьте из строя . одинаковый. Рис. 14. Схема для примера ₁ разомкнут, цепь будет состоять из R ₃ последовательно с R ₂ , а общее сопротивление будет: 1  параллельно R ₂  и общее сопротивление будет:

  Контрольные вопросы

  1. Рассчитайте общее сопротивление для каждой из следующих цепей резисторов:
     1. Последовательная цепь: R1=40 Ом, R2=75 Ом
     2. Параллельная цепь: R1=200 Ом, R2=200 Ом, R3=200 Ом
     3. Последовательная цепь: R1=2000 Ом, R2=6000 Ом, R3=2200 Ом
     4. Параллельная цепь: R1=14 Ом, R2=32 Ом
     5. Последовательная цепь: R1=4700 Ом, R2=800 Ом, R3=200 Ом
     6. Параллельная цепь: R1=60 Ом, R2=30 Ом, R3 = 15 Ом
  2. Резисторы R ₁ , R ₂ и R ₃ (50 Ом, 30 Ом и 20 Ом соответственно) соединены по применению. 200 В для формирования делителя напряжения. Используя формулу делителя напряжения, рассчитайте напряжения  E ₁ , E ₂ и E ₃ .
  3. Суммарный ток двух параллельно соединенных резисторов равен 3 А. Сопротивление R ₁ равно 10 Ом, а сопротивление R ₂ равно 40 Ом. Используя формулу делителя тока, вычислите токи I ₁ и I ₂ .
  4. Резистор 5 Ом, R ₁ и резистор 20 Ом, R ₂ , соединены параллельно друг с другом и последовательно с резистором 6 Ом, R ₃ . Вычислите полное сопротивление этой последовательно-параллельной цепи.
  5. Вам дали три резистора по 100 Ом, которые нужно соединить вместе. Опишите три возможных конфигурации цепей и рассчитайте значения их полного сопротивления.

  Контрольные вопросы – ответы

  1. (a) 115 Ом, (b) 66,7 Ом, (c) 10 200 Ом, (d) 9,74 Ом, (e) 5700 Ом, (f) 8,57 Ом
  2. E ₁ = 100 В, E ₂ = 60 В, E ₃ = 40 В
  3. I ₁ = 2,4 A, I ₂ = 0,6 A
  4. 10 ω
  5. Три 100.