Как рассчитать сопротивление при последовательном и параллельном соединении проводников. Какие законы используются для вывода формул сопротивления. Как распределяются токи и напряжения в цепи при разных типах соединений. Примеры решения задач.
Основные виды соединения проводников в электрической цепи
В электротехнике существует три основных способа соединения проводников в цепи:
- Последовательное соединение
- Параллельное соединение
- Смешанное соединение
Каждый тип соединения имеет свои особенности и законы распределения токов и напряжений. Рассмотрим подробнее последовательное и параллельное соединение проводников.
Последовательное соединение проводников
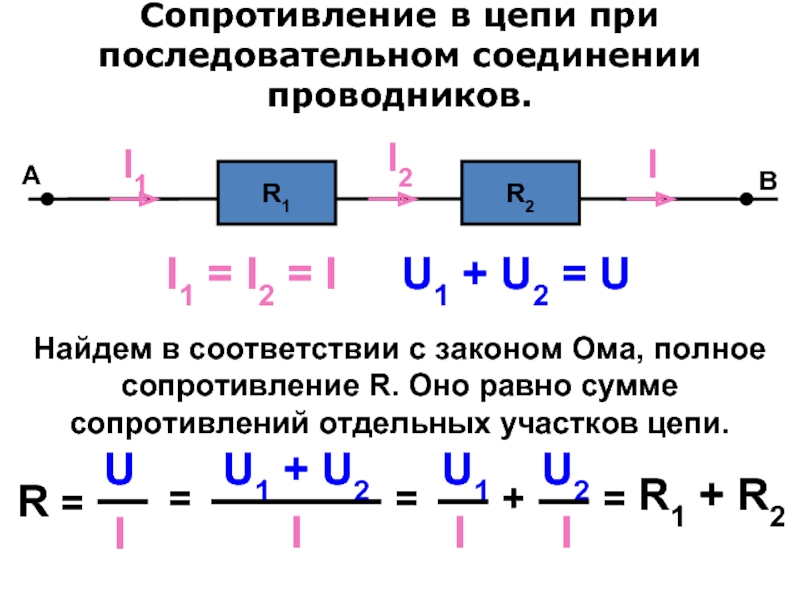
При последовательном соединении проводники соединяются друг за другом, образуя единую неразветвленную цепь. Конец первого проводника соединяется с началом второго, конец второго — с началом третьего и так далее.
Основные закономерности при последовательном соединении
- Сила тока одинакова во всех проводниках цепи: I = I1 = I2 = I3
- Общее напряжение равно сумме напряжений на отдельных проводниках: U = U1 + U2 + U3
- Общее сопротивление равно сумме сопротивлений отдельных проводников: R = R1 + R2 + R3
Как рассчитать общее сопротивление при последовательном соединении?
Формула для расчета общего сопротивления при последовательном соединении:

R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление цепи, R1, R2, R3, …, Rn — сопротивления отдельных проводников.
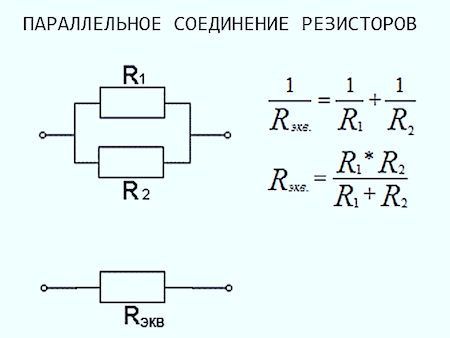
Параллельное соединение проводников
При параллельном соединении все проводники присоединяются одними концами к одной точке цепи, а другими концами — к другой точке. Образуется разветвленный участок с несколькими параллельными ветвями.
Основные закономерности при параллельном соединении
- Напряжение одинаково на всех проводниках: U = U1 = U2 = U3
- Общий ток равен сумме токов в отдельных проводниках: I = I1 + I2 + I3
- Величина, обратная общему сопротивлению, равна сумме величин, обратных сопротивлениям отдельных проводников: 1/R = 1/R1 + 1/R2 + 1/R3
Как рассчитать общее сопротивление при параллельном соединении?
Формула для расчета общего сопротивления при параллельном соединении:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
или
R = 1 / (1/R1 + 1/R2 + 1/R3 + … + 1/Rn)
где R — общее сопротивление цепи, R1, R2, R3, …, Rn — сопротивления отдельных проводников.

Распределение токов и напряжений в цепи
Как распределяются токи и напряжения при последовательном соединении?
При последовательном соединении:
- Ток одинаков во всех элементах цепи
- Напряжение распределяется пропорционально сопротивлениям элементов
- Чем больше сопротивление участка, тем больше падение напряжения на нем
Как распределяются токи и напряжения при параллельном соединении?
При параллельном соединении:
- Напряжение одинаково на всех параллельных ветвях
- Общий ток делится между ветвями обратно пропорционально их сопротивлениям
Законы, используемые для вывода формул сопротивления
При выводе формул сопротивления для последовательного и параллельного соединения используются следующие законы:
- Закон Ома для участка цепи: I = U / R
- Первый закон Кирхгофа: сумма токов, втекающих в узел, равна сумме вытекающих токов
- Второй закон Кирхгофа: сумма напряжений в замкнутом контуре равна нулю
Эти фундаментальные законы электротехники позволяют вывести все необходимые соотношения для расчета параметров электрических цепей с различными типами соединений проводников.

Примеры решения задач
Задача на последовательное соединение
Три резистора с сопротивлениями 2 Ом, 3 Ом и 5 Ом соединены последовательно. Определить общее сопротивление цепи.
Решение:
Используем формулу для последовательного соединения:
R = R1 + R2 + R3 = 2 Ом + 3 Ом + 5 Ом = 10 Ом
Ответ: общее сопротивление цепи равно 10 Ом.
Задача на параллельное соединение
Два резистора с сопротивлениями 6 Ом и 3 Ом соединены параллельно. Найти общее сопротивление участка цепи.
Решение:
Используем формулу для параллельного соединения:
1/R = 1/R1 + 1/R2 = 1/6 + 1/3 = 1/2
R = 1 / (1/2) = 2 Ом
Ответ: общее сопротивление участка цепи равно 2 Ом.
Практическое применение знаний о соединении проводников
Понимание принципов последовательного и параллельного соединения проводников имеет важное практическое значение:
- Позволяет правильно рассчитывать и проектировать электрические цепи
- Помогает выбирать оптимальные схемы соединения элементов в электронных устройствах
- Дает возможность эффективно управлять распределением токов и напряжений в сложных электрических системах
- Необходимо для безопасной эксплуатации электрооборудования
Владение этими знаниями — важная компетенция для специалистов в области электротехники, электроники и энергетики.

Лабораторная работа №5
Лабораторная работа №5ЛАБОРАТОРНАЯ
РАБОТА №5
Исследование сопротивлений резисторов при смешанном соединении.
Цель работы: опытным путем изучить законы протекания тока через последовательно и параллельно соединенные проводники и определить формулы расчета сопротивлений таких участков.
1.Пояснение к работе
Краткие теоретические сведения
Последовательным соединением
сопротивлений называется такое соединение,
при котором конец первого сопротивления соединяется с началом второго,
конец второго — с началом третьего и т. д.
Общее сопротивление последовательно
соединенных
резисторов равно сумме их сопротивлений.
Rобщ. =R1+R2+R3
=R1+R2+R3
Rобщ=5ом+10ом+25ом=40ом
Величина тока в последовательной цепи
Так как в данной цепи отсутствует
ответвление тока,
то
очевидно, что количество электричества, протекающее через поперечное
сечение проводника за единицу времени. в любой точке цепи будет
одинаковым.
Следовательно во всех точках
последовательной
цепи
величина тока одинакова.
Эти четыре амперметра покажут одинаковые величины
тока.
Поэтому при
последовательном соединении для измерения тока достаточно
включать один амперметр на любом участке цепи.
Распределение
напряжения в последовательной цепи
Напряжение источника тока приложенное к внешнему участку цепи распределяется по участкам цепи прямо пропорционально сопротивлениям этих участков.
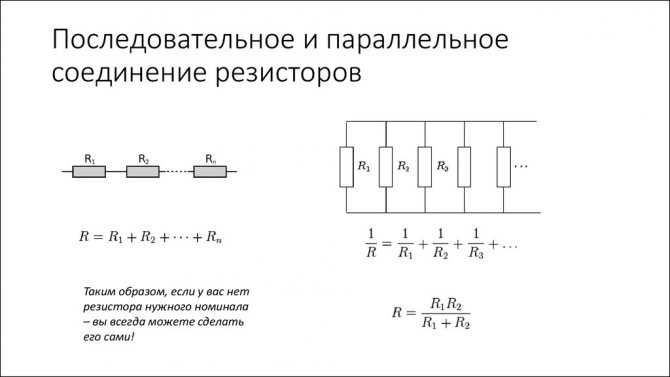 Напряжение
приложенное к каждому из этих резисторов определяется по
формуле:
Напряжение
приложенное к каждому из этих резисторов определяется по
формуле:Так как ток в последовательной цепи везде одинаков значит действительно напряжение на ее участках зависит от сопротивления чем больше сопротивление тем большее напряжение приложено к данному участку.
Сумма напряжений на участках последовательной цепи равна напряжению источника тока
Параллельным соединением сопротивлений называется
такое соединение, при
котором к одному зажиму источника подключаются начала сопротивлений, а
к другому зажиму — концы.
Общее сопротивление параллельно включенных сопротивлений определяется по формуле:
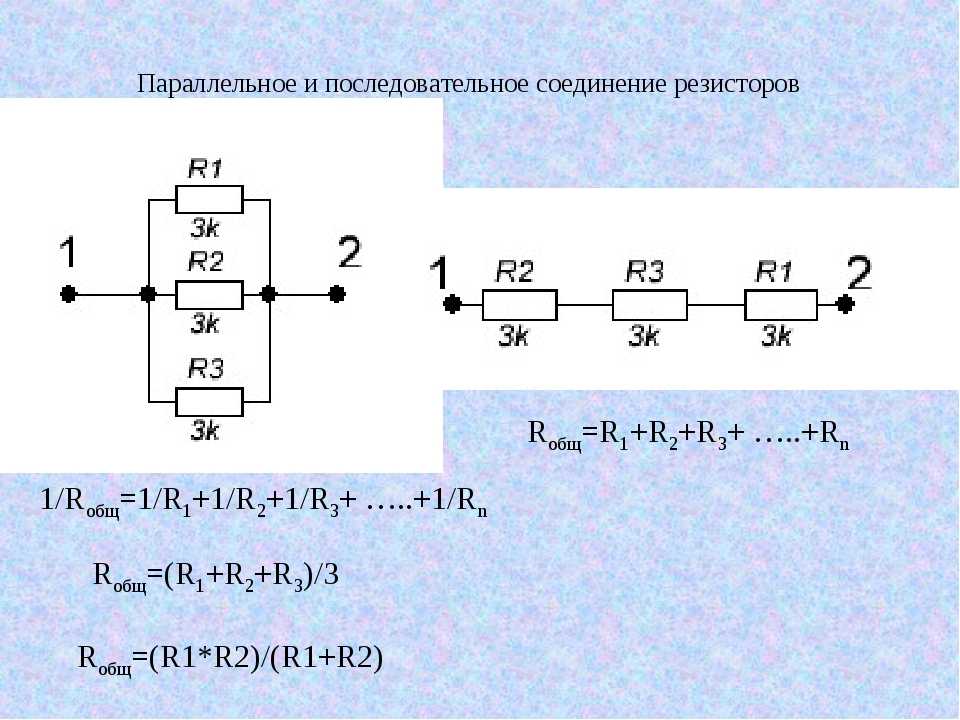
На вышеуказанном рисунке мы можем сразу сказать что общее сопротивление будет меньше 10 ом.
Первый частный случай
Если параллельно включено только два резистора то
их общее сопротивление можно определить по формуле:
Второй частный случай
Если параллельно включено любое
количество резисторов одинаковых сопротивлений то их общее
сопротивление можно определить если сопротивление одного
резистора разделить на количество резисторов.
Распределение токов и напряжения в параллельных ветвях
Так как начала всех сопротивлений сведены в одну общую точку, а концы -
в другую, то очевидно, что разность потенциалов на концах любого из
параллельно включенных сопротивлений равна разности потенциалов между
общими точками.
Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.

Если разветвление подключено непосредственно к зажимам источника тока, то напряжение на каждом из сопротивлений равно напряжению на зажимах источника.
Второе свойство цепи с параллельным соединением заключается в том, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям.
Это значит что, чем больше сопротивление, тем меньше по нему пойдет ток.
Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, I3 утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду утекающему от нее:
Следовательно, третье свойство параллельного соединения может сформулирована так:
Величина
тока в не разветвленной части цепи равна сумме токов в параллельных
ветвях.
2.Техническое задание
2.1.Собрать электрическую цепь (рисунок 1)
Рисунок
1. Схема электрическая
принципиальная.
2.2.Снять показания приборов и записать их в таблицу
2.3.Произвести расчеты
2.4.Ответить на контрольные вопросы
2.5. Сделать вывод
3.Работа в лаборатории
3.1. Собрать схему (Рисунок 2).
Рисунок 2. Схема исследования.
3.2.
Установить на схеме величины R1=1
кОм + N, R2=2
кОм + N, R3=3
кОм + N и R4=4
кОм + N,
3.
 3. Включить
источник и установить напряжение U=15 В, 24 В.
3. Включить
источник и установить напряжение U=15 В, 24 В.3.4. Определите экспериментально с помощью мультиметра (в режиме измерения сопротивлений) сопротивление между точками:
А и С; С и D; B и D; A и D.
3.5. Рассчитайте теоретические значения сопротивлений между указанными точками схемы и сравните их с измеренными.
3.6. Измерьте с помощью мультиметра (в режиме измерения тока) токи, текущие через каждое сопротивление. Запишите показания прибора в таблицу 2.
3.7. Проверьте экспериментально, что в последовательной цепи ток одинаков через все сопротивления, а в параллельной цепи разделяется так, что сумма всех токов через параллельно соединенные элементы, равна полному току через весь участок.
3.8. Измерьте с помощью мультиметра (в режиме измерения постоянного напряжения) напряжения на каждом сопротивлении.
 Запишите показания
прибора в таблицу 2.
Запишите показания
прибора в таблицу 2.3.9. Проверьте экспериментально, что в последовательной цепи напряжение на всем участке равно сумме напряжений на каждом элементе, а в параллельной цепи, напряжение одно и то же на каждом элементе.
3.10. Отключить схему.
Таблица 1 — Расчитанные параметры
|
№ вар. |
Установлено |
Рассчитано |
||||||
|
R1 |
R2 |
R3 |
R4 |
А — С |
С — D |
B — D |
A-D |
|
|
кОм |
кОм |
кОм |
кОм |
кОм |
кОм |
кОм |
кОм |
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 — Измеренные параметры
|
№ изм. |
U |
I |
I1 |
I2 |
I3 |
I4 |
U1 |
U2 |
U3 |
U3 |
|
В |
А |
А |
А |
А |
А |
В |
В |
В |
В |
|
|
1 |
15 |
|
|
|
|
|
|
|
|
|
|
2 |
24 |
|
|
|
|
|
|
|
|
|
4.
 Содержание отчета
Содержание отчета4.1. Название и цель работы
4.2. Схемы
4.3. Таблицы
4.4. Ответы на контрольные вопросы
4.5. Вывод
5.Контрольные вопросы
5.1. Может ли сопротивление участка двух параллельно соединенных проводников быть больше (меньше) любого из них? Объясните ответ.
5.2. Какие законы сохранения используются для вывода формул сопротивления параллельного и последовательного соединения проводников?
Назад в оглавление
Сайт создан в системе uCoz
Соединение проводников. Школьный курс физики
Главная | Физика 11 класс | Соединение проводников
Электрические цепи. Разветвлённые цепи.
Энергия передаётся от источника тока к потребителям (лампам, электродвигателям, радиоприёмникам и т. д.) по проводам. Источник тока, потребители (как правило, их несколько), соединительные провода и выключатели образуют электрическую цепь. Часто в цепь включают измерительные приборы — амперметры и вольтметры. Все элементы электрической цепи определённым образом соединяют между собой. На практике проводники чаще всего соединяют последовательно или параллельно.
д.) по проводам. Источник тока, потребители (как правило, их несколько), соединительные провода и выключатели образуют электрическую цепь. Часто в цепь включают измерительные приборы — амперметры и вольтметры. Все элементы электрической цепи определённым образом соединяют между собой. На практике проводники чаще всего соединяют последовательно или параллельно.
Очень часто в электрических цепях в одной точке сходится несколько (больше двух) проводников. Например, при включении вольтметра для измерения напряжения на зажимах лампы (рис. 1.16) в точках 1 и 2 сходится по три проводника. Такие точки называются точками разветвления или узлами.
Рис. 1.16
На рисунке 1.17 в точке разветвления А цепи сходятся пять проводников.
Рис. 1.17
Обозначим силу тока в них через I1, I2, I3, I4 и I5. Из рисунка видно, что токи I1, I2 и I3 направлены к узлу и за произвольный промежуток времени Δt приносят в этот узел суммарный заряд (I1 + I2 + I3)Δt. Токи I4 и I5 направлены от узла и уносят за это же время заряд (I1 + I3)Δt. Полное изменение заряда в узле за промежуток времени Δt равно
Из рисунка видно, что токи I1, I2 и I3 направлены к узлу и за произвольный промежуток времени Δt приносят в этот узел суммарный заряд (I1 + I2 + I3)Δt. Токи I4 и I5 направлены от узла и уносят за это же время заряд (I1 + I3)Δt. Полное изменение заряда в узле за промежуток времени Δt равно
В цепи постоянного тока потенциалы всех точек цепи, а следовательно, и узлов должны оставаться неизменными. Следовательно, в них не могут накапливаться ни положительные, ни отрицательные заряды. В частности, для узла А изменение заряда Δq должно равняться нулю для любого интервала времени, т. е.
е.
Рассматривая силу тока как алгебраическую величину, имеющую знак «плюс», если ток подходит к узлу, и знак «минус», если ток направлен от узла, последнее равенство можно записать в виде
Если в узле сходятся N токов, то
Алгебраическая сумма сил токов в проводниках, сходящихся в узле, равна нулю.
Это утверждение называют первым правилом Кирхгофа в честь немецкого физика Густава Кирхгофа (1824—1897), который в 1847 г. установил правила расчёта электрических цепей.
Последовательное соединение проводников.
Последовательным соединением проводников называют соединение, при котором конец первого проводника соединяется с началом второго проводника, конец второго проводника — с началом третьего и т. д.
Рис. 1.18
На рисунке 1.18 показано последовательное соединение трёх проводников, имеющих сопротивления R1, R2 и R3.
При последовательном соединении проводников выполняются следующие соотношения.
1. Сила тока во всех последовательно соединённых проводниках одинакова:
I1 = I2 = I3 = I.
2. Напряжение (или разность потенциалов) на концах рассматриваемого участка цепи равно сумме напряжений на отдельных проводниках:
U = U1 + U2 + U3. (1)
Действительно: U1 = φ0 — φ1; U2 = φ1 — φ2 и U3 = φ2 — φ3. Складывая U1, U2 и U3, получим φ0 — φ3 = U. В справедливости равенства (1) можно убедиться и непосредственным измерением при помощи вольтметра напряжений на всём участке цепи и на отдельных проводниках.
3. Согласно закону Ома, напряжения на отдельных проводниках равны: U1 = IR1, U2 = IR2, U3 = IR3.
Отсюда следует, что
При последовательном соединении напряжения на проводниках пропорциональны их сопротивлениям.
4. Разделив равенство (1) почленно на силу тока I, получим
где R — сопротивление всего рассматриваемого участка цепи.
Сопротивление участка цепи, состоящего из нескольких последовательно соединённых проводников (общее сопротивление), равно сумме сопротивлений отдельных проводников.
Параллельное соединение проводников.
Параллельным соединением проводников называют соединение, когда одни концы всех проводников соединяются в один узел (А), а другие концы — в другой узел (В) (рис. 1.19).
Рис. 1.19
При параллельном соединении различают ветви — отдельные проводники между узлами, разветвление — часть цепи между двумя узлами и неразветвлённую часть цепи, лежащую вне разветвления.
При параллельном соединении выполняются следующие соотношения.
1. Напряжения на всех ветвях и на разветвлении одинаковы, так как все они равны разности потенциалов точек А и В цепи:
U1 = U2 = U3 = U = φA — φB
2. Согласно первому правилу Кирхгофа, можно записать:
I = I1 + I2 + I3. (2)
Сила тока в неразветвлённой части цепи равна сумме сил токов в ветвях.
3. Согласно закону Ома для участка цепи,
Отсюда следует, что
Силы токов в ветвях обратно пропорциональны сопротивлениям этих ветвей.
4. Сопротивлением разветвления R называют сопротивление такого проводника, которым можно заменить разветвление без изменения силы тока в неразветвлённой части цепи и напряжения между узлами. Используя закон Ома, заменим в равенстве (2) значения сил токов:
Разделив обе части равенства на U, получим
Величина, обратная сопротивлению разветвления, равна сумме величин, обратных сопротивлениям отдельных ветвей.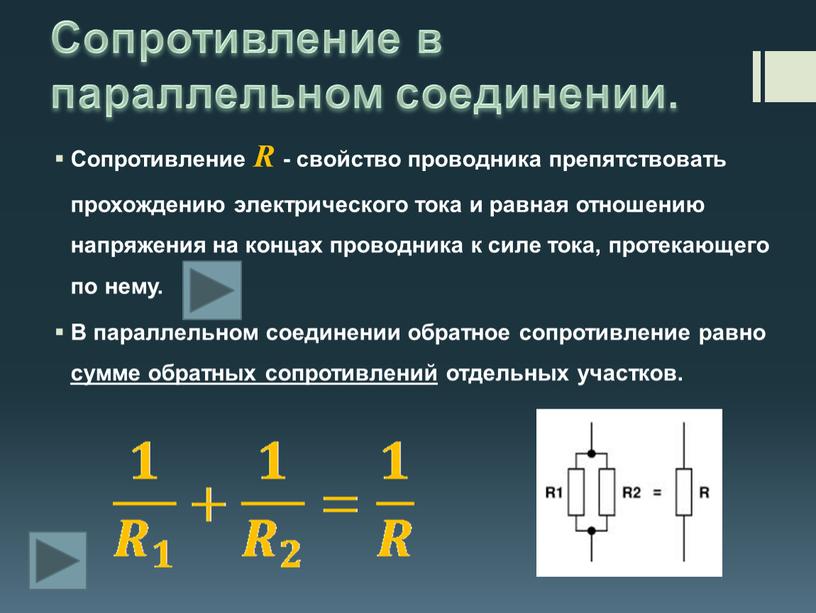
Учитывая, что 1/R = G, можно записать:
G = G1 + G2 + G3.
Проводимость разветвления равна сумме проводимостей отдельных ветвей.
Отметим, что сопротивление разветвления меньше наименьшего из сопротивлений его ветвей. В самом деле, пусть сопротивление і-й ветви является наименьшим, тогда из равенства
следует, что (сумма больше каждого из отдельных слагаемых).
Отсюда R < R1.
Если разветвление состоит из двух ветвей, то
Если сопротивления отдельных ветвей равны между собой:
Общее сопротивление п одинаковых, параллельно соединённых проводников равно сопротивлению одного проводника, делённому на их число.
Смешанное соединение проводников.
Смешанным соединением проводников называют соединение в цепи, в которой имеются и последовательное, и параллельное соединения проводников. На рисунке 1.20 в качестве примера приведена схема смешанного соединения проводников.
На рисунке 1.20 в качестве примера приведена схема смешанного соединения проводников.
Рис. 1.20
В цени имеются два последовательно соединённых участка: участок АВ, состоящий из одного резистора Rl, и участок ВС, состоящий из двух параллельных ветвей.
Так как одна параллельная ветвь имеет сопротивление R2 + R3 (ветвь содержит два последовательно соединённых резистора R2 и R3), а вторая — R4, то сопротивление участка BC равно
а общее сопротивление всех участков цепи
Вопросы:
1. Какие точки цепи называют разветвлениями или узлами?
2. В чём заключается первое правило Кирхгофа?
3. Какое соединение проводников в цепи называют:
а) последовательным;
б) параллельным;
в) смешанным?
4. Запишите основные соотношения, которые выполняются для:
Запишите основные соотношения, которые выполняются для:
а) последовательного соединения;
б) параллельного соединения трёх проводников в цепи.
Вопросы для обсуждения:
1. В ёлочной гирлянде электрические лампочки соединены последовательно. К ней последовательно подключили ещё две лампочки.
Как изменится сила тока в цепи, если напряжение на концах гирлянды осталось тем же?
2. Три одинаковых резистора, сопротивлением R каждый, включены в цепь так, как показано на рисунке 1.21. Каким будет сопротивление между точками А и В?
Рис. 1.21
Пример решения задачи
Напряжение между точками А и В участка цепи, схема которого изображена на рисунке 1.22, составляет 90 В.
Рис. 1.22
Сопротивление лампы Л2 равно сопротивлению лампы Лl, а сопротивление лампы Л3 в 4 раза больше сопротивления лампы Лl. Сила тока, текущего через лампу Лl, равна 0,5 А. Найдите сопротивление каждой лампы, напряжение на лампах Л2 и Л3 и силу тока в них.
Сила тока, текущего через лампу Лl, равна 0,5 А. Найдите сопротивление каждой лампы, напряжение на лампах Л2 и Л3 и силу тока в них.
Упражнения:
1. Четыре электрические лампы, рассчитанные на напряжение 3 В и силу тока 0,1 А, нужно включить параллельно к источнику с напряжением 5,4 В. Резистор какого сопротивления следует подключить последовательно лампам?
2. В сеть с напряжением 220 В включены последовательно десять электрических ламп с сопротивлением по 24 Ом, рассчитанных на напряжение 12 В. Определите силу тока в цепи и сопротивление реостата, который необходимо включить в цепь.
3. Электрическую лампу с сопротивлением 240 Ом, рассчитанную на напряжение 120 В, нужно подключить к сети с напряжением 220 В. Какой длины нихромовый проводник с площадью поперечного сечения 0,55 мм2 следует подключить последовательно с лампой?
4. Чему равно сопротивление цепи, схема которой показана на рисунке 1. 24, если сопротивление каждого резистора R?
24, если сопротивление каждого резистора R?
Рис. 1.24
Предыдущая страницаСледующая страница
Подробная информация – Lambda Geeks
Существует множество методов поиска параллельного сопротивления, которые мы рассмотрим в этой статье. В отличие от последовательных резисторов, резисторы, соединенные параллельно, имеют разные методы расчета эквивалентного сопротивления.
Предположим, у нас есть два резистора R 1 и R 2 , как показано на рисунке 1. Мы знаем, что общий ток в параллельной цепи = сумма токов ветвей.
Следовательно, [Latex] i = \frac{V} {R_{1}}+ \frac{V} {R_{2}} [/Latex] (потенциалы A и B одинаковы) 9{-1} [/Latex]
Как найти параллельное сопротивление – часто задаваемые вопросы
Как найти параллельное сопротивление для n резисторов?
Метод расчета эквивалентного сопротивления для более чем двух резисторов аналогичен. На рисунке 2 изображена цепь, состоящая из n параллельно расположенных резисторов. Найдем эквивалентное сопротивление в этом случае.
На рисунке 2 изображена цепь, состоящая из n параллельно расположенных резисторов. Найдем эквивалентное сопротивление в этом случае.
Мы знаем из закона Ома,
- Каждая ветвь имеет одинаковое напряжение = В 9{-1} [/Latex]
Мы можем заменить значения в соответствии с требованиями схемы и получить желаемое эквивалентное сопротивление.
Каковы особенности параллельного сопротивления?Параллельные сопротивления имеют несколько свойств в цепи. Наиболее важной особенностью параллельного сопротивления является то, что обратное эквивалентное сопротивление представляет собой сумму всех отдельных обратных сопротивлений.
Другие особенности параллельного сопротивления:
- Все резисторы имеют одинаковое напряжение, и оно равно напряжению узла
- Токи через резисторы суммируют чистый ток вне всего параллельного соединения.

- Значение эквивалентного сопротивления меньше любого резистора, присутствующего в цепи.
Подробнее….Одинаков ли ток при параллельном подключении: полная информация и ответы на часто задаваемые вопросы
Как параллельное сопротивление влияет на напряжение и ток?Нам известен тот факт, что эквивалентное сопротивление в параллельной схеме получается путем суммирования всех сопротивлений, обратных величине, и их обратного действия. Это сопротивление определяет ток в цепи.
Предположим, мы строим электрическую цепь с параллельным соединением резисторов R A и R B с источником напряжения V. Напряжение источника будет общим для обоих резисторов и падение напряжения на обоих из них будет V. Ток на пути R A будет V/R A , а ток на пути R A будет V/R B .
Подробнее….Одинаково ли напряжение при параллельном подключении: полная информация и ответы на часто задаваемые вопросы
Почему эквивалентное сопротивление при параллельном подключении меньше, чем отдельные сопротивления?Параллельно заряд, вытекающий из источника, когда он достигает узла, имеет возможность двигаться в любую ветвь.
 Так что от источника течет большое количество зарядов. Поэтому ток увеличивается.
Так что от источника течет большое количество зарядов. Поэтому ток увеличивается. Из закона Ома мы знаем, что V = IR
Напряжение будет одинаковым для всех параллельных ветвей. Таким образом, ток растет с ростом ветвей (т.е. при подключении большего сопротивления). Единственный способ, при котором напряжение может оставаться неизменным при уменьшении сопротивления. Поэтому сопротивление снижается.
Читайте также… Что такое падение напряжения в параллельной цепи: как найти, примеры проблем и подробные факты
Численные задачи
Рассчитайте эквивалентное параллельное сопротивление для этой бесконечной лестницы, показанной на рисунке 3Для этой бесконечной лестницы сопротивлений мы можем сказать, что эквивалентное сопротивление Req между точками P и Q равно сопротивлению остальной цепи. Поэтому [Latex]R_{eq} = 2+ 1|| R_{eq}[/Latex]
Итак, [Latex] R_{eq} = 2+ \frac {1\times R_{eq}}{1 + R_{eq}} = \frac{ 2 + 3R_{ eq} }{1 + R_{eq} } [/Latex]
Или [Latex] R_{eq} + R_{eq}^{2} = 2 + 3R_{eq} [/Latex] 9{2} – 2R_{eq} -2 = 0 [/Latex]
Решая приведенное выше уравнение, мы получаем [Latex] R_{eq} = 1 \pm \sqrt{3}\; ом [/Latex]
Пренебрегая отрицательной величиной, мы можем сказать [Latex] R_{eq} = 1 + \sqrt{3}\; Ом [/Latex]
Это требуемое эквивалентное сопротивление .

Если эквивалентное сопротивление для цепи на рисунке 4 равно 15 Ом, найдите недостающее значение R.На первом этапе вычислим эквивалентное сопротивление самой правой сетки. Итак, [Latex] R_{eq} = \frac{ 15R }{ 15 + R} [/Latex]. Итак, схема теперь уменьшена до изображения 4.1. Теперь рассчитаем следующую сетку из трех последовательных резисторов.
Теперь [латекс] R_{eq} = 4 + 4 + \frac{ 15R }{ 15 + R} = 8 + \frac{ 15R } { 15 + R} = \frac{ 120 + 23 R} { 15+R}[/Latex]. Далее у нас снова параллельная сетка. Таким образом, R eq теперь [Latex] 14\; ||\; \frac{ 120 + 23 R}{ 15 + R} = \frac{ 14 \times \frac{ 120 + 23 R}{ 15 + R} }{ 14 + \frac{ 120 + 23 R}{ 15 + R} } = \frac{ 14 \left (120 + 23 R \right )}{ 330 + 37R} [/Latex]. Окончательная сетка представляет собой еще одно последовательное соединение, которое дает R eq как [Latex] 5 + 3 + \frac{ 14 \left (120 + 23 R \right )}{ 330 + 37R} = 15 [/Latex] Ом. Решив это, мы получим R = 10 Ом.

Каково будет эквивалентное сопротивление Req для цепи, изображенной на рисунке 5.Мы можем перерисовать приведенную выше схему как изображение 5. Таким образом, для крайне правой сетки R eq = 4+6 = 10 Ом. Теперь у нас есть 3 параллельных резистора для правой сетки и 2 параллельных резистора для верхней сетки, как показано на 5.1.
Эквивалентное сопротивление для правой сетки [Latex] = \frac{10 \times 15\times 30}{ 10\times 15 +15\times 30 + 10\times 30} = 6\; ом[/латекс].
Эквивалентное сопротивление для верхней сетки [Latex] = \frac{ 20\times 5}{ 20 + 5} = 4\; ом[/латекс]. Теперь мы сократили систему до простой последовательной цепи с тремя резисторами 1 Ом, 4 Ом и 6 Ом, как показано в 5.2. Таким образом, окончательный R eq равен [Latex] 1 + 4 + 6 = 11 \; ом[/латекс].
Найдите эквивалентное сопротивление в приведенной ниже цепи: V S = 12 В, R 1 = 2,5 Ом, R 2 = 2 Ом, R 3 = 1,5 Ом, R 4 = 3 Ом, R 5 = 5 Ом и R 6 = 3,25 Ом.
Упрощенная схема для изображения 6 показана на 6.1. Найдем эквивалентное сопротивление самой внутренней сетки. Таким образом, R eq для сетки с R 4 и R 5 равно [Latex] \frac{ R_{4} \times R_{5} }{ R_{4} + R_{5} } = \ frac{5 \times 3}{5 + 3} = 1,875\; ом[/латекс].
Теперь у нас есть R 3 и 1,875 Ом последовательно. Итак, [латекс] R_{экв} = 1,5+ 1,875 = 3,375\; ом[/латекс]. Это сопротивление параллельно R 2 . Итак, теперь [Latex] R_{eq} = \frac{2\times 3,375}{2 + 3,375} = 1,25\; ом[/латекс]. Наконец, у нас есть это сопротивление последовательно с R 1 и R 6 . Следовательно, [Latex] R_{eq} = \left ( 2,5 + 3,25 + 1,25 \right ) = 7\; ом[/латекс]. Это эквивалентное сопротивление цепи.
Серияпротив параллельного | Сравнение последовательных и параллельных цепей
Существует три основных типа электрических цепей: последовательные, параллельные и комбинированные.
 Понимание этих схемных конфигураций поможет вам в анализе цепей, и с помощью нескольких основных правил вы сможете легко рассчитать ток и напряжение каждого компонента. Итак, в этом руководстве давайте более подробно рассмотрим основы последовательной и параллельной цепей, сравним серию с параллельной, а также перечислим некоторые области применения последовательной и параллельной цепей.
Понимание этих схемных конфигураций поможет вам в анализе цепей, и с помощью нескольких основных правил вы сможете легко рассчитать ток и напряжение каждого компонента. Итак, в этом руководстве давайте более подробно рассмотрим основы последовательной и параллельной цепей, сравним серию с параллельной, а также перечислим некоторые области применения последовательной и параллельной цепей. Краткое описание
Что такое последовательная цепь?
Простая цепь постоянного тока состоит из замкнутого пути, по которому течет постоянный ток. Простейшим источником постоянного тока является батарея, и если мы подключим небольшую лампу к клеммам батареи, то получится простая цепь постоянного тока.
Но практические схемы состоят из большего количества компонентов, чем одна лампа. Если цепь состоит из более чем одного компонента и если все они соединены встык, так что через них протекает один и тот же ток, то такая цепь называется последовательной цепью.
Если мы возьмем в качестве примера простейший электрический компонент, т.
 е. резистор, то следующая схема показывает три резистора, соединенных последовательно с источником напряжения. В последовательной цепи ток может течь только одним путем.
е. резистор, то следующая схема показывает три резистора, соединенных последовательно с источником напряжения. В последовательной цепи ток может течь только одним путем. Изображение
Поскольку ток во всех резисторах одинаков, мы можем легко рассчитать напряжение на отдельных резисторах, используя закон Ома.
Если V — напряжение питания, I — ток в цепи, R 1 , R 2 , R 3 — сопротивления, а V R1 , V R2 и V R3 — напряжения на соответствующих резисторах, то применив закон Ома, получим.
V R1 = I X R 1 , V R2 = I X R 2 и V R3 = I X R 3
V = V R1 + V R2 + V R3 = IR 1 + IR 2 + IR 3
Если R — полное сопротивление цепи, то V = IR и, следовательно,
IR = IR 1 + IR 2 + IR 3
R = R 1 + R 2 + R 3
Таким к сумме индивидуальных сопротивлений.

Делитель напряжения
Из приведенного выше объяснения последовательной схемы вы могли заметить интересный момент, касающийся напряжений на отдельных резисторах. Давайте упростим это обсуждение, рассмотрев всего два последовательно соединенных резистора.
Изображение
Здесь V — напряжение питания, R 1 и R 2 — резисторы, а V R1 и V R2 — напряжения на R 1 и R 2 соответственно.
из закона о Ом
V = IR = V R1 + V R2 = IR 1 + IR 2
Если мы рассчитываем напряжение через r 2 ,
V. R2 = В * R 2 / (R 1 + R 2 )
Напряжение на R 2 является частью входного напряжения. Это известно как схема делителя напряжения или схема делителя потенциала.
Закон Кирхгофа Закон о напряжении (KVL)
Из предыдущей серии Цепь, состоящая из трех резисторов, мы установили, что напряжение источника равно сумме напряжений на отдельных резисторах.

В = В R1 + В R2 + V R3
Преобразовывая это уравнение, мы получаем закон Кирхгофа для напряжения.
В – В R1 – В R2 – В R3 = 0
Согласно Закону Кирхгофа о напряжениях (KVL), алгебраическая сумма напряжений в замкнутом контуре равна нулю.
Применение последовательной схемы
Одним из самых известных применений последовательной схемы являются наши праздничные огни серии. Во время Рождества и праздников мы украшаем наши дома разноцветными огнями, состоящими из нескольких последовательно соединенных ламп.
Image
Основная проблема праздничных светильников этой серии заключается в том, что даже если одна лампочка перегорает, это прерывает подачу тока, и вся серия не загорается.
Что такое параллельная цепь?
В последовательной цепи есть только один путь прохождения тока. При переходе к параллельной цепи будет более одного пути для протекания тока.
 Если еще раз взять три резистора, то на следующих изображениях показаны разные конфигурации трех элементов схемы, соединенных параллельно.
Если еще раз взять три резистора, то на следующих изображениях показаны разные конфигурации трех элементов схемы, соединенных параллельно. Изображение
Схемы на изображении выше могут выглядеть по-разному, но на самом деле они одинаковы. Если присмотреться, то один конец всех элементов схемы (в данном случае резисторов) общий, а другой конец тоже. Итак, параллельная цепь из двух элементов состоит из двух общих точек.
Чтобы больше узнать о параллельных цепях, рассмотрим следующую схему, в которой у нас есть три резистора, подключенных параллельно к источнику напряжения. Поскольку все три резистора подключены к источнику напряжения, напряжение на всех резисторах одинаково.
Изображение
Но то же самое нельзя сказать о токе, поскольку он имеет несколько путей для протекания. Если I — общий ток, а I R1 , I R2 и I R3 — токи, протекающие через соответствующие резисторы, то общий ток равен сумме отдельных токов.

I = I R1 + I R2 + I R3
0007 = V / R 2 и I R3 = V / R 3
Если R — общее сопротивление цепи, I = V / R. Используя все это в приведенном выше уравнении, мы получаем
V / R = V / R 1 + V / R 2 + V / R 3
Итак, 1/R = 1/R 1 + 1/R 2 + 1/R 3
Для параллельно соединенных резисторов обратная величина общего сопротивления равна сумме обратных величин отдельных сопротивлений.
Кирхгоф Текущий закон (KCL)
Из приведенного выше обсуждения мы получаем общий ток в цепи как сумму отдельных токов в соответствующих резисторах.
I = I R1 + I R2 + I R3
Мы можем изменить приведенное выше уравнение и получить закон тока Кирхгофа.
I – I R1 – I R2 – I R3 = 0.

Согласно закону токов Кирхгофа (KCL) алгебраическая сумма токов, входящих в узел и выходящих из узла, равна нулю.
Цепь делителя тока
Точно так же, как последовательная цепь резисторов может быть сконфигурирована как цепь делителя напряжения, параллельная цепь резисторов может привести к цепи делителя тока.
Хотя делитель напряжения довольно популярен, использование делителя тока зависит от приложения.
Применение параллельной схемы
Важным применением параллельной схемы является наша домашняя электропроводка. Базовая проводка во всех домах на самом деле является параллельной конфигурацией. Таким образом, все параллельные ветви получают полные 120 В (или 240 В), а ток зависит от нагрузки.
Изображение
Даже если возникает проблема/неисправность в одной параллельной ветви или цепи, затрагиваются только приборы или устройства, подключенные к этой цепи, в то время как остальные ветви работают нормально.

Последовательные и параллельные цепи: сравнение
В следующей таблице показано простое сравнение последовательных и параллельных цепей.
Серийная цепь Параллельная цепь В последовательной цепи через все компоненты протекает одинаковый ток. В параллельной цепи ток может иметь более одного пути. Все компоненты соединены встык с одной общей точкой между компонентами. Один конец всех компонентов в параллели соединен с общей точкой, а другой конец с другой общей точкой. Итак, параллельная цепь имеет две общие точки. Напряжение на компонентах неодинаково и зависит от индивидуального сопротивления. Напряжение на всех компонентах в параллельной цепи одинаковое и равно напряжению питания. Если один компонент в последовательной цепи выходит из строя, то вся цепь перестает функционировать, так как существует только один путь тока. 
Даже если одна из параллельных ветвей выходит из строя, остальные ветки продолжают нормально работать. Ток одинаков во всех компонентах, а сумма отдельных напряжений равна напряжению питания. Напряжение одинаково для всех компонентов, включенных параллельно, а сумма отдельных токов равна общему току в цепи. Если у нас есть три последовательно соединенных резистора, то эквивалентное сопротивление представляет собой сумму отдельных сопротивлений (R = R 1 + R 2 + R 3 ). Если мы соединили три резистора параллельно, то обратная величина эквивалентного сопротивления равна сумме обратных величин отдельных сопротивлений (1/R = 1/R 1 + 1/р 2 + 1/р 3 ) Праздничные серийные светильники являются примером последовательной цепи. Жилая электропроводка имплантирована как параллельная конфигурация. Заключение
Последовательные и параллельные цепи — две основные формы электрических цепей.



