Что такое параллельное соединение проводников. Как рассчитать общее сопротивление при параллельном соединении. Каковы основные свойства параллельного соединения. Где применяется параллельное соединение на практике. Как параллельное соединение влияет на работу электрической цепи.
Что такое параллельное соединение проводников
Параллельное соединение проводников — это такой способ соединения, при котором все проводники подключены к одним и тем же двум точкам электрической цепи. При этом:
- Начала всех проводников соединены в одной точке (узле)
- Концы всех проводников также соединены в одной точке (узле)
- Ток может протекать по нескольким параллельным путям
Схематично параллельное соединение изображается следующим образом:
«` «`Основные свойства параллельного соединения проводников
Параллельное соединение проводников обладает следующими важными свойствами:
- Напряжение на всех параллельно соединенных проводниках одинаково и равно напряжению на входе цепи: U = U1 = U2 = U3 = … = Un
- Общий ток в неразветвленной части цепи равен сумме токов в параллельных ветвях: I = I1 + I2 + I3 + … + In
- Общее сопротивление параллельно соединенных проводников меньше сопротивления любого из них: 1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Расчет параллельного соединения проводников
При расчете параллельного соединения проводников используются следующие формулы:
Общее сопротивление
Для двух параллельно соединенных проводников:
R = (R1 * R2) / (R1 + R2)
Для трех и более проводников:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Токи в ветвях
I1 = U / R1
I2 = U / R2
I3 = U / R3
Общий ток
I = I1 + I2 + I3 + … + In
Применение параллельного соединения проводников
Параллельное соединение проводников широко применяется на практике в следующих случаях:
- В бытовой электропроводке для подключения различных электроприборов
- В системах освещения для подключения нескольких светильников
- В электрических цепях для создания шунтов и делителей тока
- В источниках питания для увеличения их мощности
Влияние параллельного соединения на работу электрической цепи
Параллельное соединение проводников оказывает следующее влияние на работу электрической цепи:
- Уменьшает общее сопротивление цепи
- Увеличивает общий ток в неразветвленной части цепи
- Обеспечивает независимую работу параллельно подключенных устройств
- Позволяет подключать и отключать отдельные устройства без влияния на работу остальных
- Повышает надежность цепи, так как при выходе из строя одной ветви остальные продолжают работать
Преимущества и недостатки параллельного соединения
Параллельное соединение проводников имеет следующие преимущества:

- Независимая работа параллельно подключенных устройств
- Возможность подключения устройств с разным сопротивлением
- Повышенная надежность цепи
- Возможность легкого наращивания мощности
К недостаткам параллельного соединения можно отнести:
- Увеличение общего тока в неразветвленной части цепи
- Необходимость использования проводов большего сечения
- Более сложный расчет параметров цепи
Сравнение параллельного и последовательного соединения проводников
Параллельное и последовательное соединение проводников имеют ряд существенных отличий:
| Параметр | Параллельное соединение | Последовательное соединение |
|---|---|---|
| Напряжение | Одинаково на всех элементах | Сумма напряжений на элементах |
| Ток | Сумма токов в ветвях | Одинаков во всех элементах |
| Сопротивление | Меньше минимального | Сумма сопротивлений элементов |
| Надежность | Выше | Ниже |
Как изменение одного сопротивления влияет на работу других при параллельном соединении
При параллельном соединении проводников изменение сопротивления одной ветви практически не влияет на работу других. Это объясняется следующим:
- Напряжение на всех параллельных ветвях остается неизменным
- Ток в измененной ветви изменится обратно пропорционально изменению ее сопротивления
- Токи в остальных ветвях останутся прежними, так как их сопротивления и напряжение на них не изменились
- Изменится только общий ток в неразветвленной части цепи и общее сопротивление
Например, если увеличить сопротивление одной ветви:
- Ток в этой ветви уменьшится
- Токи в других ветвях не изменятся
- Общий ток немного уменьшится
- Общее сопротивление немного увеличится
Эта особенность параллельного соединения обеспечивает независимую работу параллельно подключенных устройств, что широко используется на практике.
Доказательство свойств параллельного и последовательного соединений электрической цепи
1. Доказательство свойств параллельного и последовательного соединений
ДОКАЗАТЕЛЬСТВО СВОЙСТВПАРАЛЛЕЛЬНОГО И
ПОСЛЕДОВАТЕЛЬНОГО
СОЕДИНЕНИЙ
НАД ДОКАЗАТЕЛЬСТВОМ РАБОТАЛИ:
ВАЙНИК КИРИЛЛ
ЧЕРЕНОК НИКИТА
АЛЕКПЕРОВ ЗАУР
2. Цель:
ЦЕЛЬ:• ДОКАЗАТЬ СВОЙСТВА ПАРАЛЛЕЛЬНОГО И ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ
3. Приборы:
ПРИБОРЫ:• КЛЮЧ, ИСТОЧНИК, АМПЕРМЕТР, ВОЛЬТМЕТР, ПРОВОДА, ЛАМПОЧКИ
4. Последовательное соединение
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ• UОБЩ=U1+U2
• RОБЩ=R1+R2
• I1=I2=I3
5. Последовательное соединение
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ• ДОКАЖЕМ, ЧТО UОБЩ=U1+U2
• СОБЕРЕМ ЦЕПЬ, ПРЕДСТАВЛЕННУЮ НИЖЕ
• U2=
V
R1
R2
6. Последовательное соединение
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ• ПОМЕНЯЕМ МЕСТО ПОЛОЖЕНИЕ ВОЛЬТМЕТРА
• U1=
V
R1
R2
7. Последовательное соединение
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ• ИЗМЕРИМ НАПРЯЖЕНИЕ ОБЩЕЕ
• UОБЩ=
V
R1
R2
8. Подсчеты
ПОДСЧЕТЫ• UОБЩ=U1+U2
9. Последовательное соединение
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ• ДОКАЖЕМ, ЧТО I1=I2=I3
• СОБЕРЕМ ЦЕПЬ, ПРЕДСТАВЛЕННУЮ НИЖЕ
R1
А
R2
10. Последовательное соединение
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ• ПОМЕНЯЕМ МЕСТО ПОЛОЖЕНИЕ АМПЕРМЕТРА
• I2=
R1
А
R2
11. Последовательное соединение
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ• I3=
R1
R2
А
12. Подсчеты
ПОДСЧЕТЫ• I1=I2=I3
13. Парралельное соединение
ПАРРАЛЕЛЬНОЕ СОЕДИНЕНИЕ• IОБЩ=I1+I2
• UОБЩ=U1=U2
• 1/RОБЩ=1/R1+1/R2
14. Параллельное соединение
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ• ДОКАЖЕМ, ЧТО IОБЩ=I1+I2
• СОБЕРЕМ ЦЕПЬ, ПРЕДСТАВЛЕННУЮ НИЖЕ
• IОБЩ=
А
R2
R1
15. Параллельное соединение
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ• I1=
R1
R2
А
16. Параллельное соединение
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ• I2=
R1
А
R2
17. Подсчеты
ПОДСЧЕТЫ• IОБЩ=I1+I2
18. Параллельное соединение
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ• ДОКАЖЕМ, ЧТО UОБЩ=U1=U2
• СОБЕРЕМ ЦЕПЬ, ПРЕДСТАВЛЕННУЮ НИЖЕ
• UОБЩ=
V
R1
R2
19. Параллельное соединение
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ• U1=
V
R1
R2
20. Параллельное соединение
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ• U2=
R1
R2
V
21. Подсчеты
ПОДСЧЕТЫ• UОБЩ=U1=U2
22. Вывод:
ВЫВОД:• В ХОДЕ ПРОДЕЛАННОЙ РАБОТЫ МЫ ДОКАЗАЛИ СВОЙСТВА
ПАРАЛЛЕЛЬНОГО И ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЙ ЦЕПИ
Доказательство свойств параллельного и последовательного соединений Над Доказательством
Доказательство свойств параллельного и последовательного соединений Над Доказательством работали: Вайник Кирилл Черенок никита Алекперов Заур
Цель: Доказать свойства параллельного и последовательного соединения
Приборы: Ключ, Источник, амперметр, вольтметр, Провода, лампочки
Последовательное соединение Uобщ=U1+U2 Rобщ=R1+R2 I1=I2=I3
Последовательное соединение Докажем, что Uобщ=U1+U2 Соберем цепь, представленную ниже U2= R1 R2 V
Последовательное соединение Поменяем место положение вольтметра U1= R1 R2 V
Последовательное соединение Измерим напряжение общее Uобщ= R1 R2 V
Подсчеты Uобщ=U1+U2
Последовательное соединение Докажем, что I1=I2=I3 Соберем цепь, представленную ниже I1= R1 R2 А
Последовательное соединение Поменяем место положение амперметра I2= R1 R2 А
Последовательное соединение I3= R1 R2 А
Подсчеты I1=I2=I3
Парралельное соединение Iобщ=I1+I2 Uобщ=U1=U2 1/Rобщ=1/R1+1/R2
Параллельное соединение Докажем, что Iобщ=I1+I2 Соберем цепь, представленную ниже Iобщ= R1 R2 А
Параллельное соединение R2 А R1 I1=
Параллельное соединение I2= R2 А R1
Подсчеты Iобщ=I1+I2
Параллельное соединение Докажем, что Uобщ=U1=U2 Соберем цепь, представленную ниже Uобщ= R2 R1 V
Параллельное соединение U1= R2 R1 V
Параллельное соединение U2= R2 R1 V
Подсчеты Uобщ=U1=U2
Вывод: В ходе проделанной работы мы доказали свойства параллельного и последовательного соединений цепи
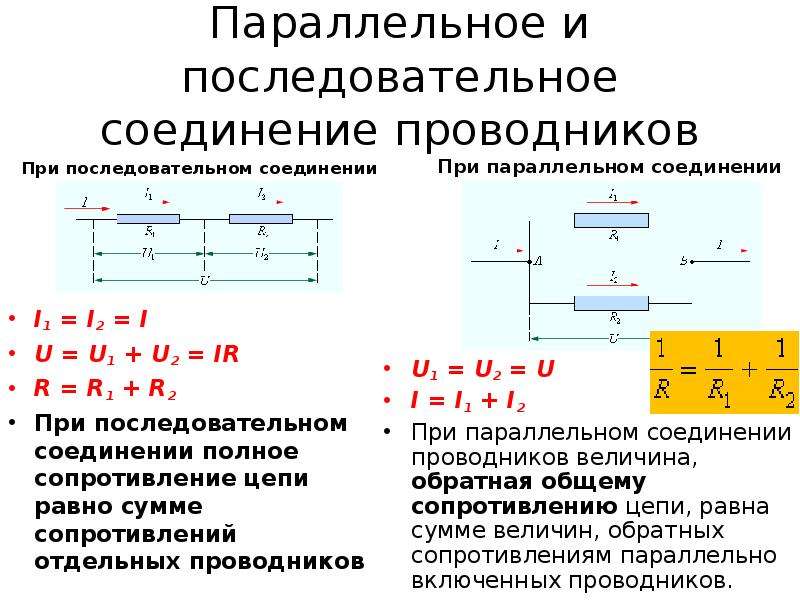
Параллельное соединение элементов электрической цепи
Параллельным называется соединение, при котором объединяются в узел начала приёмников и соответственно их концы. Напряжение подаётся на узлы.
Рис. 1.2. Схема параллельного соединения элементов
Свойства параллельного соединения элементов.
1. Параллельное соединение характеризуется общим для всех элементов напряжением, равным напряжению питающей сети:
2. Эквивалентное сопротивление параллельного участка схемы:
Эквивалентная проводимость параллельного участка схемы:
Проводимость отдельного элемента:
3. Токи в ветвях схемы распределяются обратно пропорционально сопротивлениям элементов и в совокупности равны току в неразветвленной части схемы (следует из первого закона Кирхгофа):
4. Суммарная мощность приёмников, равная мощности источника (следует из уравнения баланса мощности):
Мощность, потребляемая отдельным элементом:
Смешанное соединение элементов электрической цепи
Смешанным называется соединение, при котором имеют место и последовательное, и параллельное соединения элементов.
Рис. 1.3. Схема смешанного соединения элементов
Один из способов расчёта цепей смешанного соединения элементов – метод эквивалентных преобразований, основанный на последовательном преобразовании участков цепи, имеющих параллельное или последовательное соединение элементов
На рис. 1.3 резисторы R2 и R3 соединены параллельно, следовательно, их эквивалентное сопротивление R23 равно:
Полученный элемент R23 последовательно соединён с сопротивлением R1, следовательно, эквивалентное сопротивление всей цепи равно:
Остальные параметры схемы на рис. 1.3 определяются исходя из аналогичных рассуждений.
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ №1
Перед началом работы со стендом проверьте, что автомат под столешницей отключён (находится в нижнем положении).
Опыт №1. Последовательное соединение элементов электрической цепи
Соберите цепь по схеме на рис. 1.4 (рекомендации по сборке даны во введении).
Рис.1.4. Схема проведения опыта №1
Убедитесь, что рукоятка ЛАТРа вывернута против часовой стрелки до упора. Подайте питание на стенд, включив автомат под столешницей. Нажмите кнопку включения сети «ВКЛ». Включите источник питания «ПОСТОЯННОЕ». ЛАТРом плавно увеличивайте напряжение, подаваемое на собранную цепь, до значения, указанное преподавателем. Проведите на стенде необходимые измерения, результаты занесите в табл. 1.1. По окончании опыта выверните рукоятку ЛАТРа против часовой стрелки до упора и отключите источник питания.
Лр 1.1. Виды соединений резисторов.
1. Назвать основные свойства последовательного соединения резисторов.
Токи во всех последовательно соединенных резисторах одинаковы и равны общему току цепи
I=I1=I2=I3.
2. Падения напряжений на отдельных резисторах пропорциональны их сопротивлению Un~Rn.
3. Сумма напряжений на отдельных резисторах равна общему напряжению на зажимах цепи
U=U1+U2+U3.
4. Эквивалентное сопротивление цепи равно сумме сопротивлений всех последовательно соединенных резисторов R=R1+R2+R3.
2. Назвать основные свойства параллельного соединения резисторов.
1. Напряжения на всех параллельно соединенных резисторах одинаковы и равны общему напряжению цепи U=U1=U2=U3.
2. Токи в отдельных резисторах обратно пропорциональны их сопротивлению I~.
3. Сумма токов в отдельных резисторах равна общему току I=I1+I2+I3.
3. Как изменятся параметры цепи, если при последовательном соединении увеличить в два раза сопротивление резистора R1?
Если при последовательном соединении увеличить в два раза сопротивление резистора R1, то Rэкв цепи увеличится, ток в цепи уменьшится, падение напряжения на резисторах R2 и R3 уменьшатся, а на резисторе R1 увеличится.
4. Как изменятся параметры цепи, если при последовательном соединении уменьшить в два раза сопротивление резистора R3?
Если при последовательном соединении уменьшить в два раза сопротивление резистора R3, то Rэкв цепи уменьшится, ток в цепи увеличится, падение напряжения на резисторах R1 и R2 увеличатся, а на резисторе R3 уменьшится.
5. Как изменятся параметры цепи, если при параллельном соединении увеличить в два раза сопротивление резистора R1?
Если при параллельном соединении увеличить в два раза сопротивление резистора R1, то напряжения на параллельных ветвях останутся прежними, токи I2, I3 останутся прежними, ток I1 уменьшится в 2 раза, а, следовательно, общий ток I тоже уменьшится.
6. Как изменятся параметры цепи, если при параллельном соединении уменьшить в два раза сопротивление резистора R2?
Если при параллельном соединении уменьшить в два раза сопротивление резистора R2, то напряжения на параллельных ветвях останутся проежними, токи I2, I3 останутся прежними, ток I2 увеличится в 2 раза, а, следовательно, общий ток I тоже увеличится.
7. Как изменятся параметры цепи, если при параллельном соединении уменьшить в два раза напряжение сети?
Если при параллельном соединении уменьшить в два раза напряжение сети, то напряжения на всех параллельных ветвях уменьшатся в 2раза, а, следовательно, токи в параллельных ветвях и общий ток тоже уменьшатся в 2 раза.
Лр 2 Параллельное соединение катушки индуктивности и конденсатора.
1. Как определить опытным путём величину активного сопротивления катушки?
Активное сопротивление катушки определяется: R= P/I2 (1)
Следовательно, для определения опытным путем активного сопротивления, необходимо включить два измерительных прибора: ваттметр и амперметр. Измерив мощность Р, с помощью ваттметра и силу тока I1 с помощью амперметра активное сопротивление определим по формуле (1).
2.Как определить опытным путём величину индуктивного сопротивления катушки?
Индуктивное сопротивление катушки определяется: (2), где: Z = U/I (3), R =P/I2 (1).
Следовательно, для определения опытным путем индуктивного сопротивления катушки, необходимо включить три измерительных прибора: вольтметр, амперметр и ваттметр. Измерив, напряжение U с помощью вольтметра и силу тока I1 с помощью амперметра, определим полное сопротивление катушки Z по формуле (3). Измерив, мощность Р с помощью ваттметра и силу тока I1 с помощью амперметра, определим активное сопротивление R по формуле (1). Подставив значения Z и R в формулу (2) определим индуктивное сопротивление катушки ХL.
Параллельное соединение и его свойства
То есть общее сопротивление последовательного соединения равно сумме сопротивлений ветвей, входящих в соединение
Общая депрессия последовательного соединения равна сумме депрессий всех ветвей, входящих в соединение
Разделим обе части равенства (5.18) на квадрат расхода воздуха q =Q2
(5.19)
В соответствии с равенством (5.11) =Ri, следовательно, можно записать
(5.20)
Депрессия любой ветви последовательного соединения, как и депрессию всего соединения можно выразить через аэродинамическое сопротивление и расход воздуха т. е.
hi=Ri*q (5.21)
H=R0 Q2(5.22)
Из равенств (5.21), (5.22) q =hi /Ri ,и Q2 =H/R0, а так как в последовательном соединении qi=Q то можно записать
(5.23)
Из равенства (5.23) следует
Hi= (5.24)
В последовательном соединении депрессии отдельных ветвей пропорциональны их сопротивлениям.
Параллельное соединение горных выработок может быть простым (рис.5.9) и сложным (рис.5.10).
Простым параллельным называется такое соединение вентиляционных ветвей, в котором все начала ветвей расходятся в одном узле, а сходятся в другом (рис.5.9).
Сложным параллельным соединением называется такое соединение, когда кроме параллельных ветвей расходящихся в одном узле и сходящимся в другом в этих ветвях имеются дополнительные параллельные ветви (рис.5.10).
Рассмотрим свойства простого параллельного соединения. Согласно определению депрессии разность давления в узлах 1, 2 определяет как депрессию любой ветви входящей в соединение так и депрессию всего соединения, тогда можно записать
Р1-Р2=h1=h2= =hi= hn=H (5.25)
То есть в параллельном соединении депресии всех ветвей одинаковы и равны депрессии всего соединения.
Так как к узлу 1 притекает поток Q , равный общему потоку соединения, а вытекают из него потоки q1, q2 qi qn , а в узле 2 все наоборот, то в соответствии с первым законом сетей можно записать
Q= (5.26)
Общий поток параллельного соединения равен сумме потоков в отдельных ветвях.
Поток воздуха в любой ветви параллельного соединения, а также общий расход воздуха можно вы разить через депрессию и аэродинамическое сопротивление т. е.
Q= (5.27)
qi= (5.28)
С учетом равенств (5.27), (5.28) равенство (5.26) можно записать в виде
= (5.29)
Так как в параллельном соединении Н=hi, то сократив обе части последнего равенства на получим
(5.30)
Величина обратная корню квадратному из сопротивления называется пропускной способностью, следовательно
K= (5.31)
То есть общая пропускная способность параллельного соединения равна сумме пропускных способностей ветвей соединения.
Так как К=1/ , то равенства (5.27), (5.28) можно переписать в виде
Q=K (5.32)
qi=ki (5.33)
Так как в параллельном соединении H=hi то из равенств (5.32), (5.33) получим,
Qi= (5.34)
Потоки воздуха в отдельных ветвях параллельного соединения пропорциональны пропускной способности этих ветвей.
Теперь целесообразно выписать основные расчетные формулы последовательного и параллельного соединения и сравнить их.
Свойства параллельного и последовательного соединения проводников
Таблица знаний по электростатике (жирным шрифтом выделены векторные величины, курсивом — скалярные):
| Величина | Единица измерения в системе СИ | Общепринятое обозначение | Формула для расчёта в общем виде (без учёта знака проекции) | |
| Электрический заряд | Кулон | q(e—заряд электрона) | — | |
| Сила Кулона | Ньютон | Fкулона | F=k(q1*q2)/r2 | |
| Расстояние | Метр | r | — | |
| Напряжённость | Вольт/Метр | E | E=F/q | |
| Напряженность поля вблизи заряженного проводника | Вольт/Метр | Е |
| |
| Потенциал | Вольт | ф | ||
| Потенциал электрического поля точечного заряда | Вольт | ф | ||
| Работа по перемещению электрического заряда | Джоуль | А | ||
| Работа по перемещению электрического заряда | Джоуль | А | А=q*E*d | |
| Потенциальная энергия заряда в электрическом поле | Джоуль | Eп | — | |
| Электрическая ёмкость плоского конденсатора | Фарад | С | ||
| Ёмкость проводника | Фарад | С | ||
| Ёмкость шара | Фарад | С | ||
| Относительная диэлектрическая проницаемость | Безразмерная | ε (ε0 – для вакуума) | — | |
| Емкость батареи параллельно соединенных конденсаторов | Емкость батареи последовательно соединенных конденсаторов | |||
| Энергия конденсатора | Джоуль | W | ||
| Напряжение | Вольт | U | U=ф1-ф2 | |
| Связь напряжения с напряжённостью электрического поля | E=U/d d-расстояние между точками | |||
| Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью. Между двумя любыми точками на эквипотенциальной поверхности разность потенциалов равна нулю, поэтому работа сил электрического поля при любом перемещении заряда по эквипотенциальной поверхности равна нулю. | Линией напряженности электрического поля называется линия, касательная к которой в каждой точке совпадает с вектором напряженности Линии напряженности электростатического поля начинаются на положительных электрических зарядах и кончаются на отрицательных электрических зарядах или уходят в бесконечность. | |||
Тренировочные задания:
1. При перемещении точечного заряда +2 нКл из точки A с потенциалом 12 В в точку B с потенциалом 8 В потенциальная энергия этого заряда в электростатическом поле:
Увеличится 2. Уменьшится 3. Не изменится 4. Зависит от пути
по траектории AB, по траектории ACB и по траектории ADB.
Начало формы
В каком случае электрическим полем была совершена наибольшая работа?
1. АВ 2. АСВ 3. АDB 4. Везде одинаковая
3. На рисунке показаны силовые линии электрического поля и две эквипотенциальные поверхности (A и B). Какая эквипотенциальная поверхность имеет больший потенциал?
1. А 2.В 3. Обе одинаковы 4. Нет верного ответа
4. Два конденсатора емкостями 2C и C соединены последовательно. Полученную батарею зарядили до напряжения U. На каком конденсаторе находится больший заряд?
1. На первом 2. На втором 3. Заряды равны 4. Нет ответа
5. На горизонтальной плоскости расположены точечный заряд и заряженная пылинка (знаки их зарядов различны). Как будет двигаться заряженная пылинка в поле противоположного точечного заряда. В начале пылинка покоилась. Трением пылинки о плоскость пренебречь.
1. Равномерно 2. Равноускорено 3. Равнозамедлено 4. Ускоренно с увеличивающимся ускорением
6. На мыльном пузыре находится заряд Q. Что будет происходить с потенциалом пузыря, если из него будет выходить воздух?
1. Увеличится 2. Уменьшится 3. Не изменится 4. Может, как увеличится, так и уменьшится
7. В вершинах при основании прямоугольного равнобедренного треугольника расположены отрицательные точечные заряды, равные по модулю (см. рисунок).
Начало формы
Выберите правильное направление кулоновской силы, действующей на помещенный в точку положительный точечный заряд, равный по модулю любому из двух других зарядов.
Параллельное соединение потребителей. Схема. Свойства. Область применения. Объяснить, почему изменение одного их сопротивлений не влияет на работу других
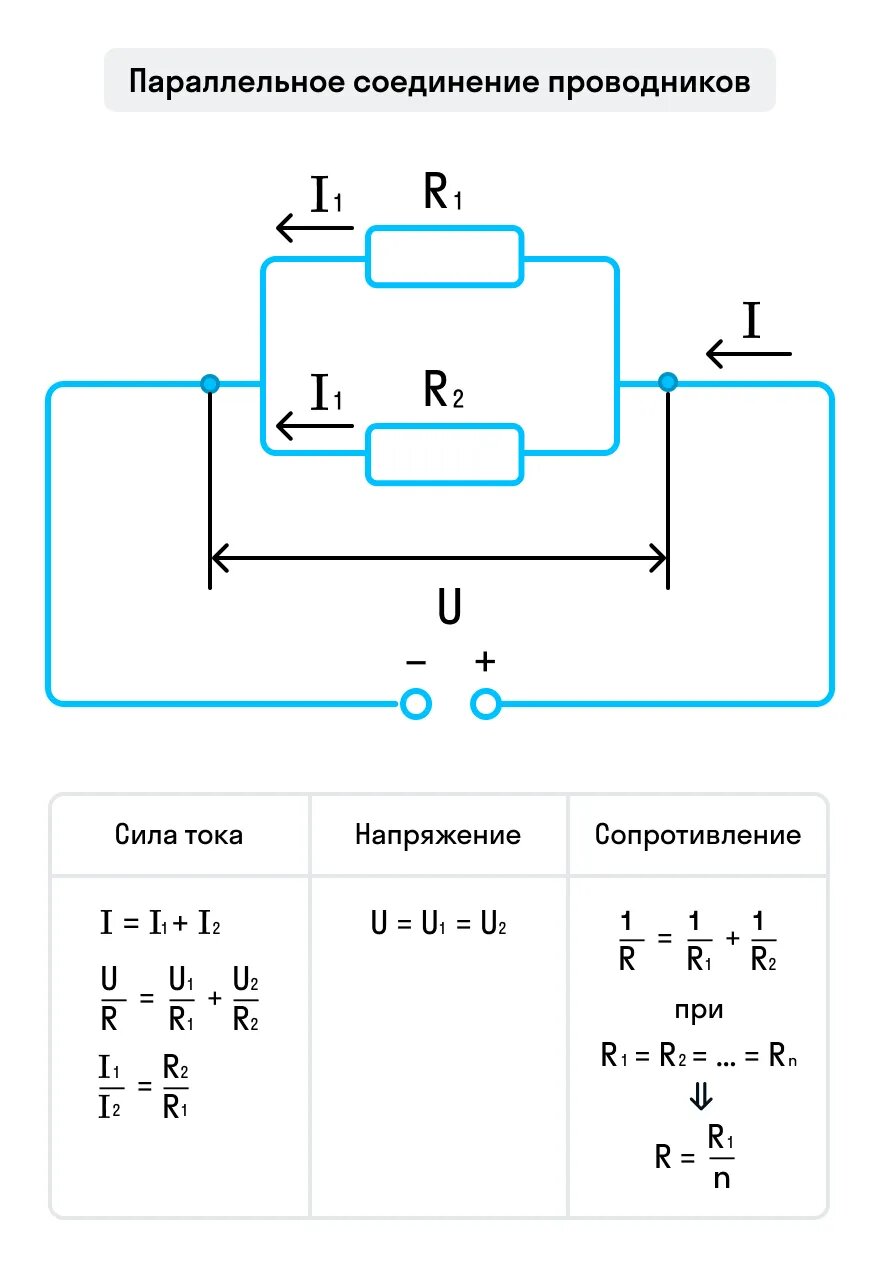
Параллельным называется соединение, когда от одной точки электрической схемы до другой ток может пройти несколькими путями (рис. 16). Левая и правая схемы, показанные на рисунке, абсолютно идентичны. Отличаются они только тем, что по разному нарисованы. На обеих схемах резисторы R1,R2, и R3 включены (соединены) параллельно.
Узлом называется точка электрической схемы, где сходится три или более проводов. На рисунке, для наглядности, узлы выделены окружностью (на левой схеме) и эллипсом (на правом). Каждая схема имеет по два узла. На схеме узел обозначается жирной точкой.
Может показаться, что на правой схеме узлов больше, чем два. Однако, это не так. На правой схеме точки 1, 2 и 3 – это разные геометрические точки. Но, для электротехники эти точки являются одной электрической точкой, одним узлом. Это объясняется тем, что точки 1, 2 и 3 соединены между собой проводником, сопротивление которого близко к нулю. Следовательно, все они имеют одини тот же потенциал и образуют одну общую точку. Из сказанного следует, что узел на схеме не всегда выглядит как геометрическая точка.
Ветвью называется участок схемы от узла до узла. В обеих схемах по три параллельные ветви. Разумеется, в других схемах их может быть больше.
Рис. 16. Параллельное соединение резисторов
Из рассмотрения схемы ясно, что на все резисторы поступает одинаковое напряжение U. В этом состоит главное свойство параллельного соединения элементов.
U1 = U2 = U3 = U
т.е. напряжение на каждом из резисторов равно напряжению,подаваемое на всю схему.
Как известно, напряжение в бытовой электросети составляет 220В. На такое напряжение рассчитаны все бытовые электроприборы. Чтобы напряжение на всех потребителях электроэнергии в квартире было одинаковым, все приёмники электроэнергии (телевизор, лампы, холодильник и др.) соединены параллельно.
Главным достоинством параллельного соединения элементов является то, что все они работают независимо друг от друга. В самом деле: мы по собственному опыту знаем, что включение телевизора не отражается на работе осветительных ламп, холодильника или других электроприборов, работающих в квартире.
Рассмотрим протекание токов в схеме. Направления токов показаны на схеме стрелками. К верхнему, по схеме, узлу подтекает общий ток всех потребителей. В узле он расходится по трём ветвям (движется по трём параллельным путям). В нижнем узле три тока вновь сливаются в один общий ток.
Для узлов электрической схемы справедлив первый закон Кирхгофа: сумма токов подходящих к узлу равна сумме токов отходящих от узла.
Закон Кирхгофа легко понять, представив вместо тока воду, текущую по трубам. Сначала вода идет по общей трубе. Затем труба разветвляется на три трубы идущие параллельно. Потом вода из трёх труб снова сливается в общий поток.
Токи в ветвях схемы вычисляются по формулам:
Эти токи могут быть равны, если все резисторы одинаковы. В противном случае токи будут различны по величине. В большем сопротивлении будет протекать меньший ток и наоборот.
Изменение одного из сопротивлений вызовет изменение тока в этой ветви. Токи в других ветвях не изменятся. Общий ток, равный сумме всех токов, изменится.
Общее сопротивление цепи (всех резисторов, включённых параллельно) меньше наименьшего из сопротивлений, входящих в параллельную цепь.
Чем больше параллельных участков, тем меньше общее сопротивление, т.к. при большем количестве параллельных путей току легче протекать.
Общее сопротивление для двух резисторов, включённых параллельно, определяется по формуле:
Если резисторов три, то сначала определяется сопротивление двух из них, затем, используя ту же формулу, определяется сопротивление резисторов иR3(см. пример 8).
Пример 8. Расчёт цепи при параллельном соединении потребителей
В схеме, показанной на рис. 16, параллельно включены резисторы: R1= 20 Ом. R2= 30 Ом и R3= 60 Ом. Напряжение, приложенное ко входу цепи U = 120 В.
Определить:
а) токи в ветвях и общий ток;
б) эквивалентное (общее) сопротивление цепи;
в) мощность, потребляемую каждым резистором и общую мощность цепи;
г) общий ток, I1 и I2 после отключения приемника R1.
Решение:
а) Напряжение U на всех ветвях (резисторах) при параллельном соединении одинаково. Находим токи в ветвях:
I1 = U / R1= 120 / 20 = 6 А,
I2 = U / R2= 120 / 30= 4 А,
I3 = U / R3= 120/ 60 = 2 А.
По первому закону Кирхгофа, общий ток (в неразветвлённой части цепи) равен сумме токов в ветвях:
Iобщ= I1+ I2 + I3 = 6+4+2 = 12 А.
б) Найдём общее (эквивалентное) сопротивление цепи. Сначала вычислим общее сопротивление для резисторов R1 и R2:
Теперь можно объединить эти два сопротивления в одно и упростить схему. Она примет вид, показанный на рис. 17.
Рис. 17. Вид цепи после объединения резисторов R1 и R2
в одно общее сопротивление R1,2
Вновь использовав формулу для двух резисторов, соединённых параллельно, найдем общее сопротивление всей цепи:
Можно найти общий ток в цепи другим способом, по закону Ома:
I = U/Rобщ = 120/10 =12A
в) Найдём мощность, выделяющуюся в каждой ветви:
P1 = U I1= 120 -6 = 720 Вт,
P2 = UI2= 120·4 = 480 Вт,
P3= UI3 = 120·2 = 240 Вт
Мощность всей цепи Робщ = U·Iобщ = 120·12= 1440 Вт.
Можно было найти общую мощность цепи сложив мощности, выделяющиеся в каждом резисторе. Результат будет совпадать с полученным ранее, что подтверждает правильность вычислений.
г) После отключения приемника R1 ток I1станет равен нулю.Токи I2 и I3 останутся прежними, а ток всей цепи уменьшится на величину тока I1 и будет равен:
Iобщ = I1 + I2 + I3 = 0 + 4 + 2= 6 А.
9. Методика расчёта схем со смешанным соединением потребителей.
Смешанное соединение резисторов представляет собой комбинацию последовательного и параллельного соединений. На рис.18а показан пример смешанного соединения. В этой схеме резисторы R2 и R3 соединены параллельно. Последовательно с этими резисторами подключён резистор R1.
При решении задач на смешанное соединение требуется прежде всего, провести анализ схемы. Необходимо нарисовать схему, обозначить все её элементы, а также токи и напряжения, действующие в схеме. Следует мысленно выделить на схеме элементы соединенные параллельно или последовательно и затем, поэтапно, упростить схему.
На рис.18а показана исходная схема, а затем этапы её упрощения на рис.18б и 18в. Заметьте, что номера токов и напряжений, обозначенных на схеме, всегда совпадают с номером соответствующего сопротивления.
Прежде всего, проведено объединение параллельно соединённых резисторов R2и R3в одно сопротивление R2,3. В результате, схема приобрела вид, показанный на рис.18б. На этой схеме видно, что сопротивления R1и R2,3соединены последовательно.
Объединяя сопротивления R1и R2,3, получим общее сопротивление, что показано на рис.18в.
Рис. 18. Смешанное соединение резисторов: а) исходная схема; б) и в) схемы после упрощения
Далее нужно проанализировать схему, рассмотреть, как в ней протекает ток. На схеме, показанной на рис.18а общий для всей схемы ток Iоб, протекая от верхней клеммы, через резистор R1, где он же обозначен как I1, доходит до узла а (см. рис. 18а).
В узле а ток разделяется на две ветви. По первому закону Кирхгофа I1 равен сумме токов I2+I3. Далее эти токи вновь сливаются в общий токIоб, который идёт к нижней клемме. Напряжения на параллельно соединённых резисторах R2и R3 одинаковы.
В схеме на рис. 18б всё уже проще. Видно, что резисторы R1 и R2,3соединены последовательно. Через всю цепь ток, одинаковый во обоих сопротивлениях. Общее напряжение, приложенное к цепи, равно сумме напряжений на резисторахR1 и R2,3.
Совсем просто выглядит схема на рис. 18в. В этой схеме только одно сопротивление.
После упрощения схемы следует записать под каждой из них соотношения для токов и напряжений, используя свойства последовательного и параллельного соединения. Такая запись показана на рис.18. Начинать запись соотношений следует с самой простой схемы, т.е. с рис.18в.
После проведения анализа схемы и её упрощения можно приступать к решению задачи на смешанное соединение? Руководствуясь записанными выше соотношениями для каждой схемы.
Пример 9. Расчёт цепи сосмешанным соединением резисторов
Для схемы, показанной на рис.18 известно общее напряжение, равное 120В
Известна величина каждого сопротивления: R1=16Ом, R2=40Ом и R3=60Ом. Найти: общее сопротивление схемы, все токи и напряжения, обозначенные на схеме.
Решение:
1. Найдём общее сопротивление цепи:
1.1. Общее сопротивление резисторов R2и R3:
1.2. Общее сопротивление всей цепи:
Rоб= R1+R2,3=16+24=40Ом
2. Находим общий ток, потребляемый схемой:
Iоб=Uоб/Rоб=120/40=3А= I1
3. Определяем напряжение на резисторе R1:
U1= I1-R1=3*16=48В
4. Найдём напряжение на параллельно включённых резисторах R2и R3:
U2,3= Uоб — U1 = 120-48=72В =U2=U3
5. Найдем токи в резисторах R2и R3:
I2=U2/R2= 72/40 = 1,8А
I3=U3/R3= 72/60 = 1,2А
Характеристики параллельной цепи
Обновлено 28 декабря 2020 г.
Автор S. Hussain Ather
Элементы схемы электрических цепей могут быть расположены последовательно или параллельно. В последовательных цепях элементы соединяются с помощью одной и той же ветви, которая пропускает электрический ток через каждую из них один за другим. В параллельных цепях элементы имеют свои отдельные ответвления. В этих цепях ток может проходить по разным путям.
Поскольку ток может проходить по разным путям в параллельной цепи, ток не является постоянным во всей параллельной цепи.Вместо этого для ветвей, которые соединены параллельно друг с другом, падение напряжения или потенциала на каждой ветви является постоянным. Это связано с тем, что ток распределяется по каждой ветви в количестве, обратно пропорциональном сопротивлению каждой ветви. Это приводит к тому, что ток становится наибольшим там, где сопротивление наименьшее, и наоборот.
Эти качества позволяют параллельным цепям пропускать заряд по двум или более путям, что делает его стандартным кандидатом в домах и электрических устройствах через стабильную и эффективную систему питания.Это позволяет электричеству течь через другие части цепи, когда какая-либо часть повреждена или сломана, и они могут распределять мощность равномерно по разным зданиям. Эти характеристики можно продемонстрировать с помощью диаграммы и примера параллельной цепи.
Схема параллельной цепи
••• Syed Hussain Ather
На схеме параллельной цепи вы можете определить поток электрического тока, создавая потоки электрического тока от положительного конца батареи к отрицательному.Положительный конец обозначен плюсом на источнике напряжения, а отрицательный -.
По мере прохождения тока по ветвям параллельной цепи помните, что весь ток, входящий в один узел или точку в цепи, должен равняться всему току, выходящему или выходящему из этой точки. Также имейте в виду, что падение напряжения вокруг любого замкнутого контура в цепи должно равняться нулю. Эти два утверждения представляют собой законы цепей Кирхгофа .
Характеристики параллельной цепи
В параллельных цепях используются ответвления, которые позволяют току проходить по разным маршрутам в цепи.Ток проходит от положительного конца батареи или источника напряжения к отрицательному. Напряжение остается постоянным по всей цепи, в то время как ток изменяется в зависимости от сопротивления каждой ветви.
Примеры параллельных цепей
Чтобы найти полное сопротивление резисторов, установленных параллельно друг другу, используйте формулу
\ frac {1} {R_ {total}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} + … + \ frac {1} {R_n}
, в котором сопротивление каждого резистора суммируется в правой части уравнения.На приведенной выше диаграмме общее сопротивление в Ом (Ом) можно рассчитать следующим образом:
- 1 / R всего = 1/5 Ом + 1/6 Ом + 1/10 Ом
- 1 / R всего = 6/30 Ом + 5/30 Ом + 3/30 Ом
- 1 / R всего = 14/30 Ом
- R всего = 15/7 Ом или около 2,14 Ом
Обратите внимание, что вы можете «перевернуть» обе стороны уравнения с шага 3 на шаг 4 только тогда, когда есть только один член с обеих сторон уравнения (в данном случае 1 / R всего слева и 14/30 Ом справа).
После того, как вы рассчитали сопротивление, ток и напряжение, можно рассчитать по закону Ома В = I / R , в котором В — напряжение, измеренное в вольтах, I — ток, измеренный в амперах. , а R — сопротивление в Ом. В параллельных цепях сумма токов, протекающих по каждому пути, является полным током от источника. Ток на каждом резисторе в цепи можно рассчитать, умножив напряжение на сопротивление резистора.Напряжение остается постоянным по всей цепи, поэтому напряжение является напряжением батареи или источника напряжения.
Параллельная и последовательная цепь
••• Syed Hussain Ather
В последовательных цепях ток постоянен на всем протяжении, падение напряжения зависит от сопротивления каждого резистора, а общее сопротивление складывается из каждого отдельного резистора. В параллельных цепях напряжение постоянно, ток зависит от каждого резистора, а величина, обратная величине общего сопротивления, является суммой величин, обратных величине каждого отдельного резистора.
Конденсаторы и катушки индуктивности могут использоваться для изменения заряда в последовательной и параллельной цепях с течением времени. В последовательной цепи общая емкость схемы (заданная переменной C ), потенциал конденсатора для накопления заряда с течением времени, является обратной суммой обратных величин каждой отдельной емкости, и общая индуктивность ( I ), мощность индукторов, выделяющих заряд с течением времени, является суммой каждой индуктивности. Напротив, в параллельной цепи общая емкость является суммой каждого отдельного конденсатора, а величина, обратная величине полной индуктивности, является суммой обратных величин каждой индивидуальной индуктивности.
Последовательные и параллельные цепи также имеют разные функции. В последовательной цепи, если одна часть сломана, ток вообще не будет течь по цепи. В параллельной цепи открытие отдельной ветви останавливает только ток в этой ветви. Остальные ветви будут продолжать работать, потому что у тока есть несколько путей, которые он может пройти по цепи.
Последовательно-параллельная цепь
••• Syed Hussain Ather
Цепи, у которых есть оба разветвленных элемента, которые также соединены таким образом, что ток течет в одном направлении между этими ветвями, как последовательно, так и параллельно.В этих случаях вы можете применять правила как для последовательного, так и для параллельного подключения, в зависимости от схемы. В приведенном выше примере R1 и R2 параллельны друг другу, чтобы сформировать R5 , а также R3 и R4 , чтобы сформировать R6 . Их можно суммировать параллельно следующим образом:
- 1 / R5 = 1/1 Ом + 1/5 Ом
- 1 / R5 = 5/5 Ом + 1/5 Ом
- 1 / R5 = 6/5 Ом
- R5 = 5/6 Ом или около 0,83 Ом
- 1 / R6 = 1/7 Ом + 1/2 Ом
- 1 / R6 = 2/14 Ом + 7/14 Ом
- 1 / R6 = 9/14 Ом
- R6 = 14/9 Ом или около 1.56 Ом
••• Syed Hussain Ather
Схема может быть упрощена для создания схемы, показанной непосредственно выше, с R5 и R6 . Эти два резистора могут быть добавлены просто, как если бы цепь была последовательной.
R_ {total} = 5/6 \ Omega + 14/9 \ Omega = 2.38 \ Omega
При напряжении 20 В в качестве напряжения закон Ома определяет, что общий ток равен В / R , или 20 В / (43/18 Ом) = 360/43 А или около 8.37 A. Используя этот общий ток, вы также можете определить падение напряжения на R5 и R6, используя закон Ома ( В = I / R ).
V_5 = \ frac {360} {43} \ times 5/6 = 6.98 \ text {V}
V_5 = \ frac {360} {43} \ times 14/9 = 13.02 \ text {V}
Наконец, эти падения напряжения для R5 и R6 можно разделить обратно на исходные параллельные цепи для расчета тока R1 и R2 для R5, и . R2 и R3 для R6 с использованием закона Ома.
I1 = (1800/258 В) / 1 Ом = 1800/258 А или около т 6,98 А.
I2 = (1800/258 В) /5 Ом = 1500/43 А или около т 34,88 А.
I3 = ( 680/129 В ) / 7 Ом = 4760/129 A или около 36,90 A .
I3 = ( 680/129 В ) / 2 Ом = 1360/129 A или около 10.54 A.
Каковы 5 характеристик параллельной цепи? — MVOrganizing
Каковы 5 характеристик параллельной цепи?
Глава 5 — Последовательные и параллельные схемы
- Напряжение: Напряжение одинаково на всех компонентах в параллельной цепи.
- Ток: Полный ток цепи равен сумме токов отдельных ответвлений.
- Сопротивление: отдельные сопротивления уменьшаются, чтобы равняться меньшему общему сопротивлению, а не складываться, чтобы составить общее.
Каковы две основные характеристики резистора?
Две основные характеристики резистора — это его сопротивление R в омах и номинальная мощность P в ваттах.
- Две основные характеристики резистора — это его сопротивление R в омах и номинальная мощность P в ваттах.
- Сопротивление R обеспечивает необходимое уменьшение тока или желаемое падение напряжения.
Какие два типа резистора?
Типы резисторов
- Постоянные резисторы.Резисторы постоянного типа являются наиболее распространенными резисторами. Когда люди говорят о резисторе, они, скорее всего, имеют в виду постоянный резистор.
- Переменные резисторы.
- Термисторы.
- Варисторы.
- Светозависимые резисторы.
Какие характеристики резистора?
Свойства резистора
- Низкотемпературный коэффициент сопротивления (TCR) TCR зависит от резистивного материала и конструкции резистора.
- Номинальная мощность.
- Шум.
- Частотная зависимость.
- Изоляция проводов.
- Защита от воздействий окружающей среды.
- Удельное электрическое сопротивление материала.
- Максимально допустимое напряжение.
Что такое резистор и его применение?
Резистор — это пассивный двухконтактный электрический компонент, который реализует электрическое сопротивление как элемент схемы. В электронных схемах резисторы используются, среди прочего, для уменьшения протекания тока, регулировки уровней сигналов, разделения напряжений, смещения активных элементов и завершения линий передачи.
Какие типы резисторов?
К типам резисторов относятся:
- Резистор из углеродного состава.
- Термистор.
- Резистор с проволочной обмоткой.
- Металлопленочный резистор.
- Углеродный пленочный резистор.
- Переменный резистор.
- Варистор
- Светозависимый резистор.
Какие факторы при выборе резистора привести пример?
Коэффициенты выбора резистора
- Сопротивление.
- Допуск.
- Номинальное рассеиваемая мощность.
- Упаковка и установка.
- Номинальное напряжение.
- Материальная конструкция.
- Паразиты (индуктивность и емкость)
- Температурный диапазон.
Как определить номинал резистора?
Выберите стандартное сопротивление резистора (10 Ом уже является стандартным значением). Пример 2: В приведенной ниже схеме вам необходимо определить значение R1. По закону Ома ток на R2 равен I = 7 В / 10 Ом = 0.7А. R1 и R2 включены последовательно, поэтому они будут иметь одинаковое значение тока.
Какой вариант подходит для параллельного включения резистора?
Для резисторов, включенных параллельно, общее сопротивление является обратной величиной суммы обратных величин отдельных резисторов.
Какой тип резистора мне следует использовать?
Практическое правило — найти резистор с удвоенной номинальной мощностью. Здесь я бы выбрал резистор 250 мВт, так как они самые стандартные. Обычно вы можете просто использовать самый дешевый резистор, который вы можете найти, с правильной номинальной мощностью.
Что такое параллельная цепь — как сделать, характеристики, применение
Поведение схемы полностью зависит от конфигурации ее компонентов схемы. В зависимости от конфигурации подключения эти схемы делятся на параллельные и последовательные схемы. В этом посте раскрывается смысл параллельной схемы, как создать параллельную схему, ее различные характеристики, приложения, преимущества и недостатки.
Что такое параллельная цепь
Схема называется параллельной цепью, когда два или более компонентов подключены к одному и тому же узлу, и обе стороны компонентов подключены непосредственно к батарее или любому другому источнику.Ток в параллельной цепи имеет два или более путей для прохождения через него.
Наиболее распространенным примером параллельной схемы является подключение автомобильных фар. Если фары автомобиля были включены последовательно, то при выходе из строя одного из фар другой также выключится, что означает потерю запаса прочности.
Рис. 1 — Пример автомобильных фар, подключенных в параллельную цепь
Как сделать параллельную цепь
Два или более компонентов схемы соединены через общий источник напряжения, образуя параллельную цепь.На рисунке ниже показана типичная параллельная схема, в которой резисторы (R1, R2, R3, R4) подключены параллельно. Обе стороны резисторов подключены непосредственно к источнику напряжения. Параллельный путь называется ветвью, и напряжение на всех ветвях одинаковое, но ток может быть разным.
Рис. 2 — Принципиальная схема параллельной цепи
Характеристики параллельной цепи
Основные характеристики параллельной цепи перечислены ниже: закон, I = E / R. Это означает, что каждый резистор в этой цепи будет потреблять ток от источника. Следовательно, полный ток, потребляемый от источника, равен сумме токов ответвления, и ток, протекающий по каждому пути, зависит от сопротивления ответвления. Однако напряжение остается прежним и создает разность потенциалов на его выводах.
Общий ток (I t ) можно рассчитать по формуле:
I t = I 1 + I 2 + I 3 +….I n
Где (I 1 + I 2 + I 3 +… .I n ) — токи ответвления
Предположим, что параллельная цепь построена с двумя резисторами ( R1 и R2) с разными значениями (10 Ом и 5 Ом) соответственно. Напряжение 10 В подается на резисторы, в результате чего ток 1 А, потребляемый от батареи через R1, и 2 А, протекающий через R2, выводится из уравнения I = E / R .
Следовательно, два тока ответвления в цепи равны 1А и 2А, что в сумме составляет 3А.
I t = 1 + 2 = 3A
Сопротивления в параллельной цепи
Суммарные сопротивления любого количества резисторов рассчитываются по формуле:
Взаимно R1 = 1 / R1 = 1/10 = 0,1
Величина, обратная R2 = 1 / R2 = 1/5 = 0,2
Сумма указанных выше обратных величин = 0,3
R t = 1 / 0,3 = 3,33 Ом
Мощность в параллельной цепи
известны значения общего тока и приложенного напряжения. Мощность может быть рассчитана по формуле P = EI .В приведенном выше примере приложенное напряжение (E) = 10 В и I = 3 A
∴P = 10 x 3 = 30 Вт
Применения параллельной цепи
Применения параллельных цепей включают:
- Электропроводка к розеткам электропитания в каждом доме в виде параллельных цепей.
- В источниках питания постоянного тока в автомобильной промышленности используются параллельные схемы.
- Компьютерное оборудование разработано с использованием параллельных схем.
Преимущества параллельной схемы
Преимущества параллельной схемы включают:
- Равное напряжение распределяется на каждый компонент в цепи.
- На ток не влияет даже при добавлении или удалении дополнительных компонентов (резисторов) из схемы.
Недостатки параллельной схемы
Недостатки параллельных схем перечислены ниже:
- Она более сложна в проектировании по сравнению с последовательными схемами.
- Дорого построить.
- Короткое замыкание в параллельной проводке может произойти случайно и быть опасным.
- Даже если один из компонентов неисправен, ток все равно может проходить через цепь.
Также читают: Цепь серии - принцип работы, характеристики, применение, преимущества Что такое цифровой вольтметр - как он работает, типы, применение, преимущества Что такое технология Li-Fi - как она работает, применение и преимущества
Характеристики параллельных цепей | Electrical Academia
Определение параллельной цепи
Говорят, что резисторы подключены параллельно , когда одинаковое напряжение появляется на каждом компоненте.При разных значениях сопротивления через каждый резистор протекают разные токи.
Сопротивление, индуктивность и емкость в параллельной цепи
Характеристика параллельной цепи заключается в том, что во всех параллельных ветвях появляется одинаковое напряжение. Мы используем это общее напряжение в качестве опорного вектора на векторных диаграммах для любых параллельных цепей переменного тока. Затем закон Ома дает ток через каждую ветвь цепи в , рис. 1, .{-1}} \ frac {{{I} _ {X}}} {{{I} _ {R}}} & {} & \ left (2 \ right) \\\ end {matrix} $
Где I X — чистый реактивный ток I C — I L .
Мы можем применить следующее уравнение для определения эквивалентного импеданса параллельной цепи:
\ [\ begin {matrix} {{\ text {Z}} _ {\ text {eq}}} \ text {=} \ frac {\ text {E}} {{{\ text {I}} _ {\ text {T}}}} & {} & \ left (3 \ right) \\\ end {matrix} \]
Это Метод решения эквивалентного импеданса параллельной цепи называется методом полного тока. {o}}} {{{X} _ {C}}} \]
Деление на E дает
\ [\ begin {matrix} \ frac {1} {\ text { Z}} = \ frac {1} {R} -j \ frac {1} {{{X} _ {L}}} + j \ frac {1} {{{X} _ {C}}} & { } & \ left (4 \ right) \\\ end {matrix} \]
В этом уравнении мы можем заменить 1 / R на проводимость G.Есть аналогичные обратные для импеданса и реактивного сопротивления.
Проводимость — это общая способность электрической цепи пропускать переменный ток. Символ допуска — Y . Полная проводимость обратно пропорциональна сопротивлению: Y = 1 / Z
Подвеска — это способность индуктивности или емкости пропускать переменный ток. Буквенное обозначение восприятия — B . Подвеска — это величина, обратная реактивному сопротивлению: B = 1 / X
В системе СИ единица измерения как проводимости, так и проводимости — это Сименс, такая же, как и для проводимости. {- 1}} \ frac {{{B} _ {eq}}} {G} & {} & \ left (6 \ right) \\\ end {matrix} \]
Где B eq — чистая эквивалентная восприимчивость, B C — В Л .
Так как B L = 1 / X L ,
\ [\ begin {matrix} {{B} _ {L}} = \ frac {1} {2 \ pi fL} = \ frac {1 } {\ omega L} & {} & \ left (7 \ right) \\\ end {matrix} \]
Аналогично
$ \ begin {matrix} {{B} _ {C}} = 2 \ pi fC = \ omega C & {} & \ left (8 \ right) \\\ end {matrix} $
Резюме
• В параллельной цепи переменного тока полный ток является векторной суммой всех ветвей токи.
• Адмиттанс — это общая способность электрической цепи пропускать переменный ток.
• Подвеска — это мера способности индуктивности или емкости пропускать переменный ток.
• Полная проводимость обратно пропорциональна импедансу.
• Прямоугольные координаты импеданса — это сопротивление и реактивное сопротивление.
• Прямоугольные координаты проводимости и проводимости:
Последовательные и параллельные резисторы — College Physics
Большинство схем имеет более одного компонента, называемого резистором, который ограничивает поток заряда в цепи.Мера этого предела для потока заряда называется сопротивлением. Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на (Рисунок). Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Резисторысерии
Когда резисторы включены последовательно? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током, должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то на (Рисунок) (a) может быть сопротивление вала отвертки, сопротивление ее ручки, сопротивление тела человека и сопротивление ее туфли.
(рисунок) показывает резисторы, последовательно подключенные к источнику напряжения. Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с резиновыми подошвами с высоким сопротивлением. прибор, уменьшающий рабочий ток.)
Три резистора, подключенных последовательно к батарее (слева) и эквивалентному одиночному или последовательному сопротивлению (справа).
Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения, в каждом резисторе (рисунок).
Согласно закону Ома падение напряжения на резисторе при протекании через него тока рассчитывается по формуле, где равно току в амперах (А), а — сопротивление в омах.Другой способ думать об этом — это напряжение, необходимое для протекания тока через сопротивление.
Таким образом, падение напряжения равно, что есть, а что есть. Сумма этих напряжений равна выходному напряжению источника; то есть
Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением, где — электрический заряд, а — напряжение. Таким образом, энергия, подаваемая источником, равна, а энергия, рассеиваемая резисторами, равна
.Связи: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе.Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, . Плата отменяется, уступая, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
Обратите внимание, что для эквивалентного одиночного последовательного сопротивления мы имеем
Это означает, что полное или эквивалентное последовательное сопротивление трех резисторов составляет.
Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление последовательного соединения составляет
, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на (Рисунок) равно, а сопротивления равны, и. а) Каково полное сопротивление? (б) Найдите ток. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:
Стратегия и решение для (b)
Ток определяется по закону Ома. Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
Стратегия и решение для (c)
Напряжение — или падение — на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает
.Аналогично
и
Обсуждение для (c)
Три капли добавляют к, как и прогнозировалось:
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля, где — электрическая мощность.В этом случае через каждый резистор протекает одинаковый полный ток. Подставляя закон Ома в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
Аналогично
и
Обсуждение для (d)
Мощность также можно рассчитать с помощью или, где — падение напряжения на резисторе (а не полное напряжение источника). Будут получены те же значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать, где — напряжение источника.Это дает
Обсуждение для (e)
По совпадению обратите внимание, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, что соответствует мощности, выдаваемой источником. То есть
Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Сопротивления серии добавить:
- Одинаковый ток течет через каждый резистор последовательно.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
Параллельные резисторы
(рисунок) показывает резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. (Рисунок) (b).)
(a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)
Чтобы найти выражение для эквивалентного параллельного сопротивления, давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны, и. Сохранение заряда подразумевает, что полный ток, производимый источником, является суммой этих токов:
Подстановка выражений для отдельных токов дает
Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление параллельного соединения связано с отдельными сопротивлениями на
.Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений.(Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления при параллельном соединении на (Рисунок) будут такими же, как и в ранее рассмотренном последовательном соединении:,, и. а) Каково полное сопротивление? (б) Найдите полный ток.(c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения. Ввод известных значений дает
Таким образом,
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны инвертировать это, чтобы найти полное сопротивление. Это дает
Суммарное сопротивление с правильным количеством значащих цифр —
.Обсуждение для (а)
, как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, заменив полное сопротивление. Это дает
Обсуждение для (б)
Ток для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,
Аналогично
и
Обсуждение для (c)
Общий ток складывается из отдельных токов:
Это соответствует сохранению заряда.
Стратегия и решение для (d)
Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.Давайте использовать, так как каждый резистор получает полное напряжение. Таким образом,
Аналогично
и
Обсуждение для (d)
Мощность, рассеиваемая каждым резистором параллельно, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общую мощность также можно рассчитать несколькими способами. Выбор и ввод полного тока дает
Обсуждение для (e)
Суммарная мощность, рассеиваемая резисторами, также 179 Вт:
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Основные характеристики параллельных резисторов
- Параллельное сопротивление получается из любого отдельного сопротивления в комбинации, и оно меньше.
- Каждый резистор, включенный параллельно, имеет то же полное напряжение, что и источник. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
- Не каждый параллельный резистор получает полный ток; они делят это.
Сочетания последовательного и параллельного
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения можно уменьшить до одного эквивалентного сопротивления, используя метод, показанный на (Рисунок).Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто единичное эквивалентное сопротивление.
Простейшая комбинация последовательного и параллельного сопротивления, показанная на (Рисунок), также является наиболее поучительной, поскольку она используется во многих приложениях.Например, это может быть сопротивление проводов от автомобильного аккумулятора к его электрическим устройствам, которые включены параллельно. и мог быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Расчет сопротивления, падения, тока и рассеиваемой мощности: объединение последовательных и параллельных цепей(рисунок) показывает резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного.Мы можем считать сопротивление проводов, ведущих к и. (а) Найдите полное сопротивление. б) Что такое падение? (c) Найдите сквозной ток. (г) Какая мощность рассеивается?
Эти три резистора подключены к источнику напряжения так, что и включены параллельно друг другу, а эта комбинация — последовательно с.
Стратегия и решение для (а)
Чтобы найти полное сопротивление, отметим, что и находятся параллельно, а их комбинация — последовательно с.Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет
.Сначала мы находим, используя уравнение для параллельных резисторов и вводя известные значения:
Инвертирование дает
Таким образом, общее сопротивление равно
.Обсуждение для (а)
Общее сопротивление этой комбинации является промежуточным между значениями чисто последовательного и чистого параллельного (и, соответственно), найденными для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти падение, отметим, что через него протекает полный ток.Таким образом, его падение составляет
.Мы должны найти, прежде чем сможем вычислить. Полный ток определяется по закону Ома для цепи. То есть
Вводя это в выражение выше, мы получаем
Обсуждение для (б)
Напряжение, приложенное к общему напряжению, и меньше его на величину. Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных и.
Стратегия и решение для (c)
Чтобы найти сквозной ток, мы должны сначала найти приложенное к нему напряжение.Мы называем это напряжением, потому что оно приложено к параллельной комбинации резисторов. Напряжение, приложенное к обоим и уменьшается на величину, так что оно составляет
.Теперь ток через сопротивление определяется по закону Ома:
Обсуждение для (c)
Ток меньше, чем 2,00 А, которые протекали, когда он был подключен параллельно к батарее в предыдущем примере параллельной цепи.
Стратегия и решение для (d)
Рассеиваемая мощность равна
Обсуждение для (d)
Мощность меньше 24.0 Вт этот резистор рассеивает при параллельном подключении к источнику 12,0 В.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если протекает большой ток, провал в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет.Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на (Рисунок). Устройство, представленное значком, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение в проводах, представленных значком, уменьшая напряжение на лампочке (которая есть), которое затем заметно гаснет.
Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
Что такое последовательная цепь? — Определение и пример — Видео и стенограмма урока
Соединение серииПоследовательное расположение компонентов имеет две отличительные характеристики. В соединении серии ток одинаков во всех компонентах, независимо от того, какие компоненты используются или их значения.Падение напряжения на каждом компоненте в цепи зависит от значений компонентов, используемых в цепи. Другой способ увидеть последовательное соединение состоит в том, что положительный конец каждого компонента соединяется с отрицательным концом предыдущего компонента по принципу «один за другим». Отрицательный конец каждого компонента также подключается к положительному концу следующего компонента.
Сравним с потоком воды по трубам. Если мы соединим вместе три трубы разных размеров, через каждую трубу будет течь одинаковое количество воды (например, ток), но давление будет пропорционально размеру трубы.Трубки меньшего размера или с большей ограниченностью похожи на резисторы с большим сопротивлением. Трубки меньшего размера будут иметь большее давление, а резисторы большего номинала будут иметь большее падение напряжения. Точно так же большие трубы будут иметь меньшее давление, так же как меньшие значения сопротивления будут иметь меньшие падения напряжения.
Параллельное соединение
Параллельное расположение компонентов аналогично последовательному соединению. В параллельном соединении ток в каждой параллельной ветви зависит от значений компонентов, используемых в ветви.Однако напряжение на компонентах одинаково. При параллельном подключении положительные концы соединяются с положительными концами, а отрицательные концы соединяются с отрицательными концами.
Давайте еще раз посмотрим на нашу аналогию с водой и трубами. Если мы соединим вместе три трубы разного размера в параллельную конфигурацию, вода разделится и будет течь по трем разным путям. Количество воды, протекающей по каждому пути, пропорционально размеру трубы. И вода, и течение идут по пути наименьшего сопротивления.Меньше воды протекает через меньшие, более узкие трубы, так же как меньший ток проходит через резисторы с более высокими значениями сопротивления. Давление или разность потенциалов одинаковы в каждой трубе, так же как напряжение одинаково на всех резисторах при параллельном подключении.
Последовательная схемаПоследовательная схема — это такая схема, в которой каждый компонент расположен в последовательном соединении. Следовательно, последовательная цепь имеет одинаковый ток во всех точках цепи.Падение напряжения на каждом компоненте в цепи суммируется с напряжением источника. Кроме того, все компоненты одного типа могут быть объединены для получения эквивалентного значения. Тогда схема будет состоять из источника напряжения и эквивалентного значения компонента.
Если используются разные компоненты, каждый тип компонента может быть объединен, чтобы сформировать эквивалент для этого типа компонента. Это обычно называется цепью RLC серии . Например, если последовательная цепь содержит несколько резисторов, катушек индуктивности и конденсаторов, каждый из них может быть объединен в цепь, содержащую один эквивалентный резистор, одну эквивалентную катушку индуктивности и один эквивалентный конденсатор.
Цепь RLC часто используется для моделирования системы электроснабжения, поскольку система питания состоит из ряда резистивных, индуктивных и емкостных нагрузок. Чтобы упростить анализ и проектирование, инженеры-электрики часто сводят это к последовательной цепи RLC. Если последовательная цепь состоит из более чем одного источника напряжения, эти источники можно суммировать, чтобы получить один комбинированный источник напряжения.
Преимущества последовательной схемы заключаются в том, что вы можете контролировать мощность, подаваемую на выход.Вы можете регулировать напряжение источника, добавлять источники напряжения и / или настраивать или добавлять последовательные компоненты для достижения желаемого выходного напряжения и мощности.
Подобно увеличению громкости стерео, вы, скорее всего, изменяете значение сопротивления переменного резистора в цепи перед выходом динамика. Если вы уменьшите сопротивление, на резисторе будет падать меньше напряжения, а на выходе — больше. Это приводит к большему объему.
Недостатками последовательной схемы является то, что при выходе из строя одного компонента вся схема становится неработоспособной.Как и в лампах на елке, если все лампочки соединены последовательно и одна лампочка не горит, ни одна из лампочек не загорится. Если светильники подключены параллельно и один свет гаснет, остальные огни продолжают гореть, потому что на них все еще есть разность потенциалов, и ток все еще может течь в их ответвлениях.
Эквивалентные схемы
Когда резисторы и катушки индуктивности соединены последовательно, эквивалентное значение находится путем сложения всех сопротивлений и индуктивностей.Например, если три резистора номиналом 10, 100 и 1000 Ом соединены последовательно, эквивалентное сопротивление составит 1110 Ом. Если две индуктивности номиналом 10 и 100 мкГенри соединены последовательно, эквивалентная индуктивность составит 110 мкГенри.
Определение эквивалентной емкости последовательно соединенных конденсаторов немного отличается. Эквивалентная емкость рассчитывается по формуле 1 / (1 / C1 + 1 / C2 + … + 1 / CN), где C1 — первый конденсатор, C2 — второй конденсатор, а CN — n-й конденсатор в цепи. .Например, если в цепи три конденсатора 0,82, 0,8 и 0,7 мкФ, эквивалентная емкость рассчитывается как:
1 / (1 / 0,82 + 1 / 0,8 + 1 / 0,7) = 1 / (1,22 + 1,25 + 1,43 ) = 1 / 3,9 = 0,26 мкФ
Если схема содержит более одного типа компонентов, необходимо рассчитать эквивалентное значение для каждого компонента.
Краткое содержание урока
Существуют два метода подключения электрической цепи:
- Последовательное соединение , при котором ток одинаков во всех компонентах в цепи независимо от того, какие компоненты используются или их значения.Падение напряжения на каждом компоненте в цепи зависит от значений компонентов, используемых в цепи.
- Параллельное соединение , в котором ток в каждой ветви зависит от значений используемых компонентов, но напряжение одинаково для всех компонентов. Последовательная схема — это такая схема, в которой каждый компонент расположен в последовательном соединении.
анализировать | Анализировать объект RFCKT в частотной области | |||||||||||||||||||||||||||||||
вычислять | Рассчитывать заданные параметры для объектов rfckt или объектов rfdata |
extract | Извлечь указанные сетевые параметры из объекта rfckt или объекта данных | ||||||
listformat | Список допустимых форматов для указанного параметра объекта цепи | ||||||
listparam параметры для указанного объекта схемы | |||||||
loglog | Нанести на график параметры объекта схемы с использованием шкалы log-log | ||||||
plot | Отобразить параметры объекта схемы на плоскости XY | ||||||
plotyy | Отображение параметров ВЧ-цепи или ВЧ-данных на плоскости XY с двумя осями Y | ||||||
getop | Отображение рабочих условий | ||||||
полярных | Отображение указанных параметров объекта в полярных координатах | ||||||
semilogx | Постройте параметры объекта ВЧ-цепи с использованием логарифмической шкалы для x - ось | ||||||
полулогия | Постройте параметры объекта ВЧ-цепи с использованием логарифмической шкалы для y - ось | ||||||
smith | Отображение параметров объекта схемы на диаграмме Смита | ||||||
запись | Запись радиочастотных данных из схемы или объекта данных в файл | ||||||
|

