Что такое таблица истинности и как ее построить. Как связаны логические операции и электрические схемы. Почему логические схемы важны для работы компьютеров. Как правильно строить логические схемы.
Что такое таблица истинности и зачем она нужна
Таблица истинности — это инструмент, используемый в математической логике для отображения всех возможных комбинаций значений логических переменных и соответствующих им результатов логических операций или выражений. Но почему таблицы истинности так важны?
- Они позволяют наглядно представить поведение логических выражений
- Помогают проверить правильность логических рассуждений
- Используются при проектировании цифровых схем
- Являются основой для минимизации логических функций
Как же правильно построить таблицу истинности? Рассмотрим основные шаги:
- Определить количество переменных в выражении
- Рассчитать число строк таблицы (2^n, где n — число переменных)
- Записать все возможные комбинации значений переменных
- Вычислить результат выражения для каждой комбинации
Связь логических операций и электрических схем
Логические операции, такие как И, ИЛИ, НЕ, лежат в основе работы цифровых устройств. Но как эти абстрактные понятия реализуются в реальных электрических схемах?
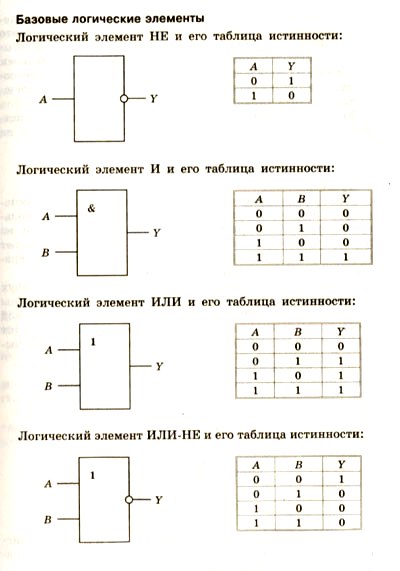
Рассмотрим три базовые логические операции и их электрические аналоги:
Конъюнкция (И)
В электрической схеме операция И реализуется последовательным соединением контактов. Ток пройдет только если замкнуты все контакты, что соответствует истинности всех входных значений в логической операции И.
Дизъюнкция (ИЛИ)
Операция ИЛИ представляется параллельным соединением контактов. Достаточно замкнуть хотя бы один контакт, чтобы ток прошел, аналогично тому, как в логической операции ИЛИ достаточно истинности хотя бы одного из входных значений.
Инверсия (НЕ)
Для реализации операции НЕ используется схема с нормально замкнутым контактом. Когда на вход подается сигнал, контакт размыкается, что соответствует переходу от истины к лжи в логической операции НЕ.
Роль логических схем в работе компьютеров
Логические схемы являются фундаментом, на котором строится вся архитектура современных компьютеров. Но почему они так важны?
- Позволяют выполнять сложные вычисления на основе простых логических операций
- Обеспечивают обработку и передачу данных внутри компьютера
- Являются основой для создания памяти и процессоров
- Позволяют реализовывать алгоритмы управления компьютерными системами
Интересный факт: современный процессор может содержать миллиарды транзисторов, каждый из которых является частью сложной логической схемы.
Правила построения логических схем
Построение корректной логической схемы — важный навык для разработчиков цифровых устройств. Каковы основные правила этого процесса?- Определить количество входных переменных
- Выявить все логические операции в выражении
- Установить порядок выполнения операций
- Подобрать соответствующие логические элементы (вентили)
- Соединить элементы в правильном порядке
- Проверить работу схемы на всех возможных входных комбинациях
При построении схем стремятся к их минимизации — использованию наименьшего возможного числа элементов. Это повышает быстродействие и надежность устройства.
Применение таблиц истинности и логических схем в информатике
Таблицы истинности и логические схемы находят широкое применение в различных областях информатики и компьютерных технологий. Где конкретно они используются?
- Проектирование цифровых устройств
- Разработка алгоритмов и программного обеспечения
- Оптимизация баз данных
- Создание систем искусственного интеллекта
- Обеспечение компьютерной безопасности
Например, в криптографии логические операции используются для шифрования данных, а в машинном обучении — для создания и оптимизации нейронных сетей.
Эволюция элементной базы компьютеров
История развития компьютерной техники тесно связана с эволюцией элементной базы, используемой для реализации логических схем. Как менялись технологии со временем?
- Электромеханические реле (1930-е годы)
- Электронные лампы (1940-е — 1950-е)
- Транзисторы (1950-е — 1960-е)
- Интегральные схемы (1960-е — настоящее время)
- Нанотехнологии (современные разработки)
Каждый этап этой эволюции приводил к значительному увеличению быстродействия, уменьшению размеров и энергопотребления компьютеров.
Перспективы развития логических схем и их применения
Какие инновации ожидают нас в будущем в области логических схем и их применения в компьютерных технологиях?
- Квантовые вычисления, использующие принципиально новые логические элементы
- Оптические компьютеры, где логические операции выполняются с помощью света
- Биокомпьютеры, использующие органические молекулы для обработки информации
- Нейроморфные вычисления, имитирующие работу человеческого мозга
Эти технологии могут привести к созданию компьютеров с невероятной производительностью и энергоэффективностью, открывая новые горизонты в области искусственного интеллекта, моделирования сложных систем и решения глобальных проблем человечества.
Таблицы истинности, с формулами и примерами
Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:
Значения логических функций определяются с помощью таблица истинности.
Таблицы истинности для основных двоичных логических функций
1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.
Обозначение:
2. Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.
Обозначение:
3. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.
Обозначение:
4. Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.
Обозначение:
5. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Обозначение:
6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.
Обозначение:
7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.
Обозначение:
Порядок выполнения логических операций
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквиваленция
- Штрих Шеффера
- Стрелка Пирса
Для последних двух операций приоритет не определен.
Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.
Примеры решения задач
Основы логики. Логические операции и таблицы истинности
Основы логики. Логические операции и таблицы истинности
На данной странице будут рассмотрены 6 логических операций: конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность и исключающие или, которых вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции.
Глоссарий, определения логики
Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
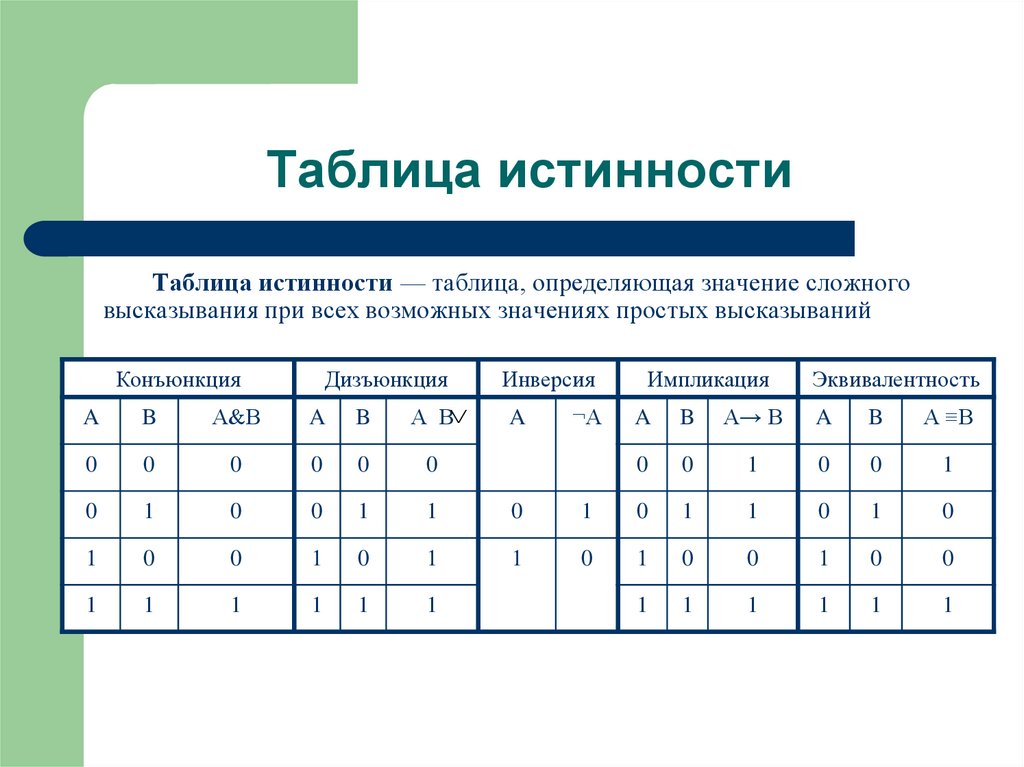
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.
Таблица истинности для дизъюнкции
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬A.
Таблица истинности для инверсии
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность. B) -> (C v not A)Построить таблицу истинности для логического выражения. Информатика в 8 классе.
Тема: «Основы алгебры логики».
Основы алгебры логики
Основы алгебры логики на уроках информатики изучаются в школе, начиная с 8 класса.
Прежде чем приступить к выполнению задания, разберем базовые понятия алгебры логики.
Алгебра логики (алгебра высказываний) — это формальная логическая теория, раздел математической логики. Основание алгебры логики положил Джордж Буль (1815 — 1864), развил же и усовершенствовал её Эрнст Шрёдер (1841-1902).
Высказывание — это предложение, о котором имеет смысл утверждать, истинно оно или ложно. Истина = 1, ложь =0.
Высказывание, включающее другие высказывания, называют сложным. Для образования сложных высказываний используют логические операции (связки).
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых.
Логические операции в порядке приоритета.
- Инверсия (отрицание)
- Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно.
В выражениях обозначается ¬A или A.
Читается «НЕ» (например, «не А»). - Конъюнкция (логическое умножение)
- Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания.
В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB).
Читается «И» (например, «А и Б») - Дизъюнкция (логическое сложение)
- Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний.
В выражениях обозначается A ∨ B, иногда A + B.
Читается «ИЛИ» (например, «А или Б») - Импликация (следование)
- Импликация
В выражениях обозначается A ⇒ B или A → B.
Читается «ЕСЛИ…ТО» (например, «если А, то Б») - Эквивалентность (равнозначность)
- Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают.
В выражениях обозначается A ⇔ B или A ≡ B.
Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)
Для записи логических функций часто используют таблицы истинности.
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
РЕШЕНИЕ
Тема таблицы истинности логические схемы
Тема: Таблицы истинности. Логические схемы.
(конспект рассчитан на 2 академических часа)
Цели: сформировать навыки построения таблиц истинности; сформировать у учащихся представление об устройствах элементной базы компьютера; сформировать навыки построения логических схем.
Требования к знаниям и умениям:
Учащиеся должны знать:
— этапы составления таблиц истинности;
— основные базовые элементы логических схем;
— правила составления логических схем.
Учащиеся должны уметь:
— составлять таблицы истинности;
— составлять логические схемы.
Тип урока – комбинированный.
Программно-дидактическое обеспечение: ПК, карточки с заданиями, элементы для сборки электрических цепей, доска.
I. Постановка целей урока
1. Таблица истинности сложного логического выражения. Как ее правильно составить и использовать?
2. Каким образом алгебра логики связана с компьютером?
3. Почему компьютер не был изобретен раньше?
II. Проверка домашнего задания
Решение задач проверьте у доски. В это время устно проверьте выполнение задания уровня применения.
Задание на карточках
|
1. Соедините правильные определения или обозначения: 1. Логика 1.А→В 2. Высказывание 2. Логическое сложение 3. Алгебра логики 3. Наука о формах и способах мышления 4. Логическая константа 4. Логическое отрицание 5. Дизъюнкция 5. ИСТИНА и ЛОЖЬ 6. Инверсия б.А↔В 7. Конъюнкция 7.& 8. Импликация 8. Наука об операциях над высказываниями 9. Эквивалентность 9. Повествовательное предложение, в кото ром что-либо утверждается или отрицается |
|
2. По мишеням произведено три выстрела. Рассмотрено высказывание: Pk = «Мишень поражена k-ым выстрелом», где k =1,2,3. Что означают следующие высказывания: А) Р1+Р1+РЗ; Б) Р1•Р2• РЗ; В) Р1+Р2+Р3. |
|
3. Даны высказывания: А = {3•3 = 9}, В = {3•3 =10}. Определите истинность высказываний: 1) А, 2) ¬В, 3)А&В, 4)В, 5)¬А, 6)AvB. |
|
4. Даны высказывания А = {5+7=13}, В ={5+7=12}. Определите истинность высказываний: 1) А , 2) ¬В, 3) А&В, 4) В, 5) ¬А, 6) AvB. |
|
5. Запишите логические выражения, соответствующие следующим высказываниям: A) Ботаника изучает растения и ботаника изучает животных; Б) В состав атома входят электроны или в состав электронов входят атомы; B) Гелий — это жидкость и вода — это газ; Г) Неверно, что положительный ион — это лишившийся электронов атом. |
|
6. Запишите логические выражения, соответствующие следующим высказываниям: A) Зоология изучает растения или ботаника изучает животных; Б) Электрон — это часть атома и электроны есть в любом веществе; B) Напряжение — это сила тока, умноженная на сопротивление; Г) Неверно, что спутник — это летательный аппарат. |
III. Изложение нового материала
1. Таблицы истинности
Решение логических выражений принято записывать в виде таблиц истинности — таблиц, в которых по действиям показано, какие значения принимает логическое выражением при всех возможных наборах его переменных.
Для составления таблицы необходимо:
Выяснить количество строк в таблице (вычисляется как 2n, где n — количество переменных).
Выяснить количество столбцов = количество переменных + количество логических операций.
Установить последовательность выполнения логических операций.
Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
Заполнить таблицу истинности по столбцам.
Пример 1
Построим таблицу истинности для выражения F = (AvB)&(¬Av¬B).
Количество строк = 22 (2 переменных) + 1 (заголовки столбцов) = 5.
Количество столбцов = 2 логические переменные (А, В) + 5 логических операций { v, &, ¬, v, ¬) = 7.
Расставим порядок выполнения операций: 1 5 2 4 3
Построим таблицу:
|
А |
В |
A v B |
¬А |
¬В |
¬AV¬B |
(AvB)&(¬Av ¬B) |
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Пример 2
Построим таблицу истинности для логического выражения X v Y& ¬ Z.
Количество строк = 23+1 = 9.
Количество столбцов = 3 логические переменные + 3 логических операций = 6.
Укажем порядок действий: 3 2 1
X VY& ¬ Z
Нарисуем и заполним таблицу:
|
X |
Y |
Z |
¬ Z |
Y& ¬ Z |
XVY& ¬Z |
|
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
2. Логические схемы
Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 — 1933), кстати несколько лет работавший в России, писал еще в 1910 году: «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить:
1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции;
2) не содержит ли она излишних усложнений. Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе — система чисто качественных… «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?». Созданная позднее М.А. Гавриловым 1903 — 1979) теория релейно-контактных схем показала, что это вовсе не утопия.
Посмотрим на микросхему. На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее при сильном увеличении она поразит нас своей стройной архитектурой. Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая Информация представлена в компьютере в виде электрических импульсов. Поговорим о них.
С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или его нет; электрическое напряжение есть или его нет… В связи с этим поговорим о различных вариантах управления включением и выключением обыкновенной лампочки (лампочка также работает на электричестве). Для этого рассмотрим электрические контактные схемы, реализующие логические операции.
Пояснение: для наглядности приготовьте электрические схемы и продемонстрируйте их в действии. Для этого используйте: источник питания, лампочки, ключи, провода.
Схема 1. Схема. 2. Схема. 3. (автоматический ключ)
На рисунках контакты обозначены латинскими буквами А и В. Введем обозначения: 1 — контакт замкнут, 0 — контакт разомкнут. Цепь на схеме I с последовательным соединением контактов соответствует логической операции «И». Цепь на схеме 2 с параллельным соединением контактов соответствует логической операции «ИЛИ». Цепь на схеме 3 (электромагнитное реле) соответствует логической операции «НЕ».
Попросите детей приготовить в тетради таблицу:
|
Конъюнкция |
Дизъюнкция |
Инверсия |
Заполняем ее по ходу объяснения материала.
Заполненная таблица
|
Конъюнкция (Логическое умножение) и |
Дизъюнкция (Логическое сложение) или |
Инверсия (Логическое отрицание) не |
|
A B A&B 0 1 0 1 0 0 1 1 1 0 0 0 |
A B AvB 0 1 1 1 0 1 1 1 1 0 0 0 A
0 1 1 0 |
|
|
Конъюнктор |
Дизъюнктор |
Инвертор |
Докажем это, рассмотрев состояния схем при различных состояниях контактов.
Схема 1 (составляем в основной таблице таблицу истинности).
Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит,
Первый контакт в положении «вкл», второй — в положении «выкл». Ток не идет, лампочка не горит.
Обратная ситуация. Лампочка не горит.
Оба контакта в положении «выкл». Тока нет. Лампочка не горит. Вывод: первая схема действительно реализует логическую операцию «И».
Схема 2 (составляем в основной таблице таблицу истинности).
Оба контакта в положении «включено». Ток через лампочку идет и она горит.
Первый контакт в положении «вкл», второй — в положении «выкл». Ток идет, лампочка горит.
Обратная ситуация. Лампочка горит.
Оба контакта в положении «выкл». Тока нет. Лампочка не горит.
Вывод: вторая схема действительно реализует логическую операцию «ИЛИ».
Схема 3 (составляем в основной таблице таблицу истинности).
В этом устройстве в качестве переключателя используется автоматический ключ. Когда тока на нем нет, пластинка замыкает контакты и лампочка горит. Если на ключ подать напряжение, то вследствие явления электромагнитной индукции пластинка прижимается и цепь размыкается. Лампочка не горит.
Вывод: схема 3 действительно реализует логическую операцию «НЕ».
Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключений в секунду. Именно такие электронные схемы нашли свое применение в качестве элементной базы ЭВМ. Вся теория, изложенная для контактных схем, была перенесена на электронные схемы. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента. Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Пояснение: историю развития элементной базы компьютера смотрите в дополнительном материале.
Почему необходимо уметь строить логические схемы?
Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом) таким образом становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.
Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.
Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.
3. Построение логических схем
Правило построения логических схем:
Определить число логических переменных.
Определить количество базовых логических операций и их порядок.
3) Изобразить для каждой логической операции соответствующий ей вентиль.
Соединить вентили в порядке выполнения логических операций.
Пример 1
Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = XvY&X.
Две переменные — X и Y.
2) Две логические операции: 2 1
XvY&X.
3) Строим схему:
010009000003f801000002008401000000008401000026060f00fe02574d464301000000000001005e830000000001000000dc02000000000000dc020000010000006c000000000000000000000015000000380000000000000000000000741a0000eb09000020454d4600000100dc0200000d00000002000000000000000000000000000000b0090000b40d0000d2000000290100000000000000000000000000005034030028880400160000000c000000180000000a0000001000000000000000000000000900000010000000200300002c010000520000007001000001000000ceffffff00000000000000000000000090010000000000cc07400012540069006d006500730020004e0065007700200052006f006d0061006e e736093000000000040000000000ae30243709300000000047169001cc0002020603050405020304ff3a00e0417800c00900000000000000ff01000000000000540069006d00650073002000000065007700200052006f006d0061006e00000000000000ce33093050dbae30401e2c0001000000000000005848110032b50230584811004c5eaf30704811006476000800000000250000000c00000001000000120000000c00000001000000180000000c0000000000000254000000540000000000000000000000150000003800000001000000df7b074139760741000000002d000000010000004c000000040000000000000000000000200300002c01000050000000200065651600000046000000280000001c0000004744494302000000ffffffffffffffff210300002d010000000000004600000014000000080000004744494303000000250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c024800c000040000002e0118001c000000fb02f4ff0000000000009001000000cc0740001254696d6573204e657720526f6d616e0000000000000000000000000000000000040000002d0100000400000002010100050000000902000000020d000000320a0b0000000100040000000000c0004800200005001c000000fb020400020000000000bc02000000cc0102022253797374656d003f00003f3f3f3f3f3f303f3f3f0800000001003f3f3f3f3f00040000002d010100030000000000
4) Ответ: l v 0 & 1= 1.
Пример 2
Постройте логическую схему, соответствующую логическому выражению
F = X&Yv ¬(YvX). Вычислить значения выражения для X = 1, Y = 0.
1) Переменных две: X и Y;
2) Логических операций три: конъюнкция и две дизъюнкции: 1432
X&Yv¬(YvX).
Схему строим слева направо в соответствии с порядком логических операций:
1
4) Вычислим значение выражения: F= l&0v¬ (0vl) = 0.
IV. Закрепление изученного
№1
Составьте таблицы истинности для следующих логических выражений:
1) А&(ВvB&C)
2) Аv (В&BvC)
№2 Заполните пустые ячейки таблицы истинности:
|
А |
B |
C |
CvA |
(CvA)B |
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
1 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
Подвидение итогов:
Таблица истинности. Базовые логические элементы.
Так же, как и стандартные Булевы выражения, информация на входах и выходах различных логических элементов или логических схем может быть собрана в единую таблицу – таблицу истинности.
Таблица истинности дает наглядное представление о системе логических функций. В таблице истинности отображаются сигналы на выходах логических элементов при всех возможных комбинациях сигналов на их входах.
В качестве примера, рассмотрим логическую схему с двумя входами и одним выходом. Входные сигналы отметим как «А» и «В», а выход «Q». Есть четыре (2²) возможных комбинаций входных сигналов, которые можно подать на эти два входа («ON — наличие сигнала» и «OFF — отсутствие сигнала»).
Однако, когда речь идет о логических выражениях и, особенно о таблице истинности логических элементов, вместо общего понятия «наличие сигнала» и «отсутствие сигнала» используют битные значения, которые представляют собой логический уровень «1» и логический уровень «0» соответственно.
Тогда четыре возможные комбинации «А» и «В» для 2-входного логического элемента можно представить в следующем виде:
- «OFF» — «OFF» или (0, 0)
- «OFF» — «ON» или (0, 1)
- «ON» — «OFF» или (1, 0)
- «ON» — «ON» или (1, 1)
Следовательно, у логической схемы имеющей три входа будет восемь возможных комбинаций (2³) и так далее. Для обеспечения легкого понимания сути таблицы истинности, мы будем изучать ее только на простых логических элементах с числом входов не превышающим двух. Но, несмотря на это, принцип получения логических результатов для многовходных элементов схемы остается таким же.
Практически, таблица истинности состоит из одного столбца для каждой из входных переменных (например, А и В), и один последний столбец для всех возможных результатов логической операции (Q). Следовательно, каждая строка таблицы истинности содержит один из возможных вариантов входных переменных (например, A = 1, B = 0), и результат операции с этими значениям.
Таблица истинности
Элемент «И»
Для логического элемента «И» выход Q будет содержать лог.1, только если на оба входа («А» и «В») будет подан сигнал лог.1
Микросхемы, содержащие логический элемент «И»:
Тестер транзисторов / ESR-метр / генератор
Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…
- К155ЛИ1, аналог SN7408N
- К155ЛИ5 с открытым коллектором, аналог SN74451N
- К555ЛИ1, аналог SN74LS08N
- К555ЛИ2 с открытым коллектором, аналог SN74LS09N
Элемент «ИЛИ»
Выход Q, элемента «ИЛИ», будет иметь лог.1, если на любой из двух входов или же на оба входа сразу подать лог.1
Микросхемы, содержащие логический элемент «ИЛИ»:
- К155ЛЛ1, аналог SN7432N
- К155ЛЛ2 с открытым коллектором, аналог SN75453N
- К555ЛЛ1, аналог SN74LS32N
Элемент «НЕ»
В данном случае выход Q, логического элемента «НЕ», будет иметь сигнал противоположный входному сигналу.
Микросхемы, содержащие логический элемент «НЕ»:
- К155ЛН1, аналог SN7404N
- К155ЛН2 с открытым коллектором, аналог SN7405N
- К155ЛН3, аналог SN7406N
- К155ЛН5 с открытым коллектором, аналог SN7416N
- К155ЛН6, аналог SN7466N
Элемент «И-НЕ»
На выходе Q элемента «И-НЕ» будет лог.1 если на обоих входах одновременно отсутствует сигнал лог.1
Микросхемы, содержащие логический элемент «И-НЕ»:
- К155ЛА3, аналог SN7400N
- К155ЛА8, аналог SN7401N
- К155ЛА9 с открытым коллектором, аналог SN7403N
- К155ЛА11 с открытым коллектором, аналог SN7426N
- К155ЛА12 с открытым коллектором, аналог SN7437N
- К155ЛА13 с открытым коллектором, аналог SN7438N
- К155ЛА18 с открытым коллектором, аналог SN75452N
Элемент «ИЛИ-НЕ»
Только если на оба входа логического элемента «ИЛИ-НЕ» подать лог.0 мы получим на его выходе Q сигнал соответствующий лог.1
Микросхемы, содержащие логический элемент «ИЛИ-НЕ»:
- К155ЛЕ1, аналог SN7402N
- К155ЛЕ5, аналог SN7428N
- К155ЛЕ6, аналог SN74128N
Элемент «Исключающее ИЛИ»
В данном случае выход Q будет содержать лог.1, если на вход элемента «Исключающее ИЛИ» поданы два противоположных друг другу сигнала.
Микросхемы, содержащие логический элемент «Исключающее ИЛИ»:
- К155ЛП5, аналог SN7486N
Подведем итог, собрав все полученные ранее результаты работы логических элементов в единую таблицу истинности:
Построение таблиц истинности для логических выражений
построим таблицу истинности для логического выражения которая представлена на экране это выражение состоит из двух логических переменных буквы a и b и различных логических операций их значки представлены перед нами чтобы построить любую таблицу необходимо знать как минимум две вещи сколько нужно построить строк и сколько столбцов поэтому в алгоритмы построения таблиц истинности первым пунктом всегда нужно узнать количество строк которые нужны для этой таблицы для этого используется формула 2 в степени n + 1 переменная n эта переменная которая обозначает количество неизвестных или переменных логического выражения для этого нам нужно посчитать сколько разных букв используются в этом выражении такое количество этих букв точнее сколько раз они повторяются не надо считать нужно просто посчитать сколько разных букв и так у нас разных букв а и b две буквы поэтому количество логических переменных будет равно 2 это значение подставляем формулу степень получим 2 в степени 2 плюс единица это будет 4 плюс 15 то есть в будущей таблицы истинности для нашего логического выражения должно быть пять строк вторым пунктом узнаем сколько же столбцов нужно для того чтобы построить эту таблицу для этого нужно использовать формулу которая выглядит примерно так первое это количество логических переменных которые записаны в выражений и второе количество операций я их обозначил а буквой о который в этом же выражение присутствует количество логических переменных букву н да мы с вами нашли в предыдущем пункте она равна 2 это буквы a и b а количество операций можно найти следующим образом либо просто посчитать количество разных значков которые используются выражение но грамотнее будет одновременно проставить порядок этих операций из одну их пересчитать для этого мы с вами записывали порядок выполнения операций 1 всегда выполняется точно так же как в математике действия в скобках поэтому операция первая которая называется с импликация и обозначается стрелочкой или следование она будет выполняться первый а второй скобке у нас есть три операции это две операции инверсия и операция дизъюнкция или логическое сложение по порядку действий инверсия или отрицание всегда выполняется первый поэтому мы будем выполнять сначала операцию отрицания переменной а затем операцию отрицания переменной b и после этого во вторых скобках выполним операцию сложения она будет у нас 4 за скобками у нас есть всего лишь одна операция эта операция называется конъюнкция или логическое умножение поэтому мы ее единственную за скобочками будем выполнять последний итак мы пронумеровали порядок операции посчитали их количество количество переменных у нас было равно двум а количество операций стала равно 5 которую мы с вами насчитали подставляем значения в формулу и получаем что столбцов нашей таблице должно быть 2 + 72 плюс 5k ровности дальше когда мы узнали сколько у нас есть строк в таблице и сколько должно быть столбцов мы можем ее построить и так строим таблицу которая будет содержать 7 столбцов и пять строк таблица готова теперь нужно ее заполнить таблицы истинности в принципе как и остальные таблицы всегда заполняются с первой строки которая называется шапкой шапка таблицы обозначает что будет происходить столбцах для первых ячеек нашей таблицы в шапочке мы отведем как раз такие места для обозначения переменных у нас их две перемены a user page of первый столбец и переменная b и и запишем во второй столбец дальше все остальные ячейки у нас отведены для самих операций операции мы уже пронумеровали их 5 поэтому мы последовательно запишем что мы будем выполнять первой операции эта операция следования вторая операция операция отрицания а третья операция операция отрицания b 4 операции это операции сложения двух предыдущих и последняя самая последняя операция операция умножения она должна по идее быть записано в виде всего выражение то есть первые скобочки которая есть и второй которая тоже уже у нас посчитан предыдущем столбце но так как эта операция и выражения слишком большое проще записать место всего выражения просто букву f то есть значение всего выражения это будет последняя операция дальше заполняется первые столбцы солце со значениями переменных них мы должны перечислить все что может произойти с переменными а и б все варианты но есть хитрый способ как это сделать просто можно например начинать выполнять запись следующим образом мы с последнего самого правого столбца переменных то есть у нас их всего 2 вот сам и правы выбираем который еще до всех остальных операций и начинаем записывать значения переменной чередуя нолики и единички через 1 то есть с наименьшего сначала 0 затем 101 дальше переходим к следующему столпу столбцу с переменной а здесь мы будем тоже чередовать значение нулей и единиц только через два знака 0011 нам осталось заполнить все операции которые мы с вами записали в остальных столбцах значит самый первый столбец возле столбца с переменами это столбец свое с выражением которое должно быть посчитано то есть операция исследований импликации для операции импликация точно так же как и для остальных операций существует специальная таблица истинности по которым можно определить значение для этого нужно посмотреть у нас получается первое это а она записана в первой строке и в первом столбце 2 в переменной b она у нас записано ее значение во втором столбце и результат этой операции можно посмотреть по таблице истинности и так я смотрю чему должна быть равна моя операция в первой ячейке которую нужно заполнить итак ноль следование 0 по таблице истинности это будет единичка поэтому в моей чей я записываю 1 следующая строка у меня уже я смотрю опять же по таблице буду смотреть чему будет равно значение 0 следует один это вторая строка таблицы здесь тоже будет единичка а с третьей строке нужно поглядеть чему будет равна операций когда с единицей следует 0 по таблице это значение равно нулю поэтому я записываю в мою таблицу истинности 0 и последняя строка из единицей следует один будет равна одному мы заполнили столбец с операция исследования следующая операция это операция отрицания для нее точно так же как и для остальных операций существуют специальные таблицы истинности а мы смотрим значение переменных в первом столбце таблицы результат операции во втором и так так как мне нужно отрицать значения переменной а я буду брать значения начальной из столбца с переменной а то есть первое значение я буду отрицать 0 по таблице истинности если я буду отрицать 0 значение будет моей операции будет равно единичке поэтому единицу я записываю мою ячейку следующее я также отрицаю 0 в следующей строке значение будет равно 5 1 когда я буду брать значения противоположной единицы не ни один это будет 0 по таблице истинности это хорошо вид поэтому две остальные строки у меня также будут записаны как нули столбец значение не б это столбец в котором нужно брать значение противоположной столбцу бы то есть если был записан 0 мои ячейки я бы написать единицу и наоборот если изначальное значение был один я запишу 0 таким образом я заполню все а строчки моего столбца дальше переходим к следующей операции эта операция называется дизъюнкция или слова логическое сложение здесь мы должны складывать два значения значение столбца не а и значение и столбца не б это то что мы посчитали только что операция дизъюнкция или сложения тоже имеет свою таблицу истинности и по ней мы узнаем что же получится в нашей таблице которую мы составляем итак первая строка мне нужно сложить значения 1 со значением 1 по таблице истинности это последняя строчка результатом это операции будет единица я пишу 1 дальше складываю один с нулем значение будет равно 1-му по таблице истинности я записываю результат 1 0 + 1 по таблице истинности это единица я пишу 1 и 0 + 0 по первой строчки таблицы истинности операции это будет равно нулю поэтому записываю в моей таблице также 0 теперь мне осталось вычислить последний результирующий столбец который будет являться значением всего логического выражения в этом столбце я должна посчитать операцию умножения двух скобочек скобочки которая нас посчитано в первом столбце то есть следования это вот этот столбец и скобочки которого посчитали только что в последнем столбце поэтому я буду по таблице истинности операции умножения логического смотреть что же получится итак мне нужно умножить 1 на 1 а таблицы истинности это будет равно единице я еще результат один дальше значение из первого столбца один из из последнего тоже один также будет равно единице 0 умножить на 1 по таблице истинности эта строчка равна будет нулю я записываю 0 и последнее значение единица должна умножить на 0 1 умножить на 0 равна нулю логическое умножение запрос запомнить проще всего она высчитывается точно также как обычное наше умножение мы с вами посчитали таблицу истинности для логического выражения которая нам задали последний столбец в котором написано и значение нашей нашей логической функции для любые значения переменных является главным которые мы хотели получить по нему можно узнать значение логической функции для кого мы захотим для любых значений переменных а и б но к сожалению редко бывает что функции заданные логически состоят только из двух переменных обычно их больше как минимум три поэтому мы построим следующую логическую до таблицу для логического выражения состоящего из трех переменных по той же самой схеме которую делали и сейчас итак для таблицы любой сначала нужно вычислить количество строк по той же самой формуле 2 в степени n + 1 мы вычисляем количество строк для нашего логического выражения н переменная это количество разных букв которые мы используем в логическом выражении здесь это а b и c второй раз и считать не надо то есть их всего три дальше мы представляем это значение формулу изначально у нас будет два в третьей степени плюс 1 это будет равно 9 в нашей таблице должно быть 9 строк вторым пунктом ищем количество столбцов для нашей таблице той же самой формуле количество переменных плюс количество операций мы будем вычислять ее и так количество переменных у нас известно с первого пункта оно равно 3 а вот количество операций мы сейчас посчитаем по тому же принципу которой было в прошлые таблице мы делаем сначала приоритет операций узнаю то есть узнаем какая операция выполняется первый а всегда выполняется точно так же как его выбрита как у нас всего две операции умножения и сложения будет выполняться в первом умножение поэтому операцию умножения мы будем выполнять последовательно начиная с самого первого до последнего итак первое второе умножение и третье по порядочку выполняется дальше осталось две операции сложения операция сложения логического выполняется тоже по порядочку с начала в конец итак 4 5 операция и так наших операций 5 считаем сколько будет столбцов количество переменных плюс количество операций 3 плюс 5 будет равно 8 строим таблицу которая будет состоять из 8 столбцов и 9 строк заполняемые по тому же принципу первые из ячейки шапки таблицы отводится на перечисление переменных эта переменная а переменная b переменная c остальные ячейки шапки таблицы а трудятся для обозначения операций не обязательно записывать эти операции как мы делали в прошлый раз можно если вы разбираетесь в том что происходит им и вас хорошо все с логическим мышлением то можно записать пост а сами номера отцу операции если вы пронумеровали порядок операций прямо как я вот так вот логическом выражении я запишу операция 1 2 3 четвертое и пятое последние а теперь самое интересное для таблицы истинности которые состоят из трех переменных заполнять значение переменных нужно примерно так же точно так же как мы делали для двух но опять же начиная с столбца с самого правого самый правый столбец до операции переменная c мы ее будем заполнять как и ранее а чередуя нули и единички через 10 10 10 10 1 2 переменная которая находится в столбце чуть левее заполняется чередуясь нулями и единицами по два знака 0 0 1 1 0 0 1 1 переменная 3 которая у нас последнее эта переменная а самом первом столбце будет чередоваться уже по 4 знака или у чередования всегда увеличивается в два раза то есть здесь будет 4 0 и 4 единицы нетрудно догадаться если переменах будет больше например будет 4 то следующая переменная которая бы стояла раньше она бы чередовалась уже по восемь нулей и 8 единиц и так а в самом первом столбце операций мы должны выполнить операцию умножения переменной а на переменную b операции умножение выполняется точно также как и в математике при умножении на 0 все будет равна нулю а 1 умножить на 1 будет равно 1-му поэтому я так и запишу умножая 0 на что угодно первые четыре строчки у меня будут однозначно 0 я запишу 0000 дальше я буду умножать переменную а которая равна единице на значение b следующей строке и нагрев двух строчках переменная b будет также равна нулю поэтому 0 умножая на единицу я получу еще два нуля и две последние строки 1 умножается на 1 получаем один и еще раз один умножается на 1 получаем 1 мы заполнили первую операцию вторая операция это уже умножение переменной а на значение переменной b то есть первое значение 100 столбец и значений из 3 столбца 0 умножая опять же на кого угодно мы получим 40 а как в первом столбце если я обнажаю единицу на 0 я получаю 50 iq единицу на единицу 1 единицу на порой значение 0 у нас получится 0 единицу на единицу получим 1 операция 3 эта операция умножения значения переменных столбца b и значений переменной c это второй и третий столбец точно также 0 умножая на калугу на будет ноль и единицу на единицу 1 итак 0 умножить на 0 0 0 на 1 0 1 на 0 0 1 на 1 единица 0 на 0 0 0 на 1 0 1 на 0 0 и последняя строчка 111 операция 4 эта операция которая складывать значение первой операции и операции 2 то есть вот эти два столбца с переменной которые обозначены цифрами 1 и цифрой 2 при сложении вы выбираете всегда наибольшее число то есть если были нули мы оставляем равное нулю но как только встречается хотя бы одна единичка значение логического сложения будет равно 1-му здесь легко видеть что практически ну значит нас получается пять первых строчек будет равны 0 и к потому что 0 складывается с нуля значит следующая строка у нас 6 будет получается и 7 и 8 будут равны единичка потому что там встречаются единицы и операция 5 последние она должна будет сложить значения всей вот этой вот большой 4 операции посчитаны в предыдущем столбцы и значение операции 3 которая записана в цэлт c под номером три при сложении я напомню нужно будет выбирать наибольшее итак ноль плюс ноль ноль ноль плюс ноль ноль ноль плюс ноль ноль один плюс ноль один ноль плюс ноль ноль ноль плюс 110 плюс 11 и 1 плюс 1 1 я напомню что при сложении двух единиц в алгебре логики получается один потому что в ней не существует других значений кроме 0 единиц и то есть истина единица и ложь 0 последний столбец который мы получили это столбец результирующий тех значений которые нам были нужны вот таким образом строится таблица истинности для логических выражений состоящих из трех логических переменных спасибо за внимание
Основы логики. Логические операции и таблицы истинности
Содержание:
На данной странице будут рассмотренны 5 логических операций: конъюнкция, дизъюнкция, инверсия, импликация и эквивалентность, которых Вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции. Советуем Вам воспользоваться нашими программами для решения задач по математике, геометрии и теории вероятности. Помоми большого количества программ для решения задач на сайте работает форум, на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
Глоссарий, определения логики
Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда
оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из
простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Слишком сложно?
Основы логики. Логические операции и таблицы истинности не по зубам? Тебе ответит эксперт через 10 минут!
таблиц истины: что это такое? (Таблицы истинности для различных логических вентилей)
Что такое таблица истинности?
Таблица истинности — это математическая таблица, в которой перечислены выходные данные конкретной цифровой логической схемы для всех возможных комбинаций ее входов. Эти таблицы истинности могут использоваться для вывода логического выражения для данной цифровой схемы и широко используются в булевой алгебре.
Таблица истинности имеет один столбец для каждой входной переменной (обычно представленной как P и Q, x и y или a и b) и один последний столбец, показывающий все возможные результаты логической операции, которую представляет таблица (для например, P И Q).
Каждая строка таблицы истинности содержит одну возможную конфигурацию входных переменных (например, P = false [0] Q = true [1]) и результат операции для этих значений (продолжая пример, P AND Q = ложь [0]).
Вопросы о логических воротах — отличный способ проверить свои знания по теме таблиц истинности.
Шлюз НЕ или таблица истинности инвертора
Шлюз НЕ — это логическое устройство с одним входом и выходом, выход которого всегда будет дополнительной формой входа.
Это означает, что выход равен 0 для входа, равного 1, и наоборот, как указано в таблице истинности. Это символически записывается как Y = X̅.
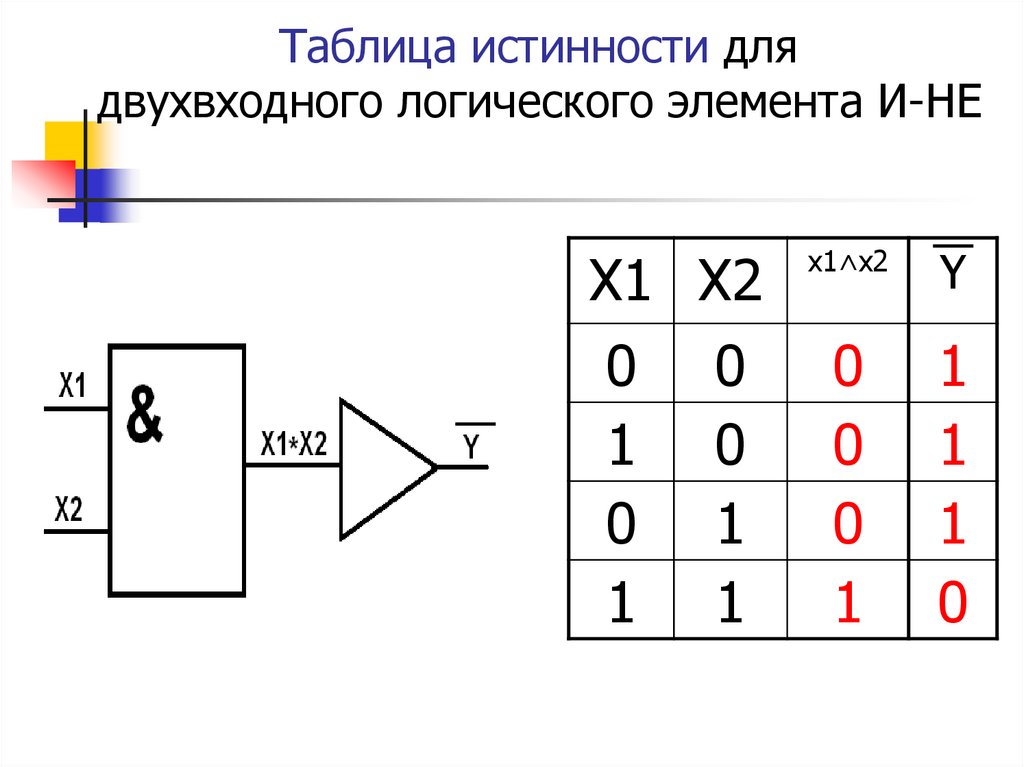
Таблица истинности логического элемента AND
Элемент AND — это базовый вентиль с несколькими входами и одним выходом. Этот вентиль имеет высокий выход только в том случае, если все его входы равны единице, в противном случае выход будет нулевым, как показано в таблице истинности . Логическое выражение, соответствующее этому вентилю, дается как Y = I 1 .Я 2 .
Таблица истинности логического элемента ИЛИ
ИЛИ — это тип базового логического элемента с характеристиками с несколькими входами и одним выходом. Здесь выход равен нулю, только если все его входные биты равны нулю, как указано в таблице истинности логического элемента ИЛИ с 2 входами. Логическое выражение для логического элемента ИЛИ дается как
Таблица истинности логического элемента И-НЕ
Элемент И-НЕ логически эквивалентен элементу И, за которым следует элемент НЕ. Таблица истинности для этого логического элемента показывает, что выход логического элемента И-НЕ имеет низкий уровень, только если все его входы имеют высокий уровень (в противном случае он равен единице).
Это означает, что выход логического элемента И-НЕ является инвертированным выходом логического элемента И, представленного промежуточным результатом M в приведенной выше таблице истинности. Логическое выражение логического элемента И-НЕ задается в виде
Таблица истинности шлюза ИЛИ
Вентиль ИЛИ является результатом объединения элемента НЕ с элементом ИЛИ. Таким образом, его выход является отрицанием выхода логического элемента ИЛИ, что означает, что он имеет высокий выход только в том случае, если все его входы низкие.
Однако для любой другой комбинации входов выход будет низким, как показано в таблице истинности.Логическое выражение для того же самого может быть дано как
Таблица истинности шлюза XOR
Элемент XOR — это логическое устройство, у которого высокий выход только тогда, когда его входы различны, как показано в таблице истинности. Это означает, что неидентичные входные данные приводят к высокому выходному сигналу затвора, в то время как идентичные входные биты вызывают низкий уровень выходного сигнала затвора.
Логически это дается далее в развернутой форме, получается
В общем, вентиль XOR используется как средство проверки четности и может иметь несколько входов.
Таблица истинности ворот XNOR
Элемент XNOR является результатом объединения элемента XOR с элементом NOT, что означает, что выход будет инвертированной формой выходов XOR.
Таким образом, получается высокий выход для идентичных входов и низкий выход для неидентичных входов, как показано таблицей истинности . Логическое выражение для элемента XNOR задается следующим образом:
Этот элемент также может иметь несколько входов и служит средством проверки четности.
Математика за минуту: таблицы истинности
В стандартной математической логике каждое утверждение — «кошка белая», «собака черная», «я голоден» — считается истинным или ложным.Имея два оператора P и Q , вы можете составить более сложные операторы, используя логические связки, такие как AND и OR.
Например, утверждение P И Q (например, «кошка белая, а собака черная») считается истинным только в том случае, если и P , и Q верны, в противном случае это ложь. Это можно резюмировать в таблице истинности:
В таблице перечислены все комбинации значений истинности для P и Q , а затем сообщается, каково соответствующее значение истинности для P И Q .
Аналогичным образом связка ИЛИ определяется следующей таблицей:
Существует также таблица истинности, которая определяет НЕ P , отрицание утверждения P (если P — «кошка белая», то НЕ P — «кошка не белая»). Неудивительно, что НЕ P истинно, когда P ложно, и наоборот:
Используя операторы OR и NOT, мы можем вывести закон для исключенного среднего , который гласит, что всегда верно P OR NOT P :
Используя таблицы истинности, вы можете выяснить, как значения истинности более сложных утверждений, таких как
P И ( Q ИЛИ НЕ R)
зависят от значений истинности его компонентов.Мы заполнили часть таблицы истинности для нашего примера, приведенного ниже, и оставляем вам заполнить остальное.
| P | Q | R | НЕ R | Q ИЛИ НЕ R | P И ( Q ИЛИ НЕ R) | T | T | F | T |
| T | T | F | T | T | |
| T | F 9014 | F | 902|||
| F | T | T | F | T | |
| T | F | F | T | T | F T |
| F | F | T | F | F | |
| F | F | F | T | T | 9017 7
Если вам это понравилось, вы также можете определить свои собственные логические связки, используя таблицы истинности.Или вы можете прочитать учебник по булевой логике или логике высказываний.
Об этой статье
Марианна Фрейбергер — редактор журнала Plus .
Эта статья является частью нашего журнала Кто смотрит? Проект физики наблюдателей , запущенный в сотрудничестве с FQXi. Щелкните здесь, чтобы увидеть больше статей о конструктивизме.
Таблица истинности: определение, правила и примеры — видео и стенограмма урока
Входные значения
Давайте возьмем утверждение: «На улице идет дождь.«Это утверждение, которое мы можем представить с помощью переменной p , истинно или ложно.
p = На улице дождь
Если идет дождь, то p истинно. Если не идет дождь, то p ложно.
Отрицание утверждения , называемое , а не p , является утверждением, которое противоречит p и имеет противоположное значение истинности.
не p = На улице нет дождя
Если на улице дождь, то not p является ложным.Если на улице нет дождя, то , а не p , верно.
Вот как обе эти возможности представлены в таблице истинности, в которой T представляет истину, а F представляет ложь:
Конъюнкция
Конъюнкция — это составное выражение, представляющее слово «и». Например, у нас есть следующие два утверждения:
p = На улице идет дождь
q = Футбольный матч отменен
Соединение p и q : ‘На улице дождь, и футбольный матч отменен.’Это утверждение будет верным только в том случае, если верны и p , и q ; то есть, если на улице идет дождь и футбольный матч отменен. Если либо p , либо q ложно, то соединение ложно.
Вот таблица истинности, показывающая возможности конъюнкции:
Дизъюнкция
Дизъюнкция — это составное выражение, представляющее слово ‘или.«Чтобы дизъюнкция была истинной, одно или оба исходных утверждения должны быть истинными. Разъединение приведенных выше утверждений p или q : «На улице идет дождь или футбольный матч отменен». Это утверждение верно, если истинны p или q или оба утверждения.
Вот как выглядит таблица истинности:
Следствие
Импликация — это условное выражение «если-то», например: «Если на улице идет дождь, то футбольный матч отменяется.Поначалу импликации могут показаться сложными, поскольку они ложны только тогда, когда антецедент (часть «если») истинен, а следствие (часть «тогда») ложно.
Итак, подтекст: «Если на улице идет дождь, футбольный матч отменяется». будет ложным, только если p истинно, а q ложно. То есть на улице идет дождь, но футбольный матч не отменяют. Смысл ложен, потому что обещание импликации было нарушено. Однако, если дождь не идет ( p ложно), то обещание импликации не может быть нарушено, поскольку первая часть (часть «если») никогда не происходила, поэтому импликация верна.Подразумевается, что не говорится, что произойдет, если на улице не будет дождя!
Вот как выглядит таблица истинности импликации:
Построение таблиц истинности
Теперь, когда вы ознакомились с некоторыми из основных таблиц истинности, вы можете приступить к построению своей собственной для оценки более сложных составных утверждений. Полезно получить несколько советов по составлению таблиц организованным образом, чтобы не упустить ни одной возможности.
Шаг 1: Подсчитайте, сколько операторов у вас есть, и сделайте столбец для каждого оператора.
Шаг 2: Введите различные возможные значения истинности для каждого столбца. Если есть только один оператор, то в первом столбце будет только два случая (TF). Если есть два оператора, то есть четыре различных возможных случая: первый столбец будет (TTFF), а второй будет чередоваться (TFTF). Если есть три утверждения, то есть восемь различных возможных случаев: первый столбец будет (TTTTFFFF), второй будет (TTFFTTFF), а третий будет чередоваться (TFTFTFTF).
Шаг 3: Добавьте столбец для каждого отрицательного утверждения и введите значения истинности.
Шаг 4: Добавьте столбцы для любых союзов, дизъюнкций или импликаций, заключенных в круглые скобки или любых группирующих символов.
Шаг 5: Добавьте последний столбец для полного составного оператора.
Противопозитивный пример
Используя два предыдущих утверждения, давайте построим таблицу истинности для составного утверждения: «Если футбольный матч не отменен, значит, на улице не будет дождя.Это противоположность первоначальному подтексту.
Напомним:
p = На улице идет дождь
q = Футбольный матч отменен
Мы можем написать контрпозитив как not q then not p .
Шаг 1. У нас есть два оператора ( p и q ), поэтому нам нужны два столбца.
Шаг 2: Поскольку есть два утверждения, у нас будет четыре разных случая. Первый столбец будет (TTFF), а второй столбец будет (TFTF).
Шаг 3: Добавьте два столбца: один для , а не p , и один для , но не q .
Шаг 4: Добавьте последний столбец для , не q , затем , не p .
Резюме урока
Мы можем использовать таблицу истинности как организованный способ увидеть все возможности при оценке того, является ли составное утверждение истинным или ложным. Буква или переменная обычно представляют утверждения. Чтобы выяснить, является ли утверждение истинным или ложным, мы используем правила логического рассуждения, такие как отрицание , конъюнкция , дизъюнкция и импликация .Эти правила также можно использовать для создания столбцов в таблице истинности, которая обычно включает два столбца case для каждого оператора и отдельные столбцы для каждого отрицательного оператора и полного составного оператора.
таблиц истинности | Блестящая вики по математике и науке
У мистера и миссис Тан пятеро детей — Альфред, Бренда, Чарльз, Дариус, Эрик — предположительно разного возраста.
-
Если Чарльз не самый старший, то Альфред.
-
Если Эрик не самый младший, то Бренда.
-
Если Дарий не самый старший, то он сразу же младше Чарльза.
-
Если Альфред старше Бренды, то Дариус — самый старший.
Определите порядок рождения пятерых детей с учетом вышеуказанных фактов.
Сдаем
- aaa предположение, что Чарльз не самый старший;
- bbb — предположение, что Альфред — самый старший;
- ccc — это утверждение, что Эрик не самый младший;
- означает, что Бренда самая младшая;
- eee быть предположением, что Дарий не самый старший;
- fff — это утверждение, что Дарий просто моложе Чарльза;
- ггг — это предположение, что Альфред старше Бренды.
Из утверждения 1, a → ba \ rightarrow ba → b.
Из утверждения 2, c → dc \ rightarrow dc → d.
Из утверждения 3, e → fe \ rightarrow fe → f.
Из утверждения 4, g → ¬eg \ rightarrow \ neg eg → ¬e, где ¬e \ neg e¬e обозначает отрицание eee.
Обратите внимание, что если Альфред самый старший (b) (b) (b), он старше всех своих четырех братьев и сестер, включая Бренду, поэтому b → gb \ rightarrow gb → g. Поскольку g → ¬eg \ rightarrow \ neg eg → ¬e (утверждение 4), b → ¬eb \ rightarrow \ neg eb → ¬e по транзитивности. Но если у нас есть b, b, b, что означает, что Альфред самый старший, из этого логически следует, что eee, потому что Дарий не может быть самым старым (только один человек может быть самым старым).Переводя это, мы имеем b → eb \ rightarrow eb → e.
Следовательно, (b → e) ∧ (b → ¬e) = (¬b∨e) ∧ (¬b∨¬e) = ¬b∨ (e∧¬e) = ¬b∨C = ¬b, ( b \ rightarrow e) \ клин (b \ rightarrow \ neg e) = (\ neg b \ vee e) \ wedge (\ neg b \ vee \ neg e) = \ neg b \ vee (e \ wedge \ neg e) = \ neg b \ vee C = \ neg b, (b → e) ∧ (b → ¬e) = (¬b∨e) ∧ (¬b∨¬e) = ¬b∨ (e∧¬e) = ¬b∨C = ¬b, где CCC означает противоречие. Единственно возможный вывод — ¬b \ neg b¬b, где Альфред не самый старший. Из утверждения 1, a → ba \ rightarrow ba → b, поэтому по модулю tollens ¬b → ¬a \ neg b \ rightarrow \ neg a¬b → ¬a.Следовательно, Чарльз — самый старый .
Обратите внимание, что по чистой логике ¬a → e \ neg a \ rightarrow e¬a → e, где Чарльз, будучи самым старым, означает, что Дарий не может быть самым старым. Из утверждения 4, g → ¬eg \ rightarrow \ neg eg → ¬e, поэтому по модулю tollens, e = ¬ (¬e) → ¬ge = \ neg (\ neg e) \ rightarrow \ neg ge = ¬ (¬e ) → ¬g. Из утверждения 3, e → fe \ rightarrow fe → f, поэтому по модусу ponens наш вывод eee приводит к другому выводу fff. С fff, поскольку Чарльз — самый старший, Дарий должен быть вторым по возрасту .
Так как ggg означает, что Альфред старше Бренды, ¬g \ neg g¬g означает Альфред моложе Бренды , поскольку они не могут быть одного возраста. Поскольку есть кто-то моложе Бренды, она не может быть самой младшей, поэтому у нас ¬d \ neg d¬d. Поскольку c → dc \ rightarrow dc → d из утверждения 2, по модулю tollens ¬d → ¬c \ neg d \ rightarrow \ neg c¬d → ¬c. Следовательно, Эрик — самый молодой .
Учитывая все вычеты, выделенные жирным шрифтом, единственно возможный порядок рождения — Чарльз, Дариус, Бренда, Альфред, Эрик .□ _ \ квадрат □
Таблица истинности
Таблица истинностиMathlet
нажав на эту кнопку. Таблица истинности появится в новом окно. Нажмите кнопку еще раз, чтобы закрыть таблицу истинности. Если он не появляется, возможно, у вас нет поддержки апплетов Java 2. См. Страницу Java 2.
Этот математический расчет создает таблицу истинности для логического соединения. предложение. Введите один (с последующим нажатием клавиши ENTER), используя следующие синтаксис:
Для переменной истинности любая строчная буква в диапазонах a-e, g-s, u-z. (я.е. опуская f и t, которые зарезервированы для false и true) могут использоваться. В оператор отрицания, ! , применяется перед всеми остальными, которые оцениваются слева направо. Круглые скобки () и квадратные скобки [] могут использоваться для принудительного применения другой порядок оценки.
Например.
p -> q
p & (q | r)
[(p -> q) & (q -> r)] -> (p -> r)
Сделать
Желтый монитор рядом с упражнением говорит о том, что вам следует решите его с помощью математики, и желтый карандаш указывает, что вычисление карандашом и бумагой может быть необходимо.
1. Познакомьтесь с математикой, создав таблицы истинности для элементарные предложения и убедитесь, что они верны! 2. Покажите, что p q логически эквивалентен p q, создавая свои таблицы истинности. 4. Покажите, что контрпозитив p q равен логически эквивалентны p q, создав свои таблицы истинности. 6. Переведите следующее предложение в логическое предложение, используя три логические переменные.Вы можете подключиться к Интернету только из своей комнаты в общежитии. если вы специализируетесь на CS или не отказались от оплаты обучения платежи.
Затем используйте таблицу истинности, чтобы создать таблицу истинности для этого предложение. При каких обстоятельствах студент , а не может подключиться к Интернет из ее комнаты в общежитии? Используйте таблицу истинности для резервного копирования утверждение. Если вы являетесь специалистом по информатике и не выплачиваете плату за обучение, ты можешь подключиться? Опять же, используйте таблицу истинности, чтобы обосновать свой вывод.Таблицы истинности
Таблицы истинностиПриложения таблиц истинности
Мы научились составлять предложения на английском языке и переводить их в логические утверждения, используя буквы и символы для логических связок. И мы узнали, как получить набор значений истинности утверждения во всех возможных случаях, составив таблицу истинности. Теперь мы можем использовать эти инструменты для решения двух важных задач:
- Мы можем доказать, что два разных логических утверждения эквивалентны или не эквивалентны друг другу.
- Мы можем проверить правильность структуры логических аргументов.
Как определить, эквивалентны ли два разных логических оператора
Чтобы определить, эквивалентны ли два логических утверждения или нет, нам нужно создать таблицу истинности для каждого утверждения и сравнить значения истинности утверждений в каждом случае. Если оба утверждения имеют таблицы истинности с точно такими же значениями истинности в последнем столбце, то два утверждения логически эквивалентны, и одно утверждение может быть заменено другим в логическом аргументе без изменения смысла.
Давайте посмотрим на несколько примеров:
Пример 1
Является ли ~ ( p ∧ q ) эквивалентом ~ p∧ ~ q?
Поскольку мы знаем, что в арифметике 2 ( x +3) = 2 x +6, мы можем начать задаваться вопросом, можем ли мы распределить знак отрицания по набору круглых скобок в логических операторах. Другими словами, ~ ( p ∧ q ) эквивалентно ~ p∧ ~ q ?
Единственный способ узнать это — составить таблицу истинности для ~ ( p ∧ q ) и таблицу истинности для ~ p∧ ~ q , а затем сравнить значения истинности в каждой таблице. :
| п. |
q |
p∧q |
~ ( p∧q ) |
| т |
т |
т |
Факс |
| т |
Факс |
Факс |
т |
| Факс |
т |
Факс |
т |
| Факс |
Факс |
Факс |
т |
| п. |
q |
~ п. |
~ q |
~ p∧ ~ q |
| т |
т |
Факс |
Факс |
Факс |
| т |
Факс |
Факс |
т |
Факс |
| Факс |
т |
т |
Факс |
Факс |
| Факс |
Факс |
т |
т |
т |
Чтобы это сравнение работало, мы должны сравнить одинаковых строк в каждой таблице истинности; например, мы должны сравнить строку, где p = T и q = T в таблице истинности для ~ ( p∧q ) со строкой, где p = T и q = T в Таблица истинности для ~ p∧ ~ q .Нас интересует, имеют ли два разных утверждения одинаковое значение истинности в абсолютно одинаковых условиях . Итак, если бы мы сравнили строку, где p = T и q = T в таблице истинности для ~ ( p∧q ), со строкой, где p = T и q = F в таблица истинности для ~ p∧ ~ q , мы будем рассматривать два разных набора условий, и поэтому сравнение значений истинности для каждого утверждения в этом случае приведет к ошибке.
В двух таблицах истинности, которые я создал выше, вы можете видеть, что я перечислил все значения истинности p и q в в том же порядке . Это сделано для того, чтобы я мог сравнивать значения в последнем столбце в двух таблицах истинности, не беспокоясь о том, сопоставляю ли я правильные строки — поскольку строки уже находятся в том же порядке, я могу просто сравнить последний столбец таблицы одна таблица с последним столбцом другой, например:
| п. |
q |
~ ( p∧q ) |
~ p∧ ~ q |
| т |
т |
Факс |
Факс |
| т |
Факс |
т |
Факс |
| Факс |
т |
т |
Факс |
| Факс |
Факс |
т |
т |
В этом случае значения истинности для ~ ( p∧q ) и ~ p∧ ~ q равны , а не , поэтому мы можем заключить, что эти два утверждения эквивалентны , а не !
Итак, это ответ на наш вопрос; если у нас есть ~ ( p∧q ), то не может просто замените его на ~ p∧ ~ q .Если мы заменим ~ ( p∧q ) на ~ p∧ ~ q , мы фактически будем , изменяя смысл нашего утверждения.
Но есть ли другой способ избавиться от скобок? Другими словами, есть ли другой оператор, эквивалентный ~ ( p∧q ), не содержащий скобок? Попробуем другой вариант:
Пример 2:
Является ли ~ ( p ∧ q ) эквивалентом ~ p∨ ~ q?
Чтобы проверить это утверждение, мы должны составить таблицу истинности для ~ ( p ∧ q ) и таблицу истинности для ~ p∨ ~ q , а затем сравнить значения истинности в каждой таблице:
| п. |
q |
p∧q |
~ ( p∧q ) |
| т |
т |
т |
Факс |
| т |
Факс |
Факс |
т |
| Факс |
т |
Факс |
т |
| Факс |
Факс |
Факс |
т |
| п. |
q |
~ п. |
~ q |
~ p∨ ~ q |
| т |
т |
Факс |
Факс |
Факс |
| т |
Факс |
Факс |
т |
т |
| Факс |
т |
т |
Факс |
т |
| Факс |
Факс |
т |
т |
т |
В двух таблицах истинности, которые я создал выше, вы можете видеть, что я перечислил все значения истинности p и q в в том же порядке .Это сделано для того, чтобы я мог сравнивать значения в последнем столбце в двух таблицах истинности, не беспокоясь о том, сопоставляю ли я правильные строки — поскольку строки уже находятся в том же порядке, я могу просто сравнить последний столбец таблицы одна таблица с последним столбцом другой, например:
| п. |
q |
~ ( p∧q ) |
~ p∨ ~ q |
| т |
т |
Факс |
Факс |
| т |
Факс |
т |
т |
| Факс |
т |
т |
т |
| Факс |
Факс |
т |
т |
В этом случае значения истинности для ~ ( p∧q ) и ~ p∨ ~ q в точности совпадают, поэтому мы можем заключить, что эти два утверждения эквивалентны:
~ ( p∧q ) ~ p∨ ~ q
Итак, если мы когда-либо встретим ~ ( p∧q ) , мы можем заменить его на ~ p∨ ~ q , не меняя логического смысла оператора !
Теперь давайте попробуем сравнить два более сложных оператора, чтобы увидеть, эквивалентны ли они:
Пример 3:
Эквивалентно ли утверждение (~ r ∧ ( p → ~ q )) → p r ∨ p?
Чтобы проверить это утверждение, мы должны составить таблицу истинности для (~ r ∧ ( p → ~ q )) → p и таблицу истинности для r ∨ p , а затем сравнить значения истинности в каждой таблице.
Будьте осторожны — поскольку мы хотим сравнить (~ r ∧ ( p → ~ q )) → p , который содержит буквы p , q и r , с r ∨ p , мы должны убедиться, что ОБЕИ таблицы истинности содержат ВСЕ ТРИ БУКВЫ p , q и r (хотя обычно, когда мы составляем таблицу истинности r ∨ p , мы будем использовать только две буквы р и р ).Это потому, что для СРАВНЕНИЯ двух таблиц истинности они должны иметь ТОЧНО ОДИНАКОВЫЕ СТРОКИ.
| п. |
q |
r |
~ д |
p → ~ q |
~ r |
~ r ∧ ( p → ~ q ) | (~ r ∧ ( p → ~ q )) → p |
| т |
т |
т |
Факс |
Факс |
Факс |
Факс |
т |
| т |
т |
Факс |
Факс |
Факс |
т |
Факс |
т |
| т |
Факс |
т |
т |
т |
Факс |
Факс |
т |
| т |
Факс |
Факс |
т |
т |
т |
т |
т |
| Факс |
т |
т |
Факс |
т |
Факс |
Факс |
т |
| Факс |
т |
Факс |
Факс |
т |
т |
т |
Факс |
| Факс |
Факс |
т |
т |
т |
Факс |
Факс |
т |
| Факс |
Факс |
Факс |
т |
т |
т |
т |
Факс |
| п. |
q |
r |
r ∨ p |
| т |
т |
т |
т |
| т |
т |
Факс |
т |
| т |
Факс |
т |
т |
| т |
Факс |
Факс |
т |
| Факс |
т |
т |
т |
| Факс |
т |
Факс |
Факс |
| Факс |
Факс |
т |
т |
| Факс |
Факс |
Факс |
Факс |
В двух таблицах истинности, которые я создал выше, вы можете видеть, что я перечислил все значения истинности p, q и r в в том же порядке .Это сделано для того, чтобы я мог сравнивать значения в последнем столбце в двух таблицах истинности, не беспокоясь о том, сопоставляю ли я правильные строки — поскольку строки уже находятся в том же порядке, я могу просто сравнить последний столбец таблицы одна таблица с последним столбцом другой выглядит так:
| п. |
q |
r |
(~ r ∧ ( p → ~ q )) → p | r ∨ p |
| т |
т |
т |
т |
т |
| т |
т |
Факс |
т |
т |
| т |
Факс |
т |
т |
т |
| т |
Факс |
Факс |
т |
т |
| Факс |
т |
т |
т |
т |
| Факс |
т |
Факс |
Факс |
Факс |
| Факс |
Факс |
т |
т |
т |
| Факс |
Факс |
Факс |
Факс |
Факс |
В этом случае значения истинности для (~ r ∧ ( p → ~ q )) → p и r ∨ p в точности совпадают, поэтому мы можем заключить, что эти два утверждения являются эквивалент:
(~ r ∧ ( p → ~ q )) → p ≡r ∨ p
Итак, если мы когда-нибудь встретим (~ r ∧ ( p → ~ q )) → p , мы можем заменить его на r ∨ p , не меняя логического смысла утверждения !
Как определить, верна ли структура логического аргумента
Мы можем использовать таблицы истинности, чтобы определить, верна ли структура логического аргумента.Чтобы определить, верна ли структура логического аргумента, нам сначала нужно преобразовать наш аргумент в серию логических утверждений, написанных с использованием букв и логических связок. Как только мы это сделаем, мы сможем создать таблицы истинности для каждого утверждения в аргументе.
Затем нам нужно создать таблицу истинности для каждого утверждения предпосылки и таблицу истинности для утверждения заключения и сравнить значения истинности утверждений предпосылки и утверждения заключения в каждом случае. Если значение истинности заключения истинно в КАЖДОМ случае, когда ВСЕ посылки истинны, то аргумент имеет допустимую структуру. Если существует хотя бы один случай , в котором все посылки верны, но заключение ложно, тогда ясно, что истинность заключения не следует непосредственно из посылок, и, следовательно, аргумент недействителен.
Примечание: Если НЕТ случаев, в которых все предпосылки верны, то аргумент действителен по умолчанию. Потому что, если невозможно, чтобы все посылки были истинными одновременно, то невозможно найти обстоятельство, при котором все посылки истинны, а вывод ложен, поэтому невозможно доказать, что аргумент недействителен; следовательно, аргумент становится действительным по умолчанию.
Давайте рассмотрим несколько примеров аргументов и определим, имеют ли они допустимую структуру или нет:
Пример аргумента 1:
Если сейчас октябрь, то занятия в сессии.
Сейчас октябрь.
Следовательно, занятия находятся в сеансе.
Если мы допустим p = «Сейчас октябрь» и q = «Классы в сеансе», то мы можем переписать этот аргумент, используя буквы и логические связки, например:
p → q
п.
Следовательно, q.
Этот аргумент имеет две посылки:
- p → q
- п.
И вывод: q .
Затем мы создаем таблицы истинности как для посылок, так и для заключения. Опять же, поскольку наш аргумент содержит две буквы: p и q , , все наши таблицы истинности должны содержать как p , так и q , и все строки должны быть в одном порядке :
Помещение 1:| p |
q |
p → q |
| т |
т |
т |
| т |
Факс |
Факс |
| Факс |
т |
т |
| Факс |
Факс |
т |
Помещение 2:
| p |
q |
п. |
| т |
т |
т |
| т |
Факс |
т |
| Факс |
т |
Факс |
| Факс |
Факс |
Факс |
Вывод:
| п |
q |
q |
| т |
т |
т |
| т |
Факс |
Факс |
| Факс |
т |
т |
| Факс |
Факс |
Факс |
В трех таблицах истинности, которые я создал выше, вы можете видеть, что я перечислил все значения истинности p и q в в том же порядке .Это сделано для того, чтобы я мог сравнивать значения в последнем столбце в каждой из таблиц истинности, не беспокоясь о том, сопоставляю ли я правильные строки — поскольку строки уже находятся в том же порядке, я могу просто сравнить последний столбец каждой таблицы с последним столбцом других таблиц, например:
| п. |
q |
p → q |
п. |
q |
| т |
т |
т |
т |
т |
| т |
Факс |
Факс |
т |
Факс |
| Факс |
т |
т |
Факс |
т |
| Факс |
Факс |
т |
Факс |
Факс |
Здесь мы отделили помещения от столбцов с первыми буквами и от столбца с выводами темными черными линиями.Теперь все, что нам нужно сделать, это посмотреть на все случаи, в которых ВСЕ предпосылки ИСТИННЫ. Мы выделяем эти примеры желтым цветом в таблице истинности:
| п. |
q |
p → q |
п. |
q |
| Т |
т |
т |
т |
т |
| т |
Факс |
Факс |
т |
Факс |
| Факс |
т |
т |
Факс |
т |
| Факс |
Факс |
т |
Факс |
Факс |
Итак, у нас есть только одна строка, в которой все помещений верны.Напомним, что для того, чтобы аргумент был действительным, всякий раз, когда все предпосылки верны, заключение также должно быть верным. Верен ли вывод и в этой строке? Да!
Таким образом, мы можем сделать вывод, что этот аргумент действителен !
Пример аргумента 2:
Если сейчас октябрь, то занятия в сессии.
Занятия идут.
Значит, октябрь.
Если мы допустим p = «Сейчас октябрь» и q = «Классы в сеансе», то мы можем переписать этот аргумент, используя буквы и логические связки, например:
p → q
q
Следовательно, п.
Этот аргумент имеет две посылки:
- p → q
- q
И вывод такой: р .
Затем мы создаем таблицы истинности как для посылок, так и для заключения. Опять же, поскольку наш аргумент содержит две буквы: p и q , , все наши таблицы истинности должны содержать как p , так и q , и все строки должны быть в одном порядке :
Помещение 1:| p |
q |
p → q |
| т |
т |
т |
| т |
Факс |
Факс |
| Факс |
т |
т |
| Факс |
Факс |
т |
Помещение 2:
| p |
q |
q |
| т |
т |
т |
| т |
Факс |
Факс |
| Факс |
т |
т |
| Факс |
Факс |
Факс |
Вывод:
| п |
q |
п. |
| т |
т |
т |
| т |
Факс |
т |
| Факс |
т |
Факс |
| Факс |
Факс |
Факс |
В трех таблицах истинности, которые я создал выше, вы можете видеть, что я перечислил все значения истинности p и q в в том же порядке .Это сделано для того, чтобы я мог сравнивать значения в последнем столбце в каждой из таблиц истинности, не беспокоясь о том, сопоставляю ли я правильные строки — поскольку строки уже находятся в том же порядке, я могу просто сравнить последний столбец каждой таблицы с последним столбцом других таблиц, например:
| п. |
q |
p → q |
q |
п. |
| т |
т |
т |
т |
т |
| т |
Факс |
Факс |
Факс |
т |
| Факс |
т |
т |
т |
Факс |
| Факс |
Факс |
т |
Факс |
Факс |
Здесь мы отделили помещения от столбцов с первыми буквами и от столбца с выводами темными черными линиями.Теперь все, что нам нужно сделать, это посмотреть на все случаи, в которых ВСЕ предпосылки ИСТИННЫ. Мы выделяем эти примеры желтым цветом в таблице истинности:
| п. |
q |
p → q |
q |
п. |
| Т |
т |
т |
т |
т |
| т |
Факс |
Факс |
Факс |
т |
| Факс |
т |
т |
т |
Факс |
| Факс |
Факс |
т |
Факс |
Факс |
Итак, у нас есть две строки, в которых все помещений верны.Напомним, что для того, чтобы аргумент был действительным, всякий раз, когда все предпосылки верны, заключение также должно быть верным. Верен ли вывод и в первом желтом ряду? Да! Верен ли вывод и во втором желтом ряду? Нет! Это означает, что существует случай, в котором все предпосылки верны, но вывод ложен, поэтому этот аргумент должен быть неверным!
Таким образом, мы можем сделать вывод, что этот аргумент недействителен !
Пример аргумента 3:
У меня проходной балл по этому классу.
Я не сдал с опозданием ни одну домашнюю работу и прошел все тесты.
Я проваливаю урок химии или этот.
Таким образом, неверно, что я плохо разбираюсь в химии, только если я поздно сдал некоторые домашние задания.
Если мы допустим p = «Я сдаю этот класс», q = «Я делаю домашнее задание поздно», r = «Я сдаю все тесты» и s = «Я сдаю мой урок химии «, то мы можем переписать этот аргумент, используя буквы и логические связки, например:
п.
~ q ∧ r
~ с ~ с
Следовательно, ~ ~ с → q .
Примечание: этот аргумент сложен, потому что нам нужно переписать очень много предложений, прежде чем мы сможем превратить их в символы, как мы сделали выше. Вот как мы бы переписали этот аргумент, чтобы было легче распознавать правильные логические связки:
Я сдаю этот курс.
Это неправда, что я поздно сдал некоторые домашние задания и прошел все тесты.
Я не сдам свой урок химии или я не сдам этот урок.
Следовательно, если неверно, что я не сдаю химию, значит, я запоздал с домашним заданием.
Вернитесь к исходному аргументу и посмотрите, сможете ли вы понять, почему мы можем переписать каждое из предложений в аргументе таким образом, не меняя их значения. (Если у вас возникли проблемы с этим, вам следует еще раз взглянуть на лекцию по логике 1).
Этот аргумент имеет три посылки:
- п.
- ~ q ∧ r
- ~ с ∨ ~ с
И вывод: ~ ~ с → q .
Затем мы создаем таблицы истинности как для посылок, так и для заключения. Опять же, поскольку наш аргумент содержит четыре буквы: p , q , r и s , , все наши таблицы истинности должны содержать обе эти четыре буквы и содержать все строки в том же порядке. :
Помещение 1:| p |
q |
r |
с |
п. |
| т |
т |
т |
т |
т |
| т |
т |
т |
Факс |
т |
| т |
т |
Факс |
т |
т |
| т |
т |
Факс |
Факс |
т |
| т |
Факс |
т |
т |
т |
| т |
Факс |
т |
Факс |
т |
| т |
Факс |
Факс |
т |
т |
| т |
Факс |
Факс |
Факс |
т |
| Факс |
т |
т |
т |
Факс |
| Факс |
т |
т |
Факс |
Факс |
| Факс |
т |
Факс |
т |
Факс |
| Факс |
т |
Факс |
Факс |
Факс |
| Факс |
Факс |
т |
т |
Факс |
| Факс |
Факс |
т |
Факс |
Факс |
| Факс |
Факс |
Факс |
т |
Факс |
| Факс |
Факс |
Факс |
Факс |
Факс |
Помещение 2:
| p |
q |
r |
с |
~ q ∧ r |
| т |
т |
т |
т |
Факс |
| т |
т |
т |
Факс |
Факс |
| т |
т |
Факс |
т |
Факс |
| т |
т |
Факс |
Факс |
Факс |
| т |
Факс |
т |
т |
т |
| т |
Факс |
т |
Факс |
т |
| т |
Факс |
Факс |
т |
Факс |
| т |
Факс |
Факс |
Факс |
Факс |
| Факс |
т |
т |
т |
Факс |
| Факс |
т |
т |
Факс |
Факс |
| Факс |
т |
Факс |
т |
Факс |
| Факс |
т |
Факс |
Факс |
Факс |
| Факс |
Факс |
т |
т |
т |
| Факс |
Факс |
т |
Факс |
т |
| Факс |
Факс |
Факс |
т |
Факс |
| Факс |
Факс |
Факс |
Факс |
Факс |
Помещение 3:
| п. |
q |
r |
с |
~ с ∨ ~ p |
| т |
т |
т |
т |
Факс |
| т |
т |
т |
Факс |
т |
| т |
т |
Факс |
т |
Факс |
| т |
т |
Факс |
Факс |
т |
| т |
Факс |
т |
т |
Факс |
| т |
Факс |
т |
Факс |
т |
| т |
Факс |
Факс |
т |
Факс |
| т |
Факс |
Факс |
Факс |
т |
| Факс |
т |
т |
т |
т |
| Факс |
т |
т |
Факс |
т |
| Факс |
т |
Факс |
т |
т |
| Факс |
т |
Факс |
Факс |
т |
| Факс |
Факс |
т |
т |
т |
| Факс |
Факс |
т |
Факс |
т |
| Факс |
Факс |
Факс |
т |
т |
| Факс |
Факс |
Факс |
Факс |
т |
| п |
q |
r |
с |
~ ~ с → q |
| т |
т |
т |
т |
т |
| т |
т |
т |
Факс |
т |
| т |
т |
Факс |
т |
т |
| т |
т |
Факс |
Факс |
т |
| т |
Факс |
т |
т |
Факс |
| т |
Факс |
т |
Факс |
т |
| т |
Факс |
Факс |
т |
Факс |
| т |
Факс |
Факс |
Факс |
т |
| Факс |
т |
т |
т |
т |
| Факс |
т |
т |
Факс |
т |
| Факс |
т |
Факс |
т |
т |
| Факс |
т |
Факс |
Факс |
т |
| Факс |
Факс |
т |
т |
Факс |
| Факс |
Факс |
т |
Факс |
т |
| Факс |
Факс |
Факс |
т |
Факс |
| Факс |
Факс |
Факс |
Факс |
т |
В ЧЕТЫРЕХ таблицах истинности, которые я создал выше, вы можете видеть, что я перечислил все значения истинности p , q , r и s в в том же порядке .Это сделано для того, чтобы я мог сравнивать значения в последнем столбце в каждой из таблиц истинности, не беспокоясь о том, сопоставляю ли я правильные строки — поскольку строки уже находятся в том же порядке, я могу просто сравнить последний столбец каждой таблицы с последним столбцом других таблиц, например:
| п. |
q |
r | с | п. |
~ q ∧ r |
~ с ∨ ~ p |
~ ~ с → q |
| т |
т |
т |
т |
т |
Факс |
Факс |
т |
| т |
т |
т |
Факс |
т |
Факс |
т |
т |
| т |
т |
Факс |
т |
т |
Факс |
Факс |
т |
| т |
т |
Факс |
Факс |
т |
Факс |
т |
т |
| т |
Факс |
т |
т |
т |
т |
Факс |
Факс |
| т |
Факс |
т |
Факс |
т |
т |
т |
т |
| т |
Факс |
Факс |
т |
т |
Факс |
Факс |
Факс |
| т |
Факс |
Факс |
Факс |
т |
Факс |
т |
т |
| Факс |
т |
т |
т |
Факс |
Факс |
т |
т |
| Факс |
т |
т |
Факс |
Факс |
Факс |
т |
т |
| Факс |
т |
Факс |
т |
Факс |
Факс |
т |
т |
| Факс |
т |
Факс |
Факс |
Факс |
Факс |
т |
т |
| Факс |
Факс |
т |
т |
Факс |
т |
т |
Факс |
| Факс |
Факс |
т |
Факс |
Факс |
т |
т |
т |
| Факс |
Факс |
Факс |
т |
Факс |
Факс |
т |
Факс |
| Факс |
Факс |
Факс |
Факс |
Факс |
Факс |
т |
т |
Здесь мы отделили помещения от столбцов с первыми буквами и от столбца с выводами темными черными линиями.Теперь все, что нам нужно сделать, это посмотреть на все случаи, в которых ВСЕ предпосылки ИСТИННЫ. Мы выделяем эти примеры желтым цветом в таблице истинности:
| п. |
q |
r | с | п. |
~ q ∧ r |
~ с ∨ ~ p |
~ ~ с → q |
| т |
т |
т |
т |
т |
Факс |
Факс |
т |
| т |
т |
т |
Факс |
т |
Факс |
т |
т |
| т |
т |
Факс |
т |
т |
Факс |
Факс |
т |
| т |
т |
Факс |
Факс |
т |
Факс |
т |
т |
| т |
Факс |
т |
т |
т |
т |
Факс |
Факс |
| т |
Факс |
т |
Факс |
т |
т |
т |
т |
| т |
Факс |
Факс |
т |
т |
Факс |
Факс |
Факс |
| т |
Факс |
Факс |
Факс |
т |
Факс |
т |
т |
| Факс |
т |
т |
т |
Факс |
Факс |
т |
т |
| Факс |
т |
т |
Факс |
Факс |
Факс |
т |
т |
| Факс |
т |
Факс |
т |
Факс |
Факс |
т |
т |
| Факс |
т |
Факс |
Факс |
Факс |
Факс |
т |
т |
| Факс |
Факс |
т |
т |
Факс |
т |
т |
Факс |
| Факс |
Факс |
т |
Факс |
Факс |
т |
т |
т |
| Факс |
Факс |
Факс |
т |
Факс |
Факс |
т |
Факс |
| Факс |
Факс |
Факс |
Факс |
Факс |
Факс |
т |
т |
Итак, у нас есть только одна строка, в которой все помещений верны.Напомним, что для того, чтобы аргумент был действительным, всякий раз, когда все предпосылки верны, заключение также должно быть верным. Верно ли заключение и в желтом ряду? Да! Это означает, что НЕТ случая, в котором все предпосылки верны, но вывод ложен, поэтому этот аргумент должен быть верным!
Таким образом, мы можем сделать вывод, что этот аргумент действителен !
Пример аргумента 4:
x ≠ y .
x = 10 тогда и только тогда, когда x = y .
Если y не четное число, то x = 10.
Следовательно, y - нечетное число.
Если мы допустим, что p будет « x = y », q будет « x = 10 », а r будет « y — четное число», то мы можем переписать этот аргумент, используя буквы и логические связки вроде этого:
~ стр.
q ↔ p
~ →
Следовательно, ~ r .
Обратите внимание, что утверждения « y — нечетное число» и « y — нечетное число» означают одно и то же и поэтому эквивалентны.
Этот аргумент имеет три посылки:
- ~ стр.
- q ↔ p
- ~ r → q
И вывод: ~ r .
Затем мы создаем таблицы истинности как для посылок, так и для заключения.Опять же, поскольку наш аргумент содержит три буквы: p , q и r , , все наши таблицы истинности должны содержать обе эти три буквы и все строки должны располагаться в том же порядке :
Помещение 1:| p |
q |
r |
~ стр. |
| т |
т |
т |
Факс |
| т |
т |
Факс |
Факс |
| т |
Факс |
т |
Факс |
| т |
Факс |
Факс |
Факс |
| Факс |
т |
т |
т |
| Факс |
т |
Факс |
т |
| Факс |
Факс |
т |
т |
| Факс |
Факс |
Факс |
т |
Помещение 2:
| p |
q |
r |
q ↔ p |
| т |
т |
т |
т |
| т |
т |
Факс |
т |
| т |
Факс |
т |
Факс |
| т |
Факс |
Факс |
Факс |
| Факс |
т |
т |
Факс |
| Факс |
т |
Факс |
Факс |
| Факс |
Факс |
т |
т |
| Факс |
Факс |
Факс |
т |
Помещение 3:
| п. |
q |
r |
~ r → q |
| т |
т |
т |
т |
| т |
т |
Факс |
т |
| т |
Факс |
т |
т |
| т |
Факс |
Факс |
Факс |
| Факс |
т |
т |
т |
| Факс |
т |
Факс |
т |
| Факс |
Факс |
т |
т |
| Факс |
Факс |
Факс |
Факс |
| п |
q |
r |
~ r |
| т |
т |
т |
Факс |
| т |
т |
Факс |
т |
| т |
Факс |
т |
Факс |
| т |
Факс |
Факс |
т |
| Факс |
т |
т |
Факс |
| Факс |
т |
Факс |
т |
| Факс |
Факс |
т |
Факс |
| Факс |
Факс |
Факс |
т |
В трех таблицах истинности, которые я создал выше, вы можете видеть, что я перечислил все значения истинности p , q, и r в в том же порядке .Это сделано для того, чтобы я мог сравнивать значения в последнем столбце в каждой из таблиц истинности, не беспокоясь о том, сопоставляю ли я правильные строки — поскольку строки уже находятся в том же порядке, я могу просто сравнить последний столбец каждой таблицы с последним столбцом других таблиц, например:
| п. | q | r | ~ стр. |
q ↔ p |
~ r → q |
~ r |
| т |
т |
т |
Факс |
т |
т |
Факс |
| т |
т |
Факс |
Факс |
т |
т |
т |
| т |
Факс |
т |
Факс |
Факс |
т |
Факс |
| т |
Факс |
Факс |
Факс |
Факс |
Факс |
т |
| Факс |
т |
т |
т |
Факс |
т |
Факс |
| Факс |
т |
Факс |
т |
Факс |
т |
т |
| Факс |
Факс |
т |
т |
т |
т |
Факс |
| Факс |
Факс |
Факс |
т |
т |
Факс |
т |
Здесь мы отделили помещения от столбцов с первыми буквами и от столбца с выводами темными черными линиями.Теперь все, что нам нужно сделать, это посмотреть на все случаи, в которых ВСЕ предпосылки ИСТИННЫ. Мы выделяем эти примеры желтым цветом в таблице истинности:
| п. | q | r | ~ стр. |
q ↔ p |
~ r → q |
~ r |
| т |
т |
т |
Факс |
т |
т |
Факс |
| т |
т |
Факс |
Факс |
т |
т |
т |
| т |
Факс |
т |
Факс |
Факс |
т |
Факс |
| т |
Факс |
Факс |
Факс |
Факс |
Факс |
т |
| Факс |
т |
т |
т |
Факс |
т |
Факс |
| Факс |
т |
Факс |
т |
Факс |
т |
т |
| Факс |
Факс |
т |
т |
т |
т |
Факс |
| Факс |
Факс |
Факс |
т |
т |
Факс |
т |
Итак, у нас есть только одна строка, в которой все помещений верны.Напомним, что для того, чтобы аргумент был действительным, всякий раз, когда все предпосылки верны, заключение также должно быть верным. Верно ли заключение и в желтом ряду? Нет! Это означает, что существует случай, в котором все предпосылки верны, но вывод ложен, поэтому этот аргумент должен быть неверным!
Таким образом, мы можем сделать вывод, что этот аргумент недействителен !
Пример аргумента 5:
Я получил высшую оценку в классе на последнем тесте, и у меня отличная посещаемость.
Если я простужусь, то всегда пропускаю хотя бы одно занятие.
На прошлой неделе я простудился.
Следовательно, если я пропустил хотя бы одно занятие, значит, я не получил наивысшую оценку в классе на последнем тесте.
Если мы допустим p = «Я получил высшую оценку в классе по последнему тесту», q = «У меня отличная посещаемость» и r будет «Я простужусь», то мы можем переписать этот аргумент с использованием букв и логических связок, например:
p∧ q
r → ~ q
р
Следовательно, ~ r → ~ p .
Обратите внимание, что утверждения «У меня не идеальная посещаемость» и «Я пропускаю хотя бы одно занятие» означают одно и то же и поэтому эквивалентны.
Этот аргумент имеет три посылки:
- p∧ q
- r → ~ q
- r
И вывод: ~ r → ~ p .
Затем мы создаем таблицы истинности как для посылок, так и для заключения.Опять же, поскольку наш аргумент содержит три буквы: p , q и r , , все наши таблицы истинности должны содержать обе эти три буквы и все строки должны располагаться в том же порядке :
Помещение 1:| p |
q |
r |
p∧ q |
| т |
т |
т |
т |
| т |
т |
Факс |
т |
| т |
Факс |
т |
Факс |
| т |
Факс |
Факс |
Факс |
| Факс |
т |
т |
Факс |
| Факс |
т |
Факс |
Факс |
| Факс |
Факс |
т |
Факс |
| Факс |
Факс |
Факс |
Факс |
Помещение 2:
| p |
q |
r |
r → ~ q |
| т |
т |
т |
Факс |
| т |
т |
Факс |
т |
| т |
Факс |
т |
т |
| т |
Факс |
Факс |
т |
| Факс |
т |
т |
Факс |
| Факс |
т |
Факс |
т |
| Факс |
Факс |
т |
т |
| Факс |
Факс |
Факс |
т |
Помещение 3:
| п. |
q |
r |
r |
| т |
т |
т |
т |
| т |
т |
Факс |
Факс |
| т |
Факс |
т |
т |
| т |
Факс |
Факс |
Факс |
| Факс |
т |
т |
т |
| Факс |
т |
Факс |
Факс |
| Факс |
Факс |
т |
т |
| Факс |
Факс |
Факс |
Факс |
| п |
q |
r |
~ r → ~ p |
| т |
т |
т |
т |
| т |
т |
Факс |
Факс |
| т |
Факс |
т |
т |
| т |
Факс |
Факс |
Факс |
| Факс |
т |
т |
т |
| Факс |
т |
Факс |
т |
| Факс |
Факс |
т |
т |
| Факс |
Факс |
Факс |
т |
В трех таблицах истинности, которые я создал выше, вы можете видеть, что я перечислил все значения истинности p , q, и r в в том же порядке .Это сделано для того, чтобы я мог сравнивать значения в последнем столбце в каждой из таблиц истинности, не беспокоясь о том, сопоставляю ли я правильные строки — поскольку строки уже находятся в том же порядке, я могу просто сравнить последний столбец каждой таблицы с последним столбцом других таблиц, например:
| п. | q | r | p∧ q |
r → ~ q |
r |
~ r → ~ p |
| т |
т |
т |
т |
Факс |
т |
т |
| т |
т |
Факс |
т |
т |
Факс |
Факс |
| т |
Факс |
т |
Факс |
т |
т |
т |
| т |
Факс |
Факс |
Факс |
т |
Факс |
Факс |
| Факс |
т |
т |
Факс |
Факс |
т |
т |
| Факс |
т |
Факс |
Факс |
т |
Факс |
т |
| Факс |
Факс |
т |
Факс |
т |
т |
т |
| Факс |
Факс |
Факс |
Факс |
т |
Факс |
т |
Здесь мы отделили помещения от столбцов с первыми буквами и от столбца с выводами темными черными линиями.Теперь все, что нам нужно сделать, это посмотреть на все случаи, в которых ВСЕ предпосылки ИСТИННЫ. Мы выделяем эти примеры желтым цветом в таблице истинности:
| п. | q | r | p∧ q |
r → ~ q |
r |
~ r → ~ p |
| т |
т |
т |
т |
Факс |
т |
т |
| т |
т |
Факс |
т |
т |
Факс |
Факс |
| т |
Факс |
т |
Факс |
т |
т |
т |
| т |
Факс |
Факс |
Факс |
т |
Факс |
Факс |
| Факс |
т |
т |
Факс |
Факс |
т |
т |
| Факс |
т |
Факс |
Факс |
т |
Факс |
т |
| Факс |
Факс |
т |
Факс |
т |
т |
т |
| Факс |
Факс |
Факс |
Факс |
т |
Факс |
т |
Но есть экземпляров НЕТ , в которых все помещений верны! Напомним, что для того, чтобы аргумент был действительным, всякий раз, когда все предпосылки верны, заключение также должно быть верным.Поскольку у нас никогда не бывает экземпляра, в котором все предпосылки истинны , это означает, что НЕ может существовать случая, в котором все предпосылки истинны, но заключение ложно, поэтому этот аргумент должен быть действительным по умолчанию .
Таким образом, мы можем сделать вывод, что этот аргумент действителен !
Будьте осторожны! Если НЕТ примеров, в которых ВСЕ посылки истинны, то у нас никогда не будет случая, когда все посылки истинны, но вывод ложен, поэтому мы не можем сказать, что аргумент неверен.Поэтому в этом случае мы всегда говорим, что аргумент действителен (по умолчанию).
Теперь вернитесь в Blackboard, чтобы ответить на вопросы лекции по логике 3: Оценка аргументов и эквивалентных утверждений!
|
|
| |||

