Таблицы истинности онлайн. Таблицы истинности: построение, СКНФ, СДНФ и полином Жегалкина

Как построить таблицу истинности для логической функции. Как получить СКНФ и СДНФ из таблицы истинности. Как составить полином Жегалкина по таблице истинности. Для чего используются таблицы истинности в математической логике.

Что такое таблица истинности и для чего она используется

Таблица истинности — это способ описания логической функции, показывающий, какие значения принимает функция при всех возможных комбинациях значений входных переменных. Таблицы истинности широко применяются в математической логике, дискретной математике и цифровой схемотехнике для следующих целей:

• Определение значений сложных логических выражений
• Сравнение логических функций на эквивалентность
• Минимизация логических функций
• Построение логических схем
• Получение аналитических выражений функций в различных формах (СДНФ, СКНФ, полином Жегалкина)

Как построить таблицу истинности

Для построения таблицы истинности логической функции необходимо выполнить следующие шаги:

1. Определить количество входных переменных функции (n)
2. Составить 2^n строк, соответствующих всем возможным наборам значений переменных
3. Вычислить значение функции для каждого набора значений переменных
4. Записать полученные значения функции в последний столбец таблицы

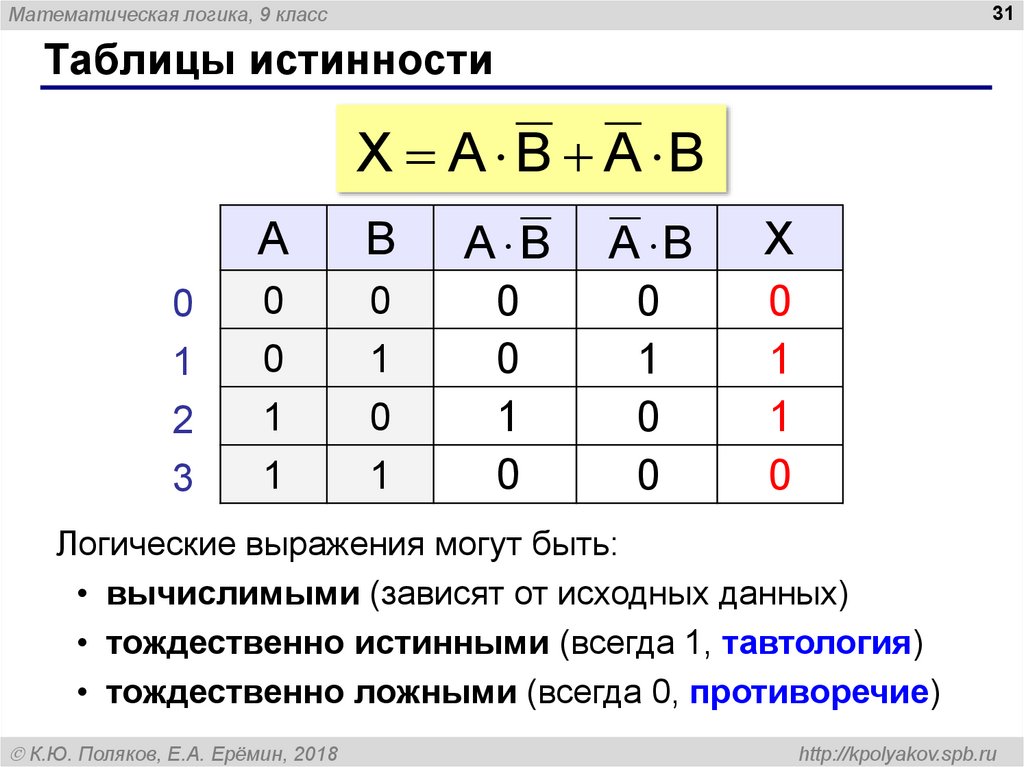
Рассмотрим построение таблицы истинности на примере функции F = A ∧ B ∨ ¬C:

A	B	C	F
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

Совершенная дизъюнктивная нормальная форма (СДНФ)

СДНФ — это представление логической функции в виде дизъюнкции элементарных конъюнкций. Для получения СДНФ из таблицы истинности нужно:

1. Выбрать строки, где функция принимает значение 1
2. Для каждой такой строки записать конъюнкцию переменных (или их отрицаний), соответствующую набору значений в этой строке
3. Объединить полученные конъюнкции знаком дизъюнкции

Для функции из примера выше СДНФ будет иметь вид:

F = (¬A ∧ ¬B ∧ ¬C) ∨ (¬A ∧ B ∧ ¬C) ∨ (A ∧ ¬B ∧ ¬C) ∨ (A ∧ B ∧ ¬C) ∨ (A ∧ B ∧ C)

Совершенная конъюнктивная нормальная форма (СКНФ)

СКНФ — это представление логической функции в виде конъюнкции элементарных дизъюнкций. Для получения СКНФ из таблицы истинности необходимо:

1. Выбрать строки, где функция принимает значение 0
2. Для каждой такой строки записать дизъюнкцию переменных (или их отрицаний), противоположных набору значений в этой строке
3. Объединить полученные дизъюнкции знаком конъюнкции

Для функции из примера СКНФ будет выглядеть так:

F = (A ∨ B ∨ ¬C) ∧ (A ∨ ¬B ∨ ¬C) ∧ (¬A ∨ B ∨ ¬C)

Полином Жегалкина

Полином Жегалкина — это представление логической функции в виде суммы по модулю 2 конъюнкций переменных. Для получения полинома Жегалкина из таблицы истинности можно использовать метод треугольника:

1. Выписать значения функции в первый столбец
2. В каждом следующем столбце записывать сумму по модулю 2 соседних элементов предыдущего столбца
3. Продолжать, пока не останется один элемент
4. Выписать коэффициенты полинома из первых элементов каждого столбца

Для нашей функции полином Жегалкина будет иметь вид:

F = 1 ⊕ C ⊕ AB

Применение таблиц истинности в цифровой схемотехнике

В цифровой схемотехнике таблицы истинности используются для описания работы логических элементов и проектирования цифровых устройств. Они позволяют:

• Определить функциональность логических схем
• Оптимизировать логические схемы
• Анализировать работу цифровых устройств
• Синтезировать новые схемы по заданной логической функции

Таким образом, таблицы истинности являются важным инструментом в математической логике и цифровой технике, позволяющим анализировать и синтезировать логические функции и схемы.

Основные логические операции и их таблицы истинности

Рассмотрим таблицы истинности для основных логических операций:

Конъюнкция (логическое И)

A	B	A ∧ B
0	0	0
0	1	0
1	0	0
1	1	1

Дизъюнкция (логическое ИЛИ)

A	B	A ∨ B
0	0	0
0	1	1
1	0	1
1	1	1

Отрицание (инверсия)

A	¬A
0	1
1	0

Законы алгебры логики

Алгебра логики имеет ряд законов, которые позволяют преобразовывать логические выражения. Вот некоторые из основных законов:

• Закон идемпотентности: A ∧ A = A, A ∨ A = A
• Закон коммутативности: A ∧ B = B ∧ A, A ∨ B = B ∨ A
• Закон ассоциативности: (A ∧ B) ∧ C = A ∧ (B ∧ C), (A ∨ B) ∨ C = A ∨ (B ∨ C)
• Закон дистрибутивности: A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C), A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C)
• Законы де Моргана: ¬(A ∧ B) = ¬A ∨ ¬B, ¬(A ∨ B) = ¬A ∧ ¬B

Эти законы позволяют упрощать логические выражения и доказывать эквивалентность различных форм записи логических функций.

Минимизация логических функций

Минимизация логических функций — это процесс нахождения наиболее простой формы записи функции, эквивалентной исходной. Основные методы минимизации включают:

• Метод карт Карно
• Метод Квайна-Мак-Класки
• Метод Петрика

Минимизация позволяет упростить логические схемы, уменьшить количество используемых логических элементов и повысить быстродействие цифровых устройств.

Заключение

Таблицы истинности являются фундаментальным инструментом в алгебре логики и цифровой схемотехнике. Они позволяют анализировать логические функции, преобразовывать их в различные формы (СДНФ, СКНФ, полином Жегалкина) и проектировать цифровые устройства. Понимание принципов работы с таблицами истинности и знание основных законов алгебры логики необходимо для эффективной работы в области цифровой электроники и компьютерных наук.

Таблица истинности онлайн с примерами

Таблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, у которой значения переменных и значение самой функции выражают истинность. Например, они принимают значения «истина» либо «ложь» (true либо false, 1 либо 0).

Таблицы истинности применяются для определения значения какого-либо высказывания для всех возможных случаев значений истинности высказываний, которые его составляют. Количество всех существующих комбинаций в таблице находится по формуле N=2*n; где N — общее количество возможных комбинаций, n — число входных переменных. Таблицы истинности нередко используются в цифровой технике и булевой алгебре, чтобы описать работу логических схем.

Таблицы истинности для основных функций

Примеры: конъюнкция — 1&0=0, импликация — 1→0=0.

Порядок выполнения логических операций

Инверсия; Конъюнкция; Дизъюнкция; Импликация; Эквиваленция; Штрих Шеффера; Стрелка Пирса.

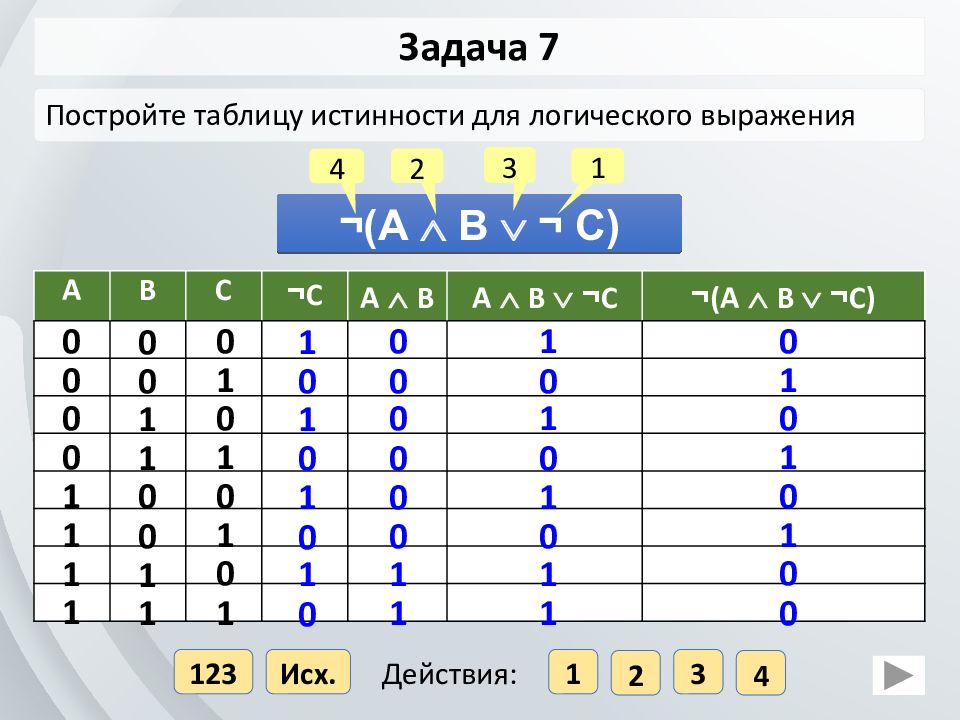
Последовательность построения (составления) таблицы истинности:

https://uchim.org/matematika/tablica-istinnosti — uchim.org

1. Определить количество N используемых переменных в логическом выражении.
2. Вычислить количество всевозможных наборов значений переменных M = 2^N , равное количеству строк в таблице.
3. Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество логических операций.
4. Озаглавить столбцы таблицы названиями переменных и названиями логических операций.
5. Заполнить столбцы логических переменных наборами значений, например, от 0000 до 1111 с шагом 0001 в случае для четырех переменных.
6. Заполнить таблицу истинности по столбцам со значениями промежуточных операций слева направо.
7. Заполнить окончательный столбец значений для функции F.

Таким образом, можно составить (построить) таблицу истинности самостоятельно.

Составить таблицу истинности онлайн

Заполните поле ввода и нажмите OK. T — истина, F — ложь. Рекомендуем добавить страницу в закладки или сохранить в социальной сети.

Обозначения

1. Множества или выражения большими буквами латинского алфавита: A, B, C, D…
2. A’ — штрих — дополнения множеств
3. && — конъюнкция («и»)
4. || — дизъюнкция («или»)
5. ! — отрицание (например, !A)
6. \cap — пересечение множеств \cap
7. \cup — объединение множеств (сложение) \cup
8. A&!B — разность множеств A∖B=A-B
9. A=>B — импликация «Если …, то»
10. AB — эквивалентность

Всё для учебы » Математика в школе » Таблица истинности онлайн с примерами — логика

Графические онлайн калькуляторы

Редактор графа

С помощью данной программы можно онлайн нарисовать любой граф (ориентированный, неориентированный, с петлями), сетевой график, дерево, граф состояний или блок-схему. Калькулятор используется для изучения таких дисциплин как Дискретная математика, Информатика, Управление проектами, Системы массового обслуживания. 12345372420181

Редактор графа

Нарисовать дерево

Простой в использовании редактор позволит быстро и легко создать граф (организационную диаграмму) в виде дерева.

Директор

Финансовый директор

Бухгалтер

Экономист

Нарисовать дерево

Код Прюфера

Восстановление дерева по коду Прюфера с выводом всех шагов построения.

Код Прюфера

Сетевой график

С помощью онлайн программы рассчитываются параметры сетевого графика (сроки свершения событий, резервы времени и критический путь), находятся коэффициенты напряженности. Оптимизация сетевого графика проводится по следующим критериям: число исполнителей, резервы-затраты, сокращение сроков. Калькулятор можно применять для изучения дисциплин

Управление проектами, Исследование операций.

Сетевой график

Диаграмма Ганта

Выбирается число этапов (мероприятий), вводятся их названия и даты проведения. Покупка оборудованияМонтажРегистрацияПолученние инвестицийПодготовка документацииРекламная кампанияНачало производстваСбытFeb 2Feb 4Feb 6Feb 8Feb 10Feb 12Feb 14Feb 16Feb 18Feb 20Feb 22Feb 24Feb 28

Диаграмма Ганта

Редактор схемы логических элементов

Возможности калькулятора позволяют создавать любые сложные схемы логических элементов с последующей минимизацией булевой функции. Имеется поддержка редактирования карты Карно. Данная программа относится к таким разделам как Информатика, Дискретная математика.

Редактор схем

Таблица истинности

По заданной булевой функции формируется таблица истинности, по которой находятся СКНФ, СДНФ и полином Жегалкина. Можно использовать для составления функциональной схемы по логическому выражению. Данная программа относится к таким разделам как Информатика, Дискретная математика.

Таблица истинности

Диаграмма Вейча

С помощью этого калькулятора производится минимизация булевой функции методом Карно-Вейча. Данная программа относится к таким разделам как Информатика, Дискретная математика.

Диаграмма Вейча

Индикаторы уровней Мюррея

Можно использовать как сигналы для покупки или продажи биржевых инструментов. Относится к тематике Рынок ценных бумаг.

Уровни Мюррея

tablica istinnosti ru

Вы искали tablica istinnosti ru? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебра логика калькулятор онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «tablica istinnosti ru».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как tablica istinnosti ru,алгебра логика калькулятор онлайн,алгебра логика онлайн калькулятор,алгебра логики калькулятор,алгебра логики калькулятор онлайн,алгебра логики онлайн,алгебра логики онлайн калькулятор,алгебра логики онлайн решение,алгебра логики решение онлайн,алгебра логики упростить выражение онлайн,булева алгебра калькулятор онлайн,булева алгебра онлайн,булева алгебра онлайн калькулятор,булевы функции онлайн калькулятор,булевых функций онлайн калькулятор,дискретная математика калькулятор онлайн,дискретная математика онлайн калькулятор,дискретная математика упростить выражение онлайн,днф и кнф онлайн,днф и кнф онлайн калькулятор,днф онлайн,днф онлайн калькулятор,доказать равносильность логических выражений онлайн,и таблица истинности,информатика упростить логическое выражение онлайн калькулятор,калькулятор алгебра логика,калькулятор алгебра логики,калькулятор алгебры логики,калькулятор алгебры логики онлайн,калькулятор булевой алгебры онлайн,калькулятор булевых функций,калькулятор булевых функций онлайн,калькулятор днф и кнф онлайн,калькулятор истинности,калькулятор истинности онлайн,калькулятор кнф онлайн,калькулятор логики,калькулятор логики онлайн,калькулятор логические операции,калькулятор логический,калькулятор логических выражений,калькулятор логических выражений онлайн,калькулятор логических выражений онлайн упрощение,калькулятор логических операций,калькулятор логических функций,калькулятор логических функций онлайн,калькулятор мат логика,калькулятор математической логики,калькулятор математической логики онлайн,калькулятор онлайн алгебра логика,калькулятор онлайн истинности,калькулятор онлайн сднф,калькулятор онлайн таблицы истинности,калькулятор онлайн упрощение логических выражений,калькулятор сднф,калькулятор сднф и скнф онлайн,калькулятор скнф и сднф онлайн,калькулятор таблиц истинности онлайн,калькулятор таблица истинности,калькулятор таблица истинности онлайн калькулятор,калькулятор таблицы истинности,калькулятор таблицы истинности онлайн,калькулятор упростить логическое выражение,калькулятор упрощение логических выражений онлайн,карта карно онлайн калькулятор,карты карно калькулятор онлайн,карты карно онлайн калькулятор,карты карно онлайн решение,карты карно решение онлайн,кнф и днф онлайн,кнф и днф онлайн калькулятор,кнф онлайн,логика алгебра онлайн калькулятор,логические выражения калькулятор онлайн,логические выражения онлайн,логические выражения онлайн калькулятор,логические выражения онлайн упростить,логические выражения упростить онлайн,логические операции калькулятор,логические операции калькулятор онлайн,логические операции онлайн,логические операции онлайн калькулятор,логические схемы онлайн,логические уравнения онлайн,логический калькулятор,логический калькулятор онлайн,мат логика калькулятор,мат логика онлайн,математическая логика калькулятор онлайн,математическая логика онлайн,математическая логика онлайн калькулятор,мднф онлайн,минимизация булевых функций онлайн,минимизация логических функций калькулятор онлайн,минимизация логических функций онлайн,минимизация логических функций онлайн калькулятор,минимизация онлайн,минимизация функции онлайн,минимизировать функцию онлайн,многочлен жегалкина онлайн калькулятор,онлайн алгебра логики,онлайн калькулятор алгебра логика,онлайн калькулятор алгебра логики,онлайн калькулятор алгебры логики,онлайн калькулятор булевой алгебры,онлайн калькулятор булевых функций,онлайн калькулятор дискретная математика,онлайн калькулятор днф,онлайн калькулятор истинности,онлайн калькулятор логики,онлайн калькулятор логические выражения,онлайн калькулятор логические операции,онлайн калькулятор логический,онлайн калькулятор логических выражений,онлайн калькулятор логических выражений упрощение,онлайн калькулятор логических функций,онлайн калькулятор математической логики,онлайн калькулятор полином жегалкина,онлайн калькулятор сднф,онлайн калькулятор таблиц истинности,онлайн калькулятор таблица истинности,онлайн калькулятор таблицы истинности,онлайн калькулятор упростить логическое выражение,онлайн калькулятор упростить логическое выражение информатика,онлайн калькулятор упрощение логических выражений,онлайн кнф,онлайн логические операции,онлайн логические схемы,онлайн логические уравнения,онлайн мат логика,онлайн математическая логика,онлайн минимизация,онлайн минимизация логических функций,онлайн минимизация функции,онлайн построение таблиц истинности,онлайн построение таблицы истинности,онлайн преобразование логических выражений,онлайн решение алгебра логики,онлайн решение карты карно,онлайн решение логических выражений,онлайн решение логических уравнений,онлайн решение таблиц истинности,онлайн решение таблицы истинности,онлайн сднф,онлайн составление таблиц истинности,онлайн составление таблицы истинности,онлайн упростите логическое выражение,онлайн упрощение логических выражений,онлайн упрощение логических функций,онлайн упрощение формул логики,полином жегалкина калькулятор онлайн,полином жегалкина онлайн,полином жегалкина онлайн калькулятор,построение онлайн таблиц истинности,построение онлайн таблиц истинности логических выражений,построение таблиц истинности логических выражений онлайн,построение таблиц истинности онлайн,построение таблицы истинности онлайн,построить логическое выражение по таблице истинности онлайн,построить логическую схему онлайн,построить онлайн таблицу истинности,построить таблицу истинности для логического выражения онлайн,построить таблицу истинности онлайн,преобразование логических выражений онлайн,привести к днф функцию онлайн,привести функцию к днф онлайн,решение алгебра логики онлайн,решение карты карно онлайн,решение логических выражений онлайн,решение логических операций онлайн,решение логических уравнений онлайн,решение онлайн логических выражений,решение онлайн таблица истинности,решение таблиц истинности онлайн,решение таблицы истинности онлайн,решить логическое уравнение онлайн,сднф и скнф онлайн,сднф и скнф онлайн калькулятор,сднф и скнф онлайн калькулятор с решением,сднф калькулятор,сднф калькулятор онлайн,сднф онлайн,сднф онлайн калькулятор,сднф по таблице истинности онлайн,скнф и сднф онлайн,скнф и сднф онлайн калькулятор,скнф онлайн,скнф упрощение онлайн,сократить днф онлайн,сокращение логических выражений онлайн,составить логическую схему онлайн,составить таблицу истинности,составить таблицу истинности онлайн,составить таблицу истинности онлайн с решением,составление таблиц истинности онлайн,составление таблицы истинности онлайн,составьте таблицу истинности,таблица истинности,таблица истинности калькулятор,таблица истинности калькулятор онлайн,таблица истинности логических операций онлайн,таблица истинности логических операций онлайн калькулятор,таблица истинности онлайн,таблица истинности онлайн калькулятор,таблица истинности онлайн решение,таблица истинности решение онлайн,таблица истинности ру,таблица истинности это,таблицы истинности калькулятор онлайн,таблицы истинности онлайн,таблицы истинности онлайн калькулятор,таблицы истинности онлайн решение,таблицы истинности решение онлайн,упростите логическое выражение онлайн,упростить выражение алгебра логики онлайн,упростить выражение дискретная математика онлайн,упростить выражение онлайн алгебра логики,упростить выражение онлайн дискретная математика,упростить логические выражения онлайн,упростить логическое выражение калькулятор,упростить логическое выражение калькулятор онлайн,упростить логическое выражение онлайн,упростить логическое выражение онлайн калькулятор,упростить логическое выражение онлайн калькулятор информатика,упростить логическое выражение онлайн калькулятор с решением,упростить логическую функцию онлайн,упростить формулу логики онлайн,упрощение булевых функций онлайн,упрощение логических выражений информатика онлайн калькулятор,упрощение логических выражений калькулятор онлайн,упрощение логических выражений онлайн,упрощение логических выражений онлайн калькулятор,упрощение логических выражений онлайн калькулятор информатика,упрощение логических функций онлайн,упрощение логического выражения онлайн,упрощение скнф онлайн,упрощение формул логики онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и tablica istinnosti ru. Просто введите задачу в окошко и нажмите «решить» здесь (например, алгебра логика онлайн калькулятор).

Где можно решить любую задачу по математике, а так же tablica istinnosti ru Онлайн?

Решить задачу tablica istinnosti ru вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Таблица истинности — это… Что такое Таблица истинности?

Таблица истинности — это таблица, описывающая логическую функцию.

Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» ( либо , либо ).

Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.

Таблицы истинности для основных двоичных логических функций

Таблицы истинности для некоторых троичных логических функций

x	2	1	0	2	1	0	2	1	0
y	2	2	2	1	1	1	0	0	0
Минимум	2	1	0	1	1	0	0	0	0

x	2	1	0	2	1	0	2	1	0
y	2	2	2	1	1	1	0	0	0
Максимум Минус.	2	2	2	2	1	1	2	1	0

x	2	1	0	2	1	0	2	1	0
y	2	2	2	1	1	1	0	0	0
Webb(x,y)	0	0	0	0	2	2	0	2	1

См. также

Примечания

Литература

• Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. — М.: Наука, 1966. — (Математическая логика и основания математики).

Ссылки

▶▷▶ алгебра логики логические законы таблица истинности

▶▷▶ алгебра логики логические законы таблица истинности

Интерфейс	Русский/Английский
Тип лицензия	Free
Кол-во просмотров	257
Кол-во загрузок	132 раз
Обновление:	26-11-2018

алгебра логики логические законы таблица истинности — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Логические законы и правила преобразования логических mir-logikiru/log_zakoni Cached Законы алгебры логики и правила преобразования логических выражений Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре Основы логики и логические основы компьютера studfilesnet/preview/5024724 Cached Базовые знания математической логики , логические элементы и таблицы истинности swf 05022016 111 Mб 14 Урок 2 Порядок выполнения логических выражений Презентация по информатике на тему «Алгебра логики» videourokinet/razrabotki/prezentatsiya-po-in Cached Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений ( истинности или ложности) и логических операций над ними Алгебра Логики Логические Законы Таблица Истинности — Image Results More Алгебра Логики Логические Законы Таблица Истинности images iMath Wiki — Алгебра логики Основные логические операции и wikilividppru/students/cs/lectures/6html Cached Алгебра логики Основные логические операции и их таблицы истинности Основные законы алгебры логики Составление таблиц истинности — YouTube wwwyoutubecom/watch?v=xK0b4ruRtjY Cached Алгебра логики : Таблицы истинности Центр онлайн-обучения «Фоксфорд» — Duration: 10:16 Онлайн-школа с 3 по 11 класс тема: «Алгебра логики Основные логические операции Таблицы открытыйурокрф/статьи/660961/prilpptx Законы и категории логики В формальной логике законы имеют абстрактную форму, в математической логике они конкретны, обладают строгой определенностью и реализуются на практике Логические выражения и логическая таблица истинности Правила mir-logikiru/virag_tabl Cached Логические выражения и таблица истинности Таблица истинности – таблица , показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний Презентация на тему «Алгебра логики» по информатике для 8 класса pptcloudru/informatika/algebra-logiki-112548 Cached Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений ( истинности или ложности) и логических операций над ними Презентация на тему Основы логики логические основы prezentaciiorg › … › Информатика Таблица истинности логического отрицания Слайд 10 Логические законы и правила преобразования логических выражений Булева алгебра (алгебра логики) function-xru/buleva_algebrahtml Cached Итак, алгебра логики (булева алгебра ) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений ( истинности или ложности) и логических операций над ними Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 14,500 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™

• для логической функции F=A?B?C (дизъюнкции) трех логических переменных А
• В
• и С таблица истинности будет иметь вид

для логической функции F=A?B?C (дизъюнкции) трех логических переменных А

и С таблица истинности будет иметь вид

• рассматриваемые со стороны их логических значений ( истинности или ложности) и логических операций над ними Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster
• обладают строгой определенностью и реализуются на практике Логические выражения и логическая таблица истинности Правила mir-logikiru/virag_tabl Cached Логические выражения и таблица истинности Таблица истинности – таблица
• в математической логике они конкретны

алгебра логики логические законы таблица истинности — Все результаты § 3 Законы алгебры логики — ЗФТШ, МФТИ Истинность этих и всех последующих законов легко можно установить, построив таблицу истинности для левого и правого логического выражения Законы алгебры логики — Дистанционная подготовка по информатике informatics-lessonru/logic/laws-logicphp Для преобразования логических формул к равносильным используются законы Докажем второй закон де Моргана с помощью таблицы истинности Таблицы истинности Законы алгебры логики Задачи, решаемые Задачи, решаемые с использованием таблиц истинности — Основы логики В алгебре логики изучаются логические операции, производимые над Законы логики на уроках информатики и ИКТ открытыйурокрф/статьи/574565/ В алгебре высказываний логические законы выражаются в виде равенства на ПК доказательство законов де Моргана, построив таблицу истинности Основные законы алгебры логики — Автор24 › Все предметы › Алгебра логики Логика как наука Рейтинг: 4,4 — ‎2 212 отзывов — ‎Бесплатно — ‎Android — ‎Обучение В алгебре высказываний логические законы выражаются в виде равенства с применением законов алгебры логики таблицы истинности совпадают Видео 10:16 Информатика Алгебра логики: Таблицы истинности Центр Онлайн-школа с 3 по 11 класс YouTube — 16 сент 2014 г 2:40 Алгебра логики: таблицы истинности Образовательный канал «Сам!» YouTube — 27 апр 2017 г 26:39 алгебра логики таблицы истинности Roman Parshykov YouTube — 31 окт 2016 г Все результаты Формулы и законы логики — MathProfi mathprofiru/formuly_i_zakony_logikihtml Похожие При выполнении логического сложения удобно использовать В алгебре высказываний такие формулы называются равносильными или тождественными: Составить таблицу истинности для формулы и убедиться в Основы алгебры логики mschoolkubsuru/mmf/indexphp?option=com_content&viewid Похожие 26 мая 2014 г — Определены аксиомы ( законы ) алгебры логики для выполнения этих таблица истинности одноместной логической операции состоит Основы формальной логики Информатика, Архив — ЯКласс › Архив › Информатика › Средняя школа Логика — наука, изучающая законы и формы мышления; учение о способах Объектами алгебры логики или булевой алгебры являются высказывания Таблица истинности логической функции n аргументов содержит 2 n строк, Урок 5 Логические законы и противоречия — 4Brain Похожие Перейти к разделу Таблицы истинности — Логики придумали для этого очень удобный метод, который получил название « таблиц истинности » Законы алгебры логики и таблицы истинности — Инфоурок › Информатика 19 сент 2016 г — 1 слайд ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ ТАБЛИЦЫ ИСТИННОСТИ 6 слайд Составим таблицу истинности логической функции F = (AVB) Логические законы и правила преобразования логических mir-logikiru/log_zakoni/ Законы алгебры логики и правила преобразования логических выражений Высказывание не может быть одновременно истинным и ложным Алгебра логики Основные логические операции и их таблицы wikilividppru/students/cs/lectures/6html Перейти к разделу Законы алгебры логики — Оказывается, алгебра логики хорошо подходит для либо составляется таблица истинности для него Таблица истинности — Википедия Похожие Таблица истинности — это таблица, описывающая логическую функцию Под « логической Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики Содержание 1 Таблицы истинности для основных двоичных логических функций; 2 Таблицы Булева алгебра (алгебра логики) Перейти к разделу Законы алгебры логики — Законы де Моргана ( законы общей инверсии или Логические схемы и таблицы истинности [PDF] Алгебра логики mospolytechru/storage/files/kaf/ite/algebra_logikipdf Похожие автор: НТ Катанаев — ‎ Похожие статьи 21 Законы , теоремы, постулаты и тождества булевой алгебры 11 действительно, из таблицы истинности логического произведения можно увидеть [PDF] ОСНОВЫ ЛОГИКИ www239ru/userfiles/file/Конспект_ОСНОВЫ%20ЛОГИКИ(3)pdf Похожие Алгебра логики определяет правила выполнения операций с логическими Таблица истинности – задает логическую функцию, то есть правила Основы логики infsusuacru/Klinachev/lc_sga_36htm Похожие Основные понятия и операции формальной логики; Логические выражения и их преобразование; Построение таблиц истинности логических выражений; Основные В алгебре логики , как и в элементарной, справедливы законы [PPT] Элементы алгебры логики lbzru/metodist/authors/informatika/3/files/eor8/presentations/8-1-3ppt алгебра логики ; высказывание; логическая операция; конъюнкция; дизъюнкция; отрицание; логическое выражение; таблица истинности ; законы логики [DOC] ГБОУ Гимназия № 1505 — Портал Гимназии №1505 — Гимназия 1505 oldgym1505ru/files/referat/ref-16869/prod20734-diplom_0doc С помощью таблиц истинности можно устанавливать эквивалентность выражений и справедливость равенств законов алгебры логики Логические основы математической логики wwwidorudnru/nfpk/inf/inf7html Похожие Мы научились составлять таблицу истинности для логической функции Попробуем Полученную формулу можно упростить, применив законы логики : Алгебра логики Таблицы истинности логической функции двух wwwinformatika-1332ru/al/al_04html Похожие Алгебра логики Таблицы истинности логической функции двух переменных Информатика Электронный учебник Помощь ученику Булева алгебра — Национальная библиотека им Н Э Баумана Алгебра логики (булева алгебра) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений ( истинности или ложности) 3) Правила выполнения логического умножения (конъюнкции) Логические схемы и таблицы истинности / Дата обращения: 260616 [PDF] Основные сведения из алгебры логики wwwccasru/wwwusers/an/dto/docs/chap4pdf Похожие основные законы формирования и преобразования логических функций от значения аргумента х в виде специальной таблицы истинности (табл 1) Таблица истинности онлайн — Онлайн-калькулятор › › Умножение двоичных чисел Построение таблицы истинности онлайн Правила ввода логической функции Вместо символа v В алгебре логики можно выделить три основные логические функции: «НЕ» (отрицание), «И» (конъюнкция), «ИЛИ» ( дизъюнкция) [PDF] ТАБЛИЦЫ ИСТИННОСТИ, ЛОГИКА, ДОКАЗАТЕЛЬСТВА wwwwilliamspublishingcom/PDF/5-8459-0498-6/partpdf ВЫСКАЗЫВАНИЯ И ЛОГИЧЕСКИЕ СВЯЗКИ В этом разделе рассматриваются таблицы истинности , знакомство с которыми будет для нас первым Основы логики Логические операции и таблицы истинности Похожие Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой Те, кому лень учить эти законы , должны вспомнить алгебру , где знание Алгебра логики synsetcom/logic/ru/intro/02_logic_algebrahtml В многзначной логике для логического ИЛИ будем использоваться всех результирующих значений в таблице истинности к сумме максимальных Кроме этого, справедливы законы поглощения (следующие 4 тождества), Примерные ответы на профильные билеты Похожие Законы логики Логические переменные Логические выражения и их преобразования Построение таблиц истинности логических выражений Алгебра Законы алгебры логики — PDF — DocPlayerru Это сделать нетрудно, так как все законы записываются для одной или двух, максимум, для трех логических переменных Поэтому таблицы истинности Алгебра логики Логические законы — Видеоуроки Самостоятельная работа по информатике » Алгебра логики Логические законы » Постройте таблицу истинности по логическому выражению МЕТОДИЧЕСКИЕ УКАЗАНИЯ по дисциплине «Математика и edutltsuru/er/book_viewphp?book_id=14aa&page_id=11240 Похожие который первым систематизировал формы и правила мышления, обстоятельно Он вывел для логических построений особую алгебру ( алгебру логики ) Таблица истинности для основных бинарных логических операций Информатика — Логика Основные сведения ege-goru › Темы Похожие Для каждого логического выражения можно составить таблицу истинности , которая описывает, какое значение принимает соответствующая логическая Картинки по запросу алгебра логики логические законы таблица истинности «id»:»ZNIRE-TJUazBpM:»,»ml»:»600″:»bh»:90,»bw»:118,»oh»:182,»ou»:»http://%D0%BE%D1%82%D0%BA%D1%80%D1%8B%D1%82%D1%8B%D0%B9%D1%83%D1%80%D0%BE%D0%BA%D1%80%D1%84/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/574565/img7jpg»,»ow»:472,»pt»:»%D0%BE%D1%82%D0%BA%D1%80%D1%8B%D1%82%D1%8B%D0%B9%D»,»rh»:»xn--i1abbnckbmcl9fbxn--p1ai»,»rid»:»yGmGk_x—YtKDM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Фестиваль педагогических идей»,»th»:90,»tu»:» \u003dtbn:ANd9GcQ2cnD2TSJKLKTI25toRbbXOWAa2eVm081NEDU56j_tgGAPuP3PckfWhU2R»,»tw»:233 «id»:»kI3yh5xXSaG2_M:»,»ml»:»600″:»bh»:90,»bw»:62,»oh»:675,»ou»:» «,»ow»:471,»pt»:»markxnarodru/bool/zalogjpg»,»rh»:»markxnarodru»,»rid»:»Vqy0kFvizuR2OM»,»rt»:0,»ru»:» «,»sc»:1,»th»:100,»tu»:» \u003dtbn:ANd9GcRkHm9vlvOp3YpRHzVPcG9DWOafUOt93Wld9lXYOQyve3d2a8BgnlUgIQ»,»tw»:69 «id»:»cMnPqwG_VpbpSM:»,»ml»:»600″:»bh»:90,»bw»:101,»oh»:392,»ou»:» «,»ow»:449,»pt»:»infolikenarodru/img/pin16gif»,»rh»:»mschoolkubsuru»,»rid»:»GhE0WOn3OXz_wM»,»rt»:0,»ru»:» \u003dcom_content\u0026view\u003darticle\u0026id\u003d211:2014-05-26-04-25-04\u0026catid\u003d27\u0026Itemid\u003d64″,»sc»:1,»th»:90,»tu»:» \u003dtbn:ANd9GcQJTdEU7j7UKHojJ-X-5PpwNoSPZ_DU9eAyRYTxc1dASbmBASkLj0Ifd0g»,»tw»:103 «cl»:3,»cr»:3,»id»:»LOuLCjsDWaXERM:»,»ml»:»600″:»bh»:90,»bw»:101,»oh»:461,»ou»:» «,»ow»:556,»pt»:»konspektanet/studopediaorg/baza14/3632097686744f»,»rh»:»studopediaorg»,»rid»:»zOEN9BP9iexaBM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»СтудопедияОрг»,»th»:90,»tu»:» \u003dtbn:ANd9GcSh4Wyf9UfeAxx34zmkXqMMHW0uWvhEzMn7ac1PkFX5XOjHk3D-Z0fEyQ»,»tw»:109 «id»:»zckeGp_dLdhg1M:»,»ml»:»600″:»bh»:90,»bw»:80,»oh»:720,»ou»:» «,»ow»:652,»pt»:»inf1info/sites/default/files/inline-images/logic»,»rh»:»inf1info»,»rid»:»9hav3HwTH0I7mM»,»rt»:0,»ru»:» «,»sc»:1,»th»:90,»tu»:» \u003dtbn:ANd9GcRq0FwOVXOmuTnAseMLTZIyRiT1SN_CazixykpW8mg3xC_L8aFzSPg5Fw»,»tw»:82 «id»:»q_JJh7My1vWGsM:»,»ml»:»600″:»bh»:90,»bw»:118,»oh»:190,»ou»:» «,»ow»:496,»pt»:»mir-logikiru/sites/default/files/pictures/virag_t»,»rh»:»mir-logikiru»,»rid»:»Y3rJC9lP1uek2M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Мир логики»,»th»:90,»tu»:» \u003dtbn:ANd9GcT8_e1KiFZusWy4hVU_lWfrE781hXDF75bs53X7xMTFJo6xf8k21GyQTqTK»,»tw»:235 Другие картинки по запросу «алгебра логики логические законы таблица истинности» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Урок Законы алгебры логики lunina21205s09edusiteru/p21aa1html Похожие Тема урока: Логические законы и правила преобразования логических С помощью таблиц истинности доказать законы поглощения и склеивания Логические основы построения компьютера иванов-амрф/informatika_09/informatika_materialy_zanytii_09_31html Похожие что изучает алгебра логики ; — какие операции возможны над высказываниями; — как составляется таблица истинности ; — каким законам подчиняются Формулы алгебры логики — СтудопедияОрг Логические операции подчиняются определенным законам Все эти формулы получаются простой проверкой по таблице истинности с учетом Глава 5 — Логические основы компьютеров bookkbsuru/theory/chapter5/1_5html Похожие Работу логических элементов описывают с помощью таблиц истинности В алгебре логики выполняются следующие основные законы , позволяющие [PPT] Основные логические операции ou30omskobr55ru/LOGICAppt Алгебра логики — это математический аппарат, с помощью которого Таблица истинности логической формулы выражает соответствие между Переместительный (коммутативный) закон : A V B = B V A и A&B = B&A 3 Основы логики — Образовательный портал города Апатиты eduapatityru/?page_id=6760 Познакомьтесьс основными понятиями алгебры логики : логические константы, переменные, функции, Научитесь строить таблицу истинности по заданному логическому выражению Изучите законы алгебры логики Используя Составление таблиц истинности для логических высказываний mtcolru/elt/logics/project/p13aa1html Логические законы и правила преобразований логических выражений Решение логических выражений принято записывать в виде таблиц истинности – таблиц, При составлении таблицы истинности для логического выражения Равносильность двух формул алгебры логики обозначается символом Логические устройства » Школа для электрика: статьи, советы electricalschoolinfo/electronica/1152-logicheskie-ustrojjstvahtml Похожие В основу алгебры логики положено понятие «событие», которое может Этот закон называется логической функцией, а переменные – аргументами удобно представить в виде таблицы состояний ( таблицы истинности ), где Элементы математической логики Читать бесплатно онлайн в windoweduru/catalog/pdf2txt/847/54847/26699 Похожие Рассматривваются понятие алгебры логики , история логики, понятие » высказывание», таблицы истинности , логические функции, основные законы логики, упрощение логических выражений, решение логических уравнений, Элементы алгебры логики — Учитель информатики murnikru/elementyi-algebryi-logikihtml 19 янв 2017 г — Алгебра логики определяет правила записи, вычисления значений Значение логических операций отражается в таблице истинности ОАЛ: Основные законы алгебры логики › › Озинский район › МОУ «СОШ рп Озинки» › ОАЛ 14 мар 2015 г — Основы алгебры логики В алгебре высказываний логические законы выражаются в виде Для этого построим таблицу истинности : Алгебра логики и логические основы компьютера 14 мар 2010 г — Законы и аппарат алгебры логики стал использоваться при проектировании Во-первых, она изучает методы установления истинности или ложности сложных логических высказываний с Таблицы истинности Логика, таблицы истинности markxnarodru/bool/tabisthtml Похожие Логика, таблицы истинности ЛОГИЧЕСКИЕ ВЫСКАЗЫВАНИЯ · Законы алгебры логики (jpg) | Законы алгебры логики (doc) · Основные законы логики Постройте таблицы истинности для логических формул и › 10 — 11 классы › Информатика Похожие Постройте таблицы истинности для логических формул и упростите формулы, используя законы алгебры логики : a·b·c… Посмотри ответы прямо Содержание и методика изучения темы «Алгебра логики» в автор: АА Федюкова — ‎2016 — ‎ Похожие статьи Изучение основных законов логики способствует развитию логического мышления у и таблицы истинности инверсия, импликация, эквивалентность Элементы алгебры логики — Информатика — Studmeorg Алгебра логики оперирует с логическими высказываниями, которые принимают значение истинности или ложности Логическое высказывание Вместе с алгебра логики логические законы таблица истинности часто ищут законы алгебры логики информатика законы алгебры логики примеры все законы алгебры логики законы алгебры логики доказательства законы алгебры логики таблица основные законы алгебры логики закон склеивания законы алгебры логики задачи Навигация по страницам

Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Знатоки Коллекции Музыка Переводчик Диск Почта Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 iMath Wiki — Алгебра логики Основные логические wikilividppru › students/cs/lectures/6html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Алгебра логики Основные логические операции и их таблицы истинности Основные законы алгебры логики Читать ещё Алгебра логики Основные логические операции и их таблицы истинности Основные законы алгебры логики Алгебра логики Логические операции Законы алгебры логики Формальное решение логических задач Алгебра логики Мы выяснили, как информация представляется в памяти вычислительных устройств и установили алгоритмы проведения операций над этими представлениями Теперь, давайте попробуем разобраться, как именно реализуются операции над двоичными представлениями Для этого, для начала, нам придется разобраться с алгеброй логики Алгебра логики является частью дискретной математики – раздела матема Скрыть 2 ОАЛ: Основные законы алгебры логики edusarsoiroru › mod/page/viewphp… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Законы алгебры высказываний Алгебра высказываний ( алгебра логики ) — раздел математической логики , изучающий логические операции над высказываниями и правила преобразования сложных высказываний При решении многих логических задач часто приходится упрощать формулы, полученные при Читать ещё Законы алгебры высказываний Алгебра высказываний ( алгебра логики ) — раздел математической логики , изучающий логические операции над высказываниями и правила преобразования сложных высказываний При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий Упрощение формул в алгебре высказываний производится на основе эквивалентных преобразований, опирающихся на основные логические законы Законы алгебры высказываний ( алгебры логики ) — это тавтологии Иногда эти законы называются теоремами В алгебре высказываний логические законы выражаются в в Скрыть 3 Алгебра логики логические Законы таблица истинности — смотрите картинки ЯндексКартинки › алгебра логики логические законы таблица Пожаловаться Информация о сайте Ещё картинки 4 Таблицы истинности , с формулами и примерами rusolverbookcom › Справочник › Таблицы › Таблицы истинности Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Значения логических функций определяются с помощью таблица истинности Таблицы истинности для основных двоичных логических функций 1 Конъюнкция ( логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него Читать ещё Значения логических функций определяются с помощью таблица истинности Таблицы истинности для основных двоичных логических функций 1 Конъюнкция ( логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения Обозначение: 2 Дизъюнкция ( логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны Обозначение Скрыть 5 Логические законы и правила преобразования mir-logikiru › log_zakoni/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Применим законы алгебры логики Покажем на примере как можно упростить логическое выражение, используя Логические законы и правила преобразования логических выражений Логические выражения и таблица истинности Законы и правила преобразования логических выражений Читать ещё Применим законы алгебры логики Покажем на примере как можно упростить логическое выражение, используя Логические законы и правила преобразования логических выражений Логические выражения и таблица истинности Законы и правила преобразования логических выражений Решение логических задач Логические основы работы компьютера Скрыть 6 Основы алгебры логики mschoolkubsuru › Малый математический факультет › indexphp?Itemid=64… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Определены аксиомы ( законы ) алгебры логики для выполнения этих операций Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний Читать ещё Определены аксиомы ( законы ) алгебры логики для выполнения этих операций Действия, которые производятся над высказываниями, записываются в виде логических выражений Логические выражения могут быть простыми и сложными Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении, например: таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции Скрыть 7 Основные законы алгебры логики spravochnickru › informatika…zakony_algebry_logiki/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Законы алгебры логики называют иногда теоремами В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул В справедливости всех законов можно убедиться, построив таблицы истинности для левой и правой частей записанного закона После упрощения Читать ещё Законы алгебры логики называют иногда теоремами В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул В справедливости всех законов можно убедиться, построив таблицы истинности для левой и правой частей записанного закона После упрощения выражения с применением законов алгебры логики таблицы истинности совпадают Справедливость части законов можно доказать, применяя инструментарий таблиц истинности Рисунок 1 Примеры Составим таблицу истинности для выражения Рисунок 2 Скрыть 8 Основы формальной логики Информатика, Архив yaklassru › materiali… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Логика — наука, изучающая законы и формы мышления ; учение о способах рассуждений и доказательств Обоснование истинности или ложности простых высказываний решается вне алгебры логики Читать ещё Логика — наука, изучающая законы и формы мышления ; учение о способах рассуждений и доказательств Законы мира, сущность предметов, общее в них мы познаем посредством абстрактного мышления Основными формами абстрактного мышления являются понятия, суждения и умозаключения Обоснование истинности или ложности простых высказываний решается вне алгебры логики Например, истинность или ложность высказывания: «Сумма углов треугольника равна 180 градусов» устанавливается геометрией, причем — в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным Истинному высказыванию ставится в соответствие 1, ложному — 0 Таким образом, А = 1, В = 0 Скрыть 9 § 13 Элементы алгебры логики иванов-амрф › informatika_08_fgos/informatika_… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте таблица истинности законы логики 131 Высказывание Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами Многие математические объекты (целые и рациональные Читать ещё таблица истинности законы логики 131 Высказывание Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами Многие математические объекты (целые и рациональные числа, многочлены, векторы, множества) вы изучаете в школьном курсе алгебры , где знакомитесь с такими разделами математики, как алгебра чисел, алгебра многочленов, алгебра множеств и т д Для информатики важен раздел математики, называемый алгеброй логики ; объектами алгебры логики являются высказывания Скрыть 10 Таблица истинности онлайн mathsemestrru › Таблица истинности Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Таблица истинности – таблица содержащая все возможные комбинации входных переменных и соответствующее им значения на выходе Функция алгебры логики называется полностью определённой если заданы все 2n её значения, где n – число выходных переменных Если определены не все значения, функция Читать ещё Таблица истинности – таблица содержащая все возможные комбинации входных переменных и соответствующее им значения на выходе Таблица истинности содержит 2n строк, где n – число входных переменных, и n+m – столбцы, где m – выходные переменные Решение онлайн Видеоинструкция Функция алгебры логики называется полностью определённой если заданы все 2n её значения, где n – число выходных переменных Если определены не все значения, функция называется частично определённой Устройство называется логическим , если его состояние описывается с помощью функции алгебры логики Для представления функции алгебры логики используется следующие способы Скрыть Основные законы алгебры логики , Таблицы studwoodru › 970591/filosofiya…zakony…logiki Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте В алгебре логики имеются законы , которые записываются в виде соотношений Например, для логической функции F=A?B?C (дизъюнкции) трех логических переменных А, В, и С таблица истинности будет иметь вид, показанный на рис 11 Для записи значений логических переменных и логической функции Читать ещё В алгебре логики имеются законы , которые записываются в виде соотношений Логические законы позволяют производить равносильные (эквивалентные) преобразования логических выражений Например, для логической функции F=A?B?C (дизъюнкции) трех логических переменных А, В, и С таблица истинности будет иметь вид, показанный на рис 11 Для записи значений логических переменных и логической функции данная таблица истинности содержит 8 строк и 4 столбца, т е число строк для записи значений аргументов и функции любой таблицы истинности будет равно 2n, где n — число аргументов логической функции, а число столбцов равно n + 1 [1] Скрыть Вместе с « алгебра логики логические законы таблица истинности » ищут: алгебра логики логические операции алгебра логики логические переменные и логические высказывания 9 класс алгебра логики логические высказывания алгебра логики логические схемы алгебра логики логические переменные и логические высказывания презентация алгебра логики логические переменные и логические высказывания алгебра логики логические выражения и функции алгебра логики логические операции законы алгебры логики алгебра логики логические выражения алгебра логики логические законы 1 2 3 4 5 дальше Bing Google Mailru Нашлось 79 млн результатов Дать объявление Регистрация Войти 0+ ЯндексБраузер: голосовое управление компьютером Установить Закрыть Попробовать еще раз Включить Москва Настройки Клавиатура Помощь Обратная связь Для бизнеса Директ Метрика Касса Телефония Для души Музыка Погода ТВ онлайн Коллекции Яндекс О компании Вакансии Блог Контакты Мобильный поиск © 1997–2018 ООО «Яндекс» Лицензия на поиск Статистика Поиск защищён технологией Protect Алиса в ЯндексБраузере Выключит компьютер по голосовой команде 0+ Установить

Онлайн-лектории по подготовке к ЕГЭ для школьников стартовали в ДГТУ

МАХАЧКАЛА, 15 марта – РИА «Дагестан». Профессорско-педагогическим составом ДГТУ ежедневно с 15 марта по 30 апреля будут проводиться онлайн-лекции для школьников Республики Дагестан. Об этом информагентству сообщили в пресс-службе вуза.

Выбор формата лекций обусловлен тем, что учащиеся школ отдаленных муниципальных образований республики не имеют возможности лично принимать участие в образовательных лекториях ДГТУ.

Теперь любой желающий через платформу FreeConferenceCall сможет получить на безвозмездной основе помощь в подготовке к Единому государственному экзамену, прослушав лекции педагогов технического университета – экспертов ЕГЭ.

Лекции будут проходить по трем дисциплинам: математике, физике и информатике, каждый день с 14:00 по ссылке.

Первая лекция по физике состоялась уже сегодня, 15 марта. Доцент кафедры физики Джавад Арсланов рассматривал с учащимися вопросы, связанные с разделом физики, изучающим движение материальных тел и взаимодействие между ними, – механикой.

Во вторник, 16 марта, состоится лекция по математике «Решение рациональных уравнений» (Ильясова С.А., ст. преподаватель.), в среду, 17 марта, – по информатике «Двоичное кодирование чисел. Запись двоичных чисел в восьмеричной и шестнадцатеричной системе» (Пиняскин В.В., к.х.н., доцент), в четверг, 18 марта, – по физике «Молекулярная физика. Термодинамика» (Ахмедов Г.Я., д.т.н., профессор), в пятницу, 19 марта, – по математике «Решение рациональных неравенств (метод интервалов)» (Асадулаева Т.Г., ст. преподаватель), в субботу, 20 марта, – по информатике «Таблицы истинности логической функции» (Исабекова Т.И., к.ф.-м.н., доцент).

С графиком проведения онлайн университетских лекториев можно ознакомиться на официальном сайте университета по ссылке.

Полином Жегалкина. Пример решения задачи на Викиматик

Полином (многочлен) Жегалкина представляет собой полином, коэффициентами которого являются числа $0$ или $1$, причем в качестве операций умножения и сложения выступают соответственно конъюнкция и сумма по модулю $2$. Например, для булевой функции $f\left(x_1,\ x_2,\ x_3\right)$ от трех переменных $x_1,\ x_2,\ x_3$ полином Жегалкина будет иметь следующий вид:

$$f\left(x_1,\ x_2,\ x_3\right)=a_0\bigoplus a_1x_1\bigoplus a_2x_2\bigoplus a_3x_3\bigoplus a_{12}x_1x_2\bigoplus a_{13}x_1x_3\bigoplus a_{23}x_2x_3\bigoplus a_{123}x_1x_2x_3.$$ 

Коэффициенты $a_0,\ a_1,\ \dots ,\ a_{123}\in \left\{0,\ 1\right\}$, то есть могут принимать значения либо $0$, либо $1$ в зависимости от того, какое значение принимает булева функция $f\left(x_1,\ x_2,\ x_3\right)$ на том или ином наборе значений переменных.

С помощью полинома Жегалкина можно представить любую булеву функцию, причем единственных образом. Поэтому можно сказать, что полином Жегалкина является еще одним способом представления булевых функций в алгебре операций $\bigoplus $ — суммы по модулю $2$, $\cdot $ — конъюнкции и константы $1$.

Операция $\bigoplus $ имеет и другие названия: сумма Жегалкина, неравнозначность, исключающее ИЛИ-НЕ. Иногда, для удобства ее обозначения используют привычную запись сложения $+$, но не стоит путать с дизъюнкцией и, тем более, с обычной арифметической операцией сложения. Таблица истинности данной операции имеет вид:

$$\begin{array}{|c|c|}
\hline
x & y & x\bigoplus y \\
\hline
0 & 0 & 0 \\
\hline
0 & 1 & 1 \\
\hline
1 & 0 & 1 \\
\hline
1 & 1 & 0 \\
\hline
\end{array}$$

Сумма $x\bigoplus y$ принимает истинное значение тогда и только тогда, когда истинно одно и только одно составляющее высказывание. Если сравнить таблицы истинности основных логических операций, то можно заметить, что $x\bigoplus y=\overline{x\leftrightarrow y}$. То есть операция сумма Жегалкина $\bigoplus $ есть отрицание эквиваленции.

Для двух введенных операций $\bigoplus ,\ \cdot $ (суммы по модулю 2 и конъюнкции) выполняются все логические законы:

1. Коммутативность: $x\bigoplus y=y\bigoplus x$;
2. Ассоциативность: $\left(x\bigoplus y\right)\bigoplus z=x\bigoplus \left(y\bigoplus z\right)$, то есть результат $x\bigoplus y\bigoplus z$ не зависит от расстановки скобок;
3. Дистрибутивность: $x\left(y\bigoplus z\right)=xy\bigoplus xz$;
4. $x\bigoplus x=0$;
5. $0\bigoplus x=x$;
6. $\overline{x}=x\bigoplus 1$.

Для построения полинома Жегалкина можно использовать различные методы:

• Метод неопределенных коэффициентов;
• Метод треугольника Паскаля;
• Преобразование ДНФ;
• Преобразование СДНФ.

Метод неопределенных коэффициентов

Найдем полином Жегалкина для функции $f\left(x_1,\ x_2,\ x_3\right)=\left(x_1x_2\vee x_3\right)\to {\overline{x}}_2$, используя метод неопределенных коэффициентов. Для этого сначала необходимо построить таблицу истинности данной булевой функции $f\left(x_1,\ x_2,\ x_3\right)$.

$\begin{array}{|c|c|}
\hline
x_1 & x_2 & x_3 & x_1x_2 & x_1x_2\vee x_3 & f\left(x_1,\ x_2,\ x_3\right)=\left(x_1x_2\vee x_3\right)\to {\overline{x}}_2 \\ 
0 & 0 & 0 & 0 & 0 & 1 \\ 
\hline
0 & 0 & 1 & 0 & 1 & 1 \\ 
\hline
0 & 1 & 0 & 0 & 0 & 1 \\ 
\hline
0 & 1 & 1 & 0 & 1 & 0 \\ 
\hline
1 & 0 & 0 & 0 & 0 & 1 \\ 
\hline
1 & 0 & 1 & 0 & 1 & 1 \\ 
\hline
1 & 1 & 0 & 1 & 1 & 0 \\ 
\hline
1 & 1 & 1 & 1 & 1 & 0 \\ 
\hline
\end{array}$

Общий вид полинома Жегалкина для функции $f\left(x_1,\ x_2,\ x_3\right)$ трех переменных $x_1,\ x_2,\ x_3$:

$$f\left(x_1,\ x_2,\ x_3\right)=a_0\bigoplus a_1x_1\bigoplus a_2x_2\bigoplus a_3x_3\bigoplus a_{12}x_1x_2\bigoplus a_{13}x_1x_3\bigoplus a_{23}x_2x_3\bigoplus a_{123}x_1x_2x_3.$$ 

Последовательно подставляем наборы значений переменных и находим коэффициенты $a_0,\ a_1,\ \dots ,\ a_{123}$.

$f\left(0,\ 0,\ 0\right)=a_0=1;$ 

$f\left(0,\ 0,\ 1\right)=a_0\bigoplus a_3=1\Rightarrow 1\bigoplus a_3=1\Rightarrow a_3=0;$ 

$f\left(0,\ 1,\ 0\right)=a_0\bigoplus a_2=1\Rightarrow 1\bigoplus a_2=1\Rightarrow a_2=0;$

$f\left(0,\ 1,\ 1\right)=a_0\bigoplus a_2\bigoplus a_3\bigoplus a_{23}=0\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus a_{23}=0\Rightarrow 1\bigoplus a_{23}=0\Rightarrow a_{23}=1;$

$f\left(1,\ 0,\ 0\right)=a_0\bigoplus a_1=1\Rightarrow 1\bigoplus a_1=1\Rightarrow a_1=0.$

$f\left(1,\ 0,\ 1\right)=a_0\bigoplus a_1\bigoplus a_3\bigoplus a_{13}=1\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus a_{13}=1\Rightarrow 1\bigoplus a_{13}=1\Rightarrow a_{13}=0;$

$f\left(1,\ 1,\ 0\right)=a_0\bigoplus a_1\bigoplus a_2\bigoplus a_{12}=0\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus a_{12}=0\Rightarrow 1\bigoplus a_{12}=0\Rightarrow a_{12}=1;$

$f\left(1,\ 1,\ 1\right)=a_0\bigoplus a_1\bigoplus a_2\bigoplus a_3\bigoplus a_{12}\bigoplus a_{13}\bigoplus a_{23}\bigoplus a_{123}=0\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus 0\bigoplus 1\bigoplus 0\bigoplus 1\bigoplus a_{123}=0\Rightarrow 1\bigoplus a_{123}=0\Rightarrow a_{123}=1;$ 

Подставляя найденные коэффициенты, получаем полином Жегалкина:

$$f\left(x_1,\ x_2,\ x_3\right)=1\bigoplus x_1x_2\bigoplus x_2x_3\bigoplus x_1x_2x_3.$$ 

Метод треугольника Паскаля

Построим полином Жегалкина для функции из предыдущего метода, используя треугольник Паскаля.

Поясним, как заполняется треугольник Паскаля. Верхняя строка треугольника задает вектор значений булевой функции $f=\left(11101100\right)$. В каждой строке, начиная со второй, любой элемент такого треугольника вычисляется как сумма по модулю $2$ двух соседних элементов предыдущей строки. Так, элементы второй строки: $1\bigoplus 1=0,\ 1\bigoplus 1=0,\ 1\bigoplus 0=1,\ 0\bigoplus 1=1,\ 1\bigoplus 1=0,\ 1\bigoplus 0=1,\ 0\bigoplus 0=0$. Аналогично вычисляются элементы других строк.

Левой стороне треугольника Паскаля соответствуют наборы значений переменных исходной функции $f\left(x_1,\ x_2,\ x_3\right)$. Соединяя знаком конъюнкции переменные, значения которых в наборе равны $1$, мы получим слагаемое в полиноме Жегалкина. Набору $\left(000\right)$ соответствует $1$, набору $\left(001\right)$ соответствует $x_3$, и т.д.

Поскольку единицам левой стороны треугольника соответствуют слагаемые $1,\ x_2x_3,\ x_1x_2,\ x_1x_2x_3$, то полином Жегалкина:

$$f\left(x_1,\ x_2,\ x_3\right)=1\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3.$$ 

Преобразование ДНФ

Используя основные законы алгебры логики, приведем сначала данную функцию к ДНФ.

$f\left(x_1,\ x_2,\ x_3\right)=\left(x_1x_2\vee x_3\right)\to {\overline{x}}_2=$ $\{$используем равносильность $x\to y=\overline{x}\vee y$$\}$ $=\overline{x_1x_2\vee x_3}\vee {\overline{x}}_2=$ $\{$используем закон де Моргана $\overline{x\vee y}=\overline{x}\ \overline{y}$$\}$ $=\overline{x_1x_2}\cdot {\overline{x}}_3\vee {\overline{x}}_2=$ $\{$используем закон де Моргана $\overline{xy}=\overline{x}\vee \overline{y}$$\}$ $=\left({\overline{x}}_1\vee {\overline{x}}_2\right){\overline{x}}_3\vee {\overline{x}}_2=$ $\{$используем закон дистрибутивности $\left(x\vee y\right)z=xz\vee yz$$\}$ $={\overline{x}}_1{\overline{x}}_3\vee \underbrace{{\overline{x}}_2{\overline{x}}_3}_{поглощается\ {\overline{x}}_2}\vee {\overline{x}}_2={\overline{x}}_1{\overline{x}}_3\vee {\overline{x}}_2$ —ДНФ.

Далее в полученной ДНФ необходимо «избавиться» от дизъюнкции, используя законы де Моргана:

$${\overline{x}}_1{\overline{x}}_3\vee {\overline{x}}_2=\overline{{\overline{{\overline{x}}_1{\overline{x}}_3}x}_2}.$$ 

Заменяем каждое отрицание $\overline{x}=1\bigoplus x$ и применяем написанные выше логические законы, получаем:

$\overline{{\overline{{\overline{x}}_1{\overline{x}}_3}x}_2}=1\bigoplus {\overline{{\overline{x}}_1{\overline{x}}_3}x}_2=1\bigoplus \left(1\bigoplus \left(1\bigoplus x_1\right)\left(1\bigoplus x_3\right)\right)x_2=1\bigoplus \left(1\bigoplus 1\bigoplus x_3\bigoplus x_1\bigoplus x_1x_3\right)x_2=1\bigoplus \left(x_3\bigoplus x_1\bigoplus x_1x_3\right)x_2=1\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3$ — полином Жегалкина.

Преобразование СДНФ

$\begin{array}{|c|c|}
\hline
x_1 & x_2 & x_3 & f\left(x_1,\ x_2,\ x_3\right) \\
\hline
0 & 0 & 0 & 1 \\
\hline
0 & 0 & 1 & 1 \\
\hline
0 & 1 & 0 & 1 \\
\hline
0 & 1 & 1 & 0 \\
\hline
1 & 0 & 0 & 1 \\
\hline
1 & 0 & 1 & 1 \\
\hline
1 & 1 & 0 & 0 \\
\hline
1 & 1 & 1 & 0 \\
\hline
\end{array}$

Для построения СДНФ по таблице истинности выбираем наборы, на которых функция $f$ принимает значение, равное 1. Если значение переменной в этом наборе равно 0, то она берется с отрицанием, если значение переменной равно 1, то переменная берется без отрицание. Соединив знаком конъюнкции переменные соответствующего набора, получим элементарную конъюнкцию. Тогда дизъюнкция всех таких элементарных конъюнкций есть СДНФ.

$$f\left(x_1,\ x_2,\ x_3\right)={\overline{x}}_1{\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1{\overline{x}}_2x_3\vee {\overline{x}}_1x_2{\overline{x}}_3\vee x_1{\overline{x}}_2{\overline{x}}_3\vee x_1{\overline{x}}_2x_3.$$ 

Чтобы построить полином Жегалкина через СДНФ, необходимо исключить операции дизъюнкции и отрицания, затем раскрыть скобки.

$f\left(x_1,\ x_2,\ x_3\right)={\overline{x}}_1{\overline{x}}_2{\overline{x}}_3\bigoplus {\overline{x}}_1{\overline{x}}_2x_3\bigoplus {\overline{x}}_1x_2{\overline{x}}_3\bigoplus x_1{\overline{x}}_2{\overline{x}}_3\bigoplus x_1{\overline{x}}_2x_3=\left(1\bigoplus x_1\right)\left(1\bigoplus x_2\right)\left(1\bigoplus x_3\right)\bigoplus \left(1\bigoplus x_1\right)\left(1\bigoplus x_2\right)x_3\bigoplus \left(1\bigoplus x_1\right)x_2\left(1\bigoplus x_3\right)\bigoplus x_1\left(1\bigoplus x_2\right)\left(1\bigoplus x_3\right)\bigoplus x_1\left(1\bigoplus x_2\right)x_3=1\bigoplus x_3\bigoplus x_2\bigoplus x_2x_3\bigoplus x_1\bigoplus x_1x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3\bigoplus x_3\bigoplus x_2x_3\bigoplus x_1x_3\bigoplus x_1x_2x_3\bigoplus x_2\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3\bigoplus x_1\bigoplus x_1x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3\bigoplus x_1x_3\bigoplus x_1x_2x_3=1\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3$ — полином Жегалкина.

Генератор таблиц истинности

— онлайн-калькулятор булевой алгебры для таблиц

Поиск инструмента

Таблица истинности

Инструмент для создания логических таблиц истинности. В булевой алгебре или электронике логические таблицы истинности позволяют определять функцию / вентиль / элемент / компонент в соответствии с его входами и выходами.

Результаты

Таблица истинности — dCode

Тег (ы): Символьные вычисления, Электроника

Поделиться

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Рекламные объявления

Ответы на вопросы (FAQ)

Что такое таблица истинности? (Определение)

Таблица истинности — это таблица, представляющая выходные логические значения логического выражения на основе их записей.Таким образом, в таблице представлены все возможные комбинации входных логических переменных (обычно 0 / ЛОЖЬ и 1 / ИСТИНА) и результат уравнения в качестве выходных данных.

Пример: Таблица функции логического НЕ:

Каждая электронная схема связана с таблицей истинности , которая ее описывает.

Как работает калькулятор таблицы истинности?

dCode таблица истинности Генератор интерпретирует логическое выражение и вычисляет, используя булеву алгебру, все возможные комбинации 0 и 1 для каждой переменной (среди запрошенных логических переменных), чтобы преобразовать логическое выражение и создать таблицу истинности .

dCode также позволяет найти функцию / выражение логической логики из таблицы истинности .

Как найти уравнение из таблицы истинности?

Есть 2 метода найти логическое уравнение из таблицы истинности , либо начав со значений 0 (вычисление Maxterms), либо начав со значений 1 (вычисление Minterms).

Пример: Таблица истинности :

Вот различные вычисления (которые дают одинаковый результат)

Расчет на основе значений 1 таблицы истинности (Minterms): для каждой 1 запишите в строке значения соответствующих записей, разделенных логическим И, затем сгруппируйте эти строки с помощью логического ИЛИ.

Пример: Строки 2 и 3 равны 1, строка 2 записывается как A AND NOT (B), строка 3 записывается как NOT (A) AND B и, следовательно, уравнение (A AND NOT (B) ) OR (NOT (A) AND B), что, возможно, упрощается до A XOR B

Расчет из значений 0 таблицы истинности (Maxterms): для каждого 0 запишите в строке значения соответствующих входов, разделенных логическим ИЛИ, затем каждую строку, разделенную логическим И.

Пример: Строки 1 и 4 равны 0, строка 1 записывается как A OR B, строка 4 записывается как NOT (A) OR NOT (B) и, следовательно, уравнение (A OR B) AND ( NOT (A) OR NOT (B)), что, возможно, упрощается до A XOR B

Какова таблица истинности для логического И?

Таблица истинности для функции И:

Что такое таблица истинности для логического ИЛИ?

Таблица истинности для функции ИЛИ:

Какова таблица истинности для логического XOR?

Таблица истинности для функции XOR:

Что такое таблица истинности для логической NAND?

Таблица истинности для функции И-НЕ:

Что такое таблица истинности для логического ИЛИ?

Таблица истинности для функции ИЛИ:

Что такое минтермы?

Minterms $ m $ — это номера строк таблицы, которые имеют выход логической 1 (нумерация строк от 0).

Пример: $ X = a + b $ таблица истинности имеет 1 выход TRUE в 3-й строке, поэтому $ X = \ sum {m (3)} $

Какие максимальные условия?

Maxterms $ M $ — номера строк таблицы, которые имеют логический выход 0 (нумерация строк от 0).

Пример: $ X = a + b $ таблица истинности имеет 3 вывода FALSE в 3 первых строках, отмеченных 0, 1 и 2, поэтому $ X = \ sum {M (0,1,2)} $

Задайте новый вопрос

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Таблица истинности».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любого алгоритма, апплета или фрагмента «Таблица истинности» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой «Таблицы истинности» ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести) написана на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.) и без загрузки данных, скрипт , копипаст или доступ к API для «Таблицы истинности» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

истина, таблица, логическое, логическое, электронное, логическое

Ссылки

Источник: https://www.dcode.fr/boolean-truth-table

© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Генератор таблиц истинности

— онлайн-калькулятор булевой алгебры для таблиц

Поиск инструмента

Таблица истинности

Инструмент для создания логических таблиц истинности. В булевой алгебре или электронике логические таблицы истинности позволяют определять функцию / вентиль / элемент / компонент в соответствии с его входами и выходами.

Результаты

Таблица истинности — dCode

Тег (ы): Символьные вычисления, Электроника

Поделиться

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Ответы на вопросы (FAQ)

Что такое таблица истинности? (Определение)

Таблица истинности — это таблица, представляющая выходные логические значения логического выражения на основе их записей.Таким образом, в таблице представлены все возможные комбинации входных логических переменных (обычно 0 / ЛОЖЬ и 1 / ИСТИНА) и результат уравнения в качестве выходных данных.

Пример: Таблица функции логического НЕ:

Каждая электронная схема связана с таблицей истинности , которая ее описывает.

Как работает калькулятор таблицы истинности?

dCode таблица истинности Генератор интерпретирует логическое выражение и вычисляет, используя булеву алгебру, все возможные комбинации 0 и 1 для каждой переменной (среди запрошенных логических переменных), чтобы преобразовать логическое выражение и создать таблицу истинности .

dCode также позволяет найти функцию / выражение логической логики из таблицы истинности .

Как найти уравнение из таблицы истинности?

Есть 2 метода найти логическое уравнение из таблицы истинности , либо начав со значений 0 (вычисление Maxterms), либо начав со значений 1 (вычисление Minterms).

Пример: Таблица истинности :

Вот различные вычисления (которые дают одинаковый результат)

Расчет на основе значений 1 таблицы истинности (Minterms): для каждой 1 запишите в строке значения соответствующих записей, разделенных логическим И, затем сгруппируйте эти строки с помощью логического ИЛИ.

Пример: Строки 2 и 3 равны 1, строка 2 записывается как A AND NOT (B), строка 3 записывается как NOT (A) AND B и, следовательно, уравнение (A AND NOT (B) ) OR (NOT (A) AND B), что, возможно, упрощается до A XOR B

Расчет из значений 0 таблицы истинности (Maxterms): для каждого 0 запишите в строке значения соответствующих входов, разделенных логическим ИЛИ, затем каждую строку, разделенную логическим И.

Пример: Строки 1 и 4 равны 0, строка 1 записывается как A OR B, строка 4 записывается как NOT (A) OR NOT (B) и, следовательно, уравнение (A OR B) AND ( NOT (A) OR NOT (B)), что, возможно, упрощается до A XOR B

Какова таблица истинности для логического И?

Таблица истинности для функции И:

Что такое таблица истинности для логического ИЛИ?

Таблица истинности для функции ИЛИ:

Какова таблица истинности для логического XOR?

Таблица истинности для функции XOR:

Что такое таблица истинности для логической NAND?

Таблица истинности для функции И-НЕ:

Что такое таблица истинности для логического ИЛИ?

Таблица истинности для функции ИЛИ:

Что такое минтермы?

Minterms $ m $ — это номера строк таблицы, которые имеют выход логической 1 (нумерация строк от 0).

Пример: $ X = a + b $ таблица истинности имеет 1 выход TRUE в 3-й строке, поэтому $ X = \ sum {m (3)} $

Какие максимальные условия?

Maxterms $ M $ — номера строк таблицы, которые имеют логический выход 0 (нумерация строк от 0).

Пример: $ X = a + b $ таблица истинности имеет 3 вывода FALSE в 3 первых строках, отмеченных 0, 1 и 2, поэтому $ X = \ sum {M (0,1,2)} $

Задайте новый вопрос

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Таблица истинности».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любого алгоритма, апплета или фрагмента «Таблица истинности» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой «Таблицы истинности» ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести) написана на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.) и без загрузки данных, скрипт , копипаст или доступ к API для «Таблицы истинности» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

истина, таблица, логическое, логическое, электронное, логическое

Ссылки

Источник: https://www.dcode.fr/boolean-truth-table

© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Генератор таблиц истинности

— онлайн-калькулятор булевой алгебры для таблиц

Поиск инструмента

Таблица истинности

Инструмент для создания логических таблиц истинности. В булевой алгебре или электронике логические таблицы истинности позволяют определять функцию / вентиль / элемент / компонент в соответствии с его входами и выходами.

Результаты

Таблица истинности — dCode

Тег (ы): Символьные вычисления, Электроника

Поделиться

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Ответы на вопросы (FAQ)

Что такое таблица истинности? (Определение)

Таблица истинности — это таблица, представляющая выходные логические значения логического выражения на основе их записей.Таким образом, в таблице представлены все возможные комбинации входных логических переменных (обычно 0 / ЛОЖЬ и 1 / ИСТИНА) и результат уравнения в качестве выходных данных.

Пример: Таблица функции логического НЕ:

Каждая электронная схема связана с таблицей истинности , которая ее описывает.

Как работает калькулятор таблицы истинности?

dCode таблица истинности Генератор интерпретирует логическое выражение и вычисляет, используя булеву алгебру, все возможные комбинации 0 и 1 для каждой переменной (среди запрошенных логических переменных), чтобы преобразовать логическое выражение и создать таблицу истинности .

dCode также позволяет найти функцию / выражение логической логики из таблицы истинности .

Как найти уравнение из таблицы истинности?

Есть 2 метода найти логическое уравнение из таблицы истинности , либо начав со значений 0 (вычисление Maxterms), либо начав со значений 1 (вычисление Minterms).

Пример: Таблица истинности :

Вот различные вычисления (которые дают одинаковый результат)

Расчет на основе значений 1 таблицы истинности (Minterms): для каждой 1 запишите в строке значения соответствующих записей, разделенных логическим И, затем сгруппируйте эти строки с помощью логического ИЛИ.

Пример: Строки 2 и 3 равны 1, строка 2 записывается как A AND NOT (B), строка 3 записывается как NOT (A) AND B и, следовательно, уравнение (A AND NOT (B) ) OR (NOT (A) AND B), что, возможно, упрощается до A XOR B

Расчет из значений 0 таблицы истинности (Maxterms): для каждого 0 запишите в строке значения соответствующих входов, разделенных логическим ИЛИ, затем каждую строку, разделенную логическим И.

Пример: Строки 1 и 4 равны 0, строка 1 записывается как A OR B, строка 4 записывается как NOT (A) OR NOT (B) и, следовательно, уравнение (A OR B) AND ( NOT (A) OR NOT (B)), что, возможно, упрощается до A XOR B

Какова таблица истинности для логического И?

Таблица истинности для функции И:

Что такое таблица истинности для логического ИЛИ?

Таблица истинности для функции ИЛИ:

Какова таблица истинности для логического XOR?

Таблица истинности для функции XOR:

Что такое таблица истинности для логической NAND?

Таблица истинности для функции И-НЕ:

Что такое таблица истинности для логического ИЛИ?

Таблица истинности для функции ИЛИ:

Что такое минтермы?

Minterms $ m $ — это номера строк таблицы, которые имеют выход логической 1 (нумерация строк от 0).

Пример: $ X = a + b $ таблица истинности имеет 1 выход TRUE в 3-й строке, поэтому $ X = \ sum {m (3)} $

Какие максимальные условия?

Maxterms $ M $ — номера строк таблицы, которые имеют логический выход 0 (нумерация строк от 0).

Пример: $ X = a + b $ таблица истинности имеет 3 вывода FALSE в 3 первых строках, отмеченных 0, 1 и 2, поэтому $ X = \ sum {M (0,1,2)} $

Задайте новый вопрос

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Таблица истинности».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любого алгоритма, апплета или фрагмента «Таблица истинности» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой «Таблицы истинности» ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести) написана на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.) и без загрузки данных, скрипт , копипаст или доступ к API для «Таблицы истинности» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

истина, таблица, логическое, логическое, электронное, логическое

Ссылки

Источник: https://www.dcode.fr/boolean-truth-table

© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Калькулятор таблицы истинности

— Найдите логику с помощью генератора таблицы истинности

Онлайн-калькулятор таблицы истинности предоставит значения таблицы истинности для данных формул логики высказываний. Утверждения логики высказываний могут быть только истинными или ложными. Многие утверждения можно комбинировать с логическими связями для образования новых утверждений. Решатель таблицы истинности генерирует все комбинации истинных и ложных утверждений и вычисляет соответствующее содержание истинности логического выражения.

Что такое таблица истины?

Таблица истинности представляет собой табличное представление всех комбинаций значений для входов и соответствующих им выходов. Это математическая таблица, которая показывает все возможные результаты, которые могут быть получены при всех возможных сценариях. Он используется для логических задач, таких как логическая алгебра и электронные схемы.

Таблица истинности показывает результат логического выражения, каждая задействованная переменная имеет отдельный столбец, а соответствующий результат имеет столбец.Слева перечислены все варианты входных данных и их параметры; вывод обычно помещается в последний столбец справа.

Таблицы предложной истинности Логика:

Предложение — это набор декларативных утверждений со значением истинности «истина» или значением истинности «ложь». Пропозициональные выражения состоят из связок и пропозициональных переменных. Мы используем заглавные буквы для обозначения пропозициональных переменных (A, B). Связки соединяют пропозициональные переменные.

Вот несколько примеров предложений —

«12 + 9 = 3-2», возвращает истину «ЛОЖЬ»

«Человек смертен», фактически возвращает «ИСТИНА»

Следующее не является предложением —

«X меньше 2».

Это потому, что, если мы не дадим X как конкретное значение, мы не сможем судить, правильно это утверждение или нет.

Однако онлайн-калькулятор с дополнением до единицы может легко реализовать логическую схему только с вентилем НЕ для каждого бита входного двоичного числа.

Как составить таблицу истинности?

Разъемы:

В калькуляторе таблицы истинности пропозициональной логики используются различные связки —

• ИЛИ (∨)
• И (∧)
• Отрицание / НЕ (¬)
• Следствие / если-то (→)
• Если и только если (⇔)
• Абсурд (#)
• Инсульт Шеффера (|)

ИЛИ (∨):

Операция ИЛИ двух предложений, таких как P и Q (записываемых как P∨Q), истинна, если по крайней мере любая пропозициональная переменная P или Q истинна.

Примеры таблицы истинности следующие —

п.	К	пол ∨
Т	Т	Т
Т	F	Т
Ф.	Т	Т
Ф.	F	F

И (∧):

Операция AND двух предложений P и Q (записываемых как P∧Q) истинна, если истинны обе пропозициональные переменные P и Q.

Таблица истинности следующая —

п.	К	пол ∧
Т	Т	Т
Т	F	F
Ф.	Т	F
Ф.	F	F

Отрицание (~):

Отрицание предложения P (записанное как ~ P) истинно, когда значение «P» ложно, и отрицание ложно, когда значение «P» истинно.

Отрицание для переменной P как:

Таблица истинности следствия / if-then (→):

Импликация P → Q — это предложение «если P, то Q». Это ложь, если P истинно, а Q ложно. Остальные случаи верны.

Таблица истинности импликации выглядит следующим образом —

Q	К	P → Q
Т	Т	Т
Т	F	F
Ф.	Т	Т
Ф.	F	Т

Следовательно, это таблица истинности для импликации с двумя разными переменными.

Если и только если (⇔):

P⇔Q — это двухусловная логическая связка, которая выполняется, когда P и Q совпадают. Например, оба верны или оба ложны.

Таблица истинности следующая —

п.	К	пол ⇔
Т	Т	Т
Т	F	F
Ф.	Т	F
Ф.	F	Т

Тавтологии:

Тавтология — это уравнение, которое всегда верно для каждого значения его переменных.

Пример:

Докажите [(P → Q) ∧ P] → Q — тавтология

Составитель таблицы истинности докажет тавтологию для переменных P и Q следующей таблицей:

п.	К	P → Q	(P → Q) ∧ P	[(P → Q) ∧ P] → Q
Т	Т	Т	Т	Т
Т	F	F	F	Т
Ф.	Т	Т	F	Т
Ф.	F	Т	F	Т

Значение [(P → Q) ∧ P] → Q из генератора таблицы истинности истинно.Следовательно, это тавтология.

Противоречия:

Противоречие — это уравнение, которое всегда неверно для каждого значения его пропозициональных ценностей.

Пример:

Докажите (P ∨ Q) ∧ [(~ P) ∧ (~ Q)] противоречие.

Решение:

Отображение калькулятора таблицы истинности и использование следующей таблицы для противоречия —

п.	К	пол ∨	~ P	~	(~ P) ∧ (~ Q)	(P ∨ Q) ∧ [(~ P) ∧ (~ Q)]
Т	Т	Т	F	F	F	F
Т	F	Т	F	Т	F	F
Ф.	Т	Т	Т	F	F	F
Ф.	F	F	Т	Т	Т	F

Если p, то q таблица истинности имеет ложные значения, то это противоречие.Однако онлайн-калькулятор дополнения до двух позволяет вычислить дополнение до 2 данного десятичного, двоичного или шестнадцатеричного числа.

На случай непредвиденных обстоятельств:

Непредвиденное обстоятельство — это уравнение, которое имеет как ложные, так и некоторые истинные значения для каждого значения его пропозициональных переменных.

Пример:

Доказать (P ∨ Q) ∧ (~ P) непредвиденный случай

Решение:

Генератор таблицы истинности отображает таблицу истинности непредвиденных обстоятельств для P, Q и ~ P:

п.	К	пол ∨	~ P	(пол. ∨ Q) ∧ (~ P)
Т	Т	Т	F	F
Т	F	Т	F	F
Ф.	Т	Т	Т	Т
Ф.	F	F	Т	F

Как мы видим, каждое значение таблиц истинности с 3 переменными имеет как истинный, так и ложный результат, это случайность.

Эквивалентность утверждений:

Два оператора A и B логически эквивалентны, если выполняется любое из следующих двух условий —

• Двуусловное утверждение A⇔B является тавтологией.
• Таблицы истинности каждого утверждения имеют одинаковые переменные истинности.

Пример:

Докажите, что ~ (P ∨ Q) и [(~ P) ∧ (~ Q)] эквивалентны

Решение:

Калькулятор таблиц истинности выполняет тестирование методом сопоставления таблиц истинности

п.	К	пол ∨	¬ (P ∨ Q)	¬ P	¬ Q	[(¬ P) ∧ (¬ Q)]
Т	Т	Т	F	F	F	F
Т	F	Т	F	F	Т	F
Ф.	Т	Т	F	Т	F	F
Ф.	F	F	Т	Т	Т	Т

Здесь мы видим, что значения истинности ~ (P ∨ Q) и [(~ P) ∧ (~ Q)] одинаковы, следовательно, все утверждения эквивалентны.

Тестирование методом двуусловности

п.	К	~ (P ∨ Q)	[(~ P) ∧ (~ Q)]	[~ (P Q)] ⇔ [(~ P) ∧ (~ Q)]
Т	Т	F	F	Т
Т	F	F	F	Т
Ф.	Т	F	F	Т
Ф.	F	Т	Т	Т

Поскольку [~ (P ∨ Q)] ⇔ [(~ P) ∧ (~ Q)] является тавтологией, утверждения эквивалентны.

Как работает калькулятор таблицы истинности?

Онлайн-генератор таблицы истинности предоставляет подробную таблицу истинности, выполнив следующие шаги:

Ввод:

• Сначала введите логическое уравнение высказываний с символами.
• Нажмите кнопку «Рассчитать», чтобы увидеть результаты.

Выход:

• Калькулятор таблицы истинности построит таблицу истинности для 4 переменных данного выражения.

FAQ:

Что такое логическая таблица истинности?

Таблица логических выражений, используемых для выражения функций логических элементов, обычно называемая логической таблицей истинности.Таблица истинности логического элемента показывает все возможные входные комбинации элемента или схемы, а выходной результат зависит от комбинации этих входов.

Что такое унарные операции?

Есть 4 унарные операции:

• Всегда верно
• Неправда, унарная ложь
• Унарный идентификатор
• Унарное отрицание

Заключение:

Используйте этот онлайн-калькулятор таблиц истинности для создания многомерных таблиц истинности логики высказываний.Логика высказываний имеет дело с утверждениями, которые могут быть значениями истинности, «истинными» и «ложными». Цель состоит в том, чтобы проанализировать эти утверждения по отдельности или в совокупности.

Артикул:

Из источника Википедии: Унарные операции, Логическая истина, Логическая ложь, Логическая идентичность, Логическое отрицание, Бинарные операции, Логическая конъюнкция (И), Логическая дизъюнкция (ИЛИ), Логическая импликация.

Из источника учебных материалов: предложная логика, связки, тавтологии, противоречия, случайность, пропозициональные эквивалентности, обратное, обратное и контрпозитивное.

Показать таблицы истинности для логических выражений

Логические выражения

Логическое выражение — это выражение, состоящее из переменных и значений истинности ( истина, и ложь, ), связанных с различными логическими операторами. Основными операторами являются и , или и , а не (отрицание), из которых могут быть получены все остальные операторы.

Есть много разных способов написать одно и то же выражение. В следующей таблице перечислены все символы, распознаваемые инструментом, и показано, для каких целей они используются.Если выражение содержит слово, которого нет в списке, оно будет рассматриваться как переменная.

Верно:	Т, 1, правда
Ложь:	F, 0, ложь
Отрицание:	¬,!, ~, -, а не	′, ‘
А:	∧, ·, *, &&, & и
или:	∨, +, ||, | или
Эксклюзив или:	⊕,! =, ^, Xor
Эквивалентность:	⇔, <=>, ==, =
Значение:	⇒, =>

Таблицы истинности

Таблица истинности показывает оценку логического выражения для всех комбинаций возможных значений истинности, которые могут иметь переменные выражения.Таблицы истинности часто упрощают понимание логических выражений и могут очень помочь при упрощении выражений. Его также можно использовать для сравнения двух разных выражений, показывая их бок о бок в одной таблице.

Не (отрицание)

Оператор , а не используется для отрицания выражения. Это означает, что истина становится ложью, а ложь становится истиной.

А (соединение)

Оператор и — это бинарный оператор, результатом которого является истина, если оба операнда истинны.Если один или оба операнда ложны, результат будет ложным.

Или (дизъюнкция)

Результат оператора или верен, если хотя бы один из операндов верен. Результат будет ложным, только если оба операнда ложны.

Эксклюзив или

Exclusive или аналогичен оператору или с той лишь разницей, что результат будет ложным, если оба операнда верны. Другой способ думать об этом состоит в том, что результат будет истинным, если два операнда имеют разные значения, иначе результат будет ложным.

905 45 905 905 905 905 905 905 905 905 905 905 905 905 905 905 F

a	b	a ⊕ b	( a ∧ ¬ b ) ∨ (¬ ¬ ¬ b ) ∨ (¬ ¬ a 9405 9140 905 905 905 905 905 9406 9406 9140 905	T	F	F
T	F	T	T
F	T	T	F

Эквивалентность

Два выражения эквивалентны, если они приводят к одному и тому же значению истинности.

a

b

a ⇔ b

( a ∧ b ) ∨ (¬ ¬ ∧ b ) ∨ (¬ ¬ ¬ 9044 ¬ 9044 9405 9044 T

T

T

T

T

F

F

F

F

T

F

F

F

F

905

T

T

Значение

Импликация ложна, если первый операнд истинен, а второй операнд ложен.Смысл верен во всех остальных случаях.

905 905 905 905 905 905 905 905 905 905 905 90592 T 905 Таблица истинности в Windows 11/10

Вот полное руководство для вас, как сгенерировать таблицу истинности в Windows 11/10.Таблица истинности в основном отображает выходы для всех возможных комбинаций входных значений для логического элемента или схемы. Он показывает либо значения Tru и False, либо значения 0 и 1. Теперь, если вы хотите вычислить таблицы истинности для логических выражений, формул высказываний и логических схем, вы можете обратиться к этому сообщению. В этой статье мы обсудим различные способы создания таблиц истинности на вашем компьютере.

Что такое таблица истинности?

Таблица истинности — это диаграмма со строками и столбцами, показывающими, как истинность или ложность предложения изменяется с его входными компонентами.Как мы упоминали выше, он в основном используется для отображения всех возможных результатов комбинации входных значений. Он используется в логике, относящейся к цифровым схемам, булевой алгебре, булевым функциям и исчислению высказываний.

Что такое генератор таблицы истинности?

Генератор таблицы истинности — это, по сути, инструмент, который может автоматически генерировать таблицу истинности на основе соответствующей логической схемы, логического выражения, предложения и т. Д. В этой статье мы собираемся перечислить несколько генераторов таблиц истинности, которые вы можете использовать в Windows. 11/10.Продолжайте читать, чтобы узнать об этих инструментах.

Как создать таблицу истинности в Windows 11/10

Вот два способа создания таблицы истинности в Windows 11/10:

1. Используйте бесплатное программное обеспечение для создания таблицы истинности.
2. Создайте таблицу истинности с помощью бесплатного веб-сервиса.

Обсудим подробно описанные выше способы!

1] Используйте бесплатное программное обеспечение для создания таблицы истинности.

Существует несколько бесплатных программ, которые позволяют создавать таблицу истинности. По сути, некоторые программы для моделирования логики позволяют создавать таблицу истинности из логических выражений, логических утверждений, схем и т. Д. или пропозициональные формулы.Вот некоторые из лучших генераторов таблиц истинности, которые вы можете использовать на ПК с Windows 11/10:

1. LogicCircuit
2. Logisim
3. SimpleSolver
4. Logicheck
5. LogicCalculus

1] LogicCircuit 2] LogicCircuit

9000 программное обеспечение, позволяющее создавать таблицы истинности в Windows 11/10. Используя его, вы можете создать таблицу истинности из логической схемы. Давайте посмотрим на шаги по созданию таблицы истинности в LogicCircuit.

Как сгенерировать таблицу истинности из логических схем в Windows 11/10:

Вот основные шаги для создания таблицы истинности из логической схемы:

Во-первых, загрузите и установите LogicCircuit на свой компьютер. Запустите его, а затем вам нужно создать логическую схему, для которой вы хотите вычислить таблицу истинности. Вы можете разработать логическую схему с несколькими компонентами, включая вход, выход, логические элементы и память. Просто перетащите нужный компонент с панели Project в главное окно дизайна.

Когда вы закончите создание принципиальной схемы, перейдите в меню Circuit и выберите опцию Truth Table . Кроме того, вы также можете нажать горячую клавишу Ctrl + T , чтобы сгенерировать таблицу истинности.

Ваша логическая схема будет обработана в течение нескольких секунд, а затем будет сгенерирована соответствующая таблица истинности. Вы увидите выходные значения, основанные на всех возможных значениях входных контактов.

Вы также можете применять фильтры для просмотра определенного набора входных и выходных значений, например x = 0, x1 = 1 и т. Д.

Это простой в использовании калькулятор таблицы истинности, который можно использовать для проектирования и экспорта логических схем. Вы можете скачать его с сайта logiccircuit.org.

2] Logisim

Logisim — портативный генератор таблицы истинности для Windows 11/10. Он в основном используется для проектирования и моделирования логических схем. Используя его, вы можете создать логическую схему, а затем сгенерировать для нее таблицу истинности. Давайте подробно обсудим весь процесс.

Загрузите это портативное приложение, а затем дважды щелкните файл приложения, чтобы запустить его основной интерфейс.Теперь вы можете просто спроектировать логическую схему, для которой вы хотите создать таблицу истинности. Используйте вентили, плексеры, арифметику, ввод, вывод, проводку и другие компоненты схемы, чтобы спроектировать схему.

Когда ваша логическая схема завершена, вы можете вычислить соответствующую таблицу истинности. Просто перейдите в меню Project и выберите опцию Analyze Circuit . Затем откроется диалоговое окно Combination Analysis . Здесь вы увидите вкладку Таблица , где вы можете в основном просмотреть таблицу истинности для созданной логической схемы.

Теперь, если вы хотите сгенерировать таблицу истинности с использованием логического выражения , вы тоже можете это сделать. Он даже позволяет автоматически генерировать схему логической схемы, используя логическое выражение.

Для этого откройте окно Combination Analysis , как мы делали в предыдущих шагах, а затем перейдите на вкладку Inputs . Здесь введите входные данные, которые вы хотите использовать в таблице истинности, а затем нажмите кнопку Добавить . Точно так же добавьте метки вывода на вкладке Outputs .

После определения входов и выходов перейдите на вкладку Expression и выберите выход для создания таблицы истинности. Введите логическое выражение в поле и нажмите кнопку Enter. Затем нажмите кнопку Build Circuit.

Это создаст логическую схему, а также таблицу истинности для введенного логического выражения.

Это хороший симулятор логических вентилей, который позволяет вычислять таблицы истинности на основе логических схем, а также булевых выражений.

3] SimpleSolver

SimpleSolver — это бесплатное программное обеспечение для вычисления таблицы истинности для Windows 11/10. В нем есть некоторые инструменты, включая логический минимизатор, логическое моделирование, генератор таблицы истинности и т. Д. В нем вы можете вводить логические выражения, и он сгенерирует соответствующую таблицу истинности. Давайте теперь проверим отсортированную процедуру.

Прежде всего, загрузите и установите SimpleSolver на свой компьютер. Затем запустите это программное обеспечение и в окне ввода введите логическое выражение, например X = A xor B xor C xor D; .Логическое выражение должно заканчиваться точкой с запятой (;). Вы можете ввести более одного логического выражения в новых строках, и оно сгенерирует таблицы истинности для всех из них.

Теперь на правой панели убедитесь, что включена опция Таблица истинности — Полная. Вы также можете включить другую информацию, которую хотите отобразить, например таблицу истинности PLA, логический дизайн, свернуть (логическое выражение) и т. Д.

Наконец, нажмите кнопку GO , и в окне Выходные данные отобразятся таблицы истинности.

Вы можете сохранить вывод как файл TXT, выбрав «Файл»> «Сохранить как».

В нем также есть несколько примеров схемотехники, которые вы можете изучить в меню Примеры . Вы можете получить его на сайте simplesolverlogic.com.

4] Logicheck

Logicheck — это специальный бесплатный портативный генератор таблиц истинности для Windows 11/10. Это простой инструмент для быстрого создания таблицы истинности из логического выражения. Посмотрим как.

Загрузите и запустите это портативное приложение.Вы увидите поле Expression на главном экране. Просто введите в это поле свое логическое выражение. Вы можете использовать логические операторы, такие как NOT, OR, AND, XOR и т. Д., Чтобы завершить логическое выражение.

После ввода выражения щелкните команду ДОБАВИТЬ, чтобы добавить его в список. Точно так же вы можете добавить в список больше логических выражений. Он также показывает синтаксические ошибки в вашем выражении (если есть) в нижней части интерфейса. Вы можете исправить ошибку позже.

По завершении добавления логических выражений выберите параметр Показать таблицу истинности .

Затем отобразится таблица истинности для всех введенных логических выражений.

Этот удобный генератор таблицы истинности можно загрузить с сайта sourceforge.net.

5] LogicCalculus

LogicCalculus — это бесплатное программное обеспечение для создания таблиц истинности с открытым исходным кодом для Windows 11/10. Он оценивает логические выражения и затем генерирует соответствующую таблицу истинности. Это один из самых простых инструментов в этом списке.

Вы можете добавить термины, используя опцию New , а затем добавить логическое выражение в средний раздел.Он предоставляет базовые логические операторы для использования в вашем выражении. Когда вы вводите выражение, оно генерирует для него таблицу истинности в специальном разделе в реальном времени.

Если во входном выражении есть ошибки, они отображаются на нижней панели.

2] Создание таблицы истинности с помощью бесплатного веб-сервиса

Вы также можете использовать онлайн-сервис для создания таблицы истинности. Вот несколько лучших сервисов генератора таблиц истинности, которые вы можете использовать:

1. mrieppel.net
2. truetablemaker.com
3. loighic.net
4. stanford.edu

1] mrieppel.net

mrieppel.net — это простой онлайн-сервис для создания таблицы истинности. Вы можете ввести логическое выражение в поле и затем нажать кнопку Generate Table , чтобы вычислить соответствующую таблицу истинности.

Вы можете выбрать значения истинности формата в выходной таблице истинности, такие как T / F, 0/1 и т. Д. Он также позволяет вам установить тип таблицы истинности Full Table, Main Connective Only, Text Table, или LaTex Таблица для создания определенного вида таблицы истинности.Кроме того, вы также можете выбрать связки для ввода выражения. Он предоставляет несколько примеров того, каким должно быть входное выражение.

Чтение: Как использовать функцию ИЛИ Excel, чтобы определить, истинно ли условие.

2] truetablemaker.com

truetablemaker.com — это специальный онлайн-сервис для генерации таблиц истинности. Просто зайдите на его веб-сайт в своем браузере и введите логическое выражение. Затем нажмите кнопку Получить таблицу истинности , чтобы сгенерировать соответствующую таблицу истинности.

Он показывает краткое руководство по его основному интерфейсу о том, как использовать этот инструмент, а также формат и символы, которые необходимо использовать в выражении.

Для просмотра таблицы истинности высказываний вы можете щелкнуть ее кнопку Расширенная таблица истинности . Затем он попросит вас ввести в это поле формулу логики высказываний. Введите формулу, и она отобразит соответствующую таблицу истинности.

3] loighic.net

loighic.net предоставляет вам онлайн-инструмент для создания таблиц истинности.Вы можете создать полную таблицу истинности, только основные соединения, таблицу LaTeX и текстовую таблицу истинности. Просто введите логическое выражение и нажмите кнопку «Создать таблицу». Это покажет таблицу истинности ниже.

4] stanford.edu

Stanford.edu — это простой инструмент для вычисления таблиц истинности для формул логической логики и логики высказываний. Вы можете ввести формулу, и она автоматически сгенерирует соответствующую таблицу истинности в веб-браузере.

Как составить логическую таблицу истинности?

Вы можете создать логическую таблицу истинности, введя соответствующее логическое выражение с правильным синтаксисом.Почти все рассмотренное выше программное обеспечение и онлайн-инструменты позволяют создать таблицу истинности из логического выражения. Из списка вы используете такое программное обеспечение, как SimpleSolver, Logicheck или LogicCalculus, как мы объясняли выше. В качестве альтернативы вы можете использовать любую из обсуждаемых веб-служб для создания логической таблицы истинности.

Как создать таблицу истинности с двумя переменными?

Чтобы создать таблицу истинности с двумя переменными, вы можете ввести логическое выражение или разработать логическую схему с двумя входами.Например, A + B = C. Здесь A и B — две входные переменные, знак + обозначает логический элемент ИЛИ, а C — результат, который генерируется комбинациями значений A и B.

Надеюсь, этот пост поможет вам создать таблицу истинности для логического выражения или логической схемы в Windows 11/10.

Сейчас читаем:

5 бесплатных онлайн-генераторов таблицы истинности для любого логического выражения

Рейтинг редактора:

Оценки пользователей:

[Всего: 0 Среднее: 0/5]

В этом посте рассказывается о бесплатном онлайн-генераторе таблицы истинности для любого логического выражения .Здесь я добавил несколько веб-сайтов, которые можно использовать для получения таблицы истинности, просто введя логическое выражение. Логическое выражение может быть простым или сложным. Они сгенерируют таблицу истинности после оценки данного выражения. В конце концов, вы можете скопировать таблицу истинности, но не можете скачать ее. Чтобы получить таблицы на свой компьютер, вы можете использовать некоторые расширения для извлечения таблиц Chrome или Firefox.

Если вы работаете в области электроники и вам нужно создать таблицу истинности для имеющегося у вас выражения, то эти веб-сайты вам пригодятся.Здесь вы просто вводите логическое выражение, добавляя соответствующие знаки и скобки, а затем позволяете одному из этих веб-сайтов оценивать его. Все эти сайты дают один и тот же результат, но на некоторых из них различается способ ввода выражений. В некоторых из них вы можете напрямую добавить выражение, используя математические операторы для функций OR и AND, но в некоторых из них вы должны добавить их в логическом выражении.

5 бесплатных онлайн-генераторов таблицы истинности для любого логического выражения:

Генератор таблицы истинности Майкла Риппеля

Генератор таблицы истинности Майкла Риппеля ( домашняя страница ) — один из лучших бесплатных инструментов для создания таблицы истинности из любого выражения.Это инструмент с открытым исходным кодом, который также можно использовать в автономном режиме. Вы получаете его исходный код и размещаете его самостоятельно или запускаете локально. Он позволяет вам выбирать различные типы таблиц истинности и поддерживает различные типы символов, а также для входного логического выражения. В целом инструмент прост: вы просто вводите логическое выражение и получаете таблицу. Просто как тот.

Откройте инструмент по указанной выше ссылке и укажите тип таблицы. Затем выберите символы значений истинности и введите окончательное выражение, для которого вы хотите получить таблицу истинности.После указания всех параметров вы просто нажимаете кнопку «Создать таблицу истинности», и тогда вам откроется финальная таблица. После этого вы можете делать все, что захотите.

Настольная машина Truth

Truth Table Maker — еще один бесплатный онлайн-генератор простой таблицы истинности, который вы можете использовать. Это очень простой генератор TT, в котором вы просто вводите логическое выражение, и он немедленно сгенерирует таблицу. Веб-интерфейс инструмента довольно минимален.Есть только текстовое поле, в которое вы ввели входное выражение, и дается простое руководство, которое вы можете использовать, чтобы увидеть синтаксис выражения. Кроме того, если вы хотите изучить основы таблиц истинности, дается небольшое руководство, и вы можете пройти его один раз, чтобы увидеть, как создаются таблицы истинности, понимая их с использованием основных логических вентилей.

Генератор таблицы истинности от Loighic.net

Это еще один генератор таблицы истинности ( домашняя страница ) из моего списка, который вы можете попробовать.Это простые веб-сайты, на которых вы можете выбрать создание итоговой таблицы в виде простого текста или LaTex. Таблицу, созданную в форме LaTex, можно использовать в научной документации, которую вы готовите для различных исследовательских проектов. Все, что вам нужно сделать, это ввести логическое выражение с правильными символами и получить итоговую таблицу.

Используйте ссылку выше, чтобы перейти на веб-сайт, а затем укажите тип таблицы, которую вы хотите создать, выбрав один из четырех перечисленных там вариантов. Затем вы вводите логическое выражение, которое хотите оценить.Дается простое руководство по созданию выражений, вы можете проанализировать его, чтобы построить выражение и увидеть некоторые примеры, перечисленные там.

Правда

Truth — это онлайн-генератор таблиц истинности для студентов-электронщиков с некоторыми дополнительными возможностями. Как и другие инструменты в списке, вы можете использовать его таким же образом. Здесь он принимает логическое выражение в простом виде с простыми математическими операторами. Вы просто вводите простое или сложное логическое выражение в правильных форматах и ​​получаете результат.Все, что вам нужно сделать, это просто перейти на домашнюю страницу этого инструмента и ввести логическое выражение.

Чтобы создать таблицу, просто нажмите кнопку «Создать таблицу истинности», и затем вы перейдете на следующую страницу, чтобы показать окончательную таблицу. Получив таблицу, вы можете либо скопировать ее, либо очистить с помощью расширений Chrome или Firefox. Чтобы помочь вам, он показывает там таблицу, которую вы можете использовать для построения логического выражения.

Генератор таблицы истинности в Стэнфорде

Это простейший генератор таблицы истинности ( домашняя страница ) в этом списке.У него минималистичный интерфейс, и вы просто вводите выражение и получаете результат. Но здесь вам нужно ввести логическое выражение, используя условные символы, которые вы используете в процедурных языках программирования, таких как C. Для использования этого простого инструмента не требуется никакой регистрации или подписки. Получите доступ к этому инструменту, используя ссылку выше, а затем просто введите логическое выражение, которое хотите оценить. Когда выражение завершится, оно немедленно сгенерирует для вас таблицу. Вы можете увидеть скриншот выше, который я добавил.

Заключительные мысли

Это лучшие бесплатных веб-сайтов генераторов таблиц истинности, которые вы можете использовать. Используйте их для быстрого создания таблицы истинности из заданного выражения, а затем вы можете просто сохранить ее.

a	b	a ⇒ b	¬ a ∨ b
T	F	F	F
F	T	T	T
F	F