Что такое электрический ток, напряжение и мощность. Как они связаны между собой. Какие единицы измерения используются для этих величин. Как рассчитать мощность электрического тока. Какие формулы применяются для расчетов в цепях постоянного и переменного тока.
Основные понятия: ток, напряжение, сопротивление
Для понимания работы электрических цепей необходимо разобраться с тремя ключевыми понятиями:
- Электрический ток — это направленное движение заряженных частиц. Измеряется в амперах (А).
- Электрическое напряжение — разность потенциалов между двумя точками электрической цепи. Измеряется в вольтах (В).
- Электрическое сопротивление — свойство проводника препятствовать прохождению электрического тока. Измеряется в омах (Ом).
Эти три величины связаны между собой законом Ома: I = U / R, где I — сила тока, U — напряжение, R — сопротивление.
Что такое электрическая мощность и как она рассчитывается
Электрическая мощность — это скорость преобразования электрической энергии в другие виды энергии. Измеряется в ваттах (Вт).
Для цепей постоянного тока мощность рассчитывается по формуле:
P = U * I
где P — мощность, U — напряжение, I — сила тока.
Также мощность можно выразить через сопротивление:
P = I^2 * R = U^2 / R
Особенности расчета мощности в цепях переменного тока
В цепях переменного тока расчет мощности имеет свои особенности. Здесь различают:
- Активную мощность P — среднюю за период мощность, преобразуемую в тепло или механическую работу.
- Реактивную мощность Q — мощность, которая периодически запасается в магнитном или электрическом поле и возвращается обратно в сеть.
- Полную мощность S — геометрическую сумму активной и реактивной мощностей.
Для расчета активной мощности используется формула:
P = U * I * cosφ
где cosφ — коэффициент мощности, показывающий сдвиг фаз между током и напряжением.
Единицы измерения электрических величин
Для измерения электрических величин используются следующие единицы:
- Сила тока — ампер (А)
- Напряжение — вольт (В)
- Сопротивление — ом (Ом)
- Мощность — ватт (Вт)
- Электрический заряд — кулон (Кл)
- Электрическая энергия — джоуль (Дж) или киловатт-час (кВт*ч)
Важно помнить соотношения между этими единицами. Например, 1 ампер — это сила тока, при которой через проводник за 1 секунду проходит заряд в 1 кулон.
Взаимосвязь тока, напряжения и мощности
Ток, напряжение и мощность тесно связаны между собой. Эту связь можно проиллюстрировать следующими формулами:
- P = U * I
- I = P / U
- U = P / I
Эти соотношения позволяют, зная две величины, легко рассчитать третью. Например, если известны мощность электроприбора и напряжение сети, можно определить потребляемый им ток.
Закон Джоуля-Ленца и тепловое действие тока
Закон Джоуля-Ленца описывает тепловое действие электрического тока. Согласно этому закону, количество теплоты Q, выделяемое проводником с током, прямо пропорционально квадрату силы тока I, сопротивлению проводника R и времени t прохождения тока:
Q = I^2 * R * t
Этот закон имеет важное практическое значение, например, при расчете нагревательных приборов или при оценке потерь энергии в проводах.
Мощность в цепях постоянного и переменного тока: сходства и различия
Расчет мощности в цепях постоянного и переменного тока имеет как сходства, так и различия:
- В обоих случаях мощность измеряется в ваттах.
- Для постоянного тока используется простая формула P = U * I.
- Для переменного тока учитывается сдвиг фаз между током и напряжением: P = U * I * cosφ.
- В цепях переменного тока различают активную, реактивную и полную мощности.
- Для переменного тока часто используют действующие (среднеквадратичные) значения тока и напряжения.
Понимание этих особенностей важно для правильных расчетов в электротехнике.
Практическое применение знаний о мощности электрического тока
Знания о мощности электрического тока имеют широкое практическое применение:
- Расчет энергопотребления бытовых приборов
- Выбор проводов и кабелей нужного сечения
- Проектирование систем электроснабжения
- Оценка эффективности электрооборудования
- Расчет стоимости потребленной электроэнергии
Эти знания позволяют грамотно использовать электроэнергию и обеспечивать безопасность электрических систем.
Влияние параметров цепи на мощность электрического тока
Мощность электрического тока зависит от параметров электрической цепи:
- Увеличение напряжения при постоянном сопротивлении ведет к росту тока и мощности.
- Уменьшение сопротивления при постоянном напряжении также увеличивает ток и мощность.
- В цепях переменного тока на мощность влияет сдвиг фаз между током и напряжением.
- Наличие реактивных элементов (катушек индуктивности, конденсаторов) изменяет соотношение активной и реактивной мощностей.
Понимание этих зависимостей позволяет эффективно управлять мощностью в электрических системах.
Физика Работа и мощность электрического тока. Работа тока
Материалы к уроку
Конспект урока
Электрический ток получил широкое применение потому, что он несет с собой электрическую энергию, которую можно преобразовать в работу или во внутреннюю энергию.
При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Эту работу принято называть работой тока.
Если за промежуток времени t через поперечное сечение произвольного участка проводника проходит заряд q, то электрическое поле совершает работу. Чтобы определить работу электрического тока на каком-либо участке цепи, надо напряжение на концах этого участка цепи умножить на электрический заряд, пошедший по нему. Т.е. A= q*U (а равно кью умножить на у), где U – напряжение на концах проводника, а q – величина прошедшего заряда, А – работа.
Так как сила тока определяется
I = q/t(и равно кью деленое на тэ), то заряд можно выразить q = I∙t, тогда работа будет
Работа электрического тока на участке цепи равна произведению силы тока, напряжения на этом участке и времени, в течение которого совершалась работа.
Работа измеряется в джоулях, сила тока – в амперах, напряжение в вольтах, время – в секундах.
Проведем опыт 1. Соберем цепь, состоящую из источника (4,5 В), лампочки (на 3 В), амперметра, включенного последовательно с лампочкой, вольтметра, включенного параллельно лампочке и выключателя. Кроме того, мы будем измерять время по секундомеру. Включим цепь и произведем замеры во время прохождения тока в течение 5 минут (300 с).
Получили:
I=0,25A ; U= 3B ; t = 300c
Вычислим работу: Работа электрического тока на участке цепи равна произведению силы тока, напряжения на этом участке и времени, в течение которого совершалась работа: 0,25А∙3В∙300с=225 Дж
В системе СИ работа измеряется в джоулях (Дж).
Мощность тока. Любой электрический прибор (лампа, электродвигатель) рассчитан на потребление определенного количества энергии за какой-то промежуток времени. Поэтому наряду с работой тока, важное значение имеет понятие мощность тока. Мощностью электрического тока называется отношение работы за время к этому интервалу времени: P = A/t Или заменив работу по ранее полученной формуле, будем иметь: P = I*U*t/t = I*U ,т.е. получаем новое выражение для мощности тока: Мощность тока равна произведению силы тока на напряжение: P = I*UЗа единицу мощности принят ватт, 1 Вт=1дж:с
Используют единицы мощности, которые кратны ватту:
1(гектоватт) гВт=100 Вт,
1(киловатт) кВт=1000 Вт,
1(мегаватт) МВт=1000 000 Вт
Проведем опыт 2. Соберем такую же цепь, как в опыте 1 и практически повторим его. Мы получим (как и ранее) 225 Дж работы за 300с. Найдем мощность электрического тока: разделим 225 Дж на 300 с и получим 0,75 Вт
Но существуют и специальные приборы, которые измеряют мощность электрического тока — ваттметры.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
2.3. Электрическое напряжение. Работа и мощность электрического тока. Тепловое действие тока — ЗФТШ, МФТИ
В электрической цепи, подключённой к источнику, возникают электрические силы, действующие на носители зарядов и приводящие их в движение. Пусть под действием электрической силы `F` частица, несущая заряд `q`, переместилась вдоль проводника из точки `1` в точку `2`, а сила `F` совершила над заряженной частицей работу `A_(12)`. Отношение работы `A_(12)` электрической силы над зарядом `q` при перемещении его из точки `1` в точку `2` к самому заряду $$ q$$ называют электрическим напряжением между точками `1` и `2`:
Единицей измерения напряжения в СИ является вольт (В).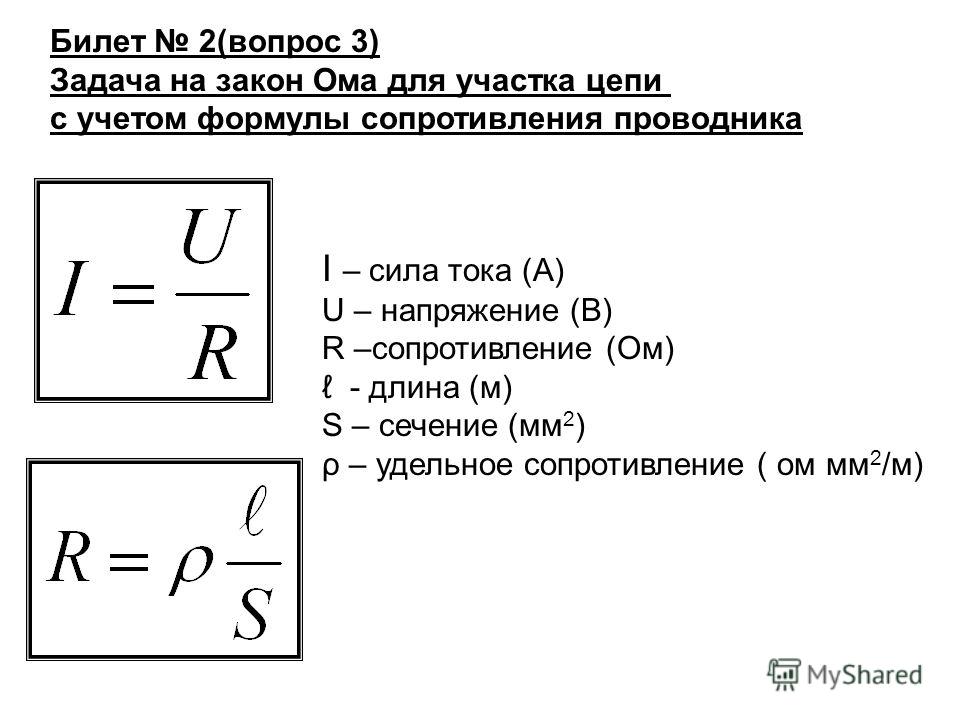
За один вольт принимается напряжение на концах проводника, при котором работа сил электрического поля по перемещению через этот проводник заряда в один кулон равна одному джоулю.
Эта единица названа в честь итальянского физика А. Вольта, который в 1800 г. изобрёл электрическую батарею и впервые получил с её помощью постоянный ток, устойчиво поддерживавшийся в электрической цепи. Это открытие ознаменовало начало новой эпохи, полностью преобразившей нашу цивилизацию: современная жизнь немыслима без использования электрического тока.
В соотношении (3) индексы `1` и `2` можно опустить, если помнить, что `1` – это точка «старта», `2` – точка «финиша».
Зная напряжение `U` на концах проводника и силу тока `I`, текущего в проводнике в течение времени `t` постоянного тока, вычислим заряд `q=I*t`, который протечёт за указанное время по проводнику. Тогда за это время силы электрического поля в проводнике совершат работу
Это позволяет судить о скорости совершения работы электрическими силами, т.
е. о мощности, развиваемой силами электрического поля. Из (4) следует, что в проводнике, напряжение на концах которого равно `U`, а сила тока `I`, силы электрического поля в единицу времени совершают работу
Напомним, что единицей измерения мощности в СИ служит ватт (Вт).
Очень часто работу и мощность электрических сил называют соответственно работой и мощностью электрического тока, тем самым подчёркивают, что это работа по поддержанию электрического тока в цепи.
Работа электрического тока может идти на изменение механической и внутренней энергий проводника. Например, в результате протекания электрического тока через электродвигатель его ротор (подвижная часть, способная вращаться, в отличие от статора) раскручивается. При этом большая часть работы электрических сил идёт на увеличение механической энергии ротора, а также других тел, с которыми ротор связан теми или иными механизмами. Другая часть работы электрического тока (в современных электродвигателях один – два процента) идёт на изменение внутренней энергии обмоток двигателя, что приводит к их нагреванию (обмотка электродвигателя представляет собой катушку, изготовленную обычно из меди, с большим числом витков).
Обсудим тепловое действие электрического тока более подробно. Из опыта известно, что электрический ток нагревает проводник. Объясняется это явление тем, что свободные электроны в металлах, перемещаясь под действием сил электрического поля, взаимодействуют с ионами вещества и передают им свою энергию. В результате увеличивается энергия колебаний ионов в проводнике, его температура растёт, при этом говорят, что в проводнике за некоторое время `t` выделяется количество теплоты `Q_(«тепл»)`. Если проводник с током неподвижен и величина тока постоянна, то работа электрических сил идёт на изменение внутренней энергии проводника. По закону сохранения энергии это количество равно работе сил электрического поля (4) в проводнике за то же самое время, т. е.
Отсюда мощность `P` тепловыделения, т. е. количество теплоты, выделяющейся в единицу времени на участке цепи, где напряжение равно `U`, а сила тока равна `I` составляет
Различия, объясненные простыми словами
Ампер, вольт и ватт — это три основных понятия, с которыми вы постоянно сталкиваетесь при работе с любой электрической системой.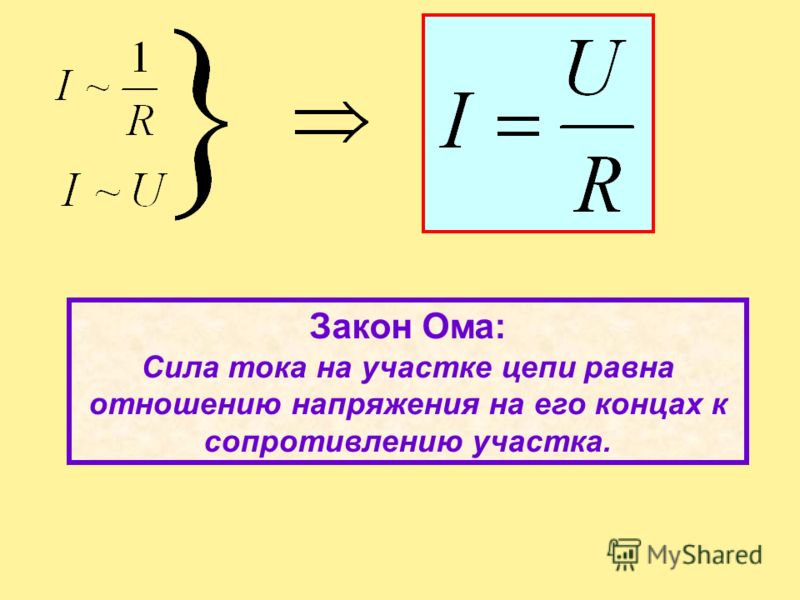
Четвертым является сопротивление, которое измеряется в омах. Это может показаться ошеломляющим, но вам не нужна степень инженера, чтобы понять, что такое электричество и как использовать его в своих интересах.
Подобно тому, как вода течет по шлангу, электричество представляет собой поток электронов через проводник. В большинстве электрических систем проводником является провод.
Электричество — это поток электронов через проводник.Так как вы не можете легко увидеть электроны, ниже мы будем использовать аналогию с водой и шлангом. Давайте перейдем к этому, объяснив каждую концепцию отдельно.
Что такое усилители?
Ампер, или сокращенно ампер, является единицей измерения электрического тока. Ток — это скорость или скорость, с которой электроны проходят через проводник, и обозначается буквой «I» в электрических уравнениях.
В нашей аналогии с водой электрический ток эквивалентен расходу или количеству воды, протекающей через шланг.
Что такое вольты?
Вольт является единицей измерения электрического напряжения и обозначается буквой «V» в электрических уравнениях.
Напряжение — это разница в электрическом потенциале или количестве электронов между любыми двумя точками электрической цепи.
В нашей аналогии с водой напряжение эквивалентно давлению воды. Давление — это сила, которая перемещает воду по шлангу точно так же, как напряжение толкает электроны по проводнику.
Что такое омы?
Ом — это единица измерения электрического сопротивления проводника, обозначаемая буквой «R» в электрических уравнениях. Сопротивление пытается замедлить поток электронов.
В нашей аналогии с водой сопротивление — это диаметр шланга. Широкий шланг имеет очень небольшое сопротивление и позволяет воде течь через него быстро. Проводники с низким электрическим сопротивлением, такие как медная проволока, позволяют электронам легко проходить через них, как и через широкий шланг.
Сопротивление представлено водой и трубкой размеромЧто такое ватты?
Мощность — это скорость, с которой электрическая энергия передается в цепи, и измеряется в ваттах.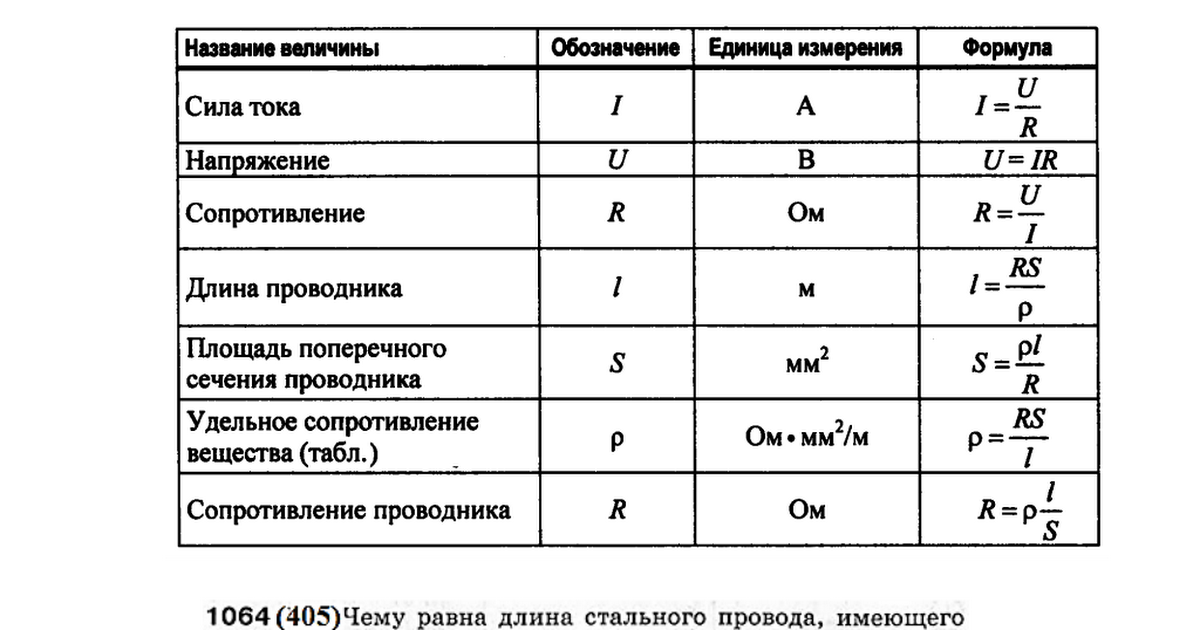
В электрических уравнениях буква «P» представляет мощность.
Силу немного сложнее объяснить, используя аналогию с водой. Со шлангом вы можете увеличить мощность, либо увеличив количество выходящей воды, либо увеличив давление воды на выходе. В электрической системе вы можете увеличить мощность, увеличив ток или увеличив напряжение.
Собираем все вместе
Важно понимать эти основные понятия сами по себе, но самое интересное получается, когда мы связываем амперы, вольты и ватты вместе.
Напряжение, ток, сопротивлениеЗакон Ома связывает напряжение, ток и сопротивление. Он представлен простым уравнением.
V = I * R
V = напряжение (вольты)
I = ток (амперы)
R = сопротивление (омы)
Если оставить сопротивление неизменным и увеличить напряжение, ток должен увеличиться . Как и в нашей аналогии со шлангом, если вы увеличите давление, через него пройдет больше воды.
Сопротивление работает против напряжения, чтобы замедлить поток электронов.
Если сопротивление увеличивается, а напряжение остается прежним, ток, протекающий через цепь, уменьшается. Точно так же, если вы сожмете шланг, чтобы уменьшить его диаметр или увеличить сопротивление, из конца выйдет меньше воды.
Чтобы свести вместе ватты (мощность), ампер (ток) и вольты (напряжение), нам нужно еще одно простое уравнение.
P = V * I
P = мощность (ватты)
V = напряжение (вольты)
I = ток (амперы)
Оглядываясь назад на наш пример воды, протекающей через шланг, мы можем теперь увидеть, какова мощность напрямую связаны с током и напряжением, используя это уравнение.
Например, представьте, что вы распыляете воду из шланга, чтобы вращать водяное колесо. Чем быстрее вращается колесо, тем больше энергии вырабатывается.
Если размер шланга останется прежним, мы можем заставить колесо вращаться быстрее двумя способами. Во-первых, увеличить скорость потока, что означает, что больше воды и веса попадает на колесо и вращает его быстрее.
Второй способ — увеличить давление воды, чтобы вода ударялась о колесо с большей силой и быстрее вращало его.
В нашей аналогии расход воды эквивалентен току, а давление воды равно напряжению. Как видно из приведенного выше уравнения, если вы увеличите ток или напряжение, ваша мощность также увеличится.
Ампер, вольт и ватт: объяснение различий!
Взаимосвязи между мощностью, током, напряжением и сопротивлением поначалу кажутся ошеломляющими, но если вникнуть, они становятся довольно простыми. Теперь, когда у вас есть общее представление об основах питания и электричества, вы сможете ваши электрические проекты RV с немного большей уверенностью.
Хотите узнать больше об электрических системах и литиевых батареях?
Мы знаем, что строительство или модернизация электрической системы может быть сложной задачей, поэтому мы здесь, чтобы помочь. Наш отдел продаж и обслуживания клиентов из Рено, штат Невада, готов ответить на ваши вопросы по телефону (855) 292-2831!
Кроме того, присоединяйтесь к нам на Facebook, Instagram и YouTube, чтобы узнать больше о том, как системы с литиевыми батареями могут обеспечить ваш образ жизни, увидеть, как другие построили свои системы, и обрести уверенность, чтобы выйти и остаться там.
Присоединяйтесь к нашему списку контактов
Подпишитесь сейчас на новости и обновления на ваш почтовый ящик.Поделитесь этим
15.4 Питание в цепи переменного тока — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Опишите, как средняя мощность от цепи переменного тока может быть выражена через пиковый ток и напряжение и среднеквадратичное значение тока и напряжения
- Определить зависимость между фазовым углом тока и напряжения и средней мощностью, известную как коэффициент мощности
Элемент схемы рассеивает или производит мощность в соответствии с P=IV,P=IV, где I — ток через элемент, а В — напряжение на нем. Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность p(t)=i(t)v(t)p(t)=i(t)v(t) также зависит от времени. График p ( t ) для различных элементов схемы показан на рис.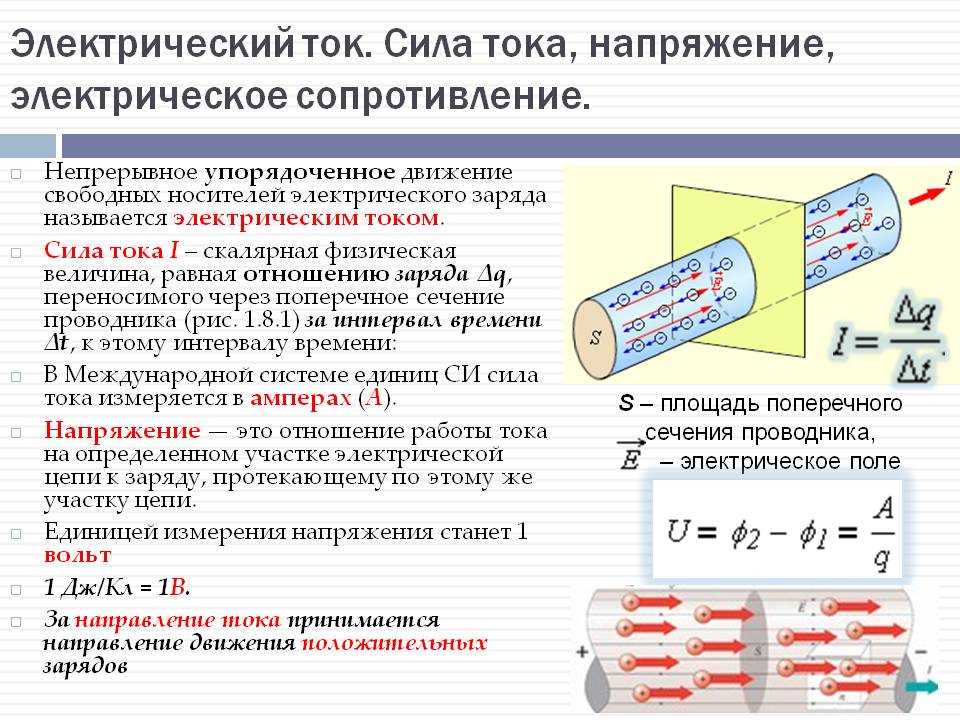
15.16. Для резистора i ( t ) и v ( t ) совпадают по фазе и поэтому всегда имеют один и тот же знак (см. рис. 15.5). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разности фаз (см. рис. 15.7 и рис. 15.9). Следовательно,
Рисунок
15.16
График мгновенной мощности для различных элементов цепи. (a) Для резистора Pave=I0V0/2, Pave=I0V0/2, тогда как для (b) конденсатора и (c) катушки индуктивности Pave=0.
Pave=0. (d) Для источника Pave=I0V0(cosϕ)/2, Pave=I0V0(cosϕ)/2, что может быть положительным, отрицательным или нулевым, в зависимости от ϕ.ϕ.
Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. Что нас почти всегда интересует, так это мощность, усредненная по времени, которую мы называем средней мощностью. Он определяется средней по времени мгновенной мощностью за один цикл:
Pave=1T∫0Tp(t)dt,Pave=1T∫0Tp(t)dt,
где T=2π/ωT=2π/ω – период колебаний. С заменами v(t)=V0sinωtv(t)=V0sinωt и i(t)=I0sin(ωt−ϕ),i(t)=I0sin(ωt−ϕ) этот интеграл принимает вид
Pave=I0V0T∫0Tsin( ωt−ϕ)sinωtdt.Pave=I0V0T∫0Tsin(ωt−ϕ)sinωtdt.
Using the trigonometric relation sin(A−B)=sinAcosB−sinBcosA,sin(A−B)=sinAcosB−sinBcosA, we obtain
Pave=I0V0cosϕT∫0Tsin2ωtdt−I0V0sinϕT∫0Tsinωtcosωtdt.Pave=I0V0cosϕT∫0Tsin2ωtdt−I0V0sinϕT∫ 0Tsinωtcosωtдт.
Вычисление этих двух интегралов дает
Следовательно, средняя мощность, связанная с элементом схемы, определяется как
Pave=12I0V0cosϕ.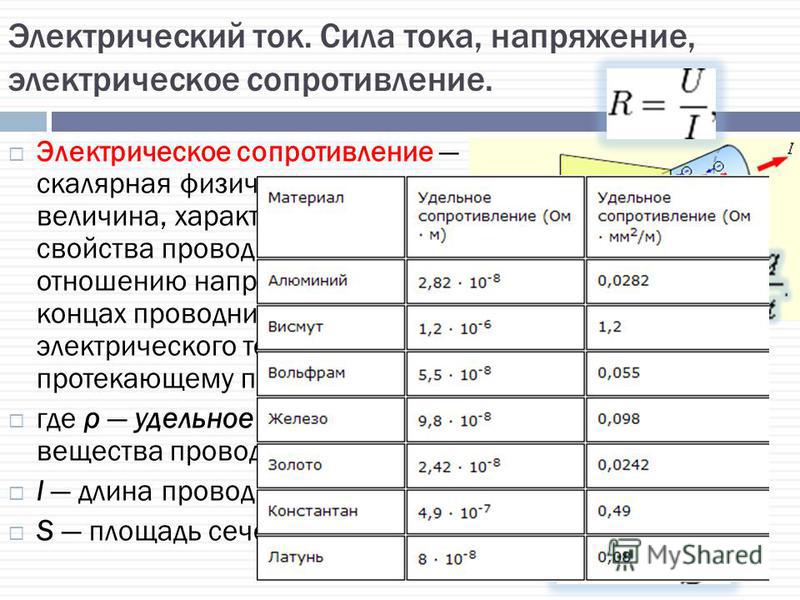
Pave=12I0V0cosϕ.
15.12
В технических приложениях cosϕcosϕ известен как коэффициент мощности, который представляет собой величину, на которую мощность, подаваемая в цепь, меньше теоретического максимума цепи из-за несовпадения фаз напряжения и тока. Для резистора ϕ=0,ϕ=0, поэтому средняя рассеиваемая мощность равна
Задать=12I0V0.Задать=12I0V0.
Сравнение p ( t ) и PavePave показано на рис. 15.16(d). Чтобы сделать Pave=(1/2)I0V0Pave=(1/2)I0V0 похожим на его аналог постоянного тока, мы используем среднеквадратичные значения IrmsandVrmsIrmsandVrms тока и напряжения. По определению это
Irms=iave2andVrms=vave2,Irms=iave2andVrms=vave2,
, где )dt и vave2=1T∫0Tv2(t)dt.
При i(t)=I0sin(ωt−ϕ) и v(t)=V0sinωt, i(t)=I0sin(ωt−ϕ)и v(t)=V0sinωt получаем
Irms=12I0и Vrms=12V0.Irms=12I0andVrms=12V0.
Затем мы можем написать для средней мощности, рассеиваемой резистором,
Pave=12I0V0=IrmsVrms=Irms2R.
15.13
Это уравнение еще раз подчеркивает, почему для обсуждения выбрано среднеквадратичное значение, а не пиковые значения. Оба уравнения для средней мощности верны для уравнения 15.13, но среднеквадратические значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не нужен.
Переменные напряжения и токи обычно описываются их среднеквадратичными значениями. Например, 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника составляет 1102 В = 156 В. 1102 В = 156 В. Поскольку большинство счетчиков переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, подключенный к бытовой розетке, покажет 110 В.
Для конденсатора и катушки индуктивности , ϕ=π/2 и −π/2рад, ϕ=π/2 и −π/2рад соответственно. Поскольку cosπ/2=cos(−π/2)=0, cosπ/2=cos(−π/2)=0, из уравнения 15.12 мы находим, что средняя мощность, рассеиваемая любым из этих элементов, равна Pave=0.
Фазовый угол генератора переменного тока может иметь любое значение. Если cosϕ>0,cosϕ>0, генератор вырабатывает мощность; если cosϕ<0,cosϕ<0, он поглощает мощность. В терминах среднеквадратичных значений средняя мощность генератора переменного тока записывается как
Pave=IrmsVrmscosϕ.Pave=IrmsVrmscosϕ.
Для генератора в цепи RLC ,
tanϕ=XL−XCRtanϕ=XL−XCR
и
cosϕ=RR2+(XL−XC)2=RZ.cosϕ=RR2+(XL−XC)2= РЗ.
Следовательно, средняя мощность генератора равна
Pave=IrmsVrmscosϕ=VrmsZVrmsRZ=Vrms2RZ2.Pave=IrmsVrmscosϕ=VrmsZVrmsRZ=Vrms2RZ2.
15.
14
Это также можно записать как
Pave=Irms2R,Pave=Irms2R,
, что означает, что мощность, вырабатываемая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.
Пример 15,3
Выходная мощность генератора
Генератор переменного тока, ЭДС которого определяется выражением
v(t)=(4,00 В)sin[(1,00×104 рад/с)t]v(t)=(4,00 В)sin[(1,00×104 рад/с)t]
подключен к RLC , для которой L=2,00×10-3HL=2,00×10-3H, C=4,00×10-6FC=4,00×10-6F и R=5,00ΩR=5,00Ω. а) Чему равно среднеквадратичное напряжение на генераторе? б) Чему равно сопротивление цепи? в) Какова средняя мощность генератора?
Стратегия
Среднеквадратичное напряжение – это амплитуда напряжения, умноженная на 1/21/2.
Полное сопротивление цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по уравнению 15.14 или, точнее, по последней части уравнения, потому что у нас есть импеданс цепи Z , среднеквадратичное значение напряжения VrmsVrms и сопротивление R .
Решение
- Поскольку V0=4,00 В, V0=4,00 В, среднеквадратичное значение напряжения на генераторе равно
Вэфф=12(4,00В)=2,83В. Вэфф=12(4,00В)=2,83В.
- Полное сопротивление цепи
Z=R2+(XL-XC)2={(5,00 Ом)2+[(1,00×104 рад/с)(2,00×10-3H)−1(1,00×104рад/с)(4,00×10-6F)] 2}1/2=7,07 Ом. Z=R2+(XL-XC)2={(5,00 Ом)2+[(1,00×104 рад/с)(2,00×10-3H)−1(1,00×104 рад/с) (4,00×10-6F)]2}1/2=7,07 Ом.
- Из уравнения 15.14 средняя мощность, передаваемая в цепь, равна
Pave=Vrms2RZ2=(2,83 В)2(5,00 Ом)(7,07 Ом)2=0,801 Вт. Pave=Vrms2RZ2=(2,83 В)2(5,00 Ом)(7,07 Ом)2=0,801 Вт.
