Что такое катушка индуктивности. Как она работает в цепи переменного тока. Какие формулы описывают ее поведение. Где применяются катушки индуктивности на практике.
Что такое катушка индуктивности и как она устроена
Катушка индуктивности представляет собой один из базовых элементов электрических цепей. Она состоит из проводника, намотанного в виде спирали на каркас. Основные части катушки индуктивности:
- Обмотка из изолированного провода
- Каркас (может быть воздушным или из диэлектрического материала)
- Магнитопровод (сердечник) — не обязателен, может отсутствовать
Главный параметр катушки — индуктивность L, измеряемая в генри (Гн). Она зависит от числа витков, геометрических размеров и свойств сердечника.
Принцип работы катушки индуктивности в цепи переменного тока
В цепи постоянного тока катушка индуктивности ведет себя как обычный проводник с некоторым активным сопротивлением. Однако в цепи переменного тока ее поведение кардинально меняется. Рассмотрим основные эффекты:

Самоиндукция
При протекании переменного тока через катушку в ней возникает ЭДС самоиндукции, направленная против изменения тока. Это приводит к отставанию тока от приложенного напряжения на 90°.
Индуктивное сопротивление
Катушка оказывает переменному току индуктивное сопротивление XL, которое прямо пропорционально частоте тока и индуктивности:
XL = ωL = 2πfL
где ω — угловая частота, f — линейная частота, L — индуктивность.
Реактивная мощность
Катушка индуктивности накапливает энергию в магнитном поле. При этом происходит обмен энергией между источником и катушкой — реактивная мощность:
Q = I2XL = U2/XL
Основные формулы для расчета цепей с катушкой индуктивности
Для анализа цепей переменного тока с катушками индуктивности используются следующие ключевые формулы:
- Закон Ома: I = U / Z, где Z = √(R2 + XL 2)
- Мгновенное значение тока: i = Imsin(ωt — φ)
- Мгновенное значение напряжения: u = Umsin(ωt)
- Угол сдвига фаз: tgφ = XL/R
- Активная мощность: P = I2R
- Реактивная мощность: Q = I2XL
- Полная мощность: S = UI = √(P2 + Q2)
Векторные диаграммы для цепей с катушкой индуктивности
Векторные диаграммы наглядно показывают соотношения между токами, напряжениями и сдвигами фаз в цепях переменного тока. Для цепи с катушкой индуктивности характерна следующая векторная диаграмма:
 «`
«`
«`
«`
На этой диаграмме:
- Синий вектор — ток I
- Красный вектор — полное напряжение U
- Зеленый вектор — напряжение на индуктивности UL
- φ — угол сдвига фаз между током и напряжением
Особенности поведения катушки индуктивности при различных частотах
Поведение катушки индуктивности существенно зависит от частоты переменного тока:
- При низких частотах индуктивное сопротивление XL мало, катушка ведет себя почти как короткозамкнутый участок цепи
- С ростом частоты XL увеличивается, катушка все сильнее препятствует прохождению тока
- На высоких частотах XL становится очень большим, катушка фактически разрывает цепь для переменного тока
Это свойство катушек индуктивности широко используется для создания частотно-зависимых цепей.
Применение катушек индуктивности в электротехнике и электронике
Благодаря своим уникальным свойствам, катушки индуктивности нашли широкое применение в различных областях:
- Фильтры высоких и низких частот
- Колебательные контуры
- Трансформаторы и дроссели
- Электромагниты и реле
- Антенны и системы беспроводной передачи энергии
- Датчики и измерительные приборы
- Стабилизаторы тока
Расчет параметров катушки индуктивности
Для практического применения часто требуется рассчитать параметры катушки индуктивности. Основные формулы для этого:
- Индуктивность многослойной катушки без сердечника: L = (μ0N2S) / l
- Индуктивность однослойной катушки: L = (d2N2) / (18d + 40l)
- Индуктивность тороидальной катушки: L = (μ0μN2S) / (2πR)
где:
- L — индуктивность (Гн)
- μ0 — магнитная постоянная
- μ — относительная магнитная проницаемость сердечника
- N — число витков
- S — площадь поперечного сечения (м2)
- l — длина катушки (м)
- d — диаметр катушки (м)
- R — средний радиус тороида (м)
Моделирование цепей с катушками индуктивности
Для анализа сложных цепей с катушками индуктивности широко применяется компьютерное моделирование. Популярные программы для этого:
- SPICE (Simulation Program with Integrated Circuit Emphasis)
- MATLAB Simulink
- LabVIEW
- Multisim
- OrCAD
Эти инструменты позволяют быстро рассчитать параметры цепи, построить графики токов и напряжений, оценить влияние различных факторов на работу схемы.
Заключение
Катушка индуктивности — фундаментальный элемент электрических цепей, обладающий уникальными свойствами в цепях переменного тока. Понимание принципов ее работы и умение рассчитывать цепи с катушками необходимо для проектирования широкого спектра электронных устройств. С развитием технологий роль катушек индуктивности в современной электронике только возрастает, открывая новые области применения.

Катушка индуктивности в цепи переменного тока кратко – формулы и опредделение (11 класс)
4.2
Средняя оценка: 4.2
Всего получено оценок: 105.
4.2
Средняя оценка: 4.2
Всего получено оценок: 105.
В цепи постоянного тока катушка индуктивности ведет себя так же, как обычный длинный провод. Однако для переменного тока ситуация существенно иная. Поговорим кратко о катушке индуктивности в цепи переменного тока.
Сущность индуктивного сопротивления
Из курса физики в 11 классе известно, что катушке индуктивности присуще явление самоиндукции. Оно состоит в том, что при изменении величины тока, протекающего по катушке, магнитное поле, порожденное этим током, также меняется. Это приводит к изменению магнитного потока через катушку. А по закону электромагнитной индукции изменение магнитного потока вызывает появление в контуре ЭДС. Эта ЭДС по правилу Ленца направлена так, чтобы препятствовать причине, ее порождающей. Иными словами, при изменении тока в катушке индуктивности в ней возникает некоторая ЭДС, которая препятствует изменению этого тока.
Получается, что катушка «сопротивляется» любым изменениям тока в ней. Если ток возрастает, она не дает ему возрастать. Если ток убывает, она не дает ему убывать. Для переменного тока, который постоянно изменяет свое значение по гармоническому закону, катушка постоянно «сопротивляется». Таким образом, для переменного тока можно говорить об особом, индуктивном, сопротивлении катушки (на постоянном токе это сопротивление равно нулю).
Это сопротивление существенно отличается от сопротивления активного. Если на активном сопротивлении работа тока преобразуется в тепло, то на сопротивлении катушки во время возрастания тока его работа преобразуется в энергию магнитного поля в катушке, а во время убывания она возвращается из магнитного поля в энергию тока. Катушка как бы «имеет реакцию» на изменение тока через нее за счет индуктивности. Поэтому такое сопротивление называется реактивным.
Реактивное сопротивление катушки индуктивности
Поскольку в первую половину периода энергия электрического тока запасается в магнитном поле катушки, а во вторую — возвращается в цепь, то в среднем работа электрического тока равна по модулю работе ЭДС самоиндукции, но имеет противоположный знак:
$$e_i =-u$$
Однако амплитудные значения напряжения и тока на катушке индуктивности достигаются неодновременно.
Мгновенное значение тока:
$$i =I_msin \omega t$$
Мгновенное значение напряжения:
$$u =L\omega I_m cos \omega t$$
Учитывая, что максимальная амплитуда напряжения $U_m$ равна $ L\omega I_m $, и приводя к синусу, получаем:
$$u =U_m sin(\omega t+{\pi \over 2})$$
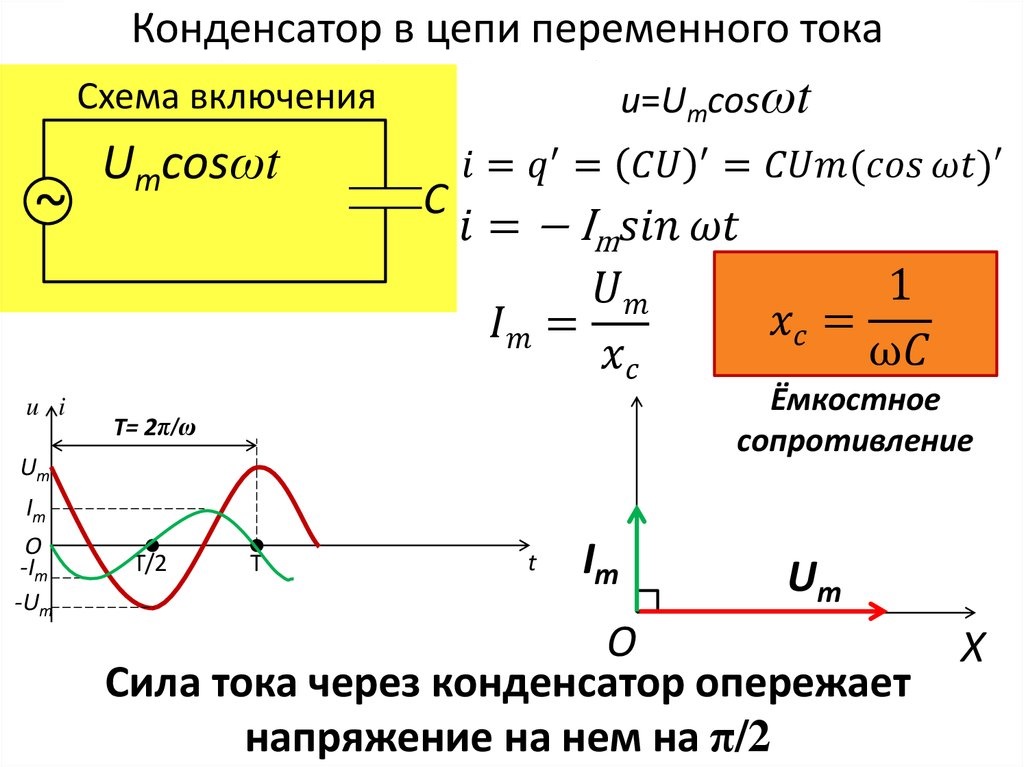
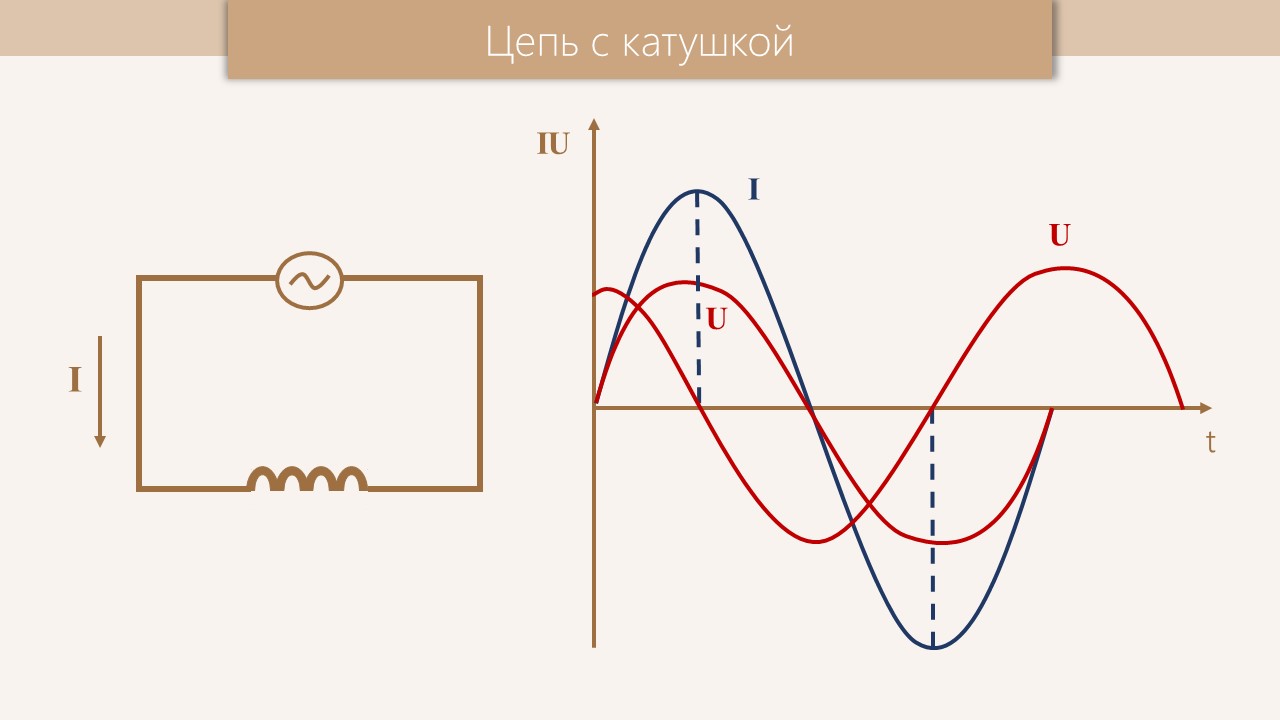
Таким образом, колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода. В этом важное отличие реактивного сопротивления от активного, где отставания между током и напряжения нет.
Рис. 2. Графики тока и напряжения для индуктивности.Амплитуда силы тока в катушке равна:
$$I_m={U_m\over \omega L}$$
Сравним эту формулу с законом Ома, который используется для определения силы тока в цепи:
$$I={U\over R}$$
Можно видеть, что эти формулы аналогичны, и величина $ \omega L$ играет роль сопротивления. То есть реактивное сопротивление катушки индуктивности (индуктивное сопротивление) равно:
$$X_L= \omega L$$
Отметим, что реактивное сопротивление катушки прямо пропорционально циклической частоте переменного тока. Чем она больше, тем больше сопротивление.
Чем она больше, тем больше сопротивление.
Поскольку любой проводник обладает некоторой индуктивностью, то на очень высоких частотах даже эта малая индуктивность обычных проводников достаточно сильно влияет на сигнал. Поэтому приходится применять специальные меры для ее компенсации. Например, применять вместо проводов волноводы — пустотелые металлические конструкции:
Что мы узнали?
Катушка индуктивности в цепи переменного тока обладает реактивным сопротивлением, пропорциональным частоте. Первую половину периода она запасает энергию электрического тока в виде магнитного поля, а вторую половину периода возвращает эту энергию электрическому току. При этом колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4. 2
2
Средняя оценка: 4.2
Всего получено оценок: 105.
А какая ваша оценка?
Основы теории цепей
Основы теории цепей
ОглавлениеПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮВВЕДЕНИЕ Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ 1-1. Элементы электрических цепей и электрических схем 1-2. Эквивалентные схемы для источников энергии 1-3. Закон Ома для участка цепи с э. д. с. 1-4. Распределение потенциала вдоль неразветвленной электрической цепи 1-5. Баланс мощностей для простейшей неразветвленной цепи 1-6. Применение законов Кирхгофа для расчета разветвленных цепей 1-7. Метод узловых потенциалов 1-8. Метод контурных токов 1-9. Уравнения состояния цепи в матричной форме 1-10. Преобразование линейных электрических схем Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ 2-2. Свойство взаимности 2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов 2-4. Применение топологических методов для расчета цепей 2-5.  Топологические формулы и правила для определения передачи электрической цепи Топологические формулы и правила для определения передачи электрической цепи2-6. Теорема о компенсации 2-7. Линейные соотношения между напряжениями и токами 2-8. Теорема о взаимных приращениях токов и напряжений 2-9. Общие замечания о двухполюсниках 2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей 2-11. Передача энергии от активного двухполюсника к пассивному Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА 3-2. Понятие о генераторах переменного тока 3-3. Синусоидальный ток 3-4. Действующие ток, э. д. с. и напряжение 3-5. Изображение синусоидальных функций времени векторами и комплексными числами 3-6. Сложение синусоидальных функций времени 3-7. Электрическая цепь и ее схема 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости 3-9. Сопротивления 3-10. Разность фаз напряжения и тока 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости 3-12.  Проводимости Проводимости3-13. Пассивный двухполюсник 3-14. Мощности 3-15. Мощности в сопротивлении, индуктивности и емкости 3-16. Баланс мощностей 3-17. Знаки мощностей и направление передачи энергии 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра 3-19. Условия передачи максимальной мощности от источника энергии к приемнику 3-20. Понятие о поверхностном эффекте и эффекте близости 3-21. Параметры и эквивалентные схемы конденсаторов 3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока 4-2. Последовательное соединение приемников 4-3. Параллельное соединение приемников 4-4. Смешанное соединение приемников 4-5. Сложные разветвленные цепи 4-6. Топографические диаграммы 4-7. Дуальность электрических цепей 4-8. Сигнальные графы и их применение для расчета цепей Глава пятая.  РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ5-2. Частотные характеристики неразветвленной цепи 5-3. Резонанс в цепи с двумя параллельными ветвями 5-4. Частотные характеристики параллельного контура 5-5. Понятие о резонансе в сложных цепях Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ 6-2. Электродвижущая сила взаимной индукции 6-3. Последовательное соединение индуктивно связанных элементов цепи 6-4. Параллельное соединение индуктивно связанных элементов цепи 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности 6-6. Эквивалентная замена индуктивных связей 6-7. Передача энергии между индуктивно связанными элементами цепи 6-8. Трансформатор без стального сердечника (воздушный трансформатор) Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ 7-1. Комплексные уравнения прямой и окружности 7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника 7-3. Круговые диаграммы для любой разветвленной цепи Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ 8-1.  Четырехполюсники и их основные уравнения Четырехполюсники и их основные уравнения8-2. Определение коэффициентов четырехполюсников 8-3. Режим четырехполюсника при нагрузке 8-4. Эквивалентные схемы четырехполюсников 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника 8-6. Идеальный трансформатор как четырехполюсник 8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом 8-9. Расчеты электрических цепей с трансформаторами 8-10. Графы пассивных четырехполюсников и их простейшие соединения Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ 9-2. Эквивалентные схемы лампового триода 9-3. Транзисторы (полупроводниковые триоды) 9-4. Эквивалентные схемы транзисторов 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы Глава десятая. ТРЕХФАЗНЫЕ ЦЕПИ 10-2. Соединения звездой и многоугольником 10-3.  Симметричный режим трехфазной цепи Симметричный режим трехфазной цепи10-4. Некоторые свойства трехфазных цепей с различными схемами соединений 10-5. Расчет симметричных режимов трехфазных цепей 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой 10-7. Напряжения на фазах приемника в некоторых частных случаях 10-8. Эквивалентные схемы трехфазных линий 10-9. Измерение мощности в трехфазных цепях 10-10. Вращающееся магнитное поле 10-11. Принципы действия асинхронного и синхронного двигателей Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений 11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей 11-4. Определение токов в симметричной цепи 11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи 11-6. Расчет цепи с несимметричной нагрузкой 11-7. Расчет цепи с несимметричным участком в линии Глава двенадцатая.  НЕСИНУСОИДАЛЬНЫЕ ТОКИ НЕСИНУСОИДАЛЬНЫЕ ТОКИ12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых 12-5. Несинусоидальные кривые с периодической огибающей 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами 12-8. Резонанс при несинусоидальных э. д. с. и токах 12-9. Мощность периодических несинусоидальных токов 12-10. Высшие гармоники в трехфазных цепях Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 13-2. Переходный, принужденный и свободный процессы 13-3. Короткое замыкание цепи r, L 13-4. Включение цепи r, L на постоянное напряжение 13-5. Включение цепи r, L на синусоидальное напряжение 13-6. Короткое замыкание цепи r, С 13-7.  Включение цепи r, С на постоянное напряжение Включение цепи r, С на постоянное напряжение13-8. Включение цепи r, С на синусоидальное напряжение 13-9. Переходные процессы в неразветвленной цепи r, С 13-10. Апериодический разряд конденсатора 13-11. Предельный случай апериодического разряда конденсатора 13-12. Периодический (колебательный) разряд конденсатора 13-13. Включение цепи r, С на постоянное напряжение 13-14. Общий случай расчета переходных процессов классическим методом 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля) 13-16. Включение пассивного двухполюсника на напряжение любой формы 13-17. Временная и импульсная переходные характеристики 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики 13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах 13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока Глава четырнадцатая.  ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ14-2. Законы Ома и Кирхгофа в операторной форме 14-3. Эквивалентные операторные схемы 14-4. Переходные процессы в цепях с взаимной индуктивностью 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям 14-6. Определение свободных токов по их изображениям 14-7. Формулы включения 14-8. Расчет переходных процессов методом переменных состояния 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций) 15-4. О переходе от преобразований Фурье к преобразованиям Лапласа 15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ 16-2.  Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника16-3. Вносимая и рабочая постоянные передачи 16-4. Цепные схемы 16-5. Частотные электрические фильтры 16-6. Низкочастотные фильтры 16-8. Полосные фильтры 16-11. Г-образный фильтр как пример несимметричного фильтра 16-12. Безындукционные (или r, C) фильтры Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы 17-3. Входные функции цепей. Положительные вещественные функции 17-4. Реактивные двухполюсники 17-5. Частотные характеристики реактивных двухполюсников 17-6. Синтез реактивных двухполюсников. Метод Фостера 17-7. Синтез реактивных двухполюсников. Метод Кауэра 17-8. Синтез двухполюсников с потерями. Метод Фостера 17-9. Синтез двухполюсников с потерями. Метод Кауэра 17-10. Понятие о синтезе четырехполюсников Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ Глава восемнадцатая.  ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ18-2. Уравнения однородной линии 18-3. Установившийся режим в однородной линии 18-4. Уравнения однородной линии с гиперболическими функциями 18-5. Характеристики однородной линии 18-6. Входное сопротивление линии 18-7. Коэффициент отражения волны 18-8. Согласованная нагрузка линии 18-9. Линия без искажений 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями 18-11. Линии без потерь 18-12. Стоячие волны 18-13. Линия как четырехполюсник Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 19-2. Общее решение уравнений однородной линии 19-3. Возникновение волн с прямоугольным фронтом 19-4. Общие случаи нахождения волн, возникающих при переключениях 19-5. Отражение волны с прямоугольным фронтом от конца линии 19-6. Общий метод определения отраженных волн 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности 19-8.  Многократные отражения волн с прямоугольным фронтом от активного сопротивления Многократные отражения волн с прямоугольным фронтом от активного сопротивления19-9. Блуждающие волны Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами 20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами 20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений) Глава двадцать первая. 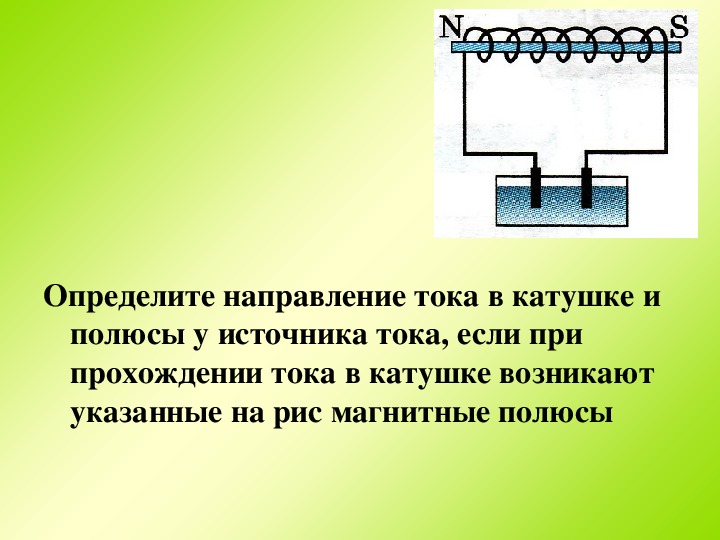 МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ21-2. Расчет неразветвленных магнитных цепей 21-3. Расчет разветвленных магнитных цепей 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников 22-3. Явления в нелинейных цепях переменного тока 22-4. Методы расчета нелинейных цепей переменного тока Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ 23-2. Форма кривой тока в цепи с вентилями 23-3. Простейшие выпрямители 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями 23-5. Утроители частоты 23-6. Формы кривых тока и напряжения в цепях с терморезисторами 23-7. 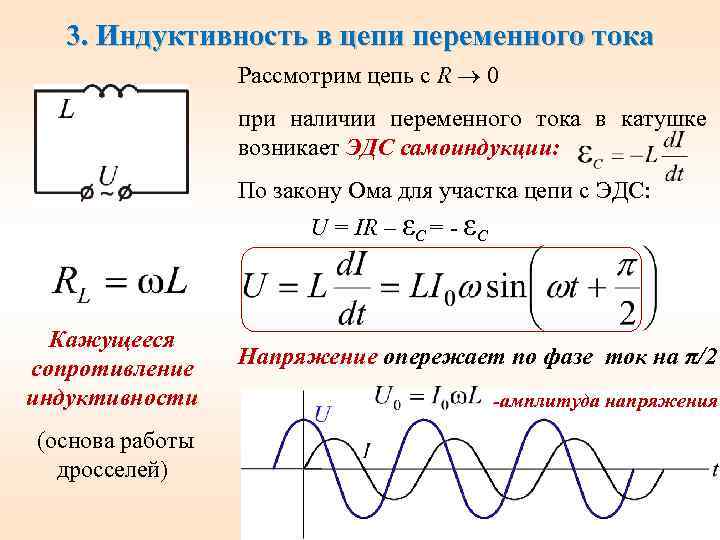 Замена реальных нелинейных элементов условно-нелинейными Замена реальных нелинейных элементов условно-нелинейными23-8. Учет реальных свойств стальных магнитопроводов 23-9. Расчет тока в катушке со стальным магнитопроводом 23-10. Понятие о расчете условно-нелинейных магнитных цепей 23-11. Явление феррорезонанса 23-12. Стабилизаторы напряжения Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот 24-2. Вентили в цепях с постоянными и переменными э. д. с. 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с. 24-5. Удвоитель частоты 24-6. Метод гармонического баланса 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли 24-8. Принцип получения модулированных колебаний 24-9. 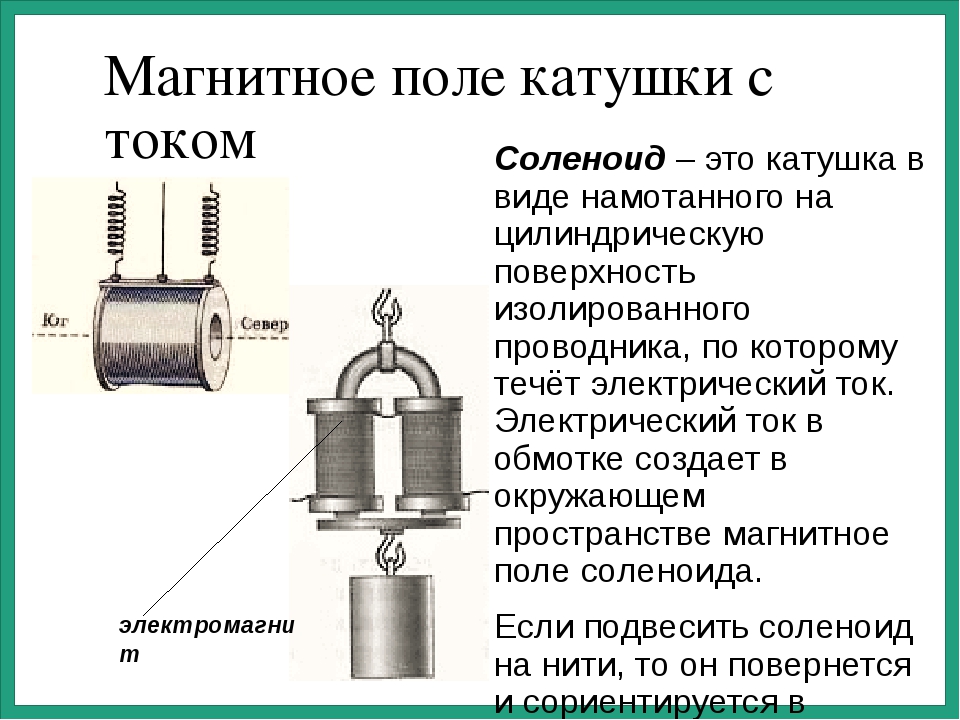 Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями24-10. Магнитные усилители мощности Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями 25-5. Понятие о простейших запоминающих устройствах 25-6. Изображение переходных процессов на фазовой плоскости 25-7. Колебательный разряд емкости через нелинейную индуктивность Глава двадцать шестая. АВТОКОЛЕБАНИЯ 26-1. Нелинейные резисторы со спадающим участком характеристики 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами 26-3. Релаксационные колебания в цепи с отрицательным сопротивлением 26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением 26-6.  Фазовые траектории процессов в генераторе синусоидальных колебаний Фазовые траектории процессов в генераторе синусоидальных колебаний26-7. Определение амплитуды автоколебаний методом гармонического баланса Приложение 1. Разложение периодических функций в тригонометрический ряд Приложение 2. Таблица оригиналов и изображений (по Лапласу) Приложение 3. Таблица функций и их частных спектров Приложение 4. Таблица функций для трапеций СПИСОК ЛИТЕРАТУРЫ |
Токовая катушка – определение, важные факторы и применение
Токовая катушка в основном представляет собой катушку, например, провод, намотанный на электрический проводник. Обычно катушка изготавливается из изолированного медного провода, а проводник представляет собой сердечник из мягкого железа. Когда катушка, намотанная на проводник, несет ток, было замечено, что катушка начинает вести себя как магнит. Это свойство проводника, намотанного на катушку с током, называется электромагнетизмом. Популярный физический эксперимент проводится с использованием того же явления. Когда гвозди кладут поперек стола с проводником, намотанным на провод с током, то гвозди стола прилипают к катушке. Причина, по которой эти гвозди приклеиваются к проводу, — электромагнетизм.
Популярный физический эксперимент проводится с использованием того же явления. Когда гвозди кладут поперек стола с проводником, намотанным на провод с током, то гвозди стола прилипают к катушке. Причина, по которой эти гвозди приклеиваются к проводу, — электромагнетизм.
Катушка тока представляет собой электрический проводник, похожий на проволочную катушку. Рассмотрим катушку из изолированного медного провода, намотанную на сердечник из мягкого железа. Ставим на стол железный гвоздь, надеваем на гвоздь катушку и смотрим, что получится. Теперь мы можем подключить батарею 9 В к клеммам катушки и посмотреть, что произойдет. Катушка работает как по волшебству. Магнит притягивает железные гвозди, поэтому повторите этот эксперимент с большим количеством витков и более мощной батареей. Обратите внимание, как меняется интенсивность. Проводник в виде катушки действует как магнит, а свойство этого проводника называется электромагнитом. Сила электромагнита зависит от количества витков в катушке. Один провод не создает достаточного магнитного поля вокруг проводника, чтобы притянуть железный гвоздь на столе, поэтому он несколько раз наматывает проводник, чтобы создать индукционно-индукционное магнитное поле. Умножая на количество витков, сила наведенного магнитного поля также зависит от величины тока, протекающего через проводник.
Один провод не создает достаточного магнитного поля вокруг проводника, чтобы притянуть железный гвоздь на столе, поэтому он несколько раз наматывает проводник, чтобы создать индукционно-индукционное магнитное поле. Умножая на количество витков, сила наведенного магнитного поля также зависит от величины тока, протекающего через проводник.
Важные факторы для токовой катушки
Существует ряд факторов, от которых зависит сила электромагнетизма.
-
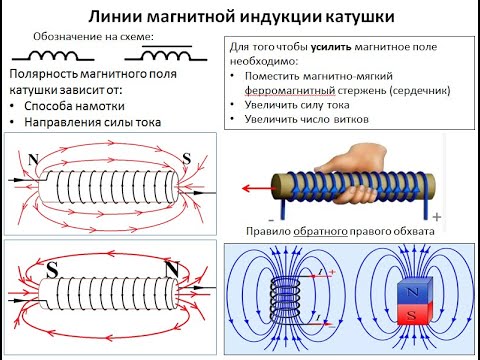
Первым фактором, определяющим силу тока катушки, является количество витков. Чем больше витков, тем больше ток в амперах. Магнитное поле также умножается на количество витков в катушке.
-
Вторым важным фактором является сила тока, протекающего по проводнику. Чем больше электрический ток, тем больше сила катушки тока.
-
Третий фактор – это материал, из которого изготовлен проводник.
 Обычно железо или железосодержащие материалы используются для улучшения электромагнетизма вокруг катушки с током. Кроме того, использование таких сплавов, как алюминий-никель-кобальт, также может создавать сильные магнитные поля.
Обычно железо или железосодержащие материалы используются для улучшения электромагнетизма вокруг катушки с током. Кроме того, использование таких сплавов, как алюминий-никель-кобальт, также может создавать сильные магнитные поля. -
Четвертый и последний фактор, который важен для катушки тока, это температура. Обнаружено, что токонесущая способность улучшается при более низких температурах. Причем самые сильные магниты сделаны из сверхпроводников, охлаждаемых жидким азотом или гелием.
Применение катушки тока
Благодаря своей уникальной способности создавать электромагнетизм, в реальном мире существует множество применений катушки тока.
-
Известно, что токовая катушка используется в качестве дробилки консервных банок. Это приложение основано на электромагнитном поле, которое генерируется, когда банка помещается внутрь катушки, которая затем получает дополнительную энергию, чтобы согнуть и деформировать банку, сжав ее в плоский диск.

-
Катушки тока также широко используются в качестве электромагнитов. Существуют также определенные типы электромагнитов, такие как соленоид, катушка Максвелла, звуковая катушка и катушка размагничивания.
-
Другим распространенным применением токовой катушки являются магнитные краны. Мусор на свалках также содержит большое количество металлов, которые либо разлагаются годами, либо могут быть просто переработаны и использованы повторно. Электромагнит может быть большим помощником здесь. Гигантский электромагнит притягивает и приклеивает все металлические детали к мусору на свалках и свалках. Более того, эти металлические обрезки легко удаляются электромагнитом, когда он обесточен. Эта функция была невозможна с постоянными магнитами, и раньше людям приходилось убирать металлический лом вручную.
Обмотка катушки тока
Понятия электричества и магнетизма пересекаются при изучении физики.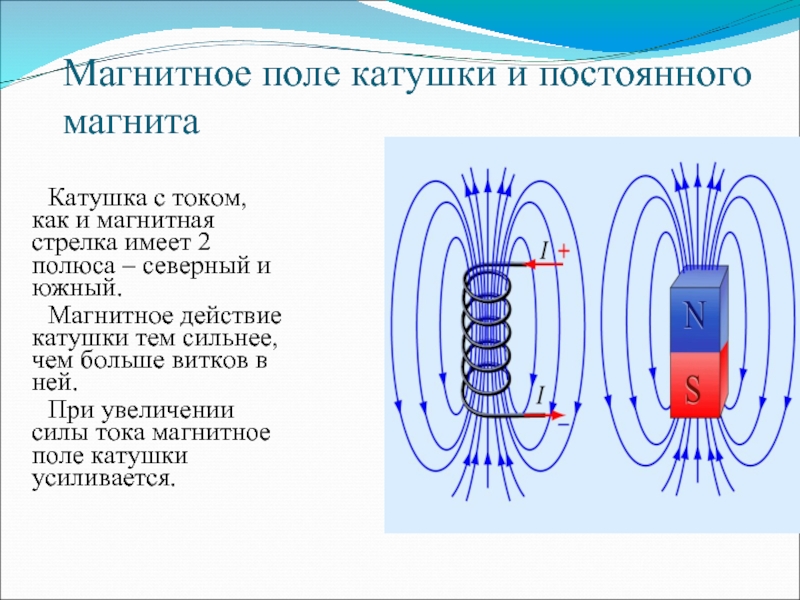 Пример катушки с током объясняет одновременное возникновение двух вышеупомянутых явлений, которые затем называются электромагнетизмом. Электромагнитное поле, создаваемое при прохождении тока через катушку с током, может служить нескольким целям. Некоторыми из этих реальных применений являются электромагниты, консервные дробилки и магнитные краны.
Пример катушки с током объясняет одновременное возникновение двух вышеупомянутых явлений, которые затем называются электромагнетизмом. Электромагнитное поле, создаваемое при прохождении тока через катушку с током, может служить нескольким целям. Некоторыми из этих реальных применений являются электромагниты, консервные дробилки и магнитные краны.
Технические характеристики электрической катушки
Электрическая катушка состоит из сердечника и проволоки, намотанной вокруг сердечника. Некоторые типы электрических катушек не имеют сердечника и просто намотаны обмотками.
-
Катушка для проволоки
Форма и размеры проволоки, используемой в катушке, выбираются для конкретной функции. Индуктивность, рассеяние энергии, диэлектрическая прочность и напряженность магнитного поля являются ключевыми факторами при выборе проводки. Наиболее эффективные рулоны ограничивают материал и объем. Между площадью электрического проводника и площадью обмотки существует зависимость, называемая рабочим циклом. Круглый провод всегда имеет некоторый зазор, который увеличивается за счет количества витков и зазора между слоями, создаваемого изолятором. Коэффициент заполнения всегда меньше 1 и находится в диапазоне от 0,01 до 0,05. Использование прямоугольной, квадратной и плоской проволоки позволяет увеличить коэффициент заполнения.
Между площадью электрического проводника и площадью обмотки существует зависимость, называемая рабочим циклом. Круглый провод всегда имеет некоторый зазор, который увеличивается за счет количества витков и зазора между слоями, создаваемого изолятором. Коэффициент заполнения всегда меньше 1 и находится в диапазоне от 0,01 до 0,05. Использование прямоугольной, квадратной и плоской проволоки позволяет увеличить коэффициент заполнения.
-
Провод катушки
В компании Sag Harbour Industries существует три типа рабочих циклов в зависимости от соотношения между площадью поперечного сечения детали и площадью поперечного сечения катушки. Расчет рабочего цикла колеблется от 0,1 до 0,5 с символическими высокими, средними и низкими рабочими циклами. Затягивание проволоки уменьшает пространство и увеличивает скорость заполнения. Это, в свою очередь, повышает эффективность электрического устройства и улучшает его проводимость. Наилучшей намоткой круглой проволоки является заполнение канавки на 300° ниже периметра катушки верхним слоем проволоки.
Наилучшей намоткой круглой проволоки является заполнение канавки на 300° ниже периметра катушки верхним слоем проволоки.
-
Коэффициент заполнения зазора
Обмотка — это изолированный проводник, используемый для обмена электрической и магнитной энергией. В большинстве случаев провод покрыт тонким слоем меди или алюминия с тонкой многослойной изоляцией, что обычно является первым выбором для большинства электрических катушек при исследовании таких факторов, как химические, физические и механические свойства меди. Медь высокой чистоты используется в высокотемпературных или высокотемпературных системах или двигателях, использующих водород для охлаждения.
-
Оцинкованная проволока
Оцинкованная проволока используется в средах, где условия могут ухудшить или повредить проводку. Оболочка провода бывает золотой, серебряной или никелевой различной толщины и покрыта изоляцией. Гальваника обеспечивает наилучшую защиту в суровых условиях. Покрытие провода значительно улучшает такие свойства, как проводимость.
Гальваника обеспечивает наилучшую защиту в суровых условиях. Покрытие провода значительно улучшает такие свойства, как проводимость.
-
Тип изоляции
В электрических катушках используются различные изоляционные материалы в зависимости от диапазона рабочих температур. Типы материалов включают поливинилхлорид (ПВХ), полиуретан, полиэстер и различные формы полиимида. При выборе изоляционного материала используется полиимид, температура которого достигает 250 °С. В процессе намотки провод нагревается и изоляционный материал прилипает друг к другу.
Изоляция повышает термостойкость и защищает провода. Основной функцией изоляции проводов является предотвращение их соприкосновения с проводом. Это может вызвать короткое замыкание. Каждый тип изоляции имеет различные свойства, включая теплоемкость, толщину и область применения.
-
Полиэстер — Полиэстер обладает высокотемпературными свойствами и очень низкой хрупкостью.
 высокая износостойкость. Отличные свойства намотки, гибкость и устойчивость к нагреву и растворителям. Полиамидное покрытие на полиэстере улучшает свойства термопласта при сминании и текучести.
высокая износостойкость. Отличные свойства намотки, гибкость и устойчивость к нагреву и растворителям. Полиамидное покрытие на полиэстере улучшает свойства термопласта при сминании и текучести.
-
Полиимид — Полиимид является одним из наиболее широко используемых типов изоляции для электромагнитных катушек. Обладает отличными механическими свойствами и может эксплуатироваться при высоких температурах. Полиимиды представляют собой полимеры, состоящие из имидных мономеров с двумя ацильными группами, связанными с азотом. Благодаря механическим и термическим свойствам полиимида он может выдерживать температуры свыше 240 °C, и его использование с электромагнитными катушками расширилось.
Интересные факты
Разница между токовой катушкой и катушкой давления.
Катушка давления также известна как катушка напряжения и обычно используется в ваттметре. Существует заметная разница между катушкой тока и катушкой давления. Катушка тока всегда подключается последовательно. При этом катушка давления подключается параллельно нагрузке. Кроме того, токовая катушка измеряет ток, а катушка давления измеряет напряжение. Обе катушки используются в шкале ваттметра и для измерения тока или напряжения в линиях электропередач.
Существует заметная разница между катушкой тока и катушкой давления. Катушка тока всегда подключается последовательно. При этом катушка давления подключается параллельно нагрузке. Кроме того, токовая катушка измеряет ток, а катушка давления измеряет напряжение. Обе катушки используются в шкале ваттметра и для измерения тока или напряжения в линиях электропередач.
Заключение
Vedantu — это целостная учебная платформа, которая предоставляет экспертные знания по концептуальному обучению, чтобы помочь учащемуся лучше понять. В Vedantu вы можете найти все, что ищете, в одном месте в формате PDF. Эти PDF-файлы легко загружаются и бесплатны. Учащиеся могут внимательно изучить концепции, определения и вопросы и понять концепции, используемые для решения этих вопросов. Это очень поможет учащимся с экзаменационной точки зрения.
О характеристиках катушки
О характеристиках катушкиО характеристиках катушки
Характеристики катушки можно использовать для упрощения настройки магнитостатических и низкочастотных электромагнитных моделей.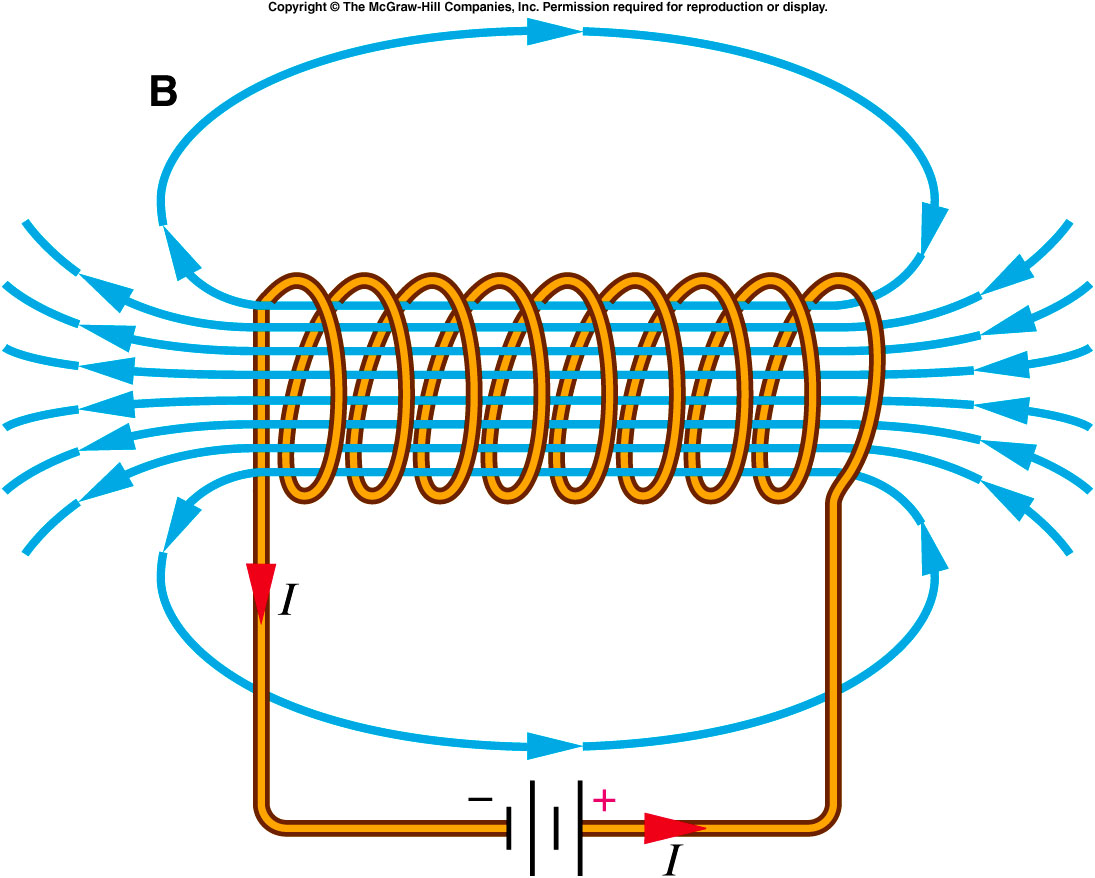 Во многих таких приложениях магнитное поле создается электрическими токами, протекающими в проводящих материалах (например, кабелях, проводах, катушках или соленоидах). Характеристики катушки можно использовать для простого моделирования этих структур и преобразования сосредоточенных величин (токов и напряжений) в распределенные величины (плотности тока и электрические поля). В этом разделе описывается основная функция катушки, которая доступна в интерфейсе магнитных полей, вращающемся оборудовании, магнитном интерфейсе и интерфейсе магнитных и электрических полей.
Во многих таких приложениях магнитное поле создается электрическими токами, протекающими в проводящих материалах (например, кабелях, проводах, катушках или соленоидах). Характеристики катушки можно использовать для простого моделирования этих структур и преобразования сосредоточенных величин (токов и напряжений) в распределенные величины (плотности тока и электрические поля). В этом разделе описывается основная функция катушки, которая доступна в интерфейсе магнитных полей, вращающемся оборудовании, магнитном интерфейсе и интерфейсе магнитных и электрических полей.
Катушка доступна как в качестве домена, так и в качестве граничного объекта. Последнее можно использовать для моделирования плоских катушек, толщина которых незначительна по сравнению с двумя другими размерами.
Функция Coil поддерживает два разных варианта модели проводника, которые отличаются представленной физической системой и деталями моделирования.
|
• |
Параметр Одиночный проводник моделирует один сплошной участок проводящего материала (например, металла), по которому течет ток. |
|
• |
Многовитковый гомогенизированный вариант реализует гомогенизированную модель катушки, состоящей из множества плотно намотанных токопроводящих проводов, разделенных электрическим изолятором. Расчет напряжения и тока катушки выполняется аналогично модели с одним проводником, но при этом также учитываются такие параметры, как количество проводов и площадь поперечного сечения. |
|
Для 2D и 2D осесимметричных геометрий ток, подаваемый катушкой, всегда направлен вне плоскости. Таким образом, емкостной (плоскостной) связью пренебрегают. Для геометрии 3D-моделей направление тока определить непросто. Домены катушки имеют настройки и подузлы для решения этой проблемы. Дополнительную информацию см. в разделе Использование катушек в 3D-моделях. |
|
Выбор несвязанных геометрических объектов с помощью Coil соединяет их параллельно. |
|
Примеры однопроводной катушки см.: .
Примеры гомогенизированной многовитковой катушки см.:
Катушка индуктивности в цепи усилителя: Путь к библиотеке приложений ACDC_Module/Inductive_Devices_and_Coils/inductor_in_circuit |
Какой материал использовать для катушки?
Домен Coil основан на законе Ампера и требует, чтобы свойства материала установили соответствующие определяющие отношения. Для граничного объекта также требуется электрическая проводимость, когда используется модель с одним проводником.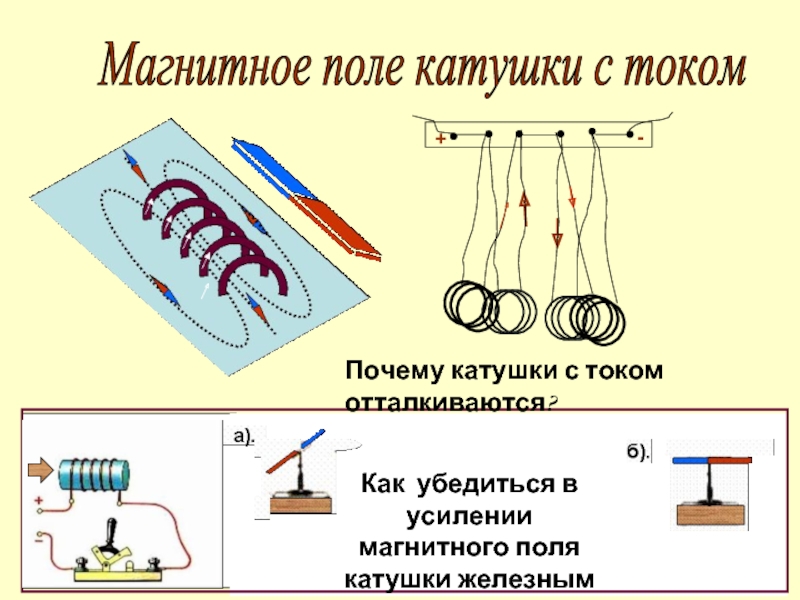 Каков правильный выбор материалов для доменов или границ Coil?
Каков правильный выбор материалов для доменов или границ Coil?
|
• |
При использовании параметра «Один проводник» катушка моделирует твердый проводящий домен (обычно металл). В этом случае следует использовать материальные свойства металла (электрическую проницаемость, магнитную проницаемость и электропроводность). |
|
• |
При использовании гомогенизированного многооборотного варианта предполагается, что ток проводимости (индуцированный ток) протекает только по проводам. Для предотвращения протекания плотности индуцированного тока в домене электропроводность области σ устанавливается равной нулю. Материал, используемый в домене, определяет только определяющие соотношения для электрического поля смещения и плотности магнитного потока. |
Другие характеристики катушки
Две функции катушек, предназначенные для специальных приложений, доступны в интерфейсе «Магнитные и электрические поля» в двухмерных и двухмерных осесимметричных компонентах:
|
• |
Функция RLC Coil Group, которая моделирует катушки, для которых емкостные эффекты между витками катушки и другими частями моделей сравнимы с индуктивными эффектами. |
|
• |
Функция «Одновитковая катушка» для подачи внешнего тока или напряжения в области, где активны функция «Закон Ампера» и «Сохранение тока». |


 Сосредоточенные напряжение и ток катушки соответствуют соответственно интегралу электрического поля по длине катушки и интегралу плотности тока по поперечному сечению. Используйте эту опцию в объекте предметной области для моделирования одиночного провода с непренебрежимо малым поперечным сечением; в граничном элементе его можно использовать для тонкого проводящего слоя, толщина которого пренебрежимо мала (например, в частотной области она мала по отношению к глубине скин-слоя).
Сосредоточенные напряжение и ток катушки соответствуют соответственно интегралу электрического поля по длине катушки и интегралу плотности тока по поперечному сечению. Используйте эту опцию в объекте предметной области для моделирования одиночного провода с непренебрежимо малым поперечным сечением; в граничном элементе его можно использовать для тонкого проводящего слоя, толщина которого пренебрежимо мала (например, в частотной области она мала по отношению к глубине скин-слоя). 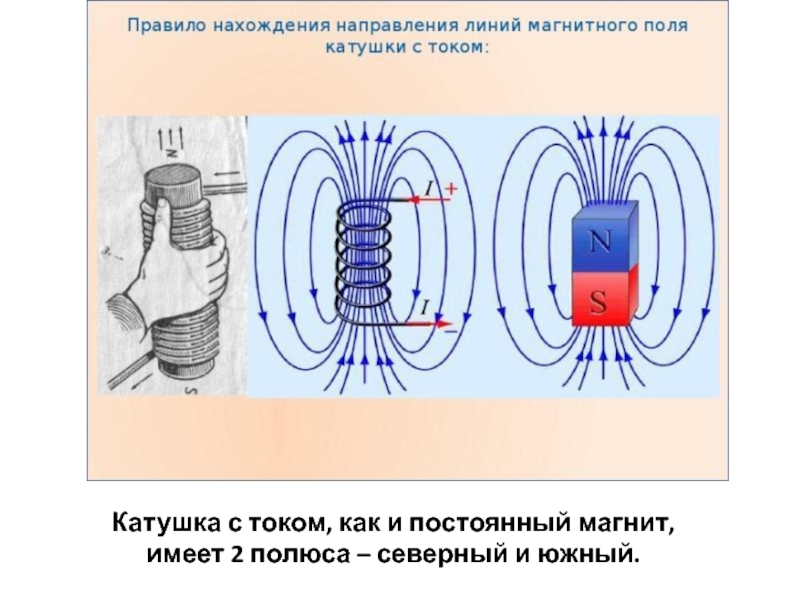 Используйте эту функцию для моделирования катушки, содержащей большое количество проводов, без необходимости моделирования каждого провода по отдельности. Граничный элемент можно использовать, когда провода расположены в тонкой области, толщина которой незначительна. Обратите внимание, что в гомогенизированной модели пренебрегают емкостной связью и скин-эффектом.
Используйте эту функцию для моделирования катушки, содержащей большое количество проводов, без необходимости моделирования каждого провода по отдельности. Граничный элемент можно использовать, когда провода расположены в тонкой области, толщина которой незначительна. Обратите внимание, что в гомогенизированной модели пренебрегают емкостной связью и скин-эффектом. 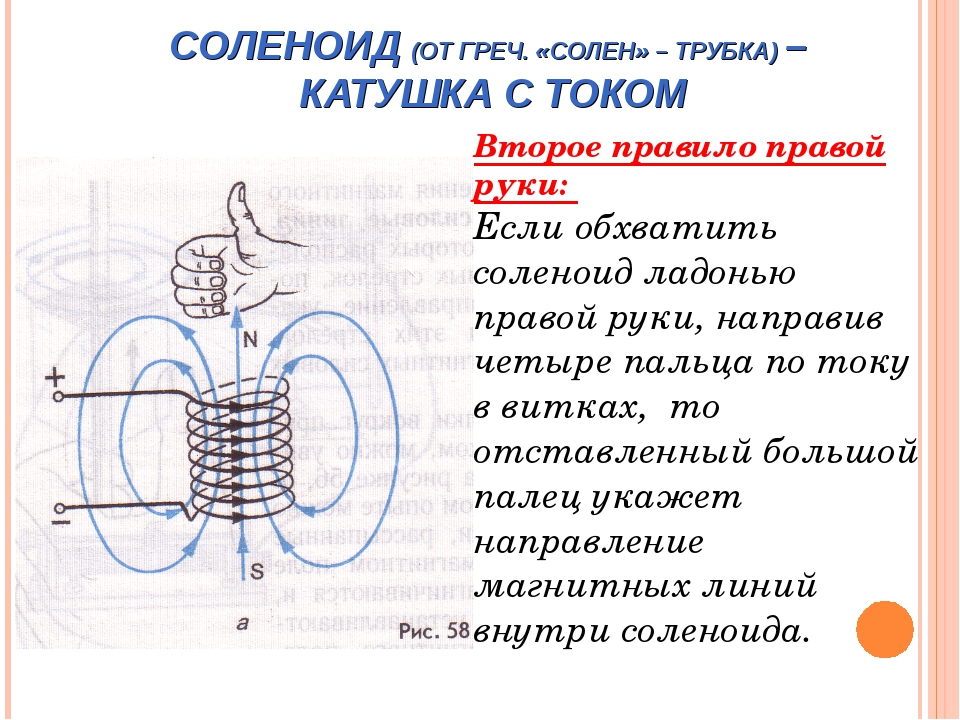

 Поэтому выберите или создайте материал, который обеспечивает определяющие отношения, представляющие всю область катушки, а не только материал, из которого состоят металлические провода.
Поэтому выберите или создайте материал, который обеспечивает определяющие отношения, представляющие всю область катушки, а не только материал, из которого состоят металлические провода. 
