В чем измеряется фаза. Фаза колебаний: измерение, физический смысл и применение в науке и технике

Что такое фаза колебаний. Как измеряется фаза. Какой физический смысл имеет фаза колебаний. Где применяется понятие фазы в науке и технике. Как рассчитать фазу колебаний.

Что такое фаза колебаний и как она определяется

Фаза колебаний — это важная характеристика любого колебательного процесса, которая определяет состояние колеблющейся системы в каждый момент времени. Фаза показывает, в какой точке своего периодического движения находится система.

Математически фаза колебаний определяется как аргумент периодической функции, описывающей колебательный процесс. Для гармонических колебаний, которые описываются синусоидальной или косинусоидальной функцией, фаза имеет вид:

φ = ωt + φ₀

Где:

• ω — циклическая частота колебаний
• t — время
• φ₀ — начальная фаза колебаний

Фаза измеряется в радианах или градусах и меняется от 0 до 2π (или от 0° до 360°) за один полный период колебаний.

Физический смысл фазы колебаний

Фаза колебаний имеет важный физический смысл, так как однозначно определяет состояние колеблющейся системы в любой момент времени. Зная фазу, можно определить:

• Смещение колеблющегося тела от положения равновесия
• Скорость движения тела
• Ускорение тела
• Потенциальную и кинетическую энергию системы

Например, для гармонических колебаний:

• При φ = 0, π, 2π и т.д. — смещение максимально, скорость равна нулю
• При φ = π/2, 3π/2 и т.д. — смещение равно нулю, скорость максимальна

Таким образом, фаза полностью характеризует мгновенное состояние колеблющейся системы.

Как измерить фазу колебаний

Существует несколько способов измерения фазы колебаний:

1. С помощью осциллографа — по сдвигу синусоид на экране
2. Методом фигур Лиссажу — по форме фигуры на экране осциллографа
3. С помощью фазометра — специального прибора для измерения разности фаз
4. Расчетным путем — по временной задержке между сигналами

Для точного измерения фазы используются цифровые фазометры, позволяющие определить разность фаз с точностью до 0.1°.

Применение понятия фазы в науке и технике

Понятие фазы колебаний широко используется во многих областях науки и техники:

• В радиотехнике — для анализа сигналов и работы электронных схем
• В акустике — при изучении звуковых волн
• В оптике — для описания световых волн и интерференции
• В квантовой механике — фаза волновой функции
• В электроэнергетике — фазовые соотношения токов и напряжений
• В системах автоматического управления

Знание фазовых соотношений критически важно для понимания многих физических явлений и работы различных технических устройств.

Расчет и анализ фазы колебаний

Для расчета фазы колебаний используются следующие формулы:

• Фаза гармонических колебаний: φ = ωt + φ₀
• Разность фаз двух колебаний: Δφ = φ₂ — φ₁
• Сдвиг фаз во времени: Δt = Δφ / ω

При анализе фазовых соотношений важно учитывать:

• Начальную фазу колебаний
• Частоту колебаний
• Форму колебаний (гармонические, негармонические)
• Наличие затухания колебаний

Для сложных колебательных систем проводится гармонический анализ с разложением сигнала на гармонические составляющие.

Фазовые соотношения в цепях переменного тока

В цепях переменного тока фазовые соотношения между током и напряжением имеют большое значение:

• На резисторе ток и напряжение совпадают по фазе
• На идеальной катушке индуктивности ток отстает от напряжения на 90°
• На идеальном конденсаторе ток опережает напряжение на 90°

Сдвиг фаз между током и напряжением определяет активную и реактивную мощность в цепи. При сдвиге 90° вся мощность является реактивной.

Фазовая плоскость и фазовые портреты колебаний

Для наглядного представления колебательных процессов используется метод фазовой плоскости. На ней по осям откладываются:

• По оси X — смещение колеблющегося тела
• По оси Y — скорость тела

Траектория движения изображающей точки на фазовой плоскости называется фазовым портретом колебаний. По виду фазового портрета можно судить о характере колебательного процесса:

• Замкнутая кривая — периодические колебания
• Спираль — затухающие колебания
• Расходящаяся спираль — нарастающие колебания

Метод фазовой плоскости позволяет наглядно анализировать сложные колебательные системы.

Интерференция колебаний и фазовые условия

При сложении колебаний одинаковой частоты важную роль играет разность фаз между ними. От нее зависит результат интерференции:

• При разности фаз 0°, 360° и т.д. — усиление колебаний
• При разности фаз 180°, 540° и т.д. — ослабление или гашение колебаний

Условие усиления колебаний при интерференции:

Δφ = 2πn, где n = 0, 1, 2…

Условие ослабления колебаний:

Δφ = π(2n+1), где n = 0, 1, 2…

Эти закономерности широко используются в оптике, акустике и радиотехнике для усиления или подавления сигналов.

Фаза колебаний – кратко что это и в чем измеряется, определение, формула, единица измерения в физике

4.6

Средняя оценка: 4.6

Всего получено оценок: 228.

4.6

Средняя оценка: 4.6

Всего получено оценок: 228.

Любой колебательный процесс, который изучается физикой, имеет ряд параметров, одним из которых является фаза. Кратко рассмотрим, что это такое, каков физический смысл фазы, в чем измеряется фаза, приведем формулу фазы колебаний.

Параметры гармонического колебания

Любой колебательный процесс — это изменения некоторого параметра около среднего значения. Колебания бывают периодическими (маятник) и непериодическими (флаг на ветру). Если построить график колебательного процесса, то среднее значение на нём будет представлено горизонтальной прямой, а значение колеблющегося параметра — кривой, постоянно возвращающейся к среднему. При этом для непериодического колебания возвраты будут хаотичными, а для периодического — строго через одинаковый промежуток времени.

Этот промежуток называется периодом колебания $T$.

Рис. 1. Периодические и непериодические колебания.

Простейшим периодическим колебанием является колебание, которое совершается по закону круговых функций (синуса или косинуса). Оно называется гармоническим. Поскольку в высшей математике доказывается, что любое колебание (в том числе непериодическое) можно представить в виду бесконечной суммы гармонических колебаний, то в первую очередь изучаются именно они. А по определению любое гармоническое колебание можно представить в виде функции:

$$A=A_0sin \Bigg ( {2\pi\over T} t +\varphi_0 \Bigg ),$$

где:

• $A_0$ — амплитуда колебания, максимальное отклонение мгновенного значения функции от нуля;
• $T$ — период колебаний;
• $t$ — свободная переменная — момент времени, для которого находится мгновенное значение амплитуды;
• $\varphi_0$ — начальная фаза колебаний.

Коэффициент ${2\pi\over T}=\omega$ при свободной переменной $t$ называется угловой частотой. Его физический смысл состоит в том, что это угол, проходимый гармонической функцией за единицу времени. Значение выражения ${2\pi\over T} t +\varphi_0=\varphi$, которое является аргументом функции синуса, называется полной фазой колебания.

Рис. 2. Фаза колебания.

Фаза гармонического колебания

Из формулы гармонического колебания можно понять физический смысл фазы. Поскольку аргументом функции $sin(x)$ является угол поворота единичного вектора на координатной плоскости, выраженный в радианах, и его период равен $2\pi$, то фаза — это часть периода колебания, соответствующая моменту $t$. Она еще выражается в радианах и тоже имеет период $2\pi$.

Из формулы также можно видеть, что если $t=0$, то $\varphi=\varphi_0$ (полная фаза в начальный момент равна начальной фазе).

Разность фаз

Для одного колебательного процесса фаза не играет большой роли. В самом деле, если брать разные моменты времени за начальные, мы можем получать любое значение фазы, колебательный процесс при этом никак не изменится.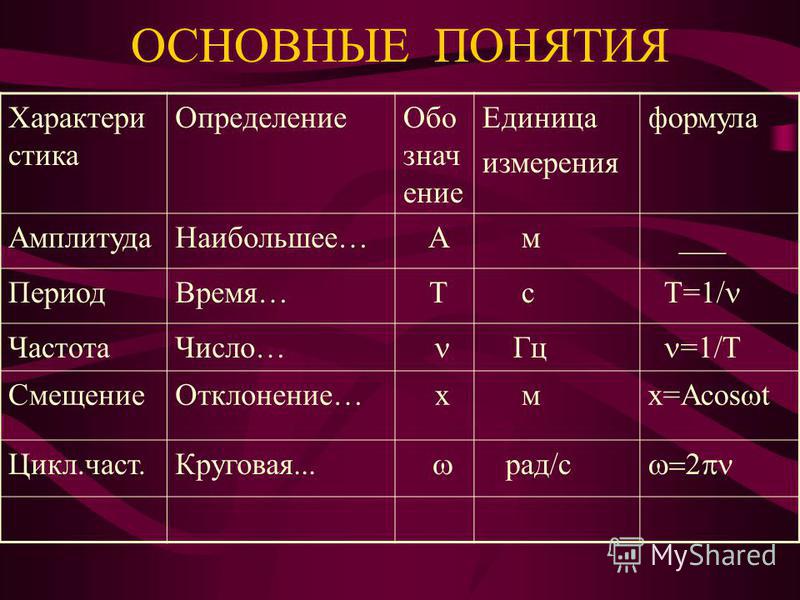 Однако, когда речь идет о нескольких колебательных процессах, то значение фазы существенно возрастает. Именно фазой определяется разница мгновенных значений двух колебаний.

Рис. 3. Графики колебаний с различными фазами.

Если частоты колебаний неодинаковы, то каждый момент времени фазы будут различны, их разность также будет изменяться. Если же частоты колебаний одинаковы, то несмотря на изменение со временем фазы каждого колебания, разность фаз этих двух колебаний будет постоянной. Это может приводить к интересным ситуациям.

Например, если мы возьмем два колебания с одинаковыми амплитудами и частотами, но у первого начальная фаза будет равна нулю, а у второго — $\pi$, то эти два колебания никогда не будут иметь одинаковых ненулевых значений. Более того, если эти колебания сложить, то их сумма всегда будет равна нулю. Говорят, что такие процессы происходят в противофазе.

Что мы узнали?

Фаза колебания — это часть периода колебания, соответствующая текущему моменту времени. Единица измерения фазы — радиана, она имеет период $2\pi$. Особо важное значение имеет разность фаз двух и более колебаний. Если частота этих колебаний одинакова, то и разность фаз будет всегда постоянной.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 228.

---

А какая ваша оценка?

Фаза колебаний, теория и онлайн калькуляторы

Фаза колебаний, теория и онлайн калькуляторы

Определение

Повторяющиеся движения или процессы называют колебаниями.

Колебательные движения имеют много общих свойств и описываются одинаковыми законами, имея разную физическую природу. Самой важной характеристикой колебаний является их многократная повторяемость через одинаковые промежутки времени. Колебания встречаются во множестве разных физических явлений.

Любую систему, которая может совершать колебания описывают некоторым физическим параметром, отклонение которого от равновесия зависит от времени по периодическому или близкому к периодическому закону. При рассмотрении механических колебаний, например, рассматривая колебания пружинного маятника, такой переменной величиной является смещение груза от положения равновесия и его скорость.

Собственными колебаниями называют колебания, в которых колебательную систему вывели из состояния равновесия и предоставили самой себе. Колебания в такой системе совершаются без воздействия на систему внешних сил.

Самым простым для описания видом колебаний являются гармонические колебания. Гармоническими колебаниями называют колебания, при которых переменная величина изменяется во времени по закону синуса или косинуса. Разные процессы, повторяющиеся через равные промежутки времени (периодические процессы) можно представить в виде совокупности наложенных гармонических колебаний.

Пусть происходят гармонические колебания некоторого параметра $s$, тогда они описываются уравнением:

\[s=A{\cos ({\omega }_0t+\varphi )\ }\ \left(1\right),\]

где $A=s_{max}$ — амплитуда колебаний; ${\omega }_0$ — циклическая (круговая) частота колебаний. Величина $s$ лежит в пределах $-A\le s\le $+A.

Определение фазы колебаний

Определение

Весь аргумент периодической функции (у нас косинуса:$\ ({\omega }_0t+\varphi )$), которая описывает процесс колебаний, называют фазой колебаний.

Значение фазы при $t=0$, то есть $\varphi $ — носит название начальной фазы.

Единицей измерения фазы является радиан (рад).

Зная амплитуду колебаний и фазу, используя уравнение (1), определяют механическое состояние системы.

Значения амплитуды и начальной фазы задаются в начальных условиях, то есть они зависят от способа возбуждения колебаний.

Фазы колеблющейся величины, ее скорости и ускорения

Найдем первую производную от параметра, который совершает гармонические колебания:

\[\frac{ds}{dt}=\frac{d}{dt}\left[A{cos \left({\omega }_0t+\varphi \right)\ }\right]=-A{\omega }_0{\sin \left({\omega }_0t+\varphi \right)=\ }A{\omega }_0{cos \left({\omega }_0t+\varphi +\frac{\pi }{2}\right)\left(2\right).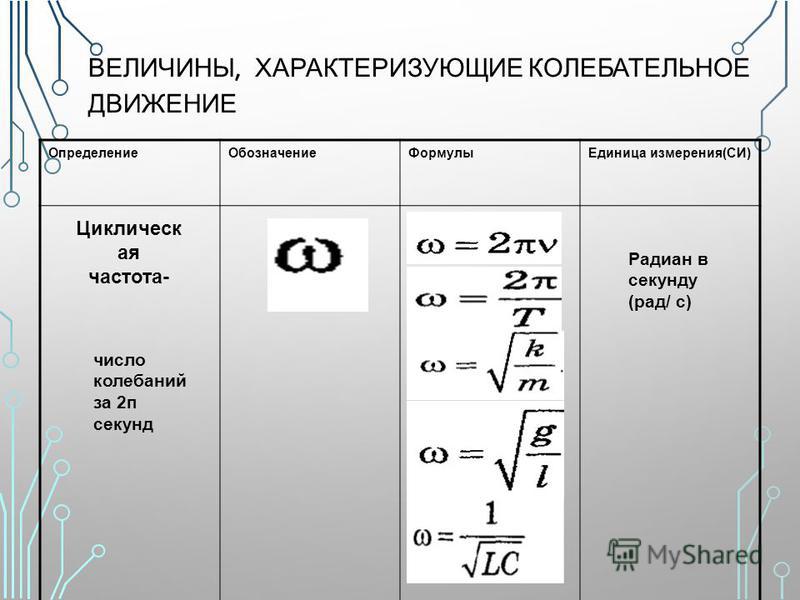 2\left(4\right).\]

Фаза скорости (${\omega }_0t+\varphi +\frac{\pi }{2}$) отличается от фазы ускорения (${\omega }_0t+\varphi +\pi $) на величину равную $\frac{\pi }{2}$. Фаза ускорения отлична от фазы колеблющейся величины на $\pi $. Это значит, что в тот момент времени, когда $s=0$ скорость ее изменения ($\frac{ds}{dt}$) достигает максимального значения. При $s$ равной максимальному отрицательному значению ее ускорение становится наибольшим положительным.

Метод векторных диаграмм

Гармонические колебания можно изображать графически при помощи метода векторных диаграмм (метод вращающейся амплитуды). С этой целью из некоторой точки О на оси X под углом $\varphi $, который равен начальной фазе, откладывают вектор $\overline{A}$. Длина этого вектора равна амплитуде ($A$) колебаний. Если этот вектор приводится во вращение с угловой скоростью ${\omega }_0$, то проекция конца этого вектора перемещается по оси X и принимает значения от $-A$ до $A$, при этом закон колеблющейся величины будет таким, как представляет уравнение (1). Получается, что гармонические колебания можно изобразить при помощи проекции на некоторую ось вектора амплитуды $\overline{A}$, который отложен из произвольной точки этой оси под углом $\varphi $, вращающимся с угловой скоростью ${\omega }_0$ вокруг избранной точки.

Примеры задач на фазу колебаний

Пример 1

Задание. Каким будет отношение кинетической энергии ($E_k$) материальной точки, совершающей колебания вдоль оси X по гармоническому закону, к ее потенциальной энергии ($E_p$), если фаза колебаний равна ${\omega }_0t+\varphi ?$\textit{}

Решение. Уравнение материальной точки, совершающей гармонические колебания, запишем как:

\[x=A{\cos \left({\omega }_0t+\varphi \right)\left(1.1\right).\ }\]

Найдем скорость движения этой точки по оси X:

\[v=\frac{dx}{dt}=-A{\omega }_0{\sin \left({\omega }_0t+\varphi \right)\ }\left(1.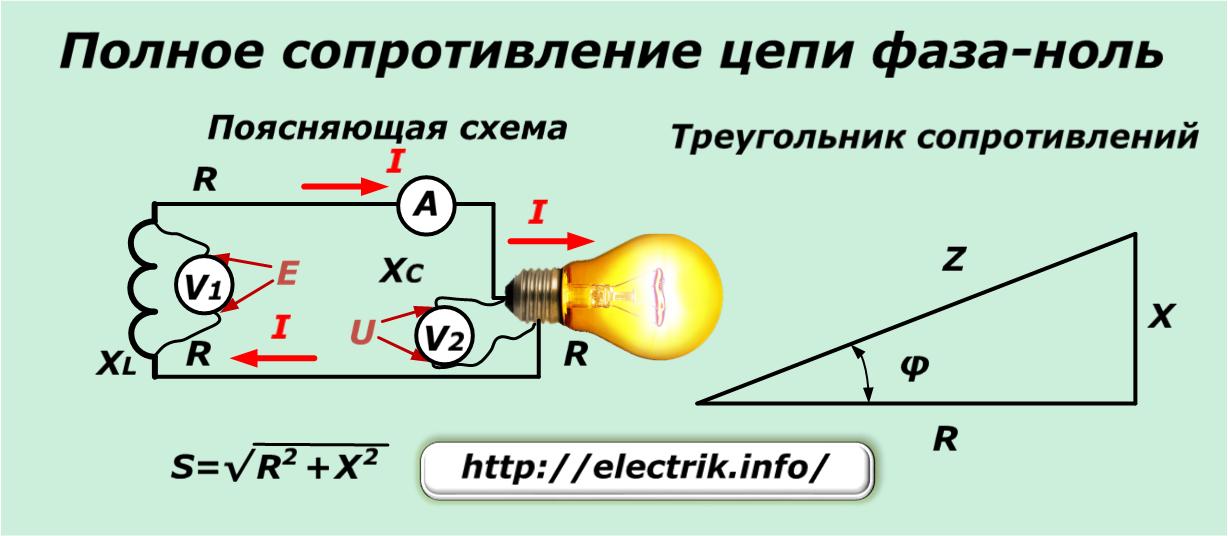 2\left({\omega }_0t+\varphi \right)$

   

Пример 2

Задание. Пружинный маятник (рис.2) совершает колебания, амплитуда которых равна $A$. В момент времени, когда возвращающая сила достигает величины $F$ в первый раз, потенциальная энергия груза на пружине равна $E_p$. Чему равна фаза в этот момент времени. Начальную фазу колебаний принять равной нулю.

Решение. Сила, под воздействием которой пружинный маятник возвращается в положение равновесия — это сила упругости, которая действует на груз со стороны упругой пружины. Считая колебания малыми можно записать закон Гука для возвращающей силы:

\[F=-kx\ \left(2.1\right).\]

где смешение груза из положения равновесия определяете гармоническим законом:

\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\cos ({\omega }_0t)\ }\left(2.2\right),\ }\]

так как по условию $\varphi =0$. 2\left({\omega }_0t\right)}{2kA{cos \left({\omega }_0t\right)\ }}\to \frac{E_p}{F}=-\frac{A}{2}{cos \left({\omega }_0t\right)\to {\omega }_0t\ }=arc{\cos \left(-\frac{2E_p}{FA}\right).\ }\]

Ответ. ${\omega }_0t=arc{\cos \left(-\frac{2E_p}{FA}\right) }$

   

Читать дальше: центр масс.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Что такое фазовая задержка и как ее измерить

Пожалуйста, включите Javascript в вашем браузере.

Сообщение в блоге

« Вернуться к началу блога

Рекомендуемые продукты

Понимание фазового запаздывания важно при сканировании на высоких скоростях с помощью пьезоизгибающих столиков. В этой статье описывается фазовое соотношение между командным сигналом и откликом каскада.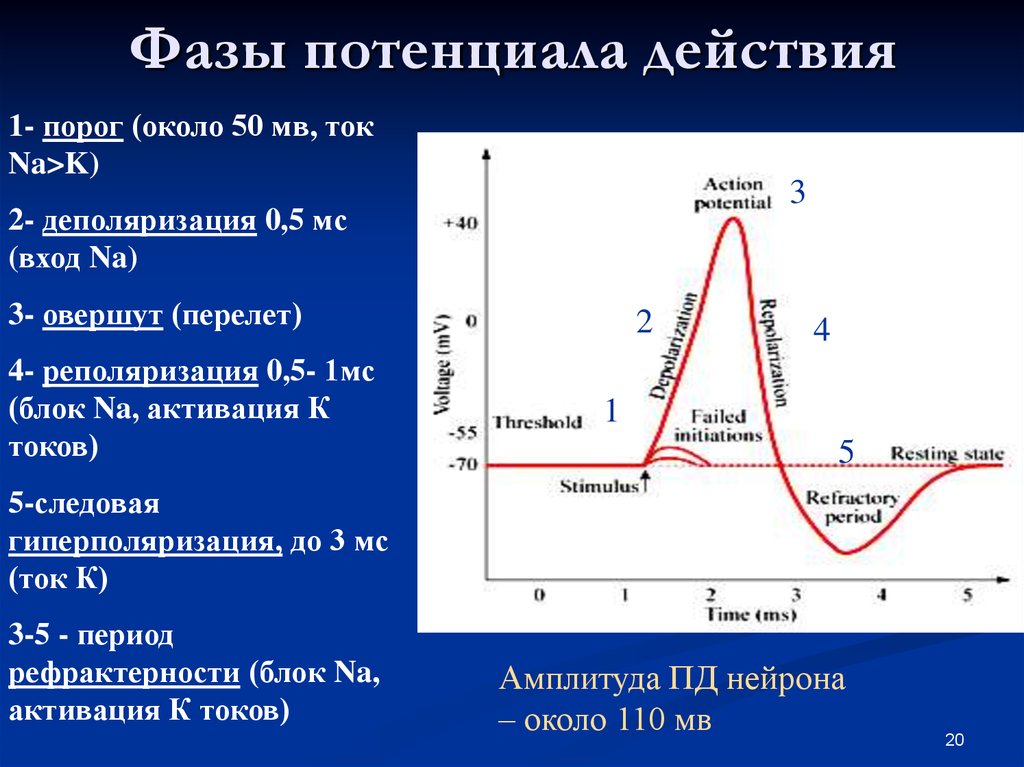 Отклик контролируется с помощью внутреннего (в данном случае емкостного) датчика. Полоса пропускания системы является ключевым элементом фазовой задержки. Используя параметры управления, можно легко получить полосу пропускания примерно 1/3 нагруженного резонанса системы. В целом пропускная способность системы зависит от резонансной частоты каскада, массы нагрузки, конфигурации монтажа, а также множества внешних факторов. Система в следующем примере целенаправленно настроена на полосу пропускания 100 Гц в демонстрационных целях.

Разность фаз обычно измеряется как разница между положительными пересечениями нуля, однако можно использовать любые две аналогичные точки на осциллограмме. Обычно это выражается в градусах (разность пересечений нуля, деленная на общий период волны, умноженная на 360 градусов). На изображениях ниже показаны пары ввода (заданное положение) и вывода (показания датчика) для четырех различных частот сканирования. Данные были получены с помощью программного обеспечения nPControl, входящего в комплект контроллеров серии LC. 400. Обратите внимание, что во время этого тестирования не использовались дополнительные функции управления, и что ошибка отслеживания может быть дополнительно уменьшена с помощью дополнительных функций контроллера. Результаты также перечислены в таблице после изображений.

Измерение фазовой задержки с помощью программного обеспечения nPControl

Синусоида 10 Гц Синусоида 20 Гц Синусоида 50 Гц Синусоида 100 Гц

В следующей таблице перечислены результаты, полученные при анализе четырех различных конфигураций сканирования. Результаты фазового отставания на разных частотах можно увидеть здесь. Также обратите внимание, что по мере увеличения частоты возбуждения отставание по фазе (во времени) остается в основном таким же, как следствие настройки контура управления, но отставание занимает все больше и больше входного периода.

Соответствующие измерения выходной синусоиды

Измерение фазовой задержки с помощью диаграммы Боде

Другой способ измерения фазы — использование результатов преобразования Фурье (БПФ) переходной характеристики системы. Шаг замкнутого контура измеряется, а БПФ рассчитывается программным обеспечением nPoint. Этот каскад настроен примерно на полосу пропускания 100 Гц. На следующих рисунках показаны графики величины и фазы системы.

Величина полосы пропускания 100 Гц График фазы полосы пропускания 100 Гц

На следующих графиках показана переходная характеристика системы с полосой пропускания 100 Гц. На этих графиках можно увидеть величину и фазу. Цифры соответствуют тому, что было видно на реальной осциллограмме.

Величина БПФ 100 Гц Фаза БПФ 100 Гц

Фазовая задержка может быть оценена на основе полосы пропускания системы нанопозиционирования. Хотя существуют функции управления, которые могут улучшить этот отклик, важно понимать, как это влияет на сканирование. Многие приложения, требующие высокоскоростного сканирования, используют выходной сигнал датчика для сопоставления полученных данных с фактическим положением. В этом случае сканирование на более высоких скоростях может происходить без фазового запаздывания, влияющего на результаты. Программное обеспечение nPControl может дать пользователю представление об отставании по фазе, присутствующем в данной системе, чтобы он мог внести необходимые корректировки для своего приложения.

«Back to Blog Home

Категории

• Тематические исследования
• Новости компании
• Focus Customer
• Engineering Insights
• Product Spotlight
• Без категории

Выберите категорию…ВсеПримеры примененияНовости компанииОриентация на клиентаИнженерные исследованияРекомендуемые продуктыОтраслевые перспективыБлог nPointНаш выборПродукт в центре вниманияБез категории

Поиск

---

---

Фазовый угол — Измерение и подробное объяснение

смещение имеет периодическое изменение со временем или расстоянием, или даже с тем и другим. Непрерывный повторяющийся рисунок этой волны помогает определить ее частоту, период и амплитуду. Фазовый угол является одной из важнейших характеристик периодической волны. Это похоже на фразу во многих свойствах. Угловой компонент периодической волны известен как фазовый угол. Это комплексная величина, измеряемая угловыми единицами, такими как радианы или градусы. Представление любой чистой периодической волны выглядит следующим образом.

 

A∠θ, где A — магнитуда, а θ — фазовый угол волны.

 

Как можно измерить фазовый угол?

Измеряется временная задержка между двумя периодическими импульсами. Разность фаз между двумя синусоидальными сигналами одной частоты и без постоянной составляющей можно легко представить, как показано на диаграмме. Как видно, Фазовый угол можно рассматривать как процент временной задержки между двумя периодическими сигналами от периода волны. Эта доля обычно указывается в угловых единицах, при этом полный цикл равен 360 градусам. Например, на рисунке напряжение v1 опережает на 360°/8 или 45° после прохождения нулевого цикла перед вторым напряжением v2.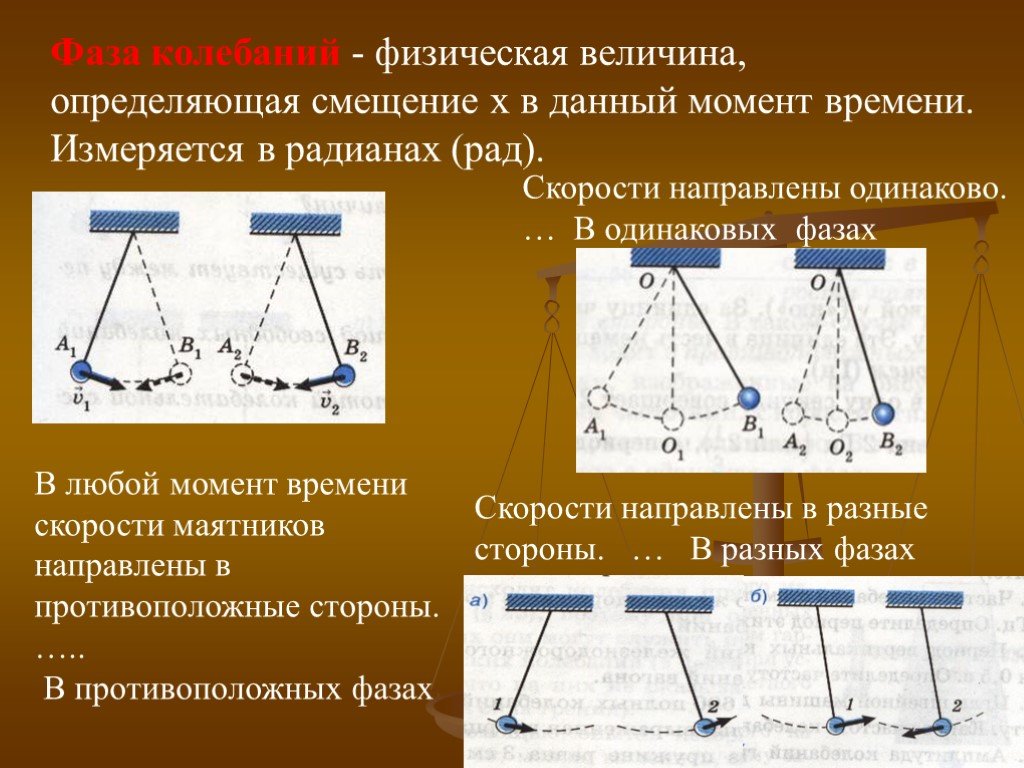 Поскольку фазовый угол часто рассчитывается на основе основной составляющей каждого сигнала, искажение одного или обоих сигналов может привести к ошибкам, величина которых зависит от характера искажения и метода измерения.

 

Большинство современных фазометров основаны на использовании детекторов перехода через нуль. Схема выпрямления (например, усилитель с перегрузкой) используется для расчета времени, за которое каждый сигнал пересекает ось нулевого напряжения, после чего следует высокоскоростной компаратор. Это генерирует триггерный импульс в каждом канале, который используется для управления бистабильным триггером. Бистабильный генератор создает прямоугольную волну с рабочим циклом, пропорциональным разности фаз между двумя входными сигналами. Когда этот сигнал интегрируется с соответствующим фильтром, создается постоянное напряжение, которое аналогично представляет угол сдвига фаз. Затем это напряжение отображается на панельном измерителе (аналоговом или цифровом) с соответствующим масштабированием в градусах или радианах.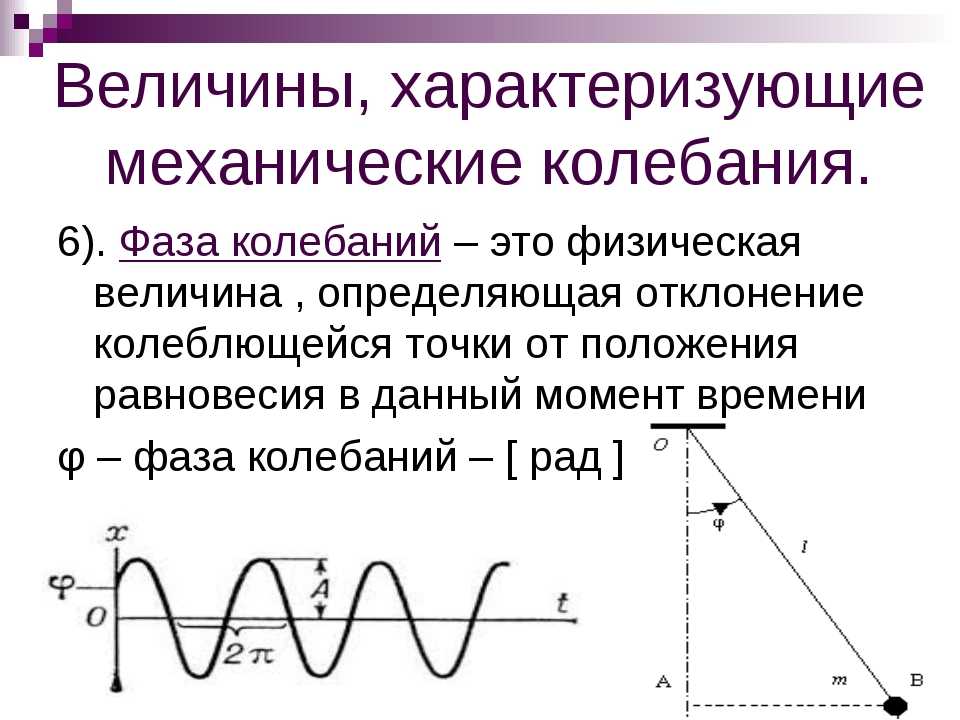 Этот принципиальный прибор может измерять фазовые отклонения с точностью до 0,05° в широком диапазоне амплитуд и частот.

 

Разность фаз

В случае синусоиды разность фаз относится к интервалу времени, на который одна волна отстает или опережает форму волны. Следовательно, это относительное свойство более чем одной формы сигнала. Он представлен греческой буквой «ɸ». В любой форме сигнала полная фаза составляет 360 градусов или 2π радиан. Ведущая фаза означает, что волна опережает другую, имеющую ту же частоту. Ниже приведены определения двух важных терминов в этой концепции.

 

Фазовая квадратура: говорят, что две волны находятся в фазовой квадратуре, если их разность фаз составляет 90 градусов (положительная или отрицательная).

 

Противофаза: если разница фаз между двумя волнами одной частоты составляет 180 градусов (положительная или отрицательная), то они находятся в противофазе друг с другом.

 

Формула фазового угла и ее связь с разностью фаз

Уравнение разности фаз синусоидального сигнала с использованием максимальной амплитуды и напряжения равно

 

A(t)  = Amax X sin(ωt ɸ)

 

Где Amax – амплитуда синусоидальной волны, ωt – угловая скорость, а ɸ – фазовый угол.

 

Если ɸ > 0, то волна имеет положительную фазу фазового угла. Точно так же, если ɸ < 0, то волна имеет отрицательную фазу фазового угла.

 

Измерение фазового угла

Рассмотрим периодическую волну. Согласно определению фазового угла, это не что иное, как угловая составляющая периодической волны. Вы можете измерить его значение, выполнив следующие шаги.

• Чтобы измерить фазовый угол, мы должны измерить количество единиц измерения угла между точкой на волне и опорной точкой. Важно отметить, что эталонная точка может присутствовать на той же волне или на другой волне.

• Проекция вращающегося вектора диаграммы Аргана на вещественную ось является точкой отсчета.

• Фазовый угол точки — это значение точки на оси абсцисс относительно точки на волне.

 

Как правило, мы можем построить волну в любой стандартной системе координат. Фазовый угол также играет решающую роль в электронике из-за наличия различных синусоидальных волн и напряжения. В электронике фазовый угол относится к отставанию или опережению в количестве электрических градусов между формами напряжения и тока в цепи.

 

Фазовые соотношения напряжения и тока в резонансной цепи

Резонансная цепь широко известна как RLC-цепь, состоящая из резистора, катушки индуктивности и конденсатора. Объяснение поведения напряжения и тока цепи RLC по отношению к фазе следующее.

 

Резистор: напряжение и ток в одной фазе резистора. Следовательно, разность фаз между этими величинами в резисторе равна нулю.

 

Конденсатор: ток и напряжение в конденсаторе не совпадают по фазе друг с другом. В этом оборудовании ток опережает напряжение на 90 градусов. Следовательно, разность фаз между ними обоими составляет 90 градусов в конденсаторе.

 

Катушка индуктивности: напряжение и ток не совпадают по фазе друг с другом и в катушке индуктивности. В этом устройстве напряжение опережает ток на 90 градусов. Следовательно, разность фаз между напряжением и током в катушке индуктивности составляет 90 градусов. Эта природа противоположна конденсатору.

 

(изображение скоро будет обновлено)

 

На изображении выше показана разность фаз между напряжением и током в катушке индуктивности.