Волновое сопротивление линии формула. Волновое сопротивление линии передачи: 6 ключевых параметров

Что такое волновое сопротивление линии передачи. Какие параметры влияют на волновое сопротивление. Как рассчитать характеристический импеданс, дифференциальный импеданс и другие важные параметры линии передачи. Почему согласование импедансов важно для высокоскоростных плат.

Что такое волновое сопротивление линии передачи

Волновое сопротивление (характеристический импеданс) линии передачи — это комплексное сопротивление, которое «видит» электромагнитная волна при распространении вдоль однородной линии передачи бесконечной длины. Оно определяется отношением напряжения к току бегущей волны:

Z = U / I

Волновое сопротивление является важнейшей характеристикой линии передачи. От него зависит распространение сигналов, обмен энергией между компонентами и возникновение нежелательных отражений. Поэтому при проектировании высокоскоростных печатных плат крайне важно обеспечить согласование импедансов.

Ключевые параметры волнового сопротивления линии передачи

При анализе линий передачи на печатных платах необходимо учитывать следующие 6 ключевых параметров импеданса:

1. Характеристический импеданс

Это волновое сопротивление одиночной линии передачи в условиях полной изоляции. Обычно обозначается Z0. Для микрополосковой линии на печатной плате характеристический импеданс можно рассчитать по формуле:

Z0 = 87 / √(εr + 1.41) * ln(5.98H / (0.8W + T))

где εr — диэлектрическая проницаемость материала подложки, H — высота над опорным слоем, W — ширина проводника, T — толщина проводника.

2. Дифференциальный импеданс

Это импеданс дифференциальной пары линий передачи. Для связанных микрополосковых линий:

Zdiff = 2Z0 * √(1 — k)

где k — коэффициент связи между линиями. Обычно дифференциальный импеданс стремятся сделать равным 100 Ом.

3. Импеданс четного и нечетного режимов

Это импедансы, возникающие при синфазном (четный режим) и противофазном (нечетный режим) возбуждении связанных линий:

Zeven = Z0 / √(1 — k)

Zodd = Z0 * √(1 + k)

4. Входной импеданс

Импеданс, измеряемый на входе линии передачи конечной длины. Зависит от длины линии и импеданса нагрузки:

Zin = Z0 * (ZL + jZ0*tan(βl)) / (Z0 + jZL*tan(βl))

где ZL — импеданс нагрузки, β — коэффициент фазы, l — длина линии.

Факторы, влияющие на волновое сопротивление печатной платы

На волновое сопротивление линий передачи на печатной плате влияют следующие основные факторы:

• Ширина и толщина сигнального проводника
• Расстояние до опорного слоя (толщина диэлектрика)
• Диэлектрическая проницаемость материала платы
• Расстояние между линиями в дифференциальной паре
• Расстояние до соседних проводников

Контролируя эти параметры при проектировании топологии, можно добиться нужных значений импеданса для высокоскоростных сигнальных линий.

Почему согласование импедансов важно для высокоскоростных плат

Согласование импедансов критически важно для обеспечения целостности сигналов в высокоскоростных платах по следующим причинам:

• Предотвращает отражения сигналов на неоднородностях линии передачи
• Минимизирует перекрестные помехи между сигнальными линиями
• Обеспечивает максимальную передачу мощности от источника к нагрузке
• Снижает уровень электромагнитных излучений от платы
• Позволяет получить качественные высокоскоростные сигналы без искажений

Поэтому при разработке высокоскоростных плат необходимо тщательно контролировать импедансы линий передачи на всем их протяжении.

Методы расчета и контроля волнового сопротивления

Для расчета и контроля волнового сопротивления линий передачи на печатных платах используются следующие основные методы:

1. Аналитические формулы

Существуют приближенные формулы для расчета характеристического импеданса микрополосковых и других типов линий. Они позволяют быстро оценить импеданс на этапе предварительного проектирования.

2. Специализированные калькуляторы

Онлайн-калькуляторы и встроенные в САПР инструменты позволяют более точно рассчитать импеданс с учетом реальной геометрии линии и свойств материалов.

3. Электромагнитное моделирование

Наиболее точные результаты дает полноволновое электромагнитное моделирование топологии в специализированных САПР. Оно позволяет учесть все тонкие эффекты.

4. Измерения тестовых структур

Измерение импеданса на специальных тестовых структурах позволяет верифицировать расчеты и уточнить параметры технологического процесса.

Рекомендации по обеспечению контролируемого импеданса

При проектировании высокоскоростных печатных плат с контролируемым импедансом рекомендуется придерживаться следующих правил:

• Использовать материалы с низким разбросом диэлектрической проницаемости
• Обеспечивать равномерную плотность меди на сигнальных слоях
• Минимизировать изменения ширины сигнальных проводников
• Избегать резких изменений конфигурации опорных слоев
• Использовать сквозные переходные отверстия с контролируемым импедансом
• Применять специальные окончания линий для критичных сигналов

Следование этим рекомендациям позволит получить стабильный импеданс сигнальных линий и обеспечить высокое качество передачи высокоскоростных сигналов.

ВОЛНОВОЕ СОПРОТИВЛЕНИЕ • Большая российская энциклопедия

Авторы: А. П. Сухоруков, К. А. Наугольных, Г. Г. Чёрный, К. В. Показеев

ВОЛНОВО́Е СОПРОТИВЛЕ́НИЕ, ме­ра спо­соб­но­сти сре­ды на­ка­п­ли­вать и пе­ре­да­вать энер­гию бе­гу­щей вол­ны. В. с. ис­поль­зу­ет­ся для ха­рак­те­ри­сти­ки длин­ных ли­ний пе­ре­дач, при опи­са­нии рас­про­стра­не­ния элек­тро­маг­нит­ных и аку­сти­че­ских волн, а так­же в аэ­ро- и гид­ро­ди­на­ми­ке для ха­рак­те­ри­сти­ки со­про­тив­ле­ния сред дви­же­нию те­ла.

В элек­тро- и ра­дио­тех­ни­ке В. с. ли­нии пе­ре­да­чи – от­но­ше­ние на­пря­же­ния к си­ле то­ка в лю­бой точ­ке ли­нии, по ко­то­рой рас­про­стра­ня­ют­ся элек­тро­маг­нит­ные вол­ны; иг­ра­ет роль внут­рен­не­го со­про­тив­ле­ния ли­нии пе­ре­да­чи. В двух­про­вод­ной элек­трич. ли­нии без по­терь ве­ли­чи­на В. с. рав­на $R_в=\sqrt{L/C}$, где $L$ и $C$ – по­гон­ные (на еди­ни­цу дли­ны) ин­дук­тив­ность и ём­кость ли­нии со­от­вет­ст­вен­но.

Ес­ли ли­ния под­клю­че­на к на­груз­ке с им­пе­дан­сом (ком­плекс­ным со­про­тив­ле­ни­ем) $Z_н$, то часть энер­гии от­ра­жа­ет­ся, ко­эф. 2$, где $\Gamma$ – от­но­ше­ние ампли­туд от­ра­жён­ной и па­даю­щей волн. От­ра­же­ние от­сут­ст­ву­ет ($\Gamma = 0$), ес­ли на­груз­ка со­гла­со­ва­на с ли­ни­ей, т. е. их со­про­тив­ле­ния рав­ны друг дру­гу, $Z_н = R_в$. Ес­ли ли­ния на кон­це ра­зомк­ну­та ($Z_н = ∞$) или замк­ну­та ($Z_н = 0$), то воз­ни­ка­ет пол­ное от­ра­же­ние ($\Gamma = 1$). Со­гла­со­ва­ние ли­нии с на­груз­кой име­ет боль­шое зна­че­ние во мно­гих уст­рой­ст­вах (в ча­ст­но­сти, при под­во­де энер­гии к ан­тен­нам).

В элек­тро­ди­на­ми­ке В. с. – от­но­ше­ние на­пря­жён­но­стей элек­три­че­ско­го и маг­нит­но­го по­лей: $Z=\sqrt{\mu /\varepsilon }$, где $μ$ и $ε$  – маг­нит­ная и ди­элек­три­че­ская про­ни­цае­мо­сти. В. с. ва­куу­ма $Z_{вак}=120π ≈ 377 Ом (СИ)$, $Z_{вак} = 1 (СГС)$.

В аку­сти­ке, в слу­чае га­зо­об­раз­ной или жид­кой сре­ды, В. с. – от­но­ше­ние зву­ко­во­го дав­ле­ния $p$ в бе­гу­щей пло­ской вол­не к ко­ле­ба­тель­ной ско­ро­сти $v$ час­тиц сре­ды. В. с. не за­ви­сит от фор­мы вол­ны и вы­ра­жа­ет­ся фор­му­лой: $p/v=ρc$, где $ρ$ – плот­ность сре­ды, $c$ – ско­рость зву­ка. В. с. пред­став­ля­ет со­бой удель­ный им­пе­данс сре­ды для пло­ских волн (см. Им­пе­данс аку­сти­че­ский).

В. с. – важ­ней­шая ха­рак­те­ри­сти­ка сре­ды, оп­ре­де­ляю­щая ус­ло­вия от­ра­же­ния и пре­лом­ле­ния волн на её гра­ни­це. При нор­маль­ном па­де­нии пло­ской вол­ны на пло­скую гра­ни­цу раз­де­ла двух сред ко­эф­фи­ци­ент от­ра­же­ния оп­ре­де­ля­ет­ся толь­ко от­но­ше­ни­ем В. с. этих сред; ес­ли В. с. сред рав­ны, то вол­на про­хо­дит гра­ни­цу без от­ра­же­ния. По­ня­ти­ем В. с. мож­но поль­зо­вать­ся и для твёр­до­го те­ла (для про­доль­ных и по­пе­реч­ных уп­ру­гих волн в не­ог­ра­ни­чен­ном твёр­дом те­ле и для про­доль­ных волн в стерж­не), оп­ре­де­ляя В. с. как от­но­ше­ние со­от­вет­ст­вую­ще­го ме­ха­нич. на­пря­же­ния, взя­то­го с об­рат­ным зна­ком, к ко­ле­ба­тель­ной ско­ро­сти час­тиц сре­ды.

В  га­зо­вой ди­на­ми­ке В. с.– од­на из со­став­ляю­щих си­лы со­про­тив­ле­ния дви­же­нию те­ла в га­зе, воз­ни­каю­щая вслед­ст­вие об­ра­зо­ва­ния удар­ных волн при око­ло- и сверх­зву­ко­вых ско­ро­стях дви­же­ния. В. с. за­ви­сит от гео­мет­рич. ха­рак­те­ри­стик те­ла и от­но­ше­ния ско­ро­сти га­за пе­ред те­лом к ско­ро­сти зву­ка – Ма­ха чис­ла M.

Тер­мин В. с. вве­дён в га­зо­вую ди­на­ми­ку в 1930-х гг. Т. фон Кар­ма­ном толь­ко для сла­бых воз­му­ще­ний не­вяз­ко­го га­за, воз­ни­каю­щих при дви­же­нии в нём с уме­рен­ной сверх­зву­ко­вой ско­ро­стью тон­ких, за­ост­рён­ных у кон­цов тел. При­чи­ной со­про­тив­ле­ния дви­же­нию яв­ля­ет­ся вяз­кость га­за и об­ра­зую­щие­ся вбли­зи те­ла удар­ные вол­ны; лишь в про­стей­ших слу­ча­ях дей­ст­вие обе­их при­чин мож­но счи­тать не­за­ви­си­мым, раз­де­ляя об­щее со­про­тив­ле­ние на вяз­кое и В. с. При более силь­ных воз­му­ще­ни­ях тер­ми­ном «В. с.» обо­зна­ча­ют со­про­тив­ле­ние, свя­зан­ное не с пе­ре­но­сом им­пуль­са от те­ла зву­ко­вы­ми вол­на­ми, как бы­ло в при­бли­жён­ной тео­рии Кар­ма­на (этот пе­ре­нос бы­ст­ро за­ту­ха­ет), а с не­об­ра­ти­мым из­ме­не­ни­ем со­стоя­ния га­за в удар­ных вол­нах. При этом ра­бо­та, со­вер­шае­мая те­лом над га­зом, идёт не толь­ко на со­об­ще­ние га­зу в сле­де за те­лом по­пут­ной ско­ро­сти, но и на его на­гре­ва­ние.

В гид­ро­ди­на­ми­ке В. с.– од­на из со­став­ляю­щих си­лы со­про­тив­ле­ния жид­ко­сти дви­же­нию те­ла. При дви­же­нии те­ла по по­верх­но­сти жид­ко­сти гра­ви­та­ци­он­ные вол­ны об­ра­зу­ют­ся на её по­верх­но­сти, а при дви­же­нии в стра­ти­фи­ци­ро­ван­ной жид­ко­сти – в ок­ру­жаю­щем те­ло про­стран­ст­ве (см. Вол­ны на по­верх­но­сти жид­ко­сти, Внут­рен­ние вол­ны). Ре­зуль­ти­рую­щая вы­зван­ных вол­на­ми сил дав­ле­ния, на­прав­лен­ная про­ти­во­по­лож­но дви­же­нию те­ла, пред­став­ля­ет со­бой си­лу В. с. Ра­бо­та, за­тра­чен­ная при дви­же­нии те­ла на пре­одо­ле­ние В. с., пре­вра­ща­ет­ся в энер­гию волн. Ве­ли­чи­на В. с. за­ви­сит от фор­мы те­ла, осад­ки или глу­би­ны его по­гру­же­ния, ско­ро­сти дви­же­ния, па­ра­мет­ров стра­ти­фи­ка­ции сре­ды, в ко­то­рой дви­жет­ся те­ло, глу­би­ны и ши­ри­ны фар­ва­те­ра. Ма­лые из­ме­не­ния фор­мы суд­на и его ско­ро­сти мо­гут при­во­дить к дос­та­точ­но боль­шим из­ме­не­ни­ям В. с., что учи­ты­ва­ет­ся при кон­ст­руи­ро­ва­нии над­вод­ных и под­вод­ных су­дов и оп­ре­де­ле­нии оп­ти­маль­ных ре­жи­мов дви­же­ния. При од­ной и той же ско­ро­сти дви­же­ния с уд­ли­не­ни­ем кор­пу­са суд­на его В. с. мо­жет как уве­ли­чи­вать­ся, так и умень­шать­ся. Это свя­за­но с ин­тер­фе­рен­ци­ей но­со­вой и кор­мо­вой сис­тем по­пе­реч­ных и, в мень­шей сте­пе­ни, про­доль­ных волн, соз­да­вае­мых дви­жу­щим­ся суд­ном. При бла­го­при­ят­ной ин­тер­фе­рен­ции вол­ны этих сис­тем ос­лаб­ля­ют друг дру­га, сле­до­ва­тель­но, ра­бо­та по соз­да­нию волн, а с ней и В. с., ста­но­вят­ся мень­ше. В од­но­род­ной сре­де при дви­же­нии те­ла под по­верх­но­стью жид­ко­сти B. с. умень­ша­ет­ся с уве­ли­че­ни­ем по­гру­же­ния те­ла.

Волновое сопротивление. Длина волны

Уравнение (26.16) запишем в таком виде:

откуда

Волновое сопротивление линии выражается отношением напряжения к току падающих волн или аналогичным отношением для отраженных волн.

Волновое сопротивление линии можно определять через входные сопротивления при холостом ходе и коротком замыкании

Большой интерес представляет также расстояние, на которое бегущая волна распространяется за время одного периода синусоидально изменяющегося напряжения или тока.

Из формулы (26.17) видно, что фазовая скорость постоянна, поэтому Х = ωt/β

Пусть, пройденный волной за время периода Т= 2π/ω, называется длиной волны

В линии без потерь фазовая скорость

а длина волны

Найдем величину фазовой скорости для воздушной линии без потерь, подставляя в формулу (26.19) Lо и С₀ двухпроводной линии, определенные ранее [см. формулы (7.31), (8.29)]:

Фазовая скорость электромагнитной волны в воздушной линии без потерь равна скорости света.

Если среда, в которой распространяется электромагнитная волна, характеризуется величинами диэлектрической ε, и магнитной проницаемости μ,., то

Принимая v = С0, при частоте f=50 Гц получим длину волны λ = С0/f = 3 10

5/50=6000км.

Режим с согласованной нагрузкой

Режим в линии называется согласованным, если сопротивление нагрузки в конце линии равно ее волновому сопротивлению: Z₂ = Zc. В этом случае U₂ =I₂Zc а уравнения (26.13) записывают так

Учитывая, что

:

уравнения (26.21) можно записать в виде

Предположим, что синусоидальное напряжение в конце линии имеет начальную фазу ψ = 0, тогда U₂ = U_2me^jωt .

Если нагрузка линии активная (R₂ = Zt), ток и напряжение совпадают по фазе: I‘₂ = I_2m e^jωt

Уравненbя напряжения и тока в линии:

В этом случае мгновенные величины напряжения и тока в любом пункте линии на расстоянии х от ее концов определяются уравнениями

Это уравнения бегущих волн напряжения и тока, распространяющихся от начала. к концу линии (прямые волны) с фазовой скоростью ύ = ω/β.

При согласованной нагрузке отраженных воли в линий нет, следовательно, энергия, которую несет падающая электромагнитная волна, полностью поглощается в нагрузке.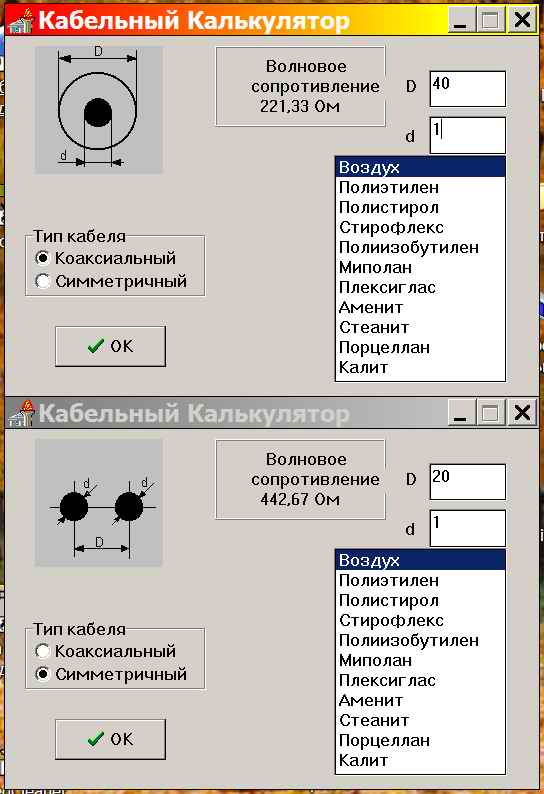

Режим с несогласованной нагрузкой

Нагрузка линии называется несогласованной, если нагрузочное сопротивление в конце линии отличается от волнового сопротивления.

Таким образом, режим в линии без потерь при несогласованной нагрузке можно рассматривать как наложение бегущих и стоячих волн напряжения и тока. Наличие бегущих волн в направлении от начала к концу линии указывает на потребление энергии в нагрузке. Однако потребляется. лишь часть энергии электромагнитной волны, другая часть отражается от конца линии.

Электромагнитная волна с прямоугольным фронтом

В цели с сосредоточенными параметрами переходный процесс начинается и протекает одновременно во всех ее элементах. Особенностью переходного процесса в длинной линии является то, что появившееся в некоторой точке возмущение распространяется по линии с определенной скоростью, поэтому переходный процесс в данном пункте линии начинается тем позднее, чем он дальше от места возмущения.

При переходных процессах в цепях с распределенными параметрами (линии, обмотки электрических машин и трансформаторов) могут возникать электромагнитные волны различной формы.

Качественную сторону явления распространения электромагнитной волны рассмотрим на примере волны с прямоугольным фронтом (рис. 26.7) в линии без потерь.

Для такой волны характерно то, что во всех пунктах линии, расположенных до фронта волны, напряжение и ток равны нулю, а в пунктах линии, расположенных за фронтом волны, напряжение и ток постоянны.

Распространение электромагнитной волны с прямоугольным фронтом означает, что напряжение и ток последовательно в каждом пункте линии изменяются скачком. Как было показано ранее, такое изменение напряжения и тока в цепях,

обладающих емкостью и индуктивностью, невозможно, так как требует источника бесконечно большой мощности. Таких источников не существует, поэтому волну с прямоугольным фронтом нужно рассматривать как некоторую идеализацию реального процесса.

Электрические и магнитные явления в лини — это две стороны единого электромагнитного процесса. Однако эти явления удобно рассматривать отдельно,

т. е. выделять из электромагнитной волны волну напряжения и волну тока.

Литература:

1. Жаворонков М.А., Кузин А.В. Электротехника и электроника. Москва,

АСАДЕМ!А, 2005.

2. Касаткин А.С., Немцов М.В. Электротехника. Москва, Высшая школа, 2003

3. Петленко Б.И. Электротехника и электроника. Москва,

АСАДЕМ!А, 2004.

4. Шихин А.Я. Электротехника. Москва, Высшая школа, 2001

5. Берикашвили В.Ш., Черепанов А.К. Электронная техника. Москва,

АСАДЕМ!А, 2005.

6. Трофимова Т.И., Курс физики. Москва, Высшая школа, 2003

7. Евдокимов.Ф.Е., Теоретические основы электротехники. Москва.

Высшая школа. 1999

Как определить импеданс цепи

Импеданс влияет на то, как сигналы распространяются через плату, как происходит обмен питанием между компонентами и как сигналы просачиваются в нежелательные участки печатной платы. Существует несколько методов определения импеданса цепи, но они не обязательно дают реалистичные результаты, если вы не включите в свои модели соответствующие паразитные элементы.

Полное сопротивление цепи

Полное сопротивление — это характеристика цепи переменного тока, которая может изменяться в зависимости от рабочей частоты. Обычно обозначается Z = R – j/ ωC + jωL, где ω= 2πf.

В чем разница между импедансом и сопротивлением?

Основное различие между сопротивлением и импедансом заключается в том, что сопротивление противодействует протеканию как постоянного, так и переменного тока, тогда как импеданс противодействует переменному току. Импеданс не имеет значения в цепи постоянного тока.

Некоторые ключевые отличия приведены в таблице ниже:

Сопротивление	Импеданс
Обозначается буквой «R»	Обозначается буквой «Z»
Не зависит от частоты питания.	В основном зависит от частоты питания.
Два или более сопротивлений, соединенных последовательно, могут быть добавлены арифметически.	Для суммирования импедансов необходимо выполнить сложение векторов.
Ток через сопротивление всегда совпадает по фазе с напряжением на нем.	Ток и напряжение не совпадают по фазе. Разность фаз зависит от индуктивности или емкости, присутствующих в импедансе.

Почему согласование импеданса важно для печатных плат?

На высоких частотах дорожки на плате действуют как линии передачи с определенными значениями импеданса в каждой точке. Согласование импеданса гарантирует, что он остается постоянным в каждой точке на протяжении всей трассы. Колебания импеданса в линии передачи приводят к отражению сигнала, нарушающему целостность сигнала. Контролируемый импеданс гарантирует, что сигналы не ухудшаются по мере их распространения по трассе.

Факторы, влияющие на контролируемый импеданс

Импеданс дорожки определяется физическими размерами дорожки (шириной и толщиной дорожки), диэлектрической проницаемостью и расстоянием до опорной плоскости (толщиной диэлектрика) материала платы.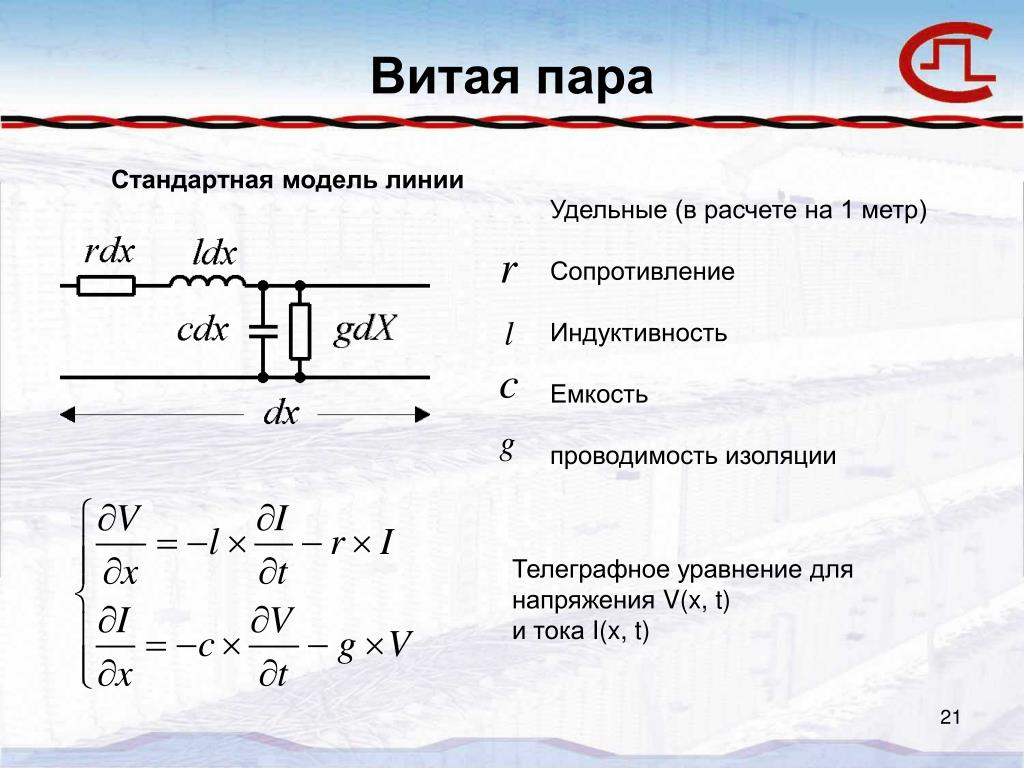 Оно колеблется между 25 и 125 Ом. На импеданс печатной платы влияют следующие факторы:

Факторы, влияющие на импеданс дорожки печатной платы

• Ширина (w) и толщина (T) медной сигнальной дорожки (вверху и внизу)
• Толщина (H) материала сердечника или препрега с обеих сторон медной дорожки
• Диэлектрическая проницаемость (ER)  материала сердечника и препрега
• Расстояние от других медных элементов

Контролируемый импеданс необходим для высокоскоростных приложений, таких как процессоры сигналов, телекоммуникации и радиочастотная передача.

Что определяет полное сопротивление печатной платы?

Полное сопротивление цепи определяется расположением компонентов. Резисторы, конденсаторы и катушки индуктивности являются одними из основных элементов схемы. Резисторы препятствуют протеканию тока, и значение сопротивления не зависит от частоты питания. Принимая во внимание, что конденсаторы и катушки индуктивности имеют реактивное сопротивление, которое зависит от частоты входного сигнала. В идеальном мире реактивное сопротивление конденсатора должно быть обратно пропорционально угловой частоте сигнала. Катушки индуктивности должны иметь реактивное сопротивление, прямо пропорциональное угловой частоте сигнала.

Помимо упомянутых выше параметров, импеданс цепи зависит от подложки печатной платы и внутренних проводящих слоев. Изолятор вместе с внутренними слоями создает паразитную емкость и индуктивность. Эти паразитные элементы вызывают перекрестные помехи и влияют на общий импеданс цепи. Теперь мы увидим несколько факторов, от которых зависит импеданс.

 

Руководство по проектированию с регулируемым импедансом

6 глав — 56 страниц — 60 минут чтения

 

Полное сопротивление линии передачи

Характеристическое сопротивление трассы

Полное сопротивление линии передачи в основном зависит от ее характеристического сопротивления, которое по существу представляет собой полное сопротивление линии передачи в условиях полной изоляции. Другими показателями, используемыми для количественной оценки импеданса линии передачи, являются импедансы четной и нечетной мод. Четный и нечетный режимы — это два основных режима распространения сигнала по парной линии передачи.

Нечетная мода — это импеданс линии передачи, когда две дорожки в паре работают по-разному (сигналы с одинаковой амплитудой и противоположной полярностью).

Четный режим   – это полное сопротивление линии передачи, когда две дорожки в паре работают равномерно (сигналы с одинаковой амплитудой и направлением).

Полное сопротивление линии передачи также зависит от того, как расположены дорожки относительно друг друга. Две дорожки, расположенные близко друг к другу, испытывают индуктивную и емкостную связь. Эта связь обычно приводит к перекрестным помехам, а также изменяет импеданс на каждой линии.

Чтобы понять, как уменьшить несоответствие импеданса на трассе печатной платы, см. как ограничить скачки импеданса и отражение сигнала в линиях передачи печатной платы.

Полное сопротивление сети подачи электроэнергии

На более низких частотах сеть подачи энергии будет иметь емкостное сопротивление, снижающее сопротивление шины питания, которая питает компоненты и ток обратного тока. Физическое разделение между шинами питания, дорожками и внутренними слоями определяет импеданс PDN. По мере увеличения входной частоты растет и импеданс PDN.

Импеданс PDN в зависимости от частоты. Изображение предоставлено: Cadence

Спектр импеданса полезен для определения полосы пропускания с наименьшим импедансом сети подачи энергии. Он должен оставаться ровным по всему рабочему диапазону доски. Для поддержания целостности питания платы решающее значение имеет расположение заземляющего слоя. При перемещении к заземляющему слою сигналы будут проходить по пути с наименьшим реактивным сопротивлением. Путь с наименьшим реактивным сопротивлением должен проходить непосредственно под проводниками на плате.  Это гарантирует, что цепи будут иметь наименьшую индуктивность контура и будут менее восприимчивы к электромагнитным помехам.

Выбор материала платы и укладка

Укладка печатных плат с требованиями к контролируемому импедансу

Укладка — это расположение материалов платы в последовательном порядке. На изображении выше показан 4-слойный стек. L1 и L4 — внешние слои, L2 и L3 — внутренние слои. Как упоминалось ранее, соседние проводящие слои в сборке платы создают паразитный эффект, влияющий на общий импеданс схемы. Несоответствие импеданса, вызванное паразитными помехами, приведет к отражениям на трассе, что в конечном итоге приведет к перекрестным помехам и проблемам с электромагнитными помехами.

Стек также выступает в качестве документации, выражающей ваши ожидания производителям. Отсутствие части информации может затруднить или сделать невозможным для производителей точное понимание требований.

Чтобы узнать об эффективной документации по контролируемому импедансу, см. Указание требований к контролируемому импедансу.

Выбор правильного материала, который наилучшим образом соответствует дизайну, является ключом к тому, чтобы избежать этих обстоятельств. Диэлектрическая проницаемость (Dk) влияет на геометрию трассы с определенным значением импеданса. Содержание смолы и толщина материала являются двумя критическими компонентами, определяющими Dk материала. Она уменьшается по мере увеличения толщины. Это означает, что чем выше содержание смолы, тем ниже значение Dk.

Приведенные ниже указатели помогут разработчикам печатных плат выбрать соответствующие материалы и избежать отклонений в общем значении импеданса.

• Определите правильную толщину слоя: Более тонкие слои уменьшают площадь контура и паразитную индуктивность, увеличивая паразитную емкость. Чтобы найти подходящую толщину слоя, вы можете использовать инструменты моделирования с различными стеками слоев.
• Выбирайте материал с более низкой диэлектрической проницаемостью:  Подложки с более высоким значением Dk создают большую паразитную емкость. Всегда выбирайте подложку с более низким значением Dk, особенно для высокоскоростных применений.
• Избегайте выбора субстрата с очень низким содержанием смолы:  Очень низкое содержание смолы может привести к нехватке смолы, что, в свою очередь, приведет к изменению импеданса.
• Не используйте более трех разных типов препрегов в стопке. : Наличие разных типов препрегов может быть рискованным, так как это увеличивает вероятность больших различий в конечной толщине. При использовании препрегов нескольких типов эффективную диэлектрическую проницаемость композиционного материала следует рассчитывать методом средневзвешенного значения.

 

Руководство по проектированию высокоскоростных печатных плат

8 глав — 115 страниц — 150 минут чтения

 

Полное сопротивление переходных отверстий

Переходные отверстия и сквозные отверстия в многослойной плате будут иметь паразитные значения между соседними проводящими элементами. Индуктивность переходного отверстия будет порядка наногенри и в основном определяется соотношением сторон. Импеданс переходных отверстий обычно составляет от 25 до 35 Ом. Следовательно, существует значительная разница между импедансами переходных отверстий и дорожек (около 50 Ом). Когда сквозное отверстие помещается на проводящие дорожки, возникает шумовая связь, вызывающая разрывы импеданса. Всегда избегайте размещения переходных отверстий между дифференциальными парами, чтобы уменьшить разрывы.

Методы определения полного сопротивления цепи

Полное сопротивление цепи можно рассчитать с помощью следующих методов.

Моделирование схемы

Блок-схема моделирования схемы

Моделирование схемы — это метод, используемый для проверки функциональности конструкции платы перед ее производством. Расчет импеданса теперь включен во многие программы проектирования печатных плат. Одним из основных преимуществ здесь является то, что расчетные параметры импеданса могут быть изменены для выполнения различных симуляций. После проведения моделирования вы можете выбрать лучший дизайн для производства.

Онлайн-калькуляторы

Контролируемый импеданс или параметры трассы можно определить с помощью онлайн-калькуляторов. Хотя они и не такие подробные, как инструменты моделирования, они могут достаточно приблизить вас к тому, где для технологичности требуются лишь минимальные корректировки со стороны вашего контрактного производителя (CM).

Калькулятор импеданса Sierra Circuits использует двумерное численное решение уравнений Максвелла для линий передачи на печатных платах. Он производит данные, которые являются достаточно точными и пригодными для производства печатных плат. Инструмент оценивает параметры трассы, такие как емкость, индуктивность, задержка распространения на единицу длины и эффективная диэлектрическая проницаемость структуры.

В отличие от нашего инструмента импеданса, большинство бесплатных онлайн-калькуляторов импеданса не очень точны, потому что они основаны на эмпирических формулах и не учитывают трапециевидную форму дорожки или влияние многочисленных диэлектрических материалов.

Практический метод

Выполните следующие шаги, чтобы быстро получить приблизительное значение контролируемого импеданса.

Рассчитайте время нарастания кривой по формуле

t _r   = 0,35 / f _max , где f _max  – максимальная рабочая частота.

Теперь рассчитайте максимальную длину трассы,

l = t _r  x 2 дюйма/нс

Волновое сопротивление дорожки можно рассчитать по следующей формуле:

Формула для расчета волнового сопротивления печатной платы trace

Где,

• εr — диэлектрическая проницаемость материала (согласно техпаспорту)
• H — высота трассы над землей
• W — ширина дорожки
• T — толщина следа

Независимо от того, как вы определяете импеданс печатной платы, вам следует сотрудничать с вашим контрактным производителем (CM), поскольку стандарты DFM и доступность материалов будут влиять на производство вашей платы. Дайте нам знать в разделе комментариев, если вам нужна помощь в разработке дизайна с контролируемым импедансом. Мы будем рады помочь вам. Проверьте наши возможности контроля импеданса, чтобы узнать больше о наших услугах.

 

 

Полное сопротивление линии передачи: шесть важных параметров | Блог

Главная Целостность сигнала Импеданс линии передачи: шесть важных параметров

Захария Петерсон

| Создано: 5 апреля 2020 г. &nbsp|&nbsp Обновлено: 25 сентября 2020 г.

При просмотре различных значений полного сопротивления линии передачи характеристическое полное сопротивление и дифференциальное полное сопротивление обычно выделяются как два важных значения, поскольку они обычно указываются в стандартах сигнализации. Однако на самом деле существует шесть значений импеданса линии передачи, которые важны при проектировании печатных плат. Иногда их семь, в зависимости от того, какие учебники или технические статьи вы читаете.

Уравнения характеристического импеданса можно легко найти в ряде статей и учебников, но другие общие значения импеданса линии передачи рассчитать сложнее. Причина этой трудности заключается в том, что она зависит от расположения нескольких линий передачи и силы связи между ними. Другим типичным значением импеданса является входной импеданс, который зависит от длины линии и любого несоответствия импеданса.

Значения импеданса линии передачи

Ниже приведены важные значения импеданса линии передачи, которые необходимо учитывать при проектировании и разводке печатной платы.

Характеристическое сопротивление

Если ввести в Google термин «импеданс линии передачи», наиболее вероятным результатом, который вы увидите на первой странице результатов поиска, будет определение характеристического сопротивления. Большинство разработчиков, вероятно, знакомы с характеристическим импедансом, поскольку он определяется в модели схемы с сосредоточенными параметрами. Эта модель возвращает следующую популярную формулу для волнового сопротивления:

Модель эквивалентной цепи и волновое сопротивление линии передачи.

При достаточно высокой частоте или с достаточно малыми потерями характеристическое сопротивление становится чисто резистивным и приближается к следующему значению:

Характеристическое сопротивление линии передачи в области высоких частот.

Обратите внимание, что здесь не учитывается скин-эффект, применимый к полосе частот до ~1 ГГц для цифровых сигналов. Вы можете получить значения L и C из задержки распространения и волнового сопротивления, используя стандартные формулы для различных геометрий трассы. Затем вы можете использовать эти значения схемы для оптимизации ширины дорожки и индуктивности, а также для минимизации переходного звона.

Характеристическое сопротивление иногда называют «импедансом перенапряжения» и связано с термином «нагрузка импеданса перенапряжения». Этот термин часто используется инженерами по энергосистемам для количественной оценки мощности, передаваемой по линии передачи и наблюдаемой при нагрузке.

Импеданс четного и нечетного режима

Две линии передачи, расположенные достаточно близко друг к другу, испытывают емкостную и индуктивную связь. Эта связь обычно определяет перекрестные помехи, но она также изменяет импеданс сигналов на каждой линии. Когда связанные линии управляются в синфазном режиме (одинаковая величина, одинаковая полярность), импеданс четной моды представляет собой импеданс, воспринимаемый сигналом, проходящим по одной линии передачи в паре. Аналогичное определение применяется, когда линии управляются в дифференциальном режиме (такая же величина, та же полярность):

Значения полного сопротивления четной и нечетной мод для двух связанных линий передачи

Обратите внимание, что значения полного сопротивления линии передачи для четной и нечетной моды определяются параметрами Z для пары связанных линий передачи:

Параметр Z для полного сопротивления линии передачи

Матрица Z (также называемая параметрами импеданса) может быть легко преобразована в S-параметры. Его также можно обобщить на несколько связанных линий передачи с синфазным или дифференциальным управлением. Взгляните на этот PDF-файл для уравнений, необходимых для преобразования Z-параметров или значения характеристического импеданса в S-параметры.

Синфазный и дифференциальный импеданс

Значения импеданса синфазного и дифференциального режима связаны со значениями импеданса четного и нечетного режима. Значения дифференциального импеданса обычно указываются для согласования импеданса дифференциальных пар, а не для импеданса нечетной моды. Полное сопротивление дифференциальной пары зависит от волнового сопротивления и расстояния между каждым концом дифференциальной пары. То же самое относится к импедансу синфазного сигнала, за исключением того, что импеданс синфазного сигнала возникает при возбуждении синфазного сигнала.

Значения импеданса дифференциального и синфазного сигнала.

Физически дифференциальный импеданс — это импеданс, измеренный между двумя соединенными линиями передачи, когда пара управляется в дифференциальном режиме.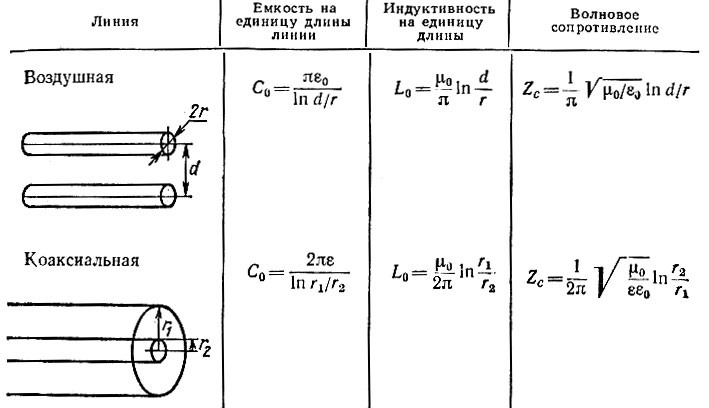 Точно так же импеданс синфазного сигнала представляет собой импеданс, измеренный между двумя соединенными линиями передачи, когда пара работает в синфазном режиме.

Входной импеданс

Это значение импеданса линии передачи важно для согласования импеданса и может использоваться для количественной оценки, когда линия передачи превышает критическую длину; взгляните на связанную статью, чтобы узнать, как можно количественно определить допустимое несоответствие импеданса. Не повторяя всего в этой статье, входное сопротивление зависит от волнового сопротивления, постоянной распространения, импеданса нагрузки и длины линии передачи:

Входное сопротивление линии передачи.

Интегрированные калькуляторы импеданса линии передачи

Здесь представлены несколько уравнений, которые описывают идеальные ситуации, не учитывающие сложную геометрию реальной печатной платы. Тем не менее, они по-прежнему являются хорошей отправной точкой при проектировании линий электропередачи. Модели цепей можно использовать для аппроксимации связи между линиями с точки зрения взаимной емкости и индуктивности, которые затем можно использовать для определения четных/нечетных и общих/дифференциальных значений импеданса.

Если вам нужны очень точные расчеты импеданса линии передачи, вам нужно использовать маршрут со встроенным решателем электромагнитного поля. Это дает вам очень точные результаты импеданса с реальными печатными платами, а также поведение сигнала на нарастающих и спадающих фронтах. Это хорошо объясняет сложные паразитные явления, которые нельзя внести в модели цепей, и позволяет разработчику учитывать геометрию настройки длины по длине связанных линий передачи.

Менеджер стека слоев и инструменты маршрутизации в Altium Designer® включают решатель электромагнитного поля, который создает точный профиль импеданса для обычных геометрий трасс. Это делает маршрутизацию с контролируемым импедансом быстрой и простой, а также обеспечивает точность менее мила при проектировании линий передачи. Теперь вы можете загрузить бесплатную пробную версию Altium Designer и узнать больше о лучших в отрасли инструментах компоновки, моделирования и планирования производства. Поговорите с экспертом Altium сегодня, чтобы узнать больше.

Об авторе

Об авторе

Захария Петерсон имеет обширный технический опыт в научных кругах и промышленности. В настоящее время он предоставляет исследовательские, дизайнерские и маркетинговые услуги компаниям электронной промышленности. До работы в индустрии печатных плат он преподавал в Портлендском государственном университете и проводил исследования в области теории случайных лазеров, материалов и стабильности. Его опыт научных исследований охватывает темы лазеров на наночастицах, электронных и оптоэлектронных полупроводниковых устройств, датчиков окружающей среды и стохастики. Его работы были опубликованы в более чем дюжине рецензируемых журналов и материалов конференций, и он написал более 2000 технических статей по проектированию печатных плат для ряда компаний. Он является членом Общества фотоники IEEE, Общества упаковки электроники IEEE, Американского физического общества и Ассоциации инженеров по печатным схемам (PCEA). Ранее он был членом с правом голоса в Техническом консультативном комитете INCITS по квантовым вычислениям, работающем над техническими стандартами для квантовой электроники, а в настоящее время он работает в рабочей группе IEEE P3186, занимающейся интерфейсом порта, представляющим фотонные сигналы с использованием симуляторов цепей класса SPICE.

Другие материалы Zachariah Peterson

Связанные ресурсы

Основы защиты от электростатического разряда с помощью диодов TVS Узнайте об основах защиты от электростатического разряда с помощью TVS-диодов, зачем они нам нужны и какие ключевые параметры составляют типичный TVS-диод. Читать статью

Все, что вам нужно знать об импедансе Действительно ли сложно понять импеданс? Эксперт Туомас Хейккила расскажет нам об основах импеданса. В этой статье вы узнаете, откуда возник импеданс, который поможет вам при разработке печатных плат или электронных проектов. Читать статью

Протоколы последовательной связи. Часть третья: RS-232 В этой серии статей мы рассмотрим некоторые из различных типов протоколов последовательной связи, доступных для передачи данных между устройствами. В статьях будут рассмотрены несколько наиболее популярных протоколов и стандартов, используемых сегодня, а в конце этой серии мы подытожим и сравним преимущества и недостатки каждого из них. Мы надеемся, что эта информация окажется полезной в следующий раз, когда вам понадобится реализовать шину последовательной связи в Читать статью Протоколы последовательной связи — Введение В этой серии статей мы рассмотрим некоторые из различных типов протоколов последовательной связи, доступных для передачи информации между микроконтроллерами, периферийными устройствами для создания и обработки данных и другими интеллектуальными устройствами. В статьях, которые следуют за этим введением в последовательную связь, будут рассмотрены некоторые из наиболее популярных широко используемых протоколов. В конце этой серии мы обобщим преимущества и Читать статью

Рекомендации по компоновке печатной платы DDR5 и целостности сигнала: что нужно знать разработчикам О выпуске стандарта DDR5 было объявлено в июле 2020 года, примерно через 18 месяцев после объявления о разработке первого модуля оперативной памяти в соответствии с предложенным стандартом. Стандарт допускает пиковые скорости более 5200 млн транзакций в секунду на контакт (сравните это с 3200 млн транзакций в секунду на контакт с DDR4), с номинальной скоростью JEDEC до 6400 млн транзакций в секунду на контакт и пропускной способностью канала, увеличенной до 300 ГБ/канал. с. Спрос на память нового поколения емкостью 8, 16 и 32 ГБ должен снизиться. Читать статью

Что такое функции импульсного отклика? Вы можете получить передаточную функцию из моделирования, но что такое функция импульсного отклика? Узнайте больше в этой статье. Читать статью

Насколько шероховатость медной поверхности печатной платы слишком велика? Когда мы говорим о шероховатости меди, мы всегда говорим об этом так, как будто это вообще что-то плохое. Дело в том, что некоторые схемы всегда будут работать нормально, даже если медь шероховатая. Пока ваши трассы изготавливаются по спецификациям во всех остальных областях, шероховатость трасс может не иметь значения, пока ваша рабочая частота или полоса пропускания достаточно низки.