Что такое закон Ома для переменного тока. Как рассчитать ток в цепи переменного тока. Какие особенности имеет закон Ома для цепей с реактивными элементами. Как определить полное сопротивление цепи переменного тока.
Основные положения закона Ома для переменного тока
Закон Ома для переменного тока является обобщением классического закона Ома для цепей постоянного тока. Он устанавливает связь между действующими значениями напряжения и силы тока в цепи переменного тока с учетом полного сопротивления цепи.
Математически закон Ома для переменного тока выражается формулой:
I = U / Z
где:
- I — действующее значение силы тока в цепи
- U — действующее значение напряжения
- Z — полное сопротивление цепи переменного тока
В отличие от цепей постоянного тока, в переменных цепях кроме активного сопротивления R учитываются также реактивные сопротивления — индуктивное XL и емкостное XC.
Особенности цепей переменного тока с реактивными элементами
В цепях переменного тока, содержащих реактивные элементы (катушки индуктивности и конденсаторы), возникают следующие особенности:
- Появляется сдвиг фаз между током и напряжением
- Возникают реактивные сопротивления XL и XC
- Полное сопротивление цепи Z отличается от активного сопротивления R
Рассмотрим подробнее, как ведут себя различные элементы в цепи переменного тока:
Цепь с активным сопротивлением
В цепи с чисто активным сопротивлением ток и напряжение совпадают по фазе. Закон Ома имеет вид:
I = U / R
Цепь с индуктивностью
В цепи с чисто индуктивным сопротивлением ток отстает по фазе от напряжения на 90°. Индуктивное сопротивление определяется как:
XL = ωL
где ω — угловая частота, L — индуктивность.
Цепь с емкостью
В цепи с чисто емкостным сопротивлением ток опережает напряжение по фазе на 90°. Емкостное сопротивление определяется формулой:
XC = 1 / (ωC)
где C — емкость конденсатора.
Расчет полного сопротивления цепи переменного тока
Полное сопротивление цепи переменного тока Z зависит от активного и реактивных сопротивлений. Для последовательного соединения элементов расчет производится по формуле:
Z = √(R² + (XL — XC)²)
где:
- R — активное сопротивление
- XL — индуктивное сопротивление
- XC — емкостное сопротивление
Для параллельного соединения элементов используется более сложная формула:
1/Z² = 1/R² + 1/(XL — XC)²
Треугольник сопротивлений в цепях переменного тока
Для наглядного представления соотношения между активным, реактивным и полным сопротивлениями используется треугольник сопротивлений:
- Катет 1 — активное сопротивление R
- Катет 2 — реактивное сопротивление X = XL — XC
- Гипотенуза — полное сопротивление Z
Из треугольника сопротивлений можно определить угол сдвига фаз φ между током и напряжением:
tg φ = X / R
Применение закона Ома для анализа цепей переменного тока
Закон Ома для переменного тока позволяет решать следующие задачи:
- Расчет действующего значения тока по известному напряжению и параметрам цепи
- Определение напряжения на участке или элементе цепи
- Нахождение полного сопротивления цепи
- Расчет параметров отдельных элементов (R, L, C)
- Анализ резонансных явлений в цепях переменного тока
При решении задач важно учитывать, что закон Ома для переменного тока применим только к действующим (эффективным) или амплитудным значениям тока и напряжения синусоидальной формы.
Особенности применения закона Ома в различных цепях переменного тока
Рассмотрим применение закона Ома для наиболее распространенных типов цепей переменного тока:
Последовательное соединение R, L и C
Для последовательного соединения активного сопротивления, катушки индуктивности и конденсатора закон Ома имеет вид:
I = U / √(R² + (ωL — 1/(ωC))²)
Параллельное соединение R и L
При параллельном соединении активного и индуктивного сопротивлений:
I = U√((1/R)² + (1/(ωL))²)
Параллельное соединение R и C
Для параллельного соединения активного сопротивления и конденсатора:
I = U√((1/R)² + (ωC)²)
Практическое применение закона Ома для переменного тока
Закон Ома для переменного тока находит широкое применение в электротехнике и энергетике:
- Расчет параметров электрических сетей
- Проектирование трансформаторов и электрических машин
- Анализ работы электронных устройств
- Настройка резонансных контуров в радиотехнике
- Расчет фильтров и цепей коррекции
Понимание закона Ома для переменного тока необходимо для эффективной работы с любыми устройствами и системами, использующими переменный ток.
Закон Ома для переменного тока
Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.
Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).
В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.
Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю
Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.
Тогда, падение напряжения на активном сопротивлении определяется по формуле:
| (1) |
где, U-напряжение на элементе цепи,
I – ток через элемент цепи
R – активное сопротивление элемента
Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:
| (2) |
где, Um-амплитудное значение напряжения на элементе цепи,
Im – амплитудное значение тока через элемент цепи
R – активное сопротивление элемента
В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).
Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением.
Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.
Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.
Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:
| (3) | |
| (4) |
где — UL-падение напряжение на чисто индуктивном сопротивлении ;
UС—падение напряжения на чисто емкостном сопротивлении;
I— значение тока в через реактивное сопротивление;
L— индуктивность реактивного элемента;
C— емкость реактивного элемента;
ω— циклическая частота.
Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.
Приведенные выше формулы являются частными случаями закона Ома для переменного тока.
Следовательно, полный закон Ома для переменного тока будет иметь вид:
| (5) |
Где Z – полное сопротивление цепи переменного тока.
Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.
Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)
Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.
Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:
| (6) |
где —эффективное значение силы тока в А;
U—эффективное значение напряжения в В;
R—активное сопротивление в Ом;
ωL—индуктивное сопротивление в ом.
Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.
В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.
Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.
А закон Ома для такой цепи принимает вид:
| (7) |
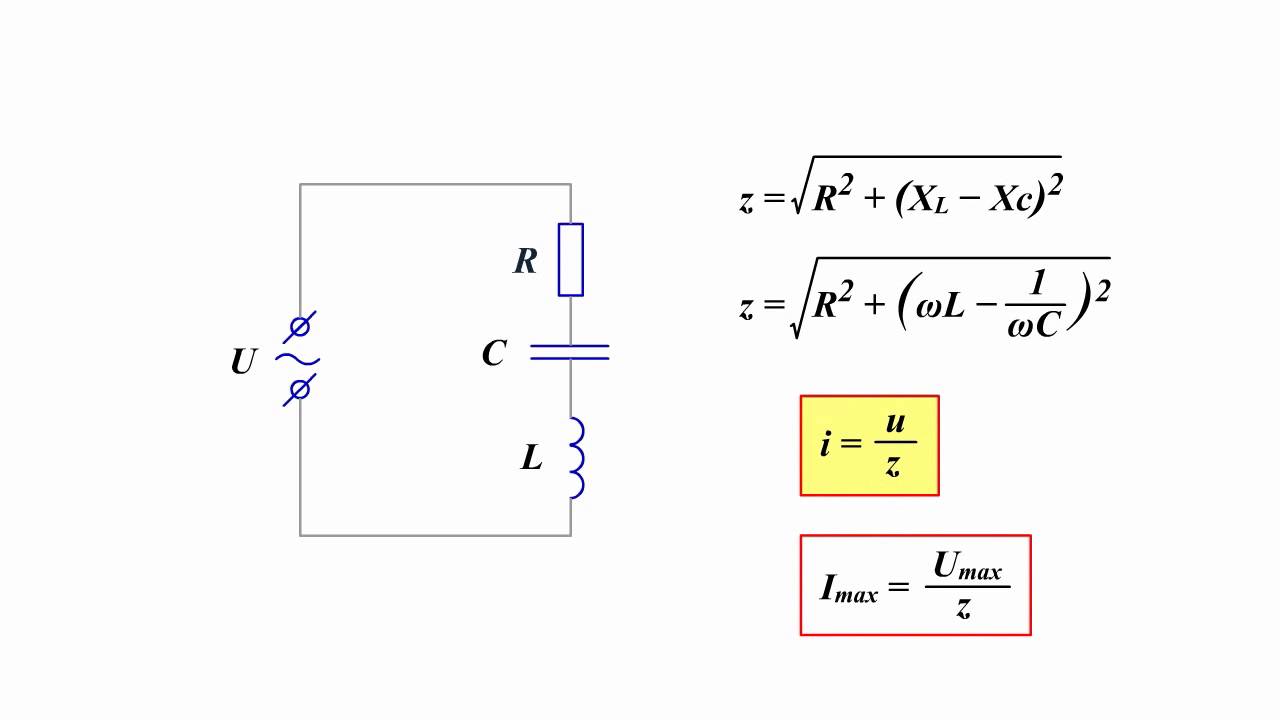
В общем случае, когда цепь содержит все три вида сопротивлений (рис.
6),
Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.
Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:
| (8) |
где I-сила тока в А;
U-напряжение в В;
R-активное сопротивление в Ом;
ωL-индуктивное сопротивление в Ом;
1/ωС-емкостное сопротивление в Ом.
Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.
Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).
Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов.
а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.
Рисунок 8. Эквивалентная схема колебательного контура.
Таким образом закон Ома для переменного тока можно сформулировать следующим образом.
Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Закон Ома для переменного тока
После открытия в 1831 году Фарадеем электромагнитной индукции, появились первые генераторы постоянного, а после и переменного тока. Преимущество последних заключается в том, что переменный ток передается потребителю с меньшими потерями.
При увеличении напряжения в цепи, ток будет увеличиваться аналогично случаю с постоянным током. Но в цепи переменного тока сопротивление оказывается катушкой индуктивности и конденсатор. Основываясь на этом, запишем закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
где
- I [А] – сила тока,
- U [В] – напряжение,
- Z [Ом] – полное сопротивление цепи.
Нужна помощь в продвижении в интернете? Пишите!!! [Нажмите на этот текст или кликните на картинку ниже]
Полное сопротивление цепи
В общем случае полное сопротивление цепи переменного тока (рис. 1) состоит из активного (R [Ом]), индуктивного, и емкостного сопротивлений. Иными словами, ток в цепи переменного тока зависит не только от активного омического сопротивления, но и от величины емкости (C [Ф]) и индуктивности (L [Гн]). Полное сопротивление цепи переменного тока можно вычислить по формуле:
где
- — индуктивное сопротивление, оказываемое переменному току, обусловленное индуктивностью электрической цепи, создается катушкой.
- — емкостное сопротивление, создается конденсатором.
Полное сопротивление цепи переменного тока можно изобразить графически как гипотенузу прямоугольного треугольника, у которого катетами являются активное и индуктивное сопротивления.
Рис.1. Треугольник сопротивлений
Учитывая последние равенства, запишем формулу закона Ома для переменного тока:
– амплитудное значение силы тока.
Рис.2. Последовательная электрическая цепь из R, L, C элементов.
Из опыта можно определить, что в такой цепи колебания тока и напряжения не совпадают по фазе, а разность фаз между этими величинами зависит от индуктивности катушки и емкости конденсатора:
Решение задач:
Цепь переменного тока состоит из последовательно соединенных конденсатора (емкостью С), катушки индуктивности (L) и активного сопротивления (R). На зажимы цепи подается действующее напряжение (U), частота которого ν. Чему равно действующее значение силы тока в цепи?
| Дано: | Решение: |
|---|---|
|
|
Нужна помощь в продвижении в интернете? Пишите!!! [Нажмите на этот текст или кликните на картинку ниже]
Хотя приведенное выше определение включает в себя постоянный ток и напряжение, то же самое определение справедливо и для применения резисторов на переменном токе.
Экспериментально зависимость от этих свойств является прямой для широкого диапазона условий, и сопротивление провода может быть выражено как
Экспериментально зависимость от этих свойств является прямой для широкого диапазона условий, и сопротивление провода может быть выражено как 9омметры 
0808
65
При микроскопическом рассмотрении закона Ома обнаруживается, что он зависит от того факта, что скорость дрейфа зарядов через материал пропорциональна электрическому полю в проводнике. Отношение напряжения к току называется сопротивлением, и если это отношение остается постоянным в широком диапазоне напряжений, материал называется «омическим». Если материал можно охарактеризовать таким сопротивлением, то ток можно спрогнозировать из соотношения:
Независимо от того, какой путь вы выберете в электрической цепи, если вы вернетесь в исходную точку, вы должны измерить одно и то же напряжение, ограничивая чистое изменение по контуру равным нулю. Поскольку напряжение представляет собой электрическую потенциальную энергию на единицу заряда, закон напряжения можно рассматривать как следствие закона сохранения энергии.
