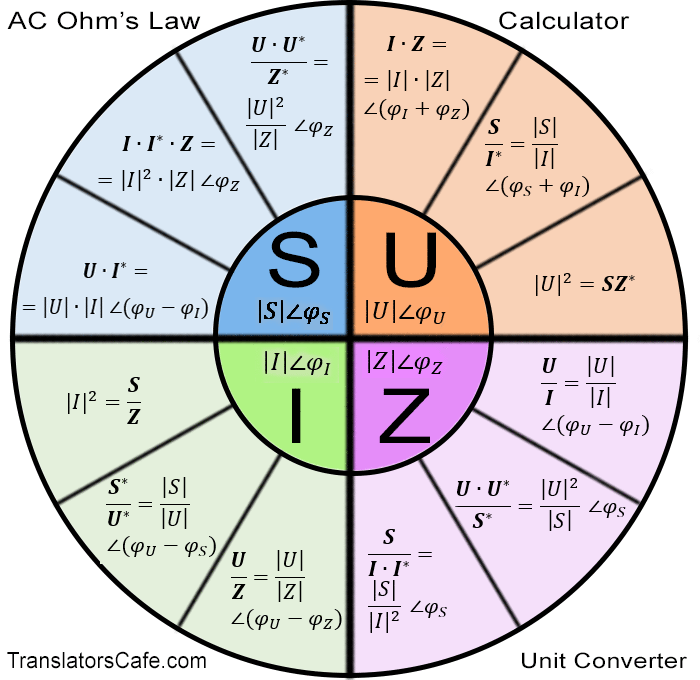
Закон ома калькулятор онлайн. Закон Ома: формулы, расчеты и онлайн калькулятор — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое закон Ома и как его применять. Как рассчитать силу тока, напряжение и сопротивление по закону Ома. Какие формулы использовать для расчетов в цепях постоянного и переменного тока.

Содержание

Что такое закон Ома и для чего он нужен

Закон Ома — это фундаментальный закон электротехники, устанавливающий связь между силой тока, напряжением и сопротивлением в электрической цепи. Он был открыт немецким физиком Георгом Омом в 1826 году.

Закон Ома формулируется следующим образом: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

Математически закон Ома выражается формулой:

I = U / R

где:

I — сила тока (в амперах, А)
U — напряжение (в вольтах, В)
R — сопротивление (в омах, Ом)

Знание закона Ома позволяет рассчитывать параметры электрических цепей и решать различные практические задачи в электротехнике.

Основные формулы закона Ома

Из базовой формулы закона Ома можно вывести следующие формулы для расчета основных электрических величин:

Сила тока: I = U / R
Напряжение: U = I * R
Сопротивление: R = U / I

Кроме того, закон Ома связан с формулой электрической мощности:

P = U * I

где P — мощность (в ваттах, Вт)

Комбинируя эти формулы, можно получить дополнительные выражения для расчета мощности:

P = I^2 * R
P = U^2 / R

Как применять закон Ома на практике

Закон Ома широко применяется при расчетах электрических цепей. Вот несколько типичных задач, которые можно решить с его помощью:

Расчет силы тока в цепи при известных напряжении и сопротивлении
Определение падения напряжения на участке цепи
Подбор сопротивления для ограничения тока до нужного значения
Расчет мощности, выделяемой на нагрузке

При решении задач важно правильно определить исходные данные и выбрать нужную формулу.

Закон Ома для полной цепи

Для полной электрической цепи, содержащей источник ЭДС с внутренним сопротивлением, закон Ома записывается в виде:

I = E / (R + r)

где:

E — электродвижущая сила источника (В)
R — сопротивление внешней цепи (Ом)
r — внутреннее сопротивление источника (Ом)

Эта формула учитывает падение напряжения внутри источника тока и позволяет более точно рассчитывать параметры реальных электрических цепей.

Закон Ома в цепях переменного тока

Для цепей переменного тока закон Ома записывается аналогично, но вместо сопротивления используется полное сопротивление (импеданс):

I = U / Z

где Z — комплексное сопротивление цепи, учитывающее активное сопротивление, индуктивность и емкость.

Импеданс для последовательной RLC-цепи рассчитывается по формуле:

Z = √(R^2 + (ωL — 1/ωC)^2)

где:

R — активное сопротивление
L — индуктивность
C — емкость
ω — угловая частота тока

Онлайн калькулятор закона Ома

Для быстрых расчетов по закону Ома удобно использовать онлайн калькуляторы. Вот простой калькулятор для основных расчетов:

«` import React, { useState } from ‘react’; import { Input, Button, Select } from ‘@/components/ui/input’; const OhmsLawCalculator = () => { const [voltage, setVoltage] = useState(»); const [current, setCurrent] = useState(»); const [resistance, setResistance] = useState(»); const [result, setResult] = useState(»); const calculate = () => { if (voltage && current) { setResistance((voltage / current).toFixed(2)); setResult(`Сопротивление: ${(voltage / current).toFixed(2)} Ом`); } else if (voltage && resistance) { setCurrent((voltage / resistance).toFixed(2)); setResult(`Сила тока: ${(voltage / resistance).toFixed(2)} А`); } else if (current && resistance) { setVoltage((current * resistance).toFixed(2)); setResult(`Напряжение: ${(current * resistance).toFixed(2)} В`); } else { setResult(‘Введите любые два значения для расчета’); } }; return (

Калькулятор закона Ома

setVoltage(e.target.value)} /> setCurrent(e.target.value)} /> setResistance(e.target.value)} />

{result}

); }; export default OhmsLawCalculator; «`

Этот калькулятор позволяет рассчитать любую из трех величин (напряжение, ток, сопротивление) по двум известным.

Примеры решения задач по закону Ома

Рассмотрим несколько типовых задач на применение закона Ома:

Задача 1: Расчет силы тока

К источнику напряжения 12 В подключен резистор сопротивлением 100 Ом. Определить силу тока в цепи.

Решение:

Дано: U = 12 В, R = 100 Ом
Используем формулу: I = U / R
I = 12 В / 100 Ом = 0.12 А

Ответ: сила тока в цепи составляет 0.12 А или 120 мА.

Задача 2: Расчет сопротивления

Через участок цепи с напряжением 220 В протекает ток 5 А. Найти сопротивление участка.

Решение:

Дано: U = 220 В, I = 5 А
Используем формулу: R = U / I
R = 220 В / 5 А = 44 Ом

Ответ: сопротивление участка цепи равно 44 Ом.

Ограничения закона Ома

Несмотря на широкое применение, закон Ома имеет ряд ограничений:

Он справедлив только для металлических проводников
Не применим к нелинейным элементам (диоды, транзисторы)
Нарушается в сверхпроводниках
Не учитывает квантовые эффекты в наноразмерных проводниках

При работе со сложными электронными схемами нужно учитывать эти ограничения и использовать более сложные модели.

Заключение

Закон Ома является фундаментальным законом электротехники, позволяющим рассчитывать основные параметры электрических цепей. Его знание необходимо для понимания работы электрических устройств и проектирования электронных схем.

Несмотря на кажущуюся простоту, закон Ома находит применение в самых разных областях — от бытовой техники до сложных промышленных систем. Умение применять этот закон на практике — важный навык для всех, кто работает с электричеством.

Закон Ома. Калькулятор онлайн.

0
AC		+/-	÷
7	8	9	×
4	5	6	—
1	2	3	+
0	00	,	=

Онлайн калькулятор Закона Ома с решением позволит вычислить силу тока, напряжение и сопротивление, единицы измерения которых, могут включать любые приставки Си, калькулятор автоматически переведет одни единицы в другие и даст подробное решение.

-24]

Вам могут также быть полезны следующие сервисы

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора.

Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка.

Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление.

Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Закон Ома — калькулятор, формулы, расчет

Закон Ома — эмпирический физический закон, определяющий связь электродвижущей силы источника (или электрического напряжения) с силой тока, протекающего в проводнике, и сопротивлением проводника. Установлен Георгом Омом в 1826 году (опубликован в 1827 году) и назван в его честь.

В данном обзоре приведены программы и калькуляторы закона Ома. Также дополнительно приведены основные формулы и методики расчетов.

Закон Ома — калькулятор онлайн

Онлайн калькулятор закона Ома позволяет быстро просчитать основные переменные для участка цепи. Для этого вам необходимо ввести любые два известных значения и нажать «рассчитать».

U Напряжение (В):
P Мощность (Вт):
R Сопротивление (Ом):
I Сила тока (А):

Закон Ома для постоянного тока — расчет, формулы

Закон Ома для постоянного тока определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи.

Закон Ома для полной цепи:

I = ε / (R + r), где:

ε — ЭДС источника напряжения, В;
I — сила тока в цепи, А;
R — сопротивление всех внешних элементов цепи, Ом;
r — внутреннее сопротивление источника напряжения, Ом.

Из закона Ома для полной цепи вытекают следующие следствия:

При r < R сила тока в цепи обратно пропорциональна ее сопротивлению, а сам источник в ряде случаев может быть назван источником напряжения.
При r > R сила тока не зависит от свойств внешней цепи (величины нагрузки), и источник может быть назван источником тока.

Часто выражение I = U / R тоже называют законом Ома. При этом формулировка следующая — сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, где:

I — сила тока, измеряемая в Амперах (A).
U — напряжение, измеряемое в Вольтах (V).
R — сопротивление, измеряемое в Омах (Ом, Ω).

Помимо закона Ома, важнейшим является понятие электрической мощности. Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U):

P = I × U, где:

P — электрическая мощность, измеряемая в Ваттах (W).
I — сила тока, измеряемая в Амперах (A).
U — напряжение, измеряемое в Вольтах (V).

Комбинируя две формулы можно получить зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:

Множительные приставки в системе СИ примирительные к закону Ома:

Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А; 1 миллиампер (1 mA) = 0,001 A; 1 микроампер (1 µA) = 0,000001 A.
Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V; 1 милливольт (1 mV) = 0,001 V; 1 микровольт (1 µV) = 0,000001 V.
Сопротивление, Омы (Ом): 1 мегаом (1 MОм) = 1000000 Ом; 1 килоом (1 kОм) = 1000 Ом.
Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W; 1 киловатт (1 kW) = 1000 W; 1 милливатт (1 mW) = 0,001 W.

Закон Ома для цепи переменного тока

В цепи переменного тока сопротивление кроме активной, может иметь как емкостную, так и индуктивную составляющие. Рассмотрим цепь переменного тока, состоящую из резистора сопротивлением R, конденсатора емкостью C и катушки индуктивностью L, соединенных последовательно.

Мгновенные значения силы тока на всех элементах этой цепи одинаковы, а мгновенное значение напряжения между концами цепи равно алгебраической сумме мгновенных значений напряжений на резисторе (UR), конденсаторе (UC) и катушке индуктивности (UL).

Для того чтобы определить амплитудные (или действующие) значения напряжения и силы тока, а также сдвиг фаз между ними удобно использовать метод векторных диаграмм. Здесь действующие значения всех напряжений и токов рассматриваются как векторы, вращающиеся с угловой скоростью ω, равной циклической частоте переменного тока, а их мгновенные значения определяются проекциями этих векторов на горизонтальную ось. Так как сила тока в цепи одинакова, то построение векторной диаграммы начинается с вектора I¯0, модуль которого равен амплитудному значению силы тока в цепи. Направление этого вектора может быть любым. Зададим угол α = ωt к горизонтали.

Колебания напряжения на активном сопротивлении совпадают по фазе с колебаниями силы тока, поэтому вектор U¯0R, модуль которого равен U0R = I0 × R, совпадает по направлению с вектором I¯0. Сдвиг фаз между колебаниями силы тока и колебаниями напряжения на индуктивном сопротивлении составляет π / 2, причем ток отстает по фазе от напряжения. Поэтому вектор U¯0L, модуль которого равен U0L = I0 × ωL, нужно повернуть относительно вектора I¯0 на угол π / 2 против часовой стрелки. Вектор U¯0C, модуль которого равен I0 / ωC, отстает по фазе от вектора I¯0 на π / 2, поэтому его нужно повернуть на этот угол по часовой стрелке.

Для того чтобы найти напряжение на зажимах цепи, необходимо сложить три вектора: U¯0 = U¯0R + U¯0L + U¯0C.

В первую очередь сложим векторы U¯0R и U¯0C. Модуль этой суммы U’0 = [U¯0R + U¯0C]. Пусть ωL > 1 / ωC, тогда: U’0 = I0 × (ωL — 1 / ωC).

Теперь сложим векторы U¯0R и U’¯0. Модуль вектора U¯0 определяется по теореме Пифагора: U0² = U0R² + (U0L — U0C)² = I0² × R² + I0² × (ωL — 1 / ωC)². Соответственно амплитудное (действующее) значение силы тока в цепи переменного тока равно отношению амплитудного (действующего) значения напряжения на концах этой цепи к его полному сопротивлению (закон Ома для цепи переменного тока):

I0 = U0 / √(R² + (ωL — 1 / ωC)²) = U0 / Z, где:

Z — полное сопротивление (импеданс) цепи.
R — его активное сопротивление.
ωL — 1 / ωC — реактивное сопротивление цепи переменного тока.
ω = 2 × π × γ — циклическая, угловая частота. γ — частота переменного тока.

Импеданс при параллельном подключении Z = 1 / √(1 / R² + 1 / (1 / ωL — ωC)²).

Сдвиг фаз между силой тока и напряжением равен углу φ между векторами U¯0 и I¯0. В соответствии с графиком выше ток отстает от напряжения на угол φ, причем tgφ = (ωL — 1 / ωC) / R.

Для того чтобы определить мгновенные значения напряжений на активном, емкостном и индуктивном сопротивлениях, необходимо спроектировать векторы U¯0R, U¯0L, U¯0C на прямую АВ.

Тогда:

UR = I0 × R × sin × (ωt + φ).
UL = I0 × ωL × sin × (ωt + φ + π / 2).
UC = (I0 / ωС) × sin × (ωt + φ — π / 2).

Если 1 / ωС > ωL, то:

U’0 = I0 × (1 / ωС — ωL).
tgφ = (1 / ωC — ωL) / R, причем ток опережает напряжение по фазе на угол φ.

Таблица удельных сопротивлений проводников

Электрическое сопротивление (ρ) 1 метра провода, сечением 1 мм², при температуре 20 С°:

Материал проводника	Удельное сопротивление ρ, Ом
Серебро	0.015
Медь	0.0175
Золото	0.023
Латунь	0,025. 0,108
Хром	0,027
Алюминий	0.028
Натрий	0.047
Иридий	0.0474
Вольфрам	0. 05
Цинк	0.054
Молибден	0.059
Никель	0.087
Бронза	0,095. 0,1
Железо	0.1
Сталь	0,103. 0,137
Олово	0.12
Свинец	0.22
Никелин (сплав меди, никеля и цинка)	0.42
Манганин (сплав меди, никеля и марганца)	0,43. 0,51
Константан (сплав меди, никеля и алюминия)	0,44-0,52
Копель (медно-никелевый сплав с 43% никеля и 0,5% марганца)	0.5
Титан	0.6
Ртуть	0.94
Хромель (хром 8,7 — 10 %; никель 89 — 91 %; кремний, медь, марганец, кобальт — примеси)	1.01
Нихром (сплав никеля, хрома, железа и марганца)	1,05. 1,4
Фехраль	1,15. 1,35
Висмут	1. 2
Хромаль (Сплав 4,5 — 6% алюминия, 17 — 30% хрома, железа)	1,3. 1,5

Сопротивление проводника определяется по формуле r = (ρ × l) / S, где:

r — сопротивление проводника, Ом.
ρ — удельное сопротивление проводника, Ом.
l — длина проводника, м.
S — сечение проводника, мм².

Закон Ома — скачать программу

Расчеты с использованием закона Ома также можно проводить в офлайн режиме. Для этого необходимо воспользоваться бесплатной программой «КИП и А». В пункте Электрика находится калькулятор, производящий расчеты по закону Ома для цепей постоянного и переменного тока:

Закон Ома, скачать программу бесплатно

Калькулятор закона

Ом онлайн

Введите любые два известных значения, выберите единицы измерения и нажмите «Отправить», чтобы найти остальные.

Напряжение (В):
Выбор напряжения:
(мВ) милливольты (В) вольты (кВ) киловольты
Ток (I):
Выберите ток:
(мА) миллиампер(А) ампер
Сопротивление (R):
Выберите сопротивление:
(Ом) ом (кОм) килоом (мОм) мегаом
Мощность (П):
Выберите мощность:
(Вт) ватт (кВт) киловатт (мВт) мегаватт

Объяснение закона Ома

Закон Ома — это взаимосвязь любой цепи постоянного тока между напряжением, током и сопротивлением, впервые открытая немецким физиком Георгом Омом. В нем говорится, что если ток приложен к проводнику между двумя точками, он прямо пропорционален напряжению в двух точках. Зная любые два значения, вы сможете найти пропущенное значение. Отличный способ запомнить формулу — использовать треугольник Омов, где напряжение находится вверху, а ток и сопротивление — внизу слева и справа.

Треугольник Ом

Найти напряжение

V = I x R

Чтобы найти напряжение с помощью треугольника, вам нужно знать ток (I) и сопротивление (R). Умножьте I X R, чтобы найти напряжение

Формула: В = I x R
Пример: 2A x 20 Ом; = 40 В

Чтобы найти ток

I = V / R

Чтобы найти ток с помощью треугольника, вам нужно знать напряжение (V) и сопротивление (R). Разделите V на R, чтобы найти текущие

Формула: I = V / R
Пример: 40 В / 20 Ом; = 2A

Чтобы найти сопротивление

R = V / I

Чтобы найти сопротивление с помощью треугольника, вам нужно знать напряжение (V) и ток (I).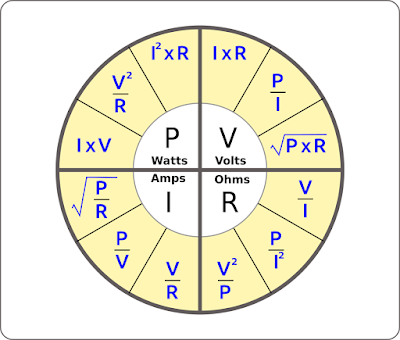 Разделите V на I, чтобы найти сопротивление.

Обычно буква (V) используется для обозначения напряжения, (I) используется для обозначения тока и (R) используется для обозначения сопротивления.

Электрическая мощность Объяснение

Электрическая мощность (P) или ватты — это скорость, с которой энергия поглощается или вырабатывается в цепи. Энергия вырабатывается многими источниками, такими как генераторы, батареи, солнечные, ветряные и другие источники. Затем электроэнергия подается в дома и на предприятия. Применяются те же принципы, что и раньше. Если вы знаете два значения, вы можете решить для других.

Треугольник силы

Найти силу

Р = I х В

Чтобы найти мощность с помощью треугольника, вам нужно знать ток (I) и напряжение (V). Умножьте I X V, чтобы найти мощность

Формула: P = I x V
Пример: 2 A x 40 В = 80 Вт

Чтобы найти ток

I = P / V

Чтобы найти ток с помощью треугольника, вам нужно знать мощность (P) и напряжение (V). Разделите P на V, чтобы найти текущий

Формула: I = P / V
Пример: 80 Вт / 40 В = 2 А

Найти напряжение

V = P / I

Чтобы найти напряжение с помощью треугольника, вам нужно знать мощность (V) и ток (I). Разделите P на I, чтобы найти напряжение

Формула: В = P / I
Пример: 80 Вт / 2 А = 40 В

Калькулятор закона

Ом — сопротивление, напряжение и ток

Рассчитать объем

Сопротивление (Ом)

Ток I(А)

Напряжение В

Рассчитать ток

Сопротивление (Ом)

Напряжение (В)

Ток I(А)

Рассчитать сопротивление

Напряжение (В)

Ток I(А)

Сопротивление (Ом)

Оставьте свой отзыв!

Худший Бедный Средний Хороший Супер

Содержание:

1	Калькулятор закона Ома
2	Как пользоваться калькулятором закона Ома?
3	Что такое закон Ома?
4	Уравнение закона Ома
5	Как рассчитать напряжение?
6	Как рассчитать сопротивление?
7	Как рассчитать ток?

Калькулятор закона Ома

Калькулятор закона Ома — это онлайн-инструмент, который вычисляет следующие величины в цепи.
•   Сопротивление
•   Напряжение
•   Ток
Если известны два значения, третье значение можно найти с помощью этого калькулятора сопротивления.
В этом посте мы обсудим закон Ома, его формулу, как найти ток, напряжение и сопротивление без использования калькулятора спирали.

Как пользоваться калькулятором закона Ома?

Чтобы использовать калькулятор закона Ома, выполните следующие действия.
•   Введите сопротивление и ток для расчета напряжения.
•   Введите сопротивление и напряжение для расчета тока.
•   Введите напряжение и ток для расчета сопротивления.
Вам не нужно нажимать какую-либо кнопку, чтобы найти напряжение с помощью калькулятора омов, потому что он вычисляет значения в режиме реального времени.

Что такое закон Ома?

Закон Ома является одним из самых основных и важных законов электрических и электронных цепей.
Закон Ома гласит, что ток, протекающий в цепи, прямо пропорционален разности потенциалов и обратно пропорционален сопротивлению цепи.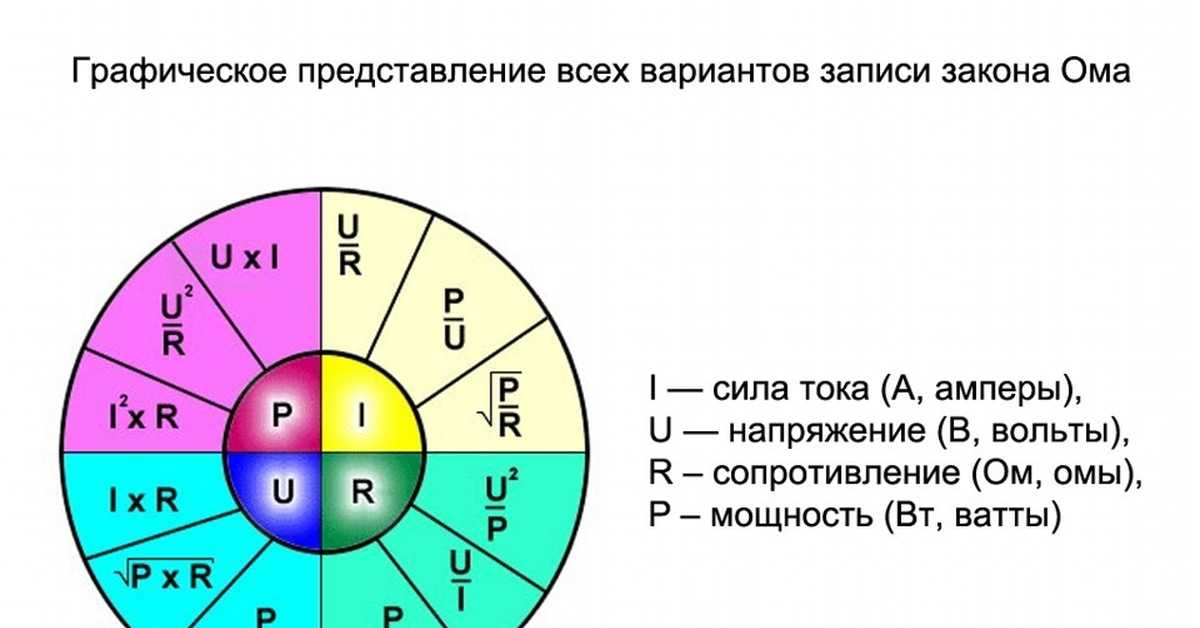 Символ Закона Ома обозначается буквой Ω.

Уравнение закона Ома

Формулу закона Ома можно выразить математически:
В = IR
В этом уравнении:
В = напряжение, выраженное в вольтах
I = ток, выраженный в амперах
R = сопротивление, выраженное в омах

Треугольник закона Ома

Чтобы запомнить формулы, можно использовать треугольную форму для представления формулы напряжения, сопротивления и силы тока. Это иногда называют треугольником закона Ома.
Закройте неизвестную величину и оцените уравнение, используя оставшиеся величины.

Колесо закона Ома

На приведенной ниже схеме закона Ома представлены отношения между P, R, V и I в законе Ома.

Как рассчитать напряжение?

Хотите знать, что такое напряжение? Напряжение есть произведение силы тока и сопротивления.
Закон Ома служит алгебраической формулой для измерения напряжения (разности потенциалов) при наличии сопротивления и тока.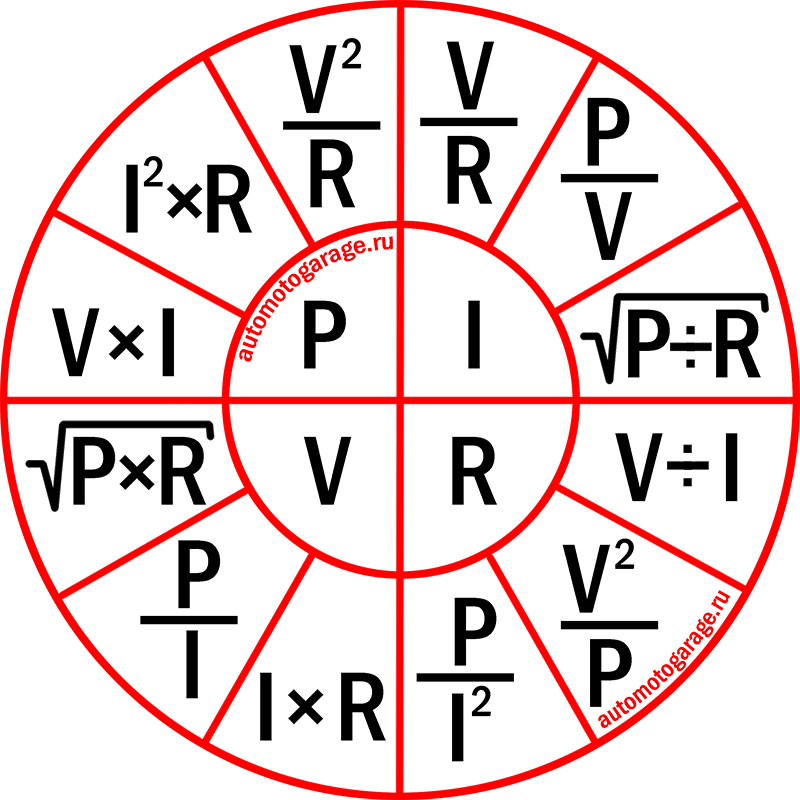
Пример:
Предположим, что в проводе есть ток 2 ампера и сопротивление 200 Ом. Рассчитать напряжение, используя эти две величины?
Решение:
Шаг 1: Прежде всего, определите значения.
I = 2 А
R = 200 Ом
Шаг 2: Запишите уравнение Ома.
V = IR
Шаг 3: Подставьте значения в уравнение и решите.
В = 2 × 200 = 400
В = 400 вольт

Как рассчитать сопротивление?

Пример:
Предположим, в цепи есть ток 3,5 ампера и напряжение 32 вольта. Рассчитать сопротивление, используя данные величины?
Решение:
Шаг 1: Сначала мы определим значения.
I = 3,5 ампера
V = 32 вольта
Шаг 2: Запишите уравнение Ома.
В = IR
Шаг 3: Подставьте значения в формулу сопротивления.
В = IR  R = В/I
R = 32/3,5
R = 9,14 Ом

Как рассчитать ток?

Пример:
Рассчитайте силу тока в амперах при сопротивлении цепи 20 Ом и разности потенциалов 40 В.

Что такое закон Ома и для чего он нужен

Основные формулы закона Ома

Как применять закон Ома на практике

Закон Ома для полной цепи

Закон Ома в цепях переменного тока

Онлайн калькулятор закона Ома

Калькулятор закона Ома

Примеры решения задач по закону Ома

Задача 1: Расчет силы тока

Задача 2: Расчет сопротивления

Ограничения закона Ома

Заключение

Закон Ома. Калькулятор онлайн.

Закон Ома — калькулятор, формулы, расчет

Закон Ома — калькулятор онлайн

Закон Ома для постоянного тока — расчет, формулы

Закон Ома для цепи переменного тока

Таблица удельных сопротивлений проводников

Закон Ома — скачать программу

Ом онлайн

Введите любые два известных значения, выберите единицы измерения и нажмите «Отправить», чтобы найти остальные.

Объяснение закона Ома

Треугольник Ом

Найти напряжение

Чтобы найти ток

Чтобы найти сопротивление

Электрическая мощность Объяснение

Треугольник силы

Найти силу

Чтобы найти ток

Найти напряжение

Ом — сопротивление, напряжение и ток

Оставьте свой отзыв!

Калькулятор закона Ома

Как пользоваться калькулятором закона Ома?

Что такое закон Ома?

Уравнение закона Ома

Треугольник закона Ома

Колесо закона Ома

Как рассчитать напряжение?

Как рассчитать сопротивление?

Как рассчитать ток?

Похожие записи

Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

Новорожденный какает слизью: причины появления слизи в кале грудничка

Гемангиома у новорожденных: причины, виды, лечение и профилактика

Добавить комментарий Отменить ответ