Закон ома сопротивление. Закон Ома и электрическое сопротивление: от теории к практике

Как возникает электрическое сопротивление. Почему закон Ома линеен. Как применять закон Ома на практике. Какие факторы влияют на сопротивление проводников. Как моделировать цепи с помощью симуляторов.

Природа электрического сопротивления

Электрическое сопротивление возникает из-за столкновений электронов с атомами проводника при их движении под действием электрического поля. При каждом столкновении электроны теряют часть своей кинетической энергии, которая превращается в тепло. Чтобы поддерживать постоянную среднюю скорость движения электронов (электрический ток), необходимо постоянно добавлять энергию для компенсации потерь при столкновениях.

Это явление аналогично сопротивлению воздуха для движущихся тел или вязкому трению в жидкостях. Во всех этих случаях для поддержания постоянной скорости движения требуется постоянный приток энергии извне.

Закон Ома и его физический смысл

Закон Ома устанавливает линейную зависимость между напряжением, током и сопротивлением:

V = IR

где V — напряжение, I — сила тока, R — сопротивление.

Физический смысл закона Ома состоит в том, что для создания тока определенной силы в проводнике с бóльшим сопротивлением требуется приложить большее напряжение. Это связано с тем, что в проводнике с большим сопротивлением электроны испытывают больше столкновений и теряют больше энергии.

Почему закон Ома является линейным

Линейность закона Ома не является универсальным свойством всех материалов. Это эмпирическое наблюдение, которое хорошо описывает поведение многих проводников в определенном диапазоне условий.

Линейность возникает из-за того, что:

• Среднее время между столкновениями электронов примерно постоянно
• Ускорение электронов пропорционально приложенному электрическому полю
• Средняя скорость дрейфа электронов пропорциональна их ускорению между столкновениями

В результате ток оказывается пропорциональным приложенному напряжению. Однако при очень сильных полях или экстремальных температурах линейность может нарушаться.

Практическое применение закона Ома

Закон Ома позволяет рассчитывать параметры электрических цепей:

• Напряжение: V = I * R
• Ток: I = V / R
• Сопротивление: R = V / I

Эти формулы широко применяются при проектировании и анализе электрических схем. Они позволяют определить неизвестный параметр, если известны два других.

На практике «известными» могут быть как заданные параметры (например, напряжение источника питания), так и измеренные значения (например, ток через резистор).

Факторы, влияющие на сопротивление проводника

Сопротивление проводника зависит от следующих факторов:

• Материал проводника (определяет удельное сопротивление ρ)
• Длина проводника L
• Площадь поперечного сечения A

Зависимость выражается формулой:

R = ρL / A

Таким образом, сопротивление прямо пропорционально длине проводника и обратно пропорционально площади его сечения. Это объясняется тем, что в более длинном проводнике электроны испытывают больше столкновений, а в проводнике с большим сечением плотность тока ниже.

Моделирование электрических цепей

Современные симуляторы электрических цепей позволяют наглядно продемонстрировать закон Ома и исследовать поведение цепей при изменении параметров. Например, можно:

• Построить вольт-амперную характеристику резистора
• Исследовать зависимость тока от сопротивления при постоянном напряжении
• Изучить влияние температуры на сопротивление проводников

Такое моделирование помогает лучше понять физические процессы в электрических цепях и развить интуитивное понимание закона Ома.

Ограничения применимости закона Ома

Несмотря на широкое применение, закон Ома имеет ряд ограничений:

• Он не применим к полупроводниковым приборам (диодам, транзисторам)
• При очень сильных электрических полях линейность нарушается
• В сверхпроводниках сопротивление отсутствует, и закон Ома не работает
• При высоких частотах необходимо учитывать реактивные составляющие сопротивления

Поэтому при анализе сложных электронных схем часто требуются более сложные модели, учитывающие нелинейные эффекты.

Применение закона Ома в электроизмерениях

Линейность закона Ома делает его чрезвычайно полезным для электрических измерений. На его основе работают:

• Амперметры (измеряют падение напряжения на известном малом сопротивлении)
• Вольтметры (измеряют ток через известное большое сопротивление)
• Омметры (подают известное напряжение и измеряют ток)

Понимание закона Ома необходимо для правильной интерпретации показаний этих приборов и учета их влияния на измеряемую цепь.

Сопротивление, проводимость и закон Ома

Электрическое сопротивление – физическая величина, характеризующая способность проводника препятствовать прохождению по нему электрического тока.

Сопротивление часто обозначается через R или r и в Международной системе единиц (СИ) измеряется в Омах.

В зависимости от среды проводника и носителей зарядов, физическая природа сопротивления может отличаться. Так, например, в металле движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решетки, теряют свой импульс, и энергия их движения преобразуется во внутреннюю энергию кристаллической решетки (то есть становится меньше).

Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления материала, из которого он выполнен.

Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и определяется согласно зависимости

где ρ – удельное сопротивление вещества проводника, Ом·м, l  — длина проводника, м, а S — площадь сечения, мм².

Удельное сопротивление ρ – скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади сечения (рисунок 1). При расчетах это значение выбирается из таблицы.

Рис. 1. Удельное сопротивление проводника, ρ

Сопротивление проводника R зависит от внешнего фактора – температуры T, но для разных групп веществ эта зависимость имеет различные зависимости. Так, при снижении температуры металлов их сопротивление снижается (то есть способность проводить ток увеличивается). Если температура металла достигает низких значений, он переходит в состояние так называемой свехрпроводимости и его сопротивление

R стремится к 0. Поведение полупроводников под воздействием температур обратное – при снижении температуры T сопротивление R растет, а при его росте наоборот падает (рисунок 2).

Рис. 2. Зависимость сопротивления R от температуры T для металлов и полупроводников

Закон Ома

В 1826 году немецкий физик Георг Ом открыл важный в электронике закон, названный впоследствии его фамилией. Закон Ома определяет количественную зависимость между электрическим током и свойствами проводника, характеризующими его способность противостоять электрическому току.

Существует несколько интерпретаций закона Ома.

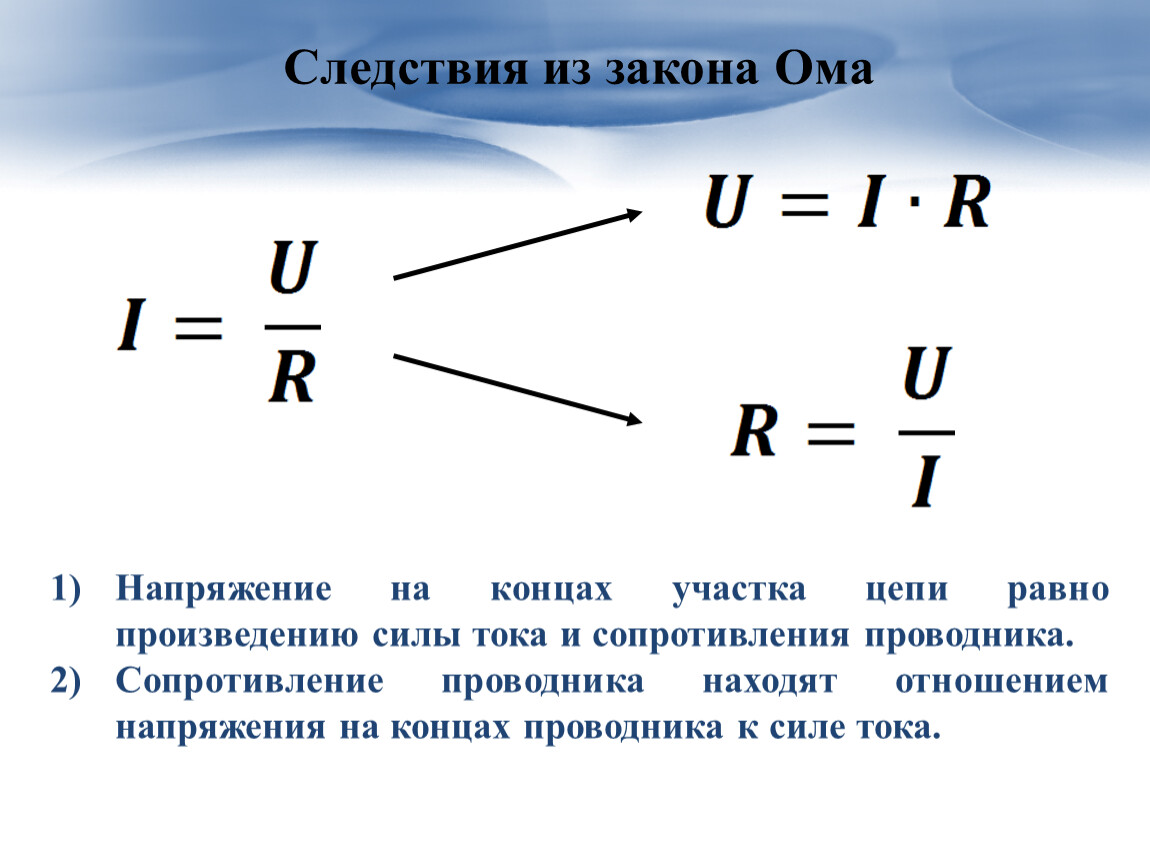
Закон Ома для участка цепи (рисунок 3) определяет величину электрического тока I в проводнике как отношение напряжения на концах проводника U и его сопротивления R

Рис. 3. Закон Ома для участка цепи

Интерпретировать закон Ома для участка цепи можно следующим образом: если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 В, тогда величина тока I в проводнике будет равна 1 А

На представленном выше простом примере разберем физическую интерпретацию закона Ома, используя аналогию электрического тока и воды. В качестве аналога проводника электрического тока возьмем воронку, сужение в которой возникает из-за наличие в проводнике сопротивления R (рисунок 4). Пусть в воронку из некоторого источника поступает вода, которая просачивается через узкое горлышко. Усилить поток воды на выходе горлышка воронки можно за счет давления на воду, например, силой поршня. В аналогии с электричеством, поршень будет являться аналогом напряжения – чем сильнее на воду давит поршень (то есть чем больше значение напряжения), тем сильнее будет поток воды на выходе из воронки (тем больше будет значение силы тока).

Рис. 4. Интерпретация закона Ома для участка цепи с использованием водной аналогии

Закон Ома может быть применен не всегда, а лишь в ограниченном числе случаев. Так закон Ома «не работает» при расчете напряжения и тока в полупроводниковых или электровакуумных приборов, содержащих нелинейные элементы. В этом случае зависимость тока и напряжения можно определить только с помощью построение так называемой вольтамперной характеристики (ВАХ). К категории нелинейных элементов относятся все без исключения полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.), а также электронные лампы.

Проводимость

Величина обратная сопротивлению, называется проводимостью:

G = 1/R.

Единица проводимости называется сименс (См): G, (g) = 1/Ом = См.

#1. Формула закона для участка цепи Ома

I = R/U

R = I/U

I = U/R

#2. Найдите сопротивление участка цепи использую закон Ома, если к концам проводника приложено U = 12 В, и в нем протекает ток I = 6 А.

2 Ом.

72 Ом.

5 Ом.

Закон Ома гласит I=U/R, следовательно R = U/I = 12/6 = 2 Ом.

#3. В чем измеряется удельное сопротивление?

Ом*мм

Ом*м

Ом

#4. Сопротивление участка цепи равно 10 Ом. Найдите проводимость участка.

5 См.

0,1 См.

10 См.

Величина обратная сопротивлению, называется проводимостью:

G = 1/R.

Так как сопротивление участка цепи R = 10 Ом, следовательно G = 1/10 = 0,1 См.

Завершить

Отлично!

Попытайтесь снова(

05.09.2020

ТОЭ

Электрические цепи постоянного тока

«Электрическое сопротивление. Закон Ома» 8 класс онлайн-подготовка на Ростелеком Лицей |

Формулы, необходимые для решения задач

 

На предыдущих уроках мы говорили, что сила тока зависит от напряжения и сопротивления проводника. Также мы выяснили, что сопротивление проводника зависит от его геометрических размеров и материала, из которого он сделан. На этом уроке будут рассмотрены задачи, связанные именно с этими двумя положениями.

 

Первая формула, которая понадобится для решения задач, – закон Ома для участка цепи:

Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Сила тока измеряется в Амперах (I=[А]), напряжение – в Вольтах (U=[В]), сопротивление – в Омах (R=[Ом]). Тогда из закона Ома можно сказать, что .

Еще одна формула, которая нам понадобится, – формула зависимости сопротивления проводника от его параметров:

Сопротивление проводника равно его удельному сопротивлению, умноженному на дробь, где в числителе – длина проводника, в знаменателе – площадь поперечного сечения проводника. При этом сопротивление измеряется в Омах (R=[Ом]), длина – в метрах (l=[м]). В единицах измерения СИ (система интернациональная) площадь измеряется в метрах квадратных, но поскольку сечение провода невелико, то имеет смысл измерять площадь поперечного сечения в миллиметрах квадратных (S=[м²]=[мм²]). Удельное сопротивление, как правило, определяется по таблицам: зная материал, из которого сделан проводник, можно определить его удельное сопротивление. Единицы измерения удельного сопротивления:

Первая запись единиц измерения используется для удобства (), а в таблицах значение обычно подается в виде второй записи (). Можно увидеть, что записи эквивалентны, т. к. если перевести миллиметры в метры, то метры сократятся.

 

Задача №1

 

 

Рассмотрим следующую задачу: надо определить силу тока в проводнике, длина которого 100 м, а сечение этого проводника – 0,5 мм².

 

Этот проводник выполнен из меди и включен в цепь таким образом, что на его концах наблюдается напряжение 6,8 В. Стоит отметить, что в задаче дан материал, из которого сделан проводник. Значит, можно узнать значение удельного сопротивления из таблицы.

Рис. 1. Решение задачи №1

Сначала следует записать краткое условие задачи. На рис. 1. слева от вертикальной черты показано, как это нужно сделать. Значение длины (l=100 м), площади поперечного сечения (S=0,5 мм²) и напряжения (U=6,8 В) дано в условии. Значение удельного сопротивления меди () мы взяли из таблицы. Под горизонтальной чертой на рис. 1 написано, что нужно найти в задаче – силу тока.

Для решения задачи запишем закон Ома для участка цепи: . Также нам потребуется выражение для сопротивления проводника: . Далее постараемся записать решение в общем виде, то есть выражение для сопротивления мы подставим в закон Ома. Поскольку R в законе Ома стоит в знаменателе, то ρ и l окажутся в знаменателе, S перейдет в числитель. Получаем:

Теперь подставим значения данных величин:

Ответ: I=2A.

Это можно понять так: если подключить амперметр последовательно к данному проводнику, то он покажет значение 2А. Стоит обратить внимание, что ничего сложного в таких задачах нет. Стоит только разобраться, какие величины куда подставить. Обычно такие задачи в дальнейшем будут использоваться как составная часть более сложных задач.

 

Задача №2

 

 

В предыдущей задаче мы находили значение силы тока. Но эту характеристику можно измерить соответствующим прибором – амперметром. Поэтому, как правило, есть другие задачи, в которых требуется найти характеристики проводника. Если мы хотим сделать какое-то сопротивление, то мы должны знать эти характеристики проводника: длину, площадь сечения, материал. Решая такие задачи, мы сможем их найти, зная силу тока и напряжение.

 

Рассмотрим пример именно такой задачи. По вольфрамовой проволоке протекает электрический ток. Длина проволоки – 4 м, сила тока составляет 0,05 А. Напряжение, под которым находится данный проводник, составляет 5 В. Необходимо определить величину площади поперечного сечения.

Рис. 2. Решение задачи №2

Как и в первом случае, запишем краткое условие задачи (рис. 2, слева от вертикальной черты). Нам даны сила тока I=0,05 А, напряжение U=5 В и длина проволоки l=4 м. Значение удельного сопротивления вольфрама  можно найти из таблицы. Под горизонтальной чертой написано то, что требуется найти: S, площадь поперечного сечения проволоки.

Как и в предыдущей задаче запишем две формулы. Первая – это формула для вычисления сопротивления проводника: . Отсюда можно выразить площадь сечения проводника:

Из этого уравнения мы не сможем сразу найти сечение, поскольку нам неизвестно сопротивление. Для его определения потребуется вторая формула – закон Ома для участка цепи: . Из него можно выразить значение сопротивления всей проволоки:

Подставив это выражение в формулу для площади сечения, получим:

Получаем дробь, где в числителе стоит произведение трех величин: удельного сопротивления, длины проводника и силы тока, а в знаменателе стоит только напряжение. Подставим численные значения:

Получаем ответ: площадь поперечного сечения проволоки . Как видим, сечение проволоки невелико, то есть проволока будет очень тонкой.

 

Применение задач на практике

 

 

Стоит отметить, что для решения конкретных технических задач, подобных решенной ранее, обычно используются данные, которые получают при помощи приборов. Например, имеется катушка с намотанным на нее проводником. Требуется измерить, например, длину этого проводника. Разматывать катушку не имеет смысла, поскольку провод может быть очень длинным. Как же тогда поступить?

 

Рис. 3. Схема для измерения длины проводника в катушке

По небольшому образцу такого провода измеряют площадь его сечения. По внешнему виду проводника можно определить материал, из которого он сделан, а значит, и узнать его удельное сопротивление. Далее катушку (обозначена желтым цветом на рис. 3) подключают к источнику тока и при помощи амперметра и вольтметра определяют напряжение на этой катушке и силу тока, протекающего по проводнику, который намотан на эту катушку. В результате получаем задачу, похожую на ту, что мы решали ранее, но найти надо длину проводника. Используя формулу для сопротивления и закон Ома, получим:

В заключение стоит сказать, что такие задачи не являются трудными, но достаточно показательны. Из большого количества величин, данных в задаче, можно легко получить значение требуемой величины.

 

Список литературы

1. Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
2. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
3. Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети интернет

1. Фестиваль педагогических идей «Открытый урок» (Источник)
2. ПроШколу.ру (Источник)
3. Электрознайка (Источник)

 

Домашнее задание

1. Стр. 106–108: вопросы № 1–4. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
2. Длина и площадь поперечного сечения алюминиевого и железного проводов одинаковые. На них подается одинаковое напряжение. В каком из проводов сила тока будет больше?
3. Можно ли вычислить напряжение в проводнике, зная силу тока в нем, его длину и площадь сечения, но не зная, из какого материала он сделан?
4. Для уменьшения потерь энергии соединительные провода делают так, чтобы ток в них был как можно меньше. Для этого их должны делать большего или меньшего диаметра?

 

Сопротивление и закон Ома | Ultimate Electronics Book

Ultimate Electronics: Практические схемы и анализ

---

≡ Оглавление

«

2,5

Земля

»

2,7

Мощность

Как решить задачи по закону Ома для резисторов. Микроскопические причины, по которым закон Ома является макроскопически линейным. 11 минут чтения

В разделе «Электроны в движении» мы обсуждали, как электрические поля вызывают силу →F=qe→E на электрон. Как и в случае с любым объектом, на который действует результирующая сила, электрон будет ускоряться →Fnet=me→a в ответ на эту силу. Со временем это ускорение вызывает увеличение скорости: →a=d→vdt . Скорость носителей заряда можно описать как электрический ток.

Для свободных электронов, летающих в вакууме, это конец истории.

Однако для электронов, движущихся в материале — обычно, но не всегда в твердом теле — столкновения между электроном и самим материалом являются невероятно доминирующим фактором в общем движении электрона.

Хотя электрон все еще ускоряется электрическим полем, он часто теряет энергию из-за столкновений с материалом. Каждое столкновение рассеивает кинетическую энергию , что электрон встраивается в материал, который становится теплом.

В результате, чтобы электроны двигались через материал с постоянной средней скоростью (нулевое среднее ускорение), нам по-прежнему необходимо добавлять энергию для компенсации кинетической энергии, теряемой при столкновениях с неподвижным материалом. Это свойство называется сопротивлением .

(Исходя из изучения механики и кинематики, существует спектр между упругими столкновениями, сохраняющими полную кинетическую энергию, и неупругие столкновения, которые не сохраняют полную кинетическую энергию, поскольку часть этой энергии преобразуется в тепло, звук, деформацию материала и т.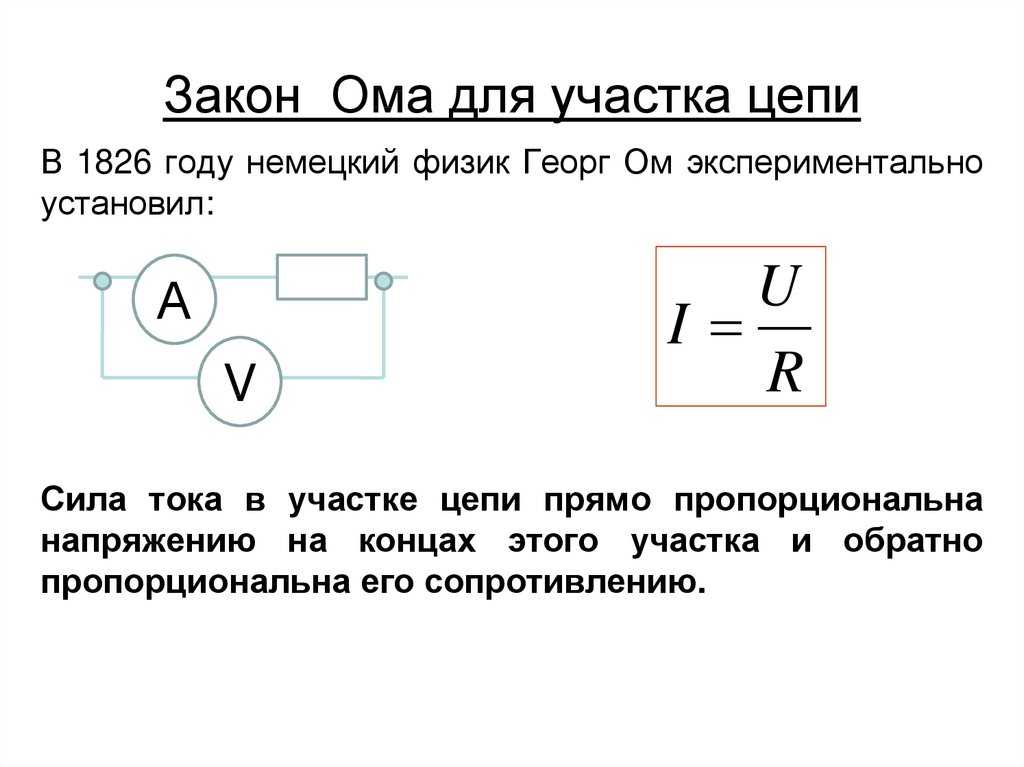 д. В случае трения или омического сопротивления мы имеем в виду неупругие столкновения.)

---

Электрическое сопротивление при столкновениях аналогично сопротивлению воздуха.

Представьте себе мячик для пинг-понга, упавший с башни. Под действием силы тяжести мяч летит к земле. Если бы не было сопротивления воздуха, скорость мяча продолжала бы увеличиваться и возрастать без ограничений. Но в воздухе между мячом и молекулами воздуха происходят столкновения, поэтому мяч достигает некоторой стационарной скорости, которую в этой ситуации часто называют «конечной скоростью». При этой установившейся скорости энергия, полученная при движении вниз в гравитационном поле потенциальной энергии, равна энергии, потерянной при столкновениях при отталкивании воздуха с пути. Когда мы усредняем многие из этих микроскопических столкновений, оказывается, что мяч не ускоряется и не замедляется, а вместо этого продолжает падать с постоянной скоростью.

Это действительно рассеивание кинетической энергии. Если бы это было не так, то добавление энергии вызвало бы дальнейшее ускорение, а не просто поддержание постоянной скорости.

Аналогия с жидкостью тоже уместна. Проталкивание жидкости через трубу требует энергии (обычно определяемой как разность давлений) для поддержания постоянной скорости (обычно определяемой как расход), потому что поток постоянно теряет энергию из-за сопротивления внутренних стенок трубы, а также к вязким взаимодействиям между молекулами жидкости. Эти силы сопротивления действительно рассеиваются в виде тепла. (Однако из-за такой высокой удельной теплоемкости воды мы обычно не замечаем этого повышения температуры в повседневной жизни!)

Автомобиль, движущийся с постоянной скоростью по ровному шоссе, демонстрирует оба этих явления: для поддержания постоянной скорости необходимо добавлять энергию за счет сопротивления воздуха, а также сопротивления жидкостей внутри двигателя и трансмиссии, трения в колесные подшипники, неупругая деформация резиновых покрышек и т. д. Если бы это было не так, мы могли бы просто поставить автомобиль на нейтраль и заглушить двигатель, как только достигнем крейсерской скорости.

Когда мы движемся через что-либо, кроме вакуума без трения (или сверхпроводника!), материалы будут взаимодействовать, сталкиваться, деформироваться и вызывать потери кинетической энергии. Независимо от того, движется ли это автомобиль по шоссе или электрон в металле, результат один и тот же: нужно постоянно добавлять больше энергии просто для поддержания постоянной средней кинетической энергии.

---

Закон Ома обычно рассматривается как:

V=IR

где R — сопротивление резистора, В — падение напряжения на резисторе, а I это ток через резистор. (См. оставшуюся часть этой главы, в том числе Закон Кирхгофа о напряжении (KVL) и Закон Кирхгофа о токе (KCL), Обозначение напряжений, токов и узлов, а также Решение систем цепей для получения дополнительной информации о правильном указании напряжения и тока!)

Поскольку напряжение — это мера работы на единицу заряда, закон Ома означает, что для материалов с более высоким сопротивлением требуется больше работы, чтобы пропустить тот же поток тока.

Закон Ома утверждает, что сопротивление является линейной функцией, но это правило не является универсальным ; на самом деле это эмпирических (основанных на наблюдениях, а не на теории). На самом деле это линеаризованная модель триллионов или более взаимодействий атомарного масштаба внутри материала, и оказывается, что в среднем , агрегированное поведение выглядит примерно линейным.

---

Если мы знаем любые два из V, I или R , мы можем решить для третьей переменной:

V=I⋅RI=VRR=VI

Это одно из самых основных практических уравнений в электронике, поэтому мы выделяем его во всех его формах.

Эти соотношения можно рассматривать с теоретической точки зрения при установлении связи между токами и напряжениями в цепи, но они также имеют практическое значение: два, чтобы получить напряжение: V=I⋅R .

Если у нас есть известных напряжение на известном сопротивлении , мы можем разделить два, чтобы получить ток: I=VR .

Наконец, если у нас есть известное напряжение и известный ток , мы можем разделить их, чтобы получить сопротивление: R=VI .

В математическом смысле, когда мы используем слово известное , мы противопоставляем его неизвестной переменной , которую ищем. (См. Системы уравнений.)

Но в практическом смысле известно может означать две немного разные вещи:

• «Известный» может означать внешне контролируемый или фиксированный . Например, если у нас есть источник тока, который всегда выдает 2 ампера, то этот ток известен, потому что он контролируется и устанавливается на определенное значение.
• «Известно» может означать измеренное . Например, мы можем измерить напряжение 6 вольт на выходе источника тока. Это напряжение известно, потому что оно измеряется, а не фиксируется каким-либо процессом.

В большинстве вопросов, связанных с законом Ома, мы комбинируем два типа «известных». Чтобы объединить два приведенных выше примера, если наши 2 A источник тока подключен к какому-то неизвестному сопротивлению, и мы измеряем 6 В на выходе мы можем определить, что неизвестное сопротивление равно:

R=VI=62=3 Ω

Линейность закона Ома чрезвычайно полезна при проведении измерений. Резисторы — это компоненты, которые линейно преобразуют разность напряжений в ток и наоборот, и это полезный эффект во многих аналоговых схемах. Подробнее о вольтметрах, амперметрах и омметрах мы поговорим в разделе «Мультиметры и измерения».

---

Наш первый пример — одиночный 100 Ом резистор R1, подключенный к источнику напряжения:

Закон Ома — постоянный резистор с источником напряжения

Circuitlab.com/cu5584wxrenxw

Править — Имитация

Упражнение Нажмите на схему, затем нажмите «Симуляция» и нажмите «Запустить DC Solver». Это покажет рассчитанный ток:

I=VR=5 В100 Ом=0,05 А=50 мА

Затем нажмите «Запустить развертку постоянным током». Это настроено для регулировки значения источника напряжения от -5 до +5. Симулятор мгновенно построит график с настройкой напряжения по оси x и результирующим током по оси y.

Вместо того, чтобы управлять сопротивлением с источником напряжения, мы можем вместо этого подключить его к фиксированному источнику тока:

Закон Ома — постоянный резистор с источником тока

Circuitlab.com/cd2yet2jf36x7

Править — Имитация

Упражнение Нажмите на схему, нажмите «Симуляция» и «Запустить DC Solver». Это покажет рассчитанное напряжение:

ВА=I⋅R=(1 А)⋅(100 Ом)=100 В

Затем нажмите «Запустить развертку постоянным током». Это настроено для настройки значения текущего источника. Симулятор мгновенно построит график с текущими настройками по оси x и результирующим напряжением по оси y.

Использование симулятора CircuitLab для изменения токов и напряжений и построения графика развертки постоянного тока является очень простой функцией. Чуть более продвинутый случай — изменение сопротивления:

.

Закон Ома — Регулируемый резистор с источником напряжения

Circuitlab.com/cqa89rtgrxx86

Править — Имитация

Упражнение Щелкните цепь, нажмите «Симуляция» и «Запустить развертку постоянным током». Теперь симулятор подключает различные резисторы от 1 до 1000 Ом и строит результирующую кривую тока с сопротивлением в Омах по оси x и током по оси y.

Это работает, если для DC Sweep установить значение «R1.R», что означает «сопротивление резистора с именем R1». Просмотр параметров компонента — мощный инструмент моделирования цепей.

---

Сопротивление зависит от выбора материала (например, алюминия или меди) и его физических размеров. Для твердого тела постоянной площади поперечного сечения A и длина L , сопротивление равно:

R=ρLA

Размеры имеют смысл: если мы сделаем резистор в два раза длиннее, расстояние, на котором могут произойти столкновения и потеря энергии, будет в два раза больше, как и в резисторах, соединенных последовательно. Вместо этого, если мы увеличим площадь поперечного сечения, средняя скорость дрейфа будет ниже при той же величине тока, поэтому при каждом столкновении теряется меньше энергии.

Удельное сопротивление ρ является свойством материала, а также функцией температуры: см. Практические резисторы: температурный коэффициент для получения дополнительной информации.

---

Почему ток линейно пропорционален напряжению в резистивном материале?

Это часто считается само собой разумеющимся, но на самом деле это не очевидно. В свободном пространстве заряд в постоянном электрическом поле имел бы линейно возрастающую скорость , а не (в среднем) постоянную скорость в резистивном материале.

Вот одна из возможных моделей:

Даже при нулевом электрическом поле (то есть при нулевом напряжении) заряды не являются остатком. Из-за теплового движения они постоянно толкаются.

Теперь применим электрическое поле (то есть ненулевое напряжение). Это поле →E Поле воздействует на заряд силой:

→F=q→E=m→a

Эта сила немного ускоряет заряд в направлении поля. Однако, прежде чем он начнет двигаться особенно быстро, заряд сталкивается с другими зарядами внутри материала. Это столкновение вызывает потерю кинетической энергии (превращающейся в тепло в материале), и заряд должен снова стартовать с нулевой скоростью. Оттуда он начинает ускоряться за счет поля, и цикл ускорения и столкновения повторяется.

Предположим, что среднее время между столкновениями равно tcollision . В этом случае в промежутках между столкновениями →E поле может ускорить заряд от v=0 до некоторой скорости vmax до столкновения. В этом случае (с фиксированным tcollision ), средняя скорость частицы будет пропорциональна ускорению, обусловленному полем. (Если это неясно, нарисуйте график зависимости скорости заряда от времени. Это будет иметь вид пилообразной формы: увеличение от 0 до vmax во время tcollision , затем внезапно падает до 0 и повторяется снова. Средняя скорость ¯¯¯¯¯vd=vmax2 .)

Чтобы узнать больше о том, как все это работает со случайными тепловыми колебаниями в трех измерениях, посмотрите модель Drude .

Вы можете задаться вопросом, почему у нас есть среднее время между столкновениями, а не среднее расстояние между столкновениями. Это связано с тем, что тепловая скорость намного больше, чем скорость дрейфа, поэтому эти случайные тепловые скорости в основном определяют, когда происходит столкновение, а не скорость дрейфа, которая важна для определения частоты столкновений.

Для большинства материалов более высокая температура означает более высокие тепловые скорости и более короткое время tстолкновения , поэтому более высокое сопротивление. Дополнительные сведения о взаимосвязи между сопротивлением и температурой см. в разделе Практические резисторы: температурный коэффициент.

---

Резисторы обычно линейны по току на многие порядки — в отличие от полупроводникового перехода, как мы увидим позже.

Резисторы обычно линейны по независимо от направления протекания тока — тоже в отличие от полупроводникового перехода.

Представьте себе механическую цилиндрическую пружину: сила линейна для маленьких толчков и для больших толчков, но в какой-то момент вы начинаете постоянно деформировать металл (пластическая деформация) и получаете нелинейное поведение.

Таким же образом, если вы превысите пределы резистора, вы можете безвозвратно заменить его, как правило, из-за перегрева. Дополнительные сведения см. в нескольких следующих разделах, посвященных мощности и практическим резисторам: номинальная мощность (мощность).

---

Сверхпроводники когда-то были экзотическими материалами, но становятся все более и более распространенными, поскольку их цена снижается, а диапазон рабочих температур растет. В настоящее время нет известных материалов, которые являются сверхпроводниками при комнатной температуре и давлении, но исследования в этой области находят материалы, которые работают при все более и более высоких температурах.

Сверхпроводники обладают не только низким сопротивлением, но и предлагают действительно нулевое сопротивление при протекании тока.

В сверхпроводнике нет внутренних неупругих столкновений между носителями заряда и веществом.

Существуют практические ограничения для сверхпроводников в нескольких измерениях:

1. Ток. Сверхпроводник может поддерживать только определенную максимальную плотность тока, известную как критический ток .
2. Магнитное поле. Сверхпроводящие материалы имеют ограничения по напряженности магнитного поля, в котором они могут работать.
3. Рабочая температура. Сверхпроводящие материалы перестают быть сверхпроводящими при превышении некоторого максимального предела температуры.

В дополнение к этому, сверхпроводники и сверхпроводящие провода по-прежнему относительно сложны в работе с производственной точки зрения. Материалы часто хрупкие, их необходимо охлаждать до чрезвычайно низких температур, и их трудно соединять и соединять с другими компонентами.

---

В следующем разделе «Мощность» мы поговорим о том, куда уходит тепло от этих резистивных столкновений, и подумаем больше о потоке энергии и мощности в целом.

≡ Оглавление

«

2,5

Земля

»

2,7

Мощность

---

Роббинс, Майкл Ф. Абсолютная электроника: проектирование и анализ практических схем. CircuitLab, Inc., 2021, Ultimateelectronicsbook.com. Доступ . (Авторское право © 2021 CircuitLab, Inc.)

Сопротивление и простые схемы – Колледж Дугласа, физика 1207

Глава 4 Электрический ток, сопротивление и закон Ома

Резюме

• Объясните происхождение закона Ома.
• Расчет напряжения, тока или сопротивления по закону Ома.
• Объясните, что такое омический материал.
• Опишите простую схему.

Что управляет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он создает разность потенциалов В , создающее электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.

Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что сила тока в металлической проволоке прямо пропорциональна приложенному напряжению :

.

И В 

Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.

Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (в общих чертах похожее на трение и сопротивление воздуха), называется сопротивлением R . Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или

Так, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает

Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление 90 272 Ом 90 273 , которое не зависит от напряжения 90 272 В 90 273 и тока 90 272 1 90 273 . Объект, который имеет простое сопротивление, называется резистор , даже если его сопротивление мало. Единицей измерения сопротивления является ом, который обозначается символом Ом (греческая омега в верхнем регистре). Преобразование I = V/R дает R = V/I , поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:

На рис. 1 ниже показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Провода, соединяющие источник напряжения с резистором, можно считать имеющими пренебрежимо малое сопротивление, или их сопротивление можно включить в Р .

Рисунок 1. Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.

Пример 1: расчет сопротивления: автомобильная фара

Чему равно сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?

Стратегия

Мы можем преобразовать закон Ома в соответствии с формулой I = V/R и использовать его для определения сопротивления.

Решение

Перестановка I = V/R и подстановка известных значений дает

Обсуждение

Это относительно небольшое сопротивление, но оно больше, чем морозостойкость фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому при первом включении лампочка имеет более низкое сопротивление и будет потреблять значительно больший ток в течение короткого периода прогрева.

Диапазон сопротивлений превышает многие порядки. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 ¹² Ом или более. У сухого человека сопротивление руки-ноги может составлять 10 ⁵ Ω , тогда как сопротивление человеческого сердца составляет около 10 ³ Ω . Метровый отрезок медного провода большого диаметра может иметь сопротивление 10 ^-5 Ом , а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в главе 20.3 Сопротивление и удельное сопротивление.

Дополнительную информацию можно получить, решив I = V/R , что даст

В = I R. 

Это выражение для В  можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I . Фраза IR падение часто используется для этого напряжения. Например, фара в примере 1 имеет падение напряжения IR 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой цепи (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку Потенциальная энергия = PE = q ΔV , и через каждый протекает одно и то же q . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. См. рисунок ниже.

Рисунок 2. Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.

Создание соединений: сохранение энергии

В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.

PhET Исследования: Закон Ома

Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой. Прямая ссылка:  https://phet.colorado.edu/sims/html/ohms-law/latest/ohms-law_en.html 

Рисунок 3.  Закон Ома

• Простая цепь — это цепь, в которой есть один источник напряжения и одно сопротивление.
• Одно из утверждений закона Ома дает отношение между током I , напряжением В и сопротивлением R в простой цепи как I = V/R .
• Сопротивление выражается в омах (Ом), связанных с вольтами и амперами по формуле 1 Ом = 1 В/1 А.
• Имеется падение напряжения или IR падение напряжения на резисторе, вызванное протеканием через него тока, определяемое выражением В = IR .