Как применяется закон Ома в цепях переменного тока. Почему нужно учитывать реактивное сопротивление. Как рассчитать импеданс цепи переменного тока. Какие особенности имеют последовательные и параллельные цепи переменного тока.
Основные принципы закона Ома для переменного тока
Закон Ома для цепей переменного тока имеет ряд особенностей по сравнению с цепями постоянного тока. Рассмотрим основные принципы его применения:
- В цепях переменного тока помимо активного сопротивления R необходимо учитывать реактивное сопротивление X, создаваемое индуктивностью и емкостью.
- Полное сопротивление цепи переменного тока называется импедансом (Z) и измеряется в омах.
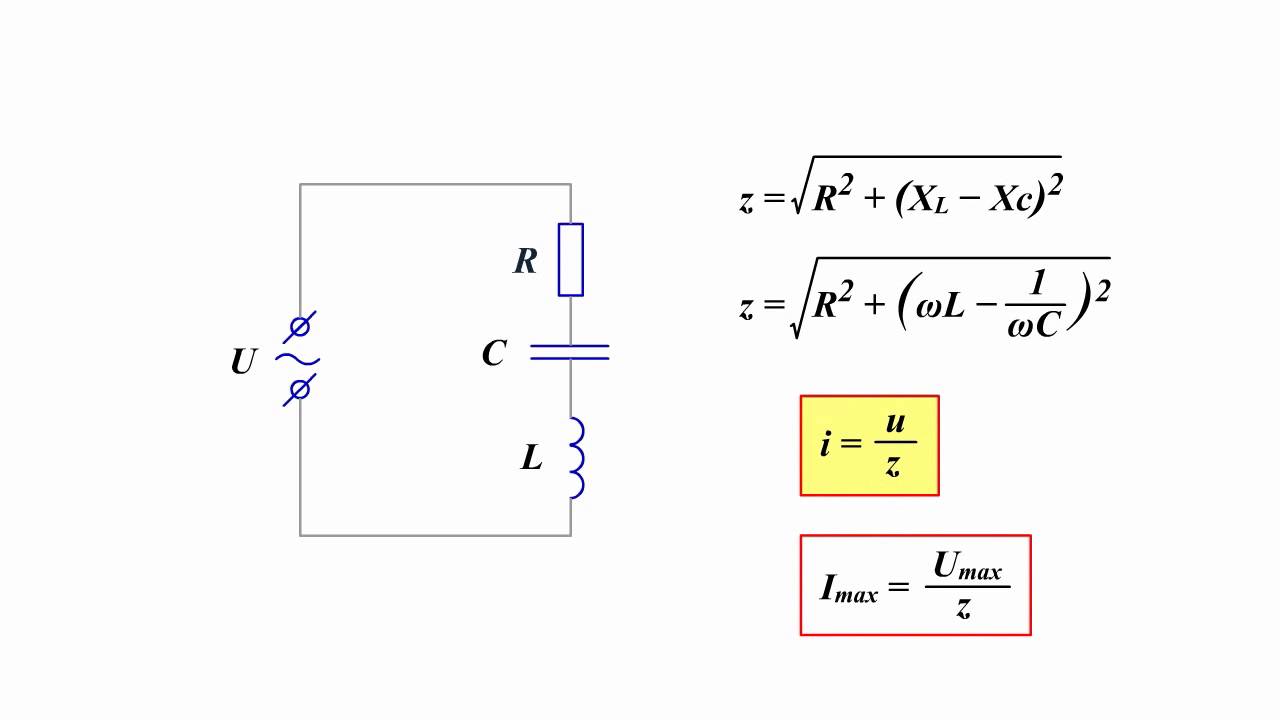
- Импеданс Z включает в себя активное R и реактивное X сопротивления: Z = √(R² + X²).
- Закон Ома для цепи переменного тока записывается как I = U / Z, где I — действующее значение тока, U — действующее значение напряжения.
Таким образом, при расчете цепей переменного тока нужно учитывать не только активное, но и реактивное сопротивление элементов. Это позволяет правильно определить токи и напряжения в цепи.
Расчет импеданса в цепях переменного тока
Импеданс Z является ключевой характеристикой цепи переменного тока. Рассмотрим, как он рассчитывается в различных случаях:
1. Цепь только с активным сопротивлением
Если цепь содержит только активное сопротивление R, то импеданс Z равен этому сопротивлению:
Z = R
2. Цепь с активным сопротивлением и индуктивностью
При наличии в цепи активного сопротивления R и индуктивности L импеданс рассчитывается по формуле:
Z = √(R² + XL²)
где XL = 2πfL — индуктивное сопротивление, f — частота переменного тока.
3. Цепь с активным сопротивлением и емкостью
Для цепи с активным сопротивлением R и емкостью C формула импеданса имеет вид:
Z = √(R² + XC²)
где XC = 1/(2πfC) — емкостное сопротивление.
4. Цепь с активным сопротивлением, индуктивностью и емкостью
В общем случае, когда цепь содержит все три элемента, импеданс рассчитывается следующим образом:
Z = √(R² + (XL — XC)²)
Здесь учитывается, что индуктивное и емкостное сопротивления действуют в противофазе.
Особенности последовательных цепей переменного тока
Рассмотрим основные характеристики последовательных цепей переменного тока:
- Ток во всех элементах цепи одинаковый.
- Напряжения на элементах складываются векторно.
- Импеданс цепи равен векторной сумме импедансов отдельных элементов.
Например, для последовательной RLC-цепи:
Z = √(R² + (XL — XC)²)
Угол сдвига фаз между током и напряжением определяется как:
φ = arctg((XL — XC) / R)
Характеристики параллельных цепей переменного тока
Параллельные цепи переменного тока имеют следующие особенности:
- Напряжение на всех элементах одинаковое.
- Токи в ветвях складываются векторно.
- Проводимость цепи равна векторной сумме проводимостей отдельных ветвей.
I = √(IR² + (IL — IC)²)
где IR, IL, IC — токи через резистор, катушку и конденсатор соответственно.
Мощность в цепях переменного тока
В цепях переменного тока различают три вида мощности:
- Активная мощность P = UI cosφ — выполняет полезную работу.
- Реактивная мощность Q = UI sinφ — циркулирует между источником и нагрузкой.
- Полная мощность S = UI — геометрическая сумма активной и реактивной мощностей.
Где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними.
Резонанс в цепях переменного тока
Резонанс — это явление, при котором индуктивное и емкостное сопротивления взаимно компенсируются. Различают два вида резонанса:
Резонанс напряжений
Возникает в последовательной RLC-цепи при условии XL = XC. При этом:
- Импеданс цепи минимален и равен активному сопротивлению Z = R.
- Ток в цепи максимален.
- Напряжения на катушке и конденсаторе могут многократно превышать общее напряжение.
Резонанс токов
Наблюдается в параллельной RLC-цепи также при XL = XC. В этом случае:
- Импеданс цепи максимален.
- Общий ток минимален.
- Токи в индуктивной и емкостной ветвях могут быть очень большими.
Резонансная частота в обоих случаях определяется формулой:
f = 1 / (2π√(LC))
Практическое применение закона Ома для переменного тока
Закон Ома для переменного тока находит широкое применение в различных областях электротехники и электроники:
- Расчет и проектирование электрических сетей переменного тока.
- Анализ работы трансформаторов и электрических машин.
- Разработка фильтров и резонансных контуров в радиотехнике.
- Создание систем передачи электроэнергии на большие расстояния.
- Проектирование систем электроснабжения зданий и промышленных объектов.
Понимание принципов работы цепей переменного тока и умение применять закон Ома позволяет эффективно решать широкий спектр инженерных задач в области электротехники.
Ограничения применения закона Ома для переменного тока
Несмотря на широкое применение, закон Ома для переменного тока имеет ряд ограничений:
- Не учитывает нелинейные эффекты в элементах цепи.
- Применим только для установившихся процессов.
- Не описывает поведение цепи на очень высоких частотах.
- Не учитывает распределенные параметры длинных линий.
В этих случаях требуется использование более сложных моделей и методов анализа цепей.
Заключение
Закон Ома для цепей переменного тока является фундаментальным принципом электротехники. Он позволяет анализировать поведение электрических цепей с учетом реактивных элементов — катушек индуктивности и конденсаторов. Понимание особенностей применения закона Ома в цепях переменного тока необходимо для эффективного проектирования и эксплуатации различных электротехнических устройств и систем.
Закон Ома для переменного тока в цепи, содержащей только емкость
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРОВЕРКА ПОЛНОГО ЗАКОНА ОМА ДЛЯ ПЕРЕМЕННОГО ТОКА
Методические указания к выполнению лабораторной работы №16 по электричеству для студентов физического факультета
УФА
РИЦ БашГУ
2010
Печатается по решению кафедры общей физики
от 17 сентября 2010г., протокол №2
Составители:
д. ф.-м. н. Альмухаметов Р.Ф.,
к. ф.-м. н. Гафуров И.Г., Горбенко А.П.
ПРОВЕРКА ПОЛНОГО ЗАКОНА ОМА ДЛЯ ПЕРЕМЕННОГО ТОКА
Цель
работы: проверка выполнения полного закона Ома
для цепи переменного тока, исследование
индуктивности и коэффициента мощности
дросселя в цепи переменного тока.
Приборы и принадлежности: катушка индуктивности (с ферромагнитным сердечником), магазин емкостей, амперметр, вольтметр, ваттметр, лабораторный автотрансформатор.
Краткая теория
При рассмотрении электрических колебаний приходится иметь дело с токами, изменяющимися во времени. Закон Ома и правила Кирхгофа были установлены для постоянного тока. Однако они остаются справедливыми и для мгновенных значений изменяющихся тока и напряжения, если только эти изменения происходят не слишком быстро (нужно помнить, что электромагнитные возмущения передаются по цепи со скоростью света).
Пусть длина цепи равна . Если за время , необходимое для передачи возмущения в самую удаленную точку цепи, сила тока изменится незначительно, то мгновенные значения силы тока во всех сечениях цепи будут практически одинаковыми. Токи, удовлетворяющие таким условиям, называются КВАЗИСТАЦИОНАРНЫМИ. Для переменного тока условие квазистационарности имеет вид
,
где
–
период изменений.
Для цепи длиной 3м время запаздывания τ=10-8 с. Таким образом, вплоть до Т~10-6 с (что соответствует частоте 106 Гц) ток в цепи можно считать квазистационарным. Ток промышленной частоты 50Гц квазистационарен для цепей длиной до 100км.
Мгновенные значения квазистационарного тока подчиняются закону Ома, следовательно, для них справедливы и правила Кирхгофа.
Для характеристики переменного тока используют сопоставление средней мощности тока с мощностью постоянного тока соответствующей силы. Полученное таким образом значение силы переменного тока
В простейшем и наиболее важном случае мгновенное значение силы I переменного тока меняется во времени t по синусоидальному закону:
(1)
где — амплитуда тока,
—
его круговая частота, — начальная фаза.
Синусоидальный (гармонический) ток создается синусоидальным напряжением U той же частоты:
(2)
где — амплитуда напряжения, — начальная фаза (рис.1).+
с.1. Графики напряжения и тока
в цепи переменного тока.
Действующие значения такого переменного тока равны:
(3)
Как уже говорилось выше, для квазистационарных токов справедлив закон Ома. Из–за наличия в цепи переменного тока индуктивности L или емкости C между силой тока I и напряжением в общем случае возникает сдвиг фаз , зависящий от параметров цепи (R, L, C, где R – активное сопротивление, L – индуктивность, С — емкость) и частоты ω. Вследствие сдвига фаз средняя мощность переменного тока, измеряемая, например, ваттметром, меньше произведения действующих значений тока и напряжения:
(4)
Закон Ома для переменного тока в цепи, содержащей только активное сопротивление
В
цепи, не содержащей ни индуктивности,
ни емкости, ток совпадает по фазе с
напряжением (рис.
2) .
рис. 2 Схема цепи и графики напряжения U(t) и силы тока I(t) в цепи, содержащей только активное сопротивление R
Закон Ома для действующих значений этой цепи имеет такую же форму, как и для цепи постоянного тока:
(5)
АКТИВНОЕ СОПРОТИВЛЕНИЕ цепи определятся по активной мощности , затрачиваемой в цепи:
Закон Ома для переменного тока в цепи, содержащей только индуктивность
При наличии в цепи индуктивности L переменный ток индуцирует в ней ЭДС самоиндукции:
(6)
рис. 3 Схема цепи и графики напряжения U(t) и
силы тока I(t) в цепи, содержащей только индуктивность L.
ЭДС
самоиндукции противодействует изменению
тока, и в цепи, содержащей только
индуктивность, ток отстает по фазе от
напряжения на четверть периода, т.
е. (рис. 3).
Действующее значение равно:
(7)
где — индуктивное сопротивление цепи.
Закон Ома для такой цепи имеет вид:
(8)
А значение
(9)
называется индуктивным сопротивлением.
При напряжении на конденсаторе с емкостью заряд на его обкладках будет равен . Периодические изменения вызывают периодическое изменение , и возникает ток, протекающий через конденсатор:
(10)
Таким образом, синусоидальный переменный ток, проходящий через емкость, опережает по фазе напряжение на её зажимах на четверть периода, т.е. (рис. 4).
рис. 4 Схема цепи и графики напряжения U(t) и
силы
тока I(t) в цепи, содержащей только емкость С.
Эффективные значения силы тока и напряжения в такой цепи связаны соотношением (закон Ома для цепи, содержащей только емкость):
(11)
где
(12)
емкостное сопротивление цепи.
Закон Ома для переменного тока в цепи, содержащей активное сопротивление, индуктивность и емкость
Если в цепь переменного тока последовательно включены активное сопротивление R, индуктивность L и емкость C, то её ПОЛНОЕ СОПРОТИВЛЕНИЕ равно:
(13)
где — реактивное сопротивление цепи.
Соответственно закон Ома переменного тока имеет вид:
( 14)
Сдвиг фаз между током и напряжением определяется отношением реактивного сопротивления к активному: .
Закон Ома для цепи
переменного тока можно получить,
используя метод векторной диаграммы
(рис.
5) на комплексной плоскости:
рис. 5
В такой цепи при совпадении частоты вынужденных колебаний, создаваемых источником переменного тока с резонансной частотой , индуктивное и емкостное сопротивление равны и полностью компенсируют друг друга, сила тока максимальна и наблюдается явление РЕЗОНАНСА. В условиях резонанса напряжения на индуктивности и емкости могут значительно (часто во много раз) превышать напряжение на зажимах цепи.
Упражнение 1. Исследование индуктивности и коэффициента мощности дросселя в цепи переменного тока.
рис. 6. Экспериментальная установка.
На рис.6 представлена схема экспериментальной установки для проведения соответствующих измерений. Дроссель с индуктивностью и активным сопротивлением питается от автотрансформатора ЛАТР. Измерительными приборами являются амперметр, вольтметр и ваттметр.
Полное сопротивление цепи определи по уравнению:
(15)
Показания измерительных приборов позволяют найти коэффициент мощности:
(16)
Активное сопротивление определяется по формуле:
(17)
Легко видеть, что индуктивность дросселя:
.
(18)
Если сопротивление соединительных проводов и обмоток дросселя обозначить , то потери энергии в сердечнике будет характеризоваться выражением:
, (19)
где — мощность, выделяемая в проводах.
Таким образом, для исследования цепи, содержащей индуктивность и активное сопротивление, следует найти индуктивность дросселя, коэффициент мощности и потери энергии в железном сердечнике дросселя.
Рекомендуется следующий порядок выполнения измерений:
Ознакомиться с устройством и принципом действия ваттметра (в нашем случае электродинамического типа) по техническому описанию; собрать схему по рис. 6, проверить правильность ее исполнения у лаборанта;
Записать в тетрадь значение активного сопротивления дросселя;
Пользуясь схемой рис.
6, определить индуктивность катушки
без ферромагнитного сердечника,
пользуясь соотношением:
6, определить индуктивность катушки
без ферромагнитного сердечника,
пользуясь соотношением:(20)
Вставить сердечник и при 3 – 5 значениях тока определить активное сопротивление (по формуле 17), коэффициент мощности (формула 16), индуктивность дросселя (18) и потери мощности в сердечнике (19). Полученные результаты внести в таблицу, в которую занести показания приборов, результаты измерений и погрешности определения измеряемых величин;
I, A | U, B | P, Вт | R, Ом | cosφ | L, Гн | N, Вт |
Согласно данным эксперимента постройте векторную диаграмму напряжений (рис.
5) на
индуктивности и активном сопротивлении.
5) на
индуктивности и активном сопротивлении.Физика для углубленного изучения. 2. Электродинамика. Оптика
Физика для углубленного изучения. 2. Электродинамика. Оптика
ОглавлениеВведениеI. ЭЛЕКТРОСТАТИКА § 1. Электрический заряд. Закон Кулона § 2. Электрическое поле. Напряженность поля § 3. Теорема Гаусса § 4. Потенциал электростатического поля. Энергия системы зарядов § 5. Расчет электрических полей § 6. Проводники в электрическом поле § 7. Силы в электростатическом поле § 8. Конденсаторы. Электроемкость § 9. Энергия электрического поля II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 10. Характеристики электрического тока. Закон Ома § 11. Соединение проводников в электрические цепи § 12. Закон Ома для неоднородной цепи § 13. Расчет цепей постоянного тока § 14. Работа и мощность постоянного тока § 15. Магнитное поле постоянного тока § 16. Действие магнитного поля на движущиеся заряды III.  ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ§ 17. Явление электромагнитной индукции § 18. Электрические машины постоянного тока § 19. Энергия магнитного поля § 20. Основы теории электромагнитного поля § 21. Квазистационарные явления в электрических цепях IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 22. Цепи переменного тока. Закон Ома § 23. Работа и мощность переменного тока. Передача электроэнергии § 24. Трехфазный ток. Электрические машины переменного тока V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ § 25. Колебательный контур § 26. Вынужденные колебания в контуре. Резонанс § 27. Незатухающие электромагнитные колебания § 28. Электромагнитные волны § 29. Свойства и применения электромагнитных волн VI. ОПТИКА § 30. Свет как электромагнитные волны. Интерференция § 31. Дифракция света § 32. Спектральные приборы. Дифракционная решетка § 33. Протяженные источники света § 34. Интерференция немонохроматического света § 35. Физические принципы голографии § 36.  Геометрическая оптика§ 37. Оптические приборы, формирующие изображение |
резисторов — Должен ли я принимать закон Ома как должное?
Закон Ома так же важен для ЭЭ, как уравнение относительности Эйнштейна (E = mc²) для физиков.
Он был создан 200 лет назад Георгом Омом, баварским физиком в 1824 году.
Позднее 20 уравнений Максвелла были объединены из многих других физических законов в полную теорию электромагнетизма. Они основаны на законах физики, которым следует вся линейная электроника. Позже Оливер Хевисайд объединил их в 4 уравнения, математически актуальные и сегодня.
Я помню, мы решали законы Ома на уроках из этих уравнений на уроках теории электромагнитного поля.
Эти уравнения также вдохновили Эйнштейна на разработку его законов относительности.
Значит ли это, что закон Ома верен для любого материала? №
Масштабирование зависит от постоянной проводимости материалов.
Материалы с нелинейностью могут быть вызваны утечкой через изолятор, экспоненциальными характеристиками полупроводника, но имеют линейное объемное сопротивление при насыщении, термические коэффициенты (tempco), напряжение пробоя, лавинные эффекты, магниторезистивные материалы и эффекты радиочастотных потерь, такие как скин-эффекты и вихревые колебания Текущие эффекты.
Имея опыт работы с перечисленными выше, вы также можете предсказать такое поведение и в некоторых случаях сделать постоянные предположения для R утечки конденсаторов, рассчитанных на максимальное напряжение, но следует понимать, что на это могут повлиять перегрев и старение. Ток утечки основан на химических законах Аррениуса и удваивается при повышении температуры на каждые 10 градусов Цельсия. Но кажущееся сопротивление коллектор-эмиттер, Rce, фиксируется по «раннему эффекту» (высокое сопротивление), когда Vce падает в сторону насыщения, достигает объемного сопротивления между границей металл-полупроводник Rce объемного сопротивления в качестве переключателя.
(от 1 до нескольких Ом для небольшого сигнального переключателя)
ESR — это эффективное последовательное сопротивление изоляторов, которые являются диэлектриками, как и конденсаторы. Это связано с границей раздела металл-изолятор и влияет на потери тепла в цоколях по закону Ома. То же самое верно для катушек с номинальным сопротивлением постоянному току или DCR, которые вызывают пусковой ток в двигателях.
Вы даже можете использовать закон Ома от постоянного тока к переменному и к высокочастотному, если вы понимаете нелинейные вклады, правила для реактивного импеданса в зависимости от f и нелинейные свойства материала..
Комбинация сопротивления R и реактивного сопротивления X равна полному сопротивлению Z(f)=R+X(f). Это ортогональные свойства, основанные на евклидовой векторной геометрии и законе Пифагора для гипотенузы R и X.
Но закон Ома по-прежнему применяется на каждой оси. Например, реактивное сопротивление 2 конденсаторов становится трансформатором напряжения переменного тока, так же как 2 пары катушек преобразуют напряжение.
Но катушки проводят тепло намного лучше, поэтому емкостные трансформаторы должны быть ограничены малыми токами, например, уменьшая 100 кВ до 100 В мониторов или 330 В до 6 В автономных преобразователей.
Означает ли это, что вы не можете эмпирически предсказать ни один компонент? Да , потому что вы не выучили зависимости для проводимости в нелинейном сопротивлении. В школе преподают основы линейных и экспоненциальных полупроводниковых материалов, затем вы изучаете нелинейные свойства материалов на собственном опыте, либо в лаборатории, либо на работе.
Значит ли это, что ваши измерения неверны? Не обязательно, но может быть. Часто линейные модели проводников слишком просты, так как металл имеет положительное увеличение сопротивления с температурой (1:10 для лампочки), или вы упустили из виду вторичные эффекты, разделяющие объемное сопротивление, или что-то еще.
OHMSLAWFORAC
OHMSLAWFORAC ЗАКОН ОМА ДЛЯ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
Правила и уравнения для цепей постоянного тока применяются к цепям переменного тока только тогда, когда
цепи содержат только сопротивление, как в случае с лампами и отоплением
элементы.
Для того, чтобы использовать действующие значения напряжения и тока в
цепи, влияние индуктивности и емкости с сопротивлением должно
быть на рассмотрении.
Совместное воздействие сопротивления, индуктивного сопротивления и емкостного сопротивления реактивное сопротивление составляет полное сопротивление току, протекающему в цепи переменного тока. Это полное сопротивление называется импедансом и обозначается буквой «З.» Единицей измерения импеданса является ом.
Серия Цепи переменного тока
| Если цепь переменного тока состоит только из сопротивления, значение импеданса совпадает с сопротивлением, а закон Ома для переменного тока цепи I = E/Z точно такая же, как и для цепи постоянного тока. На рис. 8-188 последовательная цепь, содержащая лампу с сопротивлением 11 Ом, соединенную между собой проиллюстрирован источник. Чтобы найти, какой ток будет течь, если 110 вольт применяется постоянный ток и какой ток будет течь при подаче 110 вольт переменного тока, решены следующие примеры: | |
Когда цепи переменного тока содержат сопротивление и индуктивность
или емкость, импеданс Z не совпадает с сопротивлением R. Импеданс цепи — это полное сопротивление цепи потоку
тока. В цепи переменного тока это противодействие состоит из сопротивления и
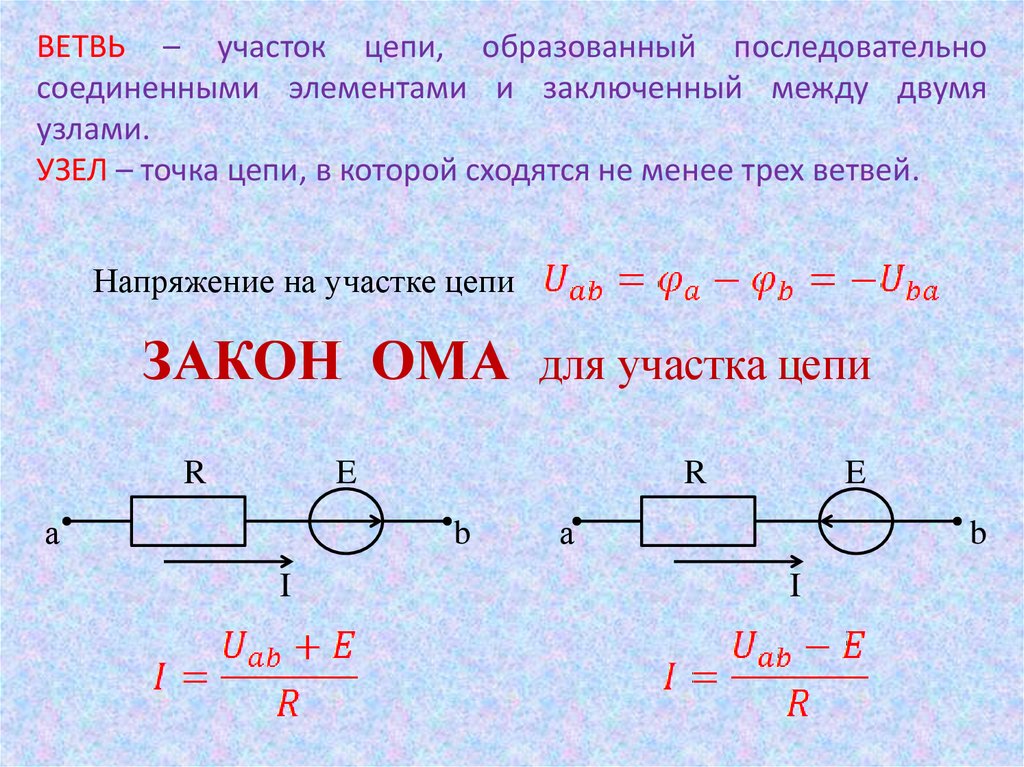
реактивное сопротивление, индуктивное или емкостное, или элементы того и другого.Сопротивление и реактивное сопротивление нельзя добавить напрямую, но их можно учитывать как две силы, действующие под прямым углом друг к другу. Таким образом, отношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать правильным треугольник, как показано на рисунке 8-189. | |
| | Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формула для нахождения импеданса или полного сопротивления току в цепи переменного тока можно найти, используя закон прямоугольных треугольников. Этот Теорема, называемая теоремой Пифагора, применима к любому прямоугольному треугольнику. Утверждается, что квадрат гипотенузы равен сумме квадратов двух других сторон.  Таким образом, стоимость любой стороны права
Треугольник можно найти, если известны две другие стороны. Если цепь переменного тока
содержит сопротивление и индуктивность, как показано на рис. 8-19.0, отношение
между сторонами можно определить как:
Квадратный корень из обеих частей уравнения дает | .
Эту формулу можно использовать для определения импеданса, когда значения
индуктивное сопротивление и сопротивление известны. Его можно изменить на
решить импеданс в цепях, содержащих емкостное реактивное сопротивление и сопротивление
подставив в формулу XC вместо XL. В цепях, содержащих
сопротивление как с индуктивным, так и с емкостным реактивным сопротивлением, реактивные сопротивления
можно комбинировать, но поскольку их действие в цепи прямо противоположно,
они объединяются вычитанием: Х = ХL — ХС или Х = ХС
— XL (меньшее число всегда вычитается из большего). В
рисунок 8-190, последовательная цепь, состоящая из сопротивления и индуктивности
соединенный последовательно подключается к источнику 110 вольт при 60 циклах
в секунду.
Резистивный элемент представляет собой лампу с сопротивлением 6 Ом, а
индуктивный элемент представляет собой катушку с индуктивностью 0,021 генри. Что
— значение импеданса и тока через лампу и
катушка?
Решение:
Сначала вычисляется индуктивное сопротивление катушки:
XL = 2 шт x ш x длина
XL = 6,28 х 60 х 0,021
XL = индуктивное сопротивление 8 Ом.
Далее вычисляется полное сопротивление:
Z = квадратный корень из R2 + XL2
Z = квадратный корень из 62 + 82
Z = квадратный корень из 36 + 64
Z = квадратный корень из 100
Z = импеданс 10 Ом.
Тогда текущий поток,
Падение напряжения на сопротивлении (ER)
ER = I x R
ER = 11 x 6 = 66 вольт.
Падение напряжения на индуктивности (EXL) составляет
РАСШ = I x ХL
EXL = 11 x 8 = 88 вольт.
Сумма двух напряжений больше подаваемого напряжения. Этот
возникает из-за того, что два напряжения не совпадают по фазе и, как таковые,
представляют максимальное напряжение. Если измерять напряжение в цепи
по вольтметру будет примерно 110 вольт, приложенное напряжение.
Это можно доказать уравнением
На рис. 8-191 показана последовательная цепь, в которой конденсатор 200 мкФ соединен последовательно с лампой на 10 Ом. Какова ценность импеданса, тока и падения напряжения на лампе? |
Решение:
Сначала емкость меняется с микрофарад на фарад. С 1
миллион микрофарад равен 1 фараду, тогда
Чтобы найти импеданс,
Чтобы найти ток,
Падение напряжения на лампе (ER) составляет
ER = 6,7 x 10
ER = 67 вольт
Падение напряжения на конденсаторе (EXC) составляет
Сумма этих двух напряжений не равна приложенному напряжению, так как
ток опережает напряжение.
Чтобы найти приложенное напряжение, формула
ET = используется квадратный корень из (ER)2 + (EXC)2.
Когда цепь содержит сопротивление, индуктивность и емкость, уравнение
Z = квадратный корень из R2 + (XL — XC)2
используется для определения импеданса.
Пример:
Чему равно сопротивление последовательной цепи (рис. 8-192), состоящей из конденсатора с реактивным сопротивлением 7 Ом, катушки индуктивности с реактивным сопротивлением сопротивлением 10 Ом, а резистор сопротивлением 4 Ом?
Предположим, что реактивное сопротивление конденсатора равно 10 Ом, а реактивное сопротивление катушки индуктивности 7 Ом, то XC больше XL. Таким образом,
Параллельные цепи переменного тока
Методы решения задач параллельных цепей переменного тока
в основном такие же, как и для последовательных цепей переменного тока.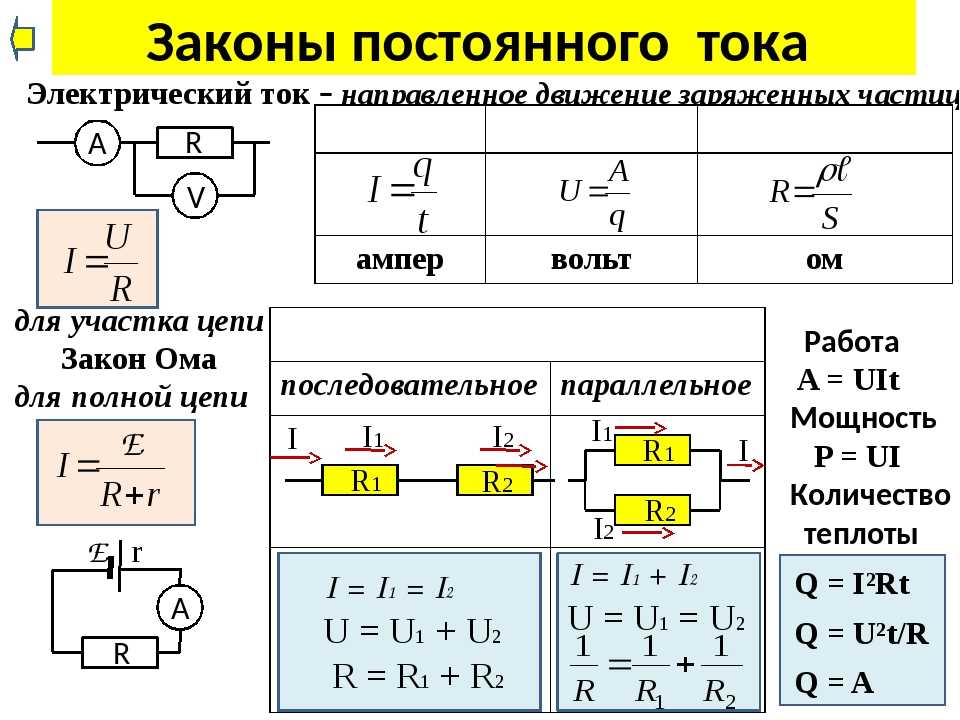 Не в фазе
напряжения и токи можно сложить, используя закон прямоугольных треугольников,
но при решении схемных задач токи по ветвям равны
добавлено, так как падение напряжения на разных ветвях одинаково
и равны приложенному напряжению. На рис. 8-193, параллельная цепь переменного тока
схематично показана индуктивность и сопротивление. Электрический ток
ток, протекающий через индуктивность IL, составляет 0,0584 ампера, а ток, протекающий
через сопротивление 0,11 ампер. Каков общий ток в
схема? |
Решение:
Поскольку индуктивное сопротивление заставляет напряжение опережать ток, общее ток, который содержит компонент индуктивного тока, отстает от приложенного Напряжение. Если ток и напряжение нанесены на график, угол между два, называемые фазовым углом, иллюстрируют величину, на которую ток отстает от Напряжение.
На рис. 8-194 генератор на 110 вольт подключен к нагрузке, состоящей из
емкостью 2 и
сопротивление 10000 Ом параллельно.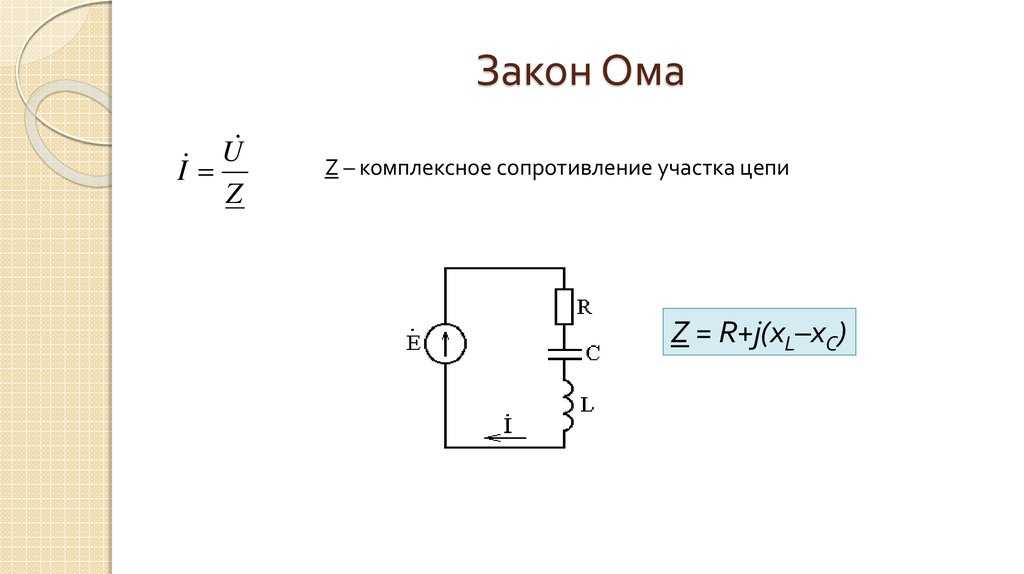
Каково значение импеданса
и общий ток?
Решение:
Сначала найдите емкостное сопротивление цепи:
Преобразование 2 в фарады и ввод значений в приведенную формулу:
Чтобы найти импеданс, формула импеданса, используемая в последовательной цепи переменного тока должны быть изменены, чтобы соответствовать параллельной схеме:
Чтобы найти ток через емкость:
Чтобы найти ток, протекающий через сопротивление:
Чтобы найти ток, протекающий через сопротивление:
Чтобы найти полный ток в цепи:
Резонанс
Было показано, что оба индуктивных сопротивления (XL = 2 f L) и емкостное сопротивление
являются функциями частоты переменного тока. Уменьшение частоты
уменьшается омическое значение индуктивного сопротивления, но уменьшение
частота увеличивает емкостное сопротивление. На определенной частоте
известная как резонансная частота, реактивные эффекты конденсатора и
индуктор будет равен.
Поскольку эти эффекты противоположны одному
другой, отменят, оставив только омическое значение сопротивления
противодействовать току в цепи. Если значение сопротивления мало
или состоит только из сопротивления в проводниках, значения тока
поток может стать очень высоким.
В цепи, где катушка индуктивности и конденсатор включены последовательно, а частота – это резонансная частота, или частота резонанса, контура говорят, что он находится «в резонансе» и называется последовательным резонансным контуром. Символ резонансной частоты — Fn.
Если на частоте резонанса индуктивное сопротивление равно к емкостному сопротивлению, то
Разделив обе стороны на 2 фл,
Извлечение квадратного корня из обеих частей дает
Где Fn — резонансная частота в циклах в секунду, C — емкость
в фарадах, а L — индуктивность в генри. По этой формуле частота
при котором конденсатор и катушка индуктивности будут резонансными, можно определить.
Чтобы найти индуктивное сопротивление цепи, используйте
Формула импеданса, используемая в последовательной цепи переменного тока, должна быть изменена на подойдет параллельная схема.
Найти параллельные сети индуктивных и емкостных реакторов использовать
Для поиска параллельных сетей с емкостным сопротивлением и индуктивностью использовать:
Поскольку на резонансной частоте XL отменяет XC, ток может стать
очень большой, в зависимости от величины сопротивления. В таких случаях напряжение
падение на катушке индуктивности или конденсаторе часто будет выше, чем приложенное
Напряжение.
| В параллельном резонансном контуре (рис. 8-195) реактивные сопротивления
равны, и через катушку и конденсатор будут протекать одинаковые токи. Поскольку индуктивное сопротивление заставляет ток через катушку
отстает от напряжения на 90 °, а емкостное сопротивление вызывает ток
через конденсатор, чтобы опережать напряжение на 90°, два тока
сдвинуты по фазе на 180°. |
Отменяющий эффект таких токов будет
означает, что ток не будет течь от генератора и параллельной комбинации
катушки индуктивности и конденсатора будет казаться бесконечным импедансом.
На практике такая схема невозможна, так как некоторое значение сопротивления
присутствует всегда, а параллельная цепь, иногда называемая баковой схемой,
действует как очень высокое сопротивление. Его также называют антирезонансным контуром,
поскольку его действие в цепи противоположно действию последовательного резонансного
цепь, в которой полное сопротивление очень низкое.
