Что такое закон Ома для полной цепи. Какова формула закона Ома для полной цепи. Как применяется закон Ома для полной цепи на практике. Какие особенности есть у закона Ома для полной цепи.
Что такое закон Ома для полной цепи
Закон Ома для полной цепи — это фундаментальный физический закон, который устанавливает связь между силой тока, электродвижущей силой (ЭДС) источника и полным сопротивлением замкнутой электрической цепи. Он был открыт немецким физиком Георгом Омом в 1826 году и является расширением закона Ома для участка цепи.
Основное отличие закона Ома для полной цепи от закона Ома для участка цепи заключается в том, что он учитывает не только внешнее сопротивление нагрузки, но и внутреннее сопротивление источника тока. Это позволяет более точно описать процессы, происходящие в реальных электрических цепях.
Формула закона Ома для полной цепи
Математически закон Ома для полной цепи выражается следующей формулой:
I = ε / (R + r)
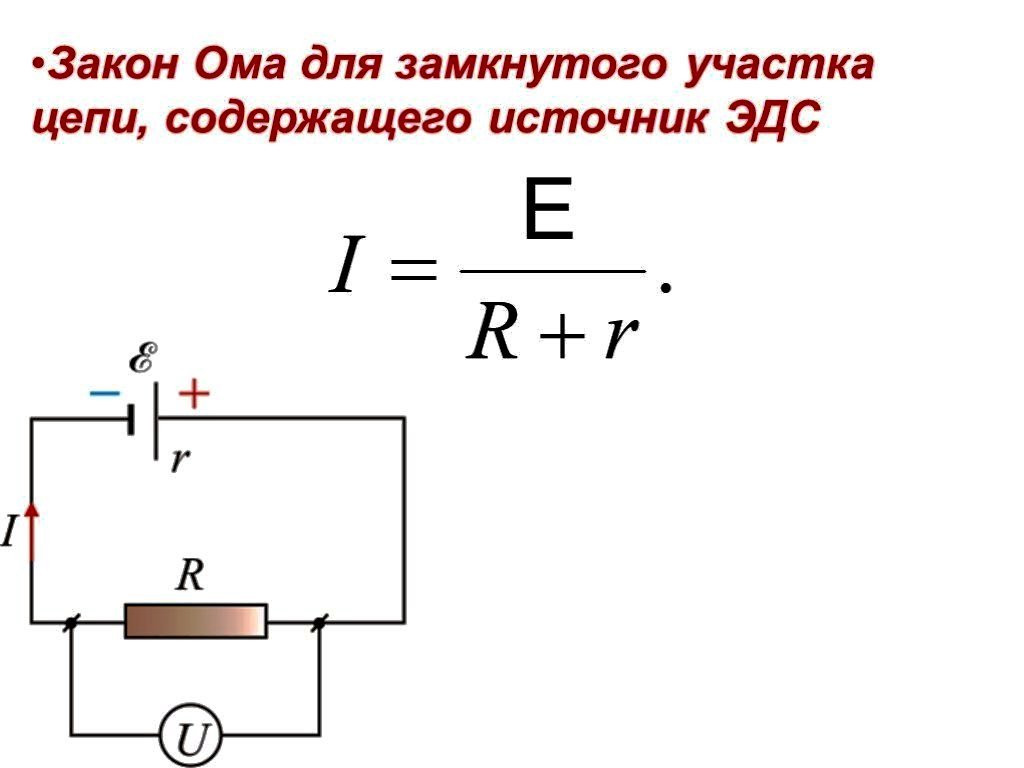
Где:
- I — сила тока в цепи
- ε — электродвижущая сила источника тока
- R — внешнее сопротивление цепи (сопротивление нагрузки)
- r — внутреннее сопротивление источника тока
Эта формула показывает, что сила тока в замкнутой цепи прямо пропорциональна ЭДС источника и обратно пропорциональна сумме внешнего и внутреннего сопротивлений.
Применение закона Ома для полной цепи
Закон Ома для полной цепи широко применяется в электротехнике и электронике для расчета параметров электрических цепей. Основные области его применения включают:
- Расчет силы тока в замкнутых электрических цепях
- Определение внутреннего сопротивления источников тока
- Анализ работы электрических генераторов и аккумуляторов
- Оптимизация электрических схем для максимальной передачи мощности
- Расчет падения напряжения на участках цепи
Особенности закона Ома для полной цепи
При использовании закона Ома для полной цепи важно учитывать следующие особенности:- Он применим только для замкнутых электрических цепей
- Учитывает внутреннее сопротивление источника тока, в отличие от закона Ома для участка цепи
- Позволяет рассчитать максимальную силу тока при коротком замыкании
- Показывает, что напряжение на полюсах источника зависит от силы тока в цепи
- Дает возможность определить КПД источника тока
Короткое замыкание и закон Ома для полной цепи
Одно из важных применений закона Ома для полной цепи — анализ ситуации короткого замыкания. При коротком замыкании внешнее сопротивление R стремится к нулю, и формула закона принимает вид:

Iкз = ε / r
Где Iкз — ток короткого замыкания. Эта формула показывает, что при коротком замыкании сила тока ограничивается только внутренним сопротивлением источника. Чем меньше внутреннее сопротивление, тем больше ток короткого замыкания, что может представлять опасность для электрических устройств.
Напряжение на полюсах источника
Закон Ома для полной цепи позволяет рассчитать напряжение на полюсах источника тока в зависимости от силы тока в цепи. Это выражается формулой:
U = ε — Ir
Где U — напряжение на полюсах источника. Эта формула показывает, что напряжение на полюсах источника уменьшается с увеличением силы тока из-за падения напряжения на внутреннем сопротивлении.
КПД источника тока
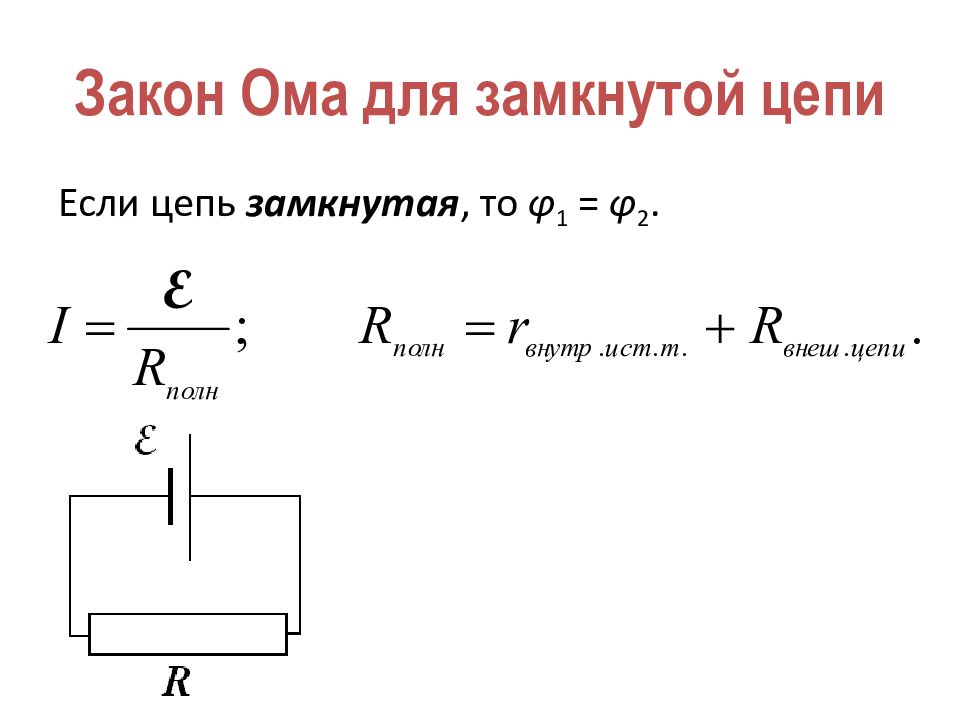
С помощью закона Ома для полной цепи можно рассчитать коэффициент полезного действия (КПД) источника тока. КПД определяется как отношение мощности, выделяемой во внешней цепи, к полной мощности источника:
η = (I²R) / (I²R + I²r) = R / (R + r)
Где η — КПД источника тока. Эта формула показывает, что КПД источника тока зависит от соотношения внешнего и внутреннего сопротивлений.
Ограничения закона Ома для полной цепи
Хотя закон Ома для полной цепи широко применяется, у него есть некоторые ограничения:
- Он применим только для постоянного тока или для переменного тока низкой частоты
- Не учитывает нелинейные эффекты, возникающие в некоторых электронных компонентах
- Предполагает, что внутреннее сопротивление источника постоянно, что не всегда верно для реальных источников
- Не учитывает электромагнитные эффекты, которые могут возникать в цепях с высокой частотой или большой силой тока
Несмотря на эти ограничения, закон Ома для полной цепи остается мощным инструментом для анализа и расчета электрических цепей в большинстве практических ситуаций.
Закон Ома для полной цепи
Закон Ома для полной цепи – эмпирический (полученный из эксперимента) закон, который устанавливает связь между силой тока, электродвижущей силой (ЭДС) и внешним и внутренним сопротивлением в цепи.
При проведении реальных исследований электрических характеристик цепей с постоянным током необходимо учитывать сопротивление самого источника тока. Таким образом в физике осуществляется переход от идеального источника тока к реальному источнику тока, у которого есть свое сопротивление (см. рис. 1).
Рис. 1. Изображение идеального и реального источников тока
Рассмотрение источника тока с собственным сопротивлением обязывает использовать закон Ома для полной цепи.
Сформулируем закона Ома для полной цепи так (см. рис. 2): сила тока в полной цепи прямо пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи, где под полным сопротивлением понимается сумма внешних и внутренних сопротивлений.
Рис. 2. Схема закона Ома для полной цепи.
Формула закона Ома для полной цепи
- R – внешнее сопротивление [Ом];
- r – сопротивление источника ЭДС (внутреннее) [Ом];
- I – сила тока [А];
- ε– ЭДС источника тока [В].
Рассмотрим некоторые задачи на данную тему. Задачи на закон Ома для полной цепи, как правило, дают ученикам 10 класса, чтобы они могли лучше усвоить указанную тему.
I. Определите силу тока в цепи с лампочкой, сопротивлением 2,4 Ом и источником тока, ЭДС которого равно 10 В, а внутреннее сопротивление 0,1 Ом.
По определению закона Ома для полной цепи, сила тока равна:
II. Определить внутреннее сопротивление источника тока с ЭДС 52 В. Если известно, что при подключении этого источника тока к цепи с сопротивлением 10 Ом амперметр показывает значение 5 А.
Запишем закон Ома для полной цепи и выразим из него внутреннее сопротивление:
III. Однажды школьник спросил у учителя по физике: «Почему батарейка садится?» Как грамотно ответить на данный вопрос?
Мы уже знаем, что реальный источник обладает собственным сопротивлением, которое обусловлено либо сопротивлением растворов электролитов для гальванических элементов и аккумуляторов, либо сопротивлением проводников для генераторов.
следовательно, ток в цепи может уменьшаться либо из-за уменьшения ЭДС, либо из-за повышения внутреннего сопротивления. Значение ЭДС у аккумулятора почти постоянный. Следовательно, ток в цепи понижается за счет повышения внутреннего сопротивления. Итак, «батарейка» садится, так как её внутреннее сопротивление увеличивается.
Закон Ома для полной (замкнутой) цепи
Закон Ома для полной цепи определяет значение тока в реальной цепи, который зависит не только от сопротивления нагрузки, но и от сопротивления самого источника тока. Другое название этого закона — закон Ома для замкнутой цепи. Рассмотрим смысл закона Ома для полной цепи более подробно.
Потребители электрического тока (например, электрические лампы) вместе с источником тока образуют замкнутую электрическую цепь. На рисунке 1 показана замкнутая электрическая цепь, состоящая из автомобильного аккумулятора и лампочки.
Рисунок 1. Замкнутая цепь, поясняющея закон Ома для полной цепи.
Замкнутая цепь, поясняющея закон Ома для полной цепи.
Ток, проходящий через лампочку, проходит также и через источник тока. Следовательно, проходя по цепи, ток кроме сопротивления проводника встретит еще и то сопротивление, которое ему будет оказывать сам источник тока (сопротивление электролита между пластинами и сопротивление пограничных слоев электролита и пластин). Следовательно, общее сопротивление замкнутой цепи будет складываться из сопротивления лампочки и сопротивления источника тока.
Сопротивление нагрузки, присоединенной к источнику тока, принято называть внешним сопротивлением, а сопротивление самого источника тока —
Если по цепи, изображенной на рисунке 1, протекает ток I, то для поддержания этого тока во внешней цепи согласно закону Ома между ее концами должна существовать разность потенциалов, равная I*R. Но этот же ток I протекает и по внутренней цепи.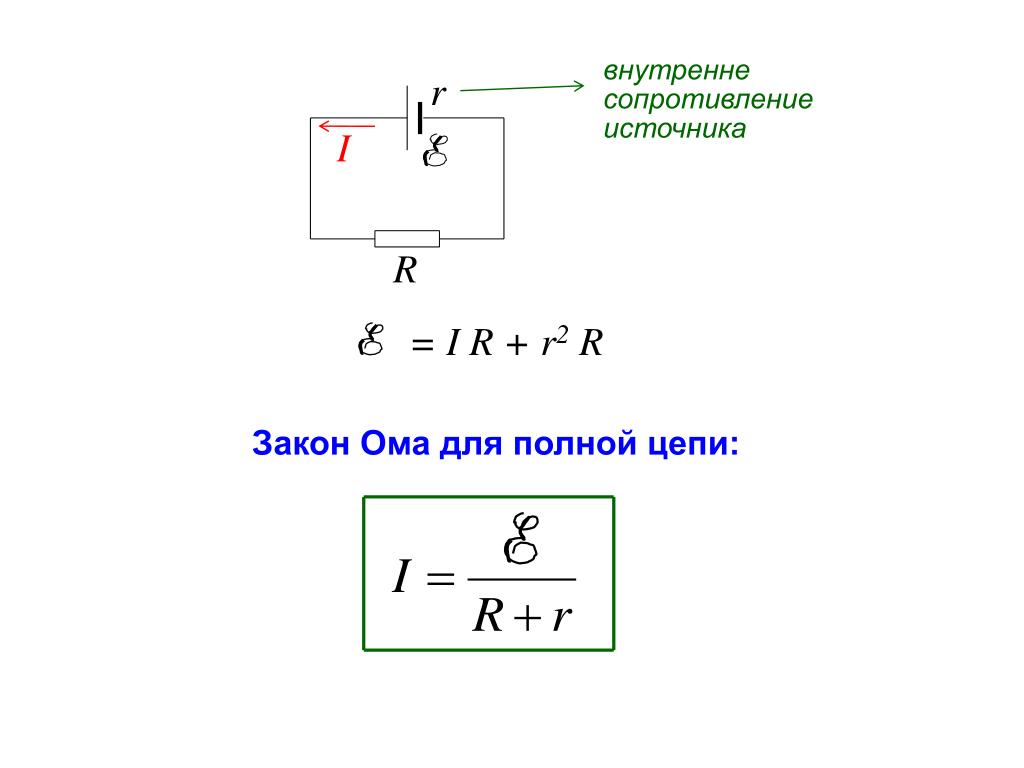 Следовательно, для поддержания тока во внутренней цепи, также необходимо существование разности потенциалов между концами сопротивления r. Эта разность потенциалов па закону Ома должна быть равна I*r.
Следовательно, для поддержания тока во внутренней цепи, также необходимо существование разности потенциалов между концами сопротивления r. Эта разность потенциалов па закону Ома должна быть равна I*r.
Поэтому для поддержания тока в цепи электродвижущая сила (ЭДС) аккумулятора должна иметь величину:
E=I*r+I*R
Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:
E=I(r+R)
или
I=E/(r+R)
Две последние формулы выражают закона Ома для полной цепи.
Закон Ома для полной замкнутой цепи формулируется так: сила тока в замкнутой цепи прямо пропорциональна ЭДС в цепи и обратно пропорциональна общему сопротивлению цепи.
Под общим сопротивлением подразумевается сумма внешнего и внутреннего сопротивлений.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Закон Ома
В 1826 величайший немецкий физик Георг Симон Ом публикует свою работу «Определение закона, по которому металлы проводят контактное электричество», где дает формулировку знаменитому закону. Ученые того времени встретили враждебно публикации великого физика. И лишь после того, как другой ученый – Клод Пулье, пришел к тем же выводам опытным путем, закон Ома признали во всем мире.
Ученые того времени встретили враждебно публикации великого физика. И лишь после того, как другой ученый – Клод Пулье, пришел к тем же выводам опытным путем, закон Ома признали во всем мире.
Закон Ома – физическая закономерность, которая определяет взаимосвязь между током, напряжением и сопротивлением проводника. Он имеет две основные формы.
Закон Ома для участка цепи
Формулировка закона Ома для участка цепи – сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению.
Это простое выражение помогает на практике решать широчайший круг вопросов. Для лучшего запоминания решим задачу.
Задача 1.1
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.
Задача простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.
Приступим.
Закон Ома для полной цепи
Формулировка закона Ома для полной цепи — сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.
Здесь могут возникнуть вопросы. Например, что такое ЭДС? Электродвижущая сила — это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электродвижущая говорит о том, что эта сила двигает электричество, то есть заряд.
В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.
Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.
А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.
Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.
Задача 2.1
Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.
Теперь решим задачу посложнее.
Задача 2.2
Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм2. Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.
Приступим.
Мнемоническая диаграмма
Для лучшего запоминания закона Ома существует мнемоническая диаграмма, благодаря которой можно всегда напомнить себе формулу. Пользоваться этой диаграммой очень просто. Достаточно закрыть искомую величину и две другие укажут, как её найти. Потренируйтесь, это может вам пригодится.
Достаточно закрыть искомую величину и две другие укажут, как её найти. Потренируйтесь, это может вам пригодится.
Успехов в изучении электричества! Рекомендуем прочесть статью — законы Кирхгофа.
формулы и определения / Блог / Справочник :: Бингоскул
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
- I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=\frac{U}{R}
- U — напряжение (в системе СИ измеряется — Вольт)
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.

- Формула: U=IR
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
- R — электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=\frac{U}{I}
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=\frac{\varepsilon}{R+r}
- \varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.

Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Закон Ома для полной цепи | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
| Рис. 5.19. Внутренняя и внешняя части электрической цепи |
Рассмотрим замкнутую электрическую цепь, состоящую из двух частей: собственно источника с электродвижущей силой Ɛ и внутренним сопротивлением r и внешней части цепи — проводника с сопротивлением R (рис. 5.19).
5.19).
Закон Ома для полной цепи устанавливает зависимость силы тока в замкнутой цепи I от электродвижущей силы источника Ɛ и полного сопротивления цепи R + r. Эту зависимость можно установить на основании закона сохранения энергии и закона Джоуля-Ленца. Если через поперечное сечение проводника за время Δt заряженными частицами переносится заряд Δq, то работа сторонних сил
Aст. = ƐΔq = ƐIΔt.
Если в цепи электрическая энергия превращается лишь в тепловую, то по закону сохранения энергии Аст. = Q и общее количество теплоты, выделяющееся в замкнутой цепи, равно сумме количеств теплоты, выделяющихся во внешней и внутренней частях цепи
Q = I2RΔt + I2rΔt.
Если
Aст. = Q = (Ɛ / R + r) • IΔt,
= Q = (Ɛ / R + r) • IΔt,
то
ƐIΔt = I2RΔt + I2rΔt.
Итак,
Ɛ = IR + Ir
и
I = Ɛ / (R + r),
что и выражает закон Ома для полной цепи.
Закон Ома для полной цепи. Сила тока в замкнутой цепи измеряется отношением электродвижущей силы источника тока, имеющегося в этой цепи, к полному ее сопротивлению.
Из сказанного выше можно сделать вывод, что
закон Ома для полной цепи является одним из выражений закона сохранения энергии.
Во многих случаях для характеристики источников тока недостаточно использовать лишь ЭДС. Пусть, например, необходимо установить, ток какой максимальной силы может дать определенный источник тока. Если исходить из закона Ома для полной цепи
I = Ɛ / (R + r), Материал с сайта http://worldofschool. ru
ru
то очевидно, что максимальной сила тока в цепи будет тогда, когда внешнее сопротивление цепи R стремится к нулю — это короткое замыкание в цепи. При этом ток короткого замыкания имеет силу Imax = Ɛ / r, поскольку Ɛ и r изменить для данного источника мы не можем, они являются характеристиками источника.
Если представить, что сопротивление внешней части цепи стремится к бесконечности (цепь становится разомкнутой), то напряжение на полюсах источника тока IR стремится к электродвижущей силе, то есть:
электродвижущая сила источника тока равна напряжению на полюсах разомкнутого источника.
На этой странице материал по темам:Закон ома для полной цепи при параллельном соединении
Закон ома при смешанном соединении
Реферат закон ома на полной цепи
Шпаргалка закон ома, что такое ток
Закон ома при параллельном соединении источников
Как определяется работа сторонних сил?
Сформулируйте закон Ома для полной цепи.

Запишите формулу закона Ома для полной цепи.
Что такое ток короткого замыкания?
Как можно определить ток короткого замыкания?
Как связаны между собой максимально возможное напряжение на полюсах источника и электродвижущая сила источника?
Закон Ома для полной цепи
1. Источник тока
При прохождении тока в проводнике выделяется некоторое количество теплоты. Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.
Может ли источником этой энергии быть электростатическое поле? Нет, не может, потому что при перемещении заряда вдоль всей цепи, то есть по замкнутой траектории, работа электростатического поля равна кулю.
Следовательно, для существования тока в замкнутой цепи в ней должен быть участок, на котором свободные заряды движутся против сил электростатического поля. Таким участком цепи является источник тока (рис. 59.1).
59.1).
В источнике тока на свободные заряды действуют силы, которые имеют не электростатическую природу. Их называют сторонними силами. В результате действия сторонних сил происходит разделение зарядов: на одном полюсе источника тока накапливается положительный заряд, а на другом – отрицательный. Вследствие этого возникает электростатическое поле, которое движет свободные заряды в электрической цепи вне источника тока, то есть во внешней цепи.
В химических источниках тока сторонние силы имеют химическую природу. Например, если погрузить цинковый и медный электроды в серную кислоту, то положительные ионы цинка будут чаще покидать электрод, чем положительные ионы меди. В результате между медным и цинковым электродами возникнет разность потенциалов: потенциал медного электрода будет больше, чем цинкового. Медный электрод станет положительным полюсом источника тока, а цинковый – отрицательным.
В генераторах электростанций сторонними силами являются силы, действующие на свободные электроны в металле со стороны вихревого электрического поля, порождаемого переменным магнитным полем. Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.
Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.
Электродвижущая сила источника тока
В источнике тока сторонние силы, перемещая свободные заряды против действия сил электростатического поля, совершают работу, которую мы обозначим Aстор.
Эта работа пропорциональна заряду q, который перемещается вдоль цепи за данный промежуток времени. Поэтому отношение работы сторонних сил к величине заряда не зависит ни от Aстор, ни от q. Следовательно, оно является характеристикой источника тока. Это отношение называют электродвижущей силой источника (ЭДС) и обозначают ξ:
ξ = Aстор/q. (1)
(Это название не совсем удачно, потому что ЭДС – не «сила» в механическом смысле, а энергетическая характеристика источника.)
ЭДС, как и напряжение, измеряют в вольтах. Например, ЭДС батарейки составляет несколько вольт.
2.
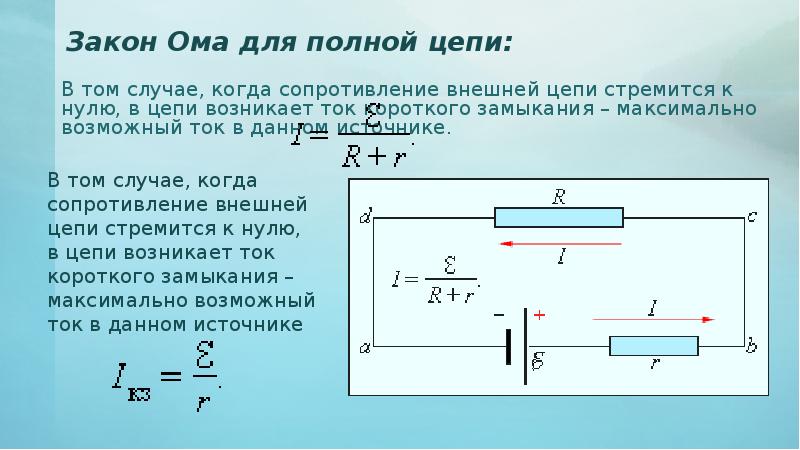 Закон Ома для полной цепи
Закон Ома для полной цепиЕсли сила тока в цепи равна I, то за время t по цепи проходит заряд q = It. Поэтому формулу (1) можно записать в виде
Aстор = ξIt. (2)
При этом во внешней цепи сопротивлением R выделяется количество теплоты
Qвнеш = I2Rt, (3)
а внутри источника тока выделяется количество теплоты
Qвнутр = I2rt, (4)
где r – сопротивление источника, которое называют его внутренним сопротивлением.
Из закона сохранения энергии следует, что
Qвнеш + Qвнутр = Aстор. (5)
? 1. Докажите, что из формул (2) – (5) следует:
I = ξ / (R + r). (6)
Это соотношение называют законом Ома для полной цепи.
Сумму сопротивлений R + r называют полным сопротивлением цепи.
? 2. ЭДС источника тока 12 В, а его внутреннее сопротивление равно 2 Ом.
а) Чему равна сила тока в цепи, если сопротивление внешней цепи равно 4 Ом?
б) Какова максимально возможная сила тока в цепи? При каком сопротивлении внешней цепи это имеет место?
? 3.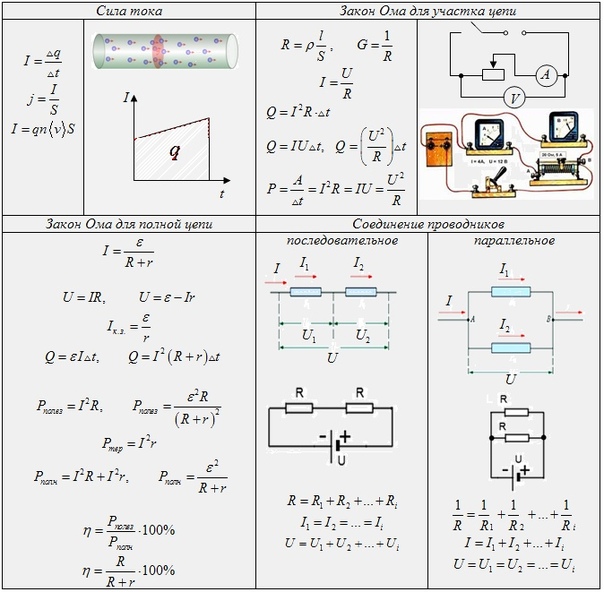 При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А.
При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А.
а) Чему равно внутреннее сопротивление источника?
б) Чему равна ЭДС источника?
Напряжение на полюсах источника
Закон Ома для полной цепи можно записать в виде
ξ = IR + Ir. (7)
Первое слагаемое в этой формуле согласно закону Ома для участка цепи равно напряжению U на полюсах источника тока:
IR = U.
Поэтому формулу (7) можно записать в виде
U = ξ – Ir. (8)
Формула (8) выражает зависимость напряжения U на полюсах источника тока от силы тока I в цепи.
Поставим опыт
Зависимость U(I) можно измерить на опыте, изменяя силу тока в цепи с помощью реостата (рис. 59.2, а, б). Красная пунктирная линия на схеме 59.2, б показывает, как идет ток в реостате. Например, если ползунок реостата, изображенного на рисунке 59,2, а, сдвинуть вправо, то сопротивление реостата увеличится, потому что увеличится длина обмотки, по которой идет ток.
? 4. На рисунке 59.3 изображен график зависимости U(I) для некоторого источника тока.
а) Чему равна ЭДС этого источника тока?
б) Чему равна наибольшая сила тока?
в) Чему равно внутреннее сопротивление источника тока?
г) Чему равно внешнее сопротивление, когда сила тока равна нулю?
д) Чему равно внешнее сопротивление, когда сила тока максимальна?
е) Чему равно внешнее сопротивление при I = 1,5 А?
Максимальное напряжение на полюсах источника равно ξ. Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).
Следовательно, напряжение между разомкнутыми полюсами источника тока равно ЭДС этого источника.
Минимальное же напряжение между полюсами источника равно нулю. Это имеет место при коротком замыкании, когда внешнее сопротивление R = 0. В этом случае сила тока максимальна. Ее называют силой тока короткого замыкания.
? 5. Покажите, что сила тока короткого замыкания выражается формулой
Покажите, что сила тока короткого замыкания выражается формулой
Iка = ξ/r. (9)
Подсказка. Воспользуйтесь законом Ома для полной цепи.
Из формулы (9) видно, что при очень малом внутреннем сопротивлении источника (как, например, у автомобильного аккумулятора) сила тока короткого замыкания будет очень большой, что может вывести источник тока из строя.
? 6. Сила тока при коротком замыкании батарейки равна 2 А. Когда к батарейке подключили резистор сопротивлением 4 Ом, сила тока стала равной 1 А.
а) Как изменилось полное сопротивление цепи?
б) Чему равно внутреннее сопротивление батарейки?
Измерив напряжение на полюсах источника и силу тока в цепи при двух различных значениях сопротивления внешней цепи, можно найти ЭДС ξ и внутреннее сопротивление r источника тока. Это можно сделать графически и аналитически.
? 7. При силе тока в цепи 2 А напряжение на полюсах источника равно 8 В, а при силе тока 4 А напряжение на полюсах равно 4 В.
а) Постройте систему координат I, U и нанесите две точки графика зависимости U(I) согласно приведенным данным.
б) Проведите прямую через эти точки и отметьте точки пересечения этой прямой с осями координат. Используя этот график, найдите, чему равны ЭДС, сила тока короткого замыкания и внутреннее сопротивление источника тока.
в) Используя уравнение (8), составьте систему двух уравнений с двумя неизвестными ξ и r и решите ее.
3. КПД источника тока
Работу тока во внешней цепи называют полезной работой. Обозначим ее Aпол. Используя формулу для работы тока, получаем:
Aпол = I2Rt.
Поскольку источник обладает внутренним сопротивлением, полезная работа меньше работы сторонних сил, потому что часть работы сторонних сил расходуется на выделение в источнике тока количества теплоты I2rt. Поскольку
Aстор = I2Rt + I2rt,
получаем для отношения полезной работы к работе сторонних сил:
η = Aпол / Aстор = (I2Rt) / (I2Rt + I2rt) = R / (R + r).
Это отношение, выраженное в процентах, называют КПД источника тока.
? 8. При каком отношении внешнего сопротивления к внутреннему сопротивлению КПД источника тока равен: 50 %; 80 %? Почему случай, когда КПД источника тока равен 100 %, не представляет практического интереса?
Дополнительные вопросы и задания
9. На рисунке 59.4 изображена схема измерения зависимости напряжения U на полюсах источника тока от силы тока I. Амперметр и вольтметр считайте идеальными. Сопротивление всей обмотки реостата 16 Ом. При первом положении ползунка реостата показания приборов 3 А и 8 В, а при втором положении – 2 А и 12 В.
а) Как сдвинули ползунок реостата между первым и вторым измерениями – влево или вправо?
б) Чему равны ЭДС источника тока и его внутреннее сопротивление?
в) Каковы будут показания приборов, если ползунок реостата передвинуть в крайнее левое положение? в крайнее правое?
10. При силе тока 6 А мощность тока во внешней цепи равна 90 Вт, а при силе тока 2 А она равна 60 Вт.
а) Чему равна ЭДС источника тока?
б) Чему равно внутреннее сопротивление источника тока?
в) Чему равно напряжение на полюсах источника в первом и втором случаях?
г) Чему равен КПД источника тока в первом и втором случаях?
Закон Ома. Для цепей и тока. Формулы и применение
Георг Симон Ом начал свои исследования вдохновляясь знаменитым трудом Жана Батиста Фурье «Аналитическая теория тепла». В этой работе Фурье представлял тепловой поток между двумя точками как разницу температур, а изменение теплового потока связывал с его прохождением через препятствие неправильной формы из теплоизолирующего материала. Аналогично этому Ом обуславливал возникновение электрического тока разностью потенциалов.
История
Исходя из этого Ом стал экспериментировать с разными материалами проводника. Для того, чтобы определить их проводимость он подключал их последовательно и подгонял их длину таким образом, чтобы сила тока была одинаковой во всех случаях.
Важно при таких измерениях было подбирать проводники одного и того же диаметра.
 Ом, замеряя проводимость серебра и золота, получил результаты, которые по современным данным не отличаются точностью. Так, серебряный проводник у Ома проводил меньше электрического тока, чем золотой. Сам Ом объяснял это тем, что его проводник из серебра был покрыт маслом и из-за этого, по всей видимости, опыт не дал точных результатов.
Ом, замеряя проводимость серебра и золота, получил результаты, которые по современным данным не отличаются точностью. Так, серебряный проводник у Ома проводил меньше электрического тока, чем золотой. Сам Ом объяснял это тем, что его проводник из серебра был покрыт маслом и из-за этого, по всей видимости, опыт не дал точных результатов.Однако не только с этим были проблемы у физиков, которые в то время занимались подобными экспериментами с электричеством. Большие трудности с добычей чистых материалов без примесей для опытов, затруднения с калибровкой диаметра проводника искажали результаты тестов. Еще большая загвоздка состояла в том, что сила тока постоянно менялась во время испытаний, поскольку источником тока служили переменные химические элементы. В таких условиях Ом вывел логарифмическую зависимость силы тока от сопротивления провода.
Немногим позже немецкий физик Поггендорф, специализировавшийся на электрохимии, предложил Ому заменить химические элементы на термопару из висмута и меди. Ом начал свои эксперименты заново. В этот раз он пользовался термоэлектрическим устройством, работающем на эффекте Зеебека в качестве батареи. К нему он последовательно подключал 8 проводников из меди одного и того же диаметра, но различной длины. Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.
Ом начал свои эксперименты заново. В этот раз он пользовался термоэлектрическим устройством, работающем на эффекте Зеебека в качестве батареи. К нему он последовательно подключал 8 проводников из меди одного и того же диаметра, но различной длины. Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.
В результате нового эксперимента Ом пришел к формуле:
Х = a / b + l
Здесь X – интенсивность магнитного поля провода, l – длина провода, a – постоянная величина напряжения источника, b – постоянная сопротивления остальных элементов цепи.
Если обратиться к современным терминам для описания данной формулы, то мы получим, что Х – сила тока, а – ЭДС источника, b + l – общее сопротивление цепи.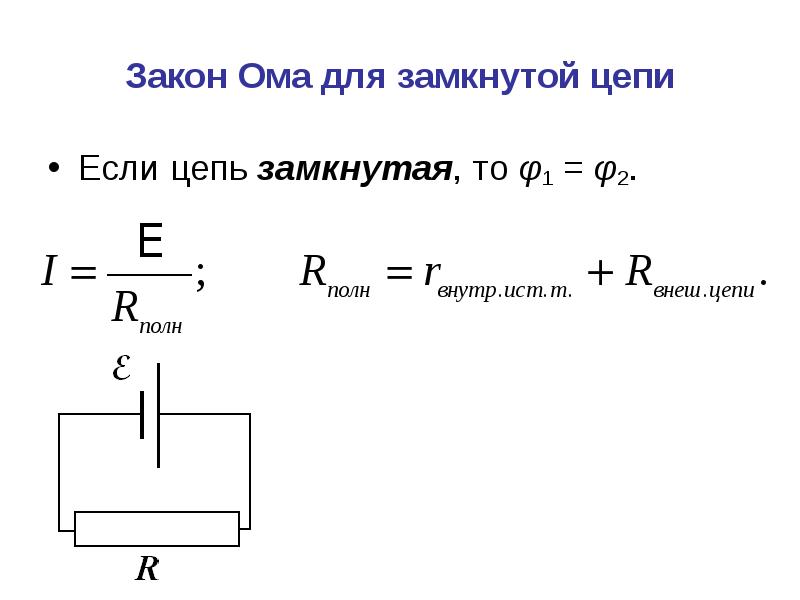
Закон Ома для отдельного участка цепи гласит: сила тока на участке цепи увеличивается при возрастании напряжения и уменьшается при возрастании сопротивления этого участка.
I = U / R
Исходя из этой формулы, мы можем решить, что сопротивление проводника зависит от разности потенциалов. С точки зрения математики, это правильно, но ложно с точки зрения физики. Эта формула применима только для расчета сопротивления на отдельном участке цепи.
Чтобы рассчитать сопротивление проводника, нужно перемножить его длину на удельное сопротивление его материала и разделить на площадь поперечного сечения.
Таким образом формула для расчета сопротивления проводника примет вид:
R = p ⋅ l / s
Закон Ома для полной цепиОтличие закона Ома для полной цепи от закона Ома для участка цепи заключается в том, что теперь мы должны учитывать два вида сопротивления. Это «R» сопротивление всех компонентов системы и «r» внутреннее сопротивление источника электродвижущей силы. Формула таким образом приобретает вид:
Это «R» сопротивление всех компонентов системы и «r» внутреннее сопротивление источника электродвижущей силы. Формула таким образом приобретает вид:
I = U / R + r
Закон Ома для переменного токаПеременный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Попробуем разобраться, в чем реальная разница между реактивным и активным сопротивлением в цепи с переменным током. Вы уже должны были понять, что значение напряжение и силы тока в такой цепи меняется со временем и имеют, грубо говоря, волновую форму.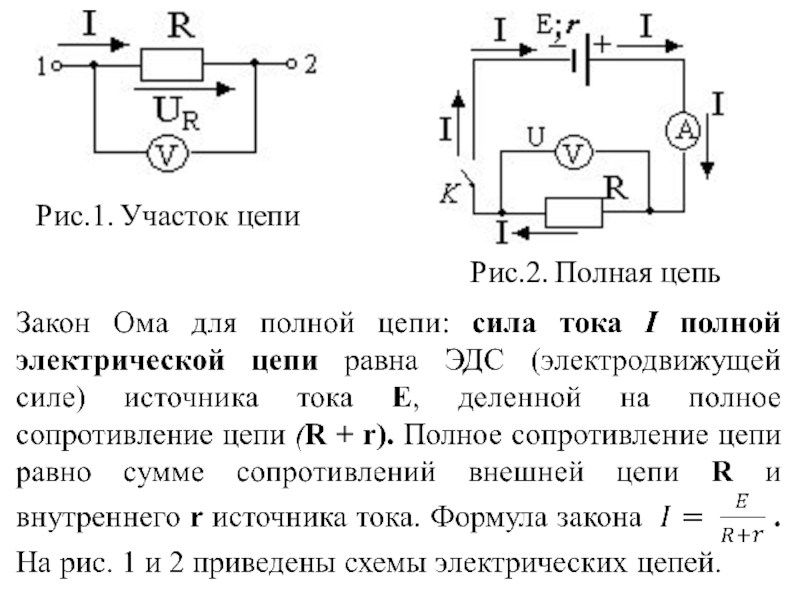
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Похожие темы:
Закон Ома и соотношение V-I-R
В физике есть определенные формулы, которые настолько мощны и распространены, что достигают уровня общеизвестных знаний. Студент, изучающий физику, записывал такие формулы столько раз, что запоминал их, даже не пытаясь. Безусловно, для профессионалов в этой области такие формулы настолько важны, что остаются в их сознании. В области современной физики E = m • c 2 . В области ньютоновской механики существует F net = m • a.В области волновой механики v = f • λ. А в области текущего электричества ΔV = I • R.
В области современной физики E = m • c 2 . В области ньютоновской механики существует F net = m • a.В области волновой механики v = f • λ. А в области текущего электричества ΔV = I • R.
Преобладающим уравнением, которое пронизывает изучение электрических цепей, является уравнение
ΔV = I • RДругими словами, разность электрических потенциалов между двумя точками в цепи ( ΔV ) эквивалентна произведению тока между этими двумя точками ( I ) и общего сопротивления всех электрических устройств, присутствующих между этими двумя точками ( R ).В остальной части этого раздела Физического класса это уравнение станет самым распространенным уравнением, которое мы видим. Это уравнение, часто называемое уравнением закона Ома , является мощным средством прогнозирования взаимосвязи между разностью потенциалов, током и сопротивлением.
Закон Ома как предсказатель токаУравнение закона Ома можно переформулировать и выразить как
В качестве уравнения это служит алгебраическим рецептом для вычисления тока, если известны разность электрических потенциалов и сопротивление. Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, это гораздо больше. Это уравнение указывает две переменные, которые могут повлиять на величину тока в цепи. Ток в цепи прямо пропорционален разности электрических потенциалов, приложенной к ее концам, и обратно пропорционален общему сопротивлению внешней цепи. Чем больше напряжение аккумулятора (то есть разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток.Заряд идет с наибольшей скоростью, когда напряжение батареи увеличивается, а сопротивление уменьшается. Фактически, двукратное увеличение напряжения батареи привело бы к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.
Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, это гораздо больше. Это уравнение указывает две переменные, которые могут повлиять на величину тока в цепи. Ток в цепи прямо пропорционален разности электрических потенциалов, приложенной к ее концам, и обратно пропорционален общему сопротивлению внешней цепи. Чем больше напряжение аккумулятора (то есть разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток.Заряд идет с наибольшей скоростью, когда напряжение батареи увеличивается, а сопротивление уменьшается. Фактически, двукратное увеличение напряжения батареи привело бы к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.
Приведенная ниже таблица иллюстрирует это соотношение как качественно, так и количественно для нескольких цепей с различными напряжениями и сопротивлением батарей.
Строки 1, 2 и 3 показывают, что удвоение и утроение напряжения батареи приводит к удвоению и утроению тока в цепи. Сравнение строк 1 и 4 или строк 2 и 5 показывает, что удвоение общего сопротивления служит для уменьшения вдвое тока в цепи.
Поскольку на ток в цепи влияет сопротивление, в цепях электроприборов часто используются резисторы, чтобы повлиять на величину тока, присутствующего в ее различных компонентах.Увеличивая или уменьшая величину сопротивления в конкретной ветви схемы, производитель может увеличивать или уменьшать величину тока в этой ветви . Кухонные приборы, такие как электрические миксеры и переключатели света, работают, изменяя ток в нагрузке, увеличивая или уменьшая сопротивление цепи. Нажатие различных кнопок на электрическом микшере может изменить режим с микширования на взбивание, уменьшив сопротивление и позволив большему току присутствовать в миксере.Точно так же поворот ручки регулятора яркости может увеличить сопротивление его встроенного резистора и, таким образом, уменьшить ток.
На схеме ниже изображена пара цепей, содержащих источник напряжения (аккумуляторная батарея), резистор (лампочка) и амперметр (для измерения тока). В какой цепи у лампочки наибольшее сопротивление? Нажмите кнопку «Посмотреть ответ», чтобы убедиться, что вы правы.
Уравнение закона Ома часто исследуется в физических лабораториях с использованием резистора, аккумуляторной батареи, амперметра и вольтметра.Амперметр — это устройство, используемое для измерения силы тока в заданном месте. Вольтметр — это устройство, оснащенное датчиками, которых можно прикоснуться к двум точкам цепи, чтобы определить разность электрических потенциалов в этих местах. Изменяя количество ячеек в аккумуляторной батарее, можно изменять разность электрических потенциалов во внешней цепи. Вольтметр может использоваться для определения этой разности потенциалов, а амперметр может использоваться для определения тока, связанного с этим ΔV.К батарейному блоку можно добавить батарею, и процесс можно повторить несколько раз, чтобы получить набор данных I-ΔV. График зависимости I от ΔV даст линию с крутизной, эквивалентной обратной величине сопротивления резистора. Это значение можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и справедливость уравнения закона Ома.
График зависимости I от ΔV даст линию с крутизной, эквивалентной обратной величине сопротивления резистора. Это значение можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и справедливость уравнения закона Ома.
Тенденция уделять внимание единицам — неотъемлемая черта любого хорошего студента-физика.Многие трудности, связанные с решением проблем, могут быть связаны с тем, что не уделили внимание подразделениям. Поскольку все больше и больше электрических величин и их соответствующих метрических единиц вводится в этот раздел учебного курса «Физический класс», становится все более важным организовать информацию в своей голове. В таблице ниже перечислены некоторые из введенных на данный момент количеств. Для каждой величины также указаны символ, уравнение и соответствующие метрические единицы.Было бы разумно часто обращаться к этому списку или даже делать свою копию и добавлять к ней по мере развития модуля. Некоторые студенты считают полезным составить пятый столбец, в котором приводится определение каждой величины.
Некоторые студенты считают полезным составить пятый столбец, в котором приводится определение каждой величины.
| Кол-во | Символ | Уравнение (я) | Стандартная метрическая единица | Другие единицы |
| Разность потенциалов (г.к.а. напряжение) | ΔV | ΔV = ΔPE / Q ΔV = I • R | Вольт (В) | J / C |
| Текущий | я | I = Q / т I = ΔV / R | Амперы (А) | Усилитель или К / с или В / Ом |
| Мощность | п | P = ΔPE / т (еще впереди) | Ватт (Вт) | Дж / с |
| Сопротивление | р | R = ρ • L / A R = ΔV / I | Ом (Ом) | В / А |
| Энергия | E или ΔPE | ΔPE = ΔV • Q ΔPE = P • t | Джоуль (Дж) | V • C или Вт • с |
(Обратите внимание, что символ C представляет собой кулоны.)
В следующем разделе Урока 3 мы еще раз рассмотрим количественную мощность. Новое уравнение мощности будет введено путем объединения двух (или более) уравнений в приведенной выше таблице.
Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие — это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Легко перетащите источник напряжения, резисторы и провода на рабочее место. Соедините их, и у вас будет схема. Добавьте амперметр для измерения тока и используйте датчики напряжения для определения падения напряжения. Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).
Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).
1. Что из перечисленного ниже приведет к уменьшению тока в электрической цепи? Выберите все, что подходит.
а. уменьшить напряжение
г. уменьшить сопротивление
г. увеличить напряжение
г.увеличить сопротивление
2. Определенная электрическая цепь содержит батарею из трех элементов, провода и лампочку. Что из перечисленного может привести к тому, что лампа будет светить менее ярко? Выберите все, что подходит.
а. увеличить напряжение АКБ (добавить еще одну ячейку)
г. уменьшить напряжение аккумулятора (удалить элемент)
г.уменьшить сопротивление цепи
г. увеличить сопротивление цепи
3. Вероятно, вас предупредили, чтобы вы не прикасались к электрическим приборам или даже к электрическим розеткам, когда ваши руки мокрые. Такой контакт более опасен, когда ваши руки мокрые (а не сухие), потому что мокрые руки вызывают ____.
а.напряжение цепи должно быть выше
г. напряжение цепи должно быть ниже
г. ваше сопротивление будет выше
г. ваше сопротивление должно быть ниже
e. ток через тебя будет ниже
4. Если бы сопротивление цепи было утроено, то ток в цепи был бы ____.
а. треть от
г. втрое больше
г. без изменений
г. … бред какой то! Сделать такой прогноз невозможно.
5. Если напряжение в цепи увеличить в четыре раза, то ток в цепи будет ____.
а.четверть от
г. в четыре раза больше
г. без изменений
г. … бред какой то! Сделать такой прогноз невозможно.
6. В схему подключены блок питания, резистор и амперметр (для измерения тока). Амперметр показывает значение тока 24 мА (миллиАмпер). Определите новый ток, если напряжение источника питания было…
а. … увеличился в 2 раза, а сопротивление осталось постоянным.
г. … увеличилось в 3 раза, а сопротивление осталось постоянным.
г. … уменьшилось в 2 раза, а сопротивление осталось постоянным.
г. … оставалось постоянным, а сопротивление увеличивалось в 2 раза.
e. … оставалось постоянным, а сопротивление увеличивалось в 4 раза.
ф…. оставалось постоянным, а сопротивление уменьшалось в 2 раза.
г. … увеличилось в 2 раза, а сопротивление увеличилось в 2 раза.
ч. … увеличилось в 3 раза, а сопротивление уменьшилось в 2 раза.
и. … уменьшилось в 2 раза, а сопротивление увеличилось в 2 раза.
7.Используйте уравнение закона Ома, чтобы дать числовые ответы на следующие вопросы:
а. Электрическое устройство с сопротивлением 3,0 Ом позволит протекать через него току 4,0 А, если на устройстве наблюдается падение напряжения ________ Вольт.
г. Когда на электрический нагреватель подается напряжение 120 В, через нагреватель будет протекать ток 10,0 А, если сопротивление составляет ________ Ом.
г. Фонарик, который питается от 3 вольт и использует лампочку с сопротивлением 60 Ом, будет иметь ток ________ ампер.
8. Используйте уравнение закона Ома для определения недостающих значений в следующих схемах.
9. См. Вопрос 8 выше. В схемах схем A и B какой метод использовался для контроля тока в схемах? А в схемах схем C и D какой метод использовался для контроля тока в схемах?
Закон Ома: сопротивление и простые цепи
Цели обучения
К концу этого раздела вы сможете:
- Объясните происхождение закона Ома.
- Рассчитайте напряжения, токи или сопротивления по закону Ома.
- Объясните, что такое омический материал.
- Опишите простую схему.
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и условно называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов В, , которая создает электрическое поле.Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
.[латекс] I \ propto {V} \\ [/ латекс].
Это важное соотношение известно как закон Ома .Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда.
Сопротивление и простые схемы
Если напряжение управляет током, что ему мешает? Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением R .Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току, или
.[латекс] I \ propto \ frac {1} {R} \\ [/ latex].
Таким образом, например, ток уменьшается вдвое, если сопротивление увеличивается вдвое. Комбинируя отношения тока к напряжению и тока к сопротивлению, получаем
[латекс] I = \ frac {V} {R} \\ [/ латекс].
Это соотношение также называется законом Ома.Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых действует закон Ома, называются омическими . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R , которое не зависит от напряжения В и тока I . Объект с простым сопротивлением называется резистором , даже если его сопротивление невелико.Единицей измерения сопротивления является Ом и обозначается символом Ω (заглавная греческая омега). Перестановка I = V / R дает R = V / I , и поэтому единицы сопротивления равны 1 Ом = 1 вольт на ампер:
[латекс] 1 \ Omega = 1 \ frac {V} {A} \\ [/ latex].
На рисунке 1 показана схема простой схемы. Простая схема имеет один источник напряжения и один резистор. Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в R .
Рис. 1. Простая электрическая цепь, в которой замкнутый путь прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленной красными параллельными линиями. Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.
Пример 1. Расчет сопротивления: автомобильная фара
Какое сопротивление проходит у автомобильной фары? 2.50 А при подаче на него 12,0 В?
СтратегияМы можем изменить закон Ома, как указано в I = V / R , и использовать его для определения сопротивления.
РастворПерестановка I = V / R и замена известных значений дает
[латекс] R = \ frac {V} {I} = \ frac {\ text {12} \ text {.} \ Text {0 V}} {2 \ text {.} \ Text {50 A}} = \ text {4} \ text {.} \ text {80 \ Omega} \\ [/ latex].
ОбсуждениеЭто относительно небольшое сопротивление, но оно больше, чем хладостойкость фары.Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампа имеет меньшее сопротивление при первом включении и потребляет значительно больший ток во время короткого периода прогрева.
Сопротивление может быть разным. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 12 Ом или более. Сопротивление между руками и ногами у сухого человека может составлять 10 5 Ом, в то время как сопротивление человеческого сердца составляет примерно 10 3 Ом.Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10 −5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделах «Сопротивление и удельное сопротивление». Дополнительное понимание можно получить, решив I = V / R для V , что дает
В = ИК
Это выражение для В можно интерпретировать как падение напряжения на резисторе, возникающее при протекании тока I .Для этого напряжения часто используется фраза IR drop . Например, фара в Пример 1 выше имеет падение IR на 12,0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления.Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как PE = q Δ V , и то же самое q протекает через каждую. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.(См. Рисунок 2.)
Рис. 2. Падение напряжения на резисторе в простой схеме равно выходному напряжению батареи.
Подключение: сохранение энергииВ простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму только с помощью резистора. Мы обнаружим, что сохранение энергии имеет и другие важные применения в схемах и является мощным инструментом анализа схем.
Исследования PhET: закон ОмаПосмотрите, как уравнение закона Ома соотносится с простой схемой. Отрегулируйте напряжение и сопротивление и посмотрите, как изменяется ток по закону Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Щелкните, чтобы запустить моделирование.
Сводка раздела
- Простая схема — это схема , в которой есть один источник напряжения и одно сопротивление.
- Одно из утверждений закона Ома дает соотношение между током I , напряжением В и сопротивлением R в простой схеме как [латекс] I = \ frac {V} {R} \\ [/ latex] . Сопротивление
- выражается в единицах Ом (Ом), относящихся к вольтам и амперам на 1 Ом = 1 В / А.
- Падение напряжения IR на резисторе, вызванное протекающим через него током, равное В = IR .
Концептуальные вопросы
- Падение напряжения IR на резисторе означает изменение потенциала или напряжения на резисторе.Изменится ли ток при прохождении через резистор? Объяснять.
- Как падение IR в резисторе похоже на падение давления в жидкости, протекающей по трубе?
Задачи и упражнения
1. Какой ток протекает через лампочку фонаря на 3,00 В, когда ее горячее сопротивление составляет 3,60 Ом?
2. Вычислите эффективное сопротивление карманного калькулятора с батареей на 1,35 В, через которую протекает ток 0,200 мА.
3.Каково эффективное сопротивление стартера автомобиля, когда через него проходит 150 А, когда автомобильный аккумулятор подает на двигатель 11,0 В?
4. Сколько вольт подается для работы светового индикатора DVD-плеера с сопротивлением 140 Ом, если через него проходит 25,0 мА?
5. (a) Найдите падение напряжения на удлинителе с сопротивлением 0,0600 Ом, через который проходит ток 5,00 А. (b) Более дешевый шнур использует более тонкую проволоку и имеет сопротивление 0.300 Ом. Какое в нем падение напряжения при протекании 5.00 А? (c) Почему напряжение на любом используемом приборе снижается на эту величину? Как это повлияет на прибор?
6. ЛЭП подвешена к металлическим опорам со стеклянными изоляторами, имеющими сопротивление 1,00 × 10 9 Ом. Какой ток протекает через изолятор при напряжении 200 кВ? (Некоторые линии высокого напряжения — постоянного тока.)
Глоссарий
- Закон Ома:
- — эмпирическое соотношение, указывающее, что ток I пропорционален разности потенциалов В, , В, ; его часто записывают как I = V / R , где R — это сопротивление
- сопротивление:
- электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V / I
- Ом:
- единица сопротивления, равная 1Ω = 1 В / A
- омическое:
- тип материала, для которого действует закон Ома
- простая схема:
- схема с одним источником напряжения и одним резистором
Избранные решения проблем и упражнения
1.0,833 А
3. 7,33 × 10 −2 Ом
5. (а) 0,300 В
(б) 1,50 В
(c) Напряжение, подаваемое на любой используемый прибор, снижается, поскольку общее падение напряжения от стены до конечного выхода прибора является фиксированным. Таким образом, если падение напряжения на удлинителе велико, падение напряжения на приборе значительно уменьшается, поэтому выходная мощность прибора может быть значительно уменьшена, что снижает способность прибора работать должным образом.
Что такое закон Ома — формульное уравнение »Электроника Примечания
Закон Ома — один из самых фундаментальных законов теории электричества. Формула или уравнение закона Ома связывает напряжение и ток со свойствами проводника, то есть с его сопротивлением в цепи.
Resistance Tutorial:
Что такое сопротивление
Закон Ома
Омические и неомические проводники
Сопротивление лампы накаливания
Удельное сопротивление
Таблица удельного сопротивления для распространенных материалов
Температурный коэффициент сопротивления
Электрическая проводимость
Последовательные и параллельные резисторы
Таблица параллельных резисторов
Закон Ома — один из самых фундаментальных и важных законов, регулирующих электрические и электронные схемы.Он связывает ток, напряжение и сопротивление для линейного устройства, так что, если известны два, можно вычислить третье.
Поскольку ток, напряжение и сопротивление являются тремя основными величинами цепи, это означает, что закон Ома также чрезвычайно важен.
Закон Ома используется во всех областях электротехники и электроники. Он используется для расчета номинала резисторов, необходимых в цепях, а также может использоваться для определения тока, протекающего в цепи, где напряжение можно легко измерить на известном резисторе, но более того, закон Ома используется в огромное количество вычислений во всех формах электрических и электронных схем — практически везде, где течет ток.
Открытие закона Ома
Существует математическая зависимость, связывающая ток, напряжение и сопротивление. Немецкий ученый по имени Георг Ом провел множество экспериментов, пытаясь показать связь между ними. В те дни, когда он проводил свои эксперименты, не было счетчиков в том виде, в каком мы их знаем сегодня.
Только после значительных усилий и со второй попытки ему удалось разработать то, что мы сегодня знаем как закон Ома.
Примечание Георга Ома:
Родившийся в Эрлангене, примерно в 50 милях к северу от Мюнхена в 1879 году, Георг Ом стал одним из тех, кто много исследовал новую науку, связанную с электричеством, обнаружив взаимосвязь между напряжением и током в проводнике — теперь этот закон действует. назвал Закон Ома, отдавая дань уважения проделанной им работе.
Подробнее о Георг Ом.
Что такое закон Ома?
Закон Ома описывает способ протекания тока через материал при приложении разных уровней напряжения. Некоторые материалы, такие как электрические провода, имеют небольшое сопротивление току, и этот тип материала называется проводником. Следовательно, если этот провод, например, проложить прямо напротив батареи, будет протекать большой ток.
В других случаях другой материал может препятствовать прохождению тока, но все же пропускать некоторые из них. В электрических схемах эти компоненты часто называют резисторами. Однако другие материалы практически не пропускают ток, и эти материалы называются изоляторами.
Посмотрите наше видео о законе Ома
Ом посмотрел на то, как ток течет в различных материалах, и смог разработать свой закон, который мы теперь называем законом Ома.
Чтобы получить первое представление о том, что происходит, можно сравнить электрическую ситуацию с течением воды в трубе.Напряжение представлено давлением воды в трубе, ток представлен количеством воды, протекающей по трубе, и, наконец, сопротивление равно размеру трубы.
Можно представить, что чем шире труба, тем больше воды будет течь. Причина этого в том, что большему количеству воды легче течь по более широкой трубе, чем по более узкой — более узкая труба оказывает большее сопротивление потоку воды. Кроме того, если давление в электронной трубе больше, то по той же трубе будет течь больше воды.
Ом определил, что для обычных материалов удвоение напряжения удваивает ток, протекающий для данного компонента. Различные материалы или одни и те же материалы с разной формой будут иметь разные уровни сопротивления току.
Определение закона Ома
Закон Ома гласит, что ток, протекающий в цепи, прямо пропорционален приложенной разности потенциалов и обратно пропорционален сопротивлению в цепи.
Другими словами, удвоив напряжение в цепи, удвоится и ток. Однако если сопротивление увеличится вдвое, ток упадет вдвое.
В этом математическом соотношении единица сопротивления измеряется в Ом.
Формула закона Ома
Формула или уравнение закона Ома очень проста.
Закон Ома можно выразить в математической форме:
Где:В = напряжение, выраженное в вольтах
I = ток, выраженный в амперах
R = сопротивление, выраженное в Ом
Формулой можно манипулировать так, чтобы, если известны любые две величины, можно было бы вычислить третью.
Треугольник закона Ома
Чтобы запомнить формулу, можно использовать треугольник, одна сторона которого горизонтальна, а вершина наверху напоминает пирамиду. Иногда это называют треугольником закона Ома.
В верхнем углу треугольника закона Ома находится буква V, в левом углу — буква I, а в правом нижнем углу — R.
Чтобы использовать треугольник, закройте неизвестное количество, а затем вычислите его из двух других. Если они выстроены в линию, они умножаются, но если один находится поверх другого, их следует разделить.Другими словами, если необходимо рассчитать ток, напряжение делится на сопротивление, то есть V / R и так далее.
Если необходимо рассчитать напряжение, оно определяется путем умножения силы тока на сопротивление, т. Е. I x R.
Пример расчета закона Ома
Если на резистор 500 Ом подается напряжение 10 В, определите величину тока, который будет протекать.
Глядя на треугольник закона Ома, ток неизвестен, а напряжение и сопротивление остаются известными значениями.
Таким образом, ток определяется делением напряжения на сопротивление.
I = VR = 10500 = 0,02 A = 20 мА
Пример 2
Аналогичным образом можно использовать закон Ома для определения сопротивления, если известны ток и напряжение. Возьмем, например, напряжение 10 вольт, а ток 0,1 А. Используя треугольник закона Ома, можно увидеть, что:
Пример 3
Наконец, другая комбинация состоит в том, что если сопротивление и ток известны, то можно рассчитать ожидаемое напряжение на сопротивлении.Возьмем, к примеру, расстояние 250 Ом, через которое протекает ток 0,1 А, тогда напряжение можно рассчитать следующим образом:
V = I R = 0,1 × 250 = 25 вольт
Проводники омические и неомические
Используя закон Ома, можно увидеть, что если бы напряжение и ток были нанесены на график для фиксированного резистора или отрезка провода и т. Д., То была бы прямая линия.
Видно, что удвоение напряжения удваивает ток, который проходит через конкретный элемент схемы.
График напряжения и тока для линейного сопротивленияНа графике есть две линии, одна для более высокого сопротивления — эта требует приложения большего напряжения для данного протекающего тока. Соответственно, у него должно быть более высокое сопротивление. И наоборот, кривая для более низкого сопротивления показывает компонент, который требует приложения более низкого напряжения для данного тока.
Компоненты, имеющие прямую или прямую линию, подчиняются закону Ома и известны как омические проводники.Однако не все электрические электронные компоненты имеют прямолинейный график для напряжения и тока. По разным причинам они могут иметь разные вольт-амперные характеристики. Эти проводники часто называют неомическими.
Закон Ома — одно из самых основных понятий в электротехнике и электронной технике. Концепция элемента, имеющего определенное сопротивление, которое определяет количество тока, протекающего через него при определенном напряжении, является ключом к работе практически всех цепей.
Другие основные концепции электроники:
Напряжение
Текущий
Мощность
Сопротивление
Емкость
Индуктивность
Трансформеры
Децибел, дБ
Законы Кирхгофа
Q, добротность
РЧ шум
Вернуться в меню «Основные понятия электроники». . .
Ом — обзор
8.2.2 Паразитная емкость
Закон Ома, как указано в уравнении. (8.1) не выполняется, когда модель устройства включает реактивные (емкостные или индуктивные) компоненты и учитываются изменяющиеся во времени напряжения / токи.В таких случаях обобщенная форма закона Ома, показанная в формуле. (8.4) описывает взаимосвязь между напряжением и током через понятие электрического импеданса Z .
(8.4) V = ZIwithZ = R + jX
Электрический импеданс Z представлен комплексным числом, действительная часть которого представляет собой сопротивление R , как определено ранее, тогда как мнимая часть X , называемое реактивным сопротивлением, учитывает реактивные эффекты.
Некоторые датчики несут информацию, относящуюся к измеряемой величине, как в резистивных, так и в реактивных компонентах импеданса, поэтому интерфейсные схемы должны иметь возможность выполнять одновременную оценку R и X .С другой стороны, если полезная информация содержится только в резистивном компоненте, как это обычно бывает с резистивными датчиками, реактивный компонент считается паразитным элементом, влияние которого следует минимизировать.
При работе с резистивными датчиками обычно основной паразитный вклад имеет емкостный характер. В отличие от неидеальности большинства компонентов схемы, эти емкостные эффекты не могут быть компенсированы правильной калибровкой схемы, поскольку они зависят от конкретного датчика и условий эксплуатации.Если не принять во внимание надлежащим образом, такие эффекты могут вызвать ошибки в оценке сопротивления, как будет разъяснено в следующих разделах.
Одна из наиболее распространенных причин возникновения паразитных емкостных эффектов связана с производством датчиков. Если эффект восприятия достигается за счет определенных явлений, происходящих на поверхности датчика (например, с фотодетекторами и датчиками газа), обычным способом повышения чувствительности датчика является максимальное увеличение поверхностных эффектов путем реализации метода, основанного на встречно-штыревых электродах, как показано на Инжир.8.3. К сожалению, эта структура приводит к увеличению паразитной емкости между электродами C ee между электродами, как показано на рис. 8.3, которая становится еще более заметной по мере повторения встречно-штыревой структуры (Polese et al., 2017).
Рисунок 8.3. Паразитно-емкостный эффект в датчиках с встречно-штыревыми электродами.
Другая ситуация, в которой появляются паразитные емкостные эффекты, характерна для газовых датчиков. Некоторым устройствам для измерения газа требуется работать при гораздо более высокой температуре, чем температура окружающей среды, и по этой причине они обычно снабжены встроенной нитью накала R h , которая действует как нагреватель (Samà et al., 2017). Нить накала нагревателя представляет собой проводник, реализованный на той же подложке чувствительного компонента R s и разделенный диэлектрическим материалом, который электрически изолирует два компонента датчика. Однако небольшой размер реализованных устройств заставляет эти два компонента взаимодействовать друг с другом из-за емкостных эффектов, как показано на рис. 8.4.
Рисунок 8.4. Паразитно-емкостный эффект в газовых датчиках со встроенной нитью нагревателя.
Помимо этих возможных внутренних источников, емкостные эффекты могут возникать из-за внешних причин, таких как соединение между датчиком и измерительной системой, как показано на рис.8.5. Фактически, разъемы и провода, используемые для соединения датчика с электронной схемой, демонстрируют распределенную емкостную характеристику C c , которая, с точки зрения приборов, наблюдается параллельно датчику.
Рисунок 8.5. Паразитно-емкостный эффект из-за связи датчика с измерительной системой.
Расчет общего емкостного паразитного эффекта далеко не прост и часто требует полного понимания характеристик датчика, в том числе на микроскопическом уровне.По этой причине, когда необходимо учитывать паразитную емкость, обычно рассматривается упрощенная модель датчика, где паразитный конденсатор C с представлен параллельно с сопротивлением датчика R с. , с учетом всех возможных емкостных паразитных эффектов. Упрощенная модель датчика, используемая в следующих разделах, показана на рис. 8.6.
Рисунок 8.6. Упрощенная модель резистивного датчика с учетом паразитно-емкостных эффектов.
Следует отметить, что когда R с очень велико (напоминает поведение, связанное с разомкнутой цепью) C с может преобладать, что приводит к значительным ошибкам в оценке сопротивления . В этих случаях (например, при работе с датчиками MOX) схемы интерфейса должны быть спроектированы так, чтобы ограничить это явление.
Закон Ома для простых электрических цепей, Рон Куртус
SfC Home> Физика> Электричество>
, автор: Рон Куртус (от 23 октября 2019 г.)
Закон Ома является наиболее фундаментальной формулой для простых электрических цепей .Он утверждает, что электрический ток, проходящий через проводник, прямо пропорционален разности потенциалов на проводнике. Впервые он был сформулирован в 1827 году немецким физиком Георгом Омом во время экспериментов по изучению того, насколько хорошо металлы проводят электричество.
ЗаконОма лучше всего демонстрируется в простой электрической цепи постоянного тока. Хотя это также относится к цепям переменного тока, необходимо учитывать другие возможные переменные.
Связь между током, напряжением и сопротивлением в цепи позволяет вычислить одну переменную, если вы используете значения двух других.
Вопросы, которые могут у вас возникнуть:
- Что означают параметры в уравнении?
- Какая конфигурация схемы?
- Как применить закон Ома?
Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц
Уравнение
ЗаконОма показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи. Самая простая форма уравнения:
В = ИК
где:
- V — напряжение в вольтах ( V )
- I — ток в амперах или амперах ( A )
- R — сопротивление в Ом ( Ом — греческая буква Омега)
Таким образом, если вы знаете ток и сопротивление, вы можете использовать формулу для определения напряжения.
Используя алгебру, вы можете изменить порядок переменных в соответствии со своими потребностями. Например, если вы знаете напряжение и сопротивление и хотите найти ток, вы можете использовать:
I = V / R
Или, если вы знаете напряжение и ток и хотите найти сопротивление, вы можете использовать:
R = V / I
Конфигурация
Простая электрическая цепь состоит из металлических проводов, идущих к источнику питания и от него, а также источника сопротивления, такого как резисторы или электрическая лампочка, соединенных последовательно с источником.Типичным источником питания является батарея постоянного тока, хотя также может применяться генератор постоянного или переменного тока.
Примечание : Если цепь переменного тока включает в себя такие компоненты, как конденсаторы или катушки индуктивности, закон Ома не применяется.
Простая цепь постоянного тока
Используя уравнение
Важность закона Ома заключается в том, что, если вы знаете значение двух переменных в уравнении, вы можете определить третью. Вы можете измерить любой из параметров с помощью вольтметра.Большинство вольтметров или мультиметров измеряют напряжение, ток и сопротивление как переменного, так и постоянного тока.
Найти напряжение
Если вам известны ток и сопротивление, вы можете найти напряжение из В = I R . Например, если ток I = 0,2 А и сопротивление R = 1000 Ом , то
В = 0,2 А * 1000 Ом = 200 В
Найти текущий
Если вы знаете напряжение и сопротивление, вы можете использовать алгебру, чтобы изменить уравнение на I = V / R , чтобы найти ток.Например, если В = 110 В и R = 22000 Ом , то
I = 110 В / 22000 Ом = 0,005 А
Найти сопротивление
Если вы знаете напряжение и ток, вы можете использовать алгебру, чтобы изменить уравнение на R = V / I , чтобы найти сопротивление. Если В = 220 В и I = 5 А , то
R = 220 В / 5 A = 44 Ом
Сводка
Закон Ома — это уравнение V = I R , которое показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи.Он может применяться как к цепям переменного, так и к постоянному току.
Будьте полны решимости сделать все возможное
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайтов
Немного истории об Ом — Краткая история
Закон Ома — Объяснение, включая калькулятор закона Ома
Основные электрические законы — Включает теорию схем
Формулы электрических цепей — Уравнения высокого уровня для решения проблем
Электроэнергетические ресурсы постоянного и переменного тока
Физические ресурсы
Книги
Научитесь электричеству и электронике Стэна Гибилиско; Макгроу-Хилл; (2001) 34 доллара.95 — Руководство для профессионалов, любителей и техников, желающих изучить цепи переменного и постоянного тока
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте. Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
electric_ohms_law.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или тезисе.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
По физике
Закон Ома для простых электрических цепей
Как применять закон Ома — Jade Learning
Как применять закон Ома
Автор: Вес Губиц | 07 августа 2019 г.
Электроэнергия работает в предсказуемых пределах.Мы пришли к выводу, что эти границы являются законом Ома. Закон Ома был разработан как средство объяснения того, как электричество работает в замкнутой цепи. Формула закона Ома помогает установить взаимосвязь между различными свойствами в электрической цепи. Мы можем использовать закон Ома, чтобы объяснить, что произошло, а также что произойдет, когда на электрическую цепь накладываются определенные условия.
Основные характеристики электрической схемы: Напряжение, ток и сопротивление .Они специфичны, определены и не меняются — при условии, что все свойства остаются постоянными. Однако измените значение только одного из этих свойств, и все свойства изменят значение соответствующим образом.
Закон Ома — это самая основная из электрических формул, он был разработан путем простого наблюдения за свойствами электричества в электрической цепи. Электричество ведет себя иначе из-за ограничений, налагаемых формулой закона Ома; формула просто представляет наши наблюдения за поведением, уже происходящим в электрической цепи.
Хотя закон Ома — всего лишь вводная ступенька на лестнице электротехники, для понимания того, как закон Ома как формула применяется к простой цепи, необходимо базовое понимание электрической цепи. Простая схема состоит из источника питания, нагрузки, проводников, устройства максимального тока и устройства управления. Ток будет течь в этой простой цепи, если имеется достаточное напряжение, чтобы преодолеть любое сопротивление цепи.
Напряжение считается давлением в электрической цепи; это уместно называется электродвижущей силой.Это давление или «сила» вызывается разными электрическими полюсами, которые хотят уравновесить себя. Толчок и притяжение, наложенные на электроны в проводнике, подключенном к этим разным полюсам, заставят электроны двигаться, если для них существует полный путь. Единственное, что может остановить движение электронов, — это приложенное сопротивление сверх того напряжения, которое заставляет их двигаться, или разрыв цепи, который нарушает поток этих электронов. Требуется один вольт (В) этой электродвижущей силы, чтобы протолкнуть один ампер (А) тока через один ом (Ом) сопротивления — это закон Ома.Напряжение (E или V) равно току (I), умноженному на сопротивление (R). Или, другими словами, E (или V) = IR.
Обозначения
- Вольт (E или V) = электродвижущая сила, опять же, это давление, которое заставляет электроны перемещаться по проводнику (и через нагрузку) в замкнутой цепи.
- Ток (I) = интенсивность, представляет ток, протекающий в цепи. Помните, что «интенсивность» тока в цепи измеряется в амперах.
- Сопротивление (R) = Ом, сопротивление току.Сопротивление может быть преднамеренным или случайным, но в любом случае оно является противодействием свободному току в цепи и отображается на вашем электрическом счетчике как Ом. Нулевое сопротивление или близкое к нему означает буквально отсутствие сопротивления току. Медь имеет очень низкое значение сопротивления на фут и является высококачественным материалом для создания эффективных проводников.
Давайте посмотрим на символы закона Ома внутри треугольника закона Ома.
Помните, что вольт (E или V) равняется току (I), умноженному на сопротивление (R)
Использование треугольника закона Ома в качестве наглядного пособия при запоминании трех уравнений закона Ома — не редкость.
Чтобы найти пропущенное значение в реальном уравнении закона Ома, просто закройте букву, представляющую пропущенное значение в треугольнике, и используйте оставшиеся два значения для вычисления этого пропущенного значения.
Например: если вы знаете, что лампа на 120 В (E или V) измеряет при использовании ток 0,625 А (I), какое сопротивление оказывает лампа?
120 В (E), деленное на 0,625 А (I), равняется 192 Ом (R) сопротивления.
Что делать, если вы знаете измеряемые амперы (I) протекающего тока и сопротивление (R) нити лампы? Можете ли вы затем рассчитать напряжение, подаваемое на эту лампу? Посмотрите на треугольник закона Ома ниже, чтобы определить свой ответ.
Ток (I), умноженный на сопротивление (R), равен напряжению, приложенному к лампе.
Треугольник Закона Ома Правило
Помните, глядя на Треугольник Закона Ома, если числа стоят рядом, вы умножаете, если числа расположены одно над другим, вы делите.
Заключение
Закон Ома и многие другие электрические формулы предоставляют нам средства, с помощью которых мы можем понять самые основные принципы протекания электричества и тока.Эти многочисленные формулы позволяют нам заглянуть в прошлое, а также в будущее электрических приложений. Можно сказать, что эти формулы дают нам своего рода поводок, если не контролировать это явление, то, возможно, хотя бы держаться!
| Электрические цепи
11,2 Закон Ома (ESBQ6)
Три величины, которые являются фундаментальными для электрических цепей: ток, напряжение (разность потенциалов) и сопротивление .Резюме:
Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
Разность потенциалов или напряжение \ (В \) — это количество энергии на единицу заряда, необходимое для перемещения этого заряда между двумя точками в цепи.
Сопротивление, \ (R \), является мерой того, насколько «трудно» протолкнуть ток через элемент схемы.
Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.
Важная взаимосвязь между током, напряжением и сопротивлением в цепи была обнаружена Георгом Симоном Омом и называется законом Ома .
- Закон Ома
Величина электрического тока через металлический проводник при постоянной температуре в цепи пропорциональна напряжению на проводнике и может быть описана как
. \ (I = \ frac {V} {R} \)где \ (I \) — ток через проводник, \ (V \) — напряжение на проводнике, а \ (R \) — сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводника постоянно, независимо от приложенного к нему напряжения или проходящего через него тока.
Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводник, прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на ось x графика, а ток — на ось y графика, мы получим прямую линию.
Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R}.\] Это можно изменить с точки зрения постоянного сопротивления как: \ [R = \ frac {V} {I}. \]
Закон Ома
Цель
Для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов (напряжением) на том же резисторе.
Аппарат
4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода
Метод
Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное к резистору напряжение и измерять результирующий ток в цепи.Во второй части мы будем изменять ток в цепи и измерять результирующее напряжение на резисторе. После получения обоих наборов измерений мы исследуем взаимосвязь между током и напряжением на резисторе.
Изменение напряжения:
Установите схему в соответствии со схемой 1), начиная с одной ячейки.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Количество ячеек
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)
Попросите учителя проверить электрическую цепь перед включением питания.
Измерьте напряжение на резисторе с помощью вольтметра и ток в цепи с помощью амперметра.
Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.
Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
Изменение тока:
Установите схему в соответствии со схемой 2), начиная с одного резистора в цепи.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
Попросите учителя проверить вашу схему перед включением питания.
Измерьте ток и напряжение на единственном резисторе.
Теперь добавьте еще один резистор последовательно в схему и снова измерьте ток и напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока у вас не будет четырех последовательно, но не забывайте каждый раз измерять напряжение только на исходном резисторе. Введите измеренные вами значения в таблицу.
Анализ и результаты
Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения.Поскольку напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная, которая будет отложена по оси \ (x \). Ток является зависимой переменной и должен быть нанесен на ось \ (y \).
Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом случае независимой переменной является ток, который должен быть нанесен на ось \ (x \), а напряжение является зависимой переменной и должно быть нанесено на ось \ (y \).
Выводы
Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резисторе, когда ток через резистор увеличивается? т.е. увеличивается или уменьшается?
Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Вопросы и обсуждение
- Для каждого из ваших графиков рассчитайте градиент и по нему определите сопротивление исходного резистора. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_0 \)?
Высокие оценки в науке — залог вашего успеха и будущих планов.Проверьте себя и узнайте больше о практике Сиявулы.
Зарегистрируйтесь и проверьте себяЗакон Ома
Упражнение 11.1Постройте график напряжения (по оси X) и тока (по оси Y).
Какой тип графика вы получите (прямолинейный, парабола, другая кривая)
прямая линия
Рассчитайте градиент графика.
Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжения:
\ begin {align *} m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\ & = \ текст {0,13} \ end {выровнять *}Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.
Как вы можете определить сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_ {0} \)?
Вы начинаете с подключения известного резистора в цепь с источником питания. Теперь вы читаете напряжение источника питания и записываете его.
Затем вы последовательно подключаете два резистора.Теперь вы можете измерить напряжение для каждого из резисторов.
Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:
\ [V = IR \]Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток одинаков во всей цепи, мы можем найти неизвестное сопротивление.
\ begin {align *} V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ end {выровнять *}Омические и неомические проводники (ESBQ7)
Проводники, подчиняющиеся закону Ома, имеют постоянное сопротивление, когда на них изменяется напряжение или увеличивается ток через них.Эти проводники называются омическими проводниками . График зависимости тока от напряжения на этих проводниках будет прямолинейным. Некоторыми примерами омических проводников являются резисторы цепи и нихромовая проволока.
Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводников называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка — типичный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.
В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается от комнатной до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, то увеличение тока приведет к увеличению температуры нити накала, что приведет к увеличению ее сопротивления. Это эффективно ограничивает увеличение тока.В этом случае напряжение и ток не подчиняются закону Ома.
Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорировать. При применении металлических нитей накала ламп, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \) и начиная с комнатной температуры), изменение довольно велико.
В общем, для неомических проводников график зависимости напряжения от тока не будет прямолинейным, что указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.
Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определят, какой из них подчиняется закону Ома. Вам потребуются лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны обнаружить, что резистор подчиняется закону Ома, а лампочка — нет.
Проводники омические и неомические
Aim
Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома
Аппарат
4 ячейки, резистор, лампочка, соединительные провода, вольтметр, амперметр
Метод
Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во второй — лампочка.Настройте обе схемы, указанные выше, начиная с 1 ячейки. Для каждой цепи:
Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметра.
Измерить ток в цепи с помощью амперметра.
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.
Результаты
Нарисуйте в своей книге две таблицы, которые выглядят следующим образом.У вас должна быть одна таблица для измерений первой цепи с резистором и другая таблица для измерений второй цепи с лампочкой.
Количество ячеек | Напряжение, В (\ (\ text {V} \)) | Ток, I (\ (\ text {A} \)) |
\ (\ text {1} \) | ||
\ (\ text {2} \) | ||
\ (\ text {3} \) | ||
\ (\ text {4} \) |
Анализ
Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs.\ (V \) (\ (x \) — ось), один для резистора и один для лампочки.
Вопросы и обсуждение
Внимательно изучите свои графики и ответьте на следующие вопросы:
Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка закону Ома?
Имеет ли лампочка омический или неомический провод?
Использование закона Ома (ESBQ8)
Теперь мы готовы увидеть, как закон Ома используется для анализа схем.
Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \), а напряжение на резисторе равно \ (\ text { 5} \) \ (\ text {V} \), то мы можем использовать закон Ома для расчета тока, протекающего через резистор. Наша первая задача — нарисовать принципиальную схему. Решая любую проблему с электрическими цепями, очень важно составить схему цепи, прежде чем производить какие-либо расчеты. Принципиальная схема для этой проблемы выглядит следующим образом:
Уравнение закона Ома: \ [R = \ frac {V} {I} \]
, который можно преобразовать в: \ [I = \ frac {V} {R} \]
Ток, протекающий через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}
Рабочий пример 1: Закон Ома
Изучите принципиальную схему ниже:
Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор, равен \ (\ text {4} \) \ (\ text {A} \ ).Какова разность потенциалов (напряжение) на резисторе?
Определите, как подойти к проблеме
Нам задают сопротивление резистора и ток, проходящий через него, и просят вычислить напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]
Решить проблему
Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \). \ begin {align *} R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}
Напишите окончательный ответ
Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).
Высокие оценки в науке — залог вашего успеха и будущих планов. Проверьте себя и узнайте больше о практике Сиявулы.
Зарегистрируйтесь и проверьте себяЗакон Ома
Упражнение 11.2Рассчитайте сопротивление резистора, разность потенциалов которого составляет \ (\ text {8} \) \ (\ text {V} \), когда ток равен \ (\ text {2} \) \ (\ text {A} \) протекает через него. Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора равно:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Какой ток будет проходить через резистор \ (\ text {6} \) \ (\ text {Ω} \) при разности потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора равно:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ end {выровнять *}Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет хоть это? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора равно:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ end {выровнять *}Резисторы последовательно и параллельно (ESBQ9)
В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы подключены последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. В параллельной цепи есть несколько путей, по которым течет ток.
Когда в цепи более одного резистора, мы обычно можем рассчитать общее суммарное сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .
Эквивалентное последовательное сопротивление
В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление — это просто сумма сопротивлений всех резисторов.
- Эквивалентное сопротивление в последовательной цепи,
Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]
Применим это к следующей схеме.
Резисторы включены последовательно, следовательно:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {align *}Эквивалентное параллельное сопротивление
В цепи, в которой резисторы включены параллельно, эквивалентное сопротивление определяется следующим определением.
- Эквивалентное сопротивление в параллельной цепи
Для резисторов \ (n \), включенных параллельно, эквивалентное сопротивление составляет:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]
Применим эту формулу к следующей схеме.
Какое полное (эквивалентное) сопротивление в цепи?
\ begin {align *} \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \верно) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text { 1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text {Ω}} {\ text {10} \ text { Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {align *}Последовательное и параллельное сопротивление
Упражнение 11.3Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) соединены последовательно. Рассчитайте эквивалентное сопротивление.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\ & = \ текст {20} \ текст {кОм} \ end {выровнять *}Два резистора соединены последовательно.Эквивалентное сопротивление равно \ (\ text {100} \) \ (\ text {Ω} \). Если один резистор равен \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ R_ {2} & = R_ {s} — R_ {1} \\ & = \ text {100} \ text {Ω} — \ text {10} \ text {Ω} \\ & = \ текст {90} \ текст {Ω} \ end {выровнять *}Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитайте эквивалентное сопротивление.
Поскольку резисторы включены параллельно, мы можем использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\ & = \ frac {1 + 10} {\ text {100}} \\ & = \ frac {11} {\ text {100}} \\ R_ {p} & = \ text {9,09} \ text {kΩ} \ end {выровнять *}Два резистора подключены параллельно.Эквивалентное сопротивление равно \ (\ text {3,75} \) \ (\ text {Ω} \). Если сопротивление одного резистора равно \ (\ text {10} \) \ (\ text {Ω} \), каково сопротивление второго резистора?
Поскольку резисторы включены параллельно, мы можем использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} \\ & = \ frac {1} {\ text {3,75}} — \ frac {1} {\ text {10}} \\ & = \ frac {\ text {10} — \ text {3,75}} {\ text {37,5}} \\ & = \ frac {\ text {6,25}} {\ text {37,5}} \\ R_ {2} & = \ текст {6} \ текст {Ω} \ end {выровнять *}Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:
a) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\ & = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\ & = \ frac {\ text {5}} {\ text {6}} \\ R & = \ текст {1,2} \ текст {Ω} \ end {выровнять *}b) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\ & = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\ & = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\ & = \ frac {\ text {25}} {\ text {12}} \\ R & = \ text {0,48} \ text {Ω} \ end {выровнять *}c) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}d) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ text {1} \ text {Ω} \\ & = \ текст {10} \ текст {Ω} \ end {выровнять *}Использование закона Ома в последовательных и параллельных цепях (ESBQB)
Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими установками.
Последовательные цепи
Рассмотрим схему, состоящую из трех резисторов и одного одиночная ячейка соединена последовательно.
Первый принцип, который нужно понять в отношении последовательных цепей, заключается в том, что величина тока одинакова через любой компонент в цепи. Это потому, что существует только один путь для движения электронов в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении будет течь ток. Мы знаем, что ток по условию течет от положительного к отрицательному.Обычный ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к A.
Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:
\ [I = I_ {1} = I_ {2} = I_ {3}. \]Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений на всех трех резисторах. Итак, мы можем написать:
\ [V = V_ {1} + V_ {2} + V_ {3} \]Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления последовательно соединенных резисторов, мы можем решить некоторые проблемы схемы.
Рабочий пример 2: Закон Ома, последовательная цепь
Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако в цепи два резистора, и нам нужно найти полное сопротивление.
Найти полное сопротивление в цепи
Поскольку резисторы включены последовательно, общее (эквивалентное) сопротивление R составляет:
\ [R = R_ {1} + R_ {2} \]Следовательно,
\ begin {align *} R & = \ текст {2} + \ текст {4} \\ & = \ текст {6} \ текст {Ω} \ end {align *}Применить закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\ I & = \ frac {V} {R} \\ & = \ frac {12} {6} \\ & = \ текст {2} \ текст {А} \ end {align *}
Напишите окончательный ответ
В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).
Рабочий пример 3: Закон Ома, последовательная цепь
Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найдите сопротивление \ (R_ {2} \), учитывая, что ток, протекающий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ ( \ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ text {V} \). \ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).
Нарисуйте схему и введите все известные значения.
Определите, как подойти к проблеме.
Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление, используя:
\ [R = R_ {1} + R_ {2} \], потому что он находится в последовательной цепи.
Найдите полное сопротивление
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {\ text {1,5}} {\ text {0,25}} \\ & = \ текст {6} \ текст {Ω} \ end {align *}Найдите неизвестное сопротивление
Мы знаем, что:
\ [R = \ text {6} \ text {Ω} \]и что
\ [R_ {1} = \ text {1} \ text {Ω} \]с
\ [R = R_ {1} + R_ {2} \] \ [R_ {2} = R — R_ {1} \]Следовательно,
\ [R_ {1} = \ text {5} \ text {Ω} \]Рабочий пример 4: Закон Ома, последовательная цепь
Для следующей схемы рассчитайте:
падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \) и \ (R_3 \)
сопротивление \ (R_3 \).
Определите, как подойти к проблеме
Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета падения напряжения на известных резисторах. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \). Теперь мы можем использовать эту информацию, чтобы найти напряжение на неизвестном резисторе \ (R_3 \).
Рассчитать падение напряжения на \ (R_1 \)
Используя закон Ома: \ begin {align *} R_1 & = \ frac {V_1} {I} \\ I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\ V_1 & = {I} \ cdot {R_1} \\ & = 2 \ cdot 1 \\ V_1 & = \ текст {2} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_2 \)
Снова используя закон Ома: \ begin {align *} R_2 & = \ frac {V_2} {I} \\ I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\ V_2 & = {I} \ cdot {R_2} \\ & = 2 \ cdot 3 \\ V_2 & = \ текст {6} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_3 \)
Поскольку падение напряжения на всех резисторах, вместе взятых, должно быть таким же, как падение напряжения на ячейке в последовательной цепи, мы можем найти \ (V_3 \), используя: \ begin {align *} V & = V_1 + V_2 + V_3 \\ V_3 & = V — V_1 — V_2 \\ & = 18-2-6 \\ V_3 & = \ текст {10} \ текст {V} \ end {align *}
Найдите сопротивление \ (R_3 \)
Нам известно напряжение на \ (R_3 \) и ток через него, поэтому мы можем использовать закон Ома для вычисления значения сопротивления: \ begin {align *} R_3 & = \ frac {V_3} {I} \\ & = \ frac {10} {2} \\ R_3 & = \ text {5} \ Omega \ end {align *}
Напишите окончательный ответ
\ (V_1 = \ text {2} \ text {V} \)
\ (V_2 = \ text {6} \ text {V} \)
\ (V_3 = \ text {10} \ text {V} \)
\ (R_1 = \ text {5} \ Omega \)
Параллельные цепи
Рассмотрим схему, состоящую из одной ячейки и трех резисторов, соединенных параллельно.
Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что напряжение одинаково на всех компонентах в цепи. Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени. Итак, для показанной схемы верно следующее:
\ [V = V_ {1} = V_ {2} = V_ {3}. \]Второй принцип параллельной схемы состоит в том, что все токи, проходящие через каждый резистор, должны составлять общий ток в цепи:
\ [I = I_ {1} + I_ {2} + I_ {3}.\]Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельных резисторов, мы теперь можем подойти к некоторым проблемам схемы, связанным с параллельными резисторами.
Рабочий пример 5: Закон Ома, параллельная цепь
Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома.Однако в цепи два резистора, и нам нужно найти полное сопротивление.
Найдите эквивалентное сопротивление в цепи
.Поскольку резисторы включены параллельно, общее (эквивалентное) сопротивление R составляет:
\ [\ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}}. \] \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {2 + 1} {4} \\ & = \ frac {3} {4} \\ \ text {Следовательно,} R & = \ text {1,33} \ Omega \ end {align *}Применить закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ cdot \ frac {I} {R} & = \ frac {V} {I} \ cdot \ frac {I} {R} \\ I & = \ frac {V} {R} \\ I & = V \ cdot \ frac {1} {R} \\ & = (12) \ left (\ frac {3} {4} \ right) \\ & = \ текст {9} \ текст {А} \ end {align *}Напишите окончательный ответ
В цепи протекает ток \ (\ text {9} \) \ (\ text {A} \).
Рабочий пример 6: Закон Ома, параллельная цепь
Два омических резистора (\ (R_1 \) и \ (R_2 \)) подключены параллельно ячейке. Найдите сопротивление \ (R_2 \), учитывая, что ток, протекающий через ячейку, равен \ (\ text {4,8} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ текст {9} \) \ (\ text {V} \).
Определите, что требуется
Нам нужно рассчитать сопротивление \ (R_2 \).
Определите, как подойти к проблеме
Поскольку резисторы омические и нам даны напряжение на ячейке и ток в ячейке, мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи.\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {\ text {4,8}} \\ & = \ text {1,875} \ \ Omega \ end {align *}
Рассчитайте значение для \ (R_2 \)
Поскольку мы знаем эквивалентное сопротивление и сопротивление \ (R_1 \), мы можем использовать формулу для параллельных резисторов, чтобы найти сопротивление \ (R_2 \). \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \ end {выровнять *} Переставляем решение для \ (R_2 \): \ begin {align *} \ frac {1} {R_2} & = \ frac {1} {R} — \ frac {1} {R_1} \\ & = \ frac {1} {\ text {1,875}} — \ frac {1} {3} \\ & = \ текст {0,2} \\ R_2 & = \ frac {1} {\ text {0,2}} \\ & = \ текст {5} \ \ Omega \ end {align *}
Напишите окончательный ответ
Сопротивление \ (R_2 \) равно \ (\ text {5} \) \ (\ Omega \)
Рабочий пример 7: Закон Ома, параллельная цепь
Ячейка на 18 В подключена к двум параллельным резисторам \ (\ text {4} \) \ (\ Omega \) и \ (\ text {12} \) \ (\ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов.
Сначала нарисуйте схему перед выполнением любых расчетов
Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.
Рассчитать ток через ячейку
Чтобы рассчитать ток через элемент, нам сначала нужно определить эквивалентное сопротивление остальной части цепи.Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {4} + \ frac {1} {12} \\ & = \ frac {3 + 1} {12} \\ & = \ frac {4} {12} \\ R & = \ frac {12} {4} = \ text {3} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {18} {3} \\ I & = \ text {6} \ text {A} \ end {align *}
Теперь определим ток через один из параллельных резисторов
Мы знаем, что для чисто параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из параллельных резисторов.Для этой схемы: \ begin {align *} V & = V_1 = V_2 = \ text {18} \ text {V} \ end {выровнять *} Начнем с расчета тока через \ (R_1 \) по закону Ома: \ begin {align *} R_1 & = \ frac {V_1} {I_1} \\ I_1 & = \ frac {V_1} {R_1} \\ & = \ frac {18} {4} \\ I_1 & = \ text {4,5} \ text {A} \ end {align *}
Рассчитайте ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_2 \): \ begin {align *} R_2 & = \ frac {V_2} {I_2} \\ I_2 & = \ frac {V_2} {R_2} \\ & = \ frac {18} {12} \\ I_2 & = \ text {1,5} \ text {A} \ end {выровнять *} Альтернативный метод вычисления \ (I_2 \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны составлять суммарный ток через ячейку: \ begin {align *} I & = I_1 + I_2 \\ I_2 & = I — I_1 \\ & = 6 — 4.5 \\ I_2 & = \ text {1,5} \ text {A} \ end {align *}
Напишите окончательный ответ
Ток через ячейку равен \ (\ text {6} \) \ (\ text {A} \).
Ток через резистор \ (\ text {4} \) \ (\ Omega \) равен \ (\ text {4,5} \) \ (\ text {A} \).
Ток через резистор \ (\ text {12} \) \ (\ Omega \) равен \ (\ text {1,5} \) \ (\ text {A} \).
Закон Ома в последовательной и параллельной цепях
Упражнение 11.4Рассчитать номинал неизвестного резистора в цепи:
Сначала мы используем закон Ома для вычисления полного последовательного сопротивления:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {1} \\ & = \ текст {9} \ текст {Ω} \ end {выровнять *}Теперь мы можем найти неизвестное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ R_ {4} & = R_ {s} — R_ {1} — R_ {2} — R_ {3} \\ & = 9 — 3 — 3 — 1 \\ & = \ текст {2} \ текст {Ω} \ end {выровнять *}Рассчитайте значение тока в следующей цепи:
Сначала находим общее сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {1} + \ text {2,5} + \ text {1,5} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать текущую:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {5} \\ & = \ текст {1,8} \ текст {А} \ end {выровнять *}Три резистора с сопротивлением \ (\ text {1} \) \ (\ text {Ω} \), \ (\ text {5} \) \ (\ text {Ω} \) и \ (\ text {10} \) \ (\ text {Ω} \) соответственно соединены последовательно с батареей \ (\ text {12} \) \ (\ text {V} \).Рассчитайте значение тока в цепи.
Рисуем принципиальную схему:
Теперь мы находим полное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ текст {1} + \ текст {5} + \ текст {10} \\ & = \ текст {16} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать текущую:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {12} {16} \\ & = \ текст {0,75} \ текст {A} \ end {выровнять *}Рассчитайте ток через ячейку, если оба резистора омические по своей природе.
Сначала находим общее сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {3}} \\ & = \ frac {3 + 1} {\ text {3}} \\ & = \ frac {4} {\ text {3}} \\ & = \ текст {0,75} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать текущую:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {\ text {0,75}} \\ & = \ текст {12} \ текст {А} \ end {выровнять *}Рассчитайте номинал неизвестного резистора \ (R_ {4} \) в цепи:
Сначала находим общее сопротивление:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {24} {\ text {2}} \\ & = \ текст {12} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать неизвестное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\ \ frac {1} {R_ {4}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} — \ frac {1} {R_ {2}} — \ гидроразрыв {1} {R_ {3}} \\ & = \ frac {1} {\ text {12}} — \ frac {1} {\ text {120}} — \ frac {1} {\ text {40}} — \ frac {1} {\ text { 60}} \\ & = \ frac {10 — 1 — 3 — 2} {\ text {120}} \\ & = \ frac {4} {\ text {120}} \\ & = \ текст {30} \ текст {Ω} \ end {выровнять *}значение тока через аккумулятор
Рисуем принципиальную схему:
Чтобы вычислить значение тока через батарею, нам сначала нужно вычислить эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {5}} + \ frac {1} {\ text {10}} \\ & = \ frac {10 + 2 + 1} {\ text {10}} \\ & = \ frac {13} {\ text {10}} \\ & = \ текст {0,77} \ текст {Ω} \ end {выровнять *}Теперь можем посчитать ток через батарею:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {0,77}} \\ & = \ текст {26} \ текст {А} \ end {выровнять *}значение тока в каждом из трех резисторов.
Для параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из резисторов. Для этой схемы:
\ [V = V_ {1} = V_ {2} = V_ {3} = \ text {20} \ text {V} \]Теперь мы можем рассчитать ток через каждый резистор. Начнем с \ (R_ {1} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {1}} \\ & = \ текст {20} \ текст {А} \ end {выровнять *}Затем мы вычисляем ток через \ (R_ {2} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {5}} \\ & = \ текст {4} \ текст {А} \ end {выровнять *}И наконец вычисляем ток через \ (R_ {3} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {10}} \\ & = \ текст {2} \ текст {А} \ end {выровнять *}Вы можете проверить, что они составляют в сумме общий ток.
Последовательные и параллельные сети резисторов (ESBQC)
Теперь, когда вы знаете, как работать с простыми последовательными и параллельными цепями, вы готовы заняться цепями, которые объединяют эти две схемы, например, следующую схему:
Рисунок 11.1: Пример последовательно-параллельной сети. Пунктирными прямоугольниками обозначены параллельные участки цепи.Проработать такие схемы относительно легко, потому что вы используете все, что вы уже узнали о последовательных и параллельных схемах.Единственная разница в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из 2 параллельных частей, которые затем включены последовательно с ячейкой. Чтобы вычислить эквивалентное сопротивление для схемы, вы начинаете с вычисления общего сопротивления каждой из параллельных частей, а затем последовательно складываете эти сопротивления. Если бы все резисторы на рисунке 11.1 имели сопротивление \ (\ text {10} \) \ (\ text {Ω} \), мы можем вычислить эквивалентное сопротивление всей цепи.
Начнем с расчета общего сопротивления параллельной цепи 1 .{-1} \\ & = \ текст {5} \, \ Omega \ end {align *}
Теперь вы можете рассматривать схему как простую последовательную схему следующим образом:
Следовательно, эквивалентное сопротивление: \ begin {align *} R & = R_ {p1} + R_ {p2} \\ & = 5 + 5 \\ & = 10 \, \ Omega \ end {align *}
Эквивалентное сопротивление цепи на рисунке 11.1 равно \ (\ text {10} \) \ (\ text {Ω} \).
Последовательные и параллельные сети
Упражнение 11.5Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {4} + \ frac {1} {2} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {3} + R_ {p} \\ & = \ текст {2} + \ текст {1,33} \\ & = \ текст {3,33} \ текст {Ω} \ end {выровнять *}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {1} + \ frac {1} {2} \\ & = \ frac {3} {2} \\ R_ {p} & = \ text {0,67} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с тремя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {3} + R_ {4} + R_ {p} \\ & = \ текст {4} + \ текст {6} + \ текст {0,67} \\ & = \ текст {10,67} \ текст {Ω} \ end {выровнять *}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}ток \ (I \) через ячейку.
Чтобы найти ток \ (I \), нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}Итак, ток через ячейку:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {12}} {\ text {2,652}} \\ & = \ текст {4,52} \ текст {А} \ end {выровнять *}ток через резистор \ (\ text {5} \) \ (\ text {Ω} \).
Ток через параллельную комбинацию резисторов равен \ (\ text {4,52} \) \ (\ text {A} \). (Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через параллельную комбинацию резисторов (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалентное сопротивление цепи):
\ begin {align *} V & = I \ cdot R \\ & = (\ text {4,52}) (\ text {0,652}) \\ & = \ текст {2,95} \ текст {V} \ end {выровнять *}Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторе \ (\ text {5} \) \ (\ text {Ω} \).
Итак, теперь мы можем рассчитать ток через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {2,95}} {\ text {5}} \\ & = \ текст {0,59} \ текст {А} \ end {выровнять *}Если ток, протекающий через ячейку, равен \ (\ text {2} \) \ (\ text {A} \), и все резисторы омические, рассчитайте напряжение на ячейке и на каждом из резисторов, \ (R_1 \ ), \ (R_2 \) и \ (R_3 \) соответственно.
Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление.Начнем с расчета эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {p} \\ & = \ text {4,66} + \ text {1,33} \\ & = \ текст {5,99} \ текст {Ω} \ end {выровнять *}Итак, напряжение на ячейке:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {5,99}) \\ & = \ текст {12} \ текст {V} \ end {выровнять *}Ток через параллельную комбинацию резисторов равен \ (\ text {2} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с нахождения напряжения на \ (R_ {1} \):
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {4,66}) \\ & = \ текст {9,32} \ текст {V} \ end {выровнять *}Теперь находим напряжение на параллельной комбинации:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {1,33}) \\ & = \ текст {2,66} \ текст {V} \ end {выровнять *}Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторах \ (R_ {2} \) и \ (R_ {3} \).
ток через ячейку
Чтобы найти ток, нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {1} + \ frac {1} {1} \\ & = 2 \\ R_ {p} & = \ text {0,5} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {4} + R_ {p} \\ & = \ text {2} + \ text {1,5} + \ text {0,5} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Итак, ток через ячейку:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {10}} {\ text {4}} \\ & = \ текст {2,5} \ текст {А} \ end {выровнять *}падение напряжения на \ (R_4 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через \ (R_ {4} \):
\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {1,5}) \\ & = \ текст {3,75} \ текст {V} \ end {выровнять *}ток через \ (R_2 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти ток через \ (R_ {2} \).
Сначала нам нужно найти напряжение на параллельной комбинации:
\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {0,5}) \\ & = \ текст {1,25} \ текст {V} \ end {выровнять *}Теперь мы можем найти ток через \ (R_ {2} \), используя тот факт, что напряжение одинаково на каждом резисторе в параллельной комбинации:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {1,25}} {\ text {1}} \\ & = \ текст {1,25} \ текст {А} \ end {выровнять *} .
