Что такое закон Ома для участка и полной цепи. Как применять формулы закона Ома на практике. Какие ограничения имеет закон Ома. Как решать задачи с использованием закона Ома.
Что такое закон Ома и для чего он нужен
Закон Ома — это один из фундаментальных законов электротехники, устанавливающий связь между током, напряжением и сопротивлением в электрической цепи. Он был открыт немецким физиком Георгом Омом в 1826 году и назван в его честь.
Закон Ома позволяет рассчитывать параметры электрических цепей и является основой для проектирования и анализа электрических схем. С его помощью можно определить:
- Силу тока при известном напряжении и сопротивлении
- Напряжение при известной силе тока и сопротивлении
- Сопротивление при известном напряжении и силе тока
Знание и умение применять закон Ома необходимо всем, кто работает с электричеством — от электриков и инженеров до радиолюбителей.
Формулировка закона Ома для участка цепи
Закон Ома для участка цепи формулируется следующим образом:

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.
Математически это выражается формулой:
I = U / R
где:
- I — сила тока (в амперах, А)
- U — напряжение (в вольтах, В)
- R — сопротивление (в омах, Ом)
Из этой базовой формулы можно вывести еще две:
U = I * R
R = U / I
Эти три формулы позволяют найти любую из величин, если известны две другие.
Закон Ома для полной цепи
Закон Ома для полной цепи учитывает не только сопротивление нагрузки, но и внутреннее сопротивление источника тока. Он формулируется так:
Сила тока в полной цепи прямо пропорциональна ЭДС источника и обратно пропорциональна сумме внешнего и внутреннего сопротивлений цепи.
Математическая запись:
I = E / (R + r)
где:
- I — сила тока
- E — электродвижущая сила (ЭДС) источника
- R — сопротивление внешней цепи
- r — внутреннее сопротивление источника
Эта формула позволяет более точно рассчитывать параметры реальных электрических цепей, учитывая особенности источников тока.
Применение закона Ома на практике
Закон Ома широко применяется в электротехнике и электронике для решения различных практических задач:
- Расчет параметров электрических цепей
- Выбор проводов нужного сечения
- Расчет мощности электроприборов
- Проектирование систем электроснабжения
- Диагностика неисправностей в электрооборудовании
Рассмотрим несколько примеров применения закона Ома.
Пример 1: Расчет тока
Задача: Определить силу тока в цепи с напряжением 220 В и сопротивлением 100 Ом.
Решение:
Используем формулу I = U / R
I = 220 В / 100 Ом = 2.2 А
Ответ: Сила тока в цепи составляет 2.2 ампера.
Пример 2: Расчет напряжения
Задача: Найти напряжение на участке цепи с сопротивлением 50 Ом, если через него протекает ток 0.5 А.
Решение:
Используем формулу U = I * R
U = 0.5 А * 50 Ом = 25 В
Ответ: Напряжение на участке цепи равно 25 вольт.
Ограничения закона Ома
Несмотря на широкое применение, закон Ома имеет ряд ограничений:
- Он применим только для проводников с постоянным сопротивлением
- Не работает для полупроводников и газовых разрядов
- Нарушается при очень высоких напряжениях и токах
- Не учитывает нелинейные эффекты в некоторых материалах
Поэтому при работе со сложными электронными схемами или специфическими материалами нужно учитывать эти ограничения и использовать более сложные модели.

Как решать задачи с использованием закона Ома
При решении задач с применением закона Ома рекомендуется следовать такому алгоритму:
- Внимательно прочитать условие задачи
- Выписать все известные величины
- Определить, какую величину нужно найти
- Выбрать подходящую формулу закона Ома
- Подставить известные значения в формулу
- Провести вычисления
- Проверить размерность полученного результата
- Записать ответ с указанием единиц измерения
Следуя этому алгоритму, можно эффективно решать большинство задач на применение закона Ома.
Значение закона Ома для развития электротехники
Открытие закона Ома стало важной вехой в развитии электротехники и электроники. Оно позволило:
- Создать научную основу для расчета электрических цепей
- Разработать методы проектирования электрооборудования
- Стандартизировать электротехнические измерения
- Заложить фундамент для дальнейших открытий в области электричества

Заключение
Закон Ома — это фундаментальный закон электротехники, устанавливающий связь между током, напряжением и сопротивлением в электрической цепи. Он широко применяется для расчета параметров электрических схем и проектирования электрооборудования.
Несмотря на некоторые ограничения, закон Ома остается мощным инструментом в руках электриков, инженеров и всех, кто работает с электричеством. Умение применять этот закон на практике — важный навык для специалистов в области электротехники и электроники.
Закон Ома для полной цепи и для участка цепи: формулы, описание и объяснение
Профессиональному электрику, специалисту электронщику никак не обойти в собственной деятельности закон Ома, решая любые задачи, связанные с наладкой, настройкой, ремонтом электронных и электрических схем.
Собственно, понимание этого закона необходимо каждому. Потому что каждому в быту приходится иметь дело с электричеством.
И хотя учебным курсом средней школы закон немецкого физика Ома и предусмотрен, но на практике не всегда своевременно изучается. Поэтому рассмотрим в нашем материале такую актуальную для жизни тему и разберемся с вариантами записи формулы.
Содержание статьи:
- Отдельный участок и полная электрическая цепь
- Расчет тока участка электрической схемы
- Вариант расчета для полной цепи
- Рассмотрение действия закона к переменной величине
- Последовательное и параллельное включение элементов
- Цепь последовательно включенных резистивных элементов
- Цепь параллельно включенных резистивных элементов
- Интегральная и дифференциальная формы закона
- Выводы и полезное видео по теме
Отдельный участок и полная электрическая цепь
Рассматривая электрическую цепь с точки зрения применения к схеме закона Ома, следует отметить два возможных варианта расчета: для отдельно взятого участка и для полноценной схемы.
Расчет тока участка электрической схемы
Участком электрической цепи, как правило, рассматривается часть схемы, исключающая источник ЭДС, как обладающий дополнительным внутренним сопротивлением.
Поэтому расчетная формула, в данном случае, выглядит просто:
I = U/ R,
Где, соответственно:
- I – сила тока;
- U – приложенное напряжение;
- R – сопротивление.
Трактовка формулы простая – ток, протекающий по некоему участок цепи, пропорционален приложенному к нему напряжению, а сопротивлению – обратно пропорционален.
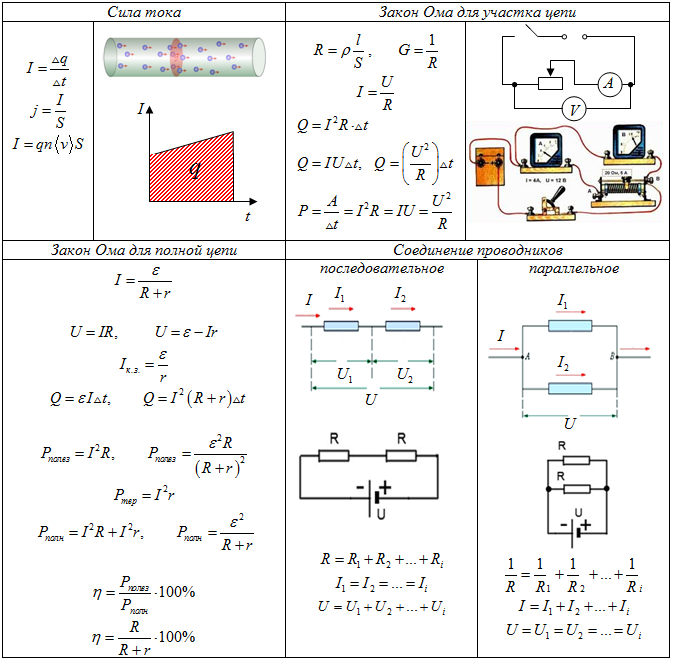
Так называемая графическая «ромашка», посредством которой представлен весь набор вариаций формулировок, основанных на законе Ома. Удобный инструмент для карманного хранения: сектор «P» — формулы мощности; сектор «U» — формулы напряжения; сектор «I» — формулы тока; сектор «R» — формулы сопротивления
Таким образом, формулой чётко описывается зависимость протекания тока по отдельному участку электрической цепи относительно определенных значений напряжения и сопротивления.
Формулой удобно пользоваться, например, рассчитывая параметры сопротивления, которое требуется впаять в схему, если заданы напряжение с током.
Закон Ома и два следствия, которыми необходимо владеть каждому профессиональному электромеханику, инженеру-электрику, электронщику и всем, кто связан с работой электрических цепей. Слева направо: 1 — определение тока; 2 — определение сопротивления; 3 — определение напряжения, где I — сила тока, U — напряжение, R — сопротивление
Вышеприведенный рисунок поможет определить, например ток, протекающий через 10-омное сопротивление, к которому приложено напряжение 12 вольт. Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.
Аналогично решаются задачи поиска сопротивления (когда известны ток с напряжением) или напряжения (когда известны напряжение с током).
Тем самым всегда можно подобрать требуемое рабочее напряжение, нужную силу тока и оптимальный резистивный элемент.
Формула, которой предложено пользоваться, не требует учитывать параметры источника напряжения. Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.
Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.
Кстати, соединительные провода любой схемы – это сопротивления. Величина нагрузки, которую им предстоит нести, определяется напряжением.
Соответственно, опять же пользуясь законом Ома, становится допустимым точный подбор необходимого сечения проводника, в зависимости от материала жилы.
У нас на сайте есть подробная инструкция по по мощности и току.
Вариант расчета для полной цепи
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.
Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС.
Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Для расчетов в условиях полноценной электрической цепи всегда берется к учету резистивное значение источника ЭДС. Это значение суммируется с резистивным сопротивлением непосредственно электрической цепи. На схеме: I — прохождение тока; R — резистивный элемент внешний; r — резистивный фактор ЭДС (источника энергии)
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины.
Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Рассмотрение действия закона к переменной величине
Понятие «сопротивление» к условиям прохождения переменного тока следует рассматривать уже больше как понятие «импеданса». Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).
Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).
Обусловлены подобные явления параметрами индуктивных элементов и законами коммутации применительно к переменной величине напряжения — синусоидальной величине тока.
Такой видится эквивалентная схема электрической цепи переменного тока под расчет с применением формулировок, исходящих из принципов закона Ома: R — резистивная составляющая; С — емкостная составляющая; L — индуктивная составляющая; ЭДС -источник энергии; I -прохождение тока
Другими словами, имеет место эффект опережения (отставания) токовых значений от значений напряжения, что сопровождается появлением активной (резистивной) и реактивной (индуктивной или емкостной) мощностей.
Расчёт подобных явлений ведётся при помощи формулы:
Z = U / I или Z = R + J * (XL — XC)
где: Z – импеданс; R – активная нагрузка; XL , XC – индуктивная и емкостная нагрузка; J – коэффициент.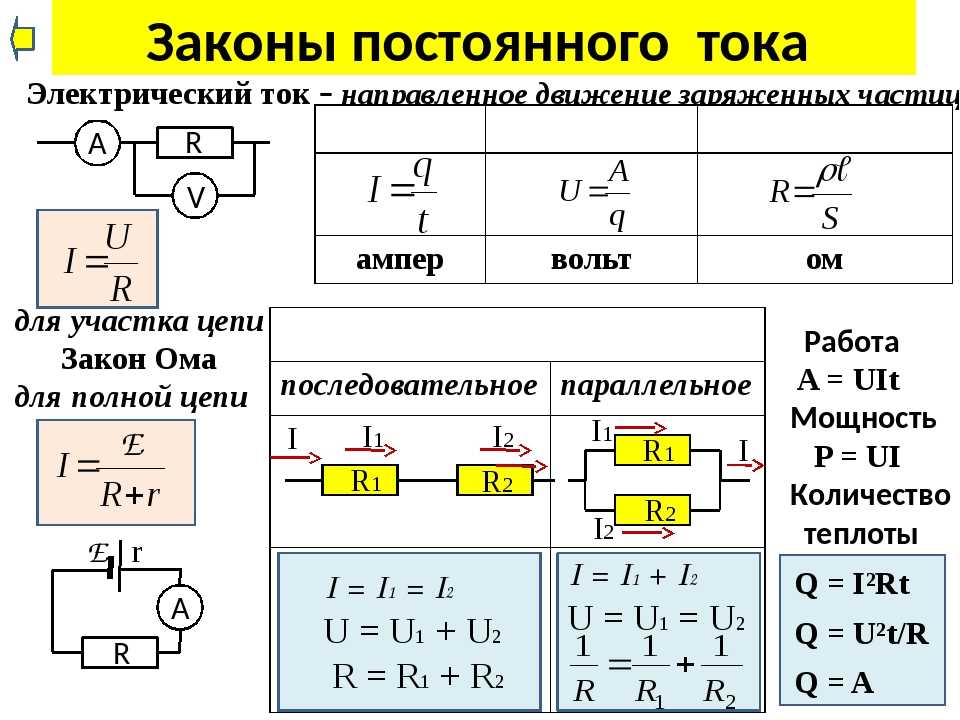
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.
Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1 = I2 ;
- U = U1 + U2 ;
- R = R1 + R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.
Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U, U1, U2 — приложенное напряжение
Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U, U1, U2 — приложенное напряжение
Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.
Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1 + I2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.
Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U — подведённое напряжение; А, В — точки входа/выхода
Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.
Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E
Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ
Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Выводы и полезное видео по теме
Подробный разбор закона Ома в видеоролике, представленном ниже, поможет окончательно закрепить знания в этом направлении.
Своеобразный видеоурок качественно подкрепляет теоретическое письменное изложение:
Работа электрика или деятельность электронщика неотъемлемо связана с моментами, когда реально приходится наблюдать закон Георга Ома в действии. Это своего рода прописные истины, которые следует знать каждому профессионалу.
Объёмных знаний по данному вопросу не требуется — достаточно выучить три основных вариации формулировки, чтобы успешно применять на практике.
Хотите дополнить изложенный выше материал ценными замечаниями или выразить свое мнение? Пишите, пожалуйста, комментарии в блоке под статьей. Если у вас остались вопросы, не стесняйтесь задавать их нашим экспертам.
Лекция № 6 — Закон Ома
Георг Симон Ом
Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.
Закон Ома для участка цепи
Строгая формулировка закона Ома может быть записана так:
сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.
Формула закона Ома записывается в следующем виде:
где
I – сила тока в проводнике, единица измерения силы тока — ампер [А];
U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];
R – электрическое сопротивление проводника, единица измерения электрического сопротивления — ом [Ом].
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза
И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.
Рассмотрим простейший случай применения закона Ома.
Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.
Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.
Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.
Где и когда можно применять закон Ома?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Задача 1.1
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.
Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.
Закон Ома для полной цепи
Формулировка закона Ома для полной цепи — сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.
Здесь могут возникнуть вопросы. Например, что такое ЭДС?
Электродвижущая сила — это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электродвижущая говорит о том, что эта сила двигает заряд.
В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.
В цепи также существует сопротивление R, оно зависит от параметров самой цепи.
Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.
Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.
Задача 2.1
Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.
Теперь решим задачу посложнее.
Задача 2.2
Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм2. Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.
Приступим.
9.4 Закон Ома – University Physics Volume 2
Глава 9. Ток и сопротивление
Ток и сопротивление
Цели обучения
К концу этого раздела вы сможете:
- Описывать закон Ома
- Распознавать, когда применяется закон Ома, а когда нет
До сих пор в этой главе мы обсуждали три электрических свойства: ток, напряжение и сопротивление. Оказывается, многие материалы демонстрируют простую зависимость между значениями этих свойств, известную как закон Ома. Многие другие материалы не показывают этой взаимосвязи, поэтому, несмотря на то, что он называется законом Ома, он не считается законом природы, как законы Ньютона или законы термодинамики. Но это очень полезно для расчетов с материалами, которые подчиняются закону Ома.
Описание закона Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
[латекс]I\phantom{\rule{0,2em}{ 0ex}}\text{∝}\phantom{\rule{0.
Это важное соотношение является основой для Закон Ома . Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, то есть экспериментально наблюдаемое явление, подобное трению. Такая линейная зависимость не всегда имеет место. Любой материал, компонент или устройство, которые подчиняются закону Ома, где ток через устройство пропорционален приложенному напряжению, известен как омический материал или омический компонент. Любой материал или компонент, который не подчиняется закону Ома, известен как неомный материал или неомический компонент.
Эксперимент Ома
В статье, опубликованной в 1827 году, Георг Ом описал эксперимент, в котором он измерял напряжение и ток в различных простых электрических цепях, содержащих провода различной длины. Аналогичный эксперимент показан на рис. 9.19. Этот эксперимент используется для наблюдения за током через резистор, возникающим в результате приложенного напряжения. В этой простой схеме резистор соединен последовательно с батареей. Напряжение измеряется вольтметром, который необходимо поставить на резистор (параллельно резистору). Ток измеряется амперметром, который должен быть подключен к резистору (последовательно с резистором).
В этой простой схеме резистор соединен последовательно с батареей. Напряжение измеряется вольтметром, который необходимо поставить на резистор (параллельно резистору). Ток измеряется амперметром, который должен быть подключен к резистору (последовательно с резистором).
В этой обновленной версии оригинального эксперимента Ома было выполнено несколько измерений тока для нескольких разных напряжений. Когда батарея была подключена, как показано на рисунке 9.19(а), ток протекал по часовой стрелке, а показания вольтметра и амперметра были положительными. Изменится ли поведение тока, если ток течет в противоположном направлении? Чтобы заставить ток течь в противоположном направлении, выводы батареи можно поменять местами. При переключении выводов батареи показания вольтметра и амперметра были отрицательными, поскольку ток протекал в противоположном направлении, в данном случае против часовой стрелки. Результаты аналогичного эксперимента показаны на рисунке 9..20.
При переключении выводов батареи показания вольтметра и амперметра были отрицательными, поскольку ток протекал в противоположном направлении, в данном случае против часовой стрелки. Результаты аналогичного эксперимента показаны на рисунке 9..20.
В этом эксперименте напряжение, приложенное к резистору, изменяется от −10,00 до +10,00 В с шагом 1,00 В. Измеряются ток через резистор и напряжение на резисторе. Строится график зависимости напряжения от тока, и результат приблизительно линейный. Наклон линии — это сопротивление или напряжение, деленное на ток. Этот результат известен как закон Ома:
[латекс]V=IR,[/латекс]
, где В — напряжение, измеренное в вольтах на рассматриваемом объекте, I — ток, измеренный через объект в амперах, а R — это сопротивление в единицах Ом. Как указывалось ранее, любое устройство, демонстрирующее линейную зависимость между напряжением и током, известно как омическое устройство. Таким образом, резистор является омическим устройством.
Как указывалось ранее, любое устройство, демонстрирующее линейную зависимость между напряжением и током, известно как омическое устройство. Таким образом, резистор является омическим устройством.
Пример
Измерение сопротивления
Угольный резистор при комнатной температуре [латекс]\left(20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}\right)[/ латекс] прикреплен к 9Батарея 0,00 В, а ток, измеренный через резистор, равен 3,00 мА. а) Чему равно сопротивление резистора в омах? (b) Если температура резистора увеличивается до [латекс]60\фантом{\правило{0.2em}{0ex}}\текст{°}\текст{С}[/латекс] путем нагревания резистора, что ток через резистор?
Стратегия
(a) Сопротивление можно найти с помощью закона Ома. Закон Ома гласит, что [латекс]V=IR[/латекс], поэтому сопротивление можно найти, используя [латекс]R=V\текст{/}I[/латекс].
(b) Во-первых, сопротивление зависит от температуры, поэтому новое сопротивление после нагревания резистора можно найти с помощью [латекс]R={R}_{0}\left(1+\alpha \text{Δ} Т\справа)[/латекс]. {3}\phantom{\rule{0.2em}{0ex}}\text{Ω}\phantom{\rule{0.2em}{0ex}}=3.00\phantom{\rule{0.2em}{0ex} }\text{k}\phantom{\rule{0.2em}{0ex}}\text{Ω}.[/latex] 9{-3}\text{A}=3.06\phantom{\rule{0.2em}{0ex}}\text{мА}.[/latex]
{3}\phantom{\rule{0.2em}{0ex}}\text{Ω}\phantom{\rule{0.2em}{0ex}}=3.00\phantom{\rule{0.2em}{0ex} }\text{k}\phantom{\rule{0.2em}{0ex}}\text{Ω}.[/latex] 9{-3}\text{A}=3.06\phantom{\rule{0.2em}{0ex}}\text{мА}.[/latex]
Значимость
Изменение температуры [латекс]40\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] привело к изменению тока на 2,00%. Это может показаться не очень большим изменением, но изменение электрических характеристик может оказать сильное влияние на схемы. По этой причине многие электронные устройства, такие как компьютеры, содержат вентиляторы для отвода тепла, рассеиваемого компонентами электрических цепей.
Проверьте свое понимание
Напряжение, подаваемое в ваш дом, изменяется как [латекс]V\left(t\right)={V}_{\text{max}}\phantom{\rule{0.2em}{0ex} }\text{sin}\phantom{\rule{0.2em}{0ex}}\left(2\pi ft\right)[/latex]. Если к этому напряжению подключить резистор, будет ли по-прежнему действовать закон Ома [latex]V=IR[/latex]?
Показать решение Да, закон Ома остается в силе.
Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Неомические устройства не демонстрируют линейной зависимости между напряжением и током. Одним из таких устройств является полупроводниковый элемент схемы, известный как диод. Диод представляет собой схемное устройство, которое позволяет току течь только в одном направлении. Схема простой цепи, состоящей из батареи, диода и резистора, показана на рисунке 9..21. Хотя мы не рассматриваем теорию диода в этом разделе, диод можно проверить, чтобы увидеть, является ли он омическим или неомическим устройством.
График зависимости тока от напряжения показан на рис. 9.22. Обратите внимание, что поведение диода показано как зависимость тока от напряжения, тогда как работа резистора показана как зависимость напряжения от тока. Диод состоит из анода и катода. Когда анод имеет отрицательный потенциал, а катод — положительный, как показано в части (а), говорят, что диод имеет обратное смещение. При обратном смещении диод имеет чрезвычайно большое сопротивление, и через диод и резистор протекает очень небольшой ток — практически нулевой ток. По мере увеличения напряжения, приложенного к цепи, ток остается практически нулевым, пока напряжение не достигнет напряжения пробоя и диод не начнет проводить ток, как показано на рисунке 9..22. Когда батарея и потенциал на диоде меняются местами, что делает анод положительным, а катод отрицательным, диод проводит ток, и ток течет через диод, если напряжение больше 0,7 В.
Ома обычно формулируется как [латекс]V=IR[/латекс], но первоначально он формулировался как микроскопический. зрения, с точки зрения плотности тока, проводимости и электрического поля. Этот микроскопический взгляд предполагает, что пропорциональность [латекс]V\propto I[/латекс] возникает из-за скорости дрейфа свободных электронов в металле, возникающей в результате приложенного электрического поля. Как указывалось ранее, плотность тока пропорциональна приложенному электрическому полю. Переформулировка закона Ома приписывается Густаву Кирхгофу, чье имя мы снова встретим в следующей главе.
Как указывалось ранее, плотность тока пропорциональна приложенному электрическому полю. Переформулировка закона Ома приписывается Густаву Кирхгофу, чье имя мы снова встретим в следующей главе.
Резюме
- Закон Ома представляет собой эмпирическую зависимость тока, напряжения и сопротивления для некоторых распространенных типов элементов схемы, включая резисторы. Это не относится к другим устройствам, таким как диоды.
- Одна формулировка закона Ома дает соотношение между током I , напряжением В и сопротивлением R в простой цепи как [латекс]В=IR[/латекс].
- Еще одно утверждение закона Ома на микроскопическом уровне: [латекс]J=\sigma E[/латекс].
Концептуальные вопросы
При определении поля по потенциалу сопротивление определялось как [латекс]R\экв\фрак{V}{I}[/латекс]. В этом разделе мы представили закон Ома, который обычно выражается как [латекс]V=IR[/латекс]. Уравнения выглядят совершенно одинаково. В чем разница между законом Ома и определением сопротивления?
В чем разница между законом Ома и определением сопротивления?
Ниже показаны результаты эксперимента, в котором четыре устройства были подключены к источнику переменного напряжения. Увеличивают напряжение и измеряют ток. Какое устройство, если таковое имеется, является омическим устройством?
Показать решение
Устройство B показывает линейную зависимость, а устройство является омическим.
Ток I измеряется через образец омического материала при приложении напряжения В . а) Какова сила тока, когда напряжение удваивается до 2 В (примем, что изменение температуры материала незначительно)? (b) Какое напряжение приложено, если измеренный ток равен 0,2 I (примем, что изменение температуры материала незначительно)? Что произойдет с током, если в материале напряжение останется постоянным, а температура материала значительно возрастет?
Проблемы
Резистор [латекс]2.2\text{-k}\phantom{\rule{0. 2em}{0ex}}\text{Ом}[/латекс] подключен к батарее типа D (1,5 В). Какой ток через резистор?
2em}{0ex}}\text{Ом}[/латекс] подключен к батарее типа D (1,5 В). Какой ток через резистор?
Резистор с номиналом [латекс]250\phantom{\rule{0.2em}{0ex}}\text{k}\phantom{\rule{0.2em}{0ex}}\text{Ом}[/latex] подключен к двум батареям D-элементов (каждая 1,50 В) последовательно, с общим напряжением 3,00 В. Производитель рекламирует, что их резисторы находятся в пределах 5% от номинального значения. Каковы возможный минимальный ток и максимальный ток через резистор? 9{5}\phantom{\rule{0.2em}{0ex}}\text{Ω}\phantom{\rule{0.2em}{0ex}},\phantom{\rule{0.8em}{0ex}}{I } _ {\ text {max}} = 11,43 \ phantom {\ rule {0.2em} {0ex}} \ mu \ phantom {\ rule {0.2em} {0ex}} \ text {A} \ hfill \ end {array }[/латекс]
Резистор соединен последовательно с источником питания 20,00 В. Мера тока 0,50 А. Чему равно сопротивление резистора?
Резистор включен в цепь с регулируемым источником напряжения. Напряжение на резисторе и ток через резистор, а также измерения показаны ниже. Оцените сопротивление резистора.
Показать решение
[латекс]R=100\фантом{\правило{0.2em}{0ex}}\текст{Ω}[/латекс]
В следующей таблице показаны измерения тока и напряжения на образце материала. Нанесите данные и, предполагая, что объект является омическим устройством, оцените сопротивление.
| I (А) | В (В) |
|---|---|
| 0 | 3 |
| 2 | 23 |
| 4 | 39 |
| 6 | 58 |
| 8 | 77 |
| 10 | 100 |
| 12 | 119 |
| 14 | 142 |
| 16 | 162 |
Глоссарий
- диод
- устройство неомической цепи, допускающее протекание тока только в одном направлении
- Закон Ома
- эмпирическое соотношение, утверждающее, что ток I пропорционален разности потенциалов V ; его часто записывают как [латекс]V=IR[/латекс], где R — сопротивление .

- омический
- тип материала, для которого справедлив закон Ома, то есть падение напряжения на приборе равно произведению силы тока на сопротивление
- неомический
- тип материала, для которого закон Ома не действует
Закон Ома. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/9-4-ohms-law. Лицензия : CC BY: Attribution . Условия лицензии : Загрузите бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction
Закон Ома и электрические цепи
Введение
В этом эксперименте вы измерите вольт-амперные характеристики резистора и проверите, чтобы
проверьте, удовлетворяет ли резистор закону Ома. В процессе вы научитесь пользоваться мультиметром для
измерять напряжение, силу тока и сопротивление. Затем вы проверите некоторые законы теории цепей.
Если разность потенциалов V , прикладывается к проводнику, электрический ток I , потечет
от конца с высоким потенциалом к концу с низким потенциалом. В общем, ток будет увеличиваться с
приложенное напряжение (разность потенциалов). График зависимости тока от напряжения называется
вольтамперная ( I — V ) характеристика. Если характеристика I — V представляет собой прямую линию, как на рис. 1, то говорят
что кусок проводника удовлетворяет закону Ома: V = IR , где R — константа, определенная как
сопротивление и измеряется в вольтах/амперах или Ω (Ом).
Затем вы проверите некоторые законы теории цепей.
Если разность потенциалов V , прикладывается к проводнику, электрический ток I , потечет
от конца с высоким потенциалом к концу с низким потенциалом. В общем, ток будет увеличиваться с
приложенное напряжение (разность потенциалов). График зависимости тока от напряжения называется
вольтамперная ( I — V ) характеристика. Если характеристика I — V представляет собой прямую линию, как на рис. 1, то говорят
что кусок проводника удовлетворяет закону Ома: V = IR , где R — константа, определенная как
сопротивление и измеряется в вольтах/амперах или Ω (Ом).
Рисунок 1 : ВАХ для омического материала
В электрической цепи провода, которые используются для соединения элементов цепи, имеют сопротивление.
Однако сопротивления проводов обычно пренебрежимо малы по сравнению с сопротивлениями проводов. элементы цепи. Существуют специальные элементы, называемые резисторами, которые контролируют распределение токов.
в цепи введением в цепь известных сопротивлений. Токи и напряжения при разных
части схемы можно рассчитать, используя теорию цепей, которая будет обсуждаться позже.
Существует много видов резисторов, но наиболее распространенными являются резисторы из углеродного композита.
показано ниже. Эти резисторы представляют собой маленькие коричневые цилиндры с цветными полосами. Цветные полосы следуют
цветовой код, указывающий сопротивление в пределах указанного производственного допуска.
элементы цепи. Существуют специальные элементы, называемые резисторами, которые контролируют распределение токов.
в цепи введением в цепь известных сопротивлений. Токи и напряжения при разных
части схемы можно рассчитать, используя теорию цепей, которая будет обсуждаться позже.
Существует много видов резисторов, но наиболее распространенными являются резисторы из углеродного композита.
показано ниже. Эти резисторы представляют собой маленькие коричневые цилиндры с цветными полосами. Цветные полосы следуют
цветовой код, указывающий сопротивление в пределах указанного производственного допуска.
Рисунок 2
В этой лабораторной работе вы будете изучать только простые схемы DC , состоящие из источника питания и одного или
больше резисторов, соединенных с проводами, сопротивления которых пренебрежимо малы по сравнению с сопротивлениями
резисторы. Основная теория анализа цепи резюмируется двумя законами, известными как закон Кирхгофа. Правила:
Правила:
-
1
Правило петли Кирхгофа - Общее изменение напряжения вокруг любого замкнутого контура равно нулю. Это очевидно, когда вы считать, что напряжение есть разность потенциалов. Это правило просто говорит о том, что разность потенциалов из одной точки в эту же точку равно нулю, как бы вы ни шли по кругу.
-
2
Правило соединения Кирхгофа - Величина тока, протекающего в любой точке провода (или в месте соединения проводов), всегда равно количеству тока, вытекающего из него.
В цепи обычно встречаются два типа соединения резисторов: последовательное и параллельное. соединение показано на рис. 3.
Рисунок 3
Используя правила Кирхгофа, можно показать, что три последовательных резистора эквивалентны одному резистор с эквивалентным сопротивлением, ·Ом , определяется по формуле:
( 1 )
Р = Р 1 + Р 2 + R 3 (резисторы последовательно)
Точно так же три резистора, соединенные параллельно, эквивалентны одному резистору с эквивалентное сопротивление, Ом , определяемое по формуле:
( 2 )
= + + (параллельные резисторы)
Аппаратура
Аппаратура для этого эксперимента состоит из регулируемого источника питания и двух мультиметров. Эти части оборудования описаны ниже.
Эти части оборудования описаны ниже.
Регулируемый блок питания
Рисунок 4
Выше показан регулируемый источник питания и его условное обозначение на схеме. Этот блок питания преобразует выход из обычной розетки 110 В, 60 Гц AC в постоянный источник питания DC с переменное напряжение от 0 до 20 В. Выдает максимальный ток 0,5 А. Поворот ручки управления на устройстве может варьироваться выходное напряжение. Рекомендуется всегда начинать с нулевого напряжения и постепенно увеличивайте его до нужного значения. Выход получается через красный и черный разъемы. К по соглашению, красный разъем — это положительный терминал, а черный разъем — отрицательный.
Измерение токов, напряжений и сопротивлений
Когда мультиметр настроен на измерение тока, он служит амперметром, когда он настроен на измерение
напряжения он служит вольтметром, а когда настроен на измерение сопротивлений, служит омметром.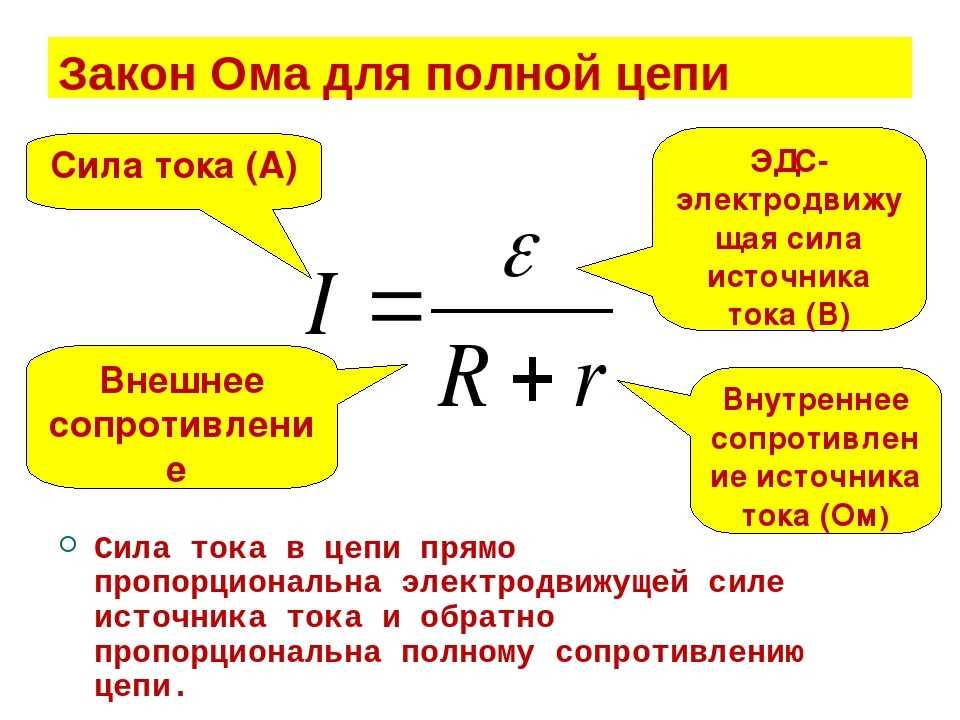 Ниже приведены символы амперметра, вольтметра и омметра.
Ниже приведены символы амперметра, вольтметра и омметра.
Рисунок 5
Чтобы измерить ток, протекающий через такой объект, как резистор, амперметр подключают к
серии с объектом, как показано на рис. 6а. Амперметры имеют очень низкое сопротивление так что когда они
помещенные в цепь, они не оказывают существенного влияния на общее сопротивление цепи и, следовательно, на ток,
измеряться.
Для измерения напряжения на объекте, таком как резистор, вольтметр подключается параллельно
с объектом, как показано на рис. 6b. Вольтметры имеют очень большое сопротивление , так что только небольшая часть
часть тока цепи будет отведена через вольтметр.
Для измерения сопротивления объекта, например резистора, омметр подключается к объекту.
как показано на рис. 6c. Если резистор подключен к цепи, то один конец резистора должен быть
отключен от цепи во время измерения. Батарейка в мультиметре поставляет
ток, необходимый для измерения сопротивления, чтобы внешний источник питания не требуется.
Рисунок 6
Выполнение одновременных измерений тока и напряжения
Рисунок 7
Существует два способа одновременного измерения A и V , как показано на рис. 7а и
Рис. 7б. На рис. 7а амперметр измеряет ток в резисторе R , а вольтметр не
измерить напряжение на резисторе, В Р . Вместо этого он измеряет напряжение на резисторе плюс
напряжение на амперметре, В А . Since V R + V A = I R + IR A , where R A is the resistance of the ammeter ,
показания вольтметра будут примерно равны В R , если R намного больше сопротивления
амперметр. Амперметры обычно имеют сопротивление 0,001 Ом или меньше. Использование метода (а) для измерения
напряжение на резисторе с малым сопротивлением, скажем, 0,1 Ом, даст ошибку в напряжении IR A / IR = 0,001/0,1 или ошибку 1%. С другой стороны, при большом сопротивлении, скажем, R = 1000 Ом, ошибка
уменьшается до
Использование метода (а) для измерения
напряжение на резисторе с малым сопротивлением, скажем, 0,1 Ом, даст ошибку в напряжении IR A / IR = 0,001/0,1 или ошибку 1%. С другой стороны, при большом сопротивлении, скажем, R = 1000 Ом, ошибка
уменьшается до
IR A / IR = 0,001/1000 или 0,0001%.
Поэтому метод, показанный на рис. 7а, следует использовать для измерения больших сопротивлений. На рис. 7б вольтметр измеряет напряжение на резисторе R , а амперметр не измерить ток через резистор I . Вместо этого он измеряет ток через резистор плюс ток через вольтметр, I V . Сумма этих токов определяется выражением:
( 3 )
Я + Я В = +
где R V сопротивление вольтметра. Следовательно, измерение амперметра будет приблизительно равно I , если R намного меньше, чем R V . Вольтметры обычно имеют сопротивления
100 000 Ом или более. Используя метод (б) для измерения тока на резисторе с большим сопротивлением, скажем
1000 Ом, погрешность измерения тока составит I V / I = R / R V = 1000/100000 или ошибка 1%.
Для небольшого сопротивления, скажем, Ом = 0,1 Ом, ошибка уменьшается до
Вольтметры обычно имеют сопротивления
100 000 Ом или более. Используя метод (б) для измерения тока на резисторе с большим сопротивлением, скажем
1000 Ом, погрешность измерения тока составит I V / I = R / R V = 1000/100000 или ошибка 1%.
Для небольшого сопротивления, скажем, Ом = 0,1 Ом, ошибка уменьшается до
Ом/Ом В = 0,1/100 000 или 0,0001%.
Поэтому метод, показанный на рис. 7b, следует использовать для измерения малых сопротивлений.
Процедура
Измерение сопротивления
-
1
Используя мультиметр в качестве омметра, измерьте и запишите сопротивления каждого из трех предусмотрены резисторы. Не забудьте включить оценки неопределенности, основанные на точности метр. -
2
Соедините три резистора последовательно. Запишите эквивалентное сопротивление, определенное с помощью омметр.
-
3
Соедините три резистора параллельно. Запишите эквивалентное сопротивление, определенное с помощью омметр.
Вольт-амперные характеристики резистора
Эта часть эксперимента требует, чтобы вы одновременно измеряли ток и напряжение на резистор. Резисторы, используемые в этом эксперименте, имеют сопротивление около 1000 Ом. Следовательно метод, показанный на рис. 7а, следует использовать для одновременного измерения I и V .
-
1
Выберите резистор с сопротивлением около 600 Ом. Подключите блок питания (не включайте его еще), вольтметр, амперметр и резистор в соответствии с принципиальной схемой, показанной на рис. Рис. 7а. Вы можете использовать Fluke 77 в качестве амперметра и Micronta в качестве вольтметра. Поскольку напряжение блока питания около 10 В, ток будет порядка миллиампер. Таким образом, клеммы «300 мА» и «COM» на Fluke 77 следует использовать для амперметра. связь.
связь.
-
2
Попросите инструктора лаборатории проверить вашу схему, прежде чем включать источник питания. -
3
С ручкой управления в минимальном положении (полностью против часовой стрелки) включите питание. питание включено. Поверните ручку управления вверх, пока вольтметр не покажет около одного вольта. Запишите тока и напряжения. -
4
Увеличивайте напряжение с шагом 2 В. Измерьте и запишите ток и напряжение. Останавливаться когда напряжение достигает примерно 15 Вольт. -
5
Полностью поверните ручку управления на блоке питания против часовой стрелки и поверните выключатель питания. выключенный. -
6
Проверьте свои данные, построив грубый график V по сравнению с I на листе технических данных или на листе миллиметровой бумаги. Проверьте, согласуется ли ваш график с законом Ома. Проверьте, дает ли наклон вашего участка правильный сопротивление. -
7
Повторите вышеуказанные шаги, чтобы измерить V vs.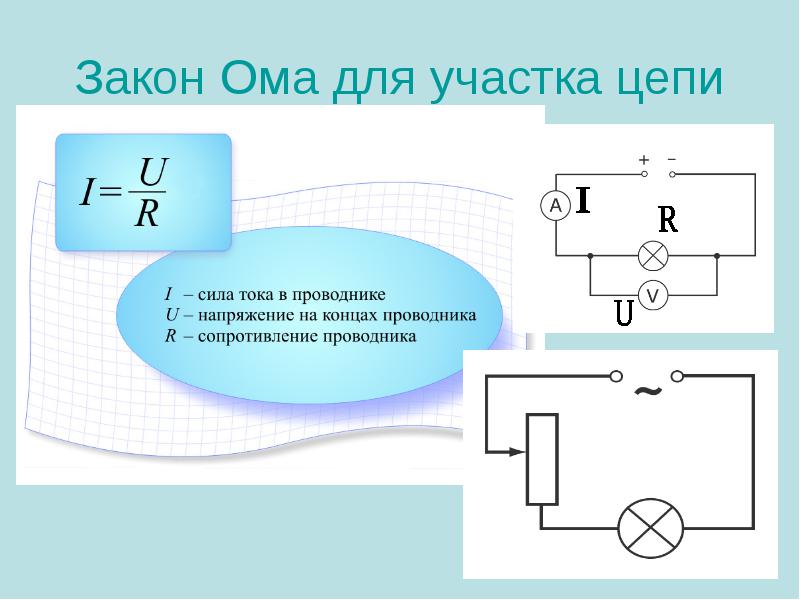 I характеристики лампочки (#53, 120 мА при
14 В). Используйте ту же схему, но замените резистор лампочкой. Возьмите показания данных в
шаг тока от 10 мА до максимум 100 мА.
I характеристики лампочки (#53, 120 мА при
14 В). Используйте ту же схему, но замените резистор лампочкой. Возьмите показания данных в
шаг тока от 10 мА до максимум 100 мА.
Правила Кирхгофа
В этом эксперименте вы проверите правила Кирхгофа на простой схеме, показанной ниже.
Рисунок 8
-
1
Подключите три резистора и блок питания в соответствии с приведенной выше схемой. Быть Обязательно определите и запишите значения трех резисторов. -
2
Попросите инструктора лаборатории проверить вашу схему, прежде чем включать источник питания. -
3
Включите источник питания и регулируйте ручку управления до тех пор, пока напряжение источника питания не станет равным 10 В. Запишите выходное напряжение В и сохраните его до конца эксперимента. -
4
Измерьте и запишите напряжения В 1 , В 2 и В 3 на каждом из резисторов. Запомни
включите оценки неопределенности для каждого из ваших измерений на основе рейтинга точности
метр.
Запомни
включите оценки неопределенности для каждого из ваших измерений на основе рейтинга точности
метр.
-
5
Измерьте и запишите токи I 1 , I 2 и I 3 через каждый из резисторов вместе с соответствующие значения неопределенности. Поскольку для этого измерения источник питания всегда включен, легко перегореть предохранитель на мультиметре, если он не подключен должным образом. Выключить мультиметр при подключении. Убедитесь, что мультиметр подключен последовательно с резистором, который вы измеряете, прежде чем включать его. Если вы не уверены, уточните у своего инструктор. -
6
Выключите мультиметр и источник питания, когда закончите эксперимент.
Когда вы закончите эксперимент, очистите свое рабочее место и верните все
провода и зажимы в свои бункеры для хранения.
Убедитесь, что вы и ваш инструктор поставили свои подписи на своих листах данных и передали копию
свои данные, прежде чем покинуть лабораторию.
Анализ данных
Измерение сопротивления
Для этой части мы будем обозначать расчетное эквивалентное сопротивление через R T , а измеренное эквивалентное сопротивление через R .
-
1
Рассчитайте сумму R T сопротивлений трех резисторов R 1 , R 2 и R 3 подключены ряд. -
2
Каковы погрешностиu R 1 , u R 2 , u R 3
в ваших измерениях сопротивлений? Что источник неопределенности? -
3
Используя ваши значения погрешностей трех резисторов, рассчитайте погрешность сумма u R T с помощью формулы распространения неопределенности для суммы.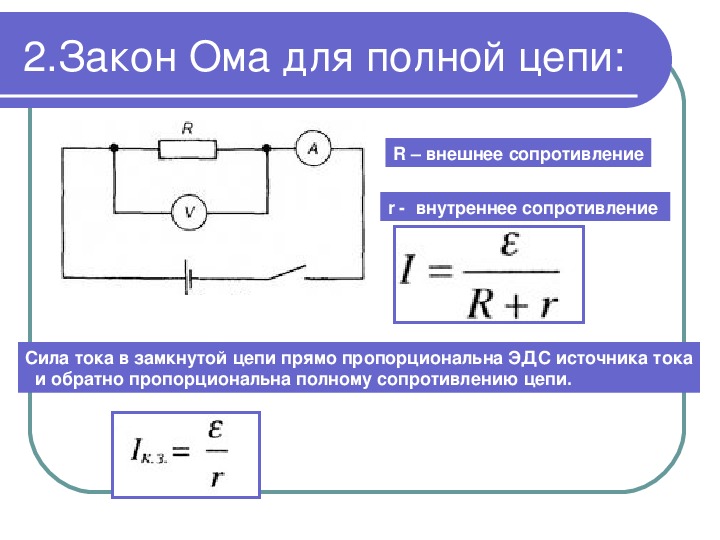
-
4
Суммируйте ваши значения R и R T , включая неопределенности. -
5
Рассчитайте общее сопротивлениеR T
для параллельного соединения. -
6
Используя формулу распространения неопределенности для отношения, покажите, что дробная неопределенность из f совпадает с дробной неопределенностью 1/ f , т.е. показывает=
u 1/f 1/f 8.7
Используя уравнение шага 6, вычислите неопределенности 1/ R 1 , 1/ R 2 и 1/ R 3 . Затем с помощью распространения неопределенности для суммы, рассчитать неопределенность 1/ R T от неопределенностей из 1/ R 1 , 1/ R 2 и 1/ R 3 . Наконец, снова используя уравнение шага 6, рассчитайте неопределенность R T от неопределенности 1/ R T .
8
Суммируйте ваши значения R и R T , включая неопределенности.Вольт-амперные характеристики резистора и лампочки
-
1
Подготовьте две таблицы (одну для резистора и одну для лампочки) токов и напряжений. из полученных данных. -
2
Сделайте график рассеяния В против I для данных резистора. -
3
Создайте линейную подгонку вашего графика по закону Ома по методу наименьших квадратов: В = ИК . Чему соответствуют параметры наклона и пересечения в подгонке? -
4
Суммируйте значение R (измеренное мультиметром) и подогнанное значение R , включая неопределенности. -
5
Постройте диаграмму рассеяния V против I для данных об лампочке.
Петля Кирхгофа и правила соединения
-
1
Каковы погрешности ваших измерений токов I 1 , I 2 и I 3 ? На основе этих погрешностей проверьте, удовлетворяют ли измеренные токи правилу соединения, т.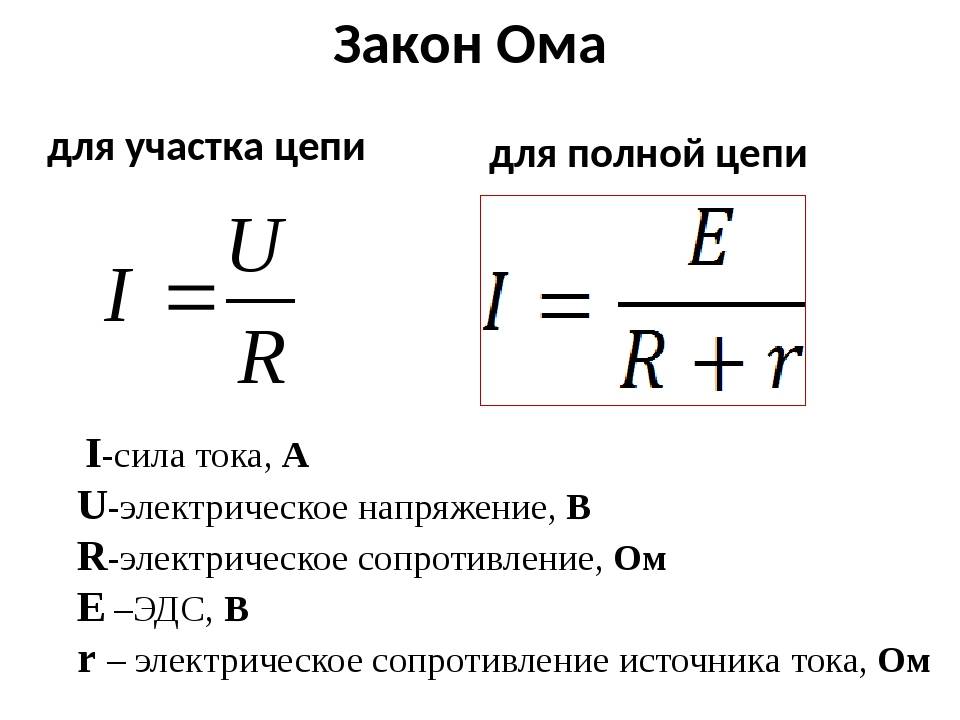 е.
е. I 1 = I 2 + I 3 .
-
2
В схеме, используемой в этой части, три петли . Запишите уравнение, данное правило цикла для каждого цикла. На основании погрешностей в ваших измерениях В 1 , В 2 и В 3 , убедитесь, что измеренные вами напряжения удовлетворяют уравнениям, полученным из правила контура.
Обсуждение
Обобщите результаты для раздела, посвященного измерению сопротивления. Какое из соединений, последовательное или параллельное, дало наименьшую суммарную сопротивление? Почему? Соответствует ли ваше измеренное значение общего сопротивления последовательного соединения и параллельное соединение соответствует расчетному эквивалентному сопротивлению? Дайте характеристику вольт-амперной характеристики резистора, изучаемого в разделе «Вольт-амперная характеристика резистора».
 .
.

