Активное сопротивление в цепи переменного тока
Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону
u = Umsinωt
Найдём ток и мощность в цепи.
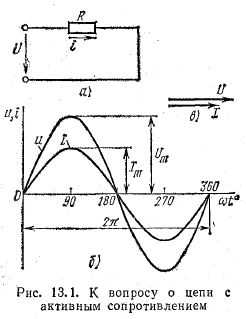

Ток в цепи переменного тока с активным сопротивлением.
По закону Ома найдем выражение для мгновенного тока:
где Im = Um/R — амплитуда тока
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).
Действующий ток найдем, разделив амплитуду на √ 2:
Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.
В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I2R = U2R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
electrikam.com
Активное сопротивление в цепи переменного тока
На векторных диаграммах можно показать, что ток и напряжение совпадают по фазе (рис. 52,а) или э. д.с. сдвинуты по фазе на некоторый угол (рис. 52,6). Условно принято считать, что векторы перемещаются в направлении против движения часовой стрелки.
Если векторы имеют различную длину, следовательно, их действующие значения разные (см. рис. 52, б).
§ 52. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением.
К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.
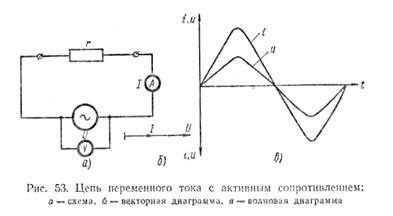
Рассмотрим цепь переменного тока (рис. 53), в которую включено активное сопротивление. В такой цепи под действием переменного напряжения протекает переменный ток. Изменение тока в Цепи, согласно закону Ома, зависит только от изменения напряжения, подключенного к ее зажимам. Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в Цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.
Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и Направление тока. Это значит, что ток и напряжение совпадают по фазе.
Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отлов жим в выбранном масштабе по горизонтали вектор напряжения Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (=0), откладываем вектор тока I по направлению вектора напряжения.
Сила тока в такой цепи определяется по закону Ома:
В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.
Пример. К цепи переменного тока с активным сопротивлением r=55 ом подключен генератор, максимальное значение напряжения которого Um=310,2 в.
Определить:
показание вольтметра, подключенного к зажимам генератора; показание амперметра, включенного в цепь; среднее значение мощности, потребляемой сопротивлением.
Решение. Известно, что электроизмерительные приборы, включенные в цепь переменного тока, измеряют действующие значения. Поэтому показание вольтметра, измеряющего напряжение,
Показание амперметра, измеряющего действующее значение тока,
Среднее значение активной мощности, потребляемой сопротивлением, Р=220х4 = 880
§ 53. ИНДУКТИВНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Прохождение электрического тока по проводнику или катушки сопровождается появлением магнитного поля. Рассмотрим электрическую цепь переменного тока (рис. 54,а), в которую включена катушка индуктивности, имеющая небольшое количество витком проволоки сравнительно большого сечения, активное сопротивления которой можно считать практически равным нулю.
Под действием э. д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции
(55)
где L — индуктивность катушки,
в омах. Таким образом, индуктивное сопротивление катушки ХL зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э. д. с. самоиндукции, зависит от скорости изменения тока в катушке (от частоты ) и от индуктивности катушки L:
где XL, — индуктивное сопротивление, ом,
ώ — угловая частота переменного тока, рад/сек,
L — индуктивность катушки, гн.
Так как угловая частота переменного тока , то индуктивное сопротивление
где, f—-частота переменного тока, гц.
Пример. Катушка, обладающая индуктивностью L=0,5 гн, присоединена к источнику переменного тока, частота которого f=50 гц. Определить:
1) индуктивное сопротивление катушки при частоте f=50 гц;
2) индуктивное сопротивление этой катушки переменному току, частота которого f=800 гц.
Решение. Индуктивное сопротивление переменному току при f=50 гц
При частоте тока f=800 гц
Приведенный пример показывает, что индуктивное сопротивление катушки повышается с увеличением частоты переменного тока, протекающего по ней. По мере уменьшения частоты тока индуктивное сопротивление убывает. Для постоянного тока, когда ток в катушке не изменяется и магнитный поток не пересекает ее витки, э. д. с. самоиндукции не возникает, индуктивное сопротивлений катушки ХL равно нулю. Катушка индуктивности для постоянного тока представляет собой лишь сопротивление
Выясним, как изменяется э. д. с. самоиндукции, когда по катушке индуктивности протекает переменный ток.
Известно, что при неизменной индуктивности катушки э. д. с. самоиндукции зависит от скорости изменения силы тока и она всегда направлена навстречу причине, вызвавшей ее.
На графике (рис. 54, в) переменный ток показан в виде синусоиды (сплошная линия). В первую четверть периода сила тока возрастает от нулевого до максимального значения. Электродвижущая сила самоиндукции ес, согласно правилу Ленца, препятствует увеличению тока в цепи. Поэтому на графике (пунктирной линией) показано, что ес в это время имеет отрицательное значение. Во вторую четверть периода сила тока в катушке убывает до нуля. В это время э. д.с. самоиндукции изменяет свое направление и увеличивается препятствуя убыванию силы тока. В третью четверть периода том изменяет свое направление и постепенно увеличивается до максимального значения; э. д. с. самоиндукции имеет положительное значение и далее, когда сила тока убывает, э. д. с. самоиндукции опять меняет свое направление и вновь препятствует уменьшению силы тока в цепи.
fiziku5.ru
2.5. Сопротивления в цепи переменного тока
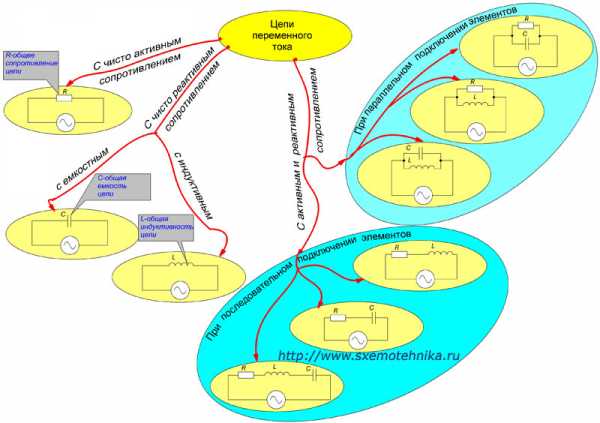
В цепях переменного тока выделяют следующие виды сопротивлений.
Активное. Активным называют сопротивление резистора. Условное обозначение
Единицей измерения сопротивления является Ом. Сопротивление резистора не зависит от частоты.
Реактивное. В разделе реактивные выделяют три вида сопротивлений: индуктивное xL и емкостное хс и собственно реактивное. Для индуктивного сопротивления выше была получена формула XL = ωL. Единицей измерения индуктивного сопротивления также является Ом. Величина xL линейно зависит от частоты.
Для емкостного сопротивления выше была получена формула XC = 1 / ωC. Единицей измерения емкостного сопротивления является Ом. Величина хс зависит от частоты по обратно-пропорциональному закону. Просто реактивным сопротивлением цепи называют величину X = XL — XC.
Полное сопротивление. Полным сопротивлением цепи называют величину
(2.28)
.
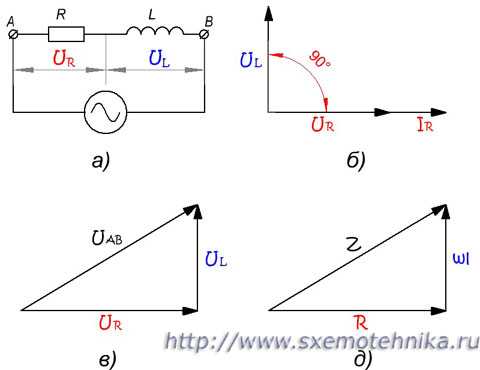
Из этого соотношения следует, что сопротивления Z, R и X образуют треугольник: Z – гипотенуза, R и X – катеты. Для удобства в этом треугольнике рассматривают угол φ, который определяют уравнением
(2.29)
φ = arctg((XL — XC) / R),
и называют углом сдвига фаз. С учетом него можно дать дополнительные связи
(2.30)
R = Z cos φ,
(2.31)
X = Z sin φ.
2.6. Мощности в цепях переменного тока
По аналогии с мощностью в цепях постоянного тока P = U I, в цепях переменного тока рассматривают мгновенную мощность p = u i. Для упрощения рассмотрим мгновенную мощность в каждом из элементов R, L и С отдельно.
Элемент r (резистор)
Зададим напряжение и ток в виде соотношений
u(t) = Um sin(ωt + ψu),
i(t) = Im sin(ωt + ψi).
Известно, что для резистора ψu = ψi, тогда для р получим
(2.32)
p(t) = u(t) i(t) = Um Im sin2(ωt + ψi
Из уравнения (2.32) видно, что мгновенная мощность всегда больше нуля и изменяется во времени. В таких случаях принять рассматривать среднюю за период Т мощность
(2.33)
.
Если записать Um и Im через действующие значения U и I: ,, то получим
(2.34)
P = U I.
По форме уравнение (2.34) совпадает с мощностью на постоянном токе. Величину Р равную произведению действующих значений тока и напряжения называют активной мощностью. Единицей ее измерения является Ватт (Вт).
Элемент l (индуктивность)
Известно, что в индуктивности соотношение фаз ψu = ψi + 90°. Для мгновенной мощности имеет
(2.35)
.
Усредняя уравнение (2.35) по времени за период Т получим
.
Для количественной оценки мощности в индуктивности используют величину Q L равную максимальному значению рL
(2.36)
QL = (Um Im) / 2
и называют ее реактивной (индуктивной) мощностью. Единицей ее измерения выбрали ВАр (вольт-ампер реактивный). Уравнение (2.36) можно записать через действующие значения U и I и используя формулу UL = I XL получим
(2.37)
QL = I2 XL.
Элемент с (ёмкость)
Известно, что в емкости соотношение фаз ψu = ψi — 90°. Для мгновенной мощности получаем
pC(t) = u(t) I(t) = (Um Im) / 2 · sin(2ωt).
Среднее значение за период здесь также равно нулю. По аналогии с уравнением (2.36) вводят величину QC = I2 XC, которую называют реактивной (емкостной) мощностью. Единицей ее измерения также является ВАр.
(2.37)
P = U I cos φ,
(2.38)
Q = QL — QC,
(2.39)
Q = U I sin φ,
где φ – угол сдвига фаз.
Вводят понятие полной мощности цепи
(2.40)
.
С учетом уравнений (2.37) и (2.39), (2.40) можно записать в виде
(2.41)
S = U I.
Единицей измерения полной мощности является ВА – вольт-ампер.
studfiles.net
Формула активного сопротивления в цепи переменного тока
В электротехнике активное сопротивление в цепи переменного тока, так же как и реактивная нагрузка, относится к разряду труднодоступных для понимания тем. Только немногие специалисты могут понятно объяснить, какие процессы происходят на участке электрической схемы. Для начала понимания нужно обратиться к словарю и узнать, что означает слово «активный». Это деятельный, инициативный и энергичный элемент или объект. В электротехнике под сопротивлением с активным свойством понимают элемент, способный потреблять электроэнергию и превращать ее в иной вид энергии (свет, тепло или химические реакции). Специалисты его называют еще ваттным сопротивлением. К активным элементам в электрической схеме тока с переменной характеристикой относят различные накаливаемые элементы и, конечно же, лампы с нитью накаливания. Графически активное сопротивление рисуют в виде резистора.
Графическое обозначение элемента с активным свойством в электротехнике
Сопротивление с активным свойством в цепи с переменной характеристикой
Если в цепь с переменной характеристикой тока подключить активную нагрузку, то по проводнику начнет протекать электрический ток по синусоидальной траектории. Это происходит за счет видоизменения напряжения по синусоиде:
u = Um sin ωt.
Отсюда и силу тока можно выразить формулой:
i = Im sin ωt,
где максимальная амплитуда силы тока считается по формуле:
Im =Um/R.
Важно знать! Сила тока в цепи с переменной характеристикой переменяется по тому закону, что и напряжение. То есть прохождение нулевой отметки у них происходит синхронно, так же как и достижение пиковой вершины.
Графика видоизменения силы тока и напряжения
Из графика видно, что за счет идеального активного в цепи сопротивления ток и напряжение совмещаются по фазе. Если в формуле:
i = Im sin ωt
каждую сторону поделить на √2, то получим формулу, выражающую закон Ома:
I=U/R.
Отсюда следует вывод, что для электрической схемы с переменной характеристикой, имеющей активное сопротивление, основополагающим законом является закон Ома.
Характеристики потерь
Причиной потерь с активной нагрузкой в схеме с переменной характеристикой тока являются:
- Омическое сопротивление самого материала проводника;
- Кроме этого, нельзя не обращать внимания на другие причины, как, например, наличие конденсатора (в электротехнике под ним можно подразумевать, например, кабель в изоляции).В такой схеме энергия теряется за счет постоянно изменяющего поляризацию диэлектрика такой изоляции. Это происходит за счет систематического «переворачивания» парных зарядов молекул, в свою очередь, приводящее к нагреву диэлектрического слоя. Такие потери в электротехнике называют диэлектрическими утечками;
- Кроме диэлектрических потерь в конденсаторном элементе, в схеме переменного тока присутствует потеря утечки. Она возникает за счет несовершенства материала изоляции;
- Также нельзя исключать потери на гистерезис, за счет постоянного присутствия переменного магнитного поля. Это приводит к нагреванию металлических частей схемы, так как наличествует систематическое переворачивание в такт с частотой переменного тока магнитиков;
- Токи Фуко также порождают высокие утраты в электрической цепи с переменной характеристикой. Они представляют собой индуктивные круговые токи и подвергают нагреванию все элементы схемы.
Присутствие всех перечисленных потерь значительно увеличивает активное сопротивление в схеме с переменным током.
Мощность в схеме с активной нагрузкой
Когда схема функционирует на переменном напряжении и токе, то напряженность преобразования электрической энергии в иной вид энергии изменяется. Отсюда получается, что такое изменение меняет мощность. Из формулы:
p = Umsinωt * Imsinωt = UmImsin2ωt
следует, что мгновенная мощность равноправна произведению мгновенного напряжения на мгновенную составляющую силы тока.
Генерация активной составляющей мощности
После тригонометрических переустройств видим, что мгновенная мощность одинакова по сумме с мгновенной и постоянной составляющими:
р = Р + р’, где Р = UmIm√2.
Важно знать! Под понятием активная мощность следует понимать, что она представляет собой среднее арифметическое мгновенных составляющих за определенный период времени.
На простом языке активная мощность – это положительная характеристика электрической схемы с переменным током. Она относится к разряду основных свойств в ходе выбора электрических нагрузок и учета потребления электрической энергии.
Взгляд на эффект с поверхностным влиянием
Активное сопротивление электрической цепи, функционирующей от переменного напряжения, постоянно больше от сопротивления с активной функцией в цепи постоянного напряжения. Основанием этому является то, что переменный ток по равноправному уровню разделяется по всей поперечной плоскости проводника. От этого полезная плоскость значительно убавляется, а сопротивление растет. Этот физический процесс называется эффектом поверхностного действия.
При поверхностном эффекте заряженные частицы в основном двигаются по внешней оболочке проводника, так как поверхность проводника становится полезным сечением. С увеличением частоты электроны двигаются, максимально приближаясь к внешним границам. Для понижения данного явления изготавливают провода специального устройства. Их делают с трубчатыми жилами или покрывают жилы металлами, имеющими идеальную проводимость. Схемы с серебряными выводами очень хорошо знакомы многим специалистам.
Понижение поверхностного эффекта
На практике для повышения активной мощности в электрических схемах применяют специальные устройства и технологии, позволяющие снизить потери и уменьшить реактивную характеристику мощности. Самыми распространенными являются компенсирующие конденсаторные установки, а в быту – это индивидуальные блоки питания. Также перед созданием электрической сети в проекты закладываются проводники с наибольшей проводимостью и требуемым от нагрузок сечением. Кроме этого, в сложных схемах немаловажным является равномерное распределение активных нагрузок потребителей.
Видео
Оцените статью:elquanta.ru
основные сведения, формулы и зависимости для цепи переменного тока
 Для проектирования электронных устройств следует рассчитывать различные параметры, одним из которых является электропроводимость или сопротивление проводника. Для цепей, питающихся постоянным током, вычислить его несложно. Но в цепях переменного тока (ПТ) существуют совсем другие соотношения. Для расчета активного сопротивления необходимо ознакомиться с основными формулами, а также альтернативными способами его вычисления.
Для проектирования электронных устройств следует рассчитывать различные параметры, одним из которых является электропроводимость или сопротивление проводника. Для цепей, питающихся постоянным током, вычислить его несложно. Но в цепях переменного тока (ПТ) существуют совсем другие соотношения. Для расчета активного сопротивления необходимо ознакомиться с основными формулами, а также альтернативными способами его вычисления.
Основные сведения об электропроводимости
Каждое вещество проводит ток по-разному. Все зависит от электронной конфигурации, которую можно получить из таблицы Д. И. Менделеева. Электронная конфигурация показывает основной параметр, от которого зависит величина сопротивления R, — количество свободных электронов (Nсэ). Вещество состоит из атомов, которые образуют кристаллическую решетку (КР). Не все электроны прочно удерживаются ядром.
Классификация веществ
В веществах присутствует несколько электронов (Э), которые имеют очень слабую силу взаимодействия с ядром. Кроме того, в металлах, кроме обыкновенных Э, есть определенное Nсэ. При приложении незначительной сторонней энергии происходит отрыв электронов от ядер атомов, и это приводит к образованию ионов. Металл остается незаряженным, так как отрицательный заряд всех Э равен положительному заряду элементарных частиц (ЭЧ), входящих в состав ядер. Ядро состоит из нуклонов, а именно:
- протонов — положительно заряженных ЭЧ;
- нейтронов — нейтральные ЭЦ.
Свободные Э движутся хаотично, однако среди них есть такие, которые летят близко к поверхности металла, и они не могут вылететь из вещества, так как их удерживает сила притяжения ионов и ядер. Исходя из Nсэ, можно разделить любое вещество на 3 группы по проводимости:
- Проводники.
- Полупроводники.
- Диэлектрики.
К проводникам (П) относятся вещества, обладающие большим Nсэ. К ним относятся металлы, электролитические растворы и ионизированные газы. В металлах свободными носителями заряда (СНЗ) являются свободные Э, в электролитах и ионизированных газах — ионы, под действием электрического поля движение СНЗ становится упорядоченным, в результате которого образуется электрический ток (ЭТ).
В полупроводниках Nсэ зависит от различных внешних факторов, при действии которых происходит освобождение некоторых Э от действия силы притяжения ядра — силы Кулона при взаимодействии 2 и более частиц. Место, которое покинул Э, называется дыркой. Движение дырок и Э является противоположным, и при этом возникает ЭТ. К веществам полупроводникового типа относятся следующие: кремний (Si), германий (Ge), селен (Se) и т. д.
К группе диэлектриков или изоляторов относятся вещества, которые вообще не обладают СНЗ, а следовательно, они не проводят электрический ток вообще. При некоторых условиях диэлектрик может стать отличным от П тока, например, если будет покрыт каплями электропроводящей жидкости. Этот момент является очень важным для избежания выхода аппаратуры из строя или поражения ЭТ. При протекании по П ЭТ оказывает тепловое действие на него. Это свойство обусловлено тем, что Э взаимодействуют с узлами КР, и кинетическая энергия Э превращается в тепловую.
В результате происходит снижение скорости Э, а затем ее полное восстановление при воздействии электромагнитного поля. Этот процесс повторяется большое количество раз и называется электрическим сопротивлением, которое обозначается для цепей постоянного тока R, а для цепей переменного тока (ПТ) существует полное сопротивление — Z. Измеряется R и Z в Ом.
Зависимость от различных параметров
R является величиной, зависящей от многих факторов. Эти факторы можно разделить на группы:
- Физические свойства: длина, площадь поперечного сечения (S) и деформация.
- Внешняя среда: температура.
- Электрические: I, U, e (электродвижущая сила — ЭДС).
R рассчитывается по закону Ома: I = U / R. Формулировка этого закона следующая: I, протекающий на участке цепи, прямо пропорционален U и обратно пропорционален R выбранного участка.
Формулировка для всей цепи: I, протекающий по всей цепи, прямо пропорционален ЭДС и обратно пропорционален R всего участка с учетом внутреннего сопротивления источника питания (ИП). Формула имеет вид: I = e / (R + Rип). Из соотношений для полной и участка цепи можно получить R:
- R = U / I.
- R = (e / I) — Rип.
Тип вещества определяется коэффициентом удельного сопротивления p, который берется из справочника. Однако следует учесть, что в справочнике приведено его значение при температуре +20 градусов. Кроме того, существует и удельная проводимость, которая обратно пропорциональна p. Она обозначается σ и равна: p = 1 / σ.
При меньшей величине S Э протекают через П и взаимодействия с КР учащаются, что иллюстрирует зависимость R от S. Для вычисления S необходимо воспользоваться справочной литературой или интернетом. Если учесть, что проводник является плоскостью, то необходимо разрезать его при помощи другой плоскости (стереометрия).
При разрезе получается плоская фигура в виде квадрата, окружности, эллипса, прямоугольника или треугольника. Затем необходимо вычислить S этой фигуры. Если П состоит из определенного количества жил, то нужно измерить S одной жилы, а затем умножить на количество жил.
R зависит прямо пропорционально от длины П (L): чем больше длина, тем больше взаимодействий совершает Э при движении. Исходя из всех зависимостей можно выразить R формулами:
- R = p * L / S.
- R = L / (σ * S).
Эти соотношения справедливы при температуре +20 градусов, но для проведения точных расчетов этого недостаточно. Некоторые сверхчувствительные элементы могут работать некорректно из-за низких значений I.
Значение p зависит от t и выражается следующим соотношением: p = p20 * [1 + a * (t — 20)]. В этом соотношении присутствуют следующие величины:
- p — удельное сопротивление, полученное при вычислении.
- p20 — величина удельного сопротивления, взятого из справочной литературы при температуре (температура +20 градусов по Цельсию).
- Температурный коэффициент a, который берется из справочной литературы. Для металлов он всегда больше 1, а для электролитических растворов — меньше.
- Температура П при конкретных условиях эксплуатации, температурная шкала по Цельсию — t.
Кроме того, p зависит еще и от уровня деформации КР. Деформация бывает упругой и пластической. При упругой происходит увеличение p, а при пластической — уменьшение. Это связано с условиями деформаций, а также со степенью затрудненности движения Э. Конечная формула при учете основных факторов примет следующий вид: R = p20 * [1 + a * (t — 20)] * L / S.
Соотношения для переменного тока
 Для того чтобы разобраться в некоторых терминах, например, какое сопротивление называется активным, и что оно из себя представляет, необходимо применить формулу полного сопротивления: sqr (Z) = sqr® +sqr (Xc-Xl). Сопротивление переменного тока является полным и состоит из активного R, индуктивного (Хl) и емкостного (Xc).
Для того чтобы разобраться в некоторых терминах, например, какое сопротивление называется активным, и что оно из себя представляет, необходимо применить формулу полного сопротивления: sqr (Z) = sqr® +sqr (Xc-Xl). Сопротивление переменного тока является полным и состоит из активного R, индуктивного (Хl) и емкостного (Xc).
Формула сопротивления
Сопротивление называется активным, если на участке или в полной цепи нет индуктивности или емкости. Для расчета необходимо измерить амплитудные значения тока и напряжения. Для этих целей применяются вольтметр и амперметр для переменного тока и напряжения. Однако минусом таких измерений является получение не амплитудных, а действующих значений. Амплитудные значения высчитываются по формулам:
- Для U: Um = 1,4142 * Ud.
- Для I: Im = 1,4142 * Id.
Исходя из этих соотношений формула активного сопротивления вычисляется по формуле: R = Um / Im. Активное сопротивление зависит еще и от Um и Im.
Простые способы измерения
 Не всегда требуются точные расчеты R, и для этих целей применяется прибор, называющиеся омметром. С ростом научного прогресса на рынке появились комбинированные приборы — мультиметры. Они имеют много функций, но основной из них является измерение значений I, R и U. Существуют также и специализированные приборы для измерения больших значений R, которые называются мегаомметрами. Мегаомметр применяется для измерения R уровня изоляции между жилами кабеля.
Не всегда требуются точные расчеты R, и для этих целей применяется прибор, называющиеся омметром. С ростом научного прогресса на рынке появились комбинированные приборы — мультиметры. Они имеют много функций, но основной из них является измерение значений I, R и U. Существуют также и специализированные приборы для измерения больших значений R, которые называются мегаомметрами. Мегаомметр применяется для измерения R уровня изоляции между жилами кабеля.
Омметр применяется и для поиска неисправностей в электроцепях, а также позволяет определить радиодеталь на предмет исправности. Для измерения значений R, а также для выявления неисправностей, необходимо соблюдать правила электробезопасности и обесточить участок цепи. Нужно разрядить и конденсаторы, так как их заряд может вывести из строя прибор, который находится в режиме измерения R.
Таким образом, активным сопротивлением в цепи переменного тока является любая нагрузка, не являющаяся емкостной или индуктивной, и зависящей от температуры, вида деформации, типа вещества, Um, Im, длины и S проводника.
220v.guru
Активное и реактивное сопротивление в цепи переменного тока
В электрической цепи переменного тока существует два вида сопротивлений: активное и реактивное. Это является существенным отличием от цепей постоянного тока.
Активное сопротивление
При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.
Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле
Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.
Реактивное сопротивление
При прохождении переменного тока через реактивные элементы возникает реактивное сопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.
Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.
Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки
Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.
Сопротивление конденсатора можно рассчитать по формуле
Треугольник сопротивлений
Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений
Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:
На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза.
electroandi.ru
6.2 Активное сопротивление в цепи переменного тока
Рассмотрим сначала частный случай, когда генератор переменного тока замкнут на внешнюю цепь, имеющую сопротивление R и настолько малые индуктивность и емкость, что ими можно пренебречь. Сопротивление резистора называется активным, так как оно обуславливает необратимый переход электрической энергии во внутреннюю энергию проводника, который при этом нагревается. Положим, что в цепи идет переменный ток
(6.2)
и найдем, по какому закону изменяется напряжение между концами внешней цепи (рисунок 6.1).
Рисунок 6.1 Рисунок 6.2
Применяя закон Ома, имеем
. (6.3)
Таким образом,
напряжение на концах участка цепи
изменяется также по гармоническому
закону, причем разность фаз между
колебаниями тока и напряжения равна
нулю. Это означает, что напряжение и ток
одновременно достигают максимальных
значений, одновременно обращаются в
нуль и т. д. (рисунок 6.2). Максимальное
значение напряжения  равно произведению амплитуды силы тока
на активное сопротивление
равно произведению амплитуды силы тока
на активное сопротивление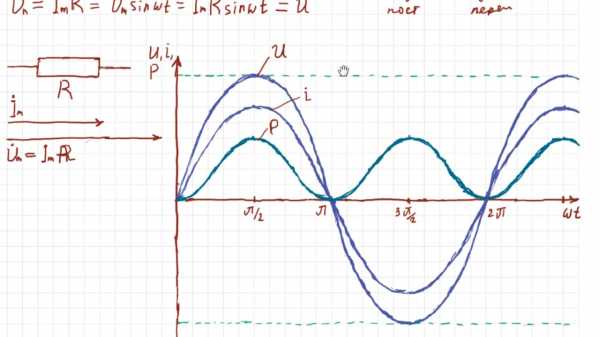 участка цепи.
участка цепи.
Гармонически изменяющиеся величины можно наглядно изображать при помощи векторных диаграмм.
Выберем ось
диаграммы таким образом, чтобы вектор,
изображающий колебания тока, был
направлен вдоль этой оси. В дальнейшем
мы будем называть его осью
токов. Вектор,
изображающий колебания напряжения,
будет направлен вдоль оси токов (рисунок
6.3). Поскольку разность фаз между током
и напряжением равна нулю, то длина этого
вектора равна амплитуде напряжения  .
.
Рисунок 6.3
6.3 Емкость в цепи переменного тока
Положим теперь,
что участок цепи содержит конденсатор
емкости  ,
причем сопротивлением и индуктивностью
можно пренебречь. Выясним, по какому
закону будет изменяться напряжение на
концах участка цепи в этом случае.
Полагаем, что сила тока изменяется по
закону.
,
причем сопротивлением и индуктивностью
можно пренебречь. Выясним, по какому
закону будет изменяться напряжение на
концах участка цепи в этом случае.
Полагаем, что сила тока изменяется по
закону.
Напряжение на конденсаторе равно
 . (6.4)
. (6.4)
Ток можно записать
через величину заряда  протекающего через сечение проводника
и увеличивающего заряд конденсатора
за промежуток времени
протекающего через сечение проводника
и увеличивающего заряд конденсатора
за промежуток времени
 . (6.5)
. (6.5)
Тогда заряд конденсатора можно найти интегрированием
 . (6.6)
. (6.6)
Поскольку сила тока в цепи изменяется по закону
, (6.7)
то заряд равен
. (6.8)
Постоянная
интегрирования 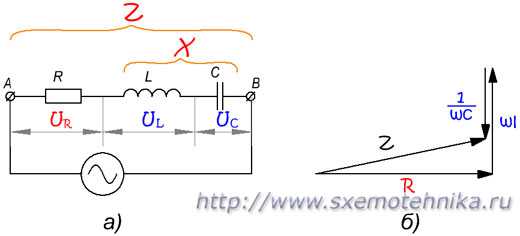 здесь обозначает произвольный постоянный
заряд конденсатора, не связанный с
колебаниями тока, и поэтому мы положим
здесь обозначает произвольный постоянный
заряд конденсатора, не связанный с
колебаниями тока, и поэтому мы положим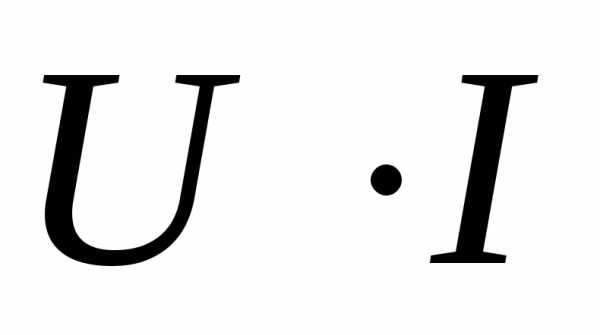 .
Следовательно, с учетом формулы (6.4)
можно записать для напряжения
.
Следовательно, с учетом формулы (6.4)
можно записать для напряжения
(6.9)
Рисунок 6.4 Рисунок 6.5
Сравнение выражений
(6.7) и (6.9) показывает, что при гармонических
колебаниях тока в цепи напряжение на
конденсаторе изменяется также по
гармоническому закону, однако колебания
напряжения на конденсаторе отстают по
фазе от колебаний тока на 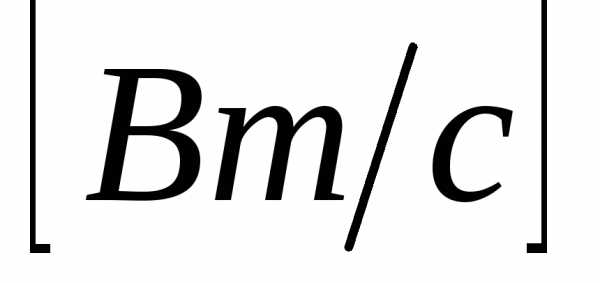
Изменение тока и напряжения во времени изображено графически на рисунке 6.5.
Полученный результат
имеет простой физический смысл. Напряжение
на конденсаторе в какой – либо момент
времени определяется существующим
зарядом конденсатора. Но этот заряд был
образован током, протекавшим предварительно
в более ранней стадии колебаний. Поэтому
колебания напряжения, как и колебания
заряда, запаздывают относительно
колебаний тока. Так, например, когда в
момент времени  сила тока равна нулю (рисунок 6.5), то на
пластинах конденсатора еще имеется
заряд, перенесенный током в предыдущий
промежуток времени, и напряжение не
равно нулю. Для обращения в нуль этого
заряда нужно, чтобы в течение промежутка
времени, равного
сила тока равна нулю (рисунок 6.5), то на
пластинах конденсатора еще имеется
заряд, перенесенный током в предыдущий
промежуток времени, и напряжение не
равно нулю. Для обращения в нуль этого
заряда нужно, чтобы в течение промежутка
времени, равного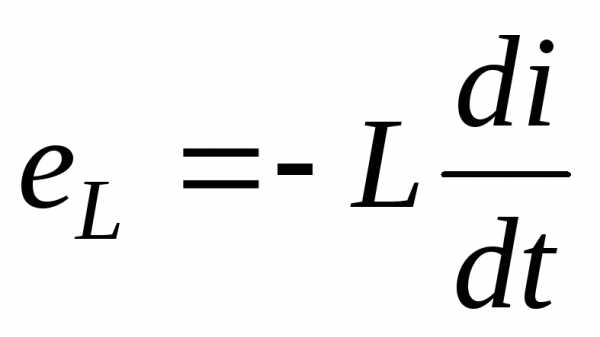 ,
проходил ток положительного направления.
Однако, когда заряд конденсатора (а
значит, и напряжение) станет равным
нулю, сила тока уже не будет равна нулю
(рисунок 6.5)–она принимает максимальное
значение.
,
проходил ток положительного направления.
Однако, когда заряд конденсатора (а
значит, и напряжение) станет равным
нулю, сила тока уже не будет равна нулю
(рисунок 6.5)–она принимает максимальное
значение.
Формула (6.9) показывает, что амплитуда напряжения на конденсаторе равна
 . (6.10)
. (6.10)
Сравнивая это
выражение с законом Ома для участка
цепи постоянного тока 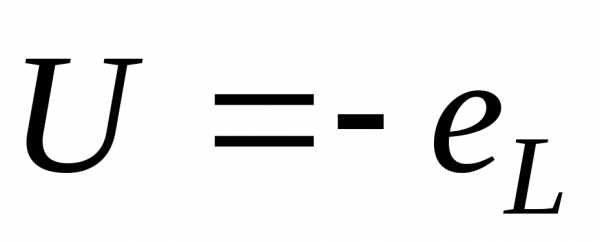 ,
мы видим, что величина
,
мы видим, что величина
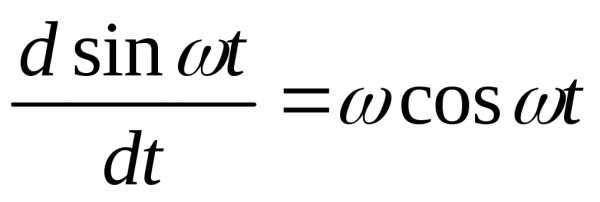 , (6.11)
, (6.11)
зависящая от
емкости конденсатора 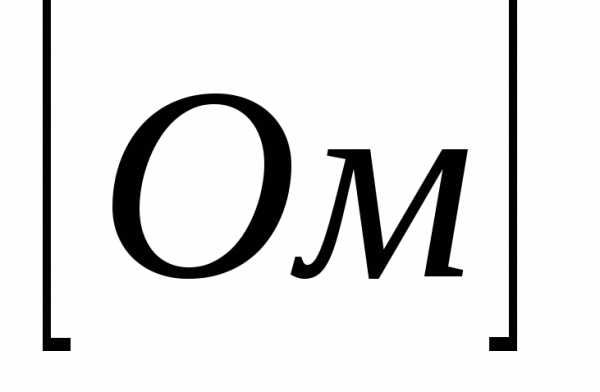 ,
играет роль сопротивления участка цепи.
Поэтому она получила названиекажушегося
сопротивления емкости или емкостным сопротивлением. Емкостное
сопротивление равно отношению амплитуды
напряжения на емкости к амплитуде силы
тока в цепи. В Международной системе
единиц СИ емкостное сопротивление
выражается в омах.
,
играет роль сопротивления участка цепи.
Поэтому она получила названиекажушегося
сопротивления емкости или емкостным сопротивлением. Емкостное
сопротивление равно отношению амплитуды
напряжения на емкости к амплитуде силы
тока в цепи. В Международной системе
единиц СИ емкостное сопротивление
выражается в омах. 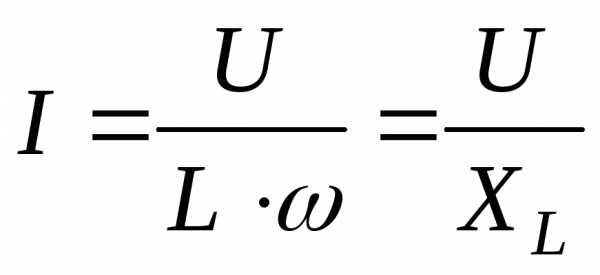 .
Емкостное сопротивление равно величине,
обратной произведению электрической
емкости ( в
.
Емкостное сопротивление равно величине,
обратной произведению электрической
емкости ( в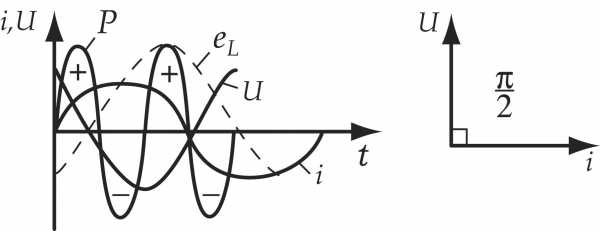 )
и циклической частоты переменного тока
)
и циклической частоты переменного тока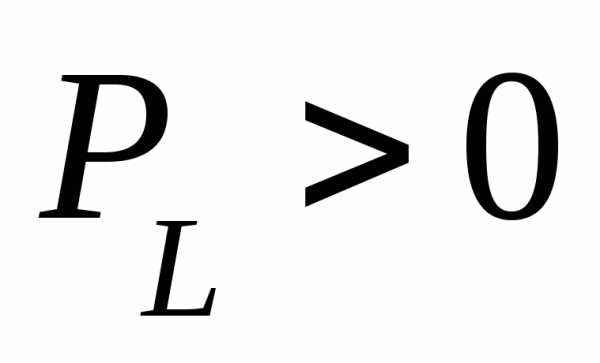 (в
(в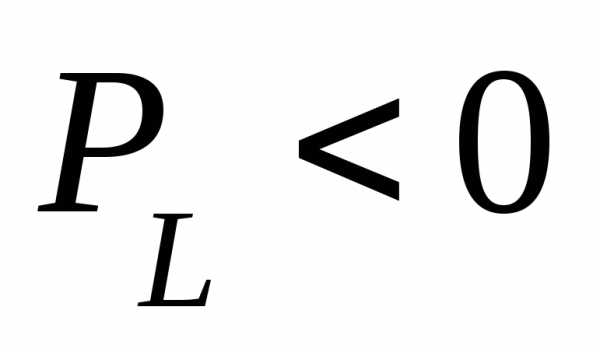 ).
).
Полученные
результаты можно представить в виде
векторной диаграммы (рисунок 6.6). Здесь
вектор, изображающий колебания напряжения,
уже не совпадает с осью токов. Он повернут
в отрицательном направлении (по часовой
стрелке) на угол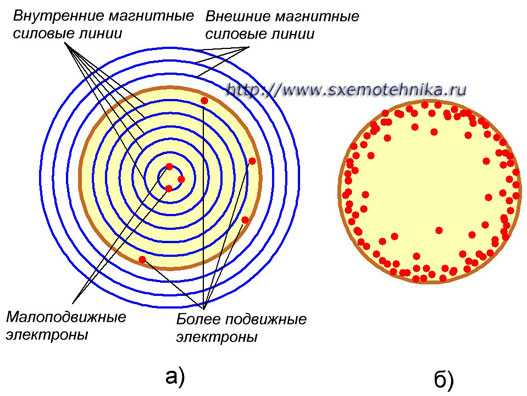 .
Модуль этого вектора равен амплитуде
напряжения
.
Модуль этого вектора равен амплитуде
напряжения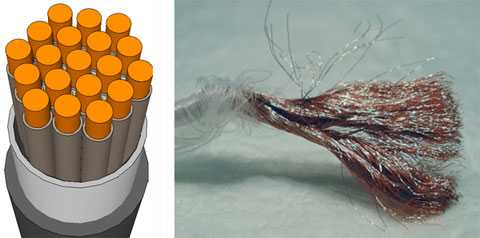 .
.
Рисунок 6.6
Из формулы (6.11)
видно, что сопротивление емкости  зависит также от частоты
зависит также от частоты .
Поэтому при очень высоких частотах даже
малые емкости могут представлять совсем
небольшое сопротивление для переменного
тока.
.
Поэтому при очень высоких частотах даже
малые емкости могут представлять совсем
небольшое сопротивление для переменного
тока.
studfiles.net

