Векторная диаграмма для цепи с емкостью

В цепи с емкостью вектор тока I опережает вектор напряжения U на 90°:

Как связаны между собой ток и напряжение на разных элементах цепи переменного тока?

Взаимосвязь между током и напряжением на разных элементах цепи переменного тока можно обобщить следующим образом:

• На активном сопротивлении ток и напряжение совпадают по фазе
• На индуктивности ток отстает от напряжения на 90°
• На емкости ток опережает напряжение на 90°

Эти соотношения наглядно отображаются на векторных диаграммах, представленных выше.

Расчет полного сопротивления цепи переменного тока

Полное сопротивление цепи переменного тока Z, содержащей активное R, индуктивное XL и емкостное XC сопротивления, рассчитывается по формуле:

Z = √(R² + (XL — XC)²)

Эта формула отражает векторное сложение активного и реактивного сопротивлений.

Резонанс в цепи переменного тока

Резонанс — это явление резкого возрастания амплитуды колебаний при совпадении частоты внешнего воздействия с собственной частотой колебательной системы. В цепи переменного тока различают два вида резонанса:

• Резонанс напряжений — возникает в последовательном колебательном контуре
• Резонанс токов — возникает в параллельном колебательном контуре

При резонансе напряжений выполняется условие:

XL = XC

то есть индуктивное и емкостное сопротивления взаимно компенсируются.

Применение знаний о сопротивлениях в цепи переменного тока

Понимание особенностей различных видов сопротивлений в цепи переменного тока имеет важное практическое значение:

• Позволяет рассчитывать параметры электрических цепей
• Помогает в проектировании электротехнических устройств
• Необходимо для анализа работы электрических машин и аппаратов
• Используется при настройке и оптимизации работы электрических систем

Эти знания широко применяются в энергетике, электронике, радиотехнике и других областях, связанных с использованием переменного тока.

Задания для административной контрольной работы по физике

Задания для административной контрольной работы.

Физика 11 класс.

Тема: «Колебания и волны»

В заданиях 1–7 выберите и запишите один правильный ответ.

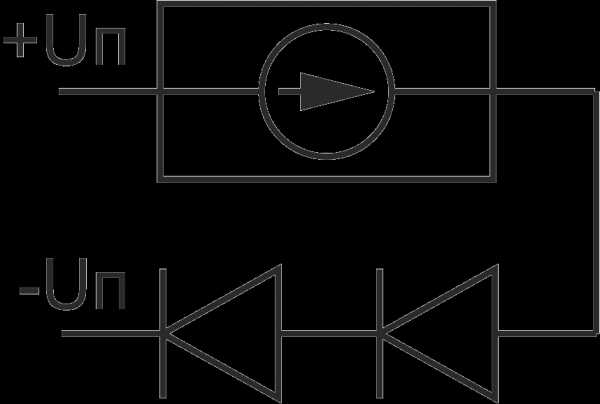
1. Цепь с активным сопротивлением изображает схема

1) А

2) Б

3) В

4) Г

2. На рисунке представлен график зависимости силы тока от времени в колебательном контуре. Значения амплитуды силы тока и частоты её изменения равны…

1) 10мА, 8Гц

2) 10мА, 4Гц

3) 5мА, 0,125Гц

4) 5мА, 0,25Гц

3. Уравнение выражает зависимость напряжения на конденсаторе от времени в колебательном контуре. В некоторый момент времени u=310В, при этом энергия

1) в конденсаторе и катушке максимальны

2) в конденсаторе максимальна, в катушке минимальна

3) в конденсаторе минимальна, в катушке максимальна

4) в конденсаторе и катушке минимальны

4. Если длину математического маятника уменьшить в 4 раза, то частота свободных гармонических колебаний маятника…

1) увеличится в 4 раза

2) увеличится в 2 раза

3) уменьшится в 4 раза

4) уменьшится в 2 раза

5. Как изменится период собственных электромагнитных колебаний в контуре, изображённом на рисунке, если ключ К перевести из положения 1 в положение 2?

1) увеличится в 3 раза

2) уменьшится в 3 раза

3) увеличится в 9 раз

4) уменьшится в 9 раз

6. Согласно теории Максвелла заряженная частица излучает электромагнитные волны в вакууме…

1) только при равномерном движении по прямой в ИСО

2) только при гармонических колебаниях по окружности в ИСО

3) только при равномерном движении по окружности в ИСО

4) при любом ускоренном движении в ИСО

7. Электромагнитные волны отличаются от звуковых…

1) наличием дифракции

2) распространением в веществе

3) распространением в вакууме

4) наличием интерференции

Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.

8. Колебательный контур радиоприёмника настроен на некоторую длину волны λ. Как изменяется период колебаний в контуре, их частота и соответствующая им длина волны, если площадь пластин конденсатора уменьшить?

9. Чему равна ёмкость конденсатора в колебательном контуре, если индуктивность катушки 0,1Гн, а частота 50Гц?

10. На какой частоте работает радиопередатчик, излучающий волну длиной 30м?

Ответы к административной контрольной работе

по теме «Колебания и волны»

Ответ

1

1

2

3

2

4

2

5

1

6

4

7

3

8

А-1; Б-2; В-1

9

100мкФ

10

1 МГц

infourok.ru

Тест по физике на тему «Колебания и волны»

КОЛЕБАНИЯ И ВОЛНЫ

1 вариант

ЧАСТЬ А

Выберите один правильный ответ.

1. Цепь с активным сопротивлением изображает схема…

1) А 2) Б 3) В 4) Г

2. На рисунке представлен график зависимости силы тока от времени в колебательном контуре. Значения амплитуды силы тока и частоты её изменения равны…

1) 10мА, 8Гц 2) 10мА, 4Гц 3) 5мА, 0,125Гц 4) 5мА, 0,25Гц

3. Уравнение выражает зависимость напряжения на конденсаторе от времени в колебательном контуре. Определите амплитуду колебаний напряжения в контуре.

1) 310 в 2) 314 в 3) 620 в 4) 628 в

4. Если длину математического маятника уменьшить в 4 раза, то частота свободных гармонических колебаний маятника…

1) увеличится в 4 раза 2) увеличится в 2 раза

3) уменьшится в 4 раза 4) уменьшится в 2 раза

5.

Как изменится период собственных электромагнитных колебаний в контуре, изображённом на рисунке, если ключ К перевести из положения 1 в положение 2?

1) увеличится в 3 раза 2) уменьшится в 3 раза

3) увеличится в 9 раз 4) уменьшится в 9 раз

6. Согласно теории Максвелла заряженная частица излучает электромагнитные волны в вакууме…

1) только при равномерном движении по прямой в ИСО

2) только при гармонических колебаниях по окружности в ИСО

3) только при равномерном движении по окружности в ИСО

4) при любом ускоренном движении в ИСО

7. В электромагнитной волне, распространяющейся в вакууме со скоростью , происходят колебания векторов напряжённости электрического поля и индукции магнитного поля . В каком из четырёх предложенных вариантов правильно указана взаимная ориентация векторов , , .

1) 2)

3) 1) 4) 1)

8. Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.

ЧАСТЬ В

Груз массой m, прикреплённый к пружине, совершает горизонтальные колебания с периодом Т и амплитудой х₀. Что произойдёт с тремя величинами – периодом, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу?

ВЕЛИЧИНА ИЗМЕНЕНИЕ

А) период 1) увеличится

Б) частота 2) уменьшится

В) максимальная потенциальная 3) не изменится

энергия пружины

9. Чему равна ёмкость конденсатора в колебательном контуре, если индуктивность катушки 0,1Гн, а частота 50Гц?

10. На какой частоте работает радиопередатчик, излучающий волну длиной 30м?

ЧАСТЬ С

11. В колебательном контуре, состоящем из катушки индуктивностью 2Гн и конденсатора ёмкостью 1,5 мкФ, максимальное значение заряда на пластинах 2 мкКл. Определить значение силы тока в контуре в тот момент, когда заряд на пластинах конденсатора станет равным 1 мкКл.

КОЛЕБАНИЯ И ВОЛНЫ

2 вариант

ЧАСТЬ А

Выберите один правильный ответ

1.

Цепь с индуктивным сопротивлением изображает схема…

1) А 2) Б 3) В 4) Г

2. На рисунке представлен график зависимости заряда от времени в колебательном контуре. Значения амплитуды заряда и периода его изменения равны…

1) 1,5нКл, 2мкс 2) 3нКл, 4 мкс

3) 1,5нКл, 4 мкс 4) 3нКл, 2 мкс

3. Изменение силы тока в зависимости от времени задано уравнением . Определите амплитуду колебаний силы тока в контуре.

1) 5А 2) 628 А 3) 2,5 А 4) 314 А

4. Маятниковые часы спешат. Чтобы часы шли точно, необходимо увеличить период колебаний маятника. Для этого надо…

1) увеличить массу маятника 2) уменьшить массу маятника

3) увеличить длину маятника 4) уменьшить длину маятника

5. Как изменится частота собственных электромагнитных колебаний в контуре, изображённом на рисунке, если ключ К перевести из положения 1 в положение 2?

1) увеличится в 4 раза 2) уменьшится в 4 раза

3) увеличится в 2 раза 4) уменьшится в 2 раза

6. При прохождении электромагнитных волн в воздухе происходят колебания…

1) молекул воздуха 2) плотности воздуха

3) напряжённости электрического и индукции магнитного полей

4) концентрации кислорода

7. В каком из приведённых случаев в пространстве вокруг описанного объекта возникает электромагнитная волна?

1) По проводнику течёт переменный ток

2) По проводнику течёт постоянный ток

3) Заряженная частица движется равномерно и прямолинейно

4) Магнит движется прямолинейно и равномерно

8. Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.

ЧАСТЬ В

Колебательный контур радиоприёмника настроен на некоторую длину волны λ. Как изменяется период колебаний в контуре, их частота и соответствующая им длина волны, если площадь пластин конденсатора уменьшить?

ВЕЛИЧИНА ИЗМЕНЕНИЕ

А) Период колебаний 1) увеличится

Б) Частота 2) уменьшится

В) Длина волны 3) не изменится

9. Определить индуктивность катушки колебательного контура, если ёмкость конденсатора равна 5 мкФ, а период колебаний 0,001с.

10. Какова длина волны телевизионного сигнала, если несущая частота равна

50 МГц?

ЧАСТЬ С

11. В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности 5мА, а амплитуда напряжения на конденсаторе 2В. В некоторый момент времени напряжение на конденсаторе равно 1,2В. Найдите силу тока в катушке в этот момент.

КОЛЕБАНИЯ И ВОЛНЫ

3 вариант

ЧАСТЬ А

Выберите один правильный ответ

1.

Цепь с ёмкостным сопротивлением изображает схема…

1) А 2) Б 3) В 4) Г

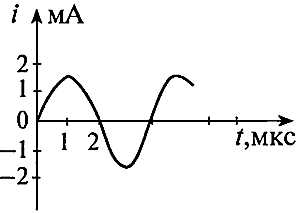
2.

На рисунке представлен график зависимости силы тока от времени в колебательном контуре. Значения амплитуды силы тока и частоты его изменения равны…

1) 1,5мА, 0,25Гц 2) 3мА, 0,25Гц 3) 1,5мА, 0,5Гц 4) 3мА, 0,5Гц

3. Уравнение выражает зависимость заряда конденсатора от времени в колебательном контуре. Определите колебания заряда в колебательном контуре.

1) 0,4Кл 2) 3,14Кл 3) 0,8Кл 4) 6,28Кл

4. Если длину математического маятника увеличить в 9 раз, то частота свободных гармонических колебаний маятника…

1) увеличится в 9 раз 2) увеличится в 3 раза

3) уменьшится в 9 раз 4) уменьшится в 3 раза

5.

Как изменится период собственных электромагнитных колебаний в контуре, изображённом на рисунке, если ключ К перевести из положения 1 в положение 2?

1) увеличится в 4 раза 2) уменьшится в 4 раза

3) увеличится в 2 раза 4) уменьшится в 2 раза

6. Согласно теории Максвелла, электромагнитные волны излучаются…

1) только при равномерном движении электронов по прямой

2) только при гармонических колебаниях заряда

3) только при равномерном движении заряда по окружности

4) при любом неравномерном движении заряда

7. При работе радиолокатора – прибора, служащего для определения местоположения тел, — используется физическое явление…

1) отражения электромагнитных волн

2) преломления электромагнитных волн

3) интерференции электромагнитных волн

4) дифракции электромагнитных волн

8. Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.

ЧАСТЬ В

Колебательный контур радиоприёмника настроен на некоторую длину волны λ. Как изменяется период колебаний в контуре, их частота и соответствующая им длина волны, если расстояние между пластинами конденсатора уменьшить?

ВЕЛИЧИНА ИЗМЕНЕНИЕ

А) Период колебаний 1) увеличится

Б) Частота 2) уменьшится

В) Длина волны 3) не изменится

9. В цепь переменного тока включена катушка с индуктивностью

20 мГн и конденсатор ёмкостью 50 мкФ. Найдите частоту переменного тока.

10. Колебательный контур излучает электромагнитную волну с длиной 450м. Чему равен период этой волны?

ЧАСТЬ С

11. В идеальном колебательном контуре амплитуда силы тока в катушке индуктивности 5мА, а амплитуда напряжения на конденсаторе 2В. В некоторый момент времени сила тока в катушке 3мА. Определите напряжение на конденсаторе в этот момент.

КОЛЕБАНИЯ И ВОЛНЫ

4 вариант

ЧАСТЬ А

Выберите один правильный ответ

1. Колебательный контур изображает схема…

1) А 2) Б 3) В 4) Г

2.

На рисунке представлен график зависимости заряда от времени в колебательном контуре. Значения амплитуды заряда и периода его изменения равны…

1) 12нКл, 8мкс 2) 12нКл, 4 мкс 3) 6нКл, 8 мкс 4) 6нКл, 4 мкс

3. Уравнение выражает зависимость силы тока от времени в колебательном контуре. Определите амплитуду колебаний силы тока в контуре.

1) 0,05А 2) 0,5А 3) 0,1 А 4) 1 А

4. Если длину математического маятника увеличить в 4 раза, то частота свободных гармонических колебаний маятника…

1) увеличится в 4 раза 2) увеличится в 2 раза

3) уменьшится в 4 раза 4) уменьшится в 2 раза

5. Как изменится частота собственных электромагнитных колебаний в контуре, изображённом на рисунке, если ключ К перевести из положения 1 в положение 2?

1) увеличится в 4 раза 2) уменьшится в 4 раза

3) увеличится в 2 раза 4) уменьшится в 2 раза

6. Основное свойство волн – …

1) перенос вещества, без переноса энергии

2) перенос энергии, без переноса вещества

3) перенос энергии и перенос вещества

4) перенос вещества и импульса

7. Электромагнитные волны отличаются от звуковых…

1) наличием дифракции 2) распространением в веществе

3) распространением в вакууме 4) наличием интерференции

8. Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.

ЧАСТЬ В

Груз массой m, прикреплённый к пружине, совершает горизонтальные колебания с периодом Т и амплитудой х₀. Что произойдёт с тремя величинами – периодом, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде увеличить массу?

ВЕЛИЧИНА ИЗМЕНЕНИЕ

А) период 1) увеличится

Б) частота 2) уменьшится

В) максимальная потенциальная

энергия пружины 3) не изменится

9. Колебательный контур состоит из катушки индуктивностью 20мкГН. Какой ёмкости конденсатор следует подключить к контуру, чтобы получить колебания с периодом 20мкс?

10. Какова длина электромагнитной волны, если радиостанция ведёт передачу на частоте 75 МГц?

ЧАСТЬ С

11. В процессе колебаний в идеальном колебательном контуре в некоторый момент времени заряд конденсатора 4нКл, а сила тока в катушке 3мА. Период колебаний 6,3 мкс. Определите амплитуду колебаний заряда.

videouroki.net

«АКТИВНОЕ, ИНДУКТИВНОЕ И ЁМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА»

бу «мЕГИОНСКИЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ»

мАГОМЕДОВ а.м.

Тест по электротехнике на тему: «Активное, индуктивное и ёмкостное сопротивления в цепях переменного тока»

вариант – 1

1. Какая схема изображает цепь переменного тока с конденсатором (рис. 1)

2. В цепи переменного тока с активным сопротивлением колебания силы тока …

а) совпадают по фазе с колебаниями напряжения;

б) отстают от колебаний силы тока по фазе на четверть периода;

в) опережают колебания силы тока по фазе на четверть периода.

3. Какая из приведенных ниже формул соответствует ёмкостному сопротивлению?

а) ; б) ; в)

4. Векторная диаграмма цепи переменного тока с катушкой индуктивности изображена на рисунке …

5. Какая из формул соответствует реактивной мощности в цепи с конденсатором?

а) ; б) Q_C = I²X_C; в) Q_L = I²X_L

Тест «Активное, индуктивное и ёмкостное сопротивления в цепях переменного тока»

вариант – 2

1. Какая схема изображает цепь переменного тока с катушкой индуктивности (рис. 1)

2. В цепи переменного тока с конденсатором колебания напряжения …

а) совпадают по фазе с колебаниями силы тока;

б) отстают от колебаний силы тока по фазе на четверть периода;

в) опережают колебания силы тока по фазе на четверть периода.

3. Какая из приведенных ниже формул соответствует ёмкостному сопротивлению?

а) ; б) ; в)

4. Векторная диаграмма цепи переменного тока конденсатором изображена на рисунке …

5. Какая из формул соответствует активной мощности в цепи переменного тока?

а) Q_C = I²X_C; б) ; в) Q_L = I²X_L

infourok.ru

Лекция по электротехнике по теме «Цепи переменного тока с активным сопротивлением, индуктивностью и емкостью»

Лекция № 9

Тема1.3.Основные положения теории переменного тока. Цепи переменно тока

План

1. Цепи переменного тока с активным сопротивлением, индуктивностью и емкостью.

1.Цепь переменного тока с активным сопротивлением. Рассмотрим цепь (рис, 4,3), в которой к активному сопротивлению (резистору) приложено синусоидальное напряжение: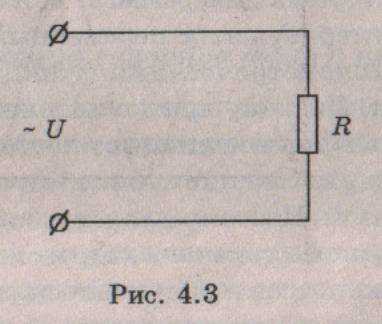

Тогда по закону Ома ток в цепи будет равен:
                   
Мы видим, что ток и напряжение совпадают по фазе. Векторная диаграмма для этой цепи приведена на рис. 4.4, а зависимости тока и напряжения от времени (временная диаграмма) — на рис. 4.5:
Выясним, как изменяется со временем мощность в цепи переменного тока с резистором.

Мгновенное значение мощности равно произведению мгновенных значений тока и напряжения:

Из этой формулы мы видим, что мгновенная мощность всегда положительна и пульсирует с удвоенной частотой (рис4.5). I,U,p .
Это означает, что электрическая энергия необратимо превращается в теплоту независимо от направления тока в цепи.
Те элементы цепи, на которых происходит необратимое преобразование электрической энергии в другие виды энергии (не только в теплоту), называются активными сопротивлениями. Поэтому резистор представляет собой активное сопротивление.

Цепь переменного тока с индуктивностью. Рассмотрим цепь (рис. 4.6), в которой к катушке индуктивности L, не обладающей активным сопротивлением (R = 0), приложено синусоидальное напряжение (4.6).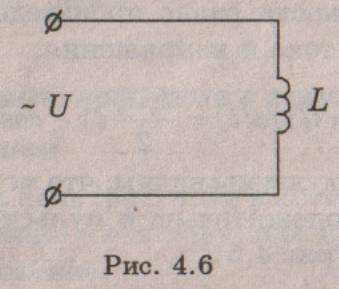

Протекающий через катушку переменный ток создает в ней ЭДС самоиндукции , которая в соответствии с правилом Ленца направлена таким образом, что препятствует изменению тока. Другими словами, ЭДС самоиндукции направлена навстречу приложенному напряжению. Тогда в соответствии со вторым правилом Кирхгофа можно записать:

(4.9)
Согласно закону Фарадея ЭДС самоиндукции
         (4.10)
Подставив (4.10) в (4.9), получим:

Решение этого дифференциального уравнения имеет вид:
       (4.12), где           (4.13)
Деля обе части равенства (4.13) на , получим для действующих значений

             (4.14)
Соотношение (4.14) представляет собой закон Ома для цепи с идеальной индуктивностью, а величина  называется индуктивным сопротивлением. Индуктивное сопротивление измеряется в омах.
Мгновенная мощность в цепи с чисто индуктивным сопротивлением равна:
        (4.15)

Положительные значения мощности соответствуют потреблению энергии катушкой, а отрицательные — возврату запасенной энергии обратно источнику. Средняя за период мощность равна нулю. Следовательно, цепь с индуктивностью мощности не потребляет — это чисто реактивная нагрузка. В этой цепи происходит лишь перекачивание электрической энергии от источника в катушку и обратно. Индуктивное сопротивление является реактивным сопротивлением.

Цепь переменного тока с индуктивностью и активным сопротивлением. Реальные цепи, содержащие индуктивность, всегда имеют и активное сопротивление: сопротивление провода обмотки и подводящих проводов. Поэтому рассмотрим электрическую цепь (рис. 4.9), в которой через катушку индуктивности L, обладающую активным сопротивлением R, протекает переменный ток
      (4.16)
Через катушку и резистор протекает один и же ток, поэтому в качестве основного выберем вектор тока и будем строить вектор напряжения, приложенного к этой цепи.
Напряжение, приложенное к цепи, равно векторной сумме падений напряжений на катушке индуктивности и на резисторе:
      (4.17)
Напряжение на резисторе, как было показано выше, будет совпадать по фазе с током:

         (4.18)
а напряжение на индуктивности будет равно ЭДС самоиндукции со знаком минус (по второму правилу Кирхгофа):
.  (4.19)
Мы видим, что напряжение на индуктивности опережает ток на угол ?/2. Построив векторы и , и воспользовавшись формулой (4.17), найдем вектор  Векторная диаграмма показана на рис. 4.10. Мы видим, что в рассматриваемой цепи ток I отстает по фазе от приложенного напряжения U, но не на / 2, как в случае чистой индуктивности, а на некоторый угол . Этот угол может принимать значения от 0 до ? / 2 и при заданной индуктивности зависит от значения активного сопротивления: с увеличением R угол уменьшается.

Как видно из векторной диаграммы, модуль вектора  равен
 , где величина        называется полным сопротивлением цепи.
Сдвиг по фазе  между током и напряжением данной цепи также определяется из векторной диаграммы:
      (4.22)

Цепь переменного тока с емкостью Рассмотрим электрическую цепь, в которой переменное напряжение (4.6) приложено к емкости С.
Мгновенное значение тока в цепи с емкостью равно скорости изменения заряда на обкладках конденсатора:
     ; но поскольку q = СU, то
    , где      (4.25)
Мы видим, что в этой цепи ток опережает напряжение на 2. Переходя в формуле (4.25) к действующим значениям переменного тока

) , получим:          (4.26)

Это закон Ома для цепи переменного тока с емкостью, а величина — называется емкостным сопротивлением. Векторная диаграмма для этой цепи показана на рис. 4.12, а временная – на рис. 4.13
Мгновенная мощность в цепи, содержащей емкость:
     (4.27)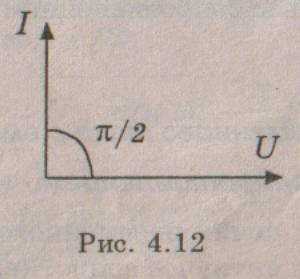

Мы видим, что мгновенная мощность изменяется с удвоенной частотой (рис. 4.13). При этом положительные значения мощности соответствуют заряду конденсатора, а отрицательные — его разряду и возврату запасенной энергии в источник. Средняя за период мощность здесь равна нулю, поскольку в цепи с конденсатором активная мощность не потребляется, а происходит обмен электрической энергией между конденсатором и источником. Следовательно, конденсатор так же, как и индуктивность, является реактивным сопротивлением.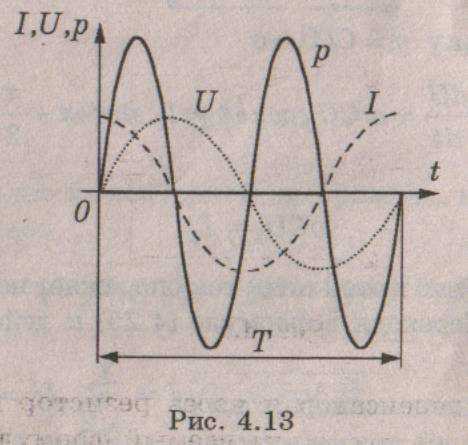

Вопросы для самопроверки:

1. Дать определение понятию « Активное сопротивление».

2. Выразить закон Ома для цепи переменного тока с активным сопротивлением.

3. Дать определение понятию « Индуктивность».

4. Выразить закон Ома для цепи переменного тока с индуктивностью.

5. Дать определение понятию « Емкость».

6. Описать основные параметры цепей переменного тока с активным сопротивлением, индуктивностью и емкостью.

7. Дать определение понятию « Активное сопротивление».

8. Дать определение понятию « Индуктивность».

9. Выразить закон Ома для цепи переменного тока.

infourok.ru

Контроль знаний по курсу «Электротехника» по теме «Сопротивление и мощность в цепи переменного тока»

Контрольные вопросы по теме «Сопротивление и мощность в цепи переменного тока. Резонанс напряжений и токов»

Вариант 1

Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется:

Варианты ответа

а) активным сопротивлением

б) индуктивным сопротивлением

в) емкостным сопротивлением

2

На рисунке изображено сопротивление:

Варианты ответа

а) индуктивное

б) активное

в) емкостное

3

Емкость – это:

Варианты ответа

а) Элемент электрической цепи, способный запасать энергию магнитного поля.

б) Элемент электрической цепи, способный запасать энергию электрического поля.

4

По данной формуле определяется:

Варианты ответа

а) индуктивное сопротивление

б) полное сопротивление

в) активное сопротивление

г) емкостное сопротивление

5

Активная мощность определяется по формуле:

Варианты ответа

а)

б)

в)

6

В Ваттах измеряется:

Варианты ответа

а) реактивная мощность

б) полная мощность

в) активная мощность

7

Формулой определяется:

Варианты ответа

а) коэффициент мощности

б) угол сдвига фаз

8

Вставьте пропущенное слово:

В цепи переменного тока, в которой индуктивность и емкость соединены ________________, может возникнуть резонанс токов.

Варианты ответа

а) параллельно

б) последовательно

в) смешанно

9

На схеме изображено:

Варианты ответа

а) резонанс токов

б) резонанс напряжений

10

Явление совпадения частоты колебаний одного тела с частотой колебаний другого – это:

Варианты ответа

а) напряжение

б) мощность

в) резонанс

Вариант 2

электрическая энергия, вырабатываемая источниками не расходуется, а возникает обмен энергии между сопротивлениями и источником энергии при:

Варианты ответа

а) активном сопротивлении

б) индуктивном сопротивлением

в) реактивном сопротивлении

2

На рисунке изображено сопротивление:

Варианты ответа

а) индуктивное

б) активное

в) емкостное

3

Индуктивность – это:

Варианты ответа

а) Элемент электрической цепи, способный запасать энергию магнитного поля.

б) Элемент электрической цепи, способный запасать энергию электрического поля.

4

По данной формуле определяется:

Варианты ответа

а) индуктивное сопротивление

б) полное сопротивление

в) активное сопротивление

г) емкостное сопротивление

5

Полная мощность определяется по формуле:

Варианты ответа

а)

б)

в)

6

В Вольт-амперах измеряется:

Варианты ответа

а) реактивная мощность

б) полная мощность

в) активная мощность

7

Формулой определяется:

Варианты ответа

а) коэффициент мощность

б) угол сдвига фаз

8

Вставьте пропущенное слово:

В цепи переменного тока с активным, индуктивным и емкостным сопротивлениями, соединенными ____________________может возникнуть резонанс напряжений.

Варианты ответа

а) параллельно

б) последовательно

в) смешанно

9

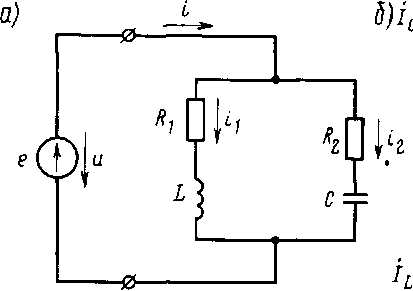
На схеме изображено:

Варианты ответа

а) резонанс токов

б) резонанс напряжений

10

Явление совпадения частоты колебаний одного тела с частотой колебаний другого – это:

Варианты ответа

а) напряжение

б) резонанс

в) мощность

Правильные ответы:

2 вариант

№ вопроса

Ответ

№ вопроса

Ответ

1

а

1

в

2

в

2

б

3

б

3

а

4

б

4

в

5

а

5

в

6

в

6

б

7

а

7

б

8

а

8

б

9

б

9

а

10

в

10

б

infourok.ru

Презентация по физике на тему «Сопротивления в цепи переменного тока. » (11 класс)

Задачи к уроку

«Сопротивления в цепи переменного тока»

1. В идеальном колебательном контуре амплитуда колебаний напряжения на конденсаторе 8 мВ, а амплитуда колебаний силы тока в катушке 2,0 мА. В определенный момент времени t сила тока в катушке составляет 1,2 мА. Определите напряжение на конденсаторе в момент времени t.

Решение

1. В идеальном колебательном контуре полная энергия электромагнитного поля контур равна сумме энергий магнитного и электрического полей:

2. Для идеального колебательного контура справедлив закон сохранения энергии, согласно которому можно записать:

3. Решаем систему двух уравнений (1) и (2):

Ответ: 6,4 мВ.

r

r

R

С

В

А

К источнику переменного напряжения с амплитудой колебаний напряжения U_m подключена электрическая цепь, представленная на схеме. Как зависит амплитуда колебаний напряжения между точками А и В от сопротивления резистора R?

Решение

Построим векторную диаграмму для цепи, изображенной на рисунке. Сила тока через конденсатор С и резистор R одинакова, значит векторы и перпендикулярны. Сумма их равна , и через концы этих векторов можно провести окружность, диаметр которой равен U_m. Напряжение U_R на резисторе сопротивлением R равно . Следовательно, искомое напряжение равно радиусу построенной окружности, т.е. , и не зависит от величины R.

При изменении сопротивления R меняется угол сдвига фазы между векторами и , так что предложенная схема может служить фазовращателем.

V

А

R

X_L

X_C

При включении катушки в цепь постоянного тока с напряжением 12 В амперметр показал силу тока 4 А. при включении той же катушки в цепь переменного тока с частотой 50 Гц и напряжением 12 В амперметр показал 2,4 А. Определить индуктивность катушки. Чему будет равна активная мощность тока в цепи, если последовательно с катушкой включить конденсатор емкостью 394 мкФ? Нарисовать векторную диаграмму для этого случая.

Дано:

U_пост = 12 В,

I_пост = 4 А,

U_перем = 12 В,

I_перем = 2,4 А,

v = 50 Гц,

С = 394 ∙ 10 ^{– 6} Ф

L — ? P — ?

Решение

Так как при постоянном токе реактивные сопротивления отсутствуют, то в этом случае по закону Ома можно найти активное сопротивление катушки . При переменном токе с помощью того же закона можно найти полное сопротивление катушки , а затем определить Х_L из формулы

.

Зная Х_L и частоту тока v и учитывая, что , найдем L.

Находим активное сопротивление катушки:

Ищем полное сопротивление катушки:

Определяем Х_L и L катушки, а также сопротивление конденсатора Х_С:

Активную мощность тока при включенном в цепь конденсаторе можно рассчитать из формулы:

, где .

Коэффициент мощности определим по формуле:

.

.

Мощность P = 12∙ 2,4∙ 0,6 = 17,3 Вт.

U_Lm

φ

I_m

U_R

U

U_Cm

При построении векторной диаграммы необходимо учитывать, что колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, поэтому вектор, изображающий амплитуду напряжения U_Rm совпадает по направлению с вектором, изображающим амплитуду силы тока I_m. Колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, поэтому вектор отстает от вектора на угол 90º. Колебания напряжения на катушке опережают колебания силы тока по фазе на π/2, поэтому вектор опережает вектор на угол 90º.

На векторной диаграмме мгновенного значения напряжения на резисторе и катушке определяется проекциями на горизонтальную ось векторов , , , вращающихся с одинаковой угловой скоростью ω против часовой стрелки. Мгновенное значение напряжений во всей цепи равно сумме мгновенных значений напряжений на отдельных элементах цепи, т.е. сумме проекций векторов , , на горизонтальную ось.

Так как Х_С больше Х_L, то в данном случае напряжение будет отставать по фазе от тока на угол φ.

Учитывая, что U_C вдвое больше U_L строим векторную диаграмму.

Ответ: индуктивность катушки равна 12, 7 мГн, активная мощность тока при последовательном соединении катушки и конденсатора составляет 17,3 Вт.

2. Резонанс в колебательном контуре, содержащем конденсатор емкостью С₁ =1 мкФ, наступает при частоте v₁ = 400 Гц. Когда же параллельно конденсатору С₁ подключили еще один емкостью С₂, резонансная частота становится равной v₂ = 100 Гц. Найдите емкость конденсатора С₂.

Решение

Здесь С₁ — емкость конденсатора в колебательном контуре, v₁ — резонансная частота этого контура, С₂ -емкость второго конденсатора, подключенного параллельно первому, v₂ – резонансная частота в контуре с двумя конденсаторами С₁ и С₂. Резонанс в приемном колебательном контуре наступает, когда собственная частота колебаний становится равной частоте вынужденных колебаний, возбуждаемых внешним передатчиком. При этом амплитуда электромагнитных колебаний в контуре становится максимальной. Частота вынужденных колебаний, равная собственной частоте колебательного контура, называется резонансной частотой.

Резонансная частота v₁ в колебательном контуре, содержащем только один конденсатор С₁, определяется формулой Томсона

Где L – индуктивность катушки этого контура.

Когда к конденсатору С₁ подключили параллельно конденсатор С₂, емкость образовавшейся батареи конденсаторов стала равна С₁ + С₂, при этом резонансная частота v₂ стала равна

Чтобы исключить индуктивность катушки, разделим обе части уравнений (1) и (2) друг на друга:

Ответ: С₂ = 1,5 ∙ 10 ^{– 5} Ф.

infourok.ru

Цепь с активным сопротивлением — Знаешь как

Содержание статьи

Напряжение и ток

Цепь, изображенная на рис. 5-17, обладает активным сопротивлением г и индуктивностью L. Примером такой цепи может служить катушка любого электромагнитного прибора или аппарата.

При прохождении переменного тока i в цепи будет индуктироваться э. д. с. самоиндукции e_L.

Согласно второму правилу Кирхгофа u + e_L = ir

откуда напряжение на зажимах цепи

и = it — e_L = ir + L (di/dt)= ua + u

Первая слагающая u_а = ir называется активным напряжением, мгновенное значение которого пропорционально току, а вторая u_L = — e_L = L(di/dt) реактивным напряжение м, мгновенное значение которого пропорционально скорости изменения тока.

Если ток изменяется по закону синуса

i — I_м sin ωt

то активное напряжение

u_а = ir = I_мr sin ωt  = U_а м sin ωt

Рис. 5-17, Цепь с активным сопротивлением и индуктивностью.

Оно изменяется также синусоидально, совпадая по фазе с током.

Амплитудное значение активного напряжения

U_а м = I_мr,

а действующее значение

U_а = Ir,

Реактивное напряжение

u_L = L di/dt = ωLI_M cos ωt = U_Lм sin(ωt + π/2)

Оно изменяется синусоидально, опережая по фазе ток на 90°.

Амплитудное значение реактивного напряжения

U_Lм = ωLI_M

а действующее значение

U_L = ωLI = x_LI

Напряжение на зажимах цепи

и= и_a + u_L = U_а м sin ωt + U_LM sin (ωt + π/2) = U_Msin (ωt + φ).

Напряжение на зажимах изменяется синусоидально, опережая ток по фазе на угол φ.

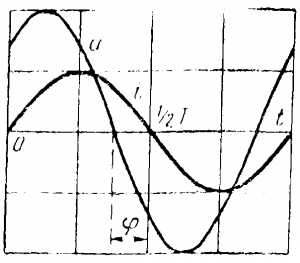
На рис. 5-18 показаны графики; i, и_a, u_L и и, а на рис. 5-19 — векторная диаграмма цепи. На диаграмме векторы напряжений U, U_a и U_L образуют прямоугольный треугольник напряжений, из которого непосредственно следует соотношение, связывающее эти величины:

U=√(U²_a + U²_L ) .

Аналогичная зависимость имеет место и для амплитудных значений

Угол сдвига фаз между напряжением на зажимах

Рис 5-18. Графики тока и напряжения в цепи с активным сопротивлением и индуктивностью.

Рис 5-19. Векторная диаграмма цепи с активным сопротивлением и индуктивностью.

цепи и током в ней находится из треугольника напряжений по одной из формул

cos φ = U_a/U и tg φ = U_L/U_a

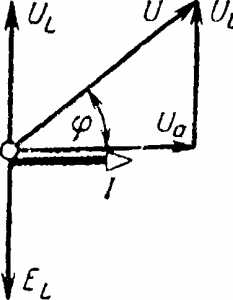Чем больше реактивное напряжение по сравнению с активным, тем на больший угол ток отстает по фазе от напряжения на зажимах цепи.

Сопротивления цепи

Уравнение (5-30) можно переписать в следующем виде

U = √(Ir)² + (Ix_L)² = I√r² + x²_L = Iᴢ

откуда ток в цепи

I = U/z = U / √(r² + x²_L)

Величина

z = √(r² + x²_L) = √(r² + ωL)²

называется полным сопротивлением цепи.

Сопротивления r, x_L и z графически можно изобразить сторонами прямоугольного треугольника — треугольника сопротивлении (рис. 5-20), который можно получить из треугольника напряжений, уменьшив каждую из его сторон в I раз.

Так как треугольники сопротивлений и напряжений подобны, то угол сдвига φ между напряжением и током, равный углу между сторонами треугольника z и r, можно определить через

cos φ = U_a /U

Рис 5-20. Треугольник сопротивлений цепи с активным сопротивлением и индуктивностью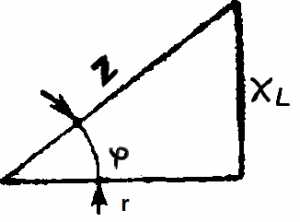

Мощности

Мгновенное значение мощности р = ui = U_м sin (ωt + φ) I_м sin ωt = U_мI_м sin (ωt + φ) sin ωt Учитывая, что

sin (со/ + φ) sin ωt = 1/2 cos φ — 1/2 cos (2ωt + φ)

а также (5-28), можно написать другое выражение ной мощности

Р = UI cos φ — UI cos (2ωt + φ)

Написанное выражение состоит из двух членов: постоянного, независимого от времени UI cos φ и переменного си-

нусоидального UI cos (2ωt + φ). Среднее значение мощности за период, которым обычно пользуются при расчете цепей переменного тока, будет равно постоянному члену UI cos φ, так как среднее значение за период синусоидальной функции равно нулю.

Таким образом, среднее значение мощности цепи равно произведению действующих значений напряжения и тока, умноженному на cos φ, т.е.

P = UI cos φ.

Так как U cos φ = U r/z = Ir = U_a,

то

P = U_аI = I₂r

Следовательно, средняя мощность цепи равна среднему значению мощности в активном сопротивлении. Поэтому среднюю мощность любой цепи называют; еще и активной мощностью.

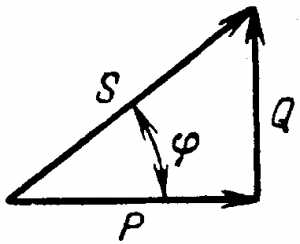
Реактивная мощность цепи:

Q = U_LI= I²x_L = I²z sin φ = UI sin φ

т.е. реактивная мощность цепи равна произведению действующих значений напряжения и тока, умножен ному на sin φ.

Рис.5-21. Треугольник мощностей

Полной мощностью цепи называется произведение действующих значений напряжения и тока, т. е.

S = UI

Учитывая, что sin² φ + cos² φ = 1 можно написать: (UI cos φ)² + (UI sin φ)² = (UI)²

или, что то же,

  P² + Q² = S²,

следовательно,

S = √(P² + Q²)

Мощности Р, Q и S графически можно изобразить сторонами прямоугольного треугольника — треугольника мощностей (рис 5-21), который можно получить из треугольника напряжений, умножая на I все его стороны.

т.е отношение активной мощности к полной называется коэффициентом мощности.

Единица полной мощности с называется вольт-ампер (в •а).

Необходимость применения понятия полной мощности обусловлена тем, что конструкция, габариты, вес и стоимость машины или аппарата определяются их номинальной полной мощностью S_н = U_нI_н а полная мощность S при том или ином режиме работы их определяет степень их использования.

Статья на тему Цепь с активным сопротивлением

znaesh-kak.com