Что такое резонанс в электрическом колебательном контуре. Как рассчитать резонансную частоту. Какие условия необходимы для возникновения резонанса. Как передаются и принимаются радиоволны. Какими свойствами обладают электромагнитные волны разных диапазонов.
Резонанс в электрическом колебательном контуре
Резонанс в электрическом колебательном контуре — это явление резкого возрастания амплитуды колебаний при совпадении частоты вынуждающей силы с собственной частотой колебательного контура. Рассмотрим подробнее условия и характеристики этого важного физического процесса.
Условия возникновения резонанса
Для возникновения резонанса в колебательном контуре необходимо выполнение следующих условий:
- Частота внешнего воздействия должна совпадать с собственной частотой контура
- Индуктивное и емкостное сопротивления должны быть равны: XL = XC
- Циклическая частота должна быть равна резонансной: ω = ω0
При выполнении этих условий амплитуда колебаний в контуре резко возрастает, что и называется резонансом.

Расчет резонансной частоты
Резонансная частота колебательного контура может быть рассчитана по формуле:
ω0 = 1 / √(LC)
Где:
- ω0 — резонансная частота
- L — индуктивность катушки
- C — емкость конденсатора
Зная индуктивность и емкость, можно определить на какой частоте будет наблюдаться резонанс в данном контуре.
Энергетические процессы в колебательном контуре
В колебательном контуре происходит периодическое преобразование энергии электрического и магнитного полей. Рассмотрим эти процессы подробнее.
Энергия электрического поля конденсатора
Энергия электрического поля конденсатора рассчитывается по формуле:
Wэл = CU^2 / 2
Где C — емкость конденсатора, а U — напряжение на его обкладках.
Энергия магнитного поля катушки
Энергия магнитного поля катушки определяется выражением:
Wмаг = LI^2 / 2
Здесь L — индуктивность катушки, а I — сила тока в ней.
Преобразование энергии в контуре
В процессе колебаний дважды за период происходит преобразование:
- Максимальной энергии электрического поля конденсатора в максимальную энергию магнитного поля катушки
- Максимальной энергии магнитного поля катушки в максимальную энергию электрического поля конденсатора
При этом выполняется закон сохранения энергии — полная энергия идеального колебательного контура остается постоянной и равной:

W = Wэл макс = Wмаг макс = CU^2 / 2 = LI^2 / 2
Излучение и прием электромагнитных волн
Электромагнитные волны могут излучаться и приниматься с помощью специальных устройств. Рассмотрим основные принципы этих процессов.
Излучение электромагнитных волн
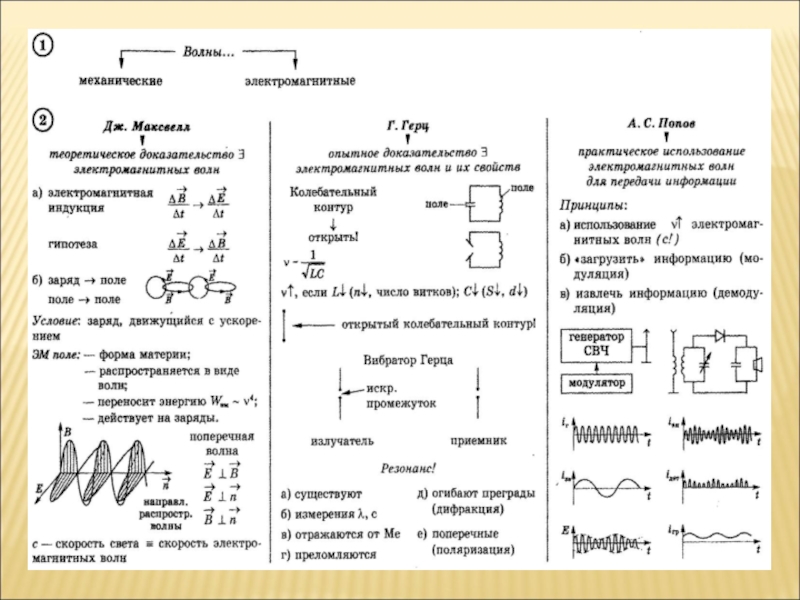
Согласно теории Максвелла, электромагнитные волны излучаются ускоренно движущимися зарядами. В радиопередатчиках используются колебательные контуры, в которых происходят высокочастотные колебания заряда, что приводит к излучению электромагнитных волн в пространство.
Прием электромагнитных волн
Для приема электромагнитных волн используются антенны, в которых под действием переменного электромагнитного поля возникают колебания тока. Эти колебания усиливаются и преобразуются в сигнал, который можно воспроизвести.
Принцип радиосвязи
Радиосвязь основана на излучении передатчиком и приеме приемником электромагнитных волн определенной частоты. Информация передается путем модуляции несущей частоты. Основные этапы радиосвязи:
- Генерация высокочастотных колебаний в передатчике
- Модуляция колебаний передаваемым сигналом
- Излучение модулированных волн антенной передатчика
- Прием волн антенной приемника
- Детектирование и усиление принятого сигнала
- Воспроизведение информации
Свойства электромагнитных волн различных диапазонов
Электромагнитные волны разных диапазонов обладают различными свойствами и применением. Рассмотрим особенности основных диапазонов.

Радиоволны
- Длина волны: от нескольких км до 1 мм
- Свойства: хорошо огибают препятствия, отражаются от ионосферы
- Применение: радиосвязь, телевидение, радиолокация
Инфракрасное излучение
- Длина волны: 1 мм — 780 нм
- Свойства: вызывает нагрев тел, невидимо для глаза
- Применение: тепловидение, обогрев, дистанционное управление
Видимый свет
- Длина волны: 380-780 нм
- Свойства: воспринимается человеческим глазом
- Применение: освещение, фотография, оптические приборы
Ультрафиолетовое излучение
- Длина волны: 10-380 нм
- Свойства: вызывает фотохимические реакции, ионизацию
- Применение: стерилизация, загар, люминесцентные лампы
Рентгеновское излучение
- Длина волны: 10^-8 — 10^-11 м
- Свойства: большая проникающая способность
- Применение: медицинская диагностика, дефектоскопия
Применение резонанса в радиотехнике
Явление резонанса широко используется в радиотехнике для настройки приемников и передатчиков на определенные частоты. Рассмотрим некоторые примеры применения резонанса.
Настройка радиоприемников
В радиоприемниках используются колебательные контуры с переменной емкостью или индуктивностью. Изменяя параметры контура, добиваются резонанса на частоте нужной радиостанции, что позволяет выделить ее сигнал из множества других.
Частотные фильтры
Резонансные контуры применяются для создания частотных фильтров, которые пропускают сигналы определенных частот и подавляют остальные. Это позволяет очистить полезный сигнал от помех и шумов.
Стабилизация частоты
Высокодобротные резонансные системы (например, кварцевые резонаторы) используются для стабилизации частоты генераторов в передатчиках и приемниках, обеспечивая высокую точность настройки.
Расчет параметров колебательного контура
При проектировании радиотехнических устройств часто требуется рассчитать параметры колебательного контура. Рассмотрим основные формулы и примеры расчетов.
Формула Томсона
Основной формулой для расчета параметров колебательного контура является формула Томсона:
f = 1 / (2π√(LC))

Где:
- f — частота колебаний
- L — индуктивность катушки
- C — емкость конденсатора
Пример расчета емкости конденсатора
Задача: Определить емкость конденсатора в колебательном контуре, если индуктивность катушки 0,1 Гн, а резонансная частота 50 Гц.
Решение:
- Используем формулу Томсона: f = 1 / (2π√(LC))
- Выразим C: C = 1 / (4π^2f^2L)
- Подставим значения: C = 1 / (4 * 3.14^2 * 50^2 * 0.1)
- Вычислим: C ≈ 101 мкФ
Ответ: Емкость конденсатора должна быть примерно 101 мкФ.
Пример расчета длины волны
Задача: На какой частоте работает радиопередатчик, излучающий волну длиной 30 м?
Решение:
- Используем формулу связи длины волны и частоты: λ = c / f, где c — скорость света
- Выразим f: f = c / λ
- Подставим значения: f = 3 * 10^8 / 30
- Вычислим: f = 10^7 Гц = 10 МГц
Ответ: Радиопередатчик работает на частоте 10 МГц.
Задания для административной контрольной работы по физике
Задания для административной контрольной работы.
Физика 11 класс.
Тема: «Колебания и волны»
В заданиях 1–7 выберите и запишите один правильный ответ.
1. Цепь с активным сопротивлением изображает схема
1) А
2) Б
3) В
4) Г
2. На рисунке представлен график зависимости силы тока от времени в колебательном контуре. Значения амплитуды силы тока и частоты её изменения равны…
1) 10мА, 8Гц
2) 10мА, 4Гц
3) 5мА, 0,125Гц
4) 5мА, 0,25Гц
3. Уравнение выражает зависимость напряжения на конденсаторе от времени в колебательном контуре. В некоторый момент времени u=310В, при этом энергия
1) в конденсаторе и катушке максимальны
2) в конденсаторе максимальна, в катушке минимальна
3) в конденсаторе минимальна, в катушке максимальна
4) в конденсаторе и катушке минимальны
4. Если длину математического маятника уменьшить в 4 раза, то частота свободных гармонических колебаний маятника…
Если длину математического маятника уменьшить в 4 раза, то частота свободных гармонических колебаний маятника…
1) увеличится в 4 раза
2) увеличится в 2 раза
3) уменьшится в 4 раза
4) уменьшится в 2 раза
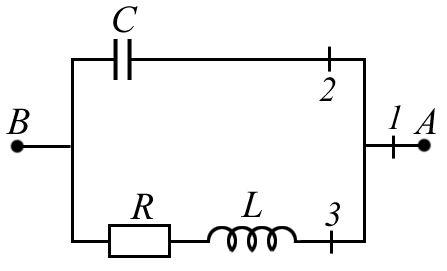
5. Как изменится период собственных электромагнитных колебаний в контуре, изображённом на рисунке, если ключ К перевести из положения 1 в положение 2?
1) увеличится в 3 раза
2) уменьшится в 3 раза
3) увеличится в 9 раз
4) уменьшится в 9 раз
6. Согласно теории Максвелла заряженная частица излучает электромагнитные волны в вакууме…
1) только при равномерном движении по прямой в ИСО
2) только при гармонических колебаниях по окружности в ИСО
3) только при равномерном движении по окружности в ИСО
4) при любом ускоренном движении в ИСО
7. Электромагнитные волны отличаются от звуковых…
1) наличием дифракции
2) распространением в веществе
3) распространением в вакууме
4) наличием интерференции
Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.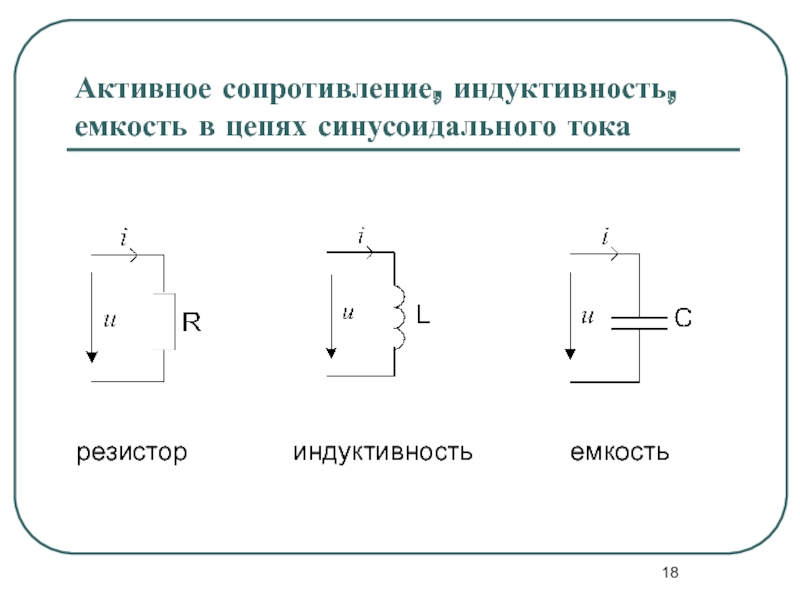
8. Колебательный контур радиоприёмника настроен на некоторую длину волны λ. Как изменяется период колебаний в контуре, их частота и соответствующая им длина волны, если площадь пластин конденсатора уменьшить?
9. Чему равна ёмкость конденсатора в колебательном контуре, если индуктивность катушки 0,1Гн, а частота 50Гц?
10. На какой частоте работает радиопередатчик, излучающий волну длиной 30м?
Ответы к административной контрольной работе
по теме «Колебания и волны»
№ заданияОтвет
1
1
2
3
3
2
4
2
5
1
6
4
7
3
8
А-1; Б-2; В-1
9100мкФ
10
1 МГц
Тест по физике на тему «Колебания и волны»
КОЛЕБАНИЯ И ВОЛНЫ
1 вариант
ЧАСТЬ А
Выберите один правильный ответ.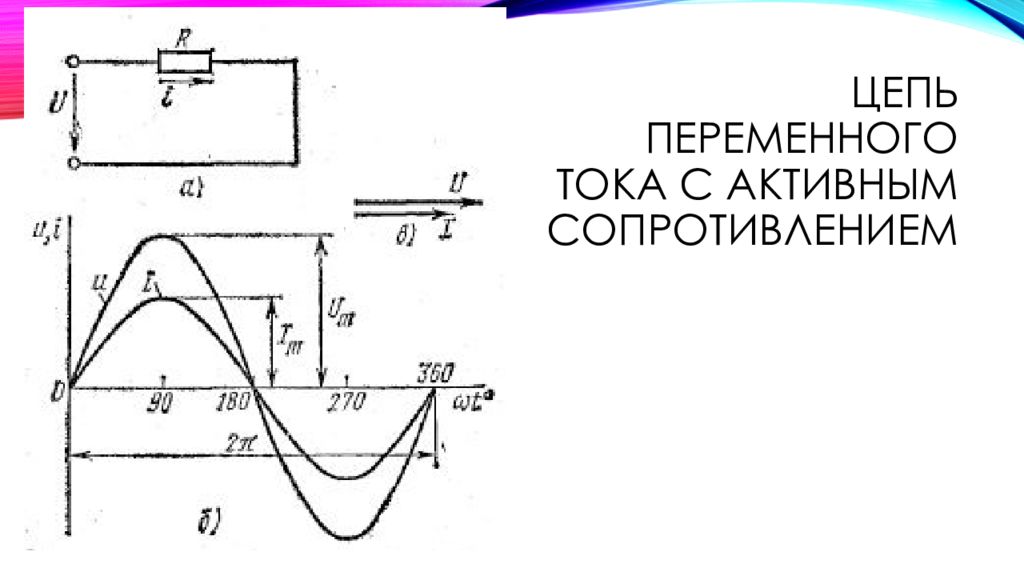
1. Цепь с активным сопротивлением изображает схема…
1) А 2) Б 3) В 4) Г
2. На рисунке представлен график зависимости силы тока от времени в колебательном контуре. Значения амплитуды силы тока и частоты её изменения равны…
1) 10мА, 8Гц 2) 10мА, 4Гц 3) 5мА, 0,125Гц 4) 5мА, 0,25Гц
3. Уравнение выражает зависимость напряжения на конденсаторе от времени в колебательном контуре. Определите амплитуду колебаний напряжения в контуре.
1) 310 в 2) 314 в 3) 620 в 4) 628 в
4. Если длину математического маятника уменьшить в 4 раза, то частота свободных гармонических колебаний маятника…
1) увеличится в 4 раза 2) увеличится в 2 раза
3) уменьшится в 4 раза 4) уменьшится в 2 раза
5.
Как изменится период собственных электромагнитных колебаний в контуре, изображённом на рисунке, если ключ К перевести из положения 1 в положение 2?
1) увеличится в 3 раза 2) уменьшится в 3 раза
3) увеличится в 9 раз 4) уменьшится в 9 раз
6. Согласно теории Максвелла заряженная частица излучает электромагнитные волны в вакууме…
Согласно теории Максвелла заряженная частица излучает электромагнитные волны в вакууме…
1) только при равномерном движении по прямой в ИСО
2) только при гармонических колебаниях по окружности в ИСО
3) только при равномерном движении по окружности в ИСО
4) при любом ускоренном движении в ИСО
7. В электромагнитной волне, распространяющейся в вакууме со скоростью , происходят колебания векторов напряжённости электрического поля и индукции магнитного поля . В каком из четырёх предложенных вариантов правильно указана взаимная ориентация векторов , , .
1) 2)
3) 1) 4) 1)
8. Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.
ЧАСТЬ В
Груз массой m, прикреплённый к пружине, совершает горизонтальные колебания с периодом Т и амплитудой х0.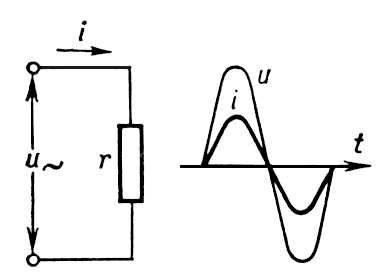 Что произойдёт с тремя величинами – периодом, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу?
Что произойдёт с тремя величинами – периодом, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу?
ВЕЛИЧИНА ИЗМЕНЕНИЕ
А) период 1) увеличится
Б) частота 2) уменьшится
В) максимальная потенциальная 3) не изменится
энергия пружины
9. Чему равна ёмкость конденсатора в колебательном контуре, если индуктивность катушки 0,1Гн, а частота 50Гц?
10. На какой частоте работает радиопередатчик, излучающий волну длиной 30м?
ЧАСТЬ С
11. В колебательном контуре, состоящем из катушки индуктивностью 2Гн и конденсатора ёмкостью 1,5 мкФ, максимальное значение заряда на пластинах 2 мкКл. Определить значение силы тока в контуре в тот момент, когда заряд на пластинах конденсатора станет равным 1 мкКл.
КОЛЕБАНИЯ И ВОЛНЫ
2 вариант
ЧАСТЬ А
Выберите один правильный ответ
1.
Цепь с индуктивным сопротивлением изображает схема…
1) А 2) Б 3) В 4) Г
2. На рисунке представлен график зависимости заряда от времени в колебательном контуре. Значения амплитуды заряда и периода его изменения равны…
1) 1,5нКл, 2мкс 2) 3нКл, 4 мкс
3) 1,5нКл, 4 мкс 4) 3нКл, 2 мкс
3. Изменение силы тока в зависимости от времени задано уравнением . Определите амплитуду колебаний силы тока в контуре.
1) 5А 2) 628 А 3) 2,5 А 4) 314 А
4. Маятниковые часы спешат. Чтобы часы шли точно, необходимо увеличить период колебаний маятника. Для этого надо…
1) увеличить массу маятника 2) уменьшить массу маятника
3) увеличить длину маятника 4) уменьшить длину маятника
5. Как изменится частота собственных электромагнитных колебаний в контуре, изображённом на рисунке, если ключ
1) увеличится в 4 раза 2) уменьшится в 4 раза
3) увеличится в 2 раза 4) уменьшится в 2 раза
6. При прохождении электромагнитных волн в воздухе происходят колебания…
При прохождении электромагнитных волн в воздухе происходят колебания…
1) молекул воздуха 2) плотности воздуха
3) напряжённости электрического и индукции магнитного полей
4) концентрации кислорода
7. В каком из приведённых случаев в пространстве вокруг описанного объекта возникает электромагнитная волна?
1) По проводнику течёт переменный ток
2) По проводнику течёт постоянный ток
3) Заряженная частица движется равномерно и прямолинейно
4) Магнит движется прямолинейно и равномерно
8. Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.ЧАСТЬ В
Колебательный контур радиоприёмника настроен на некоторую длину волны λ. Как изменяется период колебаний в контуре, их частота и соответствующая им длина волны, если площадь пластин конденсатора уменьшить?
ВЕЛИЧИНА ИЗМЕНЕНИЕ
А) Период колебаний 1) увеличится
Б) Частота 2) уменьшится
В) Длина волны 3) не изменится
9. Определить индуктивность катушки колебательного контура, если ёмкость конденсатора равна 5 мкФ, а период колебаний 0,001с.
Определить индуктивность катушки колебательного контура, если ёмкость конденсатора равна 5 мкФ, а период колебаний 0,001с.
10. Какова длина волны телевизионного сигнала, если несущая частота равна
50 МГц?
ЧАСТЬ С
11. В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности 5мА, а амплитуда напряжения на конденсаторе 2В. В некоторый момент времени напряжение на конденсаторе равно 1,2В. Найдите силу тока в катушке в этот момент.
КОЛЕБАНИЯ И ВОЛНЫ
3 вариант
ЧАСТЬ А
Выберите один правильный ответ
1.
Цепь с ёмкостным сопротивлением изображает схема…
1) А 2) Б 3) В 4) Г
2.
На рисунке представлен график зависимости силы тока от времени в колебательном контуре. Значения амплитуды силы тока и частоты его изменения равны…
1) 1,5мА, 0,25Гц 2) 3мА, 0,25Гц 3) 1,5мА, 0,5Гц 4) 3мА, 0,5Гц
3. Уравнение выражает зависимость заряда конденсатора от времени в колебательном контуре. Определите колебания заряда в колебательном контуре.
Уравнение выражает зависимость заряда конденсатора от времени в колебательном контуре. Определите колебания заряда в колебательном контуре.
1) 0,4Кл 2) 3,14Кл 3) 0,8Кл 4) 6,28Кл
4. Если длину математического маятника увеличить в 9 раз, то частота свободных гармонических колебаний маятника…
1) увеличится в 9 раз 2) увеличится в 3 раза
3) уменьшится в 9 раз 4) уменьшится в 3 раза
5.
Как изменится период собственных электромагнитных колебаний в контуре, изображённом на рисунке, если ключ К перевести из положения 1 в положение 2?
1) увеличится в 4 раза 2) уменьшится в 4 раза
3) увеличится в 2 раза 4) уменьшится в 2 раза
6. Согласно теории Максвелла, электромагнитные волны излучаются…
1) только при равномерном движении электронов по прямой
2) только при гармонических колебаниях заряда
3) только при равномерном движении заряда по окружности
4) при любом неравномерном движении заряда
7. При работе радиолокатора – прибора, служащего для определения местоположения тел, — используется физическое явление…
При работе радиолокатора – прибора, служащего для определения местоположения тел, — используется физическое явление…
1) отражения электромагнитных волн
2) преломления электромагнитных волн
3) интерференции электромагнитных волн
4) дифракции электромагнитных волн
8. Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.
ЧАСТЬ В
Колебательный контур радиоприёмника настроен на некоторую длину волны λ. Как изменяется период колебаний в контуре, их частота и соответствующая им длина волны, если расстояние между пластинами конденсатора уменьшить?
ВЕЛИЧИНА ИЗМЕНЕНИЕ
А) Период колебаний 1) увеличится
Б) Частота 2) уменьшится
В) Длина волны 3) не изменится
9. В цепь переменного тока включена катушка с индуктивностью
20 мГн и конденсатор ёмкостью 50 мкФ. Найдите частоту переменного тока.
10. Колебательный контур излучает электромагнитную волну с длиной 450м. Чему равен период этой волны?
ЧАСТЬ С
11. В идеальном колебательном контуре амплитуда силы тока в катушке индуктивности 5мА, а амплитуда напряжения на конденсаторе 2В. В некоторый момент времени сила тока в катушке 3мА. Определите напряжение на конденсаторе в этот момент.
КОЛЕБАНИЯ И ВОЛНЫ
4 вариант
ЧАСТЬ А
Выберите один правильный ответ
1. Колебательный контур изображает схема…
1) А 2) Б 3) В 4) Г
2.
На рисунке представлен график зависимости заряда от времени в колебательном контуре. Значения амплитуды заряда и периода его изменения равны…
1) 12нКл, 8мкс 2) 12нКл, 4 мкс 3) 6нКл, 8 мкс 4) 6нКл, 4 мкс
3. Уравнение выражает зависимость силы тока от времени в колебательном контуре. Определите амплитуду колебаний силы тока в контуре.
Определите амплитуду колебаний силы тока в контуре.
1) 0,05А 2) 0,5А 3) 0,1 А 4) 1 А
4. Если длину математического маятника увеличить в 4 раза, то частота свободных гармонических колебаний маятника…
1) увеличится в 4 раза 2) увеличится в 2 раза
3) уменьшится в 4 раза 4) уменьшится в 2 раза
5. Как изменится частота собственных электромагнитных колебаний в контуре, изображённом на рисунке, если ключ К перевести из положения 1 в положение 2?
1) увеличится в 4 раза 2) уменьшится в 4 раза
3) увеличится в 2 раза 4) уменьшится в 2 раза
6. Основное свойство волн – …
1) перенос вещества, без переноса энергии
2) перенос энергии, без переноса вещества
3) перенос энергии и перенос вещества
4) перенос вещества и импульса
7. Электромагнитные волны отличаются от звуковых…
1) наличием дифракции 2) распространением в веществе
3) распространением в вакууме 4) наличием интерференции
8. Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.
Используя условие задачи, установите соответствия величин из левого столбца с их изменениями в правом столбце.
ЧАСТЬ В
Груз массой m, прикреплённый к пружине, совершает горизонтальные колебания с периодом Т и амплитудой х0. Что произойдёт с тремя величинами – периодом, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде увеличить массу?
ВЕЛИЧИНА ИЗМЕНЕНИЕ
А) период 1) увеличится
Б) частота 2) уменьшится
В) максимальная потенциальная
энергия пружины 3) не изменится
9. Колебательный контур состоит из катушки индуктивностью 20мкГН. Какой ёмкости конденсатор следует подключить к контуру, чтобы получить колебания с периодом 20мкс?
10. Какова длина электромагнитной волны, если радиостанция ведёт передачу на частоте 75 МГц?
ЧАСТЬ С
11. В процессе колебаний в идеальном колебательном контуре в некоторый момент времени заряд конденсатора 4нКл, а сила тока в катушке 3мА. Период колебаний 6,3 мкс. Определите амплитуду колебаний заряда.
Период колебаний 6,3 мкс. Определите амплитуду колебаний заряда.
Тема «Резонанс в последовательной цепи переменного тока» — КиберПедия
(2ч)
Повтори теорию:
1.Резонанс в электрическом колебательном контуре – это ____________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________
2.Условие резонанса: XLXС, или ω ω0 = ______________________
3.Энергия электрического поля конденсатора: Wэл= _____________.
4.Энергия магнитного поля катушки: Wмаг= _____________.
5.Дважды за период происходит превращение максимальной энергии __________________________ поля W___=_________ в максимальную энергию ________________ поля W___=_________ и наоборот.
6.На основании закона сохранения энергии, энергия идеального колебательного контура равна ____
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
Реши задачи:
1.В колебательном контуре конденсатор ёмкостью 10нФ заряжен до максимального напряжения 40В. Найти резонансную частоту колебаний в контуре, если амплитуда колебаний силы тока в нём равна 2мА.
Дано: СИ: Решение:
Найти:
2.Электроёмкость контура 300пФ. Какова должна быть индуктивность контура , чтобы он резонировал на частоту электромагнитных колебаний 106 Гц?
Дано: СИ: Решение:
Найти:
3. При какой частоте переменного тока наступит резонанс напряжений в цепи, состоящей из последовательно соединённых катушки индуктивностью 0,5 Гн и конденсатора ёмкостью 200мкФ?
При какой частоте переменного тока наступит резонанс напряжений в цепи, состоящей из последовательно соединённых катушки индуктивностью 0,5 Гн и конденсатора ёмкостью 200мкФ?
Дано: СИ: Решение:
Найти:
4.В колебательном контуре конденсатор ёмкостью 50нФ заряжен до максимального напряжения 100В. Определить резонансную частоту колебаний свободных электронов в контуре, если максимальная сила тока в контуре равна 0,2А. Активное сопротивление равно нулю.
Дано: СИ: Решение:
Найти:
5.Определить энергии электрического и магнитного полей колебательного контура в момент, когда энергия электрического поля составляет 0,4 энергии магнитного поля, если максимальный заряд конденсатора равен 40нКл, максимальное напряжение на обкладках 500В?
Дано: СИ: Решение:
Найти:
Проверь себя:
1. Резонанс в колебательном контуре наступает при частоте 5,3кГц. Определить индуктивность катушки, если ёмкость конденсатора 6мкФ.
Определить индуктивность катушки, если ёмкость конденсатора 6мкФ.
Дано: СИ: Решение:
Найти:
2. Определить энергию электрического поля конденсатора, емкость которого 6мкФ, если напряжение на его обкладках равно 400В.
Дано: СИ: Решение:
Найти:
3. В колебательном контуре индуктивность катушки равна 0,2 Гн, а амплитуда силы тока 40 мА. Найдите энергию электрического поля конденсатора и энергию магнитного поля катушки в тот момент, когда мгновенное значение силы тока будет в 2 раза меньше амплитудного значения.
Дано: СИ: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
Дата «___» _________20____г
Задание 40 по теме
«Излучение и прием электромагнитных волн. Радиосвязь»
(2ч)
Реши задачи:
1. Колебательный контур радиопередатчика содержит конденсатор переменной ёмкости от 10нФ до 0,1нФ и катушку индуктивностью 1мкГн. Определите, в каком диапазоне длин волн работает радиопередатчик.
Колебательный контур радиопередатчика содержит конденсатор переменной ёмкости от 10нФ до 0,1нФ и катушку индуктивностью 1мкГн. Определите, в каком диапазоне длин волн работает радиопередатчик.
Дано: СИ: Решение:
Найти:
2. Радиолокатор испускает импульсы с частотой 5кГц. Длительность каждого импульса 40мкс. Определите наибольшую дальность обнаружения цели в воздухе.
Дано: СИ: Решение:
Найти:
3. Станция работает на длине волны 60м. Сколько колебаний несущей частоты происходит в течение одного периода звуковых колебаний с частотой 5кГц?
Дано: СИ: Решение:
Найти:
4. Колебательный контур радиоприёмника, содержащий катушку индуктивностью 5мкГн, настроен на приём электромагнитных волн длиной 1м. Определите электроёмкость конденсатора, включённого в колебательный контур.
Дано: СИ: Решение:
Найти:
5. Определить длину волны, на которую настроен входной контур радиоприёмника, если амплитуда заряда на обкладках конденсатора равна 10-12 Кл, а амплитуда силы тока 10-5А.
Определить длину волны, на которую настроен входной контур радиоприёмника, если амплитуда заряда на обкладках конденсатора равна 10-12 Кл, а амплитуда силы тока 10-5А.
Дано: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Г.С. Акатова/
Дата «___» _________20____г
Задание 41
Самостоятельная работа по теме «Электромагнитные колебания и волны»
(3ч)
ВАРИАНТ 1
ЧАСТЬ А Выберите один верный ответ
1. Цепь с активным сопротивлением изображает схема
1) А 2) Б 3) В 4) Г
2. На рисунке представлен график зависимости силы тока от времени в колебательном контуре. Значения амплитуды силы и частоты ее изменения равны
1) 10 мА, 8 Гц 2) 10 мА, 4 Гц 3) 5 мА, 0,125 Гц 4) 5 мА, 0,25 Гц
3. Уравнение и = 310 cos(ωt) выражает зависимость напряжения на конденсаторе от времени в колебательном контуре. В некоторый момент времени и = 310 В, при этом энергия
В некоторый момент времени и = 310 В, при этом энергия
1) в конденсаторе и катушке максимальны
2) в конденсаторе максимальна, в катушке минимальна
3) в конденсаторе минимальна, в катушке максимальна
4) в конденсаторе и катушке минимальны
4. Как изменится период собственных электромагнитных колебаний в контуре, изображенном на рисунке, если ключ К перевести из положения 1 в положение 2?
1) увеличится в 3 раза 2) уменьшится в 3 раза 3) увеличится в 9 раза
4) уменьшится в 9 раза
5. Амплитудные значения силы тока и напряжения в цепи переменного тока с катушкой индуктивности связаны
1) 2) 3) 4)
6. Согласно теории Максвелла заряженная частица излучает электромагнитные волны в вакууме
1) только при равномерном движении по прямой в инерциальной системе отсчета (ИСО)
2) только при гармонических колебаниях в ИСО
3) только при равномерном движении по окружности в ИСО
4) при любом ускоренном движении в ИСО
7. Какие из трех приведенных утверждений справедливы как для плоско поляризованных электромагнитных волн, так и для неполяризованных волн
Какие из трех приведенных утверждений справедливы как для плоско поляризованных электромагнитных волн, так и для неполяризованных волн
A. Векторы В и Е в волне колеблются во взаимно перпендикулярных плоскостях.
Б. Векторы В и Е перпендикулярны вектору скорости волны .
B. Векторы В волн колеблются в одной плоскости.
1) только А 2) только В 3) А и Б 4) Б и В
ЧАСТЬ В
8. Установите соответствия диапазонов шкалы электромагнитных волн из левого столбца таблицы с их свойствами в правом столбце.
Излучение Свойства
А. ультрафиолетовое 1) наименьшая частота волны из перечисленных
Б. радиоволны 2) обладает наибольшей проникающей способностью из
В. рентгеновское перечисленных
3) используется в приборах ночного видения
4) обеспечивает загар кожи человека
Решите задачи.
9. Чему равна емкость конденсатора в колебательном контуре, если индуктивность катушки 0,1 Гн, а резонансная частота 50 Гц?
Дано: Решение:
Найти:
10. На какой частоте работает радиопередатчик, излучающий волну длиной 30 м?
На какой частоте работает радиопередатчик, излучающий волну длиной 30 м?
Дано: Решение:
Найти:
ЧАСТЬ С
Решите задачу.
11. В колебательном контуре, состоящем из катушки индуктивностью 2 Гн и конденсатора емкостью 1,5 мкФ, максимальное значение заряда на пластинах 2 мкКл. Определить значение силы тока в контуре в тот момент, когда заряд на пластинах конденсатора станет равным 1 мкКл.
Дано: СИ: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
ВАРИАНТ 2
ЧАСТЬ А Выберите один верный ответ
1. Цепь с индуктивным сопротивлением изображает схема
1) А 2) Б 3) В 4) Г
2. На рисунке представлен график зависимости заряда от времени в колебательном контуре. Значения амплитуды заряда и периода его изменения равны
1) 1,5 нКл, 2 мкс
2) 3 нКл, 4 мкс
3) 1,5 нКл, 4 мкс
4) 3 нКл, 2 мкс
3. Уравнение выражает зависимость силы тока от времени в колебательном контуре. В некоторый момент времени , при этом энергия
Уравнение выражает зависимость силы тока от времени в колебательном контуре. В некоторый момент времени , при этом энергия
1) в конденсаторе и катушке максимальны
2) в конденсаторе максимальна, в катушке минимальна
3) в конденсаторе минимальна, в катушке максимальна
4) в конденсаторе и катушке минимальны
4. Как изменится частота собственных электромагнитных колебаний в контуре, изображенном на рисунке, если ключ К перевести из положения 1 в положение 2?
1) увеличится в 4 раза
2) уменьшится в 4 раза
3) увеличится в 2 раза
4) уменьшится в 2 раза
5. Действующие значения силы тока и напряжения на конденсаторе в цепи переменного тока связаны выражением
1) 2)3)4)
6. При прохождении электромагнитных волн в воздухе происходят колебания
1) молекул воздуха
2) плотности воздуха
3) напряженности электрического и индукции магнитного полей
4) концентрации кислорода
7. Укажите сочетание тех параметров электромагнитной волны, которые изменяются при переходе волны из воздуха в стекло
Укажите сочетание тех параметров электромагнитной волны, которые изменяются при переходе волны из воздуха в стекло
1) скорость и длина волны 2) частота и скорость 3) длина волны и частота 4) амплитуда и частота
ЧАСТЬ В
8. Установите соответствия диапазонов шкалы электромагнитных волн из левого столбца таблицы с их свойствами в правом столбце.
Излучение Свойства
А. инфракрасное 1) наименьшая длина волны из перечисленных
Б. видимое 2) используется в приборах ночного видения
В. рентгеновское 3) обеспечивает загар кожи
Решите задачи.
9. Определить индуктивность катушки колебательного контура, если емкость конденсатора равна 5 мкФ, а период колебаний 0,001 с.
Дано: СИ: Решение:
Найти:
10. Какова длина волны телевизионного сигнала, если несущая частота равна 50 МГц?
Дано: СИ: Решение:
Найти:
Часть С
Решите задачу.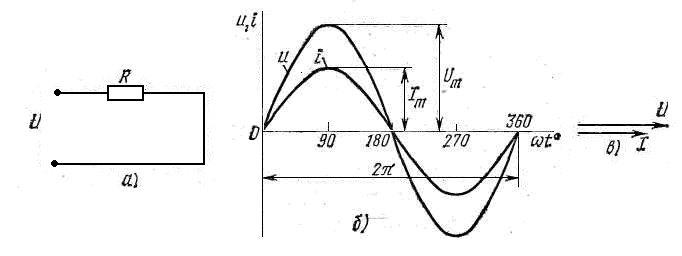
11. В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности 5 мА, а амплитуда напряжения на конденсаторе 2,0 В. В некоторый момент времени напряжение на конденсаторе равно 1,2 В. Найдите силу тока в катушке в этот момент.
Дано: СИ: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
ВАРИАНТ 3
ЧАСТЬ А Выберите один верный ответ
1. Цепь с емкостным сопротивлением изображает схема
1) А 2) Б 3) В 4) Г
2. На рисунке представлен график зависимости силы тока от времени в колебательном контуре. Значения амплитуды силы тока и частоты его изменения равны.
1) 1,5 мА, 0,25 Гц
2) 3 мА, 0,25 Гц
3) 1,5 мА, 0,5 Гц
4) 3 мА, 0,5 Гц
3. Уравнение выражает зависимость заряда конденсатора от времени в колебательном контуре. В некоторый момент времени q = 0,4 Кл, при этом энергия
В некоторый момент времени q = 0,4 Кл, при этом энергия
1) в конденсаторе и катушке максимальны
2) в конденсаторе и катушке минимальны
3) в конденсаторе минимальна, в катушке максимальна
4) в конденсаторе максимальна, в катушке минимальна
4. Как изменится период собственных электромагнитных колебаний в контуре, изображенном на рисунке, если ключ К перевести из положения 1 в положение 2?
1) увеличится в 4 раза
2) уменьшится в 4 раза
3) увеличится в 2 раза
4) уменьшится в 2 раза
5. Амплитудные значения силы тока и напряжения в цепи переменного тока с активным сопротивлением связаны
1) 2)3) 4)
6. Согласно теории Максвелла электромагнитные волны излучаются зарядом
1) только при равномерном движении заряда по прямой
2) только при гармонических колебаниях заряда
3) только при равномерном движении заряда по окружности
4) при любом ускоренном движении заряда в инерциальной системе отсчета
7. Какое явление характерно для электромагнитных волн, но не является общим свойством волн любой природы?
Какое явление характерно для электромагнитных волн, но не является общим свойством волн любой природы?
1) поляризация 2) преломление 3) дифракция 4) интерференция
Часть В
8. Установите соответствия диапазонов шкалы электромагнитных волн из левого столбца таблицы с их свойствами в правом столбце.
Излучение Свойства
А. радиоволны 1) наибольшая частота волны из перечисленных
Б. ультрафиолетовое 2) возникает при резком торможении электронов
В. видимое 3) используются в телевещании
4) обеспечивает фотосинтез
Решите задачи.
9. В цепь переменного тока включена катушка с индуктивностью 20 мГн и конденсатор емкостью 50 мкФ. При какой частоте переменного тока наступит явление резонанса?
Дано: СИ: Решение:
Найти:
10. Колебательный контур излучает электромагнитную волну с длиной 450 м. Чему равен период этой волны?
Дано: Решение:
Найти:
ЧАСТЬ С
Решите задачи.
11. В идеальном колебательном контуре амплитуда силы тока в катушке индуктивности 5 мА, а амплитуда напряжения на конденсаторе 2,0 В. В некоторый момент времени сила тока в катушке 3 мА. Определите напряжение на конденсаторе в этот момент.
Дано: Решение:
Найти
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
ВАРИАНТ 4
ЧАСТЬ А Выберите один верный ответ
1. Колебательный контур изображает схема
1) А 2) Б 3) В 4) Г
2. На рисунке представлен график зависимости заряда от времени в колебательном контуре. Значения амплитуды заряда и периода его изменения равны
1) 12 нКл, 8 мкс
2) 12 нКл, 4 мкс
3) 6 нКл, 8 мкс
4) 6 нКл, 4 мкс
3. Уравнение выражает зависимость силы тока от времени в колебательном контуре. В момент времени t= 0 с энергия
1) в конденсаторе максимальна, в катушке минимальна
2) в конденсаторе минимальна, в катушке максимальна
3) в конденсаторе и катушке максимальны
4) в конденсаторе и катушке минимальны
4. Как изменится частота собственных электромагнитных колебаний в контуре, изображенном на рисунке, если ключ К перевести из положения 1 в положение 2?
Как изменится частота собственных электромагнитных колебаний в контуре, изображенном на рисунке, если ключ К перевести из положения 1 в положение 2?
1) увеличится в 4 раза
2) уменьшится в 4 раза
3) увеличится в 2 раза
4) уменьшится в 2 раза
5. Амплитудные значения силы тока и напряжения в цепи переменного тока с емкостью связаны соотношением
1) 2) 3)4)
6. Заряженная частица не излучает электромагнитные волны в вакууме при
1) равномерном прямолинейном движении
2) равномерном движении по окружности
3) колебательном движении
4) любом движении с ускорением
7. Электромагнитные волны отличаются от звуковых
1) наличием дифракции
2) распространением в веществе
3) распространением в вакууме
4) наличием интерференции
ЧАСТЬ В
8. Установите соответствия диапазонов шкалы электромагнитных волн из левого столбца таблицы с их свойствами в правом столбце.
Излучение Свойства
А. инфракрасное 1) наибольшая длина волны из перечисленных
Б. радиоволны 2) возникает при резком торможении электронов
В. видимое 3) используется в приборах ночного видения
4) обеспечивает фотосинтез
Решите задачи.
9. Колебательный контур состоит из катушки индуктивностью 20 мкГн. Какой емкости конденсатор следует подключить к контуру, чтобы получить колебания с периодом 20 мкс?
Дано: СИ: Решение:
Найти:
10. Какова длина электромагнитной волны, если радиостанция ведет передачу на частоте 75 МГЦ?
Дано: СИ: Решение:
Найти:
ЧАСТЬ С
Решите задачу.
11. В процессе колебаний в идеальном колебательном контуре в некоторый момент времени заряд конденсатора 4 нКл, а сила тока в катушке 3 мА. Период колебаний 6,3 мкс. Определите амплитуду колебаний заряда.
Дано: СИ: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л. С. Тишкина/
С. Тишкина/
Раздел 5. Оптика
Дата «___» _________20____г
Задание 42 по теме
«Интерференция и дифракция света. Законы отражения и преломления света. Полное внутреннее отражение»
(2ч)
Реши задачи:
1.Угол падения луча света на поверхность стекла равен 360. Определить угол преломления, если отражённый и преломлённый луч взаимно перпендикулярны.
Рисунок: Решение:
2.Чему равен абсолютный показатель преломления алмаза, если относительный показатель преломления для света, идущего из стекла в алмаз, равен 1,6, а абсолютный показатель преломления стекла составляет 1,5?
Дано: Решение:
Найти:
3.Угол падения луча света на границу раздела воздух-стекло равен 600. При этом угол между отражённым и преломлённым лучами равен 900. Определить показатель преломления стекла.
Определить показатель преломления стекла.
Дано: Рисунок: Решение:
Найти:
4.Предельный угол полного отражения на границе жидкость-алмаз 410. Определите показатель преломления жидкости и скорость распространения света.
Дано: Решение:
Найти:
5.Что будет наблюдаться (усиление или ослабление света) в точке схождения двух световых волн с длиной волны 400 нм, если разность хода этих волн составляет 4 мкм?
Дано: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
Дата «___» _________20____г
Задание 43 по теме
«Получение спектра с помощью призмы. Получение спектра с помощью дифракционной решетки. Спектроскоп. Оптические приборы»
(2ч)
Реши задачи:
1. На непрозрачную пластинку с узкой щелью падает нормально параллельный пучок монохроматического света. Угол отклонения лучей, соответствующий первому дифракционному максимуму, φ=300. Определите ширину а щели, если длина волны падающего света λ=0,6мкм.
На непрозрачную пластинку с узкой щелью падает нормально параллельный пучок монохроматического света. Угол отклонения лучей, соответствующий первому дифракционному максимуму, φ=300. Определите ширину а щели, если длина волны падающего света λ=0,6мкм.
Дано: СИ: Решение:
Найти:
2.На узкую щель падает нормально параллельный пучок монохроматического света. Угол отклонения лучей, соответствующий третьему дифракционному минимуму, φ=180. Определите, сколько длин волн укладывается на ширине щели.
Дано: Решение:
Найти:
3.Определите наибольшее значение числа kmax – номер дифракционного максимума для λ=589нм при нормальном падении лучей на щель шириной 2 мкм.
Дано: СИ: Решение:
Найти:
4. Период дифракционной решетки равен 1,5 мкм. Чему равен наибольший порядок максимума в дифракционном спектре при нормальном падении на решетку монохроматического излучения длиной 0,4 мкм?
Дано: СИ: Решение:
Найти:
5. Период дифракционной решетки 2,5 мкм. Сколько линий (главных максимумов) будет содержать спектр, образующийся при нормальном падении на нее плоской монохроматической волны длиной 400 нм?
Период дифракционной решетки 2,5 мкм. Сколько линий (главных максимумов) будет содержать спектр, образующийся при нормальном падении на нее плоской монохроматической волны длиной 400 нм?
Дано: СИ: Решение:
Найти:
6. На дифракционную решётку нормально падает монохроматический свет длиной волны 0,5мкм. Угол отклонения лучей, соответствующий максимуму четвёртого порядка, φ=300. Определите число штрихов на 1 мм дифракционной решётки.
Дано: СИ: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
Тс – электромагнитные колебания
ТС – 2. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ. 1 вариант.1. Колебания в системе, которые возникают после выведения ее из положения равновесия, называются:
А. Электромагнитными колебаниями
Б. Вынужденными колебаниями
В. Свободными колебаниями
Г. Механическими колебаниями
Механическими колебаниями
Д. Резонансом
2. Колебательный контур изображает схема:
3. Индуктивное сопротивление колебательного контура может быть определено выражением:
А. Б. В. Г. Д.
4. Какой из приведенных графиков выражает зависимость емкостного сопротивления в цепи переменного тока от частоты?
5. Частота электрических колебаний в контуре равна 1 МГц. Если емкость конденсатора равна 200 пФ, то индуктивность катушки равна:
А. 1,27∙10-3 Гн Б. 2,17∙10-4 Гн В. 1,27∙10-4 Гн
Г. 7,8∙10-5 Гн Д. 2,17∙10-6 Гн
6. Действующее значение переменного напряжения имеет вид:
А. Б. В. Г. Д.
7. Амплитуда гармонических колебаний силы тока равна 10 А. Действующее значение силы тока равно:
А. 10 А Б. 5 А В. 14 А Г. 7 А Д. 9 А
8. При уменьшении частоты переменного тока в 2 раза емкостное сопротивление конденсатора:
А. Уменьшится в 4 раза Б. Уменьшится в 2 раза
В. Увеличится в 4 раза Г. Увеличится в 2 раза
Увеличится в 4 раза Г. Увеличится в 2 раза
Д. Не изменится
9. Изменение электрического заряда конденсатора в колебательном контуре происходит по следующему закону . Чему равен период колебаний заряда?
А. Б. В. 20 с Г. 40 с Д.
10. Если емкость уменьшится в 2 раза, а индуктивность возрастет в 8 раз, то частота колебаний в электрическом контуре:
А. Увеличится в раз Б. Уменьшится в раз
В. Увеличится в 2 раза Г. Уменьшится в 2 раза
Д. Уменьшится в 4 раза
11. Определите емкость конденсатора, сопротивление которого в цепи переменного тока частотой 50 Гц равно 800 Ом.
А. 4∙10-5 Ф Б. 2,5∙10-5 Ф В. 4∙10-6 Ф Г. 2,5∙10-6 Ф Д. 2∙10-5 Ф
12. Активное сопротивление 10 Ом включено в цепь переменного тока с частотой 50 Гц. Чему равна амплитуда колебаний силы тока при амплитуде колебаний напряжения на выводах активного сопротивления 50 В?
А. 5 А Б. 0 А В. 250 А Г. 0,1 А Д. 0,5 А
13. Собственные колебания контура происходят по закону . При емкости конденсатора 10 мкФ индуктивность контура равна:
Собственные колебания контура происходят по закону . При емкости конденсатора 10 мкФ индуктивность контура равна:
А. 10 Гн Б. 0,1 Гн В. 1 Гн Г. 102 Гн Д. 10-3 Гн
14. Мгновенное значение переменного тока в проводнике определяется по закону . Какое количество теплоты выделится в проводнике с активным сопротивлением 15 Ом за время, равное 10 периодам?
А. 1,2 Дж Б. 2,4 Дж В. 12 Дж Г. 24 Дж Д. 6 Дж
15. В электрическом колебательном контуре электроемкость конденсатора равна 1 мкФ, а индуктивность катушки – 1 Гн. Если для свободных незатухающих колебаний в контуре амплитуда силы тока составляет 100 мА, то амплитуда напряжения на конденсаторе при этом равна:
А. 100 В Б. 10 В В. 30 В Г. 80 В Д. 60 В
16. В колебательном контуре происходят свободные гармонические колебания. Если максимальный заряд конденсатора qm=10-6 Кл, а максимальная сила тока Im=10 А, то частота колебаний этого контура равна…
ТС – 2.
 ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ. 2 вариант.
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ. 2 вариант.1. Колебания в системе под действием внешней периодической силы называются:
А. Электромагнитными колебаниями
Б. Вынужденными колебаниями
В. Свободными колебаниями
Г. Механическими колебаниями
Д. Резонансом
2. Цепь с активным сопротивлением изображает схема:
3. Емкостное сопротивление колебательного контура может быть определено выражением:
А. UC Б. В. Г. Д.
4. Какой из приведенных графиков выражает зависимость индуктивного сопротивления в цепи переменного тока от частоты?
5. Частота электрических колебаний в контуре равна 1 МГц. Если индуктивность катушки равна 500 мкГн, то емкость конденсатора равна:
А. 5,07∙10-10 Ф Б. 0,75∙10-11 Ф В. 5,07∙10-11 Ф
Г. 7,5∙10-11 Ф Д. 5,7∙10-11 Ф
6. Действующее значение силы переменного тока имеет вид:
А. Б. В. Г. Д.
7. Амплитуда гармонических колебаний напряжения равна 10 В. Действующее значение переменного напряжения равно:
Действующее значение переменного напряжения равно:
А. 10 В Б. 5 В В. 9 В Г. 14 В Д. 7 В
8. При увеличении частоты переменного тока в 2 раза индуктивное сопротивление:
А. Увеличится в 2 раза Б. Уменьшится в 2 раза
В. Увеличится в 4 раза Г. Уменьшится в 4 раза
Д. Не изменится
9. Изменение электрического заряда конденсатора в колебательном контуре происходит по следующему закону . Чему равна частота колебаний заряда?
А. Б. В. 0,05 Гц Г. 0,025 Гц Д. 10 Гц
10. Если емкость уменьшится в 2 раза, а индуктивность возрастет в 4 раза, то период колебаний в электрическом контуре:
А. Уменьшится в раз Б. Увеличится в раз
В. Уменьшится в 2 раза Г. Увеличится в 2 раза
Д. Увеличится в 4 раза
11. Определите индуктивность катушки, сопротивление которой в цепи переменного тока частотой 50 Гц равно 10 Ом.
А. 3,2∙10-3 Гн Б. 3,2∙10-2 Гн В. 2,3∙10-4 Гн Г. 1,5∙10-2 Гн Д. 1,8∙10-3 Гн
12. Активное сопротивление 10 Ом включено в цепь переменного тока с частотой 50 Гц. Чему равна амплитуда колебаний напряжения на этом сопротивлении при амплитуде колебаний силы тока в цепи 5 А?
Активное сопротивление 10 Ом включено в цепь переменного тока с частотой 50 Гц. Чему равна амплитуда колебаний напряжения на этом сопротивлении при амплитуде колебаний силы тока в цепи 5 А?
А. 0,5 В Б. 50 В В. 1 В Г. 250 В Д. 2,5 В
13. Собственные колебания контура происходят по закону . При индуктивности катушки 10 Гн, емкость конденсатора равна:
А. 2∙10-6 Ф Б. 4∙10-5 Ф В. 8∙10-3 Ф Г. 4∙10-6 Ф Д. 2∙10-3 Ф
14. Напряжение в цепи переменного тока выражается формулой . Какое количество теплоты выделится в проводнике с активным сопротивлением 25 Ом за время, равное 4 периодам?
А. 2,4 Дж Б. 0,8 Дж В. 8 Дж Г. 24 Дж Д. 4 Дж
15. В электрическом колебательном контуре электроемкость конденсатора равна 1 мкФ, а индуктивность катушки – 1 Гн. Если для свободных незатухающих колебаний в контуре амплитуда напряжения на конденсаторе составляет 200 В, то амплитуда силы тока на катушке при этом равна:
А. 0,1 А Б.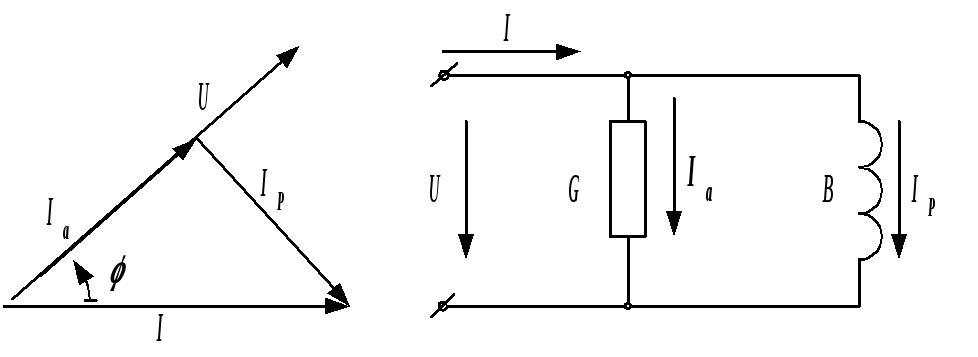 0,2 А В. 0,5 А Г. 0,4 А Д. 1 А
0,2 А В. 0,5 А Г. 0,4 А Д. 1 А
16 Максимальный заряд на обкладках конденсатора колебательного контура qm=10-4 Кл. При амплитудном значении силы тока в контуре Im=0,1 А период колебаний равен…
Задача 1. Вы кричите свое имя
В каком случае вы услышите ответ?
а) в колодец;
б) на опушке леса;
в) в степи.
Задача 2. Какое из перечисленных ниже движений является механическим колебанием?
1) Движение качелей. 2) Движения мяча падающего на землю.
А. Только 1. Б. Только 2. В. 1 и 2. Г. Ни 1, ни 2.
Задача 3. В процессе гармонических колебаний тела вдоль прямой амплитуда колебаний составляет 0.5 м. Чему равен путь, пройденный телом за период колебаний?
А. 0. Б. 0.5 м. В. 1 м. Г. 2 м. Д. Среди ответов А — Г нет правильного.
Задача 4. Максимальное значение потенциальной энергии свободно колеблющегося маятника 10 Дж., а максимальное значение его кинетической энергии 10 Дж. В каких пределах изменяется механическая энергия маятника?
В каких пределах изменяется механическая энергия маятника?
А. Не изменяется и равна 20 Дж. Б. Не изменяется и равна 10 Дж. В.
Не изменяется и равна. Г. Изменяется от 0 до 20 Дж. Д. Изменяется от 0 до 10 Дж.
Задача 5. Какова зависимость амплитуды вынужденных колебаний от частоты, если амплитуда колебаний вынуждающей силы постоянна?
А. Не зависит от частоты. Б. Непрерывно возрастает с увеличением частоты. В. Непрерывно убывает с увеличением частоты. Г. Сначала возрастает, достигает максимума, а затем убывает. Д. Сначала убывает, а затем возрастает.
Задача 6. Как изменится период колебаний груза на пружине, если массу груза увеличить в 4 раза?
А. Увеличится в 4 раза. Б. Увеличится в два раза. В. Не изменится. Г. Уменьшится в два раза. Д. Уменьшится в 4 раза.
Задача 7. После отклонения от положения равновесия на 1 см. маятник совершает свободные колебания с периодом 1 с. С каким периодом будет совершать свободные колебания тот же маятник при начальном отклонении от положения равновесия на 2 см?
А. 1 с. Б. 2 с. В 21/2 . Г. 1/2 с. Д. 1/21/2. с.
1 с. Б. 2 с. В 21/2 . Г. 1/2 с. Д. 1/21/2. с.
Задача 8. Тело массой 1 кг. совершает свободные колебания вдоль оси ОХ. Его координата изменяется по закону x=sin3t (м). По какому закону изменяется потенциальная энергия колеблющегося тела?
А. 2sin3t. Б. 6sin2 3t. B. 6cos2 3t Г. 18 sin2 3t. Д. 18 cos2 3t
Задача 9. Камертон имеет собственную частоту колебаний 440 Гц. Какой частоты надо взять другой камертон, чтобы наблюдать явление резонанса?
А. 400 Гц. Б. 300 Гц. В. 440 Гц. Г. 40 Гц. Д. 220 Гц.
Задача 10. Ухо человека наиболее чувствительно к частоте 350 Гц. Определите длину соответствующей звуковой волны в воздухе, если скорость звука в нем составляет 340 м/с. А. около 1м. Б. 2 м. В. 3 м. Г. 350 м. Д. Среди ответов нет правильного.
Ответы на задачи для самостоятельной работы 1 2 3 4 5 6 7 8 9 10
А Б А А А Б Г Д Д В А
Цепь переменного тока с активным сопротивлением и индуктивностью
Электротехника Цепь переменного тока с активным сопротивлением и индуктивностью
просмотров — 579
Рис. 2.21 изображает неразветвлённую цепь с активным сопротивлением R и индуктивностью L.
2.21 изображает неразветвлённую цепь с активным сопротивлением R и индуктивностью L.
Рис.2.21. Цепь переменного тока с активным сопротивлением и индуктивностью
Пусть мгновенный ток в цепи изменяется по закону . Тогда мгновенное напряжение на активном сопротивлении , так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке индуктивности , поскольку на индуктивности напряжение опережает по фазе ток на угол .
Построим для действующих значений напряжения и тока векторную диаграмму для рассматриваемой цепи (рис. 2.22).
Векторы и образуют треугольник напряжений. Выведем закон Ома для этой цепи. Из треугольника напряжений имеем . Но , а , где — индуктивное сопротивление, следовательно:
, откуда
. (2.22)
Рис.2.22. Векторная диаграмма действующих значений тока и напряжения цепи переменного тока с активным сопротивлением и индуктивностью
Введем обозначение , где Z — полное сопротивление цепи.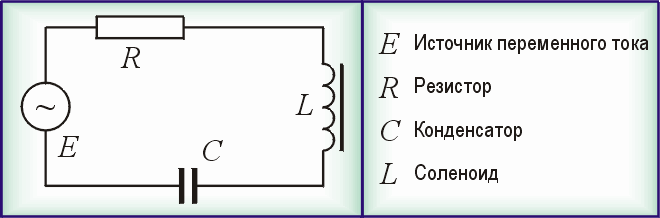 Тогда выражение закона Ома примет вид:
Тогда выражение закона Ома примет вид:
. (2.23)
Полное сопротивление Z можно определить из треугольника сопротивлений (рис. 2.23).
Рис.2.23. Треугольник сопротивлений цепи переменного тока с активным сопротивлением и индуктивностью
Сдвиг фаз между током и напряжением определяется из треугольника сопротивлений:
, (2.24)
. (2.25)
Поскольку вектор сдвинут по фазе относительно вектора на угол против часовой стрелки, данный угол имеет положительное значение.
В случае если , то мгновенная мощность . Для действующих значений произведение , откуда . Выражение . Исходя из этого,
. (2.26)
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, мгновенная мощность переменного тока может быть представлена в виде постоянной величины и, изменяющейся около неё с двойной частотой, величины (рис. 2.24).
Введем понятие средней или активной мощности:
. (2.27)
Активная мощность характеризует расход энергии на активном сопротивлении.
Реактивная мощность характеризует обмен энергий между индуктивной катушкой и источником:
. (2.28)
Полная мощность оценивает предельную мощность нагрузки:
. (2.29)
Рис.2.24. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с активным сопротивлением и индуктивностью
Совокупность всех мощностей можно определить из треугольника мощностей (рис. 2.25).
Рис.2.25. Треугольник мощностей
Так: Обозначим коэффициент мощности в виде соотношения .
Коэффициент мощности cosφ изменяется от 0 до 1. По его величине судят, какую часть полной мощности составляет активная мощность. На практике стремятся к увеличению cosφ.
2.7. Цепь переменного тока с активным сопротивлением и ёмкостью
Рассмотрим электрическую схему цепи с активным сопротивлением и ёмкостью (рис. 2.26).
Рис.2.26. Цепь переменного тока с активным сопротивлением и ёмкостью
Зададимся током , тогда . На основании приведенных выражений построим векторную диаграмму цепи (рис.2.27) для действующих значений напряжений .
На основании приведенных выражений построим векторную диаграмму цепи (рис.2.27) для действующих значений напряжений .
Рис.2.27. Векторная диаграмма действующих значений тока и напряжения цепи переменного тока с активным сопротивлением и ёмкостью
Из векторной диаграммы следует, что . Но , где — емкостное сопротивление. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, , откуда:
. (2.30)
На рис. 2.28 изображен треугольник сопротивлений. Сдвиг фаз (угол ) в этом случае отрицателен, так как напряжение отстает по фазе от тока:
. (2.31)
Пусть , тогда мгновенная мощность в цепи с R и C будет: . Опустив промежуточные преобразования, получим:
. (2.32)
Средняя или активная мощность определяется постоянной составляющей мгновенной мощности: .
Рис.2.28. Треугольник сопротивлений цепи переменного тока с активным сопротивлением и ёмкостью
Реактивная емкостная мощность характеризует интенсивность обмена энергий между источником и ёмкостью: . Так как < 0, то реактивная мощность < 0. Полная мощность определяется из треугольника мощностей (рис. 2.29): .
Так как < 0, то реактивная мощность < 0. Полная мощность определяется из треугольника мощностей (рис. 2.29): .
Рис.2.29. Треугольник мощностей
2.8. Неразветвлённая цепь переменного тока с активным сопротивлением, индуктивностью и ёмкостью. Резонанс напряжений
Рассмотрим неразветвлённую электрическую цепь (рис. 2.30).
Пусть , тогда .
Построим векторную диаграмму при условии, что действующие значения напряжений
Из векторной диаграммы (рис.2.31) следует: , откуда . Но , следовательно .
Рис.2.30. Схема неразветвлённой электрической цепи с активным сопротивлением, индуктивностью и ёмкостью
Рис.2.31. Векторная диаграмма действующих значений тока и напряжений для цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью, в которой ( )
Введя обозначение полного сопротивления цепи , найдем:
. (2.33)
Разность между индуктивным и емкостным сопротивлениями называют реактивным сопротивлением цепи X = XL — XC.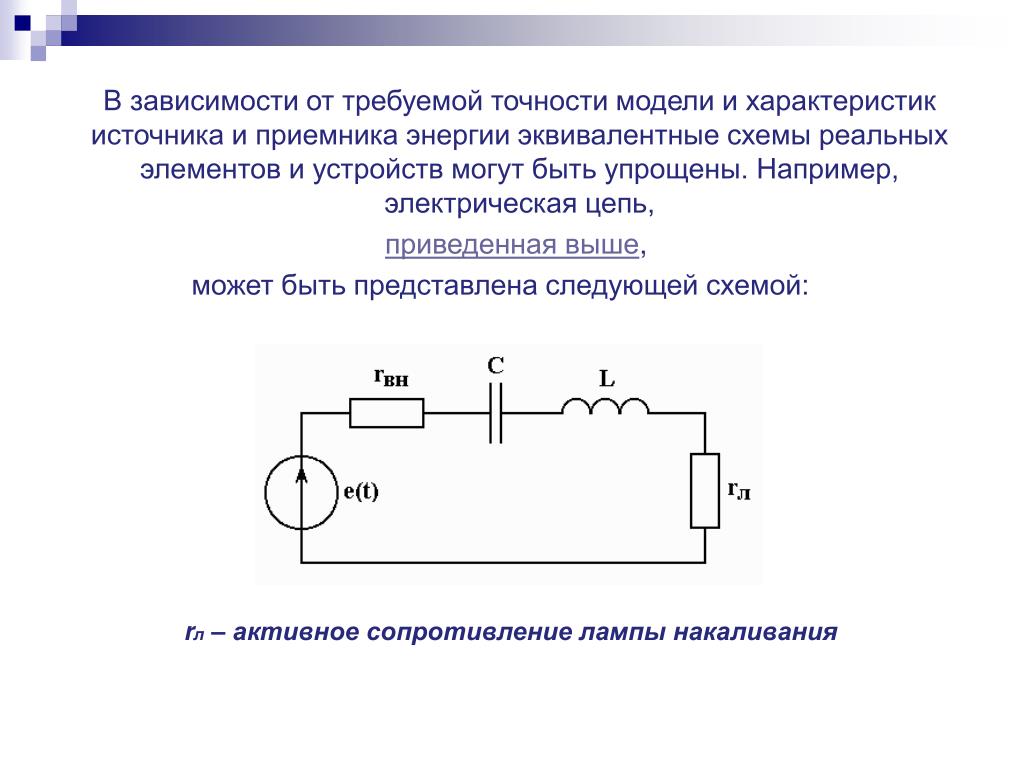 Учитывая это, получим треугольник сопротивлений для цепи с R, L и C (рис. 2.32).
Учитывая это, получим треугольник сопротивлений для цепи с R, L и C (рис. 2.32).
При XL > XC реактивное сопротивление положительно и угол > 0.
Аналогично можно построить векторную диаграмму для действующих значений напряжений (рис. 2.33) и треугольник сопротивлений (рис. 2.34).
Рис.2.32. Треугольник сопротивлений цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью ( )
Рис.2.33. Векторная диаграмма действующих значений тока и напряжений
( ) цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью
Рис.2.34. Треугольник сопротивлений цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью ( )
При XL < XC реактивное сопротивление X отрицательно и угол < 0. В случае если UL = UC и XL = XC , то векторную диаграмму можно представить в виде рис. 2.35, а зависимость тока от частоты в виде рис.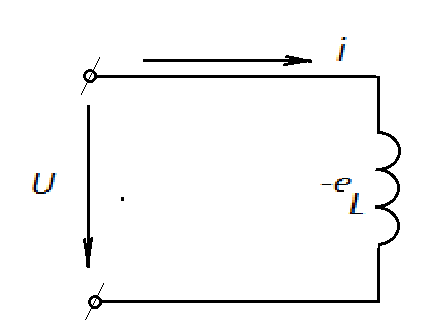 2.36.
2.36.
В этом случае наступает резонанс напряжений, когда ток в цепи совпадает по фазе с напряжением источника. При этом угол = 0, так как реактивное сопротивление равно нулю.
Рис.2.35. Векторная диаграмма резонанса напряжений
Рис.2.36. Зависимость тока от частоты питающей сети для резонанса напряжений
При резонансе напряжений частота источника равна собственной частоте колебаний LC-контура. В случае если , где f — частота источника питания, то можно записать . Решив это уравнение относительно f, получим
. (2.34)
На основании рис.2.35, 2.36 следует, что признаками резонанса напряжений являются:
а) полное сопротивление цепи равно активному сопротивлению Z = R;
б) ток в цепи совпадает по фазе с напряжением источника и имеет максимальное значение;
в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности превышает напряжение источника;
г) коэффициент мощности cos = 1.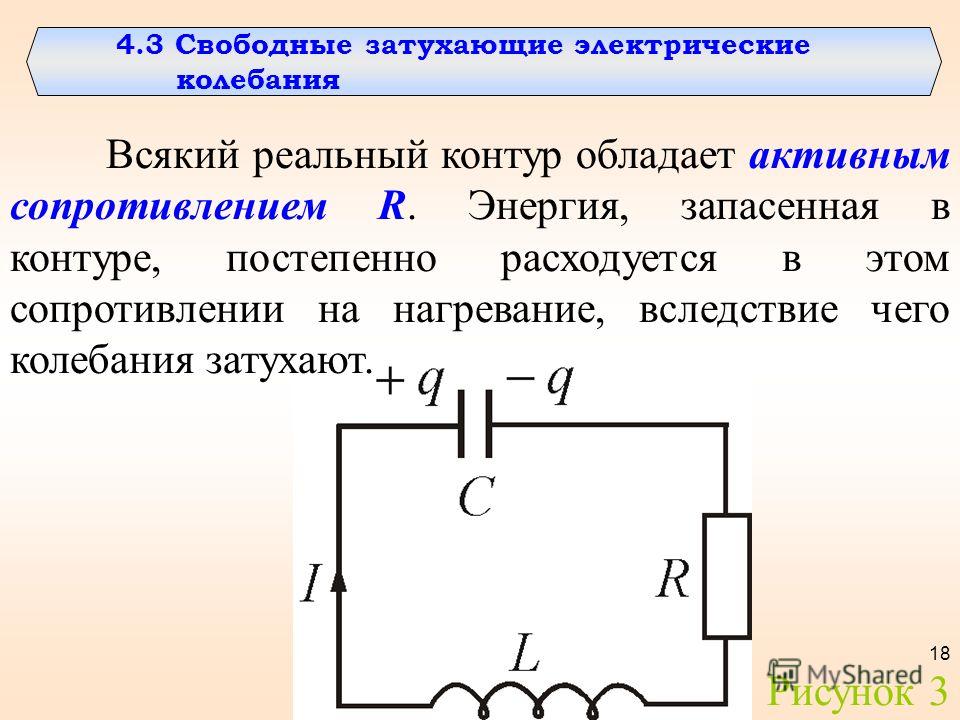
На рис.2.37 изображены примерные функциональные зависимости индуктивных и емкостных напряжений, тока и коэффициента мощности в зависимости от изменения ёмкости конденсатора, где Cp — резонансная ёмкость.
Рис.2.37. Примерное изображение зависимостей UL, UC, , cos от изменения ёмкости конденсатора C
Количественная оценка соотношения энергий источника, катушки индуктивности и конденсатора при резонансе напряжений характеризуется добротностью контура:
. (2.35)
Величину при резонансе называют волновым сопротивлением контура.
Читайте также
Рис.2.21 изображает неразветвлённую цепь с активным сопротивлением R и индуктивностью L.
Рис.2.21. Цепь переменного тока с активным сопротивлением и индуктивностью
Пусть мгновенный ток в цепи изменяется по закону . Тогда мгновенное напряжение на активном. .. [читать подробенее]
.. [читать подробенее]
С АКТИВНЫМ, ИНДУКТИВНЫМ И ЕМКОСТНЫМ
СОПРОТИВЛЕНИЯМИ
При расчетах цепей переменного тока, так же как и цепей постоянного тока, используют законы Ома и Кирхгофа. Отличие в применении этих законов заключается в том, что в цепях переменного тока необходимо учитывать углы сдвига фаз между токами и напряжениями.
Цепь переменного тока, в которую включены последовательно активное сопротивление R, индуктивность L, обладающая индуктивным сопротивлением , и емкость С, имеющая емкостное сопротивление, изображена на рис. .8, а.
Под действием переменного напряжения и в этой цепи протекает переменный ток iСогласно закону Ома определим падения напряжения на каждом элементе цепи:
Эти падения напряжения имеют соответствующие углы сдвига фаз по отношению к общему току цепи I.
Построим векторную диаграмму тока и напряжений для рассматриваемой цепи (рис. .8,б). Так как сопротивления соединены последовательно, то в них протекает одинаковый ток. Отложим по горизонтали в выбранном масштабе вектор тока I. В цепи с активным сопротивлением ток и напряжение совпадают по фазе, поэтому вектор напряжения откладываем по вектору токаI . Напряжение на индуктивности опережает ток на угол = 90°. Поэтому вектор откладываем вверх под углом 90° к вектору тока I . В цепи семкостьюи наоборот, напряжение отстает от тока на угол = 90°, поэтому вектор откладываем на диаграмме вниз под углом 90° к вектору тока I.
Рис. .8. Цепь переменного тока с последовательно включенными сопротивлением ,индуктивностью и емкостью:
а — электрическая схема; б — векторная диаграмма; в — треугольник сопротивлений
Для определения общего напряжения, приложенного к зажимам
цепи, сложим векторы и.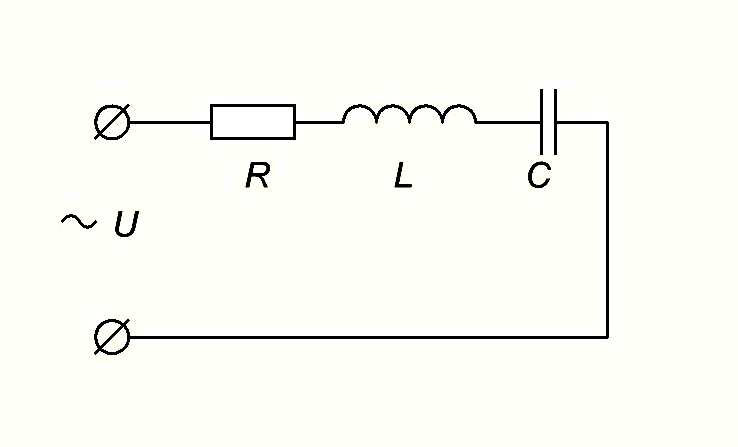 Для этого вычтем из большего вектора и
Для этого вычтем из большего вектора и
вектор и получим вектор ( ,) выражающий векторную сумму этих двух напряжений. Теперь сложим векторы ( ) .
Суммой этих векторов будет диагональ параллелограмма — вектор Uявляющийся общим напряжением на зажимах цепи:
2или 2
Полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления,
2
Полная проводимость цепи:
Угол сдвига фаз между током и напряжением цепи определяется тригонометрическими функциями:
Если >, то вектор напряжения U опережает вектор тока I, а если < то Uотстает от тока I. Треугольник сопротивлений изображен на рис..8, в
Треугольник сопротивлений изображен на рис..8, в
Пример .4. В электрическую цепь, приведенную на рисунке, с напряжением U = 220 В последовательно включены: резистор с активным сопротивлением , = 5 Ом, индуктивная катушка Lс активным сопротивлением
= 3 Ом и индуктивным сопротивлением = 4 Ом, конденсатор С с емкостным сопротивлением = 10 Ом. Определить ток в цепи и напряжение на отдельных элементах цепи. Нарисовать векторную диаграмму.
Решение
Определяем общее сопротивление
2 = =10Ом
Ток в цепи
Напряжение на отдельных элементах цепи:
В
В
В
В
Векторная диаграмма приведена на рисунке ниже.
Рассмотрим электрическую цепь, состоящую из двух приемников, подключенных параллельно к зажимам источника синусоидального напряжения u= sin
(рис. .9,а). В первом приемнике включены последовательно элементы и L, во втором соответственно и С. Оба приемника находятся под действием одного общего напряженияu. Запишем выражения для мгновенных значений токов для первой и второй ветви:
Рис. 9. Цепь переменного тока с параллельно соединенными элементам
а — электрическая схема: б — векторная диаграмма
Так как в первую ветвь включена индуктивная катушка, а во вторую— конденсатор, то электрические цепи соответственно носят индуктивны й и емкостной характер.
Действующее значение тока I и косинус угла определяем из следующих выражений:
Значение тока I в неразветвленной части цепи определяют как геометрическую сумму токов в ветвях, т. е.I = +
е.I = +
Векторная диаграмма приведена на рис. 9, б. Токи, протекающие через ветви, состоят из активной и реактивной составляющих и соответственно имеют индуктивный и емкостной характер.
Ветвь с активной составляющей характеризуется активной проводимостью
Ветвь с реактивной составляющей характеризуется реактивной проводимостью . Для первой ветви реактивная проводимость
2
Реактивная проводимость не является величиной, обратной реактивному сопротивлению, так как при ее определении учитывается и активное сопротивлении ветви. Полная проводимость ветви
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие законы используют при расчете цепей переменного тока?
2.В чем состоит принципиальное отличие расчета цепей переменного
тока от расчета цепей постоянного тока?
РЕЗОНАНС НАПРЯЖЕНИЙ
В цепи переменного тока с активным, индуктивным и емкостным сопротивлениями, соединенными последовательно (рис. 10, а), может возникнуть резонанс напряжений
10, а), может возникнуть резонанс напряжений
Резонанс напряжений наступает в том случае, если индуктивное сопротивление и емкостное сопротивление равны между собой, т.е.
Так как эти сопротивления зависят от частоты, резонанс наступает при определенной резонансной частоте :
При заданной частоте резонанс напряжений может быть достигнут изменением L и С.
Рис. 10. Цепь переменного тока при резонансе напряжения:
а — электрическая схема; б — векторная диаграмма
Когда цепь не настроена в резонанс, ее полное сопротивление
2
При резонансе напряжений в рассматриваемой цепи, когда = ее полное сопротивление
Запомните
1. Полное сопротивление цепи при резонансе напряжений равно активному сопротивлениюR.
2. Угол сдвига фаз между током и напряжением при резонансе равен нулю. Это значит, что ток и напряжение совпадают по фазе (как в цепи сактивным сопротивлением)
Уменьшение полного сопротивления цепи приводит к тому, что сила тока в ней возрастает. Напряжение генератора переменного тока, включенного в цепь, расходуется на активном сопротивлении:
Напряжение на индуктивности и емкости определяется согласно закону Ома. В связи стем что в последовательно соединенных сопротивлениях протекает одинаковый ток и при резонансе индуктивное сопротивление = напряжения на индуктивности и емкости тоже равны:
Векторная диаграмма для рассматриваемой цепи при резонансе напряжения приведена на рис 10, б. На векторной диаграмме видно, что напряжения на индуктивности и емкости равны, сдвинуты по фазе друг относительно друга на 180° и взаимно компенсируются.
Если одновременно увеличить оба реактивных сопротивления и , не нарушая при этом условия резонанса =, то соответственно возрастут оба частичных напряжения и, а сила тока в цепи при этом не изменится.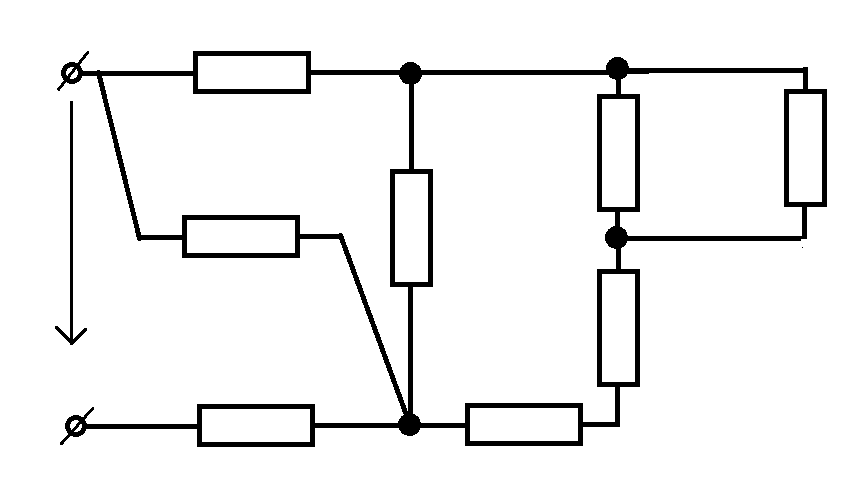 Таким образом, можно получить и во много раз большие, чем напряжение U на зажимах цепи, поэтому резонанс напряжений — опасное явление для энергетических установок.
Таким образом, можно получить и во много раз большие, чем напряжение U на зажимах цепи, поэтому резонанс напряжений — опасное явление для энергетических установок.
В электроустановках большой мощности резонанс напряжений, который может наступить внезапно, например при изменении емкостного сопротивления, может привести к опасным перенапряжениям и рассматривается как аварийный. В технике связи и автоматике явление резонанса напряжений широко используют для настройки приемных и передающих устройств на определенную частоту
Пример.5. В цепь переменного тока включены последовательно активное сопротивление R = 3 Ом, индуктивность L= 0,005 Гн и емкость С = 63,5 мкф. Генератор, включенный в цепь, вырабатывает переменное напряжение U = 2,5 В с резонансной частотой = 285 Гц. Определить индуктивное и емкостное сопротивления, полное сопротивление цепи, токпротекающий в цепи, напряжения на емкости и индуктивности.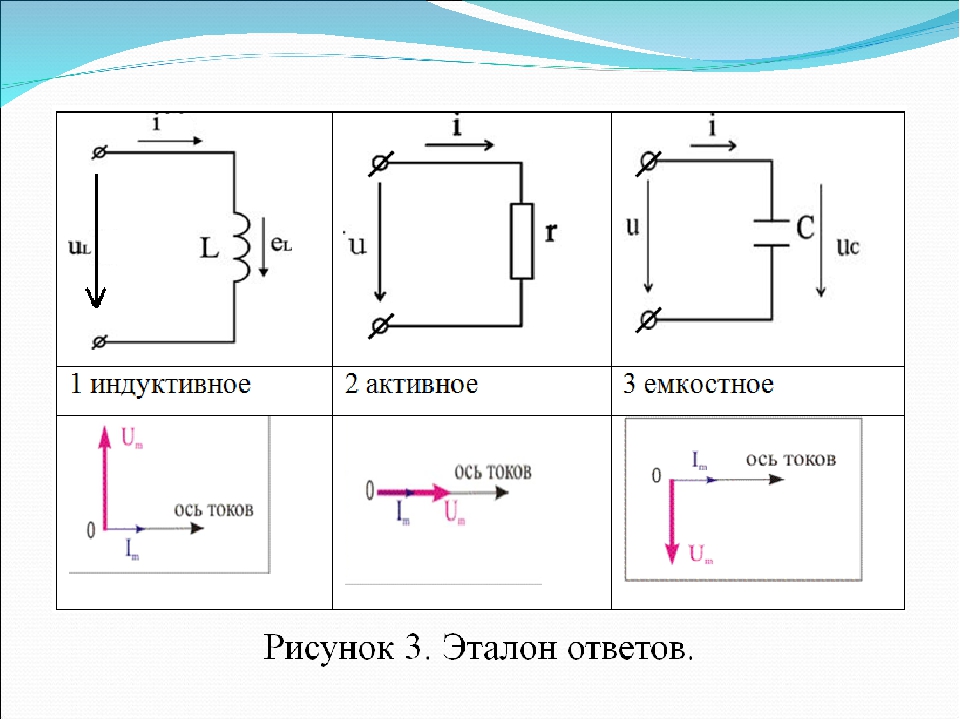
Решение
Индуктивное сопротивление
Ом
Емкостное сопротивление
Индуктивное сопротивление равно емкостному, следовательно, в цепи наступает резонанс напряжения.
Полное сопротивление цепи при резонансе напряжения
2 = 2 = 3Ом
Сила тока в цепи
Напряжение на индуктивности
Напряжение на емкости
Как видно из представленного примера, в режиме резонанса напряжения на индуктивности и емкости равны и превышают напряжение генератора.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется резонансом напряжений?
2. Чему равно полное сопротивление цепи при резонансе напряжений?
3. Чему равен угол сдвига фаз между током и напряжением при резонансе напряжений?
Чему равен угол сдвига фаз между током и напряжением при резонансе напряжений?
4. Какую опасность представляет резонанс напряжений в технике?
РЕЗОНАНС ТОКОВ
В цепи переменного тока, в которой индуктивность L, емкость Си сопротивлениеR соединены параллельно (рис. .11, а), может возникнуть резонанс токов при условии равенства реактивных сопротивлений:
Ток при резонансе достигает минимального значения I = U/R, a cos = 1, т. е. достигает своего максимального значения.
Значение резонансной частоты определяется формулой
Из формулы следует, что, изменяя величину емкости или индуктивности контура, можно изменять (регулировать) частоту свободных колебаний, т. е. настраивать контур на определенную частоту.
Векторная диаграмма изображена на рис.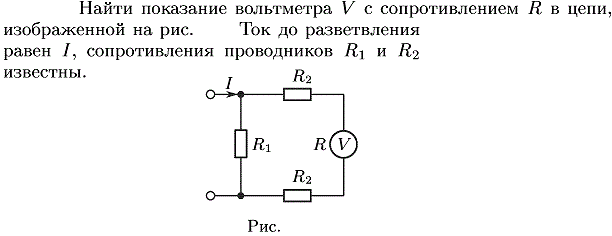 .11, б в режиме резонанса токов.
.11, б в режиме резонанса токов.
Рис .11. Цепь переменного тока при резонансе тока:
а-электрическая схема; б — векторная диаграмма
Свободные электрические колебания, возникающие в колебательном контуре, всегда затухающие. Затухание колебаний в контуре объясняется тем, что при прохождении электрического то в контуре энергия тратится на нагревание провода, из которого изготовлены индуктивная катушка и соединительные провода.
Потеря энергии в контуре вызывает постепенное уменьшение амплитуды свободных колебаний и их полное прекращение. Скорость затухания колебаний в контуре связана с потерей энергии в нем и зависит от сопротивления контура.
Запомните
■ Токи в ветвях, содержащих L и С, при резонансе тока могут быть
больше общего тока цепи.
■ Индуктивный и емкостной токи противоположны по фазе, равны по значению и по отношению к источнику энергии взаимно
компенсируются, т. е. идет обмен энергией между индуктивной
е. идет обмен энергией между индуктивной
катушкой и конденсатором.
■ Реактивная мощность цепи при резонансе токов равна нулю, поскольку равны и противоположно направлены токи . Иными словами, реактивная мощность, потребляемая в индуктивной катушке, равна реактивной мощности, генерируемой в конденсаторе.
В результате резонанса токов общий ток в цепи может быть относительно мал, а в ветвях индуктивности и емкости, где происходят электрические колебания, переменный ток значительно больше общего.
Пример 6. Разветвленная цепь, приведенная на рисунке слева, имеет
следующие параметры: = = 10 Ом, R = 40 Ом, U= 120 В. Определить токи в ветвях и общий ток цепи. Построить векторную диаграмму.
Решение
Определим токи в ветвях:
Рассчитаем общий ток цепи
Векторная диаграмма изображена на рисунке справа. Общий ток цепи при резонансе токов в четыре раза меньше тока в ветвях, содержащих реактивные элементы.
Общий ток цепи при резонансе токов в четыре раза меньше тока в ветвях, содержащих реактивные элементы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. При каких условиях возникает резонанс токов?
2. От чего зависит скорость затухания колебаний в контуре?
3. Чему равна реактивная мощность цепи при резонансе токов?
Задачи по физике и математике с решениями и ответами
Задача по физике — 7869
Катушку с активным сопротивлением $R$ и индуктивностью $L$ подключили в момент $t = 0$ к источнику напряжения $U = U_{m} \cos \omega t$. Найти ток в катушке как функцию времени $t$. ПодробнееЗадача по физике — 7870
Цепь, состоящую из последовательно соединенных конденсатора емкости $C$ и сопротивления $R$, подключили к переменному напряжению $U = U_{m} \cos \omega t$ в момент $t = 0$. Найти ток в цепи как функцию времени $t$.
Подробнее
Найти ток в цепи как функцию времени $t$.
Подробнее
Задача по физике — 7871
Длинный однослойный соленоид из проволоки с удельным сопротивлением $\rho$ имеет на единицу длины $n$ плотно расположенных витков. Толшина изоляции провода пренебрежимо мала. Радиус сечения соленоида равен $a$. Найти разность фаз между током и переменным напряжением с частотой $\nu$, которое подключено к концам соленоида. ПодробнееЗадача по физике — 7872
Концы цепи, состоящей из последовательно включенных конденсатора и активного сопротивления $R = 110 Ом$, подсоединили к переменному напряжению с амплитудным значением $U_{m} = 110 В$. При этом амплитуда установившегося тока в цепи $I_{m} = 0,50 А$. Найти разность фаз между током и подаваемым напряжением.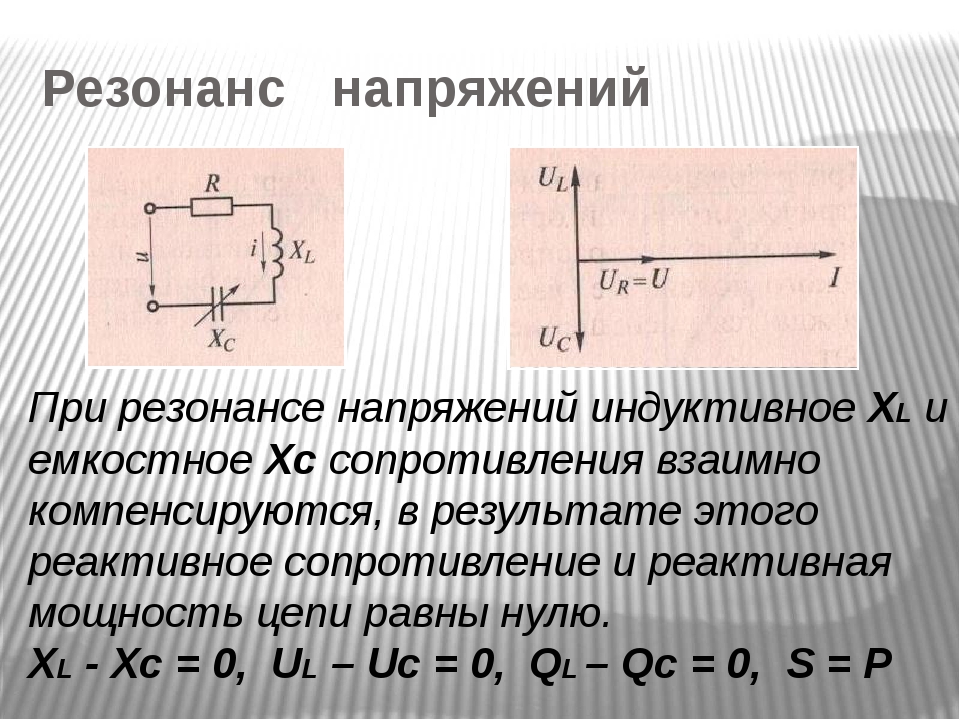 { \prime} (t)$;
{ \prime} (t)$;
б) значение величины $RC$, при котором амплитуда переменной составляющей напряжения на выходе будет в $\eta = 7,0$ раза меньше постоянной составляющей, если $\omega = 314 рад/с$.
Подробнее
Задача по физике — 7874
Изобразить примерные векторные диаграммы напряжений в электрических цепях, показанных на рис. а, б. Внешнее напряжение $U$ предполагается гармоническим с частотой $\omega$.Подробнее
Задача по физике — 7875
Цепь, состоящая из последовательно соединенных конденсатора емкости $C = 22 мкФ$ и катушки с активным сопротивлением $R = 20 Ом$ и индуктивностью $L = 0,35 Г$, подключена к сети переменного напряжения с амплитудой $U_{m} = 180 В$ и частотой $\omega = 314 рад/с$. Найти:
Найти:
а) амплитуду тока в цепи;
б) разность фаз между током и внешним напряжением;
в) амплитуды напряжения на конденсаторе и катушке. Подробнее
Задача по физике — 7876
Цепь из последовательно соединенных конденсатора емкости $C$, сопротивления $R$ и катушки с индуктивностью $L$ и пренебрежимо малым активным сопротивлением подключена к генератору синусоидального напряжения, частоту которого можно менять при постоянной амплитуде. Найти частоту, при которой максимальна амплитуда напряжения:а) на конденсаторе; б) на катушке. Подробнее
Задача по физике — 7877
Переменное напряжение с частотой $\omega = 314 рад/с$ и амплитудным значением $U_{m} = 180 В$ подключено к концам цепи, состоящей из последовательно соединенных конденсатора и катушки с активным сопротивлением $R = 40 Ом$ и индуктивностью $L = 0,36 Г$.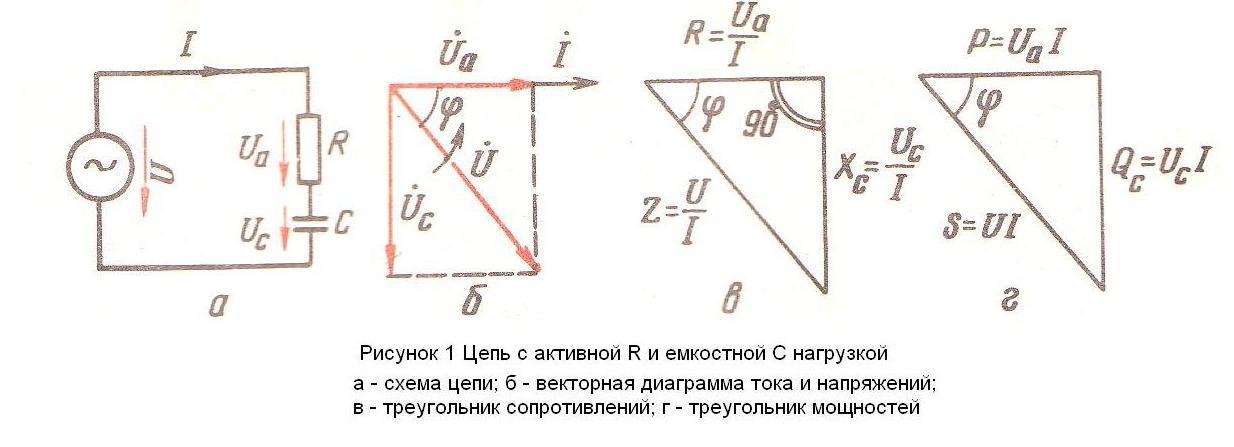 При каком значении емкости конденсатора амплитуда, напряжения на катушке будет максимальной? Чему равна эта амплитуда и соответствующая амплитуда напряжения на конденсаторе?
Подробнее
При каком значении емкости конденсатора амплитуда, напряжения на катушке будет максимальной? Чему равна эта амплитуда и соответствующая амплитуда напряжения на конденсаторе?
Подробнее
Задача по физике — 7878
Конденсатор емкости $C$, пространство между обкладками которого заполнено слабо проводящей средой с активным сопротивлением $R$, подключили к источнику, переменного напряжения $U = U_{m} \cos \omega t$. Найти установившийся ток в подводящих проводах в зависимости от времени. Сопротивление проводов пренебрежимо мало. ПодробнееЗадача по физике — 7879
Колебательный контур содержит. конденсатор емкости $C$ и соленоид с индуктивностью $L_{1}$. Соленоид индуктивно связан с короткозамкнутой катушкой, имеющей индуктивность $L_{2}$ и пренебрежимо малое активное сопротивление. Коэффициент их взаимной индуктивности равен $L_{12}$. Найти собственную частоту данного колебательного контура.
Подробнее
Коэффициент их взаимной индуктивности равен $L_{12}$. Найти собственную частоту данного колебательного контура.
Подробнее
Задача по физике — 7880
Найти добротность колебательного контура, в который последовательно включен источник переменной э. д. с, если при резонансе напряжение на конденсаторе в $n$ раз превышает напряжение на источнике. ПодробнееЗадача по физике — 7881
Цепь переменного тока, состоящая из последовательно соединенных катушки и конденсатора, подключена к источнику переменной э. д. с, причем индуктивность катушки подобрана так, что ток в цепи максимален. Найти добротность системы, если известно, что при увеличении индуктивности в $n$ раз ток в цепи уменьшается в $\eta$ раз.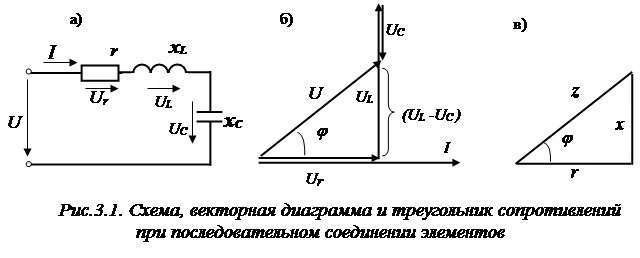 Подробнее
Подробнее
Задача по физике — 7882
Цепь, содержащая последовательно соединенные конденсатор и катушку с активным сопротивлением, подключена к источнику гармонического напряжения, частоту которого можно менять, не изменяя амплитуды напряжения. При частотах $\omega_{1}$ и $\omega_{2}$ амплитуды тока оказались в $n$ раз меньше резонансной амплитуды.Найти: а) резонансную частоту; б) добротность цепи. Подробнее
Задача по физике — 7883
Показать, что при малом затухании добротность контура, в котором совершаются вынужденные колебания, $Q \approx \omega_{0}/ \Delta \omega$, где $\omega_{0}$ — собственная частота колебаний, $\Delta \omega$ — ширина резонансной кривой $I( \omega)$ на «высоте», в $\sqrt{2}$ раз меньшей амплитуды тока при резонансе. Подробнее
Подробнее
Основы электричества: сопротивление, индуктивность и емкость
Электронные схемы являются неотъемлемой частью почти всех технологических достижений, достигнутых в нашей жизни сегодня. Сразу приходят на ум телевидение, радио, телефоны и компьютеры, но электроника также используется в автомобилях, кухонной технике, медицинском оборудовании и промышленных системах управления. В основе этих устройств лежат активные компоненты или компоненты схемы, которые электронным образом управляют потоком электронов, например, полупроводники.Однако эти устройства не могли функционировать без гораздо более простых пассивных компонентов, которые предшествовали полупроводникам на многие десятилетия. В отличие от активных компонентов, пассивные компоненты, такие как резисторы, конденсаторы и катушки индуктивности, не могут управлять потоком электронов с помощью электронных сигналов.
Сопротивление
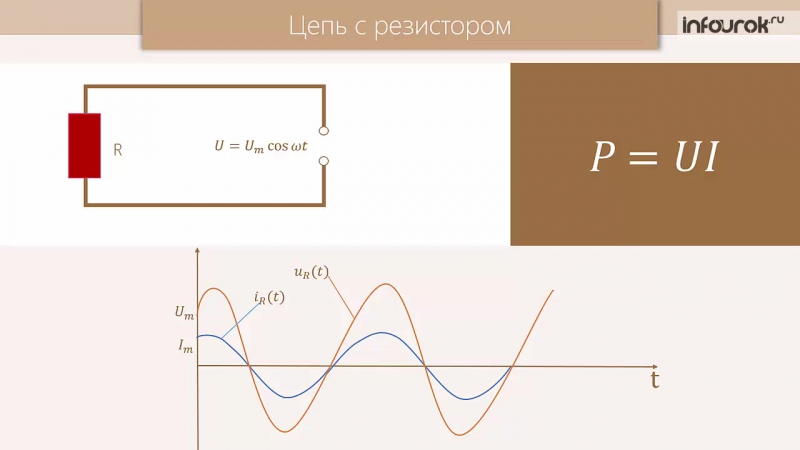
Как следует из названия, резистор — это электронный компонент, который препятствует прохождению электрического тока в цепи.
В металлах, таких как серебро или медь, которые имеют высокую электропроводность и, следовательно, низкое удельное сопротивление, электроны могут свободно переходить от одного атома к другому с небольшим сопротивлением.
Электрическое сопротивление компонента схемы определяется как отношение приложенного напряжения к протекающему через него электрическому току, согласно HyperPhysics, веб-сайту физических ресурсов, размещенному на кафедре физики и астрономии в Университете штата Джорджия. Стандартной единицей измерения сопротивления является ом, названный в честь немецкого физика Георга Симона Ома. Он определяется как сопротивление в цепи с током 1 ампер при 1 вольте. Сопротивление можно рассчитать с помощью закона Ома, который гласит, что сопротивление равно напряжению, разделенному на ток, или R = V / I (чаще записывается как V = IR), где R — сопротивление, V — напряжение, а I — ток.
Резисторы обычно делятся на постоянные и переменные. Резисторы с фиксированным значением представляют собой простые пассивные компоненты, которые всегда имеют одинаковое сопротивление в установленных пределах по току и напряжению.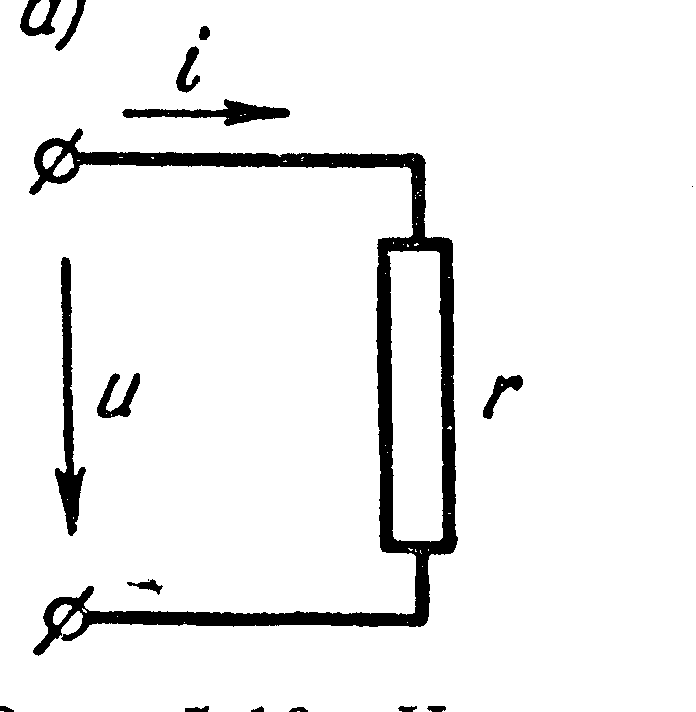 Они доступны в широком диапазоне значений сопротивления от менее 1 Ом до нескольких миллионов Ом.
Они доступны в широком диапазоне значений сопротивления от менее 1 Ом до нескольких миллионов Ом.
Переменные резисторы — это простые электромеханические устройства, такие как регуляторы громкости и диммеры, которые изменяют эффективную длину или эффективную температуру резистора, когда вы поворачиваете ручку или перемещаете ползунок.
Пример индуктора из медного провода, установленного на печатной плате. (Изображение предоставлено Shutterstock)
Индуктивность
Индуктор — это электронный компонент, состоящий из катушки с проволокой, через которую проходит электрический ток, создающий магнитное поле. Единицей измерения индуктивности является генри (H), названный в честь Джозефа Генри, американского физика, который открыл индуктивность независимо примерно в то же время, что и английский физик Майкл Фарадей. Один генри — это величина индуктивности, которая требуется для создания 1 вольт электродвижущей силы (электрического давления от источника энергии), когда ток изменяется со скоростью 1 ампер в секунду.
Одним из важных применений индукторов в активных цепях является то, что они имеют тенденцию блокировать высокочастотные сигналы, пропуская низкочастотные колебания. Обратите внимание, что это противоположная функция конденсаторов. Объединение двух компонентов в цепь может выборочно фильтровать или генерировать колебания практически любой желаемой частоты.
С появлением интегральных схем, таких как микрочипы, индукторы становятся все менее распространенными, потому что трехмерные катушки чрезвычайно трудно изготовить в двумерных печатных схемах.По этой причине, по словам Майкла Дубсона, профессора физики из Университета Колорадо в Боулдере, микросхемы разрабатываются без катушек индуктивности и вместо них используют конденсаторы для достижения практически тех же результатов.
Несколько примеров конденсаторов. Конденсаторы хранят электрический заряд. (Изображение предоставлено Питером Матисом, Университет Колорадо)
Емкость
Емкость — это способность устройства накапливать электрический заряд, и поэтому электронный компонент, который накапливает электрический заряд, называется конденсатором. Самый ранний пример конденсатора — лейденская банка. Это устройство было изобретено для накопления статического электрического заряда на проводящей фольге, которая выстилала внутреннюю и внешнюю поверхность стеклянной банки.
Самый ранний пример конденсатора — лейденская банка. Это устройство было изобретено для накопления статического электрического заряда на проводящей фольге, которая выстилала внутреннюю и внешнюю поверхность стеклянной банки.
Простейший конденсатор состоит из двух плоских проводящих пластин, разделенных небольшим зазором. Разность потенциалов или напряжение между пластинами пропорциональна разнице в количестве заряда на пластинах. Это выражается как Q = CV, где Q — заряд, V — напряжение, а C — емкость.
Емкость конденсатора — это количество заряда, которое он может хранить на единицу напряжения. Единицей измерения емкости является фарад (Ф), названный в честь Фарадея, и определяется как способность хранить 1 кулон заряда с приложенным потенциалом 1 вольт. Один кулон (C) — это количество заряда, переносимого током в 1 ампер за 1 секунду.
Для максимального повышения эффективности обкладки конденсатора уложены слоями или намотаны катушками с очень маленьким воздушным зазором между ними. В воздушном зазоре часто используются диэлектрические материалы — изоляционные материалы, которые частично блокируют электрическое поле между пластинами.Это позволяет пластинам накапливать больше заряда без искрения и короткого замыкания.
В воздушном зазоре часто используются диэлектрические материалы — изоляционные материалы, которые частично блокируют электрическое поле между пластинами.Это позволяет пластинам накапливать больше заряда без искрения и короткого замыкания.
Конденсаторы часто встречаются в активных электронных схемах, использующих колебательные электрические сигналы, например, в радиоприемниках и звуковом оборудовании. Они могут заряжаться и разряжаться почти мгновенно, что позволяет использовать их для создания или фильтрации определенных частот в цепях. Колебательный сигнал может заряжать одну пластину конденсатора, в то время как другая пластина разряжается, а затем, когда ток меняется на противоположное, он заряжает другую пластину, в то время как первая пластина разряжается.
Как правило, более высокие частоты могут проходить через конденсатор, а более низкие частоты блокируются. Размер конденсатора определяет частоту среза, при которой сигналы блокируются или пропускаются. Комбинированные конденсаторы могут использоваться для фильтрации выбранных частот в заданном диапазоне.
Суперконденсаторы производятся с использованием нанотехнологий для создания сверхтонких слоев материалов, таких как графен, для достижения емкости, в 10–100 раз превышающей емкость обычных конденсаторов того же размера; но они имеют гораздо более медленное время отклика, чем обычные диэлектрические конденсаторы, поэтому их нельзя использовать в активных цепях.С другой стороны, их иногда можно использовать в качестве источника питания в определенных приложениях, например, в микросхемах памяти компьютера, чтобы предотвратить потерю данных при отключении основного питания.
Конденсаторы также являются критически важными компонентами устройств синхронизации, например, разработанных компанией SiTime, базирующейся в Калифорнии. Эти устройства используются в самых разных приложениях, от мобильных телефонов до высокоскоростных поездов и торговли на фондовом рынке. Это крошечное устройство синхронизации, известное как МЭМС (микроэлектромеханические системы), для правильной работы полагается на конденсаторы. «Если резонатор [колебательный компонент в устройстве синхронизации] не имеет подходящего конденсатора и емкости нагрузки, схема синхронизации не будет надежно запускаться, а в некоторых случаях она вообще перестает колебаться», — сказал Пиюш Севалия, исполнительный директор. вице-президент по маркетингу в SiTime.
«Если резонатор [колебательный компонент в устройстве синхронизации] не имеет подходящего конденсатора и емкости нагрузки, схема синхронизации не будет надежно запускаться, а в некоторых случаях она вообще перестает колебаться», — сказал Пиюш Севалия, исполнительный директор. вице-президент по маркетингу в SiTime.
Дополнительные ресурсы:
Эта статья была обновлена 16 января 2019 г. участником Live Science Рэйчел Росс.
Мощность в цепи переменного тока — Университетская физика, том 2
Цели обучения
К концу раздела вы сможете:
- Опишите, как можно записать среднюю мощность в цепи переменного тока через пиковый ток и напряжение, а также среднеквадратичные значения тока и напряжения.
- Определите соотношение между фазовым углом тока и напряжения и средней мощностью, известное как коэффициент мощности.
Элемент схемы рассеивает или вырабатывает мощность в зависимости от того, где I — ток через элемент, а В, — напряжение на нем. Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность также зависит от времени. График p ( t ) для различных элементов схемы показан на (Рисунок). Для резистора i ( t ) и v ( t ) синфазны и поэтому всегда имеют один и тот же знак (см. (Рисунок)). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разницы фаз (см. (Рисунок) и (Рисунок)).Следовательно, p ( t ) положительно в некоторые моменты и отрицательно в другие, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты и поглощают ее в другие.
Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность также зависит от времени. График p ( t ) для различных элементов схемы показан на (Рисунок). Для резистора i ( t ) и v ( t ) синфазны и поэтому всегда имеют один и тот же знак (см. (Рисунок)). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разницы фаз (см. (Рисунок) и (Рисунок)).Следовательно, p ( t ) положительно в некоторые моменты и отрицательно в другие, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты и поглощают ее в другие.
Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. То, что нас почти всегда интересует, — это усредненная по времени мощность, которую мы называем средней мощностью. Он определяется средним по времени мгновенной мощностью за один цикл:
где — период колебаний.С заменами и этот интеграл становится
Используя тригонометрическое соотношение, получаем
Вычисление этих двух интегралов дает
и
Следовательно, средняя мощность, связанная с элементом схемы, равна
В технических приложениях известен как коэффициент мощности, который представляет собой величину, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе.Для резистора, поэтому средняя рассеиваемая мощность составляет
Сравнение p ( t ) и показано на (Рисунок) (d).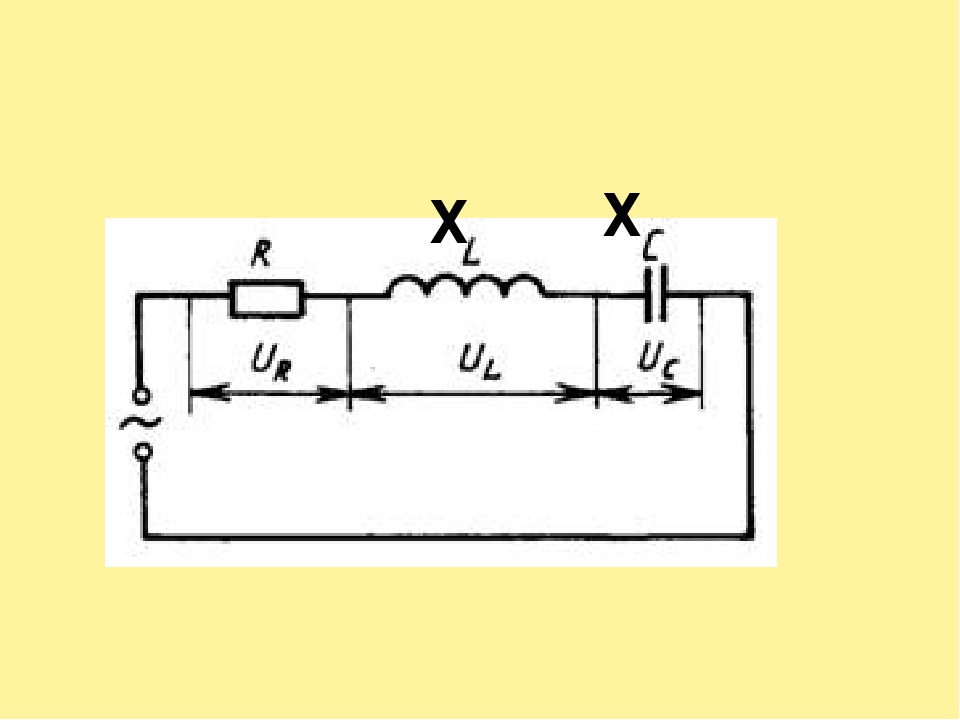 Чтобы выглядеть как его аналог постоянного тока, мы используем среднеквадратичные значения тока и напряжения. По определению это
Чтобы выглядеть как его аналог постоянного тока, мы используем среднеквадратичные значения тока и напряжения. По определению это
где
С получаем
Тогда мы можем написать для средней мощности, рассеиваемой резистором,
Это уравнение дополнительно подчеркивает, почему при обсуждении выбирается среднеквадратичное значение, а не пиковые значения.Оба уравнения для средней мощности верны для (рисунок), но среднеквадратичные значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не требуется.
Переменные напряжения и токи обычно описываются их действующими значениями. Например, напряжение 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника равна. Поскольку большинство измерителей переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, помещенный в бытовую розетку, будет показывать 110 В.
Для конденсатора и катушки индуктивности соответственно. Поскольку мы находим из (Рисунок), что средняя мощность, рассеиваемая любым из этих элементов, равна Конденсаторам, а катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем разряжают ее обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках (Рисунок), (b) и (c), которые показывают, что p ( t) колеблются синусоидально около нуля.
Поскольку мы находим из (Рисунок), что средняя мощность, рассеиваемая любым из этих элементов, равна Конденсаторам, а катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем разряжают ее обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках (Рисунок), (b) и (c), которые показывают, что p ( t) колеблются синусоидально около нуля.
Фазовый угол генератора переменного тока может иметь любое значение.Если генератор выдает мощность; если он поглощает энергию. В терминах среднеквадратичных значений средняя мощность генератора переменного тока записывается как
.Для генератора в цепи RLC ,
и
Отсюда средняя мощность генератора
Это также можно записать как
, который означает, что мощность, производимая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного значения напряжения на импеданс.
Проверьте свое понимание Вольтметр переменного тока, подключенный к клеммам генератора переменного тока 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.
Проверьте свое понимание Покажите, что среднеквадратичные значения напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичный ток выражается соответственно. Определите эти значения для компонентов цепи RLC (рисунок).
Сводка
- Средняя мощность переменного тока определяется путем умножения среднеквадратичных значений тока и напряжения.
- Закон Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного напряжения на полное сопротивление.
- В цепи переменного тока существует фазовый угол между напряжением источника и током, который можно найти, разделив сопротивление на полное сопротивление.

- Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла.
- Коэффициент мощности находится в диапазоне от –1 до 1.
Концептуальные вопросы
При каком значении фазового угла между выходным напряжением источника переменного тока и током средняя выходная мощность источника является максимальной?
Обсудите разницу между средней мощностью и мгновенной мощностью.
Мгновенная мощность — это мощность в данный момент. Средняя мощность — это мощность, усредненная за цикл или количество циклов.
Средний переменный ток, подаваемый в цепь, равен нулю.Несмотря на это, мощность в цепи рассеивается. Объяснять.
Может ли мгновенная выходная мощность источника переменного тока быть отрицательной? Может ли средняя выходная мощность быть отрицательной?
Мгновенная мощность может быть отрицательной, но выходная мощность не может быть отрицательной.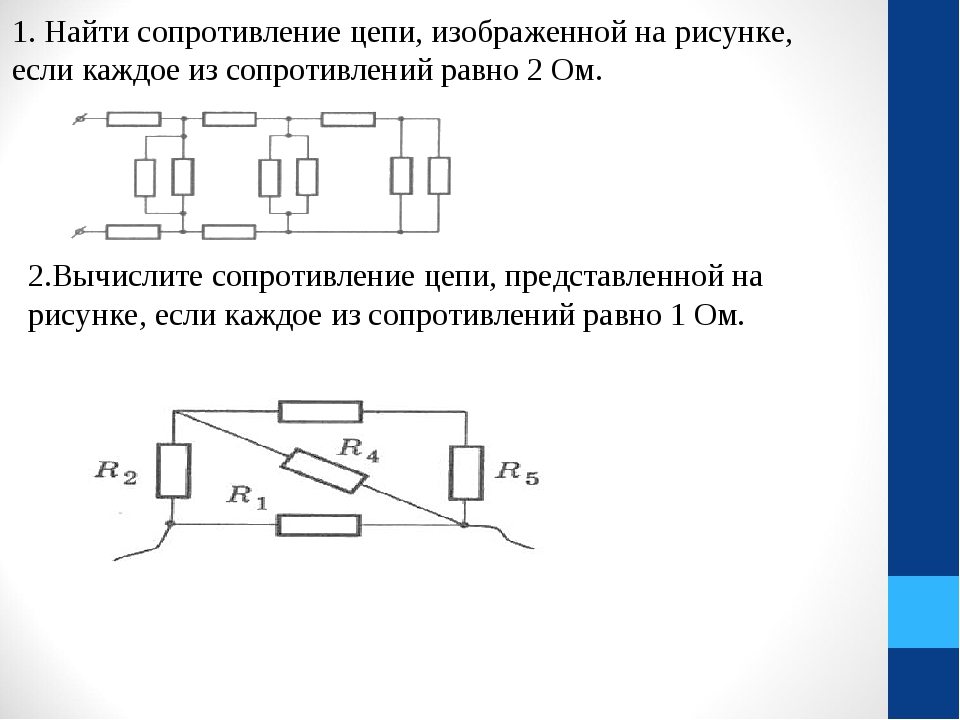
Номинальная мощность резистора, используемого в цепях переменного тока, относится к максимальной средней мощности, рассеиваемой в резисторе. Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?
Глоссарий
- средняя мощность
- среднее время мгновенной мощности за один цикл
- коэффициент мощности
- величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе
параллельная RC-цепь | Диаграмма фазора | Импеданс и мощность
В этом руководстве рассматриваются анализ параллельной RC-цепи, фазорная диаграмма, треугольник импеданса и мощности, а также несколько решенных примеров, а также ответы на вопросы для обзора.
В этом руководстве рассматривается комбинация резистора и конденсатора, подключенных параллельно источнику переменного тока, как показано на рис. 1 , называется параллельной цепью RC .
1 , называется параллельной цепью RC .
Условия, которые существуют в параллельных цепях RC , и методы, используемые для их решения, очень похожи на те, которые используются для параллельных цепей RL . Напряжение имеет одинаковое значение на каждой параллельной ветви и служит основой для выражения любых разностей фаз.Принципиальная разница — это соотношение фаз.
В чистом конденсаторе ток опережает напряжение на 90 градусов, в то время как в чистой катушке индуктивности ток отстает от напряжения на 90 градусов.
Рисунок 1 Параллельная цепь RC .
Фазорная схема параллельной RC-цепи
Взаимосвязь между напряжением и токами в параллельной цепи RC проиллюстрирована на векторной (векторной) диаграмме на рисунке 2 и резюмирована следующим образом:
- опорный вектор обозначен E и представляет собой напряжение в цепи, общее для всех элементов.
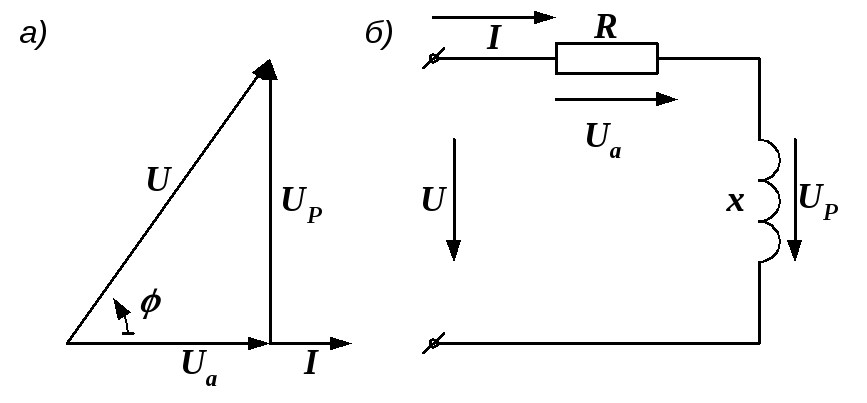
- Поскольку ток через резистор синфазен с напряжением на нем, I R (8 A) показано наложенным на вектор напряжения.
- Конденсаторный ток I C (12 А) опережает напряжение на 90 градусов и расположен в восходящем направлении, опережая вектор напряжения на 90 градусов.
- Сложение векторов I R и I C дает результат, который представляет собой общий (IT) или линейный ток (14.4 А).
- Угол тета (θ) представляет собой фазу между приложенным линейным напряжением и током.
Рисунок 2 Векторная (векторная) диаграмма цепи Parallel RC .
В параллельной цепи RC линейный ток опережает приложенное напряжение на некоторый фазовый угол меньше 90 градусов, но больше 0 градусов. Точный угол зависит от того, больше ли емкостной или резистивный ток.Если есть на больше емкостного тока, угол будет ближе к 90 градусам, , а если резистивный ток больше, угол будет ближе к 0 градусам.
Значение фазового угла можно рассчитать из значений двух токов ответвления с помощью следующего уравнения:
Ток в параллельной RC-цепи, пример 1
Для параллельной RC-цепи RC , показанной на рисунке 3 , определите:
- Ток, протекающий через резистор.
- Ток через конденсатор.
- Общий линейный ток.
- Фазовый угол между напряжением и полным током.
- Выразите все токи в полярных обозначениях.
- Используйте калькулятор, чтобы преобразовать все токи в прямоугольную форму.
Рисунок 3 Схема для примера 1.
Решение:
\ [\ text {a} \ text {. } {{\ text {I}} _ {\ text {R}}} \ text {=} \ frac {\ text {E}} {\ text {R}} \ text {=} \ frac {\ text { 120 В}} {\ text {10} \! \! \ Omega \! \! \ Text {}} \ text {= 12A} \]
\ [\ text {b} \ text {.{\ text {o}}} \\\ end {matrix} \]
\ [\ text {f} \ text {. } \ begin {matrix} \ text {} {{\ text {I}} _ { \ text {T}}} \ text {= 12 + j6} & {{\ text {I}} _ {\ text {R}}} \ text {= 12 + j0} & {{\ text {I}} _ {\ text {C}}} \ text {= 0 + j6} \\\ end {matrix} \]
} \ begin {matrix} \ text {} {{\ text {I}} _ { \ text {T}}} \ text {= 12 + j6} & {{\ text {I}} _ {\ text {R}}} \ text {= 12 + j0} & {{\ text {I}} _ {\ text {C}}} \ text {= 0 + j6} \\\ end {matrix} \]
Сопротивление параллельной RC-цепи
Импеданс ( Z ) параллельного RC-цепи Цепь аналогична параллельной цепи RL и резюмируется следующим образом:
- Импеданс можно рассчитать непосредственно из значений сопротивления и емкостного реактивного сопротивления с помощью уравнения
- Импеданс можно рассчитать с помощью Ом уравнение закона
- Импеданс параллельной цепи RC всегда меньше, чем сопротивление или емкостное реактивное сопротивление отдельных ветвей.
Импеданс в параллельной RC-цепи Пример 2
Для параллельной RC-цепи RC , показанной на рисунке 4 , определите:
- Ток, протекающий через резистор ( I R ).

- Ток через конденсатор ( I C ).
- Полный линейный ток ( I T ).
- Импеданс ( Z ).
- Фазовый угол между напряжением и полным током.
- Если цепь более резистивная или емкостная.
Рисунок 4 Схема для примера 2.
Решение:
\ [\ text {a} \ text {. } {{\ text {I}} _ {\ text {R}}} \ text {=} \ frac {\ text {E}} {\ text {R}} \ text {=} \ frac {\ text { 240V}} {\ text {200} \! \! \ Omega \! \! \ Text {}} \ text {= 1} \ text {.2A} \]
\ [\ text {b} \ text { . } {{\ text {I}} _ {\ text {C}}} \ text {=} \ frac {\ text {E}} {{{\ text {X}} _ {\ text {C}}} } \ text {=} \ frac {\ text {240V}} {\ text {100} \! \! \ Omega \! \! \ text {}} \ text {= 2} \ text {.{o}} \]
ф. Схема более емкостная по своей природе, потому что емкостной ток больше, чем резистивный ток.
Питание в параллельной RC-цепи
Силовые компоненты для параллельной RC-цепи RC показаны на Рисунке 5 .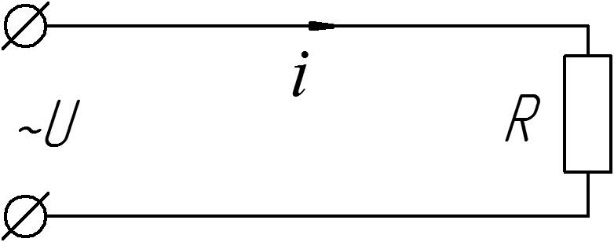 Применяемые формулы такие же, как и для параллельной цепи RL :
Применяемые формулы такие же, как и для параллельной цепи RL :
Рисунок 5 Силовые компоненты параллельной цепи RC .
Коэффициент мощности параллельной RC-цепи
Коэффициент мощности параллельной RC-цепи RC всегда опережает. Каждый раз, когда сопротивление ответвления увеличивается, через него проходит меньше тока, и цепь становится более емкостной, что приводит к более низкому коэффициенту мощности. Обратное верно, если сопротивление уменьшается.
С помощью значений тока или сопротивления и импеданса коэффициент мощности можно определить следующим образом:
Пример расчета параллельной RC-цепи 3
Для параллельной цепи RC , показанной на рисунке 6 , определите:
- Емкостное реактивное сопротивление конденсатора ( X C ).
- Ток через конденсатор ( I C ).

- Реактивная мощность конденсатора (ВАР).
- Ток через резистор ( I R ).
- Истинная мощность (Вт).
- Общий ток в линии ( I T ).
- Полное сопротивление цепи ( Z ).
- Полная мощность (ВА).
- Коэффициент мощности (PF).
- Фазовый угол цепи θ.
Рисунок 6 Схема для примера 3.
Решение:
- Шаг 1 902 10. Составьте таблицу и запишите все известные значения.
- Шаг 2 902 10. Рассчитайте емкостное реактивное сопротивление конденсатора и введите значение в таблицу.
- Шаг 3 902 10. Рассчитайте ток, протекающий через конденсатор, и введите значение в таблицу.
- Шаг 4 902 10.
 Рассчитайте реактивную мощность конденсатора и введите значение в таблицу.
Рассчитайте реактивную мощность конденсатора и введите значение в таблицу.
- Шаг 5 902 10. Рассчитайте ток, протекающий через резистор, и введите значение в таблицу.
- Шаг 6 902 10. Рассчитайте истинную мощность и введите значение в таблицу.
- Шаг 7 902 10. Рассчитайте общий ток линии и введите значение в таблицу.
- Шаг 8 902 10. Рассчитайте импеданс и введите значение в таблицу.
- Шаг 9 902 10. Рассчитайте полную мощность и введите значение в таблицу.
- Шаг 10. Рассчитайте коэффициент мощности и введите значение в таблицу.
- Шаг 11.
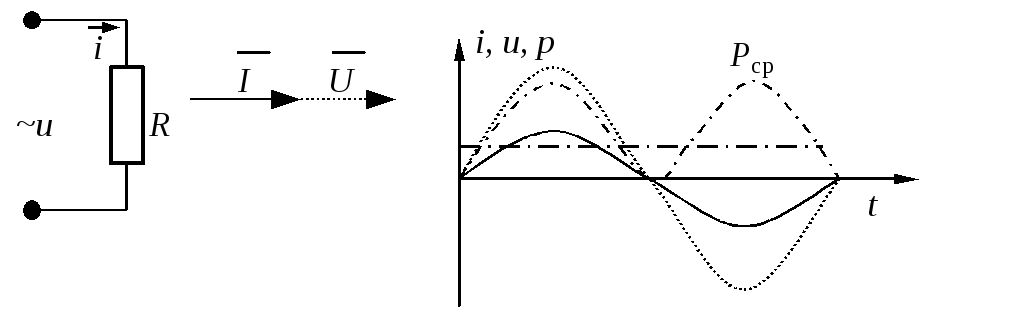 Рассчитайте фазовый угол цепи θ и введите значение в таблицу.
Рассчитайте фазовый угол цепи θ и введите значение в таблицу.
Контрольные вопросы
- В чем основное различие между параллельной схемой RL и RC ?
- Предположим, что сопротивление резистивного компонента параллельной цепи RC увеличено.Какое влияние это окажет на фазовый угол схемы?
- Параллельная цепь RC подключена к источнику 100 В, 60 Гц. Измеренный ток, протекающий через резистор, составляет 10 ампер. Измеренный ток, протекающий через конденсатор, составляет 10 ампер. Определите:
- Линейный ток ( I T ).
- Импеданс ( Z ).
- Истинная мощность (Вт).
- Реактивная мощность (ВАР).
- Полная мощность (ВА).
- ПФ в процентах.
- Для схемы, показанной на рисунке 7 , определите:
Рисунок 7 Схема для рассмотрения вопроса 4.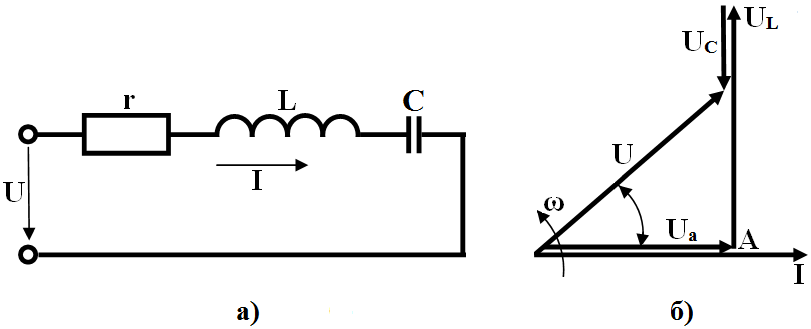
-
- Величина тока, протекающего через резистор.
- Емкостное реактивное сопротивление конденсатора.
- Величина тока, протекающего через конденсатор.
- Линейный ток.
- Полная мощность.
- ПФ в процентах.
5.Заполните таблицу для всех заданных и неизвестных величин для параллельной цепи RC , показанной на Рисунке 8 .
Рисунок 8 Цепь для контрольного вопроса 5.
Контрольные вопросы — ответы
- Принципиальная разница заключается в соотношении фаз. В чистом конденсаторе ток опережает напряжение на 90 °, в то время как в чистой катушке индуктивности ток отстает от напряжения на 90 °.
- Если сопротивление RC-цепи увеличивается, резистивный ток будет уменьшаться, цепь станет более емкостной, а фазовый угол станет больше.
- (а) 14,14 А, (б) 7,07 Ом, (в) 1000 Вт, (г) 1000 ВАр, (д) 1414 ВА, (е) 70,7%, опережение
- (а) 80 А, (б) 1,77 Ом, (в) 67,8 А, (г) 105 А, (д) 12600 ВА, (е) 76,2%, ведущий
| E | I | C | R / X C / Z | W / VA / VARs | PF | ||
| R | 440 V | 20 A | N / A | 2295 Ω | 2295 Ом 8800 Вт | 0 | |
| C | 440 V | 11. 1 A 1 A | 67 мкФ | 39,6 Ω | 4884 VAR | 90 | |
| Всего | 440 V | 22.9 A | N / A | 19.2 Ω 10076 VA 907 907 907 87,3% |
Как работает мост Уитстона для тензодатчиков?
Чтобы измерить деформацию с помощью тензодатчика сопротивления, он должен быть подключен к электрической цепи, способной измерять мельчайшие изменения сопротивления, соответствующие деформации.В тензодатчиках обычно используются четыре элемента тензодатчика, электрически соединенные для формирования мостовой схемы Уитстона (рис. 2-6).
Мост Уитстона — это схема с разделенным мостом, используемая для измерения статического или динамического электрического сопротивления. Выходное напряжение схемы моста Уитстона выражается в выходных милливольтах на входной вольт. Схема Уитстона также хорошо подходит для температурной компенсации.
Уравнение моста Уитстона: если R1, R2, R3 и R4 равны, а напряжение VIN приложено между точками A и C, то выходной сигнал между точками B и D не будет показывать разность потенциалов. Однако, если R4 изменить на некоторое значение, которое не равно R1, R2 и R3, мост станет несимметричным, и на выходных клеммах появится напряжение. В так называемой конфигурации G-моста датчик переменной деформации имеет сопротивление Rg, в то время как другие плечи представляют собой резисторы фиксированного значения.
Однако, если R4 изменить на некоторое значение, которое не равно R1, R2 и R3, мост станет несимметричным, и на выходных клеммах появится напряжение. В так называемой конфигурации G-моста датчик переменной деформации имеет сопротивление Rg, в то время как другие плечи представляют собой резисторы фиксированного значения.
Однако датчик может занимать одно, два или четыре плеча моста Уитстона, в зависимости от области применения. Общая деформация или выходное напряжение цепи (VOUT) эквивалентно разнице между падением напряжения на R1 и R4, или Rg.Это также можно записать как:
Подробнее см. Рисунок 2-6. Мост считается сбалансированным, если R1 / R2 = Rg / R3 и, следовательно, VOUT равен нулю.
Любое небольшое изменение сопротивления тензодатчика приведет к нарушению баланса моста, что сделает его пригодным для определения деформации. Когда мост настроен так, что Rg является единственным активным тензодатчиком, небольшое изменение Rg приведет к выходному напряжению с моста.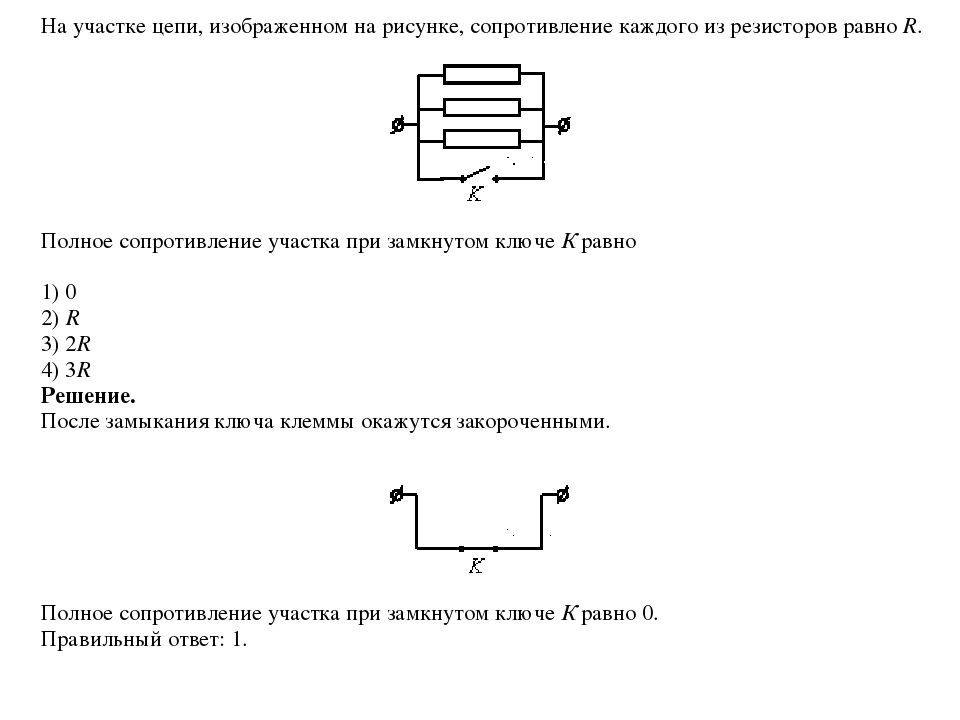 Если калибровочный коэффициент равен GF, измерение деформации связано с изменением Rg следующим образом:
Если калибровочный коэффициент равен GF, измерение деформации связано с изменением Rg следующим образом:
Количество активных тензодатчиков, которые необходимо подключить к мосту, зависит от области применения.Например, может быть полезно соединить датчики, которые находятся на противоположных сторонах балки, один при сжатии, а другой при растяжении. В такой конфигурации можно эффективно удвоить выходную мощность моста при той же деформации. В установках, где все рычаги подсоединены к тензодатчикам, температурная компенсация тензодатчиков выполняется автоматически, поскольку изменение сопротивления из-за колебаний температуры будет одинаковым для всех плеч моста Уитстона.
В четырехэлементном мосту Уитстона обычно два датчика соединены при сжатии и два — при растяжении.Например, если R1 и R3 находятся в состоянии растяжения (положительное), а R2 и R4 — в состоянии сжатия (отрицательное), то выходной сигнал будет пропорционален сумме всех деформаций, измеренных по отдельности. Для датчиков, расположенных на соседних опорах, мост становится неуравновешенным пропорционально разнице в деформации. Для датчиков на противоположных опорах мост уравновешивается пропорционально сумме деформаций. Независимо от того, измеряется ли деформация изгиба, осевая деформация, деформация сдвига или деформация кручения, устройство тензодатчика будет определять соотношение между выходной мощностью и типом измеряемой деформации.Как показано на рис. 2-6, если положительная деформация растяжения возникает на датчиках R2 и R3, а отрицательная деформация испытывается на датчиках R1 и R4, общий выходной сигнал, VOUT, будет в четыре раза больше сопротивления одного датчика. В этой конфигурации компенсируются температурные изменения измерителя пятна.
Схема моста Шеврон
Шевронный мост показан на Рисунке 2-7. Это многоканальная схема, которая служит для компенсации изменений сопротивлений перемычек путем их периодического переключения.Здесь четыре позиции каналов используются для переключения цифрового вольтметра (DVM) между конфигурациями G-моста (один активный датчик) и H-моста (два активных датчика). Измерительное устройство DVM всегда разделяет источник питания и внутренний H-мост. Эта конструкция наиболее популярна для измерения деформации вращающихся машин, где она может уменьшить количество требуемых контактных колец.
Четырехпроводная омическая цепь
Хотя схема моста Уитстона является одним из самых популярных методов измерения электрического сопротивления, можно использовать и другие методы.Основным преимуществом четырехпроводной схемы с сопротивлением Ом является то, что подводящие провода не влияют на измерение, поскольку напряжение регистрируется непосредственно на элементе тензодатчика.
Установка четырехпроводной омической схемы может состоять из вольтметра, источника тока и четырех выводных резисторов R1, соединенных последовательно с измерительным резистором Rg (рисунок 2-8). Вольтметр подключается к клеммам измерения сопротивления DVM, а источник тока подключается к клеммам источника сопротивления DVM.Для измерения величины деформации в цепь подается слабый ток (обычно один миллиампер). В то время как вольтметр измеряет падение напряжения на Rg, абсолютное значение сопротивления вычисляется мультиметром на основе значений тока и напряжения.
Измерение обычно выполняется, сначала измеряя значение сопротивления датчика в ненапряженном состоянии, а затем выполняя второе измерение с приложенной деформацией. Разница в измеренных сопротивлениях датчика, деленная на сопротивление без деформации, дает дробное значение деформации.Это значение используется с калибровочным коэффициентом (GF) для расчета деформации.
Четырехпроводная схема также подходит для автоматической компенсации смещения напряжения. Напряжение сначала измеряется при отсутствии тока. Это измеренное значение затем вычитается из показания напряжения при протекании тока. Полученная разность напряжений затем используется для вычисления сопротивления датчика. Из-за своей чувствительности четырехпроводные тензодатчики обычно используются для измерения низкочастотных динамических деформаций. При измерении деформаций более высоких частот необходимо усилить выходной сигнал моста.Эта же схема также может использоваться с полупроводниковым тензометрическим датчиком и высокоскоростным цифровым вольтметром. Если чувствительность ДВМ составляет 100 микровольт, источник тока — 0,44 миллиампера, сопротивление тензометрического элемента — 350 Ом и его коэффициент измерения — 100, то разрешающая способность измерения составит 6 микродеформаций.
Цепь постоянного тока
Сопротивление можно измерить, возбуждая мост постоянным напряжением или источником постоянного тока.Поскольку R = V / I, если либо V, либо I остается постоянным, другой будет изменяться в зависимости от сопротивления. Можно использовать оба метода.
Хотя нет теоретических преимуществ использования источника постоянного тока (рис. 2-9) по сравнению с постоянным напряжением, в некоторых случаях выход моста будет более линейным в системе постоянного тока. Кроме того, если используется источник постоянного тока, отпадает необходимость в измерении напряжения на мосту; поэтому к тензодатчику необходимо подключить только два провода.
Цепь постоянного тока наиболее эффективна при измерении динамической деформации. Это связано с тем, что, если динамическая сила вызывает изменение сопротивления тензодатчика (Rg), можно измерить изменяющуюся во времени составляющую выходного сигнала (VOUT), в то время как медленно меняющиеся эффекты, такие как изменение сопротивления выводов из-за температуры варианты будут отклонены. Используя эту конфигурацию, температурный дрейф становится практически незначительным.
Применение и установка
Выходной сигнал цепи тензодатчика представляет собой сигнал напряжения очень низкого уровня, требующий чувствительности 100 микровольт или выше.Низкий уровень сигнала делает его особенно восприимчивым к нежелательным шумам от других электрических устройств. Емкостная связь, вызванная слишком близким расположением выводных проводов к силовым кабелям переменного тока или токами заземления, является потенциальным источником ошибок при измерении деформации. Другие источники ошибок могут включать в себя магнитно-индуцированные напряжения, когда выводные провода проходят через переменные магнитные поля, паразитные (нежелательные) контактные сопротивления выводных проводов, нарушение изоляции и эффекты термопары на стыке разнородных металлов.Сумма таких помех может привести к значительному ухудшению качества сигнала.
Экранирование
Большинство проблем с электрическими помехами и шумом можно решить путем экранирования и защиты. Экран вокруг проводов измерительных выводов улавливает помехи, а также может уменьшить любые ошибки, вызванные ухудшением изоляции. Экранирование также защитит измерение от емкостной связи. Если измерительные провода проложены рядом с источниками электромагнитных помех, такими как трансформаторы, скручивание проводов сведет к минимуму ухудшение сигнала из-за магнитной индукции.При скручивании провода индуцированный магнитным потоком ток инвертируется, и области, которые пересекает магнитный поток, компенсируются. В промышленных процессах практически без исключения используются скрученные и экранированные подводящие провода.
Охрана
Защита самого оборудования так же важна, как и экранирование проводов. Ограждение представляет собой коробку из листового металла, окружающую аналоговую схему и соединенную с экраном. Если токи заземления протекают через тензометрический элемент или его подводящие провода, схема моста Уитстона не может отличить их от потока, создаваемого источником тока.Защита гарантирует, что клеммы электрических компонентов имеют одинаковый потенциал, что предотвращает протекание постороннего тока.
Подключение защитного провода между испытуемым образцом и отрицательной клеммой источника питания обеспечивает дополнительный путь тока вокруг измерительной цепи. При размещении защитного провода на пути тока, вызывающего ошибку, все задействованные элементы (т. Е. Плавающий источник питания, тензодатчик, все другое измерительное оборудование) будут иметь тот же потенциал, что и испытательный образец.Используя скрученные и экранированные подводящие провода и интегрируя цифровые видеомагнитофоны с защитой, можно практически устранить ошибку синфазного шума.
Эффекты отведений
Тензодатчики иногда устанавливают на расстоянии от измерительного оборудования. Это увеличивает вероятность ошибок из-за колебаний температуры, снижения чувствительности свинца и изменения сопротивления провода. В двухпроводной установке (рисунок 2-10A) два провода соединены последовательно с тензодатчиком, и любое изменение сопротивления подводящего провода (R1) будет неотличимо от изменений сопротивления тензодатчика. (Rg).
Чтобы скорректировать влияние проводов, можно ввести дополнительный третий вывод к верхнему плечу моста, как показано на Рисунке 2-10B. В этой конфигурации провод C действует как измерительный провод, по которому не течет ток, а провода A и B находятся на противоположных сторонах моста. Это минимально приемлемый метод подключения тензодатчиков к мосту, чтобы по крайней мере частично устранить влияние ошибок удлинительного провода. Теоретически, если подводящие провода к датчику имеют одинаковое номинальное сопротивление, одинаковый температурный коэффициент и поддерживаются при одинаковой температуре, достигается полная компенсация.На самом деле провода изготавливаются с допуском около 10%, а трехпроводная установка не исключает полностью двухпроводных ошибок, но снижает их на порядок. Если желательно дальнейшее улучшение, следует рассмотреть вариант четырехпроводной установки с компенсацией смещения (рисунки 2-10C и 2-10D).
В двухпроводных установках погрешность, вызванная сопротивлением выводного провода, является функцией отношения сопротивлений R1 / Rg. Ошибка вывода обычно не имеет значения, если сопротивление выводного провода (R1) мало по сравнению с сопротивлением датчика (Rg), но если сопротивление выводного провода превышает 0.1% от номинального сопротивления датчика, этот источник погрешности становится значительным. Поэтому в промышленных приложениях длину подводящих проводов следует минимизировать или исключить, располагая преобразователь непосредственно у сенсора.
Температура и манометрический коэффициент
Чувствительные к деформации материалы, такие как медь, изменяют свою внутреннюю структуру при высоких температурах. Температура может изменить не только свойства элемента тензодатчика, но также может изменить свойства основного материала, к которому прикреплен тензодатчик.Различия в коэффициентах расширения материала датчика и основного материала могут привести к изменению размеров чувствительного элемента. Следовательно, потребуется схема температурной компенсации.
Расширение или сжатие тензометрического элемента и / или основного материала приводит к ошибкам, которые трудно исправить. Например, изменение удельного сопротивления или температурного коэффициента сопротивления тензометрического элемента изменяет нулевую точку отсчета, используемую для калибровки устройства.
Измерительный коэффициент — это чувствительность датчика к деформации.Производитель всегда должен предоставлять данные о температурной чувствительности манометрического коэффициента. На рис. 2-11 показано изменение коэффициентов измерения для различных материалов тензодатчиков в зависимости от рабочей температуры. Медно-никелевые сплавы, такие как Advance, имеют калибровочные коэффициенты, которые относительно чувствительны к колебаниям рабочей температуры, что делает их наиболее популярным выбором для материалов для тензодатчиков.
Что такое чисто резистивная цепь? — Фазорная диаграмма и осциллограмма
Цепь, содержащая только чистое сопротивление R Ом в цепи переменного тока, известна как Чистая резистивная цепь переменного тока .Наличие индуктивности и емкости не существует в чисто резистивной цепи. Переменный ток и напряжение движутся как вперед, так и назад в обоих направлениях цепи. Следовательно, переменный ток и напряжение соответствуют форме синусоидальной волны или известной как синусоидальная форма волны.
Состав:
В чисто резистивной схеме мощность рассеивается резисторами, а фаза напряжения и тока остается прежней, т. Е., напряжение и ток одновременно достигают максимального значения. Резистор — это пассивное устройство, которое не производит и не потребляет электроэнергию. Он преобразует электрическую энергию в тепло .
Описание резистивной цепи
В цепи переменного тока отношение напряжения к току зависит от частоты источника питания, угла сдвига фаз и разности фаз. В резистивной цепи переменного тока значение сопротивления резистора будет одинаковым независимо от частоты питания.
Пусть переменное напряжение, приложенное к цепи, определяется уравнением
Тогда мгновенное значение тока, протекающего через резистор, показанное на рисунке ниже, будет:
Значение тока будет максимальным при ωt = 90 ° или sinωt = 1
Подставив значение sinωt в уравнение (2), мы получим
Фазовый угол и форма сигнала резистивной цепи
Из уравнений (1) и (3) ясно, что нет разницы фаз между приложенным напряжением и током, протекающим через чисто резистивную цепь, т.е.е. фазовый угол между напряжением и током составляет ноль . Следовательно, в цепи переменного тока, содержащей чистое сопротивление, ток находится в фазе с напряжением, как показано на рисунке ниже.
Форма волны и фазовая диаграмма чисто резистивной цепиПитание в чисто резистивной цепи
Три цвета: красный, синий и розовый, показанные на кривой мощности или на форме волны, обозначают кривую тока, напряжения и мощности соответственно. Из векторной диаграммы видно, что ток и напряжение находятся в фазе друг с другом, что означает, что значение тока и напряжения достигает своего пика в один и тот же момент времени, а кривая мощности всегда положительна для всех значений тока. и напряжение.
Как и в цепи питания постоянного тока, произведение напряжения и тока известно как мощность в цепи. Точно так же мощность такая же и в цепи переменного тока, с той лишь разницей, что в цепи переменного тока учитывается мгновенное значение напряжения и тока.
Следовательно, мгновенная мощность в чисто резистивной цепи определяется уравнением, показанным ниже:
Мгновенная мощность, p = vi
Средняя мощность, потребляемая в цепи за полный цикл, равна
Поскольку клапан cosωt равен нулю.
Итак, подставив значение cosωt в уравнение (4), значение мощности будет равно Где,
- P — средняя мощность
- В среднеквадратичное значение — среднеквадратичное значение напряжения питания
- I r.m.s — среднеквадратичное значение тока
Следовательно, мощность в чисто резистивной цепи определяется выражением:
Напряжение и ток в чисто резистивной цепи находятся в фазе друг с другом, имея отсутствие разности фаз с нулевым фазовым углом.Переменная величина достигает своего пикового значения в интервале одного и того же периода времени, когда повышение и падение напряжения и тока происходят одновременно.
Электронные нагрузки — новое поколение | Evaluation Engineering
Электронные нагрузки постоянного тока доступны для приложений электронного тестирования в течение нескольких десятилетий. Сегодняшняя продукция включает в себя переключаемые резисторы, высокоскоростные активные нагрузки, использующие силовые полупроводники, и рекуперативные нагрузки, которые возвращают энергию в сеть.Каждая технологическая группа находит свое применение в различных приложениях. В этой статье описываются некоторые преимущества и недостатки альтернативных технологий и представлена недавно разработанная гибридная топология схемы, предлагающая некоторые уникальные характеристики производительности.
Коммутируемые резистивные нагрузки
Самое старое поколение электронных нагрузок основано на переключении резистивных компонентов. В зависимости от уровня мощности резисторы обычно изготавливаются из стальных пластин, нихромовой проволоки или металлической пленки.Коммутируемые резистивные нагрузки имеют самую низкую стоимость ватт, но худшие характеристики с точки зрения динамического отклика, программируемости и защиты.
На рисунке 1 показаны две схемы, которые обычно используются с резистивной коммутацией. Две конфигурации отличаются своей способностью выбирать желаемую комбинацию резисторов, а не способностью рассеивать мощность.
Рисунок 1a , двоичная коммутация, обеспечивает наиболее точный выбор сопротивления для каждого количества компонентов.Резистор R2 имеет двойное сопротивление, чем резистор R1, R3 имеет двойное сопротивление, чем R2, и так далее. Эта схема часто используется в приложениях с низким энергопотреблением, чтобы получить цифро-аналоговое преобразование, где мощность не рассматривается. Мощность изменяется пропорционально квадрату приложенного напряжения, и как нагрузка двоичная коммутация показывает плохие характеристики с точки зрения рассеивания мощности при более низких уровнях напряжения. Двоичное переключение — лучший выбор для приложений, когда приложенное напряжение фиксировано.
Рисунок 1b , оптимизированное переключение мощности, позволяет размещать резисторы последовательно или параллельно, обеспечивая лучшую рассеиваемую мощность в более широком диапазоне приложенного напряжения.Недостатком по сравнению с двоичной коммутацией является то, что оптимизированная коммутация мощности имеет меньший выбор доступных настроек резистора на количество компонентов. С помощью трех переключателей максимальная рассеиваемая мощность может быть достигнута при половинном и полном номинальном напряжении. Также возможны другие конфигурации резисторов путем модуляции включенного состояния резистора с помощью имеющихся переключателей.
% {[data-embed-type = «image» data-embed-id = «5c3763a40114876c7c9585b8» data-embed-element = «aside» data-embed-align = «right» data-embed-alt = «1803instfig1» data- embed-src = «https: // img.ratingengineering.com/files/base/ebm/ee/image/2018/03/1803instfig1.png?auto=format&fit=max&w=1440 «data-embed-caption =» «]}% Рисунок 1. Бинарное переключение (a ) и оптимизированное переключение мощности (b)В системах постоянного тока и при использовании контакторов для коммутирующих устройств производительность обычно ограничивается номинальным постоянным током контактора. По соображениям стоимости контакторы переменного тока обычно используются для коммутации резисторных элементов, но с этими устройствами переключение ограничено низкими напряжениями, при которых искрение может быть сведено к минимуму.Это ограничение запрещает использование контакторной коммутации для приложений с мощной динамической нагрузкой. Кроме того, контакторы постоянного тока, хотя и доступны, редко используются из-за ограничений по стоимости и размерам. Использование силовых полупроводников в качестве переключающих элементов устраняет ограничения, накладываемые контакторами переменного тока, но они редко используются в пользу технологий нагрузки MOSFET.
Большинство электронных нагрузок с использованием резистивных элементов изготавливаются конечными пользователями, которым нужны мощные и недорогие решения для своих тестовых нужд, жертвуя динамической нагрузкой и возможностями программируемой защиты.
MOSFET нагрузки
Металлооксидные полевые транзисторы (MOSFET) могут использоваться в качестве современных электронных нагрузок для устранения ограничений резисторных нагрузок. Как показано на рис. 2 , в этих электронных нагрузках используются полупроводниковые устройства, работающие в линейной области, чтобы обеспечить полную мощность и полный контроль над всей номинальной мощностью продукта в ВА. МОП-транзисторы должны быть специально рассчитаны для работы в линейной области и иметь кривые безопасной работы, значительно ниже максимальной номинальной мощности при использовании в качестве электронного переключателя. 1, 2 Схема для нагрузок MOSFET требует, чтобы каждый каскад управлялся в замкнутом контуре для линеаризации отклика. Как показано на рисунке, каждое устройство производит ток нагрузки, определяемый величиной VC / Rn. Усилители с замкнутым контуром позволяют нескольким полевым МОП-транзисторам равномерно распределять ток нагрузки. Кроме того, нагрузки MOSFET обладают быстрым динамическим откликом.
% {[data-embed-type = «image» data-embed-id = «5c3763a40114876c7c9585b3» data-embed-element = «aside» data-embed-align = «right» data-embed-alt = «1803instfig2» data- embed-src = «https: // img.оценкаengineering.com/files/base/ebm/ee/image/2018/03/1803instfig2.png?auto=format&fit=max&w=1440 «data-embed-caption =» «]}% Рис. 2. Нагрузка MOSFETРегенеративная грузы
В последнее десятилетие регенеративные нагрузки начали появляться как жизнеспособный продукт. Рекуперативная нагрузка, в упрощенном смысле, представляет собой источник питания переменного тока в постоянный с измененной схемой питания, позволяющей току течь в обратном направлении. Время отклика аналогично источникам питания постоянного тока, и требуется специальная схема для остановки работы в случае отключения напряжения сети по какой-либо причине.Рекуперативные нагрузки можно сравнить с солнечными инверторами по производительности за исключением диапазона работы постоянного тока. Как и в случае нагрузок с переключаемыми резисторами, для достижения максимальной мощности в широком диапазоне напряжений требуется специальная схема, рассчитанная на максимальное напряжение и максимальный ток; такие требования к производительности могут значительно увеличить стоимость по сравнению с обычным импульсным источником питания.
Основным преимуществом регенеративных нагрузок является возможность рекуперации энергии, используемой для тестирования. Некоторые регенеративные нагрузки предназначены для работы как в качестве источника, так и в качестве поглотителя.Эти продукты, регенеративные источники питания, должны иметь двойной набор электронных переключателей.
Использование рекуперативных нагрузок в приложениях с импульсным током не рекомендуется, потому что любой импульсный ток на входе должен протекать через устройство и появляться в электросети. Экономику рекуперативных нагрузок необходимо оценивать с точки зрения капитальных затрат на оборудование по сравнению с экономией энергии.
Активные резистивные нагрузки
Активные резистивные нагрузки представляют собой смесь нагрузок с переключаемыми резисторами и нагрузок на полевых МОП-транзисторах.Преимущество резистивных нагрузок — это стоимость рассеиваемой мощности на ватт, а преимуществом нагрузок на полевых МОП-транзисторах является скорость работы и способность рассеивать мощность в широком диапазоне управления. На рисунке 3 показана основная концепция активной резистивной нагрузки. 3 Как показано, важной частью конструкции является то, что резисторы размещаются последовательно с полевыми МОП-транзисторами. МОП-транзисторы — это трансформаторы напряжения-токи. Возмущения напряжения, возникающие в результате переключения резисторов, компенсируются возмущениями обратного напряжения на полевых МОП-транзисторах.Усилители, используемые для распределения тока между устройствами, не должны быстро реагировать на эти изменения напряжения из-за профиля устройств MOSFET, когда они работают в качестве устройства крутизны. Постоянное напряжение затвора в активной области устройства обеспечивает почти постоянный ток.
% {[data-embed-type = «image» data-embed-id = «5c3763a40114876c7c9585b5» data-embed-element = «aside» data-embed-align = «right» data-embed-alt = «1803instfig3» data- embed-src = «https://img.evaluationengineering.com/files/base/ebm/ee/image/2018/03/1803instfig3.png? auto = format & fit = max & w = 1440 «data-embed-caption =» «]}% Рисунок 3. Активная резистивная нагрузкаДиапазон максимальной мощности нагрузки, как и в резистивных нагрузках, зависит от количества резисторов, количества переключателей и приложенного напряжения.Для достижения компромисса между количеством рассеивающих элементов и диапазоном максимальной мощности нагрузки применяются обе конфигурации резисторов, как показано на рис. 1a и 1b. Тщательная конструкция системы охлаждения может обеспечить максимальную выходную мощность с половинной номинальной до полного номинального напряжения.При достаточном количестве состояний переключения резистора рассеиваемая мощность может распределяться с соотношением 80% к 20% для рассеиваемой мощности резистора и полевого МОП-транзистора, соответственно.
Напряжение ниже половины номинального и, как описано ранее, максимальная рассеиваемая мощность изменяется пропорционально квадрату приложенного напряжения. Наличие последовательного подключения MOSFET позволяет получить более широкий профиль для приложений с более низким напряжением. Это требует, чтобы элементы резистора были закорочены. Если максимальная мощность ограничена 20% от общей мощности с использованием секции нагрузки MOSFET, эта часть нагрузки может обеспечить профиль максимальной мощности 20%.Хотя это не идеально, это эффективный компромисс с точки зрения рентабельности.
При закороченном МОП-транзисторе нагрузки электронная нагрузка становится чисто резистивной, и нагрузка работает в режиме реостата. Хотя это можно рассматривать как пониженную нагрузку, во многих приложениях желателен чисто резистивный профиль без управления с обратной связью. Динамически переключаемые состояния резистора исключают возможность срабатывания двух замкнутых контуров источника и нагрузки.Полоса пропускания ступенчатого изменения сопротивления зависит от скорости переключения резисторов. Активная резистивная нагрузка может обеспечивать 80% номинальной мощности нагрузки в диапазоне от половинного до полного номинального напряжения.
На рис. 4 показаны профили нагрузки полевого МОП-транзистора, резистивного и активного резистивного режимов.
Устойчивость — ключевая характеристика активных резистивных нагрузок. Ограничение тока постоянно включено с помощью последовательно включенного резистора. Внезапное изменение тока вызовет насыщение полевых МОП-транзисторов, защищая устройства от выхода за пределы их безопасной рабочей зоны.
Уравновешивание мощности между резисторами и полевыми МОП-транзисторами представляет собой одну из ключевых проблем для эффективной работы нагрузки с активным сопротивлением.Полевые МОП-транзисторы должны иметь диапазон напряжения для компенсации напряжений, создаваемых переключающими резисторами. Напряжение и ток нагрузки должны постоянно контролироваться для обеспечения изменений состояния резистора наряду с аналоговым управлением полевыми МОП-транзисторами. Высокоскоростные процессоры цифровых сигналов (DSP) необходимы для выполнения таких вычислений, чтобы гарантировать правильную работу. Для реакции на скачкообразную нагрузку требуется компенсация с прямой связью, чтобы вызвать изменение сопротивления перед изменением тока нагрузки с помощью полевых МОП-транзисторов. Если скачкообразные изменения сопротивления выполняются быстро, а полевые МОП-транзисторы заставляют срабатывать вскоре после этого, безопасная рабочая зона полевых МОП-транзисторов может быть сохранена для надежной работы.
Заключение
В этой статье представлен обзор доступных в настоящее время электронных нагрузок, а именно: коммутируемое сопротивление, полевой МОП-транзистор, рекуперативный, и недавно представленный гибридный модуль активного сопротивления. Каждая топология нагрузки имеет свои преимущества и недостатки, начиная от стоимости и скорости работы и заканчивая нагрузкой в зависимости от приложенного напряжения. Топология активного сопротивления сочетает в себе характеристики коммутируемого сопротивления и нагрузок MOSFET, а также работает независимо от других.
Список литературы
- Саттар, Абдус и Цуканов, Владимир, «МОП-транзисторы выдерживают нагрузку при работе в линейном режиме», Технология силовой электроники, апрель 2007 г., стр. 34–39.
- Додж, Дж., «Как заставить работать линейный режим», Bodo’s Power Systems, декабрь 2007 г.
- Пител И., Пител Г. и Пител А. «Электронные нагрузки», Патент США № 9 429 629.
Об авторе
Ира Дж.Pitel получил свой B.S. степень магистра Рутгерса, Государственный университет Нью-Джерси, степень магистра. степень Бакнеллского университета и его докторская степень. диплом Университета Карнеги-Меллона. С 1973 по 1976 год он работал в GTE Sylvania, изучая методы высокочастотного балласта для газоразрядного освещения. Он присоединился к Bell Laboratories в 1978 году и Exxon Enterprises в 1979 году. В Exxon он занимался конструкциями преобразователей большой мощности для приводов двигателей переменного тока и регулируемого освещения. В 1981 году он основал Magna-Power Electronics.
Ира имеет 29 патентов в области силовой электроники и является одним из соучредителей премии Society Prize Paper Award 1995 от Общества промышленных приложений. В 2000 году он был удостоен звания выдающегося выпускника инженерных наук Рутгерса. В 2008 году он получил премию Джеральда Климана за новаторство. Он является членом IEEE и занимал различные должности в IEEE, включая президента Общества отраслевых приложений. Он является членом Eta Kappa Nu и Tau Beta Pi.
Резисторы в цепях переменного тока | Мощность, напряжение и ток переменного тока
Введение
При постоянном токе (DC) поток электрического заряда является однонаправленным.В постоянном токе напряжение и ток поддерживают постоянную полярность и направление. Источником постоянного тока является аккумулятор. С другой стороны, при переменном токе (AC) поток электрического заряда периодически меняет направление на противоположное. В переменном токе напряжение меняет полярность с положительной на отрицательную и наоборот с течением времени. Это изменение полярности напряжения происходит из-за изменения направления тока. офисы, промышленность и т.д.
Наиболее распространенной формой питания переменного тока является синусоидальная волна. Математическая функция, описывающая типичное переменное напряжение:
В (t) = VMax sin ωt.
В (t) — напряжение в зависимости от времени. Напряжение меняется со временем.
t — переменное время в секундах.
VMax — пиковое значение, которого синусоидальная волна может достигать как в положительном, так и в отрицательном направлениях. Для положительного цикла это VMax, а для отрицательного — -VMax.
ω — угловая частота.ω = 2πf.
f — частота синусоидальной волны.
В цепях постоянного тока расчет тока, напряжения и мощности выполняется по закону Ома. Здесь предполагается, что полярности напряжения и тока постоянны.
В случае чисто резистивных цепей переменного тока значениями индуктивности и емкости можно пренебречь. Следовательно, расчет тока, напряжения и мощности будет следовать тем же принципам закона Ома и законов цепи Кирхгофа. Разница заключается в использовании мгновенного значения от пика до пика или среднеквадратичного значения.
Резистор с питанием постоянного и переменного тока
Резистор является пассивным устройством. Он не потребляет и не производит энергии. Энергия здесь — это электрическая энергия. Но резистор рассеивает электрическую энергию в виде тепла.
Резистор с источником питания постоянного тока указан ниже
В резистивных цепях постоянного тока сопротивление, которое представляет собой отношение напряжения к току, является линейным.
Резистор с источником питания переменного тока указан ниже.
В цепях переменного тока отношение напряжения к току в основном зависит от частоты питания f и сдвига фаз φ.Следовательно, термин импеданс используется в цепях переменного тока для обозначения сопротивления, поскольку оно обладает как величиной, так и фазой, в отличие от сопротивления в цепях постоянного тока, где оно имеет только величину. Символ сопротивления — Z.
Фазовое соотношение V-I в чисто резистивной цепи переменного тока
Значение сопротивления резистора в цепях переменного и постоянного тока одинаково независимо от частоты напряжения питания переменного тока. Изменение направления тока в сети переменного тока не влияет на поведение резисторов.Таким образом, ток в резисторе будет расти и падать в зависимости от напряжения, когда он растет и падает.
Напряжение и ток в резистивной цепи переменного тока достигают максимума, затем падают до нуля и одновременно достигают минимума. Говорят, что они находятся «в фазе», поскольку они поднимаются и опускаются в одно и то же время.
Рассмотрим следующую цепь переменного тока.
Здесь ток I (t) = IMax sin ωt.
Напряжение V (t) = VMax sin ωt. => V (t) = IMax R sin ωt.
Поскольку схема является чисто резистивной, влияние индуктивности и емкости незначительно, а разность фаз равна 0.
Следовательно, соотношение между напряжением и током в резисторе, который является частью резистивной цепи переменного тока, составляет
Мгновенные значения токов и напряжений «синфазны» по оси x кривой. Они поднимаются и опускаются одновременно и достигают своих максимальных и минимальных значений точно в одно и то же время. Это означает, что их фазовый угол θ = 00.Векторная диаграмма, представляющая этот фазовый угол, вместе со сравнением максимальных и минимальных значений напряжения и тока, показана ниже.
Расчет мощности, напряжения и тока переменного тока
Мгновенные значения тока и напряжения в резистивной цепи переменного тока можно использовать для определения сопротивления в его омической форме с помощью закона Ома.
Рассмотрим следующую резистивную схему с питанием переменного тока.
Пусть напряжение питания V (t) = VMax sin ωt подключено к резистору R.
Пусть мгновенное напряжение на резисторе будет V R .
Пусть I R будет мгновенным током, протекающим через резистор.
Поскольку приведенная выше схема является чисто резистивной по своей природе, можно применить принципы Ома.
Согласно закону Ома, напряжение на резисторе в момент t равно
В R = В Макс sin ωt.
Аналогично, ток, протекающий через резистор в момент t, может быть определен с использованием закона Ома как
I R = V R / R
Но V R = V Max sin ωt.
Следовательно, I R = (V Max * sin ωt) / R
Но значение V Max / R не что иное, как максимальный ток в цепи, обозначенный I Max ..
Следовательно I R = I Макс sin ωt.
В чисто резистивной последовательной цепи переменного тока полное напряжение цепи равно сумме напряжений отдельных резисторов, потому что все отдельные напряжения синфазны в чисто резистивной цепи. Аналогичным образом, полный ток в чисто резистивной параллельной цепи. Цепь переменного тока — это сумма токов отдельных ветвей всех параллельных резистивных ветвей.
Для расчета мощности в цепи переменного тока важную роль играет коэффициент мощности. Коэффициент мощности определяется как косинус фазового угла между током и напряжением. Фазовый угол обозначается символом φ.
Если P — активная мощность в цепи, измеренная в ваттах, а S — полная мощность цепи, измеренная в вольтах-амперах, соотношение между реальной мощностью и полной мощностью определяется выражением
P = S Cos φ.
В случае чисто резистивных цепей переменного тока фазовый угол между током и напряжением составляет 0 0 .Следовательно, φ = 0 0 . Следовательно, коэффициент мощности Cos φ равен Cos 0 0 = 1.
Следовательно, активная мощность равна полной мощности, которая является произведением напряжения и тока.
В чисто резистивных цепях переменного тока мощность в любой момент в цепи может быть определена путем вычисления произведения напряжения и тока в этот момент.
Мощность, потребляемая вышеупомянутой схемой, может быть рассчитана с использованием
P = V RMS * I RMS * Cos φ.
Поскольку φ = 0 0 в этом случае мощность равна
P = V RMS * I RMS
Мощность в чистом сопротивлении
В случае чисто резистивных цепей переменного тока мощность, потребляемая схемой, является просто произведением напряжения и тока, поскольку между током и напряжением нет фазового угла.
Форма сигнала мощности для чисто резистивной цепи переменного тока показана ниже.
Форма сигнала мощности состоит из серии положительных импульсов.Это потому, что, когда и напряжение, и ток положительны в первом полупериоде, их произведение, которое является мощностью, также положительно. А когда и напряжение, и ток отрицательны во втором полупериоде, их производительная мощность снова становится положительной (-V x -I = + P). Следовательно, значение мощности всегда больше или равно нулю.
Из приведенного выше сигнала видно, что мощность возрастает по мере увеличения как напряжения, так и тока и достигает своего максимума, когда и напряжение, и ток достигают своего максимума.Затем он падает до нуля, когда напряжение и ток падают до нуля. При изменении полярности напряжения и тока значение мощности снова возрастает и достигает максимума, когда напряжение и ток достигают своего отрицательного пика. Когда напряжение и ток падают до нуля, значение мощности падает до нуля.
В случае чисто резистивной цепи с источником питания переменного тока RMS рассеиваемая мощность такая же, как и в случае резистора, подключенного к источнику питания постоянного тока.
P = VRMS * IRMS = I2RMS * R = V2RMS / R.
VRMS и IRMS — действующие значения напряжения и тока соответственно.
P — мощность в ваттах.
R — сопротивление в Ом (Ом)
Для сравнения эффектов нагрева, вызванных переменным и постоянным током, постоянный ток следует сравнивать со среднеквадратичным значением переменного тока, но не с максимальным или пиковым током IMAX¬.
Резисторы в цепях переменного тока Примеры
Пример 1
Рассмотрим следующую схему.
Нагревательный элемент резистивной природы подключен к источнику переменного тока напряжением 240 В.Мощность, потребляемая нагревательным элементом, составляет 1,2 КВт. Значение его сопротивления можно рассчитать как
Ток, протекающий через нагревательный элемент, равен
I = P / V
P = 1,2 КВт = 1200 Вт.
В = 240 В.
Следовательно, I = 1200/240 = 5 ампер.
Значение сопротивления нагревательного элемента можно рассчитать по закону Ома как
R = V / I
R = 240/5 = 48 Ом.

