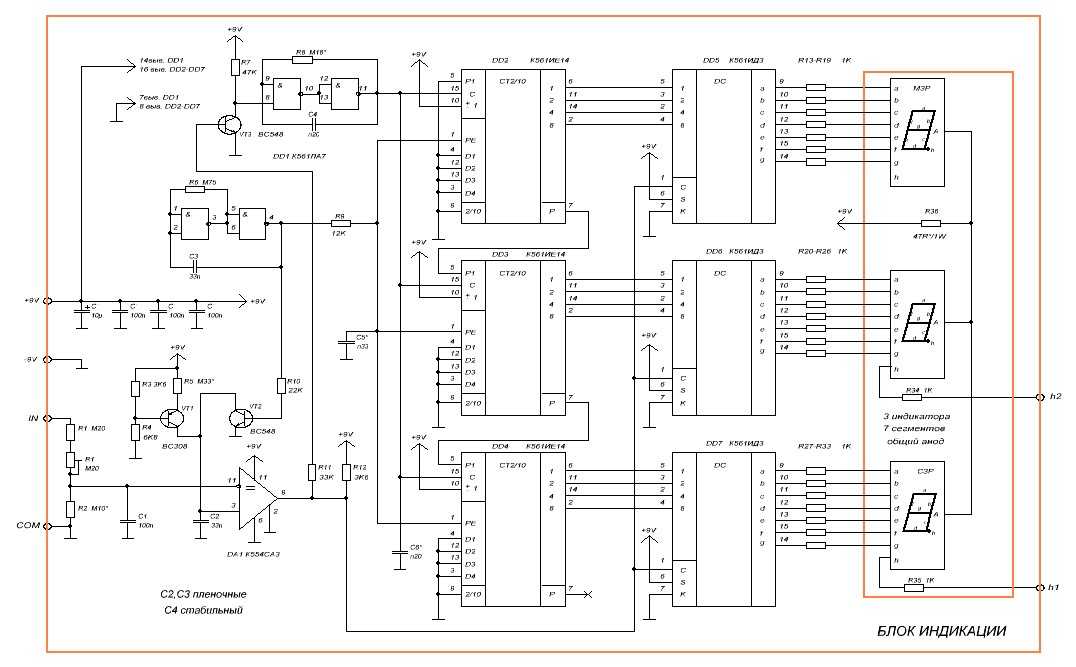
Как работает электросхема ОЗУ с подсчетом импульсов. Какие компоненты используются в такой схеме. Для чего применяется ОЗУ с портами ввода/вывода и таймером. Как реализовать счетчик импульсов на базе ОЗУ.
Принцип работы ОЗУ с подсчетом импульсов
Оперативное запоминающее устройство (ОЗУ) с функцией подсчета импульсов представляет собой специализированную схему, объединяющую в себе возможности хранения данных и счета электрических импульсов. Рассмотрим основные принципы работы такой системы:
- ОЗУ используется для временного хранения данных и промежуточных результатов вычислений
- Счетчик импульсов подключается к входу ОЗУ и регистрирует количество поступивших сигналов
- Результат счета сохраняется в выделенной области памяти ОЗУ
- Порты ввода/вывода обеспечивают взаимодействие ОЗУ с внешними устройствами
- Таймер позволяет задавать интервалы подсчета импульсов
Такая архитектура позволяет эффективно сочетать функции хранения и обработки данных в рамках одной системы. Как это работает на практике.

Ключевые компоненты схемы ОЗУ с подсчетом импульсов
В состав электросхемы ОЗУ с функцией подсчета импульсов обычно входят следующие основные элементы:
- Микросхема ОЗУ (например, КР1821РУ55) — обеспечивает хранение данных
- Счетчик импульсов — подсчитывает входящие сигналы
- Порты ввода/вывода — обеспечивают интерфейс с внешними устройствами
- Таймер — задает интервалы подсчета
- Дешифратор адреса — определяет область памяти для записи результатов
- Схема управления — координирует работу всех узлов
Рассмотрим подробнее роль каждого из этих компонентов в работе системы.
Функции портов ввода/вывода в схеме ОЗУ
Порты ввода/вывода играют важную роль в организации взаимодействия ОЗУ с внешними устройствами:
- Обеспечивают передачу данных между ОЗУ и другими компонентами системы
- Позволяют программно управлять работой ОЗУ
- Дают возможность считывать результаты подсчета импульсов
- Обеспечивают настройку параметров работы схемы
Как правило, используются 8-битные параллельные порты, которые могут работать на вход и на выход. Это позволяет гибко конфигурировать систему под различные задачи.

Применение таймера в схеме ОЗУ с подсчетом импульсов
Таймер выполняет важные функции в работе схемы ОЗУ с подсчетом импульсов:
- Задает интервалы времени для подсчета импульсов
- Формирует сигналы для синхронизации работы всех узлов
- Обеспечивает периодический опрос состояния счетчика
- Позволяет задавать частоту записи результатов в память
Использование программируемого таймера дает возможность гибко настраивать работу схемы под конкретные задачи. Как это реализуется на практике.
Реализация счетчика импульсов на базе ОЗУ
Рассмотрим основные этапы реализации счетчика импульсов с использованием ОЗУ:
- Подключение счетчика к входу ОЗУ через порт ввода
- Настройка таймера на требуемый интервал подсчета
- Выделение области памяти ОЗУ для хранения результатов
- Программирование алгоритма считывания и обработки данных
- Организация вывода результатов через порт вывода
Такой подход позволяет создать гибкую систему подсчета импульсов с возможностью программной настройки параметров работы.
Преимущества использования ОЗУ для подсчета импульсов
Применение ОЗУ в схемах подсчета импульсов дает ряд существенных преимуществ:
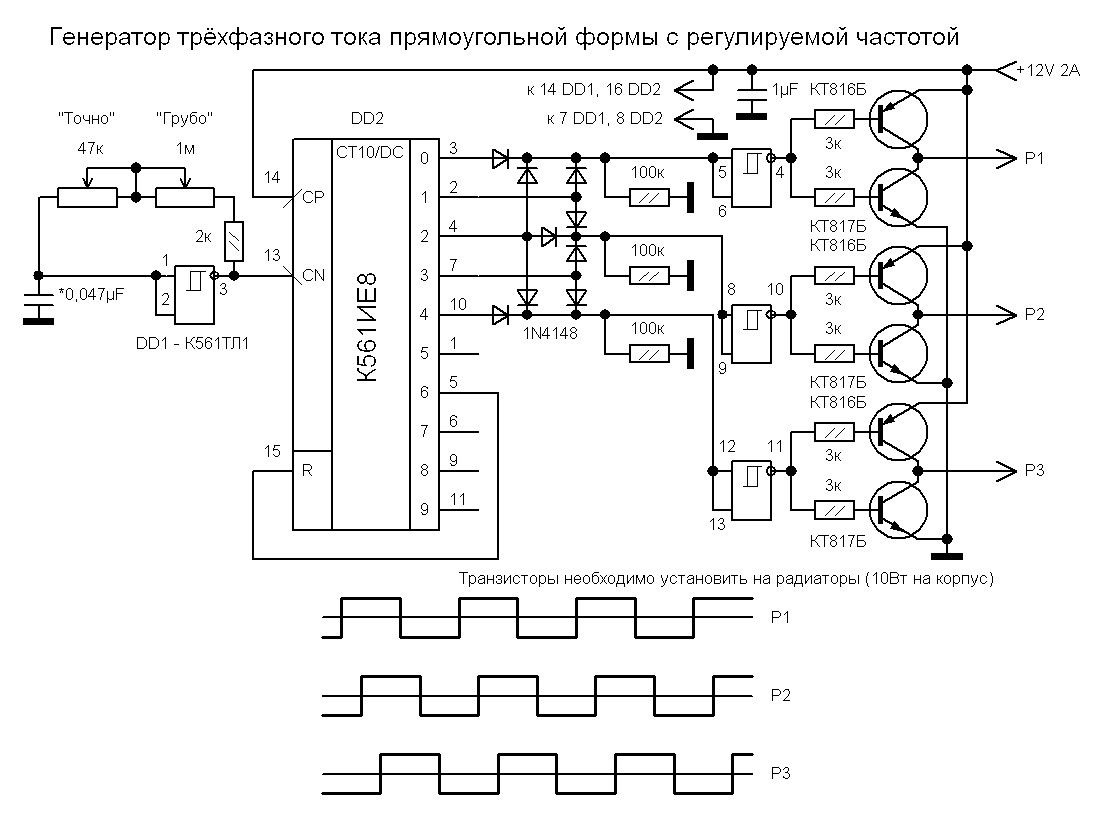
- Высокая скорость работы за счет быстродействия ОЗУ
- Возможность хранения промежуточных результатов
- Гибкость настройки параметров работы
- Простота сопряжения с микропроцессорными системами
- Возможность программной обработки результатов
Это делает такие схемы эффективным решением для широкого спектра задач, связанных с подсчетом и обработкой импульсных сигналов.
Области применения ОЗУ с функцией подсчета импульсов
Схемы ОЗУ с возможностью подсчета импульсов находят применение во многих областях:
- Измерительная техника
- Системы автоматического управления
- Телекоммуникационное оборудование
- Медицинская электроника
- Научное приборостроение
Рассмотрим некоторые конкретные примеры использования таких схем в различных устройствах и системах.
Как реализовать простой счетчик импульсов на базе ОЗУ?
Для реализации простого счетчика импульсов на базе ОЗУ можно использовать следующий алгоритм:
- Подключить выход счетчика импульсов к порту ввода ОЗУ
- Настроить таймер на требуемый интервал подсчета (например, 1 секунду)
- По прерыванию от таймера считывать значение счетчика через порт ввода
- Сохранять считанное значение в выделенной ячейке памяти ОЗУ
- Обнулять счетчик импульсов
- Повторять шаги 3-5 для накопления статистики
Такой алгоритм позволяет реализовать базовую функцию подсчета импульсов с использованием стандартных компонентов ОЗУ. При необходимости его можно дополнить более сложной обработкой данных.
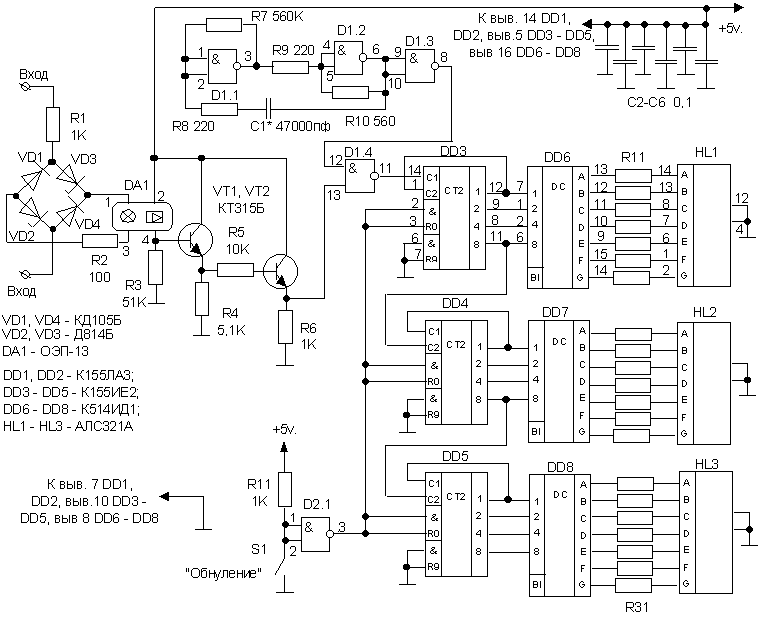
Как работает оперативная память компьютера (RAM, ОЗУ) — Железо на DTF
Строение оперативной памяти (видео)
5122 просмотров
Оперативная память это важная часть любой компьютерной системы и сейчас я объясню, почему это так.
Оперативная память (RAM)
В процессе работы память выступает в качестве буфера между накопителем и процессором, то есть данные сперва считываются с жесткого диска (или другого накопителя) в оперативную память и уже затем обрабатываются центральным процессором. Такая схема применяется, потому что процессор — очень быстрое устройство и ему требуется быстро получать доступ к нужным данным и командам, иначе он будет простаивать и производительность системы уменьшится, а так как жёсткий диск и SSD не могут обеспечить необходимую скорость, все нужные данные считываются и перемещаются в более быструю оперативную память и хранятся там, пока не понадобятся процессору для обработки.
Упрощённая схема работы памяти компьютера
Физически, оперативная память представляет собой набор микросхем припаянных к плате. Если посмотреть внутрь одной такой микросхемы, можно увидеть что она состоит из множества, соединённых друг с другом слоёв, каждый слой состоит из огромного количества ячеек, образующие прямоугольные матрицы.
Микросхемы на планке памяти
Одна ячейка может содержать 1 бит информации, а состоит она из одного полевого транзистора и одного конденсатора.
Устройство ячейки в чипе
Выглядит эта конструкция довольно сложно и может различаться в зависимости от применённых технологий, так что для наглядности лучше представить ячейку в виде схемы.
Схематичное устройство ячейки динамической памяти
Так легче понять, что именно конденсатор хранит информацию, а транзистор выполняет роль электрического ключа, который либо удерживает заряд на конденсаторе, либо открывает для считывания. Когда конденсатор заряжен, можно получить логическую единицу, а когда разряжен, ноль. Таких конденсаторов в чипе, очень много но считать заряд с одной конкретной ячейки нельзя, считывается вся страница целиком.
Когда конденсатор заряжен, можно получить логическую единицу, а когда разряжен, ноль. Таких конденсаторов в чипе, очень много но считать заряд с одной конкретной ячейки нельзя, считывается вся страница целиком.
Упрощённая схема массива ячеек, страница
Чтобы сделать это необходимо на нужную нам горизонтальную линию которая называется строка, подать сигнал, который откроет транзисторы, после чего усилители расположенные на концах вертикальных линий считают заряды которые находились на конденсаторах.
Упрощённая схема массива ячеек
Каждое такое считывание опустошает заряды на странице, из-за чего приходится её заново переписывать, для этого на строку так же подаётся открывающий транзистор заряд, а на столбцы подаётся более высокое напряжение, тем самым заряжая конденсаторы и записывая информацию. Задержки между этими операциями называются таймингами, чем они меньше тем более быстрая будет вся система в целом
Но вернёмся к модулю памяти в макро масштабе и посмотрим что, помимо самих чипов памяти, на модуль распаиваются SMD-компоненты резисторы и конденсаторы обеспечивающие развязку сигнальных цепей и питание чипов, а также Микросхема SPD – это специальная микросхема, в которой хранятся данные о параметрах всего модуля (ёмкость, рабочее напряжение, тайминги, число банков и так далее).
Компоненты плашки памяти, микросхема SPD
Так же существует несколько форм факторов модулей, модули для компьютеров называются DIMM, а для ноутбуков и компактных систем SO-DIMM, отличаются они размером и количеством контактов для подключения. Это двухрядные модули которые имеют два независимых ряда контактов по одному с каждой стороны.
DIMM и SO-DIMM
Например в старых модулях Simm контакты с двух сторон были замкнуты и они могли передать только 32 бита информации за такт, в то время как dimm могут передавать 64 бита.
DIMM и SIMM
Ко всему этому модули делятся на одноранговые, двухранговые и четырёхранговые. Ранг — это блок данных шириной 64 бита, который может быть набран разным количеством чипов память.
Ранги оперативной памяти
Так же хочется отдельно сказать о памяти с коррекцией ошибок, ECC-памяти, так как эти модули имеют дополнительный банк памяти на каждые 8 микросхем. Дополнительные банки и логика в модуле служат для проверки и устранения ошибок.
ECC- память с коррекцией ошибок
Использование буферов и коррекции ошибок незначительно ухудшает производительность, но сильно повышает надёжность данных. Поэтому ECC память широко используется в серверах и рабочих станциях
Ширина данных у ECC
Ещё немного расскажу о типах памяти, так как в современных компьютерах используется синхронная динамическая память с произвольным доступом и удвоенной скоростью передачи данных DDR SDRAM 4-го поколения и скоро будет распространено пятое.
Синхронная динамическая память (DDR)
Память типа ddr пришла на смену памяти типа SDR. SDR SDRAM работает синхронно с контроллером. В ней внутренняя и внешняя шина данных работает на одной и той же частоте. При подаче сигнала на микросхему происходит синхронное считывание информации и передача её в выходной буфер. Передача каждого бита из буфера происходит с каждым тактом работы ядра памяти. В SDR памяти синхронизация обмена данными происходит по фронту тактового импульса.
Синхронная динамическая память (SDR)
При подаче сигнала на микросхему происходит синхронное считывание информации и передача её в выходной буфер. Передача каждого бита из буфера происходит с каждым тактом работы ядра памяти. В SDR памяти синхронизация обмена данными происходит по фронту тактового импульса.
SDR (Схема)
После SDR, вышла DDR память, в ней обмен данными по внешней шине идет не только по фронту тактового импульса, но и по спаду, из-за чего на той же частоте можно передать вдвое больше информации, а чтобы воспользоваться этим увеличением, внутреннею шину расширили вдвое.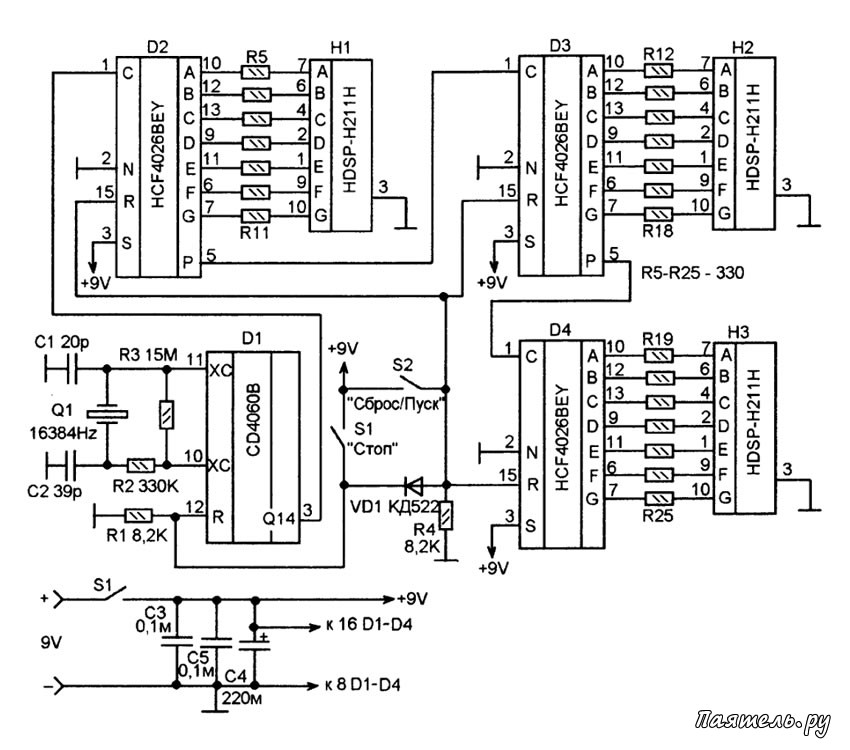 То есть работая на тех же частотах что SDR, DDR память передаёт в 2 раза больше данных.
То есть работая на тех же частотах что SDR, DDR память передаёт в 2 раза больше данных.
SDR и DDR (Схема)
Следующие поколения памяти DDR не сильно отличаются, увеличивается только частота работы буферов ввода вывода, а также расширяется шина, связывающая ядро памяти с буферами, сам принцип работы не меняется, но даже так, каждое новое поколение получает таким способом существенное увеличение пропускной способности, без увеличения частоты работы самих ячеек памяти.
(Схема) DDR 2, DDR 3, DDR 4, DDR 5
Понятно что с каждый новым поколением улучшается работа логики, техпроцесс и многое другое. Но сам принцип работы остаётся одним и для общего понимая этого достаточно.
Счетчикив цифровой логике — GeeksforGeeks
Счетчик — это устройство, которое хранит (и иногда отображает) количество раз, когда произошло определенное событие или процесс, часто по отношению к тактовому сигналу. Счетчики используются в цифровой электронике для целей подсчета, они могут подсчитывать определенные события, происходящие в цепи. Например, в счетчике UP счетчик увеличивает счет для каждого нарастающего фронта тактового сигнала. Помимо подсчета, счетчик может следовать определенной последовательности, основанной на нашем дизайне, как любая случайная последовательность 0,1,3,2…. Они также могут быть разработаны с помощью триггеров. Они используются в качестве делителей частоты, где частота заданной формы импульса делится. Счетчики представляют собой последовательные схемы, которые подсчитывают количество импульсов как в двоичном, так и в двоично-десятичном коде. Основными свойствами счетчика являются синхронизация, последовательность и подсчет. Счетчик работает в двух режимах
Счетчики используются в цифровой электронике для целей подсчета, они могут подсчитывать определенные события, происходящие в цепи. Например, в счетчике UP счетчик увеличивает счет для каждого нарастающего фронта тактового сигнала. Помимо подсчета, счетчик может следовать определенной последовательности, основанной на нашем дизайне, как любая случайная последовательность 0,1,3,2…. Они также могут быть разработаны с помощью триггеров. Они используются в качестве делителей частоты, где частота заданной формы импульса делится. Счетчики представляют собой последовательные схемы, которые подсчитывают количество импульсов как в двоичном, так и в двоично-десятичном коде. Основными свойствами счетчика являются синхронизация, последовательность и подсчет. Счетчик работает в двух режимах
UP Счетчик
Стра счетчик
Счетчик классификации
Счетчики широко разделены на две категории
- Asynchronous
- Синхронный счет
 Мы можем понять это, следуя схеме-
Мы можем понять это, следуя схеме-
Из временной диаграммы видно, что Q0 изменяется, как только встречается нарастающий фронт тактового импульса, Q1 изменяется, когда встречается нарастающий фронт Q0 (поскольку Q0 похож на тактовый импульс для второго триггера) и так далее. Таким образом, пульсации генерируются через Q0, Q1, Q2, Q3, поэтому он также называется счетчиком RIPPLE . Счетчик пульсаций представляет собой каскадное расположение триггеров, при котором выход одного триггера управляет тактовым входом следующего триггера
2. Синхронный счетчик
В отличие от асинхронного счетчика синхронный счетчик имеет один глобальный тактовый сигнал, который управляет каждым триггером, поэтому выходные данные изменяются параллельно. Одно из преимуществ синхронного счетчика по сравнению с асинхронным счетчиком заключается в том, что он может работать на более высокой частоте, чем асинхронный счетчик, поскольку он не имеет кумулятивной задержки, поскольку на каждый триггер задается один и тот же тактовый сигнал.
Схема синхронного счетчика
Временная диаграмма синхронного счетчика зависит от Q2, Q1 и Q0.
Счетчик декад
Счетчик декад подсчитывает десять различных состояний, а затем сбрасывается в исходное состояние. Простой декадный счетчик будет считать от 0 до 9.но мы также можем сделать десятичные счетчики, которые могут проходить любые десять состояний от 0 до 15 (для 4-битного счетчика).
| Clock pulse | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
Truth table для простого десятичного счетчика
Принципиальная схема декадного счетчика
Из принципиальной схемы видно, что мы использовали вентиль n-and для Q3 и Q1 и подали его на очистку входной линии, потому что двоичное представление 10:
1010
И мы видим, что Q3 и Q1 здесь равны 1, если мы зададим NAND из этих двух битов для очистки ввода, тогда счетчик будет очищен на 10 и снова начнется с начала.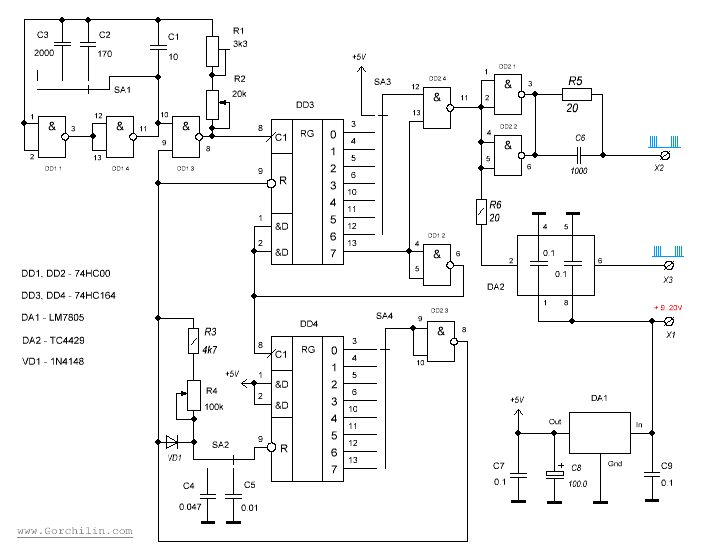
Важный момент : Количество триггеров, используемых в счетчике, всегда больше, чем равно ( log 2 n ), где n = количество состояний в счетчике.
Вопросы по счетчикам за предыдущие годы
Q1. Рассмотрим частичную реализацию 2-битного счетчика с использованием триггеров T, следующих за последовательностью 0-2-3-1-0, как показано ниже 9.0004
Для завершения схемы вход X должен быть
(A) Q2?
(B) Q2 + Q1
(C) (Q1 ? Q2)’
(D) Q1 ? Q2 (Gate-CS-2004)
Решение:
Из цепи мы видим
T1 = XQ1 ‘+X’Q1 — (1)
и
T2 = (Q2? Q1)’- -(2)
И ТРЕБУЕМЫЙ ВЫВОД 00->10->11->01->00
SO X ДОЛЖЕН БЫТЬ Q1Q2’+Q1’Q2 УДОВЛЕТВОРИТЕЛЬНО 1 И 2.
ТАКОЕ ОТВЕТ (D) ЧАСТЬ.
Q2. Ниже приведены функции управляющих сигналов 4-битного двоичного счетчика (где X означает «все равно»)
Счетчик подключается следующим образом: незначительны. Если счетчик начинается с 0, то он циклически повторяет следующую последовательность:
(А) 0,3,4
(Б) 0,3,4,5
(В) 0,1,2,3,4 9 0
9 , 1,2,3,4,5 (Gate-CS-2007)Решение:
Изначально A1 A2 A3 A4 = 0000
CLR = A1 и A3
, поэтому A1 и A3 оба являются 1 он снова переходит к 0000
Следовательно, 0000(инициал.) -> 0001(A1 и A3=0) -> 0010 (A1 и A3=0) -> 0011(A1 и A3=0) -> 0100 ( A1 и A3=1 )[ условие очистки выполнено] ->0000(инициал.), поэтому он проходит через 0->1->2->3->4
Ответ — часть (C).
Тест по цифровой логике
Статья предоставлена Ануджем Батамом, Пожалуйста, пишите комментарии, если вы обнаружите что-то неверное или хотите поделиться дополнительной информацией по теме, обсуждавшейся выше
Построение двоичного счетчика
Двоичный счетчик электронный компонент, который записывает, сколько раз он получил импульс. Это называется двоичный , потому что он хранит число в двоичном представлении. Счетчики абсолютно повсеместны в электронике и могут использоваться для создания схем, начиная от микросхем памяти и заканчивая декодерами FM-радио.
Это называется двоичный , потому что он хранит число в двоичном представлении. Счетчики абсолютно повсеместны в электронике и могут использоваться для создания схем, начиная от микросхем памяти и заканчивая декодерами FM-радио.
Поскольку счетчики очень полезны, я подумал, что было бы интересно реализовать их, используя только базовые логические элементы, такие как НЕ-И и ИЛИ. В качестве практического применения я подключил 1-битный счетчик к часам и пару светодиодов для создания генератора случайных битов:
Выход счетчика подключен к двум светодиодам. Один из них загорается, когда счетчик находится в состоянии 0, а другой загорается в состоянии 1. Когда кнопка нажата, часы начинают посылать около 100 импульсов в секунду, в результате чего счетчик колеблется между 0 и 1. Когда кнопка отпускается, таймер останавливается, а счетчик остается в своем последнем состоянии, как указано соответствующим ВЕЛ. Состояние сохраняется до следующего нажатия кнопки.
Поскольку колебания очень быстрые по сравнению с человеческими рефлексами, светодиод, который продолжает гореть после каждого отпускания кнопки, кажется выбранным случайным образом, причем каждый светодиод появляется с равной вероятностью. Другими словами, можно представить себе эту схему как имитацию подбрасывания монеты, где один из светодиодов представляет орел, а другой — решку. В конце поста я приведу некоторые доказательства того, что два исхода действительно равновероятны.
Другими словами, можно представить себе эту схему как имитацию подбрасывания монеты, где один из светодиодов представляет орел, а другой — решку. В конце поста я приведу некоторые доказательства того, что два исхода действительно равновероятны.
Основная цель этого поста — объяснить, как сделать 1-битный счетчик из простых логических вентилей. После этого мы подробно рассмотрим полную схему генератора случайных битов, показанную выше. В заключение мы покажем, как несколько однобитных счетчиков можно легко соединить вместе для получения более крупных счетчиков, таких как полезный 8-битный счетчик.
Вот общая схема однобитового двоичного счетчика, который мы хотим построить:
Теперь перейдем к требованиям к дизайну.
Счетчик имеет один вход с пометкой «Часы» и два выхода с пометкой $Q$ и $\overline{Q}$. Входные и выходные провода могут иметь «высокое» или «низкое» напряжение. В нашем случае мы будем использовать источник питания на 5 вольт, поэтому «высокий» провод будет близок к 5 вольт, а «низкий» провод будет близок к 0 вольт.
Верхняя черта на нижнем выводе указывает на то, что его состояние всегда противоположно $Q$. То есть, если $Q$ высокий, то $\overline{Q}$ низкий, и наоборот. Может показаться излишним включать $Q$ и $\overline{Q}$, но позже мы увидим, почему это полезно. Мы суммируем состояние счетчика, записывая $Q=1$, если $Q$ высокое, и $Q=0$, если $Q$ низкое.
Пока на тактовом входе низкий уровень, выходное состояние должно оставаться фиксированным. Но каждый раз, когда часы получают импульс (поясняется ниже), значения выходов должны меняться.
Более подробно, «импульс» означает, что тактовый вход повышается от низкого до высокого, а затем быстро падает обратно до низкого. Поскольку выход должен изменяться только один раз за импульс, мы хотели бы, чтобы выходы переключались всякий раз, когда тактовый вход поднимается с низкого уровня на высокий. На это особое поведение указывает треугольник рядом с тактовым входом.
Вам может быть интересно, зачем нам нужно такое причудливое поведение пульса. Почему мы не можем просто потребовать, чтобы выходы менялись всякий раз, когда на входе высокий уровень? Проблема с этим дизайном заключается в том, что каждый импульс имеет некоторую ненулевую длительность. Таким образом, даже короткий импульс приведет к тому, что выходы начнут быстро переключаться туда и обратно с момента, когда вход часов станет высоким, до конца импульса, когда он снова станет низким. Это сделало бы конечное состояние неопределенным!
Почему мы не можем просто потребовать, чтобы выходы менялись всякий раз, когда на входе высокий уровень? Проблема с этим дизайном заключается в том, что каждый импульс имеет некоторую ненулевую длительность. Таким образом, даже короткий импульс приведет к тому, что выходы начнут быстро переключаться туда и обратно с момента, когда вход часов станет высоким, до конца импульса, когда он снова станет низким. Это сделало бы конечное состояние неопределенным!
Напротив, входное напряжение повышается от низкого до высокого ровно один раз за импульс, поэтому наша конструкция гарантирует, что выходы будут переключаться ровно один раз всякий раз, когда на вход поступает импульс.
Теперь, когда мы определили поведение счетчика, переходим к реализации.
Существуют две основные проблемы реализации. Во-первых, как счетчик сохраняет свое состояние между импульсами? Во-вторых, как можно обнаружить переход от низкого уровня к высокому ровно один раз за импульс?
В следующем разделе мы сосредоточимся на первой проблеме, рассматривая более простой тип компонента, который имеет два отдельных входа «вкл. » и «выкл.», а не сложный тактовый вход. Затем мы решим проблему пульса, соединив два этих более простых компонента друг с другом!
» и «выкл.», а не сложный тактовый вход. Затем мы решим проблему пульса, соединив два этих более простых компонента друг с другом!
SR Flip-flop
В этом разделе мы создадим компонент, называемый Set Reset Flip-flop или SR Flip-flop для краткости.
Вот схема триггера SR:
Этот триггер имеет два входа: $S$ («установка») и $R$ («сброс») и два выхода: $Q$ и $\overline{Q}$. Как и раньше, $\overline{Q}$ всегда имеет значение, противоположное $Q$. Таким образом, если $Q$ высокий, то $\overline{Q}$ низкий, и наоборот.
По умолчанию на обоих входах $S$ и $R$ высокий уровень, а на выходе $Q$ низкий уровень. Если $S$ становится низким (т. е. $S=0$), этот устанавливает вентиль и приводит к тому, что выходной сигнал $Q$ становится высоким (и, следовательно, $\overline{Q}$ становится низким). Выход останется в этом состоянии, даже если $S$ снова станет высоким. С другой стороны, понижение $R$ до сбрасывает гейт, что означает, что $Q$ станет низким. Как и прежде, $Q$ останется низким, даже когда $R$ снова станет высоким.
Как и прежде, $Q$ останется низким, даже когда $R$ снова станет высоким.
Таким образом, мы можем переключаться между двумя возможными выходными состояниями, понижая либо $S$, либо $R$. Кроме того, триггер SR сохраняет свое состояние до следующей операции установки или сброса.
Оказывается, можно построить защелку SR всего из двух вентилей И-НЕ с помощью остроумного механизма, называемого защелкой И-НЕ, как показано на следующей диаграмме:
проводов означает, что провода не соприкасаются, а пересекаются друг с другом.
Как работает эта схема? Давайте посмотрим, что произойдет, если мы начнем с состояния по умолчанию ($S=R=\overline{Q}=1$, $Q=0$) и выполним операцию set :
В начальном состоянии вход в верхний И-НЕ равен $(1, 1)$, поэтому его выход равен $Q=0$. Ввод в нижний И-НЕ равен $(0, 1)$, поэтому его вывод равен $\overline{Q}=1$. Поскольку все согласовано, вентили останутся в этой конфигурации, пока мы не изменим один из входов.
Теперь давайте выполним операцию «установить», потянув $S$ в низкое состояние, чтобы получить $S=0$. Поскольку один из входов верхнего И-НЕ равен $0$, его выход будет равен $Q=1$ независимо от другого входа. Это означает, что вход нижнего И-НЕ равен $(1, 1)$, поэтому его выход равен $\overline{Q}=0$.
Наконец, давайте посмотрим, что произойдет, если мы отпустим $S$ и позволим ему вернуться в состояние высокого уровня по умолчанию $S=1$. Вход в верхний NAND теперь равен $(1, 0)$, что означает, что его выход по-прежнему равен $Q=1$. Следовательно, вывод в нижний NAND по-прежнему равен $(1, 1)$, что приводит к тому, что его вывод остается равным $\overline{Q}=0$.
Таким образом, мы можем видеть, что один цикл $S=0 \Rightarrow S=1$ устанавливает выход в $Q=1,\,\overline{Q}=0$. Аналогичный анализ показывает, что цикл $R=0 \Rightarrow R=1$ сбрасывает вывод на $Q=0,\,\overline{Q}=1$.
Реализация однобитового счетчика
Теперь вернемся к проблеме создания однобитового счетчика. Триггер SR из последнего раздела подходит к нам довольно близко: он имеет выходы $Q$ и $\overline{Q}$ и позволяет нам переключаться между ними, опуская $S$ или $R$. Чтобы превратить это в счетчик, нам нужно заменить входы установки/сброса одним входом clock .
Триггер SR из последнего раздела подходит к нам довольно близко: он имеет выходы $Q$ и $\overline{Q}$ и позволяет нам переключаться между ними, опуская $S$ или $R$. Чтобы превратить это в счетчик, нам нужно заменить входы установки/сброса одним входом clock .
Общая логика должна быть:
- Если часы низкие, тогда входы SR должны быть в состоянии по умолчанию $S=R=1$. Это приведет к тому, что $Q$ сохранит свое текущее состояние.
- Если часы высокие и $Q=1$, сбрасывает SR-триггер, устанавливая $R=0$. Это приведет к $Q=0$.
- Если часы высокие и $Q=0$, установить SR-триггер, установив $S=0$. Это приведет к $Q=1$.
Мы можем реализовать эту логику, подключив SR-триггер с двумя логическими элементами И-НЕ следующим образом:
Как и прежде, провода, пересекающиеся в X-пересечении, не касаются друг друга. Мы подключили выход $Q$ к нижнему NAND, а выход $\overline{Q}$ к верхнему NAND.
Давайте проверим, что эта схема следует логике, изложенной выше. В самом деле, если $\mathrm{Clock}=0$, то обе NAND будут иметь вход $0$, поэтому их выходы всегда будут равны $1$. Это означает, что два входа SR-триггера будут находиться в состоянии по умолчанию $1$, как и требовалось.
В самом деле, если $\mathrm{Clock}=0$, то обе NAND будут иметь вход $0$, поэтому их выходы всегда будут равны $1$. Это означает, что два входа SR-триггера будут находиться в состоянии по умолчанию $1$, как и требовалось.
Что происходит, когда часы переходят на высокий уровень ($\mathrm{Clock}=1$)? Предположим, что $Q=1,\,\overline{Q}=0$. Тогда входы в верхний И-НЕ будут $(\overline{Q}=0, \mathrm{Clock}=1)$, и поэтому его выход будет равен $1$. С другой стороны, входы в нижний И-НЕ будут $(\mathrm{Clock}=1, Q=1)$, поэтому его выход будет равен $0$. Вместе это означает, что на вход SR-триггера будет $S=1$, $R=0$, что по определению сбросит триггер в состояние $Q=0,\,\overline{Q}= 1$.
Если часы снова перейдут на высокий уровень, нетрудно заметить, что входы SR теперь будут равны $(S=0,\,R=1)$, что приведет к установить вывод обратно на $Q=0,\,\overline{Q}=1$.
Единственная проблема с этой настройкой заключается в том, что выходы будут продолжать переключаться, пока тактовый сигнал высокий! Поскольку каждый тактовый импульс имеет некоторую ненулевую длительность, эта версия счетчика будет переворачиваться много раз за импульс, а не только один раз.
Решение состоит в использовании двух триггеров SR. Один будет записывать текущий выход, а другой будет записывать выход для следующего импульса. Хитрость заключается в том, что «текущий» триггер активируется, когда часы становятся высокими, как указано выше, но «следующий» триггер будет активирован, когда часы становятся низкими. Эффект состоит в том, что счетчик обновляется только после полного цикла $\mathrm{Clock}=0 \Rightarrow \mathrm{Clock}=1$, предотвращая колебания в нашей первой версии.
Вот реализация этой идеи:
Когда часы младшие , легко увидеть, что $S_{cur}=R_{cur}=1$ означает, что «текущий» триггер будет не обновляться. Напротив, когда часы , максимум $S_{next}=R_{next}=1$, поэтому «следующие» часы не будут обновлены. Нетрудно убедиться, что в этой версии выходы $Q,\,\overline{Q}$ переворачиваются ровно один раз, когда часы получают импульс.
В этом разделе мы будем использовать 1-битный счетчик для создания генератора случайных битов, описанного во введении. Помимо того, что это забавный гаджет, это будет возможность поместить счетчик в полную рабочую схему.
Помимо того, что это забавный гаджет, это будет возможность поместить счетчик в полную рабочую схему.
Вот принципиальная схема генератора случайных битов:
Вверху слева у нас есть таймер 555, подключенный в нестабильном режиме. Когда кнопка нажата, она будет посылать импульсы на 3-й контакт с частотой около 100 Гц.
Наш 1-битный счетчик расположен внизу. Мы использовали две микросхемы 74HC00 для вентилей И-НЕ и микросхему 74HC32 для вентилей ИЛИ. Для удобства я нарисовал соединения логических вентилей внутри этих микросхем, но это только для наглядности.
Наконец, вверху справа есть два светодиода, каждый из которых подключен к разным выходам счетчика. Эти соединения выполняются через транзисторы, чтобы светодиоды не отбирали слишком много напряжения от логических элементов.
При нажатии кнопки таймер начнет посылать импульсы с 3 контакта микросхемы 555. Каждый импульс переворачивает выход счетчика, что, в свою очередь, вызывает загорание ровно одного из светодиодов. Когда кнопка отпущена, импульсы прекращаются, и тот светодиод, который когда-либо был включен, останется включенным до следующего нажатия кнопки.
Когда кнопка отпущена, импульсы прекращаются, и тот светодиод, который когда-либо был включен, останется включенным до следующего нажатия кнопки.
Чтобы проверить, имеют ли светодиоды равные шансы загореться после отпускания кнопки, я нажал кнопку 100 раз и записал, какой индикатор остался гореть. Вот результат с одним из огней, представленным 0, а другим — 1:
001100000001110011100111010010100001101011011111101 10011000110011101100010100000101010001000110111111
В последовательности 51 0 и 49 1, поэтому мы можем с уверенностью 95% заключить, что вероятность получения 1 находится в пределах $\frac{1}{\sqrt{100}} = 0,1$ от среднего значения выборки $49./ 100 = 0,49$. Другими словами, вероятность получить 1 составляет от 0,39$ до 0,59$. Мы могли бы уменьшить границы ошибки, нажимая кнопку больше раз, но этого достаточно для демонстрации.
Несложно построить N-битный двоичный счетчик из N однобитных счетчиков. Идея состоит в том, что когда выход 1-битного счетчика самого низкого порядка переключается на 0, это должно перевернуть счетчик следующего младшего бита, чтобы мы «перенесли 1».