Как устроен калькулятор изнутри. Из каких основных компонентов состоит калькулятор. Как работает жидкокристаллический дисплей калькулятора. Как происходят вычисления в процессоре калькулятора. Чем отличаются простые и научные калькуляторы.
Основные компоненты и устройство простого калькулятора
Калькулятор — это портативное электронное устройство для выполнения математических расчетов. Несмотря на кажущуюся простоту, современный калькулятор представляет собой сложное вычислительное устройство, состоящее из нескольких ключевых компонентов:
- Корпус
- Клавиатура
- Печатная плата
- Процессор
- Память
- Дисплей
- Источник питания
Рассмотрим устройство и принцип работы основных компонентов калькулятора подробнее.
Корпус и клавиатура
Корпус калькулятора обычно изготавливается из пластика и служит для защиты внутренних компонентов. На лицевой стороне корпуса располагается клавиатура с кнопками для ввода цифр и математических операций. Под кнопками находятся резиновые контакты, которые при нажатии замыкают электрическую цепь на печатной плате.
Печатная плата
Внутри корпуса калькулятора находится печатная плата — основа, на которой размещаются все электронные компоненты. В простых моделях плата может быть выполнена в виде гибкой пленки с нанесенными проводниками. На плате располагаются процессор, память, разъемы для подключения дисплея и питания.
Принцип работы жидкокристаллического дисплея калькулятора
Большинство современных калькуляторов оснащены жидкокристаллическим (ЖК) дисплеем для отображения вводимых чисел и результатов вычислений. Как же работает такой дисплей?
ЖК-дисплей состоит из следующих основных элементов:
- Два стеклянных слоя с нанесенными прозрачными электродами
- Слой жидких кристаллов между стеклами
- Поляризационные фильтры
- Отражающая подложка
Принцип работы ЖК-дисплея калькулятора следующий:
- Свет проходит через первый поляризационный фильтр и становится поляризованным в одной плоскости.
- Молекулы жидких кристаллов поворачивают плоскость поляризации света на 90°.
- Свет проходит через второй поляризационный фильтр, повернутый на 90° относительно первого.
- Свет отражается от подложки и возвращается, проходя обратный путь.
- При подаче напряжения на электроды жидкие кристаллы выстраиваются вертикально и не поворачивают плоскость поляризации.
- В результате свет не проходит через второй фильтр, и соответствующий сегмент дисплея становится темным.
Таким образом, управляя напряжением на электродах, можно формировать на дисплее нужные цифры и символы.

Как происходят вычисления в процессоре калькулятора
Сердцем любого калькулятора является микропроцессор — интегральная микросхема, выполняющая все вычислительные операции. Как же происходят вычисления в процессоре калькулятора?
Основные компоненты процессора калькулятора:
- Арифметико-логическое устройство (АЛУ)
- Регистры для хранения операндов и результатов
- Устройство управления
- Постоянное запоминающее устройство (ПЗУ) с микропрограммами
- Оперативное запоминающее устройство (ОЗУ)
Алгоритм выполнения вычислений:
- При нажатии кнопки процессор считывает ее код.
- Если это цифра, она добавляется к текущему вводимому числу в регистре.
- При нажатии кнопки операции, число из регистра сохраняется в память.
- После ввода второго числа и нажатия «равно» выполняется соответствующая операция в АЛУ.
- Результат сохраняется в регистр и выводится на дисплей.
Интересно, что простые арифметические операции (сложение, вычитание, умножение, деление) выполняются в АЛУ калькулятора примерно так же, как их выполняют люди «в столбик»:
- Сложение и вычитание — поразрядно с учетом переносов
- Умножение — последовательным сложением
- Деление — последовательным вычитанием
Более сложные функции (тригонометрические, логарифмические) обычно вычисляются с помощью разложения в ряды или специальных алгоритмов аппроксимации.
Чем отличаются простые и инженерные калькуляторы
Существует множество разновидностей калькуляторов — от самых простых моделей для базовых арифметических операций до сложных инженерных и графических калькуляторов. В чем же их основные отличия?
Простые (базовые) калькуляторы:
- Выполняют только основные арифметические действия
- Имеют минимальный набор кнопок
- Оснащены простым цифровым дисплеем
- Содержат простой процессор и минимум памяти
- Питаются от солнечной батареи или батарейки
Инженерные (научные) калькуляторы:
- Поддерживают сложные математические и статистические функции
- Имеют расширенную клавиатуру с дополнительными кнопками
- Оснащены многострочным ЖК-дисплеем
- Содержат более мощный процессор и больший объем памяти
- Могут иметь возможность программирования
- Питаются от батареек или аккумуляторов
Графические калькуляторы дополнительно оснащены большим графическим дисплеем и могут строить графики функций, что делает их похожими на миникомпьютеры.
Интересные факты из истории развития калькуляторов
История развития калькуляторов насчитывает несколько тысячелетий — от простых счетных устройств древности до современных мощных вычислительных машин. Вот несколько интересных фактов из истории калькуляторов:
- Древнейшим счетным устройством считаются абаки, использовавшиеся еще в Древнем Вавилоне около 2400 лет до н.э.
- Первый механический калькулятор изобрел французский математик Блез Паскаль в 1642 году.
- Первый массовый электронный калькулятор Anita Mk VIII появился в 1961 году и стоил как автомобиль.
- В 1967 году Texas Instruments создала первый карманный калькулятор Cal Tech.
- В 1970-х годах появились первые научные и программируемые калькуляторы.
- Современные графические калькуляторы по возможностям сравнимы с компьютерами 1980-х годов.
Сегодня калькуляторы остаются незаменимым инструментом для инженеров, бухгалтеров, студентов и многих других специалистов, несмотря на распространение смартфонов и компьютеров.
Как сделать простой механический калькулятор своими руками
Для лучшего понимания принципов работы калькулятора можно попробовать создать простую механическую модель своими руками. Это будет отличным образовательным проектом для детей и взрослых. Вот несколько идей:
Калькулятор из картона и шариков
Можно создать простой четырехбитный сумматор из картона, используя шарики для представления битов. Основные компоненты:
- Картонный корпус с дорожками для шариков
- Логические элементы AND, OR, XOR из картона
- Шарики для представления битов (1 — есть шарик, 0 — нет шарика)
Принцип работы: шарики скатываются по дорожкам, проходя через логические элементы. В результате внизу формируется сумма двух четырехбитных чисел.
Калькулятор из конструктора Lego
Из деталей конструктора Lego можно собрать более сложную модель калькулятора:
- Механические счетчики из зубчатых колес для представления разрядов
- Рычаги для ввода цифр
- Механизмы переноса между разрядами
- Устройство сброса в нулевое положение
Такая модель наглядно демонстрирует принципы работы механических вычислительных устройств.
Польза создания механических моделей калькуляторов:
- Развитие инженерного мышления
- Понимание основ двоичной арифметики
- Знакомство с логическими операциями
- Развитие навыков конструирования
- Повышение интереса к математике и информатике
Создание таких моделей помогает лучше понять принципы работы электронных калькуляторов и компьютеров в целом.

Я обратил внимание, что довольно часто спрашивают, как работает обычный калькулятор. Думал, что в интернете должно быть много статей по этому поводу, но что-то мне ничего дельного не попалось. Википедия, как обычно, слишком мудрит, и я подумал, что будет неплохо, если вкратце опишу принцип его работы.
Существует огромное количество всевозможных моделей калькуляторов. Есть простые, есть сложные. С питанием от солнечных батарей или от сети. Есть обычные, программируемые, бухгалтерские, специализированные модели. Порой, и не найдешь той грани, которая отделяет калькулятор от компьютера.
Я буду описывать работу самой простой модели калькулятора.
Это калькулятор CASIO HS-8LU. Они примерно все работают одинаково. По большому счету, в простых моделях ничего не меняется уже лет тридцать.
Калькулятор состоит из корпуса, клавиатуры с резиновыми кнопками и платы.
В данной модели плата сделана в виде пленки с нанесенными на нее проводниками. Питание — от солнечной батареи. Над солнечной батареей расположен жидкокристаллический индикатор.
На задней крышке корпуса расположены токопроводящие контакты. При нажатии на кнопку она прижимает пленку к задней крышке и происходит электрический контакт. Часто токопроводящий контакт наносят на обратную сторону кнопки. В том случае сама кнопка прижимается к плате для создания контакта.
С обратной стороны под солнечной батареей расположен чип микропроцессора. Он управляет работой калькулятора.
Как работает индикатор на жидких кристаллах.
Жидкие кристаллы — это специальные молекулы, которые при приложении между ними напряжения поворачиваются и меняют поляризацию света.
Это картиночка для одного пиксела цветного ЖКИ, но в монохромных там то же самое, только нет светофильтра.
Спереди и сзади жидких кристаллов ставят так называемый поляризационный фильтр. Он обычный свет преобразует в поляризованный (например, образно говоря, в «вертикальный»). Если напряжение не приложено, то «вертикально» поляризованный свет проходит через жидкие кристаллы, поворачивает плоскость поляризации, отражается от задней поверхности и идет обратно. Мы видим прозрачный экран. На стекле индикатора спереди нарисованы прозрачные токопроводящие линии в форме сегментов цифр, точек или других символов. Сзади также есть токопроводящая область. Когда возникает напряжение между токопроводящими проводниками (спереди и сзади), то между ними жидкие кристаллы поворачиваются и меняют свою плоскость поляризации так, что через задний поляризационный фильтр уже не проходят. Оттого на том сегменте, где есть напряжение между передней и задней поверхностью стекла, возникает невидимая область — сегмент «светится».
Если приглядеться под определенным углом, то в отраженном свете будут видны эти прозрачные проводники.
На самом деле ориентация поляризации не «вертикальная» и «горизонтальная», а «наклоненная» под углом в 45 градусов «вправо» или «влево». Если взять светофильтр и перевернуть вверх ногами, то поляризация будет не «вправо», а «влево». И изначально он будет не пропускать свет, а задерживать.
Для экономии количества один проводник отображает и подведен не к одному сегменту, а к нескольким сразу. Чтобы они не зажигались сразу все, с задней стороны стекла рисуют не один общий проводник, а тоже несколько. Получается, что спереди контакты подведены к нескольким сегментами по вертикали, а с задней стороны по горизонтали. На схеме ниже показана схема индикатора.
Там есть еще такая хитрость, что напряжение нужно прикладывать не постоянное, а переменное (прямоугольные импульсы частотой 20-40 Гц). Иначе деградирует индикатор.
Для простых индикаторов с одним общим проводником импульсы совпадают по фазе, когда не надо отображать сегмент (спереди и сзади разность потенциалов будет одинаковой) и не совпадают по фазе, когда надо отобразить (тогда спереди будет «0», и сзади «1», а через некоторое время полярность поменяется, и будет спереди «1», а сзади — «0», и так далее). В тех индикаторах на общий проводник подается меандр (просто частота), а на отображаемые сегменты — совпадение логического уровня с общим (не горит) и не совпадение (горит).
В индикаторе нашего калькулятора используется три общих проводника. Там все сложнее. Простыми логическими уровнями не обойдешься. Чтобы обеспечить переменное напряжение и отсутствие постоянной составляющей используются уровни напряжений в 1/3 и 2/3 от максимума. В итоге форма импульсов будет ступенчатой. На схеме ниже показаны эпюры таких импульсов.
А теперь самое главное и самое интересное — микросхема процессора.
Это фотографии кристаллов отечественных калькуляторов, сделанных на микросхемах К145ИП7 (слева) и К145ИП11 (справа). Фотографии взяты с интересного сайта «Радиокартинки».
Микропроцессор калькулятора принципом работы очень мало отличается от обычного персонального компьютера с процессором, памятью, клавиатурой и видеокартой.
Если быстро посмотреть на фото кристаллов, то можно примерно поделить на три области: область постоянного запоминающего устройства (ПЗУ) с программной («прошивкой»), область оперативного запоминающего устройства (ОЗУ), где хранятся регистры памяти калькулятора, и остальные цепи процессора, которые включают арифметическо-логическое устройство (АЛУ), драйвер индикатора, драйвер клавиатуры, преобразователи напряжения и другие вспомогательные цепи.
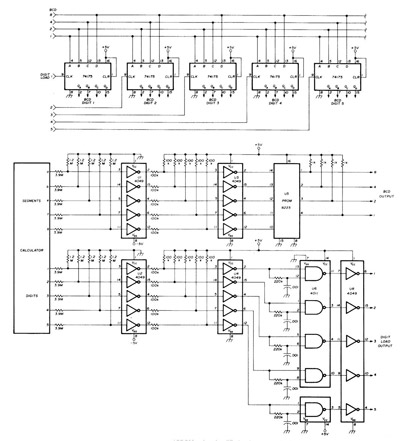
Это структурная схема процессора калькулятора МК-62.
В верхней части мы видим, что есть блоки:
— генератор опорной частоты (ГОЧ), который задает частоту, с которой регенерируется изображение на индикаторе;
— схема удвоения напряжения, умножающая напряжение солнечное батареи на два, чтобы хватило для индикатора;
— генератор, формирователь импульсов общих электродов и регистр-формирователь сегментного кода постоянно выводят заданные для вывода сегменты на индикатор. Там есть специальный регистр памяти, куда микропроцессор записывает информацию, какие надо отображать сегменты, а какие не надо. После этого процессор не отвлекается на отображение, и эти блоки выводят все сами;
— ОЗУ с регистрами данных и ПЗУ с прошивкой;
— и узел с процессором, состоящим из АЛУ с обвязкой. Счетчик адреса АЛУ выбирает очередное слово программы из ПЗУ. Разрядность этого слова может быть разной в разных калькуляторах. Отдельные биты в слове определяют работу АЛУ: например, сложить два 4-х битных числа из регистров, или считать из ОЗУ цифру, или сравнить два числа, или сдвинуть на один разряд и т. д.
Как работает микропроцессор.
Сначала срабатывает сброс по питанию. При подаче электричества специальный узел заставляет программу работать с начального адреса. Команда за командой извлекается из ПЗУ и исполняется. Вначале происходит обнуление регистров, формирование числа «0.», сброс всяких признаков переполнения, операций и прочее. После сброса программа ожидает события от клавиатуры (нажатие кнопки).
Когда нажата кнопка, то процессор через некоторое время еще раз опрашивает клавиатуру, чтобы подавить дребезг кнопок (когда из-за плохого контакта может произойти одновременно несколько нажатий).
А дальше, в зависимости от предыдущих состояний, он по программе определяет, что с этим нажатием делать. Например, если идет ввод числа и введена цифра, то продолжить ввод. Если нажата кнопка операции, то выполнить операцию.
Сам алгоритм и логика выполнения операций целиком лежит на ПЗУ и программистах, которые писали прошивки.
Что интересно, все простые операции выполняются так, как их учат в школе.
— сложение и вычитание. В столбик. Выравниваются порядки двух введенных чисел и происходит сложение или вычитание.
— умножение и деление. Так же в столбик. Разряд за разрядом. Сначала последовательным сложением умножают на младшую цифру множителя, затем вторую и так далее до старшей. Деление — последовательным вычитанием.
После выполнения операции отдельная подпрограмма нормализует результат: отбрасывает незначащие нули и сдвигает его вправо.
Если в калькуляторе есть тригонометрические функции, то они также выполняются, как их запрограммировал программист. Есть разные способы вычисления элементарных функций: разложение в ряд Тейлора или по методу «Cordic».
Вот примерно так работает калькулятор.
Я вам дам ссылку на несколько сайтов. В одном вы можете еще прочитать про то, как они работают: http://datamath.org/Story/Intel.htm#The.
А еще две ссылки — очень познавательный интерактивный сайт, где обратным реверсом считали прошивку и сделали симулятор. Там можно «прогнать» работу процессора реального калькулятора.
http://files.righto.com/calculator/TI_calculator_simulator.html и
http://files.righto.com/calculator/sinclair_scientific_simulator.html.
А также заходите в мой музей, где я собираю советскую цифровую электронику: http://www.leningrad.su/museum/
Вот, наверно, и все. Надеюсь, я вас не сильно утомил. 🙂
Вводимые числа и результат представлены в следующем формате: REG*10EXP. В регистре REG находится непосредственно шестнадцатеричный код числа с учетом знака. В регистре EXP – показатель степени с учетом знака (-127 Приципиальная электрическая схема
Для индикации используется 10-разрядный жк-индикатор с контроллером HT1611. Питание данного индикатора подается на вторую слева (GND) и на крайнюю правую клеммы (+1,5В). Вывод HK (пятая клемма) следует соединить с общим проводом. Для управления индикатором используется интерфейс SPI, поэтому вход данных индикатора DI (4 клемма) соединен через резистор R6 с выходом данных SPI, а тактовый вход CLK (3 клемма) через резистор R5, с тактовым выходом SPI. Также следует соединить общие провода индикатора и микроконтроллера. Более подробную информацию о данном индикаторе, а также и заказать его, вы можете на сайте фирмы «Телесистемы» — www.telesys.ru.
Клавиатура реализована следующим образом: выводы RB4-RB7 подтянуты к Vdd, т.е. при чтении порта возвращают логическую единицу. Четыре вывода из RA0-RA5 также находятся в высоком состоянии, а один – в низком, причем этот вывод периодически меняется. Если какая-либо из кнопок нажата, то при логическом нуле на соответствующем выводе порта А, ноль будет и на одном из выводов порта В. Таким образом, зная какие из выводов портов А и В в данный момент находятся в низком состоянии, можно определить, какая кнопка нажата.
Блок-схема программы
Рассмотрим алгоритм работы данного устройства. В начале программы подготавливаются все используемые регистры, и выводится ноль на индикацию. Затем, начинается описанное выше, сканирование клавиатуры. После нажатия кнопки, определяется, что было нажато – цифра или команда. При нажатии цифры, следует проверка на переполнение водимого числа (не больше 4-х цифр) и уменьшение его порядка, если до этого была нажата точка. Затем формируются двоично-десятичные коды для преобразования числа в двоичный код, и отдельно – для индикации. После этого вводимое число появляется на индикаторе. Если была нажата математическая команда, то ее код сохраняется в специальном регистре, и формируется двоичный код первого числа, который заносится в регистр первого числа. Затем подготавливаются регистры для ввода второго числа, и микроконтроллер снова переходит к сканированию клавиатуры. При нажатии точки, устанавливается флаг «точка», при наличии которого, происходит декрементирование порядка вводимого числа с каждой новой нажатой цифрой. Если же была нажата команда +/-, то происходит инвертирование знака вводимого числа. При нажатии кнопки «равно», формируется двоичный код второго числа, который заносится в регистр второго числа. Затем считывается код нажатой математической операции, и происходит ее выполнение. После этого результат оптимизируется и выводится на индикатор.
В данном архиве (calc.rar) находятся: calc.hex — файл-прошивка для микроконтроллера; calc.asm — файл программы MpLab с подробнейшими комментариями; bc_bcd.inc, bcd_bc.inc, degree.inc, divf.inc, minf.inc, multf.inc, sumf.inc — файлы с математическими подпрограммами; calc.sch и calc.pcb — соответственно принципиальная схема и печатная плата в формате ACCEL EDA.Источник: picro.narod.ru
Как устроен и работает калькулятор: sfrolov — LiveJournal
Я обратил внимание, что довольно часто спрашивают, как работает обычный калькулятор. Думал, что в интернете должно быть много статей по этому поводу, но что-то мне ничего дельного не попалось. Википедия, как обычно, слишком мудрит, и я подумал, что будет неплохо, если вкратце опишу принцип его работы.
Существует огромное количество всевозможных моделей калькуляторов. Есть простые, есть сложные. С питанием от солнечных батарей или от сети. Есть обычные, программируемые, бухгалтерские, специализированные модели. Порой, и не найдешь той грани, которая отделяет калькулятор от компьютера.
Я буду описывать работу самой простой модели калькулятора.
Это калькулятор CASIO HS-8LU. Они примерно все работают одинаково. По большому счету, в простых моделях ничего не меняется уже лет тридцать.
Калькулятор состоит из корпуса, клавиатуры с резиновыми кнопками и платы.
В данной модели плата сделана в виде пленки с нанесенными на нее проводниками. Питание — от солнечной батареи. Над солнечной батареей расположен жидкокристаллический индикатор.
На задней крышке корпуса расположены токопроводящие контакты. При нажатии на кнопку она прижимает пленку к задней крышке и происходит электрический контакт. Часто токопроводящий контакт наносят на обратную сторону кнопки. В том случае сама кнопка прижимается к плате для создания контакта.
С обратной стороны под солнечной батареей расположен чип микропроцессора. Он управляет работой калькулятора.
Как работает индикатор на жидких кристаллах.
Жидкие кристаллы — это специальные молекулы, которые при приложении между ними напряжения поворачиваются и меняют поляризацию света.
Это картиночка для одного пиксела цветного ЖКИ, но в монохромных там то же самое, только нет светофильтра.
Спереди и сзади жидких кристаллов ставят так называемый поляризационный фильтр. Он обычный свет преобразует в поляризованный (например, образно говоря, в «вертикальный»). Если напряжение не приложено, то «вертикально» поляризованный свет проходит через жидкие кристаллы, поворачивает плоскость поляризации, отражается от задней поверхности и идет обратно. Мы видим прозрачный экран. На стекле индикатора спереди нарисованы прозрачные токопроводящие линии в форме сегментов цифр, точек или других символов. Сзади также есть токопроводящая область. Когда возникает напряжение между токопроводящими проводниками (спереди и сзади), то между ними жидкие кристаллы поворачиваются и меняют свою плоскость поляризации так, что через задний поляризационный фильтр уже не проходят. Оттого на том сегменте, где есть напряжение между передней и задней поверхностью стекла, возникает невидимая область — сегмент «светится».
Если приглядеться под определенным углом, то в отраженном свете будут видны эти прозрачные проводники.
На самом деле ориентация поляризации не «вертикальная» и «горизонтальная», а «наклоненная» под углом в 45 градусов «вправо» или «влево». Если взять светофильтр и перевернуть вверх ногами, то поляризация будет не «вправо», а «влево». И изначально он будет не пропускать свет, а задерживать.
Для экономии количества один проводник отображает и подведен не к одному сегменту, а к нескольким сразу. Чтобы они не зажигались сразу все, с задней стороны стекла рисуют не один общий проводник, а тоже несколько. Получается, что спереди контакты подведены к нескольким сегментами по вертикали, а с задней стороны по горизонтали. На схеме ниже показана схема индикатора.
Там есть еще такая хитрость, что напряжение нужно прикладывать не постоянное, а переменное (прямоугольные импульсы частотой 20-40 Гц). Иначе деградирует индикатор.
Для простых индикаторов с одним общим проводником импульсы совпадают по фазе, когда не надо отображать сегмент (спереди и сзади разность потенциалов будет одинаковой) и не совпадают по фазе, когда надо отобразить (тогда спереди будет «0», и сзади «1», а через некоторое время полярность поменяется, и будет спереди «1», а сзади — «0», и так далее). В тех индикаторах на общий проводник подается меандр (просто частота), а на отображаемые сегменты — совпадение логического уровня с общим (не горит) и не совпадение (горит).
В индикаторе нашего калькулятора используется три общих проводника. Там все сложнее. Простыми логическими уровнями не обойдешься. Чтобы обеспечить переменное напряжение и отсутствие постоянной составляющей используются уровни напряжений в 1/3 и 2/3 от максимума. В итоге форма импульсов будет ступенчатой. На схеме ниже показаны эпюры таких импульсов.
А теперь самое главное и самое интересное — микросхема процессора.
Это фотографии кристаллов отечественных калькуляторов, сделанных на микросхемах К145ИП7 (слева) и К145ИП11 (справа). Фотографии взяты с интересного сайта «Радиокартинки».
Микропроцессор калькулятора принципом работы очень мало отличается от обычного персонального компьютера с процессором, памятью, клавиатурой и видеокартой.
Если быстро посмотреть на фото кристаллов, то можно примерно поделить на три области: область постоянного запоминающего устройства (ПЗУ) с программной («прошивкой»), область оперативного запоминающего устройства (ОЗУ), где хранятся регистры памяти калькулятора, и остальные цепи процессора, которые включают арифметическо-логическое устройство (АЛУ), драйвер индикатора, драйвер клавиатуры, преобразователи напряжения и другие вспомогательные цепи.
Это структурная схема процессора калькулятора МК-62.
В верхней части мы видим, что есть блоки:
— генератор опорной частоты (ГОЧ), который задает частоту, с которой регенерируется изображение на индикаторе;
— схема удвоения напряжения, умножающая напряжение солнечное батареи на два, чтобы хватило для индикатора;
— генератор, формирователь импульсов общих электродов и регистр-формирователь сегментного кода постоянно выводят заданные для вывода сегменты на индикатор. Там есть специальный регистр памяти, куда микропроцессор записывает информацию, какие надо отображать сегменты, а какие не надо. После этого процессор не отвлекается на отображение, и эти блоки выводят все сами;
— ОЗУ с регистрами данных и ПЗУ с прошивкой;
— и узел с процессором, состоящим из АЛУ с обвязкой. Счетчик адреса АЛУ выбирает очередное слово программы из ПЗУ. Разрядность этого слова может быть разной в разных калькуляторах. Отдельные биты в слове определяют работу АЛУ: например, сложить два 4-х битных числа из регистров, или считать из ОЗУ цифру, или сравнить два числа, или сдвинуть на один разряд и т. д.
Как работает микропроцессор.
Сначала срабатывает сброс по питанию. При подаче электричества специальный узел заставляет программу работать с начального адреса. Команда за командой извлекается из ПЗУ и исполняется. Вначале происходит обнуление регистров, формирование числа «0.», сброс всяких признаков переполнения, операций и прочее. После сброса программа ожидает события от клавиатуры (нажатие кнопки).
Когда нажата кнопка, то процессор через некоторое время еще раз опрашивает клавиатуру, чтобы подавить дребезг кнопок (когда из-за плохого контакта может произойти одновременно несколько нажатий).
А дальше, в зависимости от предыдущих состояний, он по программе определяет, что с этим нажатием делать. Например, если идет ввод числа и введена цифра, то продолжить ввод. Если нажата кнопка операции, то выполнить операцию.
Сам алгоритм и логика выполнения операций целиком лежит на ПЗУ и программистах, которые писали прошивки.
Что интересно, все простые операции выполняются так, как их учат в школе.
— сложение и вычитание. В столбик. Выравниваются порядки двух введенных чисел и происходит сложение или вычитание.
— умножение и деление. Так же в столбик. Разряд за разрядом. Сначала последовательным сложением умножают на младшую цифру множителя, затем вторую и так далее до старшей. Деление — последовательным вычитанием.
После выполнения операции отдельная подпрограмма нормализует результат: отбрасывает незначащие нули и сдвигает его вправо.
Если в калькуляторе есть тригонометрические функции, то они также выполняются, как их запрограммировал программист. Есть разные способы вычисления элементарных функций: разложение в ряд Тейлора или по методу «Cordic».
Вот примерно так работает калькулятор.
Я вам дам ссылку на несколько сайтов. В одном вы можете еще прочитать про то, как они работают: http://datamath.org/Story/Intel.htm#The.
А еще две ссылки — очень познавательный интерактивный сайт, где обратным реверсом считали прошивку и сделали симулятор. Там можно «прогнать» работу процессора реального калькулятора.
http://files.righto.com/calculator/TI_calculator_simulator.html и
http://files.righto.com/calculator/sinclair_scientific_simulator.html.
Вот, наверно, и все. Надеюсь, я вас не сильно утомил. 🙂
Кто не устал, добро пожаловать в мой музей советской цифровой электроники:
http://www.leningrad.su/museum/
Внешний вид картонного четырёхбитного калькулятора из картона. Хорошо видны полусумматор вверху и три сумматора в средней и нижней части калькулятора
Давным-давно, до изобретения электроники, люди изготавливали механические компьютеры из подручных материалов. Самым известным и сложным примером такой машины является антикитерский механизм — сложнейшее устройство из не менее чем 30 шестерёнок использовалось для расчёта движения небесных тел и позволяло узнать дату 42 астрономических событий.
В наше время механические компьютеры (калькуляторы) — скорее предмет развлечения гиков и повод устроить забавное шоу. Например, как компьютер из 10 000 костяшек домино, который складывает произвольные четырёхзначные бинарные числа и выдаёт пятизначную двухбитную сумму (математическая теория этого калькулятора и архитектура). Такие перфомансы позволяют детям лучше понять, как работают битовые логические операции в программировании, как устроены логические вентили. Да и вообще сделать маленький компьютер своими руками из подручных материалов очень интересно, тем более если вы делаете это вместе с ребёнком.
Логическая операция AND в компьютере из 10 000 костяшек домино
Для изготовления механического калькулятора отлично подходит конструктор Lego. На YouTube можно найти немало примеров таких калькуляторов.
Калькулятор из компьютера Lego
Вдохновлённый примером компьютера из домино и механических калькуляторов из конструктора Lego, программист C++ под ником lapinozz вместе со своими младшими сестричками решил соорудить в домашних условиях нечто подобное для школьного научного проекта одной из сестёр. Он задумал и реализовал полностью функциональный четырёхбитный калькулятор LOGIC (Logic cardbOard Gates Inpredictable Calculator). Для изготовления этой вычислительной машины не требуется ничего кроме картона и клея, а работает она не на электричестве, а на шариках и земной гравитации. Калькулятор умеет складывать числа от 0 до 15 с максимальной суммой 30.
В отличие от костяшек доминов и кубиков Lego, в производстве этого калькулятора не использовались никакие фабричные компоненты. Все элементы калькулятора склеены из картона с нуля, что хорошо понятно по фотографиям устройства. В этом смысле данное устройство можно считать уникальным.
Наглядное представление, как складывать бинарные числа. Обучение школьника навыкам перевода из десятичной в двоичную систему счисления и обратно. Изучение битовых логических операций и основных логических схем.
Как можно рассмотреть на фотографии калькулятора, в верхней части располагается зона для ввода данных. После прохождения всех логических операций шарики показывают результат операции внизу.
Ввод данных осуществляется шариками. Шарик есть — 1, шарика нет — 0. Бит справа — это наименьший бит числа. Перед началом работы некоторые части калькулятора следует привести в исходное положение. После указания исходных значений отодвигается полоска картона, которая удерживает шарики в исходном положении — и начинается процесс сложения.
Например, так выглядит исходное положение шариков для операции 7+5 (0111 + 0101).
Логические операции картонного калькулятора осуществляется схожим образом, как и в вышеупомянутом компьютере из домино.
Схематически логические вентили для всех логических операций показаны на схеме.
То есть логический вентиль «И» (AND) означает, что при поступлении 0 шариков на входе получается 0 на выходе. При поступлении 1 шарика на входе получается 0 на выходе. При поступлении 2 шариков на входе получается 1 на выходе.
1 на входе, 0 на выходе
2 на входе, 1 на выходе
Логический вентиль XOR сделать немного сложнее. В этом случае если поступает один шарик, он должен пройти. А если поступает два шарика, то они должны аннулировать друг друга, то есть на выходе будет 0. Автор показывает, как это делать, через вертикально висящий кусочек картона с узким горлышком. Если два шарика приходят одновременно, то они блокируют друг друга — и таким образом эффективно реализуют логическую операцию XOR.
Логический вентиль XOR
Чтобы оптимизировать систему и не городить массу логических вентилей AND и XOR, автор реализовал полусумматор — комбинационную логическую схему, имеющую два входа и два выхода. Полусумматор позволяет вычислять сумму A + B, при этом результатом будут два бита S и C, где S — это бит суммы по модулю 2, а C — бит переноса. В нашей картонной конструкции это означает, что если на входе у нас 1 шарик, то он попадает на выход C, а если на входе 2 шарика, то 1 шарик попадает на выход S, а второй никуда не попадает.
Программист придумал довольно простую и эффективную схему для полусумматора. В ней 1 шарик на входе спокойно продолжает свой путь, переворачивая барьер, и проходя в отверстие C. Но если поступают два шарика, то второй шарик уже не может пройти через барьер, перевёрнутый первым шариком — и проваливается в отверстие, прибивая новый путь S. Это и есть полусумматор.
Один шарик на входе полусумматора
Два шарика на входе полусумматора
Наконец, настоящим шедевром является сумматор. Обычно его делают из двух полусумматоров и логического вентиля «ИЛИ», но автор реализовал другую конструкцию, которая фактически является небольшой модификацией полусумматора.
Один шарик на входе — один шарик по пути 1
Два шарика на входе — один шарик по пути 2
Три шарика на входе — один шарик по пути 1, а другой по пути 2
Весь калькулятор целиком состоит из одного полусумматора и трёх сумматоров.
Калькулятор выдаёт корректный результат вычислений в случае, если шарики падают с правильной скоростью, не слишком быстро и не слишком медленно, и не отскакивают друг от друга. Сама логика безупречна, но на практике калькулятор иногда глючит.
Калькулятор своими руками

Привет всем любителям самоделок. В данной статье я расскажу, как сделать калькулятор своими руками, в сборке которой поможет кит-набор, ссылка на него будет в конце статьи. Данный кит-набор будет полезен для начинающих радиолюбителей и тех, кто хочет попробовать себя в работе с паяльником, ну и конечно же такой калькулятор можно будет использовать по прямому назначению. Для сборки такого радиоконструктора не понадобится много инструментов, поэтому собрать его сможет каждый.
Перед тем, как прочитать статью, предлагаю посмотреть видеоролик, где подобно показан процесс сборки кит-набора и его проверка на работоспособность.
Для того, чтобы сделать калькулятор своими руками, понадобится:
* Кит-набор
* Паяльник, флюс, припой
* Бокорезы
* Крестовая отвертка
Шаг первый.
В комплекте кит-набора присутствует печатная плата с металлизированными отверстиями, ее качество изготовления на высоком уровне.

В роли клавиш здесь выступают кнопки с пластиковой накладкой, их 17 штук.

Инструкция к радиоконструктору не поставляется, так как на плате не так много деталей, тем более они имеют одинаковый номинал, так что смысла в этом нет. Выводится выражение будет на семисегментные индикаторы с красной подсветкой, в темноте они также хорошо видны за счет свечения.

Разобравшись с комплектом, переходим к самой сборке.
Шаг второй.
На плату устанавливаем радиодетали. Сначала вставляем резисторы, их в комплекте шесть штук одинакового номинала, так что определять сопротивление каждого не нужно. С обратной стороны платы загинаем выводы, для того, чтобы они не выпали при пайке. После резисторов на плату устанавливаем неполярные керамические конденсаторы, их выводы также загинаем. Далее на плату ставим все 17 кнопок, а затем и семисегментные индикаторы, на них есть специальная метка в виде точке, также как и на плате, далее загибаем их ножки.
Шаг третий.
Теперь при помощи паяльника и припоя припаиваем выводы радиодеталей к контактам платы, для лучшей пайки наносим флюс. Для того, чтобы выводы не окислялись и не мешали, преждевременно удаляем их часть бокорезами. При удалении ножек радиодеталей будьте аккуратны, так как это может привести к обрыву дорожек от самой платы.


После пайки устанавливаем крепление батарейки и микросхему, ее нужно расположить так, чтобы ключ в виде выемки на корпусе совпадал по направлению с ключом, изображенным на плате.


Далее припаиваем микросхему и отсек батареи при помощи паяльника и припоя, паять микросхему желательно быстро, так как ее можно перегреть, после чего она может выйти из строя.


Лишнюю часть выводов также аккуратно удаляем.

Проверяем калькулятор, установив батарейку на место.

На семисегментном индикаторе должны отображать цифры при нажатии на все кнопки. После проверки платы калькулятора можно переходить к сборке его в корпус.
Шаг четвертый.
Для того, чтобы защитить плату и придать калькулятору нужный вид в комплекте имеется несколько частей корпуса из оргстекла. С оргстекянных пластин удаляем защитную пленку и собираем корпусе из них, друг друга скрепляя при помощи винтов и крестовой отвертки.


Чтобы было понятно на какую клавишу нажать, нужно установить пластиковые части на кнопки, в которые нужно установить подписанные бумажки, для правильного расположения можно воспользоваться картинкой с сайта продавца. В конце проверяем калькулятор в работе.


Кнопку включения данный калькулятор не имеет, через некоторое время его бездействия они сам выключается, а для включения достаточно нажать на кнопку C. Такой радиоконструктор поможет освоиться в радиоэлектронике и попробовать себя в этой сфере.

На этом у меня все, всем спасибо за внимание и творческих успехов.
Купить Kit-набор на Aliexpress
Становитесь автором сайта, публикуйте собственные статьи, описания самоделок с оплатой за текст. Подробнее здесь.Строительный калькулятор онлайн KALK.PRO
КАЛК.ПРО – разработчик современных интерактивных строительных калькуляторов, предназначенных для автоматизации и упрощения типовых расчетов. Во всех инструментах, мы стараемся учитывать положения строительных норм и правил, а алгоритмы проверяются на практике профессиональным строителями. Мы направляем все возможные усилия, чтобы конструкции получались прочными, надежными и безопасными!
Каждый третий человек, хоть раз в жизни задумывается о приобретении загородного дома, однако радужная мечта и яркая фантазия практически всегда разбивается об непреодолимую стену финансовых затрат. Для того чтобы войти в ограниченные рамки бюджета, единственным возможным выходом в данной ситуации, является отказ от дорогостоящих услуг подрядчика и попытка строительства дома своими руками.
Но самостоятельно построить дом – отнюдь не самая простая задача. Соблюдение нормативных актов, учет специфических особенностей климата, рельефа и почв, составление проекта, выполнение расчета материалов – работа ни одного профильного специалиста, а предполагается, что все эти обязанности лягут на плечи рядового семьянина без опыта в сфере строительства.
Идея проекта KALK.PRO – собрать воедино всю необходимую информацию, а также предоставить инструменты для облегчения и автоматизации расчетов с помощью строительных калькуляторов, чертежей и 3D-моделей. Мы хотим, чтобы частное строительство стало доступным каждому, чтобы это не было проблемой и не отталкивало большинство семей при реализации квартирного вопроса и достижения своей мечты.
Для тех, кто уже сталкивался со строительством и, кто понимает, насколько важно систематизировать все этапы работы, точно подготовить необходимую документацию, заранее выполнить расчет материалов для строительства дома и не допустить ошибку – наше программное обеспечение, также будет эффективным помощником.
Заблаговременно выполненный расчет строительства дома избавит вас от большинства проблем на более поздних этапах работ.
Калькулятор строительства дома
Калькуляторы строительства дома предоставляют исчерпывающую информацию об особенностях возводимых сооружений и их составных частей по параметрам, введенных пользователем. Все используемые данные в нашей базе, мы стараемся приводить в соответствие положениям нормативно-правовых актов местного законодательства и справочных данных производителей материалов, для того чтобы вы могли получить наиболее достоверную информацию, среди которой:
- расчет материалов для строительства дома и их стоимость;
- несущие способности и допустимые нагрузки силовых конструкций;
- полезные рекомендации по более комфортному расположению элементов;
- подробные детализированные чертежи строений в различных проекциях;
- интерактивную 3D-модель с возможностью взаимодействия и измерений.
Главной особенностью нашего проекта является наличие современной 3D-визуализации. Планируя строительство, вы сможете в режиме онлайн поэкспериментировать с элементами будущего дома – фундаментами, лестницами, крышами. Выбрать наиболее привлекательную и удобную конструкцию, как и рассчитать строительство дома, теперь не составит труда.
В информационном разделе нашего сайта можно ознакомиться с аннотациями, профессиональными советами специалистов, узнать много интересного об особенностях строительных работ и частной застройки. Интересные статьи с наглядными изображениями, написанные простым человеческим языком, помогут быстрее освоиться в ремонте и воплотить в реальность свою задумку.
Выбирая наш сайт в качестве помощника, вы получаете набор качественных и профессиональных инструментов с детально проработанной структурой, логикой и интерфейсом. Постоянно появляются новые калькуляторы, а алгоритмы работы совершенствуются.
Строительный калькулятор KALK.PRO – это комплексный инструмент для решения математических, инженерных и проектировочных задач с возможностью автоматизации типовых операций. С нашей помощью запутанные и утомительные расчеты исчезнут навсегда.
Также использование такого калькулятора позволяет легко построить графики различной сложности. Поэтому, его могут использовать и школьники, и студенты, и преподаватели математики, и аспиранты. Такое онлайн чудо широко используется в бухгалтерии, в современном бизнесе, а также в иных направлениях, которые связаны с постоянными вычислениями различной сложности.
Использование онлайн калькулятора очень удобно. Ведь вы можете им пользоваться с любого компьютерного устройства, находясь в любом месте, а самое главное, в любое время. Ведь некоторые из нас иногда предпочитают работать в ночное время. Заметим, для этого только нужен доступ к интернету. Также вы должны знать, что использование такого калькулятора всегда происходит бесплатно. Не стоит также волноваться за своевременную регистрацию. Она в данном случае, совершенно не нужна.
Вам не стоит переживать по поводу того, что онлайн калькулятор сложный в использовании. Поверьте, вы самостоятельно разберетесь во всех его функциях, не смотря на то, что инструкции на русском языке нет. Вы сможете найти в окне самого онлайн калькулятора специальный видеоурок, который даст возможность узнать, как работает калькулятор. Правда, некоторым пользователям этого будет не совсем достаточно, для того, чтобы воспользоваться всеми функциями такого помощника.
Но расстраиваться вам не стоит. Сегодня на многих сайтах можно найти прекрасные подсказки по использованию онлайн калькулятором. Пользователям на самом доступном языке разъясняют все обозначения, все математические тонкости, а также предлагают примеры вычислений. Благодаря этому, вы самостоятельно можете во всем разобраться. Единственное, что каждому из нас понадобиться разное время на то, чтобы все понять. Для удобства, мы рекомендуем просто скачать подобную инструкцию и иметь ее всегда под рукой. Благодаря своей уникальности, на нем можно выполнять, как самые простые вычисления (сложения, вычитания, деление и пр.), так и самые сложные, которые используют в работе ученые и инженеры.
Для того чтобы задавать необходимые функции нужно использовать мышку (как для обычного компьютера), а также кнопки на клавиатуре. Наводите на нужные кнопочки и легко получаете правильный ответ за очень короткое время. Заметим, что при использовании такого Online калькулятора, вы никогда не будете получать неправильные ответы. Поэтому, смело пользуйтесь таким компьютерным «гением». Это намного упростит и облегчит вашу работу. Мы советуем пользоваться вышеупомянутым калькулятором и учащимся старших классов. Это позволит детям быстрее разобраться во всех математических премудростях онлайн «умельца». Будучи студентами ВУЗов, они легко и быстро будут справляться с заданиями различной сложности.
Кнопки калькулятора
В списке ниже указаны все клавиши калькулятора и выполняемые ими операции.
| Клавиша | Символ | Операция |
|---|---|---|
| pi | pi | Постоянная pi |
| е | е | Число Эйлера |
| % | % | Процент |
| ( ) | ( ) | Открыть/Закрыть скобки |
| , | , | Запятая |
| sin | sin(α) | Синус угла |
| cos | cos(β) | Косинус |
| tan | tan(y) | Тангенс |
| sinh | sinh() | Гиперболический синус |
| cosh | cosh() | Гиперболический косинус |
| tanh | tanh() | Гиперболический тангенс |
| sin-1 | asin() | Обратный синус |
| cos-1 | acos() | Обратный косинус |
| tan-1 | atan() | Обратный тангенс |
| sinh-1 | asinh() | Обратный гиперболический синус |
| cosh-1 | acosh() | Обратный гиперболический косинус |
| tanh-1 | atanh() | Обратный гиперболический тангенс |
| x2 | ^2 | Возведение в квадрат |
| х3 | ^3 | Возведение в куб |
| xy | ^ | Возведение в степень |
| 10x | 10^() | Возведение в степень по основанию 10 |
| ex | exp() | Возведение в степень числа Эйлера |
| √x | sqrt(x) | Квадратный корень |
| 3√x | sqrt3(x) | Корень 3-ей степени |
| y√x | sqrt(x,y) | Извлечение корня |
| log2x | log2(x) | Двоичный логарифм |
| log | log(x) | Десятичный логарифм |
| ln | ln(x) | Натуральный логарифм |
| logyx | log(x,y) | Логарифм |
| I / II | Сворачивание/Вызов дополнительных функций | |
| Unit | Конвертер величин | |
| Matrix | Матрицы | |
| Solve | Уравнения и системы уравнений | |
| Построение графиков | ||
| Дополнительные функции (вызов клавишей II) | ||
| mod | mod | Деление с остатком |
| ! | ! | Факториал |
| i / j | i / j | Мнимая единица |
| Re | Re() | Выделение целой действительной части |
| Im | Im() | Исключение действительной части |
| |x| | abs() | Модуль числа |
| Arg | arg() | Аргумент функции |
| nCr | ncr() | Биноминальный коэффициент |
| gcd | gcd() | НОД |
| lcm | lcm() | НОК |
| sum | sum() | Суммарное значение всех решений |
| fac | factorize() | Разложение на простые множители |
| diff | diff() | Дифференцирование |
| Deg | Градусы | |
| Rad | Радианы | |
Bendingmomentdiagram.com — это бесплатный онлайн-калькулятор, который генерирует диаграммы изгибающего момента (BMD) и диаграммы силы сдвига (SFD) для большинства простых балок. Калькулятор полностью настраивается под большинство лучей; эта функция недоступна в большинстве других калькуляторов. Программное обеспечение разработано на основе SkyCiv — мощного программного обеспечения для структурного анализа и проектирования в облаке.




Инструмент полностью функционален, поэтому посетите наше Бесплатное программное обеспечение Beam, чтобы начать! Он будет работать для всех просто поддерживаемых, определяющих лучей и способен принимать точечные нагрузки, сосредоточенные моменты и распределенные нагрузки.Это также чрезвычайно настраиваемый и настраиваемый, чтобы вы могли генерировать свои собственные лучи. Это чрезвычайно точный инструмент, и в отличие от современных калькуляторов, очень удобный для пользователя. Это чрезвычайно полезный инструмент для студентов университетов, колледжей и старших классов, которым утомительно приходится перекраивать МПК и УМД для выполнения заданий и вопросов практики / обучения.
У нас также есть страница учебного пособия, которая поможет студентам университетов с расчетами, ожидаемыми в их инженерном образовании, а также старшеклассникам.Эти студенты могут научиться вычислять и генерировать диаграммы силы сдвига и изгибающего момента, и мы понимаем, что процесс анализа луча иногда может быть трудным, поэтому мы предоставили простое пошаговое руководство по вычислению диаграмм изгибающего момента и силы сдвига. Включены простые уравнения изгибающего момента и формулы, которые хорошо помогают при ваших расчетах. Есть также примеры и генераторы случайных пучков, которые позволят вам поэкспериментировать с тем, как различные нагрузки влияют на анализ пучка, а также на силу сдвига и изгибающий момент пучка.
Bending Moment Diagram разработана командой SkyCiv Engineering, которая предлагает пакеты для студентов и профессионалов, которые предоставляют пользователям доступ к различным программным средствам для проектирования конструкций для выполнения работы. Все учетные записи основаны на подписке, поэтому вы можете платить за программное обеспечение ежемесячно по мере необходимости! Больше никаких проблем с установкой, загрузкой или лицензией!
,учебник Венна по диаграмме и вероятности
Рассмотрим следующие наборы
A = {0.2,0.2,0.1,0.07} В = {0.05,0.05,0.01,0.03} С = {} 0.2,0.06 На диаграмме Венна множества A, B, C представлены в виде

Расчет P (A)
Вероятность A представлена как P (A) P (A) рассчитывается путем сложения всех значений множества A. P (A) = 0,2 + 0,2 + 0,1 + 0,07 = 0,57 На диаграмме Венна P (A) наглядно представлен как

Расчет P (B)
Вероятность B представляется как P (B) P (B) рассчитывается путем сложения всех значений множества B. P (B) = 0,05 + 0,05 + 0,01 + 0,03 = 0,14 На диаграмме Венна P (B) графически представлен как

Расчет P (AUB)
Вероятность AUB представлена как P (AUB) P (AUB) = P (A) + P (B) = 0,57 + 0,14 = 0,71 На диаграмме Венна P (AUB) графически представлен как

Расчет P (A∩B)
Вероятность A∩B представлена как P (A∩B) P (A∩B) = 0,2 + 0,06 = 0.26 На диаграмме Венна P (A∩B) графически представлен как

Расчет P (A c )
Вероятность A c представлена как P (A c ) P (A c ) = 1-P (A) = 1-0,57 = 0,43 На диаграмме Венна P (A c ) графически представлен как

Расчет P (B c )
Вероятность B c представляется как P (B c ) P (B c ) = 1-P (B) = 1-0.14 = 0,86 На диаграмме Венна P (B c ) графически представлен как

Расчет P (AUB) c
Вероятность AUB c представлена как P (AUB) c P (AUB) c = 1-P (AUB) = 1-0,71 = 0,29
Расчет P (A∩B) c
Вероятность A∩B c представляется как P (A∩B) c P (A∩B) с = 1-P (A∩B) = 1-0.26 = 0,74 На диаграмме Венна P (A∩B) c графически представлено как

Расчет P (A c ∩B c ) c
Вероятность (A c ∩B c ) c представляется как P (A c ∩B c ) c P (A c 900B c ) c = 1-P (A) -P (B) + P (A∩B) = 1-0,57-0,14 + 0,26 = 0,55
Генератор графиков стволов и листьев
Использование калькулятора
Создайте онлайновый стеблевой и листовой график или стемплот и вычислите базовую описательную статистику для выборочного набора данных с 4 или более значениями и до 1000 значений, все не отрицательные. Введите значения через запятую, например 1, 2, 4, 7, 7, 10, 2, 4, 5.
Вы также можете копировать и вставлять строки точек данных из документов, таких как электронные таблицы Excel или текстовые документы, с запятыми или без запятой в форматах, указанных в таблице ниже.
Примечания :
- В настоящее время не обрабатывает значения меньше 0.
- Не обрабатывает десятичные дроби, и они будут усечены. Если вам нужно работать с десятичными знаками, вы можете умножить все свои значения в 10 раз и рассчитать их. Вам просто нужно правильно интерпретировать результаты.
- Если вам действительно нужно работать с отрицательными значениями, пожалуйста пришлите мне запрос на расчет.
Дополнительные описательные статистические значения см. Калькулятор описательной статистики.
Ниже приведен образец стволовой и листовой диаграммы и список рассчитанных статистических значений.
Образец участка ствола и листа с разделенными стеблями
Набор данных:
42, 14, 22, 16, 2, 15, 8, 27, 6, 15, 19, 48, 4, 31, 26, 20, 28, 13, 10, 18, 13, 15, 48, 16, 15 , 5, 18, 16, 28, 11, 0, 27, 28, 5, 40, 21, 18, 7, 12, 6, 40, 12, 2, 20, 35, 3, 16, 13, 8, 15 , 7, 65, 65, 25, 15, 21, 12, 12, 35, 30, 14, 35, 20, 35, 7, 35
Стебель и лист:
1
5 5 5 5 5 5 6 6 6 6 8 8 8 9
Основные статистические формулы и вычисления, используемые в этом калькуляторе
Минимум
Заказ набора данных {x 1 ≤ x 2 ≤ x 3 ≤.{n} x_i} {n} \]
Медиана
При заказе набора данных {x 1 ≤ x 2 ≤ x 3 ≤ … ≤ x n } от младшего до максимального значения, медиана — это числовое значение, отделяющее верхнюю половину упорядоченного образца данные из нижней половины. Если n нечетно, медиана является центральным значением. Если n четное, медиана является средним из двух значений центра.
Если n нечетно, медиана — это значение в позиции p, где
\ [p = \ dfrac {n + 1} {2} \] \ [\ widetilde {x} = x_p \]Если n четное медиана, это среднее значение в позициях p и p + 1, где
\ [p = \ dfrac {n} {2} \] \ [\ widetilde {x} = \ dfrac {x_ {p} + x_ {p + 1}} {2} \]Режим
Значение или значения, которые чаще всего встречаются в наборе данных.{2}} {n — 1} \]
Приемлемый с разделителями
Форматы данных
(Новые строки)
42
54
65
47
59
40
53
42, 54, 65, 47, 59, 40, 53
с разделителями-запятыми (CSV)
42,54,
65,
47,
59,
40,
53,
или
42, 54, 65, 47, 59, 40, 53
42, 54, 65, 47, 59, 40, 53
пробелов
42 5465 47
59 40
53
или
42 54 65 47 59 40 53
42, 54, 65, 47, 59, 40, 53
Смешанные разделители
42
54 65 ,,, 47,, 59,
40 53
42, 54, 65, 47, 59, 40, 53
,Калькулятор площади
Ниже приведены калькуляторы для оценки площади семи общих фигур. Область более сложных форм обычно можно получить, разбив их на совокупные простые формы и суммируя их площади. Этот калькулятор особенно полезен для оценки земельной площади.

Прямоугольник
 |
Треугольник
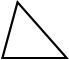
Используйте калькулятор треугольников для определения |
Трапеция
 |
Круг
 |
Сектор
 |
Эллипс
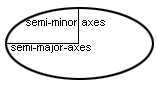 |
Параллелограмм
 |
Калькулятор площади поверхности | Калькулятор объема
Площадь — это величина, которая описывает размер или протяженность двумерной фигуры или фигуры на плоскости.Он может быть визуализирован как количество краски, которое необходимо для покрытия поверхности, и является двумерным аналогом одномерной длины кривой и трехмерного объема твердого тела. Стандартной единицей площади в Международной системе единиц (СИ) является квадратный метр или м 2 . Ниже приведены уравнения для некоторых наиболее распространенных простых форм и примеры расчета площади каждой из них.
Прямоугольник
Прямоугольник — это четырехугольник с четырьмя прямыми углами.Это одна из самых простых форм, и для расчета ее площади необходимо знать только ее длину и ширину (или их можно измерить). Четырехугольник по определению — это многоугольник, имеющий четыре ребра и вершины. В случае прямоугольника длина обычно относится к более длинным двум краям четырехугольника, тогда как ширина относится к более короткому из двух краев. Когда длина и ширина прямоугольника равны, форма представляет собой особый случай прямоугольника, называемого квадратом. Уравнение для расчета площади прямоугольника выглядит следующим образом:
площадь = длина × ширина
Фермер и его дочь — непроданная земля
Представьте себе фермера, пытающегося продать участок земли, который оказывается совершенно прямоугольным.Поскольку он владеет некоторыми коровами, которых он не хотел свободно резвиться, он ограждает участок земли и знает точную длину и ширину каждого края. Фермер также живет в Соединенных Штатах и, будучи незнакомым с использованием единиц СИ, по-прежнему измеряет свой участок земли в футах. Ступня была определена как точно 0,3048 метра в 1959 году после того, как она менялась в течение длительного периода времени, поскольку исторически сложилось, что человеческое тело часто использовалось как основа для единиц длины, и, что неудивительно, было непоследовательным в зависимости от времени и места.Касаясь в стороне, участок земли фермера имеет длину 220 футов и ширину 99 футов. Используя эту информацию:
площадь = 220 × 99 = 21780 кв. Футов
Земельный участок фермера, площадь которого составляет 21 780 квадратных футов, равняется половине акра, где акр определяется как площадь 1 цепи на 1 фарлонг, которая определяется чем-то другим, и так далее, и является почему СИ сейчас существует. К сожалению для фермера, он живет в районе, где преобладают иностранные инвесторы с меньшими ногами, которые чувствовали, что им следует получать больше квадратных футов за свои деньги, и его земля остается непроданной сегодня.
Треугольник
Существует много уравнений для расчета площади треугольника на основе доступной информации. Как упомянуто в калькуляторе выше, используйте Калькулятор треугольника для получения дополнительной информации и уравнений для расчета площади треугольника, а также определения сторон треугольника с использованием любой доступной информации. Вкратце, уравнение, используемое в калькуляторе, представленном выше, известно как формула Герона (иногда называемая формулой Героя), ссылаясь на героя Александрийского, греческого математика и инженера, которого некоторые считают величайшим экспериментатором древних времен.Формула выглядит следующим образом:
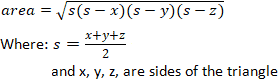
Фермер и его дочь — Треугольник Daze
На данный момент, благодаря чрезвычайным усилиям и настойчивости, фермер наконец продал свой участок земли площадью 21 780 кв. Футов и решил использовать часть заработанных денег, чтобы построить бассейн для своей семьи. К сожалению для фермера, он не учитывает тот факт, что расходы на содержание бассейна в течение одного года могут, вероятно, заплатить его детям за посещение любого бассейна или аквапарка на долгие годы.Еще больше, к сожалению, для фермера, его 7-летняя дочь, недавно отправившаяся в Египет из-за Доры Исследователь, влюбилась в треугольники и настаивает на том, что бассейн не только имеет треугольную форму, но и что размеры нужно только включить число 7, чтобы представить ее возраст и увековечить этот момент ее жизни в виде треугольного пула. Будучи любящим отцом, фермер соглашается на просьбу своей дочери и приступает к планированию строительства своего треугольного бассейна.Теперь фермер должен определить, достаточно ли у него на заднем дворе места для размещения бассейна. В то время как фермер начал больше узнавать о единицах СИ, он все еще испытывает неудобство от их использования и решает, что его единственно возможный вариант — построить пул в форме равностороннего треугольника со сторонами длиной 77 футов, поскольку любые другие варианты будет либо слишком большим, либо маленьким. Учитывая эти размеры, фермер определяет необходимую площадь следующим образом:
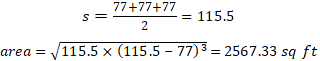
Поскольку самое длинное расстояние между любыми двумя точками равностороннего треугольника равно длине края треугольника, фермер резервирует края бассейна для плавания «кругов» в своем треугольном бассейне с максимальной длиной, приблизительно равной длине олимпийского бассейн, но с удвоенной площадью — все под пристальным взглядом председательствующей королевы бассейна, его дочери и неодобрительного взгляда его жены.
Трапеция
Трапеция — это простой выпуклый четырехугольник, имеющий как минимум одну пару параллельных сторон. Свойство быть выпуклым означает, что угол трапеции не превышает 180 ° (в отличие от вогнутого четырехугольника), хотя простота отражает то, что трапеции не являются самопересекающимися, то есть две несмежные стороны не пересекаются. В трапеции параллельные стороны называются основаниями трапеции, а две другие стороны называются ножками.Существует больше различий и классификаций для различных типов трапеций, но их площади все еще рассчитываются таким же образом, используя следующее уравнение:
где b 1 и b 2 являются основаниями. h — высота или перпендикулярное расстояние между основаниями
Фермер и его дочь — стремительные усилия
Прошло два года с тех пор, как фермерский бассейн был закончен, а его дочь выросла и повзрослела.Хотя ее любовь к треугольникам все еще сохраняется, в конце концов она пришла к пониманию, что как бы она ни была «треугольной», одни только треугольники не могут заставить мир вращаться, и что мастерская Санты не могла правдоподобно балансировать на Северном полюсе, если бы мир пирамида, а не сфера. Постепенно она начала принимать другие формы в своей жизни и преследует свои многочисленные интересы — в настоящее время фристайл BMX. Таким образом, она требует рампы, но, к сожалению, для фермера, а не просто рампы.Пандус должен состоять только из форм, которые могут быть сформированы с использованием нескольких треугольников, поскольку, как и ее рэп-идол Б.О.Б, дочь фермера все еще испытывает трудности с принятием реальности изогнутых поверхностей. Он должен, конечно, также использовать только число 9 в его измерениях, чтобы отразить ее возраст. Фермер решает, что его лучший вариант — построить пандус, состоящий из нескольких прямоугольников, причем боковая сторона пандуса имеет форму трапеции. Поскольку фермеру стало удобнее работать с СИ, он может быть более креативным с использованием единиц измерения и может построить рампу более разумного размера, придерживаясь требований своей дочери.Он решает построить пандус с трапециевидной гранью высотой 9 футов, нижним основанием длиной 29,528 футов (9 м) и верхним основанием 9 футов. Площадь трапеции рассчитывается следующим образом:
| площадь = | × 9 = 173,376 кв. Футов |
Круг
Круг — это простая замкнутая форма, образованная набором всех точек на плоскости, которые находятся на заданном расстоянии от заданной центральной точки. Это расстояние от центра до любой точки круга называется радиусом.Более подробную информацию о кругах можно найти на странице Калькулятор окружностей, но для вычисления площади необходимо знать только радиус и понимать, что значения в окружности связаны через математическую константу π . Уравнение для расчета площади круга выглядит следующим образом:
площадь = № 2
Фермер и его дочь — круг Ли (е) эс
Прошло еще шесть лет, и его дочь выросла в сильного, красивого, могущественного, уверенного в себе 15-летнего подростка, который был сосредоточен исключительно на поиске внешнего одобрения от знакомых и незнакомцев в социальных сетях, в то же время искренне игнорируя подлинную поддержку ближайших родственников и друзей. ,Поспорив с отцом о чрезмерном использовании социальных сетей, она решает охотиться на страх отца перед неизвестным и на веру в сверхъестественное, чтобы разыграть его. Не зная, с чего начать, она гуляет по городу, разговаривая с множеством незнакомцев, у каждого из которых, по-видимому, есть бесконечные источники мудрости и советов, где она узнает о кругах на полях и их связи с инопланетянами и неопознанными летающими объектами, а также о многих других темах, которые игнорировать все научные и логические объяснения.В конце концов убедившись в сферической природе Земли, удалила все свои прошлые посты в социальных сетях, связанные с BoB, и расширила свою любовь к треугольникам до принятия других форм, она решает сделать основной круг на полях, состоящий из ряда концентрических круги, и хочет определить площадь, необходимую для создания круга на полях с внешним радиусом 15 футов. Она делает это, используя следующее уравнение:
площадь = π × 15 2 = 706,858 кв. Футов
К сожалению для фермера, он не только напуган кругом на полях, который появился накануне ночью, когда его дочь сказала ему, что она была на дремоте с друзьями, что по какой-то странной причине не привело к лишним постам в Instagram (он был, конечно, первым последователем его дочери), но число «исследователей круга» и «цеологов», появившихся на его ферме, чтобы осмотреть и впоследствии подтвердить подлинность круга на полях как инопланетное сооружение, стоило ему значительного ущерба его посевам ,
Сектор
Сектор круга — это, по сути, пропорция круга, ограниченного двумя радиусами и дугой. Учитывая радиус и угол, площадь сектора может быть рассчитана путем умножения площади всего круга на отношение известного угла к 360 ° или 2π радиан, как показано в следующем уравнении:
| площадь = | × № 2 | , если θ в градусах |
или
| площадь = | × № 2 | , если θ в радианах |
Фермер и его дочь — Секционирующая семья
Фермер и его семья сталкиваются с самой серьезной на сегодняшний день дилеммой.Прошел год, и дочери фермера сейчас 16 лет, и в рамках празднования ее дня рождения ее мать испекла свой любимый десерт — ежевичный пирог. К несчастью для дочери фермера, пирог с ежевикой также является любимой едой их любимого енота, утконоса, о чем свидетельствует отсутствие пирога на 180 ° с явными признаками преступника в виде крошек, ведущих к излишне любопытному еноту. Изначально пирог можно было легко разделить между тремя людьми и одним енотом, но теперь половину пирога нужно разделить между тремя людьми как огорченные, но сытые часы из утконоса на расстоянии.Учитывая, что каждый человек получит пирог на 60 ° с радиусом 16 дюймов, площадь пирога, которую получает каждый человек, может быть рассчитана следующим образом:
Площадь= 60 ° / 360 ° × π × 16 2 = 134,041 в 2
В результате неосмотрительности Утконоса каждый человек получает на одну треть меньше пирога, а дочь созерцательно вспоминает урок американской истории, где она узнала о битве при Аламо и изображении народного героя Дейви Крокетта и его шляпы енота.
Эллипс
Эллипс является обобщенной формой окружности и представляет собой кривую в плоскости, в которой сумма расстояний от любой точки кривой до каждой из двух ее фокусных точек постоянна, как показано на рисунке ниже, где Р любая точка на эллипсе, и F 1 и F 2 являются двумя фокусами.
Когда F 1 = F 2 , полученный эллипс представляет собой круг. Большая полуось эллипса, как показано на рисунке, являющемся частью калькулятора, является самым длинным радиусом эллипса, а малая ось — самой короткой.Большая и малая оси относятся к диаметрам, а не к радиусам эллипса. Уравнение для расчета площади эллипса аналогично уравнению для вычисления площади круга, с той лишь разницей, что используются два радиуса, а не один (поскольку фокусы находятся в одном и том же месте для круга):
area = πab
, где a и b — полу мажорные
и малые оси
Фермер и его дочь — падение с орбиты
Прошло два года с тех пор, как загадочное исчезновение домашнего питомца, утконоса, и случайная победа дочери фермера за пушистым аксессуаром в школьной лотерее, которая помогла заполнить пустоту потери их любимого питомца.Дочке фермера сейчас 18 лет, и он готов сбежать из сельской Монтаны для жизни в колледже, изобилующей свободой и развратом, и, конечно, некоторого обучения на стороне. К несчастью для дочери фермера, она выросла в обстановке, наполненной позитивным подкреплением, а впоследствии и менталитетом, согласно которому следует «стрелять на Луну [с тех пор], даже если вы пропустите, вы окажетесь среди звезд», а также утверждение всех окружающих, что она может делать абсолютно все, на что она рассчитывает! Таким образом, с ее неоптимальными оценками, отсутствием каких-либо внеклассных занятий из-за того, что ее бесчисленные интересы занимают все ее свободное время, нулевое планирование и ее настойчивость только при поступлении в самые лучшие из лучших университетов, шок, который возник, когда она не была принята ни в один из университетов высшего уровня, к которым она обращалась, ее можно было бы разумно сравнить с ее метафорическим приземлением в глубоком космосе, надуванием, замерзанием и быстрым удушьем, когда она пропустила луну и приземлилась среди звезд.Наряду с ее легкими, ее мечта стать астрофизиком была в итоге разрушена, по крайней мере, на какое-то время, и она была вынуждена рассчитать эллиптическую площадь, необходимую в ее комнате, чтобы построить человеческую модель земной околоплоскостной орбиты вокруг Солнца, так что она могла с тоской смотреть на солнце в центре своей комнаты и на его олицетворение ее сердца, пылающего страстью, но окруженного холодными просторами космоса, а далекие вращения Земли насмешливо представляли расстояние между ее мечтами и твердую землю ,
площадь = π × 18 футов × 20 футов = 1130,97 кв. Футов
параллелограмм
Параллелограмм — это простой четырехугольник, который имеет две пары параллельных сторон, где противоположные стороны и углы четырехугольника имеют равные длины и углы. Прямоугольники, ромбы и квадраты — все это частные случаи параллелограммов. Помните, что классификация «простой» формы означает, что форма не является самопересекающейся. Параллелограмм можно разделить на прямоугольный треугольник и трапецию, которую можно дополнительно переставить, чтобы сформировать прямоугольник, делая уравнение для вычисления площади параллелограмма, по существу, таким же, как уравнение для вычисления прямоугольника.Однако вместо длины и ширины параллелограмм использует основание и высоту, где высота — это длина перпендикуляра между парой оснований. Исходя из рисунка ниже, уравнение для расчета площади параллелограмма выглядит следующим образом:
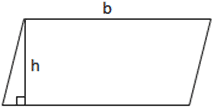
площадь = б × ч
Фермер и его дочь — Бриллиант в небе
Прошло еще два года в жизни фермера и его семьи, и хотя его дочь вызывала сильное беспокойство, она, наконец, преодолела расстояние между пылающим солнцем, которое является ее сердцем, и Землей, на которой настаивает общество она должна оставаться заземленной.Из-за борьбы, которая последовала за ее добровольной изоляцией, окруженной воображаемыми, осуждающими глазами, предполагающими ее неудачу со всех сторон, дочь фермера вышла из-под давления земли как алмаз, ярко сияя и твердо решая ее. Несмотря на все ее недостатки, она решает, что у нее нет иного выбора, кроме как остаться в астероидном поле жизни в надежде, что окончание сказки Диснея существует. В конце концов, к счастью для дочери фермера и ее семьи, надежда действительно появляется, но не в виде очаровательного принца, а скорее как знак от предполагаемых небес.Через все ее метафорические размышления и невзгоды, связанные с космосом, становится почти правдоподобным, что дочь фермера каким-то образом повлияла на массивный восьмигранный алмазный астероид, падающий прямо, но безопасно на их сельхозугодья, которые она интерпретирует как представляющие ее путешествие, образование и возможное возвращение домой. Дочь фермера продолжает измерять площадь одного из ромбовидных граней своего недавно найденного символа жизни:
площадь = 20 футов × 18 футов = 360 кв. Футов
К сожалению для дочери фермера, появление огромного алмаза привлекло внимание всего мира, и после достаточного давления она уступает человеку внутри себя и продает алмаз, само представление ее жизни и души, богатый коллекционер и продолжает проживать остаток своей жизни в щедрой снисходительности, отказываясь от своих убеждений и теряя себя в черной дыре общества.
единиц общего пользования
| Единица | Площадь в м 2 |
| квадратных метров | СИ Единица |
| га | 10000 |
| квадратных километров (км 2 ) | 1 000 000 |
| квадратных футов | 0,0929 |
| квадратный ярд | 0,8361 |
| акров | 4,046.9 (43 560 квадратных футов) |
| квадратных миль | 2 589 988 (640 акров) |

