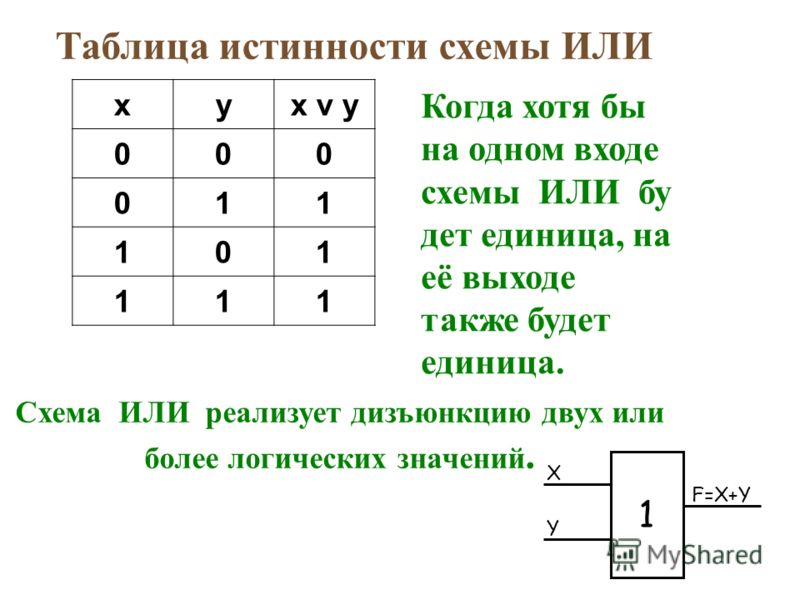
Что такое логические схемы и элементы. Как работают базовые логические элементы И, ИЛИ, НЕ. Как строятся таблицы истинности для логических схем. Какие бывают типы триггеров и как они используются в цифровой электронике.
Основные логические элементы и их функции
Логические элементы — это базовые компоненты цифровых электронных схем, выполняющие простейшие логические операции над входными сигналами. Основными логическими элементами являются:
- И (AND) — выход равен 1, только если все входы равны 1
- ИЛИ (OR) — выход равен 1, если хотя бы один вход равен 1
- НЕ (NOT) — инвертирует входной сигнал
Рассмотрим подробнее принцип работы этих элементов:
Логический элемент И
Элемент И имеет два или более входа и один выход. Выходной сигнал равен 1 только в том случае, если все входные сигналы равны 1. В остальных случаях на выходе будет 0.
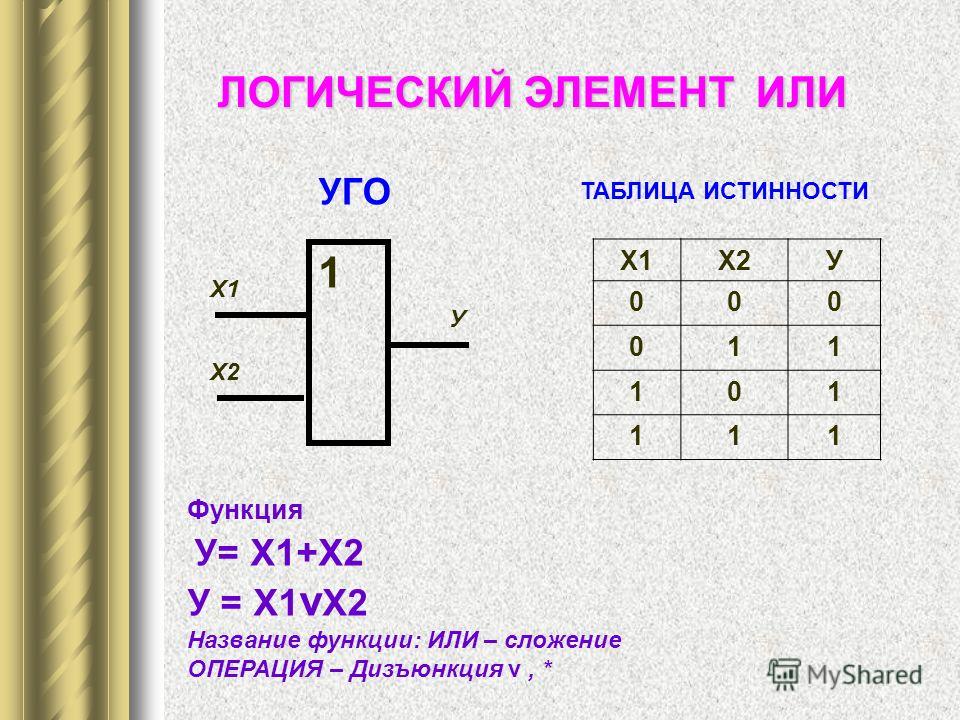
Логический элемент ИЛИ
Элемент ИЛИ также имеет несколько входов и один выход. Выходной сигнал равен 1, если хотя бы на одном из входов присутствует 1. Только когда все входы равны 0, на выходе будет 0.

Логический элемент НЕ
Элемент НЕ имеет один вход и один выход. Он инвертирует входной сигнал — если на входе 1, то на выходе 0, и наоборот.
Таблицы истинности логических элементов
Таблица истинности — это способ описания работы логического элемента, показывающий соответствие между входными и выходными сигналами. Рассмотрим таблицы истинности для основных элементов:
Таблица истинности элемента И
| Вход A | Вход B | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Таблица истинности элемента ИЛИ
| Вход A | Вход B | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Таблица истинности элемента НЕ
| Вход | Выход |
|---|---|
| 0 | 1 |
| 1 | 0 |
Применение логических элементов в цифровых схемах
Логические элементы являются строительными блоками для создания более сложных цифровых устройств. Из них конструируются:
- Триггеры — схемы для хранения одного бита информации
- Регистры — для хранения нескольких битов
- Счетчики — для подсчета импульсов
- Сумматоры — для выполнения арифметических операций
- Мультиплексоры — для коммутации сигналов
Эти базовые узлы, в свою очередь, используются для создания более сложных устройств, таких как процессоры, память и другие компоненты компьютеров.

Типы триггеров и их применение
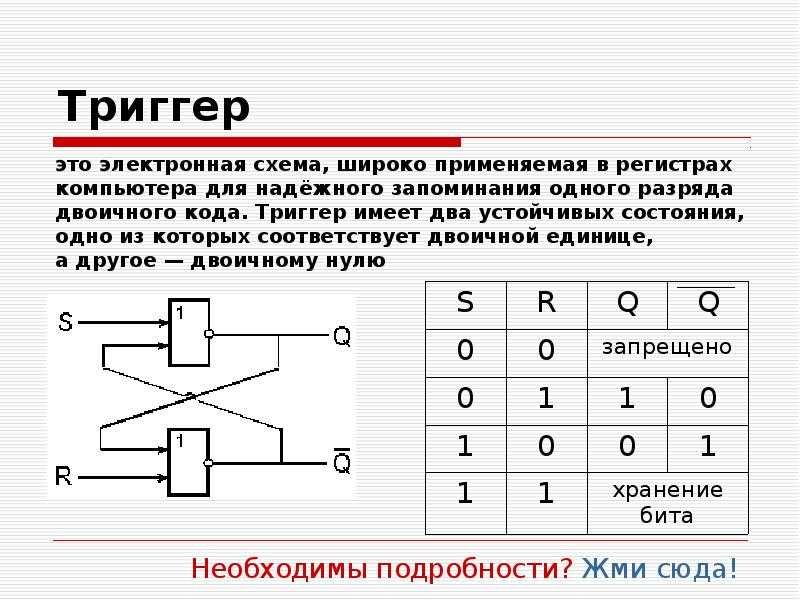
Триггер — это устройство с двумя устойчивыми состояниями, способное хранить 1 бит информации. Основные типы триггеров:
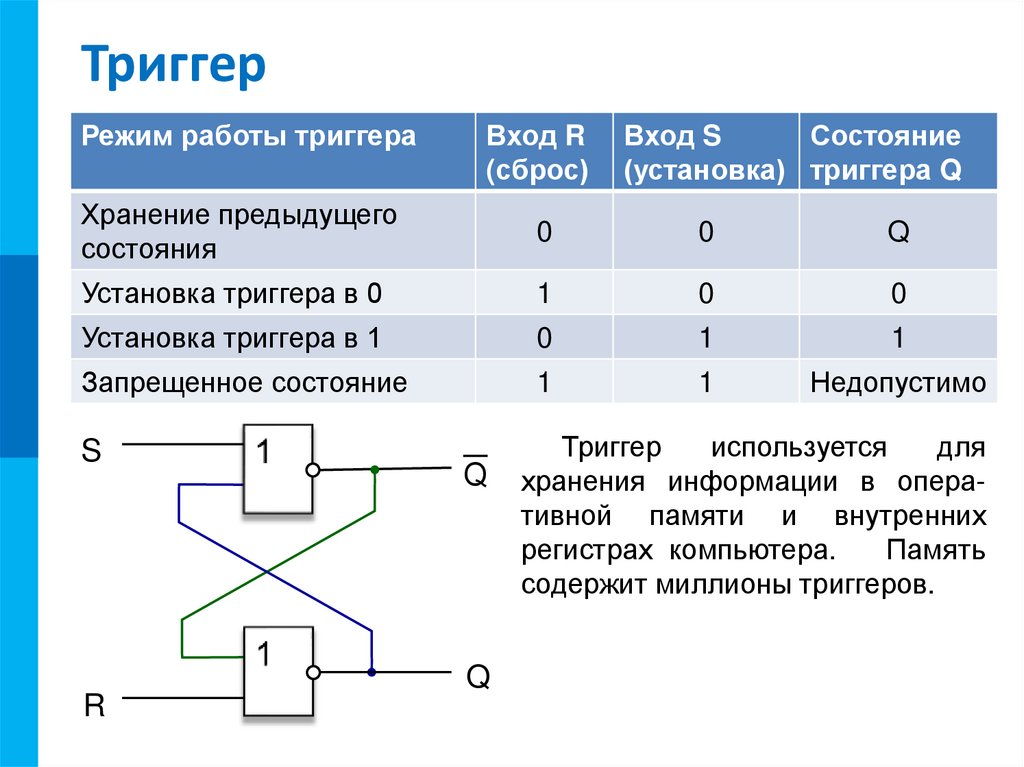
RS-триггер
Простейший тип триггера с двумя входами — Set (установка) и Reset (сброс). Имеет «запрещенное» состояние при одновременной подаче сигналов на оба входа.
D-триггер
Имеет один информационный вход D и вход синхронизации C. При подаче импульса на вход C запоминает состояние входа D.
T-триггер
Меняет свое состояние на противоположное при подаче импульса на вход T. Используется в счетчиках.
JK-триггер
Универсальный триггер, объединяющий свойства RS- и T-триггеров. Не имеет запрещенных состояний.
Триггеры широко применяются в регистрах, счетчиках, делителях частоты и других цифровых устройствах для хранения и преобразования информации.
Построение сложных логических схем
Сложные логические схемы строятся путем комбинирования базовых логических элементов. При проектировании таких схем используются следующие этапы:
- Определение требуемой функциональности схемы
- Составление таблицы истинности
- Запись логической функции по таблице истинности
- Минимизация логической функции
- Построение схемы на основе минимизированной функции
Для минимизации логических функций применяются методы алгебры логики и карты Карно. Это позволяет уменьшить количество используемых элементов и упростить схему.
Программируемые логические интегральные схемы (ПЛИС)
ПЛИС — это микросхемы, логика работы которых не определена при изготовлении, а задается посредством программирования. Основные преимущества ПЛИС:
- Возможность быстрого прототипирования цифровых устройств
- Гибкость и возможность изменения логики работы
- Параллельная обработка данных
- Низкая стоимость при мелкосерийном производстве
ПЛИС широко применяются в системах цифровой обработки сигналов, телекоммуникационном оборудовании, системах управления и других областях.
Заключение
Логические схемы и элементы являются фундаментом современной цифровой электроники. Понимание принципов их работы необходимо для проектирования и анализа цифровых устройств. С развитием технологий роль программируемой логики возрастает, открывая новые возможности для создания гибких и эффективных цифровых систем.
Цифровые логические схемы и системы
Цифровое управление — сравнительно новая область в электронике. Оно ведет свое происхождение от теории связи. Цифровое управление охватывает компьютерную технику, электронные АТС, промышленные системы управления, системы обработки данных и множество других подобных систем. Цифровые приборы работают в дискретном режиме, обычно ON (включено) или OFF (выключено). Главной и неотъемлемой особенностью цифрового прибора является переход из одного состояния в другое без «остановки» в каком-либо промежуточном положении.
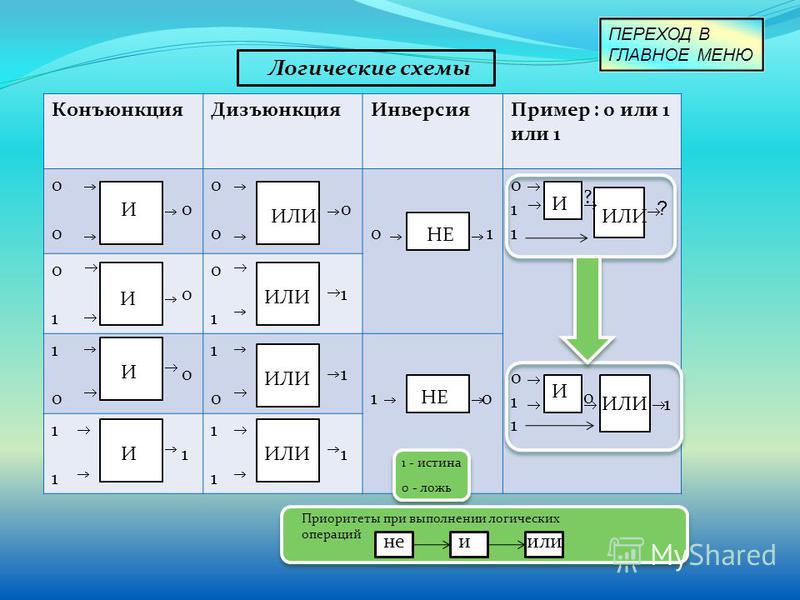
Логические схемы
Логические элементы, или схемы, — это цифровые приборы, которые имеют на выходе одно из двух состояний: нулевой выход (обозначается 0) и фиксированный выход (обозначается 1). Логическая схема может иметь несколько входов и только один выход.
Логическая схема И (рис. 11.1)
Схема И выдает на выходе логическую 1, когда на все ее входы подан сигнал, соответствующий логической 1. На рис. 11.1 показана схема И с двумя входами. Ее выход равен 1 только в том случае, если и на вход А, и на вход В подана 1. В табл. 11.1 функция И представлена в виде так называемой таблицы истинности.
На рис. 11.1 показана схема И с двумя входами. Ее выход равен 1 только в том случае, если и на вход А, и на вход В подана 1. В табл. 11.1 функция И представлена в виде так называемой таблицы истинности.
На рис. 11.2 показаны типичные формы входных и выходных сигналов.
|
Входы |
Выход |
|
|
А |
|
|
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Таблица 11. 1. Таблица истинности схемы И
1. Таблица истинности схемы И
Таблица 11.2. Таблица истинности схемы И-НЕ
|
Входы |
Выход |
|
|
А |
В |
|
|
0 |
0 |
|
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Рис. 11.1. Схема И.
11.1. Схема И.
Рис. 11.2. Входные и выходные импульсные сигналы в схеме И с двумя входами
Рис. 11.3. Схема Рис. 11.4. Входные и выходныеимпульсные Рис. 11.5. Схема ИЛИ.
И-НЕ. сигналы в схеме И-НЕ с двумя входами.
Обратите внимание, что на выходе логическая 1 появляется только тогда, когда на обоих входах присутствует 1.
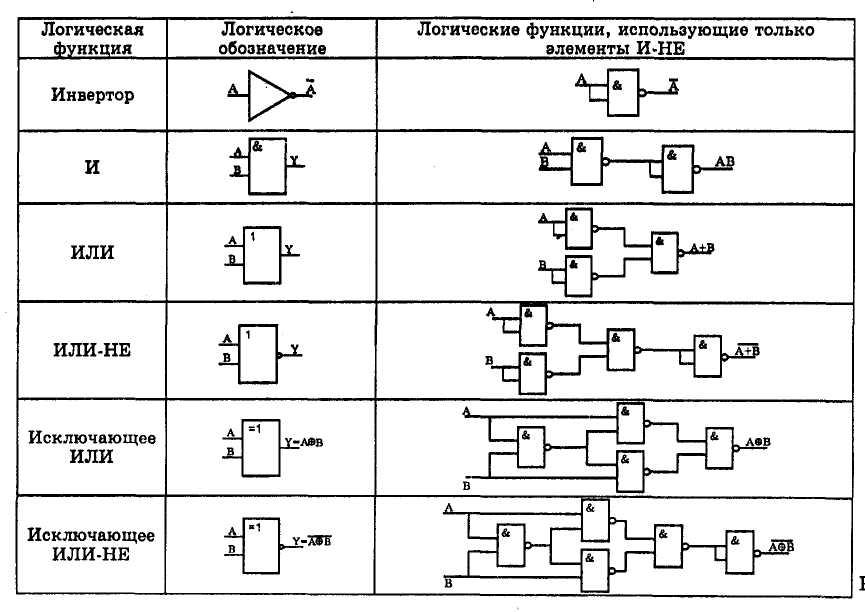
Логическая схема И-НЕ (рис. 11.3 и табл. 11.2)
Логическая схема И-НЕ имеет на выходе логический 0, когда на все ее входы поданы сигналы, соответствующие логической 1. И наоборот, если хотя бы на одномиз входов схемы И-НЕ присутствует 0, на ее выходе появляется 1 (см. рис. 11.4). Таким образом, схема И-НЕ является логической противоположностью схемы И.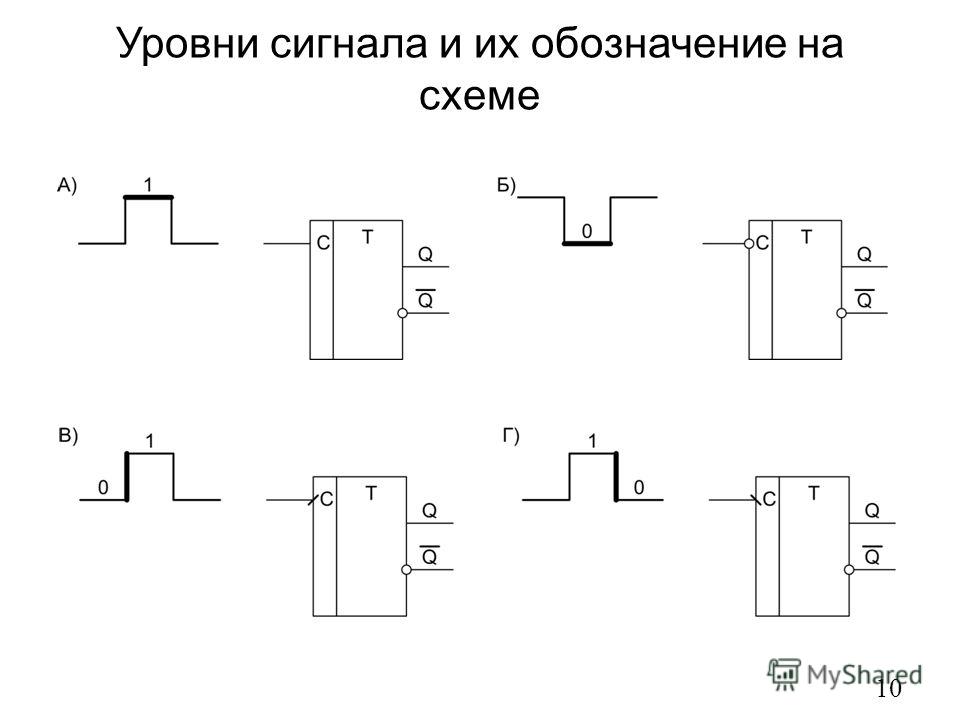
Таблица 11.3.
|
Входы |
Выход |
|
|
А |
В |
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Таблица 11.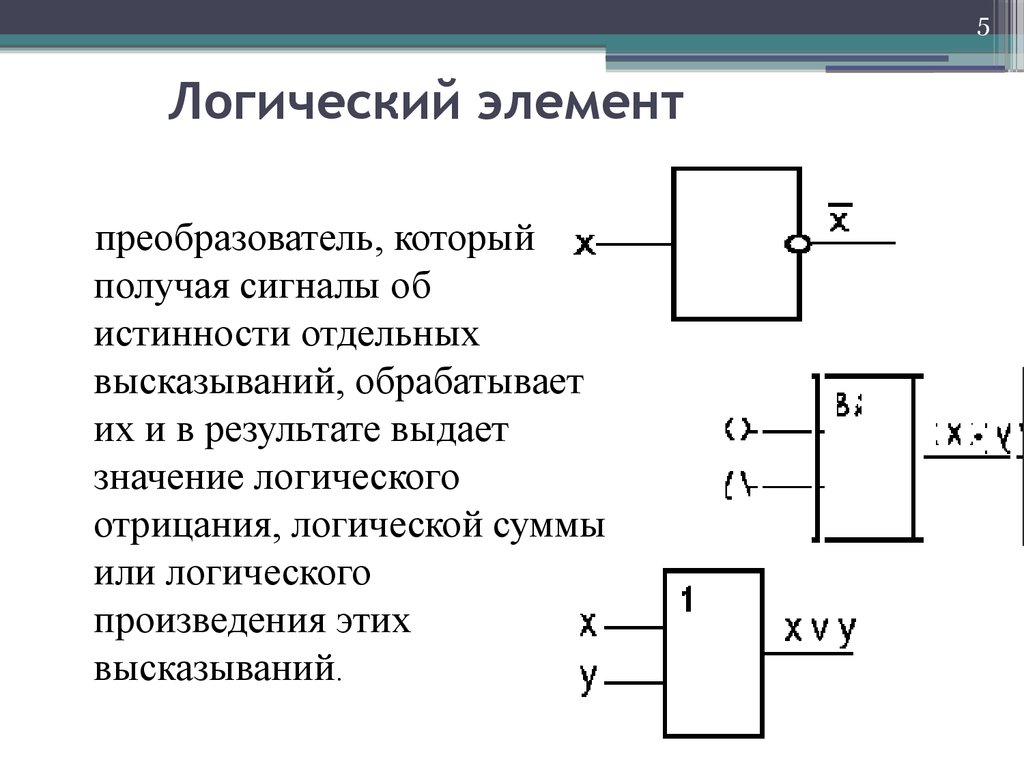 4. Таблица истинности схемы ИЛИ-НЕ
4. Таблица истинности схемы ИЛИ-НЕ
|
Входы |
Выход |
|
|
А |
В |
|
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Рис.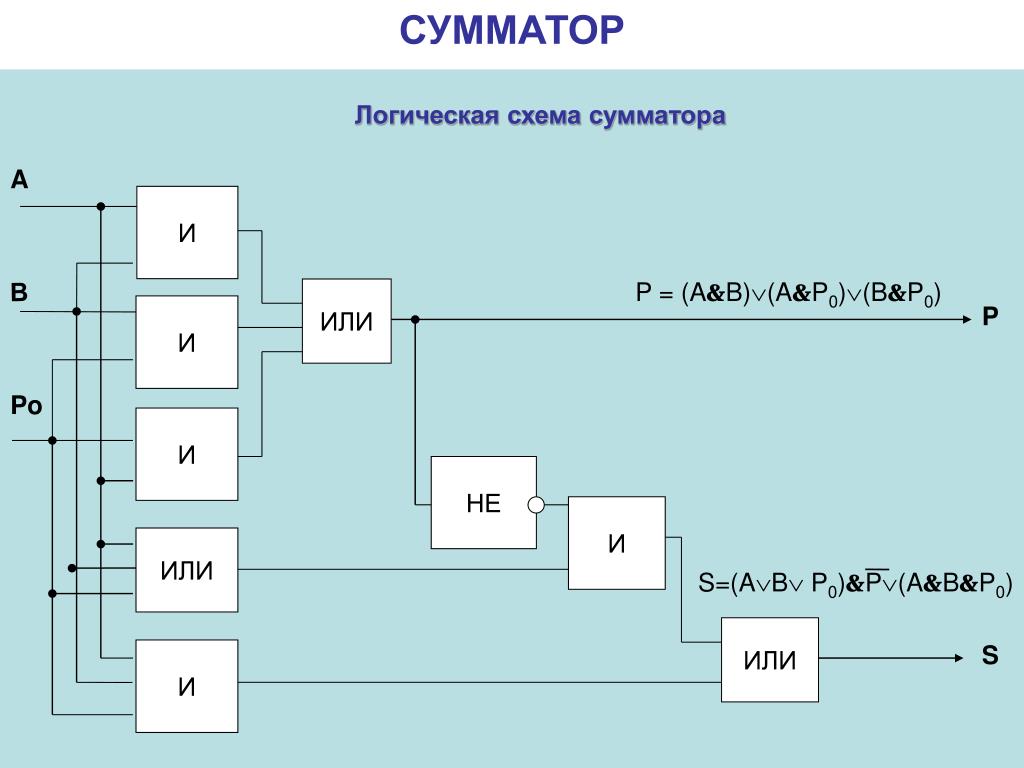 11.6. Схема ИЛИ-НЕ.
11.6. Схема ИЛИ-НЕ.
Рис. 11.7. Входные и выходные импульсные сигналы в схеме ИЛИ-НЕ с двумя входами.
Логическая схема ИЛИ (рис, 11.5 и табл. 11.3)
Логическая схема ИЛИ дает на выходе 1, если хотя бы на одном из ее входов присутствует 1. Логический 0 появляется на ее выходе только в том случае, если на всех ее входах действуют логические 0.
Логическая схема ИЛИ-НЕ (рис. 11.6 и табл. 11.4)
Схема ИЛИ-НЕ дает на выходе 0, если хотя бы на одном ее входе присутствует 1. Логическая 1 появляется на ее выходе только тогда, когда на всех ее входах присутствует логический 0. Таким образом, схема ИЛИ-НЕ является логической противоположностью схемы ИЛИ. На рис. 11.7 показаны типичные формы сигналов, действующих в схеме ИЛИ-НЕ.
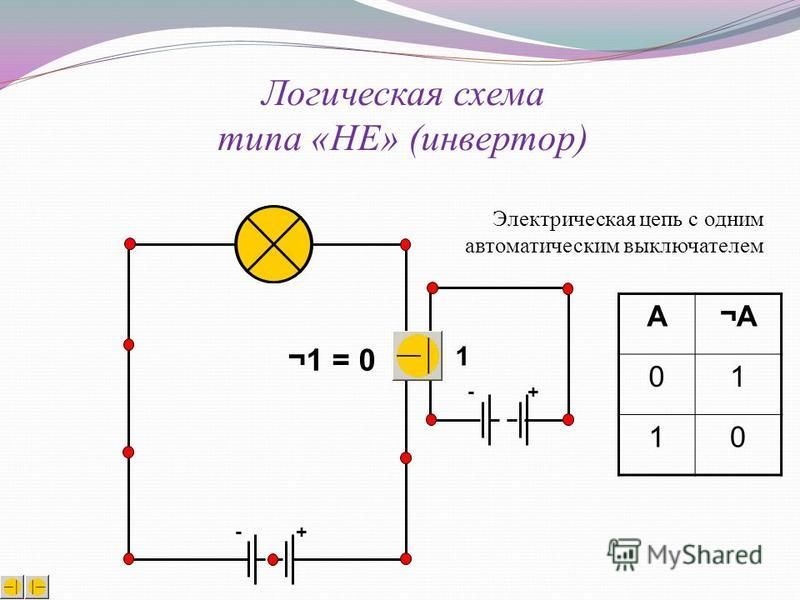
Логическая схема НЕ (рис. 11.8 и табл. 11.5)
Логическая схема НЕ является инвертором. Когда на ее входе присутствует 1, на выходе появляется 0, и наоборот. Если соединить между собой входы логических схем И-НЕ или ИЛИ-НЕ (рис. 11.8(б) и (в)), то
Когда на ее входе присутствует 1, на выходе появляется 0, и наоборот. Если соединить между собой входы логических схем И-НЕ или ИЛИ-НЕ (рис. 11.8(б) и (в)), то
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Рис.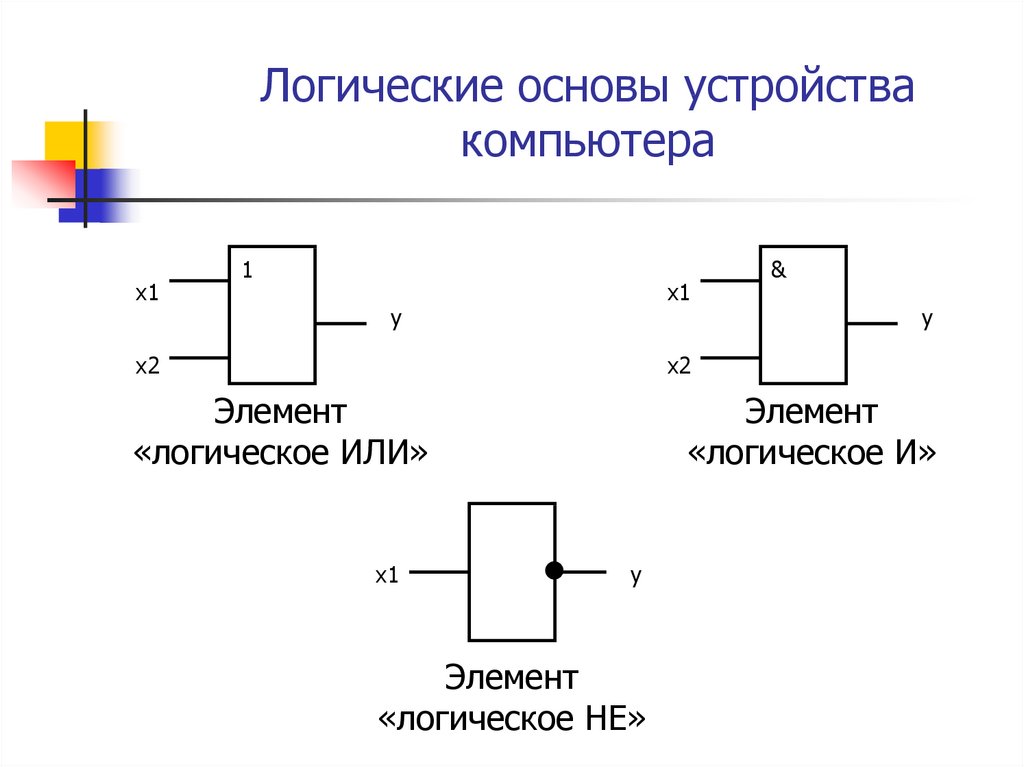 11.8. Схема НЕ.
11.8. Схема НЕ.
Рис. 11.9. Входные и выходные импульсные сигналы в схеме НЕ.
получится схема инвертора. На рис. 11.9 показаны типичные формы сигналов в схеме НЕ.
Логическая схема Исключающее ИЛИ (рис. 11.10 и табл. 11.6)
Логическая схема Исключающее ИЛИ дает на выходе 1, если только на один ее вход подается 1. Если же на обоих входах присутствуют логические 0 или 1, на выходе появляется логический 0.
Логическая схема Исключающее ИЛИ-НЕ (рис. 11Л1 и табл. 11.7)
Схема Исключающее ИЛИ-НЕ дает на выходе 1, когда на обоих ее входах присутствуют логические 0 или 1.
Рис. 11.10. Схема Исключающее ИЛИ.
Рис. 11.11. Схема Исключающее ИЛИ-НЕ,
Международные стандарты и стандарты Великобритании
На рис.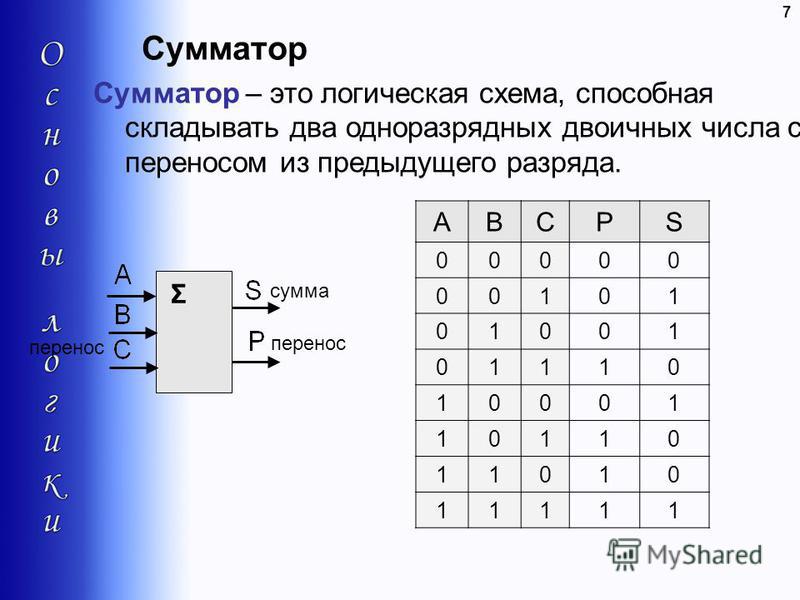 11.12 показаны условные обозначения, утвержденные международным и британским стандартами для изображении логических схем. Сводные таблицы истинности приведены в табл. 11.8.
11.12 показаны условные обозначения, утвержденные международным и британским стандартами для изображении логических схем. Сводные таблицы истинности приведены в табл. 11.8.
Рис. 11.12. Условные обозначения логических схем
Таблица 11.8. Сводные таблицы истинности логических схем
|
Входы |
Выходы |
||||||
|
А |
В |
И |
ИЛИ |
И-НЕ |
ИЛИ-НЕ |
Искл. |
Нскл, ИЛИ-НЕ |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
В видео рассказывается о логических элементах И, ИЛИ, НЕ:
Добавить комментарий
Логические схемы — презентация онлайн
1. Логические схемы
Логические схемы нужны для того чтобы в наглядной графической формеотобразить последовательность выполнения операций при вычислении логических
формул.
Входящие слева линии и цифры около них обозначают значения операндов, линия
справа и соответствующая цифра — результат операции (значение на выходе
логических элементов). 1 — это логическая единица (истина), 0 — логический ноль
(ложь).
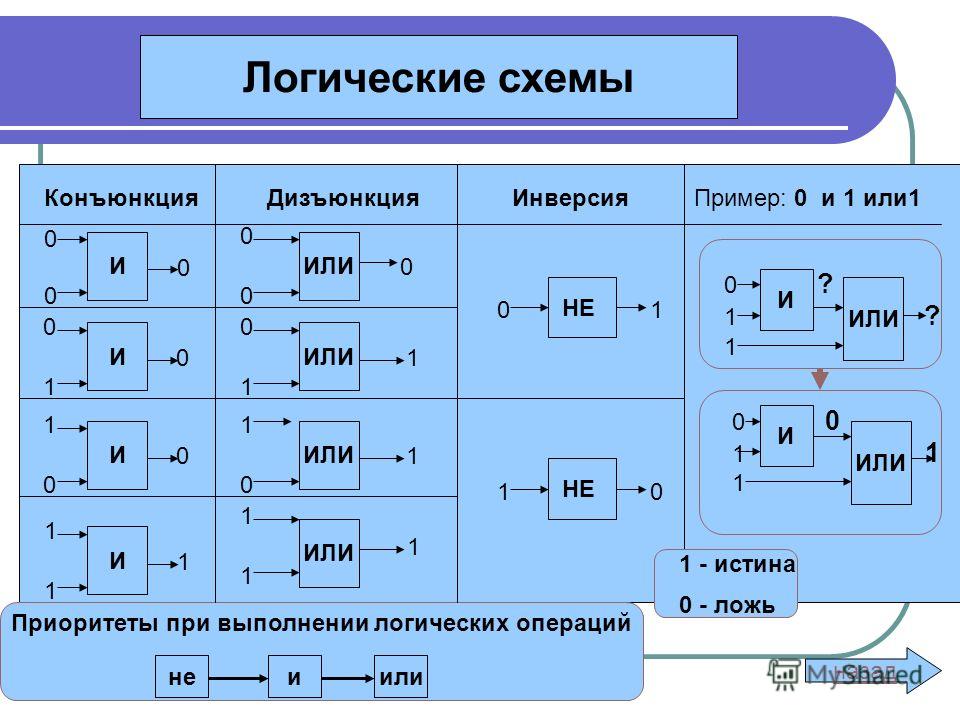
Таблицы истинности в форме логических схем будут выглядеть т.о.
3. Логический элемент НЕ (инвертор)
Логический элемент НЕ (инвертор)Простейшим логическим элементом является инвертор,
выполняющий функцию отрицания (инверсию). У этого элемента один
вход и один выход. На функциональных схемах он обозначается:
Если на вход поступает сигнал, соответствующий 1, то на выходе
будет 0.
 И наоборот.
И наоборот.вход
выход
1
0
0
1
4. Логический элемент ИЛИ (дизъюнктор)
Логический элемент, выполняющий логическое сложение, называетсядизъюнктор. Он имеет, как минимум, два входа. На функциональных схемах
он обозначается:
Если хотя бы на один вход поступает сигнал 1, то на выходе будет сигнал 1.
вход 1
вход 2
выход
0
0
0
0
1
1
1
0
1
1
1
1
5. Логический элемент И (конъюнктор)
Логический элемент, выполняющий логическое умножение, называетсяконъюнктор. Он имеет, как минимум, два входа. На функциональных
схемах он обозначается:
На выходе этого элемента будет сигнал 1 только в том случае,
когда на все входы поступает сигнал 1. Когда хотя бы на одном входе
будет ноль, на выходе также будет ноль.
вход 1
вход 2
выход
0
0
0
0
1
0
1
0
0
1
1
1
Другие логические элементы построены из трех простейших базовых
элементов и выполняют более сложные логические преобразования
информации.
Рассмотрим еще два логических элемента, которые играют роль
базовых при создании более сложных элементов и схем.
Логический элемент И-НЕ
Логический элемент И-НЕ выполняет логическую функцию штрих Шеффера (ИНЕ), он имеет, как минимум, два входа. На функциональных схемах он
обозначается:
вход 1
вход 2
выход
0
0
1
0
1
1
1
0
1
1
1
0
Логический элемент ИЛИ-НЕ
Логический элемент ИЛИ-НЕ выполняет логическую функцию стрелка Пирса (ИНЕ), он имеет, как минимум, два входа. На функциональных схемах он обозначается:
вход. 1
вход 2
выход
0
0
1
0
1
0
1
0
0
1
1
0
Логические основы компьютеров
7
значок инверсии
A
A
A
&
A
A B
B
НЕ
B
И
A
&
B
ИЛИ
A
1
B
И-НЕ
К. Поляков, 2007-2012
A B
1
ИЛИ-НЕ
A B
A B
Логические основы компьютеров
8
Любое логическое выражение можно реализовать на
элементах И-НЕ или ИЛИ-НЕ.
И: A B A B
НЕ: A A A A A
A
&
ИЛИ:
A
A
B
A
&
& A B
A
A B A B
&
B
&
B
К. Поляков, 2007-2012
&
A B
A B
9. Составление схем
Логические основы компьютеров9
Составление схем
последняя операция — ИЛИ
X A B A B C
И
A
B
C
К. Поляков, 2007-2012
A
B
&
A
B
& A B
A B
A B C
C
&
1
X
Пример 1. Нарисовать схему для логического выражения: 1 ИЛИ 0 и 1.
Читать эту схему надо слева направо. Первой выполняется операция И (что
наглядно видно на схеме), затем ИЛИ.
Теперь в порядке слева направо припишем к выходящим линиям
результаты операций:
В результате получилась 1, т.е. «истина».
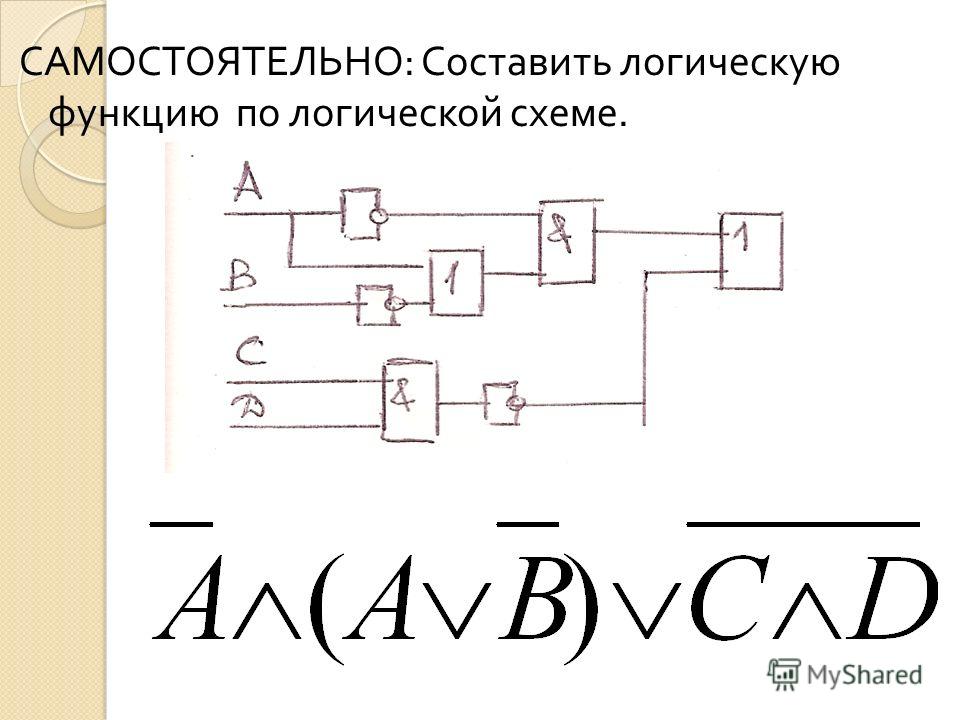
Пример 2. Представить в виде логической схемы логическую формулу:
НЕ (А И (В ИЛИ С) И D)
Логическая схема будет выглядеть так:
Теперь с помощью схемы рассчитаем значение формулы при А=С=D=1,
B=0
В результате получится логический ноль, т.
 е. «ложно».
е. «ложно».12. Функциональные схемы
Сигнал, выработанный одним логическим элементом, можноподавать на вход другого элемента, это дает возможность образовывать
цепочки из отдельных логических элементов — функциональные схемы.
Функциональная (логическая) схема – это схема, состоящая из
логических элементов, которая выполняет определённую функцию.
Анализируя функциональную схему, можно понять, как работает логическое
устройство, т.е. дать ответ на вопрос: какую функцию она выполняет.
Важной формой описания функциональных схем является структурная
формула. Покажем на примере, как выписывают формулу по заданной
функциональной схеме.
Ясно, что элемент “И” осуществляет логическое умножение значений ¬А и В.
Над результатом в элементе “НЕ” осуществляется операция отрицания, т.е.
вычисляется значение выражения:
A&B
Таким образом структурной формулой данной функциональной
схемы является формула:
C A&B
13.
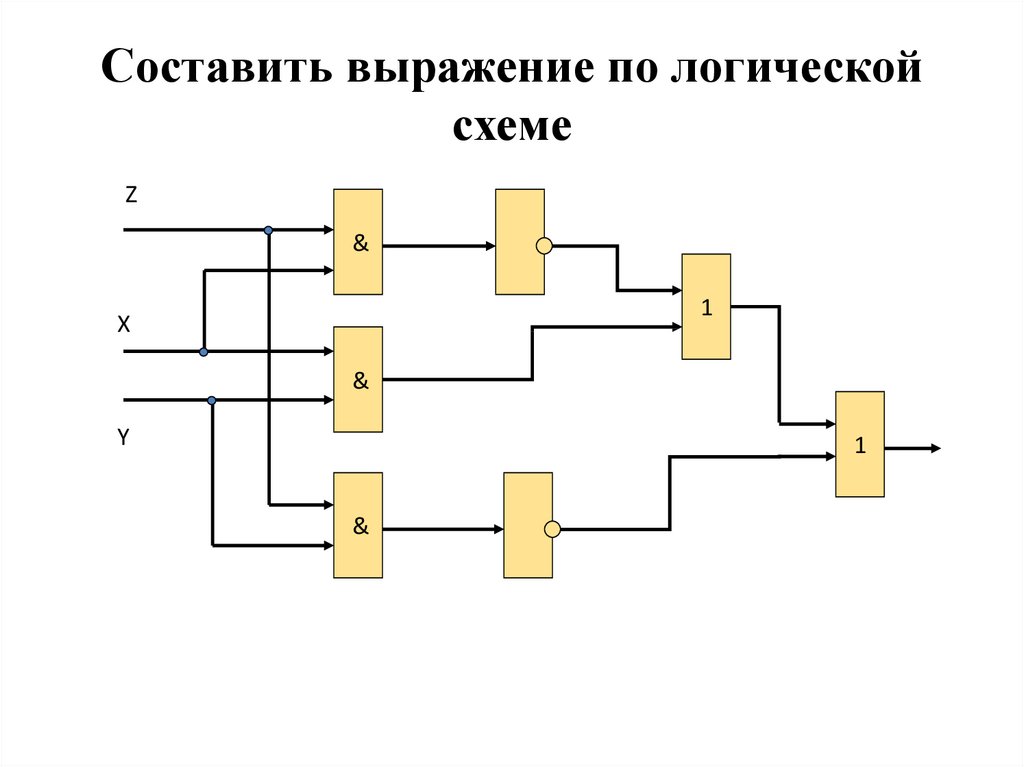 Таблица истинности функциональной схемыДля функциональной схемы можно составить таблицу истинности, то есть
Таблица истинности функциональной схемыДля функциональной схемы можно составить таблицу истинности, то естьтаблицу значений сигналов на входах и выходах схемы, по которой можно
понять какую функцию выполняет данная схема. Таблица истинности это табличное представление логической (функциональной) схемы в
котором перечислены все возможные сочетания значений входных
сигналов вместе со значением выходного сигнала для каждого из этих
сочетаний. Составим таблицу истинности для данной логической схемы:
Начертим таблицу: количество столбцов = количество входов + количество
выходов, количество строк = 2 количество входов. В данной таблице 3 столбца и 4
строки. Заполним первые столбцы всеми возможными вариантами входных
А
В
С
сигналов
(вход 1)
(вход 2)
0
0
0
1
1
0
1
1
(выход)
Рассмотрим первый вариант входных сигналов: А=0, В=0. Проследим по схеме, как проходят и
преобразуются входные сигналы.
 Результат, полученный на выходе (С=1), запишем в таблицу.
Результат, полученный на выходе (С=1), запишем в таблицу.Рассмотрим второй вариант входных сигналов: А=0, В=1. Проследим по схеме, как проходят и
преобразуются входные сигналы. Результат, полученный на выходе (С=0), запишем в таблицу.
Рассмотрим третий вариант входных сигналов: А=1, В=0. Проследим по схеме, как проходят и
преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу.
Рассмотрим четвёртый вариант входных сигналов: А=1, В=1. Проследим по схеме, как проходят
и преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу.
В результате получаем таблицу истинности данной логической схемы:
А
(вход 1)
В
(вход 2)
С
(выход)
0
0
1
0
1
0
1
0
1
1
1
1
Задание. Построить таблицу истинности для данной логической схемы и записать формулу
для данной схемы:
16. Логическая реализация типовых устройств компьютера
Обработка любой информации на компьютересводится к выполнению процессором различных
арифметических и логических операций.
 Для этого в
Для этого всостав процессора входит так называемое арифметикологическое устройство (АЛУ). Оно состоит из ряда
устройств, построенных на рассмотренных выше
логических элементах. Важнейшими из таких устройств
являются триггеры, полусумматоры, сумматоры,
шифраторы, дешифраторы, счетчики, регистры.
Выясним , как из логических элементов
разрабатываются логические устройства.
Логическая реализация типовых
устройств компьютера
17. Этапы конструирования логического устройства.
Конструирование логического устройства состоит изследующих этапов:
1. Построение таблицы истинности по заданным
условиям работы проектируемого узла (т.е. по
соответствию его входных и выходных сигналов).
2. Конструирование логической функции данного узла
по таблице истинности, ее преобразование (упрощение),
если это возможно и необходимо.
3. Составление функциональной схемы проектируемого
узла по формуле логической функции.
После этого остается только реализовать полученную
схему.
Задание. Построить логическую схему для заданной таблицы истинности:
Запишем логическую функцию по данной таблице
истинности:
F A & B &C A& B &C
Упростим полученное логическое выражение:
F С & ( A & B A & B ) С & (( A B ) A & B )
Построим логическую схему для данного выражения:
А
В
С
F
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
Попробуем, действуя по этому плану, сконструировать устройство для
сложения двух двоичных чисел (одноразрядный полусумматор).
Пусть нам необходимо сложить двоичные числа А и В. Через P и S
обозначим первую и вторую цифру суммы: A + B = PS. Вспомните таблицу
сложения двоичных чисел.
1. Таблица истинности, определяющая результат сложения, имеет вид:
Слагаемые
Перенос
Сумма
А
В
Р
S
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
2.
 Сконструируем функции P(A,B) и S(A,B) по этой таблице:
Сконструируем функции P(A,B) и S(A,B) по этой таблице:Р( A, B) A & B
S ( A, B) A & B A & B
Преобразуем вторую формулу, пользуясь законами логики:
S ( A, B) A & B A & B A & B A & B A & A B & B ( A & A A & B) ( A & B B & B )
A & ( A B) B & ( A B) ( A B) & ( A & B ) ( A B) & ( A & B)
3. Теперь можно построить функциональную схему одноразрядного
полусумматора:
Р( A, B) A & B
S ( A, B) ( A B) & ( A & B)
Чтобы убедиться в том, как работает схема, проследите за прохождением
сигналов в каждом из четырёх случаев и составьте таблицу истинности
данной логической схемы.
Условное обозначение одноразрядного
сумматора:
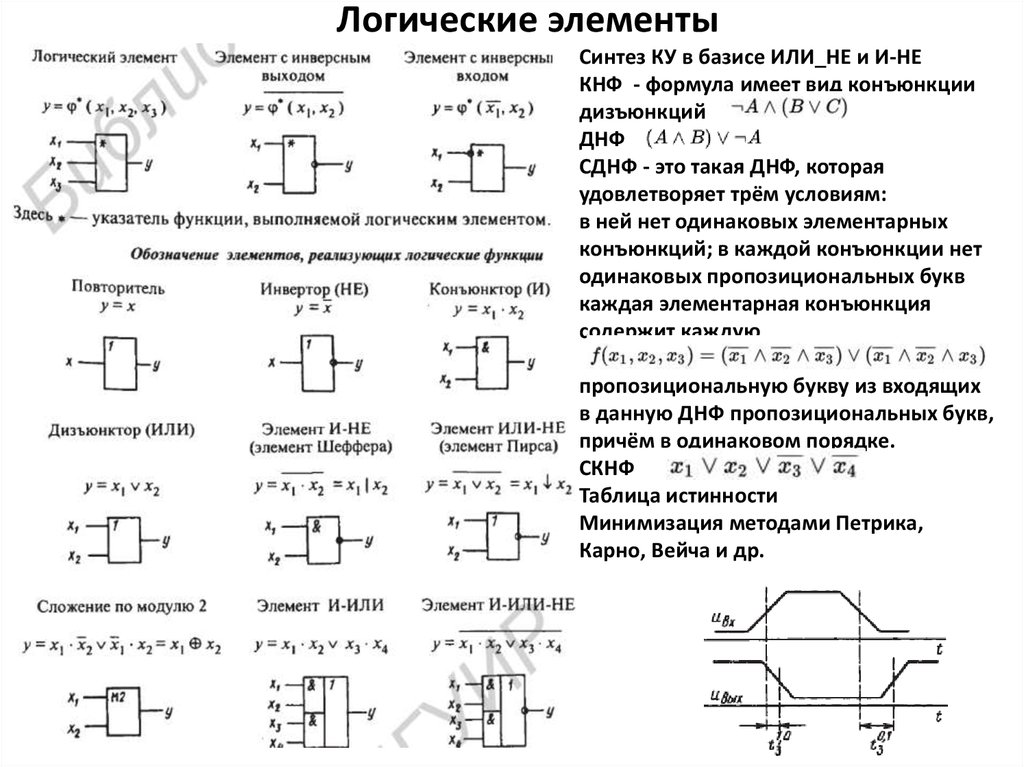
21. Полусумматор
Логические основы компьютеров21
Полусумматор
Полусумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа.
A
S сумма
A B
P
S
Σ
B
P перенос
P A B
S A B A B A B
A
B
A
B
К.
 Поляков, 2007-2012
Поляков, 2007-2012& A B
& A B
& A B
1
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
S A B A B
P
?
Схема на 4-х
элементах?
22. Полный одноразрядный сумматор.
Одноразрядный двоичный сумматор на три входа и два выхода называетсяполным одноразрядным сумматором.
Логика работы одноразрядного сумматора на три входа или полного
сумматора приведена в таблице, где А, В — суммируемые двоичные цифры
, Pо — перенос из младшего разряда, S — образующаяся сумма данного
разряда и осуществляет перенос P в следующий старший разряд.
Слагаемые
Перенос из
младшего
разряда
Сумма
Перенос
А
B
P0
S
P
0
0
0
0
0
.0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
Формула переноса:P A & B & P0 A & B & P0 A & B & P0 A & B & P0
Формула для вычисления суммы: S A & B & P0 A & B & P0 A & B & P0 A & B & P0
После преобразования формулы переноса и суммы принимают вид:
P A & B A & P0 B & P0
S ( A B P0 ) & P0 ( A & B & P0 )
Теперь можно построить схему полного одноразрядного сумматора с
учётом переноса из младшего разряда.
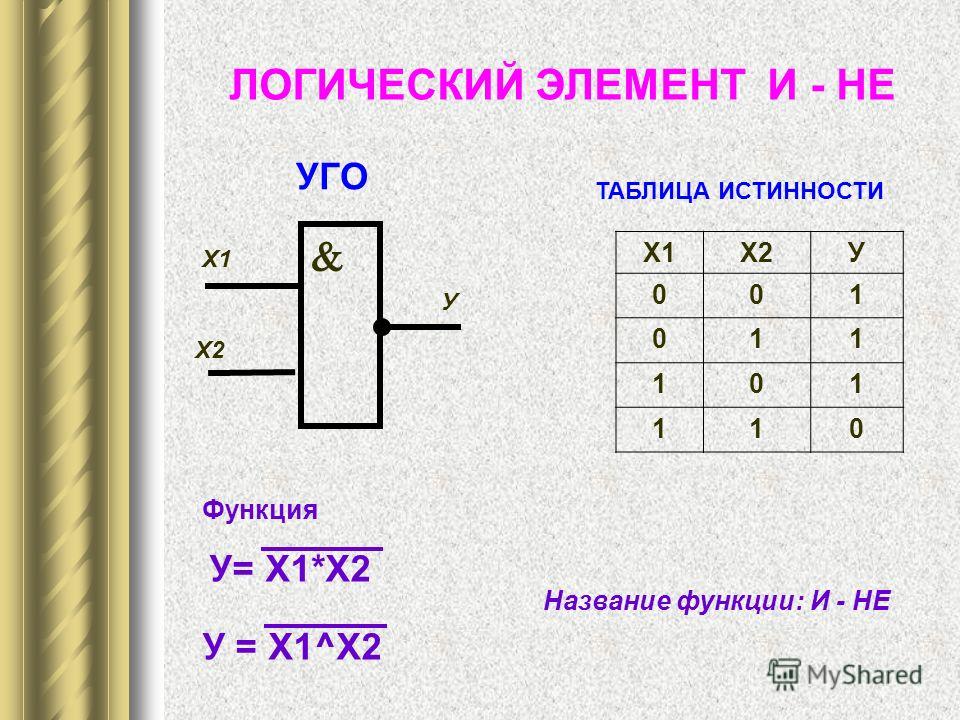
Сумматор — это электронная логическая схема,
выполняющая суммирование двоичных чисел поразрядным
сложением. Сумматор является центральным узлом
арифметико-логического устройства процессора. Находит он
применение и в других устройствах компьютера. В реальных
электронных схемах сумматор изображается так:
Сумматор выполняет сложение многозначных двоичных чисел. Он представляет собой
последовательное соединение одноразрядных двоичных сумматоров, каждый из которых
осуществляет сложение в одном разряде. Если при этом возникает переполнение разряда, то
перенос суммируется с содержимым старшего соседнего разряда.
На рисунке показано, как из N сумматоров можно составить устройство для сложения двух Nразрядных двоичных кодов, это схема многоразрядного сумматора.
25. Сумматор
Логические основы компьютеров25
Сумматор
Сумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа с
переносом из предыдущего разряда.
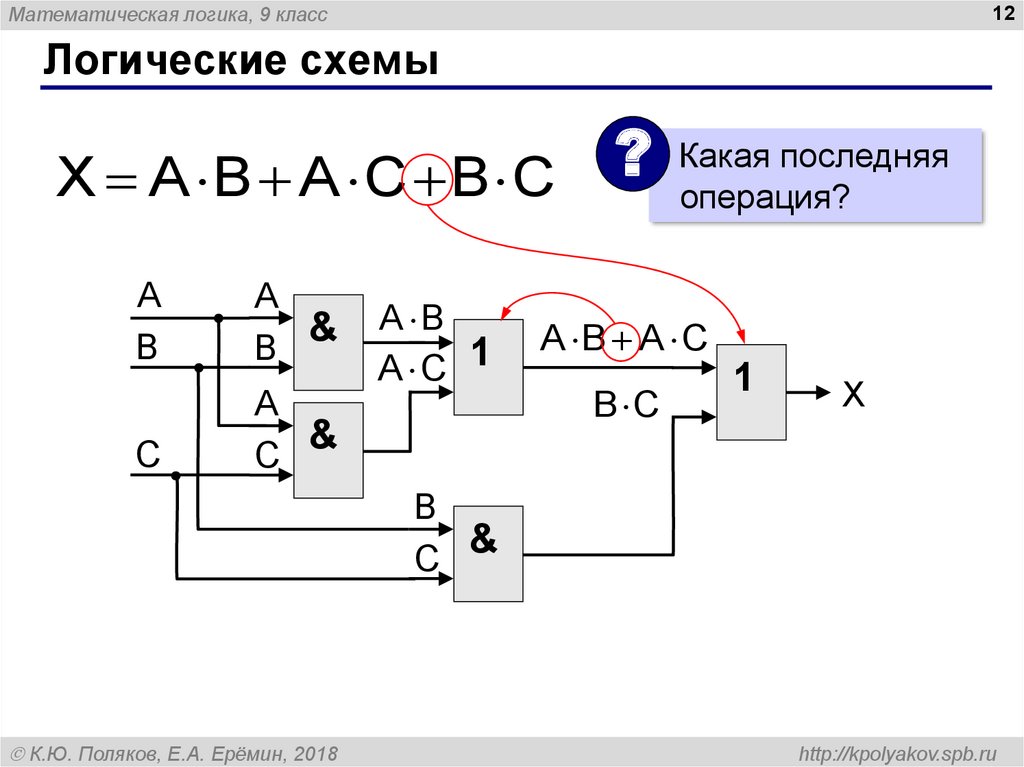
перенос
A
B
C
Σ
К. Поляков, 2007-2012
A
B
C
P
S
0
0
0
0
0
S сумма
0
0
1
0
1
P перенос
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
26. Многоразрядный сумматор
Логические основы компьютеров26
Многоразрядный сумматор
это логическая схема, способная складывать два
n-разрядных двоичных числа.
A
an an-1 a1
B
bn bn-1 b1
C p cn cn-1 c1
перенос
a1
b1
c1
Σ
0
К. Поляков, 2007-2012
p2
a2
b2
Σ
c2
p3
an
bn
pn
cn
Σ
p
перенос
27. ТРИГГЕР
Триггер — электронная схема, применяемая для хранения значенияодноразрядного двоичного кода.
Воздействуя на входы триггера, его переводят в одно из двух возможных
состояний (0 или 1). С поступлением сигналов на входы триггера в
зависимости от его состояния либо происходит переключение, либо
исходное состояние сохраняется.
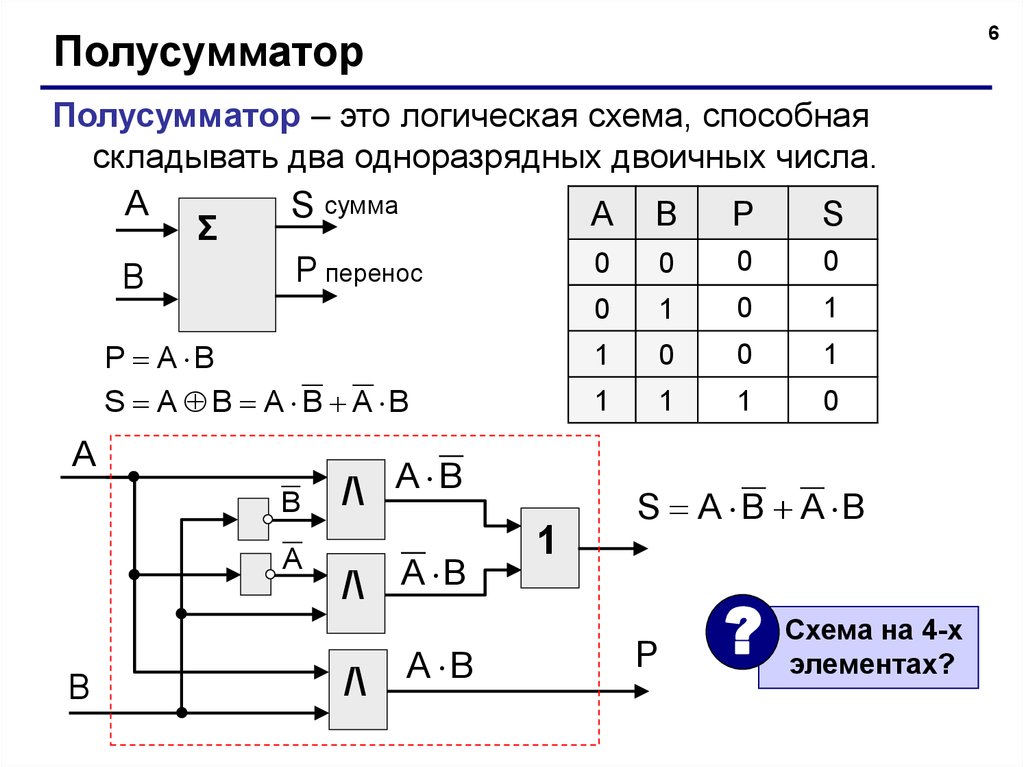 При отсутствии входных сигналов триггер
При отсутствии входных сигналов триггерсохраняет свое состояние сколь угодно долго.
Термин триггер происходит от английского слова trigger — защёлка,
спусковой крючок. Для обозначения этой схемы в английском языке чаще
употребляется термин flip-flop, что в переводе означает «хлопанье». Это
звукоподражательное название электронной схемы указывает на её
способность почти мгновенно переходить («перебрасываться») из одного
электрического состояния в другое.
Существуют разные варианты исполнения триггеров в зависимости от
элементной базы (И-НЕ, ИЛИ-НЕ) и функциональных связей между
сигналами на входах и выходах (RS, JK, T, D и другие).
Самый распространённый тип триггера — это RS-триггер (S и R
соответственно от английских set — установка, и reset — сброс). Условное
обозначение RS-триггера:
28. RS-триггер
RS-триггер построен на 2-х логических элементах: ИЛИ — НЕ либо И – НЕ.Как, правило, триггер имеет 2 выхода: прямой и инверсный Q и
Как он работает?
Пусть на вход элемента №1 подан сигнал 1, а на вход элемента № 3 — 0.
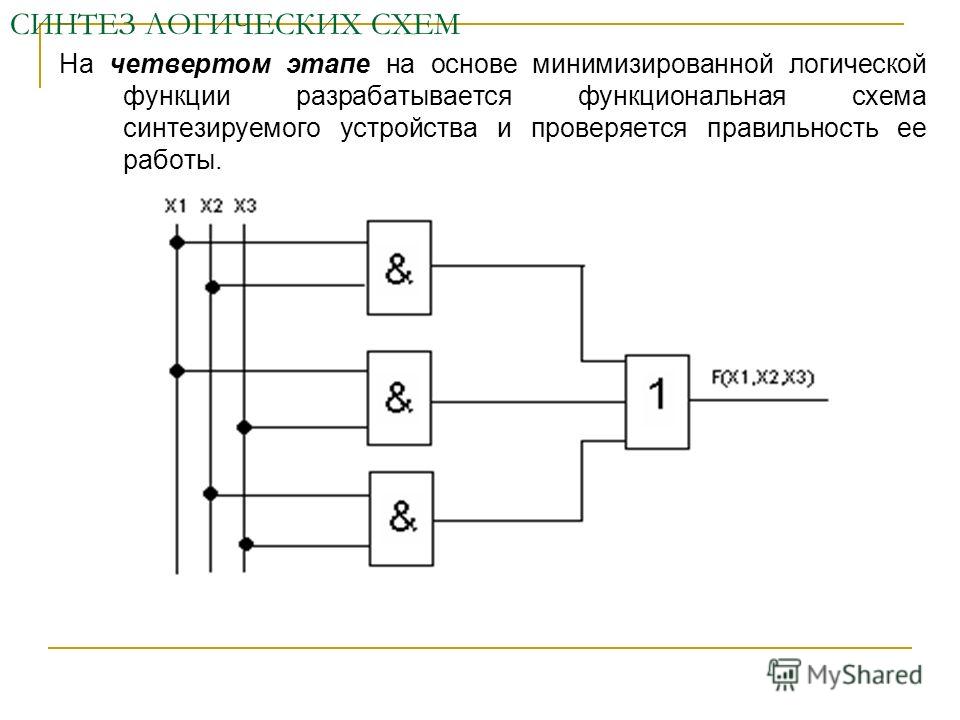 На выходе элемента №1
На выходе элемента №1независимо от того, какой второй сигнал поступит на вход, будет 1, т.к. это элемент ИЛИ (по
свойствам дизъюнкции). Пройдя через элемент № 2 сигнал примет значение 0 (Q=0).
Следовательно, и на втором входе элемента № 3 установится сигнал 0. На выходе элемента №3
— 0. Пройдя через элемент № 4 сигнал изменится на 1. Следовательно,
= 1.
Убедимся, что данное устройство сохраняет информацию. Запомните, что S=0, R=1, Q=0,
=1.
В момент прекращения входных сигналов (S=0, R=0) на выходе =1. Это напряжение подается на
вход элемента № 1. На выходе элемента №1 сохраняется 1, и на Q — сигнал 0. На входах
элемента №3 — 0, следовательно
=1. Таким образом, при отсутствии на внешних входах
сигналов 1 триггер поддерживает постоянное напряжение на своих выходах. Чтобы изменить
напряжение на выходах триггера, надо подать сигнал 1 на вход элемента № 3. Тогда Q=1, =0.
29. Триггер (англ. trigger – защёлка)
Логические основы компьютеров29
Триггер (англ.
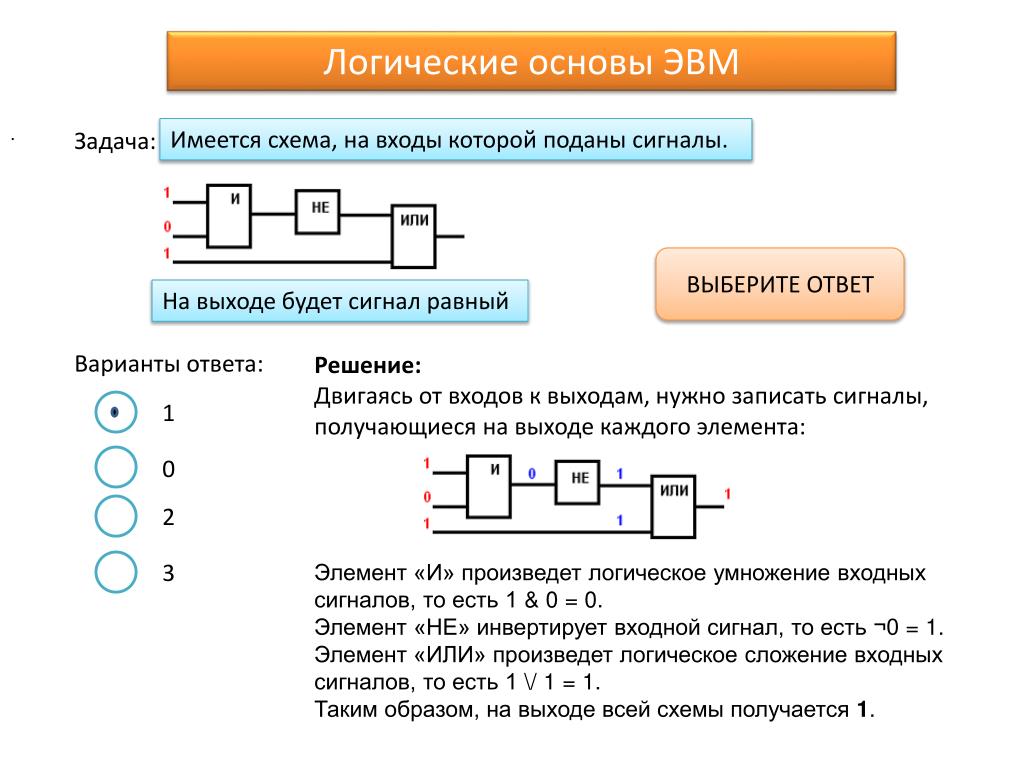 trigger – защёлка)
trigger – защёлка)Триггер – это логическая схема, способная хранить
1 бит информации (1 или 0). Строится на 2-х
элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.
set, установка
S
1
1
R
reset, сброс
К. Поляков, 2007-2012
вспомогательный
выход
Q
S R Q Q
режим
0 0 Q Q
хранение
обратные связи
0 1
0
1
сброс
Q
1 0
1 1
1
0
0
0
установка 1
основной
выход
запрещен
Логические схемы — Информатика — Уроки
Дата:
Предмет: информатика
Учитель:
Класс:
Тема урока: Логические схемы.
Цель урока: Формирование у обучающихся навыков построения логических схем для выражений.
Логические схемы
Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 — 1933), кстати, несколько лет, работавший в России, писал еще в 1910 году: «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить: 1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции; 2) не содержит ли она излишних усложнений. Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе — система чисто качественных… «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?». Созданная позднее М.А.Гавриловым (1903 — 1979) теория релейно-контактных схем показала, что это вовсе не утопия.
Например, голландский физик Пауль Эренфест (1880 — 1933), кстати, несколько лет, работавший в России, писал еще в 1910 году: «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить: 1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции; 2) не содержит ли она излишних усложнений. Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе — система чисто качественных… «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?». Созданная позднее М.А.Гавриловым (1903 — 1979) теория релейно-контактных схем показала, что это вовсе не утопия.
Посмотрим на микросхему. На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее при сильном увеличении она поразит нас своей стройной архитектурой.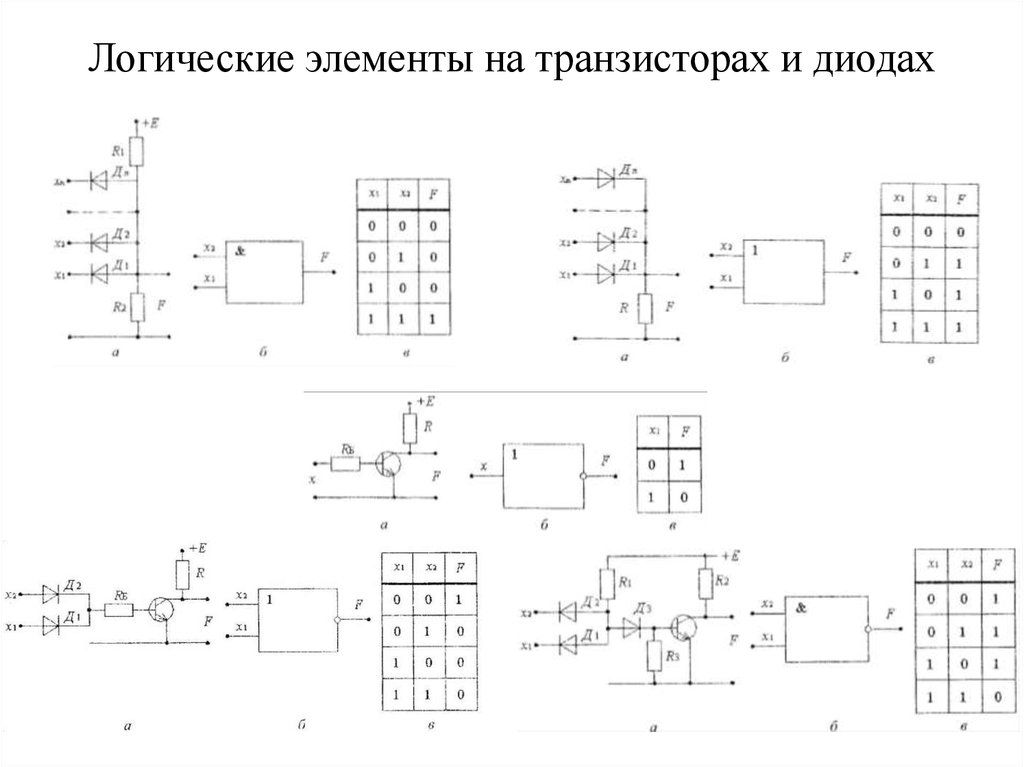 Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них.
Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них.
С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или его нет; электрическое напряжение есть или его нет… В связи с этим поговорим о различных вариантах управления включением и выключением обыкновенной лампочки (лампочка также работает на электричестве). Для этого рассмотрим электрические контактные схемы, реализующие логические операции.
На рисунках контакты обозначены латинскими буквами А и В. Введем обозначения: 1 -контакт замкнут, 0 — контакт разомкнут. Цепь на схеме 1 с последовательным соединением контактов соответствует логической операции «И». Цепь на схеме 2 с параллельным соединением контактов соответствует логической операции «ИЛИ». Цепь на схеме 3 (электромагнитное реле) соответствует логической операции «НЕ».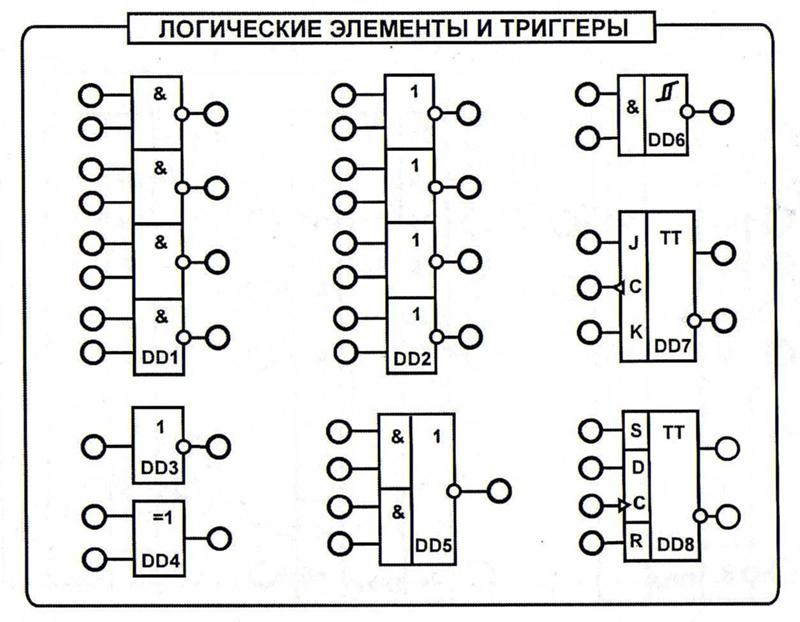
Заполняем таблицу по ходу объяснения материала.
| Конъюнкция | Дизъюнкция | Инверсия | ||||||
| | | | ||||||
| А 1 1 0 0 | В 1 0 1 0 | Результат 1 0 0 0 | А 1 1 0 0 | В 1 0 1 0 | Результат 1 1 1 0 | А 1 0 | ¬А 0 1 | |
| Конъюнктор | Дизъюнктор | Инвертор | ||||||
| | | | ||||||
Докажем это, рассмотрев состояния схем при различных состояниях контактов.
Схема 1 (составляем в основной таблице таблицу истинности).
Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит.
Первый контакт в положении «включено» второй в положении «выключено». Ток не идет, лампочка не горит.
Обратная ситуация. Лампочка не горит.
Оба контакта в положении «выключено». Тока нет. Лампочка не горит.
Вывод: первая схема действительно реализует логическую операцию «И».
Схема 2 (составляем в основной таблице таблицу истинности).
Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит.
Первый контакт в положении «включено» второй в положении «выключено». Ток идет, лампочка не горит.
Обратная ситуация. Лампочка горит.
Оба контакта в положении «выключено». Тока нет. Лампочка не горит.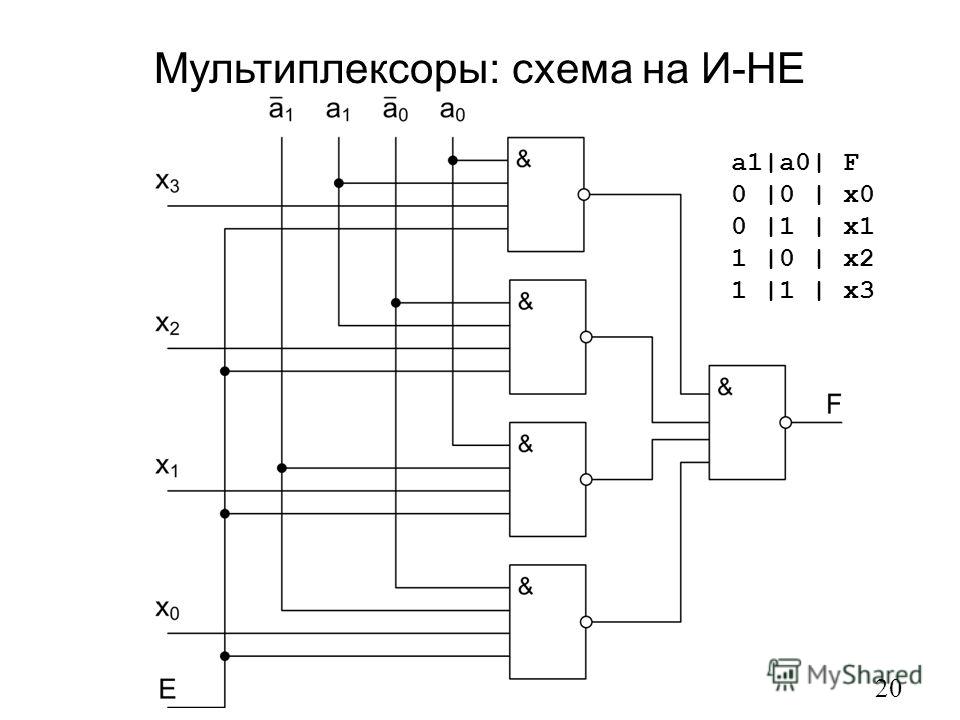
Вывод: вторая схема действительно реализует логическую операцию «ИЛИ».
Схема 3 (составляем в основной таблице таблицу истинности).
В этом устройстве в качестве переключателя используется автоматический ключ. когда тока на нем нет, пластинка замыкает контакты и лампочка горит. если на ключ подать напряжение, то вследствие явления электромагнитной индукции пластинка прижимается и цепь размыкается. Лампочка не горит.
Вывод: третья схема действительно реализует логическую операцию «НЕ».
Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключений в секунду. Именно такие электронные схемы нашли свое применение в качестве элементной базы ЭВМ.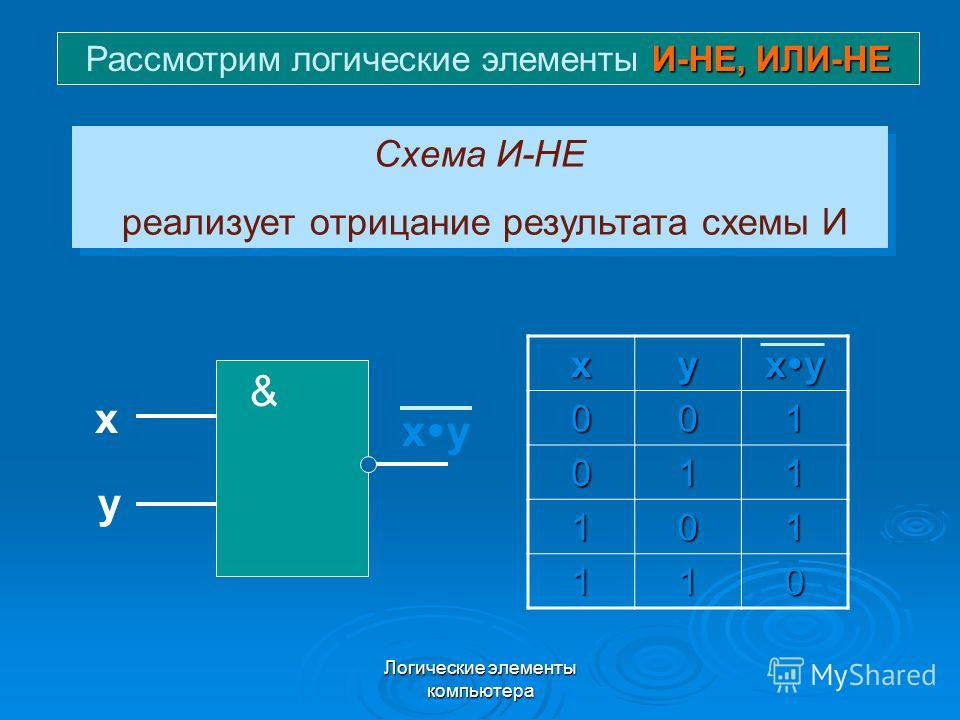 Вся теория, изложенная для контактных схем, была перенесена на электронные схемы. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента. Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Вся теория, изложенная для контактных схем, была перенесена на электронные схемы. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента. Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Почему необходимо уметь строить логические схемы?
Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом) таким образом, становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.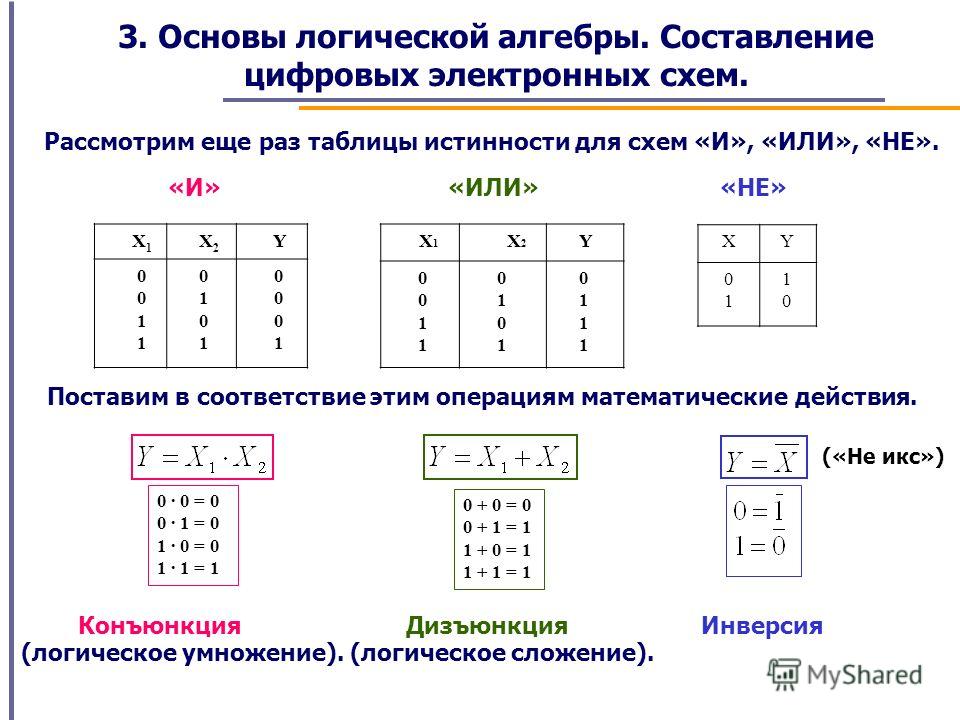
Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.
Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.
3. Построение логических схем
Правило построения логических схем:
Определить число логических переменных.
Определить количество базовых логических операций и их порядок.
Изобразить для каждой логической операции соответствующий ей вентиль.
Соединить вентили в порядке выполнения логических операций.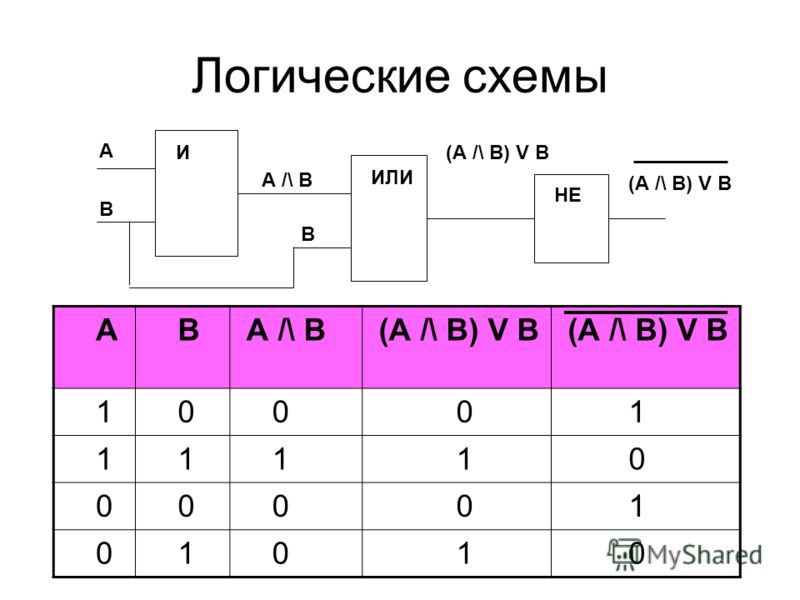
Пример 1
Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X v Y & X.
Две переменные — X и Y.
Две логические операции:
2 1
X v Y & X.
3) Строим схему:
Ответ: 1v 0 & 1 = 1.
Пример 2
Постройте логическую схему, соответствующую логическому выражению F=X&Yv¬(YvX). Найдите значение логического выражения для X=1, Y=0.
Переменных две: X и Y;
Логических операций четыре: конъюнкция, две дизъюнкции и инверсия:
1 4 3 2
X&Yv ¬ (YvX)
Схему строим слева направо в соответствии с порядком логических операций:
Вычислим значение выражения: F=1&0v ¬ (0v1) =0.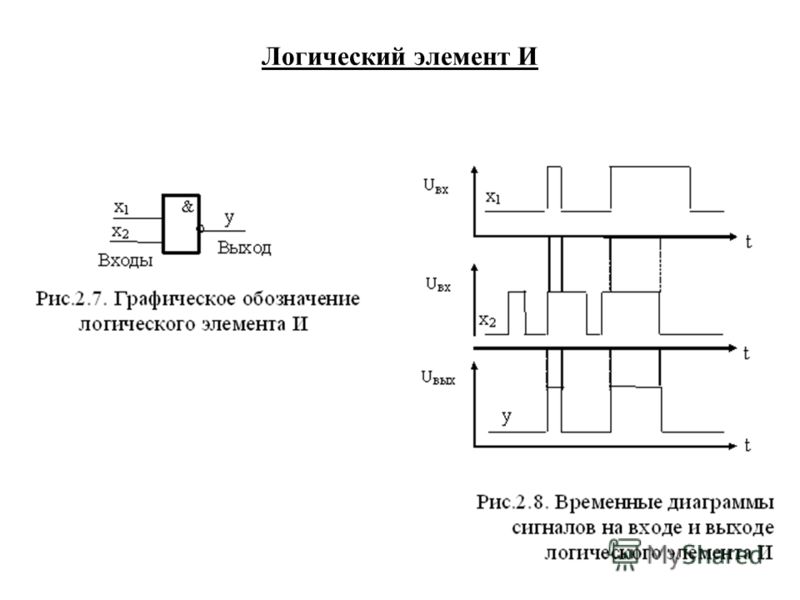
Закрепление изученного материала
Постройте логическое выражение по логической схеме:
| А)
| B) |
| C ) А В С | D ) |
Логика и схемы
Карл Берч, Колледж Хендрикса, сентябрь 2011 г.
Логика и схемы
by Carl Burch находится под лицензией Creative
Commons Attribution-Share Alike 3.0 США
Лицензия.
На основании работы в
www.cburch.com/books/logic/.
Содержание
1. Логические схемы
2. Строительные логические схемы
2.1. Булевы выражения
2.2. Законы булевой алгебры
2.3. Сумма произведений
3. Упрощение схем
Упрощение схем
3.1. Эффективность схемы измерения
3.2. Карты Карно
3.3. Более сложная карта Карно
4. Другие логические элементы и универсальность
Чтобы понять, как работают компьютеры, нам нужно понять основы цифровых схем. Как оказалось, цифровой схемы строятся на основе базовой логики.
1. Логические схемы
Конечно, на самом базовом уровне компьютер представляет собой
электрическая схема построена с использованием проводов .
Мы будем думать о каждом проводе в цепи как о переносе одной информации.
элемент, называемый бит .
Слово бит происходит от B inary dig IT ,
используя термин двоичный , потому что бит может иметь любой из
два возможных значения, 0 и 1.
В электрических терминах вы можете думать о нуле вольт
представляющие 0 и пять вольт, представляющие 1; но для нашего
целей, конкретные напряжения не важны — и
действительно, существуют разные системы интерпретации уровней напряжения.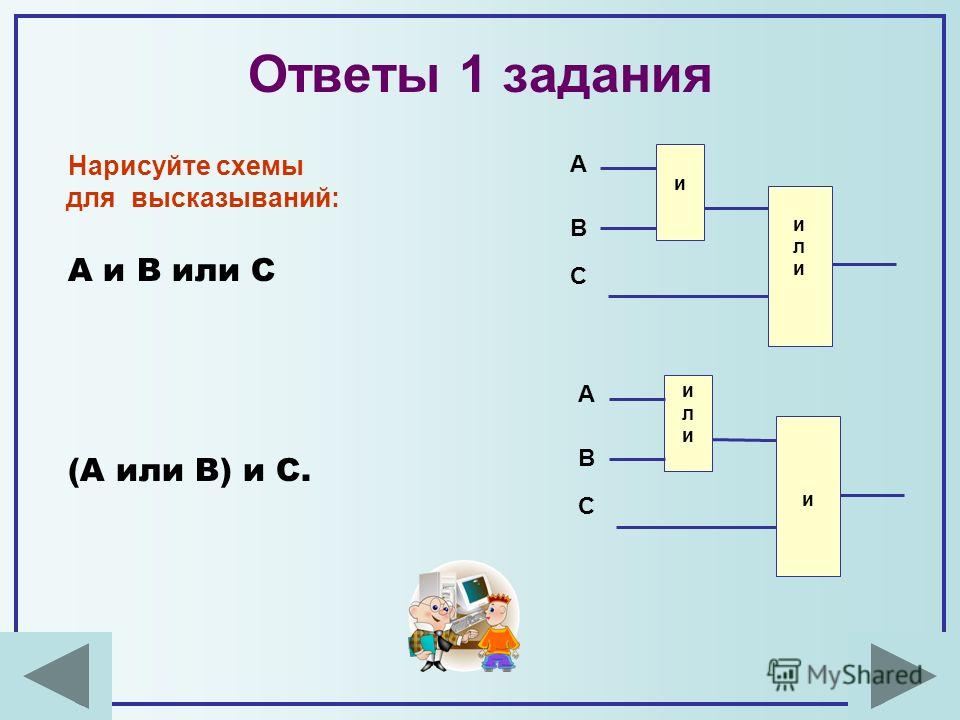 как 0 или 1.
(Люди экспериментировали с более чем двумя различными уровнями напряжения,
но в конечном итоге это приводит к более сложным и
оказываются менее эффективными, чем бинарная система.)
как 0 или 1.
(Люди экспериментировали с более чем двумя различными уровнями напряжения,
но в конечном итоге это приводит к более сложным и
оказываются менее эффективными, чем бинарная система.)
Вот пример, показывающий схему простой логической схемы.
Рисунок 1: Простая логическая схема.
Эта диаграмма состоит из некоторых своеобразных фигур, связанных некоторые линии. Линии представляют провода; фигуры представляют так называемые логические вентили , которые мы будем изучать скоро.
Мы будем думать о каждом проводе как о несущем бите, пока он не наткнется на
ворота.
Вы можете видеть, что некоторые провода пересекаются в маленьком сплошном круге:
Этот кружок указывает на то, что провода подключены, поэтому значения
в круг продолжайте вниз все провода, подключенные к кругу.
Если два провода пересекаются без окружности, это означает, что один провод
проходит над другим, как эстакада между штатами, и значение
на одном проводе не влияет на другой.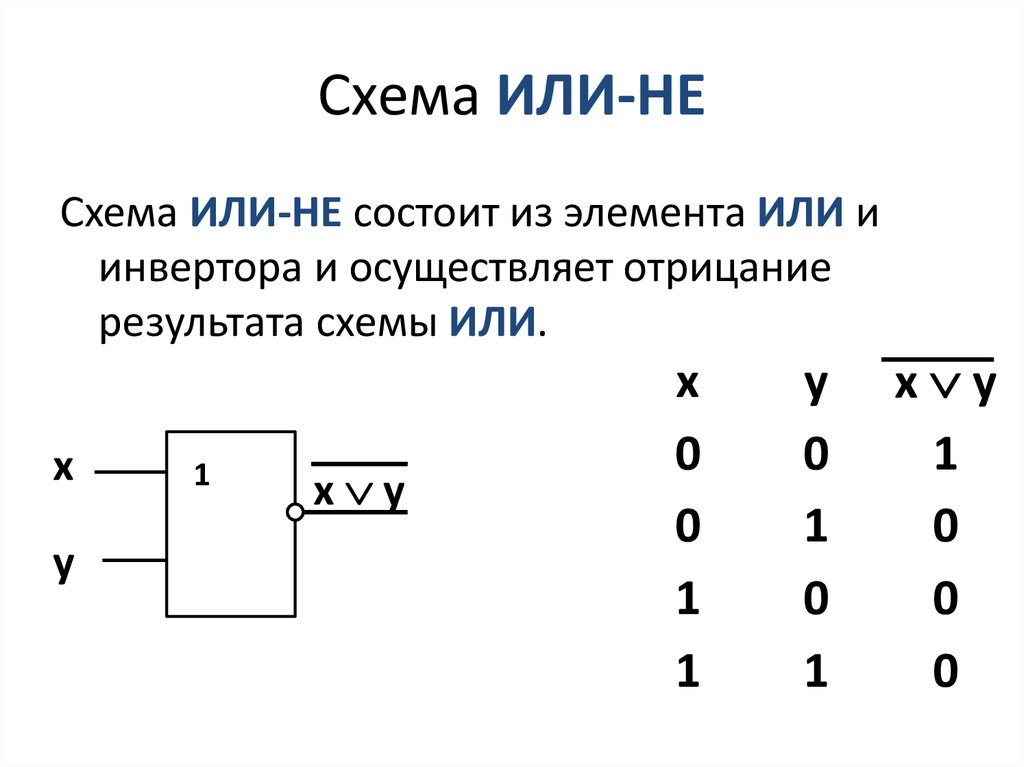
(В наших схемах мы будем рисовать системы проводов, используя разные цветов, так что вы можете сказать, что два провода не касаются когда вы видите их в разных цветах. Однако традиционно схемы нарисованы только черно-белыми, и эти точки имеют решающее значение для понимание того, когда провода пересекаются и когда они перекрываются.)
Предположим, что мы берем нашу примерную схему из Рис. 1 и отправьте бит 0 в верхнем вход ( x ) и 1 бит на нижнем входе ( y ). Затем эти входы будут перемещаться по проводам, пока не попадут в точку. логические ворота.
Итак, что происходит, когда вход достигает логического элемента? Это зависит от какой тип логических ворот это. Существует три основных типа логические вентили, изображенные с использованием трех разных форм.
| Ворота НЕ: | Берет один бит слева и производит
противоположный бит справа от него (рис.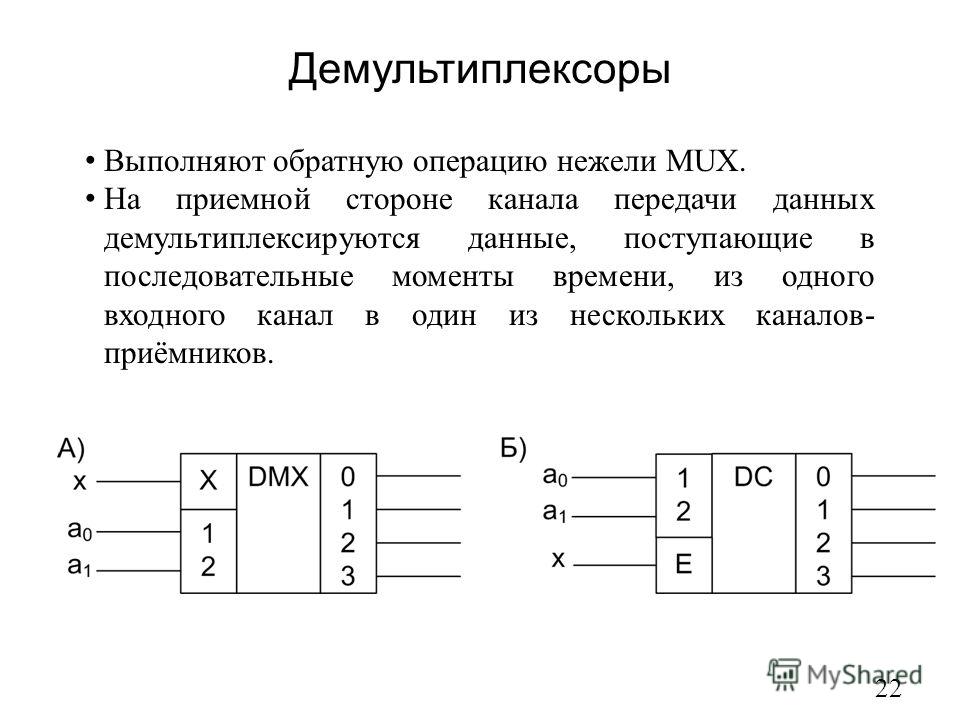 2(а)).
Для верхнего элемента НЕ в нашем примере его вход от x
равен 0, поэтому вентиль выдает 1 на выходе. 2(а)).
Для верхнего элемента НЕ в нашем примере его вход от x
равен 0, поэтому вентиль выдает 1 на выходе. |
|
| И ворота: | Принимает два входа слева и выводит 1 справа только если первый вход и второй вход равен 1 (Рисунок 2(б)). Для верхнего элемента И в нашем примере его верхний вход равен 1. от y , а его нижний вход равен 1 от верхнего НЕ ворота; оба входа равны 1, поэтому логический элемент И выдает 1 как его выход. | |
| Ворота операционной: | Принимает два входа слева и выводит 1 на это правильно, если первый вход или второй вход равен 1 (или если оба равны 1). (Рисунок 2(с)) |
Вот удобная мнемоника для различения форм ИЛИ и И:
Символ вентиля И выглядит
как заглавная буква Д , которую можно найти в слове
И .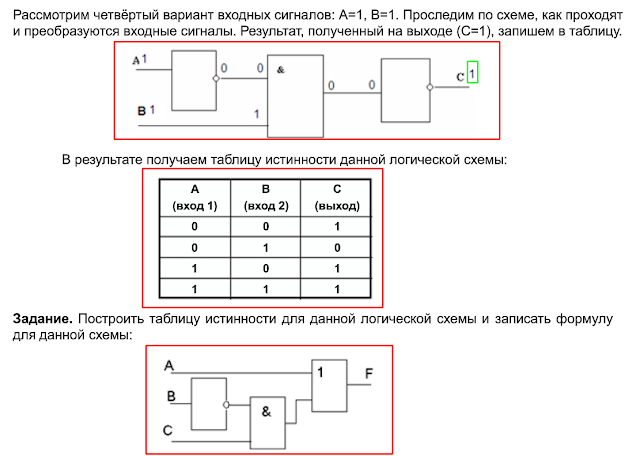
Рисунок 2: Логическое поведение вентиля.
(a) НЕ ворота (б) И ворота (c) Ворота ИЛИ
a o 0 1 1 0
a b o 0 0 0 0 1 0 1 0 0 1 1 1
а б o 0 0 0 0 1 1 1 0 1 1 1 1
После фильтрации значений через ворота на основе поведения
Рисунок 2, значения в цепи
будет следующим.
На этой диаграмме видно, что когда x равно 0, а y равно 1, вывод o равен 1.
Делая такое же распространение для других комбинаций ввода значений, мы можем построить следующую таблицу, показывающую, как это Схема ведет себя для различных комбинаций входов.
x Y O
9
9
9
9
9
9
.0071 1 1 1 0 1 71 1 1 0 1 0 71 908.908. 4 4 4 4 4 4 4 он имеет 0 в столбце x , 1 в столбце y столбец и 1 в столбце o . Это указывает на то, что если ввод x равен 0, а ввод y равен 1, тогда выход схемы или будет 1.
Такая таблица называется таблицей истинности . Таблица истинности содержит строку для каждого возможного комбинация входных значений а также каждая строка сообщает, каким будет значение выхода схемы. для этой комбинации входов. В этой примерной таблице у нас есть четыре строки, представляющие каждый возможна комбинация x и y . В нашей таблице истинности было бы восемь строк, если бы в схеме было три строки. входы; и их было бы шестнадцать, если бы схема имела четыре входа.
2. Построение логических схем
В предыдущем разделе мы видели, как работают логические схемы. это полезно когда вы хотите понять, как ведет себя схема.
Но разработчики компьютеров часто сталкиваются с противоположной проблемой. желаемое поведение, как мы можем построить схему, ведущую себя таким образом? Или задать тот же основной вопрос: как мы можем преобразовать истину таблицу в логическую схему?
В этом разделе мы рассмотрим метод систематического проектирования схемы. Однако сначала мы совершим необходимый обход через изучение Булевы выражения.
2.1. Логические выражения
В середине девятнадцатого века Джордж Буль разработал систему логики, лежащую в основе современный компьютер. Он заметил, что логические функции могут быть построены из И, ИЛИ и НЕ операции, и что это наблюдение приводит к тому, что можно рассуждать о логика в математической системе.
Поскольку Буль работал в девятнадцатом веке, он, конечно, не думаю о логических схемах. Он осматривал поле логика, создан для размышлений о справедливости философских аргументов. Философы думали об этом предмете со времен Аристотель. Логики формализовали некоторые распространенные ошибки, например, соблазн сделать вывод, что если А подразумевает В , и если B выполняется, то A также должно выполняться.
(«Гениальные люди носят очки, и я ношу очки, так что я должен быть блестящим».)
Будучи математиком, Буль искал способ кодировать предложения вот так в алгебраические выражения, и он изобрел то, что мы сейчас называем Логические выражения . Примером логического выражения является « y x + y x ». Линия над переменной (или более крупным выражением) представляет НЕ; за например, выражение y соответствует питанию y через ворота НЕ. Умножение (например, x y ) представляет собой И. В конце концов, рассуждал Буль, таблица истинности И (Рисунок 2(b)) идентичен таблица умножения на 0 и 1. Сложение (например, x + y ) представляет собой ИЛИ. Таблица истинности ИЛИ (рис. 2(c)) не соответствует таблице сложения по 0 и 1 в точности. — 1 ИЛИ 1 равно 1, но 1 плюс 1 равно 2 — но, Буль решил, это достаточно близко.
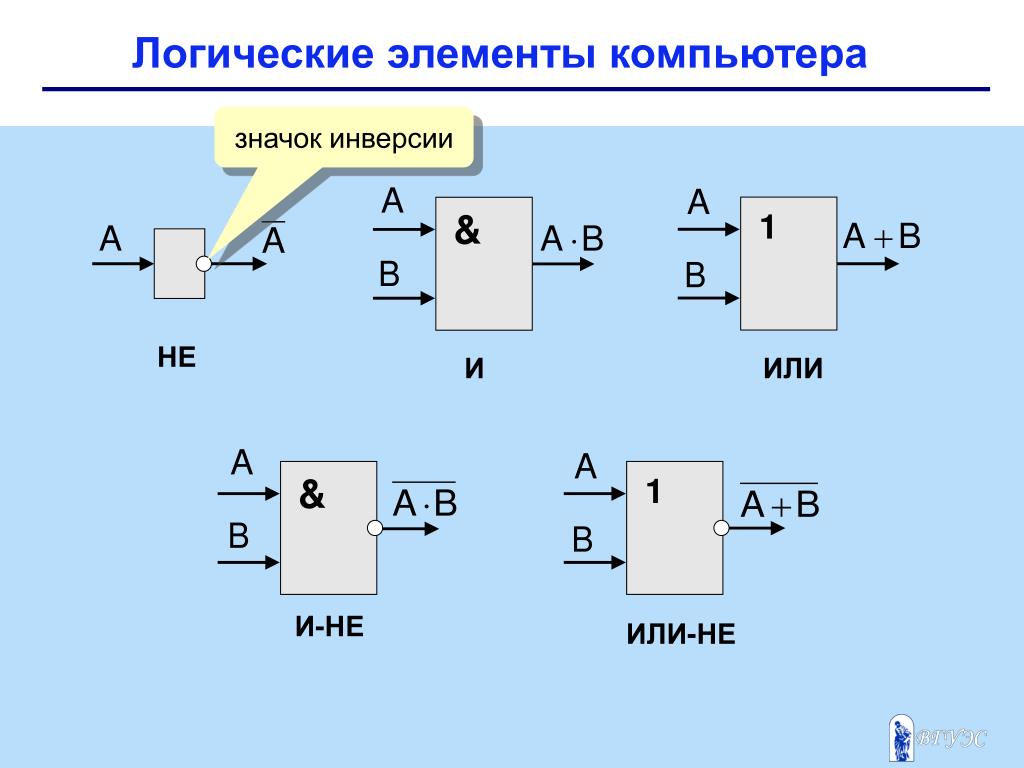
В логических выражениях соблюдается обычный порядок операций: Умножение (И) предшествует сложению (ИЛИ). Таким образом, когда мы пишем y x + y x , мы имеем в виду ( y x + y x ). Мы можем использовать круглые скобки, когда этот порядок операций не тот, который нам нужен. хочу. Для НЕ, полоса над выражением указывает степень выражение, к которому оно относится; таким образом, x + y представляет НЕ x ИЛИ y ), а x + y представляет (НЕ x ) ИЛИ (НЕ y ).
Предупреждение: Студенты, плохо знакомые с булевыми выражениями, часто пытаются сократить х у как х у — то есть, они рисуют одну линию над всем выражением, а не двумя отдельными строками над двумя отдельные куски.
Это сокращение неправильно . Первый, x y , переводится как (НЕ x ) И (НЕ y ) (то есть, оба x и y равны 0), а x y преобразуется в НЕ ( x И y ) (то есть, x и y не являются одновременно 1). Мы могли бы составить таблицу истинности, сравнивая результаты для этих двух выражения.
х у x г x 8 8x г x г 0 0 1 1 1 0 1 0 9124 1 .0124 1
1 0 0 0 1 1 0 0 1 0 0 1 1 1 0 0 0 1 0 Со времен пятой столбцы ( x y ) и Searnempenth и Se. Searne. ( x у ) не идентичны, два выражения не эквивалент.
Каждое выражение напрямую соответствует схеме и наоборот. Чтобы определить выражение, соответствующее логической схеме, мы передаем выражения через схему так же, как значения распространяются через это. Предположим, мы делаем это для нашей схемы Рисунок 1.
Входы верхнего элемента И: y и x , и поэтому он выводит y x . Нижний логический элемент И выдает y x , а логический элемент ИЛИ объединяет эти значения.
два в y x + y x .
2.2. Законы булевой алгебры
Система Буля для записи логических выражений называется Булева алгебра . Это называется алгебра , потому что мы можем манипулировать символами, используя законы, подобные те из традиционной алгебры. Например, коммутативный закон применим как к ИЛИ, так и к И. Чтобы доказать коммутативность ИЛИ (т. е. что А + В = В + А , мы можем заполнить таблицу истинности, демонстрирующую, что для каждого возможного комбинация A и B , значения A + B и B + A идентичны.
А Б А + В В + А 0 0 0 0 0 1 1 1 1 0 1 1 1 1 1 1 Поскольку третий и четвертый столбцы совпадают, мы можем заключить, что A + B = B + A – универсальный закон.

Поскольку ИЛИ (и И) коммутативны, мы можем свободно изменить порядок терминов, не меняя смысла выражения. Коммутативный закон ИЛИ позволил бы нам преобразовать г x + г x в y x + y x , а перестановочный закон И (примененный дважды) позволяет нам преобразовать это до x y + x y .
Аналогично, ИЛИ (и И) имеет ассоциативный закон (то есть, А + ( В + С ) = ( А + B ) + C . Из-за этой ассоциативности мы можем свободно писать А + В + С (и А В С ) без скобок — ведь размещение скобки вокруг первой пары ( А + В ) приводит к тому же результату, что и скобки вокруг второй пары ( B + C ).
При рисовании схем мы будем свободно рисовать логические элементы И и ИЛИ. которые имеют несколько входов. 3-входной вентиль И на самом деле будет соответствовать двум 2-входовым логическим элементам И, когда схема на самом деле проводной. Есть два возможных способа подключить это.
Из-за ассоциативного закона для И не имеет значения, что мы выбирать, и поэтому мы можем использовать двусмысленное И или ИЛИ ворота с тремя (или более) входами.
Существует много таких законов, обобщенных на рисунке 3. Это включает в себя аналоги всех важных алгебраических законов работа с умножением и сложением. Есть также много законов, которые не соблюдают . со сложением и умножением; в таблице они отмечены красным цветом звездочка.
Рисунок 3: Образец важных логических тождеств.
* Красные со звездочкой не соответствуют стандартным алгебраическим тождествам. И ИЛИ коммутативный А В = В А А + В = В + А ассоциативный A ( B C ) = ( A B ) C A + ( B + C ) = ( A + B ) + C идентификатор А ⋅ 1 = А А + 0 = А распределительный А ( В + С ) = А В + А С * A + B C = ( A + B ) ( A + C 1)) 9007 единица/ноль А ⋅ 0 = 0 * А + 1 = 1 идемпотентность * А А = А * А + А = А обратный * А А = 0 * А + А = 1 Закон Де Моргана * A B = A + B * А + В = А В двойное отрицание * А = А 2.
3. Сумма произведений
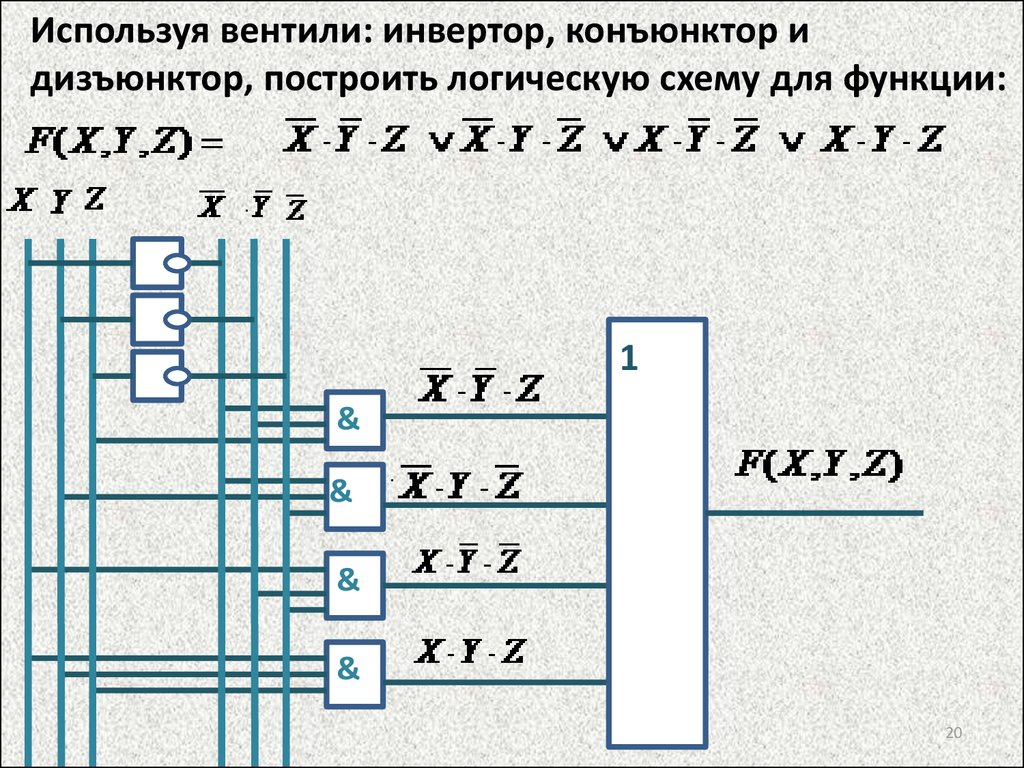
Теперь мы можем вернуться к нашей задаче: Если у нас есть конкретная логическая функция, которую мы хотим вычислить, как мы можем построить схему для ее вычисления? Мы начнем с описания логической функции в виде таблицы истинности. Предположим, мы начинаем со следующей функции, для которой мы хотим схема.
x y z o 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 Учитывая такую таблицу истинности, определяющую функцию, мы создадим логическое выражение, представляющее функцию.
Для каждого ряда таблица , где желаемый результат равен 1 , мы описываем его как И из нескольких факторов.
x y z o description 0 0 1 1 x y z 0 1 0 1 x y z 1 1 0 1 x y z 1 1 1 1 x y z Чтобы получить описание строки, мы выбираем для каждой переменной либо эта переменная или ее отрицание, в зависимости от того, является ли переменная в этой строке 1 или нет; а затем мы берем И этих вариантов.
Например, глядя на первую из строк выше, мы включаем x , так как x равно 0 в этой строке, у так как у тоже 0, и z , поскольку z равно 1; наше описание — это И из них: x y z . Это выражение дает 1 для комбинации значений в этой строке; но для других строк его значение равно 0, так как каждая вторая строка отличается некоторой переменной, и вклад этой переменной в И даст 0,
Когда у нас есть описания для всех строк, в которых требуется вывод 1, мы наблюдаем следующее: Значение желаемой схемы должно быть 1, если входы соответствуют к первому 1-му ряду, второму 1-му ряду, третьему 1-му ряду, или четвертая 1-я строка. Таким образом, мы объединим выражения, описывающие строки, с ИЛИ:
x y z + x y 9 z 418 + x y z + x y z Обратите внимание, что наше выражение не включает описания строк где таблица истинности сигнализирует, что желаемый результат равен 0: если бы мы это сделали, то это описание было бы 1, и, таким образом, ИЛИ все термины будут равны 1, а не 0, которого мы желаем.
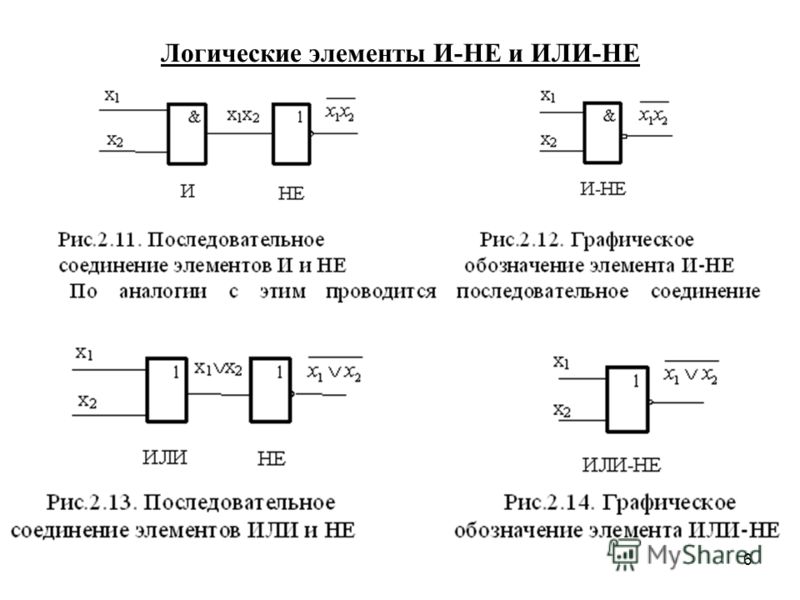
Это выражение сразу приводит к схеме Рисунок 4.
Рисунок 4: Схема, полученная из заданной таблицы истинности.
Окончательное выражение, которое мы получаем, называется суммой продукты выражение. Это называется так, потому что это ИЛИ (а сумма, если мы понимаем ИЛИ как сложение) нескольких И (продуктов, так как И соответствует умножению). Мы называем эту технику построение выражения из таблицы истинности сумма произведений техника .
Этот метод суммы произведений позволяет нам взять любую функцию над битами и построить схему для вычисления этой функции. Существование такой техники доказывает, что схемы могут вычислять любую логическую функцию.
Подводя итог: мы рассмотрели три способа описания логического значения. функция: логические схемы , таблицы истинности и Логические выражения . Кроме того, мы наблюдаем систематическое способы преобразования между тремя методами, изображенными на диаграмме ниже.
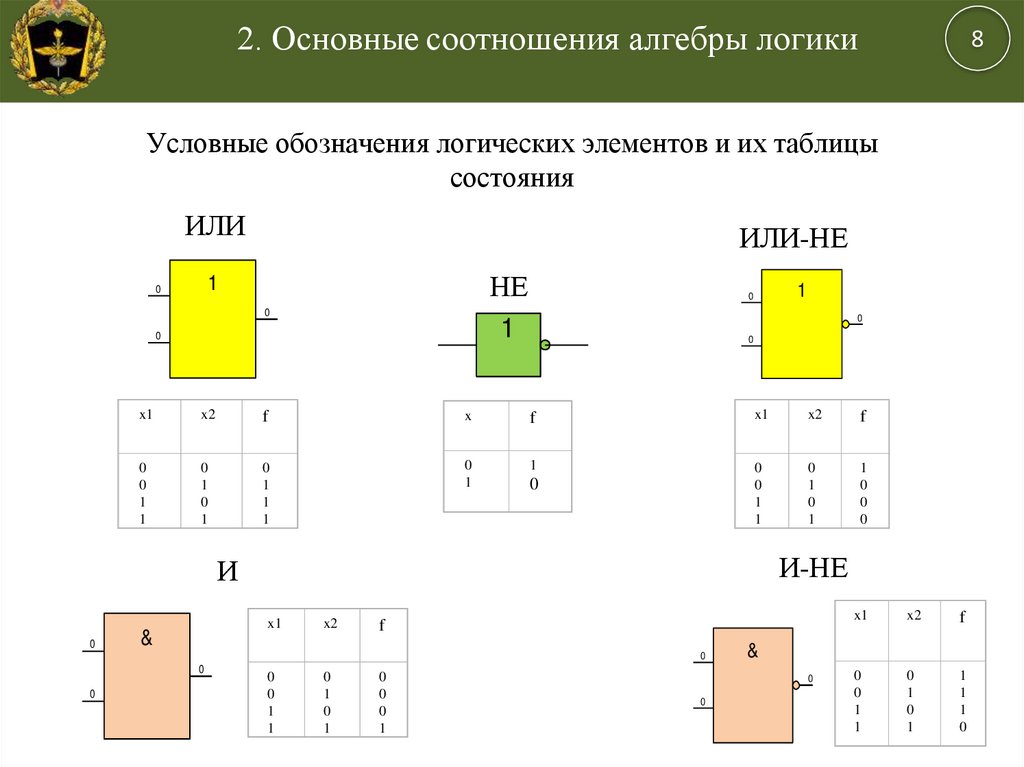
Единственной недостающей стрелкой является преобразование из таблиц истинности в схемы; мы можем справиться с этим, однако, преобразовав истину таблицу в логическое выражение (с использованием суммы произведений техника) и преобразование этого в схему.
3. Упрощение схем
Логические элементы представляют собой физические устройства, построенные с использованием транзисторов. На практике эффективность схемы имеет значение. Теперь перейдем к пониманию того, как измерить эффективности, и мы увидим технику, которая часто приводит к более эффективная схема, чем та, к которой мы пришли, используя техника суммы продуктов.
3.1. Измерение эффективности схемы
Мы можем измерить эффективность схемы в двух направлениях: пространство и скорость. Фактор пространства связан с тем, что каждый транзистор занимает место, а микросхема, содержащая транзисторы, ограничен по размеру, поэтому количество транзисторов, помещающихся на чип ограничен современными технологиями.
Поскольку разработчики ЦП хотят соответствовать многие функции на чипе, они пытаются построить свои схемы с как можно меньше транзисторов для выполнения необходимых задач. К уменьшить количество транзисторов, пытаются создавать схемы с несколько логических элементов. Таким образом, мы можем аппроксимировать использование пространства схема, просто подсчитав, сколько логических вентилей в схеме включает.
Второй фактор, скорость, связан с тем, что транзисторы требуют времени работать. Поскольку разработчики хотят, чтобы схемы работали так же быстро, как возможно, они работают, чтобы минимизировать глубину цепи , что является максимальным расстоянием от любого входа через схему до выход. Рассмотрим, например, две пунктирные линии на следующей схеме: которые указывают два разных пути от входа к выходу в схема.
Пунктирный путь, начинающийся с x проходит через трое ворот (ворота ИЛИ, затем ворота НЕ, затем еще ворота ИЛИ), в то время как пунктирный путь, начинающийся с и , идет только через два вентиля (вентиль И и вентиль ИЛИ).
Есть два других пути тоже, но ни один из путей не проходит более чем через три врата. Таким образом, мы бы сказали, что глубина этой схемы равна 3. Это грубая мера скорости цепи: Вычисление результата с помощью этой схемы занимает примерно три раза. количество времени, которое требуется одним воротам для выполнения своей работы.
«Техника суммы произведений», которую мы видели для преобразования булевой функции в схему не так уж плохо используя эти критерии. Схема, полученная в результате этой техники имеет глубину всего 3 — или немного больше, если вы настаиваете (как это сделают разработчики схем), что каждый логический элемент И и ИЛИ имеет только два входы. Но это работает хуже, чем мы могли бы надеяться с точки зрения пространство.
3.2. Карты Карно
Теперь мы обратимся к исследованию техники построения схемы из таблицы истинности, что приводит к меньшим схемам без каких-либо компромиссов в глубине.
Для логических функций с четырьмя или менее входами Карта Карно особенно удобный способ найти наименьшее возможное выражение суммы произведений.
Это простой процесс: мы преобразуем таблицу истинности в матрицу как мы увидим позже, тогда мы определяем, как лучше всего «покрыть» 1 в матрице с набором прямоугольников; каждый прямоугольник будет соответствуют термину в нашем выражении суммы произведений.
Начнем с таблицы истинности, используемой в Раздел 2.3.
x y z o 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 Поскольку в этой таблице восемь строк, мы преобразуем ее в матрицу 2×4.
(Если бы было 4 строки, это было бы Матрица 2×2. И если бы было 16 строк, это было бы Матрица 4×4.) Одна из переменных будет представлена по вертикальной оси, а две другие переменные по Горизонтальная ось. Обратите внимание, как комбинации переменных вдоль горизонтальная ось сделать вместо идут в традиционном порядке 00-01-10-11, а вместо 00-01-11-10. Это важно для Техника карты Карно в работе.
Создав эту матрицу, мы теперь заполняем ее, копируя соответствующие выходные значения в соответствующую ячейку. Правда последняя строка таблицы, например, отображается в ячейку во второй строке матрицы (поскольку x — это 1 в этой строке таблицы истинности) и третий столбец (поскольку y и z оба являются 1 в этой строке таблицу истинности). вывод в последней строке таблицы истинности равен 1, поэтому мы помещаем 1 в эту ячейку матрицы. Ниже приведена заполненная матрица, с обведенной 1, соответствующей последней строке таблицы истинности.

Теперь мы ищем наименьший набор прямоугольных областей, которые покрывают все 1 в нашей таблице, но нет 0. Высота и ширина каждого прямоугольника должно быть степенью двойки, поэтому возможности равны 1×1, 1×2, 1×4, 2×1, 2×2, 2×4, 4×1, 4×2, и 4×4. В нашем примере мы можем покрыть все 1, используя всего три прямоугольника.
Каждому из регионов будет соответствовать терм в сумме выражения продуктов, которое мы строим на основе выбранного регионы. Розовая область справа, для Например, под столбцом 10 соответствует термину, где y равно 1 и z равно 0, но x может быть либо 0, либо 1. Тогда соответствующий термин будет y z . положить вместе термины из трех регионов вместе, мы получаем:
x y z + y z 05 90 0 x Это можно перевести в схему Рисунок 5.
Обратите внимание, что эта схема имеет только 7 вентилей по сравнению с 10 ворот на рисунке 4.
Рисунок 5: Упрощенная схема, эквивалентная Рисунок 4.
3.3. Более сложная карта Карно
Другой пример иллюстрирует некоторые дополнительные возможности карты. Карта Карно. На этот раз мы будем работать с таблицей истинности над четыре входа.
w x y z o 0 0 0 0 1 0 0 0 1 0 0 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 0 0 1 1 0 1 0 1 1 1 0
w x y z o 1 0 0 0 1 1 0 0 1 0 1 0 1 0 1 1 0 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 Since we have 16 rows in this стол, мы начнем с 4×4 матрица.
Каждая строка представляет собой комбинацию значения для значений первых двух переменных, и каждый столбец будет представляют собой комбинацию значений двух последних переменных.
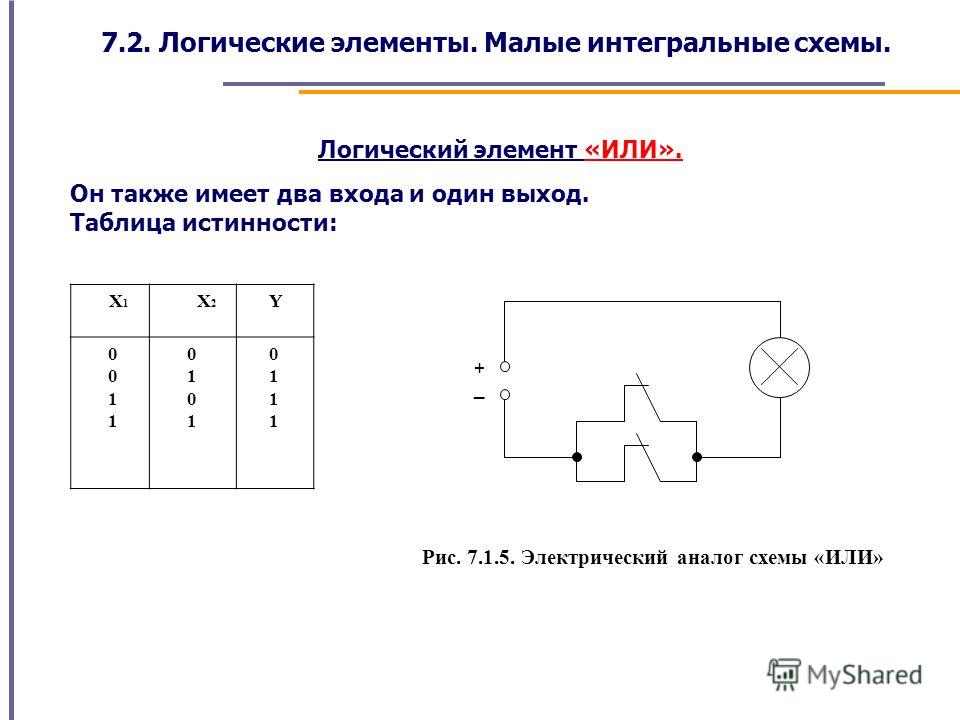
При определении прямоугольных областей введем новое правило: Области могут зацикливаться грани матрицы. (Это правило действует для трехвходовых тоже функции, хотя в нашем предыдущий пример.) Используя этот факт, мы можем покрыть 1, используя всего три прямоугольника.
Самая простая область (выделена желтым цветом) находится в правом нижнем углу; это соответствует термину w y . Верхняя область 2×2 (обозначенная розовым цветом) выходит за пределы последней столбец вокруг до первого столбца; это соответствует термину w z . Есть еще один регион (обведен синим), который переносится между столбцами, а также между строками, поэтому он охватывает все четыре угла матрицы; это соответствует термину x z .
Объединяя эти три термина, мы приходим к нашему упрощенному Логическое выражение:
w y + w z + x з Когда вы рисуете прямоугольные области, вы хотите использовать их как как можно меньше: каждому региону будет соответствовать дополнительный И ворота. В нашем примере выше мы опустили возможный прямоугольник который покрывает последний столбец, потому что он не покрывает ни одной единицы которые еще не были покрыты.
Более того, вы хотите, чтобы каждый прямоугольник покрывал столько единиц, сколько возможно, даже если в этом нет необходимости, потому что большие прямоугольники приводят к терминам, содержащим меньше переменных. В нашем более раннем Например, мы могли бы нарисовать верхний розовый прямоугольник как Прямоугольник 1×2 только во втором ряду. Но потом второй условия были бы w x z , который имеет на одну переменную больше, чем мы использовали ранее.
4. Другие логические элементы и универсальность
До сих пор мы имели дело только с элементами И, ИЛИ и НЕ. Разработчики схем часто работают с четырьмя другими вентилями: И-НЕ ( n или и ), НИ ( n или или ), XOR (e x включительно или ) и XNOR ( n или x включительно или ). Вентиль XOR выдает 1, когда один или другой из его входов равен 1, но не тогда, когда оба; то есть случай двух входов 1 исключил из ситуации, когда гейт выдает 1. Элементы И-НЕ, ИЛИ-НЕ и Исключающее-НЕ работают просто как элементы И/ИЛИ/ИСКЛЮЧАЮЩЕЕ ИЛИ с логический элемент НЕ после него — и они рисуются как И/ИЛИ/ИСКЛЮЧАЮЩЕЕ ИЛИ ворота с маленьким кружком на выходе. На рис. 6 показан внешний вид этих ворот и сводки таблицы истинности.
Рисунок 6: Больше логических вентилей.
111124 0
(а) вентиль И-НЕ (б) Ворота НЕ-ИЛИ (c) Вентиль XOR (d) Ворота XNOR
9 9008 A B O 1118 0071 0 1 0 1 1 1 0 1 1 1 0
a b o 0 0 1 0 1 0 1 0 0 1 1 0 0 0 11111124 0
0 240 4 0 4
a b o 0 0 0 0 1 1 1 0 1 1 1 0
a b o 0 0 1 0 1 0 1 0 0 1 1 1
Ранее мы не смотрели на эти ворота, потому что они могут
все они должны быть построены с использованием логических элементов И, ИЛИ и НЕ.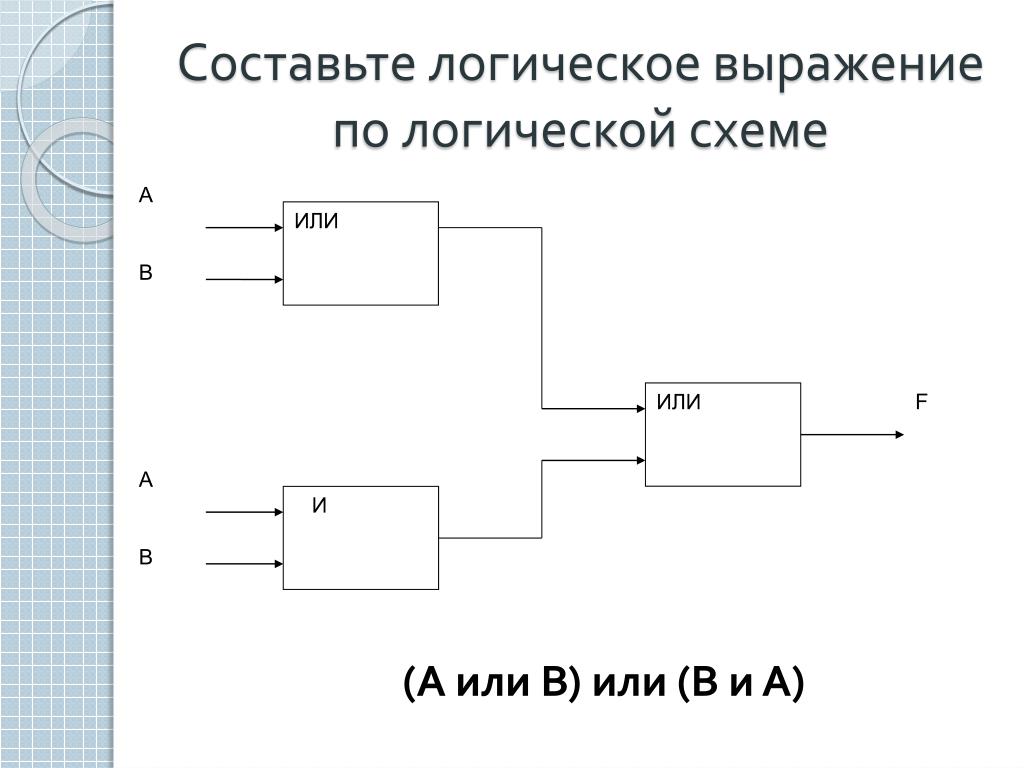 На самом деле мы видели
что каждая таблица истинности имеет схему логических элементов И, ИЛИ и НЕ
что ему соответствует —
мы просто получаем выражение суммы произведений (которое имеет только
операции И, ИЛИ и НЕ), а затем построить соответствующие
схема. Благодаря этому свойству мы называем комбинацию
И, ИЛИ, и НЕ универсальный .
На самом деле мы видели
что каждая таблица истинности имеет схему логических элементов И, ИЛИ и НЕ
что ему соответствует —
мы просто получаем выражение суммы произведений (которое имеет только
операции И, ИЛИ и НЕ), а затем построить соответствующие
схема. Благодаря этому свойству мы называем комбинацию
И, ИЛИ, и НЕ универсальный .
Несколько более удивительным является то, что только вентиль И-НЕ универсальный — то есть любая таблица истинности может быть реализована схемой, включающей только вентили И-НЕ. Чтобы убедиться в этом, начнем с того, что любой таблица истинности может быть реализована с использованием логических элементов И, ИЛИ и НЕ; а также затем мы видим, как можно заменить каждый вентиль И/ИЛИ/НЕ на система вентилей И-НЕ для получения схемы, включающей только И-НЕ ворота. На рис. 7 показан вентиль NAND. система, соответствующая каждому из И, ИЛИ и НЕ.
Рисунок 7: Построение НЕ, И и ИЛИ с использованием вентилей И-НЕ.
преобразуется в преобразуется в преобразуется в
Мы можем сделать то же самое, чтобы найти, что ворота НЕ-ИЛИ сами по себе универсальны.
Тот факт, что NAND универсален, часто используется схемой дизайнеры. Хотя дизайнеры сначала разрабатывают схему, используя И, ИЛИ, а НЕ вентили, на практике схемы проще производства, когда они используют только вентили NAND (или только вентили NOR). (Почему это так, мы здесь не будем рассматривать.) Таким образом, их первоначальные Схемы И/ИЛИ/НЕ преобразуются для использования только NAND (или NOR).
В любом случае, к этому моменту мы уже видели, как можно наращивать
достаточно маленькая схема для любой возможной логической функции.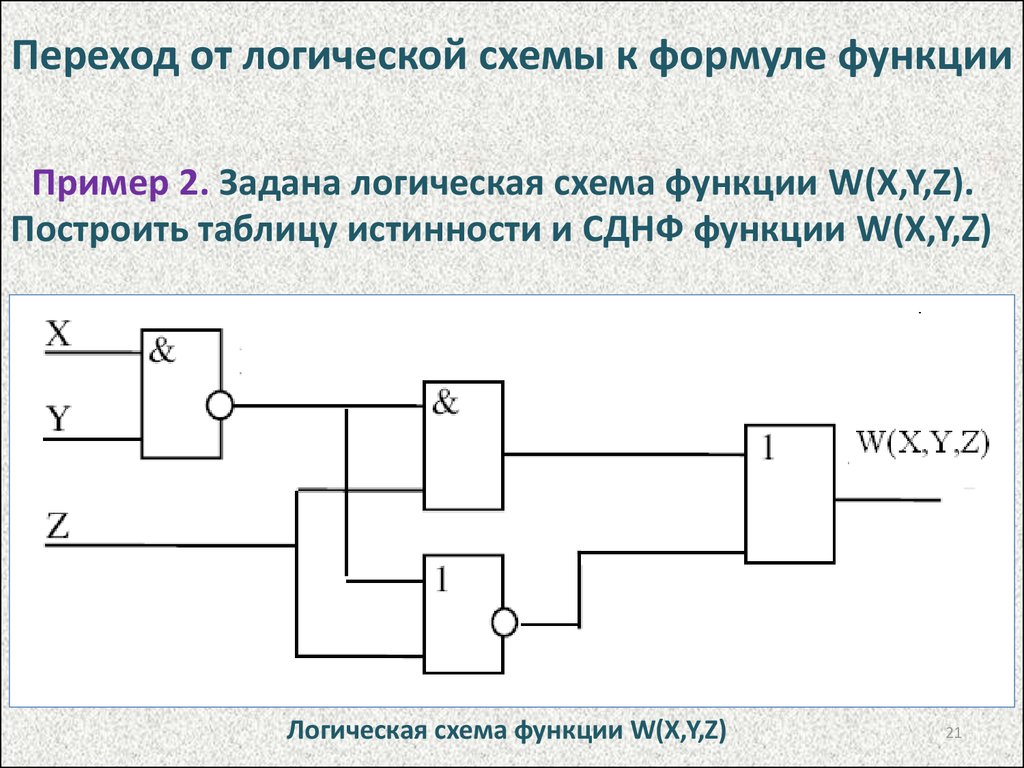 Эти знания составляют основу для создания полной вычислительной
устройства.
Эти знания составляют основу для создания полной вычислительной
устройства.
| КОМБИНАЦИОННАЯ ЛОГИКА |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
digitallogic
Хотите верьте, хотите нет, но мы можем моделировать все вычислительные процессы (о которых мы знаем) с помощью операций, в первую очередь, старой доброй классической логики.
Гейтс
Большая часть математики (особенно аксиоматическая теория множеств и теория чисел) использует бивалентную логику, в которой
утверждения либо истинны, либо ложны. Электронные компьютеры используют логические элементы для самых примитивных вычислений, принимая 0 за ложь и 1 за истину. Возможно бесконечное количество ворот; вот шесть наиболее распространенных:
Возможно бесконечное количество ворот; вот шесть наиболее распространенных:
Почему эти имена? Считайте 0 ложным, а 1 истинным. Затем:
- «не А» имеет истинностное значение, противоположное А
- «А и В» истинно тогда и только тогда, когда истинно А и истинно Б
- «А или В» истинно тогда и только тогда, когда либо А истинно, либо В истинно, либо и то, и другое
- «A xor B» истинно тогда и только тогда, когда либо A истинно, либо B истинно , но нет или оба
- «А и В» («не и») противоположны «А и В»
- «A, ни B» («не или») является противоположностью «A или B»
Упражнение : Проверьте эти описания с помощью «таблиц истинности» на рисунке выше.
Ворота можно сделать из макарон, резинок или чего угодно. Как правило, они построены из транзисторов . Вот как можно использовать КМОП-транзисторы для создания вентилей НЕ, И-НЕ и ИЛИ-НЕ (строка вверху — 1, нижняя — 0):
При изучении организации компьютерных систем мы обычно берем вентили как данность, и предоставьте инженерам-электрикам и программистам заботиться о транзисторах и обеспечить нас надежными затворами.
Логические вычисления
Операции могут быть расширены до битовых строк. Примеры:
10110 01101 01101 01101
НЕ И 10100 ИЛИ 10100 XOR 10100
----- --------- -------- ---------
01001 00100 11101 11001
Манипуляции с битами
Обратите внимание на следующие полезные формулы (всего три из многих)…
х И 0 = 0 х ИЛИ 0 = х х Исключающее ИЛИ 0 = х х И 1 = х х ИЛИ 1 = 1 х X ИЛИ 1 = ~ х х И х = х х ИЛИ х = х х X ИЛИ х = 0
…из которого вы можете узнать такие трюки, как:
- Чтобы установить биты 2, 3 и 7 в 8-битном слове, ИЛИ с 8C
- Чтобы очистить бит 6 в 16-битном слове И с помощью FFBF
- Чтобы дополнить биты 2 и 3 в 8-битном слове, XOR с 0C
- Чтобы очистить слово целиком, выполните XOR с самим собой
- Для вычисления R по модулю 8, И с 7
Функции двоичной логики
Можно создать 16 вентилей с двумя входами:
| А=0 В=0 | А=0 В=1 | А=1 В=0 | А=1 В=1 | Операция |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | $0$ |
| 0 | 0 | 0 | 1 | $A$ и $B$ $A \клин B$ $AB$ |
| 0 | 0 | 1 | 0 | $A$ и не $B$ $A \клин \neg B$ $A\overline{B}$ |
| 0 | 0 | 1 | 1 | $А$ |
| 0 | 1 | 0 | 0 | $\neg{A} \клин B$ $\overline{A}B$ |
| 0 | 1 | 0 | 1 | $В$ |
| 0 | 1 | 1 | 0 | $A$ xor $B$ $A \oplus B$ $A \neq B$ |
| 0 | 1 | 1 | 1 | $A$ или $B$ $A \vee B$ $A + B$ |
| 1 | 0 | 0 | 0 | $A$ ни $B$ $\neg(A \vee B)$ $\overline{A+B}$ $A \downarrow B$ |
| 1 | 0 | 0 | 1 | $A$ xnor $B$ $\neg(A \oplus B)$ $\overline{A \oplus B}$ $A = B$ |
| 1 | 0 | 1 | 0 | не $B$ $\neg{B}$ $\overline{B}$ |
| 1 | 0 | 1 | 1 | $A$ или нет $B$ $A \vee \neg{B}$ $A + \overline{B}$ $B \supset A$ |
| 1 | 1 | 0 | 0 | не $A$ $\neg{A}$ $\overline{A}$ |
| 1 | 1 | 0 | 1 | $\neg{A} \vee B$ $\overline{A}+B$ $A \supset B$ |
| 1 | 1 | 1 | 0 | $A$ nand $B$ $\neg(A \wedge B)$ $\overline{AB}$ $A \uparrow B$ |
| 1 | 1 | 1 | 1 | $1$ |
В Википедии есть длинные статьи о большинстве, если не обо всех из них. Не пропустите те, что на
А ТАКЖЕ,
ИЛИ ЖЕ,
XOR,
И-НЕ, и
НИ.
Не пропустите те, что на
А ТАКЖЕ,
ИЛИ ЖЕ,
XOR,
И-НЕ, и
НИ.
Упражнение . Сколько существует возможных вентилей с тремя входами? Сколько с 5 входами? Сколько с 10? Сколько атомов во Вселенной?
Эквиваленты
Это так важно. Изучите их. Знай , почему , точно, держат. Познайте их глубокий смысл. $$\begin{эквнаррай} АА & = & А \\ А+А & = & А \\ A\overline{A} & = & 0 & \tiny \textrm{A не может быть и истинным, и ложным}\\ A + \overline{A} & = & 1 & \tiny \textrm{A либо истинно, либо ложно}\\ AB & = & \overline{\overline{A} + \overline{B}} & \tiny \textrm{оба верны, если иное не верно, если одно из них ложно}\\ A + B & = & \overline{\overline{A} \: \overline{B}} & \tiny \textrm{любой из них истинен, если и только если не тот случай, когда оба ложны}\\ \overline{AB} & = & \overline{A} + \overline{B} & \tiny \textrm{не оба истинны, если и только если ложно}\\ \overline{A + B} & = & \overline{A} \: \overline{B} & \tiny \textrm{не тот случай, когда ни одно из них не истинно, если оба ложны}\\ \end{эквнаррай} $$
Полные наборы операторов
Интересным интеллектуальным упражнением является создание так называемых полных наборов операций. Полный набор — это набор операций, из которых могут быть получены все шестнадцать операций. Например, {НЕ, И, ИЛИ} завершено, так же как и {НЕ-И}. Но {ИЛИ} не завершено.
Полный набор — это набор операций, из которых могут быть получены все шестнадцать операций. Например, {НЕ, И, ИЛИ} завершено, так же как и {НЕ-И}. Но {ИЛИ} не завершено.
Докажем, что {НЕ, И, ИЛИ} завершено. Для этого мы покажем, как можно определить каждый из шестнадцати операторов, используя только НЕ, И и ИЛИ. Вот оно:
- $0 = A\overline{A}$
- $AB$ уже использует только нужные операторы
- $A\overline{B}$ уже использует только нужные операторы
- $А = АА$
- $\overline{A}B$ уже использует только нужные операторы
- $В = ВВ$
- $A \oplus B = A\overline{B} + \overline{A}B$
- $A + B$ уже использует только нужные операторы
- $\overline{A + B}$ уже использует только нужные операторы
- $\overline{A \oplus B} = AB + \overline{A}\,\overline{B}$
- $\overline{B}$ уже использует только нужные операторы
- $A + \overline{B}$ уже использует только нужные операторы
- $\overline{A}$ уже использует только нужные операторы
- $\overline{A} + B$ уже использует только нужные операторы
- $\overline{AB}$ уже использует только нужные операторы
- $1 = A + \overline{A}$
Теперь, чтобы доказать, что только {NAND} завершена, нам просто нужно показать, как определить NOT, AND и OR в терминах NAND (затем мы можем использовать версии этих трех только NAND, чтобы сделать остальные, как мы видели выше):
- $\overline{A} = \overline{AA}$
- $AB = \overline{\overline{AB}} = \overline{(\overline{AB})\:(\overline{AB})}$
- $A + B = \overline{\overline{A} \: \overline{B}}$
Отвратительно, уродливо и сверхсложно, да, знание того, что такие вещи можно делать, имеет преимущества.
Упражнение : Что такого интересного в том, что {NAND} завершена?
Упражнение : Напишите каждое из следующих действий, используя только NAND.
- $A+\overline{BC}$
- $A\oplus{\overline{C}}$
- $AB\overline{C} + AC + D$
- $1$
Логические схемы
Разработчики логики создают схемы, чтобы делать то, что они хотят. В основном они хотят реализовать функции, которые преобразуют определенные входные данные в определенные выходные данные. Например, вот логическая схема, которая складывает два четырехбитных целых числа:
Как кто-нибудь это понял? Сначала рассмотрим случай, когда мы хотим добавить только два однобитных числа. Назовите входы х и у , и выходы будут s (для суммы) и c (для переноса). Записывать поведение для всех возможных комбинаций входов:
х у | с с ------+------ 0 0 | 0 0 0 1 | 1 0 1 0 | 1 0 1 1 | 0 1
Отлично, мы видим, что s = x XOR y, а c = x AND y. Итак, вот наш
полусумматор :
Итак, вот наш
полусумматор :
Теперь, чтобы добавить многобитные числа, мы должны добавить переносы в входные данные, когда мы двигаемся справа налево, как вы учились в Elementary школа. Таким образом, полный сумматор имеет три входа, x и y и переносим в . Давайте составим таблицу и посмотрим, что нам нужно сделать:
х у син | с выходом ---------+--------- 0 0 0 | 0 0 0 0 1 | 1 0 0 1 0 | 1 0 0 1 1 | 0 1 1 0 0 | 1 0 1 0 1 | 0 1 1 1 0 | 0 1 1 1 1 | 1 1
So s = x XOR y XOR cin и cout = (y AND cin) OR (x AND cin) ИЛИ (х И у).
Вы можете построить многоразрядный сумматор, поставив половинный сумматор на справа и последовательность полных сумматоров слева, или просто используйте полные сумматоры и заставьте ноль в самый правый перенос.
Цепи памяти
Постоянное запоминающее устройство (ПЗУ) — это просто логическая схема,
ввод — это адрес, а вывод — данные по этому адресу!
Сделайте один, решив, какие значения идут по какому адресу, и создайте
схема однако вам нужно.

 6. Таблица истинности схемы ИсключающееИЛИ
6. Таблица истинности схемы ИсключающееИЛИ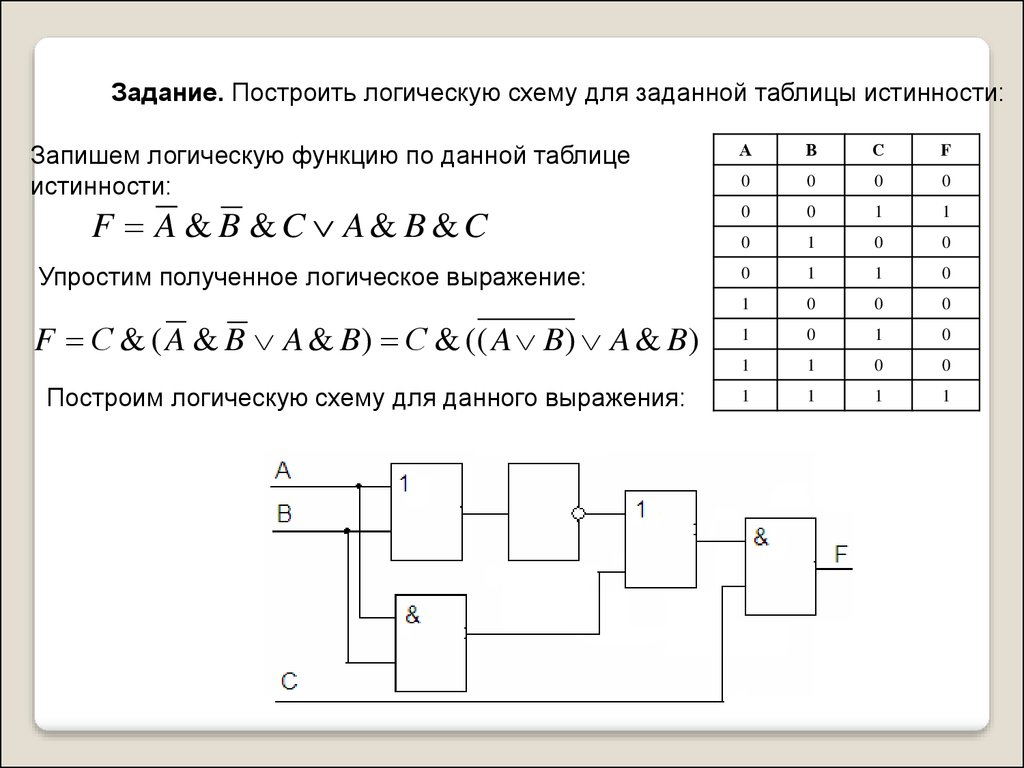 7. Таблица истинности схемы Исключающее ИЛИ-НЕ
7. Таблица истинности схемы Исключающее ИЛИ-НЕ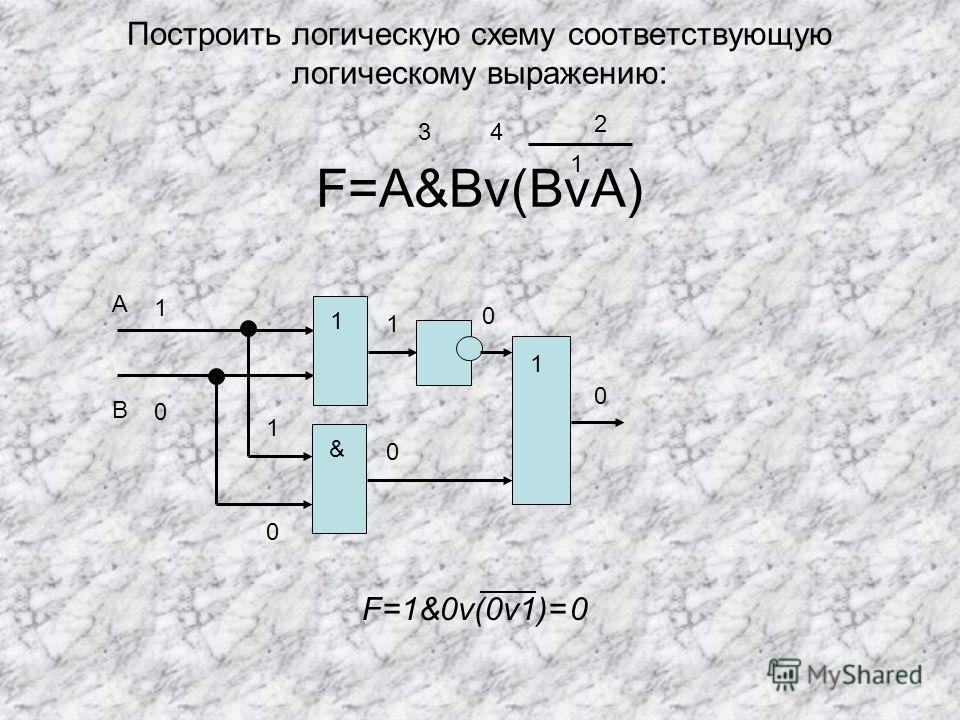 ИЛИ
ИЛИ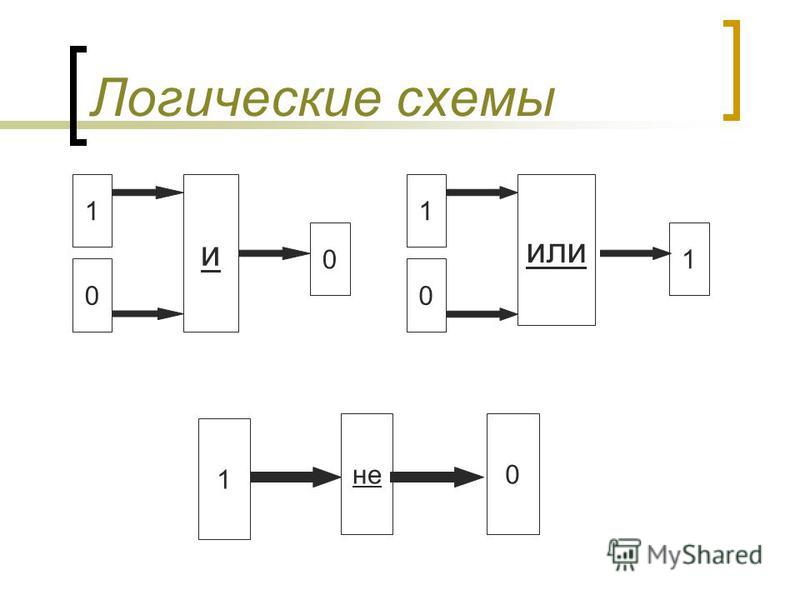

 логические схемы. Другие схемы разработаны
действительно вспомнить прошлые состояния
свои входы и производить результаты на основе
на эти прошлые сигналы, а также текущие
состояния их входов. Эти схемы
может действовать в соответствии с последовательностью
входных сигналов, и поэтому известны
как последовательные логические схемы.
логические схемы. Другие схемы разработаны
действительно вспомнить прошлые состояния
свои входы и производить результаты на основе
на эти прошлые сигналы, а также текущие
состояния их входов. Эти схемы
может действовать в соответствии с последовательностью
входных сигналов, и поэтому известны
как последовательные логические схемы. 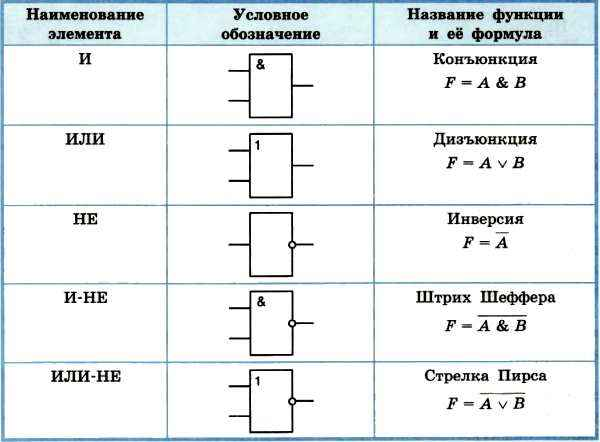 Основа
это добавление; если мы можем добавить два
двоичные числа, мы можем так же легко
вычтите их или немного пофантазируйте
и выполнить умножение и деление.
Как же тогда сложить два двоичных числа?
Основа
это добавление; если мы можем добавить два
двоичные числа, мы можем так же легко
вычтите их или немного пофантазируйте
и выполнить умножение и деление.
Как же тогда сложить два двоичных числа? 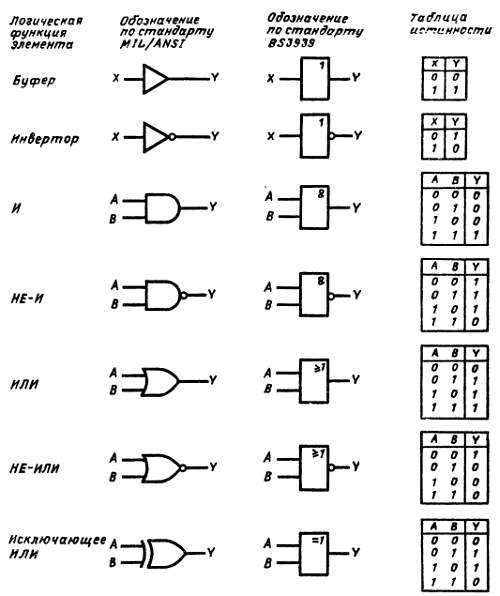 Давайте представим это как таблицу истинности
с двумя входами и двумя выходами, и см.
куда мы можем пойти оттуда.
Давайте представим это как таблицу истинности
с двумя входами и двумя выходами, и см.
куда мы можем пойти оттуда.  С
у нас будет как входной перенос, так и
выходной перенос, мы будем обозначать их как
ЦИН и КАУТ. При этом мы будем
используйте S, чтобы обозначить окончательный вывод суммы.
Вот результирующая таблица истинности:
С
у нас будет как входной перенос, так и
выходной перенос, мы будем обозначать их как
ЦИН и КАУТ. При этом мы будем
используйте S, чтобы обозначить окончательный вывод суммы.
Вот результирующая таблица истинности: 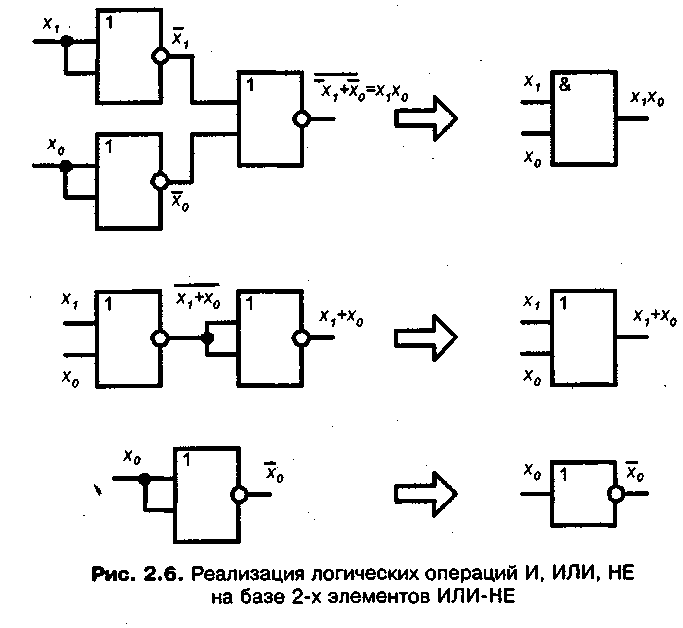 Глядя
однако, мы можем
обратите внимание, что выход S на самом деле является
XOR между входом A и полусуммером
Выход SUM с входами B и CIN. Также,
выходной перенос будет истинным, если любые два
или все три входа имеют логическую 1.
Глядя
однако, мы можем
обратите внимание, что выход S на самом деле является
XOR между входом A и полусуммером
Выход SUM с входами B и CIN. Также,
выходной перенос будет истинным, если любые два
или все три входа имеют логическую 1. 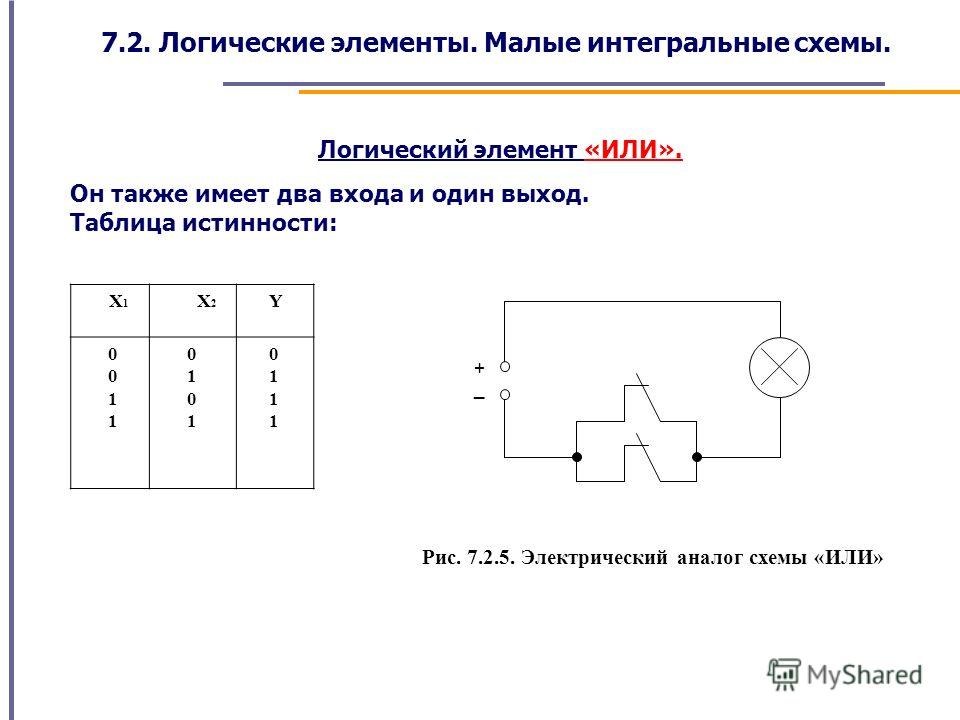 Если любой из полусумматоров дает
перенос, будет выходной перенос.
Таким образом, COUT будет функцией ИЛИ
выходы переноса полусумматора. Результирующий
полная сумматорная схема показана ниже:
Если любой из полусумматоров дает
перенос, будет выходной перенос.
Таким образом, COUT будет функцией ИЛИ
выходы переноса полусумматора. Результирующий
полная сумматорная схема показана ниже: 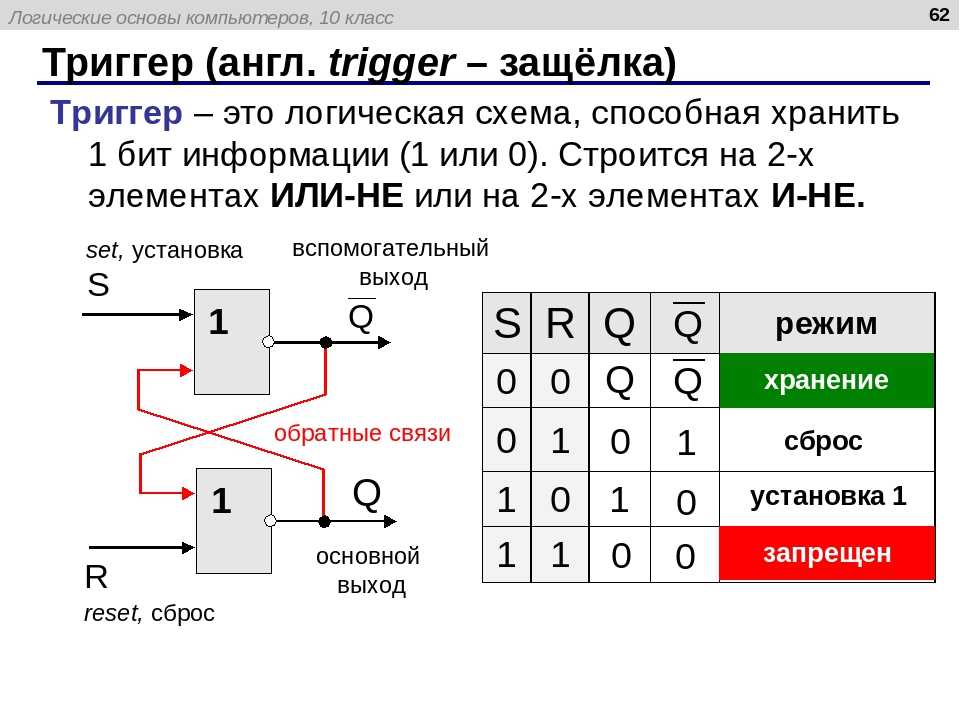 Это,
в конце концов, логическая функция, которая
важен, а не точный метод выполнения
эта функция.
Это,
в конце концов, логическая функция, которая
важен, а не точный метод выполнения
эта функция.  это не легко
описать без логической схемы, но
легко понять, когда на диаграмме
доступен.
это не легко
описать без логической схемы, но
легко понять, когда на диаграмме
доступен.  Если
вход A переключается туда и обратно в
частота, более чем в два раза превышающая частоту
любого цифрового сигнала, оба сигнала
будут точно воспроизведены и могут
быть снова разделены демультиплексором
цепь синхронизирована с мультиплексором.
Если
вход A переключается туда и обратно в
частота, более чем в два раза превышающая частоту
любого цифрового сигнала, оба сигнала
будут точно воспроизведены и могут
быть снова разделены демультиплексором
цепь синхронизирована с мультиплексором. 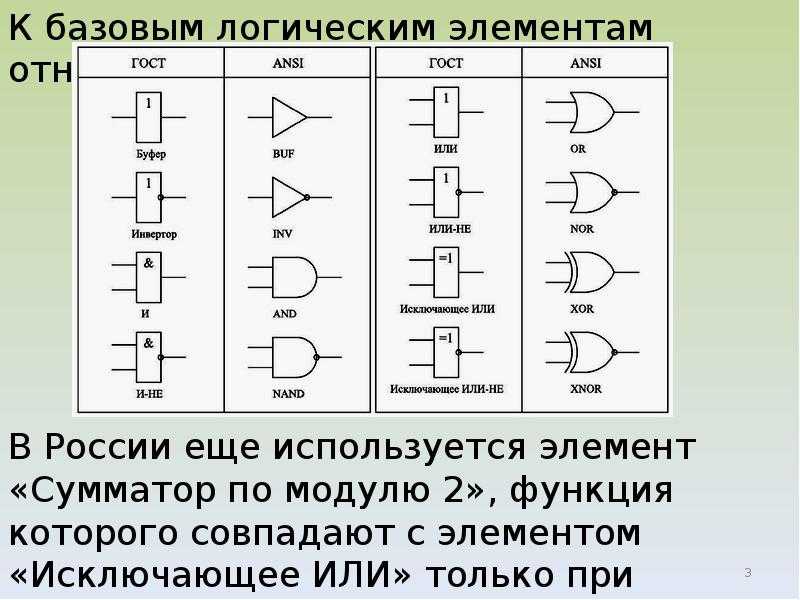 С развитием Интернета и
Всемирная паутина, большинство людей слышали
о телефонных линиях Т1. Линия T1 может
передавать до 24 отдельных телефонных
разговоры, мультиплексируя их в
таким образом.
С развитием Интернета и
Всемирная паутина, большинство людей слышали
о телефонных линиях Т1. Линия T1 может
передавать до 24 отдельных телефонных
разговоры, мультиплексируя их в
таким образом.  Эта схема
принимает один ввод данных и один или несколько
адресные входы и выбирает, какой из нескольких
выходы будут получать входной сигнал.
Эту же схему можно использовать и как
декодер, используя адресные входы как
двоичное число и создание вывода
сигнал на одном выходе, который соответствует
двоичный адресный вход. В этом приложении
линия ввода данных функционирует как схема
enabler — если схема отключена,
ни один вывод не будет показывать активность независимо
числа двоичного входа.
Эта схема
принимает один ввод данных и один или несколько
адресные входы и выбирает, какой из нескольких
выходы будут получать входной сигнал.
Эту же схему можно использовать и как
декодер, используя адресные входы как
двоичное число и создание вывода
сигнал на одном выходе, который соответствует
двоичный адресный вход. В этом приложении
линия ввода данных функционирует как схема
enabler — если схема отключена,
ни один вывод не будет показывать активность независимо
числа двоичного входа.  Принципиальное отличие состоит в том, что это
объединенные входы и выходы
что отдельные. Сделав это изменение,
мы получаем схему, обратную
двухвходовой мультиплексор. Если бы ты был
построить обе схемы на одном
макетная плата, подключите выход мультиплексора
к данным IN демультиплексора, и
управлять адресными входами (A) обеих схем
с тем же сигналом вы обнаружите, что
начальный вход X0 будет передан
на OUT0, а вход X1 будет достигать только
ВЫХ1.
Принципиальное отличие состоит в том, что это
объединенные входы и выходы
что отдельные. Сделав это изменение,
мы получаем схему, обратную
двухвходовой мультиплексор. Если бы ты был
построить обе схемы на одном
макетная плата, подключите выход мультиплексора
к данным IN демультиплексора, и
управлять адресными входами (A) обеих схем
с тем же сигналом вы обнаружите, что
начальный вход X0 будет передан
на OUT0, а вход X1 будет достигать только
ВЫХ1.  К
сохранить выходной сигнал, нам нужно добавить
схема защелки, которая может следовать за данными
сигнал, пока он активен, но будет удерживать
последнее состояние сигнала, в то время как другое
сигнал данных активен. Отличная схема
для этого является защелкой D (или данных). По
размещение защелки после каждого выхода и
используя вход Addressing (или его инверсию)
чтобы контролировать их, мы можем поддерживать оба
выходные сигналы в любое время. Если адрес
ввод меняется гораздо быстрее, чем
ввод данных, выходные сигналы будут соответствовать
входы
верно.
К
сохранить выходной сигнал, нам нужно добавить
схема защелки, которая может следовать за данными
сигнал, пока он активен, но будет удерживать
последнее состояние сигнала, в то время как другое
сигнал данных активен. Отличная схема
для этого является защелкой D (или данных). По
размещение защелки после каждого выхода и
используя вход Addressing (или его инверсию)
чтобы контролировать их, мы можем поддерживать оба
выходные сигналы в любое время. Если адрес
ввод меняется гораздо быстрее, чем
ввод данных, выходные сигналы будут соответствовать
входы
верно.
