Мостовая схема измерения сопротивления: принцип работы и применение

Как работает мостовая схема измерения сопротивления. Для чего используются мостовые схемы. Какие бывают виды мостовых схем. Как правильно настроить и откалибровать мостовую схему.

Принцип работы мостовой схемы измерения сопротивления

Мостовая схема измерения сопротивления, также известная как мост Уитстона, представляет собой электрическую цепь, позволяющую с высокой точностью измерять неизвестное сопротивление. Принцип ее работы основан на сравнении неизвестного сопротивления с эталонными резисторами.

Классическая мостовая схема состоит из четырех плеч, образующих замкнутый контур:

• Два плеча с известными сопротивлениями R1 и R2
• Плечо с регулируемым эталонным сопротивлением R3
• Плечо с измеряемым неизвестным сопротивлением Rx

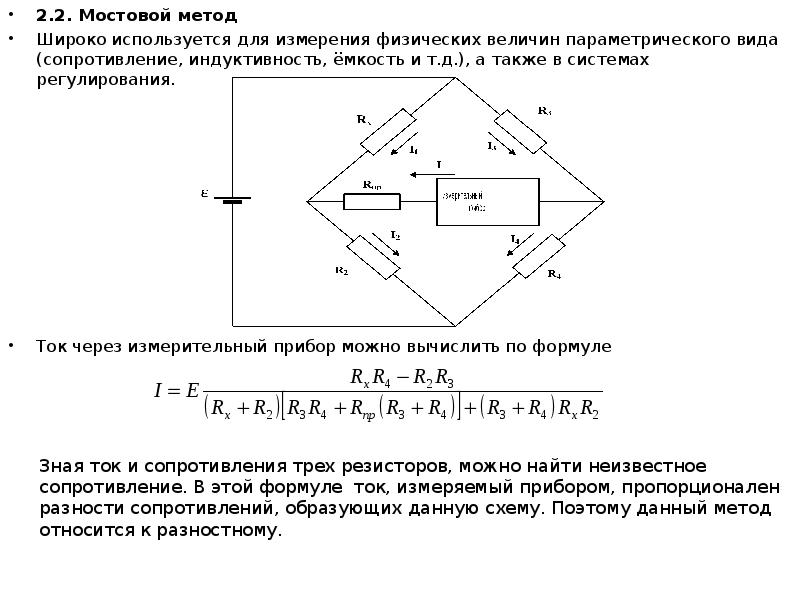
В диагональ моста включается чувствительный гальванометр. При подаче напряжения питания на мост, ток через гальванометр будет равен нулю только в случае, когда выполняется соотношение:

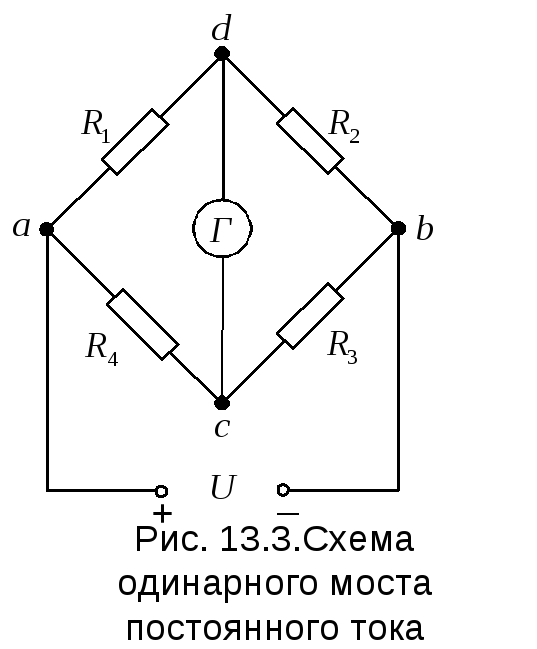
R1/R2 = Rx/R3

Это состояние называется равновесием моста. Изменяя сопротивление R3, добиваются нулевого показания гальванометра. В этом случае неизвестное сопротивление Rx можно рассчитать по формуле:

Rx = R3 * R2 / R1

Преимущества мостовой схемы измерения сопротивления

Мостовая схема обладает рядом важных преимуществ по сравнению с другими методами измерения сопротивления:

• Высокая точность измерений, особенно для малых сопротивлений
• Нечувствительность к колебаниям напряжения питания
• Возможность измерения в широком диапазоне сопротивлений
• Простота конструкции и надежность
• Возможность автоматизации процесса измерения

Благодаря этим преимуществам, мостовые схемы широко применяются в измерительной технике и системах автоматического контроля.

Области применения мостовых схем

Мостовые схемы измерения сопротивления нашли применение во многих областях науки и техники:

• Измерение электрических сопротивлений с высокой точностью
• Измерение неэлектрических величин с помощью резистивных датчиков (температуры, давления, деформации и др.)
• Контроль параметров электронных компонентов
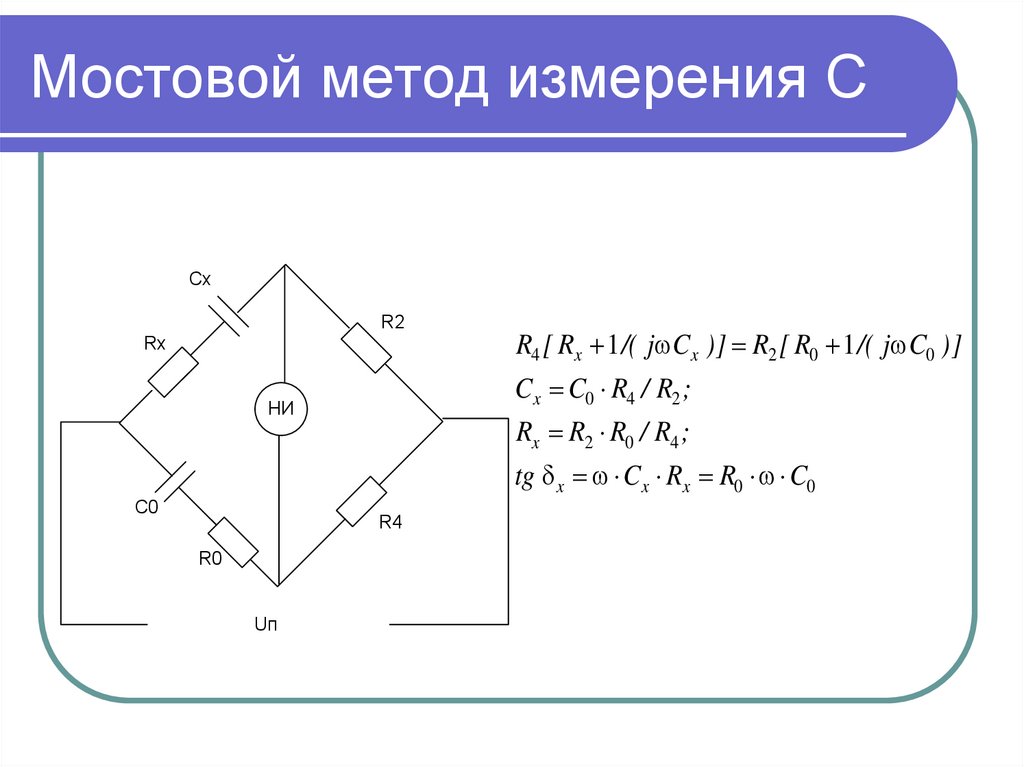
• Измерение емкости и индуктивности (мосты переменного тока)
• Системы автоматического управления и регулирования

В промышленности мостовые схемы часто используются в составе датчиков физических величин, например, тензорезисторных датчиков давления и силы.

Виды мостовых схем измерения

Помимо классического моста Уитстона, существуют и другие разновидности мостовых схем:

• Двойной мост Томсона — для измерения малых сопротивлений
• Мост Кельвина — для измерения очень малых сопротивлений
• Мосты переменного тока — для измерения емкости и индуктивности
• Автоматические мосты — с электронной схемой уравновешивания

Выбор конкретной схемы зависит от диапазона измеряемых сопротивлений и требуемой точности.

Настройка и калибровка мостовой схемы

Для получения точных результатов измерений необходимо правильно настроить и откалибровать мостовую схему. Основные этапы этого процесса:

1. Проверка исправности всех элементов схемы
2. Установка номиналов эталонных резисторов
3. Балансировка моста при отсутствии измеряемого сопротивления
4. Проверка линейности шкалы измерительного прибора
5. Калибровка с помощью эталонных резисторов

Периодическая проверка калибровки позволяет поддерживать высокую точность измерений.

Современные реализации мостовых схем

В современной измерительной технике классические мостовые схемы часто заменяются их электронными аналогами. Они имеют ряд преимуществ:

• Автоматическое уравновешивание моста
• Цифровая индикация результата измерения
• Возможность подключения к компьютеру
• Расширенные функции обработки результатов

Тем не менее, принцип работы электронных мостов остается тем же, что и у классических схем.

Проблемы и ограничения мостовых схем

При работе с мостовыми схемами измерения сопротивления следует учитывать некоторые особенности и ограничения:

• Влияние сопротивления соединительных проводов при измерении малых сопротивлений
• Нелинейность шкалы при значительном отклонении от равновесия
• Влияние температуры на точность измерений
• Ограниченный диапазон измерений для одной схемы

Правильный выбор схемы и методики измерений позволяет минимизировать влияние этих факторов.

Принцип работы мостовой схемы

Корзина: Пусто

if ($_SERVER[‘PHP_SELF’] !== «/configurator/») { // сворачиваем на странице конфигуратора ?>

} ?>

1. Как применяют измерительные мосты

Принцип работы мостовой схемы измерения продемонстрирован на рисунке 1, а способ ее применения на практике — на рисунке 2.

Рис. 1.

Сопротивление R1 вычисляется исходя из полученного при балансировке измерительно моста соотношения R4/R3, в качестве R2 используется резистор с известным значением. Конечно, сказанное дает только самое общее представление об измерительной схеме моста. На самом деле он устроен гораздо сложнее — современные мосты создаются на основе цифровых процессоров. Микропроцессорное ядро позволяет автоматизировать процедуру измерения (в первых моделях оператор должен был пользоваться калькулятором, сегодня же все расчеты выполняются аппаратурой), обеспечить многофункциональность устройства (многие мосты интегрированы с другими измерительными приборами — мультиметрами, рефлектометрами и т. п.), устранить помехи (посторонние постоянные и переменные напряжения почти всегда присутствуют на жилах кабелей), организовать дальнейшую обработку накопленных результатов измерений (хранение, обмен с компьютером, печать протоколов) и др.

Рис. 2.

Рассмотренный выше мост, используемый для измерения сопротивления, носит имя Уитстона (Wheatstone). Для подключения измеряемых цепей в нем применяются всего две клеммы (B и C). Более сложные схемы реализованы в двух других мостах — Муррея (Murray) и Купфмюллера (Kupfmuller) (рис.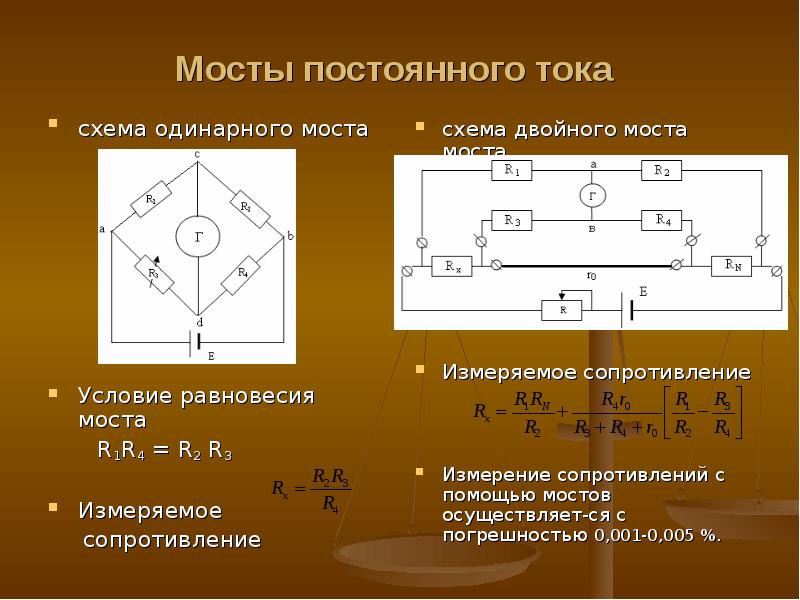

3). Здесь измеряемые цепи подключаются с помощью трех клемм (A, B и C). В более сложных схемах Хилборна/Графа (Hilborn/Graf) задействуются четыре клеммы (A, B, B’ и C). Смысл увеличения числа точек подключения станет понятен при рассмотрении схем измерения с применением мостов.

Рис. 3.

Еще один момент. Все упомянутые мостовые схемы используются для измерений при постоянном токе (определяются величины активных сопротивлений, подключенных к клеммам). Кроме того, мостовые схемы Уитстона и Муррея используются для измерений при переменном токе — определяются величины емкостей, подключенных к клеммам (рис. 4). В таких мостах источником напряжения служит генератор синусоидального напряжения.

Рис. 4.

• Методики измерений с помощью мостовых приборов
• Полезные советы
• Сравнительная таблица измерительных мостов

 

Подпишитесь на рассылку новых материалов!

Имя

Рабочий e-mail *

Согласие на отправку персональных данных *

* — Обязательное для заполнения

 

Выберите направление, по которому Вы хотите переговорить:

Мостовые схемы постоянного тока

Никакую книгу по электрическим измерениям нельзя было бы назвать полной без раздела о мостовых схемах. Эти гениальные схемы используют индикатор баланса для сравнения двух напряжений, точно так же как и лабораторные весы сравнивают две массы и указывают на то, что они равны. В отличие от «потенциометрических» схем, используемых для простого измерения неизвестного напряжения, мостовые схемы могут использоваться для измерения всех видов электрических величин, в том числе и сопротивлений.

Стандартная мостовая схема, часто называемая мостом Уитстона (Wheatstone bridge), изображена на рисунке 1.

Рис. 1.

Когда напряжение между точкой 1 и минусом батареи равно напряжению между точкой 2 и отрицательным выводом батареи, то индикатор баланса будет показывать ноль, и про такой мост говорят что он «сбалансирован». Состояние баланса моста полностью зависит от отношений R_a/R_b и R₁/R₂, и оно не зависит от напряжения питания. Для измерения сопротивлений с помощью моста Уитстона на место резисторов R_a или R_b устанавливается неизвестное сопротивление, в то время как остальные три резистора являются прецизионными и их номинал известен. Каждый из этих трёх резисторов может быть заменён сопротивлением другой величины или их номиналы могут быть скорректированы, что бы мост сбалансировался, и когда это произойдёт то величина сопротивления неизвестного резистора может быть определена из соотношения величин известных сопротивлений.

Для этого необходимо, что бы измерительная система имела набор переменных резисторов с точно известными значениями, которые могут служить эталонными стандартами. Например, если мост настроен на измерение сопротивления R_x (рисунок 2), то мы должны знать точное значение остальных трёх сопротивлений при сбалансированном мосте, что бы определить величину сопротивления R_x:

Рис. 2.

Каждое из четырёх сопротивлений в мостовой схеме называют плечом. Резистор, последовательно соединённый с неизвестным сопротивлением, R_x обычно называют реостатом моста (это будет сопротивление R_a на рисунке 2), а другие два сопротивления называют плечами отношений моста.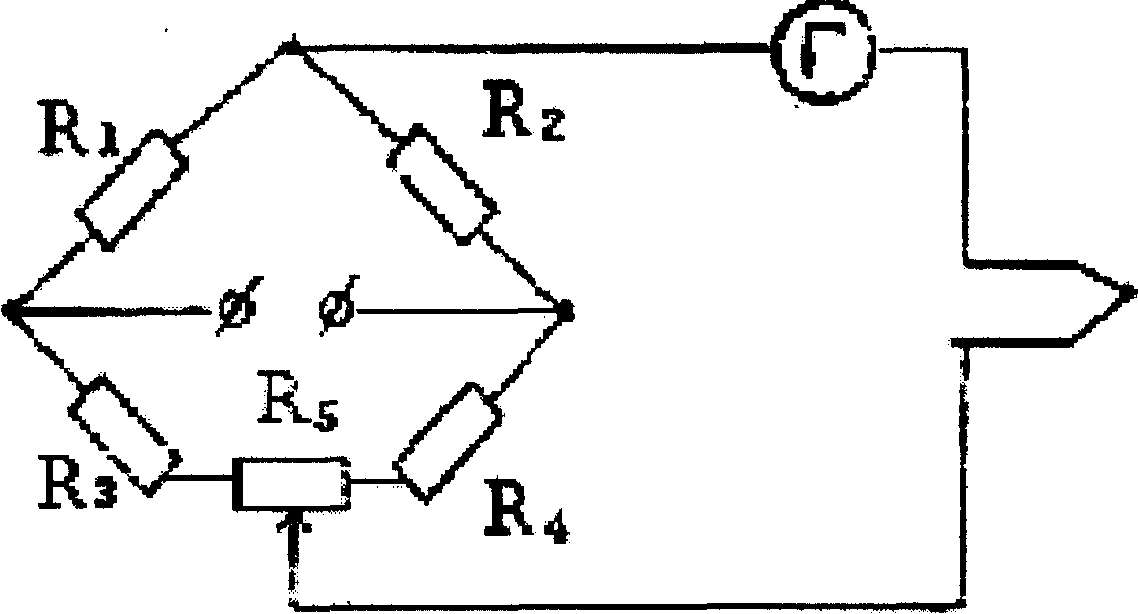

Точные и стабильные образцовые сопротивления к счастью, не сложно изготовить. В действительности они были одними из первых электрических «Стандартных» устройств, изготовленных в научных целях. На рисунке 3 приведена фотография старинного блока стандартных сопротивлений:

Рис. 3. Магазин образцовых сопротивлений

Стандарт сопротивлений, изображённый на рисунке 3, является переменным с дискретным шагом изменения сопротивления: величина сопротивления между клеммами может изменяться в зависимости от количества и положения медных вставок, вставленных в разъёмы.

Мосты Уитстона считаются превосходным средством измерения сопротивления среди схем различных омметров. Но в отличие от всех этих схем, являющихся нелинейными (и имеющих нелинейные шкалы), и связанные с этим погрешности измерений, мостовая схема является линейной (математика описания её работы основана на простых отношениях и пропорциях) и довольно точной.

Имея стандартные сопротивления достаточной точности и нуль-детектор с необходимой чувствительностью, достижимая точность измерения сопротивления может быть не хуже +-0,05% при использовании моста Уитстона.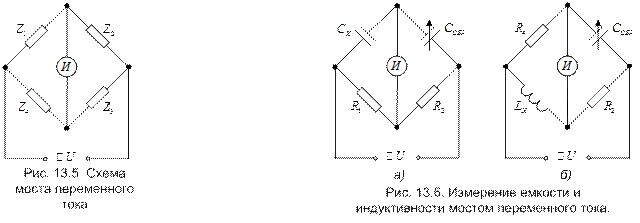 Это метод измерения сопротивления предпочитают использовать в калибровочных лабораториях из-за его высокой точности.

Существует много вариаций основной схемы моста Уитстона. Большинство мостов постоянного тока используются для измерения сопротивления, в то время как мосты переменного тока могут быть использованы для измерения различных электрических величин, таких как индуктивность, ёмкость и частота.

Интересным вариантом моста Уитстона является двойной мост Кельвина, используемый для измерения очень малых сопротивлений (обычно менее 1/10 Ома), его схема изображена на рисунке 4:

Рис. 4. Двойной мост Кельвина.
R_a и R_x являются низкоомными сопротивлениями.

Низкоомные резисторы на рисунке изображены толстой линией, так же как и проводники, соединяющие их с источником напряжения, обеспечивающим сильный ток. Принцип работы этого измерительного моста причудливой конфигурации, пожалуй, лучше всего понять, если начать объяснение принципа его работы со стандартного моста Уитстона, настроенного для измерения низкого сопротивления, этот мост развивался шаг за шагом до его нынешнего состояния в попытке преодолеть некоторые проблемы, возникшие в мосте Уитстона стандартной конфигурации.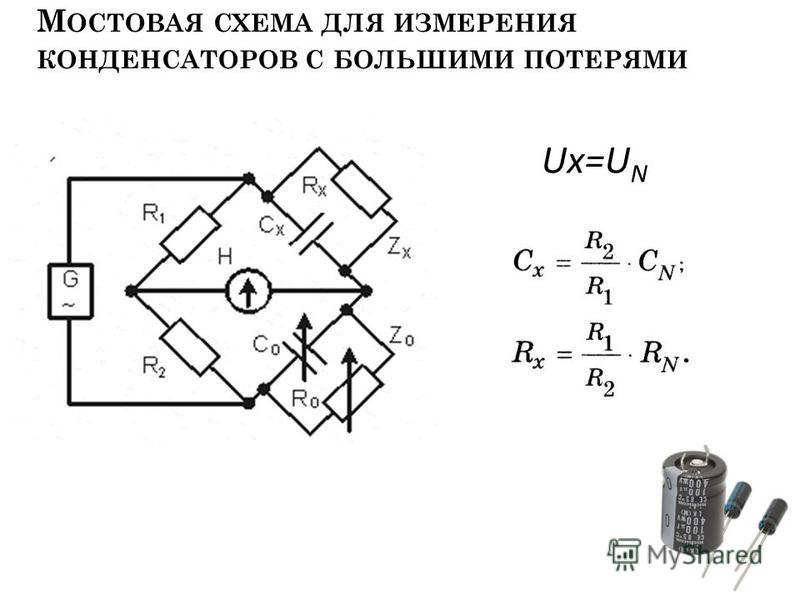

Если бы мы использовали стандартный мост Уитстона для измерения небольших сопротивлений, то его схема бы выглядела примерно так (рисунок 5):

Рис. 5.

Когда нуль-детектор указывает нулевое напряжение, мы знаем, что мост сбалансирован и что соотношение R_a/R_x и R_M/R_N математически равны друг другу. Зная значения R_a, R_M, and R_N поэтому мы имеем все необходимые данные, чтобы найти величину Rx. Почти.

Имеется проблема в том, что соединения и соединительные провода между R_a и R_x обладают неким сопротивлением, и эти паразитные сопротивления могут быть существенными по сравнению с низким сопротивлением R_a и R_x. Эти паразитные сопротивления понизят реальное напряжение, учитывая большой ток, протекающий через них, и таким образом будут влиять на показания детектора нуля и на баланс моста (Рисунок 6):

Рис. 6.
Паразитное напряжение E_пров.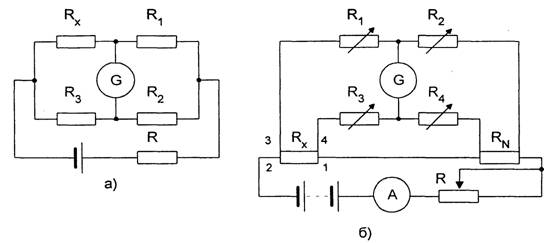 ухудшает точность измерения R_x.

Так как мы не хотим измерять сопротивление этих паразитных проводников и сопротивление соединений, а нас интересует только измерение сопротивления R_x, то надо найти такой способ включения нуль-детектора, что бы на его показания не влияли падения напряжений, протекающего через эти сопротивления. Если мы присоединим нуль-детектор и плечи отношений R_M/R_N напрямую к выводам R_a и R_x, то это приведёт нас к такой реализации измерительного моста (Рисунок 7):

Рис. 7.
Теперь только два паразитных падения напряжения E_пров. являются частями цепи нуль-детектора.

Теперь два крайних падения напряжения E_пров. не оказывают воздействия на нуль-детектор и не влияют на точность измерений сопротивления R_x. Но два оставшихся падения напряжений E_пров. являются проблемой, так как проводник, соединяющий нижний по схеме вывод R_a и верхний по схеме вывод R_x теперь шунтирует оба падения напряжения и по нему будет течь существенный ток, который создаст на этом проводнике своё падение напряжения.

Зная, что левая часть нуль-детектора должна быть подключена к двум крайним выводам сопротивлений R_a и R_x, что бы не вносить ошибки, связанные с паразитными падениями напряжения E_пров. в цепи нуль-детектора, и что любой прямой провод, соединяющий выводы этих сопротивлений R_a и R_x будет сам нести значительный ток и создавать ещё большее паразитное падение напряжения, то единственным способом преодолеть эту проблему является создание соединения, имеющее существенное сопротивление, между нижнем по схеме выводом R_a и верхнем по схеме выводом R_x (Рисунок 8):

Рис. 8.

Справится с паразитными падениями напряжений между выводами сопротивлений R_a R_x можно путём изменения сопротивления двух новых резисторов таким образом, что бы отношение их величин было бы таким же, как и отношение величин сопротивлений в плече отношений, находящихся по схеме с правой стороны от нуль-детектора. Вот почему эти резисторы были помечены R_m и R_n в оригинальной схеме двойного моста Кельвина: для обозначения их соразмерности с сопротивлениями R_M и R_N (Рисунок 9):

Рис. 9. Двойной мост Кельвина
Ra и Rx являются низкоомными сопротивлениями.

При отношении R_m/R_n равном отношению R_M/R_N, резистор в плече реостата R_a регулируется до тех пор, пока нуль-индикатор не покажет, что мост сбалансирован, и тогда можно будет сказать, что отношение R_a/R_x равно отношению R_M/R_N, или просто найти R_x из следующего уравнения:

Полное уравнение баланса двойного моста Кельвина выглядит следующим образом (R_пров. — это сопротивление толстых соединительных проводов между низкоомным образцовым сопротивлением R_a и испытуемым сопротивлением R_x):

До тех пор пока соотношение между R_M и R_N равно отношению между R_m и R_n, уравнение баланса будет не сложнее чем у обычного моста Уитстона, при R_x/R_a равном R_N/R_M, так как последнее выражение в уравнении будет равно нулю, так что будет отсутствовать влияние всех сопротивлений, кроме R_x, R_a, R_M, и R_N.

Во многих двойных мостовых схемах Кельвина R_M=R_m и R_N=R_n. Однако чем меньше значения сопротивлений R_m и R_n, тем более чувствительным должен быть нуль-детектор, потому что там будет меньше последовательное сопротивление. Увеличение чувствительности детектора является полезным, так как оно позволит обнаруживать слабые дисбалансы, и таким образом мост можно будет сбалансировать с большой точностью. Таким образом некоторые высокоточные двойные мосты Кельвина используют сопротивления R_m и R_n со значениями в 100 раз меньше, чем значения сопротивлений R_M и R_N в другом плече. К сожалению, однако, чем ниже значения сопротивлений R_m и R_n, тем больший ток по ним будет течь, что увеличит влияние любого сопротивления в точке подключения R_m и R_n к R_a и R_x. Как вы можете видеть, высокая точность инструмента требует, чтобы учитывались все ошибки различных факторов, и часто лучшее, что может быть достигнуто является компромиссом минимизации двух или более различных видов ошибок.

• ИТОГ:
• Мостовые схемы используют чувствительный индикатор нуля для сравнения двух напряжений на их равенство.
• Мост Уитстона (Wheatstone bridge) может быть использован для измерения сопротивлений путём сравнения сопротивления неизвестного номинала и образцового сопротивления с известной величиной, так же как с помощью лабораторных весов измеряют неизвестный вес путём сравнения его со стандартными грузами.
• Двойной мост Кельвина является вариантом моста Уитстона для измерения очень малых сопротивлений. Его усложнение по сравнению с базовой схемой моста Уитстона является необходимым для избежания ошибок, вносимых паразитными сопротивлениями на пути тока между низкоомным образцовым сопротивлением и сопротивлением, величина которого измеряется.

BACK

Введение в схемы моста Уитстона и дифференциальные усилители | Блоги

Если вам нужно точно измерить сопротивление, мост Уитстона — это простая схема, позволяющая сделать это путем измерения напряжения. Несмотря на простоту моста Уитстона, его эффективное использование может оказаться сложной задачей. В этой статье мы рассмотрим мостовые схемы Уитстона, как они работают и как мы можем эффективно использовать их с современной электроникой.

Во многих типах датчиков внутри используется мост Уитстона, поскольку сопротивление, измеренное в цепи, может быть связано с каким-либо другим явлением, вызывающим изменение сопротивления датчика. Вы найдете схемы моста Уитстона во всех типах устройств, основанных на сжатии и растяжении, таких как датчики давления воздуха и жидкости, тензодатчики и многое другое. Хотя в некоторых устройствах есть интегральная схема, обеспечивающая усиление мельчайших изменений напряжения, также часто используется прямой доступ к мосту, например, в тензодатчике/тензодатчике.

Мосты Уитстона — это одна из тех схем, с которыми вы, возможно, не сталкивались раньше, но которые, вероятно, есть внутри какого-то устройства или датчика, который вы используете. Например, практически во всех цифровых весах используется тензодатчик на основе моста Уитстона. Простота и эффективность моста Уитстона делают его невероятно мощной схемой, даже если она имеет относительно узкое применение.

Примечание. В этой статье есть немного математики, чтобы помочь вам понять, как определить неизвестное сопротивление, но это очень просто! Это может выглядеть как набор формул, но не отключайтесь, так как это одна и та же формула, разбитая по-разному в надежде облегчить ее объяснение.

Мост Уитстона использует две сбалансированные ветви в мостовой схеме (т. е. два делителя напряжения), чтобы обеспечить связь между напряжением на мостовой схеме и некоторым неизвестным сопротивлением одного резистора в мосте Уитстона. Мост Уитстона простейшего типа уравновешивает две ветви мостовой схемы, одна из которых включает неизвестный компонент. Другими словами, если вы знаете значения трех резисторов, вы можете рассчитать сопротивление неизвестного четвертого резистора, просто измерив напряжение на мосту. Эта схема обеспечивает изменение напряжения по мере изменения сопротивления, позволяя микроконтроллеру или другому устройству измерять сопротивление неизвестного элемента путем считывания напряжения через АЦП.

Типичные области применения схем моста Уитстона в современных устройствах, в первую очередь, включают тензометрические датчики, тензодатчики, датчики давления, датчики относительной влажности, термисторы и датчики резистивного термометра (RTD). Мост Уитстона способен измерять минимальные изменения сопротивления до уровней миллиОм, если используемый АЦП имеет достаточное разрешение (высокая разрядность). Обратите внимание, что помимо моста Уитстона существует множество топологий моста. Другие мостовые схемы могут использоваться для измерения емкости, индуктивности и импеданса; однако мы не будем рассматривать их в этой статье.

Принцип работы моста заключается в использовании четырех резисторов, обычно представленных в форме ромба. В Altium Designer® нам нужно представить это в виде коробки, как показано выше. Здесь у нас есть три известных сопротивления и четвертый резистор с неизвестным значением. Когда мы подаем напряжение на верхнюю и нижнюю клеммы моста, как показано выше, мост создает два параллельных делителя напряжения. Если напряжение измеряется в центре моста, его можно преобразовать в сопротивление, используя формулы, которые я покажу здесь. Эти формулы достаточно просты, чтобы их можно было реализовать в небольшом микроконтроллере.

Для начала, глядя на приведенную выше схему, вы должны увидеть, что напряжение между V0 и V1 будет равно 0 В, когда четыре резистора удовлетворяют следующему соотношению.

Здесь, Р? является неизвестным резистором, а остальные три резистора имеют известное значение. Здесь мы можем решить приведенную выше формулу для R? для этого конкретного случая, когда напряжение между V0 и V1 равно 0 В.

Это условие можно использовать для калибровки моста Уитстона с помощью варистора или потенциометра, но оно не помогает нам определить неизвестный резистор в других случаях .

Чтобы определить значение неизвестного резистора, давайте рассмотрим схему, показанную выше, немного дальше. Напряжение на резисторе R2, измеренное в точке V0, будет:

. В приведенном выше мосту знайте, что он будет состоять из резисторов 10 кОм, поэтому V0 будет составлять половину входного напряжения 5 В:

Другими словами, V0 всегда должен быть 2,5 В, если мы используем качественные резисторы. Это будет иметь место независимо от того, что произойдет с неизвестным резистором. Теперь делитель напряжения с портом V1 имеет неизвестный резистор, поэтому у нас есть аналогичное уравнение для напряжения на резисторе R? (измерено на порту V1):

Поскольку мы измеряем разницу между напряжениями на двух портах, мы можем написать V = V0 — V1 и подставить приведенные выше уравнения в это выражение. Это дает нам следующее:

Обратите внимание, что вы можете видеть, что у нас будет V равно 0, если неизвестный резистор R? равно R3*R2/R1, т.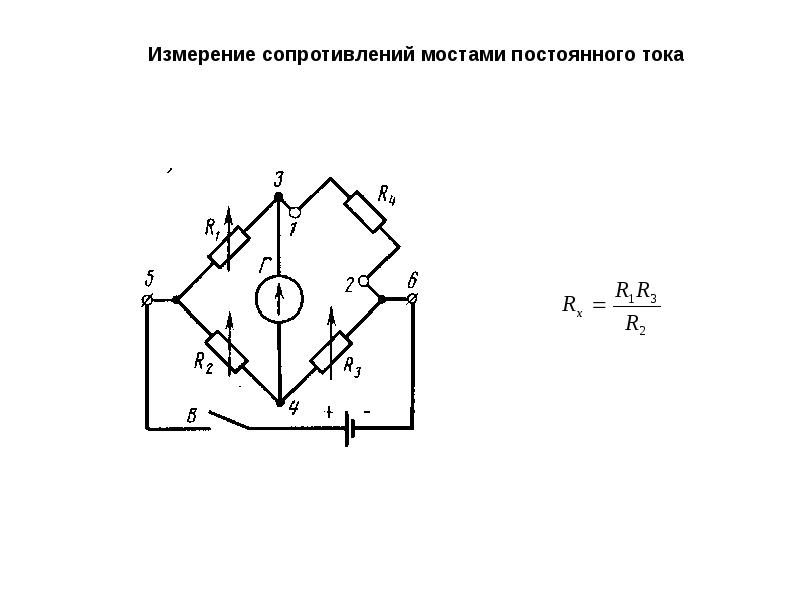 е. если мост уравновешен.

Когда V0 и V1 подключены к дифференциальному АЦП, мы можем измерить положительную и отрицательную разность напряжений с помощью микроконтроллера или другого устройства. Дифференциальное напряжение вызвано тем, что неизвестный резистор не равен другому резистору — мост не сбалансирован. Следует отметить, что в практических приложениях вам, вероятно, потребуется усилить сигнал, прежде чем подключать его к дифференциальному усилителю.

Приложив немного алгебры и измерив эту разность напряжений V, мы можем решить приведенное выше уравнение для R? и рассчитайте значение неизвестного резистора:

Помните, что V — это дифференциал между V0/V1, а VS — это напряжение питания, подаваемое на мост Уитстона. В нашем примере при R1 = R2 = R3 = 10 кОм мы можем вычислить неизвестное сопротивление R? если бы мы измерили разницу в 1 В на мосту. В этом случае неизвестное сопротивление будет:

. Вы можете подтвердить это, рассчитав выходное напряжение обоих делителей по отдельности, один обеспечивает 2,5 В (известный), а другой обеспечивает 1,5 В.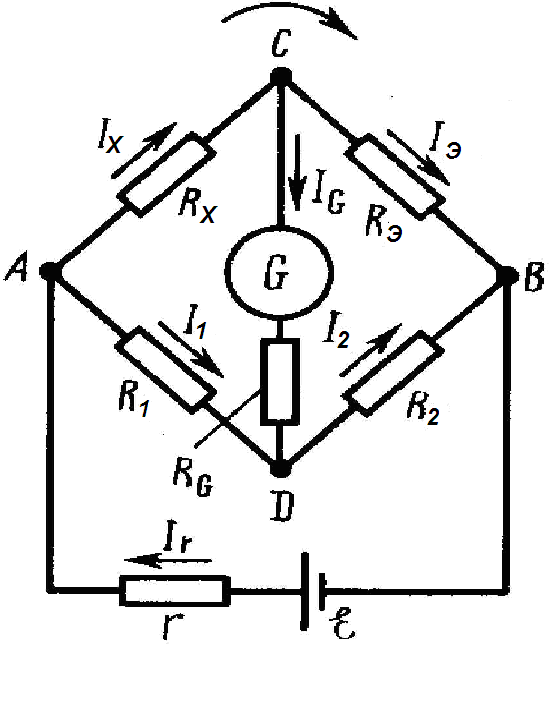 Если вам нужен онлайн-калькулятор, как проверка работоспособности, мне нравится та, что на Калькуляторе закона Ома. Как человек, страдающий дислексией, даже простые формулы могут сбить меня с толку, поэтому я обычно полагаюсь на онлайн-калькуляторы в качестве проверки здравомыслия — не расстраивайтесь, если вам тоже нужен онлайн-калькулятор!

Как правило, применение моста Уитстона в реальном мире дает гораздо менее существенные изменения сопротивления. Тем не менее, вы захотите использовать его с усилителем или АЦП с программируемым усилителем усиления. Например, с тензодатчиком я нередко использую усиление в 128 и более раз.

Хотя могут быть приложения, в которых вы можете использовать мост Уитстона напрямую, в реальных приложениях для моста Уитстона обычно возникает перепад в микровольтах или милливольтах в лучшем случае. Например, в моей статье в блоге Octopart,  Чтение напряжения слабого сигнала , я ссылаюсь на тензодатчик, в котором используется довольно типичный тензодатчик моста Уитстона. Тензодатчик на 100 кг обеспечивает изменение напряжения только на 50 мкВ на килограмм. Это не очень удобно для прямого подключения к микроконтроллеру или другой логике. Итак, как вы его используете?

Дифференциальный усилитель

Самый простой способ сделать изменение напряжения более полезным — использовать дифференциальный усилитель общего назначения, не требующий специализированного АЦП!

Используя конфигурацию дифференциального усилителя, мы можем усилить разницу между двумя делителями напряжения моста Уитстона, которые затем могут быть поданы на АЦП микроконтроллера или другое устройство. Мостовая схема Уитстона преобразует изменение сопротивления в изменение напряжения, а усилитель делает изменение напряжения полезным. Это весьма полезно при работе с датчиками, которые демонстрируют очень небольшие изменения сопротивления, так как теперь можно легко считывать разницу напряжений.

В качестве альтернативы можно использовать инструментальный усилитель вместо дифференциального усилителя общего назначения для большей точности.

Высокоимпедансный усилитель

Для большей точности мы можем сначала буферизовать выход моста Уитстона. Благодаря высокому входному сопротивлению повышается стабильность и точность схемы. Вы можете реализовать это с помощью буферных усилителей (единичное усиление) или просто использовать в качестве буфера другой операционный усилитель без усиления. Используя пакет с четырьмя усилителями, вы можете буферизовать, а затем усиливать с помощью одного пакета IC.

Инструментальный усилитель

На этом этапе мы могли бы продвинуть эту схему еще дальше, добавив несколько дополнительных резисторов для создания инструментального усилителя. Вместо этого мы возьмем более точный, компактный и точный вариант и простую конструкцию с использованием интегральной схемы инструментального усилителя. Инструментальный усилитель позволит нам очень точно усилить сигнал, не беспокоясь об использовании резисторов 0,1% или лучше для операционных усилителей или настройке каждой схемы, которую мы создаем, для точности. Производитель ИС уже сделал это на заводе. Хотя инструментальный усилитель стоит дороже, чем одиночный операционный усилитель общего назначения, он обеспечивает экономию средств, поскольку является доступным решением ИС, не требующим высокоточных внешних компонентов для правильной работы. Экономию пространства и сокращение строки спецификации (и, следовательно, запасов и питателей на линии комплектования и размещения) также нельзя игнорировать.

Инструментальный усилитель позволит нам точно усиливать сигналы между двумя входами, а также иметь отличное подавление синфазных помех. Таким образом, любые электрические помехи, обнаруженные на кабелях или дорожках нашего моста Уитстона, будут игнорироваться, поскольку они должны быть почти идентичными для обеих наших сетей. Резистор настройки усиления отделен от наших входов, его легко рассчитать и легко развести. Резистор усиления также можно настроить с помощью цифрового потенциометра, или некоторые инструментальные усилители имеют встроенные цифровые потенциометры, которые можно настроить по обычным протоколам, таким как I2C или SPI.

В качестве дополнительного бонуса многие инструментальные усилители имеют эталонный контакт, который позволяет подавать на сигнал смещение постоянного тока, что еще больше упрощает считывание выходного сигнала мостовой схемы Уитстона с устройства с однополярным питанием, такого как микроконтроллер.

Вы найдете функцию усиления для усилителя в таблице данных, например, в таблице данных Texas Instruments INA821 мы находим функцию:

Используя это уравнение, мы можем легко рассчитать правильное значение Rg для получения усиления мы хотим, чтобы наш усилитель имел. Если бы мы хотели получить усиление 100, мы могли бы упростить и изменить уравнение так:

Следовательно, резистор на 499 Ом для RG даст нам почти ровно 100 коэффициент усиления.

Если вы немного затрудняетесь с перестановкой формул/алгебраических уравнений, как всегда, есть отличный онлайн-калькулятор — в этом случае проверьте его на SymbolAB. Чтобы рассчитать усиление 100, как я сделал выше, вы можете ввести что-то вроде 100 = 1+(49400/x), и это решит x за вас.

Это даст нам схему (без развязывающих колпачков), которая выглядит так, как показано выше, — намного проще, чем другие схемы, которые мы рассматривали, верно?

Настройка усиления

Вам может быть интересно, какое усиление вам нужно и какое значение вы должны установить на эталонном выводе на инструментальном усилителе. У Analog Devices есть удобный онлайн-инструмент под названием Diamond Plot. Этот инструмент позволяет вам выбирать параметры, такие как усиление/напряжение питания и Vref, чтобы вы могли максимизировать рабочий диапазон инструментальных усилителей и настроить инструментальный усилитель на ваш АЦП или другое приложение. Используя такой инструмент, вы можете гарантировать, что вы создадите максимально возможный динамический диапазон, чтобы получить сигнал с самым высоким разрешением, которое вы можете. Инструмент также будет генерировать удобные предупреждения, если у вас есть неправильные параметры. Различные факторы могут привести к внутреннему насыщению сигнала, что может уменьшить максимальный динамический диапазон вашего сигнала или привести к отсечению и другим проблемам.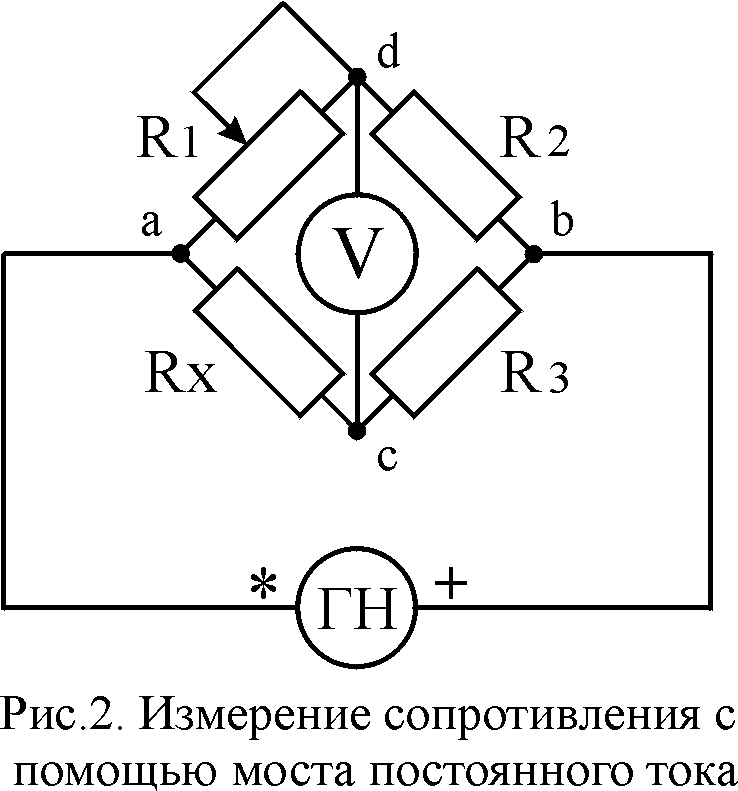

Например:

• Сигнал входного напряжения слишком высок для заданного усиления
• Слишком высокое опорное напряжение для генерируемого сигнала выходного напряжения
• Напряжение питания слишком низкое

Этот инструмент может помочь выбрать правильные параметры инструментального усилителя для вашего приложения.

Допустим, мы изменили первоначально отображаемые параметры примера. В этом случае вы можете увидеть, что он сообщит нам, что мы сделали что-то не так, и даст предложения о том, что нужно изменить, чтобы привести сигнал в соответствие с возможностями устройства.

Этот инструмент разработан специально для компонентов Analog Devices. Тем не менее, существует широкий спектр деталей Analog Devices, доступных для использования с ним. Если вы хотите использовать устройство от конкурента, вы, вероятно, можете найти часть AD с аналогичными параметрами и использовать ее в инструменте.

Примеры инструментального усилителя

Если вы хотите использовать инструментальный усилитель с мостом Уитстона, рассмотрите некоторые из этих недорогих вариантов от Analog Devices, Texas Instruments и Maxim Integrated.

Параметр	ИНА332	МАКС4208	АД8293Г160
Тип	Железнодорожный	Железнодорожный	Железнодорожный
Диапазон усиления	1000 В/В	100 В/В 1000 В/В ограниченная скорость нарастания (1000+ мкс)	160 В/В
Ошибка усиления	+/- 2 ppm/по Цельсию	+/- 25 частей на миллион/по Цельсию	+/- 5 частей на миллион/по Цельсию
Скорость нарастания	5 В/мкс	0,08 В/мкс	~1 В/мс (фильтр ограничен)
-3 дБ Полоса пропускания	2 МГц	750 кГц	500 Гц
Напряжение смещения	2 мВ	3 мкВ	9 мкВ
Напряжение смещения	2 мВ	3 мкВ	9 мкВ
Входное смещение	0,5 пА	1 пА	400 пА
Блок питания	415 мкА	1,4 мА	1 мА
Выходной ток	48 мА	25 мА	35 мА
ОКМРР	73 дБ	96 дБ	140 дБ
Напряжение питания	2,5–5,5 Одинарный +–1,25–2,75 Двойной	2,85–5,5 Одинарный +–1,425–2,25 Двойной	1,8–5,5 Одинарный +-0,9 — 2,75 Двойной
Производитель	Техасские инструменты	Максим Интегрированный	Аналоговые устройства

Эти инструментальные усилители — отличный пример недорогих вариантов, которые можно использовать в ваших проектах. Каждый из них имеет свои сильные и слабые стороны, а широкий спектр возможностей представлен только этими тремя компонентами в зависимости от ваших приложений.

В заключение

Мост Уитстона представляет собой классическую трассу с оригинальным дизайном и концепцией, насчитывающей почти двести лет. Не так много стандартных схем, которые мы используем в современной электронике, выдержали испытание временем, а также мост Уитстона. Простота схемы в сочетании с ее полезностью гарантирует, что мы продолжим использовать их в будущем.

В этой статье мы рассмотрели только основы. Существуют способы улучшить линейность мостовых схем Уитстона. В зависимости от типа датчика и того, как вы используете выходной сигнал моста, мы можем повысить точность и надежность показаний. Мы рассмотрим эти аспекты более подробно в статьях, посвященных датчикам, в будущем. Существует также широкий спектр других мостовых схем, которые, хотя и не так популярны, как мост Уитстона, все же находят применение для измерения емкости и индуктивности среди других величин.

Если вы ищете простой способ быстро улучшить существующую схему моста Уитстона, переход от одного источника питания к двойному — это очень быстрый и простой способ улучшить разрешение, сгладить кривую отклика и улучшить помехоустойчивость. Например, если вы в настоящее время используете цепь 5 В и GND, добавление инвертирующего импульсного источника питания на основе подкачки заряда обойдется вам в три дешевых компонента и даст вам питание -5 В. Имея питание +5В/-5В на вашей мостовой схеме, ваш выход будет сбалансирован на уровне 0В/земля. Это улучшит подавление, и любой универсальный или инструментальный усилитель с напряжением питания от шины до шины с двойным питанием сможет использовать выходной сигнал без каких-либо изменений. Единственное другое изменение, которое вам нужно будет рассмотреть, — это смещение выхода усилителя, чтобы гарантировать, что минимальное и максимальное напряжения находятся в пределах диапазона, который может легко прочитать ваш АЦП или другая схема.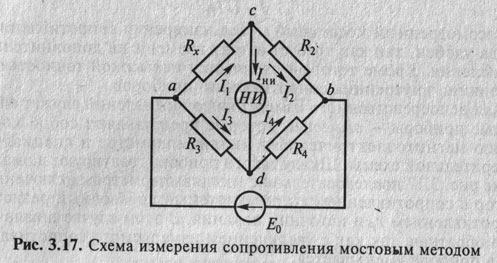

Хотите узнать больше о том, как Altium может помочь вам в разработке вашей следующей печатной платы? Поговорите с экспертом Altium.

Как работает мост Уитстона для тензодатчиков?

Чтобы измерить деформацию с помощью тензодатчика сопротивления, он должен быть подключен к электрической цепи, способной измерять мельчайшие изменения сопротивления, соответствующие деформации. В тензометрических преобразователях обычно используются четыре тензометрических элемента, электрически соединенных в мостовую схему Уитстона (рис. 2-6).

Мост Уитстона представляет собой разделенную мостовую схему, используемую для измерения статического или динамического электрического сопротивления. Выходное напряжение схемы моста Уитстона выражается в выходных милливольтах на входной вольт. Схема Уитстона также хорошо подходит для температурной компенсации.

Уравнение моста Уитстона: если резисторы R1, R2, R3 и R4 равны, а между точками A и C приложено напряжение VIN, то на выходе между точками B и D не будет разности потенциалов. Однако, если R4 изменить на некоторое значение, которое не равно R1, R2 и R3, мост станет несбалансированным, и на выходных клеммах появится напряжение. В так называемой конфигурации G-моста датчик переменной деформации имеет сопротивление Rg, а другие плечи представляют собой резисторы с фиксированным значением.
Однако датчик может занимать одно, два или четыре плеча моста Уитстона, в зависимости от применения. Полная деформация или выходное напряжение цепи (VOUT) эквивалентно разнице между падением напряжения на резисторах R1 и R4, или Rg. Это также можно записать как:

Подробнее см. Рисунок 2-6. Мост считается сбалансированным, когда R1/R2 = Rg/R3 и, следовательно, VOUT равно нулю.
Любое небольшое изменение сопротивления тензорезистора нарушит балансировку моста, что сделает его пригодным для определения деформации. Когда мост настроен так, что Rg является единственным активным тензодатчиком, небольшое изменение Rg приведет к выходному напряжению моста. Если калибровочный коэффициент равен GF, измерение деформации связано с изменением Rg следующим образом:

Количество активных тензодатчиков, которые должны быть подключены к мосту, зависит от приложения. Например, может быть полезно соединить датчики, которые находятся на противоположных сторонах балки, один на сжатие, а другой на растяжение. При таком расположении можно эффективно удвоить выходную мощность моста при том же напряжении. В установках, где все плечи подключены к тензометрическим датчикам, температурная компенсация тензорезисторов осуществляется автоматически, так как изменение сопротивления из-за колебаний температуры будет одинаковым для всех плеч моста Уитстона.
В четырехэлементном мосту Уитстона обычно два манометра подключаются на сжатие и два на растяжение. Например, если R1 и R3 находятся в растяжении (положительно), а R2 и R4 сжаты (отрицательно), то выходной сигнал будет пропорционален сумме всех деформаций, измеренных по отдельности. Для датчиков, расположенных на соседних опорах, мост становится неуравновешенным пропорционально разнице в деформации. Для калибров на противоположных опорах мост уравновешивается пропорционально сумме деформаций. Независимо от того, измеряется ли деформация изгиба, осевая деформация, деформация сдвига или деформация кручения, расположение тензодатчика будет определять взаимосвязь между выходным сигналом и типом измеряемой деформации. Как показано на рис. 2-6, если на манометрах R2 и R3 возникает положительная растягивающая деформация, а на манометрах R1 и R4 — отрицательная, общий выходной сигнал VOUT будет в четыре раза превышать сопротивление одного манометра. В этой конфигурации компенсируются изменения температуры датчика пятен.

Схема Шевронского моста

Шевронный мост показан на рис. 2-7. Это многоканальная схема, которая служит для компенсации изменений сопротивлений плеча моста путем их периодического переключения. Здесь четыре позиции канала используются для переключения цифрового вольтметра (DVM) между конфигурациями G-bridge (один активный манометр) и H-bridge (два активных манометра). Измерительное устройство DVM всегда использует общий источник питания и внутренний H-мост. Эта компоновка наиболее популярна для измерения деформации вращающихся машин, где она может уменьшить количество необходимых контактных колец.

Четырехпроводная цепь сопротивления

Хотя схема моста Уитстона является одним из самых популярных методов измерения электрического сопротивления, можно использовать и другие методы. Основное преимущество четырехпроводной омической схемы заключается в том, что подводящие провода не влияют на измерение, поскольку напряжение определяется непосредственно на тензометрическом элементе.

Установка с четырехпроводной омической схемой может состоять из вольтметра, источника тока и четырех токопроводящих резисторов R1, соединенных последовательно с калибровочным резистором Rg (рис. 2-8). Вольтметр подключается к клеммам измерения сопротивления цифрового вольтметра, а источник тока подключается к клеммам источника сопротивления цифрового вольтметра. Для измерения величины деформации в цепь подается слабый ток (обычно один миллиампер). В то время как вольтметр измеряет падение напряжения на Rg, абсолютное значение сопротивления вычисляется мультиметром по значениям тока и напряжения.
Измерение обычно проводят, сначала измеряя значение манометрического сопротивления в ненагруженном состоянии, а затем выполняя второе измерение с приложенной деформацией. Разница измеренных манометрических сопротивлений, деленная на сопротивление в ненагруженном состоянии, дает дробное значение деформации. Это значение используется с манометрическим коэффициентом (GF) для расчета деформации.
Четырехпроводная схема также подходит для автоматической компенсации смещения напряжения. Напряжение сначала измеряется, когда ток отсутствует. Затем это измеренное значение вычитается из показаний напряжения при протекании тока. Полученная разность напряжений затем используется для расчета манометрического сопротивления. Из-за своей чувствительности четырехпроводные тензодатчики обычно используются для измерения низкочастотных динамических деформаций. При измерении высокочастотных деформаций необходимо усилить выходной сигнал моста. Эту же схему можно использовать с полупроводниковым тензометрическим датчиком и быстродействующим цифровым вольтметром. При чувствительности ЦВМ 100 мкВ, источнике тока 0,44 мА, сопротивлении тензометрического элемента 350 Ом и его коэффициенте тензометрии 100 разрешение измерения составит 6 микродеформаций.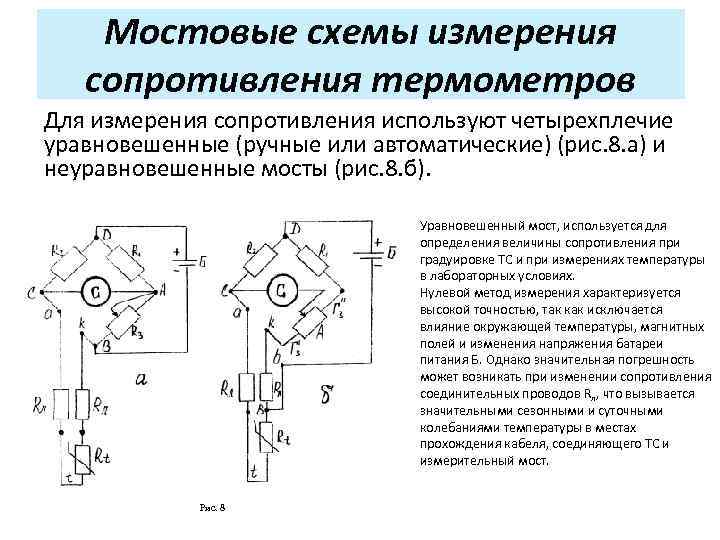

Цепь постоянного тока

Сопротивление можно измерить, возбудив мост либо постоянным напряжением, либо источником постоянного тока. Поскольку R = V/I, если либо V, либо I остаются постоянными, то другое значение будет изменяться в зависимости от сопротивления. Можно использовать оба метода.
Хотя теоретического преимущества использования источника постоянного тока (Рисунок 2-9) по сравнению с источником постоянного напряжения нет, в некоторых случаях выход моста будет более линейным в системе постоянного тока. Кроме того, если используется источник постоянного тока, это устраняет необходимость измерения напряжения на мосту; поэтому к тензометрическому элементу необходимо подключить только два провода.
Цепь постоянного тока наиболее эффективна при измерении динамической деформации. Это связано с тем, что если динамическая сила вызывает изменение сопротивления тензорезистора (Rg), можно было бы измерить изменяющуюся во времени составляющую выходного сигнала (VOUT), в то время как медленно изменяющиеся эффекты, такие как изменения сопротивления провода из-за температуры варианты будут отклонены. Используя эту конфигурацию, температурные дрейфы становятся практически незначительными.

Применение и установка

Выходной сигнал схемы тензодатчика представляет собой сигнал напряжения очень низкого уровня, требующий чувствительности 100 микровольт или выше. Низкий уровень сигнала делает его особенно восприимчивым к нежелательным помехам от других электрических устройств. Емкостная связь, вызванная слишком близкой прокладкой токоподводящих проводов к силовым кабелям переменного тока или токам заземления, является потенциальным источником ошибок при измерении деформации. Другие источники ошибок могут включать в себя магнитно-индуцированные напряжения, когда подводящие провода проходят через переменные магнитные поля, паразитные (нежелательные) контактные сопротивления подводящих проводов, нарушение изоляции и эффекты термопары на стыке разнородных металлов. Сумма таких помех может привести к значительному ухудшению сигнала.

Экранирование

Большинство проблем с электрическими помехами и шумом можно решить с помощью экранирования и ограждения.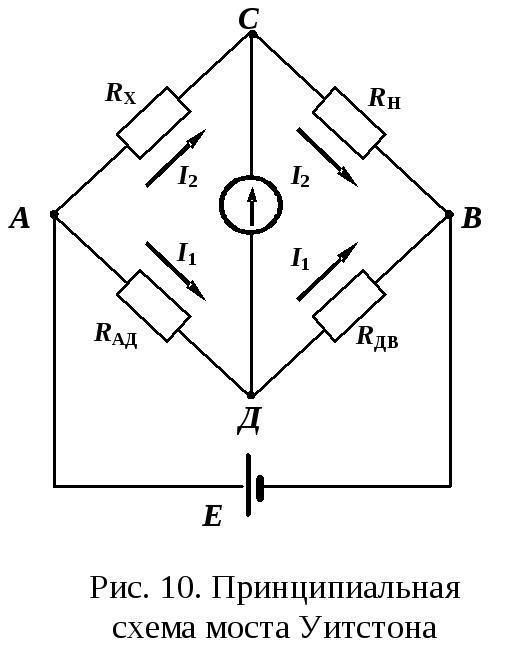 Экран вокруг измерительных проводов будет препятствовать помехам, а также может уменьшить любые ошибки, вызванные ухудшением изоляции. Экранирование также защитит измерение от емкостной связи. Если измерительные провода проложены рядом с источниками электромагнитных помех, такими как трансформаторы, скручивание проводов сведет к минимуму ухудшение сигнала из-за магнитной индукции. При скручивании провода ток, индуцированный потоком, инвертируется, и области, которые пересекает поток, компенсируются. Почти без исключения в промышленных процессах используются скрученные и экранированные провода.

Охрана

Охрана самих приборов так же важна, как и экранирование проводов. Ограждение представляет собой коробку из листового металла, окружающую аналоговую схему и соединенную с экраном. Если токи заземления протекают через тензометрический элемент или его подводящие провода, схема моста Уитстона не может отличить их от потока, создаваемого источником тока. Защита гарантирует, что клеммы электрических компонентов находятся под одинаковым потенциалом, что предотвращает протекание посторонних токов.
Подключение защитного провода между испытуемым образцом и отрицательной клеммой источника питания обеспечивает дополнительный путь тока вокруг измерительной цепи. При размещении защитного провода на пути тока, вызывающего ошибку, все задействованные элементы (т. е. плавающий источник питания, тензодатчик, все другое измерительное оборудование) будут иметь тот же потенциал, что и испытуемый образец. Используя скрученные и экранированные провода, а также интегрируя DVM с защитой, ошибка синфазного шума может быть практически устранена.

Проводные эффекты

Тензодатчики иногда монтируют на расстоянии от измерительного оборудования. Это увеличивает вероятность ошибок из-за колебаний температуры, снижения чувствительности электрода и изменения сопротивления провода. В двухпроводной схеме (рис. 2-10А) два провода соединены последовательно с тензометрическим элементом, и любое изменение сопротивления провода (R1) будет неотличимо от изменения сопротивления тензорезистора. (Рг).
Для устранения влияния проводниковых отведений к верхнему плечу мостовидного протеза можно ввести дополнительный третий электрод, как показано на рис. 2-10В. В этой конфигурации провод C действует как измерительный провод, по которому не течет ток, а провода A и B находятся на противоположных ветвях моста. Это минимально приемлемый метод подключения тензорезисторов к мосту, чтобы устранить, по крайней мере, часть влияния ошибок удлинительного провода. Теоретически, если подводящие провода к датчику имеют одинаковое номинальное сопротивление, одинаковый температурный коэффициент и поддерживаются при одной и той же температуре, достигается полная компенсация. В реальности провода изготавливаются с допуском около 10%, и трехпроводная установка не устраняет полностью двухпроводные погрешности, но снижает их на порядок. Если желательны дальнейшие улучшения, следует рассмотреть четырехпроводные установки и установки с компенсацией смещения (рис. 2-10C и 2-10D).
В двухпроводных установках погрешность, вносимая сопротивлением подводящего провода, является функцией отношения сопротивлений R1/Rg. Погрешность подвода обычно незначительна, если сопротивление подвода (R1) мало по сравнению с манометрическим сопротивлением (Rg), но если сопротивление подвода превышает 0,1 % от номинального сопротивления манометра, этот источник погрешности становится существенным. . Таким образом, в промышленных приложениях длина проводов должна быть минимизирована или устранена путем размещения преобразователя непосредственно на датчике.

Температура и манометрический коэффициент

Материалы, чувствительные к деформации, такие как медь, изменяют свою внутреннюю структуру при высоких температурах. Температура может изменить не только свойства тензометрического элемента, но и свойства основного материала, к которому прикреплен тензорезистор. Различия в коэффициентах расширения между датчиком и основным материалом могут привести к изменению размеров чувствительного элемента. Следовательно, потребуется схема компенсации температуры.
Расширение или сжатие тензометрического элемента и/или основного материала вносит ошибки, которые трудно исправить.