Что такое логические схемы и для чего они используются. Как строить логические схемы по логическим выражениям. Какие существуют методы минимизации логических выражений. Как применять карты Карно для минимизации. На что обратить внимание при минимизации логических схем.
Логические схемы: основные понятия и элементы
Логические схемы представляют собой электронные устройства, реализующие логические функции. Они широко применяются в вычислительной технике для обработки информации на логическом уровне. Основными элементами логических схем являются:
- Конъюнктор (элемент И) — реализует операцию логического умножения
- Дизъюнктор (элемент ИЛИ) — реализует операцию логического сложения
- Инвертор (элемент НЕ) — реализует операцию логического отрицания
Как строятся логические схемы на основе этих элементов? Рассмотрим пример для логического выражения:
F = (A AND B) OR (NOT C)
Соответствующая логическая схема будет выглядеть следующим образом:

- Входы A и B подаются на элемент И
- Вход C подается на инвертор
- Выходы элемента И и инвертора подаются на элемент ИЛИ
- Выход элемента ИЛИ является выходом всей схемы
Минимизация логических выражений: зачем она нужна
Минимизация логических выражений позволяет упростить логические схемы, что дает ряд преимуществ:
- Уменьшение количества логических элементов
- Повышение быстродействия схемы
- Снижение энергопотребления
- Повышение надежности за счет упрощения
Существует несколько методов минимизации логических выражений. Одним из наиболее наглядных и эффективных является метод карт Карно.
Карты Карно: принцип построения и использования
Карта Карно представляет собой графическое отображение таблицы истинности логической функции. Основные принципы построения карт Карно:
- Количество клеток карты равно количеству строк таблицы истинности
- Соседние клетки отличаются значением только одной переменной
- Крайние клетки считаются соседними (карта замыкается в тор)
Как использовать карту Карно для минимизации? Основные шаги:
- Заполнить клетки карты значениями функции из таблицы истинности
- Объединить соседние единицы в группы по 2, 4, 8 и т.д.
- Выписать логические произведения для каждой группы
- Составить логическую сумму полученных произведений
Полученное выражение и будет минимизированной формой исходной функции.
Пример минимизации логического выражения с помощью карты Карно
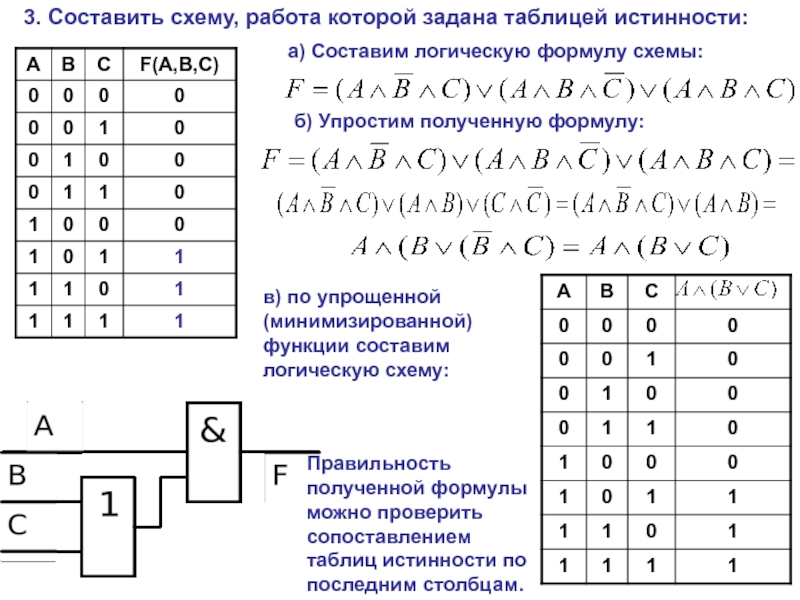
Рассмотрим пример минимизации логической функции трех переменных F(A,B,C):
F = A’B’C + A’BC + AB’C + ABC’ + ABC
Построим карту Карно для этой функции:
| A\BC | 00 | 01 | 11 | 10 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Объединяем соседние единицы в группы:
- Группа 1: A’BC + A’B’C (B не меняется)
- Группа 2: ABC + AB’C (A и C не меняются)
Минимизированное выражение: F = A’C + AC
Как видим, удалось значительно упростить исходное выражение.
Особенности минимизации функций от 4 и более переменных
При минимизации функций от 4 и более переменных следует учитывать ряд особенностей:
- Карта Карно становится четырехмерной, что усложняет ее визуальное восприятие
- Увеличивается количество возможных группировок единиц
- Возрастает вероятность пропустить оптимальное решение
В таких случаях рекомендуется:

- Использовать специализированное программное обеспечение
- Применять альтернативные методы минимизации (метод Квайна-Мак-Класки, метод Петрика)
- Разбивать функцию на подфункции меньшей размерности
Практические рекомендации по минимизации логических схем
При минимизации логических схем рекомендуется придерживаться следующих правил:
- Всегда проверяйте результат минимизации на соответствие исходной функции
- Учитывайте особенности конкретной элементной базы (стоимость, быстродействие элементов)
- При необходимости жертвуйте минимальностью в пользу лучшей структуры схемы
- Используйте симметрию функции для упрощения минимизации
- Применяйте декомпозицию сложных функций на более простые подфункции
Современные тенденции в проектировании логических схем
В настоящее время проектирование логических схем развивается в следующих направлениях:
- Автоматизация процесса синтеза и оптимизации схем с помощью САПР
- Использование программируемых логических интегральных схем (ПЛИС)
- Применение методов машинного обучения для оптимизации схем
- Разработка новых архитектур логических элементов (квантовые, оптические и др.)
Эти тенденции открывают новые возможности для создания более эффективных и производительных цифровых устройств.

Заключение: значение минимизации в современной электронике
Минимизация логических выражений и схем остается важной задачей в современной электронике. Она позволяет:
- Снизить стоимость устройств за счет уменьшения числа компонентов
- Повысить быстродействие и уменьшить энергопотребление
- Улучшить надежность и отказоустойчивость схем
- Оптимизировать использование ресурсов ПЛИС и заказных СБИС
Таким образом, владение методами минимизации логических выражений является важным навыком для разработчиков цифровых устройств и систем.
Таблица истинности онлайн с примерами
Таблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, у которой значения переменных и значение самой функции выражают истинность. Например, они принимают значения «истина» либо «ложь» (true либо false, 1 либо 0).
Таблицы истинности применяются для определения значения какого-либо высказывания для всех возможных случаев значений истинности высказываний, которые его составляют. Количество всех существующих комбинаций в таблице находится по формуле N=2*n; где N — общее количество возможных комбинаций, n — число входных переменных. Таблицы истинности нередко используются в цифровой технике и булевой алгебре, чтобы описать работу логических схем.
Таблицы истинности для основных функций

Примеры: конъюнкция — 1&0=0, импликация — 1→0=0.
Порядок выполнения логических операций
Инверсия; Конъюнкция; Дизъюнкция; Импликация; Эквиваленция; Штрих Шеффера; Стрелка Пирса.
Последовательность построения (составления) таблицы истинности:
https://uchim.org/matematika/tablica-istinnosti — uchim.org
- Определить количество N используемых переменных в логическом выражении.
- Вычислить количество всевозможных наборов значений переменных M = 2N , равное количеству строк в таблице.
- Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество логических операций.
- Озаглавить столбцы таблицы названиями переменных и названиями логических операций.
- Заполнить столбцы логических переменных наборами значений, например, от 0000 до 1111 с шагом 0001 в случае для четырех переменных.
- Заполнить таблицу истинности по столбцам со значениями промежуточных операций слева направо.
- Заполнить окончательный столбец значений для функции F.
Таким образом, можно составить (построить) таблицу истинности самостоятельно.
Составить таблицу истинности онлайн
Заполните поле ввода и нажмите OK. T — истина, F — ложь. Рекомендуем добавить страницу в закладки или сохранить в социальной сети.
Обозначения
- Множества или выражения большими буквами латинского алфавита: A, B, C, D…
- A’ — штрих — дополнения множеств
- && — конъюнкция («и»)
- || — дизъюнкция («или»)
- ! — отрицание (например, !A)
- \cap — пересечение множеств \cap
- \cup — объединение множеств (сложение) \cup
- A&!B — разность множеств A∖B=A-B
- A=>B — импликация «Если …, то»
- AB — эквивалентность
Всё для учебы » Математика в школе » Таблица истинности онлайн с примерами — логика
Таблицы истинности, с формулами и примерами
Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:
Значения логических функций определяются с помощью таблица истинности.
Таблицы истинности для основных двоичных логических функций
1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.
Обозначение:
2. Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.
Обозначение:
3. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.
Обозначение:
4. Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.
Обозначение:
5. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Обозначение:
6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.
Обозначение:
7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.
Обозначение:
Порядок выполнения логических операций
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквиваленция
- Штрих Шеффера
- Стрелка Пирса
Для последних двух операций приоритет не определен.
Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.
Примеры решения задач
Основы логики: построение логических схем
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №22 г. Владикавказа
Конспект урока по информатике
на тему:
«Основы логики:
построение логических схем»
учитель информатики
Гресева Т.В.
2015 г.
Конспект урока на тему: «Основы логики: построение логических схем».
Данный урок четвёртый в рамках темы «Основы логики». Предполагается, что обучающиеся уже знакомы с основными определениями и логическими операциями, умеют строить таблицы истинности для простых и сложных логических выражений.
Цели урока:
Задачи:
изучить принципы построения логических схем для сложных выражений;
способствовать развитию логического мышления;
сформировать у учащихся представления об устройствах элементной базы компьютера.
Тип урока:
урок совершенствования знаний, умений и навыков;
целевого применения усвоенного.
Вид урока: комбинированный.
Используемое оборудование:
компьютер;
приложение Microsoft Office PowerPoint 2003 и выше;
мультимедиа проектор;
интерактивная доска (по возможности).
План урока:
Организационный момент (1 мин)
Опрос по материалу прошлого урока (4 мин)
Представление нового материала (20 мин)
Выполнение практического задания (12 мин)
Подведение итогов урока. Задание на дом (3 мин)
Ход урока:
Организационный момент.
Приветствие учащихся. Проверка присутствующих. Настрой на урок.
Опрос по материалу прошлого урока.
На прошлом уроке мы с вами познакомились с основными логическими операциями. Обучающимся предлагается ответить на следующие вопросы:
Что такое сложное высказывание?
Сколько Вы знаете базовых логических операций? (5)
Перечислите названия базовых логических операций. (Коньюнкция, Дизъюнкция, Инверсия, Импликация, Эквивалентность)
Какими знаками обозначается логическое умножение? (& и
Как называется логическое отрицание и что оно выполняет?
Представление нового материала.
Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 — 1933) говорил «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить: 1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции; 2) не содержит ли она излишних усложнений. Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе – система чисто качественных… «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?». Созданная позднее М. А. Гавриловым (1903 – 1979) теория релейно-контактных схем показала, что это вовсе не утопия.
Посмотрим на микросхему.

На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее при сильном увеличении она поразит нас своей стройной архитектурой.
Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них.
С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или его нет; электрическое напряжение есть или его нет… В связи с этим поговорим о различных вариантах управления включением и выключением обыкновенной лампочки (лампочка также работает на электричестве). Для этого рассмотрим электрические контактные схемы, реализующие логические операции.
Виды логических элементов (вентилей):
1. Конъюнктор (И):
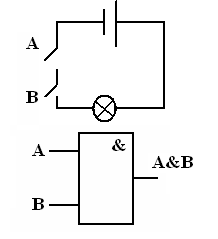
2. Дизъюнктор (ИЛИ):
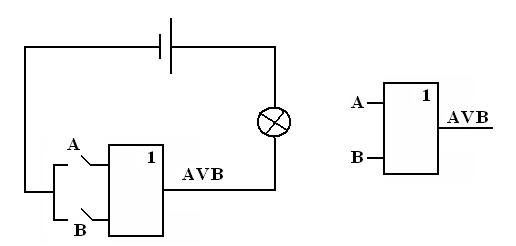
3. Инвертор НЕ:
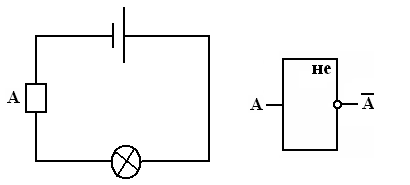
Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключений в секунду. Именно такие электронные схемы нашли свое применение к качестве элементной базы ЭВМ. Вся теория, изложенная для контактных схем, была перенесена на электронные схемы.
Логический элемент (вентиль) — это электронное устройство, реализующее одну из логических функций.
Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Логическая схема — это электронное устройство, которое реализует любую логическую функцию, описывающую работу устройств компьютера.
Физически каждый логический элемент представляет собой электронную схему, в которой на вход подаются некоторые сигналы, кодирующие 0 либо 1, а с выхода снимается также сигнал, соответствующий 0 или 1 в зависимости от типа логического элемента.
Обработка любой информации на компьютере сводится к выполнению процессором различных арифметических и логических операций. Для этого в состав процессора входит так называемое арифметико-логическое устройство. Оно состоит из ряда устройств, построенных на рассмотренных выше логических элементах.
Важнейшими из таких устройств являются регистры и сумматоры.
Регистр представляет собой электронный узел, предназначенный для хранения многоразрядного двоичного числового кода. Упрощенно можно представить регистр как совокупность ячеек, в каждой из которых может быть записано одно из двух значений: 0 или 1, то есть один разряд двоичного числа. Такая ячейка, называемая триггером, представляет собой некоторую логическую схему, составленную из рассмотренных выше логических элементов.
Под воздействием сигналов, поступающих на вход триггера, он переходит в одно из двух возможных устойчивых состояний, при которых на выходе будет выдаваться сигнал, кодирующий значение 0 или 1. Для хранения в регистре одного байта информации необходимо 8 триггеров.
Сумматор — это электронная схема, предназначенная для выполнения операции суммирования двоичных числовых кодов.
Правила построения логических схем:
1) Определить число логических переменных.
2) Определить количество базовых логических операций и их порядок.
3) Изобразить для каждой логической операции соответствующий ей логический элемент.
4) Соединить логические элементы в порядке выполнения логических операций.
Построим логическую схему для логического выражения:
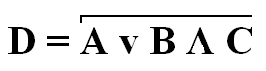
Для этого нам потребуется 3 логических элемента:
Логический элемент И
Логический элемент ИЛИ
Л
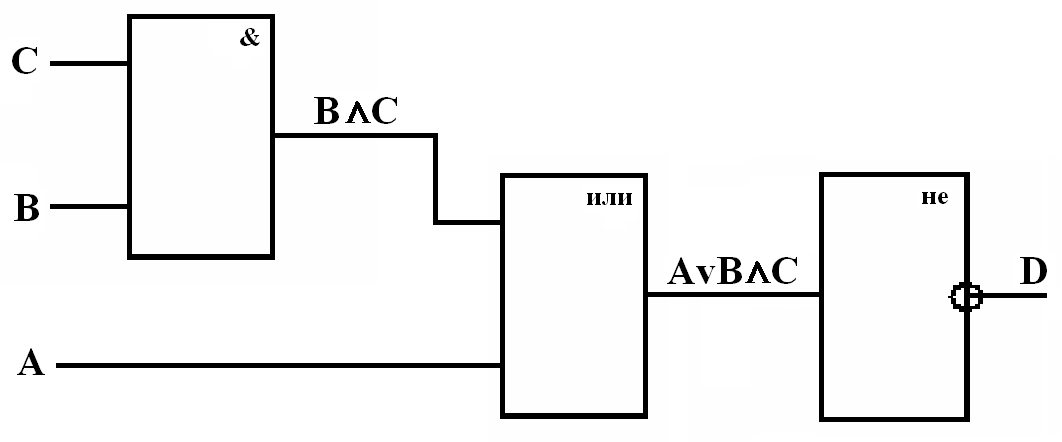 огический элемент НЕ
огический элемент НЕ
Выполнение практического задания.
Задание №1
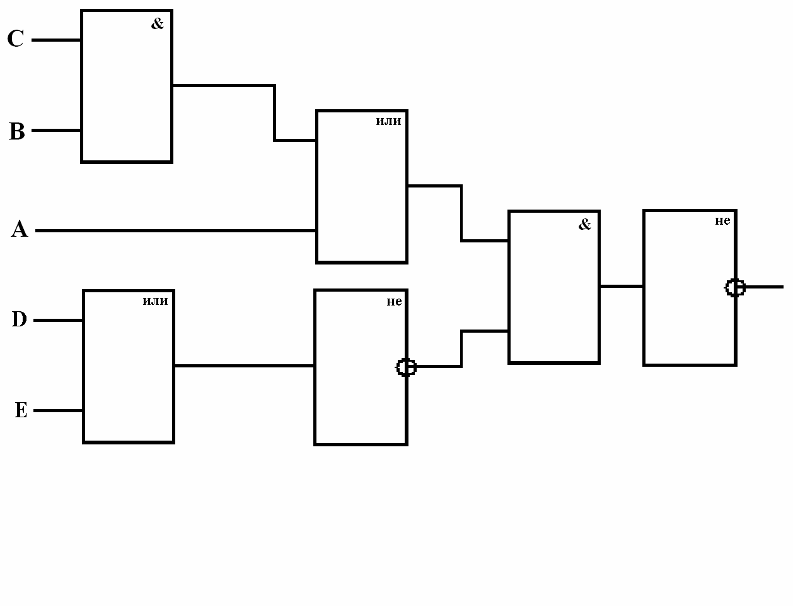
Построить логическую схему для логического выражения и выяснить, при каких входных сигналах на выходе схемы не будет напряжения?
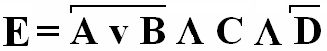
Задание №2
По построенной логической схеме составить логическое выражение
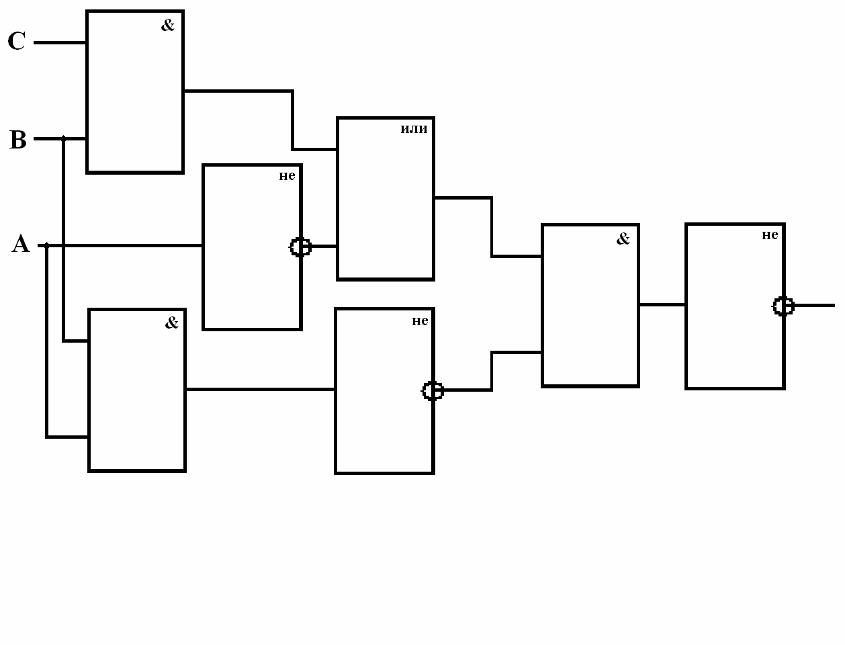
Подведение итогов урока. Задание на дом.
Ответы на вопросы учащихся. Подведение итога урока. Выставление оценок.
Домашнее задание (слайд 18).
НОУ ИНТУИТ | Лекция | Минимизация логических схем
Аннотация: Рассматривается взаимосвязь различных способов описания работы логических схем и принципы их минимизации.
Составление логических выражений по таблице истинности
Каноническая сумма минтермов
Минтерм — это полное произведение всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно логической 1. Переменная входит в минтерм с инверсией, если ее значение в данной строке таблицы равно 0, и без инверсии, если ее значение в данной строке таблицы равно 1.
Каноническая сумма минтермов — это логическая сумма всех минтермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности.Она составляется в следующей последовательности:
- В заданной таблице истинности подсчитывается
 — количество строк таблицы, в которой значение функции равно 1.
— количество строк таблицы, в которой значение функции равно 1. - Затем записывается логическая сумма
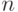 полных произведений.
полных произведений. - Далее в каждом произведении расставляются инверсии над переменными в соответствии с их значением в строке таблицы.
Для примера, представленного на рис. 1.6, каноническая сумма минтермов будет выглядеть так:
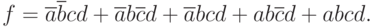 |
( 2.1) |
Из сравнения (1.1) и (2.1) видно, что одной и той же таблице истинности (рис. 1.6,б) соответствуют два разных логических выражения, причем (1.1) записывается более компактно, но возможности минимизации для него еще есть. Следовательно, есть возможность минимизировать и логическую схему, представленную на рис. 1.6, a.
Минимизация логических выражений может осуществляться с помощью различных методов на основе правил булевой алгебры, в частности, диаграммы Вейча, диаграммы Венна и табличным методом, но наиболее простым и наглядным является графический способ минимизации с помощью карт Карно, опубликованный в 1953 г. Морисом Карно.
Минимизация с помощью карт Карно
Карта Карно — графическое представление таблицы истинности. Каждой клетке карты Карно соответствует строка таблицы истинности. По осям карты расставляются сочетания переменных, а внутри карты — значения функции.
Назначение карты Карно — найти логические суммы прямого и инверсного значения переменных. Для любой переменной, например,  , такая сумма равна
, такая сумма равна 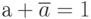 при любом значении
при любом значении  : при
: при 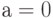 это будет
это будет 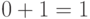 , при
, при 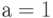 это
это 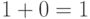 . Поэтому при вынесении за скобки в выражении:
. Поэтому при вынесении за скобки в выражении:
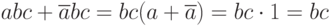
— сумму 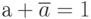 можно отбросить, при этом результат выражения не изменится. В этом и заключается минимизация логических выражений с помощью карт Карно. Для достижения поставленной цели минимизации нужно соблюдать правила разметки осей карты:
можно отбросить, при этом результат выражения не изменится. В этом и заключается минимизация логических выражений с помощью карт Карно. Для достижения поставленной цели минимизации нужно соблюдать правила разметки осей карты:
- Вертикальная ось размечается независимо от горизонтальной.
- Начинать разметку можно с любого сочетания переменных.
- Все сочетания переменных должны быть перечислены.
- Для соседних клеток карты сочетание переменных должно отличаться не более чем одним знаком, причем соседними являются крайние клетки строки (столбца).
Для функции двух переменных карта Карно — это квадрат 2×2 клетки. В этих клетках размещаются 4 значения функции из последнего столбца таблицы истинности (рис. 2.2).
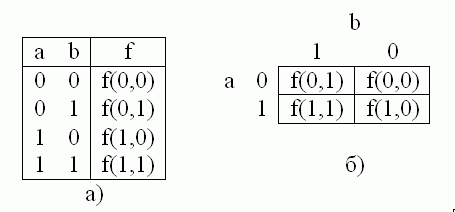
Рис. 2.2. Таблица истинности (а) и карта Карно (б) для функции 2 переменных.
Для функции трех переменных карта Карно — это прямоугольник 2×4 или 4×2 клетки. В этих клетках размещаются 8 значений функции из последнего столбца таблицы истинности (рис. 2.3). При разметке большей из осей нужно четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы соседними не оказались сочетания  и
и  , либо
, либо  и
и  , в которых одновременно меняются обе переменные.
, в которых одновременно меняются обе переменные.
Для функции четырех переменных карта Карно — это квадрат 4×4 клетки. В этих клетках размещаются 16 значений функции из последнего столбца таблицы истинности (рис. 2.4). При разметке обеих осей нужно также четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы по одной оси соседними не оказались сочетания  и
и  , либо
, либо  и
и  , в которых одновременно меняются обе переменные.
, в которых одновременно меняются обе переменные.
Для функции пяти переменных карта Карно представляет собой уже объемную фигуру — куб 4x4x4 клетки, поэтому для минимизации логических выражений она не применяется.
увеличить изображение
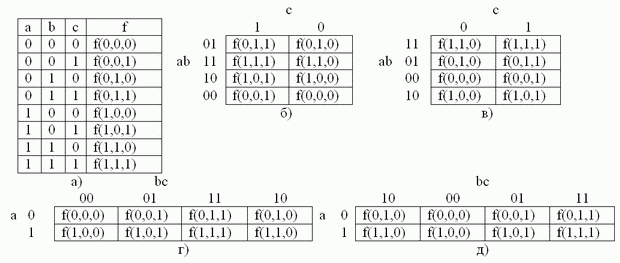
Рис. 2.3. Таблица истинности (а) и примеры заполнения карты Карно (б, в, г, д) для логической функции 3 переменных.
увеличить изображение
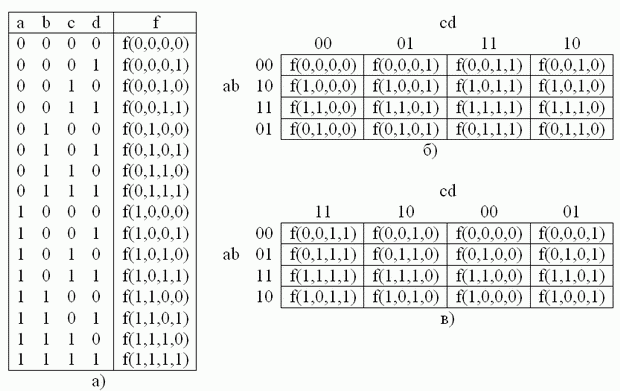
Рис. 2.4. Таблица истинности (а) и примеры заполнения карты Карно (б, в) для логической функции 4 переменных.
В конкретных случаях вместо значений функций в общем виде в клетки карты проставляются конкретные значения (логические 0 и 1) из соответствующих строк таблицы истинности. Затем рассматриваются только те клетки, которые заполнены единицами. Все эти единицы должны быть обведены контурами по следующим правилам составления контуров:
- Контуры должны быть прямоугольными и содержать количество единиц, равное
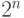 , где
, где 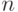 — целое число. Таким образом, в контуре может быть либо одна, либо две, либо четыре, либо восемь единиц.
— целое число. Таким образом, в контуре может быть либо одна, либо две, либо четыре, либо восемь единиц. - Количество единиц в контуре должно быть максимальным, при этом контуры могут пересекаться между собой. Нужно учитывать, что крайние строки являются соседними и крайние столбцы также являются соседними, поэтому контуры могут быть «разорванными».
- Количество контуров должно быть минимальным, но все единицы должны быть охвачены контурами. Нельзя забывать об отдельно стоящих единицах. Каждая такая единица — это контур, которому соответствует полное логическое произведение всех переменных.
После обведения контуров нужно записать минимальное выражение как логическую сумму логических произведений. Каждому произведению соответствует один контур карты Карно. В произведение входят только те переменные, которые остаются в данном контуре неизменными.При этом переменная входит в произведение с инверсией, если ее значение в данном контуре равно 0, и без инверсии, если ее значение равно 1.
Пример 1. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.5,а и нарисовать по нему логическую схему.
При одном варианте разметки осей (рис. 2.5,б) первый контур, состоящий из четырех единиц, получается разорванным. Если же принять разметку, показанную на рис. 2.5,в, то контур будет иметь нормальные очертания, а выражение, ему соответствующее, останется без изменений. Учитывая, что при данном горизонтальном начертании карты Карно крайние столбцы являются соседними, ее можно представить себе как цилиндр, развернутый на плоскости. На рис. 2.5,б представлена развертка такого цилиндра, «разрезанная» между комбинациями 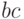 , равными
, равными  и
и  . А на рис. 2.5,в представлена развертка этого же цилиндра, «разрезанная» между произведениями
. А на рис. 2.5,в представлена развертка этого же цилиндра, «разрезанная» между произведениями 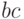 , равными
, равными  и
и 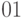 .
.
Первый контур охватывает четыре единицы, ему соответствует сумма минтермов:  ,
в которой не изменяется только переменная
,
в которой не изменяется только переменная  . Второй контур охватывает две единицы. Ему соответствует сумма минтермов
. Второй контур охватывает две единицы. Ему соответствует сумма минтермов  , в которой переменная
, в которой переменная 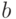 принимает оба возможных значения, а произведение
принимает оба возможных значения, а произведение 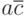 остается неизменным. Таким образом, получаем минимальное выражение:
остается неизменным. Таким образом, получаем минимальное выражение:
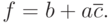 |
( 2.2) |
Ему соответствует логическая схема на рис. 2.5,г.
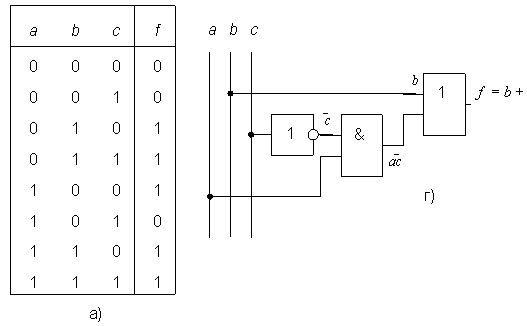
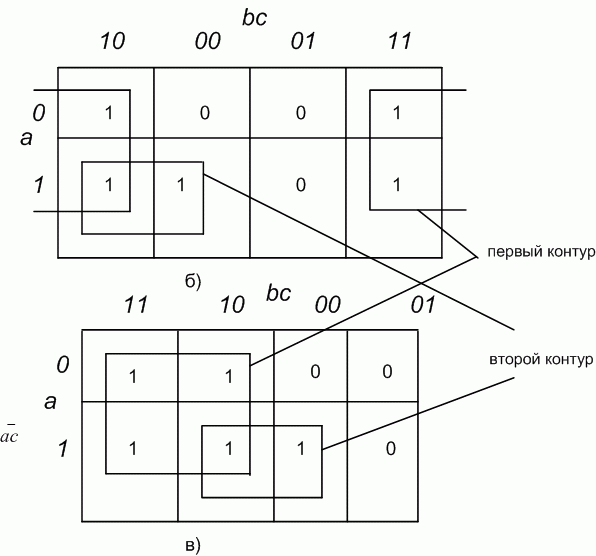
Рис. 2.5. Минимизация функции трех переменных
Для сравнения запишем максимальное выражение:
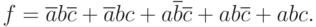 |
( 2.3) |
Разница между (2.2) и (2.3) очевидна и в комментариях не нуждается, за исключением того, что схема, реализованная по (2.3), будет на порядок сложнее и, соответственно, менее надежна, чем схема, показанная на рис. 2.5,г.
Пример 2. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.6,а, и нарисовать по нему логическую схему.
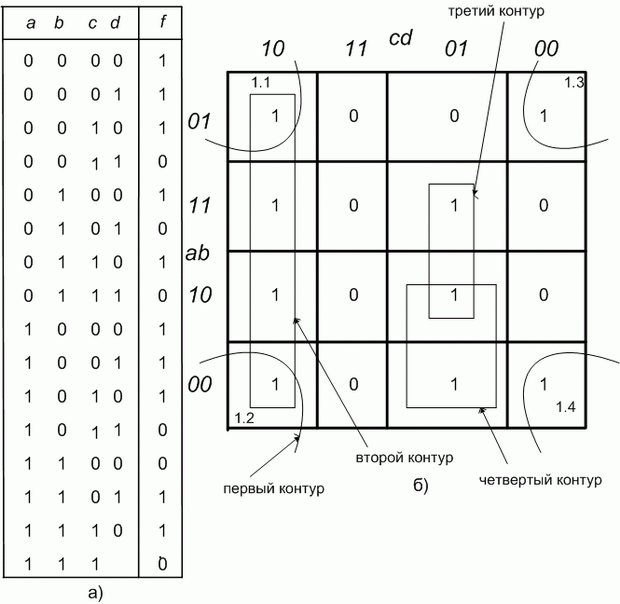
Рис. 2.6. Минимизация функции четырех переменных
При первоначально выбранной разметке осей (рис. 2.6,б) первый контур, состоящий из четырех единиц с номерами 1.1, 1.2, 1.3 и 1.4, расположенных по углам карты, получается разорванным. Если же принять разметку, показанную на рис. 2.7, то контур будет иметь очертания квадрата, а выражение, ему соответствующее, останется без изменений. Учитывая, что крайние столбцы являются соседними и крайние строки являются соседними, карту Карно для функции четырех переменных можно представить себе как торроид, развернутый на плоскости. Проще представить себе обратный процесс получения торроида из плоской фигуры — квадрата. Для этого надо сначала соединить мысленно крайние строки — получим цилиндр. После этого основания цилиндров надо мысленно соединить. Получится торроид. На рис. 2.6,б представлена развертка такого торроида, «разрезанная» между комбинациями  , равными
, равными 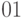 и
и  и между сочетаниями
и между сочетаниями 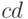 , равными
, равными  и
и  . А на рис. 2.7 представлена развертка этого же торроида, «разрезанная» между комбинациями
. А на рис. 2.7 представлена развертка этого же торроида, «разрезанная» между комбинациями 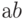 , равными
, равными  и
и  и между произведениями
и между произведениями 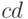 , равными
, равными  и
и 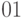 . После анализа контуров получим минимальное выражение
. После анализа контуров получим минимальное выражение 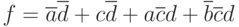 . Соответствующая ему схема приведена на рис. 2.8.
. Соответствующая ему схема приведена на рис. 2.8.
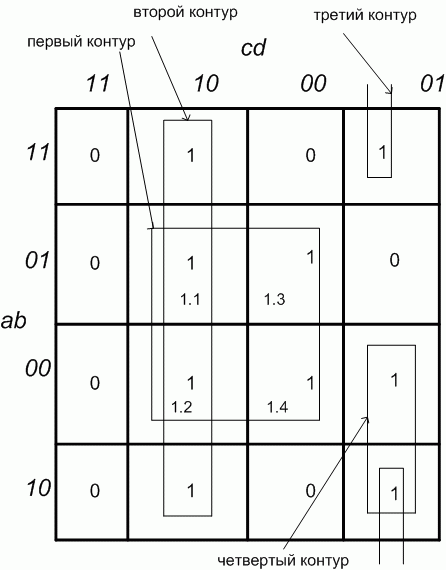
Рис. 2.7. К минимизации логической функции четырех переменных
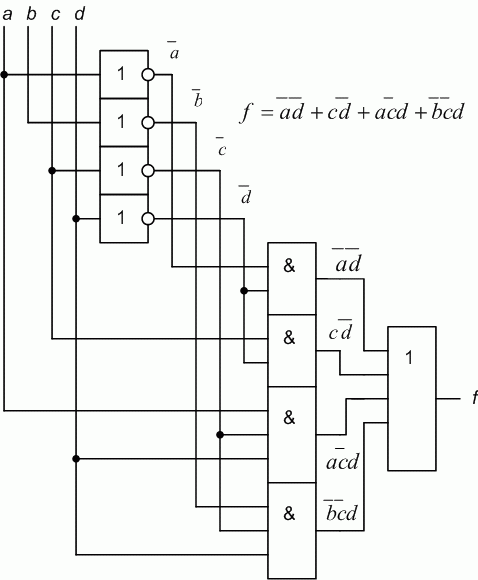
Рис. 2.8. Логическая схема для минимизированного логического выражения
python — логическое выражение списка
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Загрузка…
- Авторизоваться зарегистрироваться
-
текущее сообщество
javascript — инвертировать логическое выражение
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании

