Что такое логические элементы. Как работают базовые логические схемы И, ИЛИ, НЕ. Какие бывают типы триггеров. Как устроены счетчики и регистры сдвига. Чем отличаются ТТЛ и КМОП технологии.
Что такое логические элементы и для чего они нужны
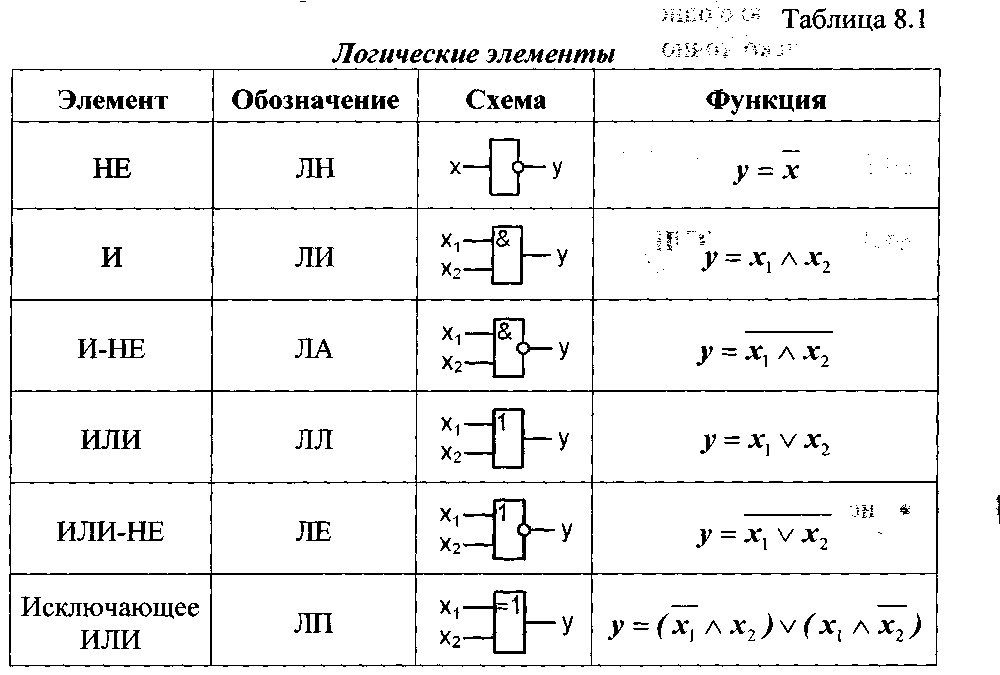
Логические элементы — это базовые «кирпичики», из которых строятся все цифровые устройства. Они выполняют элементарные логические операции над входными сигналами и формируют выходной сигнал в соответствии с заданной логической функцией.
Основные типы логических элементов:
- И (AND) — выход равен 1, только если все входы равны 1
- ИЛИ (OR) — выход равен 1, если хотя бы один вход равен 1
- НЕ (NOT) — инвертирует входной сигнал
- И-НЕ (NAND) — инвертированный выход элемента И
- ИЛИ-НЕ (NOR) — инвертированный выход элемента ИЛИ
- Исключающее ИЛИ (XOR) — выход равен 1, если входы различны
Логические элементы позволяют создавать сложные цифровые схемы для обработки и хранения информации в двоичном коде. Они являются основой для построения процессоров, памяти и других цифровых устройств.
Как работают базовые логические схемы И, ИЛИ, НЕ
Рассмотрим принцип работы трех базовых логических элементов:
Элемент И (AND)
Элемент И выполняет операцию логического умножения. Его выход равен 1 только в том случае, если все входы равны 1.
Таблица истинности элемента И с двумя входами:
| Вход A | Вход B | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Элемент ИЛИ (OR)
Элемент ИЛИ реализует операцию логического сложения. Его выход равен 1, если хотя бы один из входов равен 1.
Таблица истинности элемента ИЛИ с двумя входами:
| Вход A | Вход B | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Элемент НЕ (NOT)
Элемент НЕ выполняет операцию логического отрицания, инвертируя входной сигнал.
Таблица истинности элемента НЕ:
| Вход A | Выход Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Комбинируя эти базовые элементы, можно создавать более сложные логические схемы для решения различных задач цифровой обработки информации.
Триггеры — элементы памяти в цифровых схемах
Триггеры — это базовые элементы памяти в цифровых схемах. Они способны хранить 1 бит информации и имеют два устойчивых состояния. Основные типы триггеров:
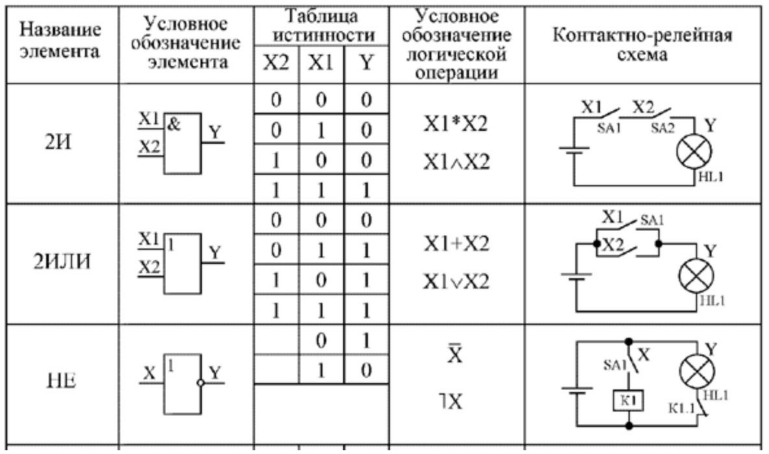
RS-триггер
Простейший тип триггера с двумя входами — Set (установка) и Reset (сброс). Имеет неопределенное состояние при одновременной подаче сигналов на оба входа.
D-триггер
Имеет один информационный вход D и тактовый вход C. При поступлении тактового импульса запоминает состояние входа D.
JK-триггер
Универсальный триггер с двумя информационными входами J и K и тактовым входом. Не имеет неопределенных состояний.
T-триггер
Счетный триггер. При поступлении импульса на вход T меняет свое состояние на противоположное.
Триггеры позволяют создавать более сложные элементы памяти — регистры, счетчики, а также служат основой для построения цифровых автоматов.
Счетчики и регистры сдвига в цифровой электронике
Счетчики и регистры сдвига — это более сложные цифровые устройства, состоящие из нескольких триггеров.
Счетчики
Счетчики предназначены для подсчета числа импульсов. Они бывают:
- Суммирующие — увеличивают свое состояние на 1 при поступлении импульса
- Вычитающие — уменьшают состояние на 1
- Реверсивные — могут работать в обоих режимах
По способу организации различают:
- Асинхронные счетчики — сигнал переноса передается последовательно между разрядами
- Синхронные — все разряды переключаются одновременно

Регистры сдвига
Регистры сдвига позволяют осуществлять последовательный ввод и вывод информации, а также выполнять операции сдвига.
Основные типы регистров сдвига:
- Последовательные — информация вводится и выводится последовательно, разряд за разрядом
- Параллельные — допускают одновременный ввод/вывод всех разрядов
- Универсальные — сочетают возможности последовательного и параллельного ввода/вывода
Регистры сдвига широко применяются для преобразования параллельного кода в последовательный и обратно, а также для выполнения арифметических операций.
Технологии изготовления логических элементов: ТТЛ и КМОП
Существует две основные технологии изготовления интегральных микросхем с логическими элементами:
ТТЛ (транзисторно-транзисторная логика)
Особенности ТТЛ:
- Высокое быстродействие
- Относительно высокое энергопотребление
- Напряжение питания 5В
- Меньшая помехоустойчивость по сравнению с КМОП
КМОП (комплементарная металл-оксид-полупроводник)
Преимущества КМОП:
- Очень низкое энергопотребление в статическом режиме
- Широкий диапазон напряжений питания (3-15В)
- Высокая помехоустойчивость
- Возможность создания схем с высокой степенью интеграции
В настоящее время технология КМОП является доминирующей при производстве цифровых интегральных схем благодаря своим преимуществам.
Применение логических элементов в современной электронике
Логические элементы являются основой для построения всех современных цифровых устройств. Вот некоторые области их применения:
- Процессоры и микроконтроллеры
- Оперативная и постоянная память
- Программируемые логические интегральные схемы (ПЛИС)
- Цифровые системы управления
- Устройства цифровой обработки сигналов
- Кодеры и декодеры информации
Несмотря на простоту отдельных логических элементов, их комбинации позволяют создавать невероятно сложные системы, лежащие в основе всей современной цифровой техники.
Логические схемы
Логические элементы, включая вентили, счетчики и запоминающие устройства, изготавливаются в виде интегральных модулей, или интегральных схем (ИС). Эти ИС разбивают на классы, называемые семействами, по числу полупроводниковых приборов, содержащихся в одной ИС. В настоящее время существуют следующие семейства.
|
1. |
ИС низкой степени интеграции |
до 10 приборов. |
|
2. |
ИС средней степени интеграции |
10-100 приборов. |
|
3. |
ИС большой степени интеграции, или большие ИС (БИС) |
100-1000 приборов. |
|
4. |
ИС сверхбольшой степени интеграции, или сверхбольшие ИС (СБИС) |
1000-10000 приборов. |
|
5. |
Ультрабольшие ИС (УБИС) |
10000-100000 приборов. |
Степень интеграции определяет сложность интегральной схемы. Каждое следующее по сложности семейство характеризуется десятикратным увеличением числа элементов по сравнению с предыдущим. К ИС низкой и средней степени интеграции относятся дискретные логические элементы, такие, как вентили, счетчики и регистры. БИС иСБИС используются в качестве запоминающих устройств, микропроцессоров и законченных систем, таких, как микрокомпьютеры.
Логические состояния
Логический элемент имеет два различных состояния: состояние логического 0, представляемое низким уровнем напряжения, обычно 0 В; и состояние логической 1. представляемое высоким уровнем напряжения (положительной полярности в случае положительной логики и отрицательной полярности в случае отрицательной логики). Уровень напряжения, который представляет логическую 1. зависит от используемого типа ИС. Для ИС, изготавливаемых по биполярной технологии, например для ПС ТТ, I (ИС на основе транзисторно-транзисторной логики), логической 1 соответствует напряжение 5 В, в то время как для ИС КМОП (ИС на комплементарных, или дополняющих, МОП-транзисторах) логическая 1 может быть представлена напряжением в диапазоне от 3 до 15 В и выше. ИС ТТЛ имеют преимущество в быстродействии, а ИС КМОП позволяют реализовать более высокую степень интеграции компонентов
представляемое высоким уровнем напряжения (положительной полярности в случае положительной логики и отрицательной полярности в случае отрицательной логики). Уровень напряжения, который представляет логическую 1. зависит от используемого типа ИС. Для ИС, изготавливаемых по биполярной технологии, например для ПС ТТ, I (ИС на основе транзисторно-транзисторной логики), логической 1 соответствует напряжение 5 В, в то время как для ИС КМОП (ИС на комплементарных, или дополняющих, МОП-транзисторах) логическая 1 может быть представлена напряжением в диапазоне от 3 до 15 В и выше. ИС ТТЛ имеют преимущество в быстродействии, а ИС КМОП позволяют реализовать более высокую степень интеграции компонентов
(т. е. позволяют разместить большее число логических элементов в одном интегральном модуле) и не требуют использования стабилизированных источников питания.
Транзисторно-транзисторные логические элементы (ТТЛ)
ТТЛ-элементы применяются в интегральных схемах и обеспечивают высокую скорость переключения.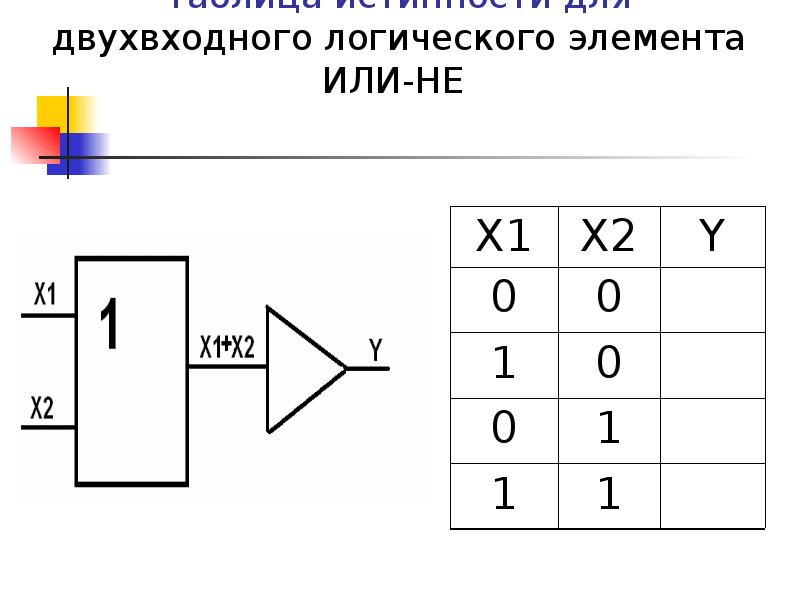 На рис. 34.1 показана упрощенная схема логического элемента И-НЕ с многоэмиттерным транзистором T1 на входе. Когда на обоих входах присутствует логический 0, транзистор T
1 насыщен и напряжение на его коллекторе близко к 0 В. Следовательно, транзистор T2 находится в состоянии отсечки, и на выходе мыимеем логическую 1. Когда на оба входа подается логическая 1, транзистор T1 закрывается и переключает транзистор T2 в состояние насыщения. В этом случае на выходе элемента мы имеем логический 0.
На рис. 34.1 показана упрощенная схема логического элемента И-НЕ с многоэмиттерным транзистором T1 на входе. Когда на обоих входах присутствует логический 0, транзистор T
1 насыщен и напряжение на его коллекторе близко к 0 В. Следовательно, транзистор T2 находится в состоянии отсечки, и на выходе мыимеем логическую 1. Когда на оба входа подается логическая 1, транзистор T1 закрывается и переключает транзистор T2 в состояние насыщения. В этом случае на выходе элемента мы имеем логический 0.
Рис. 34.1. Логический элемент И-НЕ (ТТЛ-типа).
Логические элементы на полевых транзисторах
Логические схемы в настоящее время изготавливаются только в виде интегральных схем. Огромное количество логических элементов можно разместить на мельчайшем кристалле (чипе) кремния размером 1х2 мм. В силу своей простоты полевые транзисторы применяются чаще, чем биполярные транзисторы.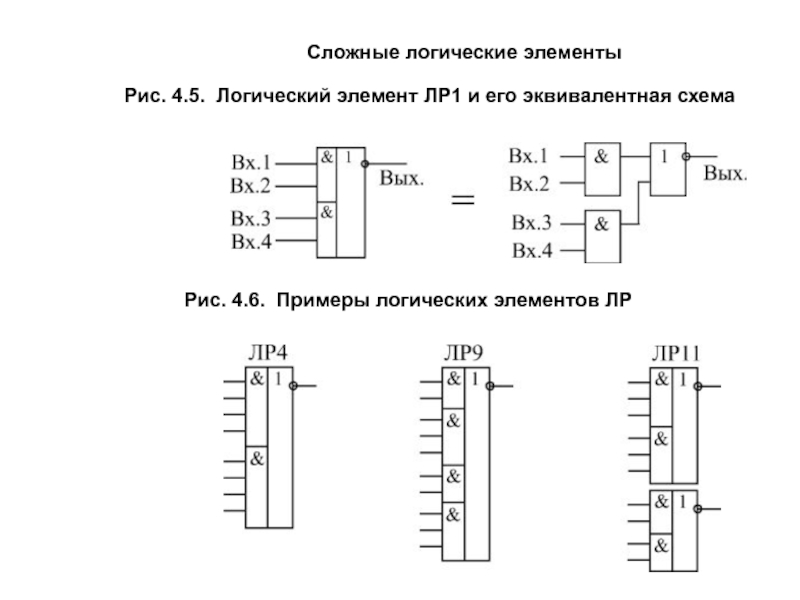 Наиболее широко распространены логические элементы на основе так называемых КМОП-ячеек (здесь они не рассматриваются). На рис. 34.2 приведена схема логического элемента ИЛИ-НЕ на МОП-транзисторах, который работает на основе отрицательной логики. В этой схеме T
Наиболее широко распространены логические элементы на основе так называемых КМОП-ячеек (здесь они не рассматриваются). На рис. 34.2 приведена схема логического элемента ИЛИ-НЕ на МОП-транзисторах, который работает на основе отрицательной логики. В этой схеме T
Рис. 34.2. Логический элемент Рис. 34.3. Логический элемент на И-НЕ
ИЛИ-НЕ на МОП-транзисторах. МОП-транзисторах.
На рис. 34. 3 показана схема логического элемента И-НЕ на основе полевых МОП-транзисторов с каналом п-типа. Поскольку используется источник питания положительной полярности, данный логический элемент работает на основе положительной логики. Транзистор T3 постоянно смещен в активную рабочую область напряжением VDD, подаваемым на затвор, и выполняет функцию активной нагрузки логического элемента. Когда на одном или на обоих входах присутствует логический 0, один или оба транзистора находятся в состоянии отсечки, выдавая логическую 1 на выходе. Ток через транзисторы будет протекать только в том случае, когда на оба входа будет подана логическая 1, и только в этом случае мы получим на выходе логический 0.
3 показана схема логического элемента И-НЕ на основе полевых МОП-транзисторов с каналом п-типа. Поскольку используется источник питания положительной полярности, данный логический элемент работает на основе положительной логики. Транзистор T3 постоянно смещен в активную рабочую область напряжением VDD, подаваемым на затвор, и выполняет функцию активной нагрузки логического элемента. Когда на одном или на обоих входах присутствует логический 0, один или оба транзистора находятся в состоянии отсечки, выдавая логическую 1 на выходе. Ток через транзисторы будет протекать только в том случае, когда на оба входа будет подана логическая 1, и только в этом случае мы получим на выходе логический 0.
Булевы выражения
Функции, реализуемые отдельным логическим элементом или комбинацией логических элементов, могут быть выражены логическими формулами, называемыми булевыми выражениями. В булевой алгебре используются следующие обозначения логических функций (см.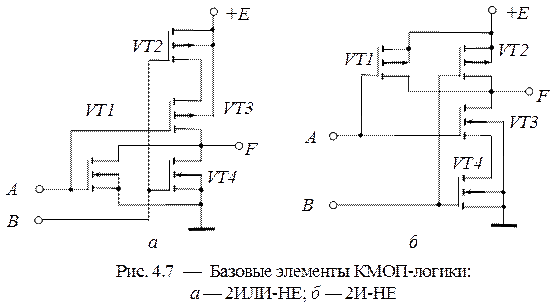 табл. 34.1):
табл. 34.1):
• Функция И обозначается символом точки (·). Двухвходовый (входы А и В) логический элемент И вырабатывает на выходе сигнал, представляемый булевым выражением А · В.
• Функция ИЛИ обозначается символом (+). Двухвходовый логический элемент ИЛИ вырабатывает на выходе сигнал, представляемый булевым выражением А + В.
Таблица 34.1. Булевы выражения
|
Функция |
Обозначение в булевой алгебре |
|
И |
А·В |
|
или |
А+В
|
|
НЕ |
|
|
И-НЕ |
|
|
ИЛИ-НЕ |
|
|
Исключающее ИЛИ |
|
|
Исключающее ИЛИ-НЕ |
• Логическая функция НЕ обозначается символом черты над обозначением входного сигнала.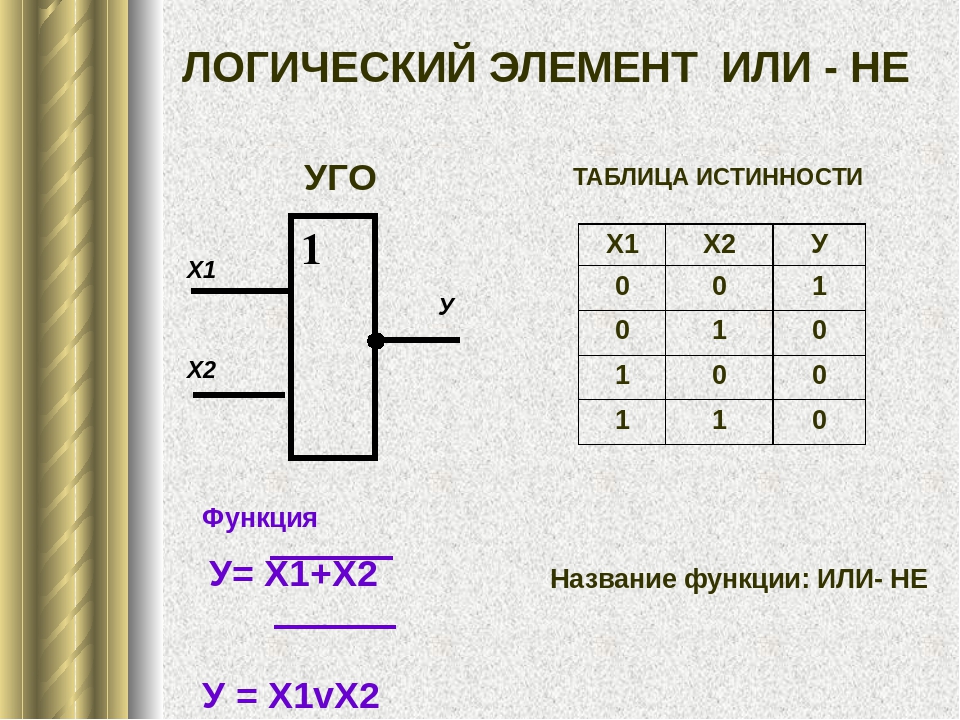 Логическая схема НЕ с одним входом А вырабатывает на выходе сигнал, представляемый булевым выражением (читается «НЕ А»).
Логическая схема НЕ с одним входом А вырабатывает на выходе сигнал, представляемый булевым выражением (читается «НЕ А»).
Через эти простые функции можно выразить более сложные:
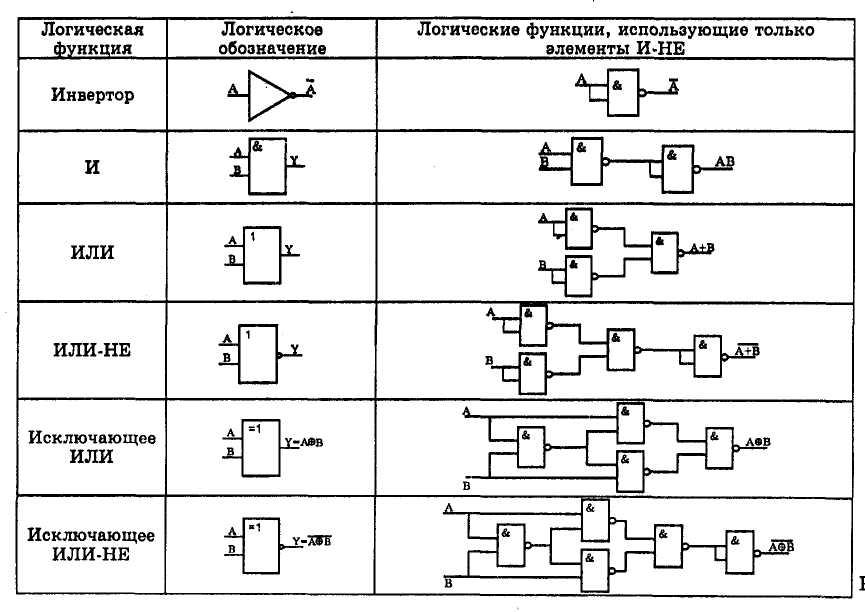
• Функция Н-НЕ записывается как .
• Функция ИЛИ-НЕ записывается как .
• Функция Исключающее ИЛИ записывается как . Ее можно также записать, используя специальное обозначение, .
• Функция Исключающее ИЛИ-НЕ записывается как . Ее можно также записать, используя специальное обозначение, .
Комбинаторная логика
Рассмотрим логическую схему на рис. 34.4. Логическую функцию, выполняемую этой схемой, можно описать с помощью следующих булевых выражений.
Выходной сигнал логического элемента ИЛИ (i): A + В
Выходной сигнал логического элемента И-ИЕ (ii):
Выходной сигнал логического элемента ИЛИ (iii): (А + В) +
Пример 1
Обратимся к рис.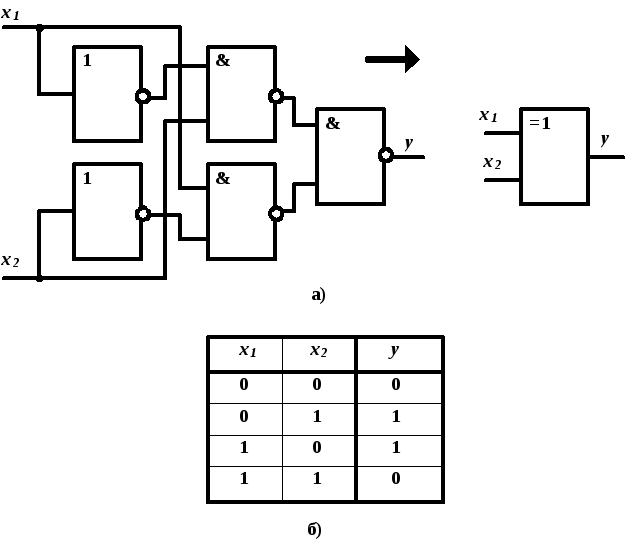 34.5.
34.5.
а) Найдите булево выражение для логической функции изображенной комбинации логических элементов.
б) Составьте таблицу истинности, показывающую логические состояния во всех точках схемы, и докажите, что эту схему можно свести к одному логическому элементу.
Решение
а) Булево выражение для точки С = .
Булево выражение для точки D= .
Булево выражение для точки F = ·.
б) Таблица истинности
|
Входы |
Точки |
Выход |
||
|
А
|
В
|
С
|
D
|
F
|
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
Как видно из таблицы истинности, приведенная комбинация логических элементов эквивалентна логическому элементу ИЛИ-НЕ.
Пример 2
Обратимся к рис. 34.6.
а) Найдите булево выражение для логической функции изображенной комбинации логических элементов.
б) Составьте таблицу истинности, показывающую логические состояния во всех точках схемы, и докажите, что эту схему можно свести к одному логическому элементу.
Решение
а) Булево выражение для точки С = .
Булево выражение для точки D = .
Булево выражение для точки F = +.
6) Таблица истинности
|
Входы |
Точки |
Выход |
||
|
А
|
В
|
С
|
D
|
F
|
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
Как видно из таблицы истинности, приведенная комбинация логических элементов эквивалентна логическому элементу И-НЕ.
Счетчики
Функцию счета в двоичном счетчике выполняет бистабильный мультивибратор, или делитель на 2, чаще называемый триггером. Цепочка из нескольких таких триггеров образует счетчик. На рис. 34.7 показан двоичный счетчик, состоящий из трех триггеров. Каждый триггер делит частоту поступающих импульсов на 2. Таким образом, два последовательных триггера обеспечивают деление на 4 (2 · 2), а три триггера – на 8 (2 · 2 · 2). Другими словами, на каждые восемь входных импульсов на выходе А появятся четыре импульса, на выходе В — два импульса и на выходе С — один импульс (рис. 34.7).
Как уже говорилось в гл. 32, бистабильный мультивибратор изменяет свое состояние только во время действия одного из фронтов входного импульса. Уровень входного импульса изменяется от 0 к 1 и обратно к 0, и так для каждого приходящего импульса. Обычно предполагается, что состояние триггера изменяется при приходе отрицательного фронта импульса (т. е. при переходе от 1 к 0).
Сигнал на выходе QА триггера А соответствует 20, или столбцу «единиц» в табл. 34.2, сигнал на выходе QB— 21, или столбцу «двоек», и наконец, сигнал на выходе QC — 22, или столбцу «четверок». После поступления 6 импульсов на вход счетчика он оказывается в следующем состоянии: А (число единиц) = 0, В (число двоек) = 1. С (число четверок) = 1; это состояние соответствует десятичному числу 6 (0 + 2 + 4).
Рис. 34.7. Двоичный счетчик на трех триггерах.
Таблица 34.2
|
Импульс |
QА единицы (20) |
QB двойки (21) |
QC четверки (22) |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
|
2 |
0 |
1 |
0 |
|
3 |
1 |
1 |
0 |
|
4 |
0 |
0 |
1 |
|
5 |
1 |
0 |
1 |
|
6 |
0 |
1 |
1 |
|
7 |
1 |
1 |
1 |
|
8 |
0 |
0 |
0 |
В двоичном исчислении это число записывается как 110 при порядке следования двоичных разрядов СВА.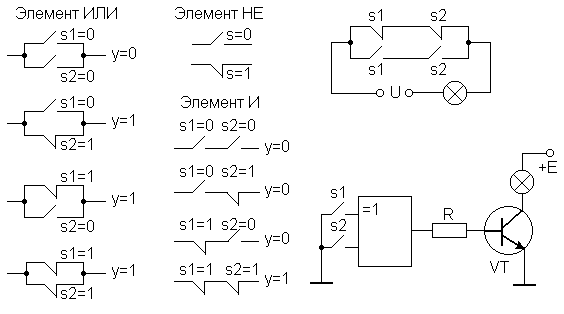 Обратите внимание, что в счетчике двоичному разряду единиц соответствует выход первого триггера, начиная от входа счетчика, а в двоичном числе разряд единиц всегда является самым правым разрядом.
Обратите внимание, что в счетчике двоичному разряду единиц соответствует выход первого триггера, начиная от входа счетчика, а в двоичном числе разряд единиц всегда является самым правым разрядом.
Когда приходит седьмой импульс, на всех выходах счетчика устанавливается 1. Восьмой импульс сбрасывает все триггеры в 0. Еще раз отметим, что выходной сигнал каждого триггера представляет столбец в таблице двоичного кода. Сам двоичный код записывается в порядке СВА.
Обратная связь
Обратная связь вводится в двоичных счетчиках для изменения коэффициента деления частоты входного сигнала. Для примера рассмотрим действие обратной связи в счетчике на рис. 34.8(а), состоящем из трех триггеров. Процесс счета происходит обычным образом до прихода третьего импульса, когда счетчик находится в состоянии 011 (см. табл. 34.3).
Рис. 34.8. (а) Счетчик-делитель на 6 с обратной связью, охватывающей триггеры В и С.
(б) Замена петли обратной связи эквивалентным модулем деления на 3.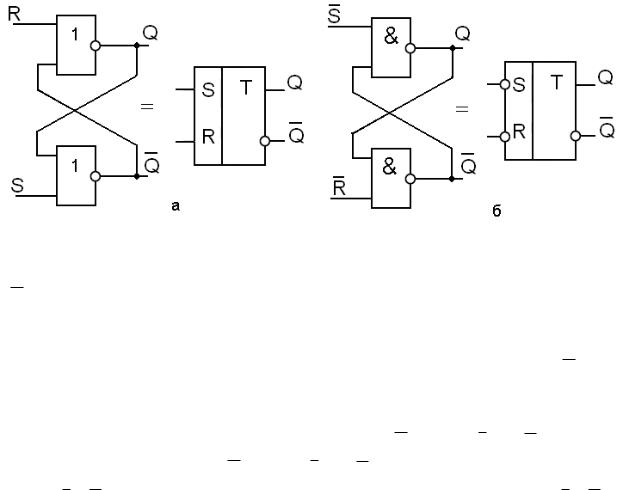
Таблица 34.3
|
Импульс |
QА |
QB |
QC |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
|
2 |
0 |
1 |
0 |
|
3 |
1 |
1 |
0 |
|
Обратная связь |
(0) |
(0) |
(1) |
|
4 |
0 |
1 |
1 |
|
5 |
1 |
1 |
1 |
|
6 |
0 |
0 |
0 |
Четвертый импульс переключает сигнал на выходах А и В к 0 и на выходе С к 1.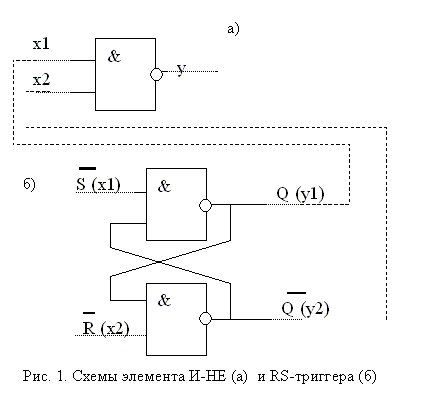 В отсутствие обратной связи счетчик переключился бы в состояние 100. Однако при включении обратной связи изменение сигнала на выходе С передается на вход триггера В, возвращая его выходной сигнал обратно к 1. Счетчик окажется в состоянии 110. Пятый импульс переключит все выходы к 1, и шестой импульс сбросит все триггеры в 0, т. е. получился счетчик-делитель на 6.
В отсутствие обратной связи счетчик переключился бы в состояние 100. Однако при включении обратной связи изменение сигнала на выходе С передается на вход триггера В, возвращая его выходной сигнал обратно к 1. Счетчик окажется в состоянии 110. Пятый импульс переключит все выходы к 1, и шестой импульс сбросит все триггеры в 0, т. е. получился счетчик-делитель на 6.
Вообще, можно показать, что петля обратной связи уменьшает коэффициент деления триггеров внутри петли на 1. В предыдущем примере внутри петли обратной связи находились триггеры В и С. Без обратной связи они осуществляли деление на 4. С обратной связью триггеры В и С образуют блок деления на 3 (= 4 – 1), как показано на рис. 34.8(б). С учетом триггера А вне петли обратной связи полный коэффициент деления счетчика равен 6 (= 2 · 3).
Десятичный счетчик
На рис. 34.9(а) изображена схема десятичного счетчика с двумя петлями обратной связи. Обратной связью охвачены : 1) блок 1, включающий триггеры С и D и обеспечивающий деление на 3 (= 4 – 1), и 2) блок 2, включающий блок 1 и триггер В.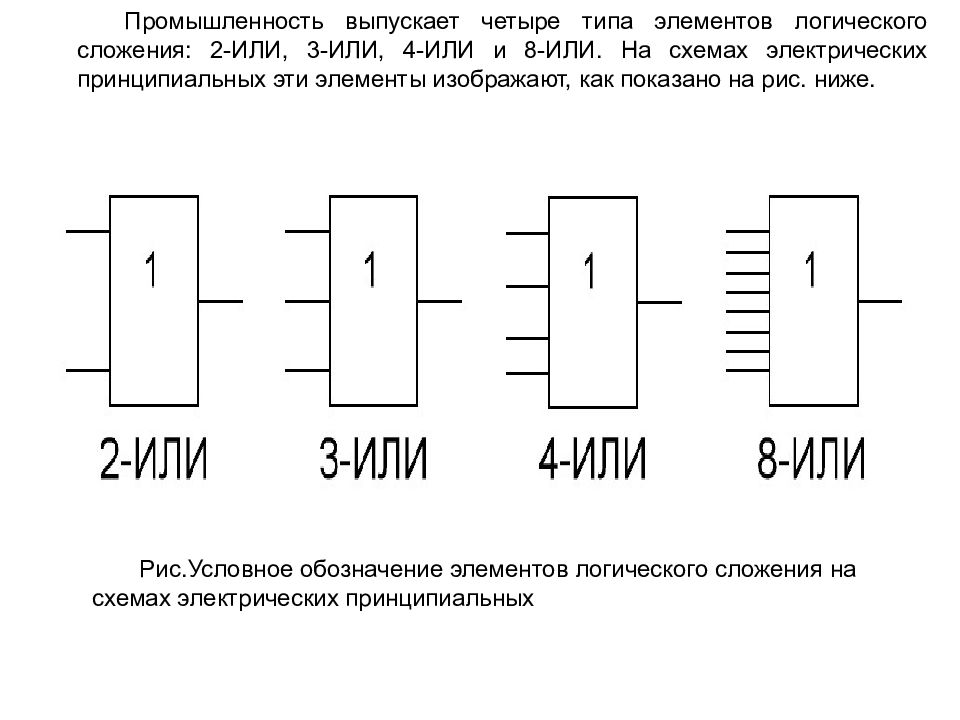 Из рис. 34.9(б) видно, что без обратной связи блок 2 делил бы на 6 (= 2 · 3). С обратной связью его коэффициент деления равен 5 (= 6 – 1). С учетом триггера А, не охваченного обратной связью, полный коэффициент деления счетчика равен 10 (= 2 · 5).
Из рис. 34.9(б) видно, что без обратной связи блок 2 делил бы на 6 (= 2 · 3). С обратной связью его коэффициент деления равен 5 (= 6 – 1). С учетом триггера А, не охваченного обратной связью, полный коэффициент деления счетчика равен 10 (= 2 · 5).
Регистр сдвига
Для передачи данных из одной части системы, например компьютера, в другую можно использовать два метода. Первый, более быстрый, заключается в одновременной передаче всех разрядов. При этом для передачи восьми разрядов требуется восемь отдельных линий. Для передачи информации на расстояния в несколько метров этот метод вполне пригоден, но при передаче на большие расстояния, например между городами, он становится слишком дорогим. В этом случае применяется второй, более медленный метод: данные передаются последовательно разряд за разрядом по одному проводу. Для одновременного сдвига всех двоичных разрядов влево или вправо применяется регистр сдвига. Он состоит из нескольких триггеров, способных передвигать двоичные разряды в последовательном порядке.
Рис. 34.9. Десятичный счетчик (а) и его представление в виде эквивалентных модулей (б).
Кольцевой счетчик
Кольцевой счетчик — это обычный счетчик, составленный из нескольких триггеров, в котором выходной сигнал подается обратно на вход, отсюда и происходит его название. Импульсы циркулируют по счетчику от входа к выходу и обратно на вход. В конце каждого цикла выходной сигнал кольцевого счетчика можно снять для переключения другого счетчика. Например, выходной сигнал десятичного, или декадного, счетчика можно использовать для переключения еще одного декадного счетчика, обеспечивая тем самым коэффициент пересчета, равный 100.
Фиксатор (триггер-защелка)
В гл. 32 рассматривались бистабильные мультивибраторы, или триггеры, построенные на дискретных компонентах. Триггеры — очень важные и нужные базовые элементы логических устройств. Они применяются в качестве делителей на 2, фиксаторов (одноразрядные ячейки памяти) и для других целей.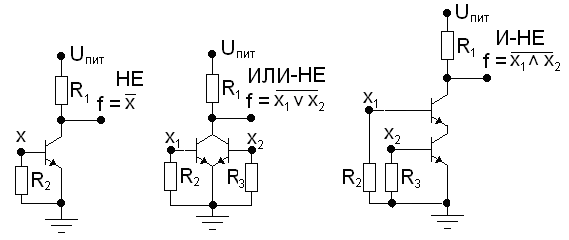
Базовый триггер, называемый RS-триггером, или триггером-защелкой, показан на рис. 34.10. Два выходных сигнала, снимаемые с выходов Q и (НЕ Q), находятся в противофазе друг к другу. Если Q = 1, то = 0, и наоборот. Таблица истинности для RS-триггера приведена на рис. 34.10(в). При подаче логической 1 на вход R (Reset — сброс) на выходе Q устанавливается уровень логического 0 (и уровень логической 1 на выходе ), при подаче логической 1 на вход S (Set — установка) на выходе Q устанавливается уровень логической 1 (и уровень логического 0 на выходе ).
|
S |
R |
|
|
0 |
0 |
Без изменений |
|
0 |
1 |
|
|
1 |
0 |
|
|
1 |
1 |
Неопределенное состояние |
(в)
Более сложным устройством по сравнению с простым RS-триггером является тактируемый JK-триггер, в котором имеется тактовый вход и отсутствует неопределенное состояние (рис. 34.11). Тактовый вход важен для синхронных систем, в которых переключение триггеров происходит лишь тогда, когда на тактовый вход подается логическая 1. При установке логической 1 на обоих входах J и К триггера его выход переключается из уровня логического 0 в логическую 1 при поступлении каждого тактового импульса.
|
Тактовый вход |
J
|
К
|
|
|
0 |
X |
X |
Без изменений |
|
1 |
0 |
0 |
Без изменений |
|
1 |
0 |
1 |
|
|
1 |
1 |
0 |
|
|
1 |
1 |
1 |
Переключение |
(а) (б)
Рис. 34.11. Условное обозначение (а) и таблица истинности (б) JK-триггера.
Логические элементы в виде ИС
Логические элементы изготавливаются в виде интегральных схем и выпускаются в виде модулей, содержащих большое число идентичных элементов на одном модуле (чипе). Известны два основных типа ИС: ИС ТТЛ и ИС КМОП. Примеры ИС ТТЛ приведены на рис. 34.12.
Рис. 34.12.
В этом видео рассказывается о элементах транзисторно-транзисторной логики:
Добавить комментарий
Урок 8.3 — Логические элементы
8.3. Логические элементы
Все, абсолютно все электронные компоненты, обрабатывающие цифровые сигналы, состоят из небольшого набора одинаковых «кирпичиков». В микросхемах малой степени интеграции могут быть единицы и десятки таких элементов, а в современных процессорах их может быть очень и очень много. Они называются логические элементы. Логическим элементом называется электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными. Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления.
Тем не менее, принцип работы цифровой логики остается неизменным – на входе логического элемента (входов может быть несколько) должен быть цифровой сигнал (сигналы, если входов несколько), который однозначно определяет сигнал на выходе логического элемента.
Конечно, логические элементы строятся, в свою очередь, из уже рассмотренных в предыдущих уроках резисторов, транзисторов и других электронных компонентов, но с точки зрения разработки цифровых схем именно логический элемент является их «элементарной» частицей.
При анализе работы логических элементов используется так называемая булева алгебра . Начала этого раздела математики было изложено в работах Джорджа Буля – английского математика и логика 19-го века, одного из основателей математической логики. Основами булевой алгебры являются высказывания, логические операции, а также функции и законы. Для понимания принципов работы логических элементов нет необходимости изучать все тонкости булевой алгебры, мы освоим ее основы в процессе обучения с помощью таблиц истинности.
Еще несколько замечаний. Логические элементы (как, впрочем, и другие элементы электронных схем) принято обозначать так, чтобы входы были слева, а выходы справа. Число входов может быть, вообще говоря, любым, отличным от нуля. Реальные цифровые микросхемы могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Условные обозначения соответствуют отечественному ГОСТу, в других стандартах они могут быть иными.
Какие же бывают логические элементы?
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
Элемент «И» (AND), он же конъюнктор, выполняет операцию логического умножения:
Условное обозначение — Таблица истинности
Здесь изображен логический элемент «2И» (цифра перед буквой «И» означает число входов). Знак & (амперсант) в левом верхнем углу прямоугольника указывает, что это логический элемент «И». Первые две буквы обозначения DD1.2 указывают на то, что это цифровая микросхема (Digital), цифра слева от точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы. Одна микросхема может содержать несколько логических элементов.
Состояние входов в таблице обозначаются «0» и «1» («ложь» и «истина»). Из таблицы видно, что выход «Y» будет иметь состояние «1» только в том случае, когда на обоих входах «Х1» и «Х2» будут «1». Это легко запомнить: умножение на «0» всегда дает «0».
Элемент «ИЛИ» (OR), он же дизъюнктор, выполняет операцию логического сложения:
Условное обозначение — Таблица истинности
Состояние «1» на выходе будет всегда, пока есть хотя бы одна «1» на входах.
Элемент «НЕ» (NOT), он же инвертор, выполняет операцию логического отрицания:
Условное обозначение — Таблица истинности
Состояние на входе обратно состоянию на входе.
Вот из этих трех элементов строятся все цифровые устройства!
Рассмотрим еще три логических элемента, которые можно получить, комбинируя уже рассмотренные. В силу исторически сложившихся схемотехнических решений эти скомбинированные схемы тоже считаются логическими элементами.
Элемент «И-НЕ» (NAND), конъюнктор с отрицанием:
Условное обозначение — Таблица истинности
Элемент И-НЕ работает точно так же как «И», только выходной сигнал противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» будет единица. И наоборот.
Элемент «ИЛИ-НЕ» (NOR), дизъюнктор с отрицанием:
Условное обозначение — Таблица истинности
Элемент работает так же как и «ИЛИ», но с инверсией выхода.
Элемент «Исключающее ИЛИ» (XOR), сумматор по модулю 2:
Условное обозначение — Таблица истинности
В этом элемента «1» на выходе будет только тогда, когда на входах разные состояния.
На таких элементах строят сумматоры двоичных многоразрядных чисел. Для этого используется еще один дополнительный выход, на котором при появлении на входах двух «1» появляется сигнал переноса разряда.
Мы рассмотрели логические элементы, которые применяются в цифровой технике для построения логических схем любого уровня сложности, но рассмотренные нами элементы не могут делать одну крайне важную работу – они не умеют хранить информацию. Для хранения используется более сложный класс устройств, называемый элементами с памятью или конечными автоматами. В этот класс входят триггеры, регистры, счетчики, шифраторы (дешифраторы), мультиплексоры (демультиплексоры) и сумматоры. Некоторый из этих устройств мы рассмотрим в следующем уроке.
Логические элементы
Логические элементыЛогические элементы
Логическим элементом называется электрическая схема, выполняющая какую-либо логическую операцию (операции) над входными данными, заданными в виде уровней напряжения, и возвращающая результат операции в виде выходного уровня напряжения. Так как операнды логических операций задаются в двоичной системе счисления, то логический элемент воспринимает входные данные в виде высокого и низкого уровней напряжения на своих входах. Соответственно, высокий уровень напряжения (напряжение логической 1) символизирует истинное значение операнда, а низкий (напряжение логического 0) — ложное. Значения высокого и низкого уровней напряжения определяются электрическими параметрами схемы логического элемента и одинаковы как для входных, так и для выходных сигналов. Обычно, логические элементы собираются как отдельная интегральная микросхема. К числу логических операций, выполняемых логическими элементами относятся конъюнкция (логическое умножение, И), дизъюнкция (логическое сложение, ИЛИ), отрицание (НЕ) и сложение по модулю 2 (исключающее ИЛИ). Рассмотрим основные типы логических элементов.
Элемент И
Логический элемент И выполняет операцию логического умножения (конъюнкция) над своими входными данными и имеет от 2 до 8 входов и один выход (как правило, выпускаются элементы с двумя, тремя, четырьмя и восемью входами). На рис. 1. изображены условные графические обозначения (УГО) логических элементов И с двумя, тремя и четырьмя входами соответственно. Элементы И обозначаются как NИ, где N — количество входов логического элемента (например, 2И, 3И, 8И и т.д.).
| Рис. 1 |
Элемент ИЛИ
Логический элемент ИЛИ выполняет операцию логического сложения (дизъюнкция) над своими входными данными и, также как и логический элемент И, имеет от 2 до 8 входов и один выход. На рис. 2. изображены УГО логических элементов ИЛИ с двумя, тремя и четырьмя входами соответственно. Элементы ИЛИ обозначаются также, как и элементы И (2ИЛИ, 4ИЛИ и т.д.).
| Рис. 2 |
Элемент НЕ (инвертор)
Логический элемент НЕ выполняет операцию логического отрицания над своими входными данными и имеет один вход и один выход. Иногда его называют инвертор, так как он инвертирует входной сигнал. На рис. 3 изображено УГО элемента НЕ.
| Рис. 3 |
Элемент И-НЕ
Логический элемент И-НЕ выполняет операцию логического умножения над своими входными данными, а затем инвертирует (отрицает) полученный результат и выдаёт его на выход. Таким образом, можно сказать, что логический элемент И-НЕ — это элемент И с инвертором на выходе. УГО элемента 3И-НЕ приведено на рис. 4.
| Рис. 4 |
Элемент ИЛИ-НЕ
Логический элемент ИЛИ-НЕ выполняет операцию логического сложения над своими входными данными, а затем инвертирует (отрицает) полученный результат и выдаёт его на выход. Таким образом, можно сказать, что логический элемент ИЛИ-НЕ — это элемент ИЛИ с инвертором на выходе. УГО элемента 3ИЛИ-НЕ приведено на рис. 5.
| Рис. 5 |
Элемент сложения по модулю 2
Этот логический элемент выполняет логическую операцию сложения по модулю 2 и, как правило, имеет 2 входа и один выход. Такой элемент, в основном, используется в схемах аппаратного контроля. УГО элемента приведено на рис. 6.
| Рис. 6 |
Комбинационные логические элементы
Существуют и более сложные логические элементы, выполняющие несколько логических операций над своими входными данными. Например, элемент 2И-ИЛИ, УГО и схема которого приведено на рис. 7, сначала выполняет операцию логического умножения над парами операндов x1, x2 и x3, x4, а затем выполняет операцию логического сложения над полученными результатами, т.е. y = x1x2 + x3x4. Можно придумать и более сложные комбинационные логические элементы, например 3-2И-ИЛИ-НЕ (рис. 8).
| Рис. 7 |
| Рис. 8 |
Универсальные логические элементы
Универсальные логические элементы могут использоваться для выполнения разнообразных операций над своими входными данными. Конкретная операция зависит от того, какие сигналы поданы на управляющие входы. Чтобы синтезировать такой универсальный логический элемент, обычно пользуются СКНФ или СДНФ, как и в синтезе комбинационных логических схем.
Электрические принципиальные схемы логических элементов
При рассмотрении электрических принципиальных схем логических элементов пользуются термином тип логики. Тип логики определяет элементную базу, на которой собран логический элемент, а также отражает некоторые особенности отдельных элементов этой элементной базы и характеристики самого логического элемента. Наиболее распространены следующие типы логик: ТТЛ, ДТЛ, МОП, КМОП, также существуют типы логик ЭСЛ, РЕТЛ и некоторые другие. Тип логики ТТЛ (транзисторно-транзисторная логика) определяет элементную базу, на которой собран логический элемент, как состоящую преимущественно из транзисторов, причём транзисторы используются и на входе, и на выходе логического элемента (отсюда и название — транзисторно-транзисторная). Тип логики ДТЛ (диодно-транзисторная логика) определяет элементную базу как состоящую преимущественно из транзисторов и диодов (диоды на входе, транзисторы — на выходе). Типы логик МОП (металл-оксид-полупроводник) и КМОП определяет элементную базу как состоящую из транзисторов МДП (металл-диэлектрик-полупроводник), причём микросхемы этого типа имеют очень низкую потребляемую мощность, засчёт особенностей МДП транзисторов оперировать малыми токами и имеющими очень малый ток утечки.
Рассмотрим электрические принципиальные схемы логического элемента И-НЕ с n входами — ДТЛ (рис. 9) и логического элемента И-НЕ с n входами — ТТЛ (рис. 10).
| Рис. 9 |
| Рис. 10 |
На рисунках +U обозначает положительный потенциал источника питания, а -U — отрицательный.
Рассмотрим сначала работу схемы на рис. 9. Если к одному из входных диодов приложено напряжение логического 0, то этот диод открыт и на базу транзистора подаётся напряжение логического 0. Транзистор закрывается и на выходе y устанавливается напряжение логической 1. Только когда ко всем входным диодам будет приложено напряжение логической 1 транзистор откроется и на выходе установится напряжение логического 0. Оставшиеся каскады на транзисторах выполняют функцию усиления сигнала и инвертирования. При подаче на вход второго транзистора напряжения логического 0, он закроется, подключив базы транзисторов оконечного каскада через резисторы к плюсу и к минусу источника питания. Один из транзисторов оконечного каскада откроется, а другой — закроется и на выходе установится напряжение логической 1. При подаче на второй транзистор напряжения логической 1, он откроется. Теперь открытый и закрытый транзисторы оконечного каскада поменяются местами и на выходе установится напряжение логического 0.
Теперь рассмотрим работу схемы на рис. 10. Вызывает некоторый интерес необычный транзистор на входе и схема его включения. Такие многоэмиттерные транзисторы всегда используются на входах логических элементов ТТЛ. Сам транзистор выполняет логическую операцию И. При подаче на один из входов напряжения логического нуля, транзистор открывается и, таким образом, на коллекторе устанавливается напряжение логического 0. Напряжение логической 1 будет на коллекторе только тогда, когда на всех входах будет напряжение логической 1. Подобный транзистор можно рассматривать как много n-p переходов, а соответственно, как много диодов. Таким образом такое включение транзистора в цепь эквивалентно диодной сборке на входе логического элемента И на рис. 9.
Применение логических элементов
Логические элементы могут использоваться как самостоятельные части схемы, так и входить в состав более сложной цифровой комбинационной схемы или схемы с памятью. Как самостоятельные части схемы, логические элементы могут применяться в качестве управляющей логики какого-либо устройства, а также в качестве генератора прямоугольных импульсов с подключённой ёмкостью или кварцевым резонатором. В качестве комбинационных схем логические элементы используются в составе микросхем БИС и СБИС, а также в дешифраторах и шифраторах, выполненных в виде отдельных микросхем. Также, логические элементы могут входить в состав схем с памятью (триггеры, регистры, счётчики и т.д.), выполненных в виде отдельной микросхемы или в составе других микросхем.
Логические элементы и логические схемы компьютера. 10-й класс
Цель урока:
- дать учащимся представление о том, как в компьютере при помощи логических элементов выполняются арифметические и логические операции.
Опорные понятия:
- логическая операция;
- сложное логическое выражение (формула).
Новые понятия:
- логический элемент,
- логическая схема.
Задачи учителя:
- на аналогиях из повседневной жизни показать, что логика хорошо реализуется при помощи электронных схем;
- познакомить учащихся с логическими элементами;
- познакомить учащихся с некоторыми логическими устройствами компьютера;
- дать представление учащимся о последовательности создания логического устройства.
Методика проведения урока
ПОВТОРЕНИЕ.
Аналоги логических операций в повседневной жизни
Примеры для повторения операции логического сложения
- Ученик должен быть толковым и усидчивым (т.е. ученик достигает хороших результатов, если он либо толковый, либо усидчивый, либо и то и другое вместе).
- Для сдачи экзамена необходимы знание или везение.
- Высказывание А: «p – четное число»; высказывание В: «p делится на 3». Каков результат операции логического сложения: А + В?
РЕШЕНИЕ. Множество всех случаев, когда А истинно: p = 2, 4, 6, 8, 10,… Множество всех случаев, когда В истинно: p = 3, 6, 9,… Множество всех случаев, когда истинно А+ В: p = 2, 3, 4, 6, 8, 9, 10,…, т.е. объединение двух множеств.
Примеры для повторения операции логического умножения
- Учитель должен быть умным и терпеливым (только одновременное наличие двух качеств, ума и терпения, делает выражение истинным).
- Только умение и настойчивость приводят к достижению цели (достижение цели возможно только при одновременной истинности двух предпосылок – наличия и умения, и настойчивости).
- Высказывание А: «p делится на 5»; высказывание В: «p меньше 20». Чему равен результат логического умножения: А & В?
РЕШЕНИЕ. Множество всех случаев, когда А истинно: p = 5, 10, 15, 20, 25, … Множество всех случаев, когда В истинно: p = 1, 2, 3,…, 19. Множество всех случаев, когда истинно А & В: p = 5, 10, 15, т.е. пересечение двух множеств.
Примеры для повторения операции импликации
- Если выучить материал, то сдашь зачет (высказывание ложно только тогда, когда материал выучен, а зачет не сдан, ведь сдать зачет можно и случайно, например если попался единственный знакомый вопрос или удалось воспользоваться шпаргалкой).
- Высказывание А: «х делится на 9»; высказывание В: «х делится на 3». Операция означает следующее: «если число делится на 9, то оно делится и на 3».
При анализе этого примера можно перебрать следующие варианты:
o А – ложно, В – ложно. Можно найти такие числа, для которых истиной является высказывание: «если А – ложно, то и В – ложно». Например, х = 4, 17, 22…
o А – ложно, В – истинно. Можно найти такие числа, для которых истиной является высказывание: «если А – ложно, то и В – истинно». Например, х = 6, 12, 21…
o А – истинно, В – истинно. Можно найти такие числа, для которых истиной является высказывание: «если А – истинно, то и В – истинно». Например, х = 9, 18, 27…
o А – истинно, В – ложно. Невозможно найти такие числа, которые делились бы на 9, но не делились на 3, т.е. истинная предпосылка не может приводить к ложному результату импликации.
Примеры для повторения операции эквивалентности
Когда в зимний день светит солнце и «кусает» мороз, это значит, что атмосферное давление высокое.
Высказывание А: «сумма цифр, составляющих число х, делится на 3», высказывание В: «х делится на 3». Операция означает следующее: «число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3».
2.РЕАЛИЗАЦИЯ ЛОГИКИ ПРИ ПОМОЩИ ЭЛЕКТРОННЫХ СХЕМ
Можно начать урок с исторической справки.
Историческая справка
С 1867 года американский логик Чарльз Сандерс Пирс ( в его честь названа одна из логических операций – «стрелка Пирса») работает над модификацией и расширением булевой алгебры. Пирс первым осознал, что бинарная логика имеет сходство с работой электрических переключательных схем. Электрический переключатель либо пропускает ток (что соответствует значению Истина), либо не пропускает (что соответствует значению Ложь). Позже Пирс даже придумал простую электрическую логическую схему, но так и не собрал ее.
Учитель предлагает учащимся самим воспроизвести возможный ход рассуждений Ч.Пирса.
ВАРИАНТ ДИАЛОГА
Вопрос: Есть электрическое устройство, которым мы пользуемся каждый день. Оно реализует логическую операцию отрицания. Подумайте, что это за устройство?
Ответ: Выключатель. Если свет не горел, он его включает, если горел – выключает.
Вопрос: Вспомните Новый год и старую елочную гирлянду. Почему она была недолговечна?
Ответ: В старых гирляндах лампочки включались последовательно. Гирлянда горела только тогда, когда все лампочки были исправны. Стоило перегореть хотя бы одной, вся гирлянда не работала.
Вопрос: На какую логическую операцию это похоже?
Ответ: На логическое умножение.
Вопрос: А в современных гирляндах как подключаются лампочки?
Ответ: Параллельно. Гирлянда горит, если хотя бы одна лампочка исправна.
Вопрос: На какую логическую операцию это похоже?
Ответ: На логическое сложение.
Учитель подводит итоги диалога: подобно Пирсу, вы сейчас убедились, как хорошо реализуются логические операции в простейших схемах. В настоящее время существуют электронные схемы, реализующие все логические операции.
3. В КАКОМ ВИДЕ ЗАПИСЫВАЮТСЯ В ПАМЯТИ КОМПЬЮТЕРА И В РЕГИСТРАХ ПРОЦЕССОРА ДАННЫЕ И КОМАНДА
Существуют различные физические способы кодирования двоичной информации, но чаще всего единица кодируется более высоким уровнем напряжения, чем нуль (или наоборот).
4.ЧТО ТАКОЕ ЛОГИЧЕСКИЙ ЭЛЕМЕНТ КОМПЬЮТЕРА.
Как при строительстве дома применяют различного рода типовые блоки – кирпичи, рамы, двери и т.п., так и при разработке компьютера используют типовые электронные схемы. Каждая схема состоит из определенного набора типовых электронных элементов.
Электронным элементом называется соединение различных деталей, в первую очередь – диодов и транзисторов, а также резисторов и конденсаторов, в виде электрической схемы, выполняющей некоторую простейшую функцию.
Электронный элемент, реализующий логическую функцию, называется логическим элементом.
ИЛИ
Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Тысячи микроскопических электронных переключателей в кристалле интегральной схемы сгруппированы в системы, выполняющие логические операции, т.е. операции с предсказуемыми результатами, и арифметические операции над двоичными числами. Соединенные в различные комбинации, логические элементы дают возможность компьютеру решать задачи, используя язык двоичных кодов.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др. (называемые также вентилями), а также триггер, регистр, сумматор.
Триггер – это логическая схема, способная сохранять одно из двух состояний до подачи нового сигнала на вход. Это, по сути, разряд памяти, способный хранить 1 бит информации.
Регистр – это устройство, состоящее из последовательности триггеров. Регистр предназначен для хранения многоразрядного двоичного числового кода, которым можно представлять и адрес, и команду, и данные.
Сумматор – это устройство, предназначенное для суммирования двоичных кодов.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния «1» и «0» в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению «истина» («1»), а низкий – значение «ложь («0»).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
Таблица истинности – это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значениями истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
5. ФИЗКУЛЬТПАУЗА.
6. ЧТО ТАКОЕ СХЕМЫ И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ.
Схема И реализует конъюнкцию двух или более логических значений.
Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис.1, а таблица истинности в таблице 1.
Таблица 1
х |
у |
х * у |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами х и у описывается отношением z = х * у (читается как «х и у»).
Операция конъюнкции на функциональных схемах обозначается знаком & (читается как «амперсэнд»), являющимся сокращенной записью английского слова and.
Схема ИЛИ реализует дизъюнкцию двух или более логических значений.
Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.
Условное обозначение схемы ИЛИ знак «1». Связь между выходом z этой схемы и входами х и у описывается соотношением z = х + у (читается как «х или у»). Рис.2 и таблица 2.
Таблица 2
х |
у |
х + у |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Схема НЕ (инвертор) реализует операцию отрицания.
Связь между входом х этой схемы и выходом z можно записать соотношением z = , где читается как «не х» или «инверсия х».
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение инвертора — на рис.3, а таблица истинности – в таблице 3
.
Таблица 3
x |
|
0 |
1 |
1 |
0 |
Схема И-НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И.
Связь между выходом z и входами х и у схемы записывают следующим образом:
z = , где читается как «инверсия х и у».
рис. 4
Таблица 4
х |
у |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Условное обозначение схемы И-НЕ представлено на рис. 4, а таблица истинности схемы И-НЕ – в таблице 4.
Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.
Связь между выходом z и входами х и у схемы записывают следующим образом:
z = , где читается как «инверсия х или у».
Таблица 5
х |
у |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
Условное обозначение схемы ИЛИ-НЕ представлено на рис. 5, а таблица истинности схемы ИЛИ-НЕ – в таблице 5.
Что такое триггер.
Триггер – это электронная схема, широко применяемая в регистрах компьютера для надежного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое – двоичному нулю.
Термин «триггер» происходит от английского слова trigger – защелка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip – flop, что в переводе означает «хлопанье». Это звукоподражательное название электронной схемы указывает на ее способность почти мгновенно переходить из одного электрического состояния в другое и наоборот.
Самый распространенный тип триггера – так называемый RS – триггер ( S и R соответственно от английских слов set – установка и reset – сброс). Условное обозначение триггера – на рис.6. Он имеет два симметричных входа S и R и два симметричных выхода Q и , причем выходной сигнал Q является логическим отрицанием сигнала . На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов. Наличие импульса на входе будем считать единицей, а его отсутствие – нулем.
На рис. 7 показана реализация триггера с помощью вентилей ИЛИ-НЕ, в таблице 6 – соответствующая таблица истинности.
Таблица 6
S |
R |
Q |
|
0 |
0 |
Запрещено |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Хранение бита |
|
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ-НЕ (см. табл. 5).
- Если на входы триггера подать S = «1», R = «0», то (независимо от состояния) на выходе Q верхнего вентиля появится «0». После этого на входах нижнего вентиля окажется R = «0», Q = «0» и выход станет равным «1».
- Точно так же при подаче «0» на вход S и «1» на вход R на выходе появится «0», а на Q – «1».
- Если на входы S и R подана логическая «1», то состояние Q и не меняется.
- Подача на оба входа R и S логического «0» может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена.
Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта соответственно 8*210=8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
Что такое сумматор.
Сумматор – это электронная логическая схема, выполняющая суммирование двоичных чисел.
Сумматор служит прежде всего центральным узлом арифметико–логического устройства компьютера, однако он находит применение также и в других устройствах машины.
Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров, с рассмотрения которых мы и начнем. Условное обозначение одноразрядного сумматора приведено на рис. 8.
При сложении чисел А и В в одном i –м разряде приходится иметь дело с тремя цифрами:
1. цифра аi первого слагаемого;
2. цифра bi второго слагаемого;
3. перенос рi-1 из младшего разряда.
В результате сложения получаются две цифры:
1) цифра сi для суммы;
2) перенос рi из данного разряда в старший.
Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности – табл.7.
Схема полусумматрора.
Таблица 7
Входы |
Выходы |
|||
Первое слагаемое |
Второе слагаемое |
Перенос |
Сумма |
Перенос |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причем для двух соседних сумматоров выход переноса одного сумматора является входом для другого.
Домашнее задание
1. Читать: стр.140 — 145.
2. Письменно: задание 3.10 стр. 145.
Логические элементы
Любые цифровые микросхемы строятся на основе простейших логических элементов «НЕ», «ИЛИ», «И». В настоящее время используется несколько технологий построения логических элементов:
- транзисторно-транзисторная логика (ТТЛ, TTL)
- логика на основе комплементарных МОП транзисторов (КМОП, CMOS)
- логика на основе сочетания комплементарных МОП и биполярных транзисторов (BiCMOS)
Простейшим логическим элементом является инвертор, который работает в соответствии со следующей таблицей:
| Рис 1 Таблица истинности логического инвертора | |
| Рис 2 Изображение логического инвертора на принципиальных схемах. |
Чаще всего существуют не отдельные схемы логического «И», а более сложные схемы, выполняющие одновременно логическую функцию «И» и логическую функцию «НЕ» Таблица истинности и изображение схемы, выполняющей логическую функцию «И-НЕ» изображены на рис 3 и 4 соответственно:
| Рис 3 Таблица истинности схемы, выполняющей логическую функцию «И-НЕ». | |
| Рис 4 Изображение схемы, выполняющей логическую функцию «И-НЕ». |
Точно также как не существует отдельных схем логического «И», выполненных по технологии ТТЛ, не существует отдельных схем логического «ИЛИ». Таблица истинности и изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ» изображены на рис 5 и 6 соответственно:
| Рис 5 Таблица истинности схемы, выполняющей логическую функцию «ИЛИ-НЕ». | |
| Рис 6 Изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ». |
Построение произвольной таблицы истинности.
Любая логическая схема без памяти полностью описывается таблицей истинности. При построении сложных логических схем с произвольной таблицей истинности используется сочетание простейших схем «И» «ИЛИ» «НЕ».
При построении схемы, реализующей произвольную таблицу истинности, каждый выход анализируется (и строится схема) отдельно. Для реализации таблицы истинности при помощи логических элементов «И» достаточно рассмотреть только те строки таблицы истинности, которые содержат логические «1» в выходном сигнале. Строки, содержащие в выходном сигнале логический 0 в построении схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую «1», реализуется схемой логического «И» с количеством входов, совпадающим с количеством входных сигналов в таблице истинности. Входные сигналы, описанные в таблице истинности логической «1» подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логическим «0» подаются на вход через иверторы. Объединение сигналов с выходов схем, реализующих отдельные строки таблицы истинности, производится при помощи схемы логического ИЛИ. Количество входов в этой схеме определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая «1».
Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 7:
Рисунок 7 Произвольная таблица истинности.
Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные красным цветом. Эти строки реализуются микросхемой D2 на рисунке 8. Каждая строка реализуется своей схемой «И», затем выходы этих схем объединяются Для построения схемы, реализующей сигнал Out2, достаточно рассмотреть строки, выделенные зеленым цветом. Эти строки реализуются микросхемой D3.
Рисунок 8. Принципиальная схема, реализующая таблицу истинности, приведенную на рисунке 7.
[Содержание] [Вперёд]
Построение тестов для константных неисправностей произвольных логических элементов комбинационных схем на основе графического представления функций элементов Текст научной статьи по специальности «Математика»
А.Ю. Матросова, А.Г. Плешков, А.С. Алемасов
ПОСТРОЕНИЕ ТЕСТОВ ДЛЯ КОНСТАНТНЫХ НЕИСПРАВНОСТЕЙ ПРОИЗВОЛЬНЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ КОМБИНАЦИОННЫХ СХЕМ НА ОСНОВЕ ГРАФИЧЕСКОГО ПРЕДСТАВЛЕНИЯ ФУНКЦИЙ ЭЛЕМЕНТОВ
Работа выполнена при финансовой поддержке гранта министерства образования РФ: грант 2003, ЕО 2-2.0-30.
Предложен алгоритм синтеза тестовых наборов для константных неисправностей произвольных логических элементов комбинационных схем. Алгоритм основан на использовании свойств ортогональных дизъюнктивных нормальных форм (ОДНФ) функций, реализуемых схемой. Графическое представление схемы композицией альтернативных графов ее элементов, названных впоследствии SSBDD-графами (Structurally Synthesized Binary Decision Diagram), наряду с информацией о структуре схемы задают ОДНФ функций этой схемы. Это позволяет, с одной стороны, использовать композицию графов при построении тестов для различных неисправностей в структуре схемы, а с другой — сокращать перебор при поиске тестов за счет графического представления ОДНФ булевых функций. Введен FSSBDD-граф (Full Structurally Synthesized Binary Decision Diagram), задающий в компактной форме ОДНФ схемы в целом. Алгоритм синтеза тестовых наборов сводится к поиску подходящих путей в FSSBDD-графе. Созданы программные реализации алгоритма. Одна из них ориентирована на построение FSSBDD-графа и последующий его анализ. Другая — на обход подмножеств путей этого графа без его явного построения за счет использования SSBDD-графов элементов схемы и информации о связях между ними. Приводятся результаты испытания программ.
Графическое представление логических схем широко используется при решении различных задач их анализа, связанных с проблемами диагностики дискретных систем. Это представление предполагает, что вершинам графа сопоставляются элементы схемы, а дугам — связи между элементами. Оно, как правило, является более компактным по сравнению с формулами, описывающими системы булевых функций, реализуемые комбинационной схемой или комбинационной частью последовательностной схемы.
Следует, однако, иметь в виду, что аналитическое представление булевых функций зачастую ориентировано на такие формулы, которые в явном виде несут информацию о свойствах функции: ее единичных наборах (ДРФ), нулевых наборах (КHФ), однородности но переменным (произвольные формулы над множеством {—, л, v } булевых функций, в которых инверсии опущены со скобок на переменные и т.д. Графическое представление логических схем такой информации в явном виде не содержит.
ROBDD-графы (Reduced Ordered Binary Decision Diagram), предложены R.E. Bryant в 1986 г. [1]. Они, в отличии от традиционных графических представлений логических схем своими путями (простыми цепями), соединяющими корень графа с 1(0)-концевой вершиной, представляют единичные (нулевые) наборы булевой функции, однако не содержат информации о структуре схемы, реализующей эту функцию.
В задачах анализа логических схем (моделирование, но-строение проверяющих и диагностических тестов для неисправностей логических элементов схем, вычисление оценок унравляемости и наблюдаемости и др.) необходима как информация о структуре схемы, так и о единичных и нулевых наборах реализуемых ею функций. Эта информация содержится в альтернативных графах, предложенных P.P. Убаром
[2].вденным точкам ветвления сопоставляются корни других SSBDD-графов и т.д. В результате одновыходная комбинационная схема задается системой SSBDD-графов. Сложность системы SSBDD-графов (число ее вершин) линейно зависит от числа элементов схемы [3].
В [4] предлагается вместо системы SSBDD-графов использовать один FSSBDD-граф (Full SSBDD), который строится аналогично SSBDD-графам но структуре схемы при движении от ее выхода к входам. Каждая переменная точки ветвления заменяется специальным BDD-графом элемента схемы, выход которого сопоставляется этой ветви или BDD-графам инверсного элемента. FSSBDD-граф в общем случае получается значительно сложнее системы SSBDD-графов, и используется главным образом для объяснения метода синтеза тестов, поскольку ближе к традиционным BDD-графам. Оба рассматриваемые графические представления содержит в себе «упакованные» ортогональные дизъюнктивные нормальные формы (ОДОФ) функций всевозможных подсхем схемы, для которой они построены. Они различаются способами «упаковки» этих ОДДФ.
В данной работе обсуждается алгоритм построения тестов для одиночных константных неисправностей комбинационной схемы [4], ориентированный на достраивание конъюнкций [5] и использование ортогональных дизъюнктивных нормальных форм (ОДДФ) [6]. Алгоритм адоптируется на схемы из произвольных логических элементов. Приводятся результаты испытания программ для схем из произвольных логических элементов.
1. FSSBDD-ГРАФЫ И ОРТОГОНАЛЬНЫЕ ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ (ОДНФ)
1.1. Построение FSSBDD-графов
Будем иметь в виду, что построение КОБББ-графов [1] основано на использовании известного разложения булевой функции по одной переменной (разложение К. Шеннона):
F (x1 >…> Xn ) = XTF (x1 >…> Xi-1 > a i > X+1V..> Xn ) V
—ai
Xi F
(x1,…,
i+1 ? F (x1>
(1)
обычно называются коэффициентами разложения, a,=1. 210
Это разложение применяется многократно сначала к самой функции, а потом к ее коэффициентам разложения с целью построения КОВББ-графа. При представлении этого разложения фрагментом ЮВББ-графа вершине фрагмента сопоставляется переменная х. Исходящая из нее дуга, помеченная 1 (1-дуга), соответствует фиксированию переменной хI функции Е константой 1 (результат фиксирования сопоставляется вершине, в которую эта дуга заходит), а дуга, помеченная 0 (0-дуга), — константой 0 (результат фиксирования сопоставляется вершине, в которую эта дуга заходит). Если на очередном шаге разложения при фиксировании перемен-
x
n
ной функция обращается в константу 1(0), то вершина, в которую заходит дуга, соответствующая функции, объявляется 1(0)-концевой вершиной. В ЯОБББ-графе все 1-кон-цевые вершины объединяются в одну 1-концевую вершину графа, также как и все 0-концевые вершины [1]. Вершина графа, отмеченная первой по порядку переменной разложения, называется корнем графа. В [1] введены операции, позволяющие сократить число вершин в графе. Построение ЮБББ-графа связано с выбранным заранее для графа в целом порядком разложения по переменным. При выбранном порядке разложения построенный граф оказывается единственным для функции, что позволяет использовать ЯОБББ-графы для верификации дискретных схем. Договоримся в дальнейшем любой граф, полученный с использованием разложения Шеннона и совмещением 1(0)-концевых вершин, называть просто БББ-графом, если другие особенности его построения нас не интересуют.
При построении 88БББ-графов [3] применяется многократное разложение по переменной элементарных функций алгебры логики произвольного числа переменных: И, ИЛИ, НЕ И, НЕ ИЛИ, НЕ с целью построения БББ-графа для каждой из элементарных функций. Причем, наряду с обычным представлением разложения Шеннона фрагментом БББ-графа, предложено использовать модификацию этого представления, в которой вершине сопоставляется переменная Хі. В этом случае 1-дуга соответствует фиксированию
переменной хі функции Е константой 0, а 0-дуга — константой 1 (это следует из формулы (1)).
К булевым функциям И, ИЛИ применяется обычное представление разложения Шеннона, а к булевым функциям НЕ И, НЕ ИЛИ, НЕ — разложение с использованием в качестве меток вершин инверсных переменных, что соответствует опусканию инверсии с функции на входные переменные и замене функции на двойственную: л заменяется на V, V заменяется на л. В результате каждый элемент комбинационной схемы представлен в системе 88БББ-графов либо элементом И, либо элементом ИЛИ, а инвертор — инверсией переменной, сопоставляемой его входу.
И = х1 х2…хп И = х1 V х1 х2 V … V х1…хи-1 хп
Рис. 2. Элементарный БББ-граф для НЕ ИЛИ. И = х1 Х2…Хп И = х1 Vх1 х2 V… Vх1…хп-1 хп
Рис. 3. Элементарный БББ-граф для ИЛИ.
И = х1 VХ1 х2 V…VХ1…Хп-1 хп И = Х1 Х2…Хп
Рис. 4. Элементарный БББ-граф для НЕ И.
И = Х1 VХ1Х2 V…VХ1…Хп-1 Хп И = Х1 Х2…Хп
і
1
0
о
Рис. 5. Элементарный ВББ-граф для НЕ. к = х1 к = х1
На рис.1-5 приведены примеры ВББ-графов для элементарных булевых функций. В дальнейшем будем называть эти графы элементарными ВББ-графами.
Дизъюнктивная нормальная форма называется ортогональной (ОДНФ), если ее конъюнкции попарно ортогональны.
Две конъюнкции ортогональны, если в одной из них некоторая переменная х, присутствует без инверсии, а в другой — с инверсией.
Каждая ОДНФ элементарной функции представляется 1-путями (простыми цепями), соединяющими корневую вершину (корень) соответствующего элементарного ВББ-графа с 1-концевой вершиной, ОДНФ инверсии
элементарной функции представляется 0-путями, соединяющими эту же корневую вершину с 0-концевой вершиной. Всякому пути, проходимому в направлении ориентации дуг из корня некоторого элементарного БББ-графа в его 1(0)-концевую вершину сопоставляется конъюнкция переменных, отмечающих вершины этого пути. Если дуга помечена константой 1, то входящая в конъюнкцию переменная имеет знак инверсии, совпадающий с меткой вершины, из которой дуга исходит, иначе эта переменная имеет противоположный знак инверсии.
На рис. 1-5 приведены ОДНФ элементарных булевых функций.
88БВБ-граф строится путем совмещения элементарных БББ-графов элементов схемы вплоть до точек ветвления схемы; точкам ветвления сопоставляются новые 88БББ-графы и т.д., пока не построим 88БББ-графы, зависящие только от входных переменных. Заметим, что элемент, выход которого является точкой ветвления, в дальнейшем может использоваться как в прямой, так и инверсной форме.
Вместо системы 88БВБ-графов для одновыходной комбинационной схемы будем строить аналогичным образом единственный граф, а именно, Р88БВБ-граф. Опишем процедуру его построения.
Будем считать, что элементы комбинационной схемы пронумерованы в соответствие с разбиением схемы на ярусы от выхода к входам схемы. Сопоставим выходам элементов внутренние переменные. Вершины Р88БББ-графа будем нумеровать в порядке их появления.
Начнем с построения элементарного БББ-графа для элемента, корень которого сопоставляется выходу схемы, а затем последовательно заменим внутренние переменные схемы элементарными БББ-графами. Пусть часть Р88БВБ-графа уже построена и представляет собой граф, в котором выделен корень и 1(0)-кон-цевые вершины. В любую вершину графа (кроме корневой) в общем случае может заходить несколько дуг. Из любой неконцевой вершины исходит ровно две дуги: одна помечена символом 1, другая — символом 0. Каждой ветви точки ветвления, как и в системе 88БББ-графов, сопоставим внутренние переменные, отличающиеся друг от друга индексом, указывающим на номер ветви, а возможно, и знаком инверсии. Внутренние переменные с индексами и знаками инверсии отмечают вершины строящегося Р88БББ-графа.
Если в уже построенном подграфе нет вершин, помеченных внутренними переменными, процедура построения закончена, и Р88БВБ-граф получен.
Иначе выбираем очередную вершину, помеченную внутренней переменной. Из нее исходит 1-дуга, заходящая в вершину построенного графа (обозначим вершину е1), и 0-дуга, заходящая в другую вершину построенного графа (обозначим вершину е0). В рассматриваемую вершину, помеченную внутренней переменной, в общем случае может заходить несколько дуг. Строим элементарный БББ-граф для элемента схемы, выход которого сопоставлен этой внутренней переменной.
Корень этого элементарного БББ-графа замещает вершину, отмеченную рассматриваемой внутренней переменной, возможно, с индексом и знаком инверсии. Все входящие в замещаемую вершину дуги теперь входят в корневую вершину замещающего элементарного БББ-
графа. Совмещаем 1-концевую вершину элементарного БББ-графа с е1, а его 0-концевую вершину — с е0. При этом метка 1(0)-концевой вершины элементарного БББ-графа исключается, метка вершины е1(е0) сохраняется.
Такая подстановка выполняется до тех пор, пока все вершины, помеченные внутренними переменными, не будут исчерпаны. В результате получим Р88БББ-граф схемы.
Рис. 6. Комбинационная схема
Рис. 7. Процесс получения FSSBDD-графа
На рис. 6 приведена комбинационная схема, а на рис. 7 представлены этапы получения для этой схемы FSSBDD-графа. При каждом замещении вершины, отмеченной внутренней переменной, возможно, с индексом и знаком инверсии, этой переменной сопоставляется номер вершины в строящемся FSSBDD-графе, являющейся корнем подставляемого элементарного BDD-графа, и номера вершин строящегося Р88БDD-графа, совмещаемые с 1(0)-концевыми вершинами этого BDD-графа. Последние номера снабжены индексами, указывающими на тип концевых вершин. Если 1(0)-концевая вершина подставляемого BDD-графа совпадает с 1(0)-концевой вершиной FSSBDD-графа (это одна и та же вершина для строящихся FSSBDD-графов и окончательного FSSBDD-графа), то номер вершины Р88БDD-графа не указывается. Соответствующий список номеров приведен на рис. 7.
1.2. Получение ОДНФ для комбинационной схемы и ее подсхем
Конъюнкцию будем называть пустой, если в ней переменная и ее инверсия присутствуют одновременно.
Конъюнкцию будем называть неэлементарной, если она пустая или содержит несколько переменных с одним и тем же знаком инверсии, иначе конъюнкция считается элементарной.
В ROБDD-графе любой простой цепи, соединяющей корень графа с его 1(0)-концевой вершиной, сопоставляется элементарная конъюнкция. Аналогичная конъюнкция в Р88БDD-графе может быть неэлементарной.
Обозначим через Д(/) дизъюнкцию попарно ортогональных, не обязательно элементарных, конъюнкций одновыходной комбинационной схемы, полученную в результате подстановки вместо внутренних переменных (например, при движении от выхода схемы к ее входам) ОДНФ элементов И, ИЛИ, НЕ И, НЕ ИЛИ, НЕ (они приведены на рис. 1-5) от входных переменных элементов и последующего раскрытия скобок. Выбрасывание пустых конъюнкций, повторяющихся букв в непустых конъюнкциях, поглощения и склеивания конъюнкций не допускаются. Такая подстановка гарантирует попарную ортогональность конъюнкций, не обязательно элементарных.
Аналогичным образом может быть получена Д (/) для инверсной схемы, в ней элемент, выход которого является выходом схемы, заменен инверсным элементом. В [4] доказано, что множество 1(0)-путей Р88БDD-графа представляет Д (/) Д (/) .
Каждому 1(0)-пути Р88БDD-графа сопоставляется конъюнкция входных переменных. Если в конъюнкции встречаются взаимно инверсные переменные, то такой путь будем называть противоречивым, то есть противоречивый путь представляет пустую конъюнкцию. Любую непустую конъюнкцию можно привести к элементарной, исключив повторение одинаковых букв. Это значит, что
из Д (/) Д (/) можно получить (ОДНФ) функции (ОДНФ инверсии функции), исключив пустые конъюнкции и повторяющиеся буквы в непустых конъюнкциях с целью превращения последних в элементарные конъюнкции. Обозначим ОДНФ через Д (/) Д (/) .
FSSBDD-граф содержит также ОДНФ и ее инверсию для любой подсхемы, выход которой сопоставляется выходу некоторого элемента схемы, а входы -входным переменным рассматриваемой схемы [4].
Выясним, как найти ОДНФ (ее инверсию) для подсхемы.
Подсхеме (будем называть ее v-подсхемой) в общем случае может быть сопоставлено в Р88БDD-графе несколько подграфов, корни которых сопоставлены символу одной и той же внутренней переменной V, возможно, с различными индексами и знаками инверсии. Обозначим символом Н функцию, реализуемую v-подсхемой, а через Н — инверсию этой функции. Каждый из подграфов задается номером вершины Р88БDD-графа, сопоставленной переменной V и являющейся корнем выделяемого подграфа, и номерами вершин Р88БDD-графа, сопоставленными 1,0-концевым вершинам этого подграфа. Непротиворечивые пути (простые цепи), соединяющие корень выделяемого подграфа с его 1(0)-концевой вершиной,
представляют функцию Н(Н) в виде ОДНФ. Номера вершин, сопоставляемых корню подграфа и его 1,0-кон-цевым вершинам были найдены при подстановке элементарного БDD-графа вместо вершины, отмеченной переменной V с соответствующим индексом и знаком инверсии. При дальнейших подстановках с целью замены других внутренних переменных элементарного БDD-графа эти вершины стали корнем и 1,0-концевыми вершинами
подграфа, представляющего рассматриваемую подсхему. Назовем выделенный подграф у-подграфом.
На рис. 7, например, подсхеме, выходом которой является выход элемента 6 комбинационной схемы, представленной на рис. 6, сопоставляется два подграфа. Корнем одного из подграфов является вершина 3 Р88БББ-графа, 1-концевая вершина подграфа совпадает с 1-концевой вершиной Р88БББ-графа, а 0-кон-цевая вершина подграфа есть вершина 2 Р88БББ-графа. Пути, ведущие из 3 в 1-концевую вершину Р88БББ-графа, представляют функцию Н, реализуе-
мую у-подсхемой, в виде дизъюнкции соответствующих путям конъюнкций: а V асё, а пути из вершины 3
в вершину 2 — инверсию этой функции: ас V асй . Корнем другого подграфа является вершина 2 Р88БББ-графа, его 1-концевая вершина есть вершина 4 Р88БББ-графа, а его 0-концевая вершина совпадает с
0-концевой вершиной Р88БББ-графа. Будем иметь ввиду, что у-подграфы, сопоставляемые внутренней переменной, возможно, с разными индексами, но одним и тем же знаком инверсии, изоморфны.
2. ПОСТРОЕНИЕ ТЕСТОВ ДЛЯ ОДИНОЧНЫХ КОНСТАНТНЫХ НЕИСПРАВНОСТЕЙ ПОЛЮСОВ ЭЛЕМЕНТОВ КОМБИНАЦИОННОЙ СХЕМЫ
В работе [6] предложен метод построения тестов для одиночных константных неисправностей полюсов элементов комбинационной схемы, основанный на использовании ОДНФ, описывающих поведение фрагментов схемы.
Пусть не исправен выход элемента схемы, сопоставляемый переменной V (выход элемента может быть точкой ветвления). Задана неисправность константа 0. Необходимо найти набор значений входных переменных схемы (тестовый набор), обнаруживающий эту неисправность. (2).
Здесь ОДНФ К представляет конъюнкции, не содержащие переменной V, ОДНФ К у представляет конъюнкции, содержащие переменную V, ОДНФ К представляет конъюнкции, содержащие переменную V. Эти ОДНФ попарно ортогональны между собой.
Обозначим через К* ОДНФ, полученную из Ку вычеркиванием переменной V. Аналогичным образом получим ОДНФ К *. Пусть Д0(Н) есть ОДНФ функции, реализуемые подсхемой, выход которой сопоставлен переменной V, (подсхеме сопоставляется v-подграф в FSSBDD-графе [4] ), а Д0(Н) — ОДНФ инверсии
этой функции. Напомним, что рассматриваемые ОДНФ зависят от входных переменных схемы. В [6] доказано, что набор значений входных переменных является тестовым для константной неисправности 0, если и только если он обращает в единицу выражение К * & Д 0(Н) и в нуль выражение К * .
Любую часть пути в графе будем называть отрезком пути. Отрезки не противоречивы, если сопоставляемые им непустые конъюнкции образуют при перемножении непустую конъюнкцию.
Приведенные ниже теоремы относятся к фрагментам упомянутых в них ОДНФ, связанных с одним и тем же v-подграфом [4].
Теорема 1. Конъюнкция из К* представляется двумя непротиворечивыми отрезками пути FSSBDD-графа. Первый из них начинается в корне графа и заканчивается в корневой вершине рассматриваемого у-под-графа, сопоставляемой переменной у( V), а второй на-
начинается в 1(0)-концевой вершине этого у-подграфа и заканчивается в 1-концевой вершине FSSBDD-графа.
Доказательство. Из построения FSSBDD у-графа следует, что рассматриваемая конъюнкция получается вычеркиванием переменной у из конъюнкции, представляемой непустым 1-путем этого графа, проходящим через полюс, помеченный переменной у( V ) и сопоставляемый рассматриваемому у-подграфу, а, возможно, и через полюсы, помеченные той же переменной и сопоставляемые подчиненным у-подграфам. Выделим в нем два отрезка: первый — из корня до первой вершины, помеченной переменной у(V ), пропускаем 1(0)-дугу этой вершины, что соответствует вычеркиванию переменной у, и рассматриваем второй отрезок — из вершины, в которую эта дуга заходит, до 1-кон-цевой вершины FSSBDD у-графа. Если во втором отрезке встречаются корневые вершины подчиненных у-под-графов, соответствующие им дуги также пропускаем. Первый отрезок начинается в корне FSSBDD-графа и заканчивается в вершине, сопоставляемой переменной у( V) рассматриваемого у-подграфа. Второй начинается в 1(0)-кон-цевой вершине этого подграфа и заканчивается в 1-кон-цевой вершине FSSBDD-графа. Теорема доказана.
Теорема 2. Конъюнкция из Д0(Н) представляется непустым 1(0)-путем V -подграфа (из корня подграфа, сопоставляемого в FSSBDD-графе переменной V ( V), в 1(0)-концевую вершину этого подграфа).
Доказательство. Утверждение теоремы следует из способа построения -подграфов. Итак, конъюнкция
ОДНФ, представленная выражением К * & Д0(Н), задается непротиворечивыми отрезками путей FSSBDD-графа, порожденными одним и тем же -подграфом рассматриваемого фрагмента. С этим же подграфом связан непротиворечивый отрезок, обеспечивающий
обращение в нуль выражения К * . Теорема доказана.
Теорема 3. Отрезок FSSBDD-графа, соединяющий 0(1)-концевую вершину рассматриваемого V -подграфа, сопоставляемого в FSSBDD-графе переменной у( V), с
0-концевой вершиной FSSBDD-графа, представляет конъюнкцию, ортогональную ОДНФ К *.
Доказательство. Фрагмент ОДНФ К * представляется путями из 0(1)-концевой вершины рассматриваемого подграфа, сопоставляемого в FSSBDD-графе переменной у( V), в 1-концевую вершину FSSBDD-графа. Каждый непустой путь из 0(1)-концевой вершины подграфа в 0-концевую вершину FSSBDD-графа представ-
ляет конъюнкцию, ортогональную всем конъюнкциям этого фрагмента. Теорема доказана.
Непротиворечивые отрезки, определяемые теоремами
1-3, вместе представляют конъюнкцию. Обращающий ее в единицу набор является тестовым набором для рассматриваемой неисправности. Исправная схема на этом наборе принимает значение один, а неисправная — нуль. Поиск таких непротиворечивых отрезков связан с перебором, однако, перебор удается сократить, во-первых, за счет рассмотрения условий существования теста для фрагментов формул, а во-вторых, за счет замены перебора формул [6] перебором путей в графе. Для нахождения тестовых наборов, обращающих исправную схему в нуль, а неисправную в единицу, необходимо рассмотреть ОДНФ для инверсной схемы и переформулировать теоремы 1-3.
Представим Д0(0) в виде Д0(0) = К V К\ V К7(3). Здесь ОДНФ К , К ‘у, К 7, К ‘I, К ‘■* аналогичны ОДНФ К , К у , К 7, К *, К* . Следовательно, для нахождения тестового набора необходимо обратить в единицу выражение Ку & Д0(Н) и в нуль выражение К7.
Теорема 4. Конъюнкция из К у представляется двумя непротиворечивыми отрезками из Р88БВБ-графа. Первый из них начинается в корне графа и заканчивается в корневой вершине рассматриваемого у-под-графа, сопоставляемого переменной у( у), а второй начинается в 1(0)-концевой вершине этого подграфа и заканчивается в 0-концевой вершине Р88БББ-графа.
Доказательство аналогично доказательству теоремы 1.
Теорема 5. Конъюнкция из Д 0(Н) представляется непустым 0(1)-путем у-подграфа (из корня подграфа, сопоставляемого переменной у ( V ) в Р88БББ-графе, в его 0(1)-концевую вершину).
Доказательство аналогично доказательству теоремы 2.
Теорема 6. Отрезок Р88БББ-графа, соединяющий 0(1)-концевую вершину рассматриваемого у-подграфа, сопоставляемую в Р88БББ-графе переменной у( V ), с
1-концевой вершиной Р88БББ-графа, представляет конъюнкцию, ортогональную ОДНФ К -.
Доказательство аналогично доказательству теоремы 2.
3. АЛГОРИТМ ПОСТРОЕНИЯ ТЕСТОВОГО НАБОРА ДЛЯ НЕИСПРАВНОСТИ КОНСТАНТА 0 НА ПОЛЮСЕ V, СОПОСТАВЛЯЕМОМ ВЫХОДУ ЭЛЕМЕНТА СХЕМЫ
Алгоритм приводится в предположении, что Р88БDD-граф построен.
1. Перебираем ближайшие к корню Р88БDD-графа у-подграфы, не обращая внимания на индексы и знаки инверсии переменной у.
2. Перебираем пути, определяемые выбранным у-подграфом, с тем чтобы найти непротиворечивые отрезки в соответствии с теоремами 1-3. Непротиворечивые отрезки представляют тестовые наборы для рассматриваемой неисправности. Если непротиворечивые отрезки найти не удается, ищем непротиворечивые отрезки в соответствии с теоремами 4-6 для того же у-подграфа.
3. Если все у-подграфы просмотрены, а тестового набора найти не удалось, то его для рассматриваемой неисправности не существует.
Для неисправности константа 0 на входном полюсе элемента схемы определяем индекс переменной у (номер
ветви точки ветвления), сопоставляемой выходу предшествующего элемента, соединенному с рассматриваемым неисправным входным полюсом. При реализации выше приведенного алгоритма перебираем только у-подграфы, сопоставляемые переменной с этим индексом.
Поиск всех совокупностей непротиворечивых отрезков обеспечивает нахождение всех тестовых наборов для рассматриваемой неисправности и представление их в виде ОДНФ.
Для неисправности константа 1 поступаем аналогично предыдущему, обращая в единицу выражение К *& Д 0(Н)(К |*& Д 0(Н)) и в нуль выражение
к *( к ;*).
При построении теста для другой константной неисправности необходимо в Р88БББ-графе выбрать соответствующие неисправному полюсу у-подграфы, а затем воспользоваться описанным выше алгоритмом.
4. РЕАЛИЗАЦИЯ АЛГОРИТМА
Составлены две программы, реализующие алгоритм и ориентированные на схемы из произвольных логических элементов. Функция, реализуемая элементом, задается либо в виде ДНФ, либо в виде КНФ.
Первая программа представляет каждый элемент как схему из двухвходовых вентилей, а затем строит FSSBDD-граф, в котором каждый вентиль подсхемы заменяется соответствующим BDD-графом. Рассматриваются неисправности на полюсах вентилей и строится тестовый набор для неисправности согласно изложенному выше алгоритму.
Результаты испытаний программы на бенч-марке 9єутт1 приведены в таблице. К сожалению, для бенчмарки С432, С499, С880, С1355 не удалось построить FSSBDD-граф из-за его большой размерности.
С целью применения алгоритма для более сложных схем была разработана другая программа. Она представляет каждый элемент графа в виде SSBDD-графа. Например, пусть
элемент задан ДНФ х7 х8 х24 V х6 х26 V х6 х10 х11. Тогда соответствующий ему граф имеет вид, представленный на рис. 8.
Рис. 8. ВББВВ-граф
Вторая программа позволяет выполнить сокращенный обход необходимых путей (простых цепей) FSSBDD-графа без построения этого графа, используя систему SSBDD-графов, соответствующих элементам схемы. Пусть строятся отрезки непротиворечивых путей с целью нахождения тестового набора. При заходе в вершину, соответствующую некоторому элементу схемы, выясняется, проходился ли SSBDD-граф этого элемента при построении тестового набора. Если да, то в строящихся отрезках содержится путь из корня SSBDD-графа в одну из его концевых вершин. Последнее означает, что булевой функции, реализуемой элементом уже приписано значение. Тогда нет необходимости заходить в SSBDD-граф рассматриваемого элемента. Достаточно из вершины, сопоставляемой элементу, пойти по соответствующей дуге, определяемой значением функции и типом инверсии вершины. Если вершина отмечена переменной без инверсии, то в случае единичного (нулевого) значения функции движемся по 1(0)-дуге, исходящей из этой вершины. В случае инверсной переменной — по 0(1)-дуге.
Если вершина, соответствующая элементу схемы, встречается впервые, то поиск пути продолжается внутри
88BDD-графа, корень которого отожествляется с этой вершиной, до тех пор, пока не встретится концевая вершина этого графа. Последнее означает приписывание значения функции, реализуемой рассматриваемым элементом.
При построении FSSBDD-графа в явном виде мы имеем возможность воспользоваться результатом обхода только V -подграфа, для которого ищется тестовый набор. Прохождение одних и тех же подграфов других элементов схемы не учитывается, поскольку это требует значительных дополнительных ресурсов памяти. Следствием этого факта является рост перебора при поиске тестового набора по FSSBDD-графу.
Программа 1, составленая Плешковым А.Г., реализует алгоритм построения тестовых наборов для константных неисправностей, используя систему SSBDD-графов. Результаты испытаний представлены в табл. и получены на ПЭВМ с 1700 МГ ц версией процессора АШопХР и 256Мб памяти.
Программа 2 составлена Алимасовым А. С., и реализует алгоритм построения тестовых наборов для константных неисправностей по FSSBDD-графу. Результаты испытаний представлены в табл. 1 и получены на ПЭВМ с 150 МГц версией процессора Репйит 1 и 64Мб памяти.
Имя файла Количество элементов в схеме Количес тво входов Количе- ство выходов Количество обнаруженных обнаружимых неисправностей Количество обнаруженных необнаружимых неисправностей Максимальное время поиска теста для необнаружи-мой неисправности Общее время построе- ния тестов
9symml (lif/9symml) (пр-ма 2) 319 9 1 1142 0 — 185,5
9symml (lif/9symml) (пр-ма 1) 57 9 1 бб2 0 — 2,0б2
С432 (С432. iscas) (пр-ма 1) 579 200 7 759 23 б523,7б5 1319б2,1 25
С499 (С499. iscas) (пр-ма 1) S59 41 32 24 0 — 27SS0
С880 (С880. iscas) (пр-ма 1) 1202 б0 2б 3230 0 — 2275,828
С1355 (С1355. iscas) (пр-ма 1) 1б87 41 32 42 0 — 4б439,б09
4. ЗАКЛЮЧЕНИЕ
Предложен и реализован метод синтеза тестовых мы. Метод основан на использовании ОДНФ функций,
наборов комбинационных схем для одиночных кон- реализуемых схемой и ее подсхемами, компактно
стантных неисправностей произвольных элементов схе- представленными композицией SSBDD-графов.
ЛИТЕРАТУРА
1. BryantR.E. Graph-based algorithms for boolean function manipulation // IEEE transactions on computers. August 1986. Vol. C-35, N° 8, P. 677-691,
2. Плакк М.П., Убар Р.Р. Построение тестов цифровых схем при помощи модели альтернативных графов // Автоматика и телемеханика. 1980. № 5. С. 152-163.
3. Jutman A., Raik J., Ubar R. SSBDDs: Advantageous model and efficient algorithms for digital circuit modeling, simulation & test // Proc. of boolean problems, 5th international workshop edited by B.Steinbach. Freiberg university of mining and technology institute of computer science. September 19-20, 2002. Freiberg(Sachsen). P. 157-165.
4. Матросова А.Ю., Плешков А.Г., Убар Р.Р. Построение тестов для неисправностей комбинационных схем на основе анализа ортогональных дизъюнктивных нормальных форм, представляемых альтернативными графами // Автоматика и телемеханика (в печати). 2004.
5. МатросоваА.Ю. Алгоритмические методы синтеза тестов. Томск: Изд-во Том. ун-та, 1990. 206 с.
6. Евтушенко Н.В., Матросова А.Ю. О вероятностном подходе к вычислению оценок управляемости и наблюдаемости узла дискретного устройства // Автоматика и телемеханика. 1993. № 11. С. 152-160.
Статья представлена кафедрой программирования факультета прикладной математики и кибернетики Томского государственного университета, поступила в научную редакцию «Кибернетика» 15 апреля 2004 г.
Программа-тренажер «Логика» для изучения логических элементов: сайт Константина Полякова
Логика
Что это такое?
Тренажер «Логика» предназначен для проведения практических занятий по теме «Математическая логика» в игровой форме. Подобная игра была ранее написана для компьютеров «Ямаха» (программисты П. Меняйло и М. Щекочихин). Оригинал программы вместе с имитатором MSX-компьютера можно скачать здесь (спасибо Михаилу Бондаревскому).
Программа работает под управлением операционных систем линейки Windows 95/98/NT/2000/XP/2003 на любых современных компьютерах. После распаковки архива она находится в работоспособном состоянии и не требует никаких дополнительных настроек.
Скачать
Программа является бесплатной для некоммерческого использования. Исходные тексты программы не распространяются.
Программа поставляется «as is», то есть, автор не несет никакой ответственности за всевозможные последствия ее использования, включая моральные и материальные потери, вывод оборудования из строя, физические и душевные травмы.
Программа содержит конструктор, позволяющий создавать новые схемы и подключать их в качестве уровней. Здесь можно скачать готовые схемы всех уровней, а также схемы триггеров на элементах «И-НЕ» и «ИЛИ-НЕ».
Достоинства
- игровая форма закрепления учебного материала;
- программа имеет встроенный набор логических схем (задач) для каждого из 10 уровней;
- существует возможность составлять новые схемы и проверять их работу, не выходя из программы;
- с каждым уровнем можно связать свою схему; список нестандартных схем хранится в файле инициализации LOGIC.INI; таким образом, можно составить несколько ini-файлов с разнотипными заданиями;
- кроме стандартного набора логических элементов (И, ИЛИ, НЕ) в схемах можно использовать включенные (непонятно почему) в школьную программу элементы «импликация», «эквивалентность», а также полусумматор, сумматор и RS-триггер.
Правила игры
Задача заключается в том, чтобы последовательно передавать кристалл с верхней площадки на нижнюю. Подавая ток на вход механизмов в правой части схемы, можно выдвигать площадки на пути кристалла. Если на входе механизма нет тока, площадка убирается.
Для управления механизмами используют выключатели в левой части поля. Их состояние изменяется щелчком мыши. Если выключатель включен, по цепи идет ток и поступает на логические схемы, включенные в эту цепь (средняя часть поля). Логические схемы преобразуют входные сигналы по следующим правилам:
- схема НЕ: на выходе будет ток (сигнал 1), если на входе тока нет (сигнал 0), и наоборот;
- схема И: на выходе будет 1, если на обоих входах 1;
- схема ИЛИ: на выходе будет 1, если хотя бы на одном входе 1;
- схема XOR (исключающее ИЛИ): на выходе будет 1, если только на одном входе 1;
- схема импликация (1—>2): на выходе будет 0, если на первом входе 1, а на втором — 0; иначе на выходе 1;
- схема эквивалентность (<—>): на выходе будет 1, если оба входа равны; иначе на выходе 0.
Кристалл нельзя передавать сразу через несколько «пролетов» — в этом случае он разбивается и приходится начинать уровень заново. Кроме того, у вас есть только 5 кристаллов на всю игру, если вы разобьете их все, задание считается невыполненным.
Игра состоит из 10 уровней. Если вы сможете пройти все уровни, сохранив хотя бы один кристалл и наберете больше нуля очков, вы увидите картинку.
Диаграммы Бора атомов и ионов
Цели
- Вспомните стабильность, связанную с атомом, который имеет полностью заполненную валентную оболочку
- Построить атом по модели Бора
Ключевые термины
- Правило октета: Правило, согласно которому атомы теряют, приобретают или делятся электронами, чтобы иметь полную валентную оболочку из 8 электронов. (Водород исключен, потому что он может удерживать максимум 2 электрона в своей валентной оболочке.)
- Электронная оболочка : Коллективные состояния всех электронов в атоме, имеющие одинаковое главное квантовое число (визуализированное как орбита, по которой движутся электроны).
Электронные оболочки
Нильс Бор предложил раннюю модель атома как центрального ядра, содержащего протоны и нейтроны, вращающиеся электронами в оболочках. Как обсуждалось ранее, существует связь между количеством протонов в элементе, атомным номером, который отличает один элемент от другого, и количеством электронов, которые он имеет.Во всех электрически нейтральных атомах количество электронов равно количеству протонов. Каждый элемент, когда он электрически нейтрален, имеет количество электронов, равное его атомному номеру.
Ранняя модель атома была разработана в 1913 году датским ученым Нильсом Бором (1885–1962). Модель Бора показывает атом как центральное ядро, содержащее протоны и нейтроны, с электронами на круговых орбиталях на определенных расстояниях от ядра (рис. \ (\ PageIndex {1} \)). Эти орбиты образуют электронные оболочки или уровни энергии, которые позволяют визуализировать количество электронов в различных оболочках.Эти уровни энергии обозначены числом и символом «n». Например, оболочка 1n представляет собой первый энергетический уровень, ближайший к ядру.
Рисунок \ (\ PageIndex {1} \): Модель Бора постулировала, что электрон вращается вокруг ядра в оболочках на фиксированном расстоянии.Электрон обычно существует в оболочке с наименьшей доступной энергией, которая является ближайшей к ядру. Энергия фотона света может подтолкнуть его к более высокой энергетической оболочке, но эта ситуация нестабильна, и электрон быстро распадается обратно в основное состояние.
Диаграммы Бора
Диаграммы Бора показывают электроны, вращающиеся вокруг ядра атома, чем-то вроде планет, вращающихся вокруг Солнца. В модели Бора электроны изображаются движущимися по кругу на разных оболочках, в зависимости от того, какой элемент у вас есть. Рисунок \ (\ PageIndex {2} \) противопоставляет диаграммы Бора для атомов лития, фтора и алюминия. Оболочка, ближайшая к ядру, называется K-оболочкой, далее идет L-оболочка, затем M-оболочка.
Рисунок \ (\ PageIndex {2} \): диаграммы Бора для нейтральных атомов лития, фтора и алюминия.Каждая оболочка может содержать только определенное количество электронов. Оболочка K может иметь 2, L может иметь 8, M может иметь 18 электронов и так далее.
- Литий имеет три электрона:
- два идут в оболочку K и
- оставшийся идет в оболочку L.
- Электронная конфигурация — K (2), L (1)
- У фтора девять электронов:
- два идут в оболочку K и
- остальные семь идут в оболочку L.
- Электронная конфигурация — K (2), L (7). Обратите внимание, что L может иметь 8 электронов.
- Алюминий имеет тринадцать электронов:
- два идут на оболочку К,
- восемь идут в оболочку L, а
- оставшихся трех идут в оболочку M.
- Его электронная конфигурация — K (2), L (8), M (3). Обратите внимание, что оболочка M может иметь 18 электронов.
Орбитали в модели Бора
Электроны заполняют оболочки орбиты в последовательном порядке.В стандартных условиях атомы сначала заполняют внутренние оболочки (ближе к ядру), что часто приводит к переменному количеству электронов во внешней оболочке. Самая внутренняя оболочка имеет максимум два электрона, но следующие две электронные оболочки могут иметь максимум восемь электронов. Это известно как правило октетов, которое гласит, что, за исключением самой внутренней оболочки, атомы более стабильны энергетически, когда у них есть восемь электронов в их валентной оболочке, самой внешней электронной оболочке.Примеры некоторых нейтральных атомов и их электронных конфигураций показаны на рисунке \ (\ PageIndex {3} \). Как показано, гелий имеет полную внешнюю электронную оболочку с двумя электронами, заполняющими его первую и единственную оболочку. Точно так же неон имеет полную внешнюю 2n-оболочку, содержащую восемь электронов. Напротив, хлор и натрий имеют семь и один электрон на своих внешних оболочках соответственно. Теоретически они были бы более энергетически стабильными, если бы следовали правилу октетов и имели восемь.
Рисунок \ (\ PageIndex {3} \):Диаграммы Бора
Диаграммы Бора показывают, сколько электронов заполняет каждую главную оболочку.Элементы группы 18 (показаны гелий, неон и аргон) имеют полную внешнюю или валентную оболочку. Полная валентная оболочка — наиболее стабильная электронная конфигурация. Элементы в других группах имеют частично заполненные валентные оболочки и приобретают или теряют электроны для достижения стабильной электронной конфигурации.
Атом может приобретать или терять электроны для достижения полной валентной оболочки, наиболее стабильной электронной конфигурации. Периодическая таблица разделена на столбцы и строки в зависимости от количества электронов и их расположения, что позволяет понять, как электроны распределяются во внешней оболочке атома.Как показано на фиг.1, группа из 18 атомов гелия (He), неона (Ne) и аргона (Ar) заполнила внешние электронные оболочки, что делает ненужным приобретение или потеря электронов для достижения стабильности; они очень стабильны как отдельные атомы. Их инертность привела к тому, что они были названы инертными газами (или благородными газами). Для сравнения, элементы группы 1, включая водород (H), литий (Li) и натрий (Na), все имеют по одному электрону на своих внешних оболочках. Это означает, что они могут достичь стабильной конфигурации и заполненной внешней оболочки, отдав или потеряв электрон.В результате потери отрицательно заряженного электрона они становятся положительно заряженными ионами. Когда атом теряет электрон, чтобы стать положительно заряженным ионом, это обозначается знаком плюс после символа элемента; например Na + . Элементы группы 17, включая фтор и хлор, имеют семь электронов на своих внешних оболочках; они стремятся заполнить эту оболочку, получая электрон от других атомов, делая их отрицательно заряженными ионами. — \).Таким образом, столбцы периодической таблицы представляют потенциальное общее состояние внешних электронных оболочек этих элементов, которое отвечает за их схожие химические характеристики.
Символы Льюиса
Символы Льюиса — это упрощенные диаграммы Бора, которые отображают электроны только на внешнем энергетическом уровне.
Сводка
- В модели атома Бора ядро содержит большую часть массы атома в его протонах и нейтронах.
- По орбите положительно заряженного ядра вращаются отрицательно заряженные электроны, которые имеют небольшой вклад в массе, но электрически эквивалентны протонам в ядре.
- В большинстве случаев электроны сначала заполняют орбитали с более низкой энергией, затем следуют орбитали с более высокой энергией, пока она не заполнится, и так далее, пока не будут размещены все электроны.
- Атомы, как правило, наиболее стабильны с полной внешней оболочкой (которая после первой содержит 8 электронов), что приводит к тому, что обычно называют «правилом октетов».
- Свойства элемента определяются его внешними электронами или электронами на орбитали с наибольшей энергией.
- Атомы, у которых нет полных внешних оболочек, будут иметь тенденцию приобретать или терять электроны, в результате чего получается полная внешняя оболочка и, следовательно, стабильность.
Авторы и авторство
Без границ (www.boundless.com)
Периодическая таблица элементов Виды деятельности
Вся материя состоит из более чем 100 различных типов атомов, которые, объединившись, могут образовать миллионы различных веществ. Эти типы атомов известны как элементы. Периодическая таблица представляет собой простую диаграмму, в которой все известные элементы упорядочены по атомному номеру. Часто это первое, с чем ученики знакомятся во время любого урока, связанного с химией, и, хотя это может показаться подавляющим, это не обязательно! Эти упражнения разработаны для того, чтобы учащимся было легко и весело осваивать таблицу Менделеева с помощью наглядных пособий.
Деятельность учащихся по элементам периодической таблицы
Атомы и Периодическая таблица
Древние греки считали, что мир состоит из пяти элементов: земли, воздуха, огня, воды и эфира. Где-то около 500 г. до н.э. Демокрит впервые выдвинул идею о том, что все в мире состоит из небольших неделимых частиц, называемых атомами. Термин atomos происходит от древнегреческого, что означает «неделимый». В начале 1800-х годов Джон Дальтон формализовал атомную теорию.Он предположил, что вся материя состоит из маленьких частиц, называемых атомами, что эти атомы перегруппировались в химических реакциях и что эти атомы обладают разными свойствами.
Дмитрий Менделеев был российским химиком, известным как отец периодической таблицы Менделеева. Он организовал элементы, известные в то время, в таблицу и оставил в ней пробелы для элементов, которые, как он предсказывал, будут обнаружены позже. Современная таблица Менделеева состоит из 118 различных элементов с 18 группами и семью периодами.
Девяносто четыре элемента встречаются в природе, 80 из которых имеют стабильные изотопы. Самый распространенный элемент на Земле — это кислород, элемент, который необходим для жизни, которую мы знаем на нашей планете. Ученые считают, что два самых легких элемента были созданы в результате Большого взрыва. Все остальные природные элементы появились в результате ядерных реакций. Звезды объединяют различные ядра вместе, чтобы произвести более тяжелые ядра, но звезды могут производить элементы весом всего 26 протонов, то есть железо.Элементы тяжелее этого были созданы в сверхновых, вплоть до атомного номера 94. Все, что больше этого, было создано людьми искусственно. Некоторые из этих сверхмассивных элементов очень нестабильны и распадаются или распадаются за доли секунды после своего создания.
Периодическая таблица — это способ организации элементов. В современной периодической таблице элементы упорядочены по их атомным номерам. Атомный номер указывает, сколько протонов находится в ядре атома.Атомная масса говорит нам, сколько протонов и нейтронов находится в ядре. Число электронов такое же, как число протонов в нейтральном атоме. Вертикальные столбцы известны как периодическая таблица , группы . Все элементы в группе имеют похожие свойства. Например, элементы первой группы — это металлы, и все они вступают в реакцию с водой. Горизонтальные строки известны как периодов . Хотя элементы в один и тот же период не имеют схожих свойств, все они имеют одинаковое количество электронных оболочек.Современная таблица Менделеева состоит из 118 различных элементов, начиная с водорода с атомным номером один и заканчивая Оганессоном с атомным номером 118.
Элементы состоят из трех типов субатомных частиц, называемых протонами, нейтронами и электронами. В то время как протоны и нейтроны находятся в ядре атома, электроны вращаются вокруг ядра в оболочках или энергетических уровнях, расположенных на разных расстояниях от ядра. Электроны удерживаются на орбите, поскольку их отрицательный заряд противоположен заряду ядра.Электроны всегда ищут в атоме состояние с наименьшей энергией. В первую оболочку мы помещаем максимум два электрона, а затем восемь электронов во вторую и третью оболочки. Например, скандий имеет атомный номер 21, что означает, что в нем 21 протон. Поскольку это нейтральный атом, здесь также 21 электрон. Снаряды наполняются от мельчайших, отходящих от центра. У скандия 21 электрон, поэтому нам нужно поместить 21 электрон в оболочки. Таким образом, их будет два в первой оболочке, восемь во второй, восемь в третьей и три в четвертой.Скандий имеет структуру 2.8.8.3.
Элементы первой группы вместе известны как щелочные металлы. Все они являются металлами, которые активно реагируют с водой. Все они имеют по одному электрону на внешней оболочке. По мере того, как вы перемещаетесь вниз по группе от лития к францию, реакционная способность увеличивается.
Элементы в группе, противоположной щелочным металлам, известны как благородные газы . Они очень инертны и имеют полную внешнюю оболочку. Они негорючие и имеют низкие температуры кипения.К ним относятся гелий, неон, аргон, криптон, ксенон и радон.
Основные вопросы для элементов и периодической таблицы
- Как элементы расположены в периодической таблице?
- Что общего у элементов в одной группе?
- Как была разработана периодическая таблица Менделеева?
- Что такое элемент?
- В чем разница между атомом гелия и атомом урана?
Идеи дополнительных действий для Периодической таблицы
- Студенты могут составить T-диаграмму, показывающую различные свойства металлов; Затем они могли бы использовать эти свойства, чтобы объяснить, почему металлы используются для определенных задач.
- Учащиеся могут создать плакат о своем любимом элементе.
- Студенты могут создать презентацию, объясняя, какой элемент был наиболее важным и почему.
Видео с вопросом: определение элементов на диаграммах Atom
Стенограмма видео
На диаграмме показаны электроны в различные электронные оболочки в атоме. Атом электрически нейтральный.Что за элемент это атом из?
Хорошо, в этом вопросе мы была дана диаграмма, которая показывает то, что кажется ядром в центре атома, а также электронные уровни энергии, которые представлены в чернить. Теперь эти электронные уровни энергии также известны как ракушки. И мы видим, что занимая эти В оболочках есть одна, две, три синие точки, обозначающие электроны.Другими словами, есть три электроны в этом атоме.
Нам сказали, что этот атом рассматриваемый электрически нейтральный. Это означает, что общая электрический заряд на атоме равен нулю, потому что он нейтрален. Теперь, чтобы понять значение Из этого следует напомнить, что электроны — это отрицательно заряженные частицы. И эти атомы нейтральны, если количество электронов в атоме равно количеству положительно заряженных протонов найдено в ядре.Итак, что говорит эта диаграмма Мы в том, что в этом атоме три электрона. И чтобы он был нейтральным, в ядре атома должно быть три протона. И тогда мы можем вспомнить, что элемент определяется количеством протонов, найденных в ядре атома этого элемент.
Итак, чтобы найти ответ Чтобы ответить на наш вопрос, нам нужно будет обратиться к таблице Менделеева. В частности, можно вспомнить, что периодическая таблица элементов показывает все элементы, расположенные в порядке атомный номер, где атомный номер атома — это просто количество протонов находится в ядре этого атома.Итак, учитывая периодические таблица расположена в порядке возрастания атомного номера, мы хотим найти элемент в периодической таблице, атомный номер которой равен трем. Поскольку в ядро этого конкретного атома. Итак, элемент с тремя протоны в его ядре — это литий. И, следовательно, это ответ на наш вопрос.
атом | Определение, структура, история, примеры, диаграммы и факты
Атом , наименьшая единица, на которую можно разделить материю без высвобождения электрически заряженных частиц.Это также мельчайшая единица вещества, обладающая характерными свойствами химического элемента. Таким образом, атом является основным строительным блоком химии.
Оболочечная модель атомаВ оболочечной модели атома электроны занимают разные энергетические уровни или оболочки. Оболочки K и L показаны для атома неона.
Encyclopædia Britannica, Inc.Исследуйте различные электронные конфигурации в электронных оболочках вокруг ядра атома
Атомная модель электронных конфигураций.
Британская энциклопедия, Inc. Посмотрите все видео по этой статьеБольшая часть атома — это пустое пространство. Остальное состоит из положительно заряженного ядра протонов и нейтронов, окруженного облаком отрицательно заряженных электронов. Ядро маленькое и плотное по сравнению с электронами, которые являются самыми легкими заряженными частицами в природе. Электроны притягиваются к любому положительному заряду своей электрической силой; в атоме электрические силы связывают электроны с ядром.
Из-за природы квантовой механики ни одно изображение не было полностью удовлетворительным для визуализации различных характеристик атома, что, таким образом, вынуждает физиков использовать дополнительные изображения атома для объяснения различных свойств.В некотором отношении электроны в атоме ведут себя как частицы, вращающиеся вокруг ядра. В других случаях электроны ведут себя как волны, застывшие вокруг ядра. Такие волновые структуры, называемые орбиталями, описывают распределение отдельных электронов. Эти орбитальные свойства сильно влияют на поведение атома, а его химические свойства определяются орбитальными группировками, известными как оболочки.
Эта статья открывается широким обзором фундаментальных свойств атома и составляющих его частиц и сил.После этого обзора следует исторический обзор наиболее влиятельных концепций об атоме, сформулированных на протяжении веков. Для получения дополнительной информации, относящейся к структуре ядра и элементарным частицам, см. субатомных частиц.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасБольшая часть вещества состоит из скоплений молекул, которые можно относительно легко разделить. Молекулы, в свою очередь, состоят из атомов, соединенных химическими связями, которые труднее разорвать.Каждый отдельный атом состоит из более мелких частиц, а именно электронов и ядер. Эти частицы электрически заряжены, и электрические силы, действующие на заряд, несут ответственность за удержание атома вместе. Попытки разделить эти более мелкие составляющие частицы требуют постоянно увеличивающегося количества энергии и приводят к созданию новых субатомных частиц, многие из которых заряжены.
Как отмечалось во введении к этой статье, атом в основном состоит из пустого пространства. Ядро является положительно заряженным центром атома и содержит большую часть его массы.Он состоит из протонов, которые имеют положительный заряд, и нейтронов, которые не имеют заряда. Протоны, нейтроны и окружающие их электроны — это долгоживущие частицы, присутствующие во всех обычных, встречающихся в природе атомах. Другие субатомные частицы могут быть обнаружены в ассоциации с этими тремя типами частиц. Однако они могут быть созданы только с добавлением огромного количества энергии и очень недолговечны.
Все атомы примерно одинакового размера, независимо от того, имеют ли они 3 или 90 электронов.Примерно 50 миллионов атомов твердого вещества, выстроенных в ряд, имеют размер 1 см (0,4 дюйма). Удобной единицей длины для измерения размеров атомов является ангстрем (Å), определяемый как 10 −10 метра. Радиус атома составляет 1-2 Å. По сравнению с общим размером атома, ядро еще более миниатюрное. Он находится в той же пропорции к атому, как шарик к футбольному полю. По объему ядро занимает всего 10 — 14 метра пространства в атоме, то есть 1 часть на 100 000.Удобной единицей длины для измерения размеров ядер является фемтометр (фм), который равен 10 −15 метра. Диаметр ядра зависит от количества содержащихся в нем частиц и колеблется от 4 фм для легкого ядра, такого как углерод, до 15 фм для тяжелого ядра, такого как свинец. Несмотря на малые размеры ядра, в нем сосредоточена практически вся масса атома. Протоны — массивные положительно заряженные частицы, тогда как нейтроны не имеют заряда и немного массивнее протонов.Тот факт, что ядра могут иметь от 1 до почти 300 протонов и нейтронов, объясняет их широкую вариацию массы. Самое легкое ядро, ядро водорода, в 1836 раз массивнее электрона, а тяжелые ядра почти в 500 000 раз массивнее.
Основные свойства
Самой важной характеристикой атома является его атомный номер (обычно обозначаемый буквой Z ), который определяется как количество единиц положительного заряда (протонов) в ядре.Например, если у атома Z из 6, это углерод, а Z из 92 соответствует урану. Нейтральный атом имеет равное количество протонов и электронов, так что положительный и отрицательный заряды точно уравновешиваются. Поскольку именно электроны определяют, как один атом взаимодействует с другим, в конечном итоге именно количество протонов в ядре определяет химические свойства атома.
Добавить ссылки на схемы
Хотя диаграмма обычно представляет собой структуру объектов моделирования, она также может выступать в качестве портала, через который вы можете получить доступ к связанным диаграммам, которые предоставляют более подробную информацию об аспекте или альтернативных представлениях структуры или представлениях других структур.Если есть много диаграмм (или, действительно, других объектов и функций), к которым нужно перейти, исходная диаграмма может стать домашней страницей для части проекта или даже всего проекта.
В диалоговом окне «Выбрать тип», которое отображается, когда вы перетаскиваете целевую диаграмму из окна браузера на главную диаграмму, предоставляется несколько вариантов связывания с другой диаграммой.
Варианты выпадения диаграммы
Выберите соответствующий вариант, чтобы настроить требуемый тип ссылки на целевую диаграмму, а затем нажмите кнопку ОК.
|
Этот параметр создает элемент кадра диаграммы, содержащий изображение перетащенной диаграммы с именем перетаскиваемой диаграммы в метке кадра. Любой пользователь, просматривающий диаграмму хоста, может дважды щелкнуть фрейм диаграммы и открыть целевую диаграмму для просмотра и, если у них есть права доступа, для редактирования. |
Рамка диаграммы | |
|
Эта опция создает пустой элемент фрейма диаграммы с именем отброшенной диаграммы в метке фрейма.Любой пользователь, просматривающий диаграмму хоста, может дважды щелкнуть фрейм диаграммы и открыть целевую диаграмму для просмотра и, если у них есть права доступа, для редактирования. |
Рамка диаграммы | |
|
Этот параметр добавляет к схеме элемент гиперссылки, содержащий значок схемы без рамки, за которым следуют имена родительского пакета и целевой схемы. Двойной щелчок по этой гиперссылке откроет целевую диаграмму. Вы можете отредактировать гиперссылку, чтобы указать на другую диаграмму или не отображать значок диаграммы, щелкнув элемент правой кнопкой мыши и выбрав параметр «Свойства». Вы также можете создать идентичный элемент гиперссылки, перетащив значок гиперссылки на диаграмму узла со страницы «Общие» панели инструментов, щелкнув элемент правой кнопкой мыши и выбрав «Свойства», а затем выбрав «Диаграмма» в раскрывающемся списке «Тип». -вниз список. |
Гиперссылки между диаграммами | |
|
Этот параметр создает ячейку навигации (элемент диаграммы UML), которая содержит имя целевой диаграммы и в правом верхнем углу значок, представляющий тип диаграммы.Сразу после того, как вы нажмете кнопку «ОК», появится диалоговое окно «Выбрать изображение», в котором вы можете выбрать изображение, представляющее характер диаграммы. Вы также можете выбрать тему диаграммы для изображения в поле «Список изображений». Если вы не хотите добавлять изображение к элементу, нажмите кнопку «Отмена». |
Ячейки навигации | |
|
Этот параметр создает диаграмму представления модели, в которой перечислены элементы целевой диаграммы.Когда вы выбираете опцию и нажимаете кнопку OK, на странице «Сведения о диаграмме> Источник» отображается диалоговое окно «Свойства» элемента представления модели, в котором отображается оператор SQL, заполняющий список. Нажмите кнопку ОК, чтобы выполнить поиск и создать диаграмму списка элементов. |
Определение диаграммы вида модели |
Другие ссылки на диаграммы из диаграмм
Существуют дополнительные способы связи и доступа к одной диаграмме из другой.К ним относятся:
- Из окна браузера перетащите пакет, содержащий целевую диаграмму (как первая диаграмма в списке пакетов), на диаграмму хоста и выберите параметр «Элемент пакета»; когда пользователь дважды щелкает элемент Package на диаграмме хоста, на целевой диаграмме отображается
- Щелкните правой кнопкой мыши подходящий элемент на главной диаграмме и выберите «Новая дочерняя диаграмма | Схема составной структуры », затем дважды щелкните элемент, чтобы отобразить первую диаграмму под элементом; если это не та диаграмма, щелкните элемент правой кнопкой мыши и выберите «Новая дочерняя диаграмма | Выберите параметр «Составная диаграмма», затем выберите целевую диаграмму в диалоговом окне «Выбор классификатора»
— Вы можете отобразить целевую составную диаграмму вместо родительского элемента на хосте
диаграмма; щелкните правой кнопкой мыши и выберите «Новая дочерняя диаграмма | Показать составную диаграмму во фрейме ‘
вариант
— В качестве альтернативы вы можете отобразить целевую диаграмму в отсеке родительского элемента
. контур; щелкните правой кнопкой мыши и выберите «Новая дочерняя диаграмма | Показать составную диаграмму в
Купе вариант - Для большинства типов ссылок диаграммы, когда пользователь щелкает ссылку, открывается целевая диаграмма; на вкладке имени диаграммы есть маленькая стрелка, которая при двойном щелчке по ней возвращает вас к исходной диаграмме (), закрывая связанную диаграмму
Учить больше
Схема атома— Вселенная сегодня
[/ caption] Изображение слева представляет собой базовую атомную диаграмму.На этом изображены протоны, нейтроны и электроны атома углерода. Каждый находится в группе по шесть человек. Это делает атом очень стабильным. На протяжении многих лет существовало много атомных моделей, но сейчас они широко считаются надежной базовой версией. Атомные диаграммы были разработаны для объяснения взаимодействия элементов Земли и космоса задолго до того, как атомы можно было наблюдать. В настоящее время ученые могут видеть частицы размером меньше атома. Эти субатомные частицы составляют основу физики элементарных частиц.
Ученые веками использовали атомные диаграммы для объяснения устройства мира. Древние греки, а до них китайцы и вавилоняне верили, что существуют невидимые силы, позволяющие соединять определенные металлы и работать на благо человека. Они этого не знали, но это был просто нагретый металл, обменивающийся субатомными частицами, чтобы стать новым металлом.
Основы химии лучше всего объясняют атом. В нем говорится, что фундаментальным строительным блоком материи является атом.Атом состоит из трех основных частей: протонов, нейтронов и электронов. Протоны имеют положительный электрический заряд. У нейтронов нет электрического заряда. Электроны имеют отрицательный электрический заряд. Протоны и нейтроны находятся вместе в так называемом ядре атома. Электроны вращаются вокруг ядра. Химические реакции включают взаимодействие между электронами одного атома и электронами другого атома. Атомы, которые имеют разное количество электронов и протонов, имеют положительный или отрицательный электрический заряд и называются ионами.Когда атомы соединяются вместе, они могут образовывать более крупные строительные блоки материи, называемые молекулами. Если бы наука не смоделировала атом, она никогда бы не поняла этот обмен электронами, и мы все еще могли бы застрять в темных веках.
Ранее я упоминал, что было разработано много моделей атомов. Некоторые из них — модель Бора, кубическая модель, модель сливового пудинга, модель Сатурна и модель Резерфорда.
Каждая из этих моделей улучшала другую и приближала науку к совершенной атомной модели.Модели Бора и Резерфорда были разработаны для квантовой механики и использовались в астрономических приложениях. Фактически, улучшение модели Бора, называемое моделью Бора-Саммерфилда, отвечает за некоторые из многих вещей, которые мы теперь знаем о квантовой механике.
Атомная диаграмма постоянно пересматривается, поскольку наука открывает все больше информации о субатомных частицах. Перейдите по этой ссылке, чтобы получить информацию о модели Бора и ее усовершенствованиях. На сайте Universe Today у нас есть две замечательные статьи: одна о протоне, а другая об электронах.Astronomy Cast предлагает хороший эпизод о материи от звезд.
Источники:
Википедия
Справка по химии
Как это:
Нравится Загрузка …
Spider Diagram
Spider Diagram
Паук-диаграмма обеспечивает полное контекстное представление набора элементов и их взаимосвязей. Являясь частью общего набора представлений, эта диаграмма объединяет концепции, представленные на диаграмме ER (отображение взаимосвязей относительно интересующей сущности), с концепциями диаграммы иерархии (показывающей несколько уровней взаимосвязей).В отличие от диаграммы иерархии, каждая сущность представлена один раз и только один раз. Кроме того, представление в произвольной форме не подразумевает искусственно иерархических отношений, которые могут не существовать. В результате получается чрезвычайно мощное представление — ни традиционное, ни SysML — для анализа и коммуникации.
Паук-диаграмма открывается для комбинации элемента и определения иерархии. Элемент определяет начальную точку диаграммы. Определение иерархии указывает отношения (и, возможно, целевые классы), которые необходимо пересечь при построении паучьей диаграммы.Диаграмма будет открываться с количеством уровней, указанным для каждого встречающегося элемента, отображаемого на диаграмме один раз и только один раз. Затем отношения между элементами отображаются в виде соединительных линий.
|
Элементы рисуются на диаграмме только один раз, потенциально представляя несколько взаимосвязей. Если вы выберете узел на диаграмме паука и попросите удалить его, вы удалите все отношения, которые связывают его с элементами на диаграмме.Если вы хотите удалить только одну связь, выберите соответствующую метку и используйте команду «Удалить цель». |
Паук-диаграмма представляет собой диаграмму произвольной формы. Диаграмма поддерживает множество различных вертикальных и горизонтальных макетов, выбираемых из параметров диаграммы или команды компоновки. Переключайтесь между макетами, чтобы выбрать предпочтительную начальную точку, а затем настройте положение узлов по своему желанию. Отдельные узлы можно перемещать в любое место на диаграмме.Кроме того, можно перемещать отдельные метки линий связи. Когда метка отделяется слишком далеко от линии связи, будет нарисована «молния», чтобы автоматически соединить метку с соответствующей линией.
Варианты схем
В дополнение к классическим параметрам диаграммы, настройки паук диаграммы включают:
-
Показать имена взаимосвязей — определяет, отображаются ли имена взаимосвязей (псевдонимы, если они определены) на линиях взаимосвязей, указывающих взаимосвязь между подключенными узлами.Когда цель состоит в том, чтобы просто понять взаимосвязь элементов (но не конкретную природу взаимосвязей), отключение отображения имен взаимосвязей минимизирует беспорядок на диаграмме и повысит удобочитаемость. Обратите внимание, что начальное значение для этого параметра берется из указанного определения иерархии и затем управляется параметром диаграммы.
-
Макет — управляет макетом диаграммы по умолчанию для использования с диаграммой. Доступные варианты макетов диаграмм включают вертикальные деревья, горизонтальные деревья, круговые, радиальные и т. Д.
-
Levels — управляет начальным количеством уровней, отображаемых на диаграмме. Затем отдельные узлы можно по желанию развернуть или свернуть.
Палитра схем
Вкладка «Конструкции» позволяет быстро украсить паук-диаграмму, а вкладка «Все сущности» позволяет связать элементы диаграммы с остальной частью определения системы.
Команды меню диаграммы
Советы и хитрости
- Удерживание элемента управления при двойном щелчке узла — это ярлык для развертывания / свертывания.Если узел свернут, он расширит его на один уровень. Если его развернуть, он свернет узел.
- Добавление элементов в паук-диаграмму лучше всего выполняется путем перетаскивания элементов на узлы из палитры диаграммы для установления требуемых взаимосвязей.
- При отслеживании одного отношения (например, физической иерархии или функциональной иерархии) отключите отображение имен отношений. Семантика ясна, а дополнительный текст может загромождать диаграмму.Если отслеживаются несколько отношений, убедитесь, что опция показывать имена отношений включена, чтобы понять природу каждой связи.
- Как правило, лучше сначала переместить узлы, а затем изменить положение меток по своему усмотрению. В противном случае, когда вы перемещаете узлы, соединительные линии также будут сдвигаться, что может вынудить вас вручную изменить положение метки.
- Благодаря своей природе свободной формы и акценту на сообщении / выделении определенных связей, паук-диаграмма является главным кандидатом на использование способности скрывать определенные узлы.Скрытие узла скроет все отношения, которые связаны с узлом, позволяя аудитории сосредоточиться на других интересующих аспектах.


