Схема калькулятора. Как работает калькулятор: устройство и принцип действия

Как устроен калькулятор изнутри. Из каких компонентов он состоит. Как происходит ввод данных и вывод результатов. Как выполняются арифметические операции. Какие типы калькуляторов существуют.

Основные компоненты калькулятора

Современный электронный калькулятор состоит из следующих основных компонентов:

• Корпус
• Клавиатура
• Дисплей (чаще всего жидкокристаллический)
• Печатная плата с электронными компонентами
• Микропроцессор
• Память (ОЗУ и ПЗУ)
• Источник питания (батарейки или солнечная батарея)

Рассмотрим подробнее, как устроены и взаимодействуют эти компоненты для выполнения вычислений.

Устройство клавиатуры калькулятора

Клавиатура калькулятора предназначена для ввода чисел и команд. Как она устроена?

• Клавиши изготовлены из резины или пластика
• Под каждой клавишей находится контактная площадка
• При нажатии клавиша замыкает контакты на печатной плате
• Микропроцессор определяет, какая клавиша была нажата

Такая конструкция обеспечивает надежный ввод данных и долговечность клавиатуры. Современные калькуляторы могут иметь сенсорные клавиатуры без механических частей.

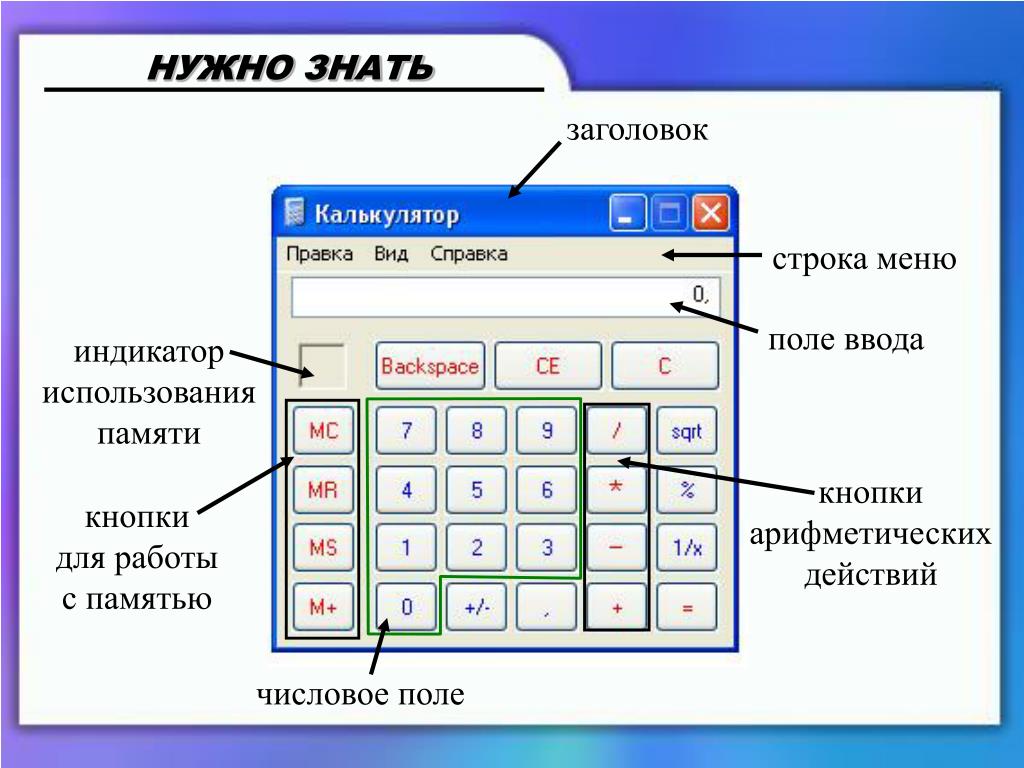
Жидкокристаллический дисплей калькулятора

Для отображения вводимых данных и результатов вычислений в калькуляторах применяются жидкокристаллические дисплеи. Как они работают?

• Дисплей состоит из сегментов в форме цифр и символов
• Каждый сегмент содержит жидкие кристаллы между двумя пластинами
• При подаче напряжения кристаллы меняют поляризацию света
• Это делает сегмент видимым на дисплее
• Микропроцессор управляет отображением нужных сегментов

ЖК-дисплеи обеспечивают контрастное изображение при низком энергопотреблении, что важно для портативных калькуляторов.

Микропроцессор — «мозг» калькулятора

Центральным элементом калькулятора является микропроцессор. Какие функции он выполняет?

• Обрабатывает сигналы от клавиатуры
• Выполняет арифметические и логические операции
• Управляет выводом информации на дисплей
• Обращается к памяти для хранения данных
• Выполняет заложенную в ПЗУ программу работы калькулятора

Микропроцессор калькулятора оптимизирован для быстрого выполнения математических вычислений при низком энергопотреблении.

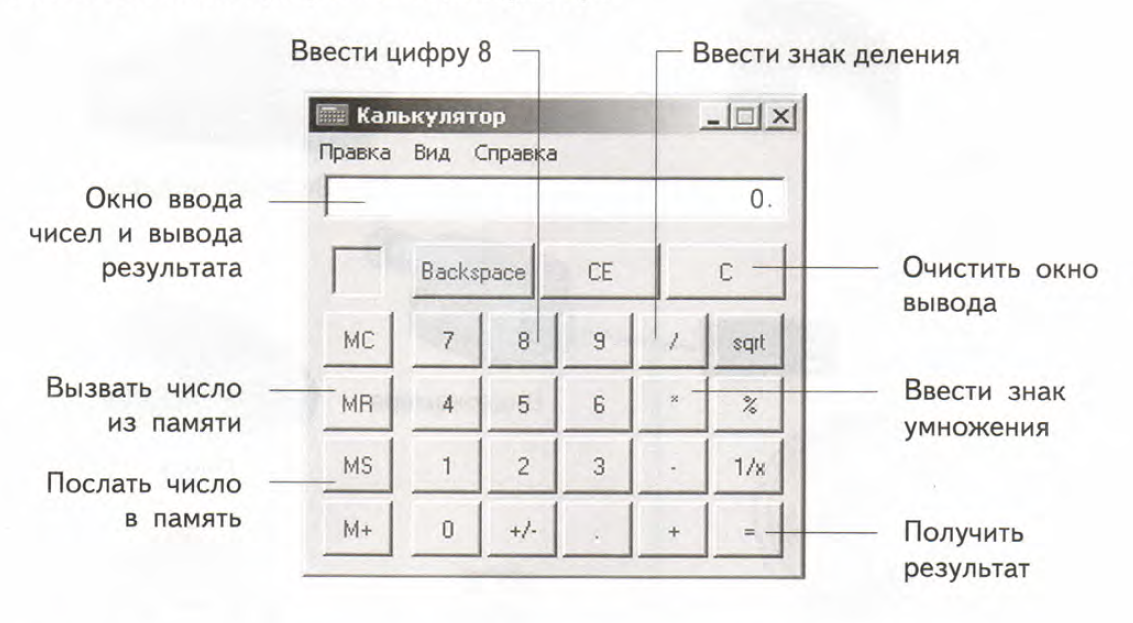
Память калькулятора: ОЗУ и ПЗУ

В калькуляторе используются два типа памяти — оперативная (ОЗУ) и постоянная (ПЗУ). Для чего они нужны?

Оперативная память (ОЗУ):

• Хранит вводимые числа и промежуточные результаты
• Обеспечивает быстрый доступ к данным
• Очищается при выключении питания

Постоянная память (ПЗУ):

• Содержит программу работы калькулятора
• Хранит константы и таблицы для вычислений
• Не теряет данные при отключении питания

Правильная организация работы с памятью обеспечивает быстродействие и функциональность калькулятора.

Выполнение арифметических операций

Как калькулятор выполняет основные математические действия?

• Сложение и вычитание производятся поразрядно, как в столбик
• Умножение выполняется последовательным сложением
• Деление реализуется последовательным вычитанием
• Более сложные функции (корень, логарифм) вычисляются по алгоритмам

Микропроцессор оптимизирован для быстрого выполнения этих базовых операций. Сложные вычисления разбиваются на простые арифметические действия.

Типы калькуляторов

Существует множество разновидностей калькуляторов для различных задач. Какие основные типы можно выделить?

• Простые (базовые арифметические действия)
• Инженерные (научные функции, системы счисления)
• Финансовые (специальные экономические расчеты)
• Графические (построение графиков функций)
• Программируемые (возможность создания программ)

Выбор типа калькулятора зависит от сложности выполняемых расчетов и области применения. Современные смартфоны также имеют функцию калькулятора.

Эволюция калькуляторов

Как развивались калькуляторы с момента появления первых моделей?

• 1960-е: первые настольные электронные калькуляторы
• 1970-е: появление карманных калькуляторов
• 1980-е: научные калькуляторы со сложными функциями
• 1990-е: графические калькуляторы
• 2000-е: интеграция калькуляторов в мобильные устройства

Несмотря на развитие компьютерной техники, отдельные калькуляторы остаются востребованными благодаря удобству, надежности и длительному времени автономной работы.

Энергопотребление и питание калькуляторов

Как обеспечивается питание калькуляторов и от чего зависит их энергопотребление?

• Простые модели работают от батареек или солнечных элементов
• Научные калькуляторы чаще используют сменные батарейки
• ЖК-дисплеи имеют низкое энергопотребление
• Микропроцессоры оптимизированы для экономии энергии
• Время автономной работы может достигать нескольких лет

Низкое энергопотребление — одно из ключевых преимуществ калькуляторов перед универсальными вычислительными устройствами.

Как устроен и работает калькулятор: engineering_ru — LiveJournal

Я обратил внимание, что довольно часто спрашивают, как работает обычный калькулятор. Думал, что в интернете должно быть много статей по этому поводу, но что-то мне ничего дельного не попалось. Википедия, как обычно, слишком мудрит, и я подумал, что будет неплохо, если вкратце опишу принцип его работы.

Существует огромное количество всевозможных моделей калькуляторов. Есть простые, есть сложные. С питанием от солнечных батарей или от сети. Есть обычные, программируемые, бухгалтерские, специализированные модели. Порой, и не найдешь той грани, которая отделяет калькулятор от компьютера.

Я буду описывать работу самой простой модели калькулятора.

Это калькулятор CASIO HS-8LU. Они примерно все работают одинаково. По большому счету, в простых моделях ничего не меняется уже лет тридцать.

Калькулятор состоит из корпуса, клавиатуры с резиновыми кнопками и платы.

В данной модели плата сделана в виде пленки с нанесенными на нее проводниками. Питание — от солнечной батареи. Над солнечной батареей расположен жидкокристаллический индикатор.
На задней крышке корпуса расположены токопроводящие контакты. При нажатии на кнопку она прижимает пленку к задней крышке и происходит электрический контакт. Часто токопроводящий контакт наносят на обратную сторону кнопки. В том случае сама кнопка прижимается к плате для создания контакта.

С обратной стороны под солнечной батареей расположен чип микропроцессора. Он управляет работой калькулятора.

Как работает индикатор на жидких кристаллах.

Жидкие кристаллы — это специальные молекулы, которые при приложении между ними напряжения поворачиваются и меняют поляризацию света.

Это картиночка для одного пиксела цветного ЖКИ, но в монохромных там то же самое, только нет светофильтра.

Спереди и сзади жидких кристаллов ставят так называемый поляризационный фильтр. Он обычный свет преобразует в поляризованный (например, образно говоря, в «вертикальный»).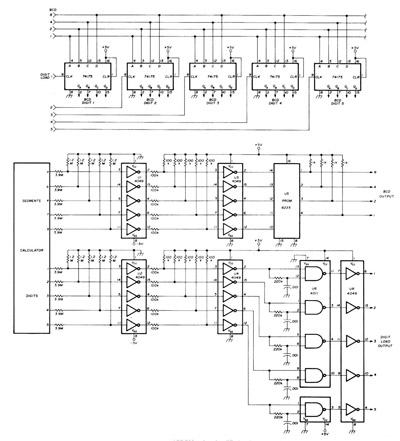 Если напряжение не приложено, то «вертикально» поляризованный свет проходит через жидкие кристаллы, поворачивает плоскость поляризации, отражается от задней поверхности и идет обратно. Мы видим прозрачный экран. На стекле индикатора спереди нарисованы прозрачные токопроводящие линии в форме сегментов цифр, точек или других символов. Сзади также есть токопроводящая область. Когда возникает напряжение между токопроводящими проводниками (спереди и сзади), то между ними жидкие кристаллы поворачиваются и меняют свою плоскость поляризации так, что через задний поляризационный фильтр уже не проходят. Оттого на том сегменте, где есть напряжение между передней и задней поверхностью стекла, возникает невидимая область — сегмент «светится».

Если приглядеться под определенным углом, то в отраженном свете будут видны эти прозрачные проводники.

На самом деле ориентация поляризации не «вертикальная» и «горизонтальная», а «наклоненная» под углом в 45 градусов «вправо» или «влево». Если взять светофильтр и перевернуть вверх ногами, то поляризация будет не «вправо», а «влево». И изначально он будет не пропускать свет, а задерживать.

Для экономии количества один проводник отображает и подведен не к одному сегменту, а к нескольким сразу. Чтобы они не зажигались сразу все, с задней стороны стекла рисуют не один общий проводник, а тоже несколько. Получается, что спереди контакты подведены к нескольким сегментами по вертикали, а с задней стороны по горизонтали. На схеме ниже показана схема индикатора.
Там есть еще такая хитрость, что напряжение нужно прикладывать не постоянное, а переменное (прямоугольные импульсы частотой 20-40 Гц). Иначе деградирует индикатор.

Для простых индикаторов с одним общим проводником импульсы совпадают по фазе, когда не надо отображать сегмент (спереди и сзади разность потенциалов будет одинаковой) и не совпадают по фазе, когда надо отобразить (тогда спереди будет «0», и сзади «1», а через некоторое время полярность поменяется, и будет спереди «1», а сзади — «0», и так далее). В тех индикаторах на общий проводник подается меандр (просто частота), а на отображаемые сегменты — совпадение логического уровня с общим (не горит) и не совпадение (горит).

В индикаторе нашего калькулятора используется три общих проводника. Там все сложнее. Простыми логическими уровнями не обойдешься. Чтобы обеспечить переменное напряжение и отсутствие постоянной составляющей используются уровни напряжений в 1/3 и 2/3 от максимума. В итоге форма импульсов будет ступенчатой. На схеме ниже показаны эпюры таких импульсов.

А теперь самое главное и самое интересное — микросхема процессора.

Это фотографии кристаллов отечественных калькуляторов, сделанных на микросхемах К145ИП7 (слева) и К145ИП11 (справа). Фотографии взяты с интересного сайта «Радиокартинки».

Микропроцессор калькулятора принципом работы очень мало отличается от обычного персонального компьютера с процессором, памятью, клавиатурой и видеокартой.
Если быстро посмотреть на фото кристаллов, то можно примерно поделить на три области: область постоянного запоминающего устройства (ПЗУ) с программной («прошивкой»), область оперативного запоминающего устройства (ОЗУ), где хранятся регистры памяти калькулятора, и остальные цепи процессора, которые включают арифметическо-логическое устройство (АЛУ), драйвер индикатора, драйвер клавиатуры, преобразователи напряжения и другие вспомогательные цепи.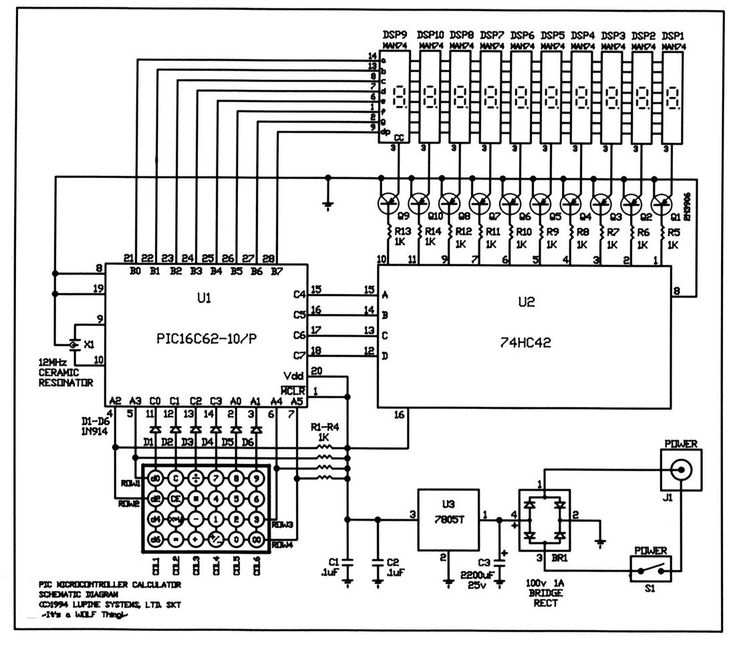

Это структурная схема процессора калькулятора МК-62.
В верхней части мы видим, что есть блоки:
— генератор опорной частоты (ГОЧ), который задает частоту, с которой регенерируется изображение на индикаторе;
— схема удвоения напряжения, умножающая напряжение солнечное батареи на два, чтобы хватило для индикатора;
— генератор, формирователь импульсов общих электродов и регистр-формирователь сегментного кода постоянно выводят заданные для вывода сегменты на индикатор. Там есть специальный регистр памяти, куда микропроцессор записывает информацию, какие надо отображать сегменты, а какие не надо. После этого процессор не отвлекается на отображение, и эти блоки выводят все сами;
— ОЗУ с регистрами данных и ПЗУ с прошивкой;
— и узел с процессором, состоящим из АЛУ с обвязкой. Счетчик адреса АЛУ выбирает очередное слово программы из ПЗУ. Разрядность этого слова может быть разной в разных калькуляторах. Отдельные биты в слове определяют работу АЛУ: например, сложить два 4-х битных числа из регистров, или считать из ОЗУ цифру, или сравнить два числа, или сдвинуть на один разряд и т.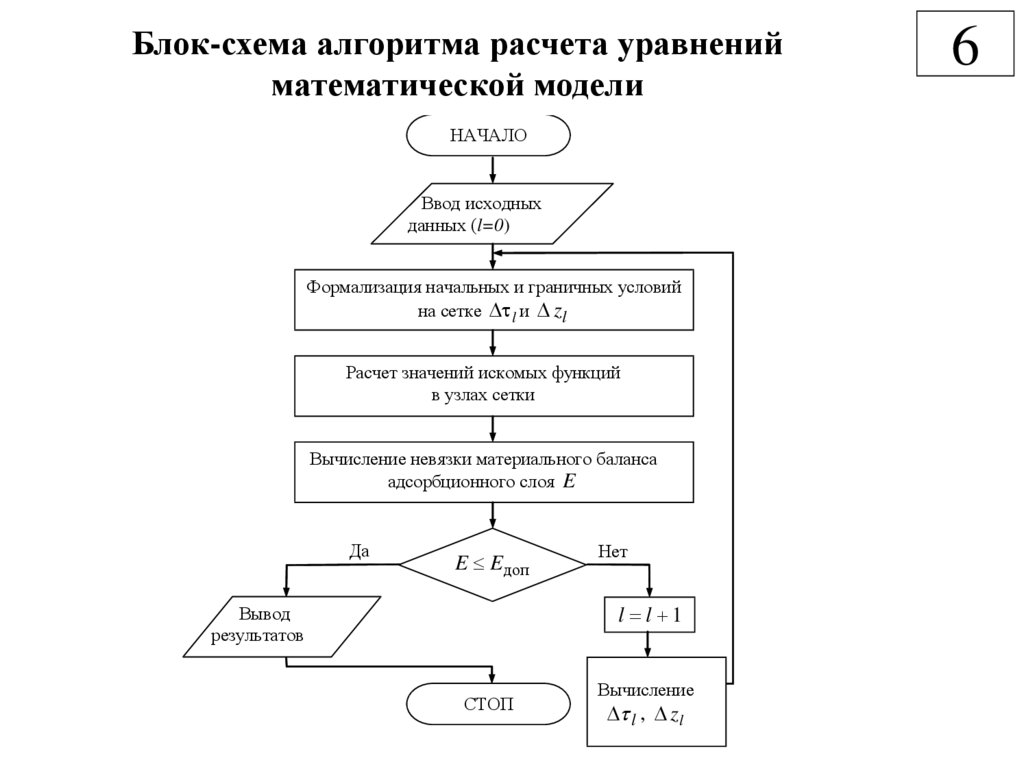 д.

Как работает микропроцессор.

Сначала срабатывает сброс по питанию. При подаче электричества специальный узел заставляет программу работать с начального адреса. Команда за командой извлекается из ПЗУ и исполняется. Вначале происходит обнуление регистров, формирование числа «0.», сброс всяких признаков переполнения, операций и прочее. После сброса программа ожидает события от клавиатуры (нажатие кнопки).
Когда нажата кнопка, то процессор через некоторое время еще раз опрашивает клавиатуру, чтобы подавить дребезг кнопок (когда из-за плохого контакта может произойти одновременно несколько нажатий).
А дальше, в зависимости от предыдущих состояний, он по программе определяет, что с этим нажатием делать. Например, если идет ввод числа и введена цифра, то продолжить ввод. Если нажата кнопка операции, то выполнить операцию.
Сам алгоритм и логика выполнения операций целиком лежит на ПЗУ и программистах, которые писали прошивки.
Что интересно, все простые операции выполняются так, как их учат в школе.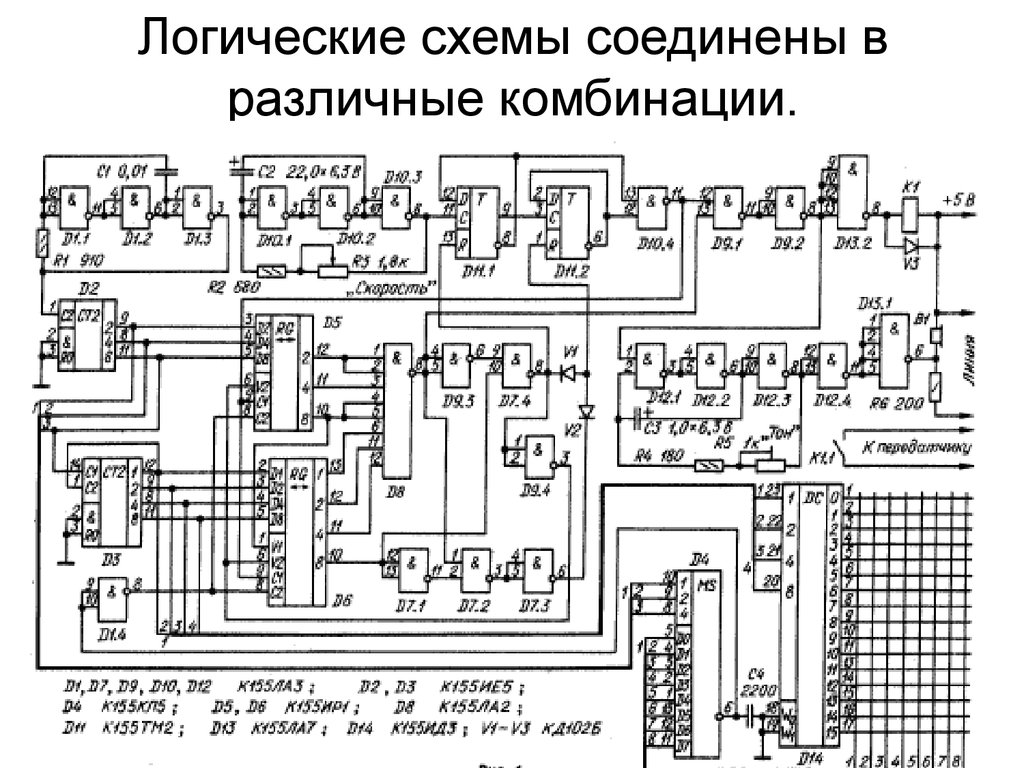
— сложение и вычитание. В столбик. Выравниваются порядки двух введенных чисел и происходит сложение или вычитание.
— умножение и деление. Так же в столбик. Разряд за разрядом. Сначала последовательным сложением умножают на младшую цифру множителя, затем вторую и так далее до старшей. Деление — последовательным вычитанием.
После выполнения операции отдельная подпрограмма нормализует результат: отбрасывает незначащие нули и сдвигает его вправо.
Если в калькуляторе есть тригонометрические функции, то они также выполняются, как их запрограммировал программист. Есть разные способы вычисления элементарных функций: разложение в ряд Тейлора или по методу «Cordic».

Вот примерно так работает калькулятор.

Я вам дам ссылку на несколько сайтов. В одном вы можете еще прочитать про то, как они работают: http://datamath.org/Story/Intel.htm#The.

А еще две ссылки — очень познавательный интерактивный сайт, где обратным реверсом считали прошивку и сделали симулятор. Там можно «прогнать» работу процессора реального калькулятора.
http://files.righto.com/calculator/TI_calculator_simulator.html и
http://files.righto.com/calculator/sinclair_scientific_simulator.html.

А также заходите в мой музей, где я собираю советскую цифровую электронику: http://www.leningrad.su/museum/

Вот, наверно, и все. Надеюсь, я вас не сильно утомил. 🙂

8.4) Создание калькулятора — Разные уроки по Программированию

Для создания любой программы нужно определить границы решаемой задачи. По этому определим для работы нашей программы седеющий круг задач. Описание работы простого калькулятора:  Описание алгоритма на естественном языке 1) Пользователь вводит 1 число сохраняем его в переменную A  2) Пользователь вводит действие в виде символов +  (сложение) —  (вычитание) *  (умножение) /  (деление) 3) Запоминаем команду в строковую переменную Moushen (действие) 4) Пользователь вводит 2 число сохраняем его в переменную B 5) Проверяем какое действие выполнить на основе выбора пользователя Если Moushen=сложение то выполняем C=A+B Если Moushen=вычитание то выполняем C=A-B Если Moushen=умножение то выполняем C=A*B Если Moushen=деление то выполняем проверку можем ли мы делить вообще: Если B = 0 выводим сообщение об ошибке Если B <>0 то производим деление C=A/B 6) Выводим результат операции на экран. 7) Спрашиваем закончил пользователь или нет          если да то выходим из программы         если нет то считаем следующее число  Блок схема     Для создания простого калькулятора воспользуемся стандартным консольным приложением в котором будем спрашивать пользователя и выводить ему результат работы на экран.  Для этого запустим Embarcadero Rad Studio XE 3     Создаем новый  консольный проект для этого выполняем следующие действия.      Выбираем пункт меню File -> New -> Other…      Далее выбираем язык программирования и ярлык консольного приложения      В мастере создания проекта просто нажимаем OK       Создается шаблон проекта все что написала среда разработки нужно оставлять так как есть     Для того чтобы вывести сообщение пользователю нужно как то вывести данные в консоль для этого подключим библиотеку Iostream. h на нашему проекту.     После отключения нам станут доступны следующие функции.      1) Функция вывода данных в консоль           cout (console out — консольный вывод) — данная функция позволяет вывести содержимое любой переменной на экран консоли     пример 1 :     Выводим на экран содержимое переменной а     пример 2 :     Выводим на экран текст например слово privet         пример 3 :    когда нужно перенести текст на новую строчку нужно вывести на экран символ переноса строки \n          2) Функция получения данных с клавиатуры:     cin (console input — консольный ввод) — данная функция позволяет записать из клавиатуры значение переменной     Пример 1:     Запись числа в переменную а и вывод его на экран         пример 2 :     Ввод пользователем символа клавиатуры и вывод его на экран     пример 3 :      Ввод нескольких символов с клавиатуры и вывод их на экран, особенность данного подхода в том что символы вводить нужно без пробела так как cin читает данные до пробела.          Задание: Реализовать консольный калькулятор. Решение. 1) Объявляем переменные которые понадобятся для калькулятора 2) Получаем 1 число от пользователя 3) Получаем действие от пользователя 4) Получаем второе число 5) На основе выбора пользователя выполняем операцию с переменными 6) Все считается ура Дополнительные задания: 1) Решить вопрос с дробными делением чисел в калькуляторе. 2) В конце расчетов калькулятор должен спрашивать закончил ли пользователь вычисления если нет то начать работу калькулятора заново. 3) Решить вопрос с делением на 0.

Калькулятор балки онлайн (расчет реакции, изгибающий момент, поперечная сила, осевая сила)

• Расчеты
• Период

Выберите необходимое количество расчетов:

2 расчета 5 расчетов 10 расчетов

Цена: 4. 99$

Выбранный тариф позволяет сделать 2 расчета балок, рам или ферм. Бессрочно.

Выберите нужный период:

1 месяц 3 месяца 12 месяцев

Цена: 39 $

Непродлеваемая подписка. Выбранный тариф позволяет произвести расчет балки, каркаса или фермы за 1 месяц без ограничений по количеству расчетов.

Количество пользователей: 1 (3 IP-адреса в день)

Узнать больше

Куда отправить код доступа ?

Согласитесь с условиями, чтобы продолжить.

Предварительно заполните данные о местоположении в платежной форме по IP-адресу.

Куда был отправлен код доступа ?

Для получения числовых значений диаграмм и подробного текста расчета необходимо Получить код доступа
(пример подробного отчета)

Конструкция рассчитывается с использованием математического аппарата метода конечных элементов. Для получения числовых значений диаграмм и опорных реакций необходимо Получить код доступа

Требуется длина балки!

Калькулятор Moody Chart — EngineerExcel

Что такое Moody Chart

Диаграмма Муди (или диаграмма Муди) — это диаграмма, используемая для расчета падения давления или потери напора из-за трения в потоке по трубе.

В частности, диаграмма Муди используется для определения коэффициента трения для потока в трубе.

Коэффициент трения отображается в зависимости от числа Рейнольдса и относительной шероховатости на диаграмме Муди. Относительная шероховатость определяется как высота шероховатости трубы, ε, деленная на внутренний диаметр, D. Число Рейнольдса, Re, представляет собой отношение эффектов инерционного потока жидкости к эффектам вязкого потока. Число Рейнольдса больше 4000 указывает на турбулентный поток, тогда как число Рейнольдса меньше примерно 2000 указывает на ламинарный поток.

Зная число Рейнольдса и относительную шероховатость, коэффициент трения можно найти по таблице и использовать в уравнении Дарси Вейсбаха для расчета потери давления из-за трения.

Уравнение Дарси Вейсбаха показано ниже:

где:

• Δp = потеря давления [Па]
• L = длина трубы [м]
• fD = коэффициент трения Дарси (или коэффициент трения Дарси Вейсбаха) [безразмерный]
• ρ = плотность жидкости [кг/м3]
• v = средняя скорость жидкости [м/с]
• D = внутренний диаметр трубы (или гидравлический диаметр для некруглых воздуховодов) [м]

Калькулятор Moody Chart: как это работает?

Основное уравнение, которое использовалось для создания диаграммы Муди, может быть решено для получения числового результата для коэффициента трения Дарси.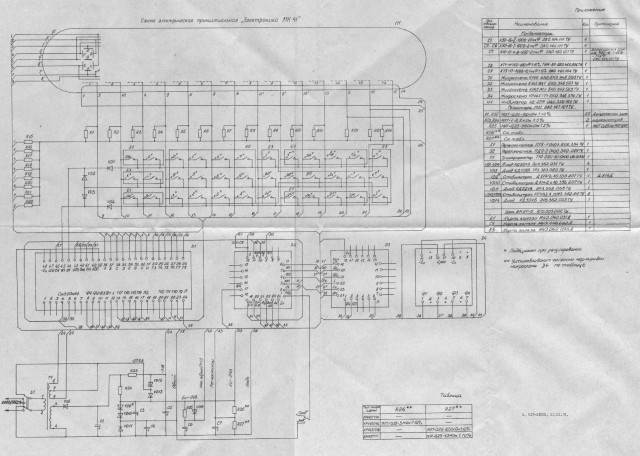

Каждая из кривых на диаграмме Муди представляет собой результат уравнения, описывающего коэффициент трения Дарси как функцию относительной шероховатости и числа Рейнольдса. Это уравнение называется уравнением Коулбрука. Она была решена Льюисом Муди в XIX веке.40 и отображается графически в виде того, что стало известно как диаграмма Муди.

Уравнение Коулбрука-Уайта — это уравнение, которое было создано путем подгонки функции к экспериментальным данным. Это также неявное уравнение, которое нельзя решить напрямую для коэффициента трения. Диаграмма Муди была необходимым инструментом для определения коэффициента трения в то время, когда не было широкого использования графических калькуляторов или электронных таблиц для решения уравнения Коулбрука.

В последние годы было предложено несколько альтернативных уравнений, связывающих коэффициент трения с относительной шероховатостью и диаметром, например уравнение Хааланда и уравнение Свами-Джейна.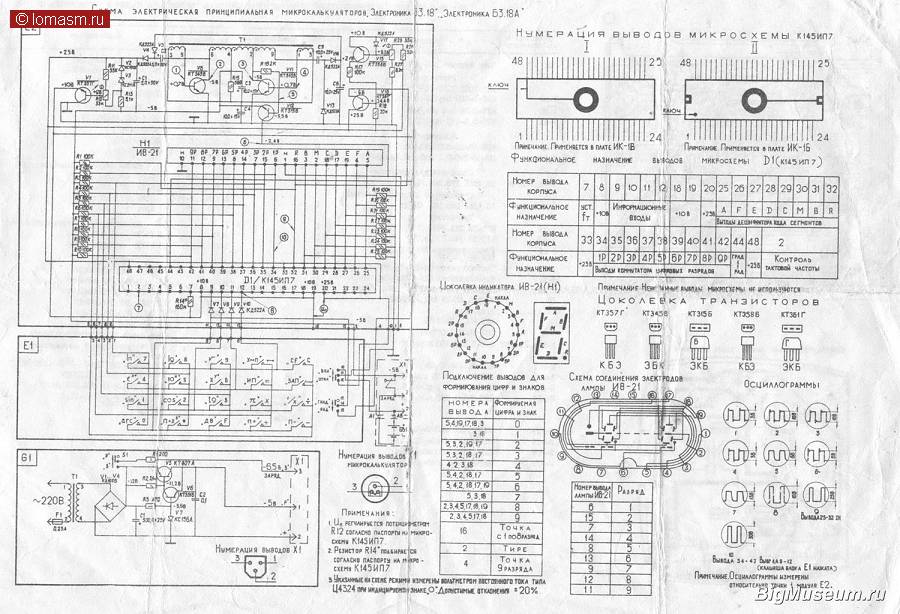 Эти явные приближения можно использовать для непосредственного решения f. Калькулятор Moody выше использует уравнение Хааланда.

Как читать диаграмму Муди

Первым шагом в чтении диаграммы Муди является расчет относительной шероховатости стенки трубы. Относительная шероховатость представляет собой безразмерное отношение высоты шероховатости ε к внутреннему диаметру трубы D. относительная шероховатость рассчитана, найдите ближайшую кривую постоянной относительной шероховатости от правой оси диаграммы Муди. Если относительная шероховатость находится между двумя кривыми, может потребоваться интерполяция.

Затем рассчитайте число Рейнольдса для потока. Число Рейнольдса рассчитывается по следующему уравнению:

где

• ρ = плотность жидкости
• v = средняя скорость жидкости
• D = внутренний диаметр трубы
• µ = динамическая вязкость жидкости

Далее найдите точку пересечения кривой относительной шероховатости с рассчитанным числом Рейнольдса.

Наконец, определите коэффициент трения, проведя горизонтальную линию от точки пересечения кривой и числа Рейнольдса до левой оси. Вам может понадобиться оценить значение коэффициента трения, если пересечение находится между двумя коэффициентами трения на правой оси.

Точность оценки коэффициента трения по диаграмме Муди зависит от двух факторов:

1. Возможность интерполяции значений между кривыми относительной шероховатости.
2. Точность значения высоты шероховатости.

При внимательном использовании диаграммы Муди или калькулятора диаграммы Муди вы можете устранить ошибку, связанную с номером 1 выше.