Как работает неинвертирующий усилитель на ОУ. Каковы его основные характеристики и преимущества. Какова формула для расчета коэффициента усиления. Чем отличается от инвертирующего усилителя. Как рассчитать входное и выходное сопротивление.
Принцип работы неинвертирующего усилителя
Неинвертирующий усилитель на операционном усилителе (ОУ) — это базовая схема аналоговой электроники, которая усиливает входной сигнал без его инверсии. Основные особенности этой схемы:
- Входной сигнал подается на неинвертирующий вход ОУ
- Используется отрицательная обратная связь
- Выходной сигнал совпадает по фазе с входным
- Коэффициент усиления всегда больше единицы
Рассмотрим принцип работы неинвертирующего усилителя на примере простейшей схемы:
Схема неинвертирующего усилителя на ОУ
Типовая схема неинвертирующего усилителя выглядит следующим образом:
«` «`Ключевые элементы схемы:
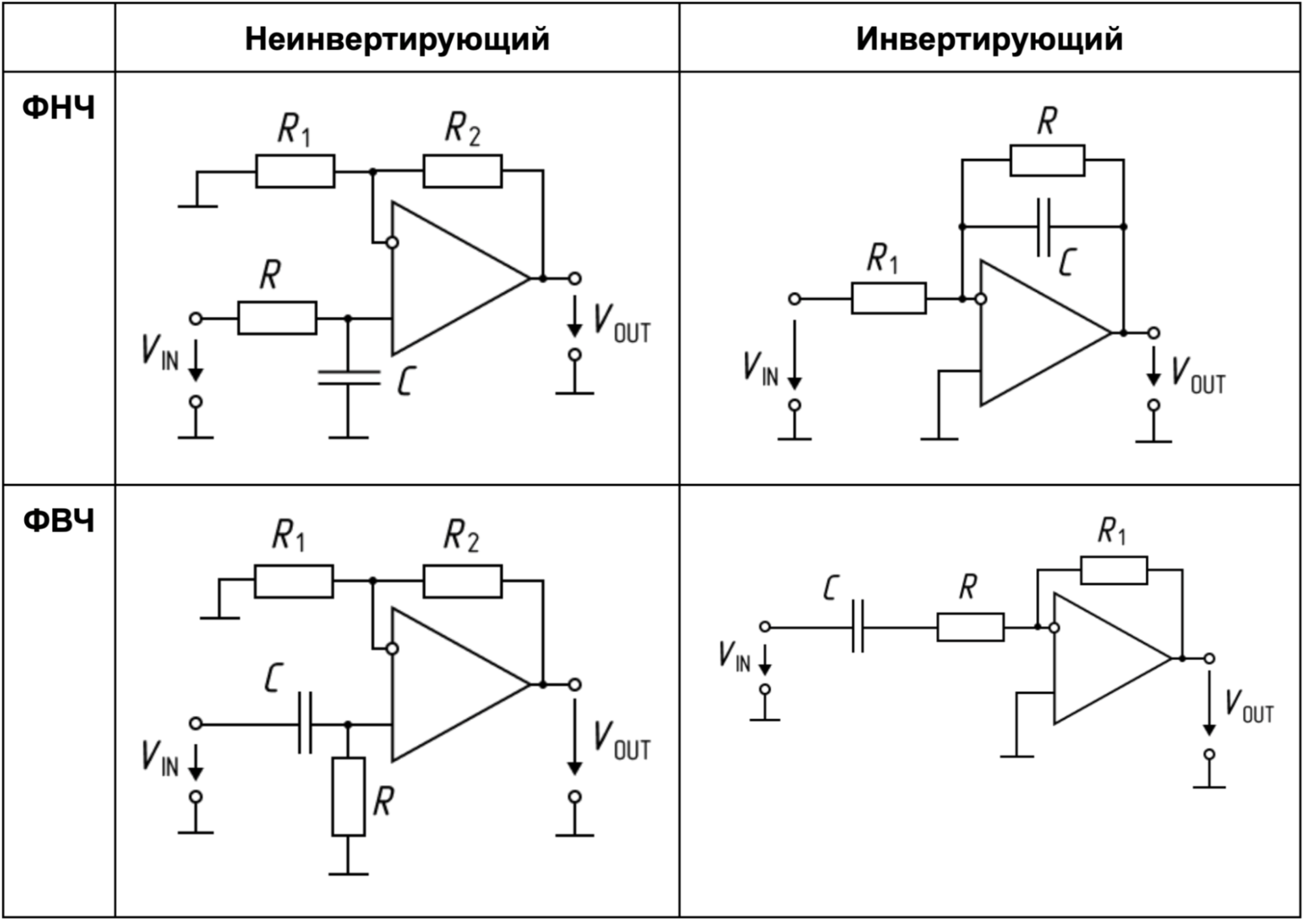
- ОУ — операционный усилитель
- Uвх — входное напряжение
- Uвых — выходное напряжение
- R1, R2 — резисторы цепи обратной связи
Как работает неинвертирующий усилитель
Принцип работы неинвертирующего усилителя основан на следующих свойствах идеального ОУ:
- Бесконечно большое входное сопротивление
- Нулевое выходное сопротивление
- Бесконечно большой коэффициент усиления
Основные этапы работы:
- Входной сигнал Uвх подается на неинвертирующий вход ОУ
- На инвертирующий вход через делитель R1-R2 подается часть выходного сигнала
- ОУ стремится уравнять напряжения на входах, усиливая сигнал
- Устанавливается равновесие, при котором Uвых = Uвх * (1 + R2/R1)
Формула коэффициента усиления
Коэффициент усиления неинвертирующего усилителя определяется отношением резисторов обратной связи:
K = 1 + R2 / R1
где:
- K — коэффициент усиления
- R1, R2 — сопротивления резисторов обратной связи
Важно отметить, что коэффициент усиления всегда больше единицы. Это означает, что схема всегда усиливает входной сигнал, в отличие от инвертирующего усилителя.
Характеристики неинвертирующего усилителя
Основные характеристики неинвертирующего усилителя:
- Высокое входное сопротивление (теоретически бесконечное)
- Низкое выходное сопротивление
- Коэффициент усиления больше единицы
- Выходной сигнал синфазен с входным
- Полоса пропускания зависит от типа ОУ
Расчет входного сопротивления
Входное сопротивление неинвертирующего усилителя очень высокое и определяется входным сопротивлением ОУ:
Rвх = Rвх.ОУ * (1 + K * β)
где:
- Rвх — входное сопротивление усилителя
- Rвх.ОУ — входное сопротивление ОУ
- K — коэффициент усиления ОУ без обратной связи
- β — коэффициент обратной связи (R1 / (R1 + R2))
На практике входное сопротивление может достигать сотен мегаом.
Расчет выходного сопротивления
Выходное сопротивление неинвертирующего усилителя очень низкое и определяется формулой:
Rвых = Rвых.ОУ / (1 + K * β)
где:
- Rвых — выходное сопротивление усилителя
- Rвых.ОУ — выходное сопротивление ОУ
- K — коэффициент усиления ОУ без обратной связи
- β — коэффициент обратной связи
Обычно выходное сопротивление составляет доли Ома.

Сравнение с инвертирующим усилителем
Основные отличия неинвертирующего усилителя от инвертирующего:
- Выходной сигнал совпадает по фазе с входным
- Коэффициент усиления всегда больше 1
- Очень высокое входное сопротивление
- Наличие синфазного сигнала на входах ОУ
Преимущества неинвертирующего усилителя
Основные достоинства неинвертирующего усилителя:
- Высокое входное сопротивление (не шунтирует источник сигнала)
- Низкое выходное сопротивление (хорошо работает на нагрузку)
- Простота схемы
- Стабильность характеристик
- Возможность получить большое усиление
Применение неинвертирующего усилителя
Благодаря своим характеристикам неинвертирующий усилитель широко применяется:
- В измерительной технике
- В аудиотехнике
- В системах сбора данных
- В активных фильтрах
- В буферных каскадах
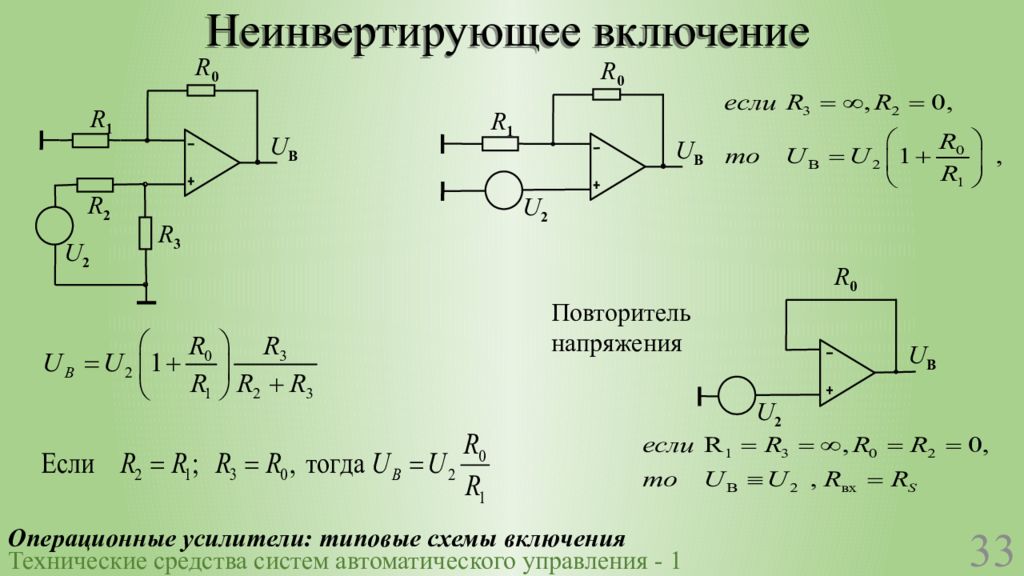
Частным случаем неинвертирующего усилителя является повторитель напряжения
Повторитель напряжения (буферный усилитель) — это частный случай неинвертирующего усилителя с коэффициентом усиления, равным единице. Его схема:
 «`
«`
«`
«`
Особенности повторителя напряжения:
- Коэффициент усиления равен 1
- Очень высокое входное сопротивление
- Очень низкое выходное сопротивление
- Используется для согласования высокоомных источников сигнала с низкоомной нагрузкой
Ограничения неинвертирующего усилителя
При проектировании неинвертирующих усилителей следует учитывать следующие ограничения:
- Ограниченная полоса пропускания на высоких частотах
- Влияние синфазного сигнала на входах ОУ
- Ограничение выходного напряжения напряжением питания ОУ
- Возможность самовозбуждения при большом усилении
Заключение
Неинвертирующий усилитель на ОУ — это мощный и гибкий инструмент аналоговой схемотехники. Его высокое входное сопротивление, низкое выходное сопротивление и возможность получить большое усиление делают его незаменимым во многих приложениях. Понимание принципов работы и основных характеристик этой схемы позволяет эффективно использовать ее в различных электронных устройствах.
Неинвертирующий усилитель на ОУ | Практическая электроника
Схема неинвертирующего усилителя на ОУ
Неинвертирующий усилитель является базовой схемой с ОУ. Выглядит он до боли просто:
В этой схеме сигнал подается на НЕинвертирующий вход ОУ.
Итак, для того, чтобы понять принцип работы этой схемы, запомните самое важное правило, которое используется для анализа схем с ОУ: выходное напряжение ОУ стремится к тому, чтобы разность напряжения между его входами была равна нулю.
Принцип работы неинвертирующего усилителя на ОУ
Итак, давайте инвертирующий вход обозначим, буквой A:
Следуя главному правилу ОУ, получаем, что напряжение на инвертирующем входе равняется входному напряжению: UA=Uвх . UA снимается с делителя напряжения, который образован резисторами R1 и R2. Следовательно:
UA = Uвых R1/(R1+R2)
Так как UA=Uвх , получаем что Uвх = Uвых R1/(R1+R2).
Коэффициент усиления по напряжению высчитывается как KU = Uвых /Uвх.
Подставляем сюда ранее полученные значения и получаем, что KU = 1+R2/R1.
Как работает неинвертирующий усилитель на ОУ на примере
Это также можно легко проверить с помощью программы Proteus. Схема будет выглядеть вот так:
Давайте рассчитаем коэффициент усиления KU. KU = 1+R2/R1=1+90к/10к=10. Значит, наш усилитель должен ровно в 10 раз увеличивать входной сигнал. Давайте проверим, так ли это. Подаем на неинвертирующий вход синусоиду с частотой в 1кГц и смотрим, что имеем на выходе. Для этого нам потребуется виртуальный осциллограф:
Входной сигнал – это желтая осциллограмма, а выходной сигнал – это розовая осциллограмма:
Как вы видите, входной сигнал усилился ровно в 10 раз. Фаза выходного сигнала осталась такой же. Поэтому такой усилитель называют НЕинвертирующим.
Но, как говорится, есть одно “НО”. На самом же деле в реальном ОУ имеются конструктивные недостатки. Так как Proteus старается эмулировать компоненты, приближенные к реальным, давайте рассмотрим амплитудно-частотную характеристику (АЧХ), а также фазо-частотную характеристику (ФЧХ) нашего операционника LM358.
АЧХ и ФЧХ неинвертирующего усилителя на LM358
На практике, для того, чтобы снять АЧХ, нам надо на вход нашего усилителя подать частоту от 0 Герц и до какого-то конечного значения, а на выходе в это время следить за изменением амплитуды сигнала. В Proteus все это делается с помощью функции Frequency Responce:
По оси Y у нас коэффициент усиления, а по оси Х – частота. Как вы могли заметить, коэффициент усиления почти не изменялся до частоты 10 кГц, потом стал стремительно падать с ростом частоты. На частоте в 1МегаГерц коэффициент усиления был равен единице. Этот параметр в ОУ называется частотой единичного усиления и обозначается как f1. То есть по сути на этой частоте усилитель не усиливает сигнал. Что подали на вход, то и вышло на выходе.
[quads id=1]
В проектировании усилителей важен такой параметр, как граничная частота среза fгр . Для того, чтобы ее вычислить, нам надо знать коэффициент усиления на частоте Kгр:
Kгр= KUo / √2 либо = KUo х 0,707 , где KUo – это коэффициент усиления на частоте в 0 Герц (постоянный ток).
Kгр = 10 х 0,707 = 7,07
Теперь проводим горизонтальную линию на уровне 7,07 и смотрим пересечение с графиком. У меня получилось около 104 кГц. Строить усилитель с частотой среза, более, чем fгр не имеет смысла, так как в этом случае выходной сигнал усилителя будет сильно затухать.
Также очень просто определить граничную частоту, если построить график в децибелах. Граничная частота будет находиться на уровне KUo-3dB. То есть в нашем случае на уровне в 17dB. Как вы видите, в этом случае мы также получили частоту среза в 104 кГц.
Ну ладно, с частотой среза вроде бы разобрались. Теперь нам важен такой параметр, как ФЧХ. В нашем случае мы вроде бы как получили НЕинвертирующий усилитель. То есть сдвиг фаз между входным и выходным сигналом должен быть равен нулю. Но как поведет себя усилитель на высоких частотах (ВЧ)?
Берем такой же диапазон частот от 0 и до 100 МГц и смотрим на ФЧХ:
Как вы видите, до частоты в 1 кГц неинвертирующий усилитель действительно работает как надо. То есть входной и выходной сигнал двигаются синфазно. Но после частоты в 1 кГц, мы видим, что фаза выходного сигнала начинает отставать. На частоте в 100 кГц она уже отстает примерно на 40 градусов.
Для наглядности АЧХ и ФЧХ можно разместить на одном графике:
Также в схемах с неинвертирующим усилителем часто вводят компенсирующий резистор RK .
Он определяется по формуле:
и служит для того, чтобы обеспечить равенство сопротивлений между каждым из входов и землей. Более подробно мы это разберем в следующей статье.
При участии Jeer
Неинвертирующий усилитель на ОУ. Принцип работы
Неинвертирующий усилитель — это, пожалуй, одним из трех самых элементарных схем аналоговой электроники, наряду со схемами инвертирующего усилителя и повторителя напряжения. Он даже проще чем инвертирующий усилитель, поскольку для работы схемы не нужно двухполярное питание.
Блок питания 0…30 В / 3A
Набор для сборки регулируемого блока питания…
Обратите внимание на единицу, содержащуюся в формуле. Это нам говорит о том, что неинвертирующий усилитель всегда имеет усиление больше 1, а это значит, что с помощью такой схемы вы не можете ослабить сигнал.
Чтобы лучше понять, как работает неинвертирующий усилитель, давайте рассмотрим схему на операционном усилителе и подумаем, какое будет напряжение на его выходе.
В первую очередь мы должны подумать о том, какие напряжения присутствуют на обоих входах нашего операционного усилителя. Вспомним первое из правил, которое описывает работу операционного усилителя:
Правило №1 — операционный усилитель оказывает воздействие своим выходом на вход через ООС (отрицательная обратная связь), в результате чего напряжения на обоих входах, как на инвертирующем (-), так и на неинвертирующем (+) выравнивается.
То есть, напряжение на инвертирующем входе составляет 3В. На следующем этапе давайте рассмотрим резистор сопротивлением 10k. Мы знаем, какое напряжение на нем и его сопротивление, а значит, из закона Ома мы можем вычислить какой ток течет через него:
I = U/R = 3В/10k = 300мкА.
Цифровой мультиметр AN8009
Большой ЖК-дисплей с подсветкой, 9999 отсчетов, измерение TrueRMS…
Этот ток, согласно правилу 2, не может быть взят с инвертирующего входа (-), таким образом, он идет с выхода усилителя.
Правило №2 — входы усилителя не потребляют ток
Ток 300мкА протекает также через резистор сопротивлением 20к. Напряжение на нем мы легко вычислим с помощью закона Ома:
U = IR = 300мкА * 20к = 6В
Получается, что это напряжение и есть выходное напряжение усилителя? Не, это не так. Напомним, что резистор 20к на одном из своих выводов имеет напряжение 3В. Обратите внимание, как направлены напряжения на обоих резисторах.
Ток течет в направлении противоположном направлению стрелки, символизирующей точку с более высоким напряжением. Поэтому к рассчитанным 6В нужно добавить еще 3В на входе. В таком случае конечный результат будет 9В.
Стоит отметить, что резисторы R1 и R2 образуют простой делитель напряжения. Помните, что сумма напряжений на отдельных резисторах делителя должно быть равно напряжению, поступающему на делитель — напряжение не может исчезнуть бесследно и возникнуть из ниоткуда.
В заключение мы должны проверить полученный результат с последним правилом:
Правило №3 — напряжения на входах и выходе должны быть в диапазоне между положительным и отрицательным напряжением питания ОУ.
То есть нам необходимо проверить, что рассчитанное нами напряжение можно получить реально. Часто начинающие думают, что усилитель работает как «Perpetuum Mobile», и вырабатывает напряжение из ничего. Но надо помнить, что для работы усилителя также нужно питание.
Классические усилители работают от напряжения -15В и +15В. В такой ситуации расчетные нами 9В являются реальным напряжением, поскольку 9В находится в диапазоне питающего напряжения. Однако современные усилители часто работают с напряжением от 5В или еще ниже. В такой ситуации нет никаких шансов, чтобы усилитель выдал на выходе 9В.
Поэтому при разработке схем необходимо всегда помнить, что теоретические расчеты всегда должны сверяться с реальностью и физическими возможностями компонентов.
Неинвертирующий усилитель
В схеме инвертирующего усилителя рис. 1.5 резисторы R1 и R2 образуют делитель, через который протекает одинаковый токИсходя из этого к инвертирующему входу ОУ приложено напряжение:
Рисунок 1.1 — Неинвертирующий усилитель
Однако, как уже отмечалось, за счет отрицательной обратной связи потенциалы инвертирующего и неинвертирующего входов будут примерно равными, т.е.
Отсюда коэффициент усиления неинвертирующего усилителя:
В отличие от инвертирующего усилителя входное сопротивление неинвертирующего усилителя определяется входным дифференциальным сопротивлением ОУ и можно считать, что
(Например, у усилителей с МОП транзисторами на входе Ом. Выходное сопротивление составляет несколько десятков-сотен Ом. Сумма сопротивлений (R1 +R2) должна быть такой, чтобы общий максимальный ток нагрузки ОУ с учетом этого сопротивления не превышал допустимого значения.
Рисунок 1.2 — Повторитель напряжения
На рис. 1.2 приведена схема неинвертирующего усилителя со 100% отрицательной обратной связью. При подаче напряжения на вход, за счет обратной связи выходное напряжение будет изменяться до тех пор, пока потенциалы инвертирующего и неинвертирующего входов не сравняются (считаем ), т.е выходное напряжение окажется приблизительно равным входному. Таким образом коэффициент усиления схемы рис. 6.7
В силу этого схема рис. 1.2 называется повторителем, так как сигнал на выходе имеет ту же амплитуду и фазу , что и входной. Повторитель часто используется в качестве буферного каскада.
При необходимости усиливать переменный сигнал можно использовать схему рис. 1.3. Для входного тока (очень небольшого) в схеме предусмотрено заземление неинвертирующего входа через резистор R. RC-цепь образует фильтр высоких частот, поэтому постоянная времени должна выбираться исходя из требуемой нижней граничной частоты пропускания усилителя.
Рисунок 1.3 – Усилитель переменного напряжения
4.05. Неинвертирующий усилитель
Операционные усилители
Основные схемы включения операционных усилителей
Рассмотрим схему на рис. 4.5. Анализ ее крайне прост: UA = Uвх. Напряжение UA снимается с делителя напряжения: UA = UвыхR1/(R1 + R2). Если UA = Uвх, то коэффициент усиления = Uвых/Uвх = 1 + R2/R1. Это неинвертирующий усилитель. В приближении, которым мы воспользуемся, входной импеданс этого усилителя бесконечен (для ОУ типа 411 он составляет 1012 Ом и больше, для ОУ на биполярных транзисторах обычно превышает 108 Ом). Выходной импеданс, как и в предыдущем случае, равен долям ома. Если, как в случае с инвертирующим усилителем, мы внимательно рассмотрим поведение схемы при изменении напряжения на входах, то увидим, что она работает, как обещано.
Рис. 4.5.
Эта схема также представляет собой усилитель постоянного тока. Если источник сигнала и усилитель связаны между собой по переменному току, то для входного тока (очень небольшого по величине) нужно предусмотреть заземление, как показано на рис. 4.6. Для представленных на схеме величин компонентов коэффициент усиления по напряжению равен 10, а точке — 3 дБ соответствует частота 16 Гц.
Рис. 4.6.
Усилитель переменного тока. Если усиливаются только сигналы переменного тока, то можно уменьшить коэффициент усиления для сигналов постоянного тока до единицы, особенно если усилитель обладает большим коэффициентом усиления по напряжению. Это позволяет уменьшить влияние всегда существующего конечного «приведенного ко входу напряжения сдвига». Для схемы, представленной на рис. 4.7, точке — 3 дБ соответствует частота 17 Гц; на этой частоте импеданс конденсатора равен 2,0 кОм. Обратите внимание, что конденсатор должен быть большим. Если для построения усилителя переменного тока использовать неинвертирующий усилитель с большим усилением, то конденсатор может оказаться чрезмерно большим. В этом случае лучше обойтись без конденсатора и настроить напряжение сдвига так, чтобы оно было равно нулю (этот вопрос мы рассмотрим позже в разд. 4.12). Можно воспользоваться другим методом — увеличить сопротивления резисторов R1 и R2 и использовать Т-образную схему делителя (разд. 4.18).
Несмотря на высокий входной импеданс, к которому всегда стремятся разработчики, схеме неинвертируюпдего усилите тя не всегда отдают предпочтение перед схемой инвертирующего усилителя. Как мы увидим в дальнейшем, инвертирующий усилитель не предъявляет столь высоких требований к ОУ и, следовательно, обладает несколько лучшими характеристиками. Кроме того, благодаря мнимому заземлению удобно комбинировать сигналы без их взаимного влияния друг на друга. И наконец, если рассматриваемая схема подключена к выходу (стабильному) другого ОУ, то величина входного импеданса для вас безразлична — это может быть 10 кОм или бесконечность, так как в любом случае предыдущий каскад будет выполнять свои функции по отношению к последующему.
Рис. 4.7.
Калейдоскоп схем на операционных усилителях
Неинвертирующий усилитель-TINA и TINACloud Resources
Неинвертирующий усилитель
Операционный усилитель может быть настроен на создание инвертированного или неинвертированного выхода. В предыдущем разделе мы проанализировали инвертирующий усилитель. Теперь мы повторим анализ для неинвертирующего усилителя, как показано на рисунке (5).
Рисунок 5 — Неинвертирующий усилитель
Мы анализируем это, используя основные свойства идеального операционного усилителя. Так как ток через R1 ноль,
(18)
Написание уравнения узла на v– выходы узла,
(19)
Мы установили v+ = V–и заменить v– чтобы получить,
(20)
Неинвертирующий коэффициент усиления определяется как
(21)
Мы проанализировали инвертирующие операционные усилители с несколькими входами в предыдущем разделе («Инвертирующий усилитель»). Теперь мы проанализируем неинвертирующие операционные усилители с несколькими входами.
Рисунок 6 — Два неинвертирующих входа
На рисунке (6) показана схема с двумя входными напряжениями. Найти v+, мы применяем текущий закон Кирхгофа к неинвертирующей входной клемме, чтобы получить (напомним, что входной ток для операционного усилителя равен нулю),
(22)
Решая тогда для v+, мы получаем
(23)
Инвертирующее напряжение, v–, находится из уравнения узла в v– с результатом,
(24)
настройка v+ равно v–, мы получаем
(25)
ЗАЯВЛЕНИЕПроанализируйте следующую схему с помощью моделирования схем с помощью TINACloud, чтобы определить Vвне с точки зрения входного напряжения, нажав на ссылку ниже.
1-Два Неинвертирующих Моделирование Цепей Входов
В практическом смысле важно кратко рассмотреть последствия погрузка на ОУ. Метод, который мы использовали для анализа, дает правильный коэффициент усиления напряжения, основанный на предположении, что ток, требуемый от зависимого источника идеальный Модель операционного усилителя находится в пределах диапазона, указанного в спецификации производителя для реальный ОУ. Хотя мы рассмотрим практические соображения в последующих главах, следующие два примера иллюстрируют эту концепцию.
При анализе как инвертирующей, так и неинвертирующей конфигурации мы должны быть уверены, что операционный усилитель способен подавать достаточный ток для управления нагрузочным резистором.
ПРИМЕНЕНИЕПроанализируйте следующие схемы с помощью онлайн-симулятора схем TINACloud, чтобы определить Vвне с точки зрения входного напряжения, нажав на ссылки ниже.
9.2. Неинвертирующий усилитель
Рассмотрим идеализированный неинвертирующий усилитель, когда на его вход подано, например, положительное напряжение (рис. 9.6). Так как дифференциальное напряжение на входе ОУ пренебрежимо мало, то инвертирующий вход также имеет потенциал Eвх, т. е. VA=Eвх. Следовательно, ток через сопротивление R1 равен IR1*=Eвх/R1, а его направление зависит от полярности этого сигнала.
Вследствие бесконечно большого (по предположению) входного сопротивления ОУ ток через сопротивлениеRо.спо величине и по направлению совпадает с током IR1*.
Выходное напряжение определяется суммой падений напряжений на сопротивлениях R1 и Rо.с.
Тогда коэффициент усиления идеализированного неинвертирующего усилителя К*=1+Rо.с/R1. В этом усилителе полярность выходного и входного сигналов всегда совпадает (отсюда и название усилителя—неинвертирующий).
Выходное сопротивление рассматриваемого усилителя равно нулю, а входное (в отличие от аналогичного параметра инвертирующего усилителя) определяется входным сопротивлением ОУ и, следовательно, является достаточно большим.
Если учесть, что коэффициент усиления ОУ конечен, то коэффициент усиления неинвертирующего усилителя примет вид (выражение для него получили ранее в разделе 8.3)
К=К0(1+К0), (9.12)
где =R1/(Rо.с+R1)—коэффициент обратной связи. Если К0>>1, то К=К*=1+Rо.c/R1. Относительная погрешность расчета коэффициента усиления усилителя по формуле (9.12) совпадает с аналогичной в случае инвертирующего усилителя.
Определим входное сопротивление неинвертирующего усилителя с учетом конечного коэффициента усиления ОУ и его входного сопротивления Rд (рис.9.7). Для входной цепи справедливо:
,
Решив совместно эти уравнения, входное сопротивление неинвертирующего усилителя получим в виде
где К* — коэффициент усиления идеализированного усилителя. Видно, что входное сопротивление неинвертирующего усилителя весьма велико.
Сопротивление Rо.с включено для компенсации ошибок за счет входного тока ОУ. Его величина находится из (9.4). Погрешность неинвертирующего усилителя, вызванная разностным входным током и температурным дрейфом, определяется теми же формулами (9.5) и (9.3), что и инвертирующего усилителя.
В отличие от последнего на входах неинвертирующего усилителя имеется синфазный сигнал. Ошибка, создаваемая им на выходе усилителя,
Uвых= КсЕс =(К0Ес)/Мс
Расчет неинвертирующего усилителя подобен расчету инвертирующего усилителя. Отличие состоит лишь в определении величины R1. В инвертирующем усилителе сопротивление R1 выбиралось исходя из требуемого входного сопротивления. Здесь же его значение находится несколько из других соображений. Как кажется на первый взгляд, величина сопротивления R1 (как и Rо.с.) зависит только от требуемого коэффициента усиления. Однако до сих пор не учитывался такой параметр ОУ, как эквивалентное шумовое напряжение, которое усиливается схемой так же, как и напряжение сдвига, создавая на выходе усилителя нежелательный шум:
Здесь еш — эквивалентное шумовое напряжение, которое при малых значениях R1 постоянно и является параметром ОУ. При больших значениях R1(R1>20 к0м) напряжение шумов возрастает прямо пропорционально R1, т. е. эквивалентное шумовое напряжение сопротивления R1 становится больше аналогичного параметра ОУ. Поэтому, исходя из требования минимального шума, сопротивление R1 целесообразно выбирать небольшим (R1~10 к0м). Для уменьшения на высоких частотах коэффициента усиления по шумам сопротивление Rо.с.часто шунтируют конденсатором малой емкости (С =3пФ).
Благодаря высокому входному и низкому выходному сопротивлениям неинвертирующий усилитель часто используют в качестве измерительного усилителя.
Широкое применение получил так называемый повторитель напряжения (рис. 9.8). Его коэффициент усиления равен единице, входное сопротивление велико, а выходное мало. Повторитель обычно включают между источником сигнала и нагрузкой с целью исключения влияния сопротивления нагрузки на выходное напряжение источника, имеющего сравнимое с нагрузкой внутреннее сопротивление. На рис. 9.9 приведена схема неинвертирующего усилителя переменного напряжения. Можно также реализовать схему неинвертирующего сумматора, например, на два входа (рис. 9.10). Потенциал точки Б, который далее усиливается схемой с коэффициентом усиленияК*=1+Rо.с/R1=2, определяется лишь цепью е1 — R — R — Е2 : Vв=(Е1+Е2)/2. Соответстренно выходное напряжение Uвых=КVв =Е1+Е2..
Неинвертирующий усилитель на основе операционного усилителя
Рассмотрим схему неинвертирующего усилителя (
рис. 2.27), где имеет место последовательная отрицательная связь по напряжению.
Вначале выполним анализ схемы, используя принятые допущения, а затем выполним анализ на основе выражений, полученных для усилителя с указанной обратной связью.
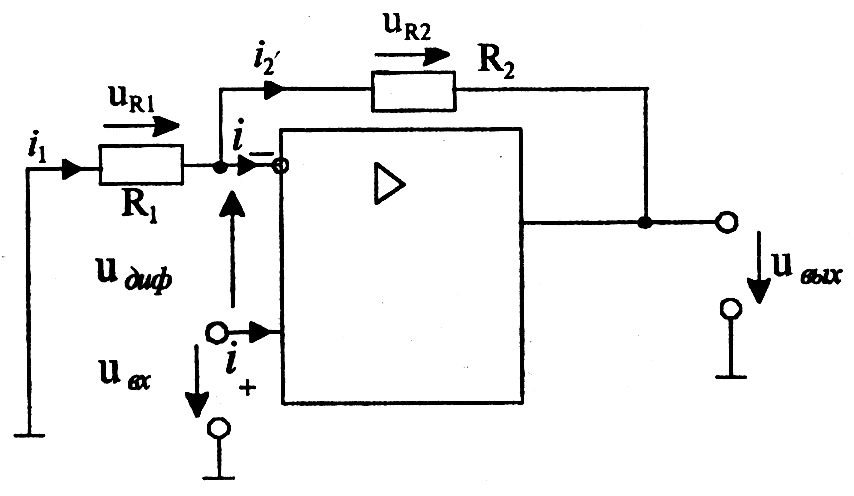
В соответствии с ранее принятыми допущениями входные токи ОУ равны нулю, т. е. i− = i+ = 0 и, следовательно, i1 = i2.
Предположим, что операционный усилитель работает в режиме усиления, тогда u диф = 0. На основании второго закона Кирхгофа получаем
uR 1 = − u вх uR 2 = u вх − u вых
Далее имеем следующие выражения:
i 1 · R 1 = − u вх i2 · R2 = u вх − u вых i1 = − u вх / R1 2 = u вх − u ых / R2 − u вх / R1 = u вх − u вых / R2 u вх · ( 1 / R1 + 1 / R2 ) = u вых / R2 u вых = u вх · ( R1 + R2 ) / R1 u вых = u вх · ( 1 + R2 / R1 )
Таким образом, неинвертирующий усилитель характеризуется коэффициентом усиления по напряжению
Ки = 1 + R 2 / R 1
Васильев Дмитрий Петрович
Профессор электротехники СПбГПУ
Задать вопрос
Воспользуемся общим выражением для коэффициента усиления усилителя, охваченного последовательной отрицательной обратной связью по напряжению. Предположим, что используется входной сигнал низкой частоты, и поэтому будем использовать вещественные коэффициенты К, β и Ки.ос. В соответствии с общим выражениемКи.ос = К / ( 1 + К · β ) При К → ∞ Ки.ос = 1 / β
Коэффициент β, как можно заметить из рис. 2.27, определяется выражением
β = R 1 / ( R 1 + R 2 )
Таким образом, при К → ∞ Ки.ос = 1 + R 2 / R 1 что совпадает с результатом, полученным на основании используемых допущений.
Пусть, например, R1 = 2 кОм, R2 = 4 кОм и u вх = 2 В. Тогда u вых = 2 · [ 1 + 4 · 103 / ( 2 · 103 ) ] = 6 В
Обратимся к общим выражениям для входного и выходного сопротивлений. Предполагая, что усилитель работает на низкой частоте, используем вещественные сопротивления Rвх, Rвх.ос , Rвых , Rвых.ос . Получаем, что входное сопротивление рассматриваемого усилителя
Rвх.ос = Rвх · [ 1 + К · R 1 / ( R 1+ R 2 ) ] причем при К → ∞ Rвх.ос → ∞ Аналогично Rвых.ос = Rвых / [ 1 + К · R 1 / ( R 1 + R 2 ) ]
Очевидно, при К → ∞ Rвых → 0. Заметим, что полученное выражение совпадает с приведенным выше выражением для усилителя с параллельной отрицательной обратной связью.
На входах операционного усилителя, использующегося в неинвертирующем усилителе, имеется синфазный сигнал, равный напряжению u вх . Это недостаток такого усилителя. В инвертирующем усилителе синфазный сигнал отсутствует.
Конфигурация неинвертирующего операционного усилителя
В этой конфигурации сигнал входного напряжения (V IN ) подается непосредственно на неинвертирующий (+) входной терминал, что означает, что выходное усиление усилителя становится «положительным» по значению в отличие от «инвертирующего» Усилитель », который мы видели в предыдущем уроке, выходное усиление которого имеет отрицательное значение. В результате выходной сигнал «синфазен» входному сигналу.
Управление с обратной связью неинвертирующего операционного усилителя достигается путем подачи небольшой части сигнала выходного напряжения обратно на инвертирующий (-) входной вывод через цепь делителя напряжения Rƒ — R2, что опять же создает отрицательную обратную связь.Эта конфигурация с обратной связью создает схему неинвертирующего усилителя с очень хорошей стабильностью, очень высоким входным сопротивлением, Rin, приближающимся к бесконечности, так как ток не течет на положительный входной контакт (идеальные условия) и низким выходным сопротивлением, Rout, как показано ниже.
Конфигурация неинвертирующего операционного усилителя
В предыдущем руководстве по инвертирующему усилителю мы сказали, что для идеального операционного усилителя «ток не течет на входной терминал» усилителя и что «V1 всегда равно V2».Это произошло потому, что соединение входного сигнала и сигнала обратной связи (V1) имеет одинаковый потенциал.
Другими словами, соединение является суммирующей точкой «виртуальной земли». Из-за этого виртуального узла заземления резисторы Rƒ и R2 образуют простую цепь делителя потенциала на неинвертирующем усилителе, причем коэффициент усиления по напряжению схемы определяется соотношением R2 и Rƒ, как показано ниже.
Схема делителя эквивалентного потенциала
Затем, используя формулу для расчета выходного напряжения сети с делителем потенциала, мы можем вычислить коэффициент усиления по напряжению с обратной связью (A В ) неинвертирующего усилителя следующим образом:
Тогда коэффициент усиления по напряжению с обратной связью неинвертирующего операционного усилителя будет представлен как:
Из приведенного выше уравнения видно, что общий коэффициент усиления в замкнутом контуре неинвертирующего усилителя всегда будет больше, но никогда не меньше единицы (единицы), он является положительным по природе и определяется соотношением значений Rƒ и R2.
Если значение резистора обратной связи Rƒ равно нулю, коэффициент усиления усилителя будет точно равен единице (единице). Если резистор R2 равен нулю, коэффициент усиления будет приближаться к бесконечности, но на практике он будет ограничен дифференциальным усилением разомкнутого контура операционных усилителей (A O ).
Мы можем легко преобразовать конфигурацию инвертирующего операционного усилителя в конфигурацию неинвертирующего усилителя, просто изменив входные соединения, как показано.
Повторитель напряжения (буфер единичного усиления)
Если мы сделаем резистор обратной связи Rƒ равным нулю (Rƒ = 0), а резистор R2 равным бесконечности (R2 = ∞), то полученная схема будет иметь фиксированный коэффициент усиления «1» (единица), как и все выходное напряжение возвращается на инвертирующий входной терминал (отрицательная обратная связь).Эта конфигурация создаст особый тип схемы неинвертирующего усилителя, называемый повторителем напряжения , также известный как «буфер единичного усиления».
Поскольку входной сигнал подключается непосредственно к неинвертирующему входу усилителя, выходной сигнал не инвертируется, в результате чего выходное напряжение равно входному напряжению, таким образом, Vout = Vin. Это делает схему повторителя напряжения идеальной в качестве источника постоянного напряжения или регулятора напряжения из-за его свойств изоляции между входами и выходами.
Преимущество конфигурации повторителя напряжения с единичным усилением заключается в том, что его можно использовать, когда согласование импеданса или изоляция цепи более важны, чем усиление напряжения или тока, поскольку он поддерживает напряжение входного сигнала на его выходном зажиме. Кроме того, входной импеданс цепи повторителя напряжения чрезвычайно высок, обычно выше 1 МОм, поскольку он равен входному сопротивлению операционных усилителей, умноженному на его коэффициент усиления (Rin x A O ). Выходное сопротивление операционного усилителя очень низкое, поскольку предполагается идеальное состояние операционного усилителя, поэтому на него не влияют изменения нагрузки.
Повторитель неинвертирующего напряжения
В этой конфигурации неинвертирующей схемы входное сопротивление Rin увеличилось до бесконечности, а полное сопротивление Rƒ обратной связи уменьшилось до нуля. Выход подключен напрямую к отрицательному инвертирующему входу, поэтому обратная связь составляет 100%, а Vin точно равно Vout, что дает ему фиксированное усиление, равное 1 или единице. Поскольку входное напряжение Vin подается на неинвертирующий вход, коэффициент усиления по напряжению усилителя определяется как:
Поскольку на неинвертирующую входную клемму ток не течет, входное сопротивление бесконечно (идеальные условия), поэтому нулевой ток будет проходить через контур обратной связи.Таким образом, любое значение сопротивления может быть помещено в петлю обратной связи, не влияя на характеристики схемы, поскольку через нее не протекает ток, поэтому на ней возникает нулевое падение напряжения, что приводит к нулевым потерям мощности.
Поскольку входной импеданс чрезвычайно высок, буфер единичного усиления (повторитель напряжения) может использоваться для обеспечения большого усиления мощности, поскольку дополнительная мощность поступает от шин питания операционных усилителей и через выходы операционных усилителей на нагрузку, а не на нагрузку. прямо со входа. Однако в большинстве реальных буферных схем с единичным усилением присутствуют токи утечки и паразитные емкости, поэтому в контуре обратной связи требуется резистор низкого номинала (обычно 1 кОм), чтобы помочь уменьшить влияние этих токов утечки, обеспечивая стабильность, особенно если операционный усилитель имеет текущий тип обратной связи.
Повторитель напряжения или буфер единичного усиления — это особый и очень полезный тип цепи неинвертирующего усилителя , который обычно используется в электронике для изоляции цепей друг от друга, особенно в переменных состояния высокого порядка или активных фильтрах типа Саллена-Ки. отделите одну ступень фильтра от другой. Типичными доступными ИС цифрового буфера являются четырехуровневый буфер 74LS125 с 3 состояниями или более распространенный восьмеричный буфер 74LS244.
Последняя мысль: коэффициент усиления по напряжению с обратной связью цепи повторителя напряжения равен «1» или Unity .Коэффициент усиления по напряжению разомкнутого контура операционного усилителя без обратной связи составляет Infinite . Затем, тщательно выбирая компоненты обратной связи, мы можем контролировать величину усиления, создаваемую неинвертирующим операционным усилителем, от единицы до бесконечности.
До сих пор мы анализировали схему инвертирующего и неинвертирующего усилителя, которая имеет только один входной сигнал Vin. В следующем уроке об операционных усилителях мы рассмотрим влияние выходного напряжения Vout при подключении дополнительных входов к усилителю.Затем получается еще один общий тип схемы операционного усилителя, называемый суммирующим усилителем, который можно использовать для «сложения» напряжений, присутствующих на его входах.
Схема неинвертирующего операционного усилителя»Примечания по электронике
Схема неинвертирующего усилителя на операционном усилителе обеспечивает высокое входное сопротивление со всеми другими преимуществами, присущими операционным усилителям.
Учебное пособие по операционному усилителю Включает:
Введение
Сводка схем
Инвертирующий усилитель
Суммирующий усилитель
Неинвертирующий усилитель
Усилитель с регулируемым усилением
Активный фильтр высоких частот
Активный фильтр нижних частот
Полосовой фильтр
Режекторный фильтр
Компаратор
Триггер Шмитта
Мультивибратор
Бистабильный
Интегратор
Дифференциатор
Генератор моста Вина
Генератор фазового сдвига
Конфигурация неинвертирующего усилителя — одна из самых популярных и широко используемых форм схемы операционного усилителя, которая используется во многих электронных устройствах.
Схема неинвертирующего усилителя на операционном усилителе обеспечивает высокое входное сопротивление и все преимущества, полученные от использования операционного усилителя.
Хотя базовая схема неинвертирующего операционного усилителя требует того же количества электронных компонентов, что и ее инвертирующий аналог, она находит применение в приложениях, где важно высокое входное сопротивление.
Схема неинвертирующего усилителя
Основная электронная схема неинвертирующего операционного усилителя относительно проста.
В этой конструкции электронной схемы сигнал подается на неинвертирующий вход операционного усилителя. Таким образом, сигнал на выходе не инвертируется по сравнению с входным.
Однако обратная связь берется с выхода операционного усилителя через резистор на инвертирующий вход операционного усилителя, где другой резистор заземляется. Он должен применяться к инвертирующему входу, так как это отрицательная обратная связь.
Значение этих двух резисторов определяет коэффициент усиления схемы операционного усилителя, поскольку они определяют уровень обратной связи.
Базовая схема неинвертирующего операционного усилителяКоэффициент усиления неинвертирующего усилителя
Коэффициент усиления неинвертирующей схемы операционного усилителя легко определить. Расчет основан на том факте, что напряжение на обоих входах одинаково. Это происходит из-за того, что усиление усилителя чрезвычайно велико. Если выход схемы остается в пределах шины питания усилителя, то деление выходного напряжения на коэффициент усиления означает, что между двумя входами практически нет разницы.
Поскольку вход операционного усилителя не потребляет ток, это означает, что ток, протекающий через резисторы R1 и R2, одинаков. Напряжение на инвертирующем входе формируется делителем потенциала, состоящим из R1 и R2, и поскольку напряжение на обоих входах одинаково, напряжение на инвертирующем входе должно быть таким же, как и на неинвертирующем входе. Это означает, что Vin = Vout x R1 / (R1 + R2). Следовательно, коэффициент усиления по напряжению схемы Av можно принять как
Где:
Av = коэффициент усиления по напряжению цепи операционного усилителя
R2 = сопротивление резистора обратной связи в Ом
R1 = сопротивление резистора относительно земли в Ом
В качестве примера, усилитель, требующий одиннадцатого усиления, можно построить, сделав R2 47 кОм и R1 4.7 кОм.
Входное сопротивление неинвертирующего усилителя
Импеданс неинвертирующей схемы операционного усилителя особенно высок.
Входное сопротивление этой схемы операционного усилителя обычно может значительно превышать 10 7 Ом.
Для большинства схемотехнических приложений любое влияние нагрузки схемы на предыдущие каскады можно полностью игнорировать, поскольку оно очень велико, если только они не являются чрезмерно чувствительными.
Это существенное отличие от инвертирующей конфигурации схемы операционного усилителя, которая обеспечивала только относительно низкий импеданс, зависящий от номинала входного резистора.
Связь по переменному току с неинвертирующим усилителем
В большинстве случаев можно подключить цепь по постоянному току. Если требуется связь по переменному току, необходимо убедиться, что у неинвертирующего устройства есть путь постоянного тока к земле для очень небольшого входного тока, необходимого для смещения входных устройств внутри ИС.
Этого можно достичь, подключив к земле резистор R3 с высоким сопротивлением, как показано ниже. Его значение обычно может составлять 100 кОм или более. Если этот резистор не вставлен, выход операционного усилителя будет подключен к одной из шин напряжения.
Базовая схема неинвертирующего операционного усилителя с конденсаторным входомПри установке резистора таким образом следует помнить, что комбинация конденсатор-резистор C1 / R3 образует фильтр верхних частот с частотой среза. Точка отсечки возникает на частоте, где емкостное реактивное сопротивление равно сопротивлению.
Аналогичным образом выходной конденсатор должен быть выбран так, чтобы он мог пропускать самые низкие частоты, необходимые для системы. В этом случае выходное сопротивление операционного усилителя будет низким, и поэтому наибольшее сопротивление, вероятно, будет у следующего каскада.
Неинвертирующий усилитель с однополярным питанием
Схемы операционного усилителя обычно предназначены для работы от двух источников питания, например + 9В и -9В. Этого не всегда легко достичь, и поэтому часто бывает удобно использовать вариант конструкции электронной схемы с односторонним или однополярным питанием. Это может быть достигнуто путем создания того, что часто называют половинной шиной питания.
Схема неинвертирующего операционного усилителя смещена на половину напряжения шины. Устанавливая рабочую точку при этом напряжении, можно получить максимальный размах на выходе без ограничения.
Схема неинвертирующего операционного усилителя с одной шиной питания.При использовании этой схемы следует отметить несколько моментов:
- Напряжение смещения: Напряжение смещения для неинвертирующего усилителя устанавливается R3 и R4. Обычно входной импеданс самого операционного усилителя выше, чем у резисторов, поэтому им можно пренебречь. Обычно напряжение смещения устанавливается равным половине напряжения шины, чтобы выход мог одинаково качаться в любом направлении без ограничения.R3 и R4 обычно имеют одинаковое значение.
- Входное сопротивление: Входное сопротивление этой схемы будет ниже, чем у операционного усилителя как такового. Входное сопротивление всей схемы неинвертирующего усилителя будет R3 параллельно с R4 параллельно входному сопротивлению операционного усилителя. На самом деле это обычно приравнивается к R3 параллельно с R4, то есть (R3 x R4) / R3 + R4).
- Конденсатор C3: Утечка конденсатора C3 должна быть очень низкой, иначе ток утечки нарушит цепь, и он попадет в шину.Электролитические конденсаторы не работают в этом положении, так как их ток утечки слишком велик, и цепь попадает в шину питания.
- Входные и выходные конденсаторы: Как и в любой конструкции электронной схемы, входные и выходные конденсаторы должны быть выбраны таким образом, чтобы пропускать самые низкие частоты без чрезмерного затухания.
Конфигурация неинвертирующего усилителя с использованием операционного усилителя особенно полезна для проектирования электронных схем в электронных устройствах, где требуется высокий входной импеданс.Схема неинвертирующего усилителя проста в сборке и работает надежно и хорошо на практике.
Другие схемы и схемотехника:
Основы операционных усилителей
Схемы операционных усилителей
Цепи питания
Конструкция транзистора
Транзистор Дарлингтона
Транзисторные схемы
Схемы на полевых транзисторах
Условные обозначения схем
Вернуться в меню «Конструкция схемы». . .
Работа и применение неинвертирующих операционных усилителей
В электронике усилитель — это схема, которая принимает входной сигнал и производит неискаженную большую версию сигнала на выходе.В этом руководстве мы узнаем о важной конфигурации операционного усилителя, называемой неинвертирующим усилителем. В неинвертирующих операционных усилителях вход подается на неинвертирующий терминал, а выход находится в фазе с входом.
Введение
Операционный усилитель, более известный как операционный усилитель, по сути, представляет собой многокаскадный дифференциальный усилитель с высоким коэффициентом усиления, который можно использовать несколькими способами. Две важные схемы типичного операционного усилителя:
- Инвертирующий усилитель
- Неинвертирующий усилитель
Неинвертирующий усилитель представляет собой конфигурацию схемы операционного усилителя, которая производит усиленный выходной сигнал и этот выходной сигнал неинвертирующего усилителя. инвертирующий операционный усилитель синфазен с приложенным входным сигналом.
Другими словами, неинвертирующий усилитель ведет себя как цепь повторителя напряжения. Неинвертирующий усилитель также использует соединение с отрицательной обратной связью, но вместо того, чтобы подавать весь выходной сигнал на вход, только часть напряжения выходного сигнала возвращается в качестве входа на инвертирующий входной терминал операционного усилителя.
Высокий входной импеданс и низкий выходной импеданс неинвертирующего усилителя делают схему идеальной для приложений с буферизацией импеданса.
Схема идеального неинвертирующего усилителя
Принципиальная схема идеального неинвертирующего усилителя показана на рисунке ниже.
Из схемы видно, что R 2 (R f на рисунке выше) и R 1 (R 1 на рисунке выше) действуют как делитель потенциала для на инвертирующий вход подается выходное напряжение и напряжение на резисторе R 1 .
Когда неинвертирующий вход подключен к земле, т. Е. V IN = 0, напряжение на инвертирующей входной клемме также должно быть на уровне земли; в противном случае любая разница напряжений между входными клеммами будет усилена, чтобы переместить инвертирующую входную клемму обратно на уровень земли (входы операционного усилителя всегда будут иметь одинаковое напряжение).
Поскольку клемма инвертирующего входа находится на уровне земли, соединение резисторов R 1 и R 2 также должно быть на уровне земли. Это означает, что падение напряжения на R 1 будет равно нулю. В результате ток, протекающий через R 1 и R 2 , должен быть равен нулю. Таким образом, на R 2 наблюдается нулевое падение напряжения, и, следовательно, выходное напряжение равно входному напряжению, которое составляет 0 В.
Когда положительный входной сигнал подается на неинвертирующую входную клемму, выходное напряжение будет сдвигаться, чтобы инвертирующая входная клемма оставалась равной приложенному входному напряжению.Следовательно, будет возникать напряжение обратной связи на резисторе R 1 ,
VR 1 = V IN = V OUT R 1 / (R 1 + R 2 )
Коэффициент усиления по напряжению неинвертирующего операционного усилителя
Из приведенного выше уравнения для V IN через V OUT , коэффициент усиления по напряжению с обратной связью неинвертирующего усилителя A CL можно рассчитать как:
A CL = V OUT / V IN
= (R 1 + R 2 ) / R 1
A CL = 1 + (R 2 / R 1 )
или A CL = 1 + (R f / R 1 )
Приведенное выше уравнение усиления положительное, что означает, что выходной сигнал будет синфазен с приложенным входным сигналом.Коэффициент усиления по напряжению с обратной связью неинвертирующего усилителя определяется соотношением резисторов R 1 и R 2 , используемых в схеме.
Практически, неинвертирующие усилители будут иметь резистор, включенный последовательно с источником входного напряжения, чтобы поддерживать входной ток одинаковым на обоих входных клеммах.
Виртуальное короткое замыкание
В неинвертирующем усилителе существует виртуальное короткое замыкание между двумя входными клеммами. Виртуальное короткое замыкание — это короткое замыкание по напряжению, но разрыв по току.Виртуальное короткое замыкание использует два свойства идеального операционного усилителя:
- Поскольку R IN бесконечен, входной ток на обоих выводах равен нулю.
- Поскольку коэффициент усиления разомкнутого контура A OL бесконечен, разность напряжений (В 1 — В 2 ) всегда равна нулю.
Хотя виртуальное короткое замыкание является идеальным приближением, оно дает точные значения при использовании с сильной отрицательной обратной связью. Пока операционный усилитель работает в линейной области (не насыщенной, положительно или отрицательно), коэффициент усиления по напряжению без обратной связи приближается к бесконечности, и между двумя входными клеммами существует виртуальное короткое замыкание.
Из-за виртуального короткого замыкания инвертирующее входное напряжение следует за неинвертирующим входным напряжением. Если неинвертирующее входное напряжение увеличивается или уменьшается, инвертирующее входное напряжение немедленно увеличивается или уменьшается до того же значения. Это действие часто называют «начальной загрузкой».
Входное сопротивление неинвертирующего усилителя
Входное сопротивление схемы операционного усилителя определяется как:
Z IN = (1 + A OL β) Z i
Где, A OL — коэффициент усиления разомкнутого контура операционного усилителя
Zi — входной импеданс операционного усилителя без какой-либо обратной связи
β — коэффициент обратной связи
Для неинвертирующего усилителя коэффициент обратной связи задается как:
β = R 2 / (R 1 + R 2 )
β = 1 / A CL
Следовательно, для схемы неинвертирующего усилителя входной импеданс определяется уравнением,
Z IN = {1 + (A OL / A CL )} Zi
Выходное сопротивление неинвертирующего усилителя
Выходное сопротивление операционного усилителя выражается как:
Z ВЫХОД = Z 0 / (1+ A OL β)
Sinc e, β = 1 / A CL для неинвертирующего усилителя, полное сопротивление задается как,
Z OUT = Z 0 / {1 + (A OL / A CL )}
Схема повторителя напряжения
Повторитель напряжения — одно из самых простых применений операционного усилителя, где выходное напряжение точно такое же, как входное напряжение, приложенное к цепи.Другими словами, коэффициент усиления цепи повторителя напряжения равен единице.
Выход операционного усилителя напрямую подключен к инвертирующей входной клемме, а входное напряжение подается на неинвертирующую входную клемму. Повторитель напряжения, как и неинвертирующий усилитель, имеет очень высокий входной импеданс и очень низкий выходной импеданс. Принципиальная схема повторителя напряжения показана на рисунке ниже.
Можно видеть, что приведенная выше конфигурация аналогична схеме неинвертирующего усилителя, за исключением того, что здесь не используются резисторы.Коэффициент усиления неинвертирующего усилителя определяется как,
A CL = 1 + (R 2 / R 1 )
В повторителе напряжения резистор R 2 равен нулю и R 1 бесконечно. Таким образом, усиление повторителя напряжения будет равно 1. Следовательно, повторитель напряжения также широко известен как буфер усиления единства.
Повторитель напряжения или буферная схема с единичным усилением обычно используется для изоляции различных цепей, т. Е. Для отделения одного каскада схемы от другого, а также используется в приложениях согласования импеданса.
На практике выходное напряжение повторителя напряжения не будет в точности равным приложенному входному напряжению, и будет небольшая разница. Это различие связано с большим внутренним усилением по напряжению операционного усилителя.
ПРИМЕЧАНИЕ: Коэффициент усиления по напряжению в разомкнутом контуре операционного усилителя бесконечен, а коэффициент усиления по напряжению в замкнутом контуре повторителя напряжения равен единице. Это означает, что путем тщательного выбора компонентов обратной связи мы можем точно контролировать коэффициент усиления неинвертирующего усилителя.
Пример неинвертирующего усилителя
Для неинвертирующего усилителя, показанного на рисунке ниже, рассчитайте следующее:
i) Коэффициент усиления усилителя, A CL
ii) Выходное напряжение, В O
iii) Ток через нагрузочный резистор I L .
iv) Выходной ток I O .
ПРИМЕЧАНИЕ: Узел A находится на неинвертирующем выводе операционного усилителя, а узел B — на инвертирующем выводе (который также является точкой делителя напряжения).Эти узлы не показаны на изображении выше.
Ответ) Потенциал в узле B равен V IN и из-за виртуального короткого замыкания
V A = V B = V IN = 0,8 V
Ток I1 задается как
I 1 = В A / R 1 = 0,8 В / 10 кОм
I 1 = 80 мкА
Поскольку входной ток операционного усилителя равен нулю, должен течь тот же I 1 через резистор R ф .
i) Коэффициент усиления неинвертирующего усилителя,
A CL = 1 + (R f / R 1 ) = 1 + (20 кОм / 10 кОм)
A CL = 3
ii) Выходное напряжение,
В O = A CL * V IN = 3 * 0,8 В
В O = 2,4 В
iii) Ток через нагрузочный резистор
I L = V O / R L = 2,4 / (2 * 10 3 Ом)
I L = 1.2 мА
iv) Выходной ток,
Из закона тока Кирхгофа (KCL), I O = I 1 + I L
I O = 80 мкА + 1,2 мА
I O = 1,28 мА
Сводка по неинвертирующему усилителю
- В неинвертирующем усилителе используется соединение с отрицательной обратной связью с делителем напряжения.
- Коэффициент усиления по напряжению всегда больше единицы.
- Коэффициент усиления по напряжению положительный, что указывает на то, что для входа переменного тока выход синфазен с входным сигналом, а для входа постоянного тока полярность выхода такая же, как полярность входа.
- Коэффициент усиления по напряжению неинвертирующего операционного усилителя зависит только от номиналов резистора и не зависит от коэффициента усиления без обратной связи операционного усилителя.
- Желаемый прирост напряжения может быть получен путем выбора соответствующих номиналов резисторов.
Заключение
Простое руководство по неинвертирующим операционным усилителям. Вы узнали схему идеального неинвертирующего усилителя, коэффициент усиления по напряжению, входное и выходное сопротивление, применение повторителя напряжения и пример схемы со всеми важными расчетами.
Базовые конфигурации усилителя: неинвертирующий усилитель
В предыдущих видеороликах мы исследовали характеристики идеального операционного усилителя, а затем представили отрицательную обратную связь как метод, который позволяет нам разрабатывать схемы высокоэффективных усилителей с использованием неидеальных реальных усилителей. операционные усилители жизни.
Усиление на ОУ
Операционные усилителиуниверсальны и могут быть включены в широкий спектр интересных и творческих схем. Однако иногда все, что нам нужно сделать, это увеличить амплитуду сигнала, и для этих приложений у нас есть базовая конфигурация неинвертирующего усилителя операционного усилителя . Эта простая топология состоит из одного операционного усилителя и двух резисторов, соединенных следующим образом:
Неинвертирующий усилитель
Когда мы говорим, что эта схема «неинвертирующая», мы имеем в виду, что она применяет положительное усиление к входному сигналу. Если вы подключите постоянное напряжение к входной клемме, выходное напряжение будет равно входному напряжению, умноженному на некоторое число, без изменения полярности. Если вы подаете синусоидальный сигнал на входной терминал, операционный усилитель увеличит амплитуду сигнала, не создавая разности фаз 180 °.
Неинвертирующий режим достигается путем подключения входного сигнала к неинвертирующей входной клемме операционного усилителя. Коэффициент усиления почти полностью определяется двумя резисторами, которые образуют цепь обратной связи, подключенную между выходом операционного усилителя и его отрицательной входной клеммой.
Как вы, возможно, помните из видео об отрицательной обратной связи, коэффициент усиления ОУ в разомкнутом контуре не бесконечен, и, следовательно, он влияет на усиление в замкнутом контуре (G CL ), но на практике эффект невелик. достаточно, чтобы быть незначительным.Таким образом, мы можем смело выразить коэффициент усиления неинвертирующего усилителя следующим образом:
Входное сопротивление
Когда мы пытаемся передать напряжение от одной подсхемы к другой, подсхема, которая генерирует сигнал, должна иметь низкий выходной импеданс, а подсхема, которая принимает сигнал, должна иметь высокое входное сопротивление. Одним из заметных преимуществ неинвертирующего усилителя является то, что он имеет очень высокий входной импеданс, поскольку входной сигнал подключается непосредственно к входной клемме операционного усилителя.Это не относится к инвертирующей конфигурации, которая обсуждается в следующем видеоуроке.
Знакомство с неинвертирующим усилителем
Из видео об отрицательной обратной связи мы узнали, что коэффициент усиления с обратной связью усилителя с отрицательной обратной связью примерно равен обратной величине коэффициента обратной связи:
Если вы рассматриваете R 1 и R 2 как цепь обратной связи с резистивным делителем, вы можете использовать это соотношение между G CL и β, чтобы получить выражение для коэффициента усиления неинвертирующего усилителя; этот метод кратко продемонстрирован в руководстве по отрицательной обратной связи.В этом видео мы найдем коэффициент усиления, используя типовой анализ цепи.
-
Входное напряжение V IN подается на неинвертирующую входную клемму, и предположение виртуального короткого замыкания позволяет нам передавать это входное напряжение непосредственно на инвертирующую входную клемму.
-
В IN на инвертирующей входной клемме генерирует ток величиной V IN / R 1 , текущий по направлению к земле.
-
Мы предполагаем, что ток не течет на входные клеммы операционного усилителя и не выходит из них, и, следовательно, ток, протекающий через R 2 , должен быть равен току, протекающему через R 1 : I R2 = V IN / R 1 . Этот ток течет от выходной клеммы операционного усилителя.
-
Падение напряжения на R 2 составляет I R2 × R 2 = (V IN R 2 ) / R 1 .
-
Поскольку клемма более низкого напряжения R 2 подключена к клемме инвертирующего входа, выходное напряжение равно V IN плюс напряжение на R 2 : V OUT = V IN + ( V IN R 2 ) / R 1 = V IN (1 + R 2 / R 1 ).
Резюме
- Мы можем добиться неинвертирующего усиления с помощью простой схемы, для которой требуется только операционный усилитель и два резистора.
- Коэффициент усиления обратной связи определяется номиналами двух резисторов.
- Конфигурация неинвертирующего операционного усилителя имеет очень высокий входной импеданс.
Буферный и неинвертирующий операционный усилитель
Буферный усилитель с единичным усилением реализован с использованием операционного усилителя в конфигурации с отрицательной обратной связью. Выход подключен к своему инвертирующему входу, а источник сигнала подключен к неинвертирующему входу. Хотя его коэффициент усиления по напряжению равен 1 или единице, он имеет высокое усиление по току, высокое входное сопротивление и низкое выходное сопротивление.Он используется, чтобы избежать загрузки источника сигнала.
Выходное напряжение операционного усилителя определяется уравнением: \ begin {уравнение} V_ {out} = {A_ {OL} \, (V _ {\! +} — V _ {\! -})} \ end {уравнение} где V + — напряжение на неинвертирующем выводе, V- — напряжение на инвертирующем выводе, а A OL — коэффициент усиления без обратной связи усилителя.
Переставьте уравнение \ begin {уравнение} {V_ {out} \ over A_ {OL}} = V _ {\! +} — V _ {\! -} \ end {уравнение}
Если предположить, что A OL равно ∞, \ begin {уравнение} V_- = V_ + \ end {уравнение} Только для схем операционных усилителей с отрицательной обратной связью мы используем уравнение 3, чтобы упростить анализ схем.
Для этого буферного усилителя, используя уравнение 3, при осмотре можно получить \ begin {уравнение} V_ {выход} = V_- = V_ + = V_ {дюйм} \ end {уравнение} и получить коэффициент усиления буферного усилителя операционного усилителя \ begin {уравнение} V_ {out} = V_ {in} \ end {уравнение}
Неинвертирующий операционный усилитель обеспечивает усиление по напряжению. Буферный усилитель можно рассматривать как частный случай этого усилителя с Rf = 0 и Rg = ∞.
Если мы позволим входному току на инвертирующий вход I- = 0 и подадим KVL на петли Vout, Rf и Rg \ begin {уравнение} V_- = {V_ {out}} {{R_g} \ over {R_f + R_g}} \ end {уравнение} Применяя уравнение 3, \ begin {уравнение} V_ {in} = V_ + = V_- = {V_ {out}} {{R_g} \ over {R_f + R_g}} \ end {уравнение} Измените уравнение, чтобы получить коэффициент усиления неинвертирующего усилителя операционного усилителя. \ begin {уравнение} V_ {out} = (1 + {{R_f} \ over {R_g}}) {V_ {in}} \ end {уравнение}
Поскольку доходы от рекламы падают, несмотря на рост числа посетителей, нам нужна ваша помощь в поддержании и улучшении этого сайта, что требует времени, денег и тяжелого труда.Благодаря щедрости наших посетителей, которые давали ранее, вы можете использовать этот сайт бесплатно.
Если вы получили пользу от этого сайта и можете, пожалуйста, отдать 10 долларов через Paypal . Это позволит нам продолжаем в будущее. Это займет всего минуту. Спасибо!
Я хочу дать!
Как получить передаточную функцию неинвертирующего усилителя — Освоение дизайна электроники
Один из наиболее распространенных усилителей в аналоговой конструкции — это неинвертирующий усилитель.
Рисунок 1
Его передаточная функция
| (1) |
Как получить эту функцию?
Прежде всего отметим, что этот операционный усилитель можно считать идеальным. Таким образом, ток на инвертирующем входе равен нулю (I = 0A, см. Рисунок 2), а токи через R1 и R2 равны.
| (2) |
Рисунок 2
Затем мы можем написать уравнение для цикла, созданного Vout, R2, V и Vin.
| (3) |
Из уравнения (3) выражение I2 равно
| (4) |
Аналогичным образом мы можем определить выражение для I1. Уравнение (5) является уравнением петли для R1, V1 и Vin.
| (5) |
и
| (6) |
Будучи идеальным операционным усилителем, мы можем считать, что неинвертирующий вход имеет тот же потенциал, что и инвертирующий вход, поэтому V = 0 В.Это связано с высоким коэффициентом усиления идеального операционного усилителя. Когда выход находится на уровне нескольких вольт, дифференциальный вход может быть на уровне нескольких десятков микровольт. Следовательно, V очень близко к нулю.
Заменив I1 и I2 в уравнении (2) и исключив V, мы можем записать это уравнение:
| (7) |
Следовательно, передаточная функция неинвертирующего усилителя равна
| (8) |
Q.E. D.
Основы инвертирующего и неинвертирующего усилителя
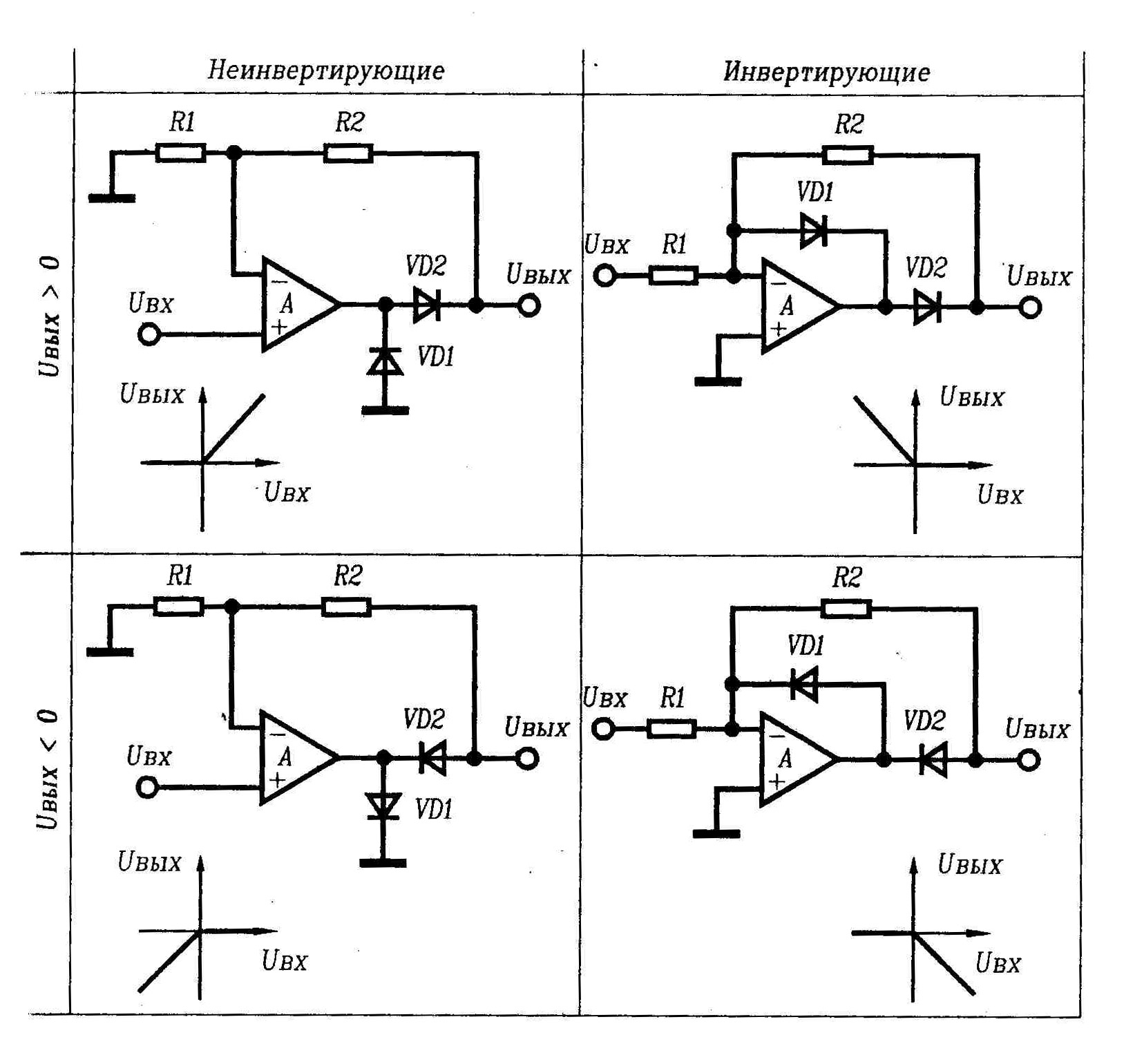
«Идеальный» или совершенный операционный усилитель — это устройство с определенными особыми характеристиками, такими как бесконечное усиление без обратной связи, бесконечное входное сопротивление, нулевое выходное сопротивление, бесконечная полоса пропускания и смещение нуля. Операционные усилители широко используются для преобразования сигналов или выполнения математических операций, поскольку они почти идеальны для усиления постоянного тока. По сути, это устройство усиления напряжения, используемое с компонентами внешней обратной связи, такими как резисторы и конденсаторы, между его выходными и входными клеммами.Операционный усилитель представляет собой трехконтактное устройство, состоящее из двух входов с высоким импедансом, один из которых называется инвертирующим входом (-), а другой — неинвертирующим входом (+). Третий вывод представляет собой выходной порт операционного усилителя, который может как потреблять, так и передавать как напряжение, так и ток.
Отрицательный отзыв
Хотя, с одной стороны, операционные усилители предлагают очень высокое усиление, это делает усилитель нестабильным и трудным для управления. Часть этого усиления можно потерять, подключив резистор через усилитель от выходной клеммы обратно к инвертирующей входной клемме для управления конечным коэффициентом усиления усилителя.Это обычно известно как отрицательная обратная связь и обеспечивает более стабильный операционный усилитель.
Отрицательная обратная связь — это процесс подачи части выходного сигнала обратно на вход. Но чтобы сделать обратную связь отрицательной, она подается на отрицательный или «инвертирующий вход» терминала операционного усилителя с помощью резистора. Этот эффект производит замкнутый контур, приводящий к усилению замкнутого контура. Инвертирующий усилитель с обратной связью использует отрицательную обратную связь для точного управления общим коэффициентом усиления усилителя, но вызывает уменьшение усиления усилителя.
Инвертирующий усилитель
В схеме инвертирующего усилителя инвертирующий вход операционного усилителя принимает обратную связь с выхода усилителя. Предполагая, что операционный усилитель идеален и применяя концепцию виртуального короткого замыкания на входных клеммах операционного усилителя, напряжение на инвертирующей клемме равно неинвертирующей клемме. Неинвертирующий вход операционного усилителя заземлен. Поскольку усиление самого операционного усилителя очень велико, а выходной сигнал усилителя составляет всего несколько вольт, это означает, что разница между двумя входными клеммами чрезвычайно мала, и ею можно пренебречь.Поскольку неинвертирующий вход операционного усилителя удерживается под потенциалом земли, это означает, что инвертирующий вход должен фактически иметь потенциал земли.
Применяя KCL в инвертирующем узле, мы можем вычислить усиление напряжения,
Коэффициент усиления напряжения (A) =
В на выходе / В на выходе = — R f / R наНеинвертирующий усилитель
Неинвертирующий усилитель — это такой усилитель, в котором выход находится в фазе по отношению к входу.Обратная связь применяется на инвертирующем входе. Однако теперь вход применяется к неинвертирующему входу. Выход представляет собой неинвертированную (с точки зрения фазы) усиленную версию входа. Коэффициент усиления схемы неинвертирующего усилителя для операционного усилителя определить легко. Расчет основан на том факте, что напряжение на обоих входах одинаково. Это происходит из-за того, что усиление усилителя чрезвычайно велико. Если выход схемы остается в пределах шины питания усилителя, то деление выходного напряжения на коэффициент усиления означает, что между двумя входами практически нет разницы.
Коэффициент усиления по напряжению можно рассчитать, применив KCL в инвертирующем узле.
Коэффициент усиления напряжения (A) =
В на выходе / В на выходе = (1+ R f / R на )Хотите запачкать руки? Ознакомьтесь с некоторыми типовыми вопросами

