Constrain arduino. Математические функции Arduino: полный обзор и применение

Какие математические функции доступны в Arduino. Как использовать тригонометрические, логарифмические и другие математические операции в скетчах Arduino. Какие константы предоставляет Arduino для математических вычислений.

Основные математические функции Arduino

Arduino предоставляет широкий набор встроенных математических функций, которые позволяют выполнять различные вычисления прямо в скетче. Рассмотрим основные категории этих функций:

Тригонометрические функции

Arduino имеет встроенные тригонометрические функции, которые работают с радианами:

• sin(x) — синус угла x
• cos(x) — косинус угла x
• tan(x) — тангенс угла x

Как использовать эти функции на практике? Например, для вычисления синуса угла 30 градусов:

float angle = 30;
float sinValue = sin(radians(angle));
Serial.println(sinValue); // Выведет примерно 0.5

Обратные тригонометрические функции

Также доступны обратные тригонометрические функции:

• asin(x) — арксинус x
• acos(x) — арккосинус x
• atan(x) — арктангенс x

Эти функции возвращают результат в радианах. Чтобы получить значение в градусах, нужно использовать функцию degrees():

float value = 0.5;
float angle = degrees(asin(value));
Serial.println(angle); // Выведет примерно 30

Экспоненциальные и логарифмические функции Arduino

Arduino также предоставляет функции для работы с экспонентами и логарифмами:

• pow(base, exponent) — возведение в степень
• sqrt(x) — квадратный корень
• exp(x) — экспонента e^x
• log(x) — натуральный логарифм
• log10(x) — десятичный логарифм

Пример использования функции pow() для вычисления квадрата числа:

float number = 5;
float square = pow(number, 2);
Serial.println(square); // Выведет 25

Функции округления в Arduino

Для округления чисел в Arduino используются следующие функции:

• round(x) — округление до ближайшего целого
• ceil(x) — округление вверх
• floor(x) — округление вниз

Как применять эти функции? Например, для округления числа до ближайшего целого:

float value = 3.7;
int rounded = round(value);
Serial.println(rounded); // Выведет 4

Константы в Arduino для математических вычислений

Arduino предоставляет ряд предопределенных констант для математических вычислений:

• PI — число пи (3.14159)
• HALF_PI — половина пи (1.57079)
• TWO_PI — два пи (6.28318)
• DEG_TO_RAD — коэффициент для перевода градусов в радианы (0.01745)
• RAD_TO_DEG — коэффициент для перевода радиан в градусы (57.2957)

Эти константы можно использовать напрямую в вычислениях. Например, для вычисления длины окружности:

float radius = 5;
float circumference = TWO_PI * radius;
Serial.println(circumference); // Выведет примерно 31.4159

Функции ограничения значений в Arduino

Arduino предоставляет полезные функции для ограничения значений в определенном диапазоне:

• min(x, y) — возвращает меньшее из двух чисел
• max(x, y) — возвращает большее из двух чисел
• constrain(x, a, b) — ограничивает значение x в диапазоне от a до b

Как использовать функцию constrain() на практике? Предположим, нам нужно ограничить показания датчика в диапазоне от 0 до 100:

int sensorValue = analogRead(A0);
int constrainedValue = constrain(sensorValue, 0, 100);
Serial.println(constrainedValue); // Значение будет в диапазоне от 0 до 100
 

Функция map() для масштабирования значений

Функция map() позволяет масштабировать значения из одного диапазона в другой. Это особенно полезно при работе с аналоговыми датчиками:

int sensorValue = analogRead(A0); // Значение от 0 до 1023
int mappedValue = map(sensorValue, 0, 1023, 0, 255);
analogWrite(9, mappedValue); // Вывод масштабированного значения на ШИМ-пин

В этом примере мы масштабируем значение с аналогового входа (0-1023) в диапазон ШИМ (0-255).

Применение математических функций в проектах Arduino

Математические функции Arduino находят широкое применение в различных проектах. Рассмотрим несколько примеров:

Создание плавных анимаций с использованием синуса

Функция sin() может быть использована для создания плавных колебаний, например, для управления яркостью светодиода:

void loop() {
  float t = millis() / 1000.0; // Время в секундах
  int brightness = 128 + 127 * sin(t); // Значение от 1 до 255
  analogWrite(LED_PIN, brightness);
}
 

Вычисление расстояния в ультразвуковом дальномере

Для вычисления расстояния в ультразвуковом дальномере часто используется функция pulseIn() вместе с простыми арифметическими операциями:

long duration = pulseIn(ECHO_PIN, HIGH);
float distance = duration * 0.034 / 2; // Расстояние в сантиметрах

Оптимизация математических вычислений в Arduino

При работе с математическими функциями в Arduino важно помнить о нескольких моментах оптимизации:

• Используйте целочисленные операции вместо операций с плавающей точкой, где это возможно, так как они выполняются быстрее.
• Предвычисляйте константные значения, чтобы избежать повторных вычислений в цикле loop().
• Используйте битовые операции вместо умножения и деления на степени двойки. Например, x << 1 быстрее, чем x * 2.

Пример оптимизации вычислений:

// Вместо этого:
float result = sin(angle) * 180 / PI;

// Используйте это:
const float radToDeg = 180.0 / PI; // Предвычисленная константа
float result = sin(angle) * radToDeg;

Работа с комплексными числами в Arduino

Arduino не имеет встроенной поддержки комплексных чисел, но вы можете создать собственную структуру для работы с ними:

struct Complex {
  float real;
  float imag;
};

Complex add(Complex a, Complex b) {
  return {a.real + b.real, a.imag + b.imag};
}

Complex multiply(Complex a, Complex b) {
  return {
    a.real * b.real - a.imag * b.imag,
    a.real * b.imag + a.imag * b.real
  };
}

Это позволит вам выполнять базовые операции с комплексными числами в ваших проектах Arduino.

Заключение

Arduino предоставляет богатый набор математических функций, которые позволяют выполнять сложные вычисления прямо на микроконтроллере. От базовых арифметических операций до тригонометрических и экспоненциальных функций, эти инструменты открывают широкие возможности для создания сложных и интересных проектов. Понимание и эффективное использование этих функций позволит вам создавать более совершенные и точные устройства на базе Arduino.

Все математические функции Arduino | AlexGyver

Приспичило в проекте использовать логарифм, полез читать – наткнулся на полный список математических функций, которые встроены в Arduino (файл math.h). Привожу его здесь с переводом на русский, пользуйтесь!
Примечание: double это тип данных для чисел с плавающей точкой, занимает 8 байт. float – то же самое, но 4 байта. Arduino поддерживает только 4 байтные числа, т.е. для неё double == float. Соответственно некоторые функции из таблицы ниже получаются “дублирующие” при использовании на Arduino.

Константы

Константа	Результат	Описание
M_E	2. 718281828	Число e
M_LOG2E	1.442695041	log_2 e
M_LOG10E	0.434294482	log_10 e
M_LN2	0.693147181	log_e 2
M_LN10	2.302585093	log_e 10
M_PI	3.141592654	pi
M_PI_2	1.570796327	pi/2
M_PI_4	0.785398163	pi/4
M_1_PI	0.318309886	1/pi
M_2_PI	0.636619772	2/pi
M_2_SQRTPI	1. 128379167	2/корень(pi)
M_SQRT2	1.414213562	корень(2)
M_SQRT1_2	0.707106781	1/корень(2)
NAN	__builtin_nan(“”)	nan
INFINITY	__builtin_inf()	infinity

Функции

Функция	Описание
cos (double x)	Косинус (радианы)
sin (double x)	Синус (радианы)
tan (double x)	Тангенс (радианы)
fabs (double x)	Модуль для float чисел
fmod (double x, double y)	Остаток деления x на у для float
modf (double x, double *iptr)	Возвращает дробную часть, целую хранит по адресу iptr http://cppstudio. com/post/1137/
modff (float x, float *iptr)	То же самое, но для float
sqrt (double x)	Корень квадратный
sqrtf (float)	Корень квадратный для float чисел
cbrt (double x)	Кубический корень
hypot (double x, double y)	Гипотенуза ( корень(x*x + y*y) )
square (double x)	Квадрат ( x*x )
floor (double x)	Округление до целого вниз
ceil (double x)	Округление до целого вверх
frexp (double x, int *pexp)	http://cppstudio. x)
cosh (double x)	Косинус гиперболический (радианы)
sinh (double x)	Синус гиперболический (радианы)
tanh (double x)	Тангенс гиперболический (радианы)
acos (double x)	Арккосинус (радианы)
asin (double x)	Арксинус (радианы)
atan (double x)	Арктангенс (радианы)
atan2 (double y, double x)	Арктангенс (y / x) (позволяет найти квадрант, в котором находится точка)
log (double x)	Натуральный логарифм х ( ln(x) )
log10 (double x)	Десятичный логарифм x ( log_10 x)
pow (double x, double y)	Степень ( x^y )
isnan (double x)	Проверка на nan (1 да, 0 нет)
isinf (double x)	Возвр. 1 если x +бесконечность, 0 если нет
isfinite (double x)	Возвращает ненулевое значение только в том случае, если аргумент имеет конечное значение
copysign (double x, double y)	Возвращает x со знаком y (знак имеется в виду + -)
signbit (double x)	Возвращает ненулевое значение только в том случае, если _X имеет отрицательное значение
fdim (double x, double y)	Возвращает разницу между x и y, если x больше y, в противном случае 0
fma (double x, double y, double z)	Возвращает x*y + z
fmax (double x, double y)	Возвращает большее из чисел
fmin (double x, double y)	Возвращает меньшее из чисел
trunc (double x)	Возвращает целую часть числа с дробной точкой
round (double x)	Математическое округление
lround (double x)	Математическое округление (для больших чисел)
lrint (double x)	Округляет указанное значение с плавающей запятой до ближайшего целого значения, используя текущий режим округления и направление

3333″ data-lineheight=»35.2px»>Что есть ещё

Далее уже от самих разработчиков Arduino есть ещё маленький пакетик удобных макро-функций!

Макро	Значение
min(a,b)	Возвращает меньшее из чисел
max(a,b)	Возвращает большее из чисел
abs(x)	Модуль числа
constrain(value,min,max)	Ограничить диапазон числа value до min и max
map(val, fromMin, fromMax, toMin, toMax)	Перевести диапазон числа value от (fromMin, fromMax) в (toMin, toMax)
round(x)	Математическое округление
radians(deg)	Перевод градусов в радианы
degrees(rad)	Перевод радиан в градусы
sq(x)	Квадрат числа
PI	Пи
HALF_PI	пол Пи
TWO_PI	дваПи
DEG_TO_RAD	Константа перевода град в рад 0. 01745329
RAD_TO_DEG	Константа перевода рад в град 57.2957786

adafruit_simplemath — документация Adafruit SimpleMath Library 1.0

adafruit_simplemath — документация Adafruit SimpleMath Library 1.0

Математические вспомогательные функции

Программное обеспечение и зависимости:

adafruit_simplemath.constrain( x: float , out_min: float , out_max: float ) → float

Ограничивает x , чтобы быть в пределах инклюзивного диапазона [ выход_мин , выход_макс ]. Иногда называется клип или зажим в других библиотеках. out_min должно быть меньше или равно out_max . Если x

меньше, чем out_min , вернуть out_min . Если x больше, чем out_max , вернуть out_max . В противном случае просто верните x . Если max_value меньше, чем min_value , они будут заменены местами.

Параметры:

• x ( с плавающей точкой ) — значение для ограничения

• out_min ( float ) — нижняя граница выходного диапазона.

• out_max ( float ) — Верхняя граница выходного диапазона.

Возвращает:

Возвращает значение, ограниченное заданным диапазоном.

Тип возврата:

поплавок

adafruit_simplemath.map_range( x: float ,

in_min: float , in_max: float , out_min: float , out_max: float ) → float

Сопоставляет число из одного диапазона с другим. Чем-то похож на Ардуино map() , но возвращает результат с плавающей запятой и ограничивает выходное значение между out_min и out_max . Если in_min больше, чем in_max или out_min больше, чем out_max , соответствующий диапазон инвертируется, что позволяет, например, отображать диапазон от 0-10 до 50-0.

См. также map_unconstrained_range()

 из adafruit_simplemath import map_range
процент = 23
screen_width = 320 # или board.DISPLAY.width
x = диапазон_карты (процент, 0, 100, 0, ширина экрана - 1)
print("Позиция X", проценты, "% слева от экрана", x)
 

Параметры:

• x ( с плавающей запятой ) — значение для преобразования

• in_min ( float ) – Начальное значение диапазона ввода.

• in_max ( float ) — конечное значение диапазона ввода.

• out_min ( float ) – Начальное значение выходного диапазона.

• out_max ( float ) — конечное значение выходного диапазона.

Возвращает:

Возвращает значение, сопоставленное с новым диапазоном.

Тип возврата:

поплавок

adafruit_simplemath.map_unconstrained_range( x: float , in_min: float , in_max: float , out_min: float , out_max: float ) → float

Сопоставляет число из одного диапазона с другим. Чем-то похож на Ардуино map() , но возвращает результат с плавающей запятой и не ограничивает выходное значение между out_min и out_max . Если in_min больше, чем in_max или out_min больше, чем out_max , соответствующий диапазон инвертируется, что позволяет, например, отображать диапазон от 0-10 до 50-0.

См. также map_range()

 из adafruit_simplemath import map_unconstrained_range
Цельсия = -20
Фаренгейты = map_unconstrained_range (цельсий, 0, 100, 32, 212)
print(celsius, "градусы Цельсия =", fahrenheit, "градусы Фаренгейта")
 

Параметры:

• x ( с плавающей запятой ) – Значение для преобразования

• in_min ( float ) – Начальное значение диапазона ввода.

• in_max ( float ) — конечное значение диапазона ввода.

• out_min ( float ) – Начальное значение выходного диапазона.

• out_max ( float ) — конечное значение выходного диапазона.

Возвращает:

Возвращает значение, сопоставленное с новым диапазоном.

Тип возврата:

поплавок

Читать документы v: последний

Версии

последний

стабильный

Загрузки

При прочтении документов

Дом проекта

Строит

FOMO: обнаружение объектов для устройств с ограничениями

Edge Impulse FOMO (быстрее объекты, больше объектов) — это новый алгоритм машинного обучения, который позволяет обнаруживать объекты на устройствах с сильными ограничениями. Он позволяет подсчитывать объекты, находить местоположение объектов на изображении и отслеживать несколько объектов в режиме реального времени, используя до 30 раз меньше вычислительной мощности и памяти, чем MobileNet SSD или YOLOv5.

Учебники

Например, FOMO позволяет обнаруживать объекты со скоростью 60 кадров в секунду на Raspberry Pi 4:

А вот FOMO выполняет обнаружение объектов со скоростью 30 кадров в секунду на Arduino Nicla Vision (MCU Cortex-M7), используя 245 КБ ОЗУ.

Полный проект Edge Impulse с моделью пива и банок, включая все данные и конфигурацию, можно найти здесь: https://studio.edgeimpulse.com/public/89078/latest.

Как это 🪄 работает?

Так как же это работает? Сначала небольшой праймер. Допустим, вы хотите определить, видите ли вы лицо перед датчиком. Вы можете подойти к этому двумя способами. Вы можете обучить простой двоичный классификатор, который говорит либо «лицо», либо «нет лица», или вы можете обучить сложную модель обнаружения объектов, которая говорит вам: «Я вижу лицо в этой точке x, y и такого размера». Таким образом, обнаружение объектов отлично подходит, когда вам нужно знать точное местоположение чего-либо или если вы хотите подсчитать несколько вещей (простой классификатор не может этого сделать), но это требует гораздо больших вычислительных ресурсов, и вам обычно требуется гораздо больше данных для этого.

Классификация изображений и обнаружение объектов

Цель разработки FOMO состояла в том, чтобы получить лучшее из обоих миров: вычислительная мощность, необходимая для простой классификации изображений, но с дополнительной информацией о местоположении и количестве объектов, которую дает нам обнаружение объектов.

Тепловые карты

Первое, что нужно понять, это то, что, хотя на выходе классификатора изображений есть «лицо» / «без лица» (и, следовательно, в результате не сохраняется местоположение), базовая архитектура нейронной сети состоит из количество сверточных слоев. Об этих слоях можно думать так: каждый слой создает рассеянное изображение предыдущего слоя с более низким разрешением. Например. если у вас есть изображение 16×16, ширина/высота слоев может быть:

Каждый «пиксель» во втором слое примерно соответствует блоку пикселей 4×4 во входном слое, и интересно то, что локальность в некоторой степени сохраняется. «Пиксель» в слое 2 в точке (0, 0) будет примерно соответствовать верхнему левому углу входного изображения. Чем глубже вы погружаетесь в обычную сеть классификации изображений, тем меньше эта локальность (или «восприимчивое поле») сохраняется до тех пор, пока вы, наконец, не получите только 1 результат.

FOMO использует ту же архитектуру, но отрезает последние слои стандартной модели классификации изображений и заменяет этот слой вероятностной картой класса для каждого региона (например, картой 4×4 в приведенном выше примере). Затем у него есть настраиваемая функция потерь, которая заставляет сеть полностью сохранять местоположение на последнем слое. По сути, это дает вам тепловую карту того, где находятся объекты.

От входного изображения к тепловой карте (красная чашка, зеленая лампа)

Разрешение тепловой карты определяется тем, где вы отсекаете слои сети. Для модели FOMO, обученной выше (на пивных бутылках), мы делаем это, когда размер тепловой карты в 8 раз меньше, чем входное изображение (входное изображение 160×160 даст тепловую карту 20×20), но это настраивается. Когда вы устанавливаете это значение на 1:1, это фактически дает вам сегментацию на уровне пикселей и возможность подсчитывать множество мелких объектов.

Вот предыдущая итерация подхода FOMO, используемого для подсчета отдельных пчел (тепловая карта в 2 раза меньше размера входных данных).

Обучение на центроидах

Отличие FOMO от других алгоритмов обнаружения объектов заключается в том, что он не выводит ограничивающие рамки, но легко перейти от тепловой карты к ограничивающим рамкам. Просто нарисуйте рамку вокруг выделенной области.

От тепловой карты к ограничивающим рамкам

Однако, работая с первыми клиентами, мы поняли, что ограничивающие рамки — это просто деталь реализации других сетей обнаружения объектов, а не типичное требование. Очень часто размер объектов не важен, поскольку камеры находятся в фиксированных местах (и объекты, таким образом, имеют фиксированный размер), а вам просто нужно местоположение и количество объектов.

Итак, теперь мы тренируемся на центроидах объектов. Это значительно упрощает подсчет близких объектов (каждая активация на тепловой карте — это объект), а сверточная природа нейронной сети гарантирует, что мы все равно осматриваем центроид в поисках объекта.

Обучение центроидам пивных бутылок. Сверху метки источника, внизу результат вывода.

Недостатком тепловой карты является то, что каждая ячейка действует как собственный классификатор. Например. если ваши классы «лампа», «растение» и «фон» каждая ячейка будет либо лампа, растение или фон. Таким образом, невозможно обнаружить объекты с перекрывающимися центроидами. Вы можете увидеть это в видео Raspberry Pi 4 выше на 00:18, где пивные бутылки расположены слишком близко друг к другу. Эту проблему можно решить, используя тепловую карту с более высоким разрешением.

Гибкость и очень, очень высокая скорость

По-настоящему классным преимуществом FOMO является то, что он полностью сверточный. Если вы установите коэффициент изображения: тепловая карта равным 8, вы можете добавить изображение 96×96 (выводит тепловую карту 12×12), изображение 320×320 (выводит тепловую карту 40×40) или даже изображение 1024×1024 (выводит тепловую карту 128×128). Это делает FOMO невероятно гибким и полезным, даже если у вас есть очень большие изображения, которые необходимо проанализировать (например, при обнаружении ошибок, когда ошибки могут быть очень и очень маленькими). Вы даже можете тренироваться на небольших участках, а затем увеличивать масштаб во время логического вывода.

Кроме того, FOMO совместим с любой моделью MobileNetV2. В зависимости от того, где модель должна работать, вы можете выбрать модель с более высокой или более низкой альфой, и трансферное обучение также работает (хотя вам нужно обучать свои базовые модели специально с учетом FOMO). Это позволяет конечным клиентам легко использовать свои существующие модели и настраивать их с помощью FOMO, чтобы также добавить местоположение (например, у нас есть клиенты с большими моделями трансфертного обучения для обнаружения диких животных).

Вместе это дает FOMO возможности масштабирования от самых маленьких микроконтроллеров до полноценных шлюзов или графических процессоров. Просто цифры:

1. 1.

   Верхнее видео классифицирует 60 раз в секунду на стандартном Raspberry Pi 4 (ввод в оттенках серого 160×160, MobileNetV2 0.1 alpha). Это в 20 раз быстрее, чем у MobileNet SSD, который делает ~3 кадра в секунду.

2. 2.

   Второе видео сверху классифицирует 30 раз в секунду на плате Arduino Nicla Vision с микроконтроллером Cortex-M7, работающим на частоте 480 МГц) в ~240 КБ ОЗУ (ввод 96×96 оттенков серого, MobileNetV2 0,35 альфа).

3. 3.

   Во время Edge Impulse Представьте себе, что мы продемонстрировали модель FOMO, работающую на Himax WE-I Plus, выполняющую 14 кадров в секунду на DSP (видео). Эта модель работала с менее чем 150 КБ ОЗУ (ввод в градациях серого 96×96, MobileNetV2 0.1 alpha). [1]

4. 4.

   Самая маленькая версия FOMO (ввод в градациях серого 96×96, MobileNetV2 0,05 альфа) работает в <100 КБ ОЗУ и ~ 10 кадров в секунду. на Cortex-M4F на частоте 80 МГц. [1]

[1] Модели, скомпилированные с помощью EON Compiler.

Как начать?

Чтобы построить свои первые модели FOMO:

1. 1.

   Создайте новый проект в Edge Impulse.

2. 2.

   Убедитесь, что выбран метод маркировки «Ограничивающие рамки (обнаружение объектов)».

3. 4.

   Добавьте к импульсу блок «Обнаружение объектов (изображения)».

4. 5.

   В разделе Изображения выберите «Оттенки серого»

5. 6.

   В разделе Обнаружение объектов выберите «Выбрать другую модель» и выберите одну из моделей FOMO.

6. 7.

   Для начала обязательно уменьшите скорость обучения до 0,001.

Выбор модели FOMO в Edge Impulse

В настоящее время FOMO совместим со всеми полностью поддерживаемыми макетными платами, имеющими камеру, а также с Edge Impulse для Linux (любой клиент). Конечно, вы можете экспортировать свою модель как библиотеку C++ и интегрировать ее, как обычно, на любое устройство или плату разработки, выходной формат моделей совместим с обычными моделями обнаружения объектов; и наш SDK работает практически на всем, что есть под солнцем (обзор см. в разделе «Локальный запуск вашего импульса»), от RTOS до «голого железа» и специальных ускорителей и графических процессоров.

Советы по экспертному режиму

Дополнительные настройки для FOMO доступны в экспертном режиме.

Доступ к экспертному режиму

Взвешивание объектов

FOMO чувствителен к соотношению объектов и фоновых ячеек в размеченных данных. По умолчанию конфигурация состоит в том, чтобы взвешивать выходные ячейки объекта x100 в функции потерь, object_weight=100 , как способ балансировки того, что обычно составляет большую часть фона. Это значение было выбрано как оптимальное для ряда примеров использования. В сценариях, где объекты для обнаружения относительно редки, это значение можно увеличить, например. до 1000, чтобы модель еще больше сосредоточилась на обнаружении объектов (за счет потенциально большего количества ложных обнаружений).

Точка отсечения MobileNet

FOMO использует

MobileNetV2

в качестве базовой модели для своей магистрали и по умолчанию выполняет пространственное сокращение на 1/8 от входа к выходу (например, ввод 96x96 приводит к 12x12 выход ).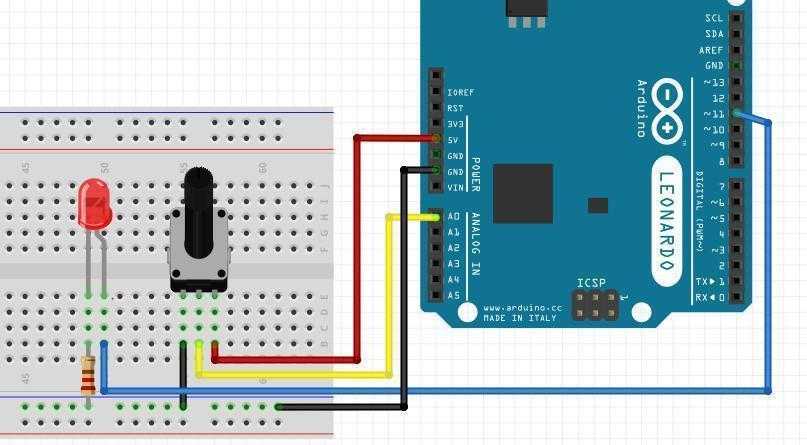 Это реализуется путем отключения MobileNet на промежуточном уровне block_6_expand_relu

MobileNetV2 cut point

Выбор другого cut_point приводит к другому пространственному сокращению; например если мы сократим выше на block_3_expand_relu FOMO вместо этого выполнит пространственное сокращение только на 1/4 (т. е. ввод 96x96 приводит к выводу 24x24 )

Обратите внимание; это означает, что требуется гораздо меньше магистрали MobileNet, и в результате получается модель только с половиной параметров. Переключение на более высокую альфу может противодействовать уменьшению этого параметра. Более поздние выпуски FOMO будут противодействовать уменьшению этого параметра с помощью архитектуры в стиле UNet.

Вместимость классификатора FOMO

FOMO логически можно рассматривать как первый раздел MobileNetV2, за которым следует стандартный классификатор, где классификатор применяется полностью свертывающимся образом.

В конфигурации по умолчанию этот классификатор FOMO эквивалентен одному плотному слою с 32 узлами, за которым следует классификатор с выходами num_classes .

FOMO использует сверточный классификатор.

Для трехстороннего классификатора, использующего точку отсечения по умолчанию, результатом является заголовок классификатора с ~3200 параметрами.

ФОРМА СЛОЯ КОЛИЧЕСТВО ПАРАМЕТРОВ

block_6_expand_relu (ReLU) (None, 20, 20, 96) 0

head (Conv2D) (None, 20, 20, 32) 3104

log его (Conv2D) (Нет, 20, 20, 3) 99

У нас есть возможность увеличить пропускную способность этой головки классификатора либо 1) увеличив количество фильтров в слое Conv2D , 2) добавив дополнительные слои, либо 3) выполнив оба действия.

Например, мы можем изменить количество фильтров с 32 до 16, а также добавить еще один сверточный слой следующим образом.

Добавление дополнительного слоя в классификатор FOMO

ФОРМА СЛОЯ КОЛИЧЕСТВО ПАРАМЕТРОВ

block_6_expand_relu (ReLU) (Нет, 20, 20, 96) 0

head_1 (Conv2D) (Нет, 2 0, 20, 16) 1552

head_2 (Conv2D) (Нет, 20, 20, 16) 272

логит (Conv2D) (Нет, 20, 20, 3) 51

Для некоторых задач дополнительный уровень может улучшить производительность, и в этом случае фактически использует меньше параметров. Однако обучение может занять больше времени и потребовать больше данных. В будущих выпусках настройка этого аспекта FOMO может выполняться с помощью EON Tuner.

Производительность и минимальные требования

Как и остальные наши обучающие блоки на основе нейронных сетей, FOMO поставляется в виде набора базовых математических процедур, свободных от зависимостей во время выполнения. Это означает, что для запуска FOMO практически нет ограничений, кроме:

1. 1.

   Убедиться, что сама модель может поместиться в память цели (флэш/ОЗУ), и

2. 2.

   убедиться, что у цели достаточно памяти для хранения буфера изображения (флэш/ОЗУ). ОЗУ) в дополнение к логике вашего приложения

В целом, мы видели, что буфер, модель и логика приложения (включая беспроводной стек) помещаются всего в 200 КБ для изображений 64×64 пикселей. Но мы определенно рекомендуем цель размером не менее 512 КБ, чтобы вы могли воспользоваться преимуществами изображений большего размера и более широкого диапазона оптимизаций модели.

Что касается задержки, скорость цели будет определять максимальное количество кадров, которые могут быть обработаны за заданный интервал (fps).