Что такое дискретное состояние в физике и математике. Как определяются дискретные состояния систем. Где применяются дискретные состояния в науке и технике. Чем отличаются дискретные и непрерывные процессы.
Что такое дискретное состояние
Дискретное состояние — это состояние системы, которое может принимать только определенные значения из ограниченного набора возможных состояний. В отличие от непрерывных систем, где состояние может плавно меняться, в дискретных системах переход между состояниями происходит скачкообразно.
Основные свойства дискретных состояний:
- Конечное или счетное множество возможных значений
- Четко выраженные границы между состояниями
- Скачкообразные переходы между состояниями
- Возможность однозначно определить текущее состояние системы
Примеры дискретных состояний в физике
В физике дискретные состояния встречаются во многих областях. Некоторые типичные примеры:
- Энергетические уровни атомов и молекул
- Квантовые состояния частиц
- Спиновые состояния электронов
- Фазовые состояния вещества (твердое, жидкое, газообразное)
Рассмотрим подробнее энергетические уровни атома водорода. Они могут принимать только дискретные значения, определяемые формулой:

E_n = -13.6 эВ / n^2
Где n — главное квантовое число, принимающее целые значения 1, 2, 3 и т.д. Электрон в атоме водорода может находиться только на этих дискретных энергетических уровнях.
Дискретные состояния в математике и информатике
В математике и информатике дискретные состояния широко используются для описания различных систем:
- Состояния конечных автоматов
- Значения переменных в компьютерных программах
- Состояния логических элементов (0 и 1)
- Дискретные значения сигналов в цифровой обработке
Как определяются дискретные состояния в этих областях. Какие преимущества дает использование дискретных моделей при решении математических и информационных задач.
Применение дискретных состояний в науке и технике
Концепция дискретных состояний находит широкое применение во многих областях науки и техники:
- Квантовая механика и физика элементарных частиц
- Проектирование цифровых электронных схем
- Теория информации и кодирования
- Моделирование сложных систем
- Теория управления дискретными системами
Рассмотрим некоторые конкретные примеры применения дискретных состояний в современных технологиях. Как используются дискретные модели при разработке компьютерных систем, средств связи, систем автоматического управления.

Дискретные и непрерывные процессы
Чем отличаются дискретные и непрерывные процессы. Основные различия:
| Дискретные процессы | Непрерывные процессы |
|---|---|
| Конечное число состояний | Бесконечное число состояний |
| Скачкообразные переходы | Плавные переходы |
| Квантованные значения | Любые значения в диапазоне |
В каких случаях целесообразно использовать дискретные или непрерывные модели для описания реальных процессов. Преимущества и недостатки обоих подходов.
Математическое описание дискретных состояний
Для математического описания систем с дискретными состояниями используются различные подходы:
- Теория конечных автоматов
- Марковские цепи
- Дискретные отображения
- Разностные уравнения
Рассмотрим простой пример описания системы с двумя дискретными состояниями с помощью марковской цепи:
Пусть система может находиться в состояниях A и B. Вероятности переходов между состояниями за один шаг:
- P(A→A) = 0.7
- P(A→B) = 0.3
- P(B→A) = 0.4
- P(B→B) = 0.6
Такую систему можно описать с помощью матрицы переходных вероятностей:

P = [0.7 0.3]
[0.4 0.6]
Эта матрица полностью определяет динамику переходов между дискретными состояниями системы.
Методы анализа систем с дискретными состояниями
Для анализа систем с дискретными состояниями применяются различные методы:
- Построение и анализ графов переходов
- Методы дискретной оптимизации
- Имитационное моделирование
Каждый из этих подходов имеет свои особенности и область применения. Выбор конкретного метода зависит от типа исследуемой системы и решаемых задач.
Проблемы и ограничения дискретных моделей
При использовании дискретных моделей для описания реальных систем возникают определенные проблемы и ограничения:
- Сложность описания систем с большим числом состояний
- Потеря информации при дискретизации непрерывных процессов
- Трудности учета непрерывных факторов
- Ограниченная точность при большом числе итераций
Как преодолеваются эти ограничения на практике. Какие подходы используются для повышения адекватности дискретных моделей.
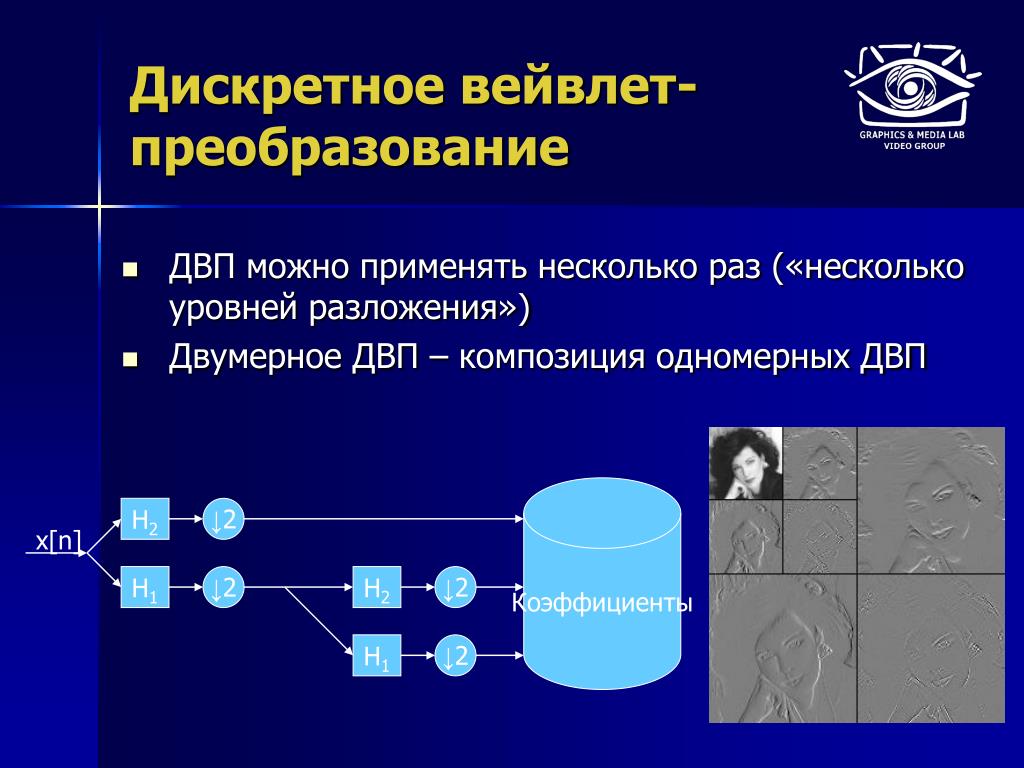
Перспективы развития теории дискретных систем
Основные направления развития теории и практики применения дискретных моделей:
- Разработка эффективных алгоритмов анализа сложных дискретных систем
- Создание гибридных дискретно-непрерывных моделей
- Применение методов машинного обучения для анализа дискретных данных
- Развитие квантовых вычислений на основе дискретных квантовых состояний
Какие новые возможности открываются в связи с развитием теории дискретных систем. Как это может повлиять на развитие науки и техники в ближайшем будущем.
Что такое дискретный процесс
Приведем общепринятые определения терминов «процесс» и «дискретный процесс», почерпнув их в википедии (открытая энциклопедия Интернета).
Определение 1. Процесс (от лат. processus — продвижение) — это последовательная смена состояний во времени некоторого объекта произвольной природы. Различают дискретные и непрерывные процессы. У дискретных процессов состояния четко отделены друг от друга, и для каждого состояния можно указать соседние (предыдущее и последующее, или только одно из них). У
 Примерами непрерывных процессов являются кипение воды, движение планет вокруг Солнца и др.
Примерами непрерывных процессов являются кипение воды, движение планет вокруг Солнца и др.Из вышеприведенной формулировки следует, что отличительной особенностью дискретного процесса является наличие у него последовательно сменяемых дискретных (т.е. четко выраженных) состояний. Отталкиваясь от этой формулировки, попытаемся разобраться с характерными свойствами дискретного процесса. Прежде всего отметим следующую его особенность. Присутствие в дискретном процессе последовательно сменяемых дискретных состояний вовсе не означает, что в нем не может быть плавно изменяемых состояний (назовем их аналоговыми). Скорее наоборот, такие состояния чаще всего в дискретном процессе присутствуют.
В самом деле, если мы вернемся к прежнему примеру с кассиром, то каждое его дискретное состояние (например, получение денег у покупателя) может быть детализировано как состояние аналоговое, длящееся определенное время и характеризующееся плавными движениями рук кассира, выполняющих определенное действие. Строго говоря, в данном случае имеют место не чисто дискретные, а дискретно-аналоговые состояния.
Строго говоря, в данном случае имеют место не чисто дискретные, а дискретно-аналоговые состояния.
Рассмотрим другой простой пример дискретного процесса, описывающего обработку станком партии деталей. Дискретность здесь выражается в укрупненном состоянии каждой детали (необработанная, обработанная или находящаяся на стадии обработки), а непрерывность — в детальном состоянии обрабатываемой в данный момент детали или в текущем состоянии станка в процессе его переналадки.
Приведем теперь пример дискретного процесса, в котором аналоговые состояния вообще отсутствуют. Это — так называемый процесс выбора вариантов, для которого фактор времени отсутствует. Типичным примером такого процесса является заполнение емкости кузова машины партией груза, который должен быть ею перевезен. В данном случае нас интересует не время, требуемое для погрузки машины, а тот набор образцов груза, который был выбран для отправки их получателю. При этом нам совершенно не важно, в какой последовательности эти образцы были погружены на машину.
Из этого простого примера следует, что для дискретного процесса выбора вариантов важен не порядок смены дискретных состояний и требуемое для этого время, а полученный при этом результат. Отсюда следует, что процесс выбора вариантов можно рассматривать как процесс мгновенный.
Здесь мы подошли к тому, чтобы разобраться с категориями неуправляемых и управляемых дискретных процессов. К первым обычно относят такие процессы, в которых порядок смены дискретных состояний является фиксированным и не может быть изменен с той или иной целью в зависимости от текущей ситуации. Для управляемых дискретных процессов такое изменение допустимо.
Типичным примером неуправляемого дискретного процесса является обслуживания продавцом покупателей в порядке их размещения в очереди. Приведем более сложный пример, когда на станке обрабатываются детали разных типов, для которых заданы приоритеты, определяющие очередность их обработки.
Независимо от того, является ли дискретный процесс управляемым или нет, в нем практически всегда присутствуют управляющие воздействия на его объекты (в дальнейшем — управления).
Управления, используемые в дискретных процессах, обладают следующими двумя свойствами:
- они применяются к объектам процесса в дискретные моменты времени, разделенные между собой конечными временными промежутками;
- каждое управление может быть либо мгновенным, либо немгновенным, т.е. растянутым во времени до момента приложения следующего управления.
Ниже приведено расширенное определение дискретного процесса, при формулировке которого мы учли изложенный выше материал текущего подраздела данного раздела сайта.
Определение 2. Дискретным процессом называется процесс последовательного изменения дискретных и аналоговых состояний для всей совокупности объектов этого процесса под воздействием последовательно применяемым к ним в дискретные моменты времени мгновенным и немгновенным управлениям.
По возможности изменения стратегии управления процессом дискретные процессы подразделяются на управляемые и неуправялемые (признак управляемости), по предсказуемости протекания процесса — на случайные (вероятностные) и детерминированные (признак поведения), а по времени его протекания — на бесконечные, ограниченные во времени и мгновенные (признак продолжительности).
Определение 3. Технологический процесс — последовательность технологических операций, необходимых для выполнения определенного вида работ. Технологический процесс состоит из рабочих операций, которые в свою очередь складываются из рабочих движений (приемов). Информационный процесс — процесс получения, создания, сбора, обработки, накопления, хранения, поиска, распространения и использования информации.
Если, к примеру, дискретный процесс описывает последовательное выполнение операций при строительстве здания или изготовлении изделия, либо при обслуживании продавцом покупателей, то такой процесс фактически является технологическим. Если же речь идет об обмене дискретными сообщениями в сети связи или о решении некоторой задачи выбора вариантов, то такой процесс является информационным.
Если же речь идет об обмене дискретными сообщениями в сети связи или о решении некоторой задачи выбора вариантов, то такой процесс является информационным.
В тех случаях, когда требуется подчеркнуть реальность рассматриваемого дискретного процесса, а также возможность эффективного управления им с помощью нашей технологии (ИТ АУ ДТИП), будем использовать применительно к нему термин «дискретный технологический или информационный процесс (сокращенно — ДТИП)».
Дискретное состояние — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Зависимость вкладов в корреляционную функцию d0o B первом бор-новском приближении от полной электронной плотности пе при Т 104 К. Показаны вклады электрон-ионного рассеяния, упругого рассеяния электронов на атомах в Is — и 25-состояниях, неупругого электрон-атомного рассеяния с переходами ls — — 2s и ls — — 2p и ионизации. Штриховыми линиями показана область неустойчивости при плотностях ниже моттовской. [1]
[1] |
Дискретные состояния, расположенные выше граничного уровня Е, рассматриваются как свободные ввиду большой протяженности их волновых функций и нестабильности этих состояний относительно тепловых столкновений. Эта трудность характерна для кулоновских систем. [2]
Дискретные состояния представляют собой колебательно-вращательные уровни молекулы, а полосы — непрерывные состояния диссоциированной молекулы, связанные с каждым электронным уровнем, При комбиняпиончом пясг. [3]
Описанные дискретные состояния молекул рассматриваются без учета их реального статистического веса. Тем не менее, где это необходимо, учитывается условная энтропия. Введенные ограничения делают расчет несколько уязвимым, но не могут существенно сказаться на относительной оценке объема информации для разных классов соединений. В реальных условиях возникают некоторые искаженные структуры, которые также трудно учесть. [4]
[4]
Пси-функции дискретных состояний атома заметно отличны от нуля только в области порядка эффективных размеров атома. [5]
Введем пять дискретных состояний, в которые постепенно переходит рассматриваемое устройство: 1 — тросе натянут; 2 — тросе ослаблен, 3 — колодки прижаты к колесу, 4 — колодки не прижаты к колесу, 5 — трение между колодками и колесом. [6]
Как функция дискретного состояния ф0 ограничена областью потенциальной ямы и ее непосредственного окружения. Поэтому величины fyL также важны только в области потенциальной ямы и в ее окрестности, поскольку оператор 901 локален. Однако для значений г, не слишком сильно превышающих Ь, функция все еще определяется в основном своей частью GL, которая по существу не зависит от энергии. Поэтому форма ft /, слабо меняется не только внутри потенциальной ямы, но также в части потенциального барьера, примыкающей к границе потенциальной ямы. [7]
Схема обнаружения двух состояний макромолекулы, претерпевающей фазовый переход типа компактизации, или поджатия ( пунктир — непрерывный переход. | Образование молекулярной мицеллы в блок-сополимере типа АВ.
[8] | Образование молекулярной мицеллы в блок-сополимере типа АВ.
[8] |
Наличие двух дискретных состояний является достаточным критерием перехода первого рода. [9]
Каждое из дискретных состояний атома характеризуется своей энергией. В этом состоянии атом пребывает некоторое время, и состояние называется стационарным. Может быть также совершен переход из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией, но для этого необходимо, чтобы энергия АЕ была сообщена атому извне. [10]
Процессы с дискретными состояниями, в которых ве роятность любого состояния в будущем зависит тольк от ее состояния в настоящий момент и не зависит с предшествующих значений процесса, называют маркое скими цепями. Полученная модель является частны случаем марковской цепи, так как выше допускались ш реходы только в соседние состояния. Рассматриваема модель определяет не только процесс перехода систем из одного состояния в другое, но и свойства входящег потока требований и обслуживающих устройств. [11]
[11]
Процессы с дискретными состояниями ( значениями Xj) и дискретными моментами ( значениями параметра t) называются цепями Маркова, по имени русского ученого акад. [12]
Обычно вводят ряд дискретных состояний, в которых может находиться рассматриваемый элемент, например: для эксплуатации изделий возникают отклонения от показателей качества, связанные с силовыми и температурными деформациями, коррозией, старением, состоянием фактического контакта сопрягаемых поверхностей, изменением свойств материала и качества слоя деталей. [13]
Для обозначения qtn дискретных состояний требуется К. [14]
Формальная структурно-логическая привязка дискретных состояний к определенным сочетаниям отказов бортовых систем и их элементов, которая может входить непосредственно в модель, а может и выходить за рамки моделирования путем проведения предварительного исследования и анализа, приводит к вынужденному определенному огрублению модели. [15]
[15]
Страницы: 1 2 3 4
scipy.signal.cont2discrete — Руководство по SciPy v1.10.0
- scipy.signal.cont2discrete( system , dt , method=’zoh’ , alpha=None )[источник]
Преобразование непрерывной системы в дискретную в пространстве состояний.
- Параметры:
- система кортеж, описывающий систему или экземпляр
lti Ниже приводится количество элементов в кортеже и интерпретация:
1: (экземпляр
lti)2: (число, ден)
3: (нули, полюса, усиление)
4: (А, Б, В, Г)
- dt float
Шаг дискретизации по времени.
- метод str, опционально
Какой метод использовать:
gbt: обобщенное билинейное преобразование
билинейная: аппроксимация Тастина («gbt» с альфа=0,5)
euler: метод Эйлера (или прямое дифференцирование) («gbt» с альфа=0)
reverse_diff: Обратное дифференцирование («gbt» с альфа=1.
 0)
0)zoh: удержание нулевого порядка (по умолчанию)
foh: удержание первого порядка ( версия добавлена: 1.3.0 )
импульс: эквивалентная импульсная характеристика ( версия добавлена: 1.3.0 )
- альфа с плавающей запятой в пределах [0, 1], необязательный
Весовой параметр обобщенного билинейного преобразования, который следует указывать только с помощью method=»gbt», иначе игнорируется
- система кортеж, описывающий систему или экземпляр
- Возвращает:
- sysd кортеж, содержащий дискретную систему
В зависимости от типа ввода вывод будет иметь вид
(num, den, dt) для входа передаточной функции
(нули, полюса, усиление, dt) для входа нули-полюса-усиление
(A, B, C, D, dt) для ввода системы в пространстве состояний
Примечания
По умолчанию подпрограмма использует метод удержания нулевого порядка (zoh) для выполнения преобразование.
 Альтернативно, обобщенное билинейное преобразование
можно использовать, включая распространенное билинейное приближение Тастина,
метод метода Эйлера или метод обратного дифференцирования.
Альтернативно, обобщенное билинейное преобразование
можно использовать, включая распространенное билинейное приближение Тастина,
метод метода Эйлера или метод обратного дифференцирования.Метод удержания нулевого порядка (zoh) основан на [1], обобщенном билинейном аппроксимация основана на [2] и [3], методе удержания первого порядка (foh) основано на [4].
Ссылки
[1]
https://en.wikipedia.org/wiki/Discretization#Discretization_of_linear_state_space_models
[2]
http://techteach.no/publications/discretetime_signals_systems/discrete.pdf
[3]
Г. Чжан, С. Чен и Т. Чен, Цифровой редизайн с помощью обобщенного билинейное преобразование, Int. Дж. Контроль, том. 82, нет. 4, стр. 741-754, 2009 г.. (https://www.mypolyuweb.hk/~magzhang/Research/ZCC09_IJC.pdf)
[4]
Г. Ф. Франклин, Дж. Д.
 Пауэлл и М. Л. Уоркман, Цифровое управление
динамических систем, 3-е изд. Менло-Парк, Калифорния: Аддисон-Уэсли,
стр. 204-206, 1998.
Пауэлл и М. Л. Уоркман, Цифровое управление
динамических систем, 3-е изд. Менло-Парк, Калифорния: Аддисон-Уэсли,
стр. 204-206, 1998.Примеры
Мы можем преобразовать непрерывную систему в пространстве состояний в дискретную:
>>> импортировать numpy как np >>> импортировать matplotlib.pyplot как plt >>> из scipy.signal импортировать cont2discrete, lti, dlti, dstep
Определить непрерывную систему в пространстве состояний.
>>> A = np.array([[0, 1],[-10., -3]]) >>> B = np.array([[0],[10.]]) >>> C = np.array([[1., 0]]) >>> D = np.массив([[0.]]) >>> l_system = lti(A, B, C, D) >>> т, х = l_system.step (T = np.linspace (0, 5, 100)) >>> рис, топор = plt.subplots() >>> ax.plot(t, x, label='Continuous', linewidth=3)
Преобразуйте его в дискретную систему в пространстве состояний, используя несколько методов.
>>> dt = 0,1 >>> для метода в ['zoh', 'bilinear', 'euler', 'backward_diff', 'foh', 'impulse']: ... d_system = cont2discrete((A, B, C, D), dt, method=method) .
 .. с, x_d = dstep (d_system)
... ax.step(s, np.squeeze(x_d), label=method, where='post')
>>> ax.axis([t[0], t[-1], x[0], 1.4])
>>> ax.legend(loc='лучший')
>>> fig.tight_layout()
>>> plt.show()
.. с, x_d = dstep (d_system)
... ax.step(s, np.squeeze(x_d), label=method, where='post')
>>> ax.axis([t[0], t[-1], x[0], 1.4])
>>> ax.legend(loc='лучший')
>>> fig.tight_layout()
>>> plt.show()
Введение в марковские процессы с дискретным временем – анализ временных рядов, регрессия и прогнозирование
И руководство по моделированию марковского процесса с дискретным временем с помощью Python
Цепь Маркова с дискретным временем можно использовать для описания поведения системы, которая переходит из одного состояния в другое с определенной вероятностью, и эта вероятность перехода в следующее состояние зависит только от того, в каком состоянии находится система в данный момент, т. е. не зависит от того, в каких состояниях находилась система до текущего состояния.
Приведенное выше определение в значительной степени подводит итог тому, что является марковским процессом с дискретным временем или цепью Маркова, как ее часто называют.
Но приведенное выше описание обманчиво просто. Как мы увидим, даже самые простые цепи Маркова могут создавать очень интересные паттерны поведения системы.
Как мы увидим, даже самые простые цепи Маркова могут создавать очень интересные паттерны поведения системы.
Мы будем использовать термины Марковский процесс и Марковская цепь взаимозаменяемо.
Марковский процесс с двумя состояниями (Изображение автора)Цепь Маркова, показанная выше, имеет два состояния, или режима , как их иногда называют: +1 и -1. Возможны четыре типа переходов между двумя состояниями:
- Состояние +1 в состояние +1: этот переход происходит с вероятностью p_11
- Состояние +1 в состояние -1 с вероятностью перехода p_12
- Состояние -1 в состояние +1 с вероятностью перехода p_21
- 7
- Состояние -1 в состояние -1 с вероятностью перехода p_22
Приведенный выше рисунок известен как диаграмма перехода состояний марковского процесса.
На следующей диаграмме показан другой способ представления этого марковского процесса. Ось X — это ось времени. Пузырьки представляют различные возможные состояния, в которых может находиться процесс на каждом временном шаге.
Пузырьки представляют различные возможные состояния, в которых может находиться процесс на каждом временном шаге.
В действительности на каждом временном шаге процесс будет находиться ровно в одном из многих возможных состояний. На следующей диаграмме черные кружки изображают одну такую реализацию марковского процесса на 4 последовательных временных шагах:
Реализация марковской цепи с двумя состояниями на 4 последовательных временных шагах (изображение автора)Таких реализаций много. возможное. В марковском процессе с двумя состояниями имеется 9N возможных реализаций цепи Маркова за N временных шагов.
Иллюстрируя марш марковского процесса по оси времени, мы получаем следующее важное свойство марковского процесса:
Реализация марковской цепи по временному измерению представляет собой временной ряд.
В цепи Маркова с двумя состояниями существует четыре возможных перехода состояний и соответствующие вероятности перехода. Мы можем представить их в виде матрицы перехода состояний P следующим образом:
Мы можем представить их в виде матрицы перехода состояний P следующим образом:
Для цепи Маркова над n-состояниями (1,2,3,…,n) , матрица переходов выглядит следующим образом:
Матрица переходов состояний P марковского процесса с n состояниями (Изображение автора)Матрица переходов состояний имеет следующие два важных свойства:
- Поскольку каждый элемент p_ij является вероятность, 0 ≤ p_ij ≤ 1
- Каждая строка P в сумме дает 1,0, т. е.
Это связано с тем, что индекс строки представляет исходное состояние в момент времени t , а индекс столбца представляет состояние назначения в момент времени (t+1) . Если процесс находится в исходном состоянии i в момент времени t , в момент (t+1) , он должен находиться в одном из допустимых состояний (1,2,3,…,n) .
Таким образом, мы можем переформулировать матрицу перехода марковского процесса с двумя состояниями следующим образом:
Матрица перехода состояний P марковского процесса с двумя состояниями (изображение автора) ввести случайную величину X_t. Суффикс t в X_t обозначает временной шаг. На каждом временном шаге t , X_t принимает значение из пространства состояний [1,2,3,…,n] согласно некоторому распределению вероятностей. Одной из возможных последовательностей значений, которые принимает X_t , является {X_0=1, X_1=3, X_2=4, X_3=0,…,X_t=k}.Вероятности перехода как условные вероятности )
задается следующей условной вероятностью: Вероятность того, что цепь Маркова будет в состоянии j в момент времени t, при условии, что она была в состоянии i в (t-1) (изображение автора)Действительно, это вероятность перехода p_ij .
Марковское свойство
Марковское свойство утверждает, что p_ij не зависит от состояния, в котором система находилась в моменты времени (t-2), (t-3),…,0 . Свойство Маркова выражается следующим образом:
Свойство Маркова выражается следующим образом:
Вероятности n-шагового перехода
Матрица перехода состояний P имеет это замечательное свойство, на которое, если вы умножите его на себя 9k представляет вероятность того, что система будет находиться в состоянии j после скачков через k число переходов, начиная с состояния i .
Например, рассмотрим следующую матрицу вероятностей перехода для двухэтапного марковского процесса:
Матрица вероятностей перехода с двумя состояниями (изображение за изображением)Вероятности двухэтапного перехода рассчитываются следующим образом:
Вероятности двухэтапного перехода марковского процесса с двумя состояниями (изображение за изображением) В P² , p_11=0,625 есть вероятность вернуться в состояние 1 после прохождения через двух состояний, начиная с состояния 1 . p_12=0,375 — вероятность достижения состояния 2 ровно за два временных шага, начиная с состояния 1 . И так один.
p_12=0,375 — вероятность достижения состояния 2 ровно за два временных шага, начиная с состояния 1 . И так один.
Мы могли бы бесконечно умножать P на себя, чтобы увидеть, как вероятности n шагов меняются со временем. Было бы еще интереснее, если бы мы могли знать, каково безусловное распределение вероятностей X_t на каждом временном шаге t .
Например, в нашем примере двухэтапного марковского процесса на каждом временном шаге t какова вероятность того, что X_t может быть +1 или -1? Эти вероятности представляют собой так называемое распределение вероятности состояния из переменной Маркова X_T во время T и обозначается π _t , (или Δ . 59505995099509,9000 59505950995099509 00 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 55 , (или Δ . 0022 ). Например, для марковского процесса с двумя состояниями, состоящего из состояний +1 и -1, распределение состояний дается следующим образом: Марковский процесс с -состояниями, работающий в состояниях [1,2,3,…,n] , может находиться в любом из этих n состояний в момент времени t , поэтому π _t — вектор длины n следующим образом:
0022 ). Например, для марковского процесса с двумя состояниями, состоящего из состояний +1 и -1, распределение состояний дается следующим образом: Марковский процесс с -состояниями, работающий в состояниях [1,2,3,…,n] , может находиться в любом из этих n состояний в момент времени t , поэтому π _t — вектор длины n следующим образом:
В общем, на каждый элемент π_t можно ссылаться, используя обозначение π _jt. π _JT индексируется с использованием двух переменных J и T , что указывает на безусловную вероятность π из процесса, находящегося в состоянии J в Time T:
.0022 π содержит безусловные вероятности того, что марковский процесс находится в состоянии j= [1,2,…n] в момент времени t (Изображение автора)(Изображение автора)распределения, его элементы всегда дают в сумме 1,0:
Как рассчитать
π_tКак правило, предполагается определенное значение для π _0 , которое является вектором вероятности для состояния 0 , а учитывая π _0 , можно показать, что π _ t можно вычислить следующим образом: t = 0 и матрица перехода P (Изображение автора)
Идея вычисления π _ t состоит в матричном умножении матрицы перехода состояния на саму себя t количество раз, чтобы получить t -шаговые вероятности перехода и умножить t-шаговые вероятности перехода на безусловное распределение вероятностей π _0 при t=0.
Обратите внимание на следующие две особенности приведенного выше уравнения:
Распределение вероятностей состояния марковского процесса в момент времени t зависит от:
- Начального распределения вероятностей =0, и
- Зависит от временного шага t. Таким образом, распределение вероятностей эволюционирует с течением времени.
Марковский процесс Пример
Давайте проработаем все изученные концепции на примере.
Предположим, что акции Acme Corporation увеличиваются или уменьшаются в соответствии со следующими правилами:
- По сравнению с ценой закрытия предыдущего дня цена закрытия текущего дня либо выше, либо ниже на несколько процентных пунктов. Для, например. в какой-то день акции Acme закрываются на 2,3% выше, чем в предыдущий день. В другие дни она может закрыться на 0,8% ниже цены закрытия предыдущего дня.
- Для любой последовательности из 3 дней, обозначенной «накануне», «вчера» и «сегодня», если Acme вчера закрылась выше, чем накануне, она закроется сегодня выше, чем вчера, с вероятностью p_11 .
 Следовательно, сегодня она закроется ниже, чем вчера, с вероятностью (1 — p_11).
Следовательно, сегодня она закроется ниже, чем вчера, с вероятностью (1 — p_11). - Давайте также предположим, что если Acme вчера закрылась ниже, чем накануне, то вероятность того, что сегодня она снова закроется ниже, составляет p_22 . И, следовательно, вероятность того, что сегодня она закроется выше, чем вчера, равна 9.0004 (1 — стр.22) .
Вы, наверное, догадались, что курс акций Acme можно смоделировать с помощью марковского процесса с двумя состояниями. Его диаграмма переходов состояний выглядит следующим образом:
Диаграмма переходов состояний для марковского процесса, используемого для моделирования движения цены акций Acme (Изображение автора)И его матрица вероятностей переходов P выглядит следующим образом:
Матрица переходов состояний P марковского процесса с двумя состояниями (изображение автора) Теперь давайте прикрепим некоторые примерные значения для этих вероятностей. Предположим, что вероятность того, что цена Acme будет двигаться вверх два дня подряд, равна 0,6, а вероятность того, что цена пойдет вниз два дня подряд, равна 0,25. Таким образом,
Таким образом,
P_11 = 0,6 и P_22 = 0,25
и, следовательно, мы имеем:
P_12 = 1 — P_11 = 0,4 и, P_21 = 1 — P22 = 0,75
. акция выглядит следующим образом:
Матрица переходов состояний для движения цены акций Acme (изображение автора)Диаграмма переходов состояний модели марковского процесса для акций Acme выглядит следующим образом:
Диаграмма переходов состояний для модели марковского процесса акций Acme движение (Изображение автора)Теперь мы хотели бы рассчитать следующее безусловное распределение вероятностей:
Распределение вероятностей состояний для марковского процесса с двумя состояниями (изображение автора) Предположим, что начальное значение равно π _0= [0,5,0,5 ], то есть равная вероятность его закрытия выше (состояние +1) или ниже (состояние — 1) в день листинга по сравнению с ценой IPO. Если мы повторно применим формулу для π _ t = π 9t , мы получим вектор распределения вероятностей π _ t для каждого временного шага t.
Следующий код Python вычисляет π _ t:
импортировать numpy как np
из matplotlib импортировать pyplot как plt
# инициализируем матрицу перехода P
P=np.массив([[0,6,0,4],[0,75,0,25]])
#инициализировать pi_0
pi_0 = np.массив ([0,5, 0,5])
# настроить массив для накопления вероятностей состояний в моменты времени от t=1 до 10
пи=[]
pi.append(pi_0)
P_mul=P.copy()
# вычислить вероятность состояния для каждого t и сохранить ее
для я в диапазоне (10):
P_mul=np.matmul(P_mul,P)
pi_t = np.matmul (pi_0, P_mul)
pi.append(pi_t)
пи = np.массив (пи)
Приведенный выше код сохраняет все вычисленные векторы π_ t в массиве π. Let’s separately plot the components π _1t and π _2t of π_ t = [ π _1t , π _2t] для t=1 от до 10.
#plot pi_2t = P(X_t = -1) в зависимости от t
рис = plt.figure()
fig.suptitle('Вероятность закрытия ниже закрытия предыдущего дня')
plt.plot (диапазон (длина (пи)), пи [:, 1])
plt.show()
#plot pi_1t = P(X_t = +1) в зависимости от t
рис = plt.figure()
fig.suptitle('Вероятность закрытия выше закрытия предыдущего дня')
plt.plot (диапазон (длина (пи)), пи [:, 0])
plt.show()
Мы получаем следующие два графика:
(Изображение автора)Мы видим, что всего за несколько временных шагов вектор безусловных вероятностей равен π_ t = [ π _1t , π _2t] settles down into the steady state value [ 0.65217391, 0.34782609 ].
На самом деле можно показать, что если марковский процесс с двумя состояниями со следующей матрицей перехода выполняется в течение «долгого времени»: распределение вероятностей состояний π_ t установившихся состояний к следующему постоянному (предельному) распределению вероятностей, которое не зависит ни от t , ни от начального распределения вероятностей π_0 :
марковский процесс с двумя состояниями (изображение автора)Моделирование движения цены акций Acme с использованием марковского процесса
Давайте смоделируем движение цены акций Acme Corp на каждом временном шаге t с использованием распределения вероятностей π_t в момент времени t. Процедура моделирования выглядит следующим образом:
Процедура моделирования выглядит следующим образом:
- Предположим, что цена IPO Acme составляет 100 долларов.
- Установите начальное распределение вероятностей:
π_0=[P(X_t = +1)=0,5, P(X_t = -1) = 0,5]. - Сопоставьте состояние Маркова +1 с действием увеличения цены закрытия Acme предыдущего дня на случайный процент в интервале [0,0%, 2,0%].
- Сопоставьте состояние Маркова -1 с уменьшением цены закрытия Acme предыдущего дня на аналогичный случайный процент в интервале [0,0%, 2,0%]. 9т.
- Генерировать равномерно распределенное случайное число в интервале [0, 1.0]. Если это число меньше или равно π_1t = P(X_t = +1) , увеличить цену закрытия по сравнению с предыдущим временным шагом на случайный процент в интервале [0,0%, 2,0%], иначе уменьшить предыдущей цене закрытия на тот же случайный процент. Повторите эту процедуру для необходимого количества временных шагов.
Вот график изменения цены акций Acme за 365 торговых дней:
Цена закрытия корпорации Acme, смоделированная с использованием марковского процесса с двумя состояниями (изображение автора)Вот исходный код для создания приведенного выше графика:
#Смоделируйте цену закрытия компании цена закрытия = 100,0 #инициализировать pi_0 pi_0 = np.i P_mul=np.matmul(P_mul,P) # умножаем на pi_0, чтобы получить вероятность состояния для времени i pi_t = np.matmul (pi_0, P_mul) # создаем случайную дельту в диапазоне [0, 2.0] дельта = случайный.случайный() * 2 # генерируем случайное число в диапазоне [0.0, 1.0] г = случайный. случайный () # если r <= P(X_t = +1), увеличить цену закрытия на дельту, # иначе уменьшите цену закрытия на дельту если г <= pi_t[0]: цена_закрытия = math.max(цена_закрытия*(100+дельта)/100,1.0) еще: цена_закрытия = цена_закрытия*(100-дельта)/100 # накапливаем новую цену закрытия close_prices.append (закрытие_цена) # построить все накопленные цены закрытия рис = plt.figure() fig.suptitle('Цена закрытия корпорации Acme, смоделированная с использованием марковского процесса') plt.xlabel('время t') plt.ylabel('Цена закрытия') plt.plot (диапазон (T + 1), закрытие_цены) plt.show()
Ссылки и авторские права
Изображения
Все изображения защищены авторским правом Sachin Date в соответствии с CC-BY-NC-SA, если под изображением не указан другой источник и авторские права.

