Докажите что при последовательном соединении двух пружин. Последовательное соединение пружин: формулы, расчеты и практическое применение

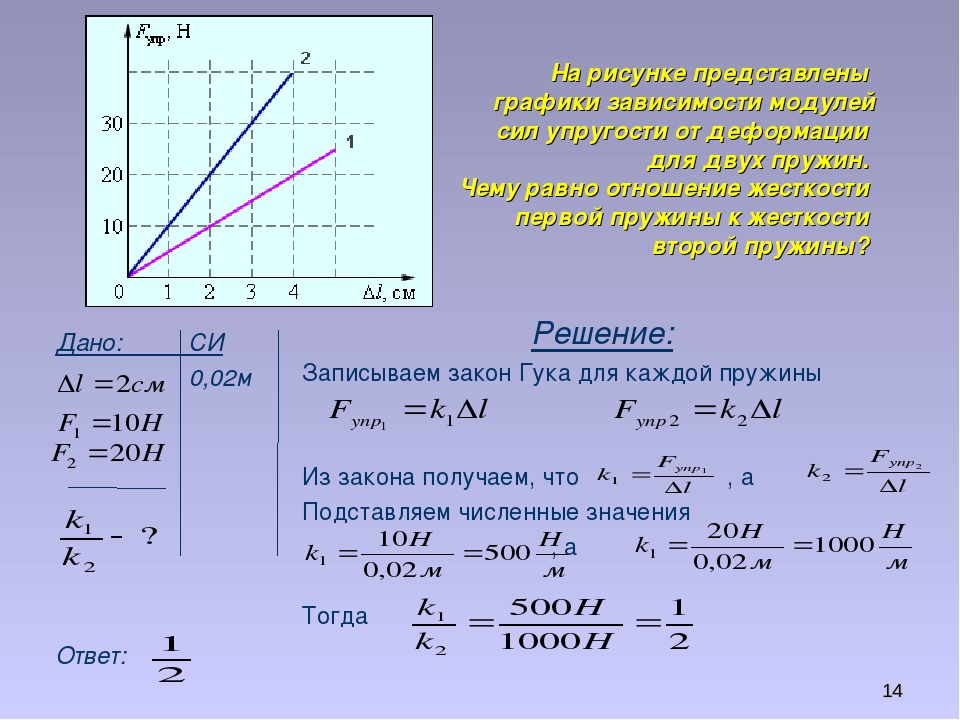
Как рассчитать жесткость и частоту колебаний при последовательном соединении пружин. Какие формулы используются для расчетов. Где применяется последовательное соединение пружин на практике.

Что такое последовательное соединение пружин?

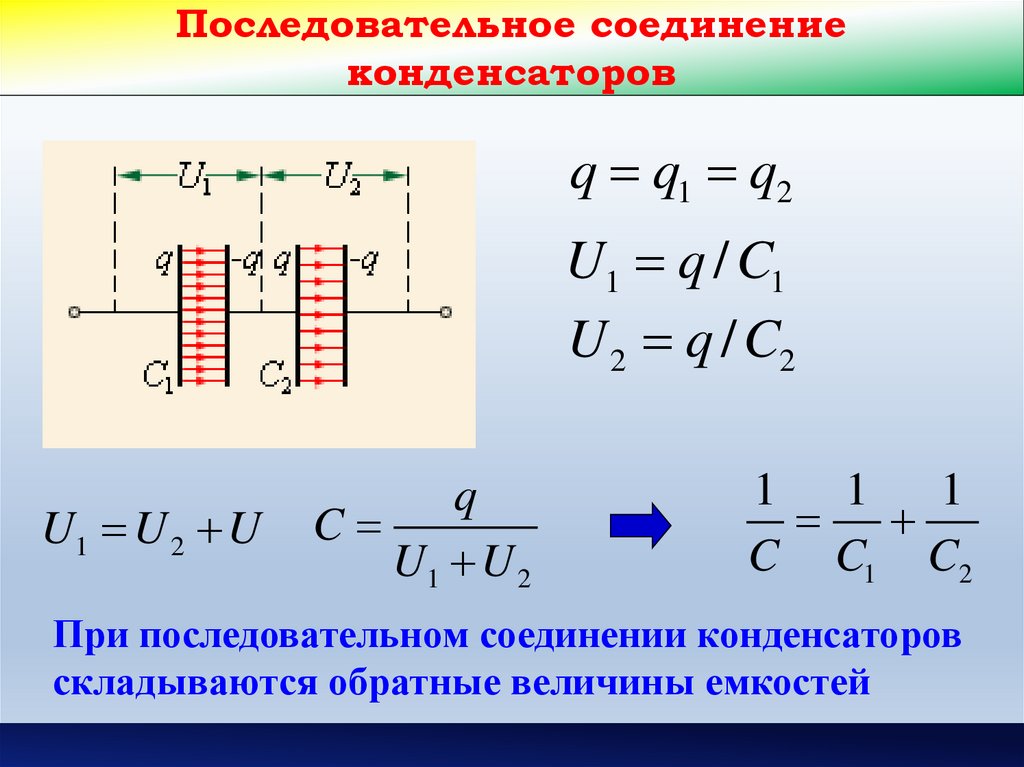
Последовательное соединение пружин — это способ соединения, при котором пружины присоединяются друг к другу концами в ряд. При таком соединении общее удлинение системы равно сумме удлинений отдельных пружин:

x = x1 + x2

где x — общее удлинение системы, x1 и x2 — удлинения первой и второй пружины соответственно.

Как рассчитать жесткость при последовательном соединении пружин?

При последовательном соединении двух пружин с жесткостями k1 и k2 эквивалентная жесткость системы k рассчитывается по формуле:

1/k = 1/k1 + 1/k2

Отсюда можно выразить эквивалентную жесткость:

k = (k1 * k2) / (k1 + k2)

Как видно из формулы, эквивалентная жесткость при последовательном соединении всегда меньше жесткости самой мягкой пружины в системе.

Как рассчитать частоту колебаний при последовательном соединении пружин?

Частота колебаний груза массой m на системе из двух последовательно соединенных пружин рассчитывается по формуле:

f = (1/2π) * √(k/m)

где k — эквивалентная жесткость системы, рассчитанная по формуле выше.

Подставляя выражение для k, получаем:

f = (1/2π) * √((k1 * k2) / (k1 + k2) / m)

Где применяется последовательное соединение пружин на практике?

Последовательное соединение пружин используется во многих технических устройствах и механизмах:

• В подвесках автомобилей для обеспечения плавности хода
• В амортизаторах различной техники
• В пружинных весах для расширения диапазона измерений
• В часовых механизмах
• В различных измерительных приборах

Как доказать формулу для эквивалентной жесткости при последовательном соединении пружин?

Для доказательства формулы эквивалентной жесткости при последовательном соединении пружин можно использовать следующий подход:

1. Запишем выражения для удлинений каждой пружины через силу F и их жесткости: x1 = F/k1 x2 = F/k2
2. Общее удлинение системы равно сумме удлинений: x = x1 + x2 = F/k1 + F/k2
3. Выразим силу: F = kx, где k — эквивалентная жесткость
4. Подставим выражение для силы в уравнение для x: x = kx/k1 + kx/k2
5. Сократим x: 1 = k/k1 + k/k2
6. Приведем к общему знаменателю: 1 = (k(k1+k2)) / (k1k2)
7. Выразим k: k = (k1k2) / (k1+k2)

Таким образом мы получили формулу для эквивалентной жесткости при последовательном соединении двух пружин.

Какие преимущества дает последовательное соединение пружин?

Последовательное соединение пружин имеет ряд преимуществ:

• Позволяет уменьшить общую жесткость системы
• Увеличивает рабочий ход пружинной системы
• Дает возможность комбинировать пружины с разными характеристиками
• Позволяет распределить нагрузку между несколькими пружинами
• Повышает надежность системы за счет дублирования элементов

Как изменяется период колебаний при последовательном соединении пружин?

При последовательном соединении пружин период колебаний груза увеличивается по сравнению с колебаниями на одной пружине. Это происходит из-за уменьшения эквивалентной жесткости системы.

Период колебаний груза массой m на системе из двух последовательно соединенных пружин рассчитывается по формуле:

T = 2π * √(m/k)

где k — эквивалентная жесткость системы.

Подставляя выражение для k при последовательном соединении, получаем:

T = 2π * √(m(k1+k2) / (k1k2))

Как видно из формулы, период колебаний увеличивается по сравнению с периодом колебаний на одной пружине.

Как влияет последовательное соединение на энергию пружинной системы?

При последовательном соединении пружин потенциальная энергия системы распределяется между пружинами. Общая потенциальная энергия системы равна сумме энергий каждой пружины:

U = U1 + U2 = (k1x1^2)/2 + (k2x2^2)/2

где U — общая потенциальная энергия, U1 и U2 — энергии первой и второй пружины, x1 и x2 — их удлинения.

При этом общая энергия системы остается такой же, как если бы груз колебался на одной пружине с эквивалентной жесткостью:

U = (kx^2)/2

где k — эквивалентная жесткость системы, x — общее удлинение.

Какие ограничения существуют при последовательном соединении пружин?

При использовании последовательного соединения пружин следует учитывать некоторые ограничения:

• Увеличение габаритов системы по сравнению с одной пружиной
• Возможность потери устойчивости при большом количестве последовательно соединенных пружин
• Сложность обеспечения точной настройки системы из-за взаимного влияния пружин
• Необходимость учета различий в характеристиках отдельных пружин
• Возможность возникновения нежелательных колебаний в системе

Учет этих ограничений позволяет эффективно использовать последовательное соединение пружин в различных технических устройствах и механизмах.

Простая физика — EASY-PHYSIC

В этой статье собраны задачи, в которых так или иначе присутствует сила упругости. Задачи прошлых лет ЕГЭ или из олимпиадных подборок.

Задача 1.

Две невесомые пружины прикреплены к верхнему и нижнему торцам неподвижного цилиндра. Концы пружин соединены. Жесткость верхней пружины равна  Н/м, жесткость нижней  Н/м. Пружины находятся в нерастянутом состоянии. Между ними вставили тонкую платформу массой  кг. Пружины прикрепляют к платформе (см. рис.). На сколько при этом растянулась верхняя пружина?

К задаче 1

Запишем уравнение по второму закону Ньютона для груза:

Здесь — сила упругости верхней пружины, она пытается вернуться в нерастянутое состояние, поэтому будет тянуть платформу вверх. — сила упругости нижней пружины, она пытается вернуться в нерастянутое состояние, поэтому будет толкать платформу вверх.

Тогда

При этом на сколько растянулась верхняя пружина, на столько же сжалась нижняя: . Следовательно,

Ответ: 40 см.

Задача 2.

К потолку прикреплена конструкция, состоящая из двух пружин и двух маленьких чашек A и B. Расстояние от пола до потолка равно 2 м. Жесткости пружин равны  Н/м и  Н/м. Длины нерастянутых пружин одинаковы и равны 30 см. Масса чашки A равна  г, чашка B невесома. Груз какой массы надо положить в чашку A, чтобы чашка B достала до пола? Какой груз надо положить в чашку B, чтобы она достала до пола (чашка A при этом пуста)?

К задаче 2

Чтобы чашка В достала до пола, нужно, чтобы первая пружина растянулась до длины 1,7 м – тогда нерастянутая вторая пружина длиной 30 см коснется пола. Тогда удлинение пружины А должно составить 1 м 40 см. Следовательно,

Но сама чаша весит 100 г, следовательно, добавив 2 кг в чашу, мы обеспечим нужную силу.

Система из двух пружинок, соединенныx последовательно, имеет жесткость

Растягивать всю систему будем на 1,4 м – именно столько чашку В отделяет от пола.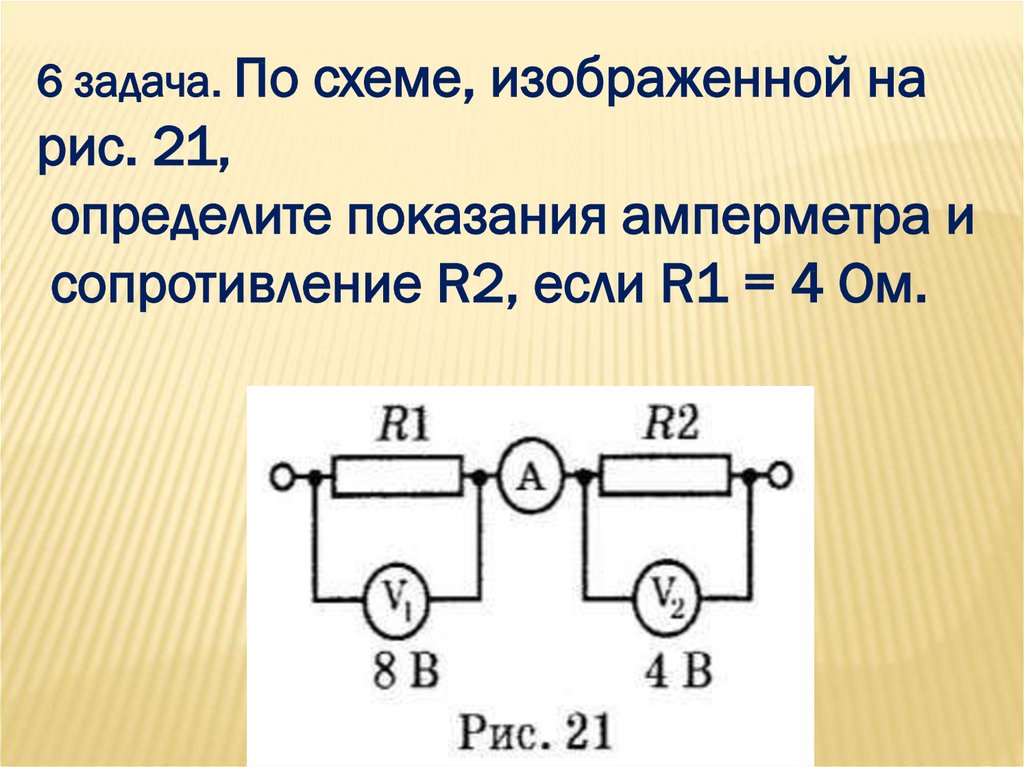

Так как чашка А весит 100 г, то в этом случае масса дополнительного груза будет 1,3 кг.

Ответ: а) 2 кг;  б)1,3 кг.

Задача 3.

Два шарика подвешены на вертикальных тонких нитях так, что они находятся на одной высоте. Между ними находится сжатая и связанная нитью пружина. При пережигании связывающей нити пружина распрямляется, отклоняя шарики в разные стороны на одинаковые углы. Во сколько раз одна нить длиннее другой, если отношение масс ? Считать величину сжатия пружины во много раз меньше длин нитей.

К задаче 3

Когда пружина толкнет шарики, они начнут двигаться по окружностям радиусов и соответственно. Первый поднимется при этом на высоту , а второй – на высоту . Определим эти высоты:

По закону сохранения импульса

Возведем в квадрат:

Или

Из равенства кинетической и потенциальной энергий следует, что

И аналогично

Поэтому

Подставим выражения, полученные вначале:

Сократим:

Ответ: .

Задача 4.

Брусок, покоящийся на горизонтальном столе, и пружинный маятник, состоящий из грузика и легкой пружины, связаны легкой нерастяжимой нитью через идеальный блок (см. рисунок). Коэффициент трения между основанием бруска и поверхностью стола равен 0,25. Груз маятника совершает колебания с периодом 0,5 с вдоль вертикали, совпадающей с вертикальным отрезком нити. Максимально возможная амплитуда этих колебаний, при которой они остаются гармоническими, равна 4 см. Чему равно отношение массы бруска к массе грузика?

К задаче 4

Координата грузика при колебаниях может быть записана как

Запишем второй закон Ньютона для грузика:

Запишем второй закон Ньютона для бруска:

Сила трения скольжения равна

Тогда, чтобы брусок не поехал под действием качаний грузика, нужно, чтобы соблюдалось условие:

Откуда отношение масс равно

Определить ускорение можно, взяв вторую производную по координате:

Максимальное ускорение равно

Подставим это ускорение в полученное отношение масс:

Ответ:

Задача 5. Пружинное ружьё наклонено под углом к горизонту. Энергия сжатой пружины равна 0,41 Дж. При выстреле шарик массой  г проходит по стволу ружья расстояние , вылетает и падает на расстоянии  м от дула ружья в точку , находящуюся с ним на одной высоте (см. рис.). Найдите расстояние . Трением в стволе и сопротивлением воздуха пренебречь.

К задаче 5

Определим скорость шарика при вылете из ружья .

По горизонтали шарик полетит равномерно со скоростью :

По вертикали шарик будет иметь начальную скорость , и она станет равной нулю в максимальной точке подъема:

Тогда время полета до максимальной точки подъема

Откуда скорость равна

Определим скорость шарика вначале. Вся энергия пружины переходит в кинетическую энергию шарика:

Таким образом, в начале трубы скорость была 4,05, а в конце – 3,4 м/с. Составим закон сохранения энергии. Учтем, что конец трубы приподнят относительно начала, следовательно, часть энергии шарика превратилась в потенциальную:

Откуда

Тогда длина ствола больше вдвое, так как катет, лежащий против угла в тридцать градусов, вдвое короче гипотенузы. .

Ответ: 48 см.

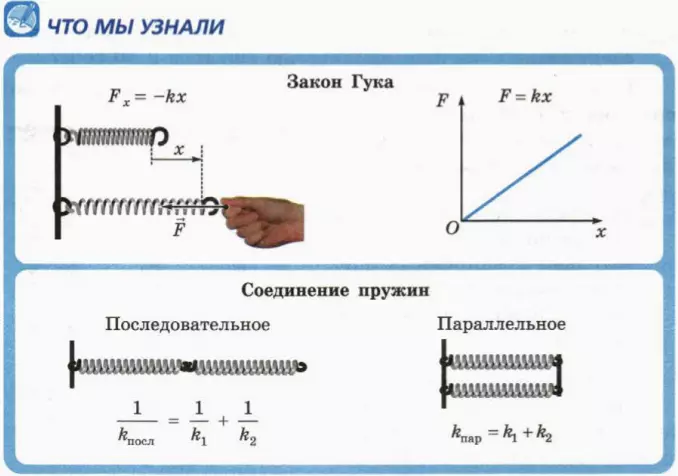
Параллельное соединение пружин

При параллельном соединении двух пружин, имеющих коэффициенты жесткости с₁, с₂ (рис. 2.5), смещение тела равно деформации каждой из пружин:

. (2.9)

Рис. 2.5 Параллельное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна сумме сил упругости двух установленных пружин, откуда с учетом (2.9) получаем

,

окончательно

. (2.10)

При последовательном соединении двух пружин, имеющих коэффициенты жесткости с₁, с₂ (рис. 2.6), смещение тела равно сумме деформаций пружин:

. (2.11)

Рис. 3.6 Последовательное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна каждой из сил упругости установленных пружин, откуда

,

,

откуда

Окончательно с учетом (2.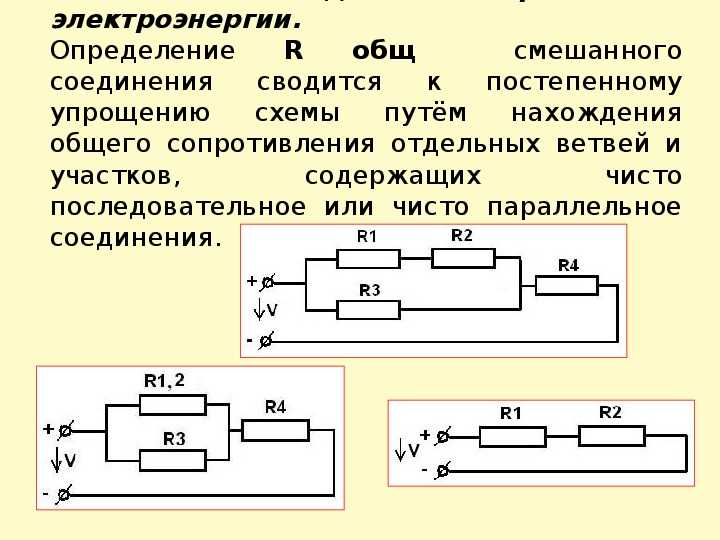 11) получаем

. (2.12)

2. Влияние сопротивления на свободные колебания

Пусть на точку массы m, совершающую прямолинейное движение, действуют две силы (рис. 2.7):

1. Восстанавливающая сила (сила упругости пружины): .

2. Сила сопротивления, пропорциональная скорости движения точки (сила сопротивления демпфера): .

Рис. 2.7 Движение массы с демпфированием

Дифференциальное уравнение движения точки запишется как

;

,

обозначая

, , (2.13)

получаем линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

. (2.14)

Характеристическое уравнение имеет вид

, (2. 15)

его корни равны

, (2.16)

где – дискриминант.

Как известно из курса высшей математики, общее решение дифференциального уравнения (2.14) существенно зависит от знака дискриминанта , т.е. от соотношения между b и k.

1-й случай (малое сопротивление): b  k , D  0.

Обозначим , причем k*  k. Тогда корни (2.16) характеристического уравнения будут комплексно сопряженными:

,

Общее решение дифференциального уравнения (2.14) в данном случае имеет вид

, (2.17)

это затухающие колебания с частотой k^* и периодом (рис.3.8).

Амплитуда колебаний убывает со временем. Отношение последующей амплитуды к предыдущей называется декрементом затухания:

< 1 (2. 18)

Рис. 2.8 Затухающие колебания

Часто используется также логарифмический декремент .

Таким образом, амплитуды образуют геометрическую прогрессию с показателем q, меньшим единицы.

Видим также, что наличие сопротивления приводит к уменьшению частоты колебаний (k^* 

k) и к увеличению их периода (Т^* > Т).

2-й случай (граничный): b = k , D = 0.

Корни (2.16) характеристического уравнения получаются кратные, , и решение дифференциального уравнения (2.14) приобретает вид

. (2.19)

Поскольку экспонента убывает быстрее, чем растёт линейная функция времени, в зависимости от начальных условий движения получим ту или иную картину затухающего апериодического (т. е. не колебательного) движения (рис.2.9).

3-й случай (большое сопротивление): b > k, D > 0.

В этом случае обозначим >0, и оба корня (2.16) характеристического уравнения будут действительными и отрицательными:

< 0, < 0,

общее решение

. (2.20)

Рис. 2.9 График затухающего апериодического движения

Здесь также получаем затухающие апериодическое движение, графики будут такие же, как и в случае b= k.

Две пружины соединены и соединены с массой m . Если константы силы пружины равны k1 и k2, то частота колебаний массы m равна ад ки рукаават ке!

Ответить

Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.

---

Похожие видео

Стержень массы m и длины l, шарнирно закрепленный на одном конце, соединен двумя пружинами жесткости k_1 и k_2 так, что в состоянии равновесия он находится в горизонтальном положении. Какова угловая частота системы? (в (рад)/(с)) (Возьмите l=1m, b=(1)/(4)m, K_1=16(N)/(m), K_2=61(N)/(m).

11446982

Две пружины с силовыми константами K и 2K соединены массой m ниже Частота колебаний массы равна из двух пружин k_(1) и k_(2), показано, что частота колебаний массы m равна

17464632

K बल नियतांक वाले स्प्रिंग से जुड़े M द्रव्यमान के की स स्वाभ कोणीय आवृति होती है है है है है है है है है है है है है है है है है है है है है है है है होती है है होती है होती होती होती तथ होती तथ तथ तथ तथ तथ तथ तथ तथ तथvenंकrehly बल तथ तथvenंकчей तथ तथ तथvenंकчей तथ तथ तथvenंकчей तथ तथvenंकrehंक तथ तथ तथven 2чей तथ तथven 2 wonglaंकrehy व बल तथven 2 wong व बलven की बलven कीven िंगें g की glo पिंड तथ. कोणीय आवृति तथ तथ तथ. द्रव्यमान m के दोलनों की आवृत्ति है

371312388

3

3

3 Сила двух пружин и k2 константы двух пружин и k2. Какой будет эквивалентная силовая постоянная пружинной системы, когда пружины соединены параллельно?

376768559

Силовые константы двух пружин равны k_1 и k_2 . Один конец пружины соединен с одним концом другого. Эквивалентная силовая постоянная пружинной системы будет равна

376768933

. Две пружины с жесткостью k_(1) и k_(2) ar соединены и связаны с массой m, как показано на рисунке. Вычислите частоту колебаний массы m.

452585887

На рис. 15.29 две пружины соединены и соединены с блоком массой 0,490 кг, который колеблется над полом без трения. Каждая пружина имеет жесткость k = 5000 Н/м. Какова частота колебаний?

482962472

जब भ भारहीन व K बल नियतांक वाली स्प्रिंग पा द द यह क क पिण पिण Как स्प्रिंग को दो बराबर भागो में काटा जाता है। स्प्रिंग के एक भाग पर 2M द्रव्यमान का पिण्ड लटकाया जाता है।।।।। है। है अब दोलनों की आवृति होगी

618401781

Когда m — масса k_1 Частота, когда пружина колеблется с частотой 3 Гц, константа колеблется k_2. Если масса комбинируется с обеими пружинами, как показано, то частота массы будет: —

641279616

Две пружины соединены и соединены с массой m, как показано на рисунке. Если пружины по отдельности имеют силовые постоянные K1 и K2 , то частота колебаний массы m равна

642793173

Текст Решение

Стержень массой m и длиной l, шарнирно закрепленный на одном конце, соединен двумя пружинами с жесткостью k1 и k2 так, чтобы в равновесии он был горизонтален. Чему равна угловая частота системы? (в радах) (Возьмите l=1м,b=14м,K1=16Нм,K2=61Нм.

644111260

Груз m подвешен на двух последовательно соединенных пружинах. Постоянная силы для пружин равна k1 и k2. Период времени подвешенной массы будет равен

644162490

Текст Решение

Две пружины с жесткостями K_1 = 1500 Н//м и K_2 = 3000 Н//м растягиваются с одинаковой силой. Соотношение потенциальной энергии, хранящейся в пружинах, будет

645748058

Текстовое решение

किसी द्रव्यमान m से बल नियत नियत नियत ंक व व की दो स स सхов चित के जुड़ी हैं की दो दो स स के के के। द्रव्यमान के दोलन की आवृत्ति f है। यदि k1 व k2 का मान उनके वास्तविक मानों से चार गुनान उनके व000

645779340

Закон Гука и простое гармоническое движение

Объектив

• •

  измерить жесткость пружины по закону Гука

• •

  исследовать статические свойства упругих предметов и пружин, соединенных последовательно и параллельно

• •

  изучить простой гармонический осциллятор, построенный из пружин и масс

• •

  чтобы убедиться, что период СГМ пропорционален квадратному корню из массы и не зависит от амплитуды

• •

  для измерения динамической жесткости пружины

• •

  проверить выполнение закона сохранения энергии

Оборудование

Часть I:

• •

  две почти одинаковые пружины
• •

  длинная резинка

• •

  опорная стойка с метровой палкой

• •

  50-граммовая вешалка

• •

  набор гирь от 100 г до 600 г

• •

  весы баланса

• •

  Интерфейс научной мастерской с датчиком силы и детектором вращательного движения, используемыми в качестве линейного датчика

Часть II:

• •

  тележка для столкновения с известной массой на горизонтальной дорожке динамики, колеблющаяся с помощью параллельных пружин

• •

  датчик движения и фотодатчик, подключенные к интерфейсу Science Workshop

• •

  нелинейные пружинящие объекты (резинки)

• •

  две прямоугольные гири по ~0,5 кг каждая для изменения массы системы

Введение и теория

Закон Гука

Сила упругости возникает в пружине, когда пружина растягивается/сжимается или деформируется (Δx) под действием внешней силы.

Сила упругости действует в направлении, противоположном внешней силе. Он пытается привести деформированный конец пружины в исходное (равновесное) положение. См. рис. 1.

Рисунок 1

Если растяжение относительно невелико, величина силы упругости прямо пропорциональна растяжению Δx в соответствии с законом Гука:

( 1 )

F _el = −kΔx

где k — константа, обычно называемая жесткостью пружины, а Δx — растяжение (разница между новым ( x ) и положением равновесия). Знак минус перед жесткостью пружины в уравнении

1

F _el = −kΔx

указывает на то, что сила упругости и растяжение действуют в противоположном направлении.

Простое гармоническое движение

Если подвесную массу сместить из положения равновесия и отпустить, то произойдет простое гармоническое движение (ГДМ). SHM означает, что положение изменяется с синусоидальной зависимостью от времени.

( 2 )

x = X _max cos( ω t)

Ниже приведены уравнения для скорости и ускорения.

( 3 )

v = −X _max ω sin( ω t) 

( 4 )

a = −X _max ω ² cos( ω t )

Подставляя уравнения

2

x = X _max cos( ω t)

,

4

a = −x _MAX ω ² COS ( ω T)

и

1

F _EL = -К

. для угловой резонансной частоты колебательной системы:

( 5 )

ω =

 

где k — жесткость пружины, а m масса системы, совершающей простое гармоническое движение.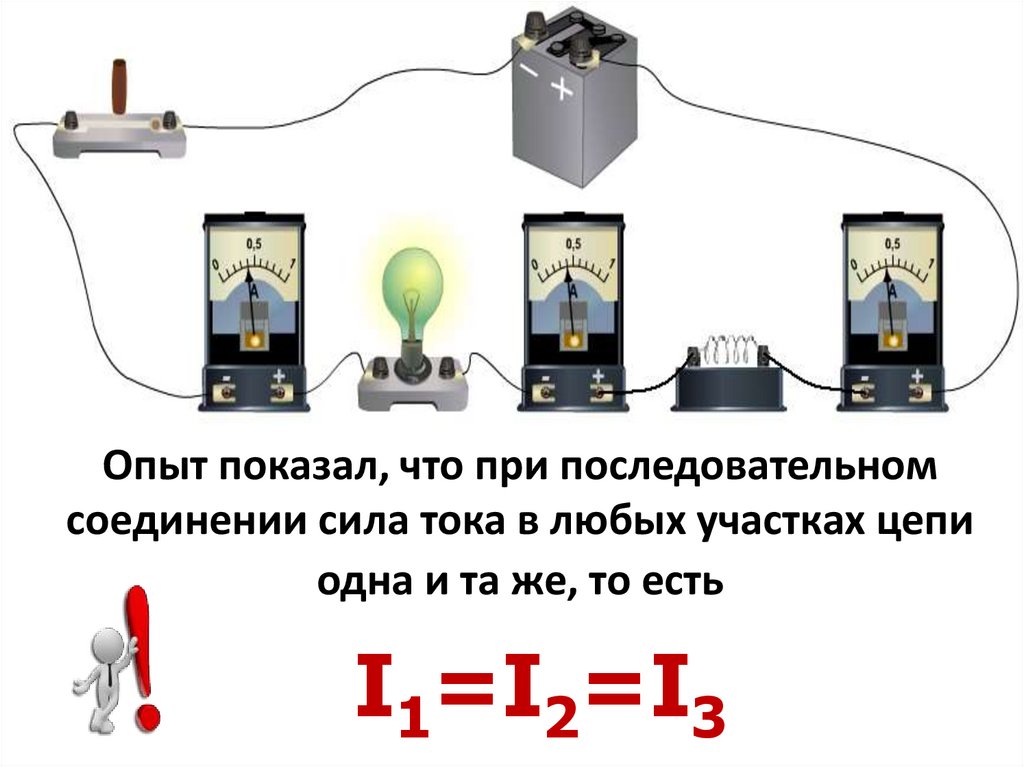 Единицей угловой частоты является

радиан в секунду = рад/с.

Собственную резонансную частоту генератора можно изменить, изменив либо постоянную пружины, либо колеблющуюся массу. Использование более жесткой пружины увеличило бы частоту колебательной системы. Добавление массы к системе уменьшит ее резонансную частоту. Двумя другими важными характеристиками колебательной системы являются период ( T ) и линейная частота (

f ). Период колебаний – это время, за которое тело совершает одно колебание. Линейная частота – это количество колебаний в одну секунду. Период обратно пропорционален линейной частоте.

( 6 )

Т =  

Единицей периода является секунда (с), а единицей частоты является Герц или с ^–1 (Гц = 1/с). Угловая частота связана с периодом и линейной частотой в соответствии со следующим выражением.

( 7 )

ω = 2 π f =  

Энергия

Чтобы возникло колебание, энергия должна быть передана в систему. Когда тело выходит из равновесия, в системе накапливается упругая потенциальная энергия. После освобождения объекта потенциальная энергия переходит в кинетическую и обратно. В гармоническом осцилляторе происходит непрерывный обмен между потенциальной и кинетической энергией. Для колеблющейся пружины ее потенциальная энергия ( E _p ) в любой момент времени равна работе ( W ) при растяжении пружины до соответствующего смещения x .

( 8 )

E _p = W = kx ²  

Кинетическая энергия ( E _k ) осциллятора для любого момента времени будет подчиняться хорошо известному уравнению:

(9)

E _k = mv ² .

Соответственно можно рассчитать максимальную потенциальную энергию и максимальную кинетическую энергию.

( 10 )

E _p = kX _max ²  

( 11 )

E _k = kV _max ²  

Согласно закону сохранения энергии: «Механическая энергия сохраняется (не уничтожается и не создается) в колебательной системе без трения».

Процедура

Пожалуйста, распечатайте рабочий лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.

Часть I. Закон Гука

Измерение жесткости пружины, метод 1

Цель этой части лабораторной работы — найти жесткость пружины. Постоянная пружины представляет собой коэффициент пропорциональности между силой упругости и смещением в соответствии с законом Гука (уравнение

1

F _el = −kΔx

).

1

Подвесьте пружину к опоре, добавьте груз, измерьте исходное положение равновесия с помощью измерительной линейки и запишите его.

2

Добавляйте гири с шагом от 100 г до 600 г и измеряйте соответствующее положение.

3

Обсудите с членами вашей группы столбцы, которые необходимо подготовить в GA для записи данных. Составьте набросок таблицы и уточните его у своего ТА. Подготовьте столбцы в GA.

4

Создайте новый расчетный столбец для данных силы упругости (ДАННЫЕ → НОВЫЙ РАСЧЕТНЫЙ СТОЛБЦ → уравнение: F = переменные « м » * г , где м в кг).

5

Создайте новую расчетную колонку для перемещения (ДАННЫЕ → НОВАЯ РАСЧЕТНАЯ СТОЛБЦА → уравнение = переменные «позиция» — начальное положение равновесия).

6

Постройте график зависимости силы от смещения.

7

Запишите наклон графика и его неопределенность в рабочий лист лабораторной работы 8. Вы будете использовать значение наклона и его неопределенность, чтобы найти постоянную пружины и ее ошибку.

Измерение жесткости пружины, метод 2

Установка аппарата, показанная на рис. 2 будет использоваться для определения жесткости пружины 2.

Рисунок 2 : Аппаратура для эксперимента по закону Гука

1

Откройте предварительно установленный файл эксперимента: desktop\pirt-labs\phy 113\PreSetUpFiles\Springs.

2

Прежде чем снимать фактические данные, откалибруйте датчик силы. Нажмите кнопку «Настройка» на панели инструментов. Затем щелкните значок датчика силы и нажмите кнопку «Калибровать датчики». Это вызовет панель калибровки, показанную на рис. 3.

Рисунок 3 : Калибровка датчика силы в Data Studio

Опция «2 точки» должна быть выбрана в качестве «Типа калибровки». При отсутствии нагрузки на датчик силы введите 0 в окне стандартного значения «Точка калибровки 1». Нажмите кнопку «Тара» на датчике силы. Это действие обнуляет показания датчика силы. Нажмите кнопку «Считать с датчика». Затем повесьте груз весом 1 кг на датчик и введите 9,8 в окне стандартного значения «Точка калибровки 2». Нажмите на кнопку «Чтение с датчика». Нажмите «ОК», чтобы сохранить эту калибровку. Закройте окна «Калибровка датчиков» и «Настройка». Теперь вы готовы к фактическим измерениям жесткости пружины.

3

Замените груз весом 1 кг на пружину. Прикрепите к нему кусок веревки. Оберните шнур вокруг большого шкива детектора вращательного движения против часовой стрелки, как показано на рис. 2. Датчик вращательного движения был откалиброван для считывания линейного расстояния.

4

Нажмите кнопку «Пуск», чтобы начать сбор данных. Осторожно потяните за веревку, наблюдая за окном отображения силы. Начинайте отпускать струну, когда усилие достигает 10 Н.

5

Примените линейную аппроксимацию к хорошей части вашей записи (см.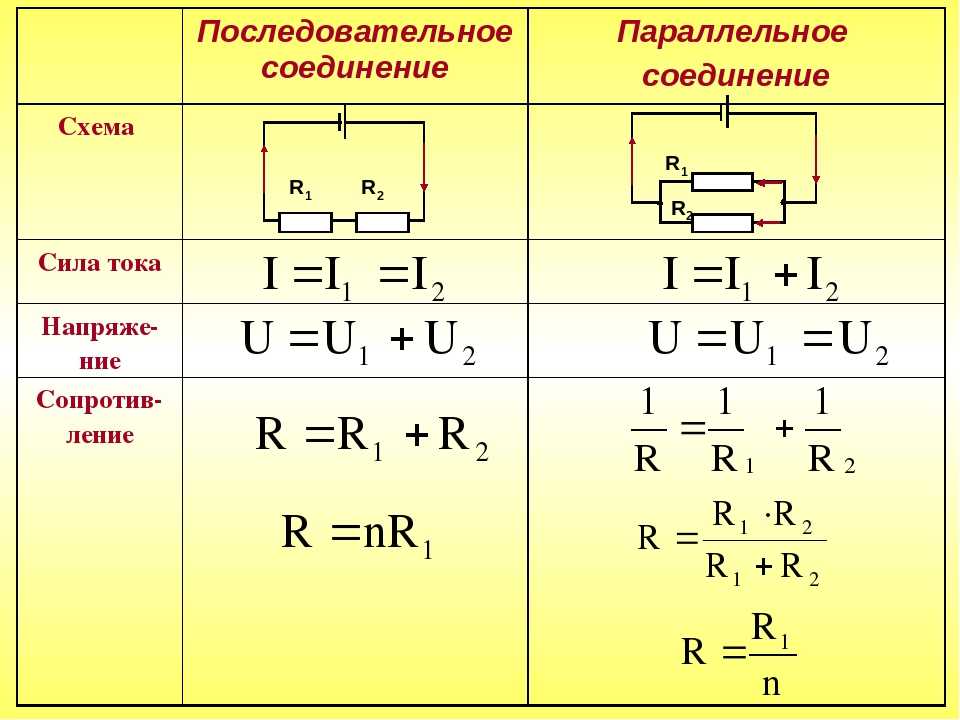 рис. 4), которая представляет собой график зависимости силы упругости от смещения. Наклон этой линии дает постоянную пружины.

6

Запишите наклон графика зависимости силы от зелья и его неопределенность в рабочем листе лабораторной работы 8. Вы будете использовать значение наклона и его неопределенность, чтобы найти постоянную пружины и ее ошибку.

7

Повторите эту процедуру для системы пружин последовательно и параллельно.

8

Запишите наклон графика зависимости силы от положения и его неопределенность в рабочем листе лабораторной работы 8. Вы будете использовать значение наклона и его неопределенность, чтобы найти постоянную пружины и ее ошибку. В разделе «Обсуждение» вам нужно будет сравнить значение жесткости пружины для системы пружин со значением каждой жесткости пружины.

Рисунок 4 : Образец файла эксперимента в DataStudio

Исследование нелинейного упругого объекта.

1

В экспериментальной установке с рис. 2, замените пружину длинной резинкой.

2

Запишите силу в зависимости от положения для движений вниз (увеличение силы) и вверх (уменьшение силы).

3

Используйте эти данные, чтобы определить, соответствует ли резинка закону Гука (

уравнение 1

F _el = −kΔx

).

Часть II — Простое гармоническое движение

В этой части эксперимента вы проверите, зависит ли период от амплитуды; рассчитать резонансную частоту и жесткость пружины системы. Вы будете записывать собранные данные в рабочий лист лабораторной работы 8.

1

Настройте эксперимент, как показано на рисунках ниже. Откройте предварительно установленный файл эксперимента: desktop\pirt-labs\phy 113\PreSetUpFiles\SHM.

Рисунок 5

Рисунок 6

2

Без дополнительной массы измерьте период колебаний для начальных амплитуд 4 см и 12 см. Сбор данных автоматически прекратится через 5 секунд. Пример записи показан на рис. 2. Период измеряется фотодатчиком и заносится в таблицу 1 слева от графика.

3

Без дополнительной массы сместите тележку из положения равновесия примерно на 8 см и начните запись. Снова запишите период колебаний тележки, измеренный фотодатчиком. Запишите все три периода колебаний в рабочий лист лабораторной работы 8.

Рисунок 7 : Пример файла для эксперимента SHM в DataStudio

4

Сопоставьте запись положения и времени с синусоидальной волной. Параметр А – амплитуда (максимальное смещение) колебаний. Параметр B дает вам период колебаний. Вы можете сравнить его значение со значением периода, измеренного фотодатчиком. Параметр D — положение равновесия. Используйте параметр B для расчета резонансной частоты и жесткости пружины системы с помощью уравнений 9.0003 7

ω = 2 π f =  

and

5

ω =

 

from the Introduction and Theory in this Lab Manual.

5

Сопоставьте запись скорости и времени с синусоидальной волной. Запишите параметр А — амплитуду (максимальное значение) графика зависимости скорости от времени.

Обратите внимание, что оба графика, положение относительно времени и скорость относительно времени, представляют собой периодические волны одной и той же частоты, только сдвинутые на 90° или

рад.

Максимальное и минимальное значения положения имеют место, когда скорость равна нулю, а также максимальное и минимальное значения скорости имеют место, когда положение находится в равновесии. С точки зрения энергии системы это означает, что когда потенциальная энергия максимальна (максимальное смещение), кинетическая энергия равна нулю. В этот момент вся энергия является потенциальной. Точно так же в момент, когда пружина не растянута (объект проходит точку равновесия), вся энергия является кинетической. Чтобы проверить теорему о сохранении энергии для колеблющейся тележки, достаточно сравнить ее максимальную потенциальную энергию с максимальной кинетической энергией, найдя процентную разницу потерь энергии.

( 12 )

%loss =

PE i − KE f

PE i

· 100%

 

Relationship between period and mass

Это часть эксперимента, в которой вы убедитесь, что период СГМ пропорционален квадратному корню из массы.

1

Загрузите тележку тяжелыми грузами (по одному) и измерьте период SHM, сохраняя постоянную амплитуду, например. 8 см.

2

Включая данные из предыдущей части эксперимента, у вас будет три точки, чтобы построить график зависимости периода от

m

.

According to the theory (equations

5

ω =

 

and

7

ω = 2 π f =  

) this graph should be a straight линия.

3

Запишите наклон графика T vs

m

 

в лист лабораторной работы 8.

4

Используйте значение наклона и его неопределенность, чтобы найти постоянную пружины.

5

На основе наклона графика рассчитайте динамическую жесткость системы.

Подсказка: Замена

• ω =  

в

• ω =

   

дает

• =

  .

   

Решение для T дает следующее.

• T =

  2 π

  k

  m

   

Обсуждение

Укажите цель лаборатории.