Что такое логические элементы. Какие бывают виды логических элементов. Как работают основные логические операции. Где применяются логические элементы в цифровой технике. Какие существуют физические реализации логических элементов.
Что такое логические элементы и для чего они нужны
Логические элементы — это устройства, предназначенные для обработки информации в цифровой форме. Они являются базовыми «кирпичиками» для построения более сложных цифровых схем и устройств.
Основные функции логических элементов:
- Выполнение простейших логических операций над входными сигналами
- Преобразование уровней сигналов
- Формирование выходных сигналов в соответствии с заданной логической функцией
Логические элементы оперируют двоичными сигналами, которые могут принимать только два значения — логический 0 и логическая 1. Это позволяет создавать на их основе сложные цифровые устройства для обработки и хранения информации.
Основные виды логических элементов
Существует несколько базовых видов логических элементов, выполняющих различные логические функции:

Элемент НЕ (инвертор)
Элемент НЕ выполняет операцию логического отрицания. Он инвертирует входной сигнал — если на входе 0, то на выходе 1 и наоборот.
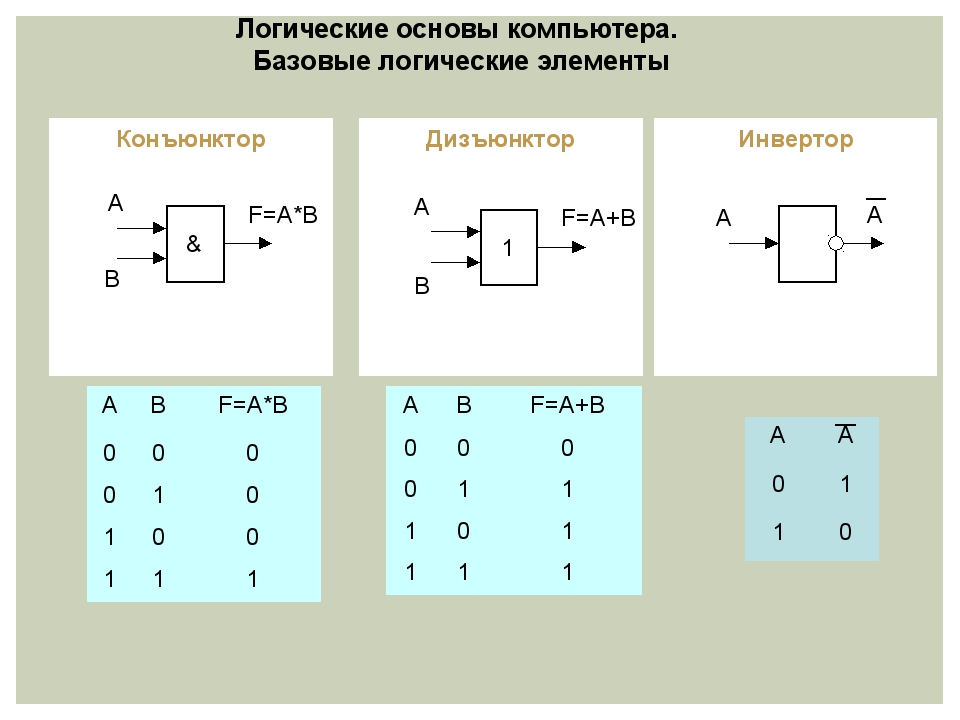
Элемент И (конъюнкция)
Элемент И реализует операцию логического умножения. Выходной сигнал равен 1 только когда все входные сигналы равны 1.
Элемент ИЛИ (дизъюнкция)
Элемент ИЛИ выполняет операцию логического сложения. Выходной сигнал равен 1, если хотя бы один из входных сигналов равен 1.
Элемент И-НЕ
Элемент И-НЕ объединяет функции элементов И и НЕ. Выходной сигнал равен 0 только когда все входные сигналы равны 1.
Элемент ИЛИ-НЕ
Элемент ИЛИ-НЕ сочетает функции элементов ИЛИ и НЕ. Выходной сигнал равен 0, если хотя бы один из входных сигналов равен 1.
Как работают основные логические операции
Рассмотрим принцип работы основных логических операций на примере двухвходовых элементов:
Операция И (конъюнкция)
Таблица истинности для операции И:
| Вход A | Вход B | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Как видно из таблицы, выходной сигнал Y равен 1 только когда оба входных сигнала A и B равны 1.
Операция ИЛИ (дизъюнкция)
Таблица истинности для операции ИЛИ:
| Вход A | Вход B | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 |
Для операции ИЛИ выходной сигнал Y равен 1, если хотя бы один из входных сигналов A или B равен 1.
Применение логических элементов в цифровой технике
Логические элементы нашли широкое применение в различных областях цифровой электроники:
- Процессоры и микроконтроллеры
- Оперативная и постоянная память
- Цифровые схемы управления
- АЦП и ЦАП
- Цифровые фильтры
- Устройства кодирования и декодирования
Рассмотрим несколько конкретных примеров использования логических элементов:
Полусумматор
Полусумматор — это устройство для сложения двух одноразрядных двоичных чисел. Он состоит из элементов И и исключающего ИЛИ:
- Элемент исключающего ИЛИ формирует сумму по модулю 2
- Элемент И формирует сигнал переноса в следующий разряд
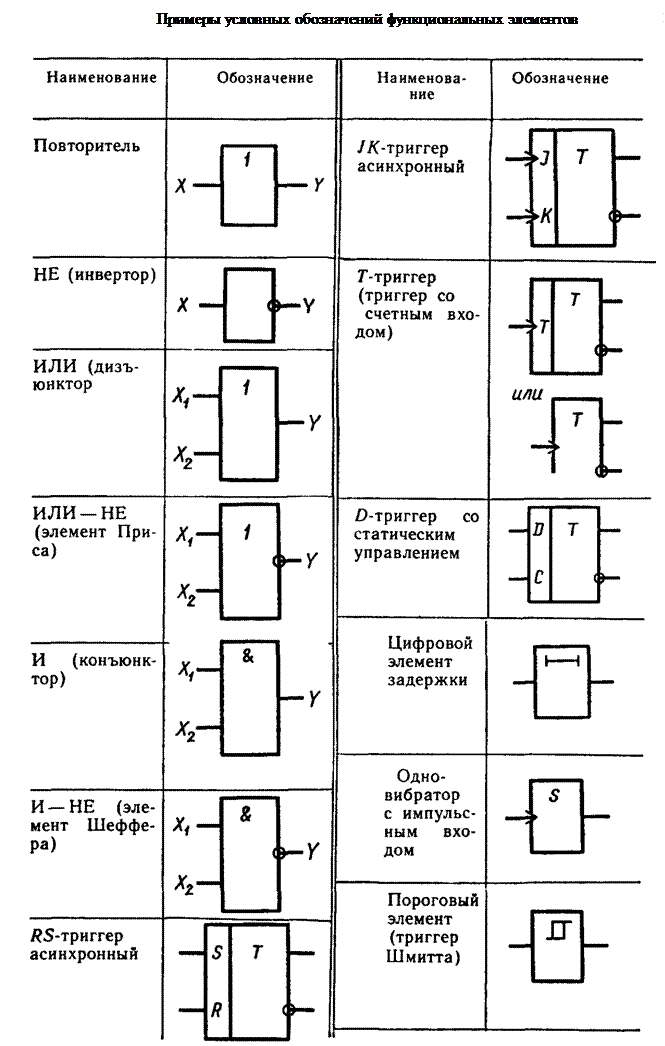
Триггер
Триггер — это устройство с двумя устойчивыми состояниями, способное хранить один бит информации. Простейший RS-триггер строится на двух элементах ИЛИ-НЕ с перекрестными обратными связями.

Физические реализации логических элементов
Существует множество способов физической реализации логических элементов:
Электронные реализации
- Транзисторно-транзисторная логика (ТТЛ)
- Эмиттерно-связанная логика (ЭСЛ)
- Комплементарная металл-оксид-полупроводниковая логика (КМОП)
Другие типы реализаций
- Механические (рычаги, шестерни)
- Гидравлические и пневматические
- Оптические (на основе управления световым потоком)
Наиболее распространенной в современной цифровой электронике является КМОП-технология, обеспечивающая высокое быстродействие при низком энергопотреблении.
Преимущества и недостатки различных типов логических элементов
Рассмотрим основные преимущества и недостатки наиболее распространенных типов логических элементов:
ТТЛ (транзисторно-транзисторная логика)
Преимущества ТТЛ:
- Высокое быстродействие
- Хорошая помехоустойчивость
- Широкий выбор микросхем
Недостатки ТТЛ:
- Относительно высокое энергопотребление
- Небольшой коэффициент разветвления по выходу
КМОП (комплементарная металл-оксид-полупроводниковая логика)
Преимущества КМОП:

- Очень низкое энергопотребление в статическом режиме
- Высокая степень интеграции
- Широкий диапазон напряжений питания
Недостатки КМОП:
- Чувствительность к статическому электричеству
- Меньшее быстродействие по сравнению с ТТЛ (в ранних реализациях)
Перспективы развития логических элементов
Развитие логических элементов идет по нескольким основным направлениям:
Уменьшение размеров
Продолжается миниатюризация логических элементов, что позволяет увеличивать плотность их размещения на кристалле. Современные технологии позволяют создавать транзисторы размером менее 10 нм.
Снижение энергопотребления
Разрабатываются новые технологии, позволяющие снизить энергопотребление логических элементов. Это особенно важно для мобильных устройств и систем Интернета вещей.
Увеличение быстродействия
Ведутся работы по созданию сверхбыстрых логических элементов на основе новых материалов и физических принципов, например, спинтроники.
Квантовые вычисления
Разрабатываются квантовые логические элементы, способные оперировать кубитами вместо классических битов. Это открывает возможности для создания квантовых компьютеров, способных решать некоторые задачи гораздо быстрее классических компьютеров.
Заключение
Логические элементы являются фундаментальными компонентами современной цифровой электроники. Они обеспечивают базовые операции обработки двоичной информации, на основе которых строятся все более сложные цифровые устройства. Несмотря на свою простоту, логические элементы продолжают развиваться, становясь меньше, быстрее и энергоэффективнее, что открывает новые возможности для создания все более совершенных цифровых систем.
Логические элементы — Википедия
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательностями «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно x(xn)∗m{\displaystyle \ x^{(x^{n})*m}} логических функций и соответствующих им логических элементов, где x{\displaystyle \ x} — основание системы счисления, n{\displaystyle \ n} — число входов (аргументов), m{\displaystyle \ m} — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны 2(22)∗1=24=16{\displaystyle 2^{(2^{2})*1}=2^{4}=16} двоичных двухвходовых логических элементов и 2(23)∗1=28=256{\displaystyle 2^{(2^{3})*1}=2^{8}=256} двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элементов и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из 2(21)=22=4{\displaystyle 2^{(2^{1})}=2^{2}=4} возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
 Инвертор, НЕ (IEC)
Инвертор, НЕ (IEC)
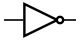 Инвертор, НЕ (ANSI)
Инвертор, НЕ (ANSI)
| A{\displaystyle A} | ¬A{\displaystyle A} |
|---|---|
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение
| A{\displaystyle A} | A{\displaystyle A} |
|---|---|
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из 2(22)=24=16{\displaystyle 2^{(2^{2})}=2^{4}=16} возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция И

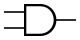
| A{\displaystyle A} | B{\displaystyle B} | A∧B{\displaystyle A\land B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть при истине на входе 1 И истине на входе 2».
Дизъюнкция (логическое сложение). Операция ИЛИ

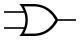
| A{\displaystyle A} | B{\displaystyle B} | A∨B{\displaystyle A\lor B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера)


| A{\displaystyle A} | B{\displaystyle B} | A|B{\displaystyle A|B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса)
В англоязычной литературе NOR.
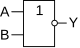
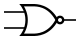
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}↓B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
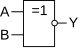 ИСКЛ-ИЛИ-НЕ (IEC)
ИСКЛ-ИЛИ-НЕ (IEC)
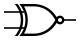 ИСКЛ-ИЛИ-НЕ (ANSI)
ИСКЛ-ИЛИ-НЕ (ANSI)
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}↔B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует чётное количество,
- «0» тогда и только тогда, когда на входе действует нечётное количество
Словесная запись: «истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2».
Сложение (сумма) по модулю 2 (Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.

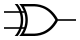
В англоязычной литературе XOR.
| A{\displaystyle A} | B{\displaystyle B} | A⊕B{\displaystyle A\oplus B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Словесное описание: «истина на выходе — только при истине на входе 1, либо только при истине на входе 2».
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}→B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| A{\displaystyle A} | B{\displaystyle B} | B{\displaystyle B}→A{\displaystyle A} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
| A{\displaystyle A} | B{\displaystyle B} | f(A,B){\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
| A{\displaystyle A} | B{\displaystyle B} | f(A,B){\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации
Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:
- механические,
- гидравлические,
- пневматические,
- электромагнитные,
- электромеханические,
- электронные,
- оптические.
Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
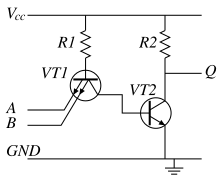 Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используется в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включённым в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включённым по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Примечания
Литература
Ссылки
Логические элементы — Википедия. Что такое Логические элементы
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательностями «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно x(xn)∗m{\displaystyle \ x^{(x^{n})*m}} логических функций и соответствующих им логических элементов, где x{\displaystyle \ x} — основание системы счисления, n{\displaystyle \ n} — число входов (аргументов), m{\displaystyle \ m} — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны 2(22)∗1=24=16{\displaystyle 2^{(2^{2})*1}=2^{4}=16} двоичных двухвходовых логических элементов и 2(23)∗1=28=256{\displaystyle 2^{(2^{3})*1}=2^{8}=256} двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элементов и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из 2(21)=22=4{\displaystyle 2^{(2^{1})}=2^{2}=4} возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
 Инвертор, НЕ (IEC)
Инвертор, НЕ (IEC)
 Инвертор, НЕ (ANSI)
Инвертор, НЕ (ANSI)
| A{\displaystyle A} | ¬A{\displaystyle A} |
|---|---|
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение

| A{\displaystyle A} | A{\displaystyle A} |
|---|---|
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из 2(22)=24=16{\displaystyle 2^{(2^{2})}=2^{4}=16} возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция И


| A{\displaystyle A} | B{\displaystyle B} | A∧B{\displaystyle A\land B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть при истине на входе 1 И истине на входе 2».
Дизъюнкция (логическое сложение). Операция ИЛИ


| A{\displaystyle A} | B{\displaystyle B} | A∨B{\displaystyle A\lor B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера)


| A{\displaystyle A} | B{\displaystyle B} | A|B{\displaystyle A|B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса)
В англоязычной литературе NOR.


| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}↓B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
 ИСКЛ-ИЛИ-НЕ (IEC)
ИСКЛ-ИЛИ-НЕ (IEC)
 ИСКЛ-ИЛИ-НЕ (ANSI)
ИСКЛ-ИЛИ-НЕ (ANSI)
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}↔B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует чётное количество,
- «0» тогда и только тогда, когда на входе действует нечётное количество
Словесная запись: «истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2».
Сложение (сумма) по модулю 2 (Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.


В англоязычной литературе XOR.
| A{\displaystyle A} | B{\displaystyle B} | A⊕B{\displaystyle A\oplus B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Словесное описание: «истина на выходе — только при истине на входе 1, либо только при истине на входе 2».
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}→B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| A{\displaystyle A} | B{\displaystyle B} | B{\displaystyle B}→A{\displaystyle A} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
| A{\displaystyle A} | B{\displaystyle B} | f(A,B){\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
| A{\displaystyle A} | B{\displaystyle B} | f(A,B){\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации
Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:
- механические,
- гидравлические,
- пневматические,
- электромагнитные,
- электромеханические,
- электронные,
- оптические.
Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
 Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используется в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включённым в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включённым по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Примечания
Литература
Ссылки
Логические элементы — Википедия
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательностями «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно x(xn)∗m{\displaystyle \ x^{(x^{n})*m}} логических функций и соответствующих им логических элементов, где x{\displaystyle \ x} — основание системы счисления, n{\displaystyle \ n} — число входов (аргументов), m{\displaystyle \ m} — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны 2(22)∗1=24=16{\displaystyle 2^{(2^{2})*1}=2^{4}=16} двоичных двухвходовых логических элементов и 2(23)∗1=28=256{\displaystyle 2^{(2^{3})*1}=2^{8}=256} двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элементов и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из 2(21)=22=4{\displaystyle 2^{(2^{1})}=2^{2}=4} возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
 Инвертор, НЕ (IEC)
Инвертор, НЕ (IEC)
 Инвертор, НЕ (ANSI)
Инвертор, НЕ (ANSI)
| A{\displaystyle A} | ¬A{\displaystyle A} |
|---|---|
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение

| A{\displaystyle A} | A{\displaystyle A} |
|---|---|
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из 2(22)=24=16{\displaystyle 2^{(2^{2})}=2^{4}=16} возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция И


| A{\displaystyle A} | B{\displaystyle B} | A∧B{\displaystyle A\land B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть при истине на входе 1 И истине на входе 2».
Дизъюнкция (логическое сложение). Операция ИЛИ


| A{\displaystyle A} | B{\displaystyle B} | A∨B{\displaystyle A\lor B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера)


| A{\displaystyle A} | B{\displaystyle B} | A|B{\displaystyle A|B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса)
В англоязычной литературе NOR.


| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}↓B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
 ИСКЛ-ИЛИ-НЕ (IEC)
ИСКЛ-ИЛИ-НЕ (IEC)
 ИСКЛ-ИЛИ-НЕ (ANSI)
ИСКЛ-ИЛИ-НЕ (ANSI)
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}↔B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует чётное количество,
- «0» тогда и только тогда, когда на входе действует нечётное количество
Словесная запись: «истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2».
Сложение (сумма) по модулю 2 (Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.


В англоязычной литературе XOR.
| A{\displaystyle A} | B{\displaystyle B} | A⊕B{\displaystyle A\oplus B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Словесное описание: «истина на выходе — только при истине на входе 1, либо только при истине на входе 2».
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}→B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| A{\displaystyle A} | B{\displaystyle B} | B{\displaystyle B}→A{\displaystyle A} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
| A{\displaystyle A} | B{\displaystyle B} | f(A,B){\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
| A{\displaystyle A} | B{\displaystyle B} | f(A,B){\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации
Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:
- механические,
- гидравлические,
- пневматические,
- электромагнитные,
- электромеханические,
- электронные,
- оптические.
Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
 Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используется в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включённым в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включённым по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Примечания
Литература
Ссылки
Логические элементы — Википедия. Что такое Логические элементы
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательностями «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно x(xn)∗m{\displaystyle \ x^{(x^{n})*m}} логических функций и соответствующих им логических элементов, где x{\displaystyle \ x} — основание системы счисления, n{\displaystyle \ n} — число входов (аргументов), m{\displaystyle \ m} — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны 2(22)∗1=24=16{\displaystyle 2^{(2^{2})*1}=2^{4}=16} двоичных двухвходовых логических элементов и 2(23)∗1=28=256{\displaystyle 2^{(2^{3})*1}=2^{8}=256} двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элементов и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из 2(21)=22=4{\displaystyle 2^{(2^{1})}=2^{2}=4} возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
 Инвертор, НЕ (IEC)
Инвертор, НЕ (IEC)
 Инвертор, НЕ (ANSI)
Инвертор, НЕ (ANSI)
| A{\displaystyle A} | ¬A{\displaystyle A} |
|---|---|
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение

| A{\displaystyle A} | A{\displaystyle A} |
|---|---|
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из 2(22)=24=16{\displaystyle 2^{(2^{2})}=2^{4}=16} возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция И


| A{\displaystyle A} | B{\displaystyle B} | A∧B{\displaystyle A\land B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть при истине на входе 1 И истине на входе 2».
Дизъюнкция (логическое сложение). Операция ИЛИ


| A{\displaystyle A} | B{\displaystyle B} | A∨B{\displaystyle A\lor B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера)


| A{\displaystyle A} | B{\displaystyle B} | A|B{\displaystyle A|B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса)
В англоязычной литературе NOR.


| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}↓B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
 ИСКЛ-ИЛИ-НЕ (IEC)
ИСКЛ-ИЛИ-НЕ (IEC)
 ИСКЛ-ИЛИ-НЕ (ANSI)
ИСКЛ-ИЛИ-НЕ (ANSI)
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}↔B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует чётное количество,
- «0» тогда и только тогда, когда на входе действует нечётное количество
Словесная запись: «истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2».
Сложение (сумма) по модулю 2 (Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.


В англоязычной литературе XOR.
| A{\displaystyle A} | B{\displaystyle B} | A⊕B{\displaystyle A\oplus B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Словесное описание: «истина на выходе — только при истине на входе 1, либо только при истине на входе 2».
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}→B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| A{\displaystyle A} | B{\displaystyle B} | B{\displaystyle B}→A{\displaystyle A} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
| A{\displaystyle A} | B{\displaystyle B} | f(A,B){\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
| A{\displaystyle A} | B{\displaystyle B} | f(A,B){\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации
Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:
- механические,
- гидравлические,
- пневматические,
- электромагнитные,
- электромеханические,
- электронные,
- оптические.
Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
 Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используется в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включённым в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включённым по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Примечания
Литература
Ссылки
Логические элементы — Википедия. Что такое Логические элементы
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательностями «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно x(xn)∗m{\displaystyle \ x^{(x^{n})*m}} логических функций и соответствующих им логических элементов, где x{\displaystyle \ x} — основание системы счисления, n{\displaystyle \ n} — число входов (аргументов), m{\displaystyle \ m} — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны 2(22)∗1=24=16{\displaystyle 2^{(2^{2})*1}=2^{4}=16} двоичных двухвходовых логических элементов и 2(23)∗1=28=256{\displaystyle 2^{(2^{3})*1}=2^{8}=256} двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элементов и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из 2(21)=22=4{\displaystyle 2^{(2^{1})}=2^{2}=4} возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
 Инвертор, НЕ (IEC)
Инвертор, НЕ (IEC)
 Инвертор, НЕ (ANSI)
Инвертор, НЕ (ANSI)
| A{\displaystyle A} | ¬A{\displaystyle A} |
|---|---|
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение

| A{\displaystyle A} | A{\displaystyle A} |
|---|---|
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из 2(22)=24=16{\displaystyle 2^{(2^{2})}=2^{4}=16} возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция И


| A{\displaystyle A} | B{\displaystyle B} | A∧B{\displaystyle A\land B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть при истине на входе 1 И истине на входе 2».
Дизъюнкция (логическое сложение). Операция ИЛИ


| A{\displaystyle A} | B{\displaystyle B} | A∨B{\displaystyle A\lor B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера)


| A{\displaystyle A} | B{\displaystyle B} | A|B{\displaystyle A|B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса)
В англоязычной литературе NOR.


| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}↓B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
 ИСКЛ-ИЛИ-НЕ (IEC)
ИСКЛ-ИЛИ-НЕ (IEC)
 ИСКЛ-ИЛИ-НЕ (ANSI)
ИСКЛ-ИЛИ-НЕ (ANSI)
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}↔B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует чётное количество,
- «0» тогда и только тогда, когда на входе действует нечётное количество
Словесная запись: «истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2».
Сложение (сумма) по модулю 2 (Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.


В англоязычной литературе XOR.
| A{\displaystyle A} | B{\displaystyle B} | A⊕B{\displaystyle A\oplus B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Словесное описание: «истина на выходе — только при истине на входе 1, либо только при истине на входе 2».
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| A{\displaystyle A} | B{\displaystyle B} | A{\displaystyle A}→B{\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| A{\displaystyle A} | B{\displaystyle B} | B{\displaystyle B}→A{\displaystyle A} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
| A{\displaystyle A} | B{\displaystyle B} | f(A,B){\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
| A{\displaystyle A} | B{\displaystyle B} | f(A,B){\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации
Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:
- механические,
- гидравлические,
- пневматические,
- электромагнитные,
- электромеханические,
- электронные,
- оптические.
Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
 Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используется в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включённым в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включённым по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Примечания
Литература
Ссылки
Логические элементы
-
Общие сведения о логических элементах
-
В любой цифровой системе присутствуют логические элементы и память.
Логическими элементами (ЛЭ) называют устройства, преобразующие входную информацию в выходную по определенным правилам.
В цифровой технике входная и выходная информация является бинарной (все переменные принимают только два значения: 1 или 0). Будем обозначать сигналы входной информации переменными Х1, Х2,…, Хn, а сигнал выходной информациипеременнымиF, Y1,Y2 и т.д..
Основные логические операции:
Логическое сложение(дизъюнкция) реализуется логическим элементом ИЛИ. Элемент, выполняющий функцию ИЛИ, имеет несколько входов и один выход. Сигнал логической единицы появляется на выходе такого устройства, если хотя бы на один из входов подана логическая единица. Функцию логического сложения математически записывают в виде
 . (1.1)
. (1.1)
Схему ИЛИ обозначают как на рис. 1.1.



Логическое умножение (конъюнкция) реализуется логическим элементом И. Сигнал логической единицы появляется на выходе такого устройства, если на все входы подана логическая единица. Функцию логического умножения математически записывают в виде
 . (1.2)
. (1.2)
Схему И (схему совпадения) обозначают как на рис. 1.2.
Логическое отрицание (инверсия) реализуется логическим элементом НЕ, который называют инвертором. Сигнал логической единицы появляется на выходе такого устройства, если на вход подан логический ноль. Функцию логического отрицания математически записывают в виде
 . (1.3)
. (1.3)
Инверсия по выходу (входу) обозначается кружком в контуре прямоугольника, изображающем схему (рис. 1.3).
-
Основные характеристики и параметры логических элементов
Характеристика передачи UВЫХ(UВХ). На рис. 1.4 представлена характеристика передачи инвертора, на которой обозначены напряженияU1 иU0 напряжения высокого и низкого уровней, соответствующие логической единице и логическому нулю,Uширина активной зоны,Umлогический перепад.


Коэффициент объединения по входу nопределяет число входов логического элемента. Обычноn 8.
Коэффициент разветвления по выходу mопределяет возможное число одновременно подключаемых логических элементов к данному логическому элементу. Обычноm ограничивают на уровнеn, но оно может доходить и до 100, и в общем случаеmот структуры логического элемента.
Параметры m иn определяютфункциональную возможностьлогического элемента.
Быстродействие характеризуется временем задержки распространения сигналов. Обычно различают (рис. 1.5) время задержки распространения сигнала при включении логического элементаtЗ+, время задержки распространения сигнала при выключении логического элементаt– и среднее время задержки распространения
 . (1.4)
. (1.4)
В зависимости отсреднего времени задержки распространения логические элементы подразделяют на:
сверхбыстродействующие элементы (tср.з. 5 нс)
быстродействующие элементы (5 нс tср.з. 10нс)
элементы со среднимбыстродействием (10 нс tср.з. 50нс)
медленнодействующие элементы (tср.з. 50нс)
Помехоустойчивость логического элемента определяется максимальной величиной помехи на входе, которая не переключает логический элемент из одного состояния в другое. В зависимости от величины помехи логические элементы подразделяют на:
Экономичность определяется мощностью, потребляемой от источника питания.
Логические элементы компьютера
Основные логические элементы реализуют 3 основные логические операции:
- логическое умножение;
- логическое сложение;
- инверсию (отрицание).
Устройства компьютера, которые выполняют обработку и хранение информации, могут быть собраны из базовых логических элементов, у которых $2$ входа и $1$ выход. К логическим устройствам компьютера относятся группы переключателей, триггеры, сумматоры.
Связь между алгеброй логики и компьютерной техникой также лежит в двоичной системе счисления, которая используется в ЭВМ. Поэтому в устройствах ПК можно хранить и обрабатывать как числа, так и значения логических переменных.
Определение 1
Логический элемент компьютера – это часть электронной схемы, которая выполняет элементарную логическую функцию.
Переключательные схемы
В ЭВМ используются электрические схемы, которые состоят из большого количества переключателей. Переключатель, находясь в замкнутом состоянии ток пропускает, в разомкнутом – не пропускает. Работа таких схем удобно описывается при помощи алгебры логики. В зависимости от состояния переключателя можно регулировать получение или неполучение сигналов на выходах.
Готовые работы на аналогичную тему
Вентили
Среди логических элементов компьютеров выделяют электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие (их называют вентили).
Эти схемы позволяют реализовать любую логическую функцию, которая описывает работу устройств ПК. Обычно вентили имеют $2–8$ входов и $1$ или $2$ выхода.
Для представления двух логических состояний ($1$ и $0$) в вентилях, входные и выходные сигналы имеют разные уровни напряжения. Например, $+3 \ B$ (вольт) для состояния $«1»$ и $0 \ B$ для состояния $«0»$.
У каждого логического элемента есть условное обозначение, выражающее его логическую функцию, но не указывающее на электронную схему, которая в нем реализована. Такой подход реализован для упрощения записи и понимания сложных логических схем.
Работа логических элементов описывается таблицами истинности.

Рисунок 1.
Триггер
Триггеры и сумматоры состоят из вентилей.
Триггер – важнейшая структурная единица оперативной памяти ПК и внутренних регистров процессора.
Определение 2
Триггер – логическая схема, которая способна хранить $1$ бит информации ($1$ или $0$). Строится на $2$-х элементах ИЛИ–НЕ или на $2$-х элементах И–НЕ.

Рисунок 2.
Самый распространённый тип триггера – $RS$-триггер (Reset/Set), который имеет $2$ входа $S$ и $R$ и два выхода $Q$ и $\bar{Q}$. На каждый из входов $S$ и $R$ могут подаваться входные сигналы в виде кратковременных импульсов (рис.3): есть импульс – $1$, нет импульса – $0$.

Рисунок 3. Кратковременный импульс
Сумматор
Сумматоры широко применяются в арифметико-логических устройствах процессора и отвечают за суммирование двоичных разрядов.
Определение 3
Сумматор – логическая схема, которая способна суммировать 2 одноразрядных двоичных числа с переносом из предыдущего разряда.

Рисунок 4.
Сумматор может находить применение и в других устройствах машины.
Для суммирования двоичных слов длиной от двух бит можно использовать последовательное соединение многоразрядных сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.
Пример реализации логической схемы

Рисунок 5.
Алгоритм реализации:
- Определим количество переменных данного выражения, значит столько входов будет иметь схема. В данном случае это входы $A, B, C$.
-
С помощью базовых логических элементов реализуются основные операции в порядке их следования:
I – инверсия переменных $A, B, C$ реализуется логическим элементом «НЕ»;
II – логическое умножение реализуется логическим элементом «И»;
III – логическое сложение реализуется логическим элементом «ИЛИ».
На выходе каждого элемента прописывается логическое выражение, которое реализуется данным элементом, что позволяет осуществить обратную задачу, т.е. по готовой схеме составить логическое выражение, которое реализует данная схема.
элементов логики
элементов логики Центр Жака Маритена: Показанияпо
Его Преосвященство кардинал Мерсье
Третье издание
Переведено
Юэн Макферсон
Нью-Йорк
Манхэттенвиль Пресс
1912
Nihil Obstat.
РЕМИГИУС ЛАФОРТ, Д.Д.
Цензор
Imprimatur
ДЖОН КАРДИНАЛ ФАРЛИ
Архиепископ Нью-Йоркский
Авторское право 1912 г.
Манхэттенвильская пресса
Введение
Глава I
Эффективная причина логического порядка
Глава II
Суть или материальная причина логического порядка
Арт.I. Концепты
§ 1. Понятие, его объект и свойства
§ 2. Разделение понятий
Арт. II. Условия.
§ 1. Термин, его объект и свойства
§ 2 Классификация терминов
Глава III
Формальная причина логического порядка
Арт. I. Решение и предложение
§ 1. Понятие решения и предложения
§ 2. Решения и предложения
И.Классификация простых предложений
II. Классификация сложных предложений
§ 3. Соотношение предложений
Арт. II. Рассуждение
§ 1. Рассуждение и силлогизм
§ 2. Силлогизмы
I. Рассмотрение силлогизмов по форме
II. Рассмотрение силлогизмов по существу
Различные виды демонстрации
Вероятные аргументы
Ошибочные и софистические аргументы
Арт.III. Научная систематизация
Предварительные замечания
§ 1. Научные процессы
§ 2. Метод и методы
Глава IV
Последняя причина логического порядка
Заключение
<< ======= >>
.элементов логики
элементов логики Центр Жака Маритена:
Чтения
Центр Жака Маритена:
Чтения по
Его Преосвященство кардинал Мерсье
Третье издание
Переведено
Эван Макферсон
Нью-Йорк
Манхэттенвиль Пресс
1912
Nihil Obstat.
РЕМИГИУС ЛАФОРТ, Д.Д.
Цензор
Imprimatur
ДЖОН КАРДИНАЛ ФАРЛИ
Архиепископ Нью-Йоркский
Авторское право 1912 г.
Манхэттенвильская пресса
Введение
Глава I
Эффективная причина логического порядка
Глава II
Суть или материальная причина логического порядка
Арт.I. Концепты
§ 1. Понятие, его объект и свойства
§ 2. Разделение понятий
Арт. II. Условия.
§ 1. Термин, его объект и свойства
§ 2 Классификация терминов
Глава III
Формальная причина логического порядка
Арт. I. Решение и предложение
§ 1. Понятие решения и предложения
§ 2. Решения и предложения
И.Классификация простых предложений
II. Классификация сложных предложений
§ 3. Соотношение предложений
Арт. II. Рассуждение
§ 1. Рассуждение и силлогизм
§ 2. Силлогизмы
I. Рассмотрение силлогизмов по форме
II. Рассмотрение силлогизмов по существу
Различные виды демонстрации
Вероятные аргументы
Ошибочные и софистические аргументы
Арт.III. Научная систематизация
Предварительные замечания
§ 1. Научные процессы
§ 2. Метод и методы
Глава IV
Последняя причина логического порядка
Заключение
<< ======= >>
.Логический элемент | Статья о «Логическом элементе» по The Free Dictionary
— простейший элемент электронного компьютера; выполняет одну конкретную логическую операцию над входными сигналами в соответствии с правилами алгебры логики. За логический элемент принимаются дискретные значения входных и выходных сигналов, независимо от их физической реализации. Обычно бывает два уровня, которые условно принимаются как «0» и «1». Различают комбинированные логические элементы, выходные сигналы которых в определенный момент определяются комбинациями входных сигналов, действующих в этот момент, и элементы хранения (памяти) или задержки, для которых выходные сигналы определяются состоянием логический элемент при передаче следующего сигнала.
Среди комбинированных логических элементов есть инвертор (элемент НЕ), элемент совпадения (конъюнктор или элемент И) и дизъюнктор (элемент ИЛИ), который представляет собой логический элемент с несколькими входами и одним выходом, на котором сигнал появляется, когда сигнал присутствует хотя бы на одном из входов. Логические элементы, состоящие из комбинаций элементов, таких как элементы НЕ И (НЕ-И) и НЕ ИЛИ (ИЛИ), широко используются. Пороговые элементы, такие как мажоритарные элементы, которые работают по «принципу большинства» (если сигнал «1» подается на большинство входов элемента, сигнал «1» также будет установлен на выходе цепи), составляют отдельный класс логических элементов.
Логические элементы являются фундаментальными элементами для построения логических схем в компьютерах и дискретных автоматических системах. Набор логических элементов составляет логическую структуру блока, узла или устройства компьютера. Набор логических элементов, состоящий из элементов И, ИЛИ и НЕ, с помощью которых можно построить логический план любой сложности, называется функционально полным. Наблюдается тенденция к созданию универсальных логических элементов, которые могут выполнять ряд логических функций.
СПИСОК ЛИТЕРАТУРЫ
Анисимов Б.В., Четвериков В.Н. Основы теории и проектирования цифровых вычислительных машин . М., 1962.Вавилов Э. Н., Портной Г. П.. Синтез схем электронных цифровых машин . Москва, 1963.
Большая Советская Энциклопедия, 3-е издание (1970-1979). © 2010 The Gale Group, Inc. Все права защищены.
.логических вентилей, триггеров, счетчиков, регистров.
Логические базы ЭВМ
Математический аппарат алгебры логики в качестве основной системы обозначений в компьютере является двоичным, в котором используются цифры 1 и 0, а также значения логических переменных тоже два, что очень удобно для описания того, как функционирует аппаратное обеспечение компьютера: 1 и 0.
Из этого факта можно сделать два вывода:
Те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных
На этапе проектирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить количество элементарных логических элементов, из которых состоят основные узлы компьютера.
Данные и команды в памяти компьютера и в регистрах процессора представлены в виде двоичных последовательностей различной структуры и длины .
Логический элемент ЭВМ — это часть электронной логической схемы, реализующая элементарную логическую функцию.
Логическими элементами компьютеров являются электронные схемы А, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и другие (называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно калитка имеет от двух до восьми входов и одного или двух выходов, узел кодируется более высоким уровнем напряжения, чем ноль (или наоборот).
Каждый логический элемент имеет символ, который выражает его логическую функцию, но не указывает, какая электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работа логических элементов описывается с помощью таблиц достоверности. Таблица достоверности — это табличное представление логической схемы (операции), в которой все возможные комбинации значений достоверности входных сигналов (операндов) вместе со значением достоверности целевого сигнала (результата операции) для каждой из этих комбинаций. перечислены.
Схема И . Схема Также реализует соединение двух или более логических значений.Условное обозначение на блок-схемах схемы И с двумя входами и его таблица годности представлены ниже.
Агрегат на схеме выход И будет только в том случае, когда на всех входах будут агрегаты. Когда хотя бы на одном входе стоит ноль, на выходе также будет ноль. Операция соединения на функциональных схемах обозначается знаком &, являющимся сокращенным обозначением английского слова And .
Схема OR
Схема OR реализует разделение двух или более логических значений.Условное обозначение на блок-схемах схемы ИЛИ с двумя входами и таблица его достоверности представлены ниже.
Значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1. Когда хотя бы на одном входе схемы ИЛИ есть единица, на ее выходе также будет единица. Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как x или y).
Схема НЕТ. Схема НЕ (инвертор) реализует операцию отказа. Обозначение схемы НЕ и таблица его применимости представлены ниже. Если на входе схемы стоит O, на выходе стоит 1. Когда на входе стоит 1, на выходе будет буква O.
Схема И-НЕ. Схема И не состоит из элемента И и инвертора и осуществляет отрицание результата схемы И .
Условное значение схемы А-НЕ и ее таблица действительности представлены ниже.
Схема ИЛИ-НЕ. Схема ИЛИ — не состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Обозначение схемы ИЛИ-НЕ и таблица его применимости представлены ниже.
Триггер — это электронная схема, широко применяемая в регистрах компьютера для надежного запоминания одной категории двоичного кода. Триггер имеет два установившихся состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю .
Термин триггер происходит от английского слова trigger a latch, триггер. Для обозначения этой схемы в английском языке чаще используется термин flip-flop, что в переводе означает хлопок. Это звукоподражательное название электронной схемы указывает на ее способность почти мгновенно переходить (перебрасываться) из одного электрического состояния в другое и наоборот .
Дата: 24.12.2015; просмотр: 1650
.

