Формула параллельных сопротивлений. Последовательное и параллельное соединение проводников: формулы, расчеты и применение

Как рассчитать общее сопротивление при последовательном и параллельном соединении проводников. Какие формулы используются для вычисления силы тока и напряжения в электрических цепях. Где применяются различные типы соединений проводников на практике.

Основные понятия и формулы для расчета электрических цепей

Прежде чем рассматривать различные виды соединений проводников, необходимо вспомнить основные понятия и формулы электротехники:

• Сопротивление (R) — свойство проводника препятствовать прохождению электрического тока. Измеряется в Омах (Ом).
• Сила тока (I) — количество заряда, проходящее через поперечное сечение проводника за единицу времени. Измеряется в Амперах (А).
• Напряжение (U) — разность потенциалов между двумя точками электрической цепи. Измеряется в Вольтах (В).
• Закон Ома: I = U / R
• Мощность электрического тока: P = U * I

Эти базовые формулы позволяют производить расчеты параметров электрических цепей при различных способах соединения проводников.

Последовательное соединение проводников

При последовательном соединении проводники подключаются друг за другом, образуя единую неразветвленную цепь. Основные свойства такого соединения:

• Сила тока одинакова во всех элементах цепи
• Общее напряжение равно сумме напряжений на отдельных участках
• Общее сопротивление равно сумме сопротивлений всех проводников

Формула для расчета общего сопротивления при последовательном соединении:

R = R1 + R2 + R3 + … + Rn

Где R — общее сопротивление цепи, R1, R2, R3 и т.д. — сопротивления отдельных проводников.

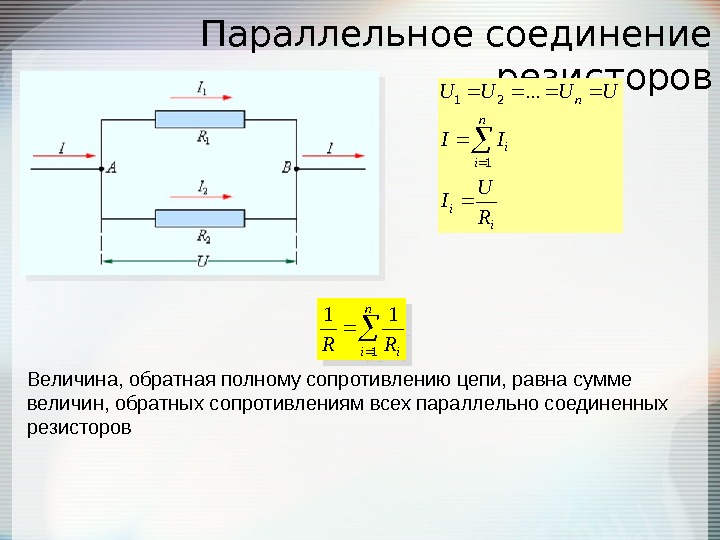
Параллельное соединение проводников

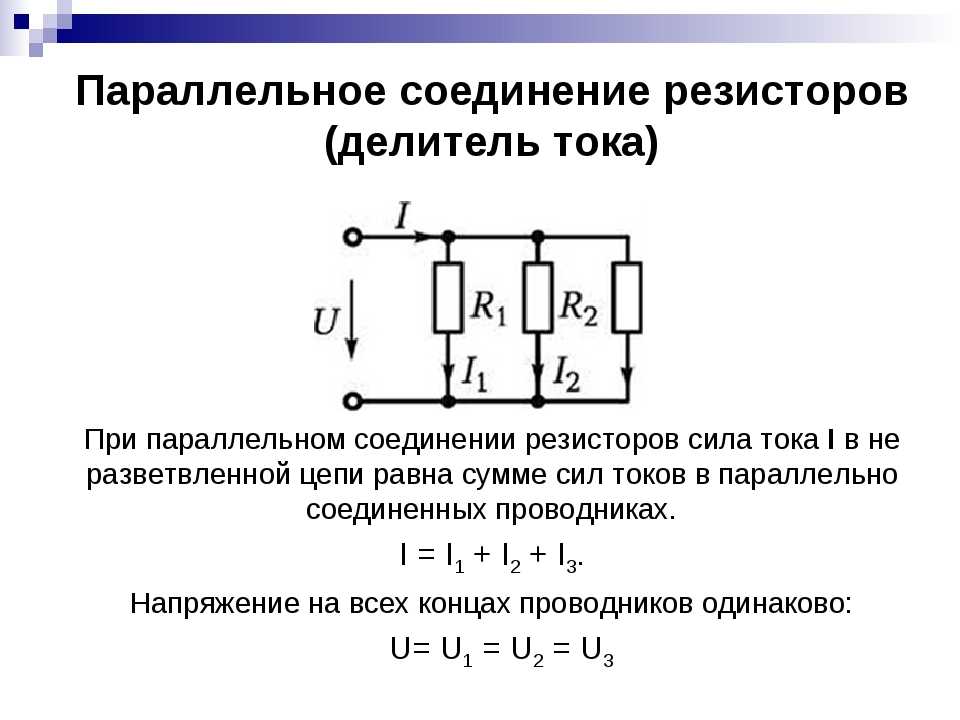
При параллельном соединении все проводники подключаются к одним и тем же точкам цепи. Особенности параллельного соединения:

• Напряжение одинаково на всех участках цепи
• Общий ток равен сумме токов через отдельные проводники
• Общая проводимость равна сумме проводимостей отдельных элементов

Формула для расчета общего сопротивления при параллельном соединении:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

Где R — общее сопротивление цепи, R1, R2, R3 и т.д. — сопротивления отдельных проводников.

Сравнение последовательного и параллельного соединения

Основные различия между двумя типами соединений:

Параметр	Последовательное соединение	Параллельное соединение
Сила тока	Одинакова во всей цепи	Разная в каждой ветви
Напряжение	Сумма напряжений на участках	Одинаково на всех участках
Общее сопротивление	Больше сопротивления любого элемента	Меньше сопротивления любого элемента

Применение различных типов соединений на практике

Последовательное и параллельное соединение проводников широко используются в различных областях электротехники и электроники:

Последовательное соединение:

• Елочные гирлянды — при перегорании одной лампочки гаснет вся цепь
• Предохранители в электрических цепях
• Реостаты для регулировки силы тока
• Делители напряжения

Параллельное соединение:

• Подключение бытовых приборов к электросети
• Соединение аккумуляторов для увеличения емкости
• Шунты в измерительных приборах
• Разветвленные электрические сети

Расчет параметров смешанных электрических цепей

На практике часто встречаются схемы, содержащие как последовательные, так и параллельные участки. Для расчета таких цепей используют следующий алгоритм:

1. Разбить схему на простые последовательные и параллельные соединения
2. Рассчитать эквивалентное сопротивление для каждого участка
3. Заменить рассчитанные участки эквивалентными сопротивлениями
4. Повторять шаги 1-3, пока не останется одно эквивалентное сопротивление
5. Рассчитать общий ток через эквивалентное сопротивление
6. Определить токи и напряжения на отдельных участках, двигаясь от общего к частному

Данный метод позволяет анализировать сложные электрические схемы, разбивая их на простые элементы.

Зависимость мощности от типа соединения проводников

Способ соединения проводников влияет на распределение мощности в электрической цепи:

Последовательное соединение:

P = I^2 * R, где I — общий ток, R — сопротивление участка

Мощность распределяется пропорционально сопротивлениям участков.

Параллельное соединение:

P = U^2 / R, где U — общее напряжение, R — сопротивление участка

Мощность распределяется обратно пропорционально сопротивлениям участков.

Понимание этих закономерностей позволяет грамотно проектировать электрические цепи с учетом требуемого распределения мощности.

Параллельное последовательное соединение резисторов. Параллельное и последовательное соединение сопротивлений. Схемы с несколькими проводниками

На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при параллельном соединении проводников и некоторые другие технические вопросы.

Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.

Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким

При расчёте сопротивления используется известная из школьного курса физики формула:

Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.

Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:

Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.

Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.

Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.

Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.

Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.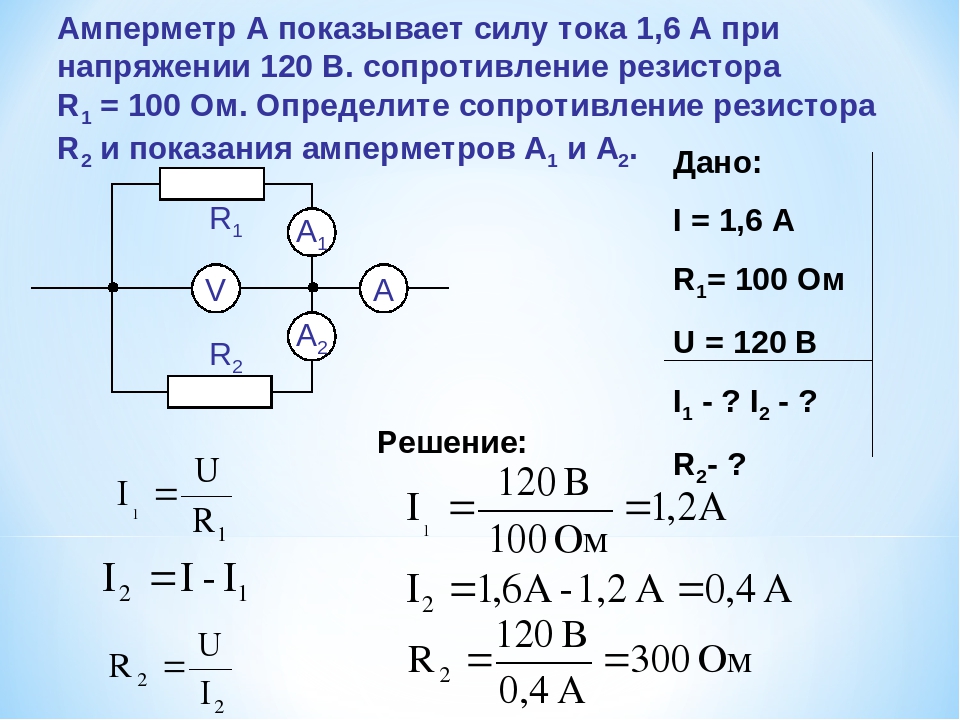

Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.

Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.

Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.

В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.

Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.

Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника сечение (провода или кабеля).

На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.

Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при двух кабелей, чтобы точнее определить их тепловыделение.

При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое падение напряжения на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.

Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.

Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей.

Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.

Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.

Содержание:

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

Свойства и технические характеристики резисторов

Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для — последовательное.

На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав , нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: + 20, + 10, + 5, + 2, + 1% и так далее до величины + 0,001%.

Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.

Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Мощность при последовательном соединение

При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, сила тока будет составлять I = U/R = 100/390 = 0,256 A.На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.

• P 1 = I 2 x R 1 = 0,256 2 x 200 = 13,11 Вт;
• P 2 = I 2 x R 2 = 0,256 2 x 100 = 6,55 Вт;
• P 3 = I 2 x R 3 = 0,256 2 x 51 = 3,34 Вт;
• P 4 = I 2 x R 4 = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.

Мощность при паралл ельном соединение

При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы — с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:

• 1/R = 1/R 1 +1/R 2 +1/R 3 +1/R 4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
• Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
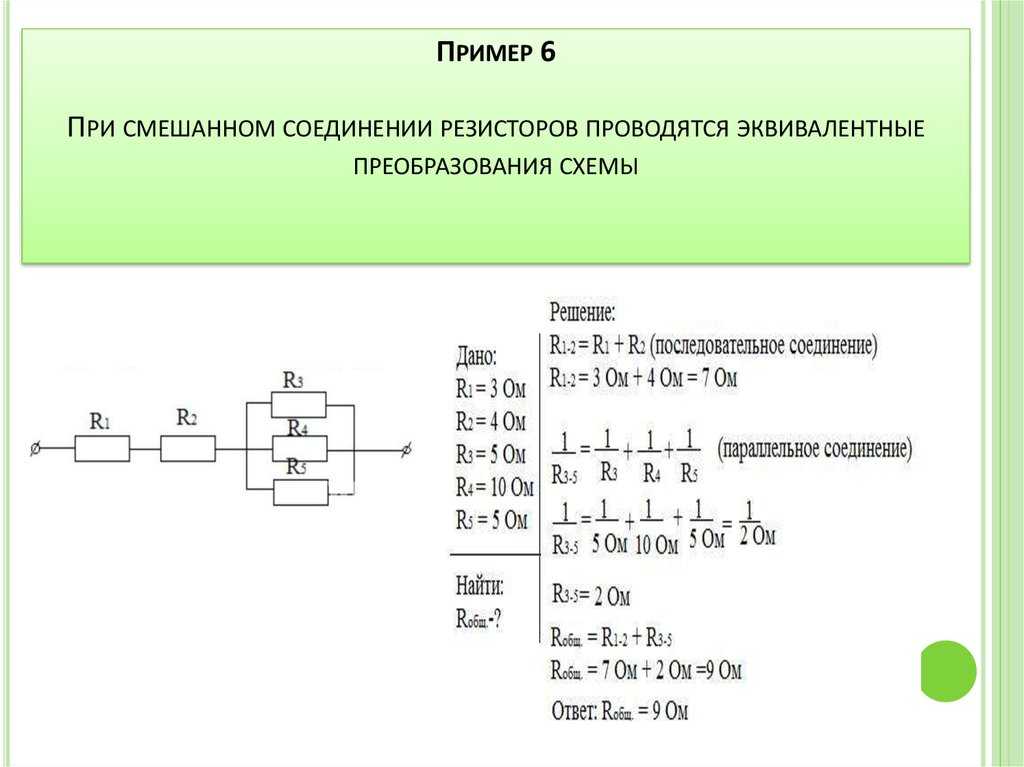
• Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
• Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
• Расчет силы тока для каждого резистора выполняется по формулам: I 1 = U/R 1 = 100/200 = 0,5A; I 2 = U/R 2 = 100/100 = 1A; I 3 = U/R 3 = 100/51 = 1,96A; I 4 = U/R 4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P 1 = U 2 /R 1 = 100 2 /200 = 50 Вт; P 2 = U 2 /R 2 = 100 2 /100 = 100 Вт; P 3 = U 2 /R 3 = 100 2 /51 = 195,9 Вт; P 4 = U 2 /R 4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р 1 +Р 2 +Р 3 +Р 4 = 50+100+195,9+256,4 = 602,3 Вт.

Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.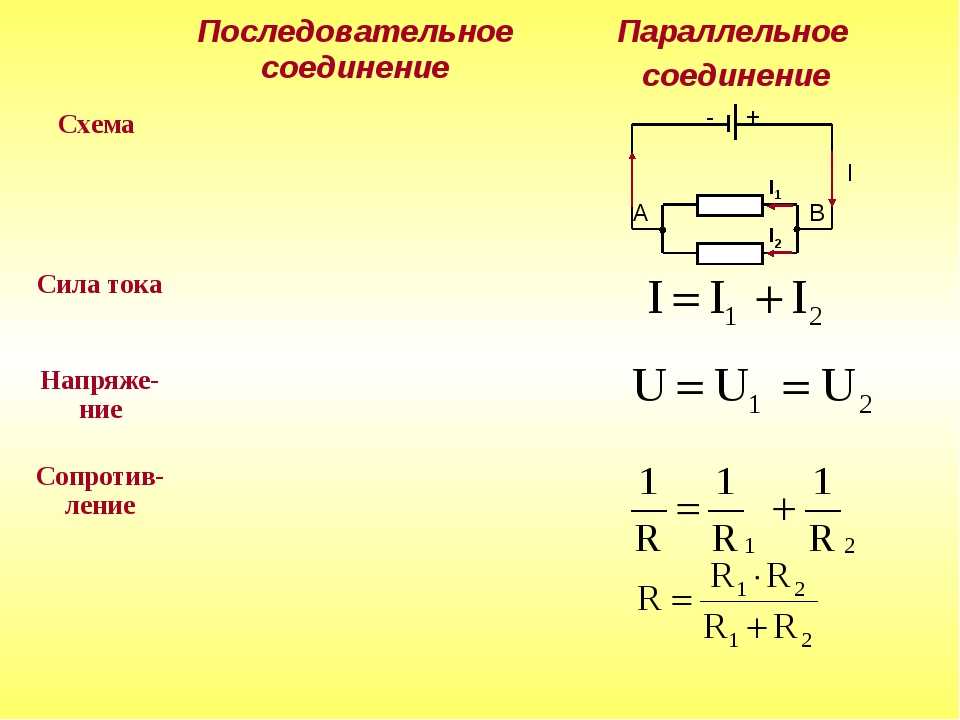

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

2) Общее сопротивление R общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Общее сопротивление R общ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.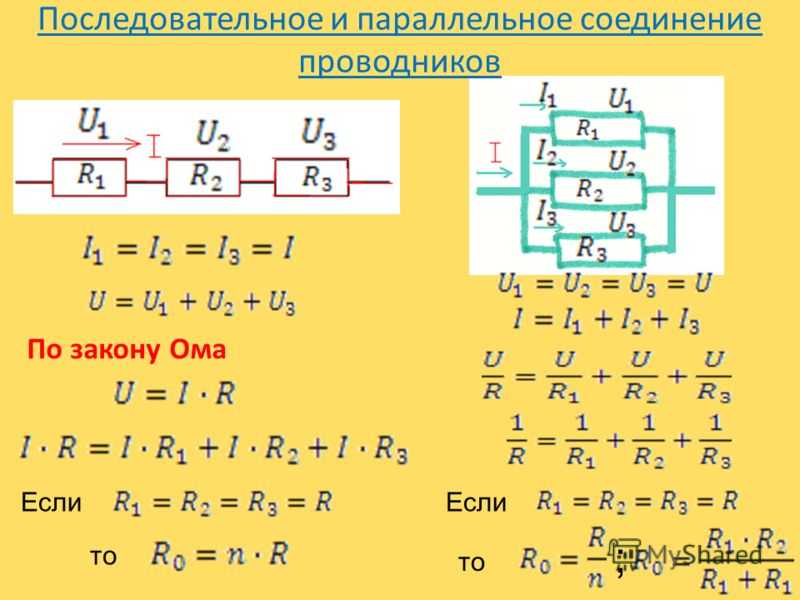

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

3)Электропроводность, электрическая проводимость, проводимость, способность тела пропускать электрический ток под воздействием электрического поля, а также физическая величина, количественно характеризующая эту способность. Тела, проводящие электрический ток, называются проводниками, в отличие от изоляторов.. .
Основная единица измерения сопротивления — Ом. Удельная проводимость — величина обратная сопротивлению, она измеряется в Сименсах, ранее назывшихся mho. Применительно к сыпучим веществам удобнее говорить об особой проводимости, обычно называемой удельной проводимостью.
Удельная проводимость — это проводимость, измеренная между противоположными сторонами куба вещества со стороной 1 см. Единицей данного типа измерений является Сименс/см. При измерении проводимости воды чаще используются более точные мкС/см (микросименс) и мС/см (миллисименс) .
Соответствующие единицы измерения сопротивления (или удельного сопротивления) — Ом/см, МегаОм/см и килоОм/см. При измерении сверхчистой воды чаще используют МегаОм/см, так как это дает более точные результаты. Сопротивление менее чистой воды, как например, водопроводной, измеряют в килоОм/см.

4) Общее сопротивление при последовательном соединении равно сумме сопротивлений Rсумм=R1+R2+R3…
Ток через все сопротивления протекает один (I). Поэтому ток вычисляешь как Отношение напряжения источника U к Rсумм.

Мощность

P=U*I или P=I*I*R (так как U=I*R).

P1=I*I*R1
P2=I*I*R2
P3=I*I*R3

5) мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:

При параллельном соединении каждая лампа подсоединяется на своё номинальное напряжение 220 В. при этом в каждой лампе появляется свой номинальный ток, обеспечивающий заданное свечение в соответствии с номинальной мощностью. мощность зависит от сопротивления нити накаливания. чем больше сопротивление нити, тем меньше ток и соответственно меньше номинальная мощность.
при последовательном соединении ток идёт один и тот же в каждой лампе. а напряжение распределяется в зависимости от доли сопротивления каждой лампы по отношению к сопротивлению всей цепи.
для цепи из двух ламп общее напряжение делится.
напряжение на лампе 40 Вт будет 220Х60:(40+60)=132; В.
напряжение на лампе 60 Вт будет 220Х40:(40+60)=80; В.

Все электронные устройства содержат резисторы, являющиеся их основным элементом. С его помощью изменяют величину тока в электрической цепи. В статье приведены свойства резисторов и методы расчёта их мощности.

Назначение резистора

Для регулировки тока в электрических цепях применяются резисторы. Это свойство определено законом Ома:

Из формулы (1) хорошо видно, что чем меньше сопротивление, тем сильнее возрастает ток, и наоборот, чем меньше величина R, тем больше ток. Именно это свойство используется в электротехнике. На основании этой формулы создаются схемы делителей тока, широко применяющиеся в электротехнических устройствах.

В этой схеме ток от источника делится на два, обратно пропорциональных

Кроме регулировки тока, резисторы используются в делителях напряжения. В этом случае опять используется закон Ома, но немного в другой форме:

Из формулы (2) следует, что при увеличении сопротивления увеличивается напряжение. Это свойство используется для построения схем делителей напряжения.

Из схемы и формулы (2) ясно, что напряжения на резисторах распределяются пропорционально сопротивлениям.

Изображение резисторов на схемах

По стандарту резисторы изображаются прямоугольником с размерами 10 х 4 мм и обозначаются буквой R. Часто указывается мощность резисторов на схеме. Изображение этого показателя выполняется косыми или прямыми чёрточками. Если мощность более 2 Ватт, то обозначение производится римскими цифрами. Обычно это делается для проволочных резисторов. В некоторых государствах, например в США, применяются другие условные обозначения. Для облегчения ремонта и анализа схемы часто приводится мощность которых выполняется по ГОСТ 2.728-74.

Технические характеристики устройств

Основная характеристика резистора — номинальное сопротивление R н, которое указывается на схеме возле резистора и на его корпусе. Единица измерения сопротивления — ом, килоом и мегаом. Изготавливаются резисторы с сопротивлением от долей ома и до сотен мегаомов. Существует немало технологий производства резисторов, все они имеют и преимущества, и недостатки. В принципе, не существует технологии, которая позволила бы абсолютно точно изготавливать резистор с заданным значением сопротивления.

Второй важной характеристикой является отклонение сопротивления. Оно измеряется в % от номинального R. Существует стандартный ряд отклонения сопротивления: ±20, ±10, ±5, ±2, ±1% и далее вплоть до значения ±0,001%.

Следующей важной характеристикой является мощность резисторов. При работе они нагреваются от проходящего по ним тока. Если рассеиваемая мощность будет превышать допустимое значение, то устройство выйдет из строя.

Резисторы при нагревании изменяют своё сопротивление, поэтому для устройств, работающих в широком диапазоне температур, вводится ещё одна характеристика — температурный коэффициент сопротивления. Он измеряется в ppm/°C, то есть 10 -6 R н /°C (миллионная часть от R н на 1°C).

Последовательное соединение резисторов

Резисторы могут соединяться тремя разными способами: последовательным, параллельным и смешанным. При ток поочерёдно проходит через все сопротивления.

При таком соединении ток в любой точке цепи один и тот же, его можно определить по закону Ома. Полное сопротивление цепи в этом случае равно сумме сопротивлений:

R=200+100+51+39=390 Ом;

I=U/R=100/390=0,256 А.

Теперь можно определить мощность при последовательном соединении резисторов, она рассчитывается по формуле:

P=I 2 ∙R= 0,256 2 ∙390=25,55 Вт.

Аналогично определяется мощность остальных резисторов:

P 1 = I 2 ∙R 1 =0,256 2 ∙200=13,11 Вт;

P 2 = I 2 ∙R 2 =0,256 2 ∙100=6,55 Вт;

P 3 = I 2 ∙R 3 =0,256 2 ∙51=3,34 Вт;

P 4 = I 2 ∙R 4 =0,256 2 ∙39=2,55 Вт.

Если сложить мощность резисторов, то получится полная P:

P=13,11+6,55+3,34+2,55=25,55 Вт.

Параллельное соединение резисторов

При все начала резисторов подключаются к одному узлу схемы, а концы — к другому. При таком соединении ток разветвляется и течёт по каждому устройству. Величина тока, согласно закону Ома, обратно пропорциональна сопротивлениям, а напряжение на всех резисторах одинаково.

1/R=1/R 1 +1/R 2 +1/R 3 +1/R 4 =1/200+1/100+1/51+1/39=0,005+0,01+0,0196+0,0256= 0,06024 1/Ом.

Сопротивление — величина, обратная проводимости:

R=1/0,06024= 16,6 Ом.

Воспользовавшись законом Ома, находят ток через источник:

I= U/R=100∙0,06024=6,024 A.

Зная ток через источник, находят мощность параллельно соединённых резисторов по формуле:

P=I 2 ∙R=6,024 2 ∙16,6=602,3 Вт.

По закону Ома рассчитывается ток через резисторы:

I 1 =U/R 1 =100/200=0,5 А;

I 2 =U/R 2 =100/100=1 А;

I 3 =U/R 1 =100/51=1,96 А;

I 1 =U/R 1 =100/39=2,56 А.

P 1 = U 2 /R 1 =100 2 /200=50 Вт;

P 2 = U 2 /R 2 =100 2 /100=100 Вт;

P 3 = U 2 /R 3 =100 2 /51=195,9 Вт;

P 4 = U 2 /R 4 =100 2 /39=256,4 Вт.

Если всё это сложить, то получится мощность всех резисторов:

P= P 1 + P 2 + P 3 + P 4 =50+100+195,9+256,4=602,3 Вт.

Смешанное соединение

Схемы со смешанным соединением резисторов содержат последовательное и одновременно параллельное соединение. Эту схему несложно преобразовать, заменив параллельное соединение резисторов последовательным. Для этого заменяют сначала сопротивления R 2 и R 6 на их общее R 2,6 , используя формулу, приведённую ниже:

R 2,6 =R 2 ∙R 6 /R 2 +R 6.

Точно так же заменяются два параллельных резистора R 4 , R 5 одним R 4,5:

R 4,5 =R 4 ∙R 5 /R 4 +R 5 .

В результате получается новая, более простая схема.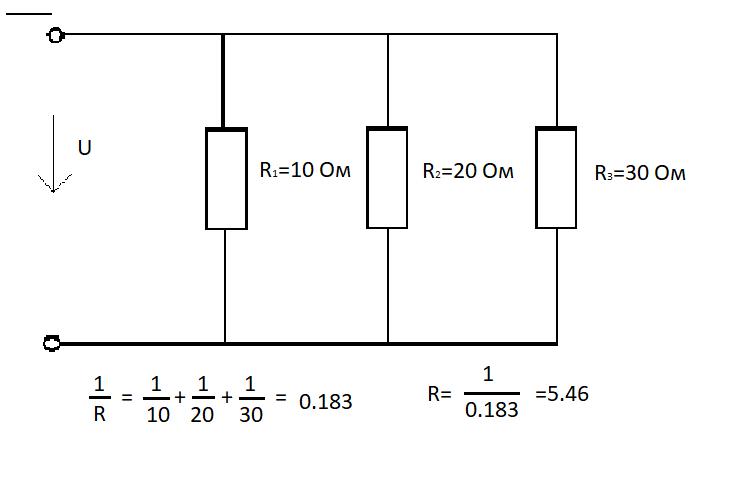 Обе схемы приведены ниже.

Мощность резисторов на схеме со смешанным соединением определяется по формуле:

Для расчёта по этой формуле сначала находят напряжение на каждом сопротивлении и величину тока через него. Можно использовать другой метод, чтобы определить мощность резисторов. Для этого используется формула:

P=U∙I=(I∙R)∙I=I 2 ∙R.

Если известно только напряжение на резисторах, то применяют другую формулу:

P=U∙I=U∙(U/R)=U 2 /R.

Все три формулы часто используются на практике.

Расчёт параметров схемы

Расчёт параметров схемы заключается в нахождении неизвестных токов и напряжений всех ветвей на участках электрической цепи. Имея эти данные, можно рассчитать мощность каждого резистора, входящего в схему. Простые методы расчёта были показаны выше, на практике же дело обстоит сложнее.

В реальных схемах часто встречается соединение резисторов звездой и треугольником, что создаёт значительные трудности при расчётах. Для упрощения таких схем были разработаны методы преобразования звезды в треугольник, и наоборот. Этот метод проиллюстрирован на схеме, представленной ниже:

Первая схема имеет в своём составе звезду, подключенную к узлам 0-1-3. К узлу 1 подсоединён резистор R1, к узлу 3 — R3, а к узлу 0 — R5. На второй схеме к узлам 1-3-0 подключены резисторы треугольника. К узлу 1 подключены резисторы R1-0 и R1-3, к узлу 3 — R1-3 и R3-0, а к узлу 0 — R3-0 и R1-0. Эти две схемы полностью эквивалентны.

Для перехода от первой схемы ко второй рассчитываются сопротивления резисторов треугольника:

R1-0=R1+R5+R1∙R5/R3;

R1-3=R1+R3+R1∙R3/R5;

R3-0=R3+R5+R3∙R5/R1.

Дальнейшие преобразования сводятся к вычислению сопротивлений. Когда будет найдено полное сопротивление цепи, находят по закону Ома ток через источник. Используя этот закон, несложно найти токи во всех ветвях.

Как определить мощность резисторов после нахождения всех токов? Для этого используют общеизвестную формулу: P=I 2 ∙R, применяя её для каждого сопротивления, найдём их мощности.

Экспериментальное определение характеристик элементов схемы

Для экспериментального определения нужных характеристик элементов требуется собрать заданную схему из реальных компонентов.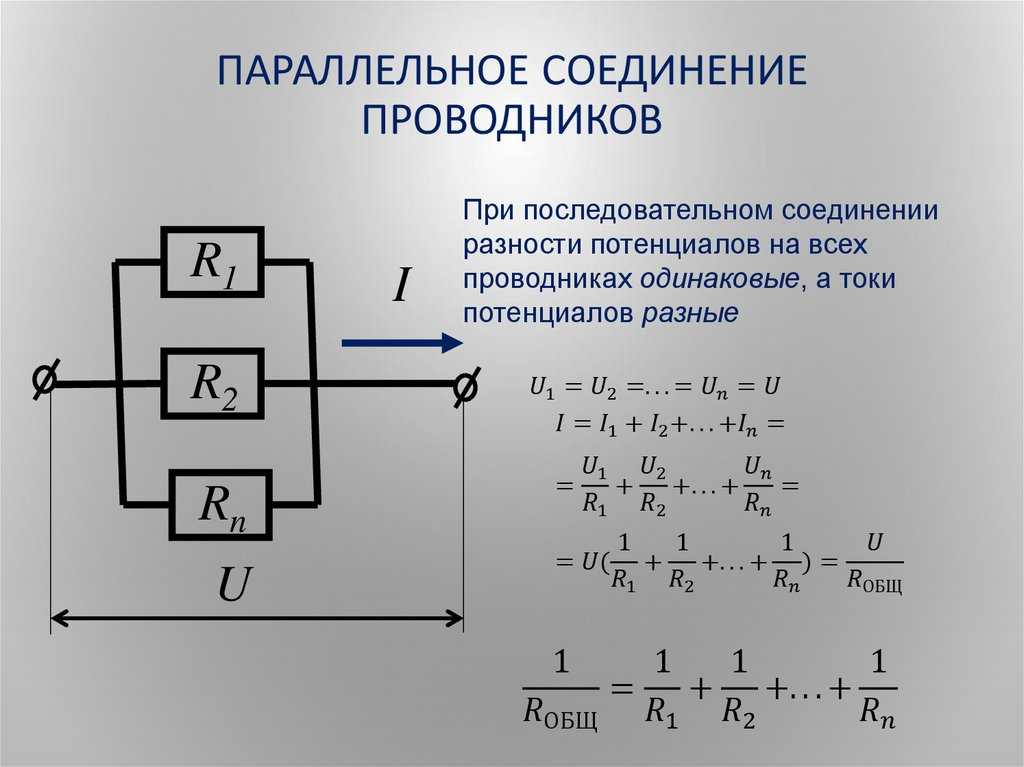 После этого с помощью электроизмерительных приборов выполняют все необходимые измерения. Этот метод трудоёмкий и дорогостоящий. Разработчики электрических и электронных устройств для этой цели используют моделирующие программы. С помощью них производятся все необходимые вычисления, и моделируется поведение элементов схемы в различных ситуациях. Только после этого собирается опытный образец технического устройства. Одной из таких распространённых программ является мощная система моделирования Multisim 14.0 фирмы National Instruments.

Как определить мощность резисторов с помощью этой программы? Это можно сделать двумя методами. Первый метод — это измерить ток и напряжение с помощью амперметра и вольтметра. Перемножив результаты измерений, получают искомую мощность.

Из этой схемы определяем мощность сопротивления R3:

P 3 =U∙I=1,032∙0,02=0,02064 Вт=20,6 мВт.

Второй метод — это непосредственное при помощи ваттметра.

Из этой схемы видно, что мощность сопротивления R3 равна P 3 =20,8 мВт. Расхождение из-за погрешности в первом методе больше. Точно так же определяются мощности остальных элементов.

Параллельное включение резисторов — схема и расчет. Как отличается параллельное и последовательное соединение резисторов?

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

1. С правого края – правый.
2. С левого края – левый.

Понятие параллельного подключения резисторов

При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.

Общее сопротивление

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.

То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

 

Схема

Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.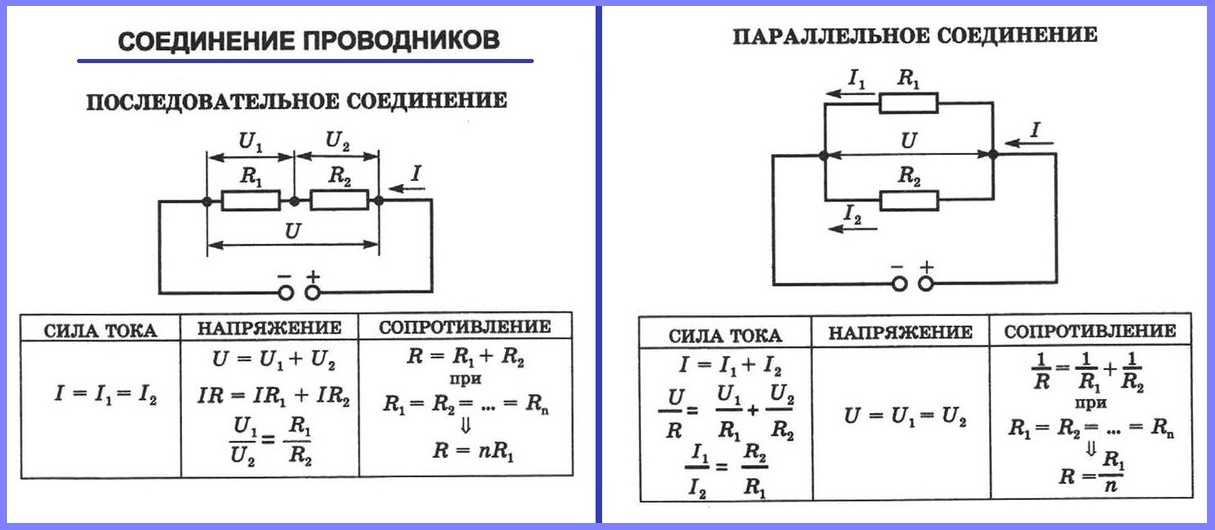

Будет интересно➡  Переменный резистор

Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.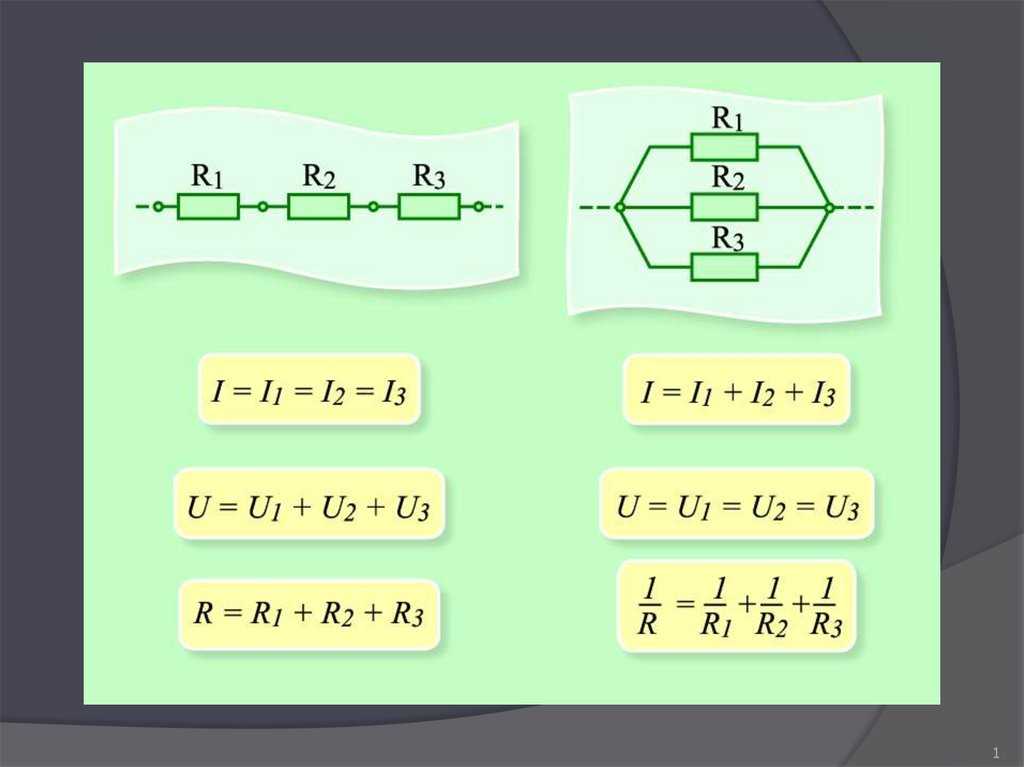

Как высчитывать

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.

Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.

Как выглядит формула Георга Ома

Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.

Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:

U1 = U2 = U.

Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:

I = I1 + I2.

Расчет силы тока при помощи закона Ома записывается как:

I = U/R;

I1 = U1/R1;

I2 = U2/R2.

Из формулы следует:

U/R = U1/R1 + U2/R2;

U = U1 = U2;

1/R = 1/R1 + 1/R2.

Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.

Последовательное подключение

При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

Пример

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

Решение

Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока.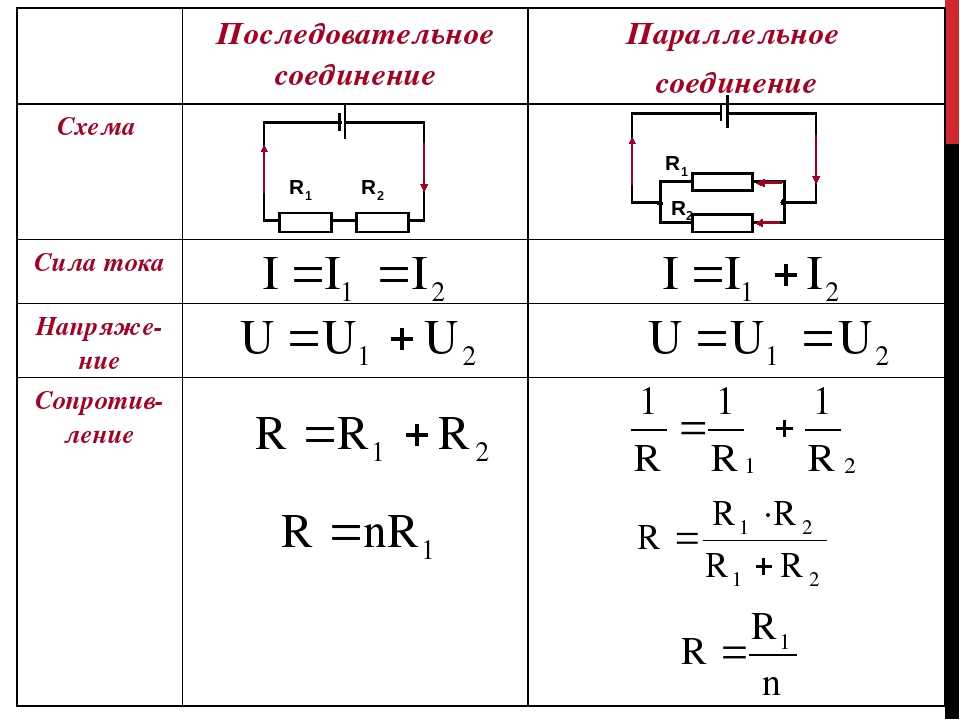 Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на  любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3  . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Следовательно,

UR1 = IR1 =1×2=2 Вольта

UR2 = IR2 = 1×3=3 Вольта

UR3 = IR3 =1×5=5 Вольт

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Получается

U=UR1+UR2+UR3

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

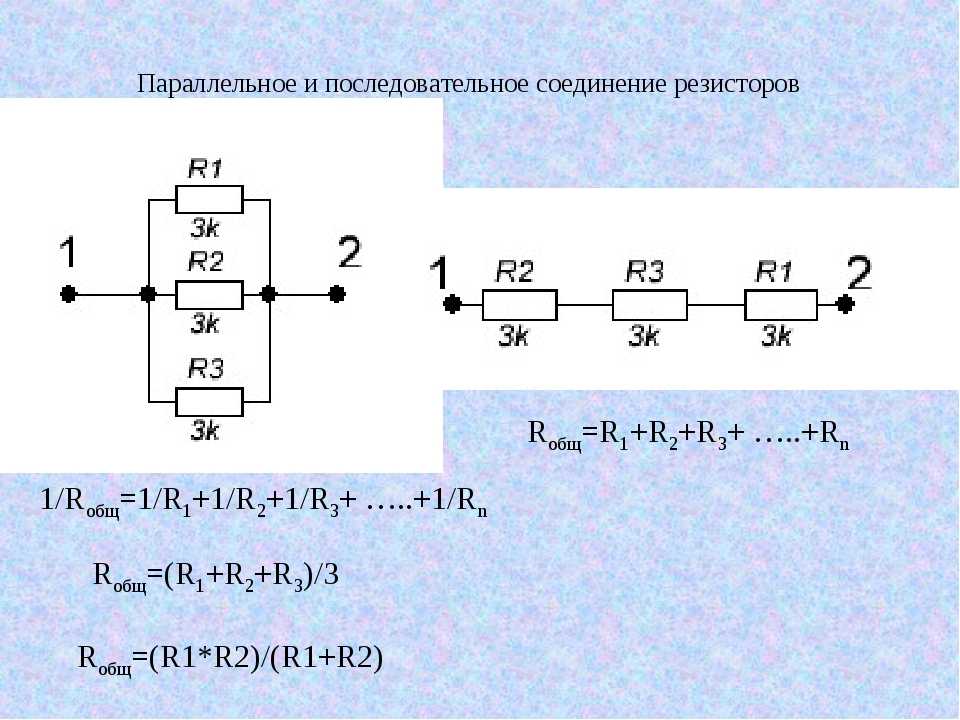
Отличия от последовательного и смешанного подключений

Параллельное соединение проводников

Иные способы соединения понятны из показанных на картинке примеров. Без специальных вычислений понятно, что параллельное включение резисторов создает несколько путей прохождения тока. Следовательно, в отдельных цепях его сила будет меньше, по сравнению с контрольными точками на входе и выходе. Вместе с тем напряжение в отмеченных местах остается неизменным.

Последовательное соединение резисторов увеличивает общее электрическое сопротивление. Ток в этой цепи (по базовым принципам) не будет изменяться. Однако на каждом пассивном элементе можно будет обнаружить измерительным прибором соответствующее падение напряжения.

Смешанный вариант – это объединение представленных выше соединений. Различные комбинации используют для деления напряжения, решения других задач. Для упрощения расчетов суммируют последовательность соединенных сопротивлений в отдельных цепях:

Rобщ = R1 + R2 + … + Rn.

Вне зависимости от сложности схемы, на входе и выходе по первому закону Кирхгофа токи будут одинаковыми.

Что ещё нужно учитывать при подключении резисторов

Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.

При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками.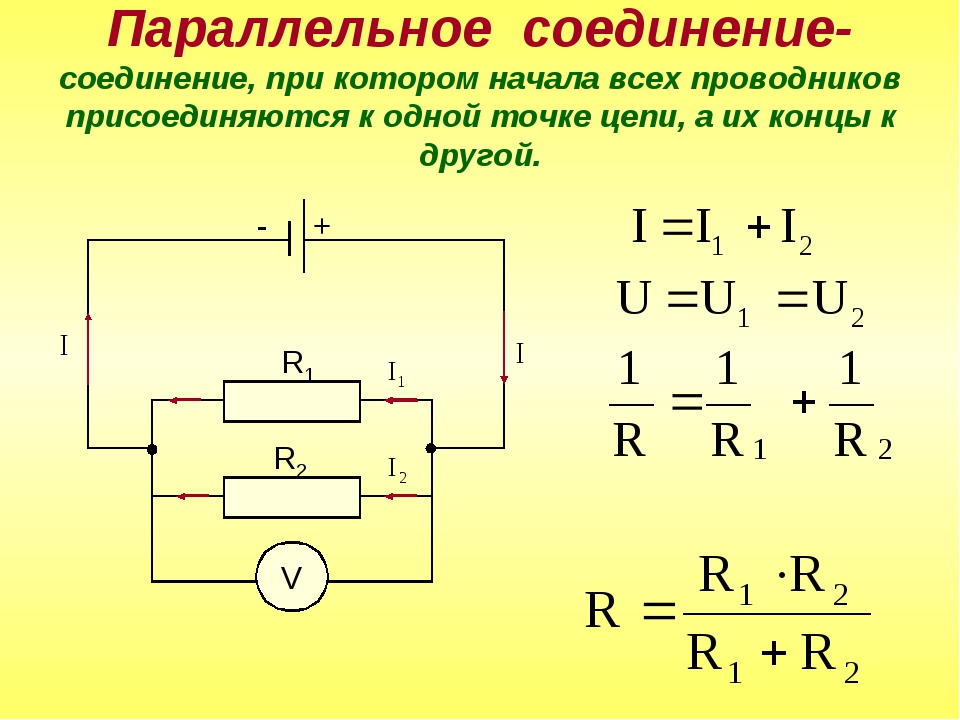 Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Установленный в мультиметре шунт для измерения ток до 20 ампер. Отметим, что если этим мультиметром измеряется большой ток непрерывно более 10 секунд, шунт перегреется и его сопротивление изменится, что приведет к ошибке измерения.

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.

Источники

• https://rusenergetics. ru/praktika/raschet-soprotivleniya-rezistorov
• https://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html
• https://ElectroInfo.net/radiodetali/rezistory/kak-otlichaetsja-parallelnoe-i-posledovatelnoe-soedinenie-rezistorov.html
• https://rusenergetics.ru/polezno-znat/parallelnoe-soedinenie
• https://www.RusElectronic.com/serial-and-parallel/
• https://amperof.ru/teoriya/parallelnoe-soedinenie-rezistorov.html
• https://www.translatorscafe.com/unit-converter/ru-RU/calculator/parallel-resistance/
• http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/

[свернуть]

21.1: Резисторы последовательно и параллельно

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2688

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Нарисовать цепь с параллельными и последовательными резисторами.
• Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
• Сравните способ расчета общего сопротивления резисторов, включенных последовательно и параллельно.
• Объясните, почему общее сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
• Рассчитайте общее сопротивление цепи, содержащей смесь резисторов, соединенных последовательно и параллельно.

Большинство цепей имеют более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением . Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рисунке \(\PageIndex{1}\). Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.

Рисунок \(\PageIndex{1}\): (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.

Резисторы серии

Когда резисторы серии относятся к серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то \(R_{1}\) на рисунке \(\PageIndex{1}\)(a) может быть сопротивлением стержня отвертки, \ (R_{2}\) сопротивление его ручки, \(R_{3}\) сопротивление тела человека и \(R_{4}\) сопротивление ее обуви.

На рисунке \(\PageIndex {2}\) показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев высокоомную обувь на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для устройство, которое уменьшило бы рабочий ток.) ​​

Рисунок \(\PageIndex{2}\): Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа).

Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потери электроэнергии, называемые падением напряжения , в каждом резисторе на рисунке \(\PageIndex {2}\).

Согласно Закону Ома , падение напряжения \(В\) на резисторе при протекании через него тока рассчитывается по уравнению \(V=IR\), где \(I\) равно току в амперах (А) и \(R\) сопротивление в омах\((\Омега)\). Другой способ думать об этом состоит в том, что \(V\) — это напряжение, необходимое для того, чтобы ток \(I\) протекал через сопротивление \(R\).

Таким образом, падение напряжения на \(R_{1}\) равно \(V_{1}=IR_{1}\), на \(V_{2}=IR_{2}\) и на \ (R_{3}\) равно \(V_{3}=IR_{3}\). Сумма этих напряжений равна выходному напряжению источника; то есть

\[V=V_{1}+V_{2}+V_{3}.\]

Это уравнение основано на законах сохранения энергии и заряда. Электрическая потенциальная энергия может быть описана уравнением \(\mathrm{PE}=qV\), где \(q\) — электрический заряд, а \(V\) — напряжение. Таким образом, энергия, подаваемая источником, равна \(qV), а энергия, рассеиваемая резисторами, равна

\[qV_{1}+qV_{2}+qV_{3}.\]

СОЕДИНЕНИЯ: ЗАКОНЫ СОХРАНЕНИЯ

Выводы выражений для последовательного и параллельного сопротивления основаны на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.

Эти энергии должны быть равны, потому что в цепи нет другого источника и другого места назначения энергии.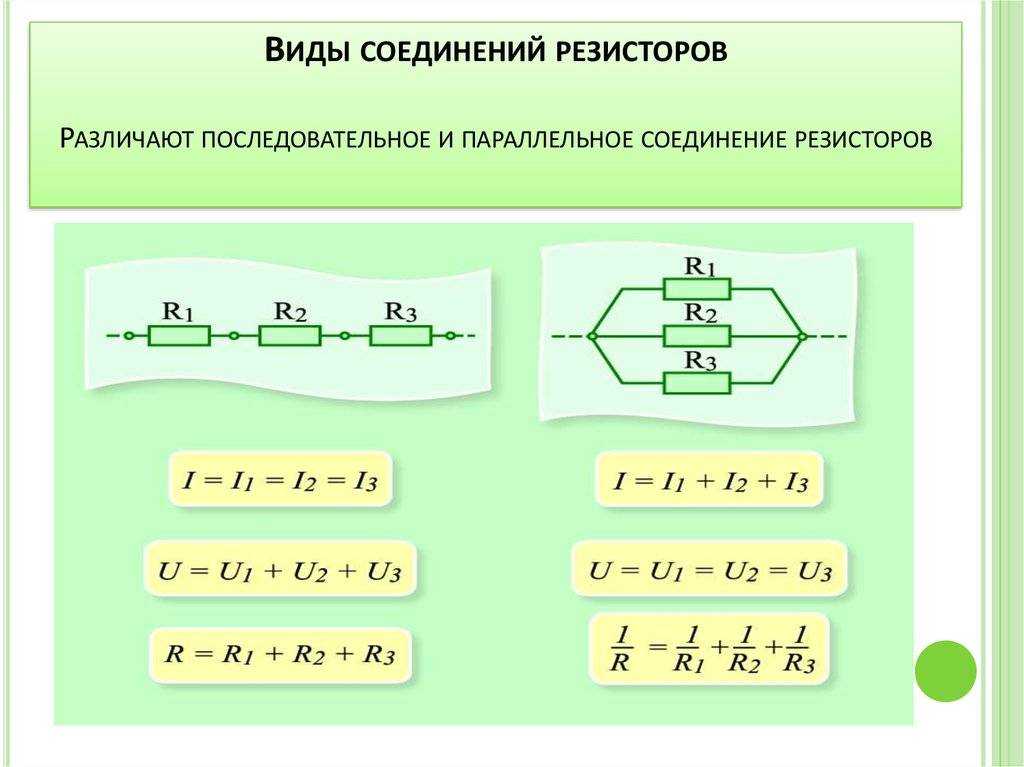 Таким образом, \(qV=qV_{1}+qV_{2}+qV_{3}\). Заряд \(q\) отменяется, что дает \(V=V_{1}+V_{2}+V_{3}\), как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется.)

Теперь подстановка значений отдельных напряжений дает

\[V=IR_{1}+IR_{2}+IR_{3}=I(R_{1}+R_{2}+R_{3}). \]

Обратите внимание, что для эквивалентного последовательного сопротивления \(R_{\mathrm{S}}\) мы имеем

\[V=IR _{\mathrm{S}}.\]

Это означает, что общее или эквивалентное последовательное сопротивление \(R_{\mathrm{S}}\) трех резисторов равно \(R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}\).

Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, полное сопротивление \(R_{\mathrm{S}}\) последовательного соединения равно

\[R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}+\dots ,\]

как предложено.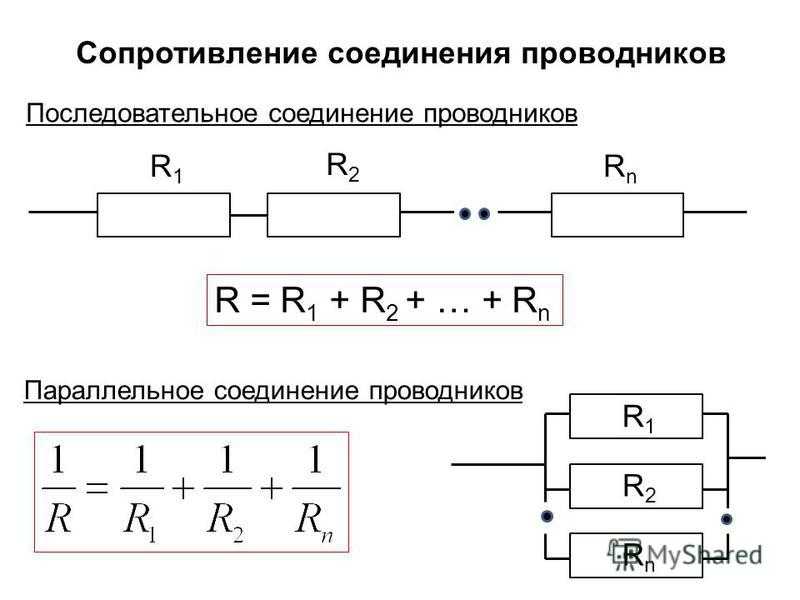 Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.

Пример \(\PageIndex{1}\): расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи

Предположим, что выходное напряжение батареи на рисунке \(\PageIndex{2}\) равно \(12,0\mathrm{V}\), а сопротивления равны \(R_{1}=1,00\Омега\), \(R_{2}=6,00\Омега\) и \(R_{3}= 13.0\Омега\). а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.

Стратегия и решение для (a)

Общее сопротивление представляет собой просто сумму отдельных сопротивлений, определяемую следующим уравнением:

\[R_{\mathrm{S}}=R_{1}+R_ {2}+R_{3}\]

\[=1,00\Омега + 6,00\Омега + 13,0\Омега\]

\[=20,0 \Омега. \]

Стратегия и решение для (b)

Ток определяется по закону Ома \(V=IR\). Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:

\[I=\dfrac{V}{R_{\mathrm{S}}}=\dfrac{12,0\Omega}{20,0\Omega}=0,600 \mathrm{A}.\]

Стратегия и решение для (c)

Падение напряжения или \(IR\) на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает

\[V_{1}=IR_{1}=(0,600\mathrm{A})(1,0\Omega)=0,600\mathrm{V}.\]

Аналогично,

\[V_{2}=IR_{2}=(0,600\mathrm{A})(6,0\Omega)=3,60\mathrm{V}\]

и

\[V_{3}= IR_{3}=(0,600\mathrm{A})(13,0\Omega)=7,80\mathrm{V}.\]

Обсуждение для (c)

Три капли \(IR\) добавляются к \(12.0\mathrm{V}\), как и предполагалось:

\[V_{1}+V_{2}+V_ {3}=(0,600+3,60+7,80)\mathrm{V}=12,0\mathrm{V}.\]

Стратегия и решение для (d)

Самый простой способ расчета мощности в ваттах (Вт) рассеивается на резисторе в цепи постоянного тока, чтобы использовать закон Джоуля , \(P=IV\), где \(P\) — электрическая мощность.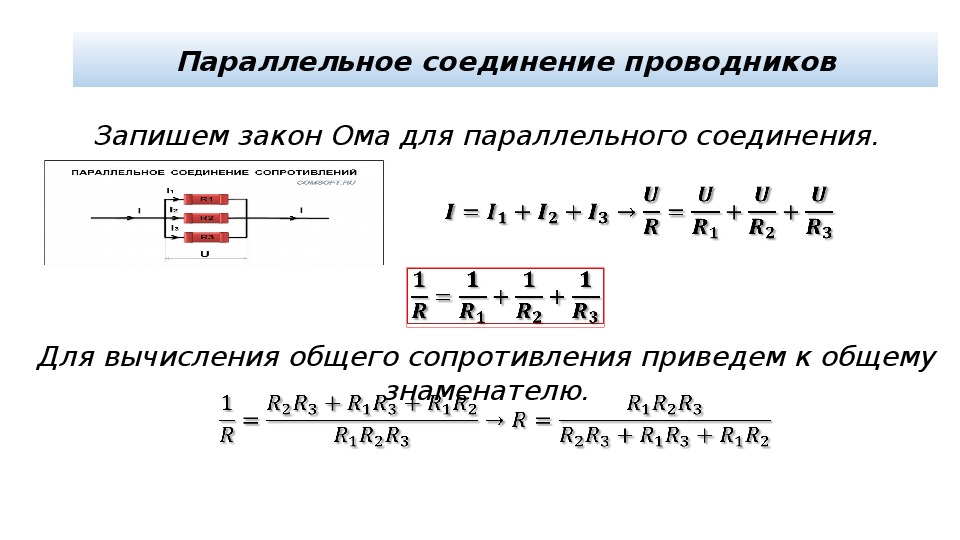 В этом случае через каждый резистор протекает одинаковый полный ток. Подставив закон Ома \(V=IR\) в закон Джоуля, мы получим мощность, рассеиваемую первым резистором, как 9{2}}{R}\), где \(V\) — падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.

Стратегия и решение для (e)

Самый простой способ рассчитать выходную мощность источника — использовать \(P=IV\), где \(V\) — напряжение источника. Это дает

\[P=(0,600\mathrm{A})(12,0\mathrm{V})=7,20 \mathrm{W}.\]

Обсуждение для (e)

Обратите внимание, по совпадению, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, как и мощность, выдаваемая источником. то есть

\[P_{1}+P_{2}+P_{3}=(0,360 +2,16+4,68)\mathrm{W}=7,20\mathrm{W}.\]

Мощность – это энергия в единицу времени ( Вт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ В СЕРИИ

1. Последовательные сопротивления добавляют: \(R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}+\dots\)
2. Один и тот же ток протекает через каждый резистор последовательно.
3. Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.

Резисторы, включенные параллельно

На рисунке \(\PageIndex{3}\) показаны резисторы, соединенные параллельно , подключенные к источнику напряжения. Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.

Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен). Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое верно и в вашем доме, или в любом здании. (См. рисунок \(\PageIndex{3}\)(b).)

Рисунок \(\PageIndex{3}\): (a) Три резистора, подключенные параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление. (b) Установка электроснабжения в доме. (кредит: Dmitry G, Wikimedia Commons)

Чтобы найти выражение для эквивалентного параллельного сопротивления \(R_{\mathrm{p}}\), давайте рассмотрим протекающие токи и то, как они связаны с сопротивлением. Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны \(I_{1}=\dfrac{V}{R_{1}}\), \(I_{2}=\dfrac{ V}{R_{2}}\) и \(I_{3}=\dfrac{V}{R_{3}}\). Сохранение заряда подразумевает, что полный ток \(I\), производимый источником, представляет собой сумму этих токов:

\[I=I_{1}+I_{2}+I_{3}.\]

Подстановка выражений для отдельных токов дает

\[I=\dfrac{V}{R_{1}} +\dfrac{V}{R_{2}}+\dfrac{V}{R_{3}}=V(\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}} +\dfrac{1}{R_{3}}). \]

Обратите внимание, что закон Ома для эквивалентного единичного сопротивления дает

\[I=\dfrac{V}{R_{\mathrm{p}}}= V(\dfrac{1}{R_{\mathrm{p}}}).\]

Члены в скобках в последних двух уравнениях должны быть равны. Обобщая на любое количество резисторов, общее сопротивление \(R_{\mathrm{p}}\) параллельного соединения связано с отдельными сопротивлениями как

\[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{ R_{3}}+\dots\]

Это соотношение приводит к тому, что общее сопротивление \(R_{\mathrm{p}}\) меньше, чем наименьшее из отдельных сопротивлений. (Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.

Пример \(\PageIndex{2}\): расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи

Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рисунке \(\PageIndex{3}\) будут такими же, как при рассмотренном ранее последовательном соединении: \(V=12.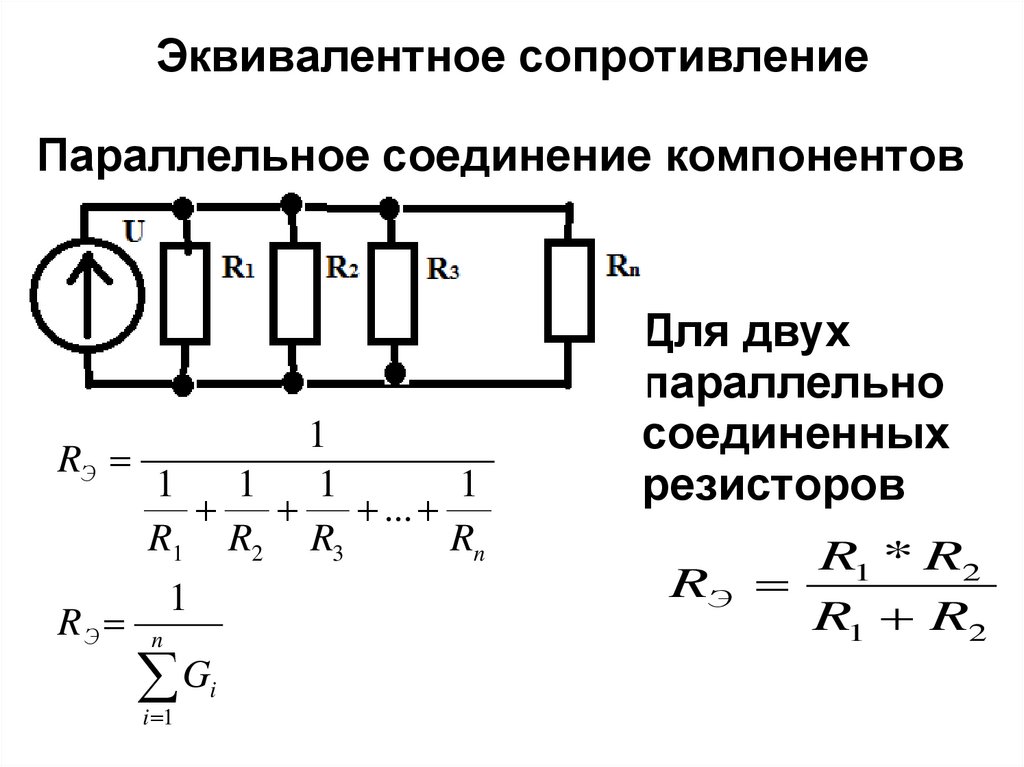 0\mathrm{V},\: R_ {1}=1,00\Омега\: R_{2}=6,00\Омега\) и \(R_{3}=13,0\Омега\). а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.

Стратегия и решение для (a)

Общее сопротивление для параллельной комбинации резисторов определяется с помощью приведенного ниже уравнения. Ввод известных значений дает

\[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac {1}{R_{3}}=\dfrac{1}{1.00\Omega}+\dfrac{1}{6.00\Omega}+\dfrac{1}{13.0\Omega}.\]

Таким образом,

\[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1,00}{\Omega}+\dfrac{0,1667}{\Omega}+\dfrac{0,07692}{\Omega}=\ dfrac{1.2436}{\Omega}.\]

(Обратите внимание, что в этих вычислениях каждый промежуточный ответ показан с дополнительной цифрой. )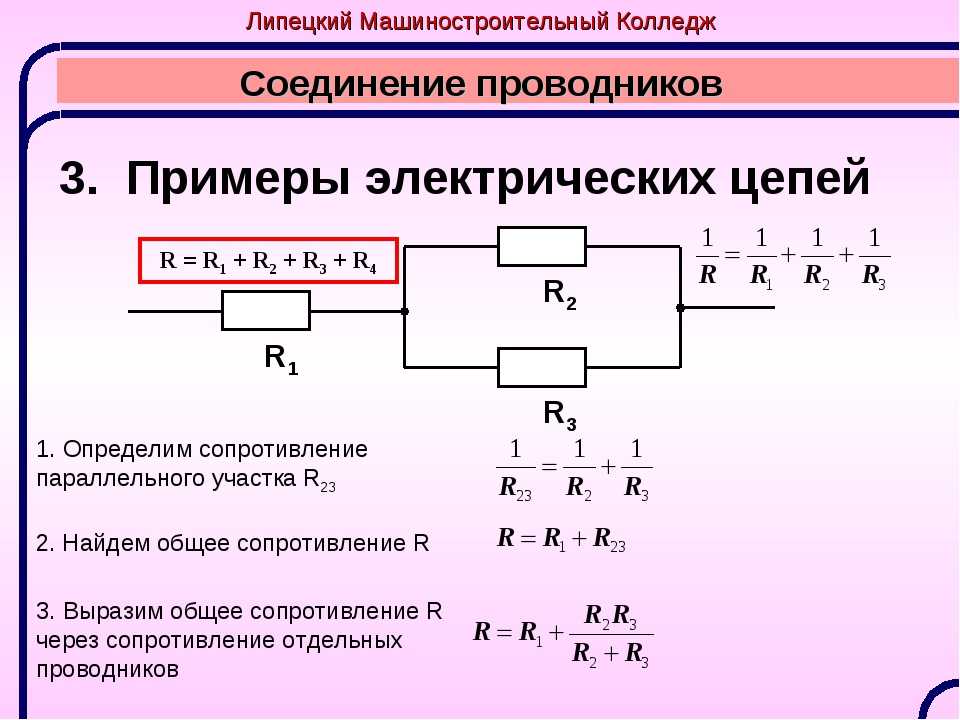

Мы должны инвертировать это, чтобы найти полное сопротивление \(R_{\mathrm{p}}\). Это дает

\[R_{\mathrm{p}}=\dfrac{1}{1,2436}\Omega=0,8041\Omega.\]

Общее сопротивление с правильным количеством значащих цифр равно \(R_{\ матрм{р}}=0,804\Омега\).

Обсуждение для (a)

\(R_{\mathrm{p}}\), как и предполагалось, меньше наименьшего индивидуального сопротивления.

Стратегия и решение для (b)

Полный ток можно найти из закона Ома, подставив \(R_{\mathrm{p}}\) вместо полного сопротивления. Это дает

\[I=\dfrac{V}{R_{\mathrm{p}}}=\dfrac{12,0\mathrm{V}}{0,8041 \Omega}=14,92 \mathrm{A}.\]

Обсуждение для (б)

Ток \(i\) для каждого устройства намного больше, чем для тех же устройств, соединенных последовательно (см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.

Стратегия и решение для (c)

Отдельные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,

\[I_{1}=\dfrac{V}{R_{1}}=\dfrac{12.0\mathrm{V}}{1.00\Omega}=12.0\mathrm{A}.\]

Аналогично,

\[I_{2}=\dfrac{V}{R_{2}}=\dfrac{12.0\mathrm{V}}{6.00\Omega}=2.00\mathrm{A}\]

и

\[I_{3}=\dfrac{V}{R_{3}}=\dfrac{12.0\mathrm{V}}{13.0\Omega}=0,92\mathrm{A}.\]

9{2}}{13.0\Omega}=11.1\mathrm{W}.\]

Обсуждение для (d)

Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к одному и тому же напряжению. источник.

Стратегия и решение для (e)

Общая мощность также может быть рассчитана несколькими способами. Выбор \(P=IV\) и ввод общего тока дает

\[P=IV=(14,92\mathrm{A})(12,0\mathrm{V})=179\mathrm{W}.\]

Обсуждение для (е)

Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт:

\[P_{1}+P_{2}+P_{3}=144\mathrm{W}+24.0\mathrm{W}+11.1\mathrm {W}=179\mathrm{W}. \]

Это согласуется с законом сохранения энергии.

Общее обсуждение

Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ, ПОДКЛЮЧЕННЫХ ПАРАЛЛЕЛЬНО

1. Параллельное сопротивление находится из \(\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1 }{R_{2}}+\dfrac{1}{R_{3}}+\dots\), и оно меньше любого отдельного сопротивления в комбинации.
2. К каждому параллельно подключенному резистору приложено одинаковое полное напряжение источника. (Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо.)
3. Параллельные резисторы не получают суммарный ток каждый; они его делят.

Комбинации последовательного и параллельного соединения

Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения.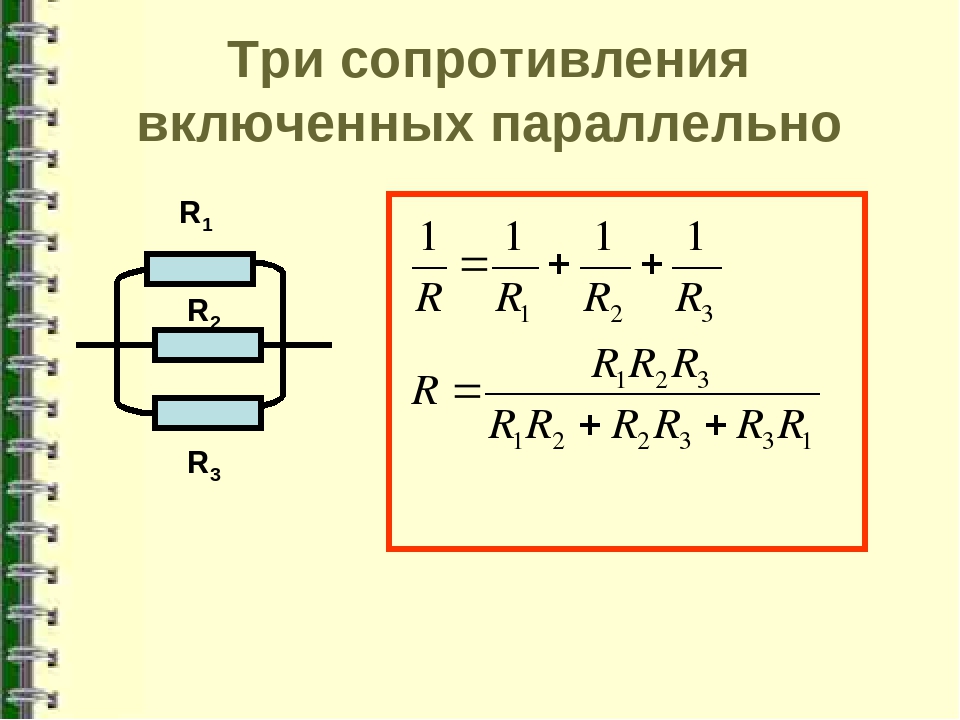 Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.

Комбинации последовательного и параллельного соединений можно привести к одному эквивалентному сопротивлению с помощью метода, показанного на рисунке \(\PageIndex{4}\). Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс скорее трудоемкий, чем сложный.

Рисунок \(\PageIndex{4}\): Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единое эквивалентное сопротивление.

Простейшая комбинация последовательного и параллельного сопротивлений, показанная на рисунке \(\PageIndex{5}\), также является наиболее поучительной, поскольку она встречается во многих приложениях.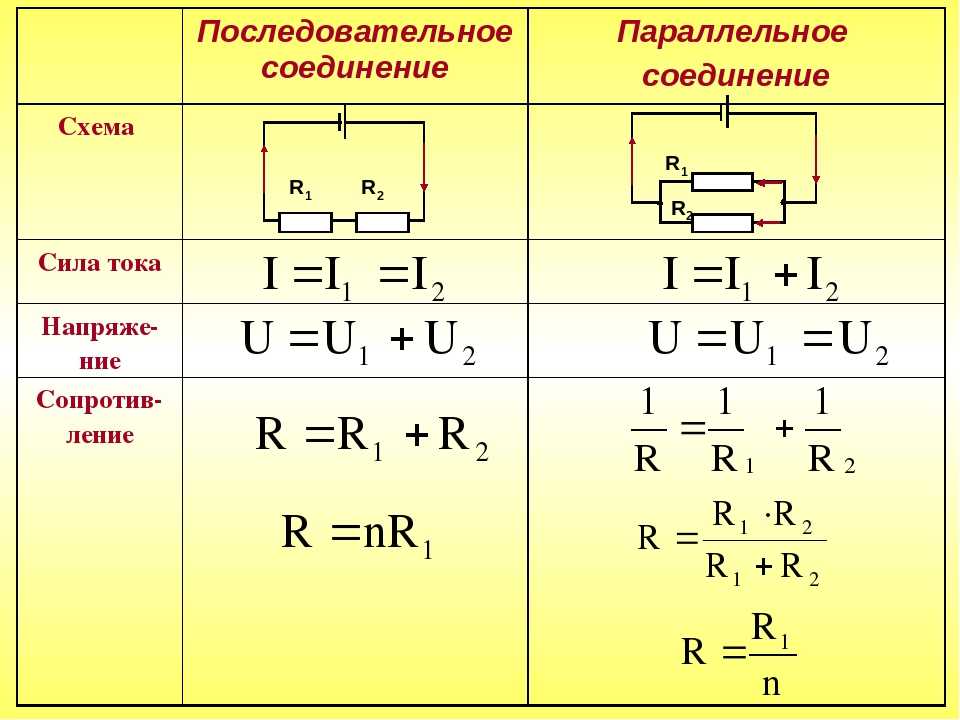 Например, \(R_{1}\) может быть сопротивлением проводов от автомобильного аккумулятора до его электрических устройств, которые включены параллельно. \(R_{2}\) и \(R_{3}\) могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.

Пример \(\PageIndex{3}\): расчет сопротивления, падения \(IR\), тока и рассеиваемой мощности: объединение последовательных и параллельных цепей

На рисунке \(\PageIndex{5}\) показаны резисторы из предыдущие два примера подключены по-другому — комбинация последовательного и параллельного. Мы можем рассматривать \(R_1\) как сопротивление проводов, ведущих к \(R_2\) и \(R_3\). а) Найдите полное сопротивление. (б) Что такое падение \(IR\) в \(R_1\)? (c) Найдите ток от \(I_2\) до \(R_2\). (d) Какая мощность рассеивается \(R_2\)?

Рисунок \(\PageIndex{5}\). Эти три резистора подключены к источнику напряжения так, что \(R_2\) и \(R_3\) параллельны друг другу, а эта комбинация последовательно с \(R_1\).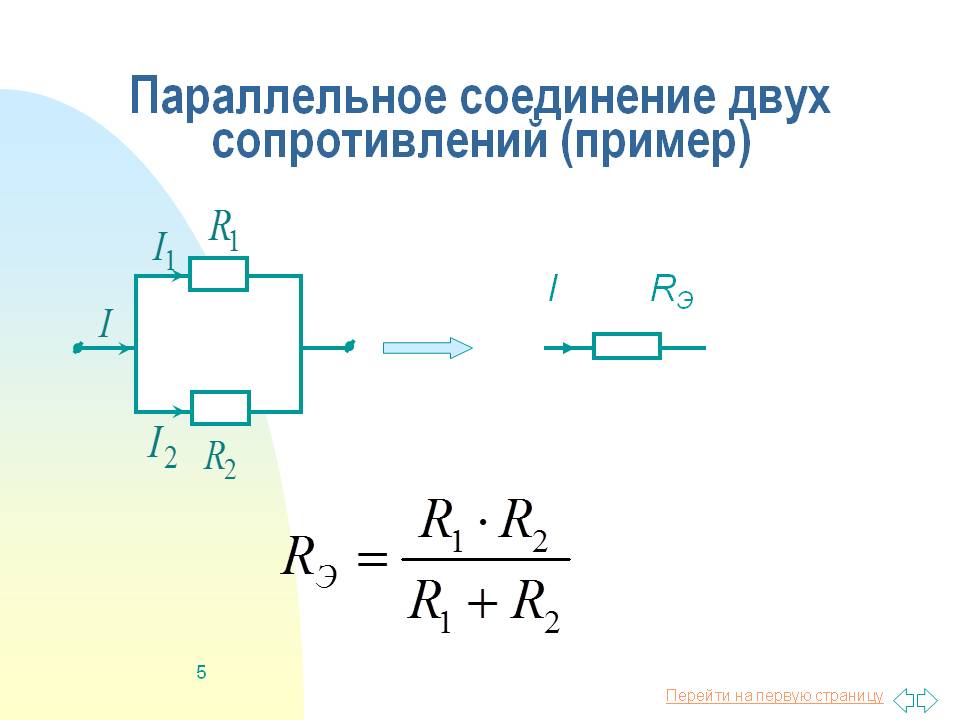

Стратегия и решение для (a)

Чтобы найти общее сопротивление, заметим, что \(R_2\) и \(R_3\) параллельны, а их комбинация \(R_p\) последовательно с \(R_1 \). Таким образом, полное (эквивалентное) сопротивление этой комбинации равно \[R_{tot} = R_1 + R_2.\]

Сначала находим \(R_p\), используя уравнение для параллельных резисторов и вводя известные значения: \[\ dfrac{1}{R_p} = \dfrac{1}{R_2} + \dfrac{1}{6,00 \, \Omega} + \dfrac{1}{13,0 \, \Omega} = \dfrac{0,2436}{\ Омега}.\]

Инвертирование дает \[R_p = \dfrac{1}{0,2436}\Omega = 4,11 \, \Omega.\] Таким образом, общее сопротивление равно \[R_{tot} = R_1 + R_p = 1,00 \Omega + 4,11 \Omega. = 5,11 \, \Омега.\]

Обсуждение для (а)

Суммарное сопротивление этой комбинации является промежуточным между чисто последовательными и чисто параллельными значениями (\(20,0 \, \Омега\) и \(0,804 \, \Omega\) соответственно), найденные для тех же резисторов в двух предыдущих примерах.

Стратегия и решение для (b)

Чтобы найти падение \(IR\) в \(R_1\), заметим, что полный ток \(I\) протекает через \(R_1\). Таким образом, его \(IR\) падение равно \[V_1 = IR_1.\]. Мы должны найти \(I\), прежде чем мы сможем вычислить \(V_1\). Полный ток \(I\) находится по закону Ома для цепи. То есть \[I = \dfrac{V}{R_{tot}} = \dfrac{12,0 \, V}{5,11 \, \Omega} = 2,35 \, A.\]. Вводя это в выражение выше, мы получить \[V_1 = IR_1 = (2,35 \, A)(1,00 \, \Omega) = 2,35 \, V.\]

Обсуждение для (б)

Напряжение на \(R_2\) и \(R_3\) меньше общего напряжения на величину \(V_1\). Когда сопротивление проводов велико, это может существенно повлиять на работу устройств, представленных \(R_2\) и \(R_3\).

Стратегия и решение для (c)

Чтобы найти ток через \(R_2\), мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение \(V_p\), потому что оно применяется к параллельной комбинации резисторов. 2(6,00 \, \ омега) = 15,5\, Вт.\]

Обсуждение для (d)

Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.

Практические выводы

Одним из следствий последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение \(IR\) в проводах также может быть значительным.

Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).

То, что происходит в таких сильноточных ситуациях, показано на рисунке \(\PageIndex{6}\). Устройство, представленное \(R_3\), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение \(IR\) в проводах, представленных \(R_1\), уменьшая напряжение на лампочке (которое равно \(R_2\)), которая затем заметно тускнеет.

Рисунок \(\PageIndex{6}\): Почему при включении крупного электроприбора свет тускнеет? Ответ заключается в том, что большой ток, потребляемый двигателем электроприбора, вызывает значительное (IR) падение напряжения в проводах и снижает напряжение на лампе.

Упражнение \(\PageIndex{1}\)

Можно ли любую произвольную комбинацию резисторов разбить на последовательные и параллельные комбинации? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательных и параллельных соединений.

Ответить

Нет, существует множество способов соединения резисторов, не являющихся комбинациями последовательного и параллельного соединения, включая петли и соединения. В таких случаях правила Кирхгофа, которые будут представлены в Правилах Кирхгофа, позволят вам проанализировать схему.

Стратегии решения проблем для последовательных и параллельных резисторов

1. Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме.
2. Определите, что именно нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
3. Определите, подключены ли резисторы последовательно, параллельно или как последовательно, так и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
4. Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных. Если в вашей задаче сочетаются последовательные и параллельные соединения, уменьшите ее пошагово, рассмотрев отдельные группы последовательных или параллельных соединений, как это делается в этом модуле и в примерах. Специальное примечание: при нахождении \(R_p\) необходимо соблюдать осторожность.
5. Проверить разумность и последовательность ответов. Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.

Резюме

• Общее сопротивление электрической цепи с последовательно соединенными резисторами представляет собой сумму отдельных сопротивлений: \(R_s = R_1 + R_2 + R_3 + ….\)
• Через каждый резистор в последовательной цепи протекает одинаковый ток.
• Падение напряжения или рассеиваемая мощность на каждом отдельном резисторе в серии различны, и их общая сумма составляет входную мощность источника питания.
• Общее сопротивление электрической цепи с параллельно соединенными резисторами меньше наименьшего сопротивления любого из компонентов и может быть определено по формуле: \(\dfrac{1}{R_p} = \dfrac{1}{R_1 } +\dfrac{1}{R_2} + \dfrac{1}{R_3} + . …\)
• К каждому резистору в параллельной цепи приложено одинаковое полное напряжение источника.
• Ток, протекающий через каждый резистор в параллельной цепи, различен в зависимости от сопротивления.
• Если более сложное соединение резисторов представляет собой комбинацию последовательного и параллельного сопротивления, его можно свести к единому эквивалентному сопротивлению, обозначив различные его части как последовательные или параллельные, сведя каждую к эквиваленту и продолжая до тех пор, пока в конечном итоге не будет достигнуто единое сопротивление .

Глоссарий

Серия

последовательность резисторов или других компонентов, включенных в цепь один за другим

резистор

Компонент, обеспечивающий сопротивление току, протекающему по электрической цепи

сопротивление

, вызывающий потерю электроэнергии в цепи

Закон Ома

соотношение между током, напряжением и сопротивлением в электрической цепи: V=IR

напряжение

электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например батареей

падение напряжения

потеря электроэнергии при протекании тока через резистор, провод или другой компонент

текущий

поток заряда через электрическую цепь, проходящий через заданную точку измерения

Закон Джоуля

Соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое как: \(P_e = IV\)

параллельный

соединение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы

---

Эта страница под названием 21. 1: Резисторы в последовательном и параллельном соединении распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. Текущий
   2. Закон Джоуля
   3. Закон Ома
   4. параллельно
   5. сопротивление
   6. Резистор
   7. Резисторы параллельно
   Резисторы
   8. в серии
   9. серия
   10. источник@https://openstax. org/details/books/college-physics
   11. падение напряжения

Сокращенные уравнения для параллельных резисторов

Патрик Форд

630views

Было ли это полезно?

Привет, ребята. Итак, в этом видео я покажу вам несколько замечательных комбинаций, которые вы можете использовать в некоторых случаях, когда у вас есть резисторы, включенные параллельно, и это избавит вас от необходимости выполнять много работы с дробями, давайте проверим это. Итак, если у вас есть два резистора, включенных параллельно, вы можете использовать сокращенное уравнение. Теперь, помните, общее уравнение таково: эквивалентное сопротивление при параллельном соединении равно единице, превышающей наши эквиваленты, равно единице, превышающей R, и единице, превышающей R. То есть, если у вас есть два резистора, это общее уравнение, хорошо? И я решу наши эквиваленты, чтобы вам никогда не пришлось делать это снова.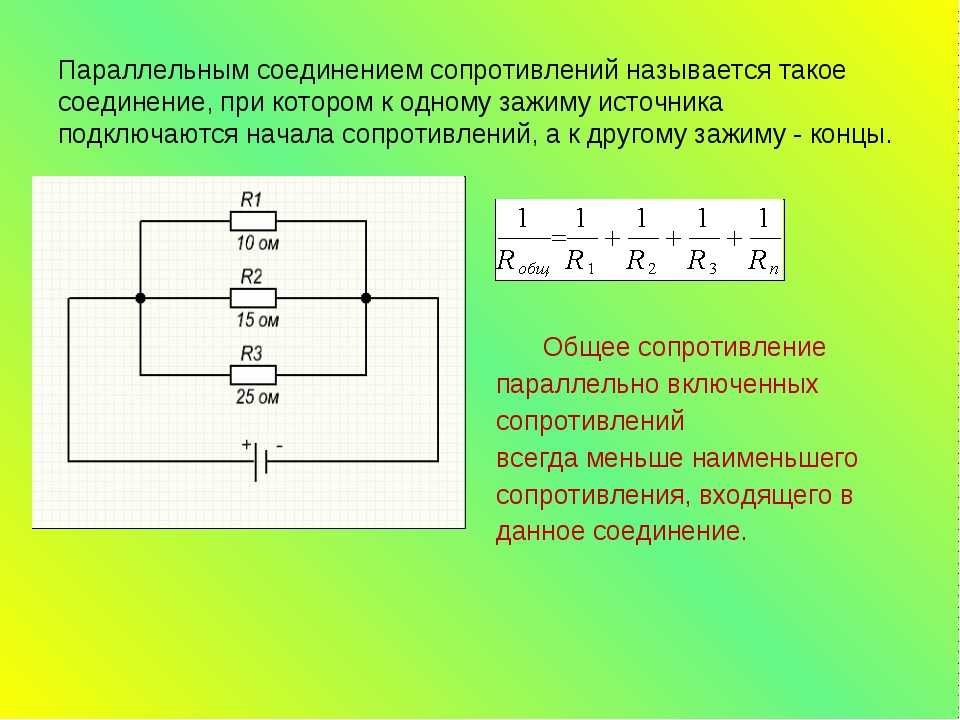 И вы можете просто использовать ярлык, если у вас есть два резистора, что является наиболее распространенной вещью, которую вы получите. Итак, первое, что, если вы помните, мы должны найти общий знаменатель. И чтобы сделать это, вы просто умножаете наш на здесь, а затем умножаете на один здесь. Так один раз тоже. Так что, если я делаю внизу, я также должен делать в верхней части или два, а затем два раза один раз один раз. Давайте расширим эту маленькую дробь. Итак, что происходит сейчас, у меня есть один или два внизу, один или два внизу. Так что у меня есть общий знаменатель. Так что я могу написать наши один раз тоже. А потом наверху у меня два плюс один или я поеду R один плюс R два. Так что в порядке. Мы закончили? Помните, мы должны перевернуть стороны. Так что, если я переверну здесь, я получу наши эквиваленты больше единицы или просто эквивалентно равны. А потом, если я переверну левый, я должен перевернуть правый, и это будет выглядеть, извините. Это была двойка прямо там. Будем надеяться, поймали, что один раз слишком за наш один плюс наши два теперь заметили. 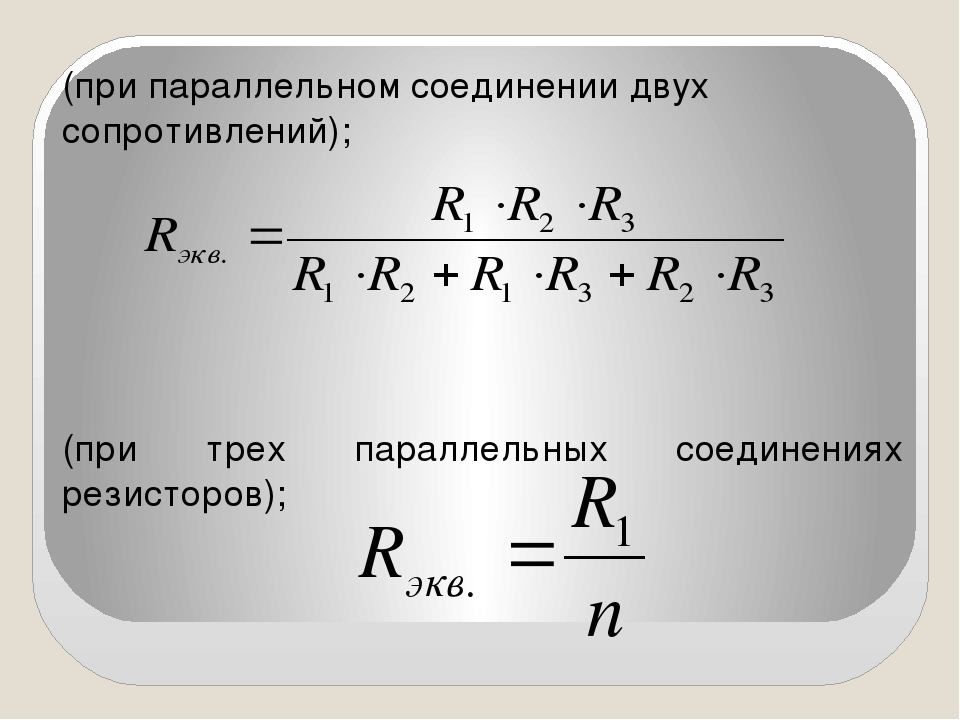Я рисую r one и r two внизу очень далеко друг от друга. И причина, по которой я это делаю, заключается в том, что одна из самых больших проблем с этим уравнением заключается в том, что люди забывают, что на первом месте: время или плюсы. Вы не знаете, что куда идет, вы можете забыть, как я помню, что глупо, но работает, потому что это точки. Это крошечные точки. R one r two очень близко друг к другу, и это большой плюс, который занимает гораздо больше места. Нижние переменные находятся дальше друг от друга, а худой верх и толстый низ образуют своего рода треугольник. Ладно, супер глупо. Но, может быть, надеюсь, это сработает для вас. Что бы ни работало, верно? Таково уравнение. Поэтому всякий раз, когда у вас есть два резистора, соединенных параллельно, вы можете просто использовать это уравнение вместо того, чтобы играть с дробями. Хорошо, теперь очень важно то, что вы не можете сделать это для трех или более резисторов, поэтому я действительно хочу, чтобы вы нарисовали вот это. Это неправильно, но я хочу, чтобы вы это написали. Скажем, вы можете подумать, что можете умножить один или два. Почему бы просто не добавить три Р здесь, а затем здесь внизу сделать плюс три Р. Что ж, это неправильно. Это не работает. Так что я хочу, чтобы вы написали это, вычеркнули и сказали: «Нет, не делай этого». Этот Onley работает на двух резисторах. Больше двух не работает. Хорошо, позвольте мне привести вам очень быстрый пример. Допустим, у вас есть четверка и шестерка, и вы хотите объединить их в один резистор. Вы бы просто использовали это уравнение и сказали, что эквивалентное сопротивление равно четырем шести, деленным на четыре плюс шесть. Я настраиваю учеников, чтобы я мог поместить числа внутри +4646 А это 24 разделить на 2,4, верно, намного быстрее, чем играть с дробями. Итак, это первый ярлык. Хм, всегда самое главное, чтобы вы знали общее уравнение, потому что оно сработает для всего. Но ярлык тоже очень удобен. Гораздо важнее использовать ярлык номер два, но путь номер два очень прост. Если у вас есть резисторы с одинаковым сопротивлением, вы также можете использовать сокращенное уравнение.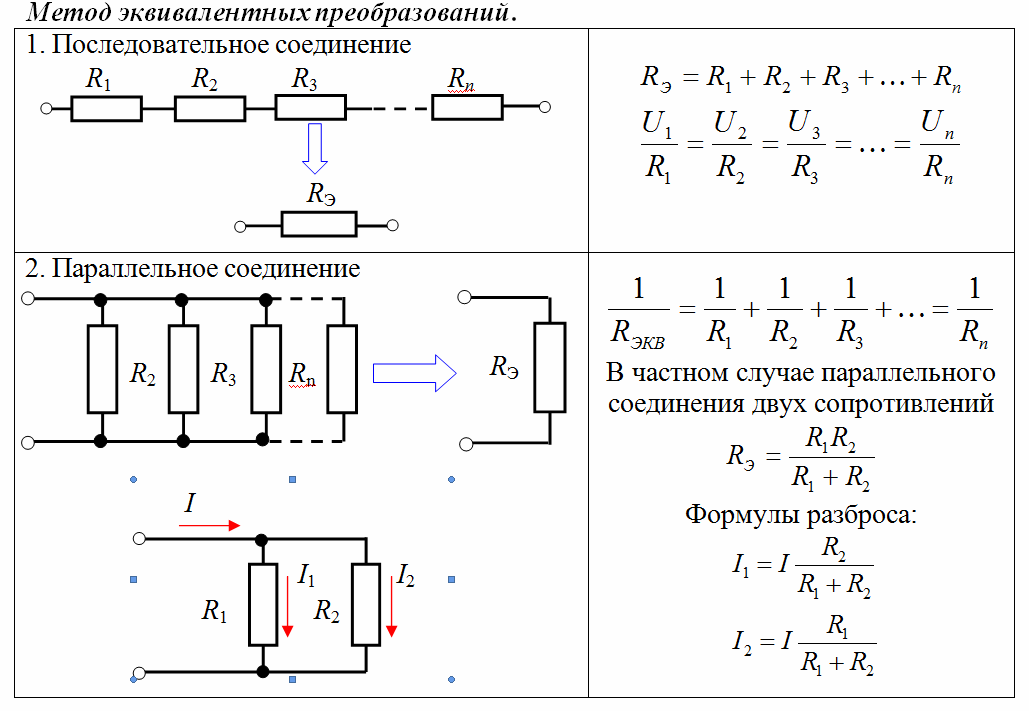 Итак, скажем, у меня есть «Давайте сделаем это жутким». 66 и шесть. Допустим, у вас есть что-то подобное. Какое эквивалентное сопротивление? Ну, если вы пишете общее уравнение, помните, вы не можете написать это уравнение прямо здесь. Тот, о котором мы только что говорили, потому что он работает только для двоих. Но если у вас есть это, вы получите что-то вроде этого 1/6, плюс 1/6, плюс 1/6. И знаменатели уже одинаковы, чтобы в итоге получить 3/6 или 6/3, что является быстрым способом сделать это, просто сказать, что эквивалентное сопротивление, когда они все одинаковые параллельно, — это одно и то же сопротивление. что в данном случае равно шести, деленным на количество резисторов. Таким образом, вы могли бы просто сделать шесть разделить на три тоже. Например, если у вас есть восемь, восемь, восемь и восемь эквивалентных сопротивлений, здесь его очень легко вычислить, его СПИД и их четыре. Эквивалентное сопротивление просто для охлаждения. Так что теперь я собираюсь сделать пример. Что-то вроде слияния всех этих идей. Вы не умеете легко сочетать одинаковые вещи. И вы знаете, как легко комбинировать, когда они имеют одинаковое сопротивление, и вы знаете, как легко комбинировать. Если сейчас двое из них используют это первое уравнение, вы действительно можете использовать эти два правила в своих интересах. Итак, если вы получите такой вопрос. Это может показаться Гарри, но на самом деле это очень просто. Итак, мы заметим, что у нас есть девятка на девятку в девятке. И даже если они не находятся рядом друг с другом, вы можете технически переставить их так, чтобы они были рядом друг с другом. И вы можете сказать, знаете что? Эта девятка с этой девяткой и с этой девяткой, потому что они одинаковые, я могу писать. Эквивалентное сопротивление трех девяток составляет всего 9/3. Я использую этот ярлык прямо здесь. Есть три девятки, так что просто девять разделить на три, что равно трем. Хорошо, вы можете сделать то же самое для 12. Там 2 12, так что я могу сказать, что эквивалентное сопротивление в сумме будет 12, деленное на два, всего шесть.