Как рассчитать общее сопротивление при последовательном и параллельном соединении проводников. Какие формулы используются для вычисления эквивалентного сопротивления цепи. Где применяются различные типы соединений проводников на практике.
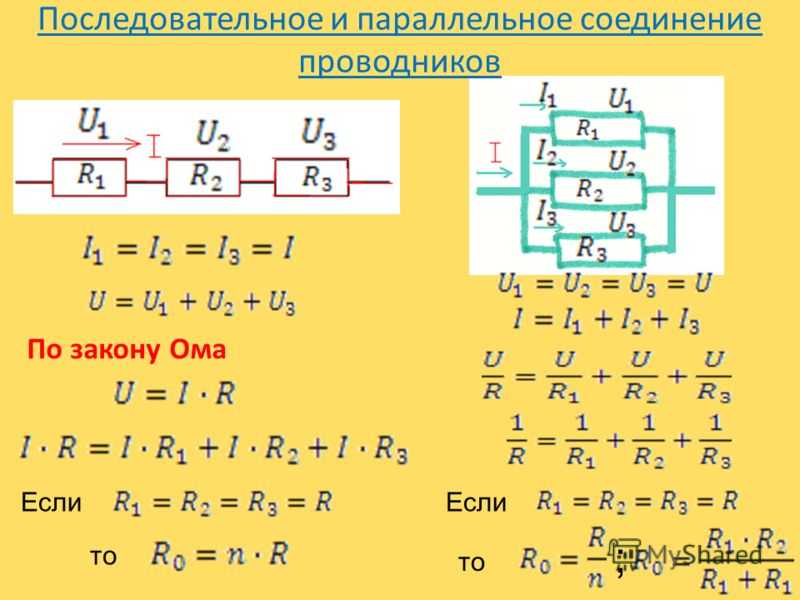
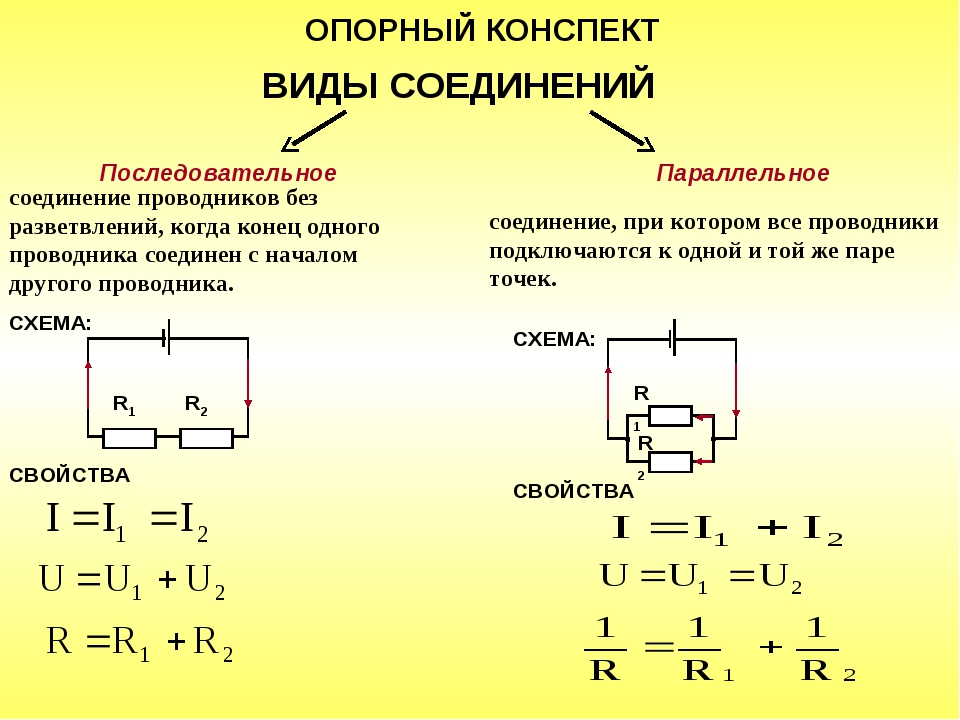
Последовательное соединение проводников
При последовательном соединении проводники подключаются один за другим, образуя единую неразветвленную цепь. Основные характеристики такого соединения:
- Сила тока одинакова во всех проводниках
- Общее напряжение равно сумме напряжений на отдельных проводниках
- Общее сопротивление равно сумме сопротивлений отдельных проводников
Формула для расчета общего сопротивления при последовательном соединении:
R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление цепи, R1, R2, R3, …, Rn — сопротивления отдельных проводников.
Параллельное соединение проводников
При параллельном соединении все проводники подключаются к одним и тем же точкам цепи. Ключевые особенности:

- Напряжение одинаково на всех проводниках
- Общий ток равен сумме токов через отдельные проводники
- Обратная величина общего сопротивления равна сумме обратных величин сопротивлений отдельных проводников
Формула для расчета общего сопротивления при параллельном соединении:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
где R — общее сопротивление цепи, R1, R2, R3, …, Rn — сопротивления отдельных проводников.
Расчет эквивалентного сопротивления сложных цепей
Для расчета эквивалентного сопротивления сложных цепей, содержащих как последовательные, так и параллельные участки, можно использовать следующий алгоритм:
- Выделить простые последовательные и параллельные соединения
- Рассчитать эквивалентные сопротивления для этих простых участков
- Заменить рассчитанные участки эквивалентными сопротивлениями
- Повторять шаги 1-3, пока не останется одно эквивалентное сопротивление всей цепи
Практическое применение различных соединений проводников
Последовательное и параллельное соединения проводников широко используются в электротехнике и электронике. Вот некоторые примеры их применения:

Последовательное соединение:
- Елочные гирлянды — лампочки соединены последовательно
- Предохранители в электрических цепях
- Резисторы в цепях делителей напряжения
Параллельное соединение:
- Подключение бытовых электроприборов к электросети
- Соединение аккумуляторов для увеличения емкости
- Шунты в измерительных приборах
Сравнение последовательного и параллельного соединений
Чем отличаются последовательное и параллельное соединения проводников? Основные различия:
| Характеристика | Последовательное соединение | Параллельное соединение |
|---|---|---|
| Сила тока | Одинакова во всех элементах | Разная в разных ветвях |
| Напряжение | Сумма напряжений на элементах | Одинаково на всех элементах |
| Общее сопротивление | Больше сопротивления любого элемента | Меньше сопротивления любого элемента |
Решение задач на соединения проводников
При решении задач на соединения проводников рекомендуется придерживаться следующего алгоритма:
- Внимательно прочитать условие задачи
- Начертить схему соединения проводников
- Определить тип соединения (последовательное, параллельное или смешанное)
- Записать формулы для расчета эквивалентного сопротивления
- Подставить известные значения и провести вычисления
- Проверить размерность полученного результата
- Записать ответ с указанием единиц измерения
Смешанное соединение проводников
Смешанное соединение представляет собой комбинацию последовательного и параллельного соединений. Для расчета эквивалентного сопротивления при смешанном соединении используется следующий подход:

- Разбить схему на участки с однотипным соединением (последовательным или параллельным)
- Рассчитать эквивалентное сопротивление для каждого участка
- Заменить рассчитанные участки их эквивалентными сопротивлениями
- Повторять процесс, пока не останется одно общее сопротивление
Пример расчета смешанного соединения:
«`python # Функция для расчета параллельного соединения def parallel_resistance(*args): return 1 / sum(1/r for r in args) # Заданные сопротивления R1 = 10 # Ом R2 = 20 # Ом R3 = 30 # Ом R4 = 40 # Ом # Шаг 1: Расчет параллельного участка R2 || R3 R23 = parallel_resistance(R2, R3) # Шаг 2: Расчет последовательного соединения R1 + (R2 || R3) + R4 R_total = R1 + R23 + R4 print(f»Эквивалентное сопротивление цепи: {R_total:.2f} Ом») «`Зависимость сопротивления от температуры
При расчете соединений проводников важно учитывать, что сопротивление металлических проводников зависит от температуры. Эта зависимость описывается формулой:

R = R0(1 + αΔT)
где:
- R — сопротивление при данной температуре
- R0 — сопротивление при начальной температуре (обычно 20°C)
- α — температурный коэффициент сопротивления материала
- ΔT — изменение температуры
Учет температурной зависимости особенно важен при проектировании электрических цепей, работающих в широком диапазоне температур.
Выведите формулы последовательного и параллельного соединений сопротивлений
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды.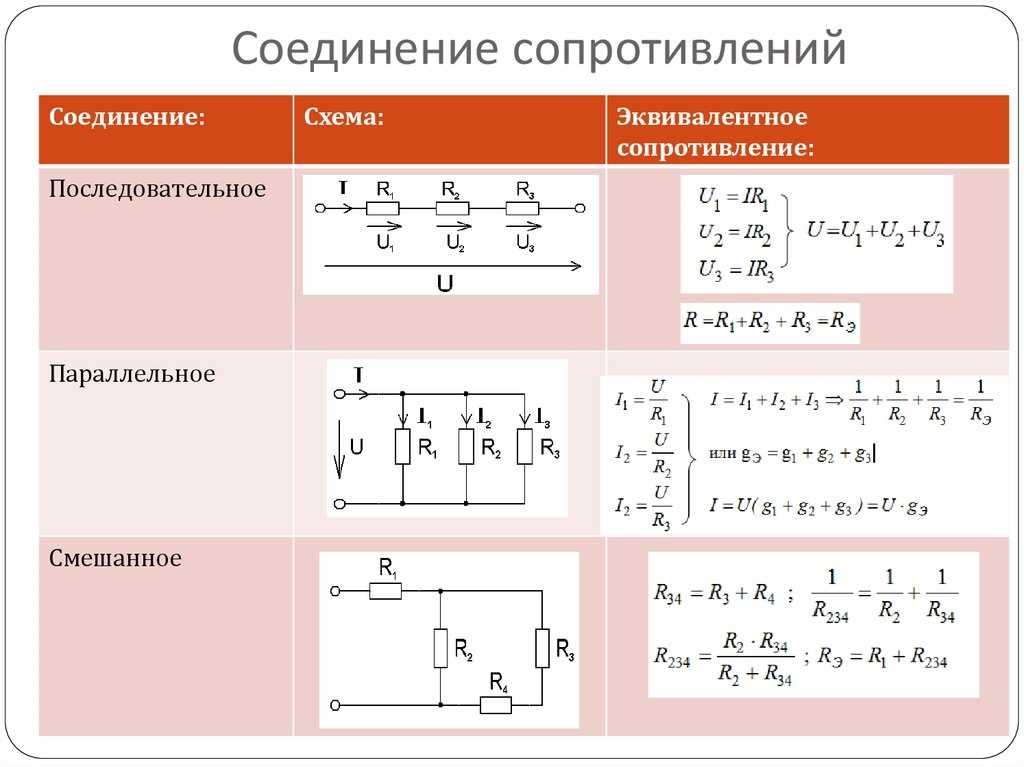 Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Параллельное соединение проводников
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Расчет сопротивления сложной цепи.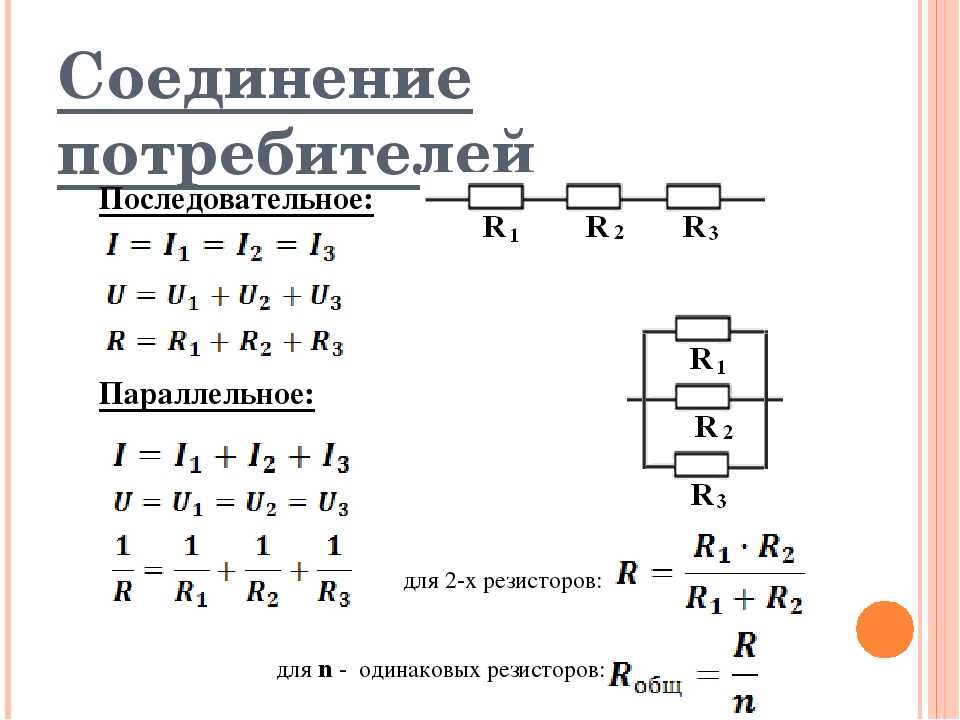 Сопротивления всех проводников указаны вомах (Ом)
Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.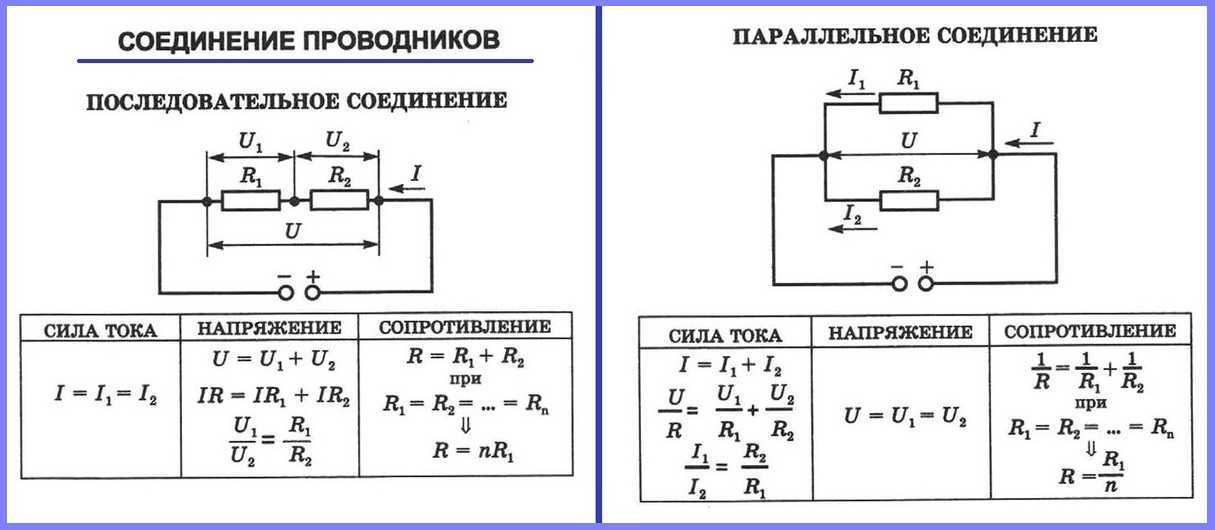
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Параллельное соединение проводников
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.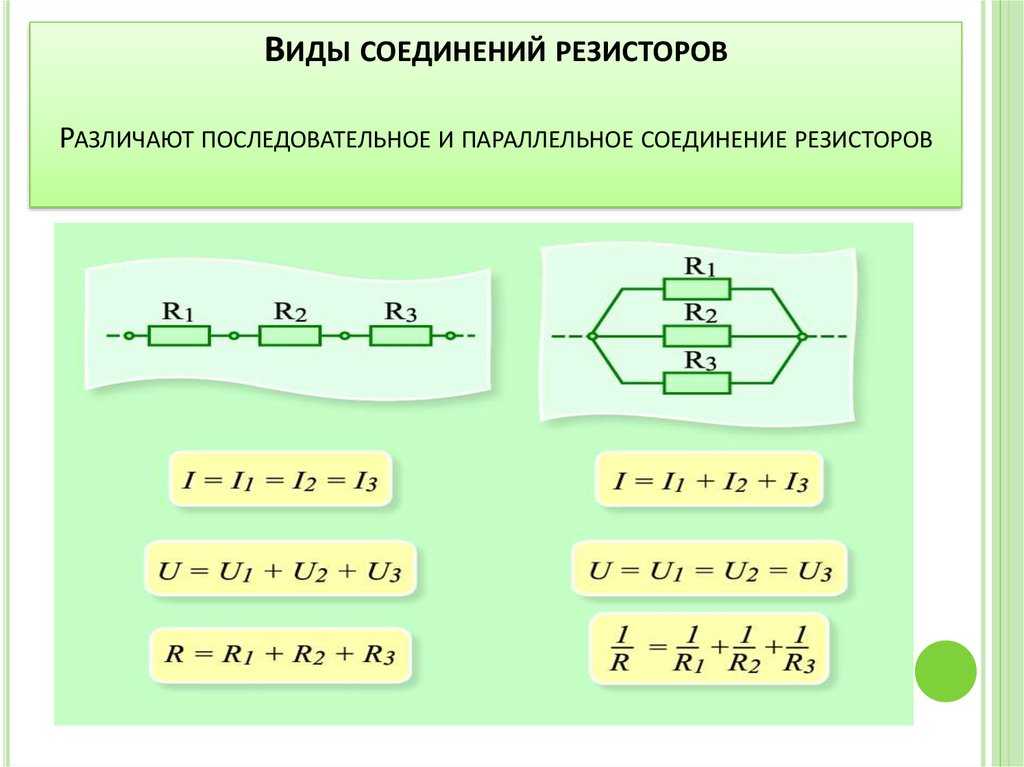
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Последовательное соединение сопротивлений
Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис.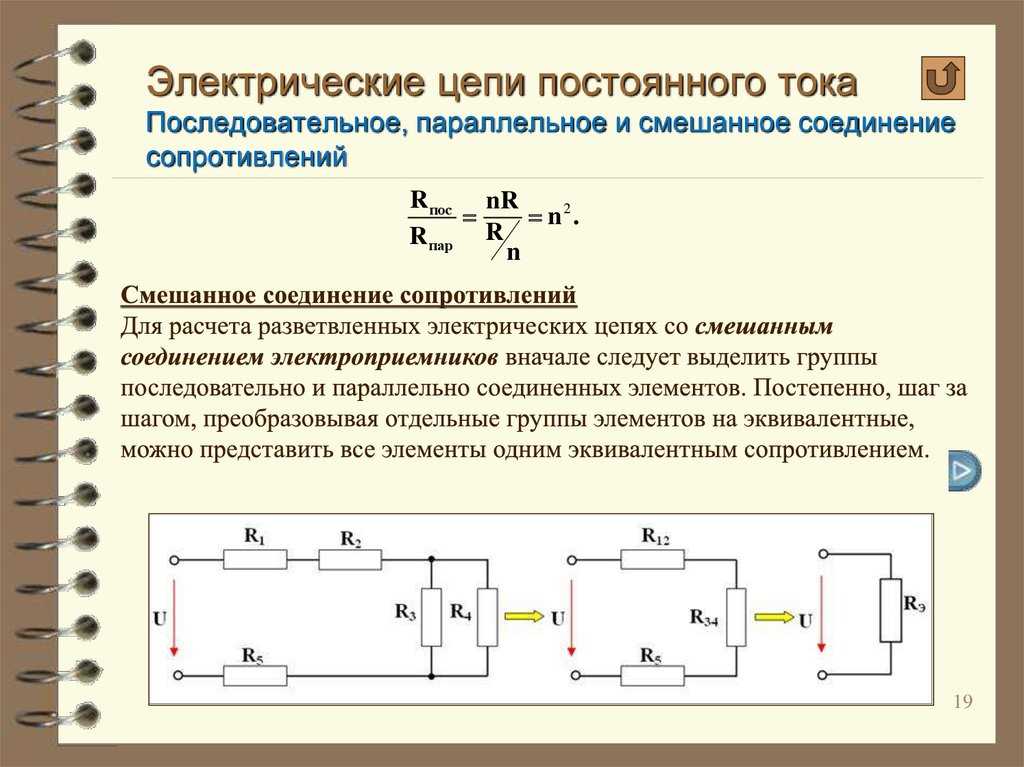 1 ).
1 ).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
Рис 1 . Последовательное соединение сопротивлений
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U1 = IR1 U2 = IR2 и U3 = IR3
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом).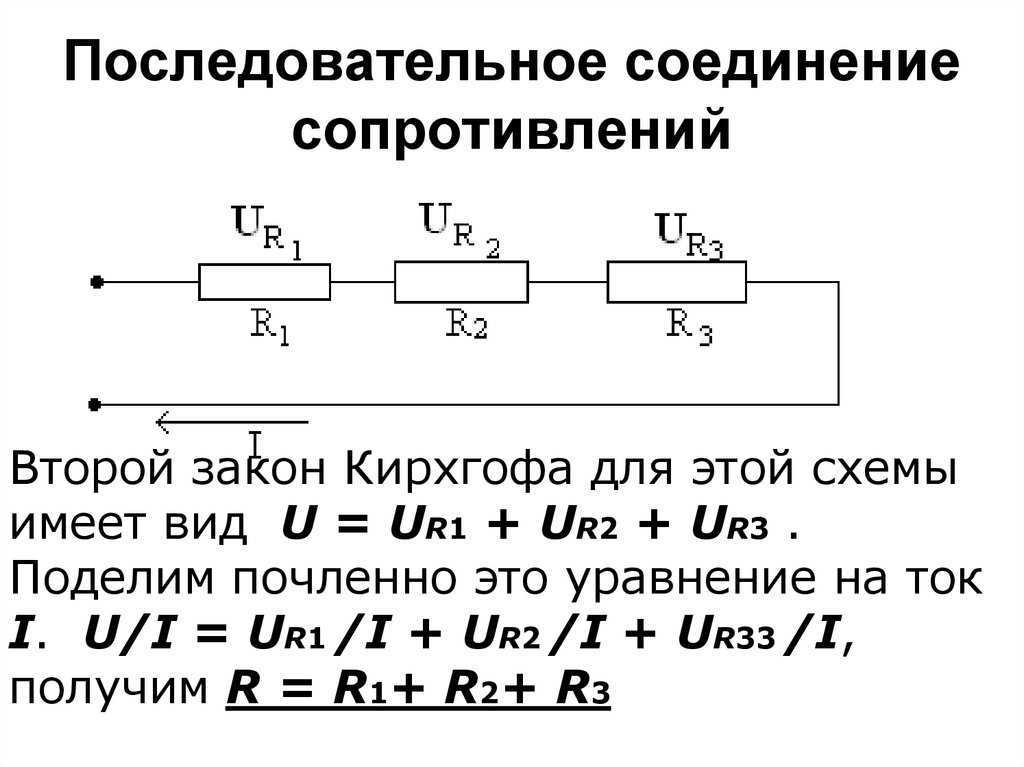 Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи по закону Ома: 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75 х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.
Параллельное соединение сопротивлений
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (—), заметим, что прибор покажет ту же величину силы тока.
Значит, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .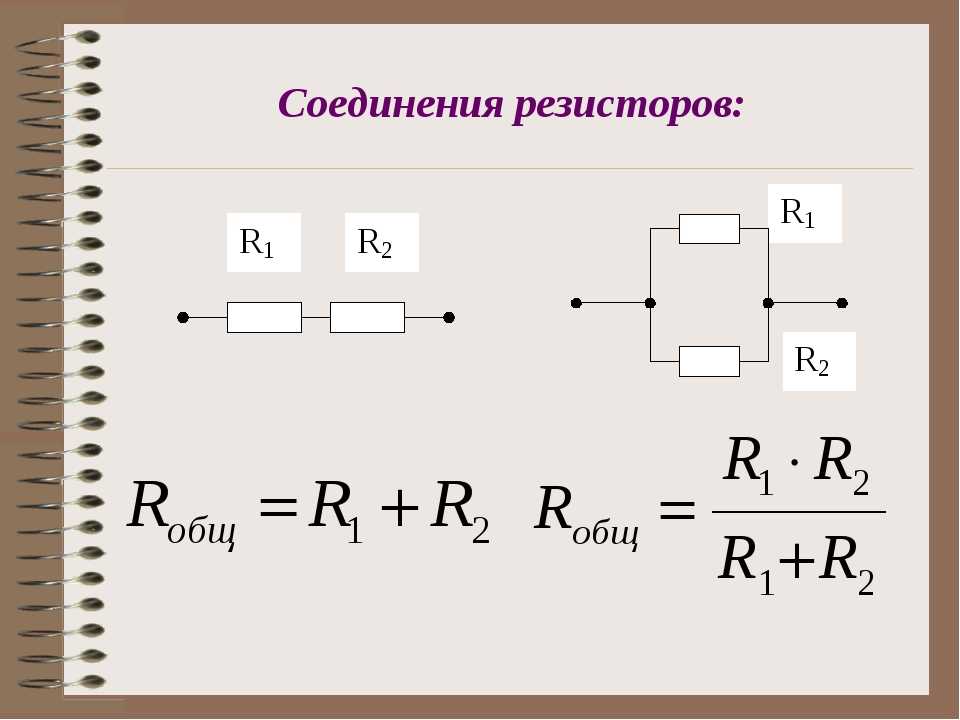
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R 1 и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U 1 — падение напряжения на сопротивлении R 1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U 1 = U2, то и I1R1 = I2R2 .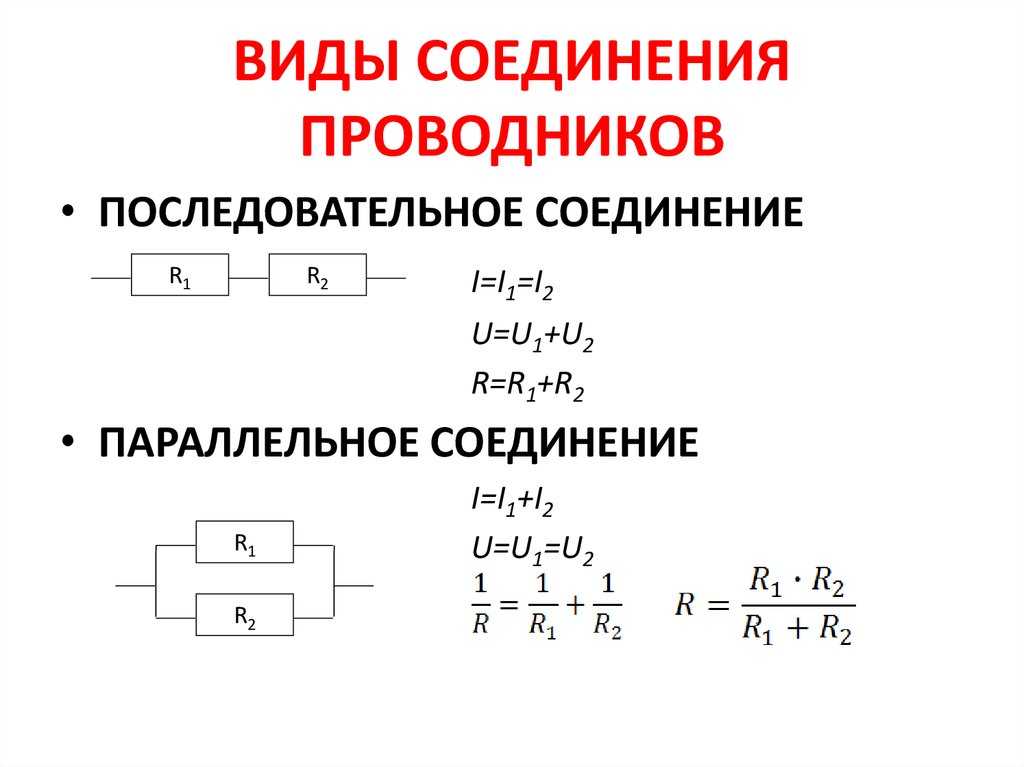
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей. Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 + I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть ( I1 = 300 мА) пошла через меньшее сопротивление ( R1 = 10 Ом), а меньшая часть ( R2 = 150 мА) — через большее сопротивление ( R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Рис. 4 . Через тонкую трубу в один и тот же промежуток времени пройдет воды меньше, чем через толстую
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.
Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U 1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ).
Определим эквивалентное сопротивление цепи (рис. 5 ).
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0, 2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 = 1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / ( R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
применение, формулы расчёта ёмкости и напряжения • Мир электрики
Содержание
- Немного теории
- Способы соединения конденсаторов
- Последовательное соединение
- Параллельное подключение
- Смешанное включение
Практически на любой электронной плате применяются конденсаторы, устанавливаются они и в силовых схемах. Для того чтобы компонент мог выполнять свои функции, он должен обладать определёнными характеристиками. Иногда возникает ситуация, когда необходимого элемента нет в продаже или его цена неоправданно завышена.
Выйти из сложившегося положения можно, используя несколько элементов, а необходимые характеристики получают, применяя параллельное и последовательное соединения конденсаторов между собой.
Немного теории
Конденсатор — пассивный электронный компонент, с переменной или постоянной величиной ёмкости, которое предназначено для накопления заряда и энергии электрического поля.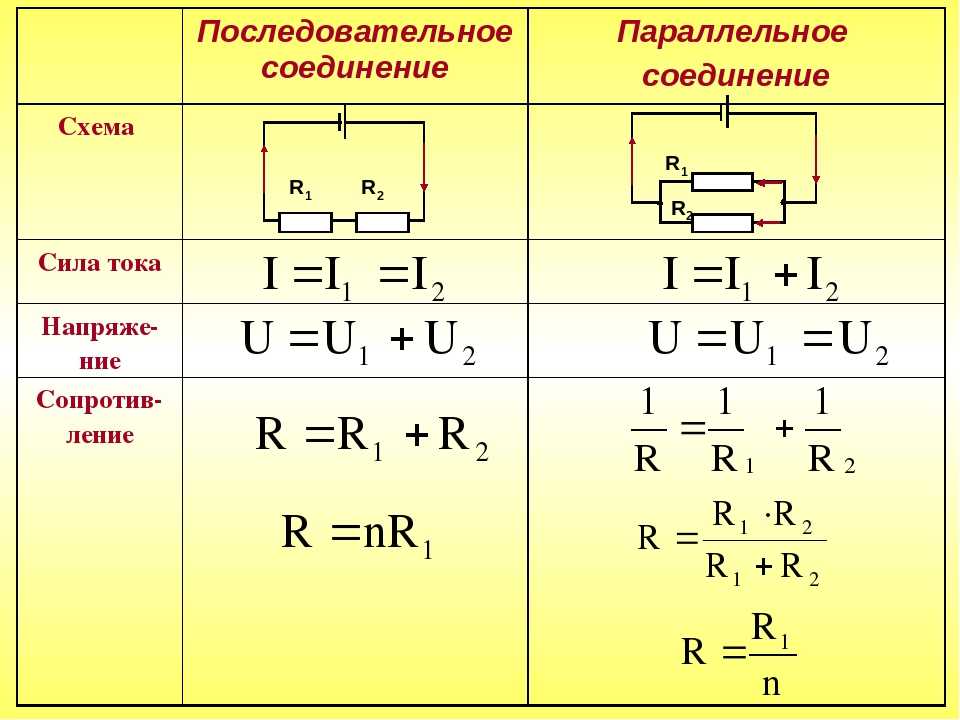
При выборе этих электронных компонентов руководствуются двумя основными характеристиками:
- Номинальная ёмкость измеряется в фарадах, но так как это очень большая величина, чаще всего применяют микрофарады. Номинальную величину этого параметра указывают на корпусе. Необходимо учитывать, что в зависимости от класса точности, отклонение действительной величины от номинальной может достигать ±20%, а иногда и более. Такие элементы подходят для большинства схем, поэтому при составлении батареи конденсаторов точного подбора ёмкости не требуется, достаточно уложиться в указанную погрешность.
- Номинальное напряжение измеряется в вольтах. Применение электронного компонента с номинальным напряжением, которое ниже чем в схеме, может привести к пробою диэлектрика и выходу элемента из строя. Поэтому эту величину необходимо выбирать с некоторым запасом.
Условное обозначение неполярного постоянного конденсатора на схеме, показано на рис. 1, а. Для полярного электронного компонента дополнительно отмечают положительный вывод — рис. 1, б.
1, а. Для полярного электронного компонента дополнительно отмечают положительный вывод — рис. 1, б.
Способы соединения конденсаторов
Составление батарей конденсаторов позволяет изменить суммарную ёмкость или рабочее напряжение. Для этого могут применяться такие способы соединения:
- последовательное;
- параллельное;
- смешанное.
Последовательное соединение
Последовательное подключение конденсаторов показано на рис. 1, в. Применяют такое соединение в основном для увеличения рабочего напряжения. Дело в том, что диэлектрики каждого из элементов расположены друг за другом, поэтому при таком соединении напряжения складываются.
Суммарная ёмкость последовательно соединённых элементов можно рассчитать по формуле, которая для трёх компонентов будет иметь вид, показанный на рис. 1, е.
После преобразования в более привычную для нас форму, формула примет вид рис. 1, ж.
Если, соединённые последовательно, компоненты имеют одинаковые ёмкости, то расчёт значительно упрощается. В этом случае суммарную величину можно определить, разделив номинал одного элемента на их количество. Например, если требуется определить, какова ёмкость при последовательном соединении двух конденсаторов по 100 мкФ, то эту величину можно рассчитать, разделив 100 мкФ на два, то есть суммарная ёмкость равна 50 мкФ.
В этом случае суммарную величину можно определить, разделив номинал одного элемента на их количество. Например, если требуется определить, какова ёмкость при последовательном соединении двух конденсаторов по 100 мкФ, то эту величину можно рассчитать, разделив 100 мкФ на два, то есть суммарная ёмкость равна 50 мкФ.
Максимально упростить расчёты последовательно соединённых компонентов, позволяет использование онлайн-калькуляторов, которые без проблем можно найти в сети.
Параллельное подключение
Параллельное подключение конденсаторов показано на рис. 1, г. При таком соединении рабочее напряжение не изменяется, а ёмкости складываются. Поэтому для получения батарей большой ёмкости, используют параллельное соединение конденсаторов. Калькулятор для расчёта суммарной ёмкости не понадобится, так как формула имеет простейший вид:
С сум = С 1 + С 2 + С 3.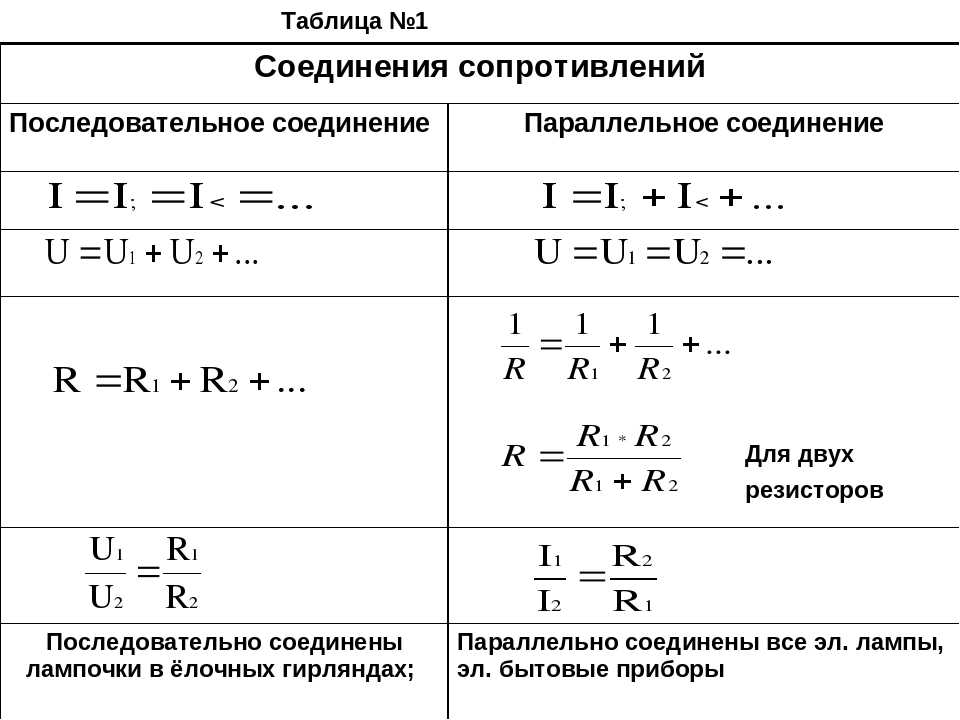
Собирая батарею для запуска трёхфазных асинхронных электродвигателей, часто применяют параллельное соединение электролитических конденсаторов. Обусловлено это большой ёмкостью этого типа элементов и небольшим временем запуска электродвигателя. Такой режим работы электролитических компонентов допустим, но следует выбирать те элементы, у которых номинальное напряжение минимум в два раза превышает напряжение сети.
Смешанное включение
Смешанное подключение конденсаторов — это сочетание параллельного и последовательного соединений.
Схематически такая цепочка может выглядеть по-разному. В качестве примера рассмотрим схему, изображённую на рис. 1, д. Батарея состоит из шести элементов, из которых С1, С2, С3, соединены параллельно, а С4, С5, С6 — последовательно.
Рабочее напряжение можно определить сложением номинальных напряжений С4, С5, С6 и напряжения одного из параллельно подключённых конденсаторов. Если параллельно соединённые элементы имеют разные номинальные напряжения, то для расчёта берут меньшее из трёх.
Если параллельно соединённые элементы имеют разные номинальные напряжения, то для расчёта берут меньшее из трёх.
Для определения суммарной ёмкости, схему разбивают на участки с одинаковым соединением элементов, производят расчёт для этих участков, после чего определяют общую величину.
Для нашей схемы последовательность вычислений следующая:
- Определяем ёмкость параллельно соединённых элементов и обозначаем её С 1-3.
- Рассчитываем ёмкость последовательно соединённых элементов С 4-6.
- На этом этапе можно начертить упрощённую эквивалентную схему, в которой вместо шести элементов изображаются два — С 1-3 и С 4-6. Эти элементы схемы соединены последовательно. Остаётся произвести расчёт такого соединения и мы получим искомую.
В жизни подробные знания о смешанном соединении могут только пригодится радиолюбителям.
Комбинация ячеек последовательно и параллельно
В сложных электрических цепях имеется много сопротивлений. Существуют методы расчета эквивалентных сопротивлений в случае, если несколько сопротивлений соединены последовательно или параллельно, а иногда и в комбинации последовательно и параллельно. Во многих ситуациях в цепях также присутствуют батареи или различные типы источников напряжения. Важно определить их влияние на цепь, поэтому важно получить результаты для расчета последовательных и параллельных комбинаций различных источников напряжения, присутствующих в цепи. Рассмотрим подробно это понятие.
Комбинация элементов
Часто в реальной жизни невозможно изготовить источники напряжения и батареи для каждого конкретного значения напряжения. На рынке доступны только определенные типы аккумуляторов. В случае, когда необходимо другое напряжение. Два или более источников напряжения используются в различных комбинациях для получения желаемого значения напряжения и тока. Эти батареи могут быть соединены в двух основных типах комбинаций. Эти комбинации составляют основу для всех остальных комбинаций. Вот эти две комбинации:
Два или более источников напряжения используются в различных комбинациях для получения желаемого значения напряжения и тока. Эти батареи могут быть соединены в двух основных типах комбинаций. Эти комбинации составляют основу для всех остальных комбинаций. Вот эти две комбинации:
- Серийная комбинация
- Параллельная комбинация.
Комбинация серий
На приведенном ниже рисунке показаны две ячейки, последовательно соединенные друг с другом. В этом случае одна клемма каждой ячейки соединена с другой, а другая клемма свободна в любой из ячеек. E 1 и E 2 — ЭДС двух элементов, а r 1 , r 2 — их внутренние сопротивления. Если потенциал в трех точках A, B и C обозначим через V(A), V(B) и V(C). Тогда разность потенциалов между этими ячейками определяется как V(A) – V(B) и V(B) – V(C).
V AB = V(A) – V(B) = E 1 – Ir 1
V BC = V(B) – V(C)2 – = E 29001 Ir 2
Таким образом, разность потенциалов между точками A и C будет равна
V(A) – V(C) = [V(A) – V(B)] – [V(C ) – V(B)]
⇒ V(A) – V(C) = E 1 + E 2 – (Ir 1 + Ir 2 )
⇒ V(A) – V (С) = Е 1 + Е 2 – (Ir 1 + Ir 2 )
Чтобы заменить эту комбинацию ячеек одной эквивалентной ячейкой со значением ЭДС E eq и r eq .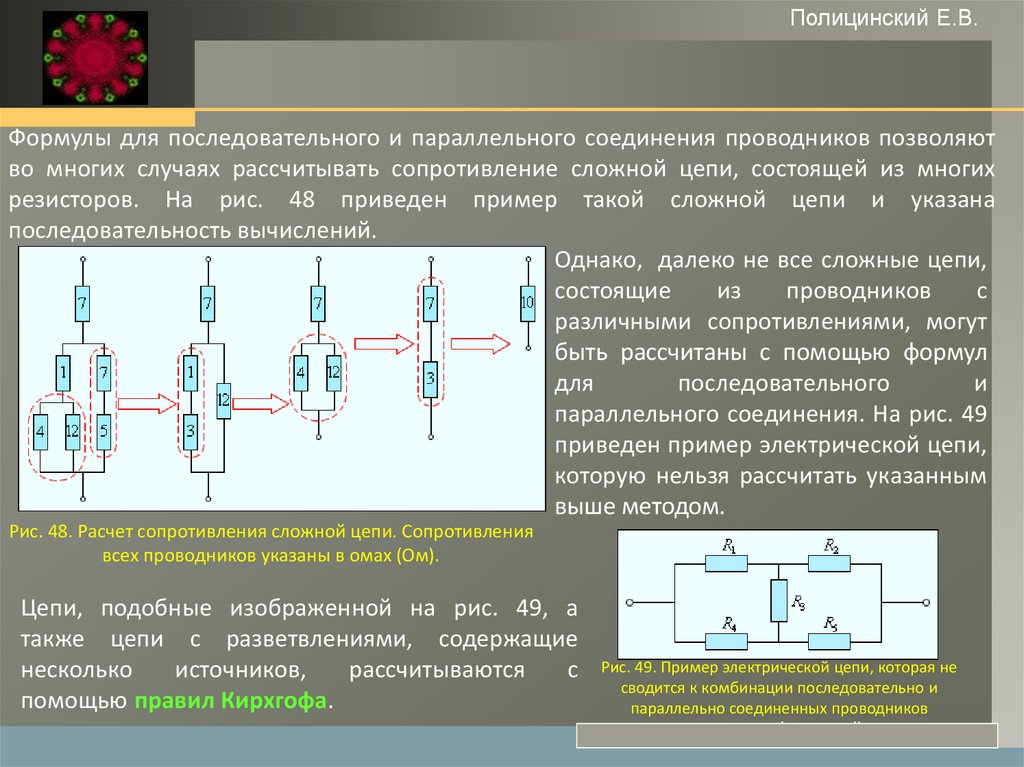 Затем,
Затем,
⇒ E Уравнение — I (R EQ ) = E 1 + E 2 — (IR 1 + IR 2 )
E EQ = E 10003 E EQ = E 10003 E EQ = E 10003 E EQ = E 10003 E EQ = E 10003 E EQ = E Это может быть расширено до любого количества ячеек, E eq = E 1 + E 2 + … и r eq = r 1 + r 2 + … электрод другой батареи. Если мы соединим их одинаковые электроды вместе, две ЭДС теперь будут указывать в противоположных направлениях. В этом случае эквивалентные значения будут E = E 1 – E 2 + … и r eq = r 1 + r 2 + … Параллельная комбинация На рисунке ниже показана параллельная комбинация батарей, в которой элементы соединены параллельно. I = I 1 + I 2 . Рассмотрим обе ячейки одну за другой: V = V(B 1 ) – V(B 2 ) = E 1 – I 1 R V = V(B 1 ) – V(B 2 ) = E 2 – I 2 R I = I 1 + I 2 Преобразование уравнения для извлечения значения V, Чтобы заменить эту комбинацию ячеек одной эквивалентной ячейкой со значением ЭДС E eq и r eq . Затем Вопрос 1. Батареи на 10 В и 5 В соединены последовательно так, что их ЭДС направлены в одном направлении. Ответ: Формула для эквивалентной серии EMF определяется, E Уравнение = E 1 + E 2 +… Дано: E 1 = 10, E 2 = 5. Заменить эти значения в уравнение, E = E 1 + E 2 ⇒ E = 10 + 5 ⇒ E = 15 В Вопрос 2: батарей 3, 5 , и 10 Ом соединены последовательно так, что их ЭДС направлены в одном направлении. Найдите эквивалентное сопротивление системы. Ответ: Формула для эквивалентной серии EMF приведена, E Уравнение = E 1 + E 2 +… . , E 2 = 5 и E 3 = 10 Заменить эти значения в уравнение, E = E 1 + E 2 + E 3 ⇒ E = 3 + 5 + 10 10. ⇒ E = 18 В Вопрос 3: Батареи 10 В и 5 В соединены последовательно так, что их ЭДС направлены в одном направлении. Внутренние сопротивления аккумуляторов равны 2 и 10 Ом соответственно. Найдите эквивалентное сопротивление системы. Ответ: Формула для эквивалентной серии EMF приведена, E Уравнение = E 1 + E 2 +… . , E 2 = 5 Заменить эти значения в уравнение, E = E 1 + E 2 ⇒ E = 10 + 5 ⇒ E = 15 В ЭКСКОВАННОЕ сопротивление также является сопротивлением. задается аналогичным уравнением, R Уравнение = R 1 + R 2 + Дано: R 1 = 2, R 2 = 10 Заменить эти значения в уравнении R = R 10002 + r 2 ⇒ r = 2 + 10 ⇒ r = 12 ом Найдите эквивалентное сопротивление системы. Ответ: Формула для эквивалентного сопротивления определяется, Дано: R 1 = 2, R 2 = 2 и R 3 = 4 . Уравнение ⇒ ⇒ ⇒ Вопрос 5. Три батареи с внутренним сопротивлением 5,5 Ом и 10,10 В соединены параллельно. Найдите эквивалентное сопротивление и ЭДС системы. Ответ: Формула для эквивалентного сопротивления определяется, Дано: r 1 = 5, R 2 = 5 Заменить эти значения. ⇒ ⇒ Эквивалентный EMF определяется как, ⇒ ⇒ ⇒ E Уравнение = 10 В ••• Jupiterimages/Pixland/Getty Images Обновлено 24 апреля 2017 г. Автор: Selma Leathem Многие сети могут быть сведены к последовательно-параллельным комбинациям, что упрощает расчет параметров цепи, таких как сопротивление, напряжение и ток. Получить ток и напряжение. Это может быть значение, данное вам в теоретической задаче, или что-то, что вы измеряете с помощью вольтметра, амперметра или мультиметра. Напряжение нужно получить только на одном резисторе, так как оно одинаково для всех. Однако для каждого резистора необходимо найти ток Ij (j = 1,2, …, n), где Ij представляет собой ток, протекающий параллельно через j-й резистор, а всего имеется n резисторов. Рассчитайте сопротивление Rj (j = 1,2, …,n) каждого элемента, где Rj представляет собой сопротивление j-го резистора, включенного параллельно, а всего резисторов n. Рассчитайте эквивалентное сопротивление цепи, если она является частью более крупной сети. Группа резисторов, включенных параллельно, может быть заменена одним эквивалентным сопротивлением Req, что упрощает расчеты при попытке получить параметры сети. Теперь вместо группы резисторов, включенных параллельно, имеется одно эквивалентное сопротивление с первоначальным напряжением V на нем и полным током I, протекающим через него, то есть суммой всех токов через каждый из резисторов, включенных параллельно. Эквивалентное сопротивление Req для параллельной цепи определяется как сумма обратных величин отдельных сопротивлений следующим образом 1 / Треб = 1 / R1 + 1 / R2 + ….1 / Rn. Эквивалентное сопротивление всегда меньше любого из отдельных сопротивлений в параллельной цепи. В частном случае двух параллельных резисторов токи обратно пропорциональны их сопротивлениям. Формулу V = I1 * R1 = I2 * R2 можно изменить, чтобы получить R1 / R2 = I2 / I1. Ссылки Советы Об авторе Selma Leathem имеет опыт написания статей для широкого круга читателей на самые разные темы, от профессиональных научных публикаций до любительского садоводства и модных советов. Имея степень по физике и опыт написания статей об электронике, инженерии, программном обеспечении, садоводстве, доме, еде и моде, она заслуживает внимания.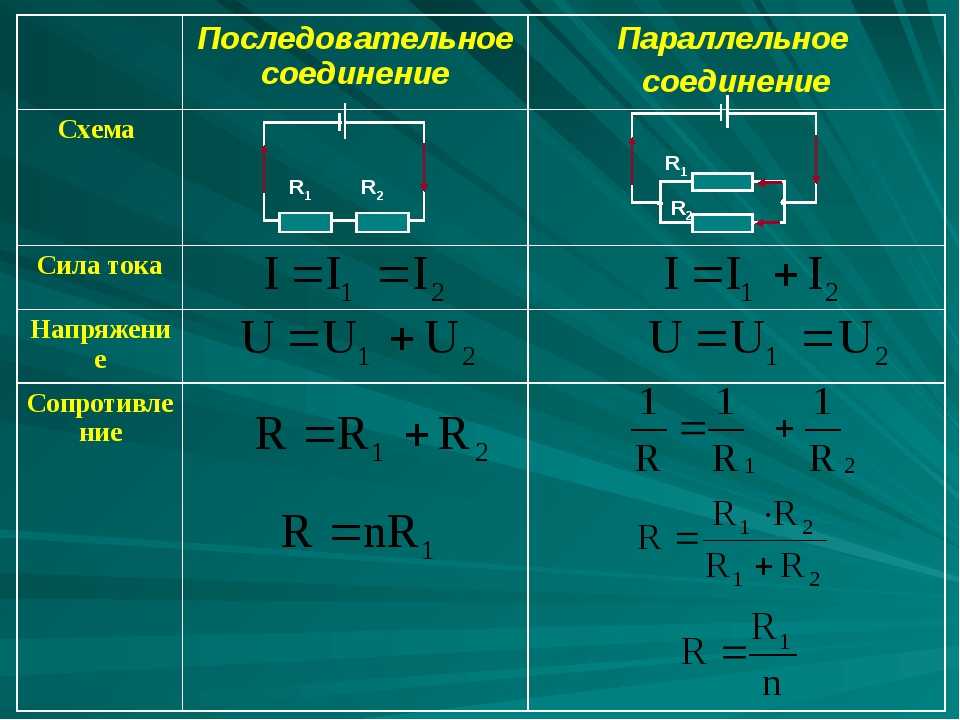 E 1 и E 2 — ЭДС двух элементов, а r 1 , r 2 — их внутренние сопротивления. На этот раз ток, протекающий через каждую ячейку, различен, и они обозначаются I 1 и I 2 , а общий ток, протекающий через цепь, обозначается I и представляет собой сумму обоих двух токов.
E 1 и E 2 — ЭДС двух элементов, а r 1 , r 2 — их внутренние сопротивления. На этот раз ток, протекающий через каждую ячейку, различен, и они обозначаются I 1 и I 2 , а общий ток, протекающий через цепь, обозначается I и представляет собой сумму обоих двух токов. Примеры задач
 Найдите эквивалентное сопротивление системы.
Найдите эквивалентное сопротивление системы.


Как вычислять сопротивление на параллели0001
 Когда несколько резисторов соединены между двумя точками только с одним путем тока, говорят, что они соединены последовательно. Однако в параллельной цепи ток делится между каждым резистором, так что больший ток проходит по пути наименьшего сопротивления. Параллельная цепь обладает свойствами, которые позволяют рассчитывать как отдельные сопротивления, так и эквивалентное сопротивление по одной формуле. Падение напряжения одинаково на каждом параллельном резисторе.
Когда несколько резисторов соединены между двумя точками только с одним путем тока, говорят, что они соединены последовательно. Однако в параллельной цепи ток делится между каждым резистором, так что больший ток проходит по пути наименьшего сопротивления. Параллельная цепь обладает свойствами, которые позволяют рассчитывать как отдельные сопротивления, так и эквивалентное сопротивление по одной формуле. Падение напряжения одинаково на каждом параллельном резисторе.
 Сопротивление каждого элемента находится по формуле Rj = V/Ij. Например, если у вас есть три резистора параллельно с падением напряжения 9Вольты и токи I1 = 3 Ампера, I2 = 6 Ампер и I3 = 2 Ампера, сопротивления R1 = 3 Ом, R2 = 1,5 Ом и R3 = 4,5 Ом.
Сопротивление каждого элемента находится по формуле Rj = V/Ij. Например, если у вас есть три резистора параллельно с падением напряжения 9Вольты и токи I1 = 3 Ампера, I2 = 6 Ампер и I3 = 2 Ампера, сопротивления R1 = 3 Ом, R2 = 1,5 Ом и R3 = 4,5 Ом. 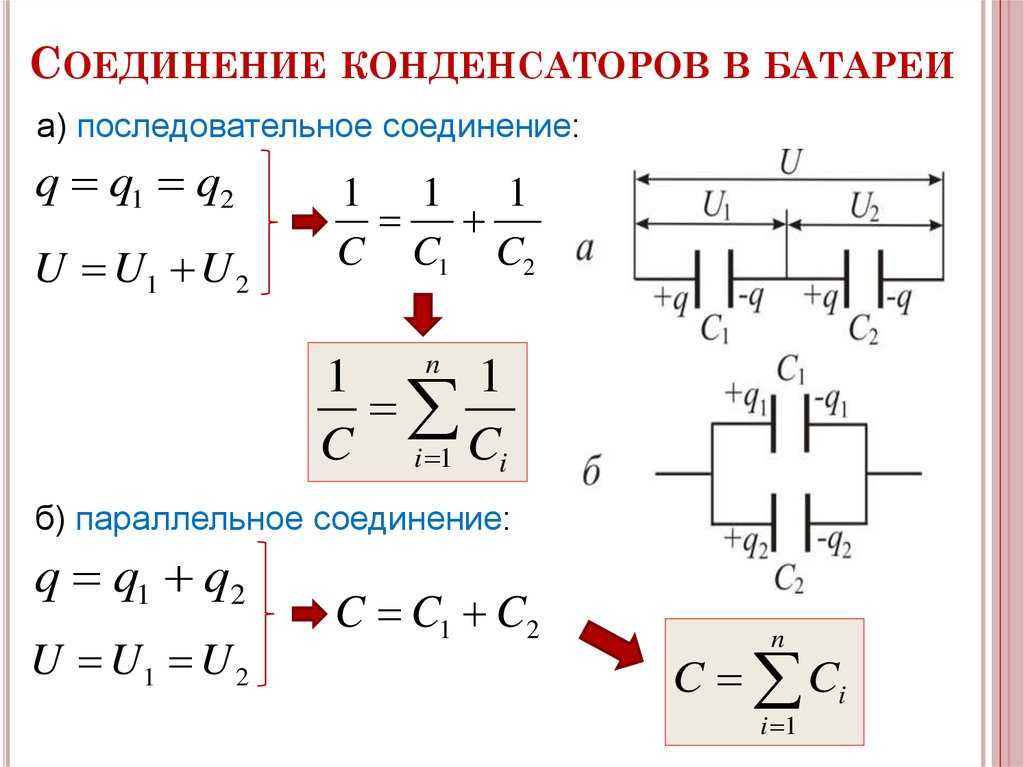 Для примера с тремя резисторами эквивалентное сопротивление Req=0,82 Ом. Это означает, что цепь можно заменить одним резистором с сопротивлением 0,82 Ом, напряжением 9 Вольт и током 11 Ампер.
Для примера с тремя резисторами эквивалентное сопротивление Req=0,82 Ом. Это означает, что цепь можно заменить одним резистором с сопротивлением 0,82 Ом, напряжением 9 Вольт и током 11 Ампер.
Связанные статьи